The correlation of histidine-ring geometry with the protonation state was analyzed in structures in the PDB and CSD. In conclusion, revised stereochemical restraints for histidine are proposed.
Keywords: imidazole, histidine protonation, hydrogen bond, X-ray crystal structure, stereochemical restraints
Abstract
The presence of H atoms connected to either or both of the two N atoms of the imidazole moiety in a histidine residue affects the geometry of the five-membered ring. Analysis of the imidazole moieties found in histidine residues of atomic resolution protein crystal structures in the Protein Data Bank (PDB), and in small-molecule structures retrieved from the Cambridge Structural Database (CSD), identified characteristic patterns of bond lengths and angles related to the protonation state of the imidazole moiety. Using discriminant analysis, two functions could be defined, corresponding to linear combinations of the four most sensitive stereochemical parameters, two bond lengths (ND1–CE1 and CE1–NE2) and two endocyclic angles (–ND1– and –NE2–), that uniquely identify the protonation states of all imidazole moieties in the CSD and can be used to predict which N atom(s) of the histidine side chains in protein structures are protonated. Updated geometrical restraint target values are proposed for differently protonated histidine side chains for use in macromolecular refinement.
1. Introduction
Protonation at the two N atoms of the imidazole moiety of histidine elicits measurable changes in the heterocyclic ring geometry. These changes, resulting from the rearrangement of the distribution of electrons in the mesomeric structures, can be further modulated by the subtler, but still detectable, effects of hydrogen bonding and metal coordination. This variability is of particular importance in protein structures, although it is also particularly recalcitrant to X-ray crystallographic characterization because of the limited resolution and the inability to detect H atoms that blight the method in routine applications. The endocyclic valence angles at the five-membered ring vary depending on which N atom (or both) is protonated. Since H atoms can only rarely be located by X-ray crystallography, even at very high resolution, one must concentrate on the ring geometry to indirectly establish the protonation state of the N atoms in histidine residues. On the other hand, if the protonation state of a particular moiety can be established by other means, such as the unequivocal presence of hydrogen bonds or the coordination of metals precluding the presence of hydrogen at certain sites, the appropriate geometric restraints may be used even at low resolution.
The accuracy of the atomic positions, and consequently of the molecular geometry, from X-ray structural analysis depends crucially on the resolution of the diffraction data. Whereas in small-molecule crystallography these parameters are usually determined solely from the diffraction data by least-squares refinement of the atomic positions, in macromolecular crystallography, owing to the paucity of experimental data at relatively low resolution, it is almost always necessary to use external a priori information about the stereochemical parameters (such as bond lengths, angles etc.) by restraining them to expected target values. The geometrical model obtained by this approach will by necessity not only reflect the genuine structural information present in the diffraction data but will also be influenced by the restraints used. Only when the diffraction data extend to a very high resolution of beyond 1.0 Å can the stereochemical restraints of the well ordered parts of a macromolecule be relaxed. In such cases the resulting model geometry depends more strongly on the diffraction data and the effect of restraints is suppressed. However, some flexible fragments, characterized by high displacement parameters or assuming multiple conformations, must still be restrained, since there is insufficient information in the diffraction data to define them satisfactorily (Dauter et al., 1992 ▸).
The widely used comprehensive set of stereochemical restraint target values and their variances for proteins was originally presented and later updated by Engh & Huber (1991 ▸, 2001 ▸) (referred to as EH91 and EH99, respectively). These target values were obtained from the analysis of small organic structures deposited in the Cambridge Structural Database (CSD; Allen, 2002 ▸). At the time when the study of Engh and Huber was initiated (1991), the CSD contained ∼80 000 entries and the total number of Protein Data Bank (PDB; Berman et al., 2000 ▸) macromolecular deposits was ∼700. Since then, the PDB has accumulated more structures (∼110 000) than were present in the CSD in 1991, with ∼2500 structures at atomic resolution (d min ≤ 1.2 Å; Sheldrick, 1990 ▸; Morris & Bricogne, 2003 ▸), making it possible to contemplate a ‘protein geometry from proteins’ approach (Jaskolski et al., 2007 ▸). Also, the size of the CSD has increased more than tenfold since 1991, suggesting that the evaluation of stereochemical targets should be revisited.
The imidazole moiety of histidine may be protonated on either or both of its N atoms, and each state is characterized by a somewhat different geometry of the five-membered ring. This is already evident from the restraint target values for the three protonation states of the His residue included in the EH91 and EH99 libraries. This issue has been addressed in the past, for example by analyzing the endocyclic bond lengths and angles in the histidine residues of a few high-resolution protein structures. Helliwell and coworkers observed convincing differences in the endocyclic angles of imidazole moieties that were correlated with their protonation states in several selected proteins (Ahmed et al., 2007 ▸; Fisher et al., 2012 ▸). Berisio et al. (1999 ▸) analyzed a series of crystal structures of RNase A at various pH values and observed gradual changes of the endocyclic bond angles of the three histidine residues and several other subtle stereochemical changes in their vicinity. Although it was not stated explicitly, the gradual geometrical changes were most probably the result of the superposition of two, singly and doubly protonated, states, with smooth changes of relative occupancies in response to the changing pH value.
In this work, we attempt to investigate the relation between the protonation state and histidine-ring geometry on the basis of a large number of high-resolution structures in the PDB and CSD. To begin with, the target values of the imidazole bond lengths and angles from the EH91 and EH99 compilations are listed in Table 1 ▸. In our approach, which was also adopted by EH91 and EH99, we assume that the imidazole moiety of a histidine can realistically exist in three discrete protonation states with protonation of ND1, NE2 or both. It has not escaped our notice that in D—H⋯A hydrogen-bond bridges, especially in those that are symmetrical (e.g. N—H⋯N), a continuum of situations with regard to the proton position is theoretically possible (Steiner, 1995 ▸). However, such a continuum is of practical significance (i.e. leading to N—H lengthening and H⋯N shortening and to concomitant modulations of the geometry of the imidazole ring) only for very strong (short) hydrogen bonds, which are not expected to be found frequently in biological systems. We have therefore assumed that the geometries considered in our analysis are not affected to a significant degree by such ‘hydrogen bonds near the transition point’.
Table 1. Bond lengths and angles in the imidazole ring in different protonation states, with standard uncertainties given in parentheses in the unit of the last decimal digit.
EH91 and EH99 refer to the stereochemical target libraries provided in two compilations by Engh and Huber in 1991 (EH91) and 2001 (EH99). The PDB statistics correspond to His residues with unambiguously deduced protonation states from high-resolution crystal structures and to all His residues in 3 resolution structures. The CSD entries were selected using the R-value criterion (R 7.5%). In both cases, the presented statistics are after outlier rejection, as described in the text. The statistics are treated separately depending on the involvement of the N atoms in metal coordination, but the overall statistics (‘all’) are also shown where appropriate.
| Bond () | CGND1 | ND1CE1 | CE1NE2 | NE2CD2 | CD2CG | No. of cases |
|---|---|---|---|---|---|---|
| ND1 protonated | ||||||
| EH91 | 1.378 (11) | 1.345 (20) | 1.319 (13) | 1.382 (30) | 1.354 (11) | |
| EH99 | 1.369 (15) | 1.343 (25) | 1.322 (23) | 1.415 (21)† | 1.353 (17) | 12 |
| PDB, no metals | 1.373 (10) | 1.337 (15) | 1.319 (16) | 1.377 (12) | 1.361(11) | 48 |
| PDB, metals‡ | 1.375 (10) | 1.337 (13) | 1.322 (11) | 1.377 (11) | 1.359 (9) | 142 |
| PDB, all | 1.375 (10) | 1.337 (13) | 1.322 (12) | 1.377 (11) | 1.360 (10) | 190 |
| CSD, no metals | 1.374 (10) | 1.345 (6) | 1.315(10) | 1.376 (9) | 1.358 (15) | 17 |
| CSD, metals‡ | 1.371 (9) | 1.337 (7) | 1.316 (9) | 1.377 (6) | 1.356 (9) | 176 |
| CSD, all | 1.371 (9) | 1.338 (8) | 1.316 (9) | 1.377 (7) | 1.356 (9) | 195 |
| NE2 protonated | ||||||
| EH91 | 1.371 (17) | 1.319 (13) | 1.345 (20) | 1.374 (21) | 1.356 (11) | |
| EH99 | 1.383 (22) | 1.323 (15) | 1.333 (19) | 1.375 (22) | 1.353 (14) | 37 |
| PDB, no metals | 1.383 (9) | 1.322 (8) | 1.335 (12) | 1.368 (10) | 1.360 (10) | 119 |
| PDB, metals‡ | 1.382 (11) | 1.326 (9) | 1.331 (12) | 1.365 (13) | 1.358 (11) | 52 |
| PDB, all | 1.382 (10) | 1.324 (9) | 1.334 (12) | 1.367 (11) | 1.359 (10) | 171 |
| CSD, no metals | 1.381 (9) | 1.319 (8) | 1.336 (13) | 1.367 (9) | 1.359 (9) | 99 |
| CSD, metals‡ | 1.385 (6) | 1.323 (7) | 1.330 (14) | 1.369 (8) | 1.357 (8) | 21 |
| CSD, all | 1.382 (9) | 1.320 (8) | 1.335 (14) | 1.367 (9) | 1.359 (10) | 123 |
| ND1 and NE2 protonated | ||||||
| EH91 | 1.378 (11) | 1.321 (10) | 1.321 (10) | 1.374 (11) | 1.354 (11) | |
| EH99 | 1.380 (10) | 1.326 (10) | 1.317 (11) | 1.373 (11) | 1.354 (9) | 54 |
| PDB, no metals | 1.375 (7) | 1.327 (6) | 1.322 (7) | 1.370 (10) | 1.352 (4) | 32 |
| CSD, no metals | 1.379 (7) | 1.325 (8) | 1.316 (9) | 1.373 (7) | 1.353 (7) | 174 |
| ND1 and NE2 deprotonated | ||||||
| CSD, metals | 1.381 (8) | 1.333 (7) | 1.325 (12) | 1.365 (9) | 1.362 (8) | 7 |
| PDB, resolution 3, all | 1.377 (11) | 1.322 (8) | 1.322 (9) | 1.372 (12) | 1.356 (9) | 39418 |
| Angle () | CG | ND1 | CE1 | NE2 | CD2 | § |
|---|---|---|---|---|---|---|
| ND1 protonated | ||||||
| EH91 | 105.2 (10) | 109.0(17) | 111.7 (13)† | 107.0 (30) | 109.5 (23) | 542.4† |
| EH99 | 106.0 (14) | 108.2 (14) | 109.9 (22) | 106.6 (25) | 109.2 (19) | 539.9 |
| PDB, no metals | 105.2 (9) | 108.3 (8) | 110.9 (14) | 105.8 (17) | 109.7 (15) | 539.9 |
| PDB, metals‡ | 105.5 (8) | 108.4 (8) | 110.4 (12) | 106.4 (14) | 109.3 (12) | 540.0 |
| PDB, all | 105.5 (8) | 108.4 (8) | 110.4 (12) | 106.4 (14) | 109.3 (12) | 540.0 |
| CSD, no metals | 104.8 (5) | 107.7 (3) | 111.8 (3) | 104.7 (5) | 111.0 (7) | 540.0 |
| CSD, metals‡ | 105.1 (4) | 108.2 (4) | 111.2 (6) | 105.3 (5) | 110.2 (5) | 540.0 |
| CSD, all | 105.1 (5) | 108.1 (5) | 111.3 (6) | 105.3 (6) | 110.3 (6) | 540.1 |
| NE2 protonated | ||||||
| EH91 | 109.2 (7) | 105.6 (10) | 111.7 (13) | 106.9 (13) | 106.5 (10) | 539.9 |
| EH99 | 109.2 (7) | 105.7 (13) | 111.5 (13) | 107.1 (11) | 106.7 (12) | 540.2 |
| PDB, no metals | 108.2 (11) | 106.4 (14) | 110.9 (14) | 107.6 (9) | 106.8 (6) | 539.9 |
| PDB, metals‡ | 107.9 (10) | 106.8 (11) | 110.3 (9) | 108.1 (8) | 106.9 (8) | 540.0 |
| PDB, all | 108.1 (11) | 106.5 (14) | 110.7 (13) | 107.8 (9) | 106.9 (7) | 540.0 |
| CSD, no metals | 109.2 (8) | 105.2 (8) | 112.1 (8) | 107.1 (7) | 106.5 (7) | 540.1 |
| CSD, metals‡ | 108.7 (6) | 105.8 (7) | 111.2 (6) | 107.8 (7) | 106.4 (8) | 539.9 |
| CSD, all | 109.1 (8) | 105.3 (9) | 111.9 (10) | 107.2 (8) | 106.5 (7) | 540.0 |
| ND1 and NE2 protonated | ||||||
| EH91 | 106.1 (10) | 109.3 (17) | 108.4 (10) | 109.0 (10) | 107.2 (10) | 540.0 |
| EH99 | 106.1 (8) | 109.0 (10) | 108.5 (11) | 109.0 (7) | 107.3 (7) | 539.9 |
| PDB, no metals | 106.2 (4) | 109.0 (7) | 108.7 (6) | 108.5 (7) | 107.7 (4) | 540.1 |
| CSD, no metals | 105.9 (5) | 109.3 (5) | 108.4 (5) | 108.9 (6) | 107.4 (5) | 539.9 |
| ND1 and NE2 deprotonated | ||||||
| CSD, metals | 107.2 (7) | 104.8 (7) | 114.0 (8) | 104.3 (6) | 109.7 (4) | 540.0 |
| PDB resolution 3.0, all | 106.3 (8) | 109.2 (9) | 108.5 (7) | 108.9 (6) | 107.1 (5) | 540.0 |
These values seem to be in error. The corrected value for the EH99 NE2CD2 bond length is 1.372 and that for the EH91 CE1 angle is 109.3, giving the sum = 540.0.
In metal complexes, ND1 is protonated when NE2 is metal-coordinated and vice versa.
Sum of the endocyclic valence angles (expected to be 540.0 for a planar five-membered ring).
2. Methods
2.1. Data mining
2.1.1. PDB
All His residues in high-resolution protein structures in the 2 September 2014 version of the PDB were analyzed which met the following selection criteria: (i) a data resolution of at least 1.0 Å, (ii) no double conformation of the His residue and (iii) all His non-H atoms with B iso/B eq less than 12 Å2. In total, there were 1414 such histidine residues (among a total number of 3689 histidine residues in protein models in this resolution interval). The selected His residues were checked for hydrogen-bonding contacts of their ND1 and NE2 atoms with the CCP4 program CONTACT (Winn et al., 2011 ▸) with the following criteria: D⋯A distance between 2.3 and 3.5 Å and D—H⋯A angle between 120 and 180°, where D is a donor N atom and A is any acceptor of a hydrogen bond.
The imidazole moieties of these His residues were classified as doubly protonated if both N atoms were in hydrogen-bond contact with a carbonyl O atom of a main-chain peptide group of any residue or of Asn or Gln side-chain amide groups, or with a carboxylate OD atom of Asp or OE atom of Glu. If a histidine ND1 or NE2 atom was likely to be a hydrogen-bond acceptor from an N—H donor (main-chain peptide except for Pro, side-chain N—H group of Asn/Gln/Trp or N+—H moiety of Lys/Arg), it was assumed to be nonprotonated, but the other imidazole N atom was then automatically treated as protonated. This approach is based on the chemically sensible assumption that, in view of the high pK a value of 14.5 (Eicher et al., 2003 ▸) of the imidazole anion, it is exceedingly unlikely that doubly deprotonated His residues will be found in protein structures. The only exception is the case where both His ring N atoms serve as ligands in the coordination of two metal centers. For the majority of the imidazole rings it was not possible to unambiguously determine the protonation state, e.g. if in contact with water molecules, but according to the specified criteria it was possible to convincingly select 70 doubly protonated, 54 ND1-protonated and 166 NE2-protonated cases.
The same subset of atomic resolution structures was analyzed for metal coordination by one (or both) of the His N atoms. All cases of contacts specified in the LINK records of a PDB file header were selected. The N atom coordinated to a metal center was assumed to be deprotonated, and the other N atom was therefore classified as protonated, unless also in a metal-coordination role. 171 histidines coordinated metal ions at NE2 and were assumed to be ND1 protonated and 59 coordinated metal ions at ND1 and were assumed to be NE2 protonated. No histidines in this set coordinated two metal ions with their two N atoms. Among the 171 ND1-protonated histidines, the NE2 atom was coordinated by the following divalent metal cations: Fe (73 cases), Zn (50), Mn (25), Cu (17), Cd (three), Co (two) and Ca (one). Among the 59 NE2-protonated histidines, the ND1 atom was coordinated by Cu (26), Zn (26), Mn (five), Ni (one) and Ca (one).
The ring geometry was also analyzed for 41 327 imidazole moieties in histidine residues of all PDB structures with a data resolution declared as 3.0 Å, excluding only those in double conformations. In addition, the exocyclic geometrical parameters at the CG atom of the imidazole moiety are presented in Table 2 ▸.
Table 2. Geometry of the exocyclic bonds and angles of CG-substituted imidazole moiety.
| Bond () or angle () | CBCG | CBCGND1 | CBCGCD2 | No. of cases |
|---|---|---|---|---|
| ND1 protonated | ||||
| EH91 | 1.497 (14) | 122.7 (15) | 129.1 (13) | |
| EH99 | 1.492 (16) | 123.2 (25) | 130.8 (31) | 12 |
| PDB, no metals | 1.492 (11) | 122.6 (12) | 132.0 (12) | 48 |
| PDB, metals | 1.496 (11) | 122.9 (11) | 131.3 (12) | 142 |
| PDB, all | 1.495 (11) | 122.9 (11) | 131.5 (12) | 190 |
| CSD, no metals | 1.479 (28) | 123.9 (22) | 131.2 (22) | 17 |
| CSD, metals | 1.476 (18) | 123.3 (11) | 131.6 (12) | 176 |
| CSD, all | 1.477 (19) | 123.4 (16) | 131.5 (16) | 195 |
| NE2 protonated | ||||
| EH91 | 1.497 (14) | 121.6 (15) | 129.1 (13) | |
| EH99 | 1.495 (18) | 121.4 (13) | 129.7 (16) | 37 |
| PDB, no metals | 1.488 (9) | 122.3 (10) | 129.4 (13) | 119 |
| PDB, metals | 1.492 (11) | 122.2 (13) | 129.8 (12) | 52 |
| PDB, all | 1.489 (10) | 122.3 (11) | 129.5 (13) | 171 |
| CSD, no metals | 1.480 (23) | 121.5 (12) | 129.3 (13) | 99 |
| CSD, metals | 1.489 (14) | 122.2 (14) | 129.0 (13) | 21 |
| CSD, all | 1.481 (22) | 121.6 (13) | 129.3(14) | 123 |
| ND1 and NE2 protonated | ||||
| EH91 | 1.497 (14) | 122.7 (15) | 131.2 (13) | |
| EH99 | 1.492 (10) | 122.5 (13) | 131.4 (13) | 54 |
| PDB, no metals | 1.491 (11) | 123.3 (16) | 130.4 (17) | 32 |
| PDB, all | 1.491 (11) | 123.3 (16) | 130.4 (17) | 32 |
| CSD, no metals | 1.490 (11) | 122.7 (12) | 131.3 (13) | 174 |
| ND1 and NE2 deprotonated | ||||
| CSD, metals | 1.471 (10) | 123.1 (12) | 129.6 (13) | 7 |
| PDB resolution 3.0, all | 1.497 (9) | 122.7 (11) | 131.0 (12) | 39418 |
Except for the calculation of hydrogen-bonding distances by CONTACT, all other calculations of the geometry of the histidine residues in the PDB were performed using locally written programs. The selection of appropriate records from PDB files was achieved with the Linux ‘grep’ command.
2.1.2. CSD
The CSD version 5.35 was searched using the CONQUEST software (Bruno et al., 2002 ▸) and further analyzed in MERCURY (Macrae et al., 2008 ▸) for all structures containing variously protonated 4-substituted imidazole rings mimicking the histidine side chain. For the purpose of this analysis, the selected fragments were renumbered using the histidine atom-labeling scheme, in which the substituted (by CB) C4 atom becomes CG and the N atoms are ND1 and NE2. The primary selection criterion was R factor ≤ 7.5%. The final selection criterion was based on the pattern of N-protonation, and the searches were divided into cases with no metal coordination by the imidazole ring (23 cases of only ND1 protonation, 126 cases of only NE2 protonation and 204 cases with both N atoms protonated) or with metal coordinated by each unprotonated N center (208 cases of ND1 protonated and 27 cases of NE2 protonated). There are also ten cases of a deprotonated imidazole ring engaged in metal coordination at both N atoms, but they are not included in the analysis since no corresponding cases are observed in the set of high-resolution protein structures.
2.1.3. Outlier rejection
The subsets of raw PDB or CSD hits were further refined using statistical analysis for outlier rejection. In each subset, a modified Z-score test (Iglewicz & Hoaglin, 1993 ▸) was used to identify and reject outliers. In this test, a data item xi is rejected as an outlier if |Mi| > 3.5. If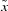 
denotes the median of the sample, Mi is calculated as follows:
 |
 |
In our application, when a data item was earmarked as an outlier the entire entry was removed from all mean calculations as potentially contaminated with gross errors. As a rule, outlier rejection leads to a drastic reduction of the standard deviation, while the mean value is generally unchanged. The geometry statistics in each case after outlier rejection are presented in Table 1 ▸. The numbers of entries in each category in Table 1 ▸ are given after outlier rejection, and are therefore different from the total numbers given in the text above.
2.2. Linear discriminant analysis (LDA)
Discriminant analysis finds a set of predictive equations based on independent variables that are used to classify individual cases into classes. Based on the rank of the function used, one can distinguish linear and quadratic discriminant analysis. The former is the simplest model with some restrictive assumptions. First of all, individual data cases should belong to two or more mutually exclusive classes. The second assumption requires that the population covariance matrices are equal for each class, something that is rarely found in practice. A further assumption is that each class is drawn from a population which has a multivariate normal distribution. Moreover, variables used in LDA should be free of outliers and correlation (McLachlan, 2004 ▸).
LDA formulates a numerical model based on a set of observations for which the classes are known. From this training set, the technique constructs linear functions of the variables X i, known as linear discriminant functions,
 |
where b i are discriminant coefficients and c is a constant. These discriminant functions are used to predict the class of a new observation of previously unknown category (Taylor & Kennard, 1982 ▸). The terms Fisher’s linear discriminant and LDA are often used interchangeably, although Fisher’s original article (Fisher, 1936 ▸) describes a slightly different discriminant which does not use some of the assumptions of LDA, such as normally distributed classes or equal class covariances.
Here, the three classes of different protonation states of the imidazole ring are derived from the ‘CSD all’ data set in Table 1 ▸. The data were already cleared of outliers, therefore in the first step Mardia’s multivariate normality test was performed (Korkmaz et al., 2014 ▸). Mardia’s test showed that none of the classes followed a multivariate normal distribution. In the second step, Box’s M test on the Fisher distribution (McLachlan, 2004 ▸) was used to test the assumption of equality for intra-class covariance matrices, and suggested that the covariances are different. Even though not all of the assumptions are strictly fulfilled, it has been shown previously that LDA can still perform a successful analysis even in such limited-compliance situations (Li et al., 2006 ▸; Duda et al., 2012 ▸).
The correlation coefficients calculated between all selected variables are presented in Table 3 ▸. Different sets of uncorrelated variables were tested as input data for the discriminative analysis. To minimize the number of variables sufficient to identify the protonation state of an imidazole ring, after each test step of iterative variable selection the least important variable, with the smallest absolute value of the discriminant coefficient, was removed from the calculations and a new discriminative analysis was performed. Eventually, four parameters were retained (i = 1, …, 4 in the equation for L above): the bond lengths ND1—CE1 and CE1—NE2 and the valence angles CG—ND1—CE1 and CE1—NE2—CD2.
Table 3. The matrix of correlation coefficients between the geometrical parameters of imidazole rings obtained from discriminative analysis of the CSD ‘all’ data set (Table 1 ▸).
Correlation coefficients with an absolute value above 0.65 are italicized and those between the four parameters selected for the final discrimination function (the bond lengths ND1CE1 and CE1NE2 and the valence angles ND1 and NE2) are in bold.
| CGND1 | ND1CE1 | CE1NE2 | NE2CD2 | CD2CG | CG | ND1 | CE1 | NE2 | CD2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| CGND1 | 1.00 | 0.24 | 0.32 | 0.27 | 0.09 | 0.01 | 0.02 | 0.08 | 0.25 | 0.20 |
| ND1CE1 | 1.00 | 0.18 | 0.10 | 0.07 | 0.12 | 0.07 | 0.19 | 0.00 | 0.25 | |
| CE1NE2 | 1.00 | 0.01 | 0.13 | 0.42 | 0.25 | 0.05 | 0.06 | 0.18 | ||
| NE2CD2 | 1.00 | 0.00 | 0.17 | 0.25 | 0.09 | 0.24 | 0.11 | |||
| CD2CG | 1.00 | 0.05 | 0.09 | 0.26 | 0.05 | 0.07 | ||||
| CG | 1.00 | 0.79 | 0.19 | 0.28 | 0.77 | |||||
| ND1 | 1.00 | 0.67 | 0.18 | 0.35 | ||||||
| CE1 | 1.00 | 0.77 | 0.26 | |||||||
| NE2 | 1.00 | 0.75 | ||||||||
| CD2 | 1.00 |
3. Results and discussion
3.1. Engh and Huber target values for histidine
Both EH libraries include bond-length and angle values for three possible protonation states of the imidazole moiety of histidine, with an H atom attached to the ND1 atom or the NE2 atom, or to both N atoms when it is positively charged. These values (as reported by Engh & Huber, 1991 ▸, 2001 ▸) are reproduced in Table 1 ▸.
A preliminary analysis of the numerical values for the case when ND1 protonation was assumed shows that some of them are inconsistent and may be in error. The five EH91 endocyclic angles sum to 542.4°, which is not possible in reality, since the sum of the internal angles in any flat pentagon is 540° and any ring puckering only makes this sum smaller. If the endocyclic angle at the CE1 atom is changed from 111.7 to 109.3° (to complement the other angles to 540°), the whole trigonometric system becomes satisfactory. The set of values given for the same case in EH99 lists 1.415 Å as the NE2—CD2 bond length, which is substantially longer than any of the corresponding bond lengths in the other cases and makes the system of bond lengths and angles trigonometrically inconsistent. The correct value for this bond length (assuming all the other parameters are correct) should be 1.372 Å.
The practical effect of these numerical discrepancies is minimized by the fact that in routine applications only one set of stereochemical targets for histidine, the EH99 case with both N atoms protonated, is implemented and used by all popular refinement programs, such as REFMAC (Murshudov et al., 2011 ▸), phenix.refine (Afonine et al., 2012 ▸) and SHELXL (Sheldrick, 2008 ▸) in their built-in restraint target libraries. In other words, all histidine residues are always treated by the refinement programs as doubly protonated. This can be viewed as a kind of compromise, since in the majority of real cases it is very difficult, if not impossible, to assign (especially automatically) the correct protonation states of histidine residues, particularly in the early stages of model refinement. However, in cases where the protonation can be unambiguously deduced from intermolecular interactions, the restraint targets can, and in fact should, be appropriately adjusted.
3.2. Geometry and protonation of imidazole rings in the PDB and CSD
The idea that the protonation or tautomeric state of a histidine side chain can be often deduced from its involvement in hydrogen bonding is not new. It was, for example, successfully applied by Thaimattam et al. (2002 ▸) to the single His25 residue in the 1.03 Å resolution PDB structure 1lu0, which was demonstrated to assume different protonation forms in the two copies of the protein in the asymmetric unit. In the present analysis, the protonation state could be determined from the intermolecular interactions of many histidine residues in PDB structures determined to better than 1 Å resolution. The results, obtained as described in §§2.1.1 and 2.1.3, are collected in Table 1 ▸.
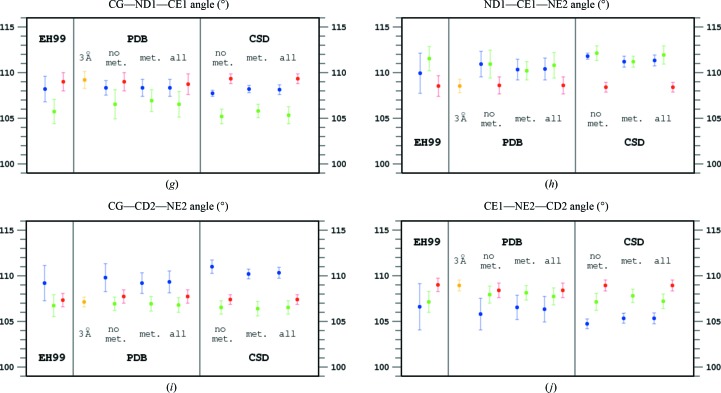
Inspection of Table 1 ▸ and Fig. 1 ▸ identifies certain differences in the geometrical characteristics of variously protonated imidazole moieties in the small molecules stored in the CSD and in the histidine residues found in atomic resolution structures of proteins in the PDB.
Figure 1.
Geometry of the imidazole rings presented in the EH99 library obtained from the analysis of atomic resolution (d min < 1 Å) protein structures in the PDB and from the CSD. The average values of the endocyclic bond lengths (a–e) and angles (f–j) are presented as circles with 1.0 r.m.s.d. values of the parameter distributions marked as vertical lines. Blue corresponds to a protonated ND1 atom, green to a protonated NE2 atom and red to both N atoms protonated. Statistics for the PDB and CSD cases when the imidazole is either engaged (‘met.’) or not engaged (‘no met.’) in metal coordination are treated separately as well as together (‘all’). In addition, values obtained from the PDB for protein structures refined at 3.0 Å resolution are marked in orange.
There is a strong and opposite imbalance between the numbers of differently protonated imidazole moieties among both protein and small-molecule structures. Whereas the statistics in Table 1 ▸ contain many more ND1-protonated histidine residues than NE2-protonated histidines among those coordinating metal ions (155 versus 54 in the PDB and 176 versus 21 in the CSD), among those without metals this ratio is reversed (49 versus 142 in the PDB and 17 versus 99 in the CSD). Interestingly, many more doubly protonated imidazole rings are identified in small structures (174 out of a total of 290 cases) than in proteins (55 out of a total of 246 cases). However, in spite of the different numbers of observations, the r.m.s.d. values of the individual geometrical parameters are similar. The level of confidence in the numerical values listed in Table 1 ▸ is therefore similar.
In general, the trends observed in small structures and in proteins are similar, but many detailed differences in bond lengths and angles among the differently protonated imidazole rings are more pronounced in the set of small structures than in proteins. This may in part be a consequence of the higher resolution of small-molecule crystal structures on the one hand and of the routine use of geometrical restraints in the refinement of macromolecular models on the other, which may to some extent bias the final geometry of protein structures, even at very high resolution. The resolution of 1.0 Å is recognized as very high in protein crystallography, but crystal structures of small molecules are usually refined at significantly higher resolution (typically a d min of 0.7–0.8 Å, corresponding to 2θmax ≃ 60° for molybdenum radiation or to a full copper sphere). The following discussion will be therefore based on the statistics obtained from the CSD.
In Table 1 ▸ and Fig. 1 ▸, the statistics of the three cases are shown separately, firstly when one of the imidazole N atoms is engaged in the coordination of metal ions (marked ‘metals’), secondly when metals are not coordinated (‘no metals’) and thirdly jointly for both situations (‘all’). It is immediately clear that involvement in metal coordination does not significantly affect the ring geometry and it is only important which N atom remains protonated after metal coordination by the other N center. Obviously, if one of the N atoms coordinates a metal ion, the imidazole moiety cannot be doubly protonated and there is no corresponding item in Table 1 ▸ and Fig. 1 ▸. However, it is possible that both imidazole N atoms are involved in coordinating two metal ions. Such cases are not observed among atomic resolution protein structures and only seven such cases exist in the CSD. As rare exceptions, which are not relevant to protein crystallography, these cases are excluded from the present analysis.
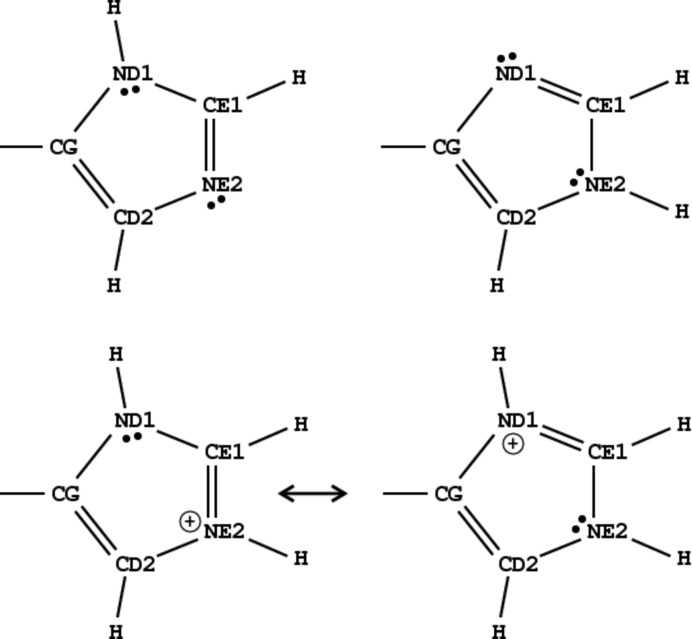
Two of the five bond distances in the imidazole ring display larger variability in response to different protonation states than the remaining three. These are the two bonds at the CE1 atom, positioned between the two N atoms of the imidazole ring. The ND1—CE2 bond is longer when only the ND1 atom is protonated than when NE2 or both N atoms are protonated. In contrast, the CE1—NE2 bond is longer when NE2 is protonated regardless of the protonation state of the other (ND1) N atom. This is in keeping with the electronic structures of differently protonated imidazoles, illustrated in Fig. 2 ▸. Obviously, the six π electrons of the imidazolium cation are delocalized over the heterocyclic ring; see Fig. 2 ▸, which shows only the principal electronic resonance structures of the systems in question. In singly protonated cases the bond between the CE1 atom and the unprotonated N atom has more double-bond character and is therefore shorter than the bond between the CE1 atom and the protonated N atom, which has more pronounced single character. If both N atoms are protonated, the two bonds between CE1 and its nitrogen neighbors have partial double-bond character and their lengths are shortened. The remaining three bonds do not show marked differences in response to the protonation state of the imidazole ring and their lengths are similar within one r.m.s.d. unit.
Figure 2.
Schemes of the electronic states of the two tautomers of neutral imidazole ring with the ND1 atom protonated (top left) and the NE2 atom protonated (top right). Two mesomeric states are shown for the positively charged imidazolium cation with both N atoms protonated (bottom).
The behavior of the endocyclic valence angles in differently protonated imidazole rings is more complicated than the variation of bond lengths. Again, similar trends in the angular features of the imidazole moiety are observed in small structures and in proteins, with more pronounced effects visible in small molecules than in the histidine residues of proteins.
The angle at the CE1 atom between the two alternatively singly protonated N atoms is not sensitive to which of the N atoms carries the H atom, since both situations are symmetric from the point of view of this C atom. However, when both N atoms are protonated the two CE1—N bonds become symmetric and the —CE1— angle diminishes by more than 3.5°, exceeding 3.0 r.m.s.d. units.
The electronic states of the two C atoms CG and CD2 are similar, but the values of their valence angles are exchanged depending on which of the N atoms is protonated. The angle at the C atom closer to the protonated N atom is smaller by ∼4° (>5.0 r.m.s.d. units) than at the C atom closer to the unprotonated N atom, i.e. it is larger at the C atom close to the N atom carrying the lone electron pair. The angles at both CG and CD2 become smaller in doubly protonated imidazole rings.
The angles at the ND1 and NE2 atoms are larger by about 2° when the N atom is protonated. The opening of endocyclic angles at N atoms in heterocycles on their protonation is well known (Singh, 1965 ▸), and the observed behavior of the N atoms of histidine follows this trend. When both N atoms are protonated, their endocyclic angles become similar and exceed the larger of the N-atom angles of singly protonated imidazole by more than 1°.
Inspection of the valence features extracted from protein structures refined at 3 Å resolution shows that they are very similar to the EH99 targets for doubly protonated imidazole. This is obviously the result of the dominating effect of the restraints over the information present in the diffraction data at low resolution. As mentioned above, the histidine-ring geometry in all popular restraint libraries is taken from the EH99 entry for doubly protonated imidazole.
In general, the values of bond lengths and angles of the imidazole ring obtained from the present analysis of the CSD are similar to the values from EH99. They differ somewhat in a few individual cases and are characterized by visibly smaller standard deviations, as a consequence of the much larger number of cases included in the present statistical analysis. The parameters that should be used as revised restraint targets in the refinement of protein crystal structures are collected in Table 4 ▸.
Table 4. Geometrical parameters of the imidazole moiety of histidine proposed as revised restraint target values and their standard uncertainties, based on statistical analysis of the CSD version 5.35.
The EH99 values are also included for comparison.
| CSD | CSD | CSD | EH99 | EH99 | EH99 | |
|---|---|---|---|---|---|---|
| Only ND1 protonated | Only NE2 protonated | ND1 and NE2 protonated | Only ND1 protonated | Only NE2 protonated | ND1 and NE2 protonated | |
| Bonds () | ||||||
| CGND1 | 1.371 (9) | 1.382 (9) | 1.379 (7) | 1.369 (15) | 1.383 (22) | 1.380 (10) |
| ND1CE1 | 1.338 (8) | 1.320 (8) | 1.325 (8) | 1.343 (25) | 1.323 (15) | 1.326 (10) |
| CE1NE2 | 1.316 (9) | 1.335 (14) | 1.316 (9) | 1.322 (23) | 1.333 (19) | 1.317 (11) |
| NE2CD2 | 1.377 (7) | 1.367 (9) | 1.373 (7) | 1.415 (21)† | 1.375 (22) | 1.373 (11) |
| CD2CG | 1.356 (9) | 1.359 (10) | 1.353 (7) | 1.353 (17) | 1.353 (14) | 1.354 (9) |
| CBCG | 1.477 (19) | 1.481 (22) | 1.490 (11) | 1.492 (16) | 1.495 (18) | 1.492 (10) |
| Angles () | ||||||
| ND1CGCD2 | 105.1 (5) | 109.1 (8) | 105.9 (5) | 106.0 (14) | 109.2 (7) | 106.1 (8) |
| CGND1CE1 | 108.1 (5) | 105.3 (9) | 109.3 (5) | 108.2 (14) | 105.7 (13) | 109.0 (10) |
| ND1CE1NE2 | 111.3 (6) | 111.9 (10) | 108.4 (5) | 109.9 (22) | 111.5 (13) | 108.5 (11) |
| CE1NE2CD2 | 105.3 (6) | 107.2 (8) | 108.9 (6) | 106.6 (25) | 107.1 (11) | 109.0 (7) |
| NE2CD2CG | 110.3 (6) | 106.5 (7) | 107.4 (5) | 109.2 (19) | 106.7 (12) | 107.3 (7) |
| CBCGND1 | 123.4 (16) | 121.6 (13) | 122.7 (12) | 123.2 (25) | 121.4 (13) | 122.5 (13) |
| CBCGCD2 | 131.5 (16) | 129.3 (14) | 131.3 (13) | 130.8 (31) | 129.7 (16) | 131.4 (13) |
This value seems to be in error. The corrected value for the EH99 NE2CD2 bond length is 1.372.
3.3. Discrimination between the different protonation states of imidazole moieties
The goal of the discriminative analysis presented in §2.2 was to formulate simple functions that could be used to assign the protonation state of histidine from the geometric (valence) parameters of the imidazole ring. The CSD data were used as input because they were more reliable as a source of the geometrical parameters and allowed unequivocal assignment to one of the three protonation groups. The first group comprises molecules with the imidazole fragment protonated at ND1, the second group those protonated at NE2 and the third group with protonation of both N atoms, regardless of metal coordination. Three separate groups allow the definition of two functions. The constant terms of the final functions were estimated in such a way that assignment to a particular class is indicated by a positive or negative sign of the function value.
The final outcome of the analysis are the following functions,
 |
 |
where X 1 and X 2 are the ND1—CE1 and CE1—NE2 distances (in Å), respectively, and X 3 and X 4 are the endocyclic valence angles —ND1— and —NE2— (in degrees), respectively. A negative value of his1 will assign a case to the ND1-protonated group, whereas a positive value shows that the imidazole is protonated either at the NE2 atom or at both atoms. The second function, his2, distinguishes between the NE2-protonated and double-protonated states. A negative value of his2 assigns a case to the NE2-protonated group and a positive value to the group with both N atoms protonated.
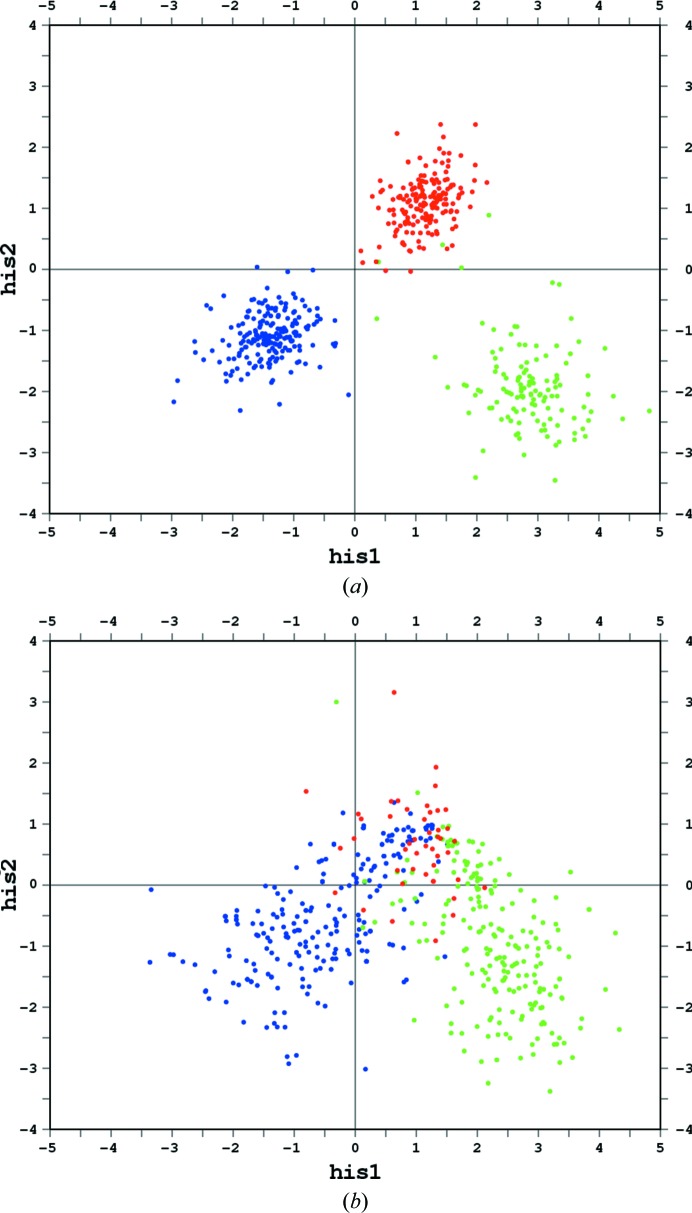
Values of the his1 and his2 functions can be plotted to visualize their clustering and test for possible misassignments of known cases. As shown in Fig. 3 ▸(a), the functions can reliably predict the protonation state of the imidazole ring in almost all cases in the CSD. Fig. 3 ▸(b) illustrates the application of these functions to the atomic resolution structures from the PDB. The division between differently protonated groups is not as clear as in the case of the CSD data. In particular, the region in Fig. 3 ▸(b) corresponding to doubly protonated imidazole is also populated by several singly protonated cases, most probably as a result of geometrical bias introduced by the restraints used during the refinement of these structures when all imidazole moieties were treated as doubly protonated. However, when the value of the his1 function is less than −1.0 it can be safely concluded that only the ND1 N atom is protonated. Similarly, if his1 is positive and his2 is less than −1.0 protonation of the NE2 atom can be predicted with high probability.
Figure 3.
Distribution plots of the values of the two discrimination functions, his1 and his2, (a) for all (with and without metal coordination) imidazole moieties from the CSD and (b) for imidazole rings in all atomic resolution (d min < 1 Å) protein structures in the PDB. Blue corresponds to ND1-protonated cases, green to NE2-protonated cases and red to both N atoms protonated.
4. Example
The predictive power of the discriminant analysis developed in this work has been tested using the recently released (and therefore not included in the previous analysis) PDB structure 4rj2 refined at 0.99 Å resolution (Timofeev et al., unpublished work). This model of Escherichia coli purine nucleoside phosphorylase comprises a hexamer of subunits (A–F), each containing six histidine residues. Their intermolecular interactions and possible involvement of the ND1 and NE2 atoms in hydrogen bonding have been analyzed and are summarized in Table 5 ▸.
Table 5. Protonation states and B-factor ranges of atoms in the imidazole moieties of the histidine residues in PDB structure 4rj2 .
If an N atom is protonated and serves as a hydrogen-bond donor it is marked ‘+’, if it is unprotonated and serves as a hydrogen-bond acceptor it is marked ‘’ and if it is not possible to deduce the protonation state it is marked ‘?’. The imidazole moieties with inflated (in excess of 202) atomic B factors after histidine-unrestrained refinement (shown in the ‘B-factor range’ columns) are shown in italics and are excluded from the analysis and from Fig. 4 ▸.
| Protonation | B-factor range (2) | |||
|---|---|---|---|---|
| Residue | ND1 | NE2 | Minimum | Maximum |
| His4A | + | ? | 9.1 | 11.3 |
| His62A | + | 7.5 | 8.6 | |
| His97A | ? | ? | 18.3 | 30.8 |
| His123A | + | 7.8 | 11.1 | |
| His205A | + | 11.6 | 12.5 | |
| His209A | ? | ? | 27.6 | 54.3 |
| His4B | + | ? | 14.6 | 17.8 |
| His62B | + | 11.7 | 13.4 | |
| His97B | ? | ? | 29.0 | 39.5 |
| His123B | + | 8.7 | 12.4 | |
| His205B | ? | ? | 21.1 | 28.1 |
| His209B | ? | ? | 84.6 | 168.9 |
| His4C | + | 10.4 | 12.4 | |
| His62C | + | 6.8 | 8.2 | |
| His97C | ? | ? | 54.9 | 68.2 |
| His123C | + | 9.5 | 12.7 | |
| His205C | + | 13.7 | 16.1 | |
| His209C | ? | ? | 26.6 | 40.3 |
| His4D | + | ? | 10.3 | 13.4 |
| His62D | + | 7.3 | 8.0 | |
| His97D | ? | ? | 18.5 | 27.0 |
| His123D | + | 9.5 | 13.1 | |
| His205D | + | + | 11.8 | 17.3 |
| His209D | + | + | 15.2 | 16.9 |
| His4E | + | ? | 8.9 | 11.5 |
| His62E | + | 6.7 | 7.7 | |
| His97E | ? | ? | 15.5 | 20.6 |
| His123E | + | 8.2 | 12.9 | |
| His205E | + | 20.1 | 34.0 | |
| His209E | ? | ? | 49.2 | 166.8 |
| His4F | + | ? | 16.2 | 19.3 |
| His62F | + | ? | 11.9 | 13.7 |
| His97F | + | 66.5 | 156.3 | |
| His123F | + | 8.3 | 12.9 | |
| His205F | + | 34.6 | 94.1 | |
| His209F | ? | ? | 85.2 | 115.8 |
The structure was submitted to two rounds of ten cycles of anisotropic REFMAC (Murshudov et al., 2011 ▸) refinement using the structure factors deposited together with the atomic coordinates; first (i) with standard restraints applied to all atoms of the model and next (ii) with the restraints of all atoms in all histidine residues removed using commands of the type ‘RESTRAINT EXCLUDE RESIDUE FROM 4A TO 4A ATOMS *’. The overall statistics after both refinements were practically identical, with R = 15.6%, R free = 17.8% and r.m.s.d.(bonds) = 0.014 Å. In the histidine-unrestrained refinement (ii), the B factors of some atoms in the histidine side chains that are extended into the solvent, mainly in the imidazole ring of residues His97 and His209 (except for His209D), inflated to very high values. These cases of highly mobile histidine side chains, represented in italics in Table 5 ▸, have been excluded from the analysis and from Fig. 4 ▸.
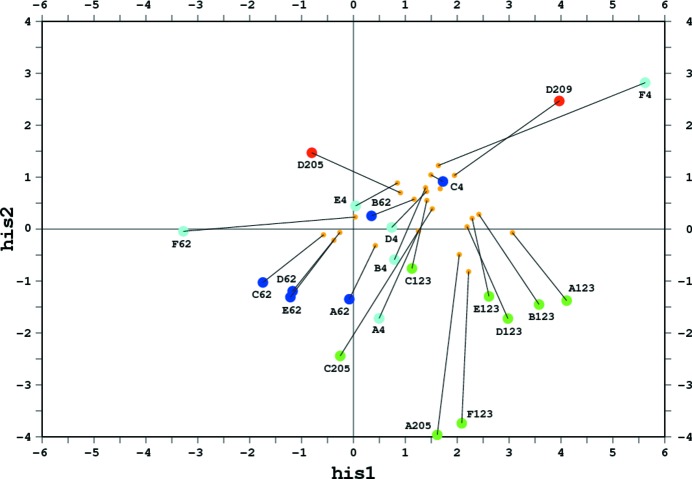
Figure 4.
Distribution plot of the his1 and his2 functions for the imidazole rings in structure 4rj2 taken from the PDB and refined with standard REFMAC stereochemical restraints applied to all residues (smaller orange circles) and with restraints removed from all histidine residues (larger circles in different colors). The protonation states of the imidazole moieties were figured out from their hydrogen-bonding interactions and are color-coded with ‘only ND1 protonated’ in dark blue, ‘only NE2 protonated’ in green and ‘both N atoms protonated’ in red. The cases corresponding to one N atom protonated without a clear indication of the protonation state of the other N atom are in cyan. The lines illustrate the changes of the his1/his2 values upon restraint removal. The histidine residues are labeled by the PDB chain identifier and residue number.
The his1 and his2 functions calculated after the fully restrained refinement (i) do not give a clear indication of the protonation states of some N atoms, and their values are concentrated close to the doubly protonated region of Fig. 4 ▸, evidently as a result of the restraints that represent this region by default. However, some discriminant values, even in scenario (i), are suggestive of ND1 protonation (C62, D62, E62) or NE2 protonation (A123, A205, B123, D123, E123, F123) (where C62 denotes His62 in chain C etc.).
After the histidine-unrestrained refinement (ii), the spread of points in Fig. 4 ▸ is much wider. Cases that were only suggestive previously became highly indicative, with the corresponding points moving into the characteristic regions, with his1 < 0 for ND1 protonation and with his1 positive and his2 negative for NE2 protonation. Among the cases that were equivocal after refinement (i), several became much clearer after refinement (ii). For example, D205 and D209 moved into a more positive his2 area, correctly indicating their double protonation. The two cases F4 and F62, in which only the ND1 atoms are engaged in hydrogen bonds as donors, became highly indicative. In the F4 case both the imidazole N atoms seem to be protonated, but the residue His62F indeed seems to be singly protonated at the ND1 atom.
The remaining cases are less strongly indicative, but the direction of their shifts in Fig. 4 ▸ upon histidine-unrestrained refinement is quite suggestive. For example, C123 moved towards the negative his2 region in keeping with its NE2 protonation, while the residues A62 and B62 moved towards positive his1 values, indicating possible ND1 protonation. The four ND1-protonated cases (A4, B4, D4 and E4) shifted closer to the positive his1 region, but not quite enough to convincingly indicate such a protonation. In two cases (C4 and C205) the his1/his2 criteria predict the wrong protonation state. Overall, however, the appearance of Fig. 4 ▸ provides a convincing indication that our test removal of histidine restraints at the conclusion of this atomic resolution protein refinement proved to be a judicious step towards a fuller analysis and better, closer to reality, restraint option of the final model.
Refinement of protein crystal structures with full stereochemical restraints (especially when tight), even at very high resolution, may hinder a univocal description of the protonation states of the imidazole moieties. However, examination of their geometry obtained after removal of histidine restraints seems to be much more indicative. In the example of PDB entry 4rj2, this approach allowed unambiguous classification of the protonation state in 13 cases and provided a suggestive indication for seven other cases within a set of 22 imidazole moieties.
5. Conclusions
The very fine features of protein stereochemistry characteristic of particular secondary-structure elements, or modulated by a specific chemical environment (such as hydrogen bonds), have been analyzed in the past. For example, it was found that the N—Cα—C angle of residues in α-helices tends to be significantly larger than that in β-strands (Jiang et al., 1995 ▸; Karplus, 1996 ▸). These observations led to the introduction of the conformation-dependent library (CDL) of restraints for protein backbone geometry (Berkholz et al., 2009 ▸). However, the geometry of some side chains may also be dependent on their electronic/tautomeric state and on the chemical environment. To our knowledge, this aspect of protein structure has not received a comprehensive analysis so far. We hope to initiate data-mining research in this direction, taking the histidine imidazole ring as the object of a pilot study.
As a conclusion of this work, we recommend a revised set of stereochemical restraints for bond lengths and angles at the imidazole ring of histidine in its three protonation states (Table 4 ▸). The target values and their standard uncertainties have been derived from the best structural information available in the CSD and confirmed by a corresponding analysis of the PDB entries. We also strongly advise macromolecular crystallographers (and software developers) to take a critical look at the interaction networks of all histidine side chains towards the end of each refinement to try to figure out the protonation state from the hydrogen-bonding/coordination puzzle whenever the data resolution warrants such an analysis (nominally from 2.7 Å on, when water molecules can be identified confidently). In our experience (based on our analysis of structural models at high resolution), in ∼20% of cases it should be possible to establish the histidine protonation state unequivocally and the stereochemical restraints should be adjusted accordingly. In the remaining ambiguous cases the double-protonation variant (Table 4 ▸) should be applied as the safest option for a ‘generic’ histidine geometry. For atomic resolution structures (starting at ∼1.2 Å), when relaxation of the initially applied restraints is possible, one might apply the discriminative analysis described in this paper and assign the most likely protonation state to each His ring based on the values of the his1 and his2 functions. The correct set of final restraints could be then selected, possibly after checking for consistency with indications from intermolecular interactions.
Acknowledgments
This project was supported in part by the Intramural Research Program of the National Cancer Institute, Center for Cancer Research and with Federal funds from the National Cancer Institute, National Institutes of Health (Contract No. HHSN261200800E). The content of this publication does not necessarily reflect the views or policies of the US Department of Health and Human Services, nor does mention of trade names, commercial products, or organizations imply endorsement by the US Government. The collaboration of MJ and ZD was supported in part by a grant (2013/10/M/NZ1/00251) from the National Science Center. MM acknowledges the Polish Ministry of Science and Higher Education for financial support through the ‘Mobility Plus’ program.
References
- Afonine, P. V., Grosse-Kunstleve, R. W., Echols, N., Headd, J. J., Moriarty, N. W., Mustyakimov, M., Terwilliger, T. C., Urzhumtsev, A., Zwart, P. H. & Adams, P. D. (2012). Acta Cryst. D68, 352–367. [DOI] [PMC free article] [PubMed]
- Ahmed, H. U., Blakeley, M. P., Cianci, M., Cruickshank, D. W. J., Hubbard, J. A. & Helliwell, J. R. (2007). Acta Cryst. D63, 906–922. [DOI] [PubMed]
- Allen, F. H. (2002). Acta Cryst. B58, 380–388. [DOI] [PubMed]
- Berisio, R., Lamzin, V. S., Sica, F., Wilson, K. S., Zagari, A. & Mazzarella, L. (1999). J. Mol. Biol. 292, 845–854. [DOI] [PubMed]
- Berkholz, D. S., Shapovalov, M. V., Dunbrack, R. L. & Karplus, P. A. (2009). Structure, 17, 1316–1325. [DOI] [PMC free article] [PubMed]
- Berman, H. M., Westbrook, J., Feng, Z., Gilliland, G., Bhat, T. N., Weissig, H., Shindyalov, I. N. & Bourne, P. E. (2000). Nucleic Acids Res. 28, 235–242. [DOI] [PMC free article] [PubMed]
- Bruno, I. J., Cole, J. C., Edgington, P. R., Kessler, M., Macrae, C. F., McCabe, P., Pearson, J. & Taylor, R. (2002). Acta Cryst. B58, 389–397. [DOI] [PubMed]
- Dauter, Z., Sieker, L. C. & Wilson, K. S. (1992). Acta Cryst. B48, 42–59. [DOI] [PubMed]
- Duda, R. O., Hart, P. E. & Stork, D. G. (2012). Pattern Classification. New York: John Wiley & Sons.
- Eicher, T., Hauptmann, S. & Speicher, A. (2003). The Chemistry of Heterocycles: Structure, Reactions, Syntheses, and Applications, 2nd ed., p. 166. New York: Wiley.
- Engh, R. A. & Huber, R. (1991). Acta Cryst. A47, 392–400.
- Engh, R. A. & Huber, R. (2001). International Tables for Crystallography, Vol. F, edited by M. G. Rossman & E. Arnold, pp. 382–392. Kluwer Academic Publishers, Dordrecht.
- Fisher, R. A. (1936). Ann. Eugen. 7, 179–188.
- Fisher, S. J., Blakeley, M. P., Cianci, M., McSweeney, S. & Helliwell, J. R. (2012). Acta Cryst. D68, 800–809. [DOI] [PubMed]
- Iglewicz, B. & Hoaglin, D. (1993). How to Detect and Handle Outliers. Milwaukee: ASQC Quality Press.
- Jaskolski, M., Gilski, M., Dauter, Z. & Wlodawer, A. (2007). Acta Cryst. D63, 611–620. [DOI] [PubMed]
- Jiang, X., Cao, M., Teppen, B., Newton, S. Q. & Schaefer, L. (1995). J. Phys. Chem. 99, 10521–10525.
- Karplus, P. A. (1996). Protein Sci. 5, 1406–1420. [DOI] [PMC free article] [PubMed]
- Korkmaz, S., Goksuluk, D. & Zararsiz, G. (2014). R J. 6, 151–162.
- Li, T., Zhu, S. & Ogihara, M. (2006). Knowl. Inf. Syst. 10, 453–472.
- Macrae, C. F., Bruno, I. J., Chisholm, J. A., Edgington, P. R., McCabe, P., Pidcock, E., Rodriguez-Monge, L., Taylor, R., van de Streek, J. & Wood, P. A. (2008). J. Appl. Cryst. 41, 466–470.
- McLachlan, G. (2004). Discriminant Analysis and Statistical Pattern Recognition. Hoboken: Wiley-Interscience.
- Morris, R. J. & Bricogne, G. (2003). Acta Cryst. D59, 615–617. [DOI] [PubMed]
- Murshudov, G. N., Skubák, P., Lebedev, A. A., Pannu, N. S., Steiner, R. A., Nicholls, R. A., Winn, M. D., Long, F. & Vagin, A. A. (2011). Acta Cryst. D67, 355–367. [DOI] [PMC free article] [PubMed]
- Sheldrick, G. M. (1990). Acta Cryst. A46, 467–473.
- Sheldrick, G. M. (2008). Acta Cryst. A64, 112–122. [DOI] [PubMed]
- Singh, C. (1965). Acta Cryst. 19, 861–864.
- Steiner, T. (1995). J. Chem. Soc. Chem. Commun., pp. 1331–1332.
- Taylor, R. & Kennard, O. (1982). J. Mol. Struct. 78, 1–28.
- Thaimattam, R., Tykarska, E., Bierzynski, A., Sheldrick, G. M. & Jaskolski, M. (2002). Acta Cryst. D58, 1448–1461. [DOI] [PubMed]
- Winn, M. D. et al. (2011). Acta Cryst. D67, 235–242.