A Bayesian Partitioning Model for Detection of Multilocus Effects in Case-Control Studies

Abstract

Background

Genome-wide association studies (GWASs) have identified hundreds of genetic variants associated with complex diseases, but these variants appear to explain very little of the disease heritability. The typical single locus association analysis in a GWAS fails to detect variants with small effect sizes and to capture higher order interaction among these variants. Multilocus association analysis provides a powerful alternative by jointly modeling the variants within a gene or a pathway and by reducing the burden of multiple hypothesis testing in a GWAS.

Methods

We have proposed here a powerful and flexible dimension reduction approach to model multilocus association. We use a Bayesian partitioning model which clusters SNPs according to their direction of association, models higher order interactions using a flexible scoring scheme, and uses posterior marginal probabilities to detect association between the SNP-set and the disease.

Results

We have illustrated our model using extensive simulation studies and applied it detect multilocus interaction in a GWAS study with type 2 diabetes in Atherosclerosis Risk in Communities (ARIC).

Conclusion

We demonstrate that our approach has better power to detect multilocus interactions than several existing approaches. When applied to ARIC dataset with 9328 individuals to study gene based associations for type 2 diabetes, our method identified some novel variants not detected by conventional single locus association analyses.

1. Introduction

The rapid progress in genotyping technology has greatly facilitated our understanding of the genetic predisposition to various diseases. Several genome-wide association studies (GWASs) have been published on various complex diseases, where genotype data on a large number of single nucleotide polymorphisms (SNPs) are collected to study the association between these SNPs and the disease. A common strategy to assess the effects of the SNPs on the disease is to perform a univariate regression with each SNP as a predictor and rank the SNPs based on their p-values from the univariate regression analysis. The top significant SNPs, which satisfy the genome-wide threshold of multiple testing are reported by the studies. Several such GWASs have successfully detected susceptibility SNPs associated with complex diseases, such as type 2 diabetes (Voight et al., 2010), and Crohn's disease and rheumatoid arthritis (Wellcome Trust Case Control Consortium, 2007). Due to huge computational requirements, most of these GWASs are often limited to single SNP association analysis.

Multilocus association analysis such as gene-based association has gained great impetus in recent days as the single locus association findings have explained very little heritability of these complex traits. Moreover with the advent of high throughput sequencing technologies, there is a dire need to generate computationally efficient statistical methodologies to perform multilocus association analysis. Numerous recent studies (Tibshirani, 1996; Gayán et al., 2008; Province and Borecki, 2008; Bush et al., 2009; Chen et al., 2010; Mukhopadhyay et al., 2010; Pan, 2010) have developed multilocus association analysis techniques and software packages that evaluate the simultaneous association of multiple loci and traits. This large group of multilocus association analysis approaches can be classified into two broad categories; one that focuses on the detection of a subset of significant SNPs associated with a disease from a large group of loci (which include many null or not-associated loci), and the other that tests for association between a large set of loci and a disease without classifying each SNP to null or non-null category (Wu et al., 2010; Larson and Schaid, 2013; Ma et al., 2013).

The set of approaches that focus on the detection of a subset of significant SNPs from a large group of loci tend to focus on modeling only the main effects of the SNPs (Tibshirani, 1996; Servin and Stephens, 2007; Park and Hastie, 2008; Guan and Stephens, 2011; Li et al., 2011). There is evidence that diseases often arise as a result of complicated interactions among SNPs (Merryweather-Clarke et al., 2003). Hence there could be significant gain in the power for detection of associated loci by allowing higher order interaction among these multiple SNPs. The major obstacle in modeling of multilocus interaction is that the number of parameters increases exponentially with the number of loci. Thus the approaches that allow for higher order interaction need to incorporate variable selection or other dimension reduction techniques in their statistical model for association between the SNP-set and the disease (Lunetta et al., 2004; Schwartz et al., 2008; McKinney et al., 2009). Bayesian model selection or variable selection approaches offer an alternative technique for selecting multiple SNPs, and interactions among them. Several Bayesian approaches (Conti and Gauderman, 2004; Lunn et al., 2006; Zhang and Liu, 2007; Wakefield et al., 2010) have been developed that include efficient variable selection. Fridley (2009) recently gave an extensive overview on the Bayesian variable and model selection methods applied to genetic association studies.

Recently several attempts have been made to incorporate higher order interaction in Bayesian multilocus modeling. Marttinen and Corander (2010) used model searching algorithm starting from the marginal model to a saturated model to identify the optimal model for a combination of SNPs. Papathomas et al. (2012) proposed a Bayesian nonparametric clustering approach combined with variable selection to search for gene-gene interaction. Another popular parametric approach to detect interaction under the Bayesian framework is the Bayesian Epistasis Association Mapping (BEAM) (Zhang and Liu, 2007; Zhang et al., 2011; Zhang, 2011), which can handle large number of markers. This approach uses dimension reduction by classifying SNPs into ‘Null’, ‘main’ or ‘interaction’ group given their disease status. It still has limitations in terms of the number of loci that could be placed in the ‘interaction’ category since the model uses the saturated model for the ‘interaction’ category.

This paper presents a new Bayesian methodology to detect multilocus effects incorporating the possibility of interaction among them in a case-control study setup. It aims to implement the data reduction strategy in Basu et al. (2010, 2011) within a Bayesian framework, by pooling the multilocus genotypes into ‘low-risk’, ‘high-risk’ and ‘not-associated’ categories based on direction of effects; and thus reducing the dimension of the genotype predictors from p to 3. An advantage over BEAM is that this approach can easily be extended to handle quantitative trait. Moreover it does not use a saturated model for interaction, rather uses different scoring algorithm to capture higher order interaction. We have considered two such scores to demonstrate the usefulness of the proposed model. Unlike Basu et al. (2010, 2011), this approach uses three parameters to classify the SNPs into ‘low-risk’, ‘high-risk’ and ‘not-associated’ categories and hence is expected to have better power to detect multilocus association. The not-associated SNPs are efficiently separated through MCMC updating, which also provides the posterior probability of each SNP in the SNP-set being associated with the disease. Unlike BEAM, our model does not distinguish between main effects or interaction effects of a group of SNPs, but our flexible scoring scheme captures high order interaction effects effectively. Although our method can potentially be applied to scan a larger number of markers for association, it is more suitable to be used for a SNP-set, such as for a gene or pathways, where associations are searched within each gene or pathway instead of the whole genome.

This paper is organized as follows. Section 2 describes our Bayesian Partitioning Model (BPM) and the reversible jump Markov chain Monte Carlo (RJMCMC) scheme in detail. In sections 3.1 and 3.2, simulation results are presented to investigate the performance of few existing methods and our BPM approach, demonstrating the advantages of the proposed method over several approaches. Section 3.4 illustrates the application of the methods to detect SNPs from a gene-based association study with type 2 diabetes data on Atherosclerosis Risk in Communities (ARIC) study. We conclude with a short summary and discussion outlining a few future research topics.

2. Method

A Dimension Reduction Approach via Bayesian Partitioning Model (BPM)

Here we propose a Bayesian approach to identify the SNPs associated with a disease from a group of p (p ≥ 2) SNPs. The model employs the data reduction strategy proposed in Basu et al. (2010, 2011) and models the joint effects of a group of SNPs on the trait and computes, via MCMC, the posterior probability of each SNP (or SNP-set) being associated with the disease. The dimension reduction strategy is to assume that the minor allele of each SNP can be either of 3 types :

• (1)low risk (LR) : minor allele is associated with decrease in disease risk (‘protective effect’)
• (2)not associated (NA) : minor allele has no effect on disease
• (3)high risk (HR) : minor allele is associated with increase in disease risk (‘deleterious effect’)

Let Y = (y₁, . . . , y_n)^T be the case-control status of n individuals; X = (X₁, . . . , X_n)^T be the n × p matrix of predictors. For the ease of explanation, we will assume that we only have data on SNPs. Hence X_i is a vector of the number of minor alleles of p SNPs for i-th individual. Each SNP can have 0, 1 or 2 minor alleles. Let ${\mathcal{A}}_j$ denote the risk-label allocation of SNP j; j = 1, 2, . . . , p, where ${\mathcal{A}}_j$ = (0,1,0), (1,0,0) or (0,0,1) denotes that SNP j belongs to NA, LR or HR category respectively. It is to be noted that the choice of which allele to code does not matter with respect to our dimension reduction strategy. It does not affect our conclusion because BPM detects SNPs associated with a disease. A priori we do not know if a SNP is NA, LR or HR. This is equivalent to the problem of model selection. For a set of p SNPs, we consider the risk allocation matrix $\mathcal{A}$, where $\mathcal{A}={({\mathcal{A}}_1,\dots ,{\mathcal{A}}_p)}^{\prime }$ is a p × 3 matrix. Hence there are potentially 3^p choices of models, which we need to search through in order to find the model that best explains the joint effect of the group of p SNPs on the trait and compute the posterior probability of observing the best model (or risk allocation) given the trait and the marker data on the n individuals.

Given a specific risk allocation $\mathcal{A}$, the effect of the group of p SNPs is assessed using logistic regression :

$$\log \left(\phantom{\mid }\frac{P(y_i=1\mid {\mathit{X}}_i,\mathcal{A})}{1-P(y_i=1\mid {\mathit{X}}_i,\mathcal{A})}\mid \alpha ,{\beta }_1,{\beta }_2\right)=\alpha +{\beta }_1{Z}_{1i}+{\beta }_2{Z}_{2i},$$ (1)

where β₁ < 0 and β₂ > 0 respectively defines the fixed effects of the LR and the HR group of SNPs, and the predictors Z_1i, Z_2i are respectively the values of scores for the LR and HR groups of an individual i, (i = 1, 2, ..., n). It is to be noted that the values of the predictors Z₁ and Z₂ depend on the allocation $\mathcal{A}$. A particular choice of this score would be Z_1i = total number of minor alleles for the i-th individual in the low-risk group and Z_2i = total number of minor alleles for the i-th individual in the high-risk group; (i = 1, 2, ..., n). We call it the ‘M-score’. The flexibility of our method lies in the fact that many other scores can be proposed in order to capture the joint effect of the SNP-set on the disease. We discuss another such choice of score in section 2.2.

Next we obtain the joint posterior distribution of $\mathcal{A}$ and β as

$$P[\mathcal{A},\beta \mid \mathit{y},\mathit{X}]\propto P[\mathit{y}\mid \mathit{X},\beta ,\mathcal{A}]P[\beta \mid \mathcal{A}]P\left[\mathcal{A}\right]$$ (2)

Here we use MCMC to study the joint posterior density given by equation (2). To construct the Markov Chain, we make 3 simplifying assumptions in the model. First, we assume equal prior probabilities for a SNP to be in the 3 categories. If applied to a genome-wide data, a more informative choice of prior would be to assign much higher probability for each SNP to be in the NA (null) group (Servin and Stephens, 2007), but we applied this model to the top genes identified by a gene-based association analysis. Hence we decided to assign high probability for each SNP to be in the non-null group. Moreover, our choice of prior gave a simplified form (equation (4)) of the acceptance probability in equation (3). Second, we assume independent prior distributions of all the SNPs, i.e., $P\left[\mathcal{A}\right]={\prod }_{j=1}^{p}P\left[{\mathcal{A}}_j\right]$ = constant. Third, we assume $P[\beta \mid \mathcal{A}]=P\left[\beta \right]$, where P [β] is the prior distribution β of = (α,β₁,β₂) following a truncated tri-variate normal distribution : β ~ N₃(μ, V) × I(β₁ < 0) × I(β₂ > 0). We let the prior parameters μ = (0,0,0)′ and set V such that we expect 95% of the SNPs to have relative risks that lie within [e^−1.5, e^1.5], as suggested by Wakefield et al. (2010). The diagonal of V is, therefore, set at {1, 0.207², 0.207²} and the off-diagonal elements are set to be zero for an uncorrelated prior setting. The joint posterior distribution (equation (2)) of $\mathcal{A}$ and β lives on a high-dimensional product space. The SNP allocation label $\mathcal{A}$ lies on a discrete space {(0,1,0),(1,0,0),(0,0,1)}^p while $\beta \in \mathbb{R}\times {\mathbb{R}}^{-}\times {\mathbb{R}}^{+}$.

2.1 Construction of the Markov Chain

We construct a Markov Chain using reversible jump (RJMCMC) with “dimension” moves, and “allocation” & “coefficient” moves within a fixed dimension. The “dimension” moves include ‘death’ and ‘birth’ steps to increase or decrease the dimension, K, by one. The dimension parameter K can take 4 values : 0; 1; 2; and 3, which refers to the case that the model has parameter(s) α; α and β₁; α and β2; and all three parameters α, β₁, β2 in equation (1), respectively. The first step in our RJMCMC is to choose one of the ‘death’, ‘birth’ and ‘fixed dimension’ moves at random. In a ‘death’ step, we drop one parameter, randomly choosing between β₁ and β₂. In a ‘birth’ step, we propose β₁ or β₂ and update $\mathcal{A}$ from its full conditionals (as described a little later). The acceptance probability for these dimension moves (from step $\overline{t-1}$ to step t) is min (1,a(K^(t–1), K^(t))), with

$$a(K^{(t-1)},K^{\left(t\right)})=\frac{P\left[K^{\left(t\right)}\right]P[{\beta }^{\left(t\right)},{\mathcal{A}}^{\left(t\right)}\mid K^{\left(t\right)}]P[\mathit{y}\mid {\mathcal{A}}^{\left(t\right)},{\beta }^{\left(t\right)},K^{\left(t\right)}]P[K^{(t-1)}\mid K^{\left(t\right)}]}{P\left[K^{(t-1)}\right]P[{\beta }^{(t-1)},{\mathcal{A}}^{(t-1)}\mid K^{(t-1)}]P[\mathit{y}\mid {\mathcal{A}}^{(t-1)},{\beta }^{(t-1)},K^{(t-1)}]P[K^{\left(t\right)}\mid K^{(t-1)}]}\times \frac{Q[D^{(t-1)}\mid D^{\left(t\right)}]}{Q[D^{\left(t\right)}\mid D^{(t-1)}]}\times \mid 1\mid$$ (3)

where Q[D^(t)|D^(t–1)] is the proposal density of the move from model D^(t–1) in step $\overline{t-1}$ 1 to D^(t) in step t. Since we assumed equal prior probabilities of a SNP to be in any of the 3 categories, P[K^(t)] = P[K^(t–1)]. The 4 possible moves are random, hence P [K^(t–1)|K^(t)] = P[K^(t)|K^(t–1)]. Also, $P[{\beta }^{\left(t\right)},{\mathcal{A}}^{\left(t\right)}\mid K^{\left(t\right)}]=P[{\beta }^{\left(t\right)}\mid {\mathcal{A}}^{\left(t\right)},K^{\left(t\right)}]P[{\mathcal{A}}^{\left(t\right)}\mid K^{\left(t\right)}]$. The possible moves along with the corresponding acceptance probabilities are listed in Section 1 of Supplementary Materials.

We now look into the general form of the proposal density Q[D^(t)|D^(t–1)]. Note that,

$$\begin{array}{cc}\hfill Q[D^{\left(t\right)}\mid D^{(t-1)}]& =P[{\beta }^{\left(t\right)},{\mathcal{A}}^{\left(t\right)},K^{\left(t\right)}\mid {\beta }^{(t-1)},{\mathcal{A}}^{(t-1)},K^{(t-1)}]\hfill \\ \hfill & =P({\beta }^{\left(t\right)}\mid {\mathcal{A}}^{\left(t\right)},K^{\left(t\right)},{\beta }^{(t-1)},{\mathcal{A}}^{(t-1)},K^{(t-1)}]P[{\mathcal{A}}^{\left(t\right)}\mid K^{\left(t\right)},{\beta }^{(t-1)},{\mathcal{A}}^{(t-1)},K^{(t-1)}]\times P[K^{\left(t\right)}\mid {\beta }^{(t-1)},{\mathcal{A}}^{(t-1)},K^{(t-1)}]\hfill \\ \hfill & =P[{\beta }^{\left(t\right)}\mid {\mathcal{A}}^{\left(t\right)},K^{\left(t\right)}]P[{\mathcal{A}}^{\left(t\right)}\mid K^{\left(t\right)}]P[K^{\left(t\right)}\mid K^{(t-1)}]\hfill \end{array}$$

So, equation (3) reduces to the simple form of a likelihood ratio :

$$a(K^{(t-1)},K^{\left(t\right)})=\frac{P[\mathit{y}\mid {\beta }^{\left(t\right)},{\mathcal{A}}^{\left(t\right)},K^{\left(t\right)}]}{P[\mathit{y}\mid {\beta }^{(t-1)},{\mathcal{A}}^{(t-1)},K^{(t-1)}]}$$ (4)

We obtain $P[\mathit{y}\mid {\beta }^{\left(t\right)},{\mathcal{A}}^{\left(t\right)},K^{\left(t\right)}]$ and $P[\mathit{y}\mid {\beta }^{(t-1)},{\mathcal{A}}^{(t-1)},K^{(t-1)}]$ using the model in equation (1). Within a fixed dimension, we update the Markov chain through “allocation” and “coefficients” moves, that is, we first update $\mathcal{A}$ from its full conditionals and then update β using Metropolis Hastings algorithm.

Updating ${\mathcal{A}}_j$ from full conditionals

We assume a multinomial prior for the configuration of SNP ${\mathcal{A}}_j$ and equal prior probabilities of being in the “low-risk”, “NA”, and “high-risk” categories. So, ${\mathcal{A}}_j$ ~ Multinomial(m = 1; p_j1 = 1/3,p_j2 = 1/3p_j3 = 1/3), where ${\mathcal{A}}_j$ ∈ {(1,0,0)′,(0,1,0)′,(0,0,1)′}. If ${\mathcal{A}}_{(-j)}$ denotes configuration of all SNPs except the j^th SNP, then the full conditional of ${\mathcal{A}}_j$ at step t also has a multinomial distribution : $[{\mathcal{A}}_j^{\left(t\right)}\mid {\beta }^{(t-1)},{\mathcal{A}}_{(-j)}^{(t-1)}]$ ~ Multinomial $(m=1;p_{j1}^{\left(t\right)},p_{j2}^{\left(t\right)},p_{j3}^{\left(t\right)})$, where $p_{j1}^{\left(t\right)},p_{j2}^{\left(t\right)},p_{j3}^{\left(t\right)}$ are the posterior probabilities of SNP j to be in the LR, NA and HR group respectively. These posterior probabilities are given by

$$p_{js}^{\left(t\right)}=\frac{P[\mathit{y}\mid {\beta }^{(t-1)},{\mathcal{A}}_{(-j)}^{(t-1)},{\mathcal{A}}_j^{\left(t\right)}={\mathit{a}}_s]P[{\mathcal{A}}_j^{\left(t\right)}={\mathit{a}}_s]}{{\sum }_{k=1}^{3}P[\mathit{y}\mid {\beta }^{(t-1)},{\mathcal{A}}_{(-j)}^{(t-1)},{\mathcal{A}}_j^{\left(t\right)}={\mathit{a}}_k]P[{\mathcal{A}}_j^{\left(t\right)}={\mathit{a}}_k]},$$ (5)

where s = 1,2,3, a_s ∈ {1,0,0)′,(0,1,0)′,(0,0,1)′} and $P[\mathit{y}\mid {\beta }^{(t-1)},{\mathcal{A}}_{(-j)}^{(t-1)},{\mathcal{A}}_j^{\left(t\right)}={\mathit{a}}_s]=P[\mathit{y}\mid {\beta }^{(t-1)},{\mathcal{A}}_{(-j)}^{(t-1)},{\mathcal{A}}_j^{\left(t\right)}={\mathit{a}}_s,K^{\left(t\right)}]$ is obtained using the model in equation (1).

Updating β using Metropolis-Hastings

After updating $\mathcal{A}$ from its full conditionals and getting ${\mathcal{A}}^{\left(t\right)}$, we sample β* from the proposal density N₃(β^(t–1),V) I(β₁ < 0)I(β₂ > 0). For each draw of β* from the proposal, we accept β* as β^(t) with probability min (1,a′(β^(t–1), β*)), where $a^{\prime }({\beta }^{(t-1)},{\beta }^{\ast })=\frac{P[\mathit{y}\mid {\beta }^{\ast },{\mathcal{A}}^{\left(t\right)}].P[{\beta }^{\ast }\mid {\mathcal{A}}^{\left(t\right)}]}{P[\mathit{y}\mid {\beta }^{(t-1)},{\mathcal{A}}^{\left(t\right)}].P[{\beta }^{(t-1)}\mid {\mathcal{A}}^{\left(t\right)}]}\times \frac{P[{\beta }^{(t-1)}\mid {\beta }^{\ast }]}{P[{\beta }^{\ast }\mid {\beta }^{(t-1)}]}$. Note that $P[\mathit{y}\mid {\beta }^{\ast },{\mathcal{A}}^{\left(t\right)}]=P[\mathit{y}\mid {\beta }^{\ast },{\mathcal{A}}^{\left(t\right)},K^{\left(t\right)}]$ and $P[\mathit{y}\mid {\beta }^{(t-1)},{\mathcal{A}}^{\left(t\right)}]$ are obtained from model in equation (1). The implementation of this RJMCMC is outlined in detail in Section 2 of Supplementary Materials.

2.2 M-score vs. P-score

The M-score corresponds to a model (equation (1)) where Z₁(Z₂) is the total number of minor alleles in the LR (HR) group. The M-score technique is theoretically equivalent to considering only main effects of the SNPs in a logistic regression model with equal effect sizes of the SNPs in the LR group and equal effect sizes of the ones in the HR group. For example, let us consider the allocation $\mathcal{A}$ where the first p₁ SNPs are in LR group and the rest p₂ SNPs are in HR group, p₁ + p₂ = p. Thus, for individual i, M-score for LR group is $Z_{1i}={\sum }_{k=1}^{p_1}{X}_{ik}$ and for HR group is $Z_{2i}={\sum }_{j=1}^{p_2}{X}_{ij}$. Equation (1) becomes

$$\mathrm{logit}\left(P[y_i=1\mid {\mathit{X}}_i,\beta ,\mathcal{A}]\right)=\alpha +{\beta }_1{X}_{i1}+\dots +{\beta }_1{X}_{i{p}_1}+{\beta }_2{X}_{i(p_1+1)}+\dots +{\beta }_2{X}_{ip}$$

Now we propose a pair-wise score to capture higher order interaction among the SNPs. The P-score is calculated as total number of pairs of minor alleles in LR and HR groups. To implement P-score in equation (1), we define Z_1i as the number of unordered samples of minor alleles of size 2 (without replacement) from the total number of minor alleles in the LR group of individual i (i = 1, 2, ..., n). Similarly Z_2i is defined for the HR group. Z_1i = 1 (Z_2i = 1) when there are only 2 minor alleles in the LR (HR) group of i^th individual. A score of 0.5 is arbitrarily assigned if there is only 1 minor allele in a group.

Each allocation $\mathcal{A}$ and the corresponding P-score is equivalent to a multiple logistic regression model with predictors as some function of the main effects and the pairwise interaction among the SNPs. For our hypothetical example with first p₁ SNPs in LR group and the rest p₂ SNPs in HR group, we consider the multiple logistic regression model (1) :

$$\begin{array}{cc}\hfill \mathrm{logit}\left(P[y_i=1\mid {\mathit{X}}_i,\beta ,\mathcal{A}]\right)& =\alpha +{\beta }_1\left(\begin{array}{c}\hfill {\sum }_{k=1}^{p_1}{X}_{ik}\hfill \\ \hfill 2\hfill \end{array}\right)+{\beta }_2\left(\begin{array}{c}\hfill {\sum }_{j=1}^{p_2}{X}_{ij}\hfill \\ \hfill 2\hfill \end{array}\right)\hfill \\ \hfill & =\alpha +{\beta }_1\left(\sum _{s,t:s\le t}{X}_{is}{X}_{it}+\sum _{k=1}^{p_1}{X}_{ik}(X_{ik}-1)∕2\right)+{\beta }_2\left(\sum _{l,m:l<m}{X}_{il}{X}_{im}+\sum _{j=1}^{p_2}{X}_{ij}(X_{ij}-1)∕2\right)\hfill \end{array}$$

Thus, through P-score we can theoretically capture main effects as well as pair-wise interaction effects among the SNPs. In practice, our simulation studies showed that P-score can capture higher order interaction effects as well (refer section 3.1). Our simulation study (refer to Section 3 of Supplementary Materials) using 1000 cases and 1000 controls showed the advantage of the proposed pair-wise-score modeling (P-score) over the main effect modeling (M-score) in presence of interaction. One can use other scoring schemes, such as Gaussian kernels, to capture interaction among SNPs.

3. Results

We performed several simulation studies to demonstrate the importance of the choice of scores for our model and to compare our approach with some existing ones.

3.1 Simulation 1

We first compared our BPM approach with BEAM (Zhang and Liu, 2007) using simulation studies on uncorrelated SNPs. We also compared our approach with the logistic kernel machine (LKM) regression method. The kernel machine regression (KMR) tests (Wu et al., 2010) are computationally efficient tests which score similarity among individuals through di erent choices of kernels (such as linear, identity-by-descent, quadratic) and use a score test to detect association between the SNP-set and the disease status.

We simulated data on 20 uncorrelated SNPs with 200 cases and 200 controls. Only the first 4 SNPs were associated with the case-control status. We considered 5 epistatic models with different main effect sizes (and directions) and interaction effect sizes. Two-way, three-way and four-way interactions were considered. We considered both additive and dominant genetic model for this power comparison. The following models were used in our simulations:

• Model 1: $\mathrm{logit}\left(\mathrm{p}\right)=-4+\frac{1}{5}{X}_1+\frac{1}{5}{X}_2-X_3-X_4$, where X_j = 0,1,2 denote SNP j with 0,1,2 minor alleles respectively.

• Model 2: logit(p) = −4 − 2X₄ + X₁X₂X₃, where X_j = 0,1,2 denote SNP j with 0,1,2 minor alleles respectively.

• Model 3: logit(p) = −4 + 2X₁X₂X₃X₄, where X_j = 0,1,2 denote SNP j with 0,1,2 minor alleles respectively.

• Model 4: $\mathrm{logit}\left(\mathrm{p}\right)=-4+\frac{1}{2}{X}_1{X}_2+\frac{1}{2}{X}_1{X}_3+X_3{X}_4$, where X_j = 0,1 for SNP j with 0, ≥ 1 minor alleles respectively.

• Model 5: $\mathrm{logit}\left(\mathrm{p}\right)=-4+\frac{1}{5}{X}_1+\frac{2}{5}{X}_2+\frac{3}{5}{X}_3-X_4$, where X_j = 0,1,2 denote SNP j with 0,1,2 minor alleles respectively.

For each of these models, we simulated 200 datasets with each SNP at minor allele frequency (maf) 0.2. We first compared, using ROCs, the power of our BPM M-score and P-score approaches with that of BEAM to detect genetic variants associated with disease. Here, we are interested in testing the null hypothesis that a chosen SNP is null. For every simulated model, we considered a range of cutoffs between 0 and 1, and for each cutoff, we calculated the number of times the posterior probabilities of each of the associated SNPs (such as SNP1, SNP2, SNP3, SNP4) in the non-null category was higher than the cutoff value. We also calculated the number of times the posterior probabilities of each of the truly null SNPs was higher than the cutoff out of 200 simulations. We generated a ROC curve by calculating the average number of truly associated SNPs (true positive rate) detected and the average number of false-positives (false positive rate) detected by BPM and BEAM for a given cutoff. The average number of false positives detected by BPM gives an estimate of BPM's type I error in testing if a chosen SNP is null. For BPM, we ran single chain of size 10,000. The first 5,000 were discarded as burn-in. For BEAM, we took the default chain size of 100,000 with a burn-in of 50,000. Thin parameter was set at 1. The default prior probabilities of 0.01 were used for each SNP to belong to marginal or interaction groups.

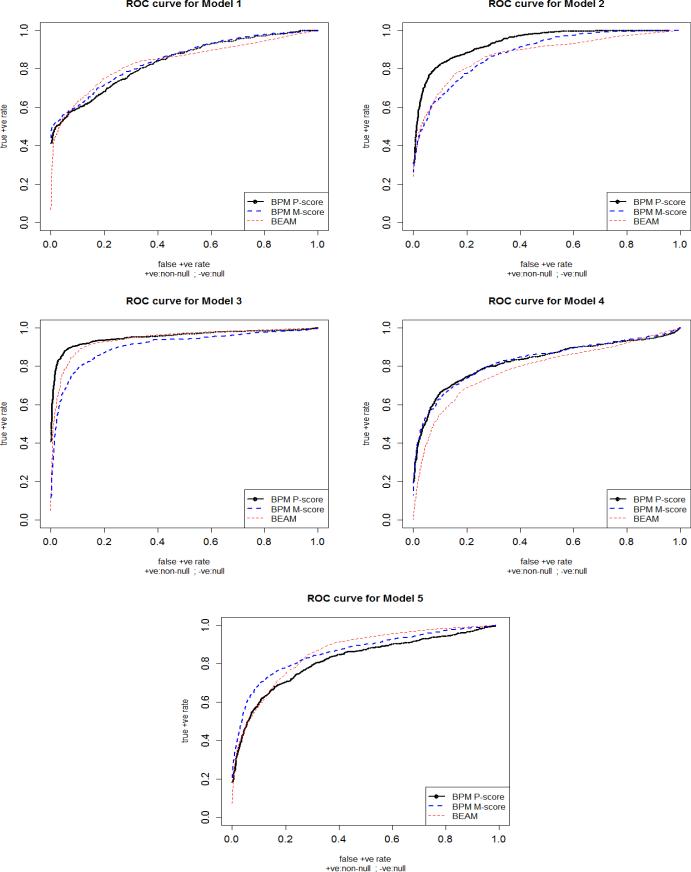
According to Figure 1 and Table 1, our BPM approach outperformed BEAM for all 5 models at Bonferroni corrected level of 0.0025 (= 0.05/20) except for Model 2 where the performances were very similar. For Model 1, we only had main effects under an additive genetic model. BEAM had lower true positive rate (tpr) than BPM for a false positive rate (fpr) < 0.1. Especially M-score performed well due to its ability to capture the main effects effectively. For a Bonferroni corrected level of 0.0025, BPM had a power of 0.48, while BEAM had only 0.26.

Figure 1.

The ROCs for BPM (M- and P-scores) and BEAM for the 5 epistatic models with 4 causal SNPs. True positive rate (tpr) or sensitivity for each dataset was calculated as the proportion of causal SNPs detected based on their posterior marginal probabilities in the non-null category and for a series of cutoff s for the posterior probabilities. It was averaged across the 200 simulated datasets with 20 uncorrelated SNPs. In a similar way, false positive rate (fpr) was calculated. As the cutoff for the posterior probability was varied, the fpr also varied. Increasing order of fpr is plotted along x-axis, and tpr along y-axis. Here, the heavy black curve represents BPM P-score, the heavy blue dashed curve is BPM M-score and the light red dashed curve is BEAM.

Table 1.

Comparison of BPM & BEAM: Power of the three methods in detecting the four associated SNPs for Bonferroni corrected error level 0.0025 (= 0.05/20) based on 200 datasets with 200 cases and 200 controls.

	Simulated Model
Method	1	2	3	4	5
BPM M-score	0.48	0.29	0.15	0.23	0.22
BPM P-score	0.41	0.31	0.55	0.21	0.19
BEAM	0.26	0.30	0.25	0.05	0.15

For Model 2, as soon as we added an interaction term to a main effect model, BPM P-score had uniformly better power than the M-score and the BEAM due to its ability to capture interaction effects. Even in the presence of a strong main effect, M-score could not outperform P-score. Here, BEAM performed marginally better than BPM M-score.

The same was true for Model 3 (an interaction-only model) where BEAM outperformed M-score marginally, but P-score captured the four-way interaction efficiently and outperformed BEAM. Here, while BEAM had very low tpr of 0.25 at a fpr of 0.0025, BPM P-score had a good tpr of 0.55 (refer Table 1). To see if BPM really performs better than BEAM in capturing higher-order interactions, we also considered another additive genetic model (figure not provided here) where the first 5 out of 20 independent SNPs were causal and were interacting with each other to increase the disease risk. The BPM P-score had uniformly better power than BEAM again.

For Model 4, we considered a dominant genetic model with only pairwise interaction effects. The true effect sizes being small, all the methods lost some power under the dominant model, but BPM had better power than BEAM (except for error levels close to 1). BPM M- and P-scores performed similar according to the ROC curve (Figure 1).

For Model 5, our method outperformed BEAM even when the basic model assumption of equal effect size was violated for our BPM approach. BEAM had lower power than BPM for an error level of < 0.2, especially for M-score due to M-score's ability to capture the main effects effectively.

Next we compared the powers of BPM, BEAM and LKM methods to detect multilocus association. Our null hypothesis of interest is that none of the SNPs is associated with the disease status. Since LKM can only test if a group of SNPs is associated or not at a given type I error level, we calculated the number of times each of these BEAM and BPM approaches detected at least one causal SNP out of the 4 SNPs for varying error levels. Table 2 (and Figure 2 of Supplementary Materials) show that at Bonferroni adjusted error of 0.0025, BPM had better power over BEAM and LKM for the main-effect-only model (Model 1). All three methods had comparable power when there was a main effect and an interaction effect in the model (Model 2). In presence of only a fourth-order interaction (Model 3) or several pairwise interaction effects (Model 4), LKM had the best performance closely followed by the BPM approach. One thing to keep in mind is that LKM can only test for association between a SNP-set and a disease; its limitation is that it cannot specifically identify the null and the non-null SNPs.

Table 2.

Comparison of BPM, BEAM & LKM: Power of the six methods in detecting at least one of the four associated SNFs for Bonferroni corrected error level 0.0025 (= 0.05/20) based on 200 datasets with 200 cases and 200 controls.

	Simulated Model
Method	1	2	3	4
BPM M-score	1.00	1.00	0.41	0.50
BPM P-score	0.93	0.98	0.91	0.48
BEAM	0.81	1.00	0.34	0.12
LKM-linear	0.91	0.995	0.84	0.56
LKM-quadratic	0.89	1.00	0.96	0.64
LKM-ibs	0.93	0.99	0.80	0.69

3.2 Simulation 2

Here we performed a simulation study with correlated SNPs to see the impact of linkage disequilibrium (LD) on our BPM approach. We considered correlation coe cients of ρ = 0, 0.5 and 0.9. The SNPs were simulated from a latent multivariate gaussian variable with an AR1(ρ) structure. As before, we simulated 200 datasets on 200 cases and 200 controls with 20 SNPs (first 4 are causal) at maf 0.2. We performed this comparison with M-score and with Model 1. The power of BPM for 3 different correlations (ρ = 0, 0.5, 0.9) at various error levels were plotted (refer Section 5 of Supplementary Materials). At low type-1 error levels, BPM lost power with the increase in LD values among the SNPs. For higher error levels, the power of the BPM M-score approach to detect association were similar for ρ = 0 and ρ = 0.5. This observation was not consistent for all our simulations. We noticed sometimes gain in power for ρ = 0.5 over ρ = 0 but fall in power for high correlation like ρ = 0.9, especially for models with interaction effect. In summary, moderate correlation among SNPs did not a ect the performance of the BPM approach significantly but for high SNP-SNP correlation, BPM lost power for stringent error levels.

3.3 Convergence diagnostics

Checking convergence of RJMCMC is not straightforward. The general consensus is to monitor common parameters (in our case, α) using popular fixed-dimensional convergence diagnostics (Sisson, 2005). Gelman and Rubin's diagnostic (Gelman and Rubin, 1992) gave point estimate for the median potential scale reduction factor (psrf) for as 1.00 (< 1.1 means the chain has converged to the stationary distribution and we need not run the chain longer). We also plotted posterior distributions of all 3 parameters α, β₁ and β₂ for 6 independent chains (using M-score) for a randomly chosen dataset under Model 1 (main effect only model) with uncorrelated SNPs (refer Section 6 of Supplementary Materials). The starting parameters β and $\mathcal{A}$ were di erent for each chain. Convergence was achieved for all these chains. Mean values of β₁ and β₂ (averaged over all 6 chains) were respectively − 0.96 (sd = 0.18) and 0.23 (sd = 0.15), which were close to the true effect sizes of −1 and 0.2 respectively.

In Figure 4 of Supplementary Materials, we presented summaries of β₁ and β₂ (using boxplots) for 15 randomly chosen datasets out of 200 datasets simulated under Model 1. In this model, the effect size of SNPs with negative direction (protective or LR SNP) was −1 and that with positive direction (deleterious or HR SNP) was 0.2. Since we are looking at M-score result, we expect the estimated β₁ and β₂ to be close to −1 and 0.2 respectively. Figure 4 shows that the estimates align quite well with the true values.

We also looked at convergence of the multivariate categorical parameter $\mathcal{A}$. For this purpose, we randomly selected 3 SNPs (out of 20), each of which was known to belong to 3 di erent groups LR, NA and HR (refer Model 1). Figure 6 of Supplementary Materials graphically compared the posterior probabilities of each of the chosen SNPs to belong to each of the groups across 6 independent chains. Stability of the posterior probabilities of the various categories over independent chains indicate convergence.

3.4 Real Data Analysis

Extensive evidence, including that gathered from twin and family studies, supports the hypothesis that genetic factors are a major contributor to the risk of type 2 diabetes (T2D). More recently, a GWAS of T2D conducted in populations of European ancestry have identified more than 50 SNPs reaching genome-wide levels of significance, most of which appear to act in the pancreatic beta-cell development or function (Voight et al., 2010; Morris et al., 2012). Several GWASs of related quantitative traits such as fasting glucose have offered additional signals. These loci are significant contributors to risk of T2D, with population attributable risks > 5% per locus in many cases. These results provide strong evidence for the existence and identification of common genetic risk factors for T2D.

The ARIC study is an ongoing prospective study designed to investigate the etiology and natural history of atherosclerosis and its clinical manifestations, and to measure variation in cardiovascular risk factors, medical care and disease by race, gender, place and time (The ARIC Investigators, 1989). ARIC has collected fasting glucose measures from the entire cohort at 4 separate visits over a 9-year period and self-reported physician diagnosis and medication use in up to 14 separate interviews over a 20-year period. Diabetes was defined as fasting glucose ≥126 mg/dL, non-fasting glucose ≥ 200 mg/dL, self-reported physician diagnosis of diabetes, or current use of diabetes medications. Details about ARIC Study samples and their genotyping can be found in Section 10 of Supplementary Materials.

We conducted single SNP association analyses on the Caucasians (sample size 9328 with 812 cases) using PLINK (Purcell et al., 2007) and a gene based association analysis in VEGAS (Liu et al., 2010). As per VEGAS, the two strongest signals were located in genes TCF7L2 (gene pvalue 8 × 10⁻⁶) on chromosome 10 and MMRN1 (gene pvalue 5.7× 10⁻⁵) on chromosome 4. PLINK identified the SNPs rs7903146 (pvalue 1.7 × 10⁻¹¹) and rs1318557 (pvalue 2.5 × 10⁻⁶) to be the most significant SNPs of genes TCF7L2 and MMRN1 respectively. Since VEGAS gives only gene-based pvalue, we wanted to explore if some additional SNPs in these two genes could be identified by our BPM approach which were not detected in the single-SNP association analysis.

To implement our BPM approach, we again focused on the Caucasian participants. We implemented the BPM approach on the SNP data separately for each of two genes mentioned above. We followed the same definition used by VEGAS for the allocation of SNPs to the genes. Our goal was to analyze each of the genes separately using our BPM approach (both M- and P-scores), find the optimal allocation of the SNPs within each gene and compare the BPM performance with single-SNP association findings.

For the gene-based association analysis, we excluded the SNPs with maf < 5% and the SNPs with absolute pairwise correlation coe cient |ρ| > 0.8 with another SNP. For a given gene data, we computed posterior probabilities for the minor allele of each of the SNPs to be in each of the three categories (LR, NA and HR) based on a long chain of 500,000 MCMC iterations. Within each iteration, β is iterated 10 times. The posterior probability of a SNP to be in a particular group was calculated as the average number of times that SNP was allocated in that group in each MCMC iteration. The starting allocation was randomly generated for each chain. Using Heidelberger-Welch (HW) tests (Heidelberger and Welch, 1983), the burn-ins were decided for each gene and each score to ensure stationarity of the common parameter α of each chain at 5% significance level.

Given the posterior probabilities of a SNP in the LR, NA and HR group, we used a cutoff 0.4 for the non-NA (LR+HR) posterior probability to assign a SNP into a non-NA group. Any SNP with a non-NA (LR+HR) posterior probability exceeding the threshold was assigned to be non-NA. The allocation of a non-NA SNP to LR or HR group was based on the group having higher posterior probability among the two. For each score and each gene, we thus obtained the final allocation $\mathcal{A}$ of the SNPs and calculated the approximate Bayes Factor (ABF) (Wakefield, 2008) as a measure of evidence in favor of null or the alternative hypothesis of association.

For the calculation of ABF₀₁ (the posterior odds of null model to the alternative model $\mathcal{A}$ selected using ≥ 0.4 posterior probability for a SNP to belong to non-NA group), we evaluated the joint likelihood of Y and β under the null as well as under the alternative. Since there is no closed form of the joint likelihood, we used Laplace approximation around the maximum a posteriori (MAP) estimate ofβ to obtain the null likelihood. On the other hand, we computed the alternative joint likelihood by using the Laplace approximation around the posterior mode of β obtained from the posterior samples (Zheng et al., 2012). In our calculations, we found the posterior mode to be almost same as the MAP estimate of β under the alternative.

We first analyzed gene MMRN1 from Chromosome 4 with 57 SNPs after screening. For BPM, the M-score chain for α passed HW stationarity test and half-width mean test at 5% level without any burn-in while a burn-in of 100,000 was needed for P-score. Figure 5 of Supplementary Materials also showed convergence of these two chains. From Table 3 we saw that, at cutoff 0.4, only 4 SNPs were detected as LR for M-score, which included the most significant SNP rs1318557 (pvalue 2.5 × 10⁻⁶) from the single-SNP association analysis. The posterior probabilities of this SNP to belong to LR category was 0.47. The other 3 SNPs chosen by BPM were not at all significant in the single-SNP association analysis (refer Table 3). M-score had −2 log₁₀(ABF₀₁) = 10.5 > 10, which indicated very strong evidence of association (Zheng et al., 2012).

Table 3.

The final allocation of the non-null SNPs selected by using a 0.4 cutoff on the posterior probability of each SNP to be in non-NA(LR+HR) group from BPM M-score analysis. The single-SNP results of these non-null SNPs in MMRN1 gene are also listed for comparison. The direction of single-SNP coefficient and the group allocation by BPM match.

SNP rsID	rs11727074	rs6812192	rs12646270	rs1318557
Final allocation $\mathcal{A}$	LR	LR	LR	LR
Posterior probability	0.38	0.48	0.43	0.47
Single-SNP coefficients	–0.2	–0.2	–0.3	–0.3
Single-SNP pvalues	6.2 × 10–2	1.4 × 10–3	4.0 × 10–2	2.5 × 10–6

On the other hand, P-score could not detect any SNP as LR/HR at the chosen cutoff , although at a lower cutoff of 0.2, it detected these above mentioned SNPs. This may indicate the fact that these SNPs in MMRN1 are not contributing through interactions and hence the P-score could not perform as well as the M-score.

We next analyzed gene TCF7L2 from chromosome 10 with 109 SNPs after screening. Using HW tests at 5% level, burn-ins of 200,000 and 150, 000 for M- and P-scores respectively ensured stationarity for common parameter α. At cutoff 0.4, with −2 log₁₀(ABF₀₁) = 15.7 > 10, M-score found only 2 SNPs rs17747324 and rs7903146, which were allocated in HR and LR group respectively (refer Table 4). Meanwhile P-score detected 11 SNPs (including the 2 non-NA SNPs from M-score) with −2 log₁₀(ABF₀₁) = 11.5 > 10 (refer Tables 5). Both scores detected the two most significant SNPs from single-SNP analysis. It is to be noted that ABF values across scores are not comparable since the two scores can give different ABF values even if the same allocation is used. As per ABF, both the allocations from BPM indicated very strong association of the selected non-NA SNPs with the disease. The high ABFs from both scores seemed to be driven by the very strong association through rs17747324 and rs7903146. Also, P-score detecting more SNPs than M-score suggested possible interaction among the selected SNPs. As seen from Tables 4 & 5, BPM captured some novel SNPs, which again emphasizes the power gain by joint modeling of SNPs within a gene over single SNP association analysis.

Table 4.

The final allocation of the non-null SNPs selected by using a 0.4 cutoff on the posterior probability of each SNP to be in non-NA(LR+HR) group from BPM M-score analysis in TCF7L2 gene. The single-SNP results of these non-null SNPs are also listed for comparison. The direction of single-SNP coefficient and the group allocation by BPM match.

SNP rsID	rs17747324	rs7903146
Posterior $\mathcal{A}$	HR	LR
Posterior probability	0.46	0.48
Single-SNP coefficients	0.42	–0.38
Single-SNP pvalues	3.6 × 10–11	1.7 × 10–11

Table 5.

The final allocation of the non-null SNPs selected by using a 0.4 cutoff on the posterior probability of each SNP to be in non-NA(LR+HR) group from BPM P-score analysis in TCF7L2 gene. The single-SNP results of these non-null SNPs are also listed for comparison. The direction of single-SNP coefficient and the group allocation by BPM match.

SNP rsID	rs7079711	rs11196181	rs17747324	rs7903146	rs7079673
Posterior $\mathcal{A}$	LR	LR	HR	LR	LR
Posterior probability	0.49	0.46	0.61	0.41	0.37
Single-SNP coefficients	–0.33	–0.24	0.42	–0.39	–0.12
Single SNP pvalues	5.2×10–4	4.2×10–2	3.6×10–11	1.7×10–11	2.8×10–1

rs11196228	rs7084875	rs290483	rs7922641	rs4918801	rs10885424
LR	LR	HR	HR	HR	LR
0.27	0.40	0.36	0.26	0.52	0.23
–0.33	–0.01	–0.02	0.001	0.11	0.01
3.1×10–2	8.8×10–1	7.3×10–1	9.9×10–1	3.7×10–1	9.2×10–1

4. Discussion

Our BPM approach makes use of the fact that we are interested in detection of the associated SNPs and not in the estimation of individual SNP effects. The main advantage of classifying the SNPs into these three groups is that for each specific choice of allocation of risk-labels to the SNPs, we can model the joint effect of the SNP-set on the disease with only three parameters. This approach could be especially advantageous when we are considering joint modeling of a large group of SNPs with a relatively small sample size. In addition to this, our proposed approach provides the flexibility of assigning scores to each of these low-risk or high-risk group of SNPs in order to capture the high-order interaction among the SNPs. Our model provides the flexibility of adjusting for other covariate effects (refer Section 9 of Supplementary Materials) and allows for modeling of epistatic and nonlinear SNP effects. Here we considered a pair-wise scoring scheme that captures such higher order interaction among the SNPs. Other scores such as Gaussian kernels can be used to capture these epistatic effects. Our simulation studies and real data analysis demonstrated the usefulness of this proposed method to detect SNPs with higher order interaction. It is to be noted that we only considered multiplicative interaction in our simulation experiments. In general, the concept of interaction is much broader than multiplicative interaction. We intend to study the performance of BPM for broader class of interactions in future.

One advantage of the BPM approach is that it models the latent state of association (risk-allocation) of the SNPs given the phenotype and genotype data and thus does not get strongly influenced by the LD among the SNPs. We conducted simulations to study the impact of the LD on power of detection of our BPM approach. In general, we found that the approach loses some power when there is strong correlation (0.9) among the SNPs, but the performance was very similar between SNPs with no LD and SNPs with moderate LD (0.5). One must note that for large number of SNPs in very high LD, the autocorrelation plots will show high autocorrelation even for large values of lag and hence more RJMCMC iterations will be needed for convergence. In such a scenario, the BPM chain (due to its single-site updating scheme) is likely to get stuck, which will be indicated clearly in the running mean plot of parameter. On the same note, our assumption of independent prior distributions for risk-allocations of all SNPs is reasonable since we model the latent state of association for each SNP. For our future work, we intend to implement some Markovian structure on the prior distribution to model the dependency among the SNPs and investigate if there is any improvement on the power for detection of association.

One big assumption for this BPM approach is that it assumes all the SNPs within each risk group have same effect-sizes. We investigated the performance of our proposed approach through simulation studies when this assumption is violated (Model 5). In our simulation studies, the proposed approach performed quite well as compared to BEAM and LKM even when the SNPs had very di erent effect sizes.

One limitation of the current version of the BPM approach is that the update of ${\mathcal{A}}_j$ is realized conditionally on ${\mathcal{A}}_{(-j)}$ for a locus j = 1, 2, . . . , p. Given that the space being explored is huge, the sampler is not very computationally efficient in exploring the entire model space. BPM was also found to be somewhat sensitive to starting parameter β for the real data analysis. We intend to implement Block-Gibbs sampler and simulated annealing strategies for better exploration of the model space. We have developed a C++ program for implementation of our BPM approach. Although potentially this approach could be applied to a large set of SNPs, the current algorithm is more suitable for gene-based association analysis.