Abstract
Purpose
The local specific absorption rate (SAR) is critical to the safety of radio frequency transmit coils. A statistical simulation approach is introduced to address the local SAR variability related to tissue property and geometric variations.
Methods
The local SAR is modeled as the output of a nonlinear transformation with factors that may affect its value being treated as random input variables. Instead of using the Monte Carlo method with a large number of sample points, the unscented transform is applied with a small set of deterministic sample points. A sensitivity analysis is further performed to determine the significance of each input variable. Electromagnetic simulations are carried out by the finite-difference time-domain method implemented on graphic processing unit.
Results
The local SAR variability of a 7 Tesla square loop coil for spine imaging and a 16-element brain imaging array as the result of tissue property and geometric changes were examined respectively. SAR limits were determined based on their means and standard deviations.
Conclusion
The proposed approach is efficient and general for the study of local SAR variability.
Keywords: specific absorption rate, statistical study, validation
INTRODUCTION
The specific absorption rate (SAR) is critical to the safety of radio frequency (RF) transmit coils (1–12). Its evaluation is typically performed by full-wave numerical simulations with available human models that may represent the subject group of interest ((1,13–15)). Because the human anatomy can vary significantly (16,17), the SAR also exhibits a certain degree of subject dependency. Besides, different subject positions and tissue properties may affect its value as well (8,9). Therefore, a safety margin is required to prevent potential overheating of subjects who are different from the numerical models in simulations (9,11).
The SAR variation has been investigated by different research groups in recent years. Tian et al computed the local SAR of a 3 Tesla (T) and a 4T 16-rung unshielded birdcage coil by using six large, medium and small head models that were obtained by scaling the Hugo model (10). Shajan et al considered three scaled head models with longitudinal shifts in the study of their 9.4T 16-channel transmit array (9). It was reported that the 10-g local SAR varies by less than 10%. In the study of a 7T 16-rung shielded high-pass birdcage coil by Wolf et al, longitudinal shift was found to decrease the local SAR by 22%. At the same time, transversal shift affects the local SAR by ±14% (8). de Greef et al studied the local SAR variation of a 7T 8-channel brain imaging transmit array by using six different human models (11). A safety margin of 1.4 was found appropriate to cover the worst-case scenario in their study. Ipek et al studied the local SAR variation of a 7T eight-channel prostate imaging transmit array by using four different human models (12). It was found that the intersubject variability is large enough to invalidate the use of generic human models. Murbach et al (18) thoroughly studied the SAR variation of a 1.5T birdcage coil in different human body models, at different positions, and with different tissue properties. The local SAR variation of 7T brain imaging coils caused by position changes was investigated in (19).
Because the variations of factors that may affect the SAR are random in nature, it is more appropriate to study the SAR in a statistical manner. In this way, the SAR can be considered as the output of a nonlinear transformation with multiple random input variables. A meaningful SAR limit can be established once its mean and standard deviation are known. Although different human models and subject positions have been considered in the aforementioned studies, SAR statistics, especially the standard deviation, have not been established and the worst-case scenario has no statistical meanings. In fact, conventional statistical simulation methods such as the Monte Carlo require a large number of random human models as its sample points (20). Even if these models are available, their full-wave simulations can be quite time-consuming. Thus it is imperative to develop a statistical simulation procedure to address the SAR variability issue efficiently.
The approach explored here applies the unscented transform for SAR variability with respect to the probability distributions of multiple random input variables (21–24). Instead of using a large number of random sample points, it only requires a few deterministic sample points to ensure good numerical accuracy. Besides sample point reduction, this method may also ease the difficulty of constructing a large number of human models that satisfy the statistical distributions of anatomical features.
METHODS
Unscented Transform
Details of the unscented transform can be found in literatures (21–24). It is briefly introduced here for the sake of completeness. Consider at first the SAR as a nonlinear transformation of one input variable x with mean μX. The nonlinear transformation can be written in terms of a zero-mean univariate random variable U = X − μX as
| [1] |
The mean and standard deviation of y can be computed by using N so-called sigma points (u1 ··· uN) with non-negative weights (w1 ··· wN) as follows
| [2] |
| [3] |
These sigma points and weights are determined by matching the first 2N central moments with those of U. As a result, only three sigma points, , 0, with weights 1/6, 2/3, 1/6, where σX is the standard deviation of input variable x, are required to get an approximation that is second-order accurate (23).
The extension of the unscented transform to multivariate case is straightforward. Suppose the SAR is a nonlinear transformation of a p-dimensional multivariate random vector, N p-dimensional sigma points can be used with appropriate weights to calculate its mean and standard deviation. In a p-dimensional parametric space where each axis is normalized by the standard deviation of the corresponding input variable, we can choose 2p points in a cube and 2p points on the axes together with the origin, i.e., N = 2p + 2p + 1. The location and weights of the first group of points are given by
| [4] |
The location and weights of the second group of points are given by
| [5] |
The weight of the origin is given by w = (2p + 4)/(p + 2)2 (23). It should be noted that the locations of these sample points are deterministic rather than random.
The sensitivity of the SAR can be studied by examining its marginal standard deviation with respect to each input variable (25), which is treated by the unscented transform as individual univariate cases (23). More specifically, three sigma points are applied with respect to the mean and standard deviation of each input variable (see Table 2), while other input variables are set at their mean values. For p input variables, this requires 3p additional numerical simulations, which is an insignificant overhead in general.
Table 2.
Normalized Sigma Points and Their Weights
| No. of sigma points | Normalized Sigma points | Weight | ||
|---|---|---|---|---|
| One variable | 2 |
|
1/6 | |
| 1 | 0 | 2/3 | ||
| Two variables | 4 | ( ) | 1/16 | |
| 4 | (±2, 0), (0, ±2) | 1/16 | ||
| 1 | 0 | 1/2 | ||
| Three variables | 8 |
|
9/200 | |
| 6 |
|
1/25 | ||
| 1 | 0 | 2/5 | ||
| Four variables | 16 |
|
1/36 | |
| 8 |
|
1/36 | ||
| 1 | 0 | 1/3 | ||
| Five variables | 32 |
|
25/1568 | |
| 10 |
|
1/49 | ||
| 1 | 0 | 2/7 | ||
| Six variables | 64 |
|
9/1024 | |
| 12 |
|
1/64 | ||
| 1 | 0 | 1/4 |
Human Models
In the first example, the Hugo model with a 5-mm isotropic spatial resolution and truncated around the waist was applied. In the second example, the Duke model with a 3-mm isotropic spatial resolution and truncated around the chest was applied as the template for model transformations. Tissue properties were specified according to literatures (26). Six geometric variables were considered for demonstration purposes. They include head breadth [mean = 154 mm; standard deviation (SD) = 6 mm], head length (mean = 199 mm; SD = 7 mm), shift along the z-direction (mean = 0 mm; SD = 15 mm), rotations around the x- (left-to-right; mean = 0°; SD = 5°), the y-(posterior-to-anterior, mean = 0°; SD = 5°), and the z-direction (mean = 0°, SD = 5°). The statistics of the head length and breadth correspond to those of Caucasians (17). When z = 0, the midpoint between the innermost points of the eyes aligns with the coil center in the longitudinal direction. The geometric center of the standard model on the transverse plane, which corresponds to the origin of the p-dimensional parametric space, aligns with that of the coil.
Generating the sigma points that correspond to different head breadths and lengths were accomplished by scaling the head in the x- and y-direction. The same spatial resolution was maintained by projecting pixels in the scaled head model back to the template model. Rotations along the three axes were performed by multiplying the coordinates of all voxels of the Duke template above the throat with the following three basic rotation matrices
| [6] |
When rotating around the z-direction, the pivot-axis went through the geometric center of the anatomy on the slice that cuts through the throat. When rotating around the x- and y-direction, the pivot-axis went through the furthest point in the direction toward which the head leans. The base of the rotated part was swept incrementally to fill the gap between the rotated and the stationary parts. The three basic rotation matrices were combined as R = Rx(θx)Ry(θy)Rz(θz) for arbitrary rotations.
Electromagnetic Simulation
The FDTD method was implemented on Nvidia Tesla C2050 GPU with 3GB of global memory and 448 processing units (1,13). A 12-fold speed-up was obtained comparing with CPU-based implementation. In all simulations, 10 layers of perfectly-matched layer (PML) were applied as the absorbing boundary with a 10-cell buffer zone from each side of the numerical model. Each coil was tuned to 297 MHz at first by adjusting its capacitor values until the input reactance at the feeding point became zero. Subsequent simulations were performed by using a 1-Volt voltage source with a 50-Ohm internal resistance. The number of time steps was long enough for the FDTD to converge to a steady state. The 10-g averaged local SAR was calculated and normalized by the total RF power deposition in the corresponding human model. It was found that changing the source internal resistance will affect the convergence rate of the FDTD, not the local SAR results normalized by power deposition.
RESULTS
Local SAR of a 7T Spine Coil
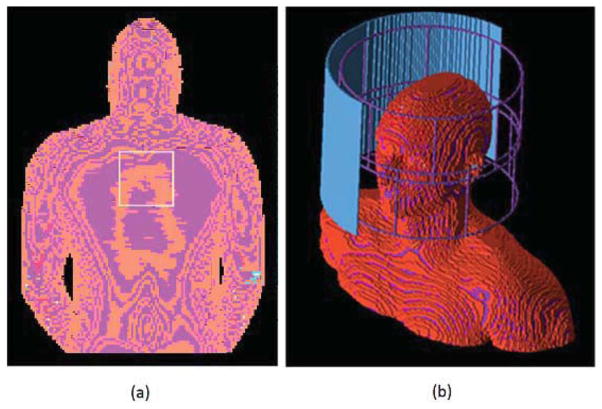
The variability of the 10-g local SAR of a 10-cm square loop coil for spine imaging with respect to tissue property changes was studied. The coil was fixed at 2-cm away from the Hugo model and numerically tuned with three capacitors (Fig. 1). The entire simulation domain consisted of 230 × 155 × 210 voxels. All tissues of the Hugo model were included except for the nail and the testicle. The average values of the dielectric property and density of each tissue were determined according to (26). A 10% standard deviation was introduced to the dielectric properties and densities of 16 tissues that are in a close range to the coil. These include blood, blood vessel, body fluid, cancellous bone, cortical bone, bone marrow, fat, glands, heart, ligament, inner lung, outer lung, lymph, muscle, spine, and skin. Properties of tissues that are far away from the coil, e.g., small intestine and gray matter, have constant values in all simulations. Thus the statistical model consisted of 48 random input variables. The local SAR variability is defined as the SD-to-mean ratio.
FIG. 1.
a: The square loop spine coil with the truncated Hugo model. b: The 16-channel transmit array with the truncated Duke model.
A sensitivity analysis was performed at first to study the impact of each input variable. The most significant ones are listed in Table 1. Next, the unscented transform was applied to study the variability of the 10-g local SAR by progressively adding more significant input variables into multivariate models. In the first batch of simulations, only the most significant variable, i.e., muscle density, was included in the statistical model. In the second batch of simulations, the first two most significant random variables, i.e., muscle density and conductivity, were included. This iterative procedure converged after the first four most significant input variables are included in the multivariate model. (Table 1; Fig. 2a). The mean and SD of the 10-g local SAR was found to be 1.38 and 0.11 Watt/kg/Watt, respectively.
Table 1.
The Most Significant Input Variables as the Result of Sensitivity Analysis
| Muscle density | Muscle conductivity | Fat density | Skin density | Muscle permittivity | Skin conductivity | |
|---|---|---|---|---|---|---|
| Marginal variability (%) | 4.8 | 4.6 | 2.6 | 2.3 | 1.8 | 1.4 |
| Multivariate variability (%) | 4.8 | 6.7 | 7.3 | 7.7 | 7.8 | 7.9 |
| Reference (%) | 5.0 | 6.9 | 7.2 | (N/A) | (N/A) | (N/A) |
(Top row) Tissue properties ranked by their significance to the 10-g local SAR of the spine coil. (Second row) Marginal variability of the 10-g local SAR with respect to the most significant variables. (Third row) The variability of the 10-g local SAR when different numbers of most significant input variables are included in multivariate models. For instance, the third column corresponds to the variability when the multivariate model consisted of the first three most significant input variables. The fourth column corresponds to the variability when the multivariate model consisted of the first four most significant input variables. (Fourth row) The reference variability obtained by the Monte Carlo method with 1500 sample points in each case.
FIG. 2.
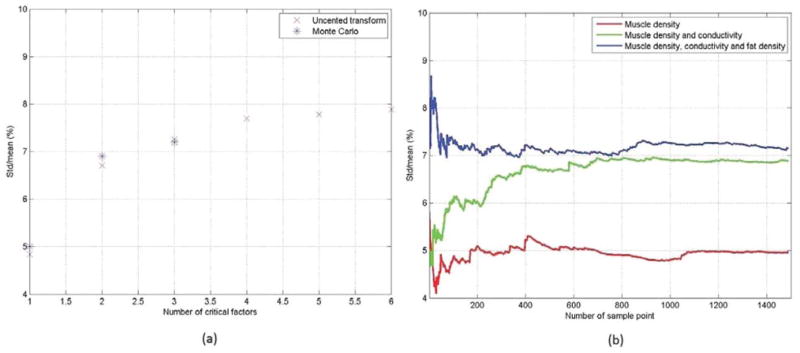
a: The variability of the 10-g local SAR of the spine coil versus the number of significant input variables in the statistical model computed by the unscented transform and the Monte Carlo method with 1500 sample points, respectively. b: The convergence history of the Monte Carlo method.
The Monte Carlo method was also applied to examine the local SAR variability with the first one, two, and three most significant input variables included in statistical models. A total of 1500 sample points were applied in each case to obtain the reference solution. The results are shown in Figure 2a and the convergence history, i.e., the variability versus the number of Monte Carlo sample points, is plotted in Figure 2b.
Local SAR of a 7T 16-Channel Transmit Array
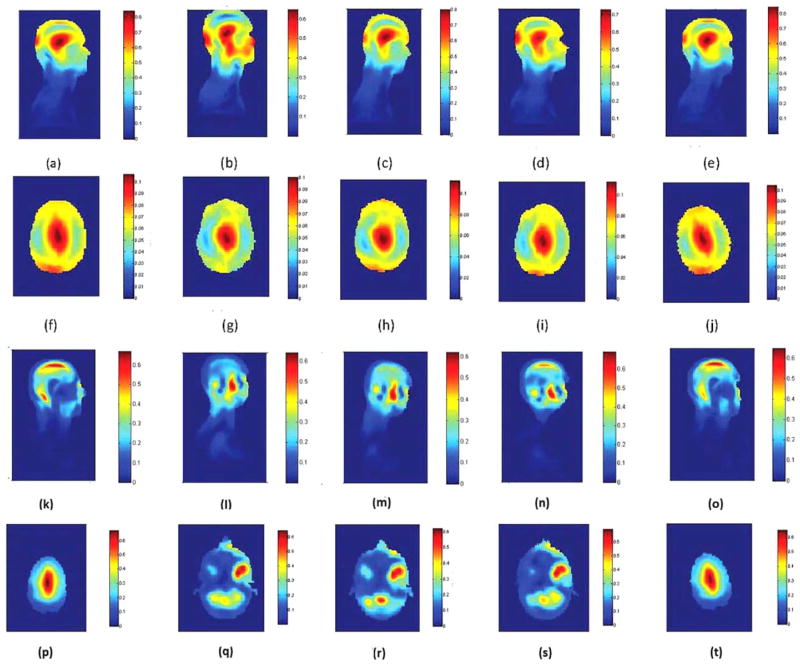
The 10-g local SAR of a 16-channel shielded transmit array caused by six geometric variations was examined. The array has two rows of loop coils (Fig. 1b). The inner diameter of this array is 28.75 cm and the height is 25 cm. The entire simulation domain for each model consisted of 230 × 155 × 210 voxels. The simulated electromagnetic fields were combined with 45° progressive phase shift to achieve a circularly polarized transverse magnetic field. Some of the combined B1+ and local SAR maps are illustrated in Figure 3. A sensitivity analysis was performed and the geometric variations ranked by their significance are longitudinal shift, head breadth, head length, rotation along y-axis, rotation along z-axis and rotation along x-axis. The mean and standard deviation of the 10-g local SAR were determined by using 77 sigma points (for six input variables). They were 0.68 and 0.07 Watt/kg/Watt, respectively.
FIG. 3.
B1+ field map in (a,f) the standard human model, (b,g) the human model shifted in z-direction by 42.4 mm, (c,h) the human model rotated alone x-axis by 14.1°, (d,i) the human model rotated alone y-axis by 14.1°, (e,j) the human model rotated alone z-axis by 14.1°. The sagittal views (a–e) cutting through the same symmetric plane of the human body. The axial views (f–j) are adjusted so that they cut through the eyes. The color bar show the B1+ magnitude as the result of 1 Watt RF power deposited in the human model. The unit is μT. 10-g averaged local SAR map in (k,p) the standard human model, (l,q) the human model shifted in z-direction by 42.4 mm, (m,r) the human model rotated alone x-axis by 14.1°, (n,s) the human model rotated alone y-axis by 14.1°, (o,t) the human model rotated alone z-axis by 14.1°. The sagittal views (k–o) and axial views (p–t) were adjusted so that they all cut through the peak local SAR location. The color bar show the 10-g averaged local SAR as the result of 1 Watt RF power deposited in the human model. The unit is Watt/kg/Watt.
DISCUSSIONS
Safety Margin
A meaningful safety margin can be determined once SAR statistics are available. In the first example, setting the 10-g local SAR limit to be three-sigma above its mean, i.e., 1.71 Watt/kg/Watt, can cover 93.3% of the cases. Setting it to be six-sigma above its mean, i.e., 2.04 Watt/kg/Watt, can cover nearly all cases. In the 16-channel transmit array example, the 10-g local SAR limit can be six-sigma above its mean, i.e., 1.1 Watt/kg/Watt, to cover the worst-case scenario of all situations being examined. Without knowing SAR statistics, the safety margin may be either overestimated or underestimated. Both will result in nonoptimal use of RF coils.
Sample Point Reduction
The first example demonstrates the accuracy and efficiency of the unscented transform. The local SAR variability calculated by the unscented transform with the first one, two, and three most significant input variables are nearly identical to those calculated by the Monte Carlo method with 1500 random sample points (Table 1; Fig. 2). The convergence of the Monte Carlo method appears to be slow and nonsmooth, which makes the use of a large number sample points necessary even if only one input variable is examined. This can be quite inefficient for sensitivity analysis. The practical sample point reduction ratio depends on how many random input variables are included in the statistical model and how confident one feels about the accuracy of the Monte Carlo method.
Sensitivity Analysis
The sensitivity analysis is especially useful in RF safety studies. First of all, it can reduce the computational complexity of statistical simulations. As demonstrated in the first example, input variables can be added one by one according to their significance in multivariate statistical models until the SAR variability converges. If all input variables are considered together, the statistical model may become too complicated to handle. Secondly, it provides a practical means of reducing the local SAR variability, and, therefore, improving the safety by decreasing the SAR margin. In the second example, the local SAR of the 16-channel array is most sensitive to longitudinal head shift, which may be understood because a virtual ground needs to be formed on the symmetric plane of the array in the longitudinal direction, and least sensitive to rotations, which may be understood because the head is approximately a sphere. Thus the local SAR variability can be reduced if the longitudinal head shift is restricted. On the contrary, using fixation devices to restrict head rotations appears to be least effective because the variations of anatomical features, which are difficult to control, have a more significant impact on local SAR variability.
What Should Be Considered as Random Input Variables?
This study provides a general framework of using the unscented transform for SAR variability studies. Which factor should be included in the statistical model is problem dependent. Naturally all physical and physiological parameters exhibit some degree of randomness. A brute force approach would be performing sensitivity analysis to all imaginable parameters and include them one by one in multivariate statistical models. Alternatively, several parameters can be excluded by physical intuitions. For instance, the properties of the brain and small intestine were assumed constant in the first example because they are far away from the spine coil. Subject positions were not treated as random variables because they are fixed when subjects lying on a spine coil. In the second example, the longitudinal head shift, which is the most significant factor, may also be excluded from the statistical model if it can be restricted. It is a good strategy in general to exclude parameters that will obviously not affect the SAR from the statistical model and perform sensitivity analysis to questionable ones.
The unscented transform is purely mathematical. The input variables are not limited to those presented in this study. For instance, the shape of the skull and the fat content of the human head, which may have a more significant impact on the local SAR, can be studied in the same manner. They were not included in this study due to the lack of their parameterized models and statistics. At the same time, geometric and tissue property variations can be studied together because they are uncorrelated. More research will be performed in the future to demonstrate the advantages of the proposed method in these cases.
CONCLUSIONS
A statistical simulation procedure based on the unscented transform is presented. Instead of using a large number of random sample points, a few weighted deterministic sigma points are applied for accurate SAR statistics. Sensitivity analysis is performed to identify significant factors to be included in multivariate statistical models. As a result, a meaningful safety margin can be established efficiently and RF coil safety may be improved by possible elimination of significant input variables. This procedure is general and factors that may affect the SAR can be examined in this framework provided that their statistics are available.
References
- 1.Jin JM. Electromagnetic analysis and design in magnetic resonance imaging. Boca Raton, FL: CRC Press; 1999. [Google Scholar]
- 2.Collins CM, Li S, Smith MB. SAR and B1 field distributions in a heterogeneous human head model within a birdcage coil. Magn Reson Med. 1998;40:847–856. doi: 10.1002/mrm.1910400610. [DOI] [PubMed] [Google Scholar]
- 3.Vaughan JT, Garwood M, Collins CM, Liu W, DelaBarre L, Adriany G, Andersen P. 7T vs. 4T: RF power, homogeneity, and signal-to-noise comparison in head images. Magn Reson Med. 2001;46:24–30. doi: 10.1002/mrm.1156. [DOI] [PubMed] [Google Scholar]
- 4.Ibrahim TS, Lee R, Baertlein BA, Robitaille PML. B1 field homogeneity and SAR calculations for the birdcage coil. Phys Med Biol. 2001;46:609. doi: 10.1088/0031-9155/46/2/324. [DOI] [PubMed] [Google Scholar]
- 5.Ingmar G, Homann H, Biederer S, Börnert P, Nehrke K, Vernickel P, Mens G, Harvey P, Katscher U. A specific absorption rate prediction concept for parallel transmission MR. Magn Reson Med. 2012;68:1664–1674. doi: 10.1002/mrm.24138. [DOI] [PubMed] [Google Scholar]
- 6.Zhu Y, Alon L, Deniz CM, Brown R, Sodickson DK. System and SAR characterization in parallel RF transmission. Magn Reson Med. 2012;67:1367–1378. doi: 10.1002/mrm.23126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bastien G, Gebhardt M, Cauley S, Adalsteinsson E, Wald LL. Local specific absorption rate (SAR), global SAR, transmitter power, and excitation accuracy trade-offs in low flip-angle parallel transmit pulse design. Magn Reson Med. 2014;71:1446–1457. doi: 10.1002/mrm.24800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wolf S, Diehl D, Gebhardt M, Mallow J, Speck O. SAR simulations for high-field MRI: how much detail, effort, and accuracy is needed? Magn Reson Med. 2013;69:1157–1168. doi: 10.1002/mrm.24329. [DOI] [PubMed] [Google Scholar]
- 9.Shajan G, Kozlov M, Hoffmann J, Turner R, Scheffler K, Pohmann R. A 16-channel dual-row transmit array in combination with a 31-element receive array for human brain imaging at 9.4 T. Magn Reson Med. 2014;71:870–879. doi: 10.1002/mrm.24726. [DOI] [PubMed] [Google Scholar]
- 10.Tian J, Snyder CJ, Delabarre1 L, Akgun C, Liu W, Collins CM, Gopinath A, Vaughan JT. Effect of head size to B1, SNR and SAR. Proceedings of the 15th Annual Meeting of ISMRM; Berlin, Germany. 2007; Abstract 1011. [Google Scholar]
- 11.de Greef M, Ipek O, Raaijmakers AJE, Crezee J, van den Berg CAT. Specific absorption rate intersubject variability in 7T parallel transmit MRI of the head. Magn Reson Med. 2013;69:1476–1485. doi: 10.1002/mrm.24378. [DOI] [PubMed] [Google Scholar]
- 12.Ipek Ö, Raaijmakers AJ, Lagendijk JL, Luijten PR, can der Berg CAT. Intersubject local SAR variation for 7T prostate MR imaging with an eight-channel single-side adapted dipole antenna array. Magn Reson Med. 2014;71:1559–1567. doi: 10.1002/mrm.24794. [DOI] [PubMed] [Google Scholar]
- 13.Taflove A, Hagness SC. Computational electrodynamics: the finite-difference time-domain method. 3. Boston, MA: Artech House; 2003. [Google Scholar]
- 14.Christ A, Kainz W, Hahn EG, et al. The virtual family—development of surface-based anatomical models of two adults and two children for dosimetric simulations. Phys Med Biol. 2010;55:N23–N38. doi: 10.1088/0031-9155/55/2/N01. [DOI] [PubMed] [Google Scholar]
- 15.Ackerman MJ. The visible human project. Proc IEEE. 1998;86:504– 511. [Google Scholar]
- 16.Tilley AR Associates HD. The measure of man and woman: human factors in design. New York: John Wiley & Sons; 2002. [Google Scholar]
- 17.Ball R, Shu C, Xi P. A comparison between Chinese and Caucasian head shapes. Appl Ergon. 2010;41:832–839. doi: 10.1016/j.apergo.2010.02.002. [DOI] [PubMed] [Google Scholar]
- 18.Murbach M, Neufeld E, Kainz W, Pruessmann KP, Kuster N. Whole-body and local RF absorption in human models as a function of anatomy and position within 1.5T MR body coil. Magn Reson Med. 2014;71:839–845. doi: 10.1002/mrm.24690. [DOI] [PubMed] [Google Scholar]
- 19.Wolf S, Diehl D, Gebhardt M, Mallow J, Speck O. SAR simulations for high-field MRI: how much detail, effort, and accuracy is needed? Magn Reson Med. 2013;69:1157–1168. doi: 10.1002/mrm.24329. [DOI] [PubMed] [Google Scholar]
- 20.Rubinstein RY, Kroese DP. Wiley series in probability and statistics. New York: John Wiley & Sons; 2007. Simulation and the Monte Carlo method. [Google Scholar]
- 21.Julier SJ, Uhlmann JK. Unscented filtering and nonlinear estimation. Proc IEEE. 2004;92:401–422. [Google Scholar]
- 22.Steiner G, Watzenig D, Magele C, Baumgartner U. Statistical robust design using the unscented transformation. COMPEL: The International Journal for Computation and Mathematics in Electrical and Electronic Engineering. 2005;24:606–619. [Google Scholar]
- 23.de Menezes LRAX, Ajayi A, Christopoulos C, Sewell P, Borges CA. Efficient computation of stochastic electromagnetic problems using unscented transforms. IET Sci Meas Technol. 2008;2:88–95. [Google Scholar]
- 24.dos Santos I, Haemmerich D, Schutt D, Ferreira da Rocha A, Menezes LR. Probabilistic finite element analysis of radiofrequency liver ablation using the unscented transform. Phys Med Biol. 2009;54:627–640. doi: 10.1088/0031-9155/54/3/010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Saltelli A, Ratto M, Andres T, Campolongo F, Cariboni J, Gatelli D, Saisana M, Tarantola S. The primer. New York: John Wiley & Sons; 2008. Global sensitivity analysis. [Google Scholar]
- 26.Gabriel C. Tech Rep AL/OE-TR-1996-0037. San Antonio, TX: Brooks Air Force; 1996. Compilation of the dielectric properties of body tissues at RF and microwave frequencies. [Google Scholar]