United polarizable multipole water model for molecular mechanics simulation

Abstract

We report the development of a united AMOEBA (uAMOEBA) polarizable water model, which is computationally 3–5 times more efficient than the three-site AMOEBA03 model in molecular dynamics simulations while providing comparable accuracy for gas-phase and liquid properties. In this coarse-grained polarizable water model, both electrostatic (permanent and induced) and van der Waals representations have been reduced to a single site located at the oxygen atom. The permanent charge distribution is described via the molecular dipole and quadrupole moments and the many-body polarization via an isotropic molecular polarizability, all located at the oxygen center. Similarly, a single van der Waals interaction site is used for each water molecule. Hydrogen atoms are retained only for the purpose of defining local frames for the molecular multipole moments and intramolecular vibrational modes. The parameters have been derived based on a combination of ab initio quantum mechanical and experimental data set containing gas-phase cluster structures and energies, and liquid thermodynamic properties. For validation, additional properties including dimer interaction energy, liquid structures, self-diffusion coefficient, and shear viscosity have been evaluated. The results demonstrate good transferability from the gas to the liquid phase over a wide range of temperatures, and from nonpolar to polar environments, due to the presence of molecular polarizability. The water coordination, hydrogen-bonding structure, and dynamic properties given by uAMOEBA are similar to those derived from the all-atom AMOEBA03 model and experiments. Thus, the current model is an accurate and efficient alternative for modeling water.

INTRODUCTION

Water is an important solvent in living systems^1,2 and many industrial applications.^3–7 There are a number of molecular mechanics models, such as the three-site TIPS,⁸ TIP3P,⁹ SPC,¹⁰ and SPC/E,¹¹ the four-site TIP4P,⁹ TIP4P-Ew,¹² TIP4P/2005,¹³ and the five site ST2,¹⁴ TIP5P,¹⁵ and TIP5P-E,¹⁶ that are commonly used in molecular simulation of water. These models use fixed atomic partial charges, with electrostatic energy evaluated in pairwise-additive fashion. Some models incorporate explicit electronic polarization to allow the charge distribution to respond to electrostatic environment and to further improve the reproduction of many water properties; these include Dang-Chang,¹⁷ Thole-Type-Model (TTM),^18–22 SWM-4DP,²³ DPP2,²⁴ and AMOEBA03.²⁵ The AMOEBA03 water model²⁶ was developed with a focus on capturing molecular polarizability, electrostatic potential, as well as the interaction energy from gas to condensed-phase, by utilizing permanent atomic monopole, dipole, and quadrupole moments and mutual atomic dipole-dipole induction.^27,28

The inexpensive AMOEBA (iAMOEBA) model was introduced recently as a way to achieve improved computational efficiency.²⁹ In this model, the induced atomic dipoles are determined directly from the permanent multipole electric fields without further interactions between induced dipoles. Thus, it captures some 3-body effects in polarization while reducing the computational cost relative to the fully self-consistent AMOEBA03 water model by a factor of 1.5-6. An alternative to improve the computational efficiency, without sacrificing the many-body effect, is to reduce the number of interaction sites within the model. Water models with single dipole moment representation have been developed since the 1980s.³⁰ Ichiye and her coworkers^31,32 introduced the “soft sticky dipole potential” for liquid water, with one spherical repulsive potential, a short-range tetrahedral “sticky” potential, and a point dipole at the center of mass. Compared with TIP3P and TIP4P models, it produced similar liquid water properties but with up to one order of magnitude speed-up. Later in 2010, the “soft-sticky dipole-quadrupole-octupole” water model was presented by the same group. It was suggested that the addition of octupole moments improved the dielectric constant (75 at 298 K).³³ Carnie and Patey reported a polarizable dipole-tetrahedral quadrupole water model and a self-consistent mean field theory was applied to account for molecular polarizability.³⁴ Later, Kusalik and Patey added the octupole moments to their water model discussed above and observed strong preferential solvation of anions at infinite dilution, suggesting an important role of octupole moments in ion solvation.³⁵ Jonsson et al.³⁶ introduced a one-site water potential based on electrostatic, induction, dispersion, and short-range repulsion interactions. Also, multipoles up to quadrupole moment for polarizability and up to hexadecapoles for permanent electrostatics were included. Previously, we have also explored one-site non-polarizable models, based on permanent molecular multipoles and the Gay-Berne potential, for molecular liquids including water.^37,38 Molinero and Moore proposed a water model (mM) that further omitted long-range intermolecular interactions. This model generally reproduces the bulk properties of liquid water—except for the self-diffusion coefficient, which is too fast.³⁹ The faster diffusion rate is likely due to the lack of long-ranged electrostatic forces in the model.

In this paper, we describe a new (nonbonded) one-site polarizable water model, united AMOEBA (uAMOEBA). This model removes two nonbonded interaction sites on H atoms to speed up the energy and force calculations by a factor of 3 to 5 times over the previous three-site AMOEBA03 model in molecular dynamics when particle-mesh Ewald (PME) is used to treat long-range electrostatics.⁴⁰ Importantly, the full many-body polarization effects are retained via mutual induction of molecular dipoles. In this model, the permanent molecular multipole (dipole and quadrupole) moments, isotropic molecular dipole polarizability, and a single van der Waals (vdW) interaction site are placed on oxygen. The remaining hydrogen atoms only carry atomic masses to define the local coordinate frames and the intramolecular geometry. For computational efficiency, uAMOEBA does not contain any octupole moment, which is a potential limitation of this model. The hydrogen atoms experience forces due to valence (bond, angle, and Urey-Bradley) interactions. In addition, the torques experienced by the molecular dipole and quadrupole moments on oxygen are translated into forces on the hydrogen atoms in the same way as all-atom AMOEBA03.²⁵ The use of a single scalar polarizability is well justified, as the three components of water molecular polarizability (1.528, 1.415, 1.468) are indeed similar in magnitude. We demonstrate the accuracy of uAMOEBA water model by evaluating a range of gas-phase and liquid properties and comparing the results with the existing AMOEBA03/iAMOEBA models and experimental data. The current work aims to extend beyond the previous one-site water models by systematically examining gas-phase clusters of increasing size and important thermodynamic properties at a wide range of temperatures. In addition, the uAMOEBA model is applied to study interactions between water and other common organic molecules (modeled by all-atom AMOEBA03⁴¹) to investigate its transferability.

METHODOLOGY

The AMOEBA03 polarizable force field

The previously published AMOEBA03 functional form⁴² has been applied in this study, except that each water molecule has a single electrostatic and vdW interaction site. The AMOEBA03 potential energy is written as a sum of valence and nonbonded contributions,

$${\displaystyle E=E_{\mathrm{angle}}+E_{\mathit{bond}}+E_{b\theta }+E_{\mathrm{vdw}}+E_{\mathrm{ele}}^{\mathit{perm}}+E_{\mathrm{ele}}^{\mathit{ind}},}$$ (1)

$${\displaystyle E_{ij}^{\mathit{buff}}={\epsilon }_{ij}{\left(\frac{1+\delta }{{\rho }_{ij}+\delta }\right)}^{n-m}\left(\frac{1+\gamma }{{\rho }_{ij}^m+\gamma }-2\right).}$$ (2)

The intramolecular valence energy is described by the first three terms. The vdW interaction is described by the buffered-14-7 vdW formula (Eq. (2)). ε_ij is the potential well depth and ρ_ij is the ratio between the actual separation of i-j sites and the minimum energy distance, described as ${\rho }_{ij}=R_{ij}/R_{ij}^0$.⁴³ The electrostatic potential energy is evaluated from the permanent molecular dipole and quadrupole moments (Eq. (3)) and molecular isotropic dipole polarizability (Eq. (4)). All electrostatic energy and force terms, including polarization, are calculated using the PME approach,^40,44

$${\displaystyle E_{\mathit{ele}}^{\mathit{perm}}\left(ij\right)=M_i{}^T{T}_{ij}{M}_j,}$$ (3)

$${\displaystyle {\mu }_{i,\alpha }^{\mathit{ind}}={\alpha }_i\left(\sum _{\left\{j\right\}}{T}_{\alpha }^{ij}{M}_j+\sum _{\left\{\stackrel{\prime }{j}\right\}}{T}_{\alpha \beta }^{i{j}^{\prime }}{\mu }_{j^{\prime },\beta }^{\mathit{ind}}\right)\text{for}\alpha ,\beta =1,2,3.}$$ (4)

In Eq. (4), the first term represents the dipole induced at site i by the electric field generated from the permanent multipoles of the neighboring molecules. The second term represents the contributions due to the field of induced dipoles on all other sites. In order to avoid the polarization catastrophe, the polarization is modified at short-range with the Thole damping scheme.⁴⁵

Parameterization data set

The data utilized for fitting the parameters were composed of a combination of experimentally determined liquid properties as well as high-level ab initio quantum mechanics (QM)-derived properties. The liquid properties considered were density, enthalpy of vaporization, isothermal compressibility, isobaric heat capacity, thermal expansion coefficient, and dielectric constant. The temperature and pressure combinations were: 1 atm at temperatures ranging from 249 K to 373 K (32 total) and 298 K at pressures from 1 kbar to 4 kbar (4 total).

The ab initio QM reference data included properties for systems ranging in size from the monomer to clusters of 23 water molecules. For the monomer, the molecular dipole, quadrupole, polarizability, vibration, and geometry were considered. The ab initio QM interaction energy and geometries for the ground state dimer, Smith dimer set (10 total),⁴⁶ trimer, tetramer, pentamer, eight hexamers,⁴⁷ two octamers,⁴⁸ five 11-mers,⁴⁹ five 16-mers, two 17-mers, and four 20-mers^50,51 were utilized for calibration. In previous work,²⁹ over 42 000 cluster (ranging from 2 to 22 water molecules) geometries were obtained from AMOEBA03 simulations of liquid water for temperatures ranging from 249 K to 373 K. Energy and gradients for the clusters were determined via RI-MP2^52,53/heavy-aug-cc-pVTZ⁵⁴ as implemented in Q-Chem 4.0.⁵⁵ This large compilation of theoretical data was included in the fitting of the model parameters.

Parameter optimization

We applied ForceBalance, an automatic optimization method, to parameterize the uAMOEBA water model using the expanded data set described above. ForceBalance supports many different optimization algorithms, and the calculation in this work was carried out using the trust-radius Newton-Raphson (or Levenberg-Marquardt^56,57) algorithm with an adaptive trust radius.^58,59 This algorithm requires the first and second derivatives of the objective function in the parameter space, which we derive from the first derivatives of the simulated properties using the Gauss-Newton approximation.

A major challenge in force field parameterization is the significant statistical noise in the objective function from the sampling of properties to be matched to experiment. The parametric derivatives are challenging to evaluate because numerical differentiation requires running multiple simulations and evaluating small differences between statistically noisy estimates. ForceBalance uses thermodynamic fluctuation formulas to calculate accurate parametric derivatives of simulated properties without running expensive multiple simulations.^60,61 For instance, the ensemble average of a generic observable A that does not depend explicitly on the force field parameters (for example, the density or an order parameter) can be expressed as follows:

${\displaystyle {〈A〉}_{\lambda }=\frac{1}{Q\left(\lambda \right)}\int A(r,V)exp(-\beta (E(r,V;\lambda )+PV))drdV,}$${\displaystyle Q\left(\lambda \right)=\int exp(-\beta (E(r,V;\lambda )+PV))drdV,}$ (5)

where A is the observable, r a given molecular configuration in a periodic simulation cell, λ the force field parameter, E the potential energy, β ≡ (k_BT)⁻¹ the inverse temperature, k_B the Boltzmann constant, T the temperature, P the pressure, V the volume, Q the isothermal-isobaric partition function, and the angle brackets with a λ subscript represent an ensemble average in the thermodynamic ensemble of the force field parameterized by λ. In practice, this integral is evaluated numerically using molecular dynamics or Monte Carlo simulation in the NPT ensemble.

Since the expression for A depends on λ only through the potential energy E, we can differentiate Eq. (5) analytically,

$${\displaystyle \frac{d}{d\lambda }{〈A〉}_{\lambda }=\frac{1}{Q\left(\lambda \right)}\int A(r,V)exp(-\beta (E(r,V;\lambda )+PV))\left(-\beta \frac{dE(r,V)}{d\lambda }\right)drdV-\frac{1}{Q{\left(\lambda \right)}^2}\frac{dQ}{d\lambda }\int A(r,V)exp(-\beta (E(r,V;\lambda )+PV))drdV=-\beta \left({〈A\frac{dE}{d\lambda }〉}_{\lambda }-{〈A〉}_{\lambda }{〈\frac{dE}{d\lambda }〉}_{\lambda }\right).}$$ (6)

The potential energy derivative $\frac{dE}{d\lambda }$ is evaluated by numer-ically differentiating the potential energies at the sampled structures. Eq. (6) provides a way to evaluate the parametric derivative of thermodynamic properties without running additional sampling simulations, though the derivative of any observable always manifests as a higher order correlation function and has a larger statistical error than the observable itself. This equation may be directly applied to obtain derivatives of ensemble-averaged observables with implicit parametric dependence through the thermodynamic ensemble, such as the density. Eq. (6) is easily extensible to obtain derivatives of observables with explicit parameter dependence, such as the enthalpy; derivatives for higher-order thermodynamic response properties such as the dielectric constant are obtained using the chain rule.²⁹ We omit the calculation of second parametric derivatives for reasons of computational cost and statistical noise, relying instead on the least-squares form of the objective function and the Gauss-Newton approximation to obtain the Hessian.

The problem of overfitting is treated by regularization via a penalty function, which corresponds to imposing a prior distribution of parameter probabilities in a Bayesian interpretation. The prior widths reflect the expected variations of the parameters during the optimization. We used a Gaussian prior distribution, corresponding to a parabolic penalty function in parameter space centered at the original AMOEBA03 parameter values with the chosen force constants. Since the various parameters have different physical meanings (e.g., vdW well depth, O–H bond length), each parameter type was assigned its own prior width.

We ran the optimization until fluctuations from numerical noise prevented further improvement. The calculation converged to within the statistical error after about 15 nonlinear iterations, though we performed several optimizations with different choices of weights for the reference data and prior widths before arriving at the final answer.

COMPUTATIONAL DETAILS

Parameterization calculations

ForceBalance carried out the condensed phase simulations in the optimization by interfacing with OpenMM 6.1,^62–64 a graphics processing unit (GPU)-accelerated molecular dynamics software package with an extensively validated implementation of AMOEBA03, which provides a speedup of an order of magnitude over the reference implementation in TINKER 6.3.⁶⁵ At each optimization step, the set of 36 simulations at different phase points (32 temperatures at 1.0 atm pressure plus 4 pressures at 298.15 K temperature) is performed simultaneously on multiple nodes in a GPU cluster; the Work Queue library^66–68 allows ForceBalance to act as a distributed computing server and coordinate many OpenMM simulations running on multiple compute nodes in different physical locations. Finally, the data from the finished simulations were analyzed using the multistate Bennett acceptance ratio (MBAR) estimator,^69,70 which allows each simulation to contribute to the estimated properties of all other simulations. This combination of methods allowed us to optimize the condensed phase properties very accurately. Due to the non-overlapping features of the simulation codes, we combined OpenMM 6.1 and TINKER 6.3 during the optimization to evaluate quantities for comparison with the ab initio and gas phase reference data, using OpenMM to evaluate the potential energies and forces, and TINKER to evaluate the binding energies and monomer properties. ForceBalance,⁷¹ TINKER,⁶⁵ OpenMM,⁶⁴ and Work Queue⁶⁸ are freely available on the web.

Validation calculations

The validation calculations were conducted using the TINKER 6.3 modeling package. PME summation was used to handle the electrostatic interactions (real-space cutoff at 7 Å) and the atom-based switching window was applied to restrict the vdW interactions with a cutoff of 12 Å. During the MD simulation of NPT ensembles, we utilized the Nose-Hoover algorithm to integrate the equation of motion and control pressure and temperature.⁷²

Diffusion

The diffusion coefficient is typically computed from the slope of the mean-square displacement as a function of time, averaged over the MD trajectories of individual particles,

$${\displaystyle D_{\mathit{PBC}}=\underset{t\to \infty }{lim}\frac{1}{6}\frac{d〈{\left|r\left(t\right)-r\left(0\right)\right|}^2〉}{dt}.}$$ (7)

Yeh and coworkers⁷³ showed that for a system of nearly 2000 water molecules in a cell with periodic boundary conditions (PBC), the diffusion coefficient could be underestimated by around 10%; correcting for such systematic errors is particularly crucial in comparisons of simulation to experiment when transport properties are used to assess interaction potentials.^74–76 A correction to the system-size dependence was proposed,

$${\displaystyle D_0=D_{\mathit{PBC}}+\frac{2.837\hspace{0.17em}297k_{B}T}{6\pi \eta L},}$$ (8)

where L is the length of the cubic simulation box, D_PBC is the diffusion coefficient calculated in the simulation, k_B the Boltzmann constant, T the absolute temperature, and η the shear viscosity.

To obtain the system-size independent diffusion coefficient D₀, we calculated the diffusion coefficients D_PBC under periodic boundary conditions with N = 216, 343, 512, 1000, 1600, and 2500 water molecules. The production time of the simulations is 6 ns (N ≤ 512), 5 ns (N = 1000, 1600), or 3 ns (N = 2500). In practice, each MD trajectory was divided into 500 ps blocks from which the water diffusion coefficient was evaluated. The final D_PBC was computed as the average over these blocks (TABLE SXI).⁸³ The size-independent diffusion coefficient D₀ was obtained by fitting a straight line to D_PBC vs. 1/L and extrapolating to 1/L = 0.

Viscosity

No significant system-size dependence of viscosity was observed in computer simulations of Lennard-Jones fluids.^77,78 Here, we used the slope of Eq. (8) and data from Table SXI⁸³ to obtain the average viscosity. To estimate the error bar for size-independent viscosity and self-diffusion coefficient, the size-dependent diffusion coefficient for each box size was computed from a randomly selected 500 ps block of trajectory. These diffusion coefficients for the 6 box sizes were then combined to compute the size-independent viscosity and diffusion coefficient according to Eq. (8). The above process was repeated for 16 times to calculate the standard error.

RESULTS AND DISCUSSION

Optimized parameters

The final parameters for the new uAMOEBA, AMOEBA03, and iAMOEBA models are compared in Table I. The first six rows contain the intramolecular parameters for uAMOEBA. The equilibrium bond length was set to 0.9499 Å, which is slightly shorter than the experimental value of 0.9572 Å.⁷⁹ The ideal bond angle parameter of 105.9° is reduced by 1°-2° from the iAMOEBA and AMOEBA03 values. The slightly increased value from the experimental gas-phase angle of 104.52° is necessary to reproduce the experimental liquid properties such as the dielectric constant^7,80,25 (Fig. 3). The three force constants for the valence terms were fit to reproduce the experimental gas-phase vibrational frequencies of the water monomer.⁸¹ The bond, angle, and the Urey-Bradley force constants for uAMOEBA are essentially unchanged from the iAMOEBA values.

TABLE I.

Parameters for uAMOEBA water model.

Parameter name	Units	uAMOEBA	AMOEBA0325	iAMOEBA29
O–H equilibrium bond length	Å	0.949 9	0.957 2	0.958 4
O–H bond force constant	kcal/mol Å−2	557.55	529.60	557.63
H–O–H equilibrium angle	deg	105.95	108.50	106.48
H–O–H angle force constant	kcal/mol Å−2	48.93	34.05	49.90
H–H Urey–Bradley length	Å	1.516 8	1.553 7	1.535 7
H–H Urey–Bradley force constant	kcal/mol Å−2	−9.74	38.25	−10.31
Oxygen vdW sigma	Å	3.755 3	3.405 0	3.645 3
Oxygen vdW epsilon	kcal/mol	0.142	0.110	0.197
Hydrogen vdW sigma	Å	…	2.655	…
Hydrogen vdW epsilon	kcal/mol	…	0.013 5	…
Hydrogen vdW reduction factor	none	…	0.91	…
Oxygen charge	e	…	−0.519 66	−0.594 02
Oxygen dipole Z-component	e bohr	0.708 89	0.142 79	0.088 48
Oxygen quadrupole XX-component	e bohr2	2.080 11	0.379 28	0.226 18
Oxygen quadrupole YY-component	e bohr2	−2.088 28	−0.418 09	−0.322 44
Oxygen quadrupole ZZ-component	e bohr2	0.008 17	0.038 81	0.096 26
Hydrogen charge	e	…	0.259 83	0.297 01
Hydrogen dipole X-component	e bohr	…	−0.038 59	−0.093 91
Hydrogen dipole Z-component	e bohr	…	−0.058 18	−0.125 60
Hydrogen quadrupole XX-component	e bohr2	…	−0.036 73	0.187 54
Hydrogen quadrupole YY-component	e bohr2	…	−0.107 39	0.021 74
Hydrogen quadrupole XZ-component	e bohr2	…	−0.002 03	−0.036 35
Hydrogen quadrupole ZZ-component	e bohr2	…	0.144 12	−0.209 28
Oxygen polarizability	Å3	1.720 9	0.837 0	0.806 4
Hydrogen polarizability	Å3	…	0.496 0	0.504 8
Polarization damping factor	Å−1	0.390	0.390	0.236

FIG. 3.

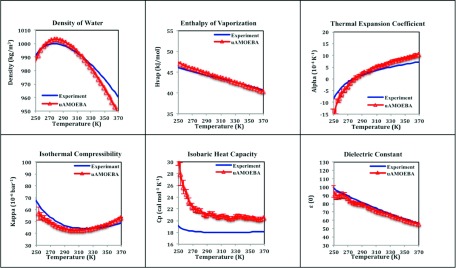
Thermodynamic properties of uAMOEBA liquid water as a function of temperature. Error bars indicate one standard error.

In uAMOEBA, the non-bonded interaction sites on the hydrogen atoms are removed. The repulsion-dispersion parameters (vdW radius and well-depth), permanent molecular multipole (dipole and quadrupole) moments, isotropic molecular dipole polarizability, and a single vdW interaction site are assigned to oxygen, which is slightly shifted from the molecular center of mass.

The next five rows contain the vdW parameters, followed by twelve rows containing the permanent multipole parameters. uAMOEBA has a larger vdW radius and well depth compared to AMOEBA03, which is largely due to the removal of vdW interaction sites from hydrogen. With no partial charges in this model, the electrostatic representation relies on high order molecular moments, which are significantly different from the atomic multipole moments of AMOEBA03 or iAMOEBA. In this case, it is more meaningful to compare molecular properties as described below.

Fitted gas phase water properties of uAMOEBA

Recently, Abascal and Vega pointed out that water multipole moments, specifically quadrupole moments, are crucial for capturing water properties from the vapour and liquid to solid phases accurately in multi-site models.⁸² In Table II, a comparison of the experimental, ab initio QM, and calculated molecular dipole moments, quadrupole moments, and polarizability of an isolated water molecule at equilibrium geometry is given. The uAMOEBA water monomer possesses a molecular dipole of 1.801 D, similar to that of the all-atom AMOEBA14 water model with revised parameters (1.808 D). The yy and zz components of the uAMOEBA molecular quadrupole moments are in better agreement with experimental values than the previous AMOEBA14 or iAMOEBA model. The isotropic molecular polarizability of the uAMOEBA model is noticeably greater than the AMOEBA14 or experimental value but slightly lower than that of iAMOEBA.

TABLE II.

Gas phase monomer properties of the uAMOEBA, AMOEBA14, and iAMOEBA models compared with experiment, evaluated at the energy-minimized geometry. The molecular multipole moments were evaluated at the center of mass of water molecule.

Property		Expt.	QMa	uAMOEBA	AMOEBA14b	iAMOEBA
Vibrational frequencies (cm−1)	Antisymmetric stretch	3755c	…	3754	3755	3755
	Symmetric stretch	3656c	…	3658	3656	3656
	Bend	1594c	…	1594	1594	1594
Dipole (D)	dz	1.855d	1.840	1.802	1.808	1.864
Quadrupole (D Å)	Qxx	2.63e	2.57	2.913	2.626	2.584
	Qyy	−2.50e	−2.42	−2.693	−2.178	−2.178
	Qzz	−0.13e	−0.14	−0.220	−0.045	−0.406
Polarizability (Å3)	αxx	1.528f	1.47	1.721	1.767	1.816
	αyy	1.415f	1.38	1.721	1.308	1.816
	αzz	1.468f	1.42	1.721	1.420	1.816

^aReference 89.

^bReference 84.

^cReference 88.

^dReference 85.

^eReference 86.

^fReference 87.

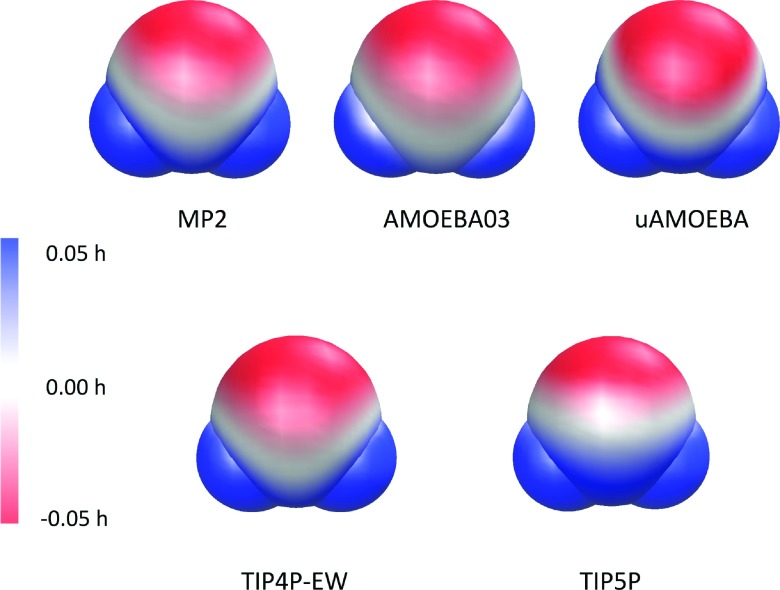
Figure 1 shows the plots of the electrostatic potential of different water models on the vdW surface. The water structure (O and H) used in calculations was based on the MP2/cc-pVTZ optimized geometry. In general, both uAMOEBA and AMOEBA03 compare well with the MP2/6-311++G(2d,2p) electrostatic potential (ESP). The similarity between the uAMOEBA and MP2 potentials around H is notable given that uAMOEBA has no electrostatic parameters on H. However, uAMOEBA is slightly more negative around the oxygen site; this is also possibly a consequence of the missing hydrogen sites, which leads to larger multipole moments on oxygen and stronger electrostatic interactions at short range. This may also explain the slightly over-structured radial distribution function (RDF) plot around the second solvation shell, due to the stronger electrostatic interaction. The fixed charge TIP4P-EW model displays a very reasonable ESP surface while the TIP5P model seems not negative enough around the O. Nonetheless, due to the lack of explicit polarization, both TIP4P-EW and TIP5P models give a water dipole moment of ∼2.3 D, about 30% higher than the experimental or uAMOEBA/AMOEBA03 value for a gas-phase water monomer (Table II).

FIG. 1.

Electrostatic potential plotted on the vdW surface, with blue representing 0.05 h and red −0.05 h. The MP2 result was obtained using the 6-311++G (2d, 2p) basis set.

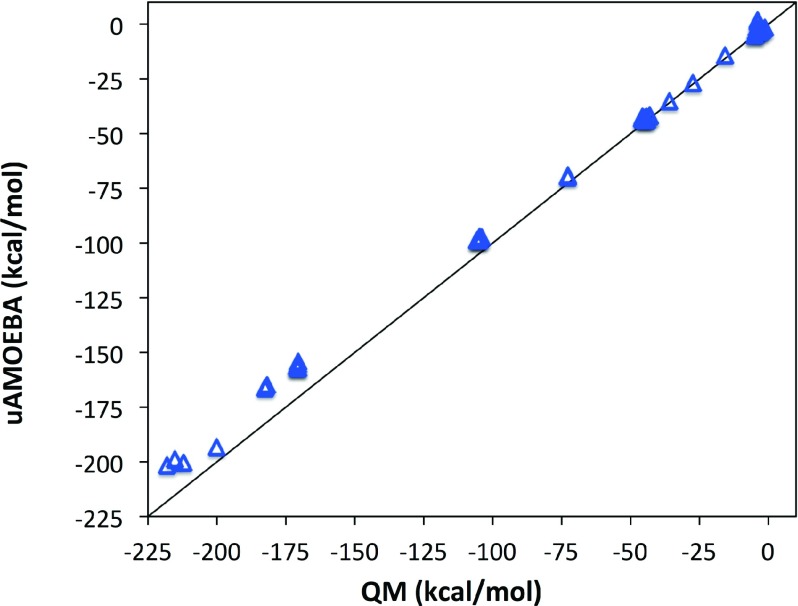
The interaction energies of water clusters ranging from dimers to clusters of 20 water molecules⁸³ are shown in Figure 2. The predicted cluster energies are in generally good agreement with ab initio QM results, with a root-mean-square error (RMSE) value of 0.85 kcal/mol per molecule and a correlation coefficient r² of 0.988. The error increases for larger clusters. Despite the overall success, uAMOEBA has trouble with certain molecular orientations due to its isotropic, spherical nature. For example, it finds 1.056 and 1.841 kcal/mol for the Smith5 and Smith6 dimer interaction energies, while the experimental value is ∼ − 4 kcal/mol. Besides, clusters provide a critical calibration for the increasing importance of polarization as one move from the gas-phase toward bulk phases. uAMOEBA is able to accurately reproduce the optimal structures of the water clusters; the root-mean-square deviations (RMSDs) to the reference QM-optimized structures are around 0.15 Å for all of the clusters in the parameterization data set except a couple of hexamers and one eleven-mer (hexamer07, hexamer08, and n11_434 in the Table SI).⁸³

FIG. 2.

Cluster energy of gas phase geometry-optimized clusters ranging from size 2 to 20.

Fitted liquid water properties of uAMOEBA

Figure 3 shows the temperature dependence of thermodynamic properties water simulated using uAMOEBA and compared to experiment: the density, enthalpy of vaporization, thermal expansion coefficient, isothermal compressibility, isobaric heat capacity, and dielectric constant, which are included as part of the parameterization data set. Overall, the coarse-grained uAMOEBA model is able to describe the liquid properties as well as the previous AMOEBA03 models and other non-polarizable and polarizable models in the literature (Table III).

TABLE III.

Comparison of experimental and simulated liquid data from different water models (T = 298.15 K, P = 1 atm). Numbers in parentheses include one standard error in terms of the least significant digit.

Property	Expt.	TIP3P	TIP4P-Ew	SWM4-NDP	TTM3-F	GCPM	SWM6	BK3	AMOEBA03	uAMOEBA
Enthalpy of vaporization/kcal mol−1
ΔHvap	10.52	10.45	10.583	10.44	11.40	11.30	10.52	10.94	10.48	10.599 (7)
Density of water/g cm−3
ρ	0.997	0.982	0.995	0.994	0.994	1.007	0.996	0.997	1.000	0.999 (1)
Isothermal compressibility/10−6 bar−1
κ	45.3	57.4	48.1	…	…	…	…	44.4	66.0	42.7 (5)
Isobaric heat capacity/cal/mol K−1
Cp	18.0	16.8	19.2	…	…	22.5	…	22.0	21.3	21.2 (3)
Static dielectric constant
ε	78.5	94.0	63.90	78.0	67.7	84.0	78.1	79.0	81.4	76.3 (12)
Thermal expansion coefficient/10−4 K−1
α	2.56	4.10	3.40	…	…	4.20	…	3.01	1.90	3.38 (26)
Self-diffusion coefficient/10 cm2 s−1
D0	2.30	6.14	2.70	2.85	2.37	2.26	2.14	2.28	2.00	2.41 ± 0.03
Viscosity/cP
η	0.896	0.321	0.573	0.66	…	…	0.87	0.95	1.08	0.72 ± 0.05
References	102	9, 103, 104	92, 103, 105, 106	104	19, 107, 108	109, 110	104	109	25

The enthalpy of vaporization, thermal expansion coefficient, isothermal compressibility, and dielectric constant all show excellent agreement with experiment over a range of temperatures after the parameter fit. The density of liquid uAMOEBA shows a correct maximum at 277 K. Small deviations in density of up to 1.4% are observed at very high temperatures (373.15 K). As the AMOEBA03 model, uAMOEBA overestimates the water heat capacity at room temperature by 3 cal/mol K⁻¹, similar to the other two polarizable models that have reported Cp, GCPM (22.5), and SWM6 (22.0). This deficiency is likely due to the approximated quantum correction to the heat capacity applied to the classical, flexible model.^12,25,90

The dielectric constant of water is a critical property that is tightly coupled to the electrostatic model. However, the evaluation of dielectric constant by computer simulation is difficult due to the slow convergence near ambient conditions⁹¹ and its dependence on the long-range interactions,⁷ as well as the H–O–H angle.⁸⁰ Previous model shows that the non-polarizable models tend to underestimate the dielectric constant (68 for SPC/E⁸⁰ and 62 for TIP4P-Ew⁹²), likely due to the fixed atomic charges.⁹³ Our simulated value for the dielectric constant, 78.4 ± 1, matches perfectly with the experimental measurement of 78.5 at 298 K. The use of quadrupole moments and incorporation of many body polarization, even though at a coarse-grained molecular level, seems sufficient to capture the dielectric response of water.

In liquid phase, the instantaneous water dipole moment according to density functional theory (DFT) simulations ranges between 2.6 and 3.0 D at room temperature.⁹⁴ The average molecular dipole moment predicted by uAMOEBA, including both the permanent and induced components, is 2.80 ± 0.19 D, which is consistent with the 2.78 D given by the all-atom AMOEBA03 model. Due to the induced dipoles, the liquid phase principle molecular quadrupole moments, located at the water center of mass, changed slightly to (2.962, −2.645, and −0.317).

Validation of uAMOEBA

In this section, we validate the uAMOEBA model by predicting several properties not used in parameterization, including the RDF, O–O–O angle distribution, self-diffusion coefficient, viscosity, and interaction energy with molecules other than water.

Radial distribution function

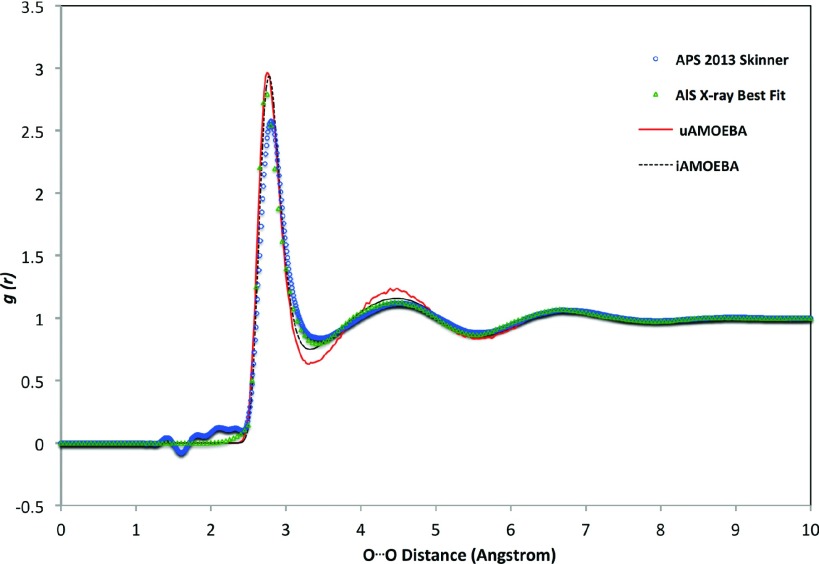
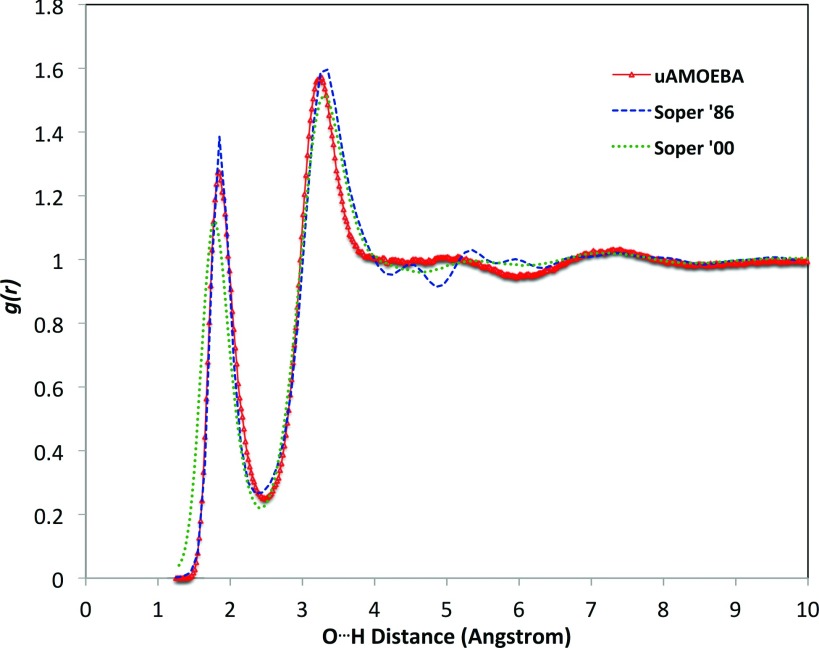
To characterize the liquid structure, the O–O and O–H radial distribution functions were sampled from the NPT molecular dynamics simulations. As shown in Fig. 4, the O–O RDF displays two well-defined peaks, similar to the experimentally derived RDFs from X ray scattering data taken by Hura and co-workers using the Advanced Light Source (ALS),⁹⁵ more recently by Skinner and co-workers using the Advanced Photon Source (APS)⁹⁶ and simulations using the 2013 iAMOEBA model.²⁹ The positions of the first and second peaks of the uAMOEBA g_OO(r) agree very well with the experimental data, especially the ALS data. Like iAMOEBA, the position of the first trough is slightly shifted to the left. The first peak height is almost identical to that of iAMOEBA, both similar to the ALS RDF. The second peak height is notably higher than the rest, and accordingly the first trough is 0.1 lower than the experimental RDF, which suggests that the second shell of uAMOEBA water is somewhat over structured. The positions of the first and second peaks of uAMOEBA g_OH(r) show excellent agreement with the experimental curve (Fig. 5). The first peak appears around 1.9 Å, which matches the reported hydrogen bond length (1.5–2.5 Å⁹⁷). The first peak of the uAMOEBA g_OH(r) is lower than the Soper 1986 data⁹⁸ but higher than the Soper 2000 results.⁹⁹ Features in the first trough and second peak are similar to the Soper 1986 data.

FIG. 4.

The oxygen-oxygen RDF curves of the uAMOEBA water model, compared with experimentally derived RDFs.

FIG. 5.

The oxygen-hydrogen RDF curves of the uAMOEBA water model, compared with experimentally derived RDFs.

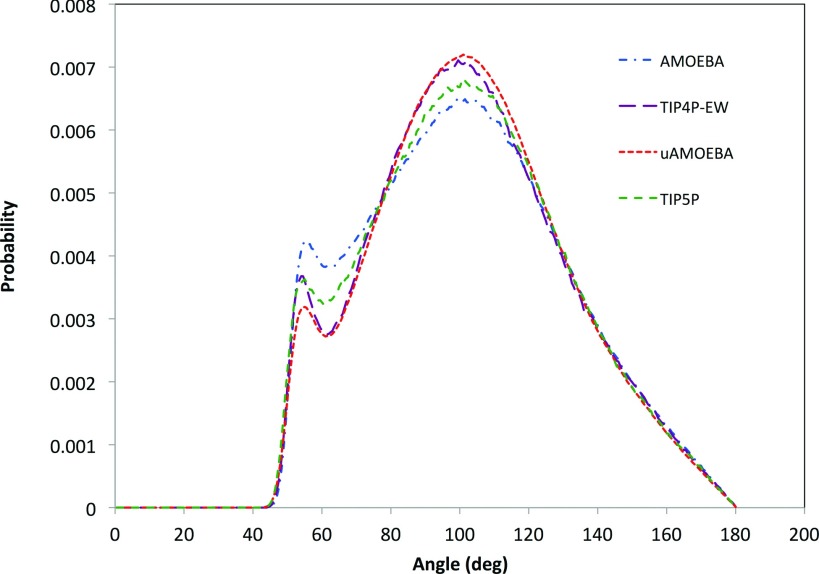
The O⋯O⋯O angle distributions sampled using uAMOEBA, AMOEBA03, TIP4P-EW, and TIP5P models are shown in Fig. 6. From MD trajectories, we computed the O⋯O⋯O angle distribution within 3.4 Å of each oxygen atom. Overall, the O⋯O⋯O angle distribution in these models suggests a tetrahedron-like structure, as the maximum probability appears around 101°-105°. All models display a small shoulder at 55°-58°, indicating a fifth atom entering the first solvation shell. This is strong evidence that the uAMOEBA model can describe hydrogen bonding as well as the other all-atom models. Note that the uAMOEBA profile is particularly similar to that of TIP4P-Ew.

FIG. 6.

The O⋯O⋯O angle distributions of uAMOEBA, AMOEBA03, TIP4P-Ew, and TIP5P water models.

The results for the self-diffusion coefficient as a function of system size are reported in Table SXI⁸³ and the corresponding size-independent diffusion coefficient D₀ and viscosities η are summarized in Table III. Polarizable water models generally produce reasonable diffusion constants compared to nonpolarizable ones,⁷ except for SWM4-NDP which is slightly under-polarized. Fig. SX and Table SXI⁸³ illustrate the strong dependence of the calculated diffusion constant on the system size. With a small box of 216 water molecules, the simulated D using uAMOEBA is 1.95 × 10⁻⁵ cm² s⁻¹, which increases to 2.21 × 10⁻⁵ cm² s⁻¹ when the simulation box contains 2500 molecules. By using extrapolation, the system-independent self-diffusion constant by uAMOEBA is 2.41 × 10⁻⁵ cm² s⁻¹, in excellent agreement with the experimental value.

For the viscosity, which is considered system size-independent, most models underestimate the viscosity except the BK3 and AMOEBA03 model. The deviation in viscosity given by the uAMOEBA model is similar to AMOEBA03 models and larger than those of SWM6, BK3, and iAMOEBA (0.85 cP).²⁹

To investigate the transferability of the uAMOEBA model and its ability to interact with the all-atom AMOEBA03 model, we have computed the dimer equilibrium interaction energy between water and several small molecules (Table IV). For the water-water dimer, AMOEBA03 or uAMOEBA was used for both molecules. For the other heterodimers, the water was modeled with either uAMOEBA or AMOEBA03 (as labeled in the 3rd and 4th column in Table IV) while the other molecule was always modeled with AMOEBA03. These comparisons allow us to understand the potential differences between the AMOEBA03 and uAMOEBA water models as solvent. Starting from QM optimized structures,¹⁰⁰ each dimer was optimized using force fields to obtain the corresponding interaction energy. These molecules were chosen to test performance of uAMOEBA water model as the hydrogen bond donor, acceptor and interacting with aromatic benzene. The overall trend given by uAMOEBA model is in good agreement with the SAPT2+/CBS data (calculated using PSI4¹⁰¹). The correlation coefficient (R²) between uAMOEBA and SAPT2+/CBS results is 0.83 while the correlation coefficient between all-atom AMOEBA03 and SAPT2+/CBS is 0.92. As a hydrogen bond acceptor, uAMOEBA performs equally well compared to all–atom AMOEBA03, even in the more complicated peptide–water interaction (−5.35 for uAMOEBA, −5.16 for AMOEBA03, and −5.14 kcal/mol for SAPT2+/CBS). In addition, uAMOEBA accurately captures the OH-pi interaction when facing the aromatic molecules. We also tested the hybrid water dimer where one of the water is described AMOEBA03 while the other is uAMOEBA. The dimer interaction energy is −4.11 kcal/mol when uAMOEBA is the H-bond donor in the dimer, and −5.90 kcal/mol when uAMOEBA is the H-bond acceptor. The average of the two is −5.0 kcal/mol, matching very well with AMOEBA03 or QM values. Overall, the uAMOEBA water model performs reasonably when replacing the AMOEBA03 model in the hybrid uAMOEBA-AMOEBA03 application even though there are no electrostatic or vdW parameters on the hydrogen atoms at all.

TABLE IV.

Dimer equilibrium interaction energy between water and small molecules. Compared results from uAMOEBA, AMOEBA03 water model, and SAPT2+/CBS (calculated using PSI4¹⁰¹). For the water-water dimer, AMOEBA03 or uAMOEBA was used for both molecules. For the other heterodimers, the water was modeled with either uAMOEBA or AMOEBA03 (as labeled in the 3rd and 4th column) while the other molecule was always modeled with AMOEBA03. The structural RMSD values in parentheses represent the structure different from the MP2/cc-pVTZ optimized structures.¹¹¹

Dimer	Dimer structure	uAMOEBA ΔEint	AMOEBA03 ΔEint	SAPT2+/CBS ΔEint
(a) Water-water		−5.16 (0.13)	−4.99 (0.06)	−4.92
(b) Peptide-water		−5.35 (0.10)	−5.16 (0.13)	−5.14
(c) MeOH-water		−5.61 (0.07)	−4.83 (0.05)	−5.03
(d) Benzene-water		−3.14 (0.25)	−3.16 (0.23)	−3.25
(e) Water-MeNH2		−6.69 (0.13)	−8.53 (0.08)	−7.18
(f) Water-peptide		−6.48 (0.35)	−8.28 (0.26)	−8.04
(g) Water_pyridine		−6.46 (0.10)	−7.26 (0.05)	−7.15
(h) Water-MeOH		−4.84 (0.24)	−6.77 (0.19)	−5.61

Computational efficiency

The main motivation for developing uAMOEBA is to improve computational efficiency by reducing the number of nonbonded interaction sites. We compared the simulation time between the uAMOEBA model and the all-atom AMOEBA03 model in 1000 steps of gradient evaluation (see Table V). The same simulation settings were used for both models and the only difference is the model parameters that distinguish the one-site model from the three-site model. The efficiency ratio is defined by the simulation time from the all-atom AMOEBA03 model divided by that of the one-site model. For relatively small systems containing less than 1000 atoms, the speed up is almost a factor of 5, while for large water box the improvement is about a factor of 3; this is expected as the computational cost of the PME method scales as N log (N).

TABLE V.

Efficiency test for the uAMOEBA water model. For all simulations, the vdW cutoff was set to 12 Å and Ewald real-space cutoff was 7 Å. For the first 3 systems of 512 molecules or less, no neighbor-list was used for the vdW calculation. Computer hardware: Intel E5-2697 v2 @ 2.70 GHz, 8 threads.

No. of molecules	AMOEBA03 models/1000 force evaluations	uAMOEBA models/1000 force evaluations	Ratio
216	59.6	12.3	4.8
512	95.6	22.4	4.3
1000	97.3	35.2	2.8
1600	155.4	59.9	2.6
2500	245.2	88.2	2.8
4000	386.0	132.1	2.9

CONCLUSION

Advancement in molecular simulation relies on accurate potential models and efficient sampling methods.¹¹² In this work, we present the development of a coarse-grained polarizable water model, “uAMOEBA,” where all nonbonded interactions, including the polarizability, are placed on the oxygen atom. The parameters of this model are determined from a wide range of ab initio and experimental data using the automated ForceBalance procedure. The model and parameters are validated by comparing with additional ab initio and experimental results, including liquid structural properties, self-diffusion coefficient, shear viscosity, and interaction energies with other small organic molecules. Overall, uAMOEBA shows good transferability between gas and liquid phases, polar and nonpolar environments, most likely because of the incorporation of molecular polarizability. The water structural and dynamic properties given by uAMOEBA are in very good agreement with those derived from all-atom AMOEBA03 model and experiments. The dimer interaction energy between AMOEBA03 small molecules and uAMOEBA water are mixed together also show a satisfying trend in comparison with all-AMOEBA03 and SAPT results. Meanwhile, the computational efficiency is improved by a factor of three compared to atomistic AMOEBA03. We expect uAMOEBA to be a useful solvent model in simulations of biological systems such as proteins and nucleic acids and it can be readily combined with the existing all-atom polarizable protein force field.¹¹³