Image-based reconstruction of three-dimensional myocardial infarct geometry for patient-specific modeling of cardiac electrophysiology

Abstract

Purpose:

Accurate three-dimensional (3D) reconstruction of myocardial infarct geometry is crucial to patient-specific modeling of the heart aimed at providing therapeutic guidance in ischemic cardiomyopathy. However, myocardial infarct imaging is clinically performed using two-dimensional (2D) late-gadolinium enhanced cardiac magnetic resonance (LGE-CMR) techniques, and a method to build accurate 3D infarct reconstructions from the 2D LGE-CMR images has been lacking. The purpose of this study was to address this need.

Methods:

The authors developed a novel methodology to reconstruct 3D infarct geometry from segmented low-resolution (Lo-res) clinical LGE-CMR images. Their methodology employed the so-called logarithm of odds (LogOdds) function to implicitly represent the shape of the infarct in segmented image slices as LogOdds maps. These 2D maps were then interpolated into a 3D image, and the result transformed via the inverse of LogOdds to a binary image representing the 3D infarct geometry. To assess the efficacy of this method, the authors utilized 39 high-resolution (Hi-res) LGE-CMR images, including 36 in vivo acquisitions of human subjects with prior myocardial infarction and 3 ex vivo scans of canine hearts following coronary ligation to induce infarction. The infarct was manually segmented by trained experts in each slice of the Hi-res images, and the segmented data were downsampled to typical clinical resolution. The proposed method was then used to reconstruct 3D infarct geometry from the downsampled images, and the resulting reconstructions were compared with the manually segmented data. The method was extensively evaluated using metrics based on geometry as well as results of electrophysiological simulations of cardiac sinus rhythm and ventricular tachycardia in individual hearts. Several alternative reconstruction techniques were also implemented and compared with the proposed method.

Results:

The accuracy of the LogOdds method in reconstructing 3D infarct geometry, as measured by the Dice similarity coefficient, was 82.10% ± 6.58%, a significantly higher value than those of the alternative reconstruction methods. Among outcomes of electrophysiological simulations with infarct reconstructions generated by various methods, the simulation results corresponding to the LogOdds method showed the smallest deviation from those corresponding to the manual reconstructions, as measured by metrics based on both activation maps and pseudo-ECGs.

Conclusions:

The authors have developed a novel method for reconstructing 3D infarct geometry from segmented slices of Lo-res clinical 2D LGE-CMR images. This method outperformed alternative approaches in reproducing expert manual 3D reconstructions and in electrophysiological simulations.

1. INTRODUCTION

Myocardial infarction (MI) results from prolonged tissue ischemia, typically related to coronary artery occlusion, and is associated with serious long-term complications such as heart failure and ventricular arrhythmia.^1–3 Tissue in infarcted regions undergoes significant electrophysiological and structural remodeling, which plays a central role in the mechanisms that lead to heart dysfunction.^2–6 Recently, computational modeling of hearts with ischemic cardiomyopathy has emerged as a promising tool to guide patient-specific diagnosis and the treatment of associated rhythm disorders.^7–12 However, to accurately represent patient-specific structural remodeling, computational models must incorporate accurate geometric reconstructions of infarct regions. In particular, experimental and clinical studies using late-gadolinium enhanced cardiac magnetic resonance (LGE-CMR) imaging^6,10 have demonstrated that both the core component of the infarct and the surrounding border zone, also termed gray zone, play an important role in cardiac arrhythmogenesis. Thus, accurate reconstruction of these zones is paramount to their representation in patient-specific models.

While experimental LGE-CMR imaging protocols can acquire three-dimensional (3D) images in vivo with an isotropic voxel size below 1.7 mm,^13–15 routine clinical protocols are limited to acquiring a low-resolution (Lo-res) stack of short-axis (SAX) slices.⁶ This two-dimensional (2D) LGE- CMR imaging protocol is preferred in the clinic because critically ill patients are often unable to hold their breath for 20–30 s as required by 3D LGE-CMR imaging methods.¹⁶ Also the 3D LGE-CMR images are affected by respiratory motion artifacts to a higher degree, and removing these artifacts requires reacquisition of the entire 3D image. However, the resolution of the 2D LGE-CMR images is coarse, particularly in the out-of-plane direction, where it is between 6 and 10 mm. Building 3D reconstructions of infarct regions for patient-specific modeling from such Lo-res 2D LGE-CMR images requires an accurate interpolation method, because the voxel size of the reconstruction needs to be smaller than 0.4 mm, to resolve the electrical activation front.¹⁷ This interpolation is a challenging task, given the inherent variation in infarct size, topology, and geometry.

Numerous interpolation methods have been developed for the reconstruction of 3D organ geometries from Lo-res stacks of image slices. These methods can be categorized into two broad groups, namely, parametric and implicit. Parametric techniques require explicit correspondences between landmark points on adjacent slices.¹⁸ However, such landmark points cannot be identified in infarct image slices, as the shape and topology of myocardial infarct regions are not uniform. Implicit methods, on the other hand, rely on functions, such as characteristic functions,¹⁹ signed distance maps,^20–22 and radial basis functions,^23,24 to implicitly define the organ shape in 2D slices, which are then interpolated on a voxelwise or global basis. While effective implicit methods have been reported for the reconstruction of certain organs, e.g., the cardiac ventricles,^25,26 there is a lack of such a methodology that is specifically developed and tested for infarct reconstruction. The objective of our study was to address this need.

The infarct reconstruction methodology we have developed has two steps, the first of which involved delineation of the infarct regions from the 2D slices of the clinical image via manual or automated segmentation. The second step consisted of interpolation of the segmented data to build a 3D reconstruction with the desired voxel size. Since established methods for infarct segmentation from Lo-res 2D LGE-CMR images^6,10,27–29 are available, the focus of the present study was on the development and evaluation of the interpolation step. The main contribution of this paper is twofold. First, we developed a methodology based on logarithm of odds (LogOdds)³⁰ for the interpolation of slices of infarct segmentation. Second, we thoroughly evaluated the efficacy of the proposed interpolation scheme in replicating manually segmented infarct geometries (i.e., manual infarct reconstructions), using metrics based on infarct geometry as well as outcomes of simulations of cardiac electrophysiology. In particular, we assessed the effect of errors in reconstruction on wavefront activation maps and pseudo-ECGs of electrophysiological simulations during both sinus rhythm and ventricular tachycardia (VT). Several alternative interpolation methods were implemented and compared with the proposed method.

2. METHODS

2.A. Infarct geometry reconstruction method based on LogOdds

Shapes of 2D objects have been represented in prior studies via discrete probability or signed distance maps.^22,31 However, when these representations are used for interpolation of shapes, the computations are limited to convex combinations, as the spaces of discrete probability or signed distance maps are not closed under addition or scalar multiplication.³⁰ LogOdds is an example of a class of functions that map the space of discrete probability maps to a Euclidean space.³² This mapping facilitates the use of linear combinations in interpolation, as opposed to being limited to only convex combinations. The application of LogOdds functions in image analysis was originally demonstrated by Pohl et al.³⁰ in the representation of object shape, generation of probabilistic atlas maps for segmentation, and temporal interpolation of 3D brain structures.

More precisely, let p ∈ ℙ≜{p|p ∈ [0, 1]} be the probability that a voxel is assigned to a particular anatomical structure. The LogOdds of p, denoted by logit(.) : ℙ → ℝ, is the logarithm of the odds ratio between the probability p and its complement, that is,

$${\displaystyle \text{logit}\left(p\right)\cong log\frac{p}{(1-p)}.}$$ (1)

The LogOdds space is defined as 𝕃≜{logit(p)|p ∈ ℙ}. The inverse of the LogOdds function logit(.) is the generalized logistic function,

$${\displaystyle T\left(t\right)\cong \frac{1}{1+e^{-t}},}$$ (2)

where T(.) maps each element t ∈ 𝕃 to a unique probability p ∈ ℙ. Thus, the function logit(.) and its inverse comprise a homomorphism between ℙ and 𝕃.³⁰ Let s be the number of slices in the Lo-res image, n the number of pixels per slice, and m the number of voxels in the interpolated image. The discrete probability maps P : Ω → ℙⁿ, where Ω ⊂ ℝ², are obtained from discrete label maps B : Ω → 𝔹ⁿ of segmentation. LogOdds maps L : Ω → 𝕃ⁿ are created from discrete probability maps using logit(.) function.

In this work, we represented the infarct region shapes using LogOdds maps, where the boundary of the infarct was given by the zero level set of a function of type Ω → 𝕃ⁿ. Specifically, we used smoothing by Gaussian filtering to map values of pixels in 2D binary image slices that contain infarct region segmentations to probabilities. When a binary image slice representing the segmentation of an infarct region was smoothed using the Gaussian kernel, each pixel was assigned a value in the interval [0, 1], which we interpreted as the probability of that pixel belonging to the infarct region. Similarly to Pohl et al.,³⁰ we used a probability value (T_p) of 0.5, which maps to a LogOdds value to 0, to define the object boundary. The standard deviation σ of the Gaussian function was determined empirically. Although it was possible to use alternatives, such as signed distance map, to convert binary image values to probabilities, our experiments yielded more accurate results when Gaussian smoothing was used. This difference in accuracy may be due to the increased precision in shape representation when probability maps generated using Gaussian filtering are employed.³⁰ The 2D probability maps resulting from Gaussian smoothing were converted into LogOdds maps using the logit(.) function. A cubic spline method was then used in the interpolation 𝕃^sn → 𝕃^m of the stack of 2D LogOdds maps into a 3D image. Next, a 3D probability map P : Ω → ℙ^m was generated from the interpolated image via logistic transformation. Finally, the 3D probability map was thresholded to generate a 3D reconstruction of the infarct region. In the present study, the core and border zones of the infarct were reconstructed in two consecutive steps. In the first step, the total infarct (i.e., core and border zone combined) was considered as the region of interest, and a 3D reconstruction of that region was obtained. In the second step, a reconstruction of the core region alone was obtained. From the reconstructions of the total infarct and core regions, the border zone reconstruction was obtained by subtracting the core region reconstruction from the total infarct reconstruction.

2.B. Data acquisition

We used three high-resolution (Hi-res) ex vivo LGE-CMR canine datasets for optimizing the standard deviation σ of the Gaussian smoothing term and 36 high-resolution in vivo LGE-CMR human datasets for evaluating the proposed method. To acquire the canine heart datasets, myocardial infarctions were induced in adult mongrel dogs. Gd-DTPA (Magnevist) was then injected (0.2 mmol/kg), and the animals were sacrificed 20 min after injection. T1-weighted gradient recalled echo MRI was then performed on the explanted hearts, at a resolution of 0.25 × 0.25 × 0.50 mm³, to obtain the LGE images. More details about image acquisition can be found in previous publications.^26,33 The data acquisition procedures were approved by the Animal Care and Use Committee at the Johns Hopkins University.

The human data were acquired from study subjects presenting with myocardial infarction recruited for the Cardiovascular MRI Clinical Research (CMCR) program at Robarts Research Institute of Western University (London, ON). All subjects received LGE-CMR imaging examination using a whole-heart, respiratory navigated, 3D inversion recovery gradient echo pulse sequence (Siemens 3 T Trio, Erlangen, GER) during and 30 min following infusion of 0.2 mmol/kg Gadovist (Bayer, Toronto, ON). The study protocol was approved by the Research Ethics Board of Western University, after receiving written consent from the subjects. The images were acquired at a voxel size of 0.625 × 0.625 × 1.3 mm³. More details about these acquisitions have been reported previously.³⁴

2.C. Evaluation of infarct reconstruction accuracy based on geometry

Our processing pipeline to evaluate the proposed method using the Hi-res 3D LGE-CMR images of patient hearts is shown in Fig. 1. Initially, an expert manually segmented left-ventricular (LV) infarct regions in a given 3D image using itk-snap.³⁵ As mentioned previously, infarct tissue comprises of scar (also known as infarct core) and semiviable myocardium (or border zone),⁶ and it is important to represent the two regions differently in electrophysiological models.¹⁰ In this paper, the segmented 3D infarct regions were automatically subdivided into the core and border zones using the full-width at half maximum (FWHM) thresholding technique,⁶ where the intensity at 95% percentile of the cumulative intensity histogram corresponding to the total infarct was chosen as maximum intensity. Next, the image was downsampled to reduce the resolution in the SAX plane to 1.3 mm and out of the plane to 6–12 mm, to mimic the resolution of clinical LGE-CMR data. The LogOdds method was then used to interpolate the downsampled total infarct and core regions separately back to the original voxel size. The border zone reconstruction was obtained by subtracting the reconstructed core region from the reconstructed total infarct. Finally, the computed reconstructions of the infarct regions were compared to manually generated ones using a variety of geometry-based metrics. All computed reconstructions were built using matlab (Mathworks, Inc., Natick, MA) on an ubuntu 12.04 workstation with eight Intel Core i7 CPU of 3.4 GHz and 32 GB RAM.

FIG. 1.

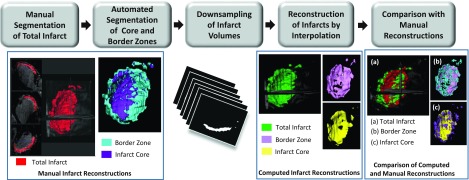
Our processing pipeline for evaluation of the reconstruction accuracy of the proposed method using metrics based on infarct geometry. The pipeline involves manual segmentation of the infarcted regions in 3D LGE-CMR images, downsampling of the segmented images to the desired resolution, computation of infarct reconstructions from downsampled images by the LogOdds method, and comparison between computed and manual reconstructions.

2.D. Evaluation of infarct reconstruction accuracy based on outcomes of electrophysiological simulations

Simulations of both normal and abnormal cardiac functions, in which cardiac electrical activity was modeled from ionic channels to the whole organ, were performed. As these multiscale simulation experiments were computationally very expensive, they were conducted with models generated from only a subset of seven LGE-CMR images randomly chosen from our testing set. The block diagram for generation of electrophysiological models of individual hearts and execution of simulations is shown in Fig. 2. For each image, LV and right-ventricular (RV) contours were first manually extracted from each 2D SAX slice in the image using ImageJ.³⁶ Ventricular geometry was then reconstructed from the contours at an isotropic resolution of 0.4 mm using a variational implicit (VI) function approach reported previously.^24,26 Using the ventricular reconstruction, and the corresponding infarct reconstructions (obtained as in Sec. 2.C), two finite element models, one with manually generated infarct reconstruction and the other with computed infarct reconstruction, were built.³⁷ Here, infarct reconstructions were computed from a downsampled image with an out-of-plane resolution (R_out) of 8 mm. The two finite element models were identical except for the differences in tissue labels of some of the elements that reflect the differences in the two infarct reconstructions. The fiber orientations for the models were estimated using a rule-based scheme published previously.³⁸

FIG. 2.

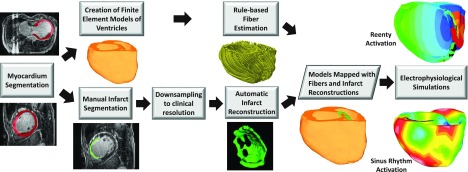
Block diagram for generation of models of individual hearts from LGE-CMR images for our electrophysiological simulation studies. Infarct reconstructions were performed as in Fig. 1. For each patient, two ventricular models, one with manually generated infarct reconstruction and the other with computed infarct reconstruction, were built. Ventricular fiber orientations were estimated using a rule-based method. The outcomes of electrophysiological simulations with computed infarct reconstructions were compared to those with manual reconstructions.

Electrical propagation was modeled using the monodomain formulation.¹⁷ Intracellular conductivities in the normal myocardium were assigned such that the resulting conduction velocity matched those recorded in human ventricular experiments.^39,40 To represent connexin 43 remodeling and lateralization in the remodeled border zone, transverse conductivity was decreased by 90%, resulting in increased tissue anisotropy.⁴¹ The scar was modeled as passive tissue with zero conductivity.

A human ventricular action potential model was used to represent the membrane kinetics in the healthy human myocyte.⁴² For the remodeled border zone, the action potential model was modified to represent electrophysiological changes that have been observed experimentally (reduction in peak sodium current to 38% of the normal value,⁴³ in peak L-type calcium current to 31% of normal,⁴⁴ and in peak potassium currents IKr and IKs to 30% and 20% of the maximum,⁴⁵ respectively). These modifications resulted in border zone action potential morphology that had decreased upstroke velocity, decreased amplitude, and increased duration, consistent with experimental recordings,⁴⁶ as previously described by Arevalo et al.⁴⁷

Sinus rhythm was simulated in all models by replicating activation originating from the Purkinje network. As a surrogate for Purkinje excitation, the ventricular models were activated at six locations on the endocardium by stimuli with a cycle length of 600 ms.^48,49 The six locations included one on the RV free wall, three on the LV septum, and two on the LV free wall. Appropriate timings of the stimuli were chosen such that the resultant 3D electrical propagation matched experimental data.⁵⁰ Simulations of VT induction were also performed in all models by applying at the apex a programmed electrical stimulation (PES) protocol similar to the one used in the clinic.⁵¹ Since the electrophysiological remodeling within infarct tissue is known to play a crucial role in the initiation and sustenance of arrhythmias,^10,47 we expected the fidelity of infarct reconstruction to affect the outcomes of VT simulations to a higher degree than those of simulations of normal electrical activity. The PES protocol consisted of six pacing (S1) stimuli with a coupling interval of 350 ms, followed by a premature stimulus (S2) whose cycle length was shortened until sustained VT was initiated or the last stimulus failed to capture. If needed, two additional extrastimuli were delivered to attempt arrhythmia induction. An arrhythmia was classified as sustained if it persisted for at least 2 s. All simulations were performed using the software package carp (CardioSolv, LLC)^52,53 on a parallel computing platform.

2.E. Accuracy metrics for evaluation of the computed infarct reconstructions

The performance of the LogOdds method was evaluated using two sets of metrics. First, the accuracy of computed reconstructions of the total infarct region, infarct core, and the infarct border zones was assessed separately using boundary distance-, spatial overlap-, smoothness-, and topology-based metrics. In addition, clinically relevant measurements, including infarct volume and surface area,³ were compared between computed infarct reconstructions and manually generated ones. Second, the differences between the outcomes of electrophysiological simulations conducted with ventricular models incorporating computed and manual infarct reconstructions were examined.

The root mean square error (RMSE) was used as the boundary distance metric. RMSE was defined as the RMS of the shortest distance from each point on the surface of the computed reconstruction to the surface of the manual reconstruction. As a measure of spatial overlap, we used the Dice similarity coefficient (DSC),⁵⁴ a widely used metric for evaluation of segmentations. The DSC measures the spatial fidelity of the computed reconstruction volume to manual reconstruction, the ground truth used in our study. To compare smoothness of the computed reconstructions to manual ones, we used a metric based on curvature of the surface. This metric was defined as the Bhattacharyya distance $\text{Bh}\left(\kappa \right)=\sum _{\kappa \in P}\sqrt{\left(h\left(\kappa \right)\hat{h}\left(\kappa \right)\right)}$ (Ref. 55) between the probability distribution functions, h(κ) and $\hat{h}\left(\kappa \right)$, of mean curvature κ of the surfaces of the computed and manual reconstructions. To examine the topological accuracy of the reconstructed infarct volumes, we used absolute differences in Euler characteristic (δχ) between the computed and manual reconstructions. The metrics based on volume and surface area included relative absolute volume difference (δRV) and relative absolute surface area difference (δRSA), expressed as a percentage of the volume and surface area of manual reconstructions. Statistical analyses were performed using GraphPad Prism 6.2 (GraphPad Software, Inc., La Jolla, CA), and an α of 0.05 was considered as the level of significance.

Prior to the evaluations, the parameters of the LogOdds method (i.e., the Gaussian standard deviation σ and the probability threshold T_p) were iteratively refined to maximize the DSC between computed and manually generated reconstructions in the three canine datasets (see Fig. 1). Note that each parameter was refined separately. After the parameter refinement, the LogOdds method yielded a highest mean DSC of 75.5% ± 7.4% at σ = 3 voxels and T_p = 0.5. The method with the optimized parameters was then tested using the 36 human LGE-CMR images.

For all simulations, pseudo-ECGs (Ref. 56) were generated by taking the difference between the extracellular potentials calculated at two points in an isotropic conductive medium surrounding the heart, as described previously.⁵⁷ The differences between the pseudo-ECG signals corresponding to computed and manual reconstructions were calculated using RMSE, mean absolute deviation (MAD), and correlation coefficient (CORR) metrics. The rationale behind our use of the MAD and CORR metrics was the application of these metrics in prior clinical studies to compare ECGs of reentrant activity.⁵⁸ Mathematically, let X and Y be two waveforms with length n. MAD is then defined as⁵⁸

$${\displaystyle \text{MAD}=\frac{\sum _{i=1}^n|(X_i-\overline{X})-(Y_i-\overline{Y})|}{\sum _{i=1}^n|(X_i-\overline{X})+(Y_i-\overline{Y})|}.}$$ (3)

MAD varies between 0% and 100% corresponding to identical and completely different waveforms.

Activation maps for all simulations were derived by determining, at each node of the finite element mesh, the instant in time at which the upstroke of the action potential at that node reached a threshold of 0 mV. The difference between the activation maps corresponding to computed and manual infarct reconstructions, expressed in milliseconds, was calculated as

$${\displaystyle \text{ATD}=\sum _{i=1}^{n_n}|\underset{i}{\overset{A}{T}}-\underset{i}{\overset{M}{T}}|/n_n,}$$ (4)

where n_n was the number of nodes in the 3D finite element model and $T_i^A$ and $T_i^M$ the activation times corresponding to computed and manual reconstructions for node i. The infarct core was excluded from this analysis, as it was modeled as passive tissue and did not activate. All metrics based on simulation results were computed in the steady state, where activation from beat to beat was stable.

2.F. Comparison of infarct reconstructions by the LogOdds method with those by alternative methods

We implemented four reconstruction methods already being used in medical imaging applications, including the signed distance transform-based method (SDM),²² the modified signed distance based-method (MSDM),²⁰ nearest neighbor (NN) interpolation, and VI method.²⁴ The SDM (Ref. 22) was an implicit interpolation method, in which the segmented slices were first converted to gray scale images, where the pixel intensity was its shortest distance to the boundary of the segmentation. These gray scale image slices were then linearly interpolated. The MSDM was similar to SDM except that it used cubic splines for the interpolation. The NN method, the interpolation that underlies the widely employed Simpson’s rule⁵⁹ for calculating volumes in the clinic, directly interpolated the binary label maps. The VI method used thin-plate spline interpolation, in which a function was computed to fit the given data and maximize the smoothness of the reconstruction. The accuracies of infarct reconstructions by all these alternative methods were evaluated using metrics based on geometry as in Fig. 1, and the results compared to those of the LogOdds method. To test whether relatively inferior performance of one method compared to another in evaluations based on geometry led to relatively poorer performance of the former in evaluations based on simulations, we selected one representative method from the alternative methods and evaluated its accuracy based on outcomes of electrophysiological simulations (see Fig. 2). The representative method we chose was the one with the highest accuracy in terms of DSC, which is widely regarded in the image processing community as an effective metric in evaluating 3D geometries.

3. RESULTS

3.A. Assessment of infarct reconstruction accuracy with metrics based on geometry

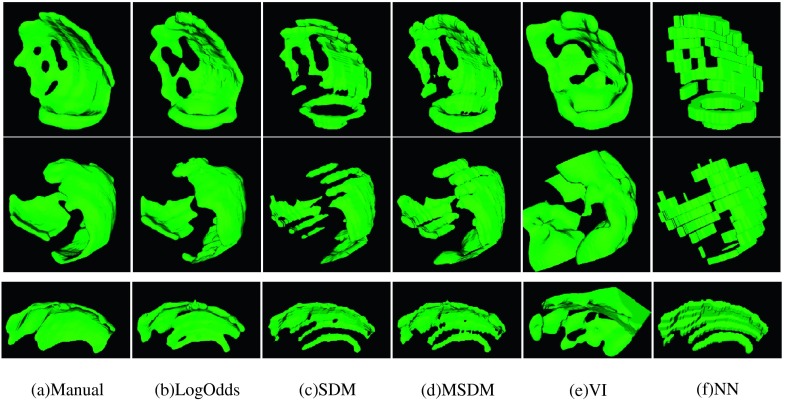
Surfaces of the total infarct region reconstructed by each of the methods from three example human subject images are shown in Fig. 3. Here, the interpolation was performed from a resolution of 1.3 × 1.3 × 8 mm³ to an isotropic resolution of 0.625 mm³. The mean computation time for the VI method was about 33 s, while it was less than 3 s for all the other methods. Except for the NN and VI methods, all methods generated smooth and anatomically realistic surfaces. Qualitatively, the LogOdds method generated surfaces that matched most closely with the surfaces of manual reconstructions. Summary of quantitative evaluation of the methods for reconstructing the total infarct for the 36 human LGE-CMR images is given in Table I. The LogOdds method yielded a mean DSC of 82.10% ± 6.58%. Normality test using Shapiro–Wilk test showed that DSCs do not follow a Gaussian distribution. Therefore, Wilcoxon signed rank sum tests were used to identify statistically significant differences between the mean DSC of the LogOdds method and that of the others. The LogOdds method yielded significantly higher DSC than all the other methods. Paired t-tests were performed on log-transformed volumes of total infarct regions, after testing for normality using Shapiro–Wilk test. Volumes of the infarct reconstructions generated by the LogOdds method were significantly closer to those of manual reconstructions. Similar to the volume measurements, the LogOdds method yielded smaller error for the surface area of the infarct. With respect to topological measures, the LogOdds method provided the smallest δχ. The accuracy of the LogOdds method in terms of the smoothness metric Bh was comparable to those of other methods, except the NN method, which reported a substantially lower value.

FIG. 3.

Comparison of the surfaces of total infarct reconstructions obtained using the various interpolation methods (columns) from three LGE-CMR images (rows). The different methods are the manual segmentation (manual), LogOdds approach we have developed (LogOdds), signed distance transform-based method (SDM), MSDM, VI technique, and NN method. Here, all methods were applied to input images of resolution 1.3 × 1.3 × 8 mm³ to obtain interpolated images of resolution 0.625 mm³.

TABLE I.

Summary of geometry-based evaluations of accuracy of the various methods in reconstructing the total infarct for the 36 human LGE-CMR images. An asterisk before a number indicates a statistically significant difference between the corresponding method and the LogOdds method.

Method	DSC (%)	δRV (%)	RMSE (mm)	δRSA (%)	Bh	Euler δχ
LogOdds	82.10 ± 6.58	7.23 ± 6.2	1.08 ± 0.15	7.29 ± 5.58	0.89 ± 0.02	6.25 ± 4.94
SDM	∗65.43 ± 12.86	∗48.77 ± 14.3	1.34 ± 0.21	28.15 ± 11.3	0.90 ± 0.01	11.6 ± 12.37
MSDM	∗75.99 ± 8.57	∗25.67 ± 10.15	1.20 ± 0.28	12.22 ± 8.94	0.90 ± 0.02	9.12 ± 11.83
VI	∗60.35 ± 17.36	∗96.32 ± 60.66	4.31 ± 3.36	18.02 ± 17.5	0.89 ± 0.02	5.36 ± 5.1
NN	∗74.13 ± 6.90	∗8.1 ± 14.56	1.54 ± 0.19	9.94 ± 4.7	0.68 ± 0.02	12.51 ± 8.10

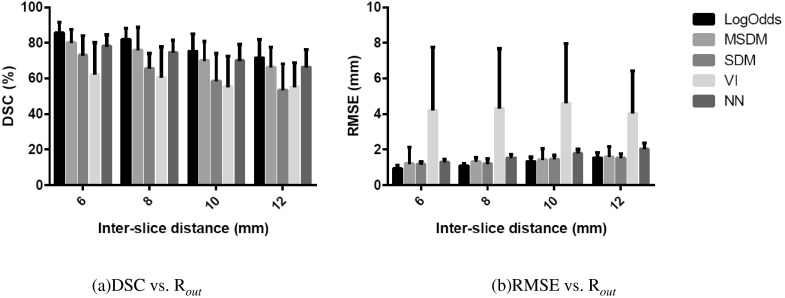
The summary of evaluations of the various methods in reconstructions of the core and border zones separately is given in Table II. Statistical testing was performed for DSC and infarct volumes. The DSC values in Table II are smaller than those for the total infarct (see Table I). Nevertheless, similarly to the results for total infarct, the LogOdds method yielded a significantly higher mean DSC than those of the other methods, for both core and border zone reconstructions. In the volume measurements, the LogOdds method yielded significantly smaller mean volume error for both core and border zone reconstructions than the alternative methods. Furthermore, the LogOdds method reported smaller RMSE error than other methods for both core and border zones. To evaluate the robustness of the various infarct reconstruction methods, we examined the efficacy of each approach for R_out values ranging from 6 to 12 mm. The variations of DSC and RMSE with R_out are shown in Fig. 4. For each method, DSC gradually decreased with the increase in R_out. However, the LogOdds method consistently yielded higher DSC and lower RMSE than those of the other methods, for all values of R_out.

TABLE II.

Summary of geometry-based evaluations of accuracy of the various methods in reconstructing the core and border zones separately for the 36 human LGE-CMR images. An asterisk before a number indicates significant difference between the corresponding method and the LogOdds method.

	DSC (%)		δRV (%)		RMSE (mm)
Method	Core	Border zone	Core	Border zone	Core	Border zone
LogOdds	70.44 ± 10.26	59.45 ± 15.36	11.93 ± 7.89	7.5 ± 7.73	1.33 ± 0.23	1.56 ± 0.40
SDM	∗51.42 ± 13.20	∗43.60 ± 18.89	∗60.1 ± 11.8	∗38.87 ± 16.4	1.33 ± 0.16	2.25 ± 0.57
MSDM	∗65.34 ± 11.20	∗53.02 ± 15.89	∗33.6 ± 12.28	∗20.7 ± 12.4	1.46 ± 0.57	2.48 ± 0.90
VI	∗45.54 ± 18.96	∗32.35 ± 34.35	∗93.17 ± 45.05	∗120.5 ± 143.3	5.02 ± 2.95	2.36 ± 1.18
NN	∗64.8 ± 9.70	*52.94 ± 14.54	∗11.2 ± 7.14	∗10.4 ± 10.1	1.60 ± 0.20	1.73 ± 0.47

FIG. 4.

Variations in DSC (left) and RMSE of distance (right) of the different methods as a function of R_out. The error bars represent one standard deviation.

3.B. Assessment of infarct reconstruction accuracies with metrics based on outcomes of electrophysiological simulations

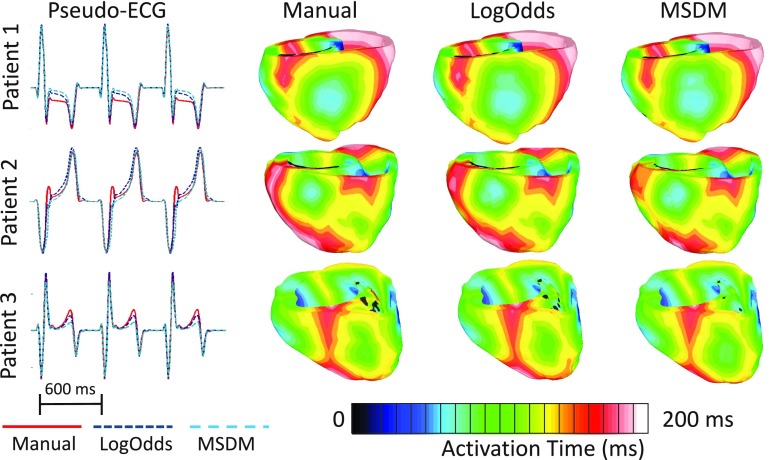
Figure 5 shows, for three patient hearts, the activation maps and the corresponding pseudo-ECGs, during one beat of sinus rhythm simulation. The scar regions appear in black in the activation maps. Visually, the activation maps simulated with manual and computed infarct reconstructions matched closely. Between the LogOdds method and MSDM, the pseudo-ECGs corresponding to the former were visually more similar to the ones corresponding to the manual reconstructions. The quantitative analyses of outcomes of the sinus rhythm simulations are shown in Table III. We did not test for statistically significant differences in outcomes of simulations between MSDM and LogOdds methods because of the small sample size that we used in the simulation experiments (i.e., seven patient hearts). The results for the metrics based on both pseudo-ECGs and activation maps indicated that, between the two infarct reconstruction methods, the outcomes of the simulations with infarct reconstructions by the LogOdds method more closely matched those with manual reconstructions.

FIG. 5.

Comparison of pseudo-ECGs and activation maps from one beat of sinus rhythm simulated for three patient hearts, with models that incorporate different infarct reconstructions. The activation maps are displayed in posterior views of the ventricles.

TABLE III.

Summary of quantitative evaluation of accuracies of the various infarct reconstruction methods based on outcomes for simulations of sinus rhythm. Seven LGE-CMR images were used in the simulation experiments.

Method	RMSE (mV)	MAD (%)	CORR (ms)	ATD
LogOdds	0.0117 ± 0.0064	10.15 ± 5.13	0.97 ± 0.042	1.19 ± 0.55
MSDM	0.0141 ± 0.0137	12.8 ± 5.56	0.95 ± 0.018	1.91 ± 1.28

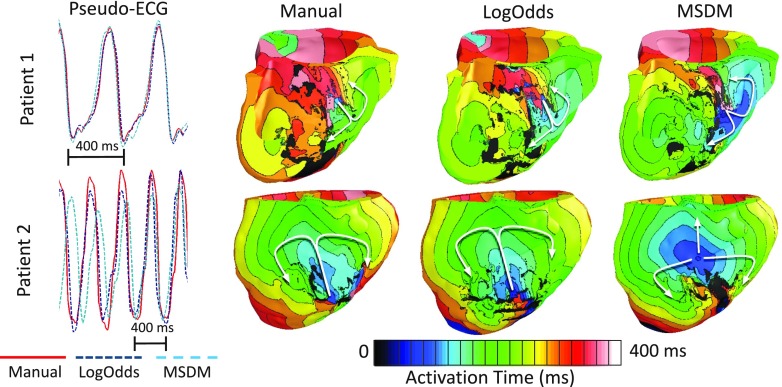
Out of the seven LGE-CMR images selected for electrophysiological simulation studies, sustained VT was induced in models corresponding to only two LGE-CMR images for all three types of reconstructions. The pseudo-ECGs and activation maps for these two cases are shown in Fig. 6. The arrhythmogenic border zones corresponding to these two images were larger than those of the rest, and thus, the models derived from these images were inducible regardless of the infarct reconstruction method.⁴⁷ The reentrant propagation patterns in the VT simulations performed for Patient 1 were similar across all three infarct reconstruction methodologies (i.e., figure-of-8 reentry on the RV side of the septum). However, in simulations performed for Patient 2, between the reentrant patterns corresponding to the LogOdds method and MSDM, only the former closely matched the one corresponding to the manual reconstruction (i.e., epicardial figure-of-8 reentry). Furthermore, visual comparison of the pseudo-ECGs reveals that, between the LogOdds method and MSDM, pseudo-ECGs corresponding to the former were visually more similar to those corresponding to the manual reconstructions. The RMSE, MAD, and CORR corresponding to the LogOdds method were 0.09 ± 0.07 mV, 12.53% ± 9.6%, and 0.93 ± 0.07, respectively. The values for the same metrics corresponding to the MSDM were 0.18 ± 0.18 mV, 36.0% ± 38.8%, and 0.73 ± 0.43. Note that the differences in the RMSE, MAD, and CORR values between the LogOdds method and MSDM were 90 μV, 23.47%, and 0.2, respectively, in VT simulations. These differences were substantially larger than their corresponding values of 2.4 μV, 2.65%, and 0.02 in sinus rhythm simulations (see Table III).

FIG. 6.

Comparison of pseudo-ECGs and activation maps for one beat of VT simulated for two patient hearts, with models that incorporate different infarct reconstructions. Activation maps are shown in septal and anterior views of the ventricles for Patients 1 and 2, respectively. The arrows highlight reentrant propagation patterns.

4. DISCUSSION

The main goal of this paper was to develop an accurate method for 3D reconstruction of myocardial infarct geometry from clinical LGE-CMR images and to thoroughly evaluate the efficacy of the developed method in comparison with alternatives. The evaluation included metrics based not only on infarct geometry but also outcomes of simulations of cardiac electrophysiology. Our results demonstrate that the LogOdds method was superior to all alternatives in evaluations based on geometry. Also, the LogOdds method outperformed the MSDM, the representative alternative method selected based on DSC, in the evaluations based on the outcomes of electrophysiological simulations. To our knowledge, this study is the first to develop and evaluate a method for image-based reconstruction of infarcts specifically. Furthermore, our study shows that the errors in infarct reconstructions affect outcomes of VT simulations to a substantially higher degree than those of sinus rhythm simulations and thereby underscores the importance of using accurate infarct reconstructions in simulations of arrhythmia. As the 3D reconstruction of the infarct geometry is crucial to patient-specific modeling of the heart in ischemic cardiomyopathy, the development of the LogOdds method and its comprehensive evaluation constitute an important step in advancing the clinical applications of personalized simulations of cardiac function. Additionally, the LogOdds method will enable more accurate calculations of image-based indices, such as volume,⁶ surface area,³ and geometry⁶⁰ of the infarct, which have been shown to predict clinical outcomes, including ventricular arrhythmia and sudden cardiac death.

Similarly to previous studies on 3D reconstructions of organs,^20,22 our infarct reconstruction pipeline involves segmentation of the 2D image slices, followed by interpolation of the segmented data. We assume that the segmentation step accounts for the noise and artifacts in clinical LGE-CMR images and produces an accurate delineation of the infarct in 2D. Notably, an alternative would be to interpolate on the 2D gray scale image slices directly and then segment the resulting 3D image. However, this alternative involves not only increased burden of computation and manual interaction in segmenting a Hi-res 3D image but also higher amount of interpolation artifacts that may affect the delineation of the core and border zones in the 3D image. Moreover, numerous well-established methods already exist for infarct segmentation from a stack of 2D LGE-CMR image slices.^29,61–63 Though an attempt⁶⁴ to simultaneously segment and reconstruct an object of interest from Lo-res medical images has been reported recently, this method required acquisitions of multiple views of the object and was tested only on structures with known topology. Note that, in our approach, the border zone of the infarct was reconstructed indirectly by subtracting the reconstruction of core from that of the total infarct. A direct reconstruction of the border zone may lead to larger errors than the ones in our approach, as the border zone is typically more complex in topology than the core zone.

The LogOdds method yielded a mean DSC that was at least 5% greater than the second highest DSC in our evaluations. As expected, accuracy in reconstruction gradually decreased with the increase in the value of R_out. However, the consistently higher accuracy yielded by the LogOdds method for all R_out values demonstrated its superiority to the other methods in robustness. The LogOdds method yielded significantly smaller volume errors for the total infarct and the border zone. Although the NN method was the closest to the LogOdds method in terms of δRV, the NN method generated rough surfaces with holes, especially along a curved boundary, and hence reported the largest errors in terms of smoothness- and topology-based metrics, i.e., Bh and δχ. The LogOdds method had the second smallest δχ among all the methods. The MSDM was more accurate than the SDM in terms of δRV, because the cubic spline interpolation was more suitable for interpolation of objects with curved surfaces, such as some infarct regions (see row 2 of Fig. 3). Even though the VI method has been proven highly suitable for reconstruction of cardiac ventricles,²⁶ it performed poorly in this study, due to the more complex topology and higher surface curvature of the infarcts. Note that, although there is a correlation between some of the geometry-based metrics used in our evaluation, e.g., δRV and δRSA, no metric is completely redundant, as the ranking of the various methods was different for different metrics.

Our study examined the effect of reconstruction errors on outcomes of simulations of normal as well as abnormal cardiac electrical activity. One alternative method, namely, the MSDM, was chosen as the representative method for comparison with the LogOdds approach in evaluations of computed infarct reconstructions based on simulations. Between the LogOdds method and MSDM, the outcomes of simulations with reconstructions generated by the former were more similar to those with manual reconstructions. Thus, relatively inferior performance of the MSDM compared to the LogOdds method in evaluations based on geometry translated into relatively poorer performance of the former in evaluations based on simulations. Since the MSDM was the best among alternative methods in terms of DSC, which effectively measures accuracy of computed infarct reconstructions based on geometry, we expect the LogOdds method to perform better than all the alternative methods in electrophysiological simulations. It is important to note that, irrespective of the reconstruction method, the same error in geometry reconstructions affected the outcomes of VT simulations to a substantially higher degree than the results of sinus rhythm simulations. This is because the reentrant circuits that drive the propagation pattern throughout the ventricles in VT are largely determined by the morphology of the infarct zone.^10,47 Notably, between the VT reentrant propagation patterns corresponding to the LogOdds method and MSDM, only the former closely matched the ones corresponding to manual reconstructions in both cases (see Fig. 6). It was evident from the surface reconstructions illustrated in Fig. 3, and δχ values in Table I, that the infarct reconstructions by MSDM had more gaps in them than the ones by the LogOdds method. We believe that this difference in infarct reconstructions between the two methods is the main reason for the inferior performance of the MSDM in our evaluations based on the outcomes of VT simulations. These results indicate that the guidance provided by patient-specific models of cardiac electrophysiology^9,10 to clinicians may be more effective when the models incorporate infarct reconstructions by the LogOdds method.

Our study has some limitations. While the absolute difference in Euler characteristic (δχ) represented the topological accuracy of the infarct reconstructions, this metric did not specifically quantify the preservation of arrhythmogenic conduction channels in the infarct. However, our evaluations of infarct reconstruction accuracy based on outcomes of VT simulations indirectly examined the preservation of the arrhythmogenic site(s). Ideally, the outcomes of simulations of cardiac electrophysiology performed with infarct reconstructions generated by the LogOdds method and MSDM methods should have been compared to electroanatomical mapping data. Since such data were not available to us, we utilized outcomes of simulations performed with manual reconstructions as a surrogate. Nonetheless, we believe that our findings remain valid, because the simulation methodology we used has been validated with experimental data, e.g., from optical imaging,^65,66 and the manual delineations of the infarct boundaries were drawn by experts. Also Lo-res and Hi-res images of the same heart were not available to us, and accordingly, we relied on mimicked Lo-res image segmentations in our evaluations. However, we believe that the mimicked Lo-res data were sufficient for our study, as ours was a comparative evaluation of various infarct reconstruction methods, and all methods received the same image segmentations as input.

5. CONCLUSION

We have developed a novel method for reconstructing 3D infarct geometry from segmented slices of Lo-res clinical LGE-CMR images. The developed method has outperformed alternative approaches in reproducing expert manual reconstructions and in electrophysiological simulations of both normal and abnormal cardiac function. This study is the first that has developed and evaluated a method specifically for 3D infarct reconstruction from Lo-res clinical images and constitutes an important step in advancing clinical applications of personalized simulations of cardiac electrophysiology.