Abstract
Purpose:
Cortical bone supports and protects human skeletal functions and plays an important role in determining bone strength and fracture risk. Cortical bone segmentation at a peripheral site using multirow-detector CT (MD-CT) imaging is useful for in vivo assessment of bone strength and fracture risk. Major challenges for the task emerge from limited spatial resolution, low signal-to-noise ratio, presence of cortical pores, and structural complexity over the transition between trabecular and cortical bones. An automated algorithm for cortical bone segmentation at the distal tibia from in vivo MD-CT imaging is presented and its performance and application are examined.
Methods:
The algorithm is completed in two major steps—(1) bone filling, alignment, and region-of-interest computation and (2) segmentation of cortical bone. After the first step, the following sequence of tasks is performed to accomplish cortical bone segmentation—(1) detection of marrow space and possible pores, (2) computation of cortical bone thickness, detection of recession points, and confirmation and filling of true pores, and (3) detection of endosteal boundary and delineation of cortical bone. Effective generalizations of several digital topologic and geometric techniques are introduced and a fully automated algorithm is presented for cortical bone segmentation.
Results:
An accuracy of 95.1% in terms of volume of agreement with manual outlining of cortical bone was observed in human MD-CT scans, while an accuracy of 88.5% was achieved when compared with manual outlining on postregistered high resolution micro-CT imaging. An intraclass correlation coefficient of 0.98 was obtained in cadaveric repeat scans. A pilot study was conducted to describe gender differences in cortical bone properties. This study involved 51 female and 46 male participants (age: 19–20 yr) from the Iowa Bone Development Study. Results from this pilot study suggest that, on average after adjustment for height and weight differences, males have thicker cortex (mean difference 0.33 mm and effect size 0.92 at the anterior region) with lower bone mineral density (mean difference −28.73 mg/cm3 and effect size 1.35 at the posterior region) as compared to females.
Conclusions:
The algorithm presented is suitable for fully automated segmentation of cortical bone in MD-CT imaging of the distal tibia with high accuracy and reproducibility. Analysis of data from a pilot study demonstrated that the cortical bone indices allow quantification of gender differences in cortical bone from MD-CT imaging. Application to larger population groups, including those with compromised bone, is needed.
Keywords: osteoporosis, cortical bone, image segmentation, CT imaging, fuzzy digital topology and geometry
1. INTRODUCTION
Cortical bone is one of the two types of osseous tissue and forms the cortex of individual bones and facilitates supporting and protecting their function. Adult bone diseases, especially osteoporosis, lead to increased risk of fracture associated with substantial morbidity, mortality, and financial costs.1 Although osteoporosis is defined by low bone mineral density (BMD), BMD explains 60%–70% of the variability in bone strength,2,3 with the remaining variability due to the cumulative and synergistic effects of other factors, including geometry and microarchitecture of cortical and trabecular bones.2,4 Trying to discern the relative contributions of trabecular and cortical bones to load bearing during locomotion and falling has been challenging.5–7 Several clinical studies have reported that cortical bone thinning and high porosity are associated with increased risk of osteoporotic low-trauma fractures.8–13 There is evidence in the literature indicating that age-related bone loss for both men and women leads to reduced cortical bone density as well as thinner cortex;14–17 however, the loss is larger for women, especially after menopause.14,15 Several researchers have studied effects of drug treatment in cortical bone.18–21 In a study on postmenopausal women (N = 179), Eastell and colleagues20 observed cortical bone volume in the total hip and trochanteric regions increased (7% and 9%, respectively) in the once-yearly zoledronic acid treatment group versus placebo. Black et al.18 reported a similar finding studying the effects of alendronate treatment in cortical bone. Several studies have investigated degeneration of cortical bone loss properties, such as bone content, thickness, and porosity, under osteoporosis.22–24 Recently, a thorough review in cortical bone assessed with computed tomography at the proximal femur and its relation with fracture risk, aging, and drug treatment have been reported by Johannesdottir et al.25
Most of the existing cortical bone segmentation algorithms at peripheral sites are dedicated to microcomputed tomography (μ-CT)26,27 and high resolution peripheral quantitative CT (HR-pQCT)19,22,28,29 imaging. Laib et al.30 applied a semiautomated slice-by-slice hand contouring technique for cortical bone segmentation on three-dimensional (3-D) quantitative CT (QCT) images. Gelaude et al.31 incorporated region growing and spline-fitting approaches in a deformable model to develop a semiautomated cortical bone segmentation method. Gomberg et al.32 combined region growing and morphological operations with cortical edge detection on locally orthogonal sample lines to develop a cortical bone segmentation algorithm for magnetic resonance imaging (MRI). Buie et al.27 presented a cortical bone segmentation algorithm for μ-CT imaging using dual thresholding and connective filters. Valentinitsch et al.29 developed a machine learning based classifier algorithm to label cortical bone voxels in HR-pQCT bone data. Treece et al.33 used a CT point spread function to calculate femur cortex thickness and later improved his method by assuming a fixed density value.34 A few algorithms have been dedicated for cortical bone segmentation at femur using 3-D QCT imaging.33,35–38 Recent advancements in multirow-detector CT (MD-CT) imaging technologies have enabled a resolution that allows in vivo segmentation of individual trabeculae and their microarchitectural analysis at peripheral anatomic sites, e.g., distal tibia.39 A major advantage of bone CT imaging at a peripheral site as compared to a central site, e.g., proximal femur is that a peripheral bone CT requires significantly lower radiation dose as compared to a femur CT—a few days of background radiation for a peripheral bone CT versus two or three years of background radiation for a bone CT at a central site. Thus, peripheral bone CT imaging may be performed on low risk individuals, while a bone CT at a central site on low risk individuals may be difficult to justify. To maximally benefit from MD-CT bone imaging at a peripheral site, it is important to derive cortical bone properties and outcomes from such images. A fully automated and thoroughly validated cortical bone segmentation algorithm for MD-CT bone imaging at a peripheral anatomic site has not yet been established. The segmentation methods cited above were developed for different image resolution regimes or for different anatomic sites and may not work for cortical bone segmentation with peripheral MD-CT imaging. In this paper, a fully automated cortical bone segmentation algorithm is presented for in vivo MD-CT imaging of human distal tibia. This algorithm will advance the medical physics science by extending the role of MD-CT imaging for assessment of bone quality at a peripheral anatomic site. The accuracy of the method was examined using in vivo MD-CT scans of the distal tibia in young adults as well as high resolution micro-CT images of cadaveric specimens. The reproducibility of the method was evaluated using three repeat scans of cadaveric specimens. The application of the algorithm was assessed in a human pilot study that examined gender differences in cortical bone properties.
2. METHODS
Cortical bone segmentation for in vivo MD-CT imaging at a peripheral site offers several challenges, including limited image resolution, noise, presence of cortical pores, and structural complexity over the transition between trabecular and cortical bones, which prohibits thresholding and conventional morphological approaches to accomplish the task. In this paper, we meet these challenges by using larger contextual and topological modeling of the tibial bone through a new generalization of the fuzzy distance transform (FDT)40,41 and connectivity analysis (see the Appendix).42,43 A preliminary version of this method was reported in a conference paper44 for image processing and pattern recognition community. The overall method is completed in two major steps—(1) bone filling, alignment, and region-of-interest (ROI) computation and (2) segmentation of cortical bone. The purpose of the first step is to fill the bone region providing a well-defined periosteal surface and then to realign the axis of the distal tibia with the coordinate z-axis. This step facilitates accurate and robust identification of the distal tibial end-plateau as well as location of subject-specific ROIs at different tibial lengths.
2.A. Bone filling, alignment, and ROI computation
This step begins with conversion of image CT numbers into BMD values [Fig. 1(a)] using a calibration phantom. A calibration CT phantom scan was acquired immediately after each CT bone scan. The CT calibration curve describing the relation between CT Hounsfield units (HU) and electron density was separately computed for each bone CT scan from its matching calibration phantom scan. The relation curve was derived using the set of pairs each consisting of the average CT number and the known material density corresponding to a cylinder in the phantom. All subsequent operations are applied on BMD images. The next task is to generate a filled-in shape for the tibia after separating the tibia from the assembly of other bones and soft-tissues. To accomplish this task, first, a simple thresholding at 1233 mg/cm3 is applied on the BMD image to isolate the bone structure from marrow and other soft-tissues. The BMD threshold value of 1233 mg/cm3 was selected as the average of threshold values manually selected by three independent users on five randomly selected in vivo MD-CT images. Each user was asked to select a threshold value to isolate bone from marrow and other soft-tissues. The standard deviation and the range of user specified BMD threshold values observed were 39 and [1190, 1350], respectively. It may be noted that the constant BMD threshold of 1233 mg/cm3 was applied to all MD-CT ankle images used in this paper. Thus, the algorithm requires no user interaction while applying it to individual images. For a different MD-CT scanner or an imaging protocol with moderately different kVp and mAs, the BMD characteristic should not alter significantly. It is expected that the same BMD threshold will work for such situations. However, a different scanner or imaging protocol with significantly different spatial resolutions or noise characteristics may require a different BMD threshold and a similar experiment should be performed to determine the optimum threshold for such scanners or imaging protocols. In the current study, all images were acquired at 0.2 mm slice thickness and 0.2 × 0.2 mm2 pixel-size, and at SNR of 23.4 computed over the representative cortical bone cylinder in the CT image of the density calibration phantom used in our experiments. On the thresholded image, the largest component was computed [Fig. 1(b)] to remove the fibula and other bones at the ankle assembly. Let Sbone denote the set of bone voxels of tibia and let Snonbone denote the set of nonbone voxels, including marrow, soft-tissues, and the space outside the tibia. The filled-in bone shape was computed using the following sequence of operations:
-
(1)
Computation of the distance transform (see the Appendix) DTbone from Sbone providing the Euclidean distance of a voxel from Sbone [Fig. 1(c)].
-
(2)
Computation of fuzzy connectivity, denoted as FCmorpho, on the distance field DTbone with a set of seed S preset at corner voxels of the image space. It may be noted that these seed points are automatically selected by the algorithm and no user interaction is required. Marrow voxels inside the tibia are expected to be disconnected from the background, so ideally FCmorpho values at marrow voxels should be zero. However, often, the cortex contains small leaks and fuzzy connectivity paths (see the Appendix) sneak through such leaks. Since such leaks are small holes on the cortex with low values of DTbone(p), any path through those holes possesses a low value of FCmorpho. Thus, FCmorpho at marrow voxels are always small because a path from the background to marrow has to pass though one of those leaks on the cortex [Fig. 1(d)]. We refer to this unique connectivity on a distance transform field as morpho-connectivity, because it can be shown that, for any two object voxels p, q, their morpho-connectivity determines the minimum scale of a morphological erosion operator disconnecting p, q.
-
(3)
Computation of dilated tibia by thresholding the morpho-connectivity image FCmorpho at a threshold value of thr barely avoiding marrow cavity formation on the proximal-most axial slice; let Snontibia be the set of voxels in the thresholded nontibia region [Fig. 1(e)].
-
(4)
Computation of DT DTnontibia from Snontibia [Fig. 1(f)] and selection of the filled-in tibia as the region obtained by thresholding DTnontibia at the value of thr determined in the previous step [Fig. 1(g)].
FIG. 1.
Intermediate results of bone filling. (a) An axial slice from an in vivo MD-CT ankle image after converting CT intensity numbers into BMD values. (b) The largest component (Sbone) of the thresholded BMD image of (a). (c) The FDT map from bone voxels in Sbone. (d) The fuzzy connectivity image on the FDT map of (c) with seeds chosen at corner voxels of the image space. (e) Results of thresholding on the fuzzy connectivity image of (d) at the value barely avoiding marrow cavity formation on the proximal-most axial slice. (f) The FDT map from the surrounding white region in (e). (g) The filled bone region derived by thresholding the image of (f) at the same threshold as used for (e). (h) Bone volume fraction image within the filled bone region.
The filled-in representation of the tibial bone was used to reorient the tibia and to identify the distal tibial end-plateau defined as the most proximal location on the distal tibial end plate after aligning the tibial axis with the coordinate z-axis. Finally, the reoriented bone and the location of the distal tibial end-plateau were used to determine the matching ROIs in individual bones. The method works as follows. First, a rough estimate of the distal tibial end-plateau location is performed by analyzing cross sectional images of filled-in tibial bone and the end-plateau is located just above the first image slice containing a 2-D cavity in the filled-in bone while tracing slices from proximal to distal [Fig. 2(c)]. In general, such a 2-D cavity consists of multiple voxels; therefore, the center of gravity of the cavity is used as the location of the distal tibial end-plateau. After a rough estimate of the distal tibial end-plateau, image slices above 8% of the tibial length from the end-plateau are used to compute the tibial axis. Also, a 40% peel is applied to this region to make it thinner and easier to determine the axis [Fig. 2(c)]. The axis of the tibia is computed as the best-fit line to the thinned region. The bone is reoriented to align its axis with the image z-axis [Fig. 2(d)] and, simultaneously, the image is interpolated at 150 μm isotropic voxel and the distal tibial end-plateau is relocated using the same logic as before. Four adjacent axial cylindrical ROIs, each covering 2% of the tibial length, were located at 8%, 10%, 12%, and 14% proximal to the distal endplate as shown in Fig. 2(d). All cortical bone segmentation and analysis were applied within the axial cylindrical ROIs covering 8% of the tibial length. Tibia length was acquired from the MD-CT scout scans.
FIG. 2.
Bone alignment and ROI computation. (a) An original MD-CT image slice. (b) Filled bone region for the distal tibia. (c) Initial location of the distal tibial end-plateau (white dot) and the shaded region used for bone alignment. (d) Final location of the tibial end-plateau and the ROI covering 8%–16% of the tibia. Although, the process is applied in 3-D, 2-D illustrations are used for demonstration.
2.B. Cortical bone segmentation
Cortical bone segmentation is applied on the output of the previous step with well-defined periosteum surface—the outer cylindrical boundary of the filled tibia bone ROIs. The algorithm works as follows. At a given periosteal voxel, the cortical thickness is computed as the distance of the voxel from the endosteum. Finally, the cortical bone region is delineated as the set of all bone voxels whose distance from some periosteal voxel is less than or equal to its thickness value. Here, a major challenge emerges due to the presence of cortical pores artificially reducing local thickness at nearby periosteal voxels. This challenge is overcome by identifying possible cortical bone pores through connectivity analysis and then confirming actual pores by matching possible pores with sudden recession points of cortical thickness along the periosteal boundary. These steps are iterated until no more cortical pores are confirmed. A workflow diagram of the cortical bone segmentation algorithm is presented in Fig. 3 and three major tasks are identified as follows—(1) detection of marrow space and possible pores (task blocks on the top row), (2) computation of cortical bone thickness, detection of recession points, and confirmation and filling of true pores (task blocks on the middle two rows), and (3) detection of endosteal boundary and delineation of cortical bone (task blocks on the bottom row).
FIG. 3.
Workflow diagram of the cortical bone segmentation algorithm after bone filling, reorientation, and ROI detection. See text for further discussion.
2.B.1. Connectivity analysis and detection of possible pores
First, bone structures are isolated by thresholding the BMD image at 1233 mg/cm3. Possible cortical pores are detected in the thresholded image as follows. Let Stibia denote the set of all voxels in the filled and reoriented tibia within the target ROI [Fig. 4(a)] and let give the BMD value at each voxel in Stibia. Also, let Sbone ⊂ Stibia denote the set of bone voxels and Snonbone = Stibia − Sbone be the set of marrow and cortical pore voxels [Fig. 4(c)]. Let Speriosteum denote the set of voxels forming the periosteum which fall outside Stibia but 26-adjacent to it; thus, the periosteum Speriosteum [Fig. 4(c)] wraps around the ROI Stibia. The set of voxels outside Stibia∪Speriosteum, denoted by Sbackground, is excluded from all subsequent processing. Nonbone voxels Snonbone ⊂ Stibia inside the tibia are further classified into confident marrow (green) and possible cortical pore (blue) voxels; let Smarrow and Spore denote these two sets. The set Smarrow is computed as the largest 6-component of Snonbone and Spore = Snonbone − Smarrow.
FIG. 4.
Results of intermediate steps during cortical bone segmentation. (a) ROI volume and an image slice chosen for illustration. (b) BMD image on the chosen slice. (c) Marrow space (marked), possible cortical pores (marked by the gray circle), and the periosteal boundary (outlined). (d) The FDT map from marrow space and possible cortical pores; a possible cortical bone pore and the matching thickness are marked with a circle. (e) Same as (d) after filling the confirmed cortical pore. (f) The generalized FDT from the periosteum with the negative of local thickness value initialized at each periosteal voxel; see text for explanation. (g) Cortical bone segmented as the region with nonpositive FDT values in (f). (h) Segmented trabecular bone region. (i) Overlaid cortical bone region on the CT image.
2.B.2. Computation of cortical bone thickness, detection of recession points, and confirmation and filling of true pores
Here, the overall goal is to confirm and fill true cortical pores and to refine local cortical thickness values at individual periosteal voxels, which works as follows. Cortical pores are confirmed by identifying sudden recessions in thickness values along the periosteum and then linking such recession points with possible pores. Initial thickness values at periosteal voxels are computed as their FDT values from the set of marrow or possible pore voxels, i.e., Smarrow∪Spore. Sudden recession points of computed thickness appear along the periosteal border due to the presence of cortical pores. On a given image slice, a periosteal boundary is represented as a four-path, say, p0, p1, …, pi−1, pi, pi+1, …, pN−1. A given voxel pi on the periosteum is a recession voxel if the computed thickness value at pi is smaller than half of the average of the thickness values at voxels pi±j, where j = L, L + 1, …, H. Let o denote the center of gravity (c.g.) of the tibia on the given image slice. The values H and L were chosen such that the three points pi, o, and pi+L create an angle of 5° while the points pi, o, and pi+H represent an angle of 10°. After a recession voxel pi is detected, the nonbone voxel, say q, nearest to pi is identified. Finally, if q is a possible pore voxel, i.e., q ∈ Spore, then the 6-component Cq of Spore containing q is confirmed as a true cortical pore. To fill the true pore Cq, the set Snonbone of nonbone voxels is reduced to Snonbone − Cq while the set Sbone of bone voxels is augmented to Sbone∪Cq. After all recession voxels are identified and matching pores are filled, the cortical bone thickness is recomputed along the periosteal boundary and the process continues until no new true pores are confirmed. For all images used in this paper, the process converged in three or fewer iterations. It may be worth mentioning that, at the current MD-CT resolution, it is not possible to identify small pores. In this paper, we do not aim to analyze cortical pore morphology. Instead, the method described here aims to detect all cortical pores surviving at the current resolution so that the artificial reduction in cortical bone thickness at the vicinity of a cortical pore is reverted. Once, the correct measure of cortical bone thickness is obtained, the method of segmenting the cortical bone region is described in Sec. 2.B.3. Also, it should be clarified that the pore filling process fills the pore cavities in a topologic sense only and no increase in actual BMD values takes place. Thus, the pore filling process does not artificially inflate cortical bone measures.
2.B.3. Detection of endosteal boundary and delineation of cortical bone
The goal of this step is to delineate the cortical bone region, which is accomplished using the cortical thickness distribution along the periosteum computed in the previous step. Let denote the cortical bone thickness at a periosteal voxel p ∈ Speriosteum, which is computed as the FDT value from the marrow space after filling all cortical pores as described in the previous step. The cortical bone region Scortex is computed as the set of all voxels whose distance from some periosteal voxel p is less than its cortical thickness and this task is accomplished using the generalized FDT (see the Appendix). At each voxel p ∈ Speriosteum, the FDT value is initialized as , the negative of the cortical bone thickness at p. A large value is initialized at each voxel inside Sbone. Finally, the path propagation is confined to the set of voxels Sbone∪Speriosteum. Thus, each bone voxel, which is closer to a periosteal voxel than its cortical thickness, gets a generalized FDT value greater than or equal to zero. Finally, the outer layer Souter-cortex on cortex is defined as the set of cortex bone voxels, which are 6-adjacent to Speriosteum. Results of cortical bone segmentation on a sagittal and a coronal image planes are shown in Fig. 5, which show the continuity of the endosteal boundary in the Z-direction.
FIG. 5.
Results of cortical bone segmentation on a coronal (a) and sagittal (b) MD-CT image planes. It illustrates the continuity of the endosteal boundary in the Z-direction.
2.C. Experimental methods
This study was designed to accomplish the following milestones—(1) evaluation of the accuracy of the cortical bone segmentation algorithm in terms of its agreement with manual outlining, (2) evaluation of repeat MD-CT scan reproducibility of different cortical bone measures, and (3) assessment of the method’s ability to detect gender differences in cortical bone properties. All images were obtained at the distal tibia site. To examine the accuracy of the method, two experiments were conducted. The first experiment was aimed to assess the performance of the segmentation algorithm, which was achieved by comparing the results of automated cortical segmentation with the manual outlining of cortical bone on matching in vivo MD-CT images. The second experiment was designed to examine the accuracy of cortical bone segmentation at MD-CT imaging resolution. It was accomplished on a cadaveric ankle study where MD-CT-based automated cortical bone segmentation results were compared with the results of manual outlining on postregistered high resolution micro-CT images. To evaluate the method’s reproducibility, three repeat-scan MD-CT images were obtained on human cadaveric ankle specimens. Also, MD-CT scans of the distal tibia were obtained for the human pilot study. Different materials and methods for these applications are described in the following.
2.C.1. Cortical bone thickness and density measures
Each MD-CT image was processed through the following cascade of steps: (1) computation of the BMD image, (2) bone reorientation, interpolation, and ROI selection, (3) application of cortical segmentation of the ROI image data, and (4) computation of cortical measures. MD-CT image numbers in the HU were converted to BMD (mg/cm3) values using a calibration phantom. The INTable™ Calibration Phantom: Solid Calcium Hydroxyapatite Design (Image Analysis, Inc., Columbia, KY) was used for all cadaveric specimen scans which were acquired before human scans. Later, the Gammex RMI 467 Tissue Characterization Phantom (Gammex RMI, Middleton, WI) was obtained and used for all in vivo scans. The Gammax RMI 467 phantom was preferred and adopted for in vivo scans because it has calibration cylinders with high material density suitable for characterization of the relation between CT numbers and electron density for materials similar to bone. To reduce any phantom-induced density bias, a correspondence was established between the density values of the INTable and the RMI calibration phantoms using their CT images and cadaveric images were recalibrated with the RMI phantom.
Following Sec. 2.A, four axial tibial sections, namely, T8−10, T10−12, T12−14, and T14−16, covering 8%–16% of the tibia were used as ROIs. Also, the section of 8%–16% of the tibia was subdivided into four angular sections,19 namely, Alateral, Aanterior, Amedial, and Aposterior, using the reference line joining the centers-of-gravity of the cross sections of the tibia and fibula (Fig. 6). Cortical bone thickness and density measures were computed over each ROI using the following equations:
| (1) |
| (2) |
FIG. 6.
Illustration of angular ROIs Alateral, Aanterior, Amedial, and Aposterior using the reference line joining the center of gravity (c.g.) of the tibia with that of the fibula. Each angular section covers 90° of the angular space.
2.C.2. Cadaveric specimens
Fifteen fresh-frozen human cadaveric ankle specimens were obtained from 11 body donors (age at death: 55–91 yr). Bodies were obtained under the Deeded Bodies Program, The University of Iowa, Iowa City, IA, and the ankle specimens were removed at the midtibia region. Exclusion criteria for this study were evidence of previous fracture or knowledge of bone tumor or bone metastasis. These ankle specimens were kept frozen until the performance of MD-CT imaging following the protocol described in Sec. 2.C.3.
2.C.3. Multirow-detector CT imaging
High resolution MD-CT scans of the distal tibia were acquired at the University of Iowa Comprehensive Lung Imaging Center on a 128 slice SOMATOM Definition Flash scanner (Siemens, Munich, Germany) using the following CT parameters: single tube Spiral acquisition at 120 kV, 200 effective mAs, 1 s rotation speed, pitch factor: 1.0, nominal collimation: 16 × 0.3 mm, scan length of 10 cm beginning at the distal tibia end-plateau, and total effective dose equivalent: 170 μSv ≈ 10 days of environmental radiation in the U.S. One AP projection scout scan of the entire tibia was acquired to locate the field of view (FOV) for the CT scan as well as to determine the tibial length. Tibial length was determined by locating the distal and proximal tibial plateaus in the AP projection MD-CT scout scan of the entire tibia. For cadaveric specimens, gender-specific average tibia lengths, computed from in vivo scans, were used. High resolution MD-CT scan mode: The Siemens Flash scanner has 2 × 64 rows of 0.6 mm detectors under two x-ray guns allowing operation in both single and dual source scan modes. The highest resolution single gun scan mode was used, which activated 16 of the most central detectors to maximize beam quality. Siemens double z sampling allowed for a dual sampling of the 0.6 mm detectors, splitting the signal so that each detector created a 0.3 mm slice in the z plane.45,46 As specified by the manufacturer, the z-UHR scan mode within the Siemens Flash scanner enabled high spatial resolution with 14.0 line-pairs/cm at 10% modulation transfer function (MTF). Images were reconstructed at 0.2 mm slice thickness and 0.2 × 0.2 in-plane resolution using a normal cone beam method with a special U70u kernel achieving high structural resolution. Three repeat MD-CT scans of each distal tibia specimen were acquired after repositioning the specimen on the CT table before each scan.
2.C.4. Micro-CT imaging
Following MD-CT repeat scans, six randomly chosen cadaveric ankle specimens were further scanned on a Micro-cat II (Siemens Pre-Clinical, TN) cone beam micro-CT scanner after removing soft-tissue and dislocating the tibia from the ankle joint to fit the specimen in the scanner. The following micro-CT parameters were used: 100 kV, 200 mAs, 720 projections over 220°, exposure 1 s/projection, and 2 mm Al filter for beam hardening. The images were reconstructed using filtered back-projection: image size 1536 × 1536 and 1024 slices at 28.8 μm isotropic voxel size.
2.C.5. In vivo pilot studies
In vivo MD-CT distal tibia bone scans were obtained for 46 healthy males and 51 healthy females (age: 19–20 yr) as part of the ongoing Iowa Bone Development Study (IBDS). MD-CT scans were obtained on the left lower leg following the same protocol used for cadaveric specimens (Sec. 2.C.3). Tibial length was determined by locating the distal and proximal tibial plateaus in the AP projection MD-CT scout scan of the entire tibia. All human scans were acquired following the protocol approved by the IRB at the University of Iowa.
2.C.6. Image processing and statistical analysis
For the first experiment examining the accuracy of the new segmentation algorithm, the computerized segmentation results of the cortical bone region were compared with the results of manual outlining on 20 axial image slices from each MD-CT image. Among the 20 slices, 5 consecutive slices were randomly chosen from each of the four tibial sections T8−10, T10−12, T12−14, and T14−16. Segmentation of the periosteal boundary is straight-forward and easily obtained by thresholding and region growing.47 Therefore, we restrained ourselves from manual delineation of the periosteal boundary and considered computerized segmentation of the periosteum as the ground truth. On every target image slice, the endosteal boundary was manually outlined and was linked with the computerized segmentation of the periosteum to generate the ground truth for cortical bone mask. Manual outlining of the endosteal boundary was performed by an independent expert using the itk-snap software.48 Let be the set of voxels falling inside the true segmentation of the cortical bone region and let denote the computerized segmentation for the same. The Jaccard index (JI) was used to characterize the accuracy of a computerized segmentation result as follows:
| (3) |
Also, the Dice coefficient was computed as another accuracy index. Further, Type I error of cortical bone segmentation was computed as the over segmentation or false positive error as compared to the known truth. Similarly, Type II error was computed as the under segmentation or false negative error. Both Type I and Type II errors were normalized by the volume of the known truth for the cortical bone region.
For the second accuracy experiment, each MD-CT image was registered onto the matching micro-CT image using the rigid transformation registration toolkit inside the analyze 12.0 software, AnalyzeDirect, Inc., Overland Park, KS. The automatically segmented cortical bone mask was mapped onto the micro-CT image by applying the same rigid transformation used for registration. A 1 cm axial section of the micro-CT image, scanned between 10% and 14% of the tibia of each specimen, was used in this experiment. Two subregions, each consisting of five contiguous slices, were randomly selected in each micro-CT image. Manual outlining of cortical bone was performed by an expert user on each selected micro-CT image slice, which was used as the ground truth for this experiment. Finally, the Jaccard index and Dice coefficient as well as Type I and Type II errors were computed to assess the accuracy of the MD-CT-based cortical bone segmentation results.
To assess the reproducibility of the method, intraclass correlation coefficients (ICC) of bone measures were computed from three repeat MD-CT scans of 15 cadaveric ankle specimens.
In vivo statistical analysis investigated gender differences in cortical measures for healthy young adults (IBDS cohort). Descriptive statistics for cortical thickness and density measures for male and female participants for four tibial sections and four angular ROIs were calculated. Gender differences in cortical bone thickness and density measures were tested by first fitting a simple linear regression model with only gender included, and then fitting a multivariable linear regression model that included height and weight as covariates.49 The difference in gender-specific least-squares means was compared and the effect size was estimated as the difference between the gender-specific least-squares means standardized by , where MSE is the mean square error from the corresponding regression model.
3. RESULTS
Results of intermediate steps during cortical bone segmentation on an in vivo MD-CT image are illustrated in Fig. 4. Final results of cortical bone delineation are visually satisfactory. Results of accuracy, reproducibility, and in vivo experiments are presented in the following.
3.A. Accuracy of cortical bone segmentation
The first accuracy experiment was conducted on in vivo MD-CT images of distal tibia for ten randomly chosen IBDS cohort members (5 M, 5 F). As described in Sec. 2.C.6, the accuracy was computed by comparing computerized segmentation with manually outlining of cortical bone regions on 20 axial image slices from each MD-CT image. A visual comparison of between computerized and manual segmentations of cortical bone on in vivo MD-CT image slices of distal tibia is presented in Fig. 7. An average accuracy of 95.1% with a standard deviation of 1.0% was observed from data for the ten randomly chosen in vivo MD-CT images. Considering the challenges of cortical bone segmentation at the relatively low resolution of MD-CT imaging, the observed accuracy results are encouraging. Also, the Dice coefficient was computed for cortical bone segmentation results by the new algorithm and the coefficient value was 97.5%. Type I and Type II errors in overlapping areas of automated cortical bone segmentation, as compared to manual outlining on MD-CT images, are plotted in Fig. 8. Here, each data point represents the results from one subregion consisting of five axial MD-CT image slices.
FIG. 7.
Comparison between computerized segmentation and manual outlining of cortical bone regions on a MD-CT image. The figure on the left shows the slice locations of (a)–(d) along the tibial axis. The area of agreement between the two segmentation results along with Type I and Type II errors in mismatch areas are marked. Zoomed in panels of Type I and Type II errors are displayed in (c) and (d).
FIG. 8.
Type I and Type II errors in mismatch areas between computerized segmentation and manual outlining of cortical bone regions on matching MD-CT image slices. Note that Type I and Type II errors represent the over segmentation and under segmentation errors, respectively.
The second accuracy experiment was performed on MD-CT and micro-CT images of six cadaveric ankle specimens. MD-CT-based computerized segmentation and micro-CT-based manual outlining results of cortical bone are qualitatively compared in Fig. 9. For each cadaveric specimen, two subregions, each consisting of five consecutive axial micro-CT image slices, were used for the accuracy analysis. An average accuracy of 88.5% in terms of area of overlap with the manual outlining of micro-CT images was found. The distribution of Type I and Type II errors as a function of cross-sectional area is presented in Fig. 10. Each data point in Fig. 10 represents the data from one subregion consisting of five axial micro-CT image slices. The observed Dice coefficient of MD-CT-based automated cortical bone segmentation as compared to manual outlining on micro-CT images was 93.8%.
FIG. 9.
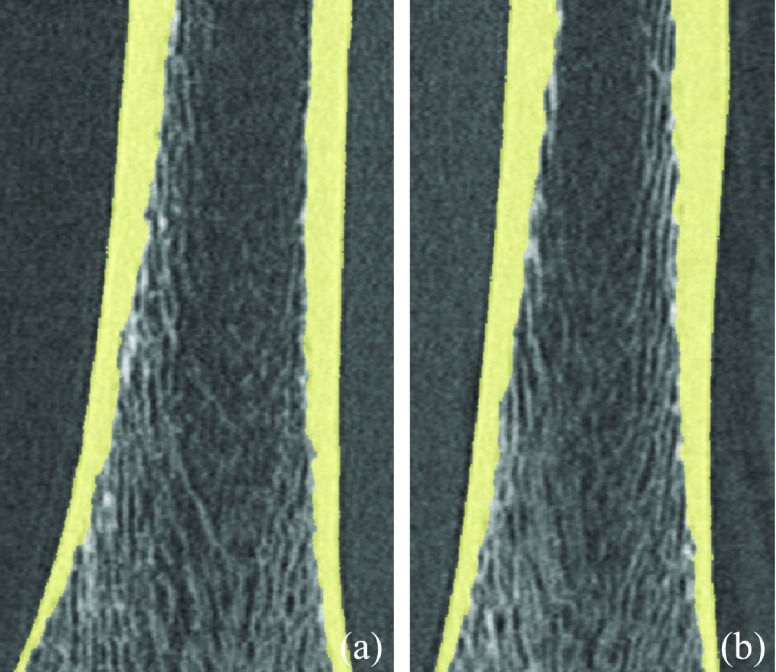
Comparison between MD-CT based computerized segmentation of cortical bone region and manual outlining on postregistered micro-CT image slices. The area of agreement between the two segmentation results along with Type I and Type II errors in mismatch areas are marked. [(a) and (b)] Comparative results on micro-CT image slices with thin (a) and thick (b) cortical bones.
FIG. 10.
Type I and Type II errors in mismatch areas between MD-CT based computerized segmentation of cortical bone region and manual outlining on postregistered micro-CT image slices.
3.B. Repeat-scan reproducibility of cortical bone segmentation in cadaveric ankle specimens
To assess reproducibility of the cortical bone segmentation algorithm, repeat-scan ICC were computed for each of the two cortical measures CBTh and CBDensity over each of the eight ROIs, namely, T8−10, T10−12, T12−14, T14−16, Alateral, Aanterior, Amedial, and Aposterior. The observed ICCs for both cortical bone thickness and density measures were high for each of the eight ROIs (Table I). The mean and standard deviation of ICCs over different ROIs were 0.982 and 0.015, respectively, for cortical bone thickness and 0.979 and 0.099, respectively, for cortical bone density. Observed results of repeat-scan reproducibility of cortical bone measures were highly satisfactory, confirming the repeatability of cortical bone segmentation and the resulting measures.
TABLE I.
Mean, standard deviation (SD), and intraclass correlation coefficient (ICC) for cortical bone measures over eight ROIs computed from MD-CT repeat scans of the 15 cadaveric ankle specimens mentioned in Sec. 2.C.2.
| CBTh (mm) | CBDensity (mg/cm3) | |||
|---|---|---|---|---|
| ROI | Mean ± SD | ICC | Mean ± SD | ICC |
| T8−10 | 1.16 ± 0.36 | 0.97 | 1599.0 ± 91.5 | 0.98 |
| T10−12 | 1.33 ± 0.39 | 0.98 | 1653.8 ± 78.1 | 0.98 |
| T12−14 | 1.44 ± 0.43 | 0.99 | 1684.8 ± 68.8 | 0.98 |
| T14−16 | 1.57 ± 0.49 | 0.99 | 1710.0 ± 65.9 | 0.99 |
| Alateral | 1.38 ± 0.40 | 0.98 | 1675.5 ± 71.7 | 0.98 |
| Aanterior | 1.37 ± 0.47 | 0.97 | 1650.0 ± 83.0 | 0.97 |
| Amedial | 1.38 ± 0.45 | 0.97 | 1648.2 ± 79.7 | 0.98 |
| Aposterior | 1.37 ± 0.44 | 0.99 | 1673.9 ± 74.3 | 0.99 |
3.C. In vivo pilot study results
IBDS participants were 19–20 yr old and included 51 females (height mean ± SD = 165.2 ± 6.8 cm and weight 67.9 ± 21.0 kg) and 46 males (height 180.4 ± 8.0 cm and weight 83.6 ± 14.8 kg). Cortical bone thickness and density measures for male and female participants for four tibial sections and four angular ROIs are described in Table II. Males showed significantly higher height-weight-adjusted cortical bone thickness than females, specifically in the anterior region (region with the highest cortical thickness) (F-statistic p-value < 0.01), and significantly lower height-weight-adjusted cortical bone density across all regions (F-statistic p-value < 0.01) with large effect sizes (average effect size across T8−10 − T14−16 was −1.31), which could demonstrate adaptation of longer and wider bones to bending. The reduced bone density may also be an adaptation toward maintaining lightness needed for mobility.
TABLE II.
Comparison of cortical bone thickness (mm) and density (mg/cm3) measures between male and female cohort members from the Iowa Bone Development Study.
| Males (N = 46) | Females (N = 51) | Effect sizea | |||
|---|---|---|---|---|---|
| ROI | Mean ± SD | Mean ± SD | Unadjusted | Adjusted | p valueb |
| Thickness (mm) | |||||
| T8−10 | 1.53 ± 0.23 | 1.33 ± 0.18 | 0.97 | 0.73 | 0.02 |
| T10−12 | 1.81 ± 0.24 | 1.58 ± 0.20 | 1.05 | 0.80 | <0.01 |
| T12−14 | 2.06 ± 0.26 | 1.80 ± 0.19 | 1.14 | 0.83 | <0.01 |
| T14−16 | 2.28 ± 0.27 | 2.02 ± 0.20 | 1.12 | 0.74 | 0.01 |
| Alateral | 1.77 ± 0.25 | 1.57 ± 0.29 | 0.72 | 0.56 | 0.06 |
| Aanterior | 2.15 ± 0.30 | 1.82 ± 0.24 | 1.24 | 0.92 | <0.01 |
| Amedial | 1.94 ± 0.33 | 1.67 ± 0.25 | 0.94 | 0.65 | 0.03 |
| Aposterior | 1.81 ± 0.32 | 1.65 ± 0.25 | 0.54 | 0.36 | 0.23 |
| Bone mineral density (mg/cm3) | |||||
| T8−10 | 1850.23 ± 26.11 | 1879.67 ± 29.86 | −1.05 | −1.26 | <0.0001 |
| T10−12 | 1882.49 ± 17.74 | 1909.13 ± 19.53 | −1.42 | −1.35 | <0.0001 |
| T12−14 | 1898.28 ± 14.04 | 1922.44 ± 16.14 | −1.59 | −1.30 | <0.0001 |
| T14−16 | 1907.18 ± 12.89 | 1929.64 ± 13.96 | −1.67 | −1.32 | <0.0001 |
| Alateral | 1883.47 ± 22.41 | 1912.14 ± 23.21 | −1.26 | −1.29 | <0.0001 |
| Aanterior | 1890.26 ± 18.67 | 1909.94 ± 19.80 | −1.02 | −0.88 | <0.01 |
| Amedial | 1887.58 ± 18.00 | 1913.21 ± 20.63 | −1.32 | −1.25 | <0.0001 |
| Aposterior | 1876.86 ± 18.05 | 1905.59 ± 20.44 | −1.48 | −1.35 | <0.0001 |
Effect size was calculated as the difference (males − females) between least-squares means for male and female IBDS cohort members standardized by , where MSE is the mean square error from the linear regression models with (adjusted) and without (unadjusted) adjustment for height and weight.
p-value from multivariable linear regression models with adjustment for height and weight differences.
4. DISCUSSION
Our studies showed that this new cortical bone segmentation algorithm worked fully automatically, i.e., it required no user intervention when applied to individual images, both cadaveric and human, from our study. The algorithm runs on a standard desktop computer, requiring 15–20 min to compute cortical measures for each MD-CT image including preprocessing, bone alignment, ROI selection, and cortical bone segmentation steps. The algorithm requires only one imaging protocol-specific parameter—the BMD threshold, which can be optimized using an independent observer experiment described in Sec. 2.A.
Major challenges in segmentation of cortical bone regions in in vivo MD-CT imaging emerge from limited image resolution, partial voluming, noise, nonuniformity of cortical bone thickness, presence of cortical pores, and structural complexity over the transition between trabecular and cortical bones. These challenges were effectively dealt with using this approach that is based on larger contextual and topological modeling of the tibial bone through a generalized fuzzy distance transform and connectivity analysis on the distance field.
A Dice coefficient of 97.5% was observed for the new MD-CT-based computerized cortical bone segmentation results as compared to manual outlining on matching MD-CT images. On the other hand, a Dice coefficient of 93.8% was observed for the MD-CT-based computerized results when compared with the results obtained using manual outlining on postregistered high resolution micro-CT images. Both Dice coefficients observed for the new method were higher than the Dice coefficient of 90.4% reported by Valentinitsch et al.29 Further, it should be clarified that the accuracy results reported by Valentinitsch et al. were derived from an experiment where automated segmentation results were compared with manual outlining on the same image avoiding the challenges of cross-modality validations such as resolution difference and registration errors.
The distribution of Type I and Type II errors in both accuracy experiments is reported in Figs. 8 and 10. It is observed in these figures that there is a small bias in our computerized algorithm toward over segmentation, i.e., larger Type I errors as compared to Type II errors. This bias is diminished for cortical bones with larger cross-sectional areas. Generally, a small cross-sectional area of cortical bone occurs at a distal location of the tibia where the interconnection between trabecular and cortical bones is high, and some of the small marrow holes near the endosteal boundary may be misjudged as cortical pores. Despite this challenge, the performance of the current method is better than that of the previously reported cortical bone segmentation methods29,50 on HR-pQCT.
The ICC values of computed cortical bone thickness and bone mineral density in repeat MD-CT scans, reported in Table I, suggest that the method is reproducible. Unlike the results reported in Table II for young adults, the observed cortical bone thickness values at different angular sections in cadaveric specimens were mostly uniform. A probable reason behind this observation is that the specimens were collected from cadavers who died at older ages. At an older age, the bone-muscle biomechanical interaction is significantly reduced causing diminished localized angular variations in the cortical thickness. Also, the observed BMD for the cadaveric specimens was low, i.e., increased porosity as compared to the results reported in Table II for young adults. To compare our cortical bone thickness results with the HR-pQCT based results, reported by Burghardt et al.,50 the cortical bone thickness was computed from cadaveric repeat-scan MD-CT images over a 9 mm axial section at 22.5 mm proximal to the distal tibial end-plateau. The observed MD-CT-based mean cortical bone thickness of 1.07 mm at the 22.5 mm location was close to the mean cortical bone thickness of 1.13 mm reported by Burghardt et al. for older individuals. The observed root mean square coefficient of variation (RMSCV) of 0.81% by the MD-CT-based method at the 22.5 mm location was better than the value of 1.5% reported by Burghardt et al. The observed results suggest that, using novel and advanced image processing algorithms, MD-CT imaging offers automated segmentation of cortical bone and computation of thickness and density measures at the distal tibia whose accuracy and reproducibility are comparable to the performance using HR-pQCT imaging. It may be worth examining whether the cortical bone segmentation method provides a similar performance for other scanners and imaging protocols with similar spatial resolution and noise characteristics.
In vivo data from a human pilot study involving 46 male and 51 female young adults showed that males have a thicker cortex, but reduced cortical bone mineral density, i.e., more porous cortex at the distal tibia as compared to females. This observation was consistent across all axial as well as angular regions and statistically significant for most regions. However, cortical bone thickness differences between males and females were not significant at lateral (p = 0.06) and posterior (p = 0.23) angular regions. Based on a HR-pQCT study, Kazakia et al.51 reported the cortical thickness and porosity at the tibia among young and elderly males and females. Their reported data show a 7.0% difference in cortical bone thickness between young males and females, which is lower than the difference of 13.1% observed in our study between young males and females at 8%–10% of the tibia. The results observed in this study are important because the lower cortical bone thickness observed in females puts them at higher risk of osteoporosis and/or low-trauma fractures during age-related bone loss at later phases of life or during bone loss incurred due to other disease processes. Reduced cortical bone mineral density in males could demonstrate adaptation of longer and wider bones to bending and may be a factor to counteract the higher cortical thickness and thus, balance the net skeletal weight. The trade-off of a thicker but more porous cortex to mechanical strength and risk of fracture is yet to be investigated.
5. CONCLUSION
A fully automated cortical bone segmentation algorithm with regional cortical measures was developed for in vivo MD-CT bone imaging at a peripheral site. The algorithm was applied to cadaveric as well as in vivo MD-CT images of the distal tibia. Experimental results demonstrate that the new method is accurate and reproducible. After optimizing the threshold parameter for a specific CT imaging protocol, the algorithm can automatically compute cortical bone measures from acquired images. The method was applied in a human pilot study describing gender differences in cortical bone properties. Observed results are presented and discussed.
ACKNOWLEDGMENTS
This work was supported by the NIH Grant Nos. R01-AR054439 and R01-DE012101. The authors wish to thank Mr. Jered Sieren for performing MD-CT cadaveric and human bone imaging.
APPENDIX: GENERALIZED FUZZY DISTANCE TRANSFORM AND CONNECTIVITY ANALYSIS
A MD-CT image is represented by a CT intensity function fCT on a 3-D rectangular voxel grid Z3, where Z is the set of integers. Two voxels are as 26-adjacent if ∀i = 1, 2, 3, ||pi − qi|| ≤ 1; those are 6-adjacent if .52 Here, 26-adjacency is used for bone voxels, while 6-adjacency is used for marrow voxels. A fuzzy object is a fuzzy subset of Z3 where is its membership function. An α-path π, , is a sequence of voxels p0, p1, …, pN−1 where every two successive voxels are α-adjacent. The length of the path π in the fuzzy object is
| (A1) |
Fuzzy distance40 between any two voxels p, q, denoted as , is the length of the shortest path between p, q, i.e.,
| (A2) |
where is the set of all possible paths between p, q. For any voxel p inside the support of , the fuzzy distance transform or FDT at p, denoted as , is the fuzzy distance of p from the background B = Z3 − O, i.e.,
| (A3) |
The FDT is computed in two steps. The first step is to initialize a zero FDT value within the background B where the FDT value is trivially defined and a large value in O, i.e., not known at the beginning. The second step performs an iterative propagation of FDT values that is governed by the following equation:
| (A4) |
where is the set of voxels adjacent to p excluding p itself. The iterative propagation step of the FDT computation terminates in a finite number of iterations when the FDT values at all voxels stabilize and no further changes are possible.40 In the following, we introduce a simple yet effective generalization of the FDT algorithm that may be useful in several applications. First, let us define the following three sets: (1) L: set of voxels initialized with a large positive value, i.e., the set of voxels with an unknown FDT value at the time of initialization, (2) U: set of voxels initialized with nonlarge values, i.e., the set of voxels with known FDT values at initialization, and (3) V: the set of voxels where no path propagation is allowed, i.e., outside the region of interest. Note that the sets L, U, V are mutually exclusive and exhaustive, i.e., L∩U = U∩V = L∩V = 0̸ and L∪U∪V fills the entire image space. Unlike the case of conventional FDT,40 here, the initial values of the voxels in U may be nonzero, nonuniform, and may include negative values depending upon the target application. This generalization provides an effective and efficient solution to delineate an object after computing locally varying thickness of the object along its centerline or along an edge of the object. Introduction of the notion of V into the framework allows geodesic distance analysis.
Fuzzy connectivity47,53 between any two voxels p, q in the fuzzy object , denoted as , is the connectivity strength of the strongest path between p, q where the strength of connectivity of a path is the smallest membership value on the path, i.e.,
| (A5) |
The connectivity strength, denoted by FC, of a fuzzy connected object induced by a set S of seed voxels is
| (A6) |
REFERENCES
- 1.Singer A. J. and Boonen S., “Osteoporosis management: Translating research into optimal fracture protection II,” Curr. Med. Res. Opin. 24(6), 1789–1796 (2008). 10.1185/03007990802115887 [DOI] [PubMed] [Google Scholar]
- 2.Ammann P. and Rizzoli R., “Bone strength and its determinants,” Osteoporosis Int. 14(Suppl 3), S13–S18 (2003). 10.1007/s00198-002-1345-4 [DOI] [PubMed] [Google Scholar]
- 3.Wehrli F. W., Saha P. K., Gomberg B. R., Song H. K., Snyder P. J., Benito M., Wright A., and Weening R., “Role of magnetic resonance for assessing structure and function of trabecular bone,” Top. Magn. Reson. Imaging 13, 335–356 (2002). 10.1097/00002142-200210000-00005 [DOI] [PubMed] [Google Scholar]
- 4.Seeman E. and Delmas P. D., “Bone quality–the material and structural basis of bone strength and fragility,” N. Engl. J. Med. 354(21), 2250–2261 (2006). 10.1056/NEJMra053077 [DOI] [PubMed] [Google Scholar]
- 5.Holzer G., von Skrbensky G., Holzer L. A., and Pichl W., “Hip fractures and the contribution of cortical versus trabecular bone to femoral neck strength,” J. Bone Miner. Res. 24(3), 468–474 (2009). 10.1359/jbmr.081108 [DOI] [PubMed] [Google Scholar]
- 6.Lotz J. C., Cheal E. J., and Hayes W. C., “Stress distributions within the proximal femur during gait and falls: Implications for osteoporotic fracture,” Osteoporosis Int. 5(4), 252–261 (1995). 10.1007/BF01774015 [DOI] [PubMed] [Google Scholar]
- 7.Verhulp E., van Rietbergen B., and Huiskes R., “Load distribution in the healthy and osteoporotic human proximal femur during a fall to the side,” Bone 42(1), 30–35 (2008). 10.1016/j.bone.2007.08.039 [DOI] [PubMed] [Google Scholar]
- 8.Cheng X., Li J., Lu Y., Keyak J., and Lang T., “Proximal femoral density and geometry measurements by quantitative computed tomography: Association with hip fracture,” Bone 40(1), 169–174 (2007). 10.1016/j.bone.2006.06.018 [DOI] [PubMed] [Google Scholar]
- 9.Yang L., Burton A. C., Bradburn M., Nielson C. M., Orwoll E. S., and Eastell R., “Distribution of bone density in the proximal femur and its association with hip fracture risk in older men: The osteoporotic fractures in men (MrOS) study,” J. Bone Miner. Res. 27(11), 2314–2324 (2012). 10.1002/jbmr.1693 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yang L., Udall W. J., McCloskey E. V., and Eastell R., “Distribution of bone density and cortical thickness in the proximal femur and their association with hip fracture in postmenopausal women: A quantitative computed tomography study,” Osteoporosis Int. 25(1), 251–263 (2014). 10.1007/s00198-013-2401-y [DOI] [PubMed] [Google Scholar]
- 11.Johannesdottir F., Poole K. E., Reeve J., Siggeirsdottir K., Aspelund T., Mogensen B., Jonsson B. Y., Sigurdsson S., Harris T. B., Gudnason V. G., and Sigurdsson G., “Distribution of cortical bone in the femoral neck and hip fracture: A prospective case-control analysis of 143 incident hip fractures; the AGES-REYKJAVIK study,” Bone 48(6), 1268–1276 (2011). 10.1016/j.bone.2011.03.776 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Crabtree N., Loveridge N., Parker M., Rushton N., Power J., Bell K. L., Beck T. J., and Reeve J., “Intracapsular hip fracture and the region-specific loss of cortical bone: Analysis by peripheral quantitative computed tomography,” J. Bone Miner. Res. 16(7), 1318–1328 (2001). 10.1359/jbmr.2001.16.7.1318 [DOI] [PubMed] [Google Scholar]
- 13.Bousson V. D., Adams J., Engelke K., Aout M., Cohen-Solal M., Bergot C., Haguenauer D., Goldberg D., Champion K., Aksouh R., Vicaut E., and Laredo J. D., “In vivo discrimination of hip fracture with quantitative computed tomography: Results from the prospective European femur fracture study (EFFECT),” J. Bone Miner. Res. 26(4), 881–893 (2011). 10.1002/jbmr.270 [DOI] [PubMed] [Google Scholar]
- 14.Riggs B. L., Melton III L. J., Robb R. A., Camp J. J., Atkinson E. J., Peterson J. M., Rouleau P. A., McCollough C. H., Bouxsein M. L., and Khosla S., “Population-based study of age and sex differences in bone volumetric density, size, geometry, and structure at different skeletal sites,” J. Bone Miner. Res. 19(12), 1945–1954 (2004). 10.1359/jbmr.040916 [DOI] [PubMed] [Google Scholar]
- 15.Nicks K. M., Amin S., Melton III L. J., Atkinson E. J., McCready L. K., Riggs B. L., Engelke K., and Khosla S., “Three-dimensional structural analysis of the proximal femur in an age-stratified sample of women,” Bone 55(1), 179–188 (2013). 10.1016/j.bone.2013.02.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sigurdsson G., Aspelund T., Chang M., Jonsdottir B., Sigurdsson S., Eiriksdottir G., Gudmundsson A., Harris T. B., Gudnason V., and Lang T. F., “Increasing sex difference in bone strength in old age: The age, gene/environment susceptibility-reykjavik study (AGES-REYKJAVIK),” Bone 39(3), 644–651 (2006). 10.1016/j.bone.2006.03.020 [DOI] [PubMed] [Google Scholar]
- 17.Poole K. E., Mayhew P. M., Rose C. M., Brown J. K., Bearcroft P. J., Loveridge N., and Reeve J., “Changing structure of the femoral neck across the adult female lifespan,” J. Bone Miner. Res. 25(3), 482–491 (2010). 10.1359/jbmr.090734 [DOI] [PubMed] [Google Scholar]
- 18.Black D. M., Greenspan S. L., Ensrud K. E., Palermo L., McGowan J. A., Lang T. F., Garnero P., Bouxsein M. L., Bilezikian J. P., and Rosen C. J., “The effects of parathyroid hormone and alendronate alone or in combination in postmenopausal osteoporosis,” N. Engl. J. Med. 349(13), 1207–1215 (2003). 10.1056/NEJMoa031975 [DOI] [PubMed] [Google Scholar]
- 19.Burghardt A. J., Kazakia G. J., Sode M., de Papp A. E., Link T. M., and Majumdar S., “A longitudinal HR-pQCT study of alendronate treatment in postmenopausal women with low bone density: Relations among density, cortical and trabecular microarchitecture, biomechanics, and bone turnover,” J. Bone Miner. Res. 25(12), 2558–2571 (2010). 10.1002/jbmr.157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Eastell R., Lang T., Boonen S., Cummings S., Delmas P. D., Cauley J. A., Horowitz Z., Kerzberg E., Bianchi G., Kendler D., Leung P., Man Z., Mesenbrink P., Eriksen E. F., and Black D. M., “Effect of once-yearly zoledronic acid on the spine and hip as measured by quantitative computed tomography: Results of the HORIZON pivotal fracture trial,” Osteoporosis Int. 21(7), 1277–1285 (2010). 10.1007/s00198-009-1077-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yang L., Sycheva A. V., Black D. M., and Eastell R., “Site-specific differential effects of once-yearly zoledronic acid on the hip assessed with quantitative computed tomography: Results from the HORIZON pivotal fracture trial,” Osteoporosis Int. 24(1), 329–338 (2013). 10.1007/s00198-012-2200-x [DOI] [PubMed] [Google Scholar]
- 22.Nishiyama K. K., Macdonald H. M., Buie H. R., Hanley D. A., and Boyd S. K., “Postmenopausal women with osteopenia have higher cortical porosity and thinner cortices at the distal radius and tibia than women with normal aBMD: An in vivo HR-pQCT study,” J. Bone Miner. Res. 25(4), 882–890 (2010). 10.1359/jbmr.091020 [DOI] [PubMed] [Google Scholar]
- 23.Rigotti N. A., Neer R. M., Skates S. J., Herzog D. B., and Nussbaum S. R., “The clinical course of osteoporosis in anorexia nervosa. A longitudinal study of cortical bone mass,” JAMA 265(9), 1133–1138 (1991). 10.1001/jama.1991.03460090081037 [DOI] [PubMed] [Google Scholar]
- 24.Ritzel H., Amling M., Posl M., Hahn M., and Delling G., “The thickness of human vertebral cortical bone and its changes in aging and osteoporosis: A histomorphometric analysis of the complete spinal column from thirty-seven autopsy specimens,” J. Bone Miner. Res. 12(1), 89–95 (1997). 10.1359/jbmr.1997.12.1.89 [DOI] [PubMed] [Google Scholar]
- 25.Johannesdottir F., Turmezei T., and Poole K. E., “Cortical bone assessed with clinical computed tomography at the proximal femur,” J. Bone Miner. Res. 29(4), 771–783 (2014). 10.1002/jbmr.2199 [DOI] [PubMed] [Google Scholar]
- 26.Barck K. H., Lee W. P., Diehl L. J., Ross J., Gribling P., Zhang Y., Nguyen K., van Bruggen N., Hurst S., and Carano R. A., “Quantification of cortical bone loss and repair for therapeutic evaluation in collagen-induced arthritis, by micro-computed tomography and automated image analysis,” Arthritis Rheum. 50(10), 3377–3386 (2004). 10.1002/art.20557 [DOI] [PubMed] [Google Scholar]
- 27.Buie H. R., Campbell G. M., Klinck R. J., MacNeil J. A., and Boyd S. K., “Automatic segmentation of cortical and trabecular compartments based on a dual threshold technique for in vivo micro-CT bone analysis,” Bone 41(4), 505–515 (2007). 10.1016/j.bone.2007.07.007 [DOI] [PubMed] [Google Scholar]
- 28.Boutroy S., Van Rietbergen B., Sornay-Rendu E., Munoz F., Bouxsein M. L., and Delmas P. D., “Finite element analysis based on in vivo HR-pQCT images of the distal radius is associated with wrist fracture in postmenopausal women,” J. Bone Miner. Res. 23(3), 392–399 (2008). 10.1359/jbmr.071108 [DOI] [PubMed] [Google Scholar]
- 29.Valentinitsch A., Patsch J. M., Deutschmann J., Schueller-Weidekamm C., Resch H., Kainberger F., and Langs G., “Automated threshold-independent cortex segmentation by 3D-texture analysis of HR-pQCT scans,” Bone 51(3), 480–487 (2012). 10.1016/j.bone.2012.06.005 [DOI] [PubMed] [Google Scholar]
- 30.Laib A., Hauselmann H. J., and Rüegsegger P., “In vivo high resolution 3D-QCT of the human forearm,” Technol. Health Care 6, 329–337 (1998). [PubMed] [Google Scholar]
- 31.Gelaude F., Vander Sloten J., and Lauwers B., “Semi-automated segmentation and visualisation of outer bone cortex from medical images,” Comput. Methods Biomech. Biomed. Eng. 9(1), 65–77 (2006). 10.1080/10255840600604474 [DOI] [PubMed] [Google Scholar]
- 32.Gomberg B. R., Saha P. K., and Wehrli F. W., “Method for cortical bone structural analysis from magnetic resonance images,” Acad. Radiol. 12, 1320–1332 (2005). 10.1016/j.acra.2005.06.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Treece G. M., Gee A. H., Mayhew P. M., and Poole K. E., “High resolution cortical bone thickness measurement from clinical CT data,” Med. Image Anal. 14(3), 276–290 (2010). 10.1016/j.media.2010.01.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Treece G. M., Poole K. E., and Gee A. H., “Imaging the femoral cortex: Thickness, density and mass from clinical CT,” Med. Image Anal. 16(5), 952–965 (2012). 10.1016/j.media.2012.02.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kang Y., Engelke K., and Kalender W. A., “A new accurate and precise 3-D segmentation method for skeletal structures in volumetric CT data,” IEEE Trans. Med. Imaging 22(5), 586–598 (2003). 10.1109/tmi.2003.812265 [DOI] [PubMed] [Google Scholar]
- 36.Lang T. F., Keyak J. H., Heitz M. W., Augat P., Lu Y., Mathur A., and Genant H. K., “Volumetric quantitative computed tomography of the proximal femur: Precision and relation to bone strength,” Bone 21(1), 101–108 (1997). 10.1016/S8756-3282(97)00072-0 [DOI] [PubMed] [Google Scholar]
- 37.Hangartner T. N. and Short D. F., “Accurate quantification of width and density of bone structures by computed tomography,” Med. Phys. 34(10), 3777–3784 (2007). 10.1118/1.2769102 [DOI] [PubMed] [Google Scholar]
- 38.Prevrhal S., Fox J. C., Shepherd J. A., and Genant H. K., “Accuracy of CT-based thickness measurement of thin structures: Modeling of limited spatial resolution in all three dimensions,” Med. Phys. 30(1), 1–8 (2003). 10.1118/1.1521940 [DOI] [PubMed] [Google Scholar]
- 39.Saha P. K., Xu Y., Duan H., Heiner A., and Liang G., “Volumetric topological analysis: A novel approach for trabecular bone classification on the continuum between plates and rods,” IEEE Trans. Med. Imaging 29(11), 1821–1838 (2010). 10.1109/TMI.2010.2050779 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Saha P. K., Wehrli F. W., and Gomberg B. R., “Fuzzy distance transform: Theory, algorithms, and applications,” Comput. Vision Image Understanding 86, 171–190 (2002). 10.1006/cviu.2002.0974 [DOI] [Google Scholar]
- 41.Saha P. K. and Wehrli F. W., “Measurement of trabecular bone thickness in the limited resolution regime of in vivo MRI by fuzzy distance transform,” IEEE Trans. Med. Imaging 23, 53–62 (2004). 10.1109/TMI.2003.819925 [DOI] [PubMed] [Google Scholar]
- 42.Saha P. K. and Chaudhuri B. B., “Detection of 3-D simple points for topology preserving transformations with application to thinning,” IEEE Trans. Pattern Anal. Mach. Intell. 16, 1028–1032 (1994). 10.1109/34.329007 [DOI] [Google Scholar]
- 43.Saha P. K. and Chaudhuri B. B., “3D digital topology under binary transformation with applications,” Comput. Vision Image Understanding 63, 418–429 (1996). 10.1006/cviu.1996.0032 [DOI] [Google Scholar]
- 44.Li C., Jin D., Burns T. L., Torner J. C., Levy S. M., and Saha P. K., “A new algorithm for cortical bone segmentation with its validation and applications to in vivo imaging,” Presented at the 17th International Conference on Image Analysis and Processing (ICIAP), Naples, Italy, 2013, pp. 349–358. [DOI] [PMC free article] [PubMed]
- 45.Petersilka M., Bruder H., Krauss B., Stierstorfer K., and Flohr T. G., “Technical principles of dual source CT,” Eur. J. Radiol. 68(3), 362–368 (2008). 10.1016/j.ejrad.2008.08.013 [DOI] [PubMed] [Google Scholar]
- 46.Flohr T., Stierstorfer K., Raupach R., Ulzheimer S., and Bruder H., “Performance evaluation of a 64-slice CT system with z-flying focal spot,” Rofo 176(12), 1803–1810 (2004). 10.1055/s-2004-813717 [DOI] [PubMed] [Google Scholar]
- 47.Saha P. K., Udupa J. K., and Odhner D., “Scale-based fuzzy connected image segmentation: Theory, algorithms, and validation,” Comput. Vision Image Understanding 77, 145–174 (2000). 10.1006/cviu.1999.0813 [DOI] [Google Scholar]
- 48.ITK: The NLM Insight Segmentation and Registration Toolkit, http://www.itk.org. [DOI] [PubMed]
- 49.Ming K. and Rosenbaum P. R., “Substantial gains in bias reduction from matching with a variable number of controls,” Biometrics 56(1), 118–124 (2000). 10.1111/j.0006-341X.2000.00118.x [DOI] [PubMed] [Google Scholar]
- 50.Burghardt A. J., Buie H. R., Laib A., Majumdar S., and Boyd S. K., “Reproducibility of direct quantitative measures of cortical bone microarchitecture of the distal radius and tibia by HR-pQCT,” Bone 47(3), 519–528 (2010). 10.1016/j.bone.2010.05.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kazakia G. J., Nirody J. A., Bernstein G., Sode M., Burghardt A. J., and Majumdar S., “Age-and gender-related differences in cortical geometry and microstructure: Improved sensitivity by regional analysis,” Bone 52(2), 623–631 (2013). 10.1016/j.bone.2012.10.031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Saha P. K., Chaudhuri B. B., Chanda B., and Dutta Majumder D., “Topology preservation in 3D digital space,” Pattern Recognit. 27, 295–300 (1994). 10.1016/0031-3203(94)90060-4 [DOI] [Google Scholar]
- 53.Udupa J. K. and Saha P. K., “Fuzzy connectedness and image segmentation,” Proc. IEEE 91, 1649–1669 (2003). 10.1109/JPROC.2003.817883 [DOI] [Google Scholar]