The relationship between gamma frequency and running speed differs for slow and fast gamma rhythms in freely behaving rats

Abstract

In hippocampal area CA1 of rats, the frequency of gamma activity has been shown to increase with running speed (Ahmed and Mehta, 2012). This finding suggests that different gamma frequencies simply allow for different timings of transitions across cell assemblies at varying running speeds, rather than serving unique functions. However, accumulating evidence supports the conclusion that slow (~25–55 Hz) and fast (~60–100 Hz) gamma are distinct network states with different functions. If slow and fast gamma constitute distinct network states, then it is possible that slow and fast gamma frequencies are differentially affected by running speed. In this study, we tested this hypothesis and found that slow and fast gamma frequencies change differently as a function of running speed in hippocampal areas CA1 and CA3, and in the superficial layers of the medial entorhinal cortex (MEC). Fast gamma frequencies increased with increasing running speed in all three areas. Slow gamma frequencies changed significantly less across different speeds. Furthermore, at high running speeds, CA3 firing rates were low, and MEC firing rates were high, suggesting that CA1 transitions from CA3 inputs to MEC inputs as running speed increases. These results support the hypothesis that slow and fast gamma reflect functionally distinct states in the hippocampal network, with fast gamma driven by MEC at high running speeds and slow gamma driven by CA3 at low running speeds.

INTRODUCTION

Gamma oscillations (~25–100Hz) are widespread in the entorhinal-hippocampal network and are thought to coordinate distributed neurons during spatial memory processing (Buzsaki and Wang, 2012; Colgin and Moser, 2010; Csicsvari et al., 2003). Gamma rhythms split into two distinct subtypes, which differentially route information streams in the entorhinal-hippocampal network (Colgin et al., 2009). Slow gamma (25–55Hz) links hippocampal subfield CA1 to neighboring subfield CA3, a region that is thought to play a role in memory retrieval (Brun et al., 2002; Steffenach et al., 2002; Sutherland et al., 1983). Fast gamma (60–100Hz) coordinates activity in CA1 and the superficial layers of medial entorhinal cortex (MEC), which transmit information to hippocampus about current spatial location (Brun et al., 2008; Hafting et al., 2005). In line with these findings, separate ~40 Hz and ~90 Hz gamma components have been observed in CA1 stratum radiatum and stratum lacunosum-moleculare, respectively (Schomburg et al., 2014). Moreover, recent work suggests that hippocampal neurons code spatial location differently during slow and fast gamma. Hippocampal place cells, neurons with spatial receptive fields (O’Keefe, 1976; O’Keefe and Dostrovsky, 1971), predict upcoming locations during slow gamma and encode recent locations during fast gamma (Bieri et al., 2014). Also, fast gamma power increases relative to slow gamma power when animals use landmarks, rather than a sequence memory-based strategy, to solve a spatial memory task (Cabral et al., 2014). In an object recognition task, slow, but not fast, gamma coherence between CA3 and CA1 was significantly higher during exploration of objects that were later well remembered compared to those that were later poorly remembered (Trimper et al., 2014). Also, fast, but not slow, gamma power in CA1 was significantly enhanced prior to the choice point in a spatial working memory task (Yamamoto et al., 2014). Taken together, these findings suggest that slow and fast gamma constitute distinct network states that perform different spatial memory functions in the entorhinal-hippocampal network.

Cells within an assembly that represents a particular place are thought to activate within the same gamma cycle (Harris et al., 2003; Senior et al., 2008), with successive gamma cycles representing sequences of locations (Lisman and Jensen, 2013). More cell assemblies, representing longer distances, activate within a single theta cycle as running speeds increase (Maurer et al., 2012). These results suggest that more gamma cycles should occur within a theta cycle at higher running speeds. Accordingly, the frequency of gamma rhythms increases with running speed (Ahmed and Mehta, 2012). These findings raise the possibility that fast gamma rhythms may simply support faster transitions across cell assembly sequences at higher running speeds, rather than performing specific functions that differ from those performed by slow gamma. However, this remains an open question because the study by Ahmed and Mehta did not investigate slow and fast gamma separately.

An alternative hypothesis is that slow and fast gamma rhythms mediate different operations that tend to occur at different running speeds. In line with this idea, a previous study showed that CA1 and CA3 slow gamma power decreased with increasing running speed, whereas fast gamma power in CA1, CA3, and MEC increased as running speed increased (Kemere et al., 2013). This study also found that the strength of CA3 input to CA1 decreased as running speed increased and that coordination of CA3-CA1 cell ensembles was stronger at low running speeds compared to high running speeds. Also, CA1 slow gamma power and CA3-CA1 slow gamma coherence have been shown to increase during sharp wave-ripples (Carr et al., 2012), which occur during immobility (Buzsaki, 1986). These findings are in line with the hypothesis that slow and fast gamma rhythms are separate states, with slow gamma performing functions that tend to occur during low running speeds and immobility, while fast gamma rhythms carry out functions associated with fast movement.

Here, we hypothesized that slow and fast gamma frequencies exhibit different relationships with running speed. To test this hypothesis, we recorded local field potentials (LFPs) and single unit activity in CA1, CA3, and MEC superficial layers as rats traversed a linear track. The results suggest that slow gamma frequencies change minimally as a function of running speed, whereas fast gamma frequencies increase continuously with increasing running speed.

MATERIALS AND METHODS

Animals

Eight male Long Evans rats weighing approximately 350–500 grams were used in this study. Four of the rats had recordings in CA3 and CA1; 3 had recordings in superficial layers of MEC, and 1 had recordings in CA3 only. They were housed on a reverse light dark cycle (lights off from 8 a.m.–8 p.m. and lights on from 8 p.m.–8 a.m.); behavioral sessions took place during the dark phase. Rats were pre-trained to run on a linear track (see below) prior to surgical implantation of the recording drive. After surgery, rats were housed individually in custom-built acrylic cages (~40 cm × 40 cm × 40 cm). Cages contained enrichment materials (e.g., plastic balls, wooden blocks, cardboard tubes). Rats recovered from surgery for at least one week before behavioral testing resumed and data collection began. During the data collection period, rats were food-deprived to ~90% of their free-feeding weight. All experiments were conducted according to the guidelines of the United States National Institutes of Health Guide for the Care and Use of Laboratory Animals under a protocol approved by the University of Texas at Austin Institutional Animal Care and Use Committee.

Surgery

All rats were implanted with a chronic ‘hyperdrive’ recording device containing 13–14 independently movable tetrodes (13 in one rat, 14 in 7 rats). Tetrodes were constructed from 17 μm polyimide-coated platinum-iridium (90%–10%) wire (California Fine Wire). Electrode tips of tetrodes targeted toward cell body layers were plated with platinum to reduce single channel impedances to ~150–300 kΩ at 1kHz. Five rats were implanted with a hyperdrive above dorsal hippocampus at the coordinates: AP −3.8 mm, ML 3.0 mm and DV 1 mm. The other three rats were implanted with a hyperdrive above MEC at the coordinates: 0.2–0.3 mm anterior to the transverse sinus, ML 4.5 mm and DV 1 mm. Bone screws were placed in the skull, and the screws and the base of the drive were covered with dental cement to secure the drive to the skull. Two screws in the anterior skull were connected to the recording drive to serve as an electrical ground.

Tetrode placement

Over the next few weeks after surgery, tetrodes were slowly lowered toward their target locations. For five rats, tetrodes were lowered to stratum pyramidale in either CA1 or CA3. For the other three rats, tetrodes were lowered to superficial layers of MEC. In the rats with hyperdrives implanted above hippocampus, one tetrode was lowered to the distal apical dendritic region of CA1 (see Supporting Information Figs. S4 and S13). In each hyperdrive, another tetrode was used as a reference for differential recording. In hippocampus, it was placed at the level of the corpus callosum or higher. For MEC hyperdrive recordings, the most anterior tetrode was selected as the reference for differential recording and was targeted toward the angular bundle. Reference tetrodes were continuously recorded against ground to ensure that they were placed in a quiet location. All recording locations were verified histologically after experiments were finished (see Fig. 1D–F and Supporting Information Fig. S1).

Figure 1.

A–C, Color-coded gamma power as a function of running speed, averaged across all recordings in CA1 (A), CA3 (B) and MEC (C). Note that both the x- and y-axes are shown in log scale. As is apparent, frequencies within the slow gamma band (i.e., 25–55 Hz) are associated with low running speeds in CA1 and CA3. Fast gamma frequencies (i.e., 60–100 Hz) are associated with high running speeds in CA1, CA3, and MEC. D–F, Histological sections showing examples of recording sites in CA1 (D), CA3 (E), and MEC (F).

Data collection

Data were collected using the Neuralynx data acquisition system (Neuralynx, Bozeman, MT, USA). The recording drive was connected to a multichannel, unity gain headstage (HS-54, Neuralynx, Bozeman, MT, USA). The rat’s position was tracked at a 30 Hz sampling rate using light-emitting diodes (LEDs) on the headstage. The output of the headstage was conducted via two lightweight tether cables through a multichannel slip-ring commutator to a data acquisition system that processed the signals through individual 24 bit AD converters (Digital Lynx, Neuralynx, Bozeman, MT, USA). Experiments began when spikes emerged with amplitudes that were approximately five times the noise levels and when depth estimates and oscillatory activity indicated that tetrodes were in target regions (i.e., robust theta rhythms for hippocampus and MEC; prominent sharp wave-ripples for hippocampus). For spike detection, signals were digitally bandpass filtered between 600 and 6000 Hz; events that exceeded a threshold set by the experimenter (~55–75 μV) were detected as spikes and sampled at 32 kHz. Additionally, continuous LFP recordings were digitally filtered in the 0.1–500Hz band and sampled at 2000 Hz. LFPs were recorded differentially against a reference tetrode placed in an electrically silent region (see above). This reference signal was duplicated using a breakout board (MDR-50 breakout board, Neuralynx, Bozeman, MT, USA) and recorded continuously against ground. The hippocampal data (5 rats) used for this study were also included in a previously published study (Bieri et al., 2014).

Behavior

After recovering from surgery, rats resumed behavioral training, which consisted of three 10-minute sessions per day on a linear track (2 m long, 10 cm wide, and 64 cm above the floor). Rats were trained to run back and forth on the track, as described previously (Bieri et al., 2014). Rats were rewarded with small pieces of sweet cereal or cookies at both ends of the track. Before data acquisition began, rats were trained on the track for at least 3 days to ensure environmental familiarity. Each recording session was preceded and followed by ~10-minute rest sessions. During each rest session, rats were placed in a towel-lined, elevated flower pot.

Results, statistics, and data analyses

Data were analyzed using custom software written in MATLAB (MathWorks, Natick, MA), unless indicated otherwise. Specific analysis methods are described in detail below. Results are depicted in figures as means ± SEM. The results of all statistical tests are described in the Results section. Reported t-tests are 2-tailed.

Spike sorting and cell classification

Spike sorting was performed offline usinggraphical cluster-cutting software (MClust; A.D. Redish, University of Minnesota, Minneapolis). Spikes were clustered manually in two-dimensional projections of the multidimensional parameter space. Autocorrelation and crosscorrelation functions were additionally used to identify single units. In hippocampal recordings, putative place cells were distinguished from putative interneurons on the basis of spike width, average firing rate, and bursting properties (Fox and Ranck, 1981; Frank et al., 2001; Harris et al., 2000; Henze et al., 2000). In MEC, we examined the activity of spatially modulated ‘grid cells’ (Hafting et al., 2005) and putative interneurons without spatial receptive fields. Because bursting properties are not reliable criteria for identifying interneurons in MEC (Frank et al., 2001; Mizuseki et al., 2009; Quilichini et al., 2010), units in MEC without spatial receptive fields that fired at a high rate (mean rate >10 Hz) were classified as putative interneurons.

Estimation of power spectra across running speeds (Figs. 1A–C and 4A; Supporting Information Figs. S3–S4)

Figure 4.

Correlation of peak frequency of slow and fast gamma with running speed. A, Color-coded power as a function of running speed, averaged across periods in which slow and fast gamma activity was detected in CA1 (left), CA3 (middle) and MEC (right). B, Correlation of peak slow (blue) and fast (red) gamma frequencies with running speed. Note that results are plotted on a log-log scale. Each blue and red line represents the regression line for the relationship between the peak frequency of slow and fast gamma, respectively, and running speed in each rat. C, Average correlation between running speed and peak frequency of slow or fast gamma. Note that, for all three regions, the correlation between running speed and fast gamma frequencies is significantly higher than that for slow gamma. * indicates p < 0.05, and ** indicates p < 0.01.

The measurement of power spectra across different running speeds was performed, as described previously (Ahmed and Mehta, 2012). The Chronux toolbox (http://chronux.org/) was used to estimate power spectra using multitaper spectral analysis (Mitra and Bokil, 2008). Briefly, the absolute power spectrum was calculated for successive 200 ms time windows of the LFP recordings. The time-bandwidth product parameter (TW) was set at 3, and the number of tapers (K) was set at 5 (Ahmed and Mehta, 2012; Jarvis and Mitra, 2001), resulting in spectral smoothing of ±12.5 Hz. For each day’s recording, the absolute power for each frequency was z-scored across time for the LFP recording from each tetrode, in order to allow for comparisons across different frequencies that would otherwise be difficult due to the 1/f decay of power in physiological signals. Running speed was calculated (as described in Bieri et al., 2014) in each 200 ms time window corresponding to the LFP segments. To produce power estimates across running speed bins, z-scored absolute power at each frequency was averaged across all the time windows that fell within a given speed bin. Speed and frequency were plotted on a log-log scale, as in Ahmed and Mehta (2012). This allows for better visualization of the relatively narrow band of slow gamma frequencies (i.e., compared to the fast gamma band) and the reduced range of running speeds associated with slow gamma compared to fast gamma.

Gamma detection (Figs. 4A, Supporting Information Figs. S5–S8, and S12)

Slow and fast gamma episodes were detected using a similar method as described previously (Bieri et al., 2014; Colgin et al., 2009). For fast and slow gamma estimates, time-varying power was computed across the 60–100 Hz and 25–55 Hz frequency bands, respectively, using a wavelet transform method (Tallon-Baudry et al., 1997). LFP power at each time point was averaged across the slow and fast gamma frequency ranges to obtain estimates of slow and fast gamma power, respectively, for each time point. In hippocampal gamma studies, a detection threshold is typically applied to accurately detect gamma occurrence and reject noise. This is necessary because gamma is a non-stationary signal, and its frequency overlaps with the frequency of power-line noise. A threshold of 2 SD above the mean was selected here based on its use in a fundamental hippocampal gamma study (Csicsvari et al., 2003). In addition, our examination of detected events using various thresholds revealed that the 2 SD threshold accurately detects gamma events and rejects noise most of the time (data not shown). Thus, time points were collected during which slow and fast gamma power exceeded 2 SD above the mean slow and fast gamma power, respectively. Time windows, 200 ms in length, were cut around the selected time points. In each window, slow and fast gamma maxima were determined from slow and fast gamma bandpass filtered versions of the signals, respectively, and windows were centered around the maxima. Duplicate windows were avoided by discarding identical maxima values within a gamma subtype and requiring maxima to be separated by at least 100 ms.

Fitting mixture models to gamma frequency-running speed distributions (Figs. 2 and 3)

Figure 2.

Contour plots of the probability density functions of the mixture models with 1–5 normal density functions (top to bottom rows) in CA1 (left column), CA3 (middle column), and MEC (right column). Note that the x- and y-axes are shown in log scale. For each mixture model, the weights of the components are shown in the center, or near the center, of the contours.

Figure 3.

The average log-likelihood parameters (λ_L) with L = 1, 2, 3, 4, and 5 across recordings from CA1 (A), CA3 (B), and MEC (C). Note that in CA1 and CA3, the fitting of the probability density functions improves substantially from L = 1 to L = 2, but adding additional components does not apparently improve the fit. In MEC, however, the fit is improved substantially by adding a third component, but then the increase in likelihood tapers off after L = 3.

In order to identify whether the power of slow and fast gamma is differentially modulated as a function of running speed, we assessed how well the color-coded power spectra across running speed plots were fit by mixture models with one to five components. To do so, we adapted a method that has been used previously to assess the bimodality of theta phase precession (Yamaguchi et al., 2002). In our case, the speed-frequency color map was assumed to be a Gaussian mixture model, i.e., a probability density function represented as the weighted sum of a number of normal density functions. In order to fit a Gaussian mixture model to our data, we first transformed the speed-frequency color map into a scatter plot reflecting the z-scored power value associated with each bin. Specifically, for each color-coded plot of gamma power by running speed and gamma frequency, we first normalized the power value (z) in each frequency-speed bin to [0,1] in the following manner:

$$z\_\mathit{norm}(f_i,{\mathit{vel}}_j)=\frac{z(f_i,{\mathit{vel}}_j)-min(z(f_{\mathit{all}},{\mathit{vel}}_{\mathit{all}}))}{max(z(f_{\mathit{all}},{\mathit{vel}}_{\mathit{all}}))-min(z(f_{\mathit{all}},{\mathit{vel}}_{\mathit{all}}))},$$

where i and j are the indices of frequency (f) and velocity (vel) bins, respectively. We then set z_norm values that were smaller than mean z_norm values to zero. For each frequency-speed bin, we generated z_norm(f_i, vel_j) × 50 points, such that bins with higher power values included more points in the scatter plot. The points were randomly assigned to specific frequency and velocity values using the ‘mvnrnd’ function in MATLAB, with (μ_f, μ_vel) being the center of the bin, ${\sigma }_f^2$ and ${\sigma }_{\mathit{vel}}^2$ being 1/4 of each bin width, and σ_f,vel = 0. In this way, the generated points almost covered the bin [min(f_i), max(f_i)] × [min(vel_j), max(vel_j)]. This method generated a distribution that matched our data, which was then used to estimate parameters in a Gaussian mixture model, as described below.

The expectation maximization (EM) algorithm (Dempster et al., 1977; Redner and Walker, 1984) was employed to estimate the parameters of the component normal density functions in a Gaussian mixture model. Given L components in the mixture model, the best fit of its probability density function in the (x, y) plane was estimated by the EM algorithm, defined as:

$$\mathrm{P}(x,y)=\sum _{i=1}^L{\alpha }_i{\mathrm{\Psi }}_i^{-1}\mathit{exp}\left\{-\frac{1}{2(1-r_i^2)}\left[\frac{{(x-{\mu }_{xi})}^2}{{\sigma }_{xi}^2}+\frac{{(y-{\mu }_{yi})}^2}{{\sigma }_{yi}^2}-2r_i\frac{(x-{\mu }_{xi})(y-{\mu }_{yi})}{{\sigma }_{xi}{\sigma }_{yi}}\right]\right\}$$

with

$$\begin{array}{c}{\mathrm{\Psi }}_i=2\mathrm{\pi }{\sigma }_{xi}{\sigma }_{yi}{(1-r_i^2)}^{1/2}\\ r_i=\frac{{\sigma }_{\mathit{xiyi}}}{{\sigma }_{xi}{\sigma }_{yi}}\end{array}$$

and

$$\sum _{i=1}^L{\alpha }_i=1$$

In our case, the variables x and y correspond to the rat’s velocity v and gamma frequency f in each color map. The suffix i signifies the ith normal density function (i = 1, 2, …, L). The symbol α_i represents the relative weight of the ith normal density function, and the summation of all α_i is equal to 1. For the parameters in the ith normal density function, μ_xi and μ_yi are the mean values of the x and y variables, and ${\sigma }_{xi}^2,{\sigma }_{yi}^2$, and σ_xiyi represent the variance of x and y, and their covariance, respectively. The variable r_i is the correlation coefficient. In this study, the value of L was varied from 1 to 5 for comparison purposes.

The mixture model with L normal density functions can be represented by Π_L, with the probability density function of the mixture model denoted by P(f, v|Π_L). In order to determine how many components were required to get the best fit for the speed-frequency representations of color-coded power, the log-likelihood ratio function (McLachlan et al., 1996; Redner and Walker, 1984) was employed (as in Yamaguchi et al., 2002). The test parameter λ_L, which assesses the fewest number of components in the model that can provide a good fit with the data, is defined by the log likelihood function as

$${\lambda }_L=\sum _{\mathit{all}k,h}log\frac{P(f_k,v_h\mid {\mathrm{\Pi }}_L)}{P(f_k,v_h\mid {\mathrm{\Pi }}^{\ast })}$$

Here, (f_k, v_k) denotes the value of (f, v) for all the points in the scatter plots. P(f_k, v_h|Π_L) and P(f_k, v_h|Π^*) represent the value of the conditional probability density for the (f_k, v_h) bin in the models Π_L and Π^*, respectively. In this study, Π^* is defined as the mixture model with the maximum number of density functions (i.e., L =5). In other words,

$$P(f,v\mid {\mathrm{\Pi }}^{\ast })=P(f,v\mid {\mathrm{\Pi }}_5)$$

Obviously, λ_L is a monotonically increasing function of L, so the appropriate number of parameters cannot simply be determined by selecting the model with the maximum value of λ_L. However, at some value of L, L_n, the increase in likelihood should taper off, thereby indicating that L_n−1 is the correct number of components to include in the mixture model (McLachlan et al., 1996). This is the point that the difference value of λ_Ln − λ_Ln−1 (L_n−1 < L_n) is much larger than λ_Ln+1 − λ_Ln (L_n+1 > L_n).

Correlation between gamma frequency and running speed (Fig. 4B–C; Supporting Information Fig. S9)

In order to calculate the correlation between running speed and slow or fast gamma separately, we first defined a border between slow gamma-associated running speeds and fast gamma-associated running speeds. For CA1 and CA3, this border was defined by the speed at which the slow gamma- and fast gamma-associated contours from the two-component mixture models (shown in the second row of Fig. 2) intersected with each other and exhibited equivalent probability densities. For MEC, the border between fast and slow gamma-associated running speeds was defined in the same manner, except that two of the contours from the three-component mixture model were used (i.e., the fast-gamma associated component seen at high running speeds and the relatively low frequency gamma component seen at relatively low running speeds; see right panel in third row of Fig. 2) instead of the contours from the two-component mixture model. In order to calculate the correlation between speed and gamma frequency, frequencies exhibiting power greater than 90% of the maximal gamma power (‘peak frequencies’) were identified for each running speed bin. For each rat, and for each running speed bin, these peak frequencies were then used to estimate the correlation between gamma frequency and running speed for slow and fast gamma (reported in Fig. 4C). For the slow and fast gamma components within each rat, these frequency values were also linearly regressed as a function of running speed using the ‘regression’ function in Matlab (see Fig. 4B).

Relationships between firing rate and gamma power (Figs. 5–6)

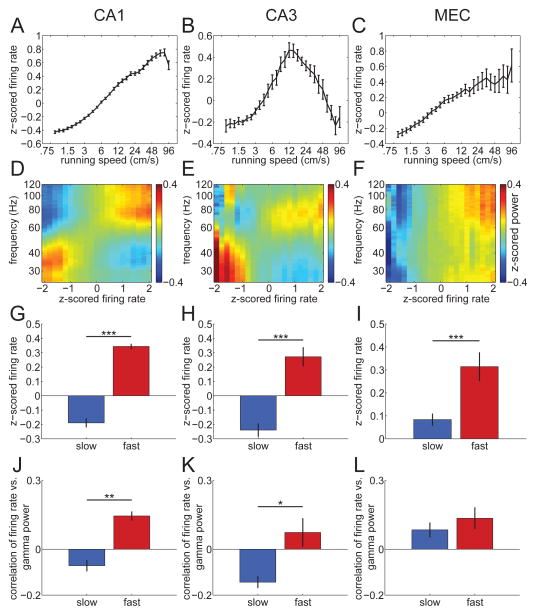
Figure 5.

Relationship between firing rates of place or grid cells, running speed, and frequency of gamma oscillations. A–C, Z-scored firing rate of place or grid cells plotted as a function of speed for CA1 (A), CA3 (B), and MEC (C). Note how firing rate generally increases with increasing running speed for CA1 and MEC, whereas CA3 firing rates initially increase with running speed but then start to decrease at intermediate running speeds. D–F, Color-coded, z-scored gamma power is plotted as a function of z-scored firing rates of place cells in CA1 (D) and CA3 (E), and grid cells in MEC (F). Note how, for all three areas, high firing rates are associated with strong power in the fast gamma range. For CA1 and CA3, power in the slow gamma range is seen when firing rates are relatively low. G–I, Average z-scored firing rates of place or grid cells during periods when slow and fast gamma activity was detected in CA1 (G), CA3 (H), and MEC (I). Firing rates were significantly higher during periods when fast gamma activity was detected compared to periods when slow gamma activity was detected. *** indicates p < 0.001. J–L, Average correlations between z-scored firing rates of place or grid cells and power of slow and fast gamma in CA1 (J), CA3 (K) and MEC (L). In all regions, the correlation between place/grid cell firing rates and fast gamma power was significantly higher than the correlation between firing rates and slow gamma power. * indicates p < 0.05. *** indicates p < 0.001.

Figure 6.

Relationship between interneuron firing rates, running speed, and frequency of gamma activity. A–C, Z-scored firing rate of interneurons plotted as a function of speed for interneurons in CA1 (A), CA3 (B), and MEC (C). Note that firing rates of interneurons generally increase with increasing running speed for CA1 and MEC. For CA3, however, firing rates initially increase but then begin to decrease at intermediate running speeds. D–F, Color-coded gamma power is plotted as a function of z-scored firing rates of interneurons in CA1 (D), CA3 (E), and MEC (F). Note how low interneuron firing rates are associated with power in the slow gamma range for CA1 and CA3 and how high firing rates are associated with power in the fast gamma range in all three regions. G–I, Average z-scored firing rate of interneurons during periods of slow and fast gamma in CA1 (G), CA3 (H), and MEC (I). *** indicates p < 0.001. Note how CA1 and CA3 interneuron firing rates were significantly higher during fast gamma than during slow gamma. J–L, Average correlations between z-scored interneuron firing rates and the power of slow and fast gamma activity in CA1 (J), CA3 (K) and MEC (L). In CA1 and CA3, the correlation between interneuron firing rates and gamma power was significantly higher for fast gamma than for slow gamma. * indicates p < 0.05, and ** indicates p < 0.01.

In each session, recordings were separated into non-overlapping time windows, 200 ms in length. The firing rate of putative interneurons, assemblies of simultaneously recorded grid cells, or assemblies of simultaneously recorded place cells, was measured in each time window. Gaussian kernel smoothing was applied to the firing rate series, for each interneuron or grid or place cell assembly. Next, for each interneuron or each cell assembly, firing rates were z-scored across windows. If there were multiple interneurons recorded from the same tetrode, z-scored firing rates were averaged across all interneurons on a given tetrode. For LFP recordings from each tetrode, slow and fast gamma power estimates were obtained using multitaper spectral analysis (as described above) and then z-scored. The mean power of fast and slow gamma in each window was obtained by averaging the z-scored power across the fast and slow gamma frequency ranges, respectively. For all regions, the 60–100 Hz frequency band was used for fast gamma. For CA1 and CA3, the 25–55 Hz band was used for slow gamma, but a 35–55 Hz band was used for MEC to prevent contamination from the third theta harmonic (see Supporting Information Fig. S5). Then, for individual tetrodes, the correlation between firing rate and slow or fast gamma power was calculated (as shown in Fig. 5J–L and Fig. 6J–L). For the results shown in Figs. 5G–I and 6G–I, slow and fast gamma windows were detected as windows in which slow or fast gamma power exceeded 2 SD above the mean slow or fast gamma power, respectively (see Gamma detection, above). The mean z-scored firing rates associated with the slow or fast gamma windows were then averaged to produce the bar plots shown in Figs. 5G–I and 6G–I.

RESULTS

We applied methods similar to those used in a previous study describing changes in gamma frequency as a function of running speed (Ahmed and Mehta, 2012). Within each frequency bin, power was z-scored and plotted against running speed for recordings from CA1 s. pyramidale, CA3 s. pyramidale, and MEC superficial layers (Fig. 1). As is apparent in Fig. 1A for data from CA1, the relationship between frequency and running speed does not appear to be the same across all gamma frequencies. Rather, fast gamma frequencies appear to increase as a function of relatively high running speeds, whereas slow gamma frequencies change less across lower running speeds. Consistent results were also observed when data were randomly down-sampled to control for different amounts of time spent at low and high running speeds (Supporting Information Figs. S2–S3) and when gamma was recorded from dendritic layers (Supporting Information Fig. S4). In CA3, as in CA1, slow gamma was also dominant at low running speeds (< 5 cm/s), whereas fast gamma was dominant at higher running speeds (Fig. 1B). However, unlike in CA1, the power of fast gamma in CA3 was weak when rats ran at speeds greater than 24 cm/s. This suggests that inputs to CA1 from MEC may drive fast gamma in CA1 when rats are running at high speeds. In support of this idea, fast gamma in MEC superficial layers was greatly enhanced at speeds greater than 24 cm/s compared to lower running speeds (Fig. 1C). In MEC, little to no slow gamma was apparent at low running speeds, suggesting that CA3 preferentially drives slow gamma in CA1 at low running speeds. Power in the slow gamma range was apparent in MEC at high running speeds. However, closer inspection revealed that power in this range in MEC primarily reflected a theta harmonic that emerged at relatively high running speeds (Supporting Information Fig. S5).

The above-described results suggest that the peak frequency of gamma oscillations does not increase uniformly with running speed for slow and fast gamma frequency ranges. Thus, we tested the bimodality of the gamma frequency-running speed relationship using a method that has previously been used to assess the bimodality of theta phase precession (Yamaguchi et al., 2002; see Materials and Methods). We hypothesized that the speed-frequency color-coded representations of power reflect a statistical population that is a mixture of two distinct components, corresponding to slow and fast gamma (Supporting Information Fig. S6), with separate probability density functions. For each region, the results with 1, 2, 3, 4 and 5 components in the mixture model are shown in Fig. 2. The top row shows contour plots representing the probability density functions for the mixture models with one component. In these cases, slow and fast gamma are encompassed within the same cluster. The second row shows the results for the mixture models with two probability density functions. The probability density functions in the slow and fast gamma frequency ranges were fully separated in CA1. Interestingly, the weight associated with the fast gamma cluster in CA1 (α_fast = 0.79) was higher than that of the slow gamma cluster (α_slow = 0.21), which suggests that fast gamma may be the dominant gamma state in CA1 during exploration of a familiar environment, as has been suggested previously (Colgin et al., 2009). In CA3, the clusters were well separated; however, the weights of the fast gamma cluster (α_fast = 0.48) and the slow gamma cluster (α_slow = 0.52) were approximately equal. This is consistent with the hypothesis that slow gamma exerts a stronger influence on CA3 than on CA1, as has been reported previously (Colgin et al., 2009). In MEC, however, the two-component mixture model only fit fast gamma and the theta harmonic (see above), with each of these components weighted approximately equally (α = 0.54 for fast gamma component and α = 0.46 for theta harmonic). In CA1 and CA3, including a third component in the mixture model revealed a third cluster in the high frequency range (~100–120 Hz). It is possible that this component represents activity in the ‘epsilon’ range, which likely reflects cell spiking (Belluscio et al., 2012). In MEC, the third cluster corresponded to relatively low gamma frequencies (~50–80 Hz) and running speeds. This third component in MEC may reflect a mixture of slow gamma activity in MEC (Newman et al., 2013) and lower frequency fast gamma at lower running speeds. As is apparent in the lower two panels of Fig. 2, adding additional components to the mixture model did not appear to provide a better fit for the data from any of the regions.

Fig. 3 shows the log-likelihood value of the parameter estimation for the mixture models with 1 to 5 probability density functions. The log-likelihood value monotonically increases with increasing number of probability density functions, as described in the Materials and Methods, but the improvement gained by adding additional density functions levels off after L = 2 for CA3 and CA1 (Fig. 3A, 3B). That is, the log-likelihood value difference between λ₁ andλ₂ is substantially larger than that between λ₂ and λ₃. However, in MEC, the log-likelihood function levels off after L=3 (Fig. 3C). Specifically, in MEC, the difference between λ₂ and λ₃ is substantially greater than the difference between λ₃ and λ₄. These results suggest that fitting the data with a mixture model containing more than 2 probability density functions is unlikely to be meaningful for CA1 and CA3, with the two components in CA1 and CA3 reflecting slow and fast gamma at low and high running speeds, respectively. In MEC, fitting the data with a mixture model comprised of 3 probability density functions is likely optimal. The three components likely correspond to fast gamma at high running speeds, slower gamma at lower running speeds, and a theta harmonic that emerges at high running speeds (Supporting Information Fig. S5).

The above-described results suggest that the relationship between gamma frequency and running speed differs for slow and fast gamma. Therefore, we assessed the relationship between gamma frequency and running speed separately for periods of slow and fast gamma. We detected periods of slow or fast gamma, using methods applied previously (Bieri et al., 2014; see Materials and Methods). Briefly, time windows were detected during which slow or fast gamma power exceeded 2 standard deviations above the mean slow and fast gamma power, respectively (Supporting Information Figs. S7–S8). Fig. 4A shows power across running speeds after these detected gamma episodes were combined. In these plots, the distinct slow and fast gamma components are again apparent, as in Fig. 1A–C. In order to assess the relationship between gamma frequency and running speed separately for slow and fast gamma, we first separated the slow and fast gamma components according to the speed value that corresponded to the border between the two density functions for slow and fast gamma (see Materials and Methods). Then, gamma power within each gamma frequency bin was z-scored and assessed as a function of running speed separately for slow and fast gamma. The frequency associated with maximum power in each speed bin (‘peak frequency’) was then found for the slow and fast gamma components. For each region recorded within each rat, the peak frequency-running speed values were fit with two lines, one for slow gamma and one for fast gamma (Fig. 4B). In CA1, the linear fits for the slow gamma component tended to show relatively flat slopes, as was also typically the case in CA3 and MEC. However, the fast gamma components in all three regions were best fit by lines with a positive slope, indicative of a positive correlation between peak gamma frequency and running speed. Indeed, the correlation between peak fast gamma frequency and running speed was significantly higher than the correlation between peak slow gamma frequency and running speed (Fig. 4C; in CA1 (t(3) = 6.1, p = 0.009), CA3 (t(4) = 5.8, p = 0.004), and MEC (t(2) = 4.8, p = 0.04); see also Supporting Information Figs. S9, and see S10A–B and S11A–B for slope of the relationship between gamma power and running speed (as in Kemere et al., 2013). This could be due to the reduced dynamic range of speeds associated with high slow gamma power. To address this possibility, we assessed the relationship between running speed and gamma power separately for slow and fast gamma frequencies. Again, we found that the correlation between fast gamma frequencies and running speed was higher than the correlation between slow gamma frequencies and running speed (Supporting Information Fig. S12). It should be noted that correlations between slow gamma frequency and running speed, although lower than correlations between fast gamma frequency and running speed, were nonetheless significantly positive for CA1 and MEC (CA1 (n = 4): Z = 2.3, p = 0.01; MEC (n = 3): Z = 1.9, p = 0.03, Wilcoxon rank sum test (one-sided)). The correlation between slow gamma frequency and running speed in CA3 (n = 5), however, was not significantly positive (Z = 1.1; p = 0.1).

The firing rates of hippocampal place cells (Diba and Buzsaki, 2008), hippocampal interneurons (Ahmed and Mehta, 2012), and MEC grid cells (Sargolini et al., 2006) increase with increasing running speed. These single unit firing rate changes with running speed may explain gamma frequency increases at higher running speeds (Ahmed and Mehta, 2012). Thus, we next asked how firing rates in place or grid cells and interneurons were affected by running speed and how these firing rate changes correlated with slow and fast gamma activity. Individual place cells in hippocampus, by definition, are silent in the majority of locations (i.e., they fire sparsely). Therefore, for place cells, we assessed the firing rate of multiple simultaneously recorded units rather than single units (for consistency purposes, the same was also done for MEC grid cells). As shown in Fig. 5A, the firing rate of place cells in CA1 (n = 1197) increased with increasing running speed and tended to decrease at speeds higher than 48 cm/s. For CA3, place cell (n = 118) firing rates first increased with increasing running speeds and then gradually decreased at higher running speeds (Fig. 5B). In contrast, MEC grid cell (n = 52) firing rates increased with running speed, and remained high across high running speeds. Fig. 5D–F shows the power of gamma oscillations across different frequencies as a function of the normalized place cell or grid cell population firing rate (see also Supporting Information Figs. S10C–D, S11C–D, and S13). In CA3 and CA1, slow gamma activity was associated with low firing rates. In MEC, strong power in the slow gamma range was apparent at high firing rates; however, this power likely reflects a theta harmonic that emerges at high running speeds (Supporting Information Fig. S5) rather than slow gamma oscillations. In all three areas, higher frequency gamma activity was associated with relatively high firing rates. We also examined the normalized population firing rate during periods of slow and fast gamma and found that the population firing rate was greater during fast gamma than during slow gamma in CA1 (t(520) = 19.7, p < 0.00001), CA3 (t(56) = 4.5, p = 6.8 × 10⁻⁵), and MEC (t(27) = 4.3, p = 1.8×10⁻⁴) (Fig. 5G–I).

A previous study showed a positive correlation between place cell firing rate and fast gamma power, and a negative correlation between firing rate and slow gamma power, in CA1 (Ahmed and Mehta, 2012). These results were replicated in this study (Fig. 5J). Correlations between place cell firing rates and fast gamma power were significantly higher than correlations between place cell firing and slow gamma power for CA1 (t(3) = 4.0, p = 0.03; Fig. 5J) and also CA3 (t(4) = 10.6, p = 0.0005; Fig. 5K). Additionally, in MEC, a positive correlation was found between grid cell firing and fast gamma power, which was significantly higher than the correlation between grid cell firing and slow gamma power (t(2) = 4.7, p = 0.04; Fig. 5L).

Basket cell interneurons have previously been reported to fire at gamma frequencies, phase-locked to gamma oscillations in CA1 (Penttonen et al., 1998). Thus, we hypothesized that the firing rate of putative basket cells (i.e., fast-spiking interneurons recorded in or near the hippocampal cell body layers) would increase with running speed and that such firing rate increases would be associated with higher frequency gamma activity. Consistent with what was found in a previous study (Ahmed and Mehta, 2012), the firing rate of interneurons in CA1 increased with increasing running speed, although rates decreased slightly at very high running speeds (Fig. 6A; n = 94 interneurons). CA3 interneuron firing rates first increased with increasing running speed and then gradually decreased at higher running speeds (Fig. 6B; n = 16 interneurons). The maximum firing rate occurred at the ~12 cm/s speed, which corresponded to the running speed at which fast gamma power was maximal in CA3 in Fig. 4A. MEC putative interneuron (n = 14) firing rates increased with running speed and remained high across high running speeds (Fig. 6C), consistent with the hypothesis that gamma-generating interneurons in MEC are highly active at high running speeds. Moreover, in CA1 and CA3, low interneuron firing rates were associated with robust slow gamma activity, and high interneuron firing rates were associated with robust fast gamma activity (Fig. 6D–E). In MEC, little gamma activity was observed when putative interneurons fired at a low rate, whereas strong gamma activity focused in the fast gamma range emerged at high firing rates (Fig. 6F). The normalized interneuron firing rate during periods of slow and fast gamma was also examined. In all three areas, interneuron firing rates were significantly higher for fast gamma than for slow gamma (t(93) = 15.7, p < 1.0 × 10⁻⁵ for CA1; t(15) = 5.4, p = 7.7 × 10⁻⁵ for CA3; and t(13) = 5.0, p = 2.6 × 10⁻⁴ for MEC; Fig. 6G–I; see also Supporting Information Figs. S10E–F and S11E–F). In CA1, interneuron firing rates were positively correlated with fast gamma power and negatively correlated with slow gamma power, consistent with previous work (Ahmed and Mehta, 2012). Correlations between CA1 interneuron firing rates and fast gamma power were significantly higher than correlations between interneuron firing rates and slow gamma power (t(3) = 9.6, p = 0.002; Fig. 6J). In CA3, the pattern of results was similar to CA1, with significantly higher correlations between fast gamma power and interneuron firing than between slow gamma power and interneuron firing (t(3) = 3.5, p = 0.04; Fig. 6K). In MEC, interneuron firing rates were positively correlated with both slow and fast gamma power, with no significant difference between the correlations for slow and fast gamma (Fig. 6L). However, slow gamma measures in MEC may have been affected by the theta harmonic at high running speeds (Supporting Information Fig. S5). Taken together, these findings support the conclusion that increased firing rates in interneurons drive higher frequency gamma oscillations in the hippocampal network.

DISCUSSION

A previous study reported that the frequency of hippocampal gamma oscillations increases continuously as a function of running speed in rats (Ahmed and Mehta, 2012; but see Chen et al., 2011 for results in mice). Different relationships between gamma power and running speed were previously reported for slow and fast variants of gamma. Slow gamma power decreased with increasing running speed, whereas fast gamma power increased with increasing running speed (Ahmed and Mehta, 2012; Kemere et al., 2013). However, previous studies did not examine whether running speed differentially correlates with frequency for slow and fast variants of gamma. Here, we replicate the previous results regarding gamma power and running speed but also report the novel finding that slow and fast gamma frequencies change differentially as a function of running speed. For CA1, CA3, and superficial layers of MEC, we show that fast gamma frequencies increase continuously as running speeds increase. In contrast, for CA1 and CA3, slow gamma frequencies change to a lesser extent across the range of relatively low running speeds associated with strong slow gamma power. In MEC superficial layers, relatively little slow gamma activity is seen at low running speeds; high power in the slow gamma range at high running speeds primarily reflects a theta harmonic.

Additionally, the results are consistent with previous reports that ~40 Hz slow gamma is driven by inputs from CA3 and ~80 Hz fast gamma is driven by inputs from MEC (Colgin et al., 2009; Schomburg et al., 2014). In the present study, the slow gamma component in the 2 component mixture model for CA3 was more heavily weighted than the fast gamma component. In the mixture model for MEC, the fast gamma component at high running speeds was dominant, compared to the weak slow gamma component at low running speeds. A previous study by Kemere and colleagues (2013) showed that responses evoked by Schaffer collateral stimulation decreased as running speeds increased. This result provides a mechanism to explain why slow gamma in CA1 decreases at higher running speeds.

The first study to report a positive correlation between gamma frequency and running speed suggested that the observed gamma frequency increases allow for faster transitions across cell assemblies coding sequences of locations (Ahmed and Mehta, 2012). This interpretation assumes that each location is represented by an active cell assembly within a single gamma cycle, as suggested by Lisman (2005) and supported by experimental results showing gamma phase-locked firing during theta phase precession (Senior et al., 2008). This interpretation fits well with the fast gamma results presented here. Fast gamma frequencies continuously increase with increasing running speed in CA1 and superficial layers of MEC. This suggests that fast gamma allows place cells and grid cells to keep track of the animal’s current location. In line with this idea, CA1 place cells preferentially represent recent locations during periods of fast gamma (Bieri et al., 2014).

On the other hand, the present results show that slow gamma frequencies do not change much as a function of running speed. This may signify that cell assemblies do not code positions that strictly correspond to the animal’s current trajectory during slow gamma states. In support of this idea, slow gamma power is heightened during sharp wave-ripples (Bieri et al., 2014; Carr et al., 2012), a state during which the hippocampal network reactivates representations of previously experienced locations rather than representing current position (Kudrimoti et al., 1999; Nadasdy et al., 1999). Moreover, place cells do not tend to code current positions, but rather predict upcoming positions, during periods of slow gamma (Bieri et al., 2014). Additionally, during slow gamma, place cells show reduced theta phase precession (Bieri et al., 2014), a phenomenon that allows sequences of spatial locations to be represented within a theta cycle (O’Keefe and Recce, 1993; Skaggs et al., 1996). Together, these findings suggest that slow gamma is not involved in mediating transitions across representations of spatial sequences in real time but instead involved in triggering activation of previously stored spatial representations.

Kemere and colleagues (2013) showed that experience is a key variable that affects the relationship between running speed and slow and fast gamma power. Specifically, novelty was associated with stronger speed modulation of both slow and fast gamma power in CA1. This raises the possibility that relationships between running speed and slow and fast gamma frequency are also affected by novelty. This question remains open, however, because rats in the present study were highly familiar with the testing environment. In any event, the study by Kemere and colleagues (2013) showed negative correlations between running speed and slow gamma power in CA1 and CA3 that remained significant across many days of experience. Moreover, positive correlations between running speed and fast gamma power in CA1 and MEC also remained significant across multiple exposures to the testing environment. Thus, the present results from familiar environments showing heightened slow gamma power in CA3 and CA1 at low running speeds and increased fast gamma power in CA1 and MEC at high running speeds are in line with previously published results (Kemere et al., 2013).

Single unit data point to possible explanations as to why slow and fast gamma power, and fast gamma frequencies, are affected by running speed. Fast gamma rhythms in the hippocampus are coupled with fast gamma activity in MEC (Colgin et al., 2009), and the firing of many cells in MEC is positively correlated with running speed (Fig. 5C; Kropff-Causa et al., 2014; Sargolini et al., 2006). Considering that hippocampal gamma rhythms are thought to be driven primarily by interneurons (Lasztoczi and Klausberger, 2014; Penttonen et al., 1998; Pernia-Andrade and Jonas, 2014; Soltesz and Deschenes, 1993; Tukker et al., 2007), it is possible that increasing MEC cell firing drives faster spiking in fast gamma-generating interneurons at high running speeds. This notion is supported by results showing that the firing rate of CA1 interneurons positively correlates with running speed (Fig. 6A; Ahmed and Mehta, 2012; McNaughton et al., 1983). On the other hand, CA3 interneurons increase their firing rates with increasing running speed up until approximately 12 cm/s, after which CA3 interneuron firing slowly decreases (Fig. 6B). This result could partially explain why slow gamma diminishes, and fast gamma predominates, at high running speeds, considering that CA3-entrained gamma is thought to be driven by feedforward inhibition from CA3 (Csicsvari et al., 2003). However, CA3 excitatory inputs to CA1 also decrease with increasing running speed (Kemere et al., 2013), suggesting that excitatory inputs from CA3 may also play a role in CA1 slow gamma generation.

The present pattern of results supports the following scenario. At low running speeds, projection neurons in MEC fire at a relatively low rate and do not powerfully entrain fast gamma in the hippocampus. Instead, slow gamma rhythms, driven by CA3, predominate. During slow gamma, hippocampal place cells tend to represent spatial locations separate from the current location. This can occur as part of the sharp wave-triggered reactivation process (Carr et al., 2012) or as maps of upcoming locations are activated during exploration (Bieri et al., 2014). As running speed increases, animals likely need to rely more on self-motion cues, conveyed by MEC (Jacob et al., 2014; McNaughton et al., 2006; Parron and Save, 2004; Van Cauter et al., 2013), to accurately keep track of where they are. Under these conditions, MEC spiking increases, and MEC-driven fast gamma becomes the dominant gamma activity in CA1. Fast gamma frequency increases as running speed increases, allowing place cells to accurately keep track of rapid transitions across spatial locations. If the above interpretations are correct, then manipulations that block the fast variant of gamma (e.g., Yamamoto et al., 2014) should greatly reduce the correlation between gamma frequency and running speed and impair spatial navigation at high running speeds.