miRNA-Target Gene Regulatory Networks: A Bayesian Integrative Approach to Biomarker Selection with Application to Kidney Cancer

Summary

The availability of cross-platform, large-scale genomic data has enabled the investigation of complex biological relationships for many cancers. Identification of reliable cancer-related biomarkers requires the characterization of multiple interactions across complex genetic networks. MicroRNAs are small non-coding RNAs that regulate gene expression; however, the direct relationship between a microRNA and its target gene is difficult to measure. We propose a novel Bayesian model to identify microRNAs and their target genes that are associated with survival time by incorporating the microRNA regulatory network through prior distributions. We assume that biomarkers involved in regulatory networks are likely associated with survival time. We employ non-local prior distributions and a stochastic search method for the selection of biomarkers associated with the survival outcome. We use KEGG pathway information to incorporate correlated gene effects within regulatory networks. Using simulation studies, we assess the performance of our method, and apply it to experimental data of kidney renal cell carcinoma (KIRC) obtained from The Cancer Genome Atlas. Our novel method validates previously identified cancer biomarkers and identifies biomarkers specific to KIRC progression that were not previously discovered. Using the KIRC data, we confirm that biomarkers involved in regulatory networks are more likely to be associated with survival time, showing connections in one regulatory network for five out of six such genes we identified.

1. Introduction

High-throughput tools for nucleic acid characterization provide the means to investigate human cancer genomes through comprehensive lists of genomic and epigenomic alterations present in diverse human cancers (Chin et al., 2011). The integration of data from multiple genomic platforms promises to provide insights into the complex nature of cancer, contributing to early cancer detection, improved treatments and even prevention. The Cancer Genome Atlas (TCGA) is a large public repository for cancer-related genomic data. In addition to detailed patient clinical information, TGCA has data on DNA methylation, mRNA expression, microRNA (miRNA) expression, protein expression, single nucleotide polymorphism and copy number variations across 20 different cancers (Do et al., 2013). The availability of multi-platform genomic data from TCGA for the same patient set motivates researchers to integrate multiple aspects of the genome with biological information to investigate the complex phenotypes of cancer.

Data integration studies can be categorized into three groups: 1) studies that analyze sequentially heterogeneous data from different sources; 2) studies that merge different data sets by cross-referencing sequence identifiers (Waters et al., 2006); and 3) studies that integrate multiple platforms into a statistical model to select the most relevant features (Daemen et al., 2009). Our approach can be classified in the third group, as it integrates mRNA and miRNA expression profiles to define a structured biomarker profile for survival time prediction. More specifically, we consider the genomic feature selection problem, where mRNA expression, miRNA expression and the miRNA regulatory network are the structured biomarkers that may affect the overall survival of individuals with cancer. Our work is particularly motivated by a TCGA dataset of kidney renal cell carcinoma (KIRC). Cancer consists of thousands of distinct molecular changes, from multiple types of genetic and epigenetic alterations to the interactions between them. The incorporation of information across multiple platforms can increase statistical power and lower the false discovery rates in identifying biomarkers that are related to clinical outcomes (Wang et al., 2013).

miRNAs are small non-coding RNAs that regulate the expression of complementary mRNAs (Ambros, 2004). They have been shown to be involved in gene regulation and to affect clinical outcome (Qin, 2008; Tseng et al., 2011; Herranz and Cohen, 2010). For this research, genes regulated by miRNAs are called target genes. It is believed that miRNAs down-regulate their target genes (Jackson and Standart, 2007) by either promoting the post-transcription degradation of mRNA (Bagga et al., 2005) or repressing protein synthesis translation (Petersen et al., 2006). The current research follows the biological paradigm of miRNA-target gene post-transcriptional de-regulation, and dismisses positive associations between miRNA and gene expression. There are three major approaches for the identification of miRNA regulatory networks: sequence analysis, experimental methods, and expression analysis (Muniategui et al., 2012). Here, we present a new method for assessing miRNA regulatory networks that integrates expression data, prior knowledge and experimental information.

Earlier research used lasso models (Simon et al., 2011; Long et al., 2011) or Bayesian variable selection (Sha et al., 2006) to identify either mRNA or miRNA biomarkers. It is common in biological studies to take into account the known interaction between features to improve the results (Li and Li, 2008; Pan et al., 2010; Stingo et al., 2011). In an attempt to best capture the true biological variation present in the experimental data, our proposed method both uses known biological information and infers novel interactions among biomarkers through a Bayesian approach that fully accounts for uncertainty. Specifically, we develop an innovative Bayesian statistical approach to identify a small set of potential target genes and miRNA regulators for censored survival times in the context of accelerated failure time (AFT) models. We adopt a stochastic search method for variable selection using mixture priors for the regression coefficients, where the selected coefficients follow non-local prior densities (Johnson and Rossell, 2012). Our approach incorporates gene-miRNA interactions via a novel variable selection prior. We hypothesize that a gene regulated by many miRNAs is more likely to affect clinical outcomes. Similarly, the selection of miRNAs depends positively on the corresponding number of target genes. The miRNA regulatory network is built upon the graphical model approach of Stingo et al. (2010). Due to the inherent nature of miRNA markers to regulate their target genes within gene networks, we introduce pathway-specific random effects that account for the correlation between genes within the same biological pathways. We account for the down-regulation constraints of miRNAs on target genes by imposing a generalized gamma distribution on the regression coefficients that define the regulatory network. To the best of our knowledge, our work represents the first attempt to define an integrative statistical model for survival time that is based on miRNA expression, mRNA expression, and the miRNA regulatory network.

2. Model specification

We depict our proposed model formulation as a Bayesian hierarchical model that includes the selection of miRNAs and mRNAs, prior distributions that incorporate biological knowledge and miRNA regulatory networks that capture structural dependencies among the biomarkers. First, we briefly introduce the following notations:

1. (y, δ) = (y_n, δ_n)_N×2, an N × 2 matrix where y_n = min(t_n, c_n), t_n is the event time for the patient n, c_n is the censoring time and δ_n = I₀(t_n < c_n) is the censoring indicator, with n = 1, …, N, and where I₀ (·) is a Dirac delta function.

2. X = (x₁, x₂, …, x_G) = (x_ng)_N×G, an N × G matrix of standardized mRNA expression levels of G genes.

3. Z = (z₁, z₂, …, z_M) = (z_nm)_N×M, an N × M matrix of standardized expression levels of M miRNAs.

4. P = (ρ_gk)_G×K, a G × K binary matrix indicating membership of genes in biological pathways, where ρ_gk = 1 if gene g belongs to pathway k, and ρ_gk = 0 otherwise. This matrix is constructed using information from the KEGG pathway database (Kanehisa and Goto, 2000).

5. C = (c_gm)_G×M, a G × M binary matrix indicating the candidate miRNA target genes, with c_gm = 1 if gene g is a candidate target gene of miRNA m, and c_gm = 0 otherwise. This matrix is obtained using the bioinformatics methods described in Doecke et al. (2014).

Our model approach consists of two main levels. Given a set of candidate targets, C, and the pathway information, P, the first level aims to identify a miRNA regulatory network based on both experimental and expression data, see Section 2.1. The second level aims to identify a set of significant genes and miRNAs that are associated with survival time, y, see Section 2.2 and 2.2.1. In Section 2.2.2 we present a prior distribution that links the two levels, as it gives biomarkers highly connected in the regulatory network an higher probability to be associated with the survival time. Figure 1 provides a schematic representation of our model, illustrating the probabilistic dependencies among the observed variables and model parameters.

Figure 1.

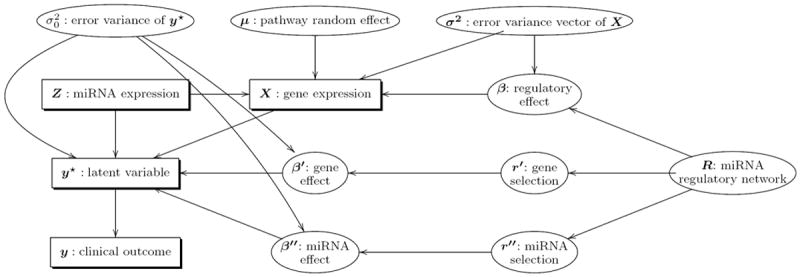
Schematic representation of our proposed approach

2.1 miRNA regulatory network

We model the miRNA regulatory network as a directed graphical model (Bayesian network). This approach is equivalent to a system of linear equations, where each regression corresponds to a target gene that is potentially affected by all its candidate corresponding miRNAs. For each target gene, we are interested in identifying a small number of regulatory associations with high confidence. This goal can be accomplished via a variable selection approach by introducing a G × M binary matrix, R = (r₁, r₂, …, r_G)^T = (r_gm)_G×M, with r_gm = 1 if gene g is a target of miRNA m, and r_gm = 0 otherwise. The matrix R represents the miRNA regulatory network. We take into account that miRNAs down-regulate gene expression by assuming negative regression coefficients. We incorporate the biological pathway information by allowing genes belonging to the same pathway, k, to have the same random effect, μ_k. Our model formulation naturally accounts for genes belonging to more than one pathway ( ${\sum }_{k=1}^K{\rho }_{\mathit{gk}}>1$). We write the model as

$${\mathit{x}}_{\mathit{g}}=\sum _{k=1}^K{\rho }_{gk}{\mu }_k{1}_N­{\mathit{Z}}_{({\mathit{r}}_{\mathit{g}})}{\mathit{\beta }}_{\mathit{g}(\mathit{R})}+{\mathit{\epsilon }}_{\mathit{g}},g=1,\dots ,G,$$ (1)

where β_g = (β_g1, …, β_gM)^T is the vector of the non-negative regulatory effects of miRNAs on gene g, β_g(R) is the vector of the nonzero elements of β_g, and Z_(rg) is the matrix obtained by taking the corresponding columns of Z. The error terms, ε_g’s, are assumed to be independent, $N(0,{\sigma }_g^2{I}_N)$. The scalar random effects, μ_k’s, are independent and follow a normal distribution, $N(0,{\sigma }_{{\mu }_k}^2)$. The random effects capture the residual correlation between genes within the same pathway (Wilczynski and Furlong, 2010). In these biological pathways, information pertaining the edges between nodes are taken from experimentally validated research, with the directional networks indicating direct regulation of “target genes” within networks. Thus a gene within a directional network that is up/down regulated in cancer, may have direct effects on the expression of other genes in that network. More precisely, the covariance between two genes, g and g′, is $\mathit{cov}(x_{\mathit{ng}},x_{n^{\prime }{g}^{\prime }})={\sum }_{k=1}^K{\rho }_{\mathit{gk}}{\rho }_{g^{\prime }k}{\sigma }_{{\mu }_k}^2$. If genes g and g′ both belong to pathways k and k′, their correlation is $({\sigma }_{{\mu }_k}^2+{\sigma }_{{\mu }_{k^{\prime }}}^2)/{[({\sigma }_{{\mu }_k}^2+{\sigma }_{{\mu }_{k^{\prime }}}^2+{\sigma }_g^2)({\sigma }_{{\mu }_k}^2+{\sigma }_{{\mu }_{k^{\prime }}}^2+{\sigma }_{g^{\prime }}^2)]}^{0.5}$. Given the regulatory network R, each coefficient β_gm follows an independent mixture prior distribution

$$p({\beta }_{\mathit{gm}}\mid \mathit{R},\tau ,{\sigma }_g^2,r)=r_{\mathit{gm}}\mathit{GG}({\beta }_{\mathit{gm}};2r+1,\sqrt{2\tau }{\sigma }_g,2)+(1-r_{\mathit{gm}})I_0({\beta }_{\mathit{gm}}),$$ (2)

where $\mathit{GG}({\beta }_{\mathit{gm}};2r+1,\sqrt{2\tau }{\sigma }_g,2)$ is the generalized gamma (GG) density with shape parameters 2r + 1 and scale parameter $\sqrt{2\tau }{\sigma }_g$, and r ∈ ℕ⁺ and τ ∈ ℝ⁺ are hyperparameters to be specified. For non-negative β_gm, the GG function is defined by

$$\begin{array}{lll}\mathit{GG}({\beta }_{\mathit{gm}};2r+1,\sqrt{2\tau }{\sigma }_g,2)& =& 2{\left[(2r-1)!!\right]}^{-1}{(2\pi )}^{-0.5}{(\tau {\sigma }_g^2)}^{-r-0.5}{\beta }_{\mathit{gm}}^{2r}\exp \left\{­\frac{1}{2\tau {\sigma }_g^2}{\beta }_{\mathit{gm}}^2\right\}\\ & \propto & {\beta }_{\mathit{gm}}^{2r}\mathit{HN}({\beta }_{\mathit{gm}};\tau {\sigma }_g^2),\end{array}$$ (3)

where $\mathit{HN}({\beta }_{\mathit{gm}};\tau {\sigma }_g^2)$ is the half normal distribution with variance $\tau {\sigma }_g^2$. Prior (3) has two desirable features: 1) it accounts for the down-regulatory effect of miRNAs on genes, giving positive mass to only positive values of β_gm (Stingo et al., 2010; Huang et al., 2007); and 2) it gives a low prior probability to coefficients close to 0, eliminating regression models that contain unnecessary explanatory variables, a property that is common to the non-local prior distributions (Johnson and Rossell, 2012). In contrast, local prior densities assign positive density values to regression coefficient vectors with components equal to 0. For the error variances, we assume conjugate inverse-gamma priors, ${\sigma }_g^2~\mathrm{Inv}­\mathrm{Gamma}(\alpha ,\psi )$. The Bernoulli random variable, r_gm, indicates whether there is a relationship between gene g and miRNA m. We choose to model the success probability of r_gm as a function of c_gm, where the binary matrix C encodes the validated miRNA-target gene connections from the experimental methods (see Section 5 for more details). Thus, the prior of r_gm can be defined as r_gm∣c_gm, q ~ c_mgq^r_gm (1 − q)^{1 − r_gm} + (1 − c_gm)I₀(r_gm), where q is the probability that a candidate gene-miRNA connection is selected. This prior excludes all the miRNA-target gene connections not supported by prior biological knowledge. Such connections are possible only under a myriad of binding conditions, underpinning the necessity of a strict prior for plausible miRNA-target gene networks that excludes regulatory mechanisms that are biologically improbable (Huang et al., 2007; Li et al., 2009, 2014).

2.2 Building a survival time model

We aim to build a model to predict survival time using gene expression and microRNA expression. We use an accelerated failure time (AFT) model and apply the latent variable approach of Sha et al. (2006). We introduce a latent variable y^★ such that $y_n^{★}=\log (t_n)$ if δ_n = 1, and $y_n^{★}>\log (y_n)$, otherwise. The proposed AFT model can be written as

$${\mathit{y}}^{★}=1_N{\beta }_0+{\mathit{X}}_{({\mathit{r}}^{\prime })}{\mathit{\beta }}_{({\mathit{r}}^{\prime })}^{\prime }+{\mathit{Z}}_{({\mathit{r}}^{″})}{\mathit{\beta }}_{({\mathit{r}}^{″})}^{″}+\mathit{\nu },\mathit{\nu }~N(0,{\sigma }_0^2{\mathit{I}}_N),$$ (4)

where ${\mathit{\beta }}_{({\mathit{r}}^{\prime })}^{\prime }$ and ${\mathit{\beta }}_{({\mathit{r}}^{″})}^{″}$ are the nonzero regression coefficients for genes and miRNAs, respectively, β₀ is the intercept term, and ${\mathit{r}}^{\prime }={(r_1^{\prime },\dots ,r_G^{\prime })}^T$ and ${\mathit{r}}^{″}={(r_1^{″},\dots ,r_M^{″})}^T$ are the binary indicators of the selected genes and miRNAs associated with survival outcome, with $r_g^{\prime }=1(r_m^{″}=1)$ if gene g (miRNA m) is selected, and $r_g^{\prime }=0(r_m^{″}=0)$ otherwise. In what follows, r_y = (r′^T, r″^T)^T are the indicators of biomarkers related to the clinical outcome, Θ = (β₀, β′^T, β″^T)^T the regression coefficients, and Θ_(ry) the vector of nonzero values of Θ.

2.2.1 Prior distributions for the regression parameters

The elements of vector β′ are stochastically independent, given the selection indicators r′, and have the following mixture prior distribution:

$$p({\mathit{\beta }}^{\prime }\mid {\mathit{r}}^{\prime },{\tau }_0,{\sigma }_0^2,r_0)=\prod _{g=1}^G\{r_g^{\prime }\mathit{PM}({\beta }_g^{\prime };r_0,{\tau }_0,{\sigma }_0^2)+(1-r_g^{\prime })I_0({\beta }_g^{\prime })\},$$ (5)

where $\mathit{PM}({\beta }_g^{\prime };r_0,{\tau }_0,{\sigma }_0^2)$ is the product moment distribution (pMOM) density of parameters r₀, τ₀ and ${\sigma }_0^2$, where τ₀ is a scale parameter that determines the dispersion of ${\beta }_g^{\prime }$ around 0. pMOM distributions are defined on ℝ and can be written as $\mathit{PM}({\beta }_g^{\prime };r_0,{\tau }_0,{\sigma }_0^2)=\mathit{GG}({\beta }_g^{\prime };2r_0+1,\sqrt{2{\tau }_0}{\sigma }_0,2)/2$. These priors are then symmetric at zero and the positive part of this distribution is actually the GG distribution defined in (3). Such pMOM distributions have been efficiently used by Johnson and Rossell (2012) for Bayesian model selection. Given the selection indicator of the miRNAs r″, we can analogously assume a mixture prior distribution on the regression coefficients β″ of the miRNAs. We also assume a non-local prior on the intercept term β₀ by $p({\beta }_0\mid {\tau }_{00},{\sigma }_0^2,r_0)=\mathit{PM}({\beta }_0;r_0,{\tau }_{00},{\sigma }_0^2)$, with scale parameter τ₀₀, and a conjugate inverse gamma prior for ${\sigma }_0^2$, with parameters α₀ and ψ₀. The intercept term is not subject to variable selection and it is always included in our inference procedure.

2.2.2 Priors for variable selection indicators

For the latent gene selection indicator r′ and the miRNA selection indicator r″, we specify prior distributions that account for the miRNA regulatory network as defined by the matrix R. These priors define a probabilistic dependency between the miRNA regulatory network, i.e., our structured biomarker, and the clinical outcome. We choose to model the success probability of $r_g^{\prime }$ as a function of R, as follows:

$$P(r_g^{\prime }=1\mid \mathit{R},{\nu }^{\prime },{\tau }^{\prime })=\frac{\exp ({\nu }^{\prime }+{\tau }^{\prime }{\sum }_{m=1}^M{r}_{\mathit{gm}})}{1+\exp ({\nu }^{\prime }+{\tau }^{\prime }{\sum }_{m=1}^M{r}_{\mathit{gm}})},$$ (6)

where ν′ ∈ ℝ and τ′ ∈ ℝ⁺ are unknown parameters. The elements of r′ are stochastically independent given R, ν′ and τ′. These prior probabilities are an increasing function of the number of miRNAs that regulate each gene. An analogous prior p(r″∣R, ν″, τ″) is defined for r″; this prior is an increasing function of the number of target genes for each miRNA. The parameters ν′ and ν″ control the sparsity of the model, and their inverse logit transformation can be interpreted as the a priori false positive rate associated with R. The higher the value of τ′ and τ″, the stronger is the effect of the regulatory network on the selection process. We hypothesize that genes and miRNAs involved in the regulatory network are more likely to be significantly correlated with survival time. Prior (6) gives higher probabilities of being selected to genes that are targeted by many miRNAs and to miRNAs that regulate many genes. Therefore, we expect this prior to increase the selection probability of true positive biomarkers as it accounts for additional biological information. This assumption is biologically intuitive since it is known that miRNAs play important roles in cancer outcomes (Qian et al., 2011). We specify a hyper-prior distribution for τ′ and τ″ to be half normal ${\tau }^{\prime }~\mathit{HN}({\sigma }_{{\tau }^{\prime }}^2)$ and ${\tau }^{″}~\mathit{HN}({\sigma }_{{\tau }^{″}}^2)$. We summarize the hierarchical formulation of our full model in Table 1. We present an extension of our model that includes prior distributions on ν′, ν″, and q in Web Appendix C.

Table 1.

The proposed probabilistic model

Complete data likelihood:

$\begin{array}{lll}L(·\mid {\mathit{y}}^{★},\mathit{X},\mathit{Z})& =& L_1({\beta }_0,{\mathit{\beta }}^{\prime },\mathit{\beta }″\mid {\mathit{y}}^{★},\mathit{Z},\mathit{X})L_2(\mathit{\mu },\mathit{\beta },\mathit{\sigma },\mathit{X}\mid \mathit{Z})\\ & =& N({\mathit{y}}^{★};1_N{\beta }_0+\mathit{X}{\mathit{\beta }}^{\prime }+\mathit{Z}{\mathit{\beta }}^{″},{\sigma }_0^2{\mathit{I}}_N)\prod _{g=1}^{G}N({\mathit{x}}_{\mathit{g}};­\mathit{Z}{\mathit{\beta }}_{\mathit{g}}+\sum _{k=1}^K{\rho }_{\mathit{gk}}{\mu }_k{1}_N,{\sigma }_g^2{\mathit{I}}_N)\end{array}$

Model parameters:

$\begin{array}{lll}\hfill p({\mathit{\sigma }}_{\mathit{\mu }}^{\mathbf{2}}\mid {\alpha }_{\mu },{\psi }_{\mu })& =& {\prod }_{k=1}^K\mathit{IG}({\sigma }_{{\mu }_k}^2;{\alpha }_{\mu },{\psi }_{\mu })\\ \hfill p(\mathit{\mu }\mid {\mathit{\sigma }}_{\mathit{\mu }}^{\mathbf{2}})& =& {\prod }_{k=1}^{K}N({\mu }_k;0,{\sigma }_{{\mu }_k}^2)\\ \hfill p({\mathit{\sigma }}^{\mathbf{2}}\mid \alpha ,\psi )& =& {\prod }_{g=1}^G\mathit{IG}({\sigma }_g^2;\alpha ,\psi )\\ \hfill p({\beta }_{gm}\mid \mathit{R},\tau ,{\sigma }^2,r)& =& r_{\mathit{gm}}\mathit{GG}({\beta }_{\mathit{gm}};2r+1,\sqrt{2\tau }{\sigma }_g,2)+(1-r_{\mathit{gm}})I_0({\beta }_{\mathit{gm}}),\\ & & g=1,\dots ,G;m=1,\dots ,M.\\ \hfill p({\sigma }_0^2\mid {\alpha }_0,{\psi }_0)& =& \mathit{IG}({\sigma }_0^2;{\alpha }_0,{\psi }_0)\\ \hfill p({\mathit{\beta }}^{\prime }\mid {\mathit{r}}^{\prime },{\tau }_0,{\sigma }_0^2,r_0)& =& {\prod }_{g=1}^G\{r_g^{\prime }\mathit{PM}({\beta }_g^{\prime };r_0,{\tau }_0,{\sigma }_0^2)+(1-r_g^{\prime })I_0({\beta }_g^{\prime })\}\\ \hfill p(\mathit{\beta }″\mid \mathit{r}″,{\tau }_0,{\sigma }_0^2,r_0)& =& {\prod }_{m=1}^M\{r_m^{″}\mathit{PM}({\beta }_m^{″};r_0,{\tau }_0,{\sigma }_0^2)+(1-r_m^{″})I_0({\beta }_m^{″})\}\\ \hfill p({\beta }_0\mid {\tau }_{00},{\sigma }_0^2,r_0)& =& \mathit{PM}({\beta }_0;r_0,{\tau }_{00},{\sigma }_0^2)\end{array}$

Variable selection parameters:

$\begin{array}{lll}\hfill p({\mathit{r}}^{\prime }\mid \mathit{R},{\nu }^{\prime },{\tau }^{\prime })& \propto & {\prod }_{g=1}^G{[\exp ({\nu }^{\prime }+{\tau }^{\prime }{\sum }_{m=1}^M{r}_{\mathit{gm}})]}^{r_g^{\prime }}\\ \hfill p({\tau }^{\prime }\mid {\sigma }_{{\tau }^{\prime }}^2)& =& \mathit{HN}({\tau }^{\prime };{\sigma }_{{\tau }^{\prime }}^2)\\ p({\mathit{r}}^{″}\mid \mathit{R},{\nu }^{″},{\tau }^{″})& \propto & {\prod }_{m=1}^M{[\exp ({\nu }^{″}+{\tau }^{″}{\sum }_{g=1}^G{r}_{\mathit{gm}})]}^{r_m^{″}}\hfill \\ \hfill p({\tau }^{″}\mid {\sigma }_{{\tau }^{″}}^2)& =& \mathit{HN}({\tau }^{″};{\sigma }_{{\tau }^{″}}^2)\\ \hfill p(r_{\mathit{gm}}\mid \mathit{C},q)& =& c_{\mathit{mg}}{q}^{r_{\mathit{gm}}}{(1-q)}^{1-r_{\mathit{gm}}}+(1-c_{\mathit{gm}})I_0(r_{\mathit{gm}}),g=1,\dots ,G;m=1,\dots ,M\end{array}$

Model hyperparameters : τ, τ0, τ00, r, r0, α, ψ, α0, ψ0, αμ, ψμ.

Variable selection hyperparameters: ${\sigma }_{{\tau }^{\prime }}^2$, ${\sigma }_{{\tau }^{″}}^2$, q, ν′, ν″.

3. Posterior inference and prediction

We define an MCMC procedure to fit the model and subsequently conduct posterior inference. For posterior inference, our primary interest is in the selection of the arrows in the miRNA regulatory network and of the covariates that affect survival time, as captured by the selection parameters R and r_y. To increase computational efficiency, we integrate out all regression coefficients and variance parameters to obtain the marginal distribution p(y^★, X∣Z, μ, R, r_y). This is accomplished by analytically integrating out the variance parameters, approximating the resulting marginal likelihood by its limiting normal distribution, and applying a standard Laplace approximation (Johnson and Rossell, 2012), see Web Appendix A. Thus, we design an algorithm that draws samples from the marginal posterior distribution of (μ, R, r_y, τ′, τ″, ${\sigma }_{\mu }^2$). Employing a stochastic search, our MCMC algorithm efficiently explores the model space and can quickly find the most probable set of covariates with high posterior probabilities, while spending less time in regions with low posterior probabilities. We detail the MCMC implementation in the Web Appendix B. Model selection can be performed by either using the maximum a posteriori estimate of (R, r_y) or selecting biomarkers and edges in the regulatory network by looking at their marginal probabilities of inclusion. The latter solution is preferred in practice since the model space is quite large and the posterior mode may be encountered only a few times in the MCMC runs.

Survival times are predicted using a Bayesian model averaging approach (Sha et al., 2006). Let x^new and z^new be the vector of the gene and miRNA expressions of a new patient, and let x^★ = (1, x^new, z^new) be the vector of all the covariates for that patient. Let Ŷ^★ be the augmented data, with the censored failure times imputed from the mean of the values sampled in the course of the MCMC algorithm; (τ̂′, τ̂″) be the posterior mean of (τ′, τ″); and R̂ be the selected regulatory network, defined by the miRNA-gene connections that correspond to the arrows with the highest posterior probabilities. In what follows, θ̂ = (τ̂′, τ̂″, R̂) is the set of the estimated parameters. The log-survival time for a new patient can be estimated as $y^{\mathrm{new}}={\sum }_{{\mathit{r}}_{\mathit{y}}}{\widehat{\mathit{x}}}^{★}{\mathrm{\Theta }}_{({\mathit{r}}_{\mathit{y}})}^{★}p({\mathit{r}}_{\mathit{y}}\mid \mathit{X},\mathit{Z},{\widehat{\mathit{Y}}}^{★},\widehat{\theta },\widehat{\mathit{R}})\approx {\sum }_{s=1}^S{\widehat{\mathit{x}}}^{★}{\mathrm{\Theta }}_{({\mathit{r}}_{\mathit{y}}^{(s)})}^{★}p({\mathit{r}}_{\mathit{y}}^{(s)}\mid \mathit{X},\mathit{Z},{\widehat{Y}}^{★},\widehat{\theta },\widehat{\mathit{R}})$, where vector ${\mathrm{\Theta }}_{({\mathit{r}}_{\mathit{y}}^{(s)})}^{★}$ is the posterior mode of Θ=(β₀, β′^T, β″^T)^T for model ${\mathit{r}}_{\mathit{y}}^{(s)}$, visited at the s-th iteration of our MCMC algorithm, and x̂^★ = (1, x̂^new, ẑ^new), ${\widehat{x}}_g^{\mathrm{new}}=(x_g^{\mathrm{new}}-{\overline{x}}_g)/{\widehat{\sigma }}_g^X$ is the expression of gene g, standardized with its arithmetic mean x̄_g and its empirical standard deviation ${\widehat{\sigma }}_g^X$, obtained from a training set. Similarly, ${\widehat{z}}_m^{\mathrm{new}}=\left(z_m^{\mathrm{new}}-{\overline{z}}_m\right)/{\widehat{\sigma }}_m^Z$ is the standardized expression of miRNA m. Following Gelfand (1996), the predictive survival function can be estimated by $\widehat{S}(t\mid {\mathit{x}}^{\mathrm{new}},{\mathit{z}}^{\mathrm{new}})\approx {\sum }_{s=1}^{S}P(y^{★}>\log (t)\mid {\widehat{x}}^{★},\mathit{X},\mathit{Z},{\widehat{Y}}^{★},\widehat{\theta },{\mathit{r}}_{\mathit{y}}^{(s)},{\mathrm{\Theta }}_{({\mathit{r}}_{\mathit{y}}^{(s)})}^{★})p({\mathit{r}}_{\mathit{y}}^{(s)}\mid \mathit{X},\mathit{Z},{\widehat{\mathit{Y}}}^{★},\widehat{\theta },\widehat{\mathit{R}})$, where $P({\mathit{y}}^{★}>\log (t)\mid {\widehat{\mathit{x}}}^{★},\mathit{X},\mathit{Z},{\widehat{Y}}^{★},\widehat{\theta },{\mathit{r}}_{\mathit{y}}^{(s)},{\mathrm{\Theta }}_{({\mathit{r}}_{\mathit{y}}^{(s)})}^{★})$ is the survivor function of a log-student distribution.

4. Simulation studies

We investigated the performance of our method by using simulated data that mimic the KIRC dataset. To highlight the importance of the miRNA regulatory network in our model, we compared the BNL method with a version of our method that does not include priors (6) (the BNLR method), with the latter approach failing to take into account the gene-miRNA interactions. The BNLR method is simply defined by setting τ′ = τ″ = 0 and corresponds to a simpler two-stage approach, where the two stages are performed independently. We compare BNL and BNLR to asses the benefits of joint framework for the miRNA regulatory networks and the survival analysis over a simpler two-stage approach. We also compared the performance of these two models with those of the L₁ penalized Cox proportional hazards regression (CPH-L1) of Simon et al. (2011) and the AFT Bayesian variable selection (AFT-BVS) approach of Sha et al. (2006) by simply using genes and miRNAs as covariates. This approach assumes local distributions (normal distributions) on the regression coefficients. The synthetic data roughly mimic the KIRC data that motivated the development of our model. We generated training and validation sets with similar sizes to the original KIRC data application (167 and 85 patients, respectively) and used the matrix of observed miRNA expression Z to ensure that the realistic pattern of correlation across miRNAs is preserved. We randomly simulated three different scenarios, with K ∈ {161, 229, 253} biological pathways from KEGG, which respectively contain G ∈ {208, 516, 1003} genes, with several genes belonging to multiple pathways. We simulated different scenarios with 0%, 30% and 50% censored data. Details on the procedure used to generate the model parameters are given in Web Appendix D. We report results on 30 simulated data sets for 9 scenarios. Details on hyperparameter setting are given in Web Appendix E.

4.1 Results

We fit the CPH-L1 method by choosing the optimal tuning parameter from a 10-fold cross validation implemented in the R package glmnet. We ran the AFT-BVS model using standard normal priors for the regression coefficients. The AFT-BVS results were obtained from an MCMC run of 120,000 iterations, with 40,000 as burn-in. The MCMC sampler of our BNL and BNLR methods was run for 25,000 iterations, 5,000 discarded as burn-in. The initialization of the parameters is discussed in Web Appendix H and MCMC diagnostics are discussed in Web Appendix I. To evaluate prediction performances, we reported the C-index and the integrated Brier score (IBS) for the validation set, see Web Appendix F. To assess performance in terms of variable selection, we computed the area under the curve (AUC), sensitivity and specificity (Table 2). Sensitivity analyses with different choices of q, ν′, ν″, u, υ, α₀ and ψ₀ show that the posterior inference is quite robust (see Web Appendix G). Our method perfectly reconstructed the miRNA regulatory networks, R (AUCs close to 1 for all simulation scenarios), implying that the regulatory network feature selection is robust to changes in the number of genes. The highest performance, in terms of both variable selection and prediction, was achieved using our BNL method across almost all of the different scenarios. These findings reinforce the importance of incorporating miRNA regulatory network information into the inferential process. Overall, the performance of the CPH-L1 method was not as good as those of the Bayesian approaches in terms of variable selection. The CPH-L1 method exhibited good predictive performances, but tended to have very low sensitivity. When G was large with at least 30% censoring, the BNLR approach performed as well as the AFT-BVS and CPH-L1 methods. We performed additional simulation studies to investigate the robustness of our model to miss-specification of these biological assumptions, see Web Appendix J. The perturbation of the miRNA/gene candidate connections has a slight negative impact on both selection and prediction, whereas the perturbation of the pathway information does not have a significant impact on our model performances.

Table 2.

Simulation results under different numbers of genes, G, and different percentages of censored data. Cens stands for the percentage of censored data, Sens for sensitivity, Spec for specificity, and IBS for integrated Brier score. The best values are shown in boldface.

G	Cens	Method	AUC	Sens	Spec	C-index	IBS
208	0	BNL	0.993 (0.014)	0.975 (0.032)	0.999 (0.002)	0.956 (0.015)	0.014 (0.011)
208	0	BNLR	0.989 (0.023)	0.950 (0.096)	0.999 (0.003)	0.960 (0.040)	0.016 (0.019)
208	0	CPH-L1	0.742 (0.083)	0.571 (0.188)	0.912 (0.031)	0.793 (0.09)	0.098 (0.046)
208	0	AFT-BVS	0.990 (0.016)	0.968 (0.035)	0.999 (0.002)	0.964 (0.015)	0.013 (0.008)
208	30	BNL	0.991 (0.019)	0.950 (0.083)	0.994 (0.008)	0.931 (0.033)	0.051 (0.032)
208	30	BNLR	0.856 (0.084)	0.509 (0.171)	0.981 (0.01)	0.826 (0.078)	0.126 (0.074)
208	30	CPH-L1	0.646 (0.064)	0.367 (0.146)	0.925 (0.033)	0.759 (0.078)	0.174 (0.079)
208	30	AFT-BVS	0.862 (0.110)	0.586 (0.286)	0.983 (0.013)	0.837 (0.095)	0.105 (0.071)
208	50	BNL	0.983 (0.034)	0.870 (0.142)	0.988 (0.013)	0.903 (0.055)	0.084 (0.067)
208	50	BNLR	0.831 (0.064)	0.448 (0.136)	0.979 (0.008)	0.811 (0.075)	0.174 (0.088)
208	50	CPH-L1	0.595 (0.048)	0.250 (0.112)	0.94 (0.027)	0.737 (0.085)	0.227 (0.093)
208	50	AFT-BVS	0.711 (0.085)	0.274 (0.153)	0.974 (0.011)	0.760 (0.078)	0.195 (0.089)
516	0	BNL	1.00 (0.00)	0.999 (0.001)	0.999 (0.001)	0.962 (0.010)	0.012 (0.010)
516	0	BNLR	0.950 (0.073)	0.761 (0.282)	0.989 (0.014)	0.921 (0.079)	0.029 (0.032)
516	0	CPH-L1	0.683 (0.061)	0.412 (0.135)	0.953 (0.018)	0.792 (0.055)	0.083 (0.039)
516	0	AFT-BVS	0.999 (0.001)	0.997 (0.009)	0.997 (0.002)	0.967 (0.009)	0.011 (0.009)
516	30	BNL	0.976 (0.030)	0.812 (0.153)	0.981 (0.015)	0.866 (0.046)	0.102 (0.063)
516	30	BNLR	0.769 (0.087)	0.369 (0.133)	0.969 (0.013)	0.784 (0.062)	0.161 (0.081)
516	30	CPH-L1	0.606 (0.049)	0.25 (0.11)	0.962 (0.018)	0.763 (0.065)	0.169 (0.074)
516	30	AFT-BVS	0.717 (0.085)	0.335 (0.141)	0.963 (0.008)	0.775 (0.071)	0.155 (0.088)
516	50	BNL	0.920 (0.073)	0.650 (0.197)	0.973 (0.012)	0.844 (0.060)	0.134 (0.070)
516	50	BNLR	0.739 (0.060)	0.333 (0.103)	0.968 (0.012)	0.779 (0.075)	0.204 (0.096)
516	50	CPH-L1	0.580 (0.038)	0.194 (0.087)	0.965 (0.015)	0.742 (0.069)	0.217 (0.084)
516	50	AFT-BVS	0.652 (0.065)	0.215 (0.073)	0.961 (0.008)	0.730 (0.082)	0.212 (0.083)
1003	0	BNL	0.888 (0.087)	0.713 (0.208)	0.972 (0.019)	0.860 (0.075)	0.060 (0.050)
1003	0	BNLR	0.763 (0.07)	0.286 (0.116)	0.969 (0.008)	0.762 (0.06)	0.105 (0.056)
1003	0	CPH-L1	0.631 (0.051)	0.288 (0.106)	0.974 (0.009)	0.760 (0.073)	0.090 (0.054)
1003	0	AFT-BVS	0.825 (0.121)	0.578 (0.261)	0.974 (0.012)	0.830 (0.086)	0.072 (0.061)
1003	30	BNL	0.851 (0.066)	0.407 (0.152)	0.966 (0.005)	0.773 (0.065)	0.186 (0.076)
1003	30	BNLR	0.688 (0.054)	0.208 (0.091)	0.961 (0.007)	0.736 (0.062)	0.185 (0.064)
1003	30	CPH-L1	0.583 (0.042)	0.188 (0.088)	0.978 (0.009)	0.742 (0.064)	0.167 (0.069)
1003	30	AFT-BVS	0.681 (0.069)	0.274 (0.111)	0.964 (0.007)	0.749 (0.068)	0.183 (0.080)
1003	50	BNL	0.818 (0.067)	0.375 (0.141)	0.970 (0.006)	0.750 (0.068)	0.255 (0.110)
1003	50	BNLR	0.651 (0.062)	0.203 (0.078)	0.961 (0.006)	0.724 (0.073)	0.268 (0.109)
1003	50	CPH-L1	0.561 (0.039)	0.142 (0.084)	0.980 (0.009)	0.712 (0.094)	0.205 (0.094)
1003	50	AFT-BVS	0.626 (0.052)	0.147 (0.072)	0.962 (0.006)	0.707 (0.083)	0.250 (0.110)

5. Application to TCGA Kidney Data

Our study was motivated by the challenges presented in analyzing multi-platform genetic data and unraveling the biological complexities associated with disease patterns. We applied our newly developed methodology to 267 samples from TCGA (2013) KIRC data, using the mRNA and miRNA expression information collected from Illumina sequencing platforms. Briefly, we obtained mRNA expression data produced from the Illumina HiSeq2000 platform (~ 20, 000 protein coding genes), and miRNA data from the Illumina miSeq platform (~ 800 miRNA markers) for our analyses. We downloaded pathway information from the KEGG database (Kanehisa and Goto, 2000), and used the Bioconductor R package KEGGgraph (Zhang and Wiemann, 2009) to map the Entrez Gene ID to the Pathway ID. We identified a total of 264 pathways and 6,362 Entrez Gene IDs. As candidates for miRNA-target gene connections, we used a set of validated miRNA target genes obtained from three online databases (see Doecke et al. (2014)). The target gene matrix consisted of 307 miRNAs that map to 3,293 target genes with 8,583 gene-miRNA connections. Mapping target genes with the KEGG pathway gene set, we identified 1,761 genes within 252 KEGG pathways. We removed markers with > 40% missing data and imputed markers with < 40% missing data by using the k-nearest neighbor algorithm (Troyanskaya et al., 2001), with k = 10. We further filtered the mRNA transcripts with minimal variance or those that were not included in known KEGG pathways. We retained a total of 222 miRNAs and 1,082 mRNAs, with 3,183 miRNA-target gene connections. We defined the event time as the number of days from the patient’s entrance into the study until the patient’s death. Patients who died of causes other than KIRC or who were lost to follow-up were considered censored cases. Only samples with complete data for miRNA, mRNA and survival time were analyzed (n = 252, with 166 censored cases). We randomly split the data into training (N=167) and validation (85) subsets, keeping the same proportion of censoring in each subset (65%). A comprehensive discussion and exploratory analyses of the TCGA Kidney data supporting our biological assumptions are presented in Web Appendix K. Overall, our approach (BNL) results in improved prediction performances with respect to a simpler two-stage analysis (BLNR), see Table 3.

Table 3.

Comparison of predictive performance

	Training data		Validation data
Method	C-index	IBS	C-index	IBS
BNL	0.95 (0.02)	0.07	0.75 (0.10)	0.19
BNLR	0.94 (0.02)	0.07	0.66 (0.14)	0.22
CPH-L1	0.79 (0.06)	0.14	0.77 (0.09)	0.17
AFT-BVS	0.94 (0.02)	0.08	0.63 (0.13)	0.22

5.1 Results

We ran two MCMC chains with different starting points. We used the same hyperparameter settings as in the simulation studies. MCMC diagnostics confirm that our chains have been run for a satisfactory number of iterations, see Web Appendix I. We compared the prediction performance of our methods (BNL and BNLR) to those of the CPH-L1 and AFT-BVS methods (Table 3). Our BNL method performed better than the AFT-BVS method for both the training and validation sets. The CPH-L1 method performed very well on the validation data, but showed the worst performances for the training data. These results should be interpreted cautiously since the estimated 95% confidence intervals for the C-indices overlapped for the three models. Our BNL approach identified 103 genes connected to 49 miRNAs (Figure 2). We found many miRNA markers connected to multiple genes, with hsa-miR-21, hsa-miR-221, hsa-miR-155 and hsa-miR-29a having the highest proportions of connections. Further, 24 genes were associated with survival time, with a posterior probability ≥ 0.5, 6 of these genes were involved in the miRNA regulatory network. In particular, MYCN, PDCD4, and RBL2 were associated with increased survival time (posterior mode of the regression coefficient of 0.45, 0.74, and 1.01, respectively) while PNPT1, TBK1, and NDUFA2 were associated with decreased survival time (-0.92, -0.47, and -0.45). Our method also identified two miRNA markers (hsa-miR-21, hsa-miR-130b) that were associated with decreased survival time (-0.16 and -0.14), while hsa-miR-133a, hsa-miR-579, and hsa-miR-9-1 were associated with increased survival time (0.16, 0.28, and 0.24).

Figure 2.

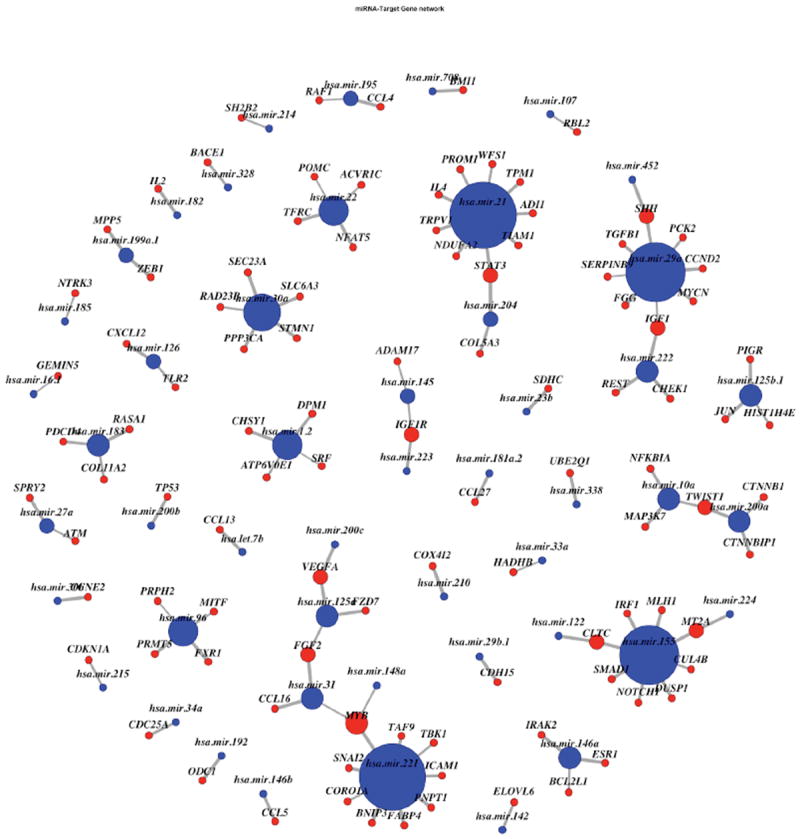
miRNA regulatory network using a threshold of 0.5 on its marginal posterior probability. The diameter of each node is proportional to its number of edges. Thicker edges correspond to higher marginal posterior probabilities. Red nodes correspond to genes; blue nodes correspond to miRNAs.

We conducted downstream analyses of the six genes identified both within the regulatory networks and in association with cancer survival via Ingenuity Pathway Analyses (IPA; Ingenuity^® Systems, www.ingenuity.com). Five of the six genes are involved in the cell cycle, cellular development, or cellular growth and proliferation networks (Figure 3). Interestingly, we discovered similar cancer-related functions from multiple molecules. In particular, PNPT1 and MYCN both regulate CDKN1A, a regulator of cell cycle progression that is tightly coupled to the tumor suppressor gene p53. NDUFA2 and PNPT1 are both mitochondrial membrane genes. NDUFA2, part of mitochondrial complex I, has recently been shown to influence cell metastatic properties (He et al., 2013); whereas TBK1 regulates the NFkB complex (Pomerantz and Baltimore, 1999), leading to increased expression of genes that promote survival.

Figure 3.

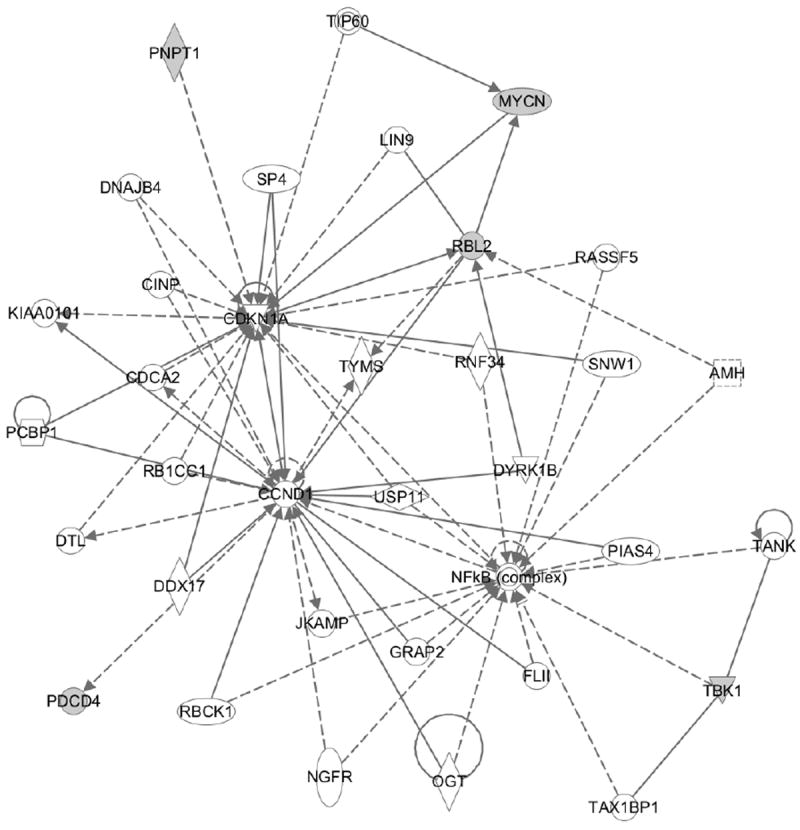
Gene regulatory network obtained from IPA. From the six genes identified, five (colored grey) could be mapped to a regulatory network based around NFκ B, CCND1 and CDKN1A, markers of immune response, cell cycle activity and tumor suppression.

With an increase in research into miRNAs, the downstream effects of miRNA-target gene repression are becoming well characterized (Maia et al., 2013). The miRNA hsa-miR-21 has been associated with many different cancers, targeting a large number of genes that are associated with disease processes (Lawrie, 2013). In the current study, we found hsa-miR-21 to have a significant association with cancer survival, directly targeting nine genes with a posterior probability of greater than 0.5. One of the genes directly targeted by has-miR-21, NDUFA2, was also associated with cancer survival. Other miRNAs of interest identified as regulating the top six genes included hsa-miR-221 (PNPT1, TBK1), hsa-miR-107 (RBL2), hsa-miR-29a (MYCN) and hsa-miR-183 (PDCD4). All five miRNAs identified in regulatory networks with a posterior probability of greater than 0.5 have been previously associated with at least one cancer. Note that 28 genes and 5 miRNAs were identified to be associated to the survival time by BNLR, of which 12 genes and 2 miRNAs were also selected by BNL. This set of 12 genes includes RBL2, PDCD4, and PNPT1 but excludes several other relevant genes, implying that BNLR failed to provide some of the important biological insights provided by BNL; a detailed comparison of biological findings from BNL and BNLR is presented Web Appendix L.

6. Discussion

In this article, we proposed an innovative hierarchical model of feature selection for the analysis of high-dimensional data with censored information. Motivated by the availability of multi-platform TCGA KIRC data, we integrated two different genomic platforms (mRNA and miRNA) in order to build a predictive model for survival outcome. Our approach incorporates biological information from the miRNA regulatory networks, accounting for correlations between multiple mRNAs within commonly known pathways, and demonstrates the feasibility of inferring reliable gene-miRNA networks associated with KIRC survival data. We showed through an extensive simulation study that our model outperforms models that do not consider interactions between miRNA and mRNA biomarkers, both in terms of biomarker selection and prediction. The Bayesian model we have developed has several innovative characteristics: 1) it is integrative since it combines both miRNA and gene expression to select an informative set of biomarkers; 2) it infers the miRNA regulatory network by integrating expression levels of miRNAs with their candidate target mRNAs; 3) it employs variable selection priors that capture the complex miRNA regulatory network, so that biomarkers more involved in the network are more likely to be selected; and 4) it achieves sharper biomarker selection through the specification of non-local prior distributions on the regression coefficients of both the regulatory network and the AFT model. The application of this new methodology supported our hypothesis that biomarkers highly connected in the regulatory network are associated to the survival time. The application of our method to the TCGA KIRC data defined five out of six genes within one regulatory network. Similar to other research findings (Becker Buscaglia and Li, 2011), we found that miR21 regulates many different genes, while miR221 and miR29a also regulate many cancer-related genes. All six genes identified (MYCN, TBK1, NDUFA2, PDCD4, RBL2, PTPN1) have been previously implicated with either the etiology of cancer or with the survival time of individuals with cancer. Interestingly, one of the genes that was shown to be regulated by miR21 (NDUFA2) has previously been associated with cell metastatic properties (indirectly through mitochondrial complex I), suggesting a relationship between metastatic disease and the KIRC samples tested. Our proposed approach is general and the method used to understand the regulatory network can be applied to any feature selection with constraints on the regression coefficients. Moreover, the approach used to predict survival time can be adapted for the analysis of categorical data. Further, our method can be extended to include three or more biological platforms. This will require a deeper understanding of the fundamental biological relationships that link the different platforms.

Supplementary Material

Supplement

Web Appendices A-K, referenced in Sections 2-5, the TCGA Kideny cancer data analyzed in Section 5, and the accompanying computer code are available with this paper at the Biometrics website on Wiley Online Library.