Significance
An outstanding issue in protein science is identifying the relationship between sequence and folding, e.g., do sequences having similar structures have similar folding pathways? The homologs Proteins G & L have been cited as a primary example where sequence variations dramatically affect folding dynamics. However, our new results indicate that the homologs have similar folding behavior. At the highest point on the reaction surface, the pathways converge to similar ensembles. These findings are distinct from descriptions based on the widely used mutational ϕ analysis, partly due to nonnative behavior. Our study emphasizes that significant challenges remain both in characterizing and predicting transition state ensembles even for relatively simple proteins whose folding behavior is believed to be well understood.
Keywords: protein folding, ψ analysis, ϕ analysis, bi-histidine, transition state ensemble
Abstract
Experimental and computational folding studies of Proteins L & G and NuG2 typically find that sequence differences determine which of the two hairpins is formed in the transition state ensemble (TSE). However, our recent work on Protein L finds that its TSE contains both hairpins, compelling a reassessment of the influence of sequence on the folding behavior of the other two homologs. We characterize the TSEs for Protein G and NuG2b, a triple mutant of NuG2, using ψ analysis, a method for identifying contacts in the TSE. All three homologs are found to share a common and near-native TSE topology with interactions between all four strands. However, the helical content varies in the TSE, being largely absent in Proteins G & L but partially present in NuG2b. The variability likely arises from competing propensities for the formation of nonnative β turns in the naturally occurring proteins, as observed in our TerItFix folding algorithm. All-atom folding simulations of NuG2b recapitulate the observed TSEs with four strands for 5 of 27 transition paths [Lindorff-Larsen K, Piana S, Dror RO, Shaw DE (2011) Science 334(6055):517–520]. Our data support the view that homologous proteins have similar folding mechanisms, even when nonnative interactions are present in the transition state. These findings emphasize the ongoing challenge of accurately characterizing and predicting TSEs, even for relatively simple proteins.
Although different sequences can adopt similar structures, each one encodes for a unique free energy surface that may lead to distinct folding behavior. This issue has been investigated by probing how folding transition state ensembles (TSEs) differ for homologous proteins (1, 2). Both experimental and computational studies of the α/β homologs Proteins L & G typically identify their TSEs as being polarized, consisting of either the N- or C-terminal hairpin, respectively (3–16). Moreover, NuG2, a variant of Protein G designed to have a more stable N-terminal β1 + β2 hairpin, is thought to fold through a TSE featuring this hairpin rather than the C-terminal β3 + β4 hairpin found in its parent’s TSE (15).
However, we recently demonstrated that Protein L’s TSE contains both hairpins in a four-stranded β sheet, whereas the native helix remains weakly formed, if at all (17). The difference between this and prior studies emerges from our use of ψ analysis with engineered bi-histidine (biHis) metal ion binding sites to directly identify the residue-residue contacts in the TSE (18–20), whereas the earlier investigations used mutational ϕ analysis (10–16). The revised picture of Protein L’s TSE provides the present motivation for a corresponding analysis on Protein G and NuG2 to properly investigate their sequence–folding relationship.
Accordingly, we apply ψ analysis to Protein G and NuG2b, a fast folding, triple mutant of NuG2 studied by Shaw and coworkers in all-atom molecular dynamics (MD) simulations (21). These two proteins have 73% sequence identity, whereas Proteins G & L share only 13% identity (22). In common with Protein L, their TSEs are deduced to contain four β strands, in contrast to the polarized TSEs previously identified (15). This significant discrepancy is due in part to the presence of nonnative hairpin structures in the TSEs of the two naturally occurring proteins (15, 16). These nonnative turns are likewise found in silico using our TerItFix folding algorithm (23–26), which uses sequence-dependent Ramachandran maps to predict native structures and folding pathways. Moreover, our experimental TSE for NuG2b proves to be in partial agreement with all-atom simulations (21).
Results
ψ Analysis.
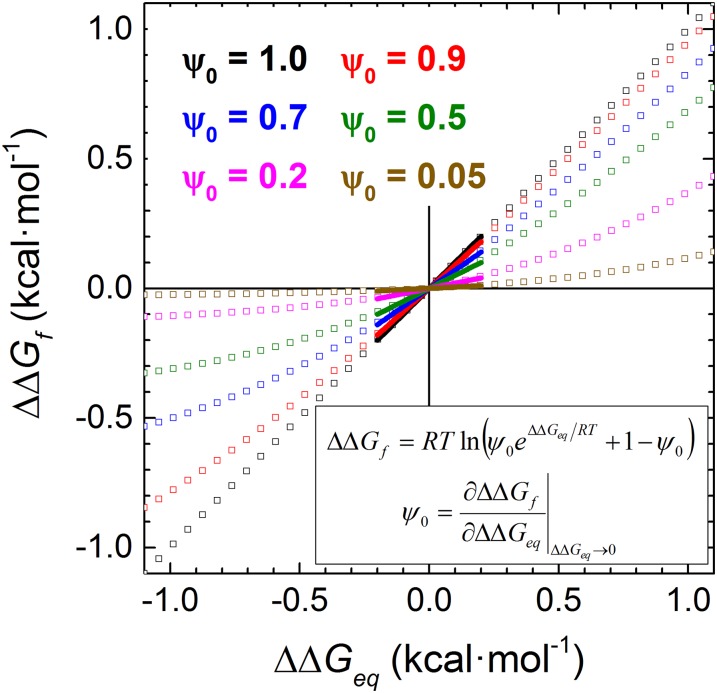
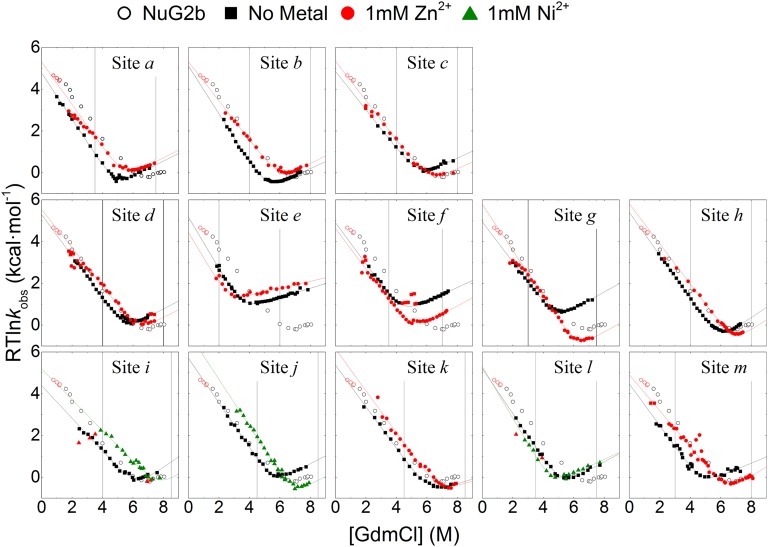
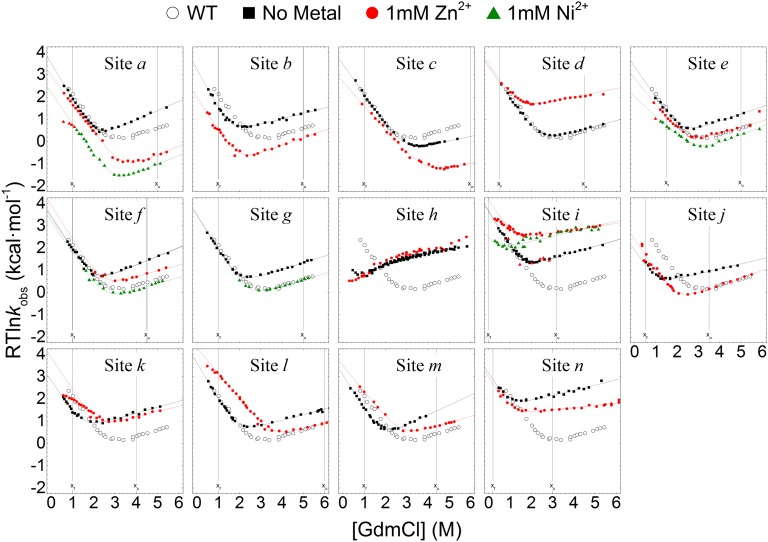
A total of 28 biHis sites were individually introduced into Protein G and NuG2b at locations designed to probe the TSE for the presence of strand-strand pairings, helix formation, and a long-range contact (Fig. 1). The addition of zinc or nickel ions, which can coordinate the pair of histidines, alters the protein’s stability and activation free energy for folding (ΔΔGeq and ΔΔGf, respectively) due to differences in binding and disassociation constants KDSE, KN, and KTSE for the denatured state ensemble (DSE), native state ensemble (NSE or N), and TSE (SI Materials and Methods and Fig. S1). The ion-induced changes in the folding rate and stability are used to define the ψ value, a parameter analogous to the standard mutational ϕ value, with ψ being the instantaneous change in ΔΔGf relative to ΔΔGeq
| [1] |
Any potential artifacts related to the alteration of the folding behavior by the metal ion binding are alleviated by evaluating ψ in the limit of zero perturbation
| [2] |
As defined, ψ0 reflects the intrinsic degree of contact formation in the TSE in the absence of metal ions. This ability to calculate ψ in the limit of vanishing metal ion concentration provides information on the conformation of the TSE before any ion-induced perturbation.
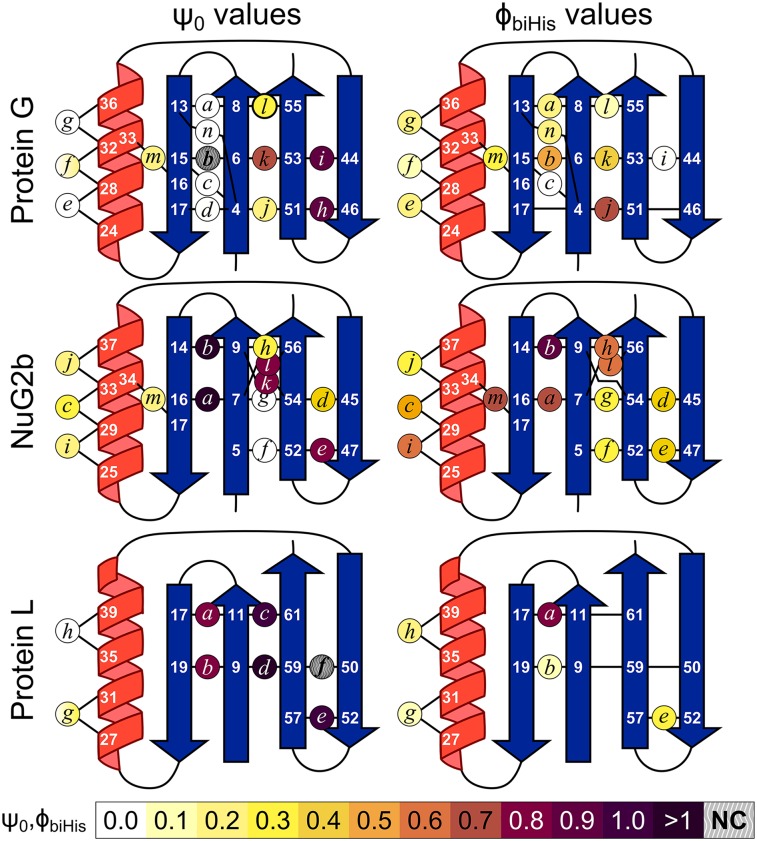
Fig. 1.
ψ0 and ϕbiHis values for the biHis mutations. NC, noncanonical ψ0 values where ΔΔGeq → 0 and ΔΔGf ≠ 0 on addition of metal ions, such that ψ0 → ±∞. ϕbiHis values for which < 0.3 kcal/mol are not shown.
Fig. S1.
Relationship between the change in activation energy ΔΔGf and the stability ΔΔGeq. The two values are related by a single parameter ψ0, the instantaneous slope as ΔΔGeq → 0.
ψ0 values of zero or unity indicate that the ion binding affinity of the biHis site is the same as found in the unfolded or native site, respectively. These two behaviors are interpreted as the biHis site being absent or native-like in the TSE, respectively. A fractional ψ0 value indicates that the biHis site either is native-like in a subpopulation of the TSE or contains nonnative binding affinity (e.g., a distorted site with less favorable binding geometry or a flexible site that must be restricted before ion binding), or some combination thereof (18–20, 27). ψ0 values greater than unity are possible and can reflect the presence of the biHis site in the TSE but with a stronger affinity for ion binding than the native state. Mutational ϕbiHis values also are calculated for each biHis site using double mutant data (in the absence of metal ions) and the WT protein data as a reference point.
Structural Variations Within a Common TSE Topology.
The pattern of ψ0 values indicates that the three homologs share a common TSE topology. Each TSE features interactions among the four strands to varying extents (Figs. 1 and 2, Figs. S2–S4, and Tables S1 and S2). Notably, ψ0 values for biHis sites within the hairpins are typically higher than for sites on β1 + β4 bridging the two hairpins. At least one significant ψ0 value is present for each of the strand-strand pairings for Protein G and NuG2b, indicating that all three interstrand interactions are present in the respective TSEs. Both hairpins in NuG2b contain at least one near-unity ψ0 value, whereas the interhairpin ψ0 value is 0.8 at sites k and l. Protein G exhibits two near-unity ψ0 values on its C-terminal hairpin (ψ0 = 0.9 for sites h and i) and another high value between the hairpins (). A noncanonical ψ0 value (where ψ0 ∉ [0,1]) occurs for site b in Protein G (). This result coupled with the nearly vanishing ψ0 values at sites a, c–e, and n implies that the N-terminal hairpin is partially formed in the TSE and has nonnative interactions.
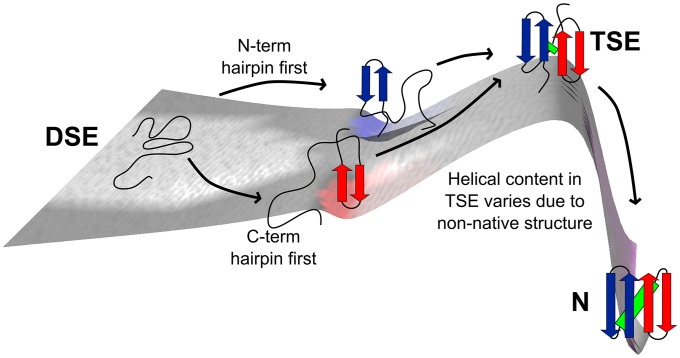
Fig. 2.
Folding landscape of Proteins G & L and NuG2b.
Fig. S2.
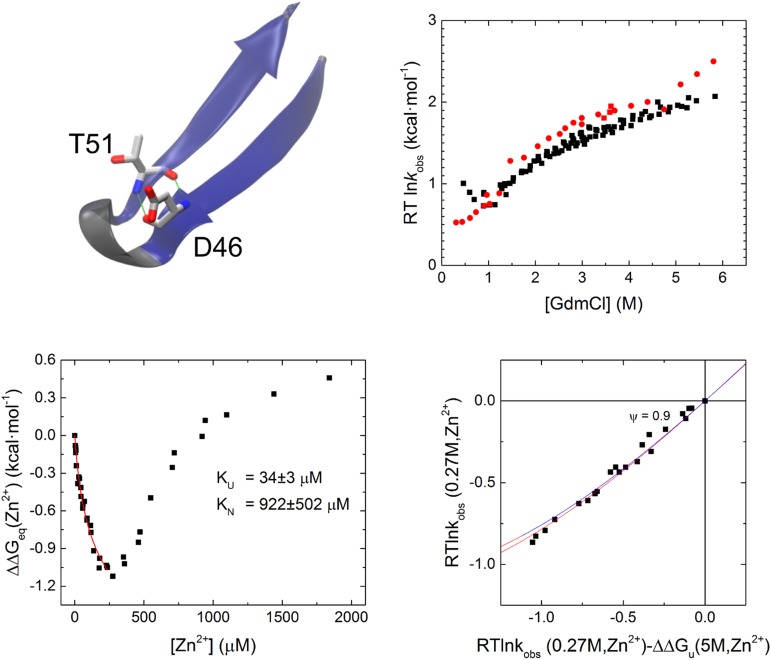
Destabilization of the native state in the carboxyl-terminal hairpin of Protein G (site i). The hairpin is able adopt a better binding geometry in the unfolded state than in the native state (and TSE). Although NuG2b is able to tolerate the destabilizing mutation (site e; Fig. 3), site h in Protein G is not, and therefore a full chevron is not possible in 1 mM Zn2+. A Leffler analysis for folding and unfolding kinetics up to ∼200 mM Zn2+ is sufficient to calculate the ψ value.
Fig. S4.
Folding chevrons of NuG2b biHis mutants in the absence and presence of metal. Vertical lines designate the [GdmCl] at which the ΔΔGf and ΔΔGu are calculated. The NuG2b chevron is shown for comparison (〇).
Table S1.
Summary of biHis sites in NuG2b
| Location | Site | Mutation | ψ0* | ϕbiHis | ΔΔGeqMetal | ΔΔGeqbiHis | ΔΔGfMetal | m0 | m0Metal | βT† | βTMetal | Metal |
| WT | − | − | − | − | − | − | 1.29(7) | − | 0.78(5) | − | − | |
| β1 + β2 | a | V7H/T16H | 1.45(15) | 0.67(7) | 0.90(11) | −1.91(18) | 0.83(5) | 1.52(3) | 1.38(5) | 0.72(2) | 0.81(4) | Ni2+ |
| b | V9H/T14H | 1.65(23) | 0.89(9) | 0.81(6) | −1.21(13) | 1.01(3) | 1.48(2) | 1.32(4) | 0.78(2) | 0.71(4) | Zn2+ | |
| α | c | K29H/Q33H | 0.26(3) | 0.47(6) | 0.92(6) | −1.42(19) | 0.40(4) | 1.27(4)§ | 1.29(4) | 0.73(3) | 0.73(3) | Zn2+ |
| β3 + β4 | d | T45H/T54H | 0.36(5) | 0.38(6) | 0.97(6) | −1.13(14) | 0.55(3) | 1.37(4)§ | 1.30(5) | 0.72(3) | 0.71(3) | Zn2+ |
| e | D47H/T52H | 0.80(2) | 0.39(2) | −1.08(6) | −2.84(13) | −0.65(5) | 1.46(4)¶ | 1.41(5) | 0.85(1) | 0.88(1) | Zn2+ | |
| β1 + β4 | f | K5H/T52H | −0.14(3) | 0.32(2) | 0.70(4) | −2.55(13) | −0.22(3) | 1.33(3) | 1.35(2) | 0.74(2) | 0.72(2) | Zn2+ |
| g | V7H/T54H | 0.02(0) | 0.31(3) | 2.27(5) | −2.22(15) | 0.35(3) | 1.37(3)§ | 1.51(3) | 0.70(2) | 0.73(3) | Zn2+ | |
| h | V9H/T56H | 0.28(2) | 0.55(12) | 1.27(3) | −0.78(17) | 0.67(2) | 1.52(3)§ | 1.45(3) | 0.68(1) | 0.66(1) | Zn2+ | |
| α | i | A25H/K29H | 0.19(9) | 0.63(17) | 1.84(24) | −0.85(28) | 0.98(7) | 1.29(12)§ | 1.25(13) | 0.61(7) | 0.59(7) | Ni2+ |
| j | Q33H/D37H | 0.15(2) | 0.30(7) | 2.00(8) | −0.83(15) | 1.00(4) | 1.45(5)§ | 1.50(5) | 074(3) | 0.75(3) | Ni2+ | |
| β1 + β4 | k | V9H/T54H | 0.79(15) | ND | 0.85(12) | −0.06(9) | 0.75(6) | 1.23(3)§,‡ | 1.23(3) | 0.81(0) | 0.81(0) | Zn2+ |
| l | V7H/T56H | 0.84(6) | 0.57(6) | −0.60(7) | −1.72(19) | −0.46(4) | 1.47(3) | 1.57(6) | 0.73(2) | 0.79(2) | Ni2+ | |
| β2 + α | m | Y17H/Y34H | 0.22(3) | 0.74(12) | 1.60(7) | −1.65(25) | 0.85(4) | 1.35(4)§ | 1.25(4) | 0.73(3) | 0.71(3) | Zn2+ |
Values in parentheses represent SEs of the fitting and derived parameters, e.g., 1.45(15) = 1.45 ± 0.15. ND, not determined.
ψ0 value is calculated directly in the fit of the chevron data that includes data for strongly folding and unfolding condition, xf and xu, respectively (Fig. S4).
βT = mf/m0, where mf and m0 are the denaturant dependences of the ΔGf and ΔGeq, respectively (Materials and Methods).
mu is a shared parameter.
mf is a shared parameter.
mu is set to the value obtained from fitting the chevron in the absence of metal ions.
Table S2.
Summary of biHis sites in WT Protein G
| Location | Site | Mutation | ψ0* | ϕbiHis | ΔΔGeqMetal | ΔΔGeqbiHis | ΔΔGfMetal | m0 | m0Metal | βT† | βTMetal | Metal |
| WT | − | − | − | − | − | − | 1.69(2) | − | 0.83(1) | − | − | |
| β1 + β2 | a | N18H/K13H | −0.02(0) | 0.18(3) | 1.76(5) | −0.97(5) | −0.23(3) | 1.99(4) | 1.66(4) | 0.79(1) | 0.77(2) | Zn2+ |
| −0.10(2) | 1.30(7) | −1.11(7) | 1.77(4) | 0.78(2) | Ni2+ | |||||||
| b | I6H/E15H | −5.13(386) | 0.48(2) | 0.09(6) | −1.28(4) | −1.00(8) | 1.99(9) | 1.82(6) | 0.78(2) | 0.71(4) | Zn2+ | |
| c | K4H/E15H | −0.24(3) | 0.01(4) | 0.72(4) | 0.57(3) | −0.50(3) | 1.56(3) | 1.29(2) | 0.73(3) | 0.73(3) | Zn2+ | |
| d | K4H/T17H | −0.22(7) | ND | −1.43(3) | −0.21(3) | 0.11(3) | 1.63(2) | 1.57(3) | 0.72(3) | 0.71(3) | Zn2+ | |
| α | e | A24H/K28H | −0.34(8) | 0.18(5) | 0.38(4) | −0.73(5) | −0.22(3) | 1.71(6) | 1.45(4) | 0.81(2) | 0.81(2) | Zn2+ |
| −0.83(17) | 0.34(5) | −0.61(4) | 1.27(4) | 0.70(2) | Ni2+ | |||||||
| f | K28H/Q32H | 0.24(4) | 0.13(3) | 1.05(12) | −1.18(5) | 0.46(12) | 1.88(7) | 1.76(8)§ | 0.80(2) | 0.85(2) | Zn2+ | |
| −0.05(3) | 1.00(9) | −0.16(8) | 1.71(8)§ | 0.84(2) | Ni2+ | |||||||
| g | Q32H/D36H | 0.03(3) | 0.21(2) | 0.82(5) | −0.94(3) | 0.05(5) | 1.84(2) | 1.82(3)§ | 0.70(2) | 0.73(3) | Zn2+ | |
| β3 + β4 | h | D46H/T51H | 0.90(1)¶ | ND | ND | ND | ND | ND | ND | ND | ND | Zn2+ |
| i | T44H/T53H | −2.57(53) | 0.04(2) | −0.49(5) | −1.54(4) | 0.52(5) | 1.85(4) | 1.72(5)§ | 0.85(1) | 0.92(1) | Zn2+ | |
| 0.93(2) | −2.42(17) | −1.44(17) | 1.82(10)§ | 0.88(1) | Ni2+ | |||||||
| β1 + β4 | j | K4H/T51H | 0.17(2) | 0.70(1) | 1.30(10) | −2.34(5) | 0.51(9) | 1.59(7) | 1.70(6)§ | 0.74(3) | 0.75(3) | Zn2+ |
| k | I6H/T53H | 0.71(5) | 0.41(2) | 1.21(14) | −1.75(5) | 1.04(14) | 1.71(10) | 1.68(11)§ | 0.81(0) | 0.81(0) | Zn2+ | |
| l | N8H/T55H | 0.30(1) | 0.13(2) | 1.77(4) | −0.80(3) | 1.13(3) | 1.85(1) | 1.42(2) | 0.73(2) | 0.79(2) | Zn2+ | |
| β2 + α | m | T16H/Y33H | 0.24(2) | 0.33(2) | 1.47(5) | −1.67(6) | 0.77(3) | 1.95(3) | 1.45(4) | 0.73(3) | 0.71(3) | Zn2+ |
Values in parentheses represent SEs of the fitting and derived parameters, e.g., 0.18(3) = 0.18 ± 0.03. ND, not determined.
ψ0 value is calculated directly in the fit of the chevron data that includes data for a strongly folding and unfolding condition, xf and xu, respectively (Fig. S3).
βT = mf/m0, where mf and m0 are the denaturant dependences of ΔGf and ΔGeq, respectively (Materials and Methods).
mf is a shared parameter.
Estimated from measuring the dependence of folding and unfolding kinetics in a Leffler style analysis (Fig. S2).
Fig. S3.
Folding chevrons of Protein G biHis mutants in the absence and presence of metal. Vertical lines designate the [GdmCl] at which the ΔΔGf and ΔΔGu are calculated when presented in a Leffler plot. The WT Protein G chevron is shown for comparison (〇).
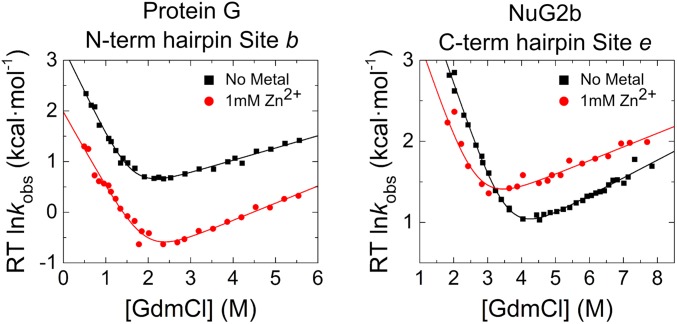
The results for site b in Protein G, which is located in the middle of the hairpin, are particularly informative as they indicate the presence of nonnative interactions in the TSE. Both folding and unfolding rates diminish approximately fivefold for this site on the addition of 1 mM Zn2+ (Fig. 3), indicating that the free energy of the TSE increases by 1 kcal/mol relative to both the NSE and DSE, whereas the stability of the native state is effectively unchanged (ΔΔGeq < 0.2 kcal/mol). This unusual behavior is explained by the formation of a binding site with similar affinity in both the NSE and the DSE (KN = 23 ± 1 μM; KDSE = 33 ± 2 μM), but the site in the TSE has nonnative character and an ∼10-fold weaker binding affinity (KTSE = 333 ± 38 μM).
Fig. 3.
ψ values for two unusual sites. ψ values can be calculated from the denaturant dependence of a biHis site in the absence and presence of 1 mM Zn2+. The addition of Zn2+ to site b of the N-terminal hairpin of Protein G slows folding and unfolding rates equally, indicating that the site has nonnative properties in the TSE. Site e in the C-terminal hairpin of NuG2b experiences destabilization with increasing metal ion concentration, both in the native state and in the TSE by a similar amount, which produces a near unity ψ0 = 0.8.
The nearly vanishing ψ0 and ϕbiHis values for the helical sites indicate that the helix is only weakly formed or absent within Protein G’s TSE. This finding mirrors previous observations derived for Protein L from both ψ (17) and ϕ analyses (12). Despite having nearly the same sequence as Protein G, NuG2b’s helix is present to a greater degree in its TSE. We infer that the lower helical content of Protein G’s TSE is related to it having a poorer helix-hairpin interface due to the presence of the nonnative N-terminal hairpin.
The similarity of the fractional ψ0 (0.2–0.3) and ϕbiHis values (0.3–0.6) for the three exterior sites along NuG2b’s helix is consistent with most of the helix being folded approximately one third of the time in a rapid equilibrium between docked and unfolded conformations (corresponding to a Keq = [docked]/[unfolded] ∼ 1/2 within the TSE). Alternatively, the helix could be present but distorted in a more homogenous TSE, as observed for Protein A (28).
Notably, the global chain topologies within the TSEs for Protein G and NuG2b are similar. Insertion of a biHis site between the center of the β2 strand and a residue that becomes helical in the native state yields similar ψ0 values () for the two proteins, whereas = 0.33 and 0.74 for Protein G and NuG2b, respectively. These data indicate that the overall fold is formed in the TSE for both proteins even though the helix is largely unfolded in Protein G’s TSE.
In Silico Folding.
We conducted folding simulations using TerItFix (17, 23, 25, 26, 29), our homology-free, Cβ-level folding program that uses realistic sampling of the Ramachandran dihedral angles and authentic backbone H-bonding. Its Monte Carlo (MC) search strategy uses the principle of sequential stabilization to iteratively promote the formation of tertiary contacts and H-bonds across multiple rounds of folding. Each round involves ∼1,000 individual MC simulations that are analyzed to identify consensus interactions and backbone geometries, which are incorporated as energetic biases in subsequent rounds of folding. This iterative process continues until the consensus properties converge. In addition, the multiround nature identifies potential intermediate species, albeit without an explicit time scale.
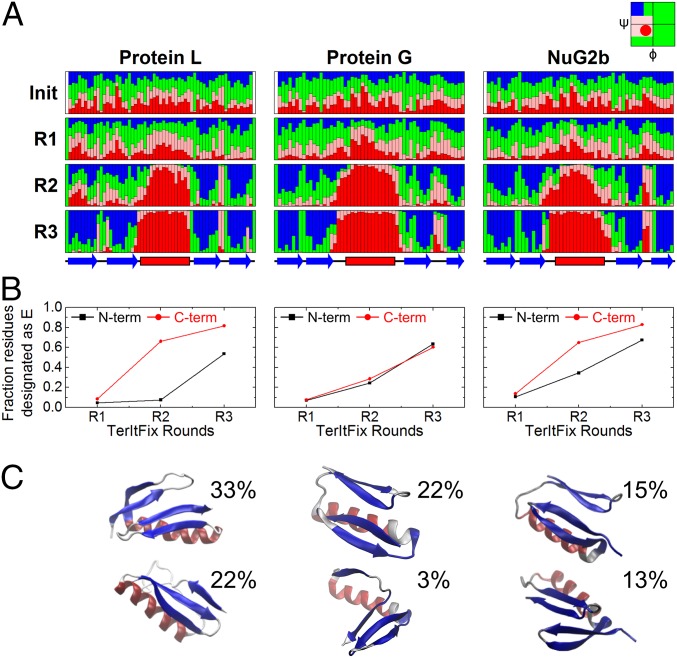
A similar evolution of structure is found for the three homologs (Fig. 4). Although only nascent structures are observed at the end of the first round, the four strands and the helix become identifiable by the end of round 2. Very native-like structures appear at the end of round 3 where the algorithm has converged.
Fig. 4.
TerItFix simulations. (A) Evolution of Ramachandran angles and secondary structure from the initial sampling library to the end of round 3 (color coded according to Ramachandran basin). (B) Fraction of residues in each hairpin forming extended structure. (C) Possible TS structures obtained from the two largest clusters at the end of round R2 (centroids).
The folding behavior, however, does vary between the three homologs, specifically in their ability to form the native hairpins. The most accurate structure generated for NuG2b is very close to the native structure (Cα-RMSD < 2 Å), whereas the best predictions for Proteins G & L (17) are not nearly as good (Cα-RMSD ∼ 4–5 Å).
The success for NuG2b and seemingly weaker performance for the other two proteins lies in the latter pair’s lower backbone propensities for formation of their native turns (Fig. 5). TerItFix’s predictions for both of NuG2b’s hairpins are good, e.g., Cα-RMSD = 0.8 and 1.0 Å across residues K5-T18 and E43-T56, respectively. Likewise, Protein G’s C-terminal hairpin is well predicted with Cα-RMSD = 0.8 Å for E42-T55.
Fig. 5.
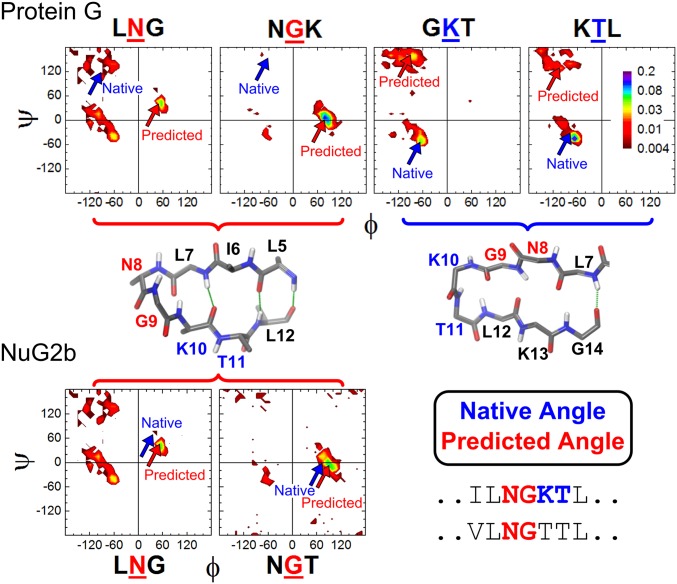
Differences in the Ramachandran propensities of the N-terminal hairpin in Protein G and NuG2b. The dihedral angles of N8 and G9 in Protein G have high propensities for the nonnative type I′ turn, whereas K10 and T11 yield low propensities for the native type I turn. NuG2b eliminates the competition by removing the K10-T11 turn and allowing the N8-G9 pair to take advantage of their high propensity for a type I′ turn, which becomes the native turn in this designed protein.
However, Protein G’s N-terminal turn region is not as well described. The native state adopts a type I turn involving residues K10 and T11, but the Ramachandran sampling distributions strongly favor the formation of a nonnative type I′ turn involving N8 and G9 (Fig. 5). Consequently, the nonnative turn outcompetes the native form in the simulations, and the predicted structure contains a two-amino-acid register shift with an RMSD to the native state of 5.4 Å across K4-T17. A very similar result occurs for the C-terminal hairpin for Protein L (17). The nonnative register shifts observed in silico for Proteins G & L rationalize the noncanonical and the nearly vanishing ψ0 values observed for the relevant hairpins, in particular, for Protein G ( and ).
Nauli et al. (15) modified Protein G to encourage the N-terminal hairpin to adopt a type I′ turn. The ensuing design, NuG2, thus avoids the conflicting turn preferences present in the WT protein (Fig. 5). With this redesign, both NuG2b hairpins adopt native-like geometries in the TerItFix simulations and the experimental TSE, and the predicted structure is better compared with results for the other two homologs.
Despite not reflecting true kinetics, TerItFix is capable of predicting the order of folding events. By the end of round 2, the diversity of contacts and H-bonds is greatly diminished, and the predicted ensemble becomes more homogeneous. Therefore, we analyze the round 2 structures for comparison with the experimental data. Candidate structures from round 2 are culled based on the observation that the TSEs of two-state folders adopt a high fraction of the native topology, as defined using the relative contact order (RCO) parameter, RCOTSE ∼ 0.7∙RCON (17, 30, 31). The culled structures are clustered, and the two largest clusters are considered potential members of the TSE.
The largest cluster (22%) for Protein G contains the N-terminal hairpin in a nonnative geometry and docked to an incompletely formed C-terminal hairpin. The helix is present in both clusters, contrary to the experimental findings. The two major clusters for NuG2b contain native-like hairpins that fold before docking, as also seen in the simulations for Protein G. The largest cluster includes structures with multiple docking poses for the two hairpins, but not necessarily in the native registry. The helix in NuG2b’s TSE is found to be partially to fully folded. The results for NuG2b are generally consistent with the experimental ψ values.
Comparison with DESRES Trajectories for NuG2b.
We also analyzed the all-atom MD trajectories for NuG2b taken from the landmark study of Shaw and coworkers (21). The trajectories for this protein contain 13 discrete folding and 14 unfolding transition paths (TPs) between the NSE and the DSE (Fig. S5). The DSE is described by the simulations as collapsed and highly H-bonded, whereas experimentally, the DSE is expanded and devoid of measurable H-bonding (32). Nevertheless, we examined the simulations to identify the sequence of structure formation along the TPs for comparison with experiment.
Fig. S5.
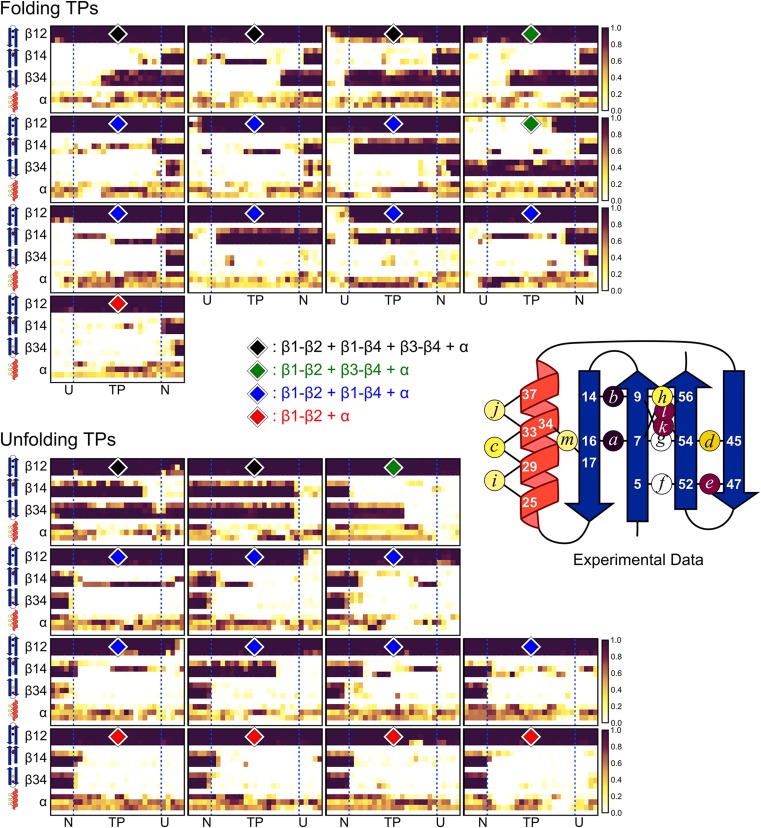
Structure formation along the 13 folding and 14 unfolding transition paths observed in the all-atom MD simulations. The helix is formed across all transition paths (TPs), but the level of strand formation is variable. In the largest class containing 14 members (blue diamond), the amino hairpin is formed along the entire TP, and it is often associated with β4, but β3 is unfolded. Five TPs (black diamond) agree with the experimental data in that both hairpins are formed near the middle of the TP, although the level of hairpin-hairpin contact often is lower than indicated by the ψ values for the folding TPs. For five TPs (red diamond), the amino but not the carboxy hairpin is formed. For three TPs, the carboxy but not the amino hairpin is formed (green diamond). Experimental ψ values mapped on to NuG2b is shown for comparison (color scale as in Fig. 1).
The helix is at least partially formed across all 27 TPs, but the degree of β strand formation is heterogeneous. The β4 strand in 14 TPs is docked against the N-terminal hairpin, but the C-terminal hairpin is absent (Fig. S5). Five TPs largely agree with the experimental data in that both hairpins are formed, although the degree of hairpin-hairpin contact often is lower in the TP than indicated by the ψ values. Another five TPs only contain a formed N-terminal hairpin. The remaining three TPs only have the C-terminal hairpin formed.
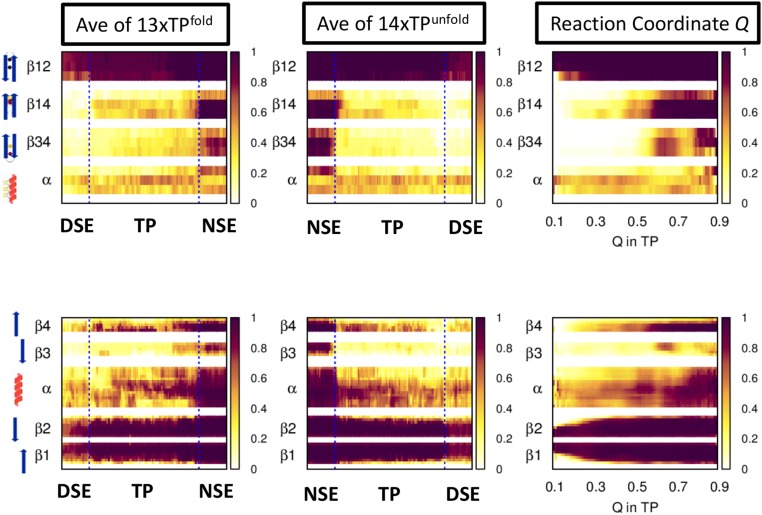
A mean folding TP is generated by averaging the 13 folding TPs (as defined in ref. 21) after normalizing the reaction coordinate of each TP to begin and finish at 0 and 1, respectively (Fig. S6). The N-terminal hairpin is already folded in the DSE before any progression along the mean TP. Interestingly, β4 docks to the N-terminal hairpin in a nonnative, antiparallel orientation near the beginning of the TP, but adopts the native parallel orientation by the end of the TP, suggesting that this change in topology is a critical folding event. β3 does not fold until the end of the TP, if at all. The helix is formed at approximately the level indicated by the ψ values. The major difference between the mean TP and the experimental data are the formation of the C-terminal hairpin only after the TP in the simulations. A PFold-style analysis was conducted using all 27 TPs to identify a 328 member TSEMD having 0.4 < PFold < 0.6 (Fig. S7 and SI Materials and Methods). The average structural content in the TSEMD is consistent with the analysis of the mean TPs.
Fig. S6.
Structure formation along the mean transition path of the MD simulations. Illustration on the left edge denotes the level of contacts for the biHis sites (Upper) and the secondary structure of the four strands and helix (Lower).
Fig. S7.
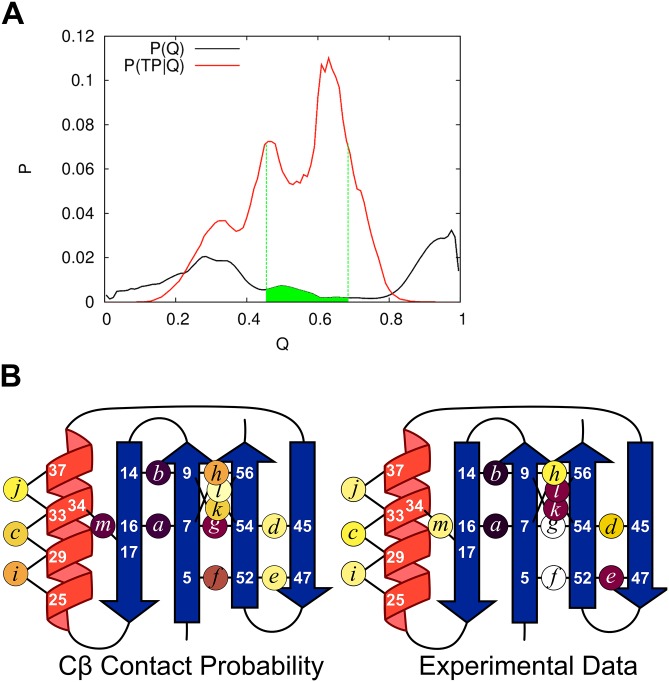
Quasi-PFold analysis of the MD trajectories on NuG2b. (A) Selection of the TSEMD begins by calculating P(TP|Q), i.e., the probability of having Q native contacts across the 27 TPs. Candidate TSE structures are selected according to P(TP| 0.45 < Q < 0.68, green). For each such candidate structure, the number of structures is identified from all other structures in the trajectory that have Cα-RMSD < 2 Å but are not in any TP. If at least 10 such structures can be found, PFold is calculating as the fraction of the 10+ structures that folds to the native basin within 1 μs. The TSE is composed of all structures having 0.4 < PFold < 0.6. (B) Cβ contact probability of the TSEMD obtained from Quasi-PFold analysis using the same color scale as Fig. 1. The ensemble displays the N-terminal hairpin as folded with a contacting β4 in its native parallel orientation, and the helix is found to be partially formed. Overall, despite the challenges in reproducing full experimental data even with today’s state-of-the-art all-atom molecular dynamics simulations (partially due to the deficiencies in modern force fields), 19% of the TSEMD structures feature all four strands arranged in a native-like conformation, consistent with the four strands being present in 5 of 27 transition paths.
SI Materials and Methods
Proteins.
The sequences for the pseudo WT of Protein G (Protein Data Bank ID code 3GB1) (66) and of NuG2b (Protein Data Bank ID code of NuG2 is 1MI0) (67) are MEYKLILNGKTLKGETTTEAVDAATAEKVFKQYANDNGVDGEWTYDDATKTFTVTE and MDTYKLVIVLNGTTFTYTTEAVDAATAEKVFKQYANDAGVDGEWTYDAATKTFTVTE, respectively.
Data Analysis.
The kinetic data are analyzed using the chevron analysis of the denaturant dependence of folding rate constants where ΔGeq, ΔGf, and ΔGu are linearly dependent on denaturant concentration
| [S1a] |
| [S1b] |
| [S1c] |
where R is the universal gas constant, and T is the absolute temperature. The dependence on denaturant concentration, i.e., the m values, report on the degree of surface area burial during the folding process. Equilibrium values of m can be calculated from the kinetic measurements according to ΔΔGeq = ΔΔGf − ΔΔGu and mo = mu + mf. To minimize extrapolation errors, ΔΔGf and ΔΔGu are evaluated in the linear regions of the folding and unfolding arms of the chevron, typically 1.5–2 and 5–8 M GdmCl, respectively. ψ- alues are determined from a simultaneous fit to the vanishing and high Me2+ chevrons, with ψ0 included as one of the fitting parameters and using nonlinear least-squares algorithms implemented in the Origin software package (OriginLab).
ψ Analysis.
ψ analysis uses engineered biHis sites to probe the fraction of native metal ion binding energy realized in the TSE. The kinetic response as a function of metal ion concentration quantifies the degree to which the biHis site is present in the TSE (see refs. 18 and 45 for detailed treatment). In a manner analogous to the ϕ analysis performed using point mutations, the kinetic response due to metal induced binding can be obtained from the denaturant dependence of folding rates (chevron analysis) in the limits of zero and high metal ion concentrations or by measuring the metal ion dependence of the folding and unfolding rates for strongly folding (0.3–1.9 M GdmCl) and unfolding conditions (5–5.5M GdmCl), respectively (Leffler analysis). To obtain ψ0, the data are fit using the equation relating the changes in activation energy and stability
| [S2] |
When side chain substitution or metal binding only affects the unfolding rate ku and not the free energy of the TSE relative to the unfolded state, the sites probed by the biHis inserts are absent in the TSE, and the corresponding ϕ or ψ vanishes. Conversely, when the perturbation only affects the folding rate, kf, the structure probed is likely to be native-like in the TSE, and the associated ϕ or ψ value is unity. When both the folding and unfolding arms shift, the ϕ or ψ value is a fractional quantity whose origin can be challenging to discern in both methods. Fractional ϕ may arise either because of partial structure formation in the TSE or of the presence of multiple, distinct TSE structures. A fractional ψ value indicates that the biHis site is either native-like in a subfraction of the TSE, or has nonnative binding affinity in the entire TSE (e.g., a distorted site with less favorable binding geometry or a flexible site that must be restricted before ion binding), or some combination thereof. In the limit of homogenous TSEs with nonnative binding affinities, ΔΔGeq and ΔΔGf become
| [S3a] |
| [S3b] |
where KDSE, KN, and KTSE are the cation binding disassociation constants of the denatured state ensemble, native state, and TSE, respectively.
PFold Analysis of DESRES MD Trajectories.
A PFold-style analysis was conducted using all 27 TPs to identify the TSE (Fig. S7). First, the members of the TP were ranked according to P(TP|Q), the probability of having Q native contacts. The top 32% or 83,105 members were selected. For each structure X in this set of structures, a family of structures similar to X was created by selecting structures that were within 2 Å (Cα-RMSD) from the rest of the trajectories excluding all TP regions. For families with at least 10 members, the PFold for the family’s parent structure X was defined as the fraction of the 10+ structures that folded to the native state within 1 μs. The TSE was taken as the composite of structures for which 0.4 < PFold < 0.6.
Discussion
Our experimental data indicate that the TSEs of three homologous α/β proteins, Proteins L & G and NuG2b, adopt a similar four-stranded structure (Fig. 2). These findings contrast with the long held view that this family possesses small, polarized TSEs whose structure is strongly sequence dependent (1–16). Despite the conserved topology, sequence does exert notable effects. The TSE of Protein G contains an N-terminal hairpin with nonnative features. Protein L similarly contains a nonnative turn in its TSE, albeit at the C terminus (17). According to the ψ values and TerItFix folding simulations, these features are due to alternative turn geometries in the TSE with a two-amino-acid register shift. The nonnative properties are not present in the TSE of NuG2b for both experiments and the TerItFix simulations, consistent with the design goal of Nauli et al. of a less frustrated N-terminal hairpin with a single preferred geometry (15). The helix is present in the NuG2b’s TSE but not in Protein G or Protein L.
Nonnative interactions provide a partial explanation for the differences in the TSE and folding rate between the three proteins. The helical amino acid sequence of Protein G and NuG2b are nearly identical with the same low average helical propensity (5.4–5.5%) (33). Given this similarity, and the presence of the helix and the two native-like β turns only in NuG2b’s TSE, we suggest that two native-like hairpins are required to create a hydrophobic surface suitable for docking the helix. Without the two native-like turns in the TSE of the naturally occurring proteins, the helix remains unfolded in their TSE and the kinetic barrier is higher.
The TSEs of Protein G and NuG2b both contain a tertiary contact between one of the outer strands (β2) and a central residue in the segment that becomes helical in the native state (this aspect was not investigated for Protein L). Hence, the folding of both Protein G and NuG2b converges to a late TSE with a native-like topology.
Overall, we believe that the folding behavior of the homologs and other proteins can be explained by a common mechanism, the principle of sequential stabilization (34, 35). Here, pieces of H-bonded structure, or foldons, template onto existing H-bonded structure and often bury a commensurate amount of hydrophobic surface. This templating occurs both on the route up to the TSE (20) and on the descent down (34, 35). The incremental buildup of secondary and tertiary structure mostly produces native- or unfolded-like regions, as suggested by the frequent observation of ψ = 0 or 1 and the cooperative pattern of hydrogen exchange (HX) protection factors within secondary structures (36–39). Folding steps can involve both local and nonlocal contacts and H-bonds even during the early stages of folding. This view differs from models that either favor the folding of one class over the other, such as secondary structure formation followed by hydrophobic collapse or vice versa, or ones that stress long-range side-chain contacts before secondary structure formation.
ψ and ϕ Analyses in the Homologs and Other Proteins.
The differences between our study and previous studies arise in part because of our use of ψ analysis as opposed to ϕ analysis. The primary variance between the two methods is that ψ analysis directly probes residue-residue contacts between two known partners, whereas ϕ analysis uses energetic perturbations to infer structure. This inference can be challenging because the perturbations introduced by mutations may be the consequence of multiple factors, including changes in side-chain interactions and backbone dihedral propensities. In addition, ϕ values can underreport the structural content of the TSE if the TSE relaxes energetically (40) or involves nonnative features (41–44).
Another situation where ϕ analysis can underreport structure occurs when a residue’s side chain is buried in the native state but not in the TSE due to a portion of the protein being unfolded. This situation applies to residues on the hydrophobic face of the four β strands in Proteins G & L as the helix is absent in their TSEs. As a result, a substitution on a strand can yield a smaller energy signature in the TSE than in the native state. Consequently, small ϕ values are observed even for residues participating in the sheet, leading to erroneous inferences about the degree of sheet structure in the TSE of these two proteins. This issue, along with relaxation of the TSE, applies to β sheet sites in other proteins including ubiquitin, e.g., where a value of ϕL67A = 0 is found for a position that is structured in the TSE according to ψ analysis (19).
We believe these and other factors lead to many ϕ values for structured regions in the TSE being in the range of 0.2–0.5, rendering them difficult to interpret. In fact, ϕ analysis has been found to underreport the structure and topology of the TSE in all cases where both ϕ and ψ analyses have been performed, namely for acyl phosphatase (45, 46), ubiquitin (19, 31), the B domain of Protein A (28), Protein L (17), Protein G, and NuG2b (see figure 6 in ref. 17). We suspect underreporting also occurs with other proteins, particularly those characterized as having a polarized TSE, such as cold shock protein (47) or src SH3 (48). Overall, the ambiguities in the interpretation of low to moderate ϕ values probably has led to an unrealistically diverse range of folding models and mechanisms, as well as to an overestimation of the magnitude of sequence effects, as demonstrated here for the Proteins G & L homologs.
The consistent theme of extensive TSE structure implied by the ψ values provides additional support for its use in identifying folding principles. The TSEs of the six globular proteins studied using ψ analysis share a common and high degree of native topology, RCOTSE ∼ 0.7∙RCON. This finding rationalizes the well-known correlation between kf and RCO (49). In contrast, the TSE deduced from ϕ analysis often barely defines a protein’s fold and the ensuing RCO levels of the TSE are variable for different proteins.
Furthermore, whereas a 1:1 relationship between H-bond content and surface burial is found in the TSEs of a variety of proteins (50, 51), the H-bond content of the ϕ-determined TSE for the Proteins G & L homologs is inadequate to match the ∼80% surface burial (mf/m0) in the TSE. A recent transfer study by Record and coworkers (52) supports our conclusion based on ψ analysis that the TSEs of many proteins have a substantial level of H-bonded structure.
The binding of increasing concentrations of ions in ψ analysis produces a continuous increase in the stability of TSE structures that contain the biHis site. Hence, stability is perturbed in an isosteric and isochemical manner. The resulting series of data can be justifiably combined, and the ψ0 value can be extracted, devoid of any perturbation due to ion binding. This ability to extrapolate to zero ion concentration addresses a potential misconception that metal binding induces structure in the TSE and, therefore, biases the outcome.
The implementation of ψ analysis using biHis sites does have some issues, however. The biHis sites are limited to surface positions. Furthermore, the introduction of the two histidines can be destabilizing (<ΔΔGbiHis > Protein G, NuG2b = −1.3 ± 0.8 kcal/mol), just as any substitution may be when implementing ϕ analysis (particularly as large values of ΔΔG often are viewed as necessary for accuracy) (53).
Fractional ψ values raise the same issues of interpretation as fractional ϕ values, including the possibility that they arise from either TS heterogeneity or partial structure formation (19). Nevertheless (and significantly), the conclusion that the ψ-determined TSE has near-native topology emerges even when only the sites with near-unity ψ values are considered.
As NuG2 was designed to shift the TSE from the C- to the N-terminal hairpin by resolving the nonnative behavior (15), those results warrant some discussion. The ϕ values were determined in the background of a variant already having a destabilizing hairpin mutation, D46A, i.e., the analysis focused on the NuG2D46A variant rather than NuG2 itself. The D46A mutation destabilizes the C-terminal hairpin by removing a side-chain to backbone H-bond between D46 and A48 and a possible H-bond between D46 and T49 (ΔΔGD46A = −1.5 kcal/mol). In the D46A background, the T49A substitution has a reduced kinetic effect that can explain the decrease in ϕT49A from 1.1 in Protein G to 0.3 in NuG2D46A, rather than the actual absence of the hairpin in the TSE of WT NuG2. In fact, ϕD46A = 0.6 for NuG2 (using values in table 2 in ref. 15). Hence, we believe that the prior data are consistent with both hairpins being present in NuG2’s TSE.
Pathway Diversity.
The mechanism of sequential stabilization produces few low energy routes, particularly for proteins with nested or asymmetric folds. Multiple pathways are possible (54) for symmetric proteins, although energetic heterogeneity due to sequence differences can reduce the degree of pathway diversity (55). Hence, even for symmetric folds, a given sequence may have a major route, but the entire family may traverse different routes due to sequence variation.
This multipath scenario may be occurring with the Proteins L & G homologs, where alternative routes may be traversed up to the TSE. Either hairpin can form before the other, with the relative flux being influenced by the hairpins’ relative stabilities. Potentially, one hairpin might form along with the adjoining strand before the formation of the other hairpin (e.g., β2 + β1 + β4 ˗ β2 + β1 + β4 + β3). Both types of pathways appear in the TerItFix and all-atom simulations, although generally the coarse-grained simulations describe the hairpin formation as arising independently, whereas the all-atom simulations typically follow the three-strand motif pathway. The helix of NuG2b may fold before the folding of both hairpins, as all three elements can be found in the experimental TSE. However, we suspect that this possibility does not occur because the helical sequence is nearly identical to Protein G’s and the helix forms after the four strands in Proteins G & L.
In two classes of pseudo-1D proteins, coiled coils (56, 57) and repeat proteins (58–60), local energetic differences alter the location of the TS nucleus and reduce the extent of pathway degeneracy. The TSEs of IgG-like domains exhibit some structural diversity but share a common nucleus that can shift along the strands (2) or be localized to a subset thereof for one homolog having parallel unfolding pathways (61). The variable pattern of ϕ values for engrailed homeodomains (62) and spectrin domain families (2) has been interpreted as a change in folding mechanism. Our ψ studies find that the TSE of Protein A, a small three-helix bundle, converges to an ensemble involving all three helices and with the terminal helices forming contacts that define the overall fold (28). As mentioned above, the general RCOTSE ∼ 0.7∙RCON trend suggests that other three helix bundles have similar TS topologies.
In addition to changes in the TSE, the protein sequence can influence the energy landscape of homologs by altering the energetics of intermediates (2). A partially misfolded intermediate accumulates in the folding of Im7, but not its homolog, Im9 (63, 64). HX studies indicate that the intermediates are different for meso- and thermophilic versions of Rnase H (65). Hence, pathway diversity is not limited to symmetric folds.
Conclusion
The folding behavior of the Proteins L & G and NuG2b has been widely viewed as the major example of sequence variation influencing TS structure. However, our application of ψ analysis reveals that the homologs fold through a similar and nonpolarized TSE having near-native topology. The variability in the TSE mostly relates to helix formation and likely arises from nonnative turn propensities for the naturally occurring proteins. This study and prior studies emphasize that even for small proteins such as these α/β proteins, as well as for the three helix bundle Protein A (28), considerable challenges remain in correctly characterizing and predicting TSEs. Furthermore, integrated approaches, such as the present combination of ψ analysis with TertItFix and all-atom simulations, often are necessary for accurately describing the folding process.
Materials and Methods
Sample Preparation.
BiHis sites were inserted into the WT plasmid using the Quikchange protocol and prepared according to ref. 17.
Folding Kinetics.
Kinetic data were collected at 10–20 μM protein concentration in 50 mM Hepes and 100 mM NaCl, pH 7.5, at 20 °C using a BioLogic SFM400/40000 stopped-flow apparatuses connected to a PTI A101 arc lamp.
Further descriptions of the methods are listed in SI Materials and Methods.
Supplementary Material
Acknowledgments
We thank S. Piana-Agostinetti, B. Kuhlman, J. Weber, and members of our group for helpful discussions. We also thank C. Antoniou and I. Gagnon for assisting in preparing protein samples. Trajectories of NuG2b were kindly provided by DE Shaw Research. This work was supported by National Institutes of Health Grant GM055694 and National Science Foundation Grant CHE-1363012. W.Y. was supported in part by National Creative Research Initiatives (Center for Proteome Biophysics) of National Research Foundation, Korea (Grant 2011-0000041).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1503613112/-/DCSupplemental.
References
- 1.Nickson AA, Clarke J. What lessons can be learned from studying the folding of homologous proteins? Methods. 2010;52(1):38–50. doi: 10.1016/j.ymeth.2010.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Nickson AA, Wensley BG, Clarke J. Take home lessons from studies of related proteins. Curr Opin Struct Biol. 2013;23(1):66–74. doi: 10.1016/j.sbi.2012.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Clementi C, García AE, Onuchic JN. Interplay among tertiary contacts, secondary structure formation and side-chain packing in the protein folding mechanism: All-atom representation study of protein L. J Mol Biol. 2003;326(3):933–954. doi: 10.1016/s0022-2836(02)01379-7. [DOI] [PubMed] [Google Scholar]
- 4.Karanicolas J, Brooks CL., 3rd The origins of asymmetry in the folding transition states of protein L and protein G. Protein Sci. 2002;11(10):2351–2361. doi: 10.1110/ps.0205402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Brown S, Head-Gordon T. Intermediates and the folding of proteins L and G. Protein Sci. 2004;13(4):958–970. doi: 10.1110/ps.03316004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yang Q, Sze SH. Predicting protein folding pathways at the mesoscopic level based on native interactions between secondary structure elements. BMC Bioinformatics. 2008;9:320. doi: 10.1186/1471-2105-9-320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zhao L, Wang J, Dou X, Cao Z. Studying the unfolding process of protein G and protein L under physical property space. BMC Bioinformatics. 2009;10(Suppl 1):S44. doi: 10.1186/1471-2105-10-S1-S44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ejtehadi MR, Avall SP, Plotkin SS. Three-body interactions improve the prediction of rate and mechanism in protein folding models. Proc Natl Acad Sci USA. 2004;101(42):15088–15093. doi: 10.1073/pnas.0403486101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Koga N, Takada S. Roles of native topology and chain-length scaling in protein folding: A simulation study with a Go-like model. J Mol Biol. 2001;313(1):171–180. doi: 10.1006/jmbi.2001.5037. [DOI] [PubMed] [Google Scholar]
- 10.Scalley ML, et al. Kinetics of folding of the IgG binding domain of peptostreptococcal protein L. Biochemistry. 1997;36(11):3373–3382. doi: 10.1021/bi9625758. [DOI] [PubMed] [Google Scholar]
- 11.Gu H, Kim D, Baker D. Contrasting roles for symmetrically disposed beta-turns in the folding of a small protein. J Mol Biol. 1997;274(4):588–596. doi: 10.1006/jmbi.1997.1374. [DOI] [PubMed] [Google Scholar]
- 12.Kim DE, Yi Q, Gladwin ST, Goldberg JM, Baker D. The single helix in protein L is largely disrupted at the rate-limiting step in folding. J Mol Biol. 1998;284(3):807–815. doi: 10.1006/jmbi.1998.2200. [DOI] [PubMed] [Google Scholar]
- 13.Kim DE, Fisher C, Baker D. A breakdown of symmetry in the folding transition state of protein L. J Mol Biol. 2000;298(5):971–984. doi: 10.1006/jmbi.2000.3701. [DOI] [PubMed] [Google Scholar]
- 14.McCallister EL, Alm E, Baker D. Critical role of beta-hairpin formation in protein G folding. Nat Struct Biol. 2000;7(8):669–673. doi: 10.1038/77971. [DOI] [PubMed] [Google Scholar]
- 15.Nauli S, Kuhlman B, Baker D. Computer-based redesign of a protein folding pathway. Nat Struct Biol. 2001;8(7):602–605. doi: 10.1038/89638. [DOI] [PubMed] [Google Scholar]
- 16.Kuhlman B, O’Neill JW, Kim DE, Zhang KY, Baker D. Accurate computer-based design of a new backbone conformation in the second turn of protein L. J Mol Biol. 2002;315(3):471–477. doi: 10.1006/jmbi.2001.5229. [DOI] [PubMed] [Google Scholar]
- 17.Yoo TY, et al. The folding transition state of protein L is extensive with nonnative interactions (and not small and polarized) J Mol Biol. 2012;420(3):220–234. doi: 10.1016/j.jmb.2012.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sosnick TR, Krantz BA, Dothager RS, Baxa M. Characterizing the protein folding transition state using psi analysis. Chem Rev. 2006;106(5):1862–1876. doi: 10.1021/cr040431q. [DOI] [PubMed] [Google Scholar]
- 19.Sosnick TR, Dothager RS, Krantz BA. Differences in the folding transition state of ubiquitin indicated by phi and psi analyses. Proc Natl Acad Sci USA. 2004;101(50):17377–17382. doi: 10.1073/pnas.0407683101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Krantz BA, Dothager RS, Sosnick TR. Discerning the structure and energy of multiple transition states in protein folding using psi-analysis. J Mol Biol. 2004;337(2):463–475. doi: 10.1016/j.jmb.2004.01.018. [DOI] [PubMed] [Google Scholar]
- 21.Lindorff-Larsen K, Piana S, Dror RO, Shaw DE. How fast-folding proteins fold. Science. 2011;334(6055):517–520. doi: 10.1126/science.1208351. [DOI] [PubMed] [Google Scholar]
- 22.Zhang Y, Skolnick J. TM-align: A protein structure alignment algorithm based on the TM-score. Nucleic Acids Res. 2005;33(7):2302–2309. doi: 10.1093/nar/gki524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.DeBartolo J, et al. Mimicking the folding pathway to improve homology-free protein structure prediction. Proc Natl Acad Sci USA. 2009;106(10):3734–3739. doi: 10.1073/pnas.0811363106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Colubri A, et al. Minimalist representations and the importance of nearest neighbor effects in protein folding simulations. J Mol Biol. 2006;363(4):835–857. doi: 10.1016/j.jmb.2006.08.035. [DOI] [PubMed] [Google Scholar]
- 25.Adhikari AN, Freed KF, Sosnick TR. Simplified protein models: Predicting folding pathways and structure using amino acid sequences. Phys Rev Lett. 2013;111(2):028103. doi: 10.1103/PhysRevLett.111.028103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Adhikari AN, Freed KF, Sosnick TR. De novo prediction of protein folding pathways and structure using the principle of sequential stabilization. Proc Natl Acad Sci USA. 2012;109(43):17442–17447. doi: 10.1073/pnas.1209000109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Krantz BA, Dothager RS, Sosnick TR. Erratum to Discerning the structure and energy of multiple transition states in protein folding using psi-analysis. J Mol Biol. 2004;347(5):1103. doi: 10.1016/j.jmb.2004.01.018. [DOI] [PubMed] [Google Scholar]
- 28.Baxa MC, Freed KF, Sosnick TR. Quantifying the structural requirements of the folding transition state of protein A and other systems. J Mol Biol. 2008;381(5):1362–1381. doi: 10.1016/j.jmb.2008.06.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Adhikari AN, et al. Modeling large regions in proteins: Applications to loops, termini, and folding. Protein Sci. 2012;21(1):107–121. doi: 10.1002/pro.767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sosnick TR, Barrick D. The folding of single domain proteins—Have we reached a consensus? Curr Opin Struct Biol. 2011;21(1):12–24. doi: 10.1016/j.sbi.2010.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Baxa MC, Freed KF, Sosnick TR. Psi-constrained simulations of protein folding transition states: Implications for calculating. J Mol Biol. 2009;386(4):920–928. doi: 10.1016/j.jmb.2009.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Skinner JJ, et al. Benchmarking all-atom simulations using hydrogen exchange. Proc Natl Acad Sci USA. 2014;111(45):15975–15980. doi: 10.1073/pnas.1404213111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lacroix E, Viguera AR, Serrano L. Elucidating the folding problem of alpha-helices: Local motifs, long-range electrostatics, ionic-strength dependence and prediction of NMR parameters. J Mol Biol. 1998;284(1):173–191. doi: 10.1006/jmbi.1998.2145. [DOI] [PubMed] [Google Scholar]
- 34.Maity H, Maity M, Krishna MM, Mayne L, Englander SW. Protein folding: The stepwise assembly of foldon units. Proc Natl Acad Sci USA. 2005;102(13):4741–4746. doi: 10.1073/pnas.0501043102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Englander SW, Mayne L. The nature of protein folding pathways. Proc Natl Acad Sci USA. 2014;111(45):15873–15880. doi: 10.1073/pnas.1411798111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bai Y, Sosnick TR, Mayne L, Englander SW. Protein folding intermediates: native-state hydrogen exchange. Science. 1995;269(5221):192–197. doi: 10.1126/science.7618079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Chamberlain AK, Handel TM, Marqusee S. Detection of rare partially folded molecules in equilibrium with the native conformation of RNaseH. Nat Struct Biol. 1996;3(9):782–787. doi: 10.1038/nsb0996-782. [DOI] [PubMed] [Google Scholar]
- 38.Feng H, Vu ND, Bai Y. Detection and structure determination of an equilibrium unfolding intermediate of Rd-apocytochrome b562: Native fold with non-native hydrophobic interactions. J Mol Biol. 2004;343(5):1477–1485. doi: 10.1016/j.jmb.2004.08.099. [DOI] [PubMed] [Google Scholar]
- 39.Zheng Z, Sosnick TR. Protein vivisection reveals elusive intermediates in folding. J Mol Biol. 2010;397(3):777–788. doi: 10.1016/j.jmb.2010.01.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Bulaj G, Goldenberg DP. Phi-values for BPTI folding intermediates and implications for transition state analysis. Nat Struct Biol. 2001;8(4):326–330. doi: 10.1038/86200. [DOI] [PubMed] [Google Scholar]
- 41.Neudecker P, et al. Identification of a collapsed intermediate with non-native long-range interactions on the folding pathway of a pair of Fyn SH3 domain mutants by NMR relaxation dispersion spectroscopy. J Mol Biol. 2006;363(5):958–976. doi: 10.1016/j.jmb.2006.08.047. [DOI] [PubMed] [Google Scholar]
- 42.Feng H, Vu ND, Zhou Z, Bai Y. Structural examination of phi-value analysis in protein folding. Biochemistry. 2004;43(45):14325–14331. doi: 10.1021/bi048126m. [DOI] [PubMed] [Google Scholar]
- 43.Zarrine-Afsar A, Dahesh S, Davidson AR. A residue in helical conformation in the native state adopts a β-strand conformation in the folding transition state despite its high and canonical Φ-value. Proteins. 2012;80(5):1343–1349. doi: 10.1002/prot.24030. [DOI] [PubMed] [Google Scholar]
- 44.Di Nardo AA, et al. Dramatic acceleration of protein folding by stabilization of a nonnative backbone conformation. Proc Natl Acad Sci USA. 2004;101(21):7954–7959. doi: 10.1073/pnas.0400550101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Pandit AD, Jha A, Freed KF, Sosnick TR. Small proteins fold through transition states with native-like topologies. J Mol Biol. 2006;361(4):755–770. doi: 10.1016/j.jmb.2006.06.041. [DOI] [PubMed] [Google Scholar]
- 46.Taddei N, et al. Stabilisation of alpha-helices by site-directed mutagenesis reveals the importance of secondary structure in the transition state for acylphosphatase folding. J Mol Biol. 2000;300(3):633–647. doi: 10.1006/jmbi.2000.3870. [DOI] [PubMed] [Google Scholar]
- 47.Garcia-Mira MM, Boehringer D, Schmid FX. The folding transition state of the cold shock protein is strongly polarized. J Mol Biol. 2004;339(3):555–569. doi: 10.1016/j.jmb.2004.04.011. [DOI] [PubMed] [Google Scholar]
- 48.Grantcharova VP, Riddle DS, Santiago JV, Baker D. Important role of hydrogen bonds in the structurally polarized transition state for folding of the src SH3 domain. Nat Struct Biol. 1998;5(8):714–720. doi: 10.1038/1412. [DOI] [PubMed] [Google Scholar]
- 49.Plaxco KW, Simons KT, Baker D. Contact order, transition state placement and the refolding rates of single domain proteins. J Mol Biol. 1998;277(4):985–994. doi: 10.1006/jmbi.1998.1645. [DOI] [PubMed] [Google Scholar]
- 50.Krantz BA, et al. Understanding protein hydrogen bond formation with kinetic H/D amide isotope effects. Nat Struct Biol. 2002;9(6):458–463. doi: 10.1038/nsb794. [DOI] [PubMed] [Google Scholar]
- 51.Krantz BA, Moran LB, Kentsis A, Sosnick TR. D/H amide kinetic isotope effects reveal when hydrogen bonds form during protein folding. Nat Struct Biol. 2000;7(1):62–71. doi: 10.1038/71265. [DOI] [PubMed] [Google Scholar]
- 52.Guinn EJ, Kontur WS, Tsodikov OV, Shkel I, Record MT., Jr Probing the protein-folding mechanism using denaturant and temperature effects on rate constants. Proc Natl Acad Sci USA. 2013;110(42):16784–16789. doi: 10.1073/pnas.1311948110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Sánchez IE, Kiefhaber T. Origin of unusual phi-values in protein folding: Evidence against specific nucleation sites. J Mol Biol. 2003;334(5):1077–1085. doi: 10.1016/j.jmb.2003.10.016. [DOI] [PubMed] [Google Scholar]
- 54.Klimov DK, Thirumalai D. Symmetric connectivity of secondary structure elements enhances the diversity of folding pathways. J Mol Biol. 2005;353(5):1171–1186. doi: 10.1016/j.jmb.2005.09.029. [DOI] [PubMed] [Google Scholar]
- 55.Cho SS, Levy Y, Wolynes PG. Quantitative criteria for native energetic heterogeneity influences in the prediction of protein folding kinetics. Proc Natl Acad Sci USA. 2009;106(2):434–439. doi: 10.1073/pnas.0810218105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Moran LB, Schneider JP, Kentsis A, Reddy GA, Sosnick TR. Transition state heterogeneity in GCN4 coiled coil folding studied by using multisite mutations and crosslinking. Proc Natl Acad Sci USA. 1999;96(19):10699–10704. doi: 10.1073/pnas.96.19.10699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Krantz BA, Sosnick TR. Engineered metal binding sites map the heterogeneous folding landscape of a coiled coil. Nat Struct Biol. 2001;8(12):1042–1047. doi: 10.1038/nsb723. [DOI] [PubMed] [Google Scholar]
- 58.Tripp KW, Barrick D. Rerouting the folding pathway of the Notch ankyrin domain by reshaping the energy landscape. J Am Chem Soc. 2008;130(17):5681–5688. doi: 10.1021/ja0763201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Aksel T, Barrick D. Direct observation of parallel folding pathways revealed using a symmetric repeat protein system. Biophys J. 2014;107(1):220–232. doi: 10.1016/j.bpj.2014.04.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Werbeck ND, Rowling PJ, Chellamuthu VR, Itzhaki LS. Shifting transition states in the unfolding of a large ankyrin repeat protein. Proc Natl Acad Sci USA. 2008;105(29):9982–9987. doi: 10.1073/pnas.0705300105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Wright CF, Lindorff-Larsen K, Randles LG, Clarke J. Parallel protein-unfolding pathways revealed and mapped. Nat Struct Biol. 2003;10(8):658–662. doi: 10.1038/nsb947. [DOI] [PubMed] [Google Scholar]
- 62.Banachewicz W, Religa TL, Schaeffer RD, Daggett V, Fersht AR. Malleability of folding intermediates in the homeodomain superfamily. Proc Natl Acad Sci USA. 2011;108(14):5596–5601. doi: 10.1073/pnas.1101752108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Ferguson N, Capaldi AP, James R, Kleanthous C, Radford SE. Rapid folding with and without populated intermediates in the homologous four-helix proteins Im7 and Im9. J Mol Biol. 1999;286(5):1597–1608. doi: 10.1006/jmbi.1998.2548. [DOI] [PubMed] [Google Scholar]
- 64.Capaldi AP, Kleanthous C, Radford SE. Im7 folding mechanism: Misfolding on a path to the native state. Nat Struct Biol. 2002;9(3):209–216. doi: 10.1038/nsb757. [DOI] [PubMed] [Google Scholar]
- 65.Hollien J, Marqusee S. Structural distribution of stability in a thermophilic enzyme. Proc Natl Acad Sci USA. 1999;96(24):13674–13678. doi: 10.1073/pnas.96.24.13674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Kuszewski J, Gronenborn AM, Clore GM. Improving the packing and accuracy of NMR structures with a pseudopotential for the radius of gyration. J Am Chem Soc. 1999;121(10):2337–2338. [Google Scholar]
- 67.Nauli S, et al. Crystal structures and increased stabilization of the protein G variants with switched folding pathways NuG1 and NuG2. Protein Sci. 2002;11(12):2924–2931. doi: 10.1110/ps.0216902. [DOI] [PMC free article] [PubMed] [Google Scholar]