Theta–gamma coordination between anterior cingulate and prefrontal cortex indexes correct attention shifts

Significance

During flexible goal-directed behavior, our frontal cortex coordinates goal-relevant information from widely distributed neuronal systems to prioritize the relevant over irrelevant information. This coordination may be realized by entraining multiple distributed systems with slow activity oscillation to phase-align their local fast oscillatory activity. We analyzed this spatially distributed oscillatory coupling in macaques during actual attentional stimulus selection. We identified that successful—but not failed—selection of relevant information followed the coupling of slow and fast frequencies at narrow oscillation phases, with interareal anatomical specificity, and based on a reset mechanism for the slow oscillation. These findings suggest a specific functional and mechanistic solution to the fundamental coordination problem in primate brains.

Abstract

Anterior cingulate and lateral prefrontal cortex (ACC/PFC) are believed to coordinate activity to flexibly prioritize the processing of goal-relevant over irrelevant information. This between-area coordination may be realized by common low-frequency excitability changes synchronizing segregated high-frequency activations. We tested this coordination hypothesis by recording in macaque ACC/PFC during the covert utilization of attention cues. We found robust increases of 5–10 Hz (theta) to 35–55 Hz (gamma) phase–amplitude correlation between ACC and PFC during successful attention shifts but not before errors. Cortical sites providing theta phases (i) showed a prominent cue-induced phase reset, (ii) were more likely in ACC than PFC, and (iii) hosted neurons with burst firing events that synchronized to distant gamma activity. These findings suggest that interareal theta–gamma correlations could follow mechanistically from a cue-triggered reactivation of rule memory that synchronizes theta across ACC/PFC.

The anterior cingulate and prefrontal cortex (ACC/PFC) of primates are key structures that ensure the flexible deployment of attention during goal-directed behavior (1, 2). To achieve such flexible control, diverse streams of information need to be taken into account, which are encoded by neuronal populations in anatomically segregated subfields of the ACC/PFC (3, 4). Information about the expected values of possible attentional targets are prominently encoded in medial prefrontal cortices and ACC, whereas the rules and task goals that structure goal-directed behavior are prominently encoded in the lateral PFC (5, 6). Flexible biasing of attention thus requires the integration of information across anatomically segregated cortical circuits. One candidate means to achieve such interareal integration is by synchronizing local processes in distant brain areas to a common process. A rich set of predominantly rodent studies have documented such interareal neuronal interactions in the form of a phase–amplitude (P–A) correlations between low-frequency periodic excitability fluctuation and high-frequency gamma-band activity (7–9). It is, however, unknown whether there are reliable cross-frequency P–A interactions between those primate ACC/PFC nodes that underlie flexible attention shifts and, if so, whether P–A correlations are reliably linked to the actual successful deployment of attention (10, 11). We thus set out to test for and characterize P–A interactions during covert control processes by recording local field potential (LFP) activity in macaque ACC/PFC subfields during attentional stimulus selection.

Results

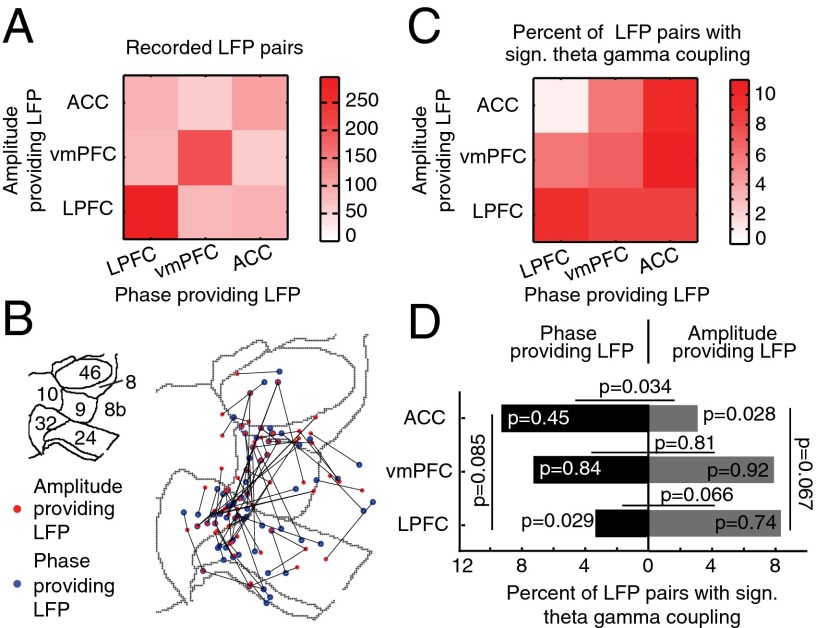
We recorded LFP activity from 1,104 between-channel pairs of electrodes (344 individual LFP channels) within different subfields in ACC/PFC of two macaques engaged in an attention task (Fig. 1A). In the following, we report results pooled across monkeys and show that individual monkey results were consistent and qualitatively similar in SI Result S1. These recordings were from a dataset that was previously analyzed with respect to neuronal firing and burst–LFP synchronization (3, 12, 13) (SI Methods). During each trial, covert spatial attention had to be shifted toward one of two peripheral stimuli in response to the color of a centrally presented cue stimulus (Fig. 1A). Covert spatial attention then had to be sustained on the target stimulus until it transiently rotated clockwise or counterclockwise. The animals obtained fluid reward when they correctly discriminated the rotation of the attended stimulus. On one-half of the trials, the distracting nontarget stimulus rotated before the target stimulus. Both monkeys successfully ignored this distractor change, indicating correct attentional deployment on the target with an average accuracy of 82.6 ± 0.7% SE and errors committed in response to the distractor rotation in 4.5 ± 0.2% SE) (SI Result S2).

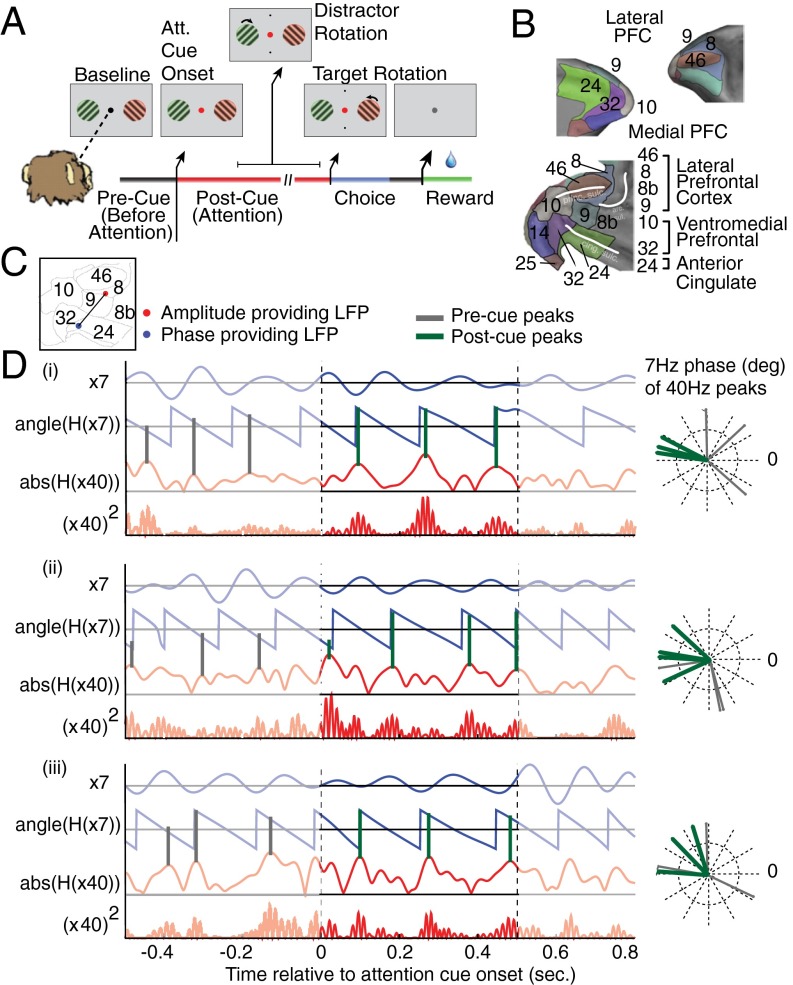
Fig. 1.

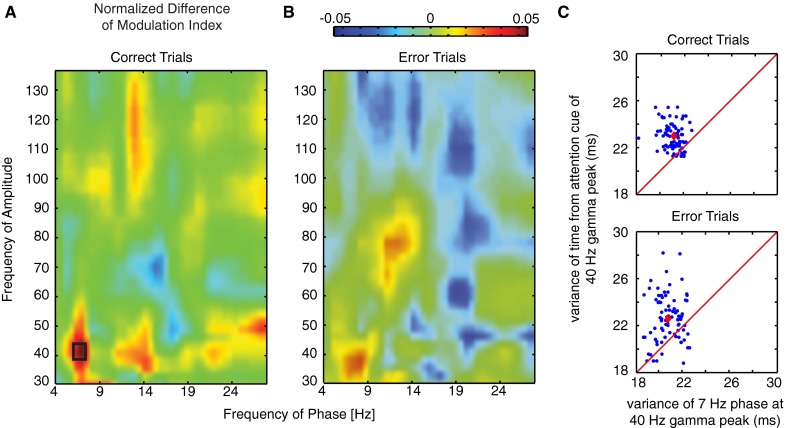
Task and illustration of example theta–gamma correlation. (A) The selective attention task required monkeys to keep fixation on a central cue throughout a trial, while presented with two peripheral grating stimuli. First, both grating stimuli changed their color simultaneously to either green or red, the location of which was random. Then, the fixation point changed its color to match the stimulus to which the monkey has to covertly shift attention. The attended stimulus rotated transiently at unpredictable times, requiring the monkey to judge a clockwise/counterclockwise rotation to receive fluid reward. Rotations of the nonattended stimulus had to be ignored (filtered). (B) Lateral and medial prefrontal cortex of macaques rendered in 3D (upper panels) and represented as 2D flat map (bottom panel) with a standard labeling of cortical fields (for details, see Fig. S1). Adapted from ref. 3. (C) Anatomical locations on the 2D flat map of an example LFP pair in which the LFP theta phase of one recording site in the ACC (blue dot) correlated with the low-gamma amplitude of a second LFP recording site in LPFC area 8 (red dot). (D) Filtered phase and amplitude traces for the example LFP–LFP pair that is shown in C for three trials (i–iii). For each trial, the bandpass-filtered low-frequency activation and its phase evolution are shown with blue lines, and the amplitude envelope and the squared gamma amplitude of the amplitude-providing LFP recording are shown in red. Gray (green) vertical lines highlight the phases at which the gamma-amplitude variations show peaks within the 500 ms before (after) attention cue onset. The polar plot on the Right shows these peak phases in the precue and postcue epoch. For this ACC–LPFC example pair, the gamma-amplitude peaks of the PFC channel correlate with similar theta phases of the ACC channel in the postcue period. For more examples, see Fig. S2.

Attention Cue Triggers Theta–Gamma P–A Correlations.

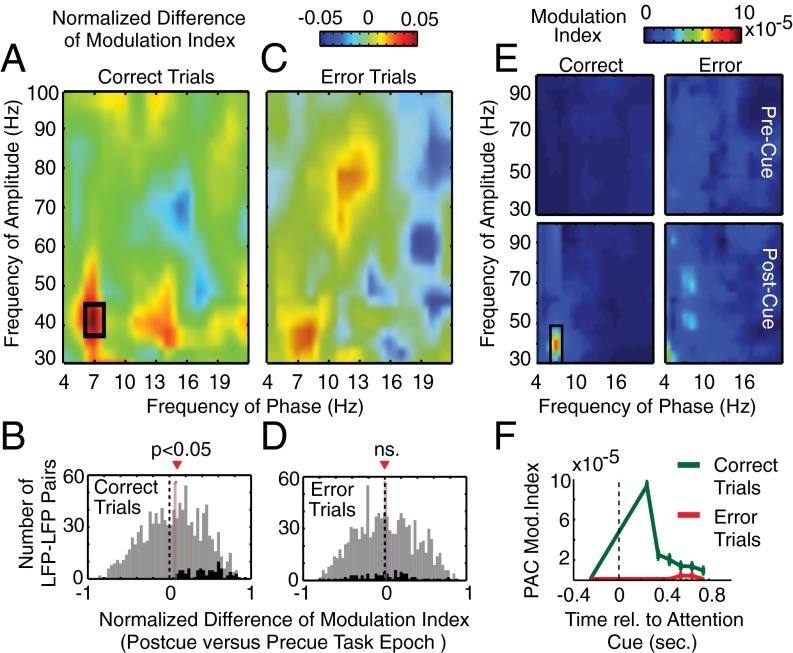
In the outlined task, attention shifts required the use of task knowledge to successfully combine color and location information to prioritize the correct stimulus. ACC/PFC subfields are core circuits supporting the flexible integration of information to shift attention (2, 3). To test whether the attention shift is accompanied by cross-frequency interactions, we selected LFP pairs recorded from different sites in ACC and PFC (Fig. 1B and Figs. S1 and S2) and quantified how high-frequency activity variations related to the phases of slow frequency activity modulation around the time of the attention cue. In multiple-example LFP pairs, we observed that the attention cue onset triggered sequences of brief bursts of gamma-band activity that synchronized to a narrow phase range of periodic 5- to 10-Hz theta-band activity recorded at distant sites (Fig. 1C and Fig. S2). To quantify whether these cross-frequency correlations were reliably linked to attention shifts, we calculated the change in Tort’s modulation index (MI) (14) in 0.5-s time windows following the attention cue vs. before the cue. Across all between-channel LFP pairs, we found a significant increase in cross-frequency correlations between the phase of a ∼7-Hz theta frequency, and the amplitude of ∼40-Hz gamma-frequency activity [Wilcoxon sign-rank test, P = 1.6*10⁻⁴, false discovery rate (FDR) corrected; Fig. 2 A and B and Fig. S3]. Across all LFP pairs, the theta–gamma P–A correlations increased on average by 61.73 ± 0.037% SE (average normalized change in MI: 0.0556 ± 0.0109 SE; Fig. 2B). For the 7- to 40-Hz theta–gamma frequency combination that showed maximal correlation, n = 85 LFP pairs (85 of 1,104; 7.7%) showed a statistically significant increase in P–A correlation following the attention cue (Monte Carlo surrogate test, at least P < 0.05; Fig. 2B). In the following, we characterize these 85 LFP pairs that showed an increased theta–gamma correlation in the postcue period that was also evident in the average across the population of LFP pairs [see SI Result S3 for a characterization of n = 46 (4.2%) LFP pairs showing significant reductions in theta–gamma correlation in the postcue epoch]. Theta–gamma correlation of these 85 LFP pairs was based on 74 of 344 (21.5%) LFP channels contributing theta phases, and 67 of 344 (19.5%) LFPs contributing gamma-amplitude variations. Overall, 122 of 344 (35.5%) unique LFPs contributed to LFP pairs with theta–gamma correlation that was significant and consistently evident in both monkeys (SI Result S1.1). Observing reliable theta–gamma correlation was not dependent on the metric used to measure P–A correlation, as we found essentially identical results when we applied the weighted phase-locking factor (15) (Fig. S4). Consistent with this finding, we observed in 73% of those LFPs that provided the theta phase for significantly P-A–correlated pairs an apparent theta-band peak in the power spectra (Figs. S5 and S6). Power modulations at theta did not, however, correlate with cue-triggered increases of theta–gamma correlations (SI Result S4).

Fig. S1.

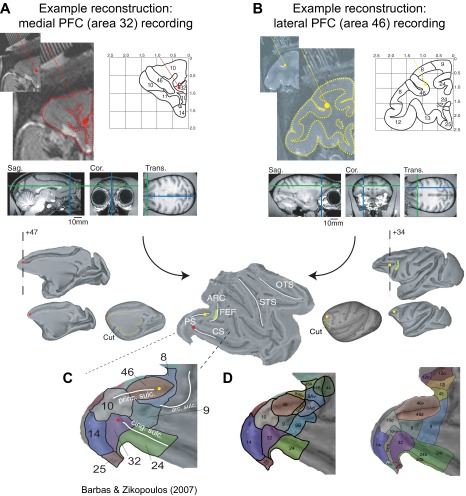
Illustration of the reconstruction of recording sites. (A and B) Reconstruction of a medial PFC (area 32; A), and a LPFC (area 46; B) recording site started from the 7-T anatomical MR, which was obtained with (iodine-based) visualization of electrode trajectories within the electrode grid placed inside the recording chamber. The outline of the cortical folding was sketched on the coronal MR slice to ease identification of areas and landmarks according to standard brain atlases, and to place the depth of the electrode tip (red dot in A and yellow dot in B) with custom MATLAB code. The electrode tip position was then placed into a standardized macaque brain available in the MR Caret software package. Caret allowed rendering the MR slice into a 3D volume and to inflate the volume before the spherically inflated brain was cut (indicated as yellow line) to represent it as 2D flat map. White lines on the flat map demarcate the principal sulcus (PS), the arcuate sulcus (ARC), and the cingulate sulcus (CS). The location of the frontal eye field (FEF) within the ARC is indicated by a green patch. (C) As a last step, the anatomical subdivision of areas in the prefrontal-cingulate cortex were visualized following the nomenclature from Barbas and Zikopoulus (46). The area 32 and area 46 recording sites are visualized throughout the panels by a red and a yellow dot, respectively. (D) Similar format to C, but using major anatomical reference schema as indicated in ref. 3. Adapted from ref. 3.

Fig. S2.

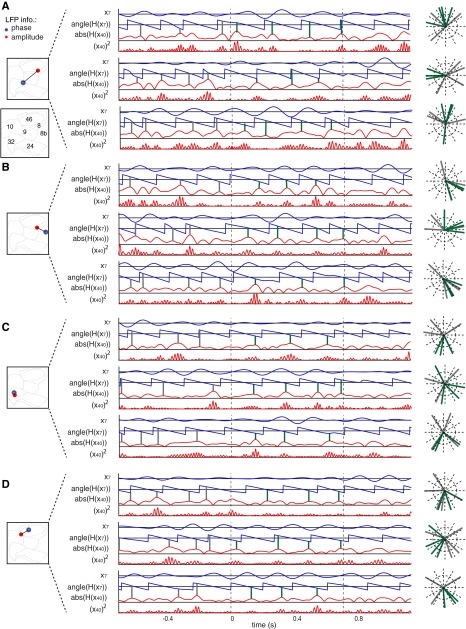
Example LFP–LFP pairs showing theta–gamma correlation in the postcue period. (A–D) Example LFP–LFP pairs shown in same format as Fig. 1D in the main text. Filtered phases and amplitude traces for the example LFP–LFP pairs that are shown in Insets of the 2D ACC/PFC representation. For each of three trials (i–iii) the bandpass-filtered low-frequency activation and its phase evolution are shown with blue lines, and the amplitude envelope and the squared gamma amplitude of the amplitude-providing LFP recording are shown in red. Gray (green) vertical lines highlight the phases at which the gamma-amplitude variations show peaks within the 500 ms before (after) attention cue onset. The polar plot on the Right shows these peak phases in the precue and postcue period. For all example LFP–LFP pairs, the gamma-amplitude peaks in the 0.5-s time after cue onset couple to similar theta phases of the phase channels in the postcue period across trials.

Fig. 2.

Theta–gamma correlation is significantly enhanced after attention cue onset on correct trials. (A) Comodulograms of the normalized difference in the phase (x axis)-to-amplitude (y axis) correlation (measured as MI) in the postcue relative to the precue task epoch on correct trials (n = 1,104). Positive values indicate increases of P–A correlation after attention cue onset. The black rectangle denotes significant (P < 0.05) comodulation difference. (B) Histogram of the difference in theta–gamma P–A correlation MI in the postcue relative to precue task epoch across all LFP–LFP pairs on correct trials (n = 1,104). Black bars in both panels highlight those LFP pairs that exhibited an individually significant P–A correlation increase with attention on correct trials (n = 85). Red and blue vertical bars denote mean and median of the distribution, and the dotted line highlights the difference in MI of zero. (C and D) Same format as A and B but for error trials. Note that, in D, the black bars in the histogram show the theta–gamma MI values for the same LFP pairs highlighted in B. (E) Comodulograms showing the average P–A MI on correct trials (left column) and error trials (right column), and in the precue task epoch (upper row) and the postcue epoch (bottom row) (n = 85). Shown are the average MIs of those LFP–LFP pairs with significantly increased theta-to-gamma P–A correlation (the black-colored bars in B). (F) Temporal evolution of theta–gamma P–A correlation for those LFP pairs with a significant P–A correlation effect on correct trials (n = 85) during correct (green) and error (red) trials at different 500-ms time windows relative to the attention cue onset (x axis).

Fig. S3.

Theta–gamma correlation is significantly enhanced after attention cue onset on correct trials in a narrow theta–gamma coupling range. (A and B) Same format as Fig. 2 A and B in the main text. Comodulograms of the normalized difference in the phase (x axis)-to-amplitude (y axis) correlation (measured as MI) in the postcue relative to the precue task epoch (n = 1,104). Positive values indicate increases of P–A correlation after attention cue onset. The left and right panels shows PAC difference for correct and error trials, respectively. The black rectangle denotes significant (P < 0.05, FDR corrected) comodulation difference. (C) Scatter plot of the variance of the time from attention cue onset (y axis) and circular variance of the phase (x axis) relative to the maximum peak of the gamma envelope (n = 85). The red line denotes where variances are equal, and the red dot is defined by the average variance.

Fig. S4.

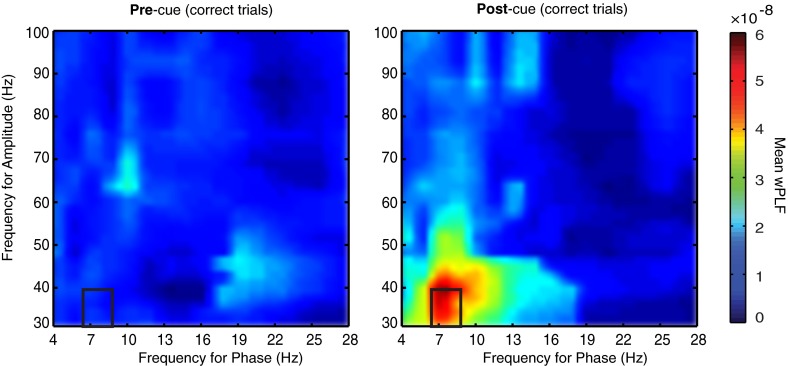
Theta–gamma correlation indexed with Maris’ weighted phase-locking factor. Comodulograms of average wPLF in the precue (Left) and postcue (Right) for the LFP–LFP pairs (n = 85) that showed a significant increase (P < 0.05) in coupling on correct trials. The black rectangle denotes frequency pairs that show a significant normalized difference in coupling at the population level.

Fig. S5.

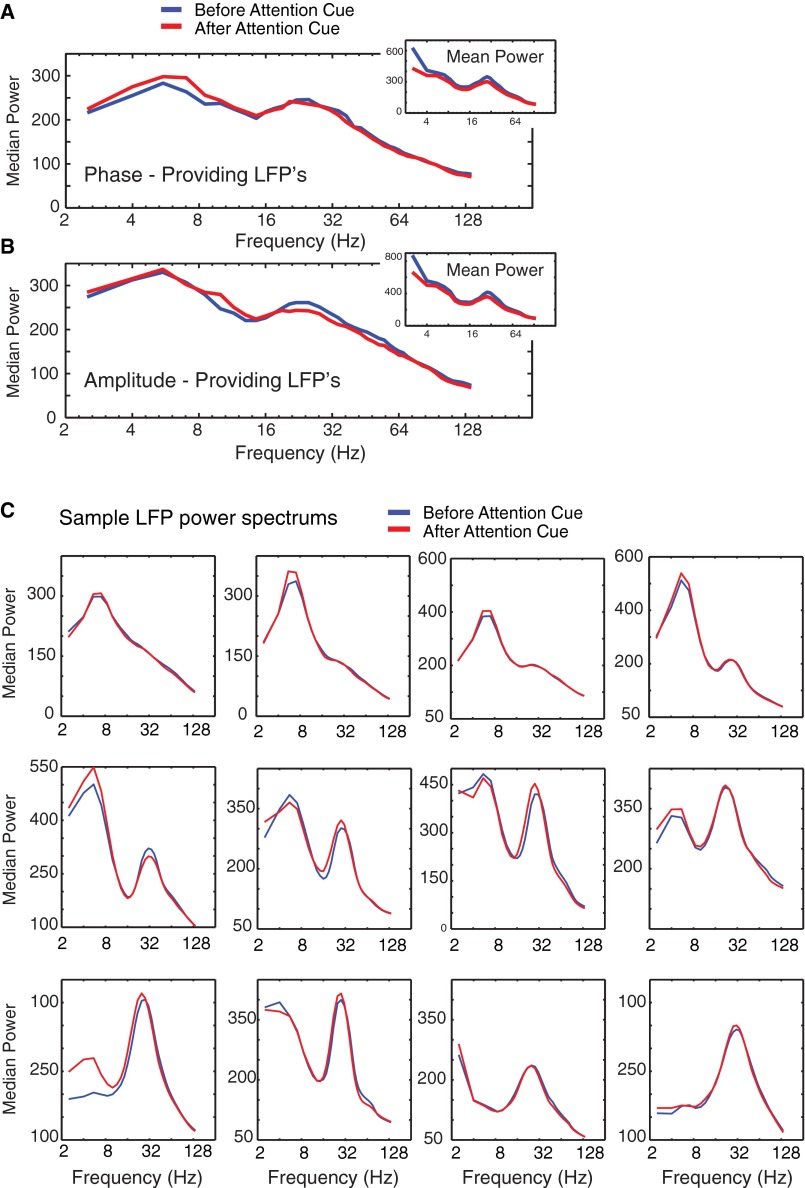
Average power spectral densities for phase- and amplitude-providing LFP recordings. (A) Median power spectral density (y axis) for unique LFP recordings (n = 74) that provided the low-frequency phase information to the LFP–LFP pairs that showed significant theta–gamma P–A correlation in the post-attention cue epoch but not in the pre-attention cue epoch. Line colors denote the median power in 0.5-s time windows immediately before the attention cue (blue) and immediately after the attention cue onset (red). The Inset shows the mean power spectral density instead of the median. (B) Same format as A but in unique LFP recordings that provided the amplitude information (n = 67) to the theta–gamma P–A correlation. (C) Average power spectral densities (y axis) for 12 example LFPs that engaged in significant cross-frequency P–A correlation in the 500 ms after the onset of the attention cue (red), but not before the attention cue onset (blue). Power spectra were arranged so that LFPs with a stronger theta power component are shown earlier, and LFPs with relatively stronger beta LFP peak are shown later in the sequence. The examples illustrate the range of LFP power spectral densities evident in the PFC/ACC, and they show that there were no apparent LFP power modulations between the precue and postcue attention epoch.

Fig. S6.

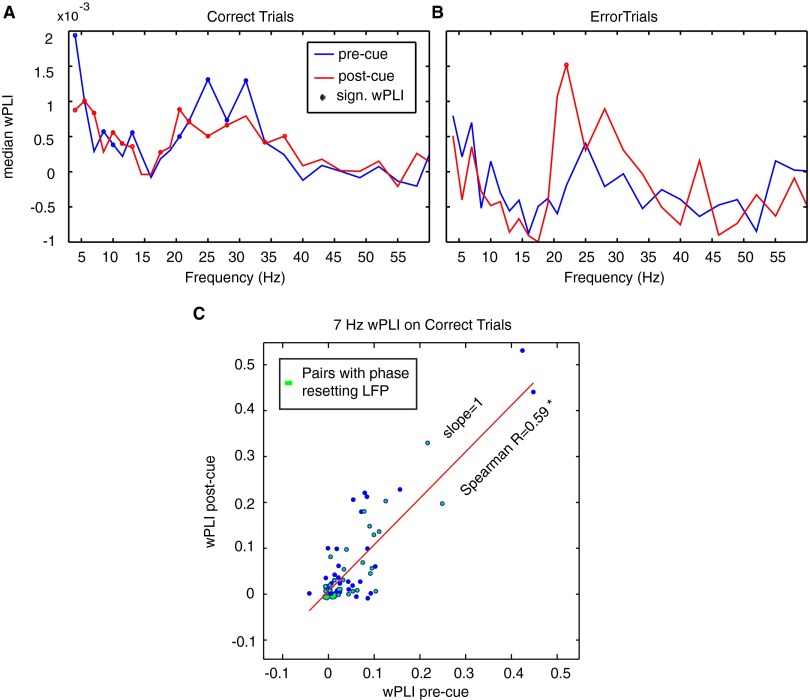
Phase synchronization in the P–A correlation network during attention switching. (A and B) Average phase synchronization (measured as wPLI) across LFP pairs (n = 85) that showed a reliable increase in phase–amplitude theta–gamma correlation, for correct (A) and error (B) trials. There was no significant change in phase synchronization between the precue and postcue epochs (SI Result S7). The dots mark frequencies where the average wPLI was significantly higher than zero (Wilcoxon sign rank). (C) Spearman rank correlation and linear regression (red line) of the wPLI in the precue and postcue epoch. Spearman R was significant (P < 0.05). Green crosses highlight those P–A correlation LFP pairs where the theta-providing LFP showed a significant phase reset 100–300 ms after attention cue onset. Phase-resetting channels are broadly distributed even among weakly P–A correlated LFP pairs.

We next tested whether the LFP gamma-amplitude variations were statistically more precisely locked to the theta phases of LFPs or to the cue onset. If the latter were the case, then theta–gamma correlations could be secondary to cue-triggered gamma-amplitude changes (10). However, we found on average across the n = 85 LFP pairs with significant theta–gamma correlations that the maximum gamma amplitudes showed less variance in the phase of their theta-band modulation than in their time to attention cue onset (SI Result S5; Fig. S3C).

Theta–Gamma Correlations Fail to Emerge on Error Trials.

Theta–gamma P–A correlations could accompany attention cues irrespective of whether attention shifted correctly, which would render the phenomenon functionally unimportant. We thus compared correctly performed trials to error trials, where subjects either responded to the distractor (indicating either wrong attention shifts or low attentional control levels) or made wrong choices to the target (indicating, e.g., failed perceptual discrimination of the attended stimulus likely also related to low attentional control levels) (2, 16). In contrast to correct trials, the attention cue did not trigger a significant increase in P–A correlation on error trials (Wilcoxon sign-rank test, P = 1, FDR corrected; Fig. 2C). The lack of P–A correlation was evident across the whole population of LFP pairs as well as for the subset of LFP pairs that showed individually significant P–A correlation on correct trials (Fig. 2D). This functional effect is readily visible in the average MI comodulograms (Fig. 2E) and remained robust when equalizing the number of correct trials to the lower number of error trials (SI Result S6). Testing the temporal specificity of this error-predicting effect across all LFP pairs showed that theta–gamma correlations were maximal on correct trials immediately following cue onset, but remained higher than chance levels, and higher than on error trials, over the entire postcue analysis period (up to 0.75 ± 0.25 s) (Fig. 2F).

The lack of P–A correlations on error trials may follow from a larger variability of theta phases at which gamma activity synchronizes, from a systematic shift in theta-frequency locked phases, or a combination of both (17). To elucidate these possibilities, we characterized the theta phase at which gamma-activity modulations aligned on correct and on error trials (Fig. 3). Across LFP pairs with significant theta–gamma correlation, gamma bursts on correct trials phase locked on average close to the peak of the theta cycle after the attention cue (mean phase of −14.69°, 95% CI [−41.01°, 11.63°]), with a significantly nonuniform circular phase distribution (Hodjes–Ajne test, P = 3.6*10⁻⁴; Fig. 3A). In contrast, the distribution of phases on error trials only revealed a statistical trend to deviate from uniformity (Hodjes–Ajne test, P = 0.064), with a mean phase that was about 90° offset from the mean phase on correct trials (−94.28°, 95% CI [−131.40°, −57.16°]; Fig. 3B). Importantly, correct and error trial phase distributions were significantly different (Kuiper test, P < 0.005), suggesting that, on error trials, theta phases shifted and showed a larger variability compared with correct trials (Fig. 3C; see SI Result S1.2 for consistent effect across monkeys). Control analyses revealed the same functional effects when we accounted for the lower overall modulation strength on error trials compared with correct trials (SI Result S7 and Table S1), as well as for the differences in trial numbers (SI Result S6). Moreover, we found that the average field potential of the LFP around the attention cue onset did not distinguish correct from error trials, suggesting that possible nonstationary transients do not account for the functionally significant P–A correlations (10) (SI Result S8).

Fig. 3.

Preferred theta phase of theta–gamma correlation on correct and error trials. (A) Polar histogram of the amplitude-weighted mean preferred phases in the postcue period at which gamma activity phase locked in those LFP pairs with significant theta–gamma coupling in the postcue period (n = 85). Colors denote the distributions expected by chance (green) and from the post-attention cue epoch (blue) on correct trials. The outer dotted ring corresponds to a proportion of 20%. The red dot and line denote circular mean and 95% confidence range. (B) Same as in A, but for error trials. (C) Illustration of the mean and 95% confidence range of the preferred theta phases on correct (green) and error trials (red) at which gamma amplitudes couple for the LFP pairs that showed a significant increase in theta–gamma P–A correlation after attention cue onset.

Table S1.

The distribution of preferred phases of coupling is significantly nonuniform for correct but not error trials

Statistical test			Method of phase extraction
	Null hypothesis		MI	wPLF	Peaksmax	Peaks80	Peaks70	Peaks50
Hodjes–Ajne test	Correct trials: the distribution of phases is nonuniform	Mean ± 95% CI phase (deg)	−14.7 ± 26.3	9.0 ± 27.2	−8.1 ± 69.7	−1.6 ± 51.2	1.0 ± 46.8	−6.7 ± 37.9
		P value	0.00036	0.00088	0.0045	0.0127	0.0113	0.00067
	Error trials: the distribution of phases is nonuniform	Mean ± 95% CI phase (deg)	−94.3 ± 37.1	110.19 ± 53.2	−77.2 ± 90	−73.9 ± 90	−92.4 ± 90	−131.8 ± 90
		P value	0.0642	0.1772	0.2716	0.0669	0.665	0.1732
Kuiper test	Error and correct trial distributions are the same	P value	0.005	0.002	1	1	1	1

The average (±confidence intervals) of preferred phases are shown for correct trials and error trials. We report P values associated with either the Hodjes–Ajne test for circular nonuniformity (n = 85, each), or the Kuiper test for the difference between two sample distributions. Bolded values are significant at P < 0.05. Different methods of analyzing the distribution of phases to which gamma activity coupled agree that correct trials are nonuniform, whereas error trials are not. Moreover, two different metrics (MI and wPLF) agree that the two distributions are different from one another.

Interareal Cross-Frequency Correlation Is Anatomically Specific.

We next asked whether the anatomical location of the theta-phase– and gamma- amplitude–providing LFPs in ACC/PFC mattered for P–A correlations. One assumption of this analysis is that theta-phase–providing sites may more likely serve as modulating sources for attention, whereas gamma-amplitude–providing sites relate to implementing attention. To test this, we reconstructed the LFP recording locations (Fig. S1) and grouped them into the ventromedial PFC (vmPFC) (areas 32 and 10), ACC (area 24), and LPFC (areas 46, 8, and 9) (Fig. 4A). We found that, among the significantly theta–gamma correlated pairs, phase- and amplitude-providing LFPs were found in each of the subareas, but with an apparent asymmetry between areas (Fig. 4 B and C; SI Result S9 and SI Result S1.3). Testing each area for whether they contained more phase or amplitude LFPs, we found that LPFC theta phases were significantly less likely to correlate with ACC gamma amplitudes (Z test, P = 0.0089; Fig. 4C). More specific testing of the interareal P–A correlations showed that the LPFC had overall less interareal theta-phase–providing LFPs than expected by chance (Z test, P = 0.029; Fig. 4D), whereas the ACC had less interareal amplitude-providing LFPs (Z test, P = 0.028; Fig. 4D). Consistent with this finding, the ACC provided overall significantly more theta-phase LFPs than gamma-amplitude LFPs during interareal theta–gamma correlations (McNemar χ² test, P = 0.034; Fig. 4D), whereas the LPFC showed a trend for more amplitude- than phase-providing LFPs (McNemar χ² test, P = 0.066; Fig. 4D). These results were similar in both monkeys (SI Result S1.3).

Fig. 4.

Anatomical origins of cortical sites with phase and amplitude modulation during theta–gamma P–A correlation. (A) Combination matrix showing the total number of LFP–LFP pairs (n = 1,104) recorded from the ventromedial PFC (vmPFC) (areas 32 and 10), the anterior cingulate cortex (ACC) (area 24), and the LPFCs (areas 46, 8, and 9). The brain area of the phase-providing channels is on the x axis, and the origin of the amplitude-providing LFP channels is on the y axis. (B) Anatomical recording location of phase (blue)- and amplitude (red)-providing LFPs (n = 85 LFP pairs; connected with black lines) and plotted on the 2D flat-map representation of the ACC and PFC. Gray contours denote area boundaries (see Inset for area labels; Fig. 1B). (C) Same as in A, but for the proportion of theta–gamma P-A–correlated LFP pairs (n = 85) relative to all LFP pairs recorded for an area combination. Color indexes the proportion. (D) Likelihood to find a phase-providing channel (values Left from zero) and an amplitude-providing channel (Right from zero) in the vmPFC, ACC, and LPFC during cross-area theta–gamma correlation (n = 32; y axis).

Cue Induced Theta-Phase Reset in LFPs Showing Theta–Gamma Correlation.

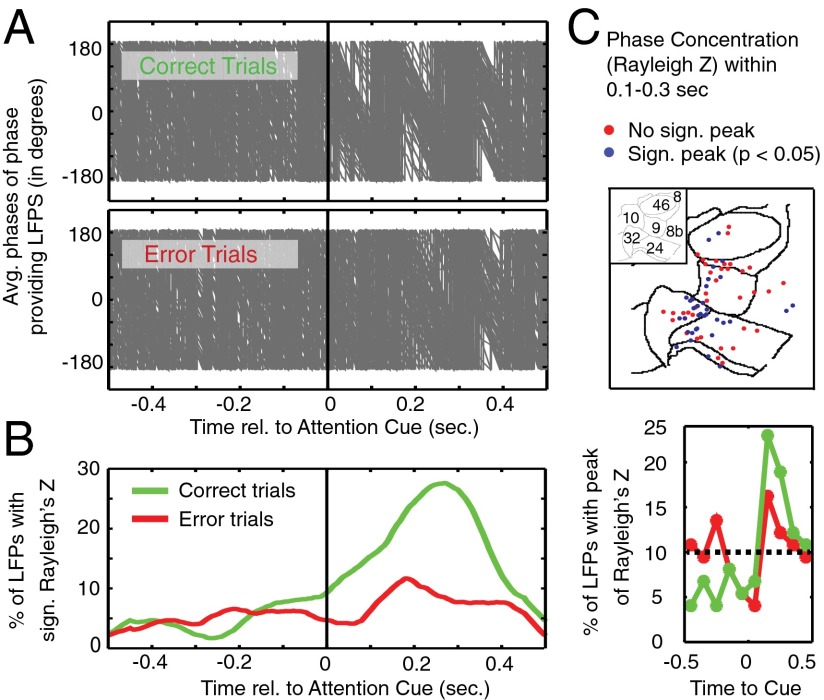
Theoretical studies suggest that the modulation of low-frequency phase is instrumental in triggering high-frequency bursts during theta–gamma correlations (17, 18). Such precedence of low-frequency activity for P–A correlation would empirically become evident as a realignment, or reset, of phases (19). We tested for the presence of an attention cue-triggered theta-phase reset and its putative relation to theta–gamma correlation, and found that immediately following the attention cue the average theta-band phases became highly similar across individual LFPs that showed significant theta–gamma correlations. This phase alignment was visually apparent on correct trials but not on error trials (Fig. 5A). To quantify this phase reset, we calculated the significance of the instantaneous theta-phase consistency across trials for each LFP around attention cue onset and found that the greatest number of LFP channels exhibited significant theta-phase consistency 268 ms after attention cue onset (Fig. 5B, Left). The rise in theta-phase–consistent LFPs was evident on correct trials and failed to emerge on error trials. To validate this finding, we extracted the time at which the Rayleigh Z time course peaked in the 1,000 ms around the time of the attention cue onset for each LFP. Corroborating the previous result, we found that 41.89% of the theta-phase–providing LFP sites (31 of 74) showed peak phase consistency 150–250 ms (±50 ms) after attention cue onset on correct trials (Fig. 5B, Right). This distribution of peak phase consistency was significantly nonuniform on correct trials, but not on error trials (Pearson’s χ² test, P = 0.0012 and P = 0.465, respectively). In the 150- to 250-ms (±50-ms) time window, 35 of 74 LFP sites showed a significant theta-band phase consistency, and clustered at the nexus of the ACC, vmPFC, and LPFC (Fig. 5C).

Fig. 5.

Phase-providing LFPs engaging in significant theta–gamma phase–amplitude correlation show a theta-phase reset after attention cue onset on correct trials. (A) Progression of the average phase (y axis) for all phase-providing LFP channels (n = 74) engaging in significant theta–gamma correlation around the time of the attention cue onset (x axis). Each gray line represents the average phase across trials of one such LFP. Top and bottom panels show the progression of mean phases on correct trials and on error trials, respectively. (B) The left panel shows the percentage of phase-providing channels with significant phase concentration (y axis, measured as Rayleigh’s Z) around the time of the attention cue onset (x axis). Green and red lines show the average Rayleigh’s Z across LFP channels for correct and for error trials, respectively. The panel on the Right shows the percentage of LFPs whose peak phase concentration fell within 1 of 10 nonoverlapping time bins (around attention cue onset). (C) The anatomical distribution of recorded LFPs that showed a significant phase concentration (blue) or that did not show significant phase concentration (red) in the 0.1–0.3 s following attention cue onset. See Fig. 1B for the labeling of PFC/ACC brain areas on the 2D flat-map representation (and Figs. 1 and 2).

The presence of a theta-phase reset could synchronize LFP theta phases across multiple ACC/PFC subfields. Thus, the correlation of gamma amplitudes to theta phases could be understood as a direct consequence of such large-scale theta-band coherence. However, we found that LFP–LFP theta-phase synchronization did not change from pre- to post-attention cue, was not different between correct and error trials, and did not correlate with the increase of interareal theta–gamma correlation during attention shifts (SI Result S10).

Selective Theta–Gamma Correlation for Target Locations and Its Relation to Firing-Rate Information.

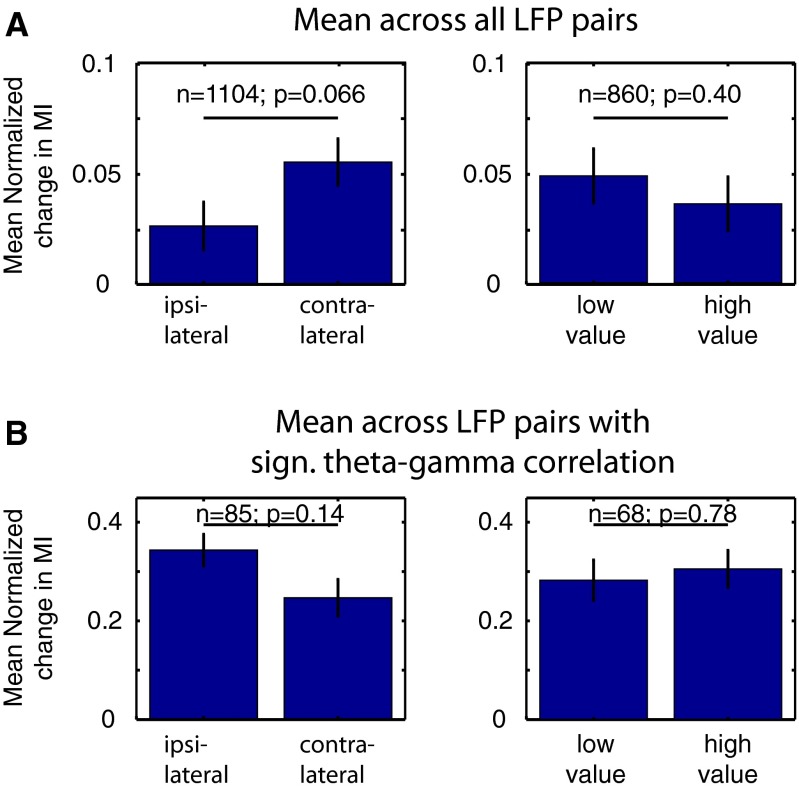
Theta–gamma correlation may not only emerge selectively on correct vs. erroneous attention shifts but may carry specific task-relevant information about direction of the attention shift. Across the entire population of LFP pairs, we found a statistical trend for larger theta–gamma correlation when attention shifted to the contralateral vs. ipsilateral stimulus (Wilcoxon sign-rank test, P = 0.066; Fig. S7A and SI Result S11.1). Testing for significant differences in theta–gamma correlation between spatial conditions at the single LFP pair level revealed that a small subset of LFP pairs (4.4%; 49 of 1,104) showed significant effects (Monte Carlo surrogate test, two-sided, P < 0.05), with n = 32 (n = 17) LFP pairs showing larger theta–gamma correlations for contralateral (ipsilateral) attention shifts (SI Result S11.1). This spatially selective theta–gamma correlation may relate to previously reported spatially selective firing-rate modulations of neurons in ACC/PFC (3, 20). However, we found that spatial selectivity in theta–gamma correlations were not consistently related to spatially selective firing of neurons recorded from the LFP recording sites that provided theta-phase or gamma-amplitude variations underlying theta–gamma correlations (all r < 0.1, P > 0.05; SI Result S12). In addition to spatial attention, we tested in a subset of sessions whether theta–gamma correlations emerged differentially when the cue directed attention to a target stimulus with higher vs. lower reward association, but did not find consistent differences of theta–gamma correlations for higher or lower rewarded attention targets (SI Result S11.2). Theta–gamma correlations for location or reward were largely unrelated to LFP pairs with theta–gamma correlations predictive of correct choices (Fig. S7B and SI Result S11.1 and SI Result S11.2).

Fig. S7.

Representation of spatial information and information about target-associated reward outcome in theta–gamma P–A correlation. (A) The average change in theta–gamma correlation across all LFP pairs for different spatial and reward outcome conditions (n = 1,104 for spatial conditions; n = 860 for value conditions), represented as the mean and SE. There is a higher increase in correlation on contralateral vs. ipsilateral trials (Left), but no difference between attention to lower vs. higher rewarded targets (Right). (B) Same as in A, but only for LFP pairs where theta–gamma correlation showed reliable increase in the postcue period on correct trials (n = 85 for spatial conditions; n = 68 for value conditions). Insignificant theta–gamma correlation was masked to zero. There is no difference between contralateral and ipsilateral trials, or between high- and low-value target trials.

Theta–Gamma Correlation and Its Relation to Synchronization of Burst Firing Events.

Although overall firing-rate modulations of neurons were not statistically associated with theta–gamma correlations (SI Result S12), it is possible that finer-grained burst firing events relate to long-range theta–gamma correlations, similar to burst firing events synchronizing long-range to mid-gamma–band (55–75 Hz) LFP activity (12). We thus correlated burst–LFP synchronization of neurons recorded at LFP recording sites that provided theta-phase or gamma-amplitude variations for theta–gamma correlations (SI Result S13). We found that burst synchronization to remote LFP gamma activity varied proportionally with the degree of theta-phase correlation with low-gamma amplitudes (35–50 Hz), an effect that was limited to those LFP sites that showed significant theta–gamma correlations (Spearman rank correlation r = 0.2, P = 0.044; Table S2 and SI Result S13). To our knowledge, these findings provide the first quantitative evidence that recording sites with LFP theta phases that engage in long-range gamma correlations also host neurons whose burst firing events synchronize long-range to gamma activity.

Table S2.

The relationship of theta–gamma P–A correlation and burst–LFP synchronization across all types of channel combination

Channel of burst-LFP synchronization pair	Frequency band applied to LFP signal in burst-LFP synchronization	Theta-phase–providing LFP channels		Gamma-amplitude–providing LFP channels
		All	Those with significant theta–gamma correlation	All	Those with significant theta–gamma correlation
“LFP channel” of burst–LFP synchronization pair; LFP recorded at the same channel as used for the cross-frequency analysis	Theta (5–10 Hz) burst–LFP synchronization	P = 0.261	P = 0.713	P = 0.027*	P = 0.702
		r = 0.036	r = 0.038	r = 0.072*	r = 0.040
	Beta (15–25 Hz) burst–LFP synchronization	P = 0.155	P = 0.016†	P = 0.086	P = 0.032†
		r = −0.046	r = −0.246†	r = 0.056	r = −0.219†
	Gamma (55–75 Hz) burst–LFP synchronization	P = 0.069	P = 0.701	P = 0.138	P = 0.163
		r = 0.059	r = −0.040	r = 0.048	r = 0.143‡
“Burst channel” of burst–LFP synchronization pair; burst firing of neurons at the same channel as used for the cross-frequency analysis	Theta (5–10 Hz) burst–LFP synchronization	P = 0.728	P = 0.255	P = 0.657	P = 0.266
		r = 0.010	r = 0.114‡	r = 0.013	r = 0.111‡
	Beta (15–25 Hz) burst–LFP synchronization	P = 0.482	P = 0.406	P = 0.581	P = 0.234
		r = 0.021	r = 0.083	r = −0.017	r = 0.119‡
	Gamma (55–75 Hz) burst–LFP synchronization	P = 0.070	P = 0.044*	P = 0.750	P = 0.476
		r = 0.055	r = 0.200*	r = 0.010	r = 0.071

The table shows the Spearman rank correlations and their respective significance levels. Columns are split into the theta-phase–providing channels and the gamma-amplitude–providing channels. Different columns show either all channels, or channels from LFP pairs that showed significantly increased P–A correlation in the postcue period. Rows show the results separately for channels at which either the LFP (upper three rows) or the burst firing of neurons (lower three rows) were part of a burst–LFP pairs. For recording channels with more than one single cell, the average burst–LFP synchronization across cells for that channel was used for calculating the correlation. Significant (P < 0.05) correlations are indicated in bold.

^*Positive correlations at P < 0.05.

^†Negative correlations at P < 0.05.

^‡Correlations >0.1.

Discussion

We found that a centrally presented attention cue induces a correlation of 5–10 Hz theta-band phase fluctuations and 35–55 Hz gamma-band activations between cortical subfields in ACC/PFC. This theta–gamma P–A correlation failed to increase on erroneous trials and thus signified successful shifts of attention, i.e., cue utilization. On error trials, preferred theta phases were earlier and more variable in the theta cycle compared with correct trials. This suggests that failures of shifting attention are associated with the decoherence of theta to gamma interactions in a network comprising the ACC/PFC. In this network, the theta–gamma P–A correlations were supported disproportionally often by theta phases from within the ACC compared with the LPFC. This finding indicates that it is particularly the ACC (the rostral part of area 24) that provides a critical, slow theta-periodic influence on gamma-mediated processes within the LPFC during the implementation of attention shifts. A further major characteristic of theta–gamma correlation is its close association with a cue-induced theta-phase reset. More than one-third of phase-providing LFPs for significant theta–gamma P–A correlation showed the largest theta-phase consistency within the first 0.3 s following cue onset, suggesting that a theta-phase reset could mechanistically be a source of anatomically widespread theta–gamma correlation. Taken together, these findings provide a unique perspective on how the control of attention is implemented by circuits in primate ACC/PFC and corroborate a long-held hypothesis that theta–gamma cross-frequency interactions are an essential means of interareal integration of distributed activities in multinode cortical networks (9, 21).

Frequency Specificity of P–A Correlation in ACC/PFC.

Our main finding characterized the statistical relation of two band-limited activity fluctuations comprising a narrow ∼5- to 10-Hz (peak at 7 Hz) theta band and a ∼35- to 55-Hz (peak at 40 Hz) gamma band. Previous studies have documented that a 5- to 10-Hz theta band is a widespread LFP signature in ACC/PFC that increases with specific demands to control goal-directed behavior (22–25). Our study corroborates these reports (Fig. S5) revealing that theta-band activity synchronizes distributed bursts of gamma activity in ACC/PFC to preferred phases of the theta oscillation. This further supports the notion that theta–gamma P–A correlation is a ubiquitous phenomenon evident across multiple circuits including hippocampal-cortical circuits (26), hippocampal-striatal networks (27), cortico-striatal networks (28), and cortico-cortical networks (29, 30). Our results extend the role of theta–gamma P–A correlation to PFC circuits, with ∼35% of LFP sites contributing to significant theta–gamma interactions. However, these sites show anatomically specific clustering, with a moderate maximal ∼8–10% of interareal ACC–theta to LPFC–gamma pairs showing individually significant effects (Fig. 4).

In previous studies, 5- to 10-Hz activity fluctuations were shown to organize distinct band-limited gamma-frequency bands categorized as low (∼35–55 Hz), medium (∼50–90 Hz), and high (epsilon; ∼90–140 Hz) bands, each likely originating in separable underlying circuit motifs (8, 11, 26). The observation that ACC/PFC circuits theta-synchronized the activation at a low-gamma–frequency band (35–55 Hz) is, to our knowledge, unprecedented in LFP recordings in the primate brain. However, a similar theta to low-gamma P–A correlation has been found in rodents to emerge in medial frontal, entorhinal, and hippocampal circuits (8, 26, 27, 31). In the cortex of nonhuman primates, synchronization of a low (35–55 Hz) gamma-frequency band has recently been described to characterize local LFP and spike–LFP coherence within the macaque frontal eye field (FEF) during sustained selective attention (32) (for a lower 30- to 40-Hz beta/gamma in LPFC, see ref. 33). The cortical ACC/PFC fields engaging in theta-locked low-gamma activation in our study anatomically connect to the FEF. This makes it likely that the theta-phase reset we observed in ACC/PFC also synchronizes FEF gamma-activity bursts and spiking activity of visually selective FEF neurons that most strongly synchronize to the local, low-gamma activity in FEF during sustained selective attentional processing (34). We can thus speculate that the band-limited neuronal activation of the specific theta and gamma bands that interact during attention shifts in our study may serve as general band-limited signatures of neuronal coordination of attention information during goal-directed behaviors.

Functional Significance of Theta-Phase Resets in the ACC/PFC.

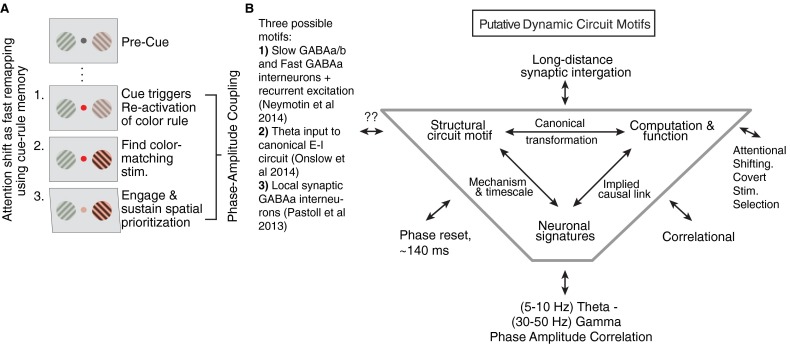
The attention cue-triggered P–A correlations we observed were associated with a prominent theta-phase reset. Similar to the absence of theta–gamma P–A correlation on error trials, the theta phase failed to reset following the attention cue on error trials (Fig. 5B), illustrating that the LFP theta-phase resets of the theta-gamma–correlated network also indexed whether attention shifts are successful. A plausible mechanism for such a far-reaching consequence of phase-aligned theta activation can be found in recent studies that identified how a cue-induced phase reset effectively gates the outflow of a cortical circuit (35–37). These studies suggest that the phase reset-gated output of a local circuit can serve as the causal trigger of distant gamma activity phase locked to theta activity. For example, one optogenetic study documented that a locally generated theta-phase reset in rodent frontal cortices develops in conjunction with learning the meaning of a (classically conditioned) cue (37). Following learning, the cue-triggered theta-phase reset predicted when projection neurons phase lock their spike output to the peak of theta oscillation cycles (37). Moreover, the theta-phase reset effectively synchronized the spiking activity of those projection neurons in rodent mPFC that activated fear-related target structures that modified behavior. The attention cue-induced phase reset we report may be analogous to such a sequence of events. In our task, the cue signified a color-matching rule (“find the peripheral stimulus matching the color of the cue and enhance its representation against other stimuli”). Correctly interpreting the cue required reactivating neural assemblies coding for the rule representation and applying the rule to the visually available information to eventually prioritize processing of the attended stimulus and filter out uncued stimuli (3, 38) (Fig. S8A). Such an attentional remapping of functional connectivity occurred in the first 0.5 s following attention cue onset (3), and it is during this process that theta phases were most consistent across trials and began to synchronize remote gamma activities across ACC/PFC. We therefore speculate that the cue-triggered theta reset is instrumental to synchronize ACC/PFC neural circuits to theta rhythmic, ∼140-ms-long activation periods that provide a reference for phase-locked gamma-activity bursts.

Fig. S8.

Cue-triggered attention shifts during memory reactivation and remapping and hypothetical dynamic circuit motifs of theta–gamma P–A correlation. (A) Illustration of three separable component processes underlying the cue-triggered (covert) attention shift. The panel shows the succession from precue (top panel) to postcue period (bottom three panels). The panels show that attention shifting proceeds from (i) the reactivation of a color rule, (ii) applying the rule by finding the color matching peripheral stimulus and filtering out nonmatching stimuli, and (iii) engaging and sustaining stimulus selection. (B) The framework of the tripartite dynamic circuit motifs helps understand how an activation signature (theta–gamma P–A correlation) links to a function (attentional shifting and stimulus selection). Completion of a dynamic motif would require identification of the structural (cellular and synaptic) origin of the activation state. (For details, see ref. 11.) The shown putative motif makes it explicit that the link of theta–gamma P–A correlation and attentional prioritization is correlational. Moreover, we can only speculate which synaptic or cellular mechanisms implement theta–gamma P–A correlation, but outline three generic cortical circuits that are powerful candidates.

Three additional sources of evidence support this prediction and are in line with our results. First, studies in rodents suggest that theta-phase resets and theta coupling to gamma emerges in a prefrontal–hippocampal network to widely varying types of instructional cues, ranging from (Pavlovian) cues in classical conditioning contexts (31, 37), to instrumental cues in spatial choice tasks and item-context association tasks (27, 39). Second, computational studies have identified canonical circuit motifs of theta–gamma correlation in which the theta phase can be instrumental in triggering and even generating gamma-band activities in postsynaptic target circuits (17, 40). Key assumptions of such “theta-reset models” are the existence of a robust gamma-generating feedback circuit in the target structure, and a low-frequency (theta periodic)–modulated input to inhibitory cells in the circuit (17, 41, 42). This low-frequency (theta)–modulated input may likewise be generated de novo from within the circuit from theta-generating or theta-resonating interneuron populations (figure 1A in ref. 11; see Fig. S8 for other dynamic circuit motifs). Third, a large set of studies have documented how attentional expectancies realign phases of low frequencies in sensory cortices to the time when attentionally relevant stimuli are expected to occur to support goal-directed behavior (19). Such anticipatory phase entrainment resembles “resets” and can synchronize high-frequency activities at beta and gamma bands that correlate with sensory detection speed and the efficiency of subjects to filter out distractors in attention tasks (19, 43). Consistent with these findings, we found that, in a situation without externally imposed entrainment of events, attention cues induce a rapid phase reset and thereby possibly implement a covert selection of relevant sensory stimuli according to the cue-dependent instructional rule.

Theta–Gamma Correlation as Means to Coordinate Attention Information.

It is important to acknowledge that we found the theta-phase reset and theta–gamma P–A correlation in precisely those cortical circuits of the ACC/PFC that are functionally essential for the flexible control and biasing of attention- and goal-directed behavior (1, 6). To realize such a control/bias function, ACC/PFC likely continuously interact with fronto-parietal attention networks during goal-directed behavior to ensure continued attention to relevant information that relate to the task goals and other working memory contents (1, 2). We believe that such biasing during attentive processes is realized through theta–gamma cross-frequency interactions involving circuits in ACC/PFC.

An important piece of information supporting the proposed “P–A correlation hypothesis of attentional control” is that burst spiking events related to theta–(low) gamma correlation. We found that burst firing of neurons synchronized to remote (mid) gamma-band activity at those LFP recording channels that provided the theta phases for LFP pairs with significant theta–gamma correlation. This result links findings on interareal burst synchronization (12) with the current report of functionally relevant theta–gamma correlations and suggests that interareal theta–gamma interactions of different LFPs may directly or indirectly relate to burst firing of neurons within the theta-frequency–modulated circuits. Intriguingly, firing of bursts or firing of sequences during brief periods of theta-nested gamma-band activity is strongly implicated in rodent hippocampus and striatum to carry unique information about internally maintained goals (e.g., the location of the most rewarded outcome) (44, 45). Our results suggest that theta-nested gamma modulations may serve as a means to organize and integrate such covertly (internally) generated information to ensure the flexible control of attention during goal-directed behaviors.

Methods

Two macaque monkeys were trained on a selective attention task that required using a centrally presented color cue to covertly select (i.e., in the absence of overt eye movements) a color matching peripheral stimulus and ignore the nonmatching stimulus (Fig. 1A). During attention performance, we recorded LFPs from microelectrodes in anatomically reconstructed locations in the medial and lateral PFC (Fig. 1B). The full task is detailed in Fig. 1 A and B and Supporting Information. The experiment followed the guidelines of the Canadian Council of Animal Care policy on the use of laboratory animals and was approved by University of Western Ontario Council on Animal Care.

SI Methods

The local field potential (LFP) recordings and anatomical reconstruction of recording sites reported in this manuscript are from the dataset and experiment described in detail in ref. 3.

Electrophysiological Recording and Data Acquisition.

We recorded and analyzed the LFP in two awake and behaving macaque monkeys in 102 experimental sessions (26 and 76 for monkeys M and R, respectively) as described in detail in ref. 3 and following the guidelines of the Canadian Council of Animal Care policy on the use of laboratory animals and of the University of Western Ontario Council on Animal Care. Extracellular recordings commenced with one to six tungsten electrodes (impedance, 1.2–2.2 MΩ; FHC) through standard recording chambers (19-mm inner diameter) implanted over the left hemisphere in both monkeys. Electrodes were lowered through guide tubes with software-controlled precision microdrives (NAN Instruments Ltd.) on a daily basis, through a recording grid with 1-mm interhole spacing. Before recordings began, anatomical 7-T MRIs were obtained from both monkeys, visualizing possible electrode trajectories through a recording grid within the chamber using iodine. Data amplification, filtering, and acquisition were done with a multichannel processor (Map System; Plexon), using headstages with unit gain.

The recording experiments were performed in a sound attenuating isolation chamber (Crist Instrument Company) with monkeys sitting in a custom-made primate chair viewing visual stimuli on a computer monitor (85-Hz refresh rate; distance of 58 cm). The monitor covered 36° × 27° of visual angle at a resolution of 28.5 pixel/deg. Eye positions were monitored using a video-based eye-tracking system (ISCAN; sampling rate, 120 Hz) calibrated before each experiment to a five-point fixation pattern (one central fixation point and the remaining four points offset by vertical 8.8° and horizontal 6° toward the four corners of the monitor). Eye fixation was controlled within a 1.4–2.0° radius window. During the experiments, stimulus presentation, monitored eye positions, and reward delivery were controlled via the software MonkeyLogic (open-source software, www.monkeylogic.net) running on a Pentium III PC (for details, see ref. 3). Liquid reward was delivered by a custom-made, air compression-controlled, mechanical valve system with a noise level during valve openings of 17 dB within the isolation chamber.

Behavioral Task.

LFPs were recorded while the monkeys were performing a selective attention, two–forced-choice discrimination task (for details, see ref. 3). The task involved 2-s intertrial intervals, before a small gray fixation point was presented centrally on the monitor. Monkeys had to direct their gaze and keep fixation onto that fixation point until the end of the trial. After 300-ms fixation, two black/white grating stimuli were presented to the left and right of the center and contained oblique movements of the grating within their circular aperture. After 0.4 s, each stimuli changed color to either black/red or black/green. After a variable time (0.05–0.75 s), the color of the central fixation point changed to either red or green, which cued the monkeys to covertly shift attention toward the location where the color of the grating matched the color of the fixation point. Monkeys maintained central fixation and sustained covert peripheral attention on the cued stimulus until it underwent a transient clockwise or counterclockwise rotation, ignoring possible rotations of the nonattended (uncued) stimulus, which occurred in 50% of the trials. To obtain a liquid reward, the monkeys had to discriminate the rotation by making upward or downward saccades for clockwise/counterclockwise rotations (the mapping was reversed between monkeys). Following this choice and a 0.4-s waiting period, the animals received fluid reward. In the majority of experimental sessions (including experimental sessions and sessions with at least one LFP that was in ACC/PFC, 70 of 80 sessions of monkey R, and 70 of 73 sessions of monkey M), the magnitude of the fluid reward varied as a function of the color of the attended stimulus that the monkeys acted upon. High- and low-reward magnitude was 0.76 and 0.4 mL per successfully performed trial. High/low rewards were linked to the red/green color of the attended stimuli (with the color–reward mapping changing across blocks of 30 correctly performed trials). A key component of the task is that the location of covert spatial attention on one of the two colored stimuli (left or right periphery) is distinct from the possible locations to which the animal made a saccade (upward and downward) to indicate the transient rotation of the attended stimulus.

Anatomical Reconstruction.

The anatomical site of each recorded LFP was reconstructed for each monkey and projected onto the 2D flat-map representation of a standardized macaque brain (“F99”) available within the MR software Caret (3). Fig. S1 surveys the main procedure for two example reconstructions. Reconstruction began by projecting each electrode’s trajectory onto the 2D brain slices obtained from 7-T anatomical MRI images, using the open-source OsiriX imaging software and custom-written MATLAB programs (The Mathworks), using the iodine visualized electrode trajectory within the electrode grid placed within the recording chamber during MR scanning. We drew the coronal outline of the cortical folding of the MR grayscale image to ease the comparison of the individual monkey brain slices to standard anatomical atlases, before projecting the electrode tip position into the standardized macaque brain (F99) available in Caret. Note that we initially reproduced the individual monkey brains within the Caret software to validate similarity and derive the scaling factors to match the lower-resolution monkey MRs to the higher-resolution standard F99 brain. We then manually projected, under visual guidance, the electrode position to the matched location in the standard brain in Caret. In the MATLAB scripts, we adjusted the anteroposterior angle of the electrode trajectory (the four chambers in the two animals had anteroposterior angles of 0°, 0°, 5°, and 10°, respectively) so that the projected 3D electrode tip position was the actual position of the tip in the correct coronal place.

After identifying all recording sites within the standard brain, we used the Caret software to render the sliced brain into a 3D volume, spherically inflated, and cut it to unfold the brain into 2D space (Fig. 1B and Fig. S1). In an independent procedure, we visualized major anatomical subdivision schemes of the fronto-cingulate cortex, using the labeling scheme from Barbas and Zikopoulos (46) (Fig. S1C). We also visualized two other prefrontal/cingulate cortex subdivision schemes that are used in the literature in the same 2D flat map in Fig. S1D to allow comparison with the Barbas and Zikopoulus scheme of the cortical fields (for details, see ref. 3). These alternate subdivision schemes are highly similar to the schema we used for assigning cells to anatomically defined brain areas.

Definition of Error Trials.

Error trials were defined as those where the monkey either made an error in discriminating the transient rotation of the target or responded during the 600 ms following a rotation event in the distractor stimulus. Thus, all errors were committed after a stimulus change (rotation) happened (16).

Analysis of Phase–Amplitude Correlations Cross-Frequency.

We analyzed how phase variations of low-frequency activity relate to variations of high-frequency activity amplitudes. Following methodological guidelines proposed in ref. 10, we consider this phase–amplitude (P–A) cross-frequency analysis to reflect P–A correlations instead of the more common label P–A coupling, as our experiment does not include direct manipulations for testing whether there are direct interactions of activity across different frequencies.

All main analysis steps and statistical routines described in the following are available publicly online under a GNU license at attentionlab.ca/doku.php?id=analysis-tutorials from the time of publication.

We hypothesized that cross-frequency correlations subserves attentional selection. As a first step, raw LFP signals were bandpass filtered with a fourth-order, two-pass Butterworth filter and subsequently Hilbert transformed. We used a variable bandpass filter defined as ±1/3 of the center frequency (e.g., 7 ± 2.3 Hz as [4.7 9.3] Hz, or 40 ± 13.3 Hz as [26.7 53.3] Hz), which has been shown to improve detection of cross-frequency interactions (10). We quantified P–A correlation between low frequencies in the range of 4–29 Hz (with 1.5-Hz steps) and high frequencies in the 30- to 130-Hz range (with 3-Hz steps). We selected channel combinations where the phase and amplitude channels are recorded from different electrodes to avoid spurious coupling as a result of a nonstationary input (10). We quantified cross-frequency correlation between the low-frequency (f_p) phase of the analytic signal x_fp(t) and the high-frequency (f_a) amplitude of the analytic signal x_fa(t) using Tort’s modulation index (MI) (14) and Maris’ weighted phase-locking factor (wPLF) (47). These signals were derived by concatenating, for a single channel, all recorded trials into one signal. The procedures are summarized here.

Analysis of Cross-Frequency Interactions Using Tort’s MI.

The MI is based on the Kullbeck–Leiber distance between two empirical distributions and is closely related to Shannon entropy. In calculating the MI, the phases of signal x_fp(t) are extracted and binned (n = 18 bins; see ref. 14). The mean amplitude M(j)_mean of x_fa(t) is then calculated over each phase bin j. Finally, each M(j)_mean bin is normalized by the mean of all M_mean, yielding the distribution P(j).

The null hypothesis of the test is that the expected amplitude distribution is uniform. The Kullbeck–Leiber distance (D) is as follows:

$$D\left(P\mathrm{,}Q\right)\mathrm{=}{\displaystyle \sum _{j\mathrm{=}1}^{N}P\left(j\right)\mathrm{\cdot }\log \left(\frac{P\left(j\right)}{Q\left(j\right)}\right)},$$ [S1]

where distribution P is the observed amplitude distribution, distribution Q is the uniform distribution, and N is the number of samples. The MI is the normalized KL distance:

$$MI\mathrm{=}\frac{D\left(P\mathrm{,}Q\right)}{\log \left(N\right)}.$$ [S2]

Analysis of Cross-Frequency Interactions Using the Weighted Phase Locking Factor.

The wPLF is an inner product of the complex signals x_fp(t) and x_fa(t) (47). Its magnitude indexes the strength of P–A correlation, whereas its phase indexes the preferred phase of high-frequency activity (47). Each signal is mean centered (mean amplitude over the signal subtracted from each entry) and normalized. The magnitude of the derived high-frequency signal A(t) is taken, resulting in a real-valued signal, whereas the low-frequency P(t) derived signal remains complex valued. The wPLF is then as follows:

$$wPLF=\hspace{0.17em}<A\left(t\right),P\left(t\right)>.$$ [S3]

Testing for Changes in Cross-Frequency Correlation.

Across the population of LFP–LFP recording pairs, we compared cross-frequency correlation in the 500 ms before attention cue onset (“precue”) to the 500 ms in the post-attention cue period (“postcue”) (Figs. 1 and 2). The pairwise difference in P–A correlation was normalized such that:

$$\mathrm{dCFC}\mathrm{=}\frac{\mathit{CF}{\mathit{C}}_{\mathit{post}}\mathrm{-}\mathit{CF}{\mathit{C}}_{\mathit{pre}}}{\mathit{CF}{\mathit{C}}_{\mathit{post}}\mathrm{+}\mathit{CF}{\mathit{C}}_{\mathit{pre}}},$$ [S4]

where CFC is the cross-frequency correlation as measured using the MI or wPLF (see above).

We tested the significance of the change in P–A correlation across the population of LFPs by applying a Wilcoxon sign-rank test for each phase-to-amplitude frequency combination (α = 0.05), corrected for the false discovery rate (FDR) using the Bonferroni–Holm method. Analysis was performed separately for correct and error trials.

Statistical Surrogate Analysis of Single LFP Pair Cross-Frequency Correlation.

We further analyzed cross-frequency correlation by selecting LFP pairs that showed a significant change in P–A correlation, as determined by a surrogate shuffling method. To this end, a surrogate high-frequency signal was derived by offsetting x_fa(t) by a random, large amount (in other words, by splicing the signal in two). This procedure was repeated 200 times, which allowed the derivation of a P value. Because the wPLF has the potential to be biased by power in the low-frequency band, we used the MI to select significant channels. All subsequent analysis (regarding preferred phase and anatomical specificity) was conducted on those LFP pairs that individually showed a significant increase in P–A correlation.

Temporal Specificity of Theta–Gamma P–A Correlation.

We determined the time of maximal (peak) P–A correlation by calculating the MI in 500-ms windows analyzed every 100 ms, first in the 500-ms precue period and subsequently every 100 ms from 0 to 1,000 ms (seven windows total; Fig. 2E). MI values were masked to a value of zero if they did not achieve statistical significance, and averaged in the LFPs in the P–A correlated frequencies of interest determined earlier.

Controlling for Differences in Trial Number Between Correct and Error Trials.

On average, there were less error trials than correct trials. To control for a bias related to the different number of trials, we used a shuffling procedure whereby for each LFP pair identified above, we selected at random the same number of correct trials as there were error trials. This procedure was repeated 1,000 times, from which we built a distribution of shuffled MI values. We then compared the observed difference in MI on error trials (Eq. S4) with the distribution of shuffled MI difference values from correct trials for the pair of P-A–correlated frequencies identified in the previous analysis. We also tested whether the MI across different LFP pairs was higher on each distribution of error-matched correct trials vs. error trials (Wilcoxon sign-rank test, 1,000 surrogates).

Analysis of the Low-Frequency Phases of Gamma-Frequency Correlation.

The MI allowed determining the preferred phase by finding the circular average of the phase bins, weighted by the amplitude probability in each phase bin. Circular statistics were performed using the CircStats toolbox (48). We determined the circular distribution of the mean preferred phases of the LFPs channels with significant theta–gamma P–A correlation for both correct and error trials, and used the nonparametric Hodjes–Ajne test to determine whether these distributions differed significantly from a uniform angular distribution. We also tested whether two distributions differed from one another via the Kuiper test.

If there would exist multiple preferred coupling phases, the MI amplitude distribution would be multimodal. In such a case, it may be that the mean preferred phase is in fact a trough of the amplitude distribution. To control for the effects of multimodality, we extracted preferred phases by finding the mean phase of peaks in the amplitude distribution. A bin was considered a peak if it was higher than a set threshold of the difference between the global maximum and minimum of the amplitude distribution (threshold = 100%, 80%, 70%, 50%). We assessed uniformity using the Hodjes–Ajne test, and similarity between distributions using the Kuiper test.

We repeated the analysis of preferred phase of the amplitude distribution after equalizing the number of correct trials to that of error trials. Multiple surrogates were thus created. For each LFP pair, we took the circular average of phases across surrogates. Where the number of correct trials was less than the number of error trials, we used the observed preferred phase in lieu of the average across surrogates. All subsequent analysis (of the preferred phase, uniformity, and comparison with error trials) mirrored the analysis described above.

As mentioned previously, the phase of the wPLF is the mean preferred phase of high-frequency activity. We also determined the distribution of preferred phases and their similarity to the preferred phase distributions described above via the Hodjes–Ajne and Kuiper tests.

The summary of the results using different phase extraction methods is shown in Table S1.

Anatomical Specificity of Theta–Gamma P–A Correlation.

We used adjacency matrices to visualize the anatomical specificity of theta–gamma P–A correlation (Fig. 4 A and B). The x axis (y axis) corresponds to the areas where channels from which the low-frequency phase information (high-frequency amplitude information) were derived. Because there are a different number of recorded channels in each area, we report on the proportion of channels exhibiting theta–gamma P–A correlation for each area combination using statistical analyses outlined by Zar (49).

We assessed whether the global distribution of P-A–correlated channels was independent of anatomical recording location via a χ² test on a 3 × 3 × 2 contingency table crossing location of phase LFPs with location of amplitude LFPs with the LFP pairs’ status of coupling (i.e., was significant theta–gamma correlation found?; Fig. 4). We used a Z score with a Yates correction for continuity for each individual area pair. Z scores were assessed at a significance of α = 0.05 (corresponding to a Z score of 1.96).

We also asked whether a particular subarea within the ACC/PFC was more likely to contribute phase or amplitude information for the interareal P–A correlations. To this end, we found the number N(t,a) of all channels where either the phase or amplitude channel came from a particular area:

$$N\left(t\mathrm{,}a\right)\mathrm{=}{\displaystyle \sum _i^n{\displaystyle \sum _j^n{m}_{i\mathrm{,}j}}},$$ [S5]

where N is the number of type t = {amplitude, phase} channels found in area a = {1, …, n} during theta–gamma P–A correlation, and n is the number of areas. The matrix m is an adjacency matrix indexing the number of LFP pairs per area combination (as described above). When considering either phase or amplitude channels, i or j remains constant, respectively, and is equal to a. In other words, we sum across a column or row of matrix m, depending on whether we are concerned with phase- or amplitude-providing LFPs. Because we considered only interareal P–A correlation in this analysis, we ignored entries where i = j = a. Finally, the likelihood P(t,a) that a particular area is more likely to contribute phase or amplitude information during interareal P–A correlation is as follows:

$$P\left(t\mathrm{,}a\right)\mathrm{=}\frac{N_{couple}\left(t\mathrm{,}a\right)}{N_{all}\left(t\mathrm{,}a\right)},$$ [S6]

where the subscript “couple” refers to LFP pairs that exhibited significant P–A correlation, and “all” refers to all recorded LFP pairs (Fig. 4D).

As a first step, we determined whether the distribution of phase or amplitude channels across all recorded areas is significantly different than expected using a χ² test. Second, we asked whether the difference in the proportion of the observed amplitude or phase channels was significant for a particular area. Because channels in an area are not independent, we used the Mcnemar test on a 2 × 2 contingency table, crossing the kind of information the LFP contributed during theta–gamma P–A correlation (i.e., did the LFP contribute phase information, yes/no? amplitude information, yes/no?). We performed the test using the mcnemar.m function available at www.mathworks.com/matlabcentral/fileexchange/15472-mcnemar-est. Finally, we assessed whether the individual observed frequencies of amplitude or phase information donation during P–A correlation across all recorded areas was different from expected by chance using a Z-score test.

Relation of Maximal Gamma Amplitude to Cue Onset Time and Low-Frequency Phase.

We compared the variability (i.e., jitter) of the peak in the gamma envelope relative to the cue onset time and relative to the phase of the theta-frequency band (10). We extracted the peak in the gamma (40-Hz–filtered)-amplitude envelope and recorded the time from cue onset as well as the concurrent phase in the theta-frequency signal. We then computed the variance of the time, and the circular variance of the phase. The phase variance was converted to milliseconds, which allowed a direct comparison between the time and phase.

Relation of P–A Correlation to Changes in LFP Power.

We assessed whether the P–A theta–gamma correlation we identified was related to LFP power. To this end, we first calculated the power for individual trials by squaring the amplitude envelope (derived from the Hilbert transform) in the epoch of interest, and summing in the 500 ms precue and postcue epoch individually. We then took the average power across trials in low- and high-frequency ranges and correlated this with the MI from LFP channels showing P–A correlations using the Spearman rank correlation.

Relation of P–A Correlation to Theta Phase.

We assessed the phase consistency across trials for unique channels from which the theta signal (and subsequent phase data) was taken. For each channel, the instantaneous mean angle of either correct or error trials was determined using the circ_mean function across trials (48). Statistical significance of phase consistency was determined by taking the instantaneous Rayleigh Z score and associated P value using the circ_rtest function (48). These data were used to assess the temporal latency of maximal phase consistency. First, we determined the proportion of phase channels that showed a significant Rayleigh Z score for each point in time (Fig. 5B, Left). Second, we divided the −500- to 500-ms time-resolved Rayleigh’s Z data into 10 equally spaced time bins. For each phase channel, we recorded the time in which the peak Rayleigh Z value occurred (Fig. 5B, Right). In this way, we generated a proportion of channels that peak within a particular time bin, allowing us to perform a χ² test to determine whether the distribution of Rayleigh Z peaks in time is significantly different from the null hypothesis that the distribution is uniform. Finally, we determined which phase channels showed phase consistency 100- to 300-ms postcue (as determined from the prior analysis) at P < 0.05 to locate them on the cortical sheet (Fig. 5C).

Relation of P–A Correlation to the Average Field Potential.

We determined the average LFP potential aligned to the attention cue onset using the fieldtrip function ft_timelockanalysis on correct trials and on error trials separately for all phase- or amplitude-providing LFPs. The average field potential was plotted in relation to the cue onset time.

We then used the behavioral outcome as a way to dissociate the influence of the average field potential on attention processing, using cluster-level analysis reviewed by Maris and Oostenveld (50). Briefly, a time-resolved t test was performed across average cue-aligned field potentials for individual phase- or amplitude-LFPs between correct and error trials. We then determined temporal clusters of interest by summing the t value for adjacent time points with a similar sign that showed a significant (P < 0.05) difference. Statistical reliability was determined by a Monte Carlo surrogate test. Average field potentials of different phase- or amplitude-channels associated with either correct or error trials were shuffled, and then surrogate correct and error sets were reconstructed by randomly sampling from the pool, and the cluster statistic recalculated. A cluster was deemed significant if its value was greater than 95% of permuted clusters (i.e., P < 0.05). The analysis was run on a temporal window spanning −700 to +500 ms (aligned to attention cue onset), as determined by a visual inspection of the average field potential.

Relation of P–A Correlation to LFP Phase Synchronization.

We next determined the degree of phase synchronization across theta–gamma P-A–correlated LFPs, and whether they were related to either the degree of P–A correlation or to the cue-triggered LFP phase reset. We determined phase synchronization with the debiased weighted phase lag index (wPLI) (25) using the FieldTrip toolbox. (Note that this is not related to the “weighted phase-locking factor” described above.) This measure is sensitive to noise and volume-conduction effects, and also corrects for the positive bias the wPLI has for small sample size. We will refer to the debiased wPLI as the wPLI in this text.

We calculated the wPLI for both correct (Fig. S6A) and error trials (Fig. S6B) in the 85 theta–gamma P–A correlation channels we identified across a wide range of frequencies. To compare them to the MI values we obtained, we restricted wPLI time of interest to the 500 ms before and after attention cue onset.

We determined, independently for each behavioral outcome and temporal epoch, whether the wPLI was significantly different from 0 with Wilcoxon sign-rank test. To determine whether there was a change in wPLI after attention cue onset, we used a Wilcoxon sign-rank test for paired samples. Tests were significant if P < 0.05, after the Bonferroni–Holm correction for the FDR.

To compare the phase synchronization to P–A correlation, we restricted further phase synchrony analysis to the same frequency range as determined by the P–A correlation analysis. We tested for a difference in wPLI across behavioral outcomes with a Wilcoxon signed-rank test for paired samples, independently for the precue and postcue epoch. We also correlated the MI with the wPLI using Spearman rank correlation. Finally, to draw a link between the phase-resetting LFPs and phase coupling, we correlated wPLI in the postcue epoch, and then highlighted those data points where the phase-donating LFP showed a significant phase reset in the 100–300 ms postcue (Fig. S6C).

Dissociating Value and Spatial Information Contribution to Theta–Gamma P–A Correlation.

It may be the case that cross-frequency correlation is selective for ipsilateral or contralateral shifts of attention. By the same token, shifting attention to a target stimulus with a higher or lower associated reward may influence the strength of theta–gamma cross-frequency correlation. We thus tested whether we could find evidence whether cross-frequency correlation shows spatial selectivity or selectivity for the relative reward magnitude associated with targets.

As a first step, we calculated the normalized change in theta–gamma P–A correlation (quantified using the MI; Eq. S4) from pre- to post-attention cue separately for contralateral vs. ipsilateral conditions, or high vs. low rewarded targets. We tested whether the average change in theta–gamma P–A correlation change across all LFP pairs could dissociate between two separate attention conditions via a Wilcoxon sign-rank test. This was performed across the entire population of LFP pairs, and across those n = 85 LFP pairs that showed individually significant increases in theta–gamma P–A correlation (unless stated otherwise).

As a second analysis approach, we tested whether theta–gamma P–A correlation of individual LFP pairs is selective for attention conditions. We assessed this via a Monte Carlo surrogate test. First, the change in theta–gamma P–A correlation as indexed using the MI (dMI; Eq. S4) was calculated for two attention conditions separately (e.g., dMI_contra vs. dMI_ips). Next, we calculated the difference across the conditions. For spatial conditions, we used the following:

$$D_{spatial}=dM{I}_{contra}-dM{I}_{ips},$$ [S7]

whereas for value conditions we used the following:

$$D_{reward}=dM{I}_{high}-dM{I}_{low}.$$ [S8]

For example, positive value of D_spatial (>0) indexes a relative increase in theta–gamma correlation when the cue shifts attention contralaterally, whereas negative (<0) values reflect a relative increase in theta–gamma correlation with attention ipsilateral to the recording site.

To assess significance, we shuffled the trial labels, and recalculated D′. This procedure was repeated 200 times, and the observed D was compared against the distribution of D′. Finally, we determined whether LFP pairs informative of correct attentional deployment overlapped with LFP pair informative of ipsilateral or contralateral attention, or of high- vs. low-reward magnitude. We determined LFP pairs that individually differentiated between two conditions via the change in MI in the previous analysis, and compared these to those comprising the functional network analyzed in the main text.

Quantifying Attention Information in the Firing Rate of Recorded Neurons.

Firing rate at LFP sites engaged in cross-frequency correlation may be different from those sites that are not thus engaged. To test for this possibility, we extracted the firing rate of neurons from those electrodes that provided either LFP phase or LFP amplitude information in the theta–gamma P–A correlation analysis. We tested for a difference between firing rate in the postcue epoch in the theta–gamma paired sites and all others via a Wilcoxon rank test. Likewise, we used the same test but on the change in firing rate after cue onset compared with before onset. We determined whether there was a more subtle relationship between absolute MI and firing rate, or the change in MI and firing rate, by computing Spearman R correlations.

We quantified attention selective modulation of firing by computing the normalized difference in firing when attention shifted contralateral vs. ipsilateral:

$$A{I}_{rate}\mathrm{=}\frac{firin{g}_{contra}\mathrm{-}firin{g}_{ips}}{firin{g}_{contra}\mathrm{+}firin{g}_{ips}}.$$ [S9]

The AI_rate is positive when firing was larger with contralateral than ipsilateral attention shifts, and negative when the firing was larger for ipsilateral attention trials. We quantified attention modulation in theta–gamma correlation in the same way as the firing rate by indexing the strength of theta–gamma correlation during contralateral vs. ipsilateral attention shift in the same 0.5-s postcue time window as the firing-rate modulation. Additionally, we also quantified spatially specific changes in theta–gamma correlation as we have done in the main analysis. We thus calculated the change from theta–gamma correlation form the precue interval to the postcue interval separately for the condition when the cue indicated a contralateral or an ipsilateral shift (Eq. S4). We then contrasted this attention cue-specific change in theta–gamma correlation between attention conditions (Eq. S7).

Comparison of Theta–Gamma Correlation of LFP–LFP Pairs with the Strength of Burst–LFP Synchronization.

We tested whether the strength of theta–gamma LFP–LFP correlation is related to the strength of burst–LFP synchronization following procedures outlined in ref. 12 and described in brief below. To test for this, we performed the following analysis steps.

First, we selected for analysis those single isolated neurons that showed within either 0.5 s before or 0.5 s after the attention cue onset at least n = 30 burst spike events across all trials where monkeys shifted attention either contralaterally or ipsilaterally. Burst spike events were defined (as before) as spike successions with ≤5-ms interspike intervals. Spike recording techniques are described in detail in ref. 12.

Second, we calculated burst–LFP synchronization for all electrode combinations at which we recorded LFPs for the theta–gamma P–A correlation analysis. Analysis was restricted to burst–LFP recording pairs from different (spatially distant) recording sites. To quantify the strength of burst–LFP synchronization, we followed the procedure described in detail in ref. 12. In brief, we selected for all burst events the first spike of the burst and calculated how phase consistent these burst spikes were to the LFP at the three frequencies described above (theta: 5–10 Hz; low beta: 15–25 Hz; mid-gamma: 55–75 Hz). LFP phases were obtained by Hanning-tapered fast Fourier transforms of the LFP in a time window ±0.25 s around the time of the first burst spike. We indexed the synchronization of burst spikes to the phase of theta/low-beta/mid-gamma frequencies using the pairwise phase consistency, which is a measure that is unbiased with regard to the number of observations (i.e., not biased by the number of spike events; see ref. 23).

Third, we sorted the burst–LFP pairs into different conditions based on whether the electrode providing the burst firing neurons was the same as the theta LFP-phase–providing channel, or the gamma-amplitude–providing channel, or whether the LFP channel that was paired with the burst firing neutron channel was the same as the theta- or gamma-providing channel (see Table S2 for the complete matrix of conditions). For each condition, we then obtained the Spearman rank correlation coefficients between burst–LFP synchronization and theta–gamma LFP–LFP correlation, which we report in Table S2.

SI Results

SI Result S1. Results of LFP–LFP Pairs from Individual Monkeys.

For all primary results reported in the main text, the LFP–LFP pairs were pooled from the individual monkeys. To ensure that the pooled results are qualitatively evident also in LFP–LFP pairs recorded from individual monkeys, we performed all analyses steps separately for each monkey’s LFP–LFP pairs and report the results below in the same succession as they are mentioned in the main text.

In summary, all primary results were qualitatively replicated for each monkey (points S1.1–S1.4), and the majority of secondary (or control) results (points S1.5–S1.9) likewise were replicated in individual monkeys.

Primary results.

S1.1. Theta–gamma correlation on correct and error trials.

• Our main results show that (7-Hz) theta-phase to (∼40-Hz) gamma-amplitude correlations between distant LFP pairs significantly increased after the attention cue onset on correct trials (Fig. 2A). We found this theta–gamma correlation to significantly increase in 85 LFP pairs (7.7% of all LFP pairs) that were coming from both animals proportional to their overall number of LFP pairs. In monkey M, 31 of 446 LFP pairs (7.0%), and in monkey R, 54 of 658 LFP pairs (8.2%) showed significant theta–gamma correlation from pre- to post-attention cue. The overall significant increase in theta–gamma correlation across the restricted population of LFP pairs for individual monkeys was statistically significant for pairs of monkey R (P = 0.0045, FDR corrected), but did not reach significance across the smaller sample of n = 31 LFP pairs of monkey M (P = 1, FDR corrected).

• Compared with the increased theta–gamma correlations, we found that a smaller total number of LFP pairs (n = 46; 4.2%) showed individually significant decreases in the theta–gamma correlations from the pre- to post-attention cue periods. This decrease was evident in 15 LFP pairs (of 446 pairs; 3.4%) in monkey M and in 31 LFP pairs (of 658 pairs; 4.7%) in monkey R.

• We found on average no (7-Hz) theta-to-(∼40-Hz) gamma correlation on error trials (Fig. 2C). In line with this average finding, there was no consistent increase in theta–gamma correlation on error trials in either monkey R (P = 1, FDR corrected), nor in monkey M (P = 0.63, FDR corrected).

S1.2. Theta-phase preferences for gamma-amplitude modulation.

• Pooled data showed that gamma correlations were evident in correct trials on average at theta phases around −14.69°, 95% CI [−41.01°, 11.63°] (Fig. 3A). The average phase on correct trials was similar in both animals: monkey R’s average phase on correct trials was −24.93°, 95% CI [−48.60° −1.26°]. Monkey M’s average phase on correct trials was −32.33°, 95% CI [−57.67° −122.33°]. The phase distributions were significantly different from nonuniformity for the pooled data and for monkey R phases (P = 0.00017), but not for monkey M’s phase distribution (P = 0.45).

• Compared with correct trials, the theta phases of the gamma-amplitude modulations on error trials were more variable and shifted to more negative phases with an average theta phase for the pooled data of −94.28°, 95% CI [−131.40°, −57.16°] (Fig. 3B). A similar shift in mean phase was evident in monkey R (−97.61°, 95% CI [−144.06° −51.17°]) and in monkey M (−87.27, 95% CI [−177.27°, 2.73°]). Similar to the pooled distribution, none of the phase distributions on error trials from individual monkeys were significantly different from a random distribution (Hodjes–Ajne test, all P > 0.05).

S1.3. Anatomical distribution of theta–gamma correlation.

• For the pooled n = 85 significant LFP pairs, we found that LFP theta-phase–providing channels showed a preference for the ACC, and LFP gamma-amplitude–providing channels showed a preference for the LPFC, respectively (Fig. 4D). We separately quantified the anatomical origins of phase- and amplitude-providing channels for n = 51 and n = 31 LFP pairs with significant theta–gamma correlations for monkey R and monkey M, respectively, as the proportion of significant pairs relative to all recorded LFP pairs. We found the same trend in each of the monkeys. Both monkeys showed more theta-phase–providing channels in ACC than in LPFC (monkey R: 9% in ACC vs. 3.5% in LPFC; monkey M: 9.7% in ACC vs. 3.2% in LPFC). Similarly, both monkeys showed more gamma-amplitude–providing LFPs in LPFC than in the ACC (monkey R: 5.9% in LPFC vs. 3.0% in ACC; monkey M: 10.5% in LPFC vs. 3.2% in lateral ACC). For vmPFC, the proportion of significant LFP pairs ranged from 4.6% to 10.7% between monkeys and phase/amplitude LFP channel comparisons.

S1.4. Analysis of theta-phase reset.

• We found that, for a significant proportion of LFPs that showed theta–gamma P–A correlation increases during the attention shift period, the theta phases became more phase consistent across trials in the postcue period on correct trials, but not on error trials (Fig. 5D). A similar result pattern was found in each monkey separately. In monkey R, 70% (35 of 50) of the LFPs that donated theta to significant theta–gamma P–A correlation showed peak theta-phase consistency in the (0.5-s) postcue period compared with the (0.5-s) precue period on correct trials, whereas there were less peaks in the postcue period (30%; 15 of 50) on error trials. In monkey M, 75% (16 of 24) of the LFPs showed peak theta-phase consistency in the postcue period on correct trials, whereas only 25% (8 of 24) showed maximum phase consistency in the postcue period on error trials. The difference in proportions between precue and postcue period was significant in both monkeys on correct trials (P < 0.015) but not error trials (P > 0.2).

Secondary results and results from control analysis.

S1.5. Analysis of LFP power.

• In our pooled analysis, we found that peaks in the LFP power spectra were evident in the theta-frequency band in 73% of LFPs that engaged in P–A correlations, and that power modulations did not correlate with theta–gamma P–A correlation changes (SI Result S3). Both of these pooled findings were evident at the single-monkey level. Monkeys M and R showed a median theta-power peak (within ∼5.5–8.5 Hz) of those LFPs that engaged in P–A correlations. In neither monkey did theta-band power change from precue to postcue and thus did not correlate with the functional theta–gamma correlation increase (Spearman rank correlation, in either phase- or amplitude-providing LFPs, P > 0.20).

S1.6. Average cue-aligned field effects.

• Similar to the pooled LFP average field effect, the LFP average field in each monkey showed no significant difference between the pattern of activation on correct trials, or on error trials (Monte Carlo surrogate test, all P > 0.05). Average pericue field potentials therefore cannot account for the functional precue to postcue changes we observe.

S1.7. Theta-frequency phase coherence analysis.

• We found for the pooled data that theta-band phase coherence between areas in PFC did not change from precue to postcue and was not different in correct vs. error trials (SI Result S10). The same results were found in each monkey. Both monkey’s had a spectral peak of coherence at ∼7 Hz (P < 0.05 in monkey R, but P > 0.05 in monkey M, FDR corrected), but this coherence did not change significantly from before to after attention cue onset.

S1.8. Temporal jitter of gamma-amplitude phase to theta vs. cue onset time.

• Similar to the pooled results (SI Result S4), in both monkeys, the gamma peaks aligned more consistently to the phase of theta, rather than to the attention cue onset (monkey R: 47 of 54 LFP pairs, 87%; monkey M: 30 of 31 LFP pairs, 97%).

S1.9. Comparison of trial number matched correct and error trials.

• In pooling data across monkeys, we found that correct trial MI changes were reliably higher than error trial MI changes (Monte Carlo surrogate test, evident in 968 of 1,000 surrogates), when reducing the number of correct trials to that of error trials. Similar results were evident in each monkey independently. In both, the distribution of MI changes on correct trials was higher on average than the distribution of error MI changes (R: 54 LFP pairs = 767 of 1,000 surrogates showed this trend; M: 31 LFP pairs = 770 of 1,000 surrogates showed this trend).

SI Result S2. Behavioral Analysis.

Both animals performed the task at accuracy levels well above chance (R = 78.9 ± 0.9% SE; M = 86.7 ± 0.6% SE) across all (80/73 in monkey R/M) behavioral sessions of the monkeys. This definition of accuracy takes into account all correctly performed trials. On the other hand, errors were defined as all other trials in which the animal maintained fixation on the central fixation point at least until the time of the cue onset. Thus, errors were committed during or after the selective attention period of the task.

Considering all these trials, both monkeys committed only 3.9/5.1% of errors during the 0.55 s following a rotation of distractors (i.e., false-positive errors) (R = 3.9 ± 0.2% SE; M = 5.1 ± 0.3% SE). Erroneous fixation breaks during the 0.55 s after rotation of the cued target stimulus occurred in monkey R at 4.1 ± 0.2% SE, and for monkey M at 1.3 ± 0.1% SE. Incorrect saccadic responses to the rotation of the target stimulus occurred 3.4 ± 0.2% SE of the time for monkey R and 0.8 ± 0.1% SE for monkey M. Responses that were late or did not occur after 0.55 s after the rotation onset occurred for monkey R at 8.3 ± 0.6% SE and for monkey M at 1.3 ± 0.2% SE. The remainder of error trials were fixation breaks between cue onset and onset of the first rotation (either of the distractor or the target stimulus).

Across experimental sessions, overall accuracy levels were higher for ipsilateral (left) than contralateral (right) cued target trials in monkey R (t test, ipsilateral: 83.6 ± 0.7% SE; contralateral: R = 75.2 ± 1.2% SE, P < 0.001, t test). Monkey M showed similar accuracy for ipsilaterally than contralaterally cued target trials and thus did not exhibit a bias (t test, ipsilateral: M = 86.5 ± 0.6% SE; contralateral: M= 87.2 ± 0.8% SE; P = 0.511, respectively).

For the majority of sessions (70 of 80 sessions of monkey R, and 70 of 73 sessions of monkey M), attentional targets were differentially rewarded with 0.76 mL vs. 0.4 mL. In these sessions, monkeys performed at high, above chance for both conditions, i.e., when cued to the higher rewarded target (R = 79.3%, SE = 1.1; M = 89.0%, SE = 0.7), and when cued to the lower rewarded target (R = 79.5 ± 1.0% SE; M = 85.4 ± 0.7% SE) with false-alarm rates (responses during the distractor rotations) between 3.3% and 5.7% of all trials (for higher rewarded target trials: R = 3.3 ± 0.2% SE, M = 3.7 ± 0.3% SE; for lower rewarded target trials: R = 3.4 ± 0.2% SE, M = 5.7 ± 0.4% SE). For monkey R, the overall performance for high and low rewarded trials were statistically not different (t test, P = 0.858), whereas for monkey M accuracy was higher across sessions in trials that cued attention to high vs. lower rewarded target stimuli (t test, P = 0.0004).

SI Result S3. Analysis of LFP Pairs Showing Significantly Reduced Theta–Gamma Correlation Following Attention Cue Onset.

The main population effect was an increase in theta–gamma correlation in the postcue compared with the precue epoch (Fig. 2 A and B). In the main text, we characterized how the n = 85 (7.7%) LFP pairs with an individually significant theta–gamma increase in the postcue period evolve over time and in anatomical space. Despite the overall positive effect at the population level, we also found a subset of n = 46 LFP pairs (4.2% of total pairs) that showed a significant reduction of theta–gamma correlation in the postcue compared with the precue period when tested at the individual LFP pair level. We therefore asked whether these LFP pairs were also modulated on error trials and whether they showed an anatomically distribution in ACC/PFC that was comparable to the LFP pairs with significant enhanced theta–gamma correlation.

First, we found that none of the LFP pairs with significantly reduced theta–gamma correlation on correct trials showed a significant reduction from precue to postcue on error trials. This finding could be due to lower cross-frequency correlation in the precue period on error compared with correct trials, or it can be due to continuously enhanced cross-frequency correlation in the postcue period on error trials, or a combination of both. We found that on error trials these LFP pairs did not show significant theta–gamma correlation (P > 0.05) in the precue period, revealing that the lack of reduction was dominated by already lower correlation before the cue.

Second, we next analyzed the anatomical distribution of LFP pairs showing significantly reduced theta–gamma correlations (similar to Fig. 4). We found that there was no anatomical specificity of the distribution of LFP phase-providing channels and LFP amplitude-providing channels for these n = 46 LFP pairs with only one exception: There was a significant smaller than expected number of phase–amplitude LFP pairs with reduced theta–gamma correlations from vmPFC to ACC than would be expected by chance. These anatomical results suggest that LFP pairs with theta–gamma decorrelations were anatomically segregated from those LFP pairs showing increased theta–gamma correlations.

Taken together, these results suggest that LFP pairs showing a reduced cross-frequency correlation after the attention cue onset may constitute a phenomenon that relates to a decoupling of local brain circuits that are not engaged in actual attentional stimulus selection.

SI Result S4. Relation of Cross-Frequency Correlations to LFP Power Modulation at Theta- and Gamma-Frequency Bands.

We tested for a relationship between theta–gamma correlation and overall power modulation after observing apparent theta-band peaks in the power spectra but no overall gamma-band peak across theta–gamma P-A–correlated channels (Fig. S5). Of the LFP pairs with significant theta–gamma correlations, we found that 73% (50 of 74) of the unique phase-modulating LFPs showed theta (4–9 Hz) peaks of individual power spectra. The difference in MI from pre- to post-attention cue did not correlate with the change in overall power in either the phase-providing, or the amplitude-providing LFPs, which showed significant P–A correlations after the attention cue. However, in the gamma-amplitude–providing LFPs in these LFP pairs, the strength of postcue MI correlated with gamma power on correct trials (at 40 Hz, r = 0.22, P = 0.0.048; Spearman rank correlation).

SI Result S5. Relation of Gamma-Amplitude Variations to the Time of Cue Onset vs. the Phase of Remote Theta-Band Fluctuations.

We validated that the high-frequency gamma amplitude more precisely locked to the theta-band phase of a distant recording sites than to the time of attention cue onset. If gamma amplitudes lock more precisely to cue onset, then this would suggest that the cross-frequency correlation effect is secondary to a cue-triggered gamma response at some neuronal recording site (10). We evaluated this scenario by quantifying (i) the variance across trials of the time difference between cue onset and the time of the maximum amplitude of the high-frequency gamma component and (ii) the jitter (variance) of the phase of the theta-frequency component at the time of the maximum amplitude of the high-frequency gamma component. We compared the two types of variance of the gamma amplitude across LFP–LFP pairs. We found that the gamma amplitudes were more precisely locked (i.e., showed less variance) to the phase of the theta-band modulation than to the attention cue onset. On average, across the 85 LFP pairs that showed significant P–A correlation, 90.6% of LFP pairs showed maximum gamma amplitudes that were more precisely locked to theta phase than to cue onset (Fig. S3C). This finding supports the conclusion that the gamma LFP events were tightly linked to the theta phases measured at distant electrodes, rather than constituting statistically independent or only spuriously linked events.

SI Result S6. Equalizing the Number of Correct and Error Trials Using a Randomization Approach.

We ran a shuffling procedure with 1,000 surrogates and recalculated the normalized difference in MI for theta–gamma correlation using the same number of correct trials as error trials to determine any trial-number related bias in cross-frequency correlation.

We first quantified the population-level comparison of error and correct theta–gamma correlations (across the 84 of 85 LFP pairs that had more trials in correct than error trials) for each surrogate of correct trials against the observed error MI values (1,000 Wilcoxon one-tailed signrank tests in total). We found that the difference in precue to postcue change in theta–gamma correlation on correct trials was significantly (P < 0.05) higher than the corresponding change in error trials in 968 of 1,000 (96.8%) of surrogates. In other words, the increase in P–A correlation found on correct, but not error trials is highly reliable when controlling for the number of trials. Moreover, we quantified for each LFP pair how often correct shuffled MIs were higher than the observed error MIs when equating the number of trials. We found that, on average across LFP pairs, 64 ± 3.1% SE of correct shuffled MIs were higher than the observed error MIs.

We next corroborated the phase preference evident during theta–gamma correlation on correct trials after equalizing for the number of error trials. To this end, we took the average phase for individual LFP pairs and calculated the preferred phase as before. We found that the distribution of preferred phases of the trial-equated shuffled amplitude distributions (mean phase of −14.03°, 95% CI [−40.26°, 12.20°]) was the same as the observed amplitude distribution, deviated from uniformity (Hodjes–Ajne test, P = 0.00036), and was dissimilar to the error amplitude distribution (Kuiper test, P < 0.005).

SI Result S7. Accounting for Differences of Overall Modulation Strength of Correct and Error Trials on Phase Preference.

The main text describes the preferred phase analysis based on the MI. We repeated the phase analysis with another metric that weights the low-frequency phase alignment of high-frequency activity by overall modulation strength (47). The phase analysis of the wPLF confirmed that correct and error phase distributions were significantly different from each other (Table S1). In addition, this analysis also showed that error trials were not associated with a statistically reliably preferred phase across LFP channels (Table S1). In contrast, the wPLF analysis confirmed that correct trials showed a nonuniform, preferred mean phase for theta–gamma correlation (Table S1). Control analysis of the peaks of the amplitude distribution also confirmed a statistically significant preferred phase of theta–gamma correlation on correct but not error trials (Table S1). Together with the results in SI Result S6 above, correct trials were characterized by high-frequency gamma-band activity that correlated with reliably similar phases across pairs of LFPs engaging in theta–gamma correlation.

SI Result S8. Testing for the Effect of the Average Field Potential to Explain the Difference of P–A Correlation in Correct vs. Error Trials.

We observed a pericue average LFP potential that was an evoked field from the stimulus color onset preceding the attention cue onset. We tested whether this nonstationary pericue event influenced the postcue enhanced theta–gamma correlation effect (10) and found that the average field was not different on correct vs. error trials for those LFPs that provided the phases or the amplitudes of the theta-gamma–correlated LFP pairs.

SI Result S9. Testing Global Distribution of Phase or Amplitude LFPs.

Despite the fact that all subareas contained phase- and amplitude-providing LFPs engaging in theta–gamma correlation (Fig. 3 B and C), the relative proportion of all theta–gamma P-A–correlated LFP pairs across vmPFC, ACC, and LPFC was not significantly different than expected by chance (Fig. 3C; χ² test with Yates correction, χ² =9.67, P = 0.65). Moreover, the relative proportion of interareal phase- and amplitude-providing LFPs showed a trend but was not different significantly from a uniform distribution (Fig. 3D; χ² test, χ² = 5.4, P = 0.067 and χ² = 4.93, P = 0.085, phase- and amplitude-providing LFPs, respectively).

SI Result S10. The Relation of Phase Synchronization, Phase Resetting, and P–A Correlation.

Gamma-amplitude modulation, and thus theta–gamma P–A correlation, in a target region may be the result of bidirectional theta-phase synchronization across regions. One possibility is that there is a large-scale phase reset across ACC/PFC subfields, which would align oscillations and result in large-scale theta-phase synchrony. However, we showed that the theta-phase reset is rather localized to the nexus of vmPFC, ACC, and LPFC (Fig. 4), which instead suggests that theta-phase synchronization may not necessarily spread across all ACC/PFC fields that show significant theta–gamma correlations. To address these considerations, we analyzed phase synchronization in the same LFP pairs that showed significant theta–gamma P–A correlation to describe the interaction between phase synchronization, P–A correlation, and phase resetting.

First, we quantified phase synchronization (using the wPLI), defined its temporal specificity, and determined its functional relevance. This measure removes artifactual coherence from volume conduction. There was significant phase coupling in the 4- to 7-Hz range and the 17- to 34-Hz range on correct trials in both the precue and postcue epochs (Fig. S6A; Wilcoxon sign-rank test, P < 0.05 for both, correct and error trials, FDR corrected). On error trials, peak phase coupling shifted from 25 Hz in the precue period to 21.5 Hz in the postcue period (Fig. S6B, Wilcoxon sign-rank test, P < 0.05 for both, correct and error trials, FDR corrected). Furthermore, there was no significant change in phase synchronization after attention cue onset at any of the frequencies considered (Wilcoxon sign rank test for paired samples, P > 0.05, FDR corrected).

Because we wanted to compare theta-phase synchronization with theta–gamma P–A correlation, we restricted further analysis to the theta-frequency phase. The wPLI did not significantly differ between correct and error trials in either the precue or postcue epochs (Wilcoxon sign-rank test for paired samples, P > 0.05), suggesting that in the network of LFP pairs we identified, theta-phase synchronization does not predict behavioral outcome.

We next determined the link between the cross-frequency P–A correlation and phase synchronization. We limited this correlation analysis to correct trials because both measures showed significant phase synchronization and theta–gamma correlations on these trials. We found a weakly negative, but significant correlation of the wPLI in the postcue epoch with theta–gamma P–A correlations (Spearman rank correlation, r = −0.22, P = 0.048). To test whether phase synchronization tended to decrease when P–A correlation increases, we compared the change in phase synchronization with the change in P–A correlation from precue to postcue, but found no correlation (Spearman rank correlation, R = 0.067, P = 0.54).

Finally, we tested for a possible link between phase synchronization and the phase reset we identified. We correlated the phase synchronization in the precue period and the postcue period. In line with the conclusion that phase synchronization did not change in time, we observed a positive correlation (Fig. S6C). We highlighted the LFP pairs where the phase channel showed a significant phase reset in the 150–250 (±50) ms after attention cue onset in the previous analysis. We note that the highlighted phase-resetting LFPs are broadly distributed among those LFP pairs that showed either weak or strong coupling.

In summary, the observed theta–gamma P–A correlation does not apparently relate to LFP–LFP theta-band phase synchronization. Phase synchronization neither tracks attention cue onset nor indexes the behavioral outcome. Moreover, the negative correlation with theta–gamma P–A correlation suggests that the two phenomena may be involved in different processes. In support of this, significant phase resets (associated with P–A correlation, but not phase coupling) occurred even when the network showed weak phase coupling.

SI Result S11. Selectivity of Theta–Gamma Correlation for the Attended Target Location or Reward Outcome Associated with the Target Location.

To quantify whether theta–gamma P–A correlations carried information about the location of the attentional target stimulus and about the reward outcome associated with the attended target stimulus, we performed two types of analysis (see Methods for details). First, we conducted a population-level analysis to discern the overall selectivity across LFP pairs. Second, we applied single-LFP pair statistics to infer how often selectivity is reliably (statistically significant) evident across trials of single LFP pairs.

S11.1. Selectivity for the location of the attended target stimulus.

First, at the population level, we found a trend for higher increases in theta–gamma correlation when attention was cued contralaterally vs. ipsilaterally (Fig. S7A, Left; Wilcoxon sign-rank test, P = 0.066). This statistical trend suggests that individual LFP pairs may carry significant spatial attention information in theta–gamma P–A correlation. We thus determined in a second step whether individual pairs showed a significant preference for the contralateral or ipsilateral attention conditions. We found 49 of 1,104 (4.4%) LFP pairs with a preference for a specific spatial location (Monte Carlo surrogate test, two-sided, P < 0.05). Among those 49 LFP pairs, n = 32 (65%) showed stronger theta–gamma correlation when attention shifted to a contralateral stimulus, whereas n = 17 (35%) showed stronger theta–gamma correlation for ipsilateral attention.

In the theta-gamma–correlated subnetwork (i.e., the n = 85 LFP pairs that showed significant theta–gamma correlation on correct trials), there was no statistically reliable, average difference in theta–gamma correlation between contralateral and ipsilateral attention (Fig. S7B, Left; Wilcoxon sign rank, P = 0.14). Considering the single-LFP pair statistics, we found that 5 of the 85 individual LFP pairs showed a significant preference for spatial allocation, as evidenced by the differential change in theta–gamma correlation between spatial conditions (Monte Carlo surrogate test, P < 0.05). In summary, these results suggest that theta–gamma correlation at the single LFP pair encodes spatially specific attention information in a small subset of LFP pairs (4.4%), but that a larger proportion of LFP pairs engage in theta–gamma correlation without apparent, single-LFP pair level selectivity for the spatial hemifield of the attentional target stimulus.

S11.2. Selectivity for the reward outcome associated with the attended target stimulus.

In the majority of experimental sessions, we manipulated the reward outcome associated with the cued attentional target stimulus by associating the color of the stimulus to higher or lower reward magnitude (Methods). This reward outcome association was not instrumental for solving the task (attention had to be shifted to the cued location irrespective of the associated reward magnitude), but it could influence the LFP activity during the attention shift period, similar to its influence on the firing rate of a subset of neurons (3).

To test for this, we calculated theta–gamma P–A correlations for trials where the cued target was associated with higher or lower reward outcome. Among 860 LFP pairs recorded in sessions with reward outcome manipulations, we found on average no difference in the change of the theta–gamma correlations when attention shifted to a higher or lower rewarded attentional target stimulus (Fig. S7A, Right; Wilcoxon sign-rank test, P = 0.40). At the level of the individual LFP pairs, 45 of 860 (5.2%) LFP pairs showed a statistically significant difference in theta–gamma P–A correlation for high vs. low targets (Monte Carlo surrogate test, P < 0.05), with 21 (47%) and 24 (53%) showing a greater increase on trials with attention to a lower and higher rewarded target, respectively.

These results were largely preserved when analyzed separately for those LFP pairs that showed a postcue increase in theta–gamma correlation on correct trials and that were recorded in experimental session with a reward outcome difference between attentional targets (n = 68 of the 85). The change in theta–gamma correlation was not different between higher- vs. lower-reward outcome conditions (Fig. S7B, Right; Wilcoxon sign rank, P = 0.78). Only 1 of these 68 LFP pairs showed a statistically reliable difference in the theta–gamma correlation between higher- vs. lower-reward outcome conditions (Monte Carlo surrogate test, P < 0.05). In summary, these results illustrate that a small subset of single LFP pairs engages in theta–gamma correlation significantly stronger when attention is deployed to a high (vs. low)-rewarded attentional target, and a similarly small subset engages in significantly stronger theta–gamma correlation with attention to a lower (vs. higher)-rewarded attentional target. Consistent with this result, there was no preference for higher- or lower-rewarded targets at the grand average population level.

Taken together, these results show that, for subsets of recorded LFP pairs, the strength of theta–gamma correlation provides statistically reliable information about task-relevant variables. This finding calls upon future studies to test specifically how theta–gamma correlation contributes to the encoding of task-relevant variables. These more specific tests may explicitly focus on those LFP recording sites in which variations in the LFP phase, or the LFP amplitude carry already specific information about task-relevant variables about, e.g., the location or expected reward magnitude. One possible result of these future analysis may be that theta–gamma P–A correlation emerges particularly for pairs of LFP recording sites that encode separable types of task-relevant information (including stimulus features and their spatial location, reward expectancies, or rule-based stimulus–response mapping rules) that is integrated or gated through theta–gamma correlation (9).

SI Result S12. The Relation of Theta–Gamma Correlations and Firing-Rate Modulation During Attention Shifts.

In previous analyses of the same ACC/PFC dataset, we have shown that neuronal spiking activity carries significant information about the target location to which attention is shifted (3). A large proportion of neurons increased firing when attention was shifted to a contralateral stimulus, whereas a slightly lower proportion of cells increased the firing when attention shifted ipsilaterally.

One possibility is that these firing-rate modulations at single recording sites are linked to cross-frequency correlations of the LFP at the same recording site. For example, if the theta phase of the LFP at a recording site couples with the gamma amplitude of a distant recording site during the attention shift, then this LFP phase-providing site may also have single neurons with firing-rate modulations about the direction of the attention shift. Similarly, if the LFP gamma amplitudes at one recording site couple to the phase of distant recording sites during the attention shift, then neurons at the gamma-amplitude–providing LFP site may also modulate their firing. In both these hypothetical scenarios, the overall strength of cross-frequency correlation could relate to the information in firing rates about the spatial location of attention during the postcue attention period.

We tested these scenarios by performing two broader analyses that we report in this section: first, we tested whether firing-rate information (e.g., larger firing rate for attend contralateral rather than for attend ipsilateral) is related to the overall strength of cross-frequency correlation of the LFP recorded at the recording site as the neuronal firing rates were recorded. This analysis rests on the assumption that the overall strength of theta–gamma correlation could be important for firing-rate increases and decreases.

Second, we tested whether actual differences in theta–gamma cross-frequency correlations between attention conditions (e.g., the strength of P–A correlation during attend contralateral compared with attend ipsilateral) relate to actual differences in firing-rate modulation in the attention conditions. This analysis is based on the assumption that recording sites with attention information about the direction of the attention shift in the firing rates (e.g., higher firing for contralateral shifts) may also show more likely LFPs that engage in interareal cross-frequency correlation. For example, if neuron firing is stronger for contralateral attention shifts, then the LFP theta phase or the LFP gamma amplitudes may be also stronger for contralateral attention shifts.

In a final analysis, we quantified the relation of attentional modulation of theta–gamma correlation with attention to a higher- vs. lower-rewarded target stimulus to the firing-rate modulation in both conditions.

S12.1. Relation of overall theta–gamma cross-frequency correlation with the degree of firing-rate information.

With regard to the first analysis, we extracted the firing of neurons from those electrodes that provided either LFP phase or LFP amplitude for theta–gamma P–A correlation analysis. Firing-rate information was quantified as the absolute z-normalized difference of neuronal firing when attention was shifted to a stimulus contralateral vs. ipsilateral from the recorded hemisphere. We used for this analysis the same 0.5-s time window after the attention cue onset in which theta–gamma correlations were calculated (see Methods for details).

We found that firing-rate information was not different for neurons recorded at recording sites that provided either the LFP phase or the LFP amplitude for significant theta–gamma correlation increases following the attention cue compared with recording sites that did not participate in significant theta–gamma correlation (Wilcoxon rank test on the differences in firing-rate information: P = 0.22 for the LFP phase channels, and P = 0.44 for the LFP amplitude channels; the average firing-rate Z score for sites with significant theta–gamma correlation: LFP phase channels: 1.12 ± 0.07 SE; for LFP amplitude channels: 1.11 ± 0.07 SE; the average firing-rate Z score for sites without theta–gamma correlation: LFP phase channels: 1.26 ± 0.03 SE; LFP amplitude channels showed identical results: 1.26 ± 0.03 SE). These results were consistent across monkeys with no significant effect when data from each monkey was tested separately (all P values ≥ 0.09).

We next repeated the previous analysis but considered not the absolute cross-frequencies correlation in the postcue epoch but whether the LFP site showed significant increases or decreases in P–A correlation from the precue to the postcue epoch. Similarly to the previous analysis, the firing-rate information was not different for LFP phase or LFP amplitude channels that showed significantly increased MI compared with LFP channels that did not show significant cross-frequency modulation (for LFP phase channels: Wilcoxon rank-sum test, P = 0.33; average Z score for LFP phase channels with significant P–A modulation = 1.16 ± 0.09 SE; for channels without P–A modulation = 1.24 ± 0.03 SE; for LFP amplitude channels, P = 0.84; average Z score for LFP phase channels with significant P–A modulation = 1.16 ± 0.08 SE; for channels without P–A modulation, 1.25 ± 0.03 SE). We repeated this analysis also for the subset of LFP channels that showed a significant decrease in cross-frequency modulation following the attention cue. Similar to the previous analyses, we found that the firing-rate information was not different for neurons at recording sites showing significant decreased MI vs. channels showing no significant MI modulation (Wilcoxon rank-sum test, all P > 0.05). All but one of these analyses provided results similar across monkeys with no significant effect when data from each monkey was tested separately. The exception was for LFP phase-providing channels from monkey R. The firing rates of neurons at these channels carried on average significantly more spatial attention information than neurons at channels with LFPs that did not significantly change theta–gamma correlation (Wilcoxon rank-sum test, P = 0.009; average Z score = 1.88, ±0.197 SE).

To exclude the possibility that the previous analyses overlooked a more gradual or subtle relationship of a change in cross-frequency correlation and firing-rate information in the postcue epoch, we calculated Spearman rank correlations of both variables. We found that firing-rate information was not significantly correlated with the change in MI from precue to postcue (for LFP phase-providing channels: r = −0.012, P = 0.72; LFP amplitude-providing channels: r = −0.05, P = 0.16). These results did not change when we removed data points that qualified as outliers (defined as values >3 SD from the mean). These results were consistent across monkeys with no significant correlations when data from each monkey was tested separately (P values for monkeys M: P = 0.86; and R: P = 0.73).

In summary, these results suggests that LFP recordings that engage in long-range theta–gamma correlations are not more likely than other recording sites to coincide with neuronal firing-rate modulation about the spatial target location.

S12.2. Relation of spatially specific theta–gamma cross-frequency correlation with spatially specific firing-rate information.

The previous analyses were based on z-transformed firing-rate differences between spatial attention conditions that were rectified and not sensitive to the sign of the modulation (i.e., enhanced firing for contralateral vs. ipsilateral attention or vice versa was not distinguished). In this second analysis, we considered the sign of the firing-rate modulation. We quantified attentional modulation of firing by computing the normalized difference in firing when attention shifted contralateral vs. ipsilateral as attention index for firing rate (Eq. S9), and contrasted the change in theta–gamma correlation on contralateral vs. ipsilateral conditions (Eq. S7).

We found similar results using other methods of contrasting P–A correlation between conditions (e.g., that contrasted only the postcue epoch cross-frequency correlation, as opposed to D_spatial).

We first tested whether attentional modulation of firing rates was associated with attentional modulation of cross-frequency correlations. Spearman rank correlations of AI_rate and D_spatial across all channels were significantly, positively correlation (r = 0.07; P = 0.0416), but it was of modest size and was only a statistical trend when outliers (values >3 times SD) were removed (r = 0.06; P = 0.056). Similarly, the correlation of AI_rate and D_spatial were marginally positive and nonsignificant when testing the LFP/neuron channels separately in the LPFC, ACC, and vmPFC. The same null results (all P > 0.05) were obtained when the correlation was restricted to those recording channels at which the attentional firing-rate modulation (AI_rate) was significant (at P < 0.05) based on a Wilcoxon rank-sum tests.

In conclusion, there is no prominent association of spatially specific firing-rate modulation and spatially specific cross-frequency P–A correlations, but rather modest positive correlations that only partly satisfy statistical trends (P < 0.1).

S12.3. Relation of reward-specific theta–gamma cross-frequency correlation with reward-specific firing-rate information.

In addition to the shift to a right vs. left stimulus location, the cue also directed attention to a relatively higher vs. relatively lower rewarded target stimulus in the majority of sessions (Methods). Although the reward magnitudes were not instrumental for performance (i.e., the animals had to perform the task irrespective of whether they were cued to a higher- or lower-rewarded stimulus), we wondered whether the modulation of theta–gamma P–A correlation with the attend-high vs. attend-low condition was related to the firing-rate modulation in the attend-high vs. attend-low condition. We thus calculated the attention index for rate and P–A correlation in the same way as for the spatial attention condition, but for the different reward conditions [where AI_rate = (firing_high − firing_low)/(firing_high + firing_low) as in Eq. S9, and D_reward is as defined in Eq. S8].

Across all LFP pairs, we found only marginal positive correlations between D_reward and AI_rate for higher vs. lower reward comparison, which were not significant (r = 0.051, P = 0.135; after outlier removal: r = 0.034, P = 0.325). Similarly, no correlation was significant when we computed them separately for phase-providing LFPs from the individual subareas in PFC/ACC (vmPFC, LPFC, ACC, all P > 0.1) or for amplitude-providing LFPs from the individual subareas in PFC/ACC (vmPFC, LPFC, ACC, all P > 0.5). Likewise, there were no significant correlations when restricting the correlation analysis to neurons with large or small attentional firing-rate modulations.

In conclusion, we did not find a prominent association of target value-specific firing-rate modulation and target value-specific cross-frequency P–A correlations.

SI Result S13. The Relation of Theta–Gamma LFP–LFP Correlations and Burst–LFP Synchronization.

In a previous study, we have shown that the LFPs in ACC and LPFC synchronized long-range to burst firing events of single isolated neurons at narrow frequency bands of the LFP (12). This previous analysis was based on the same dataset and anatomical reconstruction of recording sites as used here, but included a smaller subset of all LFP recording sites based on whether they were recorded simultaneously with single (spiking and bursting) neurons. Based on these previous insights, we were interested in whether the increase in theta–gamma LFP–LFP cross-frequency correlation following the attention cue that we report here is related to the previously reported interareal burst–LFP synchronization.

In particular, the previous study reported that burst firing events in about one-third of single neurons synchronized bursts to remote LFP activity at 15- to 25-Hz beta-band frequencies, and another one-third of neurons synchronized bursts to LFPs at a midrange 55- to 75-Hz gamma-frequency band (the last one-third of burst firing neurons did not show synchronization). In addition, we reported as a secondary finding in the previous manuscript that about a quarter of those neurons with burst synchronization at beta- and gamma-band frequency also showed significant synchronization of burst firing events to a 5- to 10-Hz theta-frequency band of the LFP at remote sites (supplementary figures S5 in ref. 12).

Based on these previous findings, we tested whether there was any relationship between theta–gamma P–A correlation in the 0.5-s postcue period and the strength of burst synchronization in the same epoch. We (i) selected for this analysis the three frequency ranges for which burst–LFP synchronization was reliably shown (5- to 10-Hz theta, 15- to 25-Hz low-beta, and 50- to 75-Hz mid-gamma frequencies), (ii) calculated the average burst–LFP synchronization for each frequency band, and (iii) calculated Spearman rank correlations between the strength of burst–LFP synchronization and LFP–LFP theta–gamma P–A correlations (for details, see Methods). We summarize three major findings below and report the results of all correlations in Table S2.

First, we found that in those LFP channels that provided the theta phases for significantly theta–gamma P-A–correlated channels, single neurons showed stronger burst–LFP synchronization to mid-gamma–frequency activity at remote channels (Spearman rank correlation, r = 0.20, P = 0.044, uncorrected for multiple comparisons; Table S2). This finding suggests that the existence of reliable (i.e., significant) theta–gamma cross-frequency interactions between two channels also allows inference of burst firing events in the theta-phase–providing LFP channels likewise coupled to remote gamma events. In other words, task-modulated, interareal coupling of theta LFP activities to remote narrow LFP-band gamma activity may translate to interareal coupling of burst events to remote narrow-band LFP gamma activity.

Second, we found a another significant positive correlation indicating that theta phases in LFP channels donating gamma during theta–gamma correlations were synchronized to remote burst events (Spearman rank correlation, r = 0.072, P = 0.027, uncorrected for multiple comparisons; Table S2). This finding suggests that LFP channels with gamma activity that was modulated by remote LFP theta phases (Results), also locked remote burst events via theta-phase modulation.

Third, beyond the two positive correlations of theta–gamma P–A correlations and burst synchronization, we found two negative relationships that suggest a decoupling of theta–gamma interactions of LFPs and burst events from activity at beta frequencies (marked in blue font in Table S2). LFP channels that were participating in reliable (significant) theta–gamma cross-frequency interactions showed lower LFP beta-frequency synchronization with burst events from remote channels (theta-phase–providing LFPs: r = −0.246, P = 0.016, uncorrected for multiple comparisons; gamma-amplitude–providing LFPs: r = −0.219, P = 0.032, uncorrected for multiple comparisons). This finding suggests that LFPs with theta–gamma interactions are not engaged at the same time as beta-frequency modulations.