Human population dynamics in Europe over the Last Glacial Maximum

Significance

Despite its importance for understanding genetic, cultural, and linguistic evolution, prehistoric human population history has remained difficult to reconstruct. We show that the dynamics of the human population in Europe from 30,000 to 13,000 y ago can be simulated using ethnographic and paleoclimate data within the climate envelope modeling approach. Correspondence between the population simulation and archaeological data suggests that population dynamics were indeed driven by major climate fluctuations, with population size varying between 130,000 and 410,000 people. Although climate has been an important determinant of human population dynamics, the climatic conditions during the last glacial were not as harsh as is often presented, because even during the coldest phases, the climatically suitable area for humans covered 36% of Europe.

Abstract

The severe cooling and the expansion of the ice sheets during the Last Glacial Maximum (LGM), 27,000–19,000 y ago (27–19 ky ago) had a major impact on plant and animal populations, including humans. Changes in human population size and range have affected our genetic evolution, and recent modeling efforts have reaffirmed the importance of population dynamics in cultural and linguistic evolution, as well. However, in the absence of historical records, estimating past population levels has remained difficult. Here we show that it is possible to model spatially explicit human population dynamics from the pre-LGM at 30 ky ago through the LGM to the Late Glacial in Europe by using climate envelope modeling tools and modern ethnographic datasets to construct a population calibration model. The simulated range and size of the human population correspond significantly with spatiotemporal patterns in the archaeological data, suggesting that climate was a major driver of population dynamics 30–13 ky ago. The simulated population size declined from about 330,000 people at 30 ky ago to a minimum of 130,000 people at 23 ky ago. The Late Glacial population growth was fastest during Greenland interstadial 1, and by 13 ky ago, there were almost 410,000 people in Europe. Even during the coldest part of the LGM, the climatically suitable area for human habitation remained unfragmented and covered 36% of Europe.

Growing populations of anatomically and behaviorally modern humans have been partly responsible for past ecosystem changes such as the extinctions of Pleistocene megafauna and Neanderthal humans (1, 2). In addition to the destiny of other species, human population size also influences our own cultural and genetic evolution. Large pools of interacting individuals can create and maintain adaptive skills, as well as phonological variation, more effectively than small populations, and they are also capable of faster cumulative cultural evolution (3–5). A decrease in population size may even result in a loss of complex cultural traits (6). The effects of population size on cultural variation are thus roughly similar to the effects of population size on genetic variation (7).

The study of the role of human population size in cultural and genetic evolution and past ecosystem changes necessitates estimates of population dynamics extending far beyond historical times. The archaeological record illustrates patterns of human population range and size dynamics (8–10), but it does not offer quantitative population size data. Archaeological reconstructions of population dynamics are also bound to the regions and time periods that offer a sufficiently rich archaeological record. In addition to archaeological data, information on past population patterns can be inferred from genetic data using skyline-plot methods (11) and pairwise or multiple sequentially Markovian coalescent analyzes (12, 13). However, these methods depend on estimates of DNA mutation rate and molecular clock calibrations, which are still debated (14, 15) and imprecise, leading to poor temporal resolution. Furthermore, these methods track changes in effective population size that does not have a straightforward relationship with the actual census population size (16). Together with poor resolution, this makes it extremely difficult to meaningfully compare DNA-based population reconstructions with the records of cultural or environmental changes.

Here, we take a different approach and model human population size and range dynamics in the last glacial Europe independently of archaeological and genetic data. Ethnographic studies have found a link between climate and the diet, mobility, and territory size of hunter-gatherers (17–20). We hypothesize that correlation exists also between climate and hunter-gatherer population density. We take advantage of this potential climate connection and use an approach made possible by recent developments in climate envelope modeling.

Climate envelope or niche models use associations between aspects of climate and the occurrences of species to estimate the conditions that are suitable for maintaining viable populations (21–23). By using information on how the climate affects modern hunter-gatherer population densities, this framework allows us to evaluate climatic suitability for humans and simulate their potential distribution and abundance under the changing climatic conditions of the last glacial, thus overcoming the above-mentioned limitations of approaches using only archaeological or genetic data. We use ethnographic data on terrestrially adapted mobile hunter-gatherers and their climatic space (24) (Dataset S1) to construct a calibration model that predicts hunter-gatherer presence and population density by three climatic predictors: potential evapotranspiration and water balance, both of which exert strong influence on ecosystem productivity and species richness, and the mean temperature of the coldest month that affects wintering conditions, such as winter mortality (25, 26). This model is extrapolated over the European landscape for 30–13 ky ago using climate predictor values obtained by statistical downscaling of the CLIMBER-2 climate model simulation data (27, 28) (Dataset S2). The period in question was chosen because it extends from the end of the Marine Isotope Stage 3 (MIS-3) to the Last Glacial Termination and includes the coldest phase and the largest ice sheet extent of the last glaciation (29).

In practice, estimates of absolute prehistoric population size or density cannot be truly verified with any existing data. Because our model is not archaeologically informed, it is, however, possible to use the dataset of archaeological radiocarbon dates (30) (Dataset S3) to evaluate the simulated spatial and temporal patterns and, in that sense, the realism of our simulation. Such archaeological data are increasingly used as a proxy in studies of prehistoric human population dynamics (8–10, 31, 32).

Results

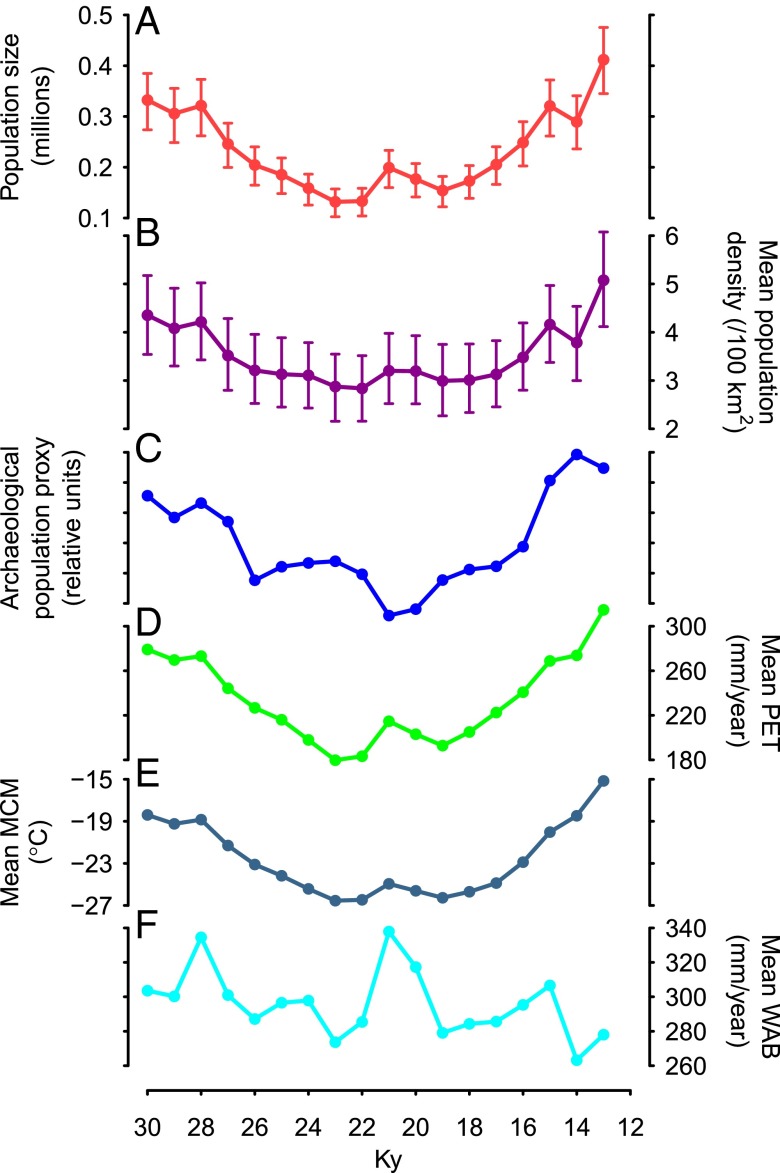
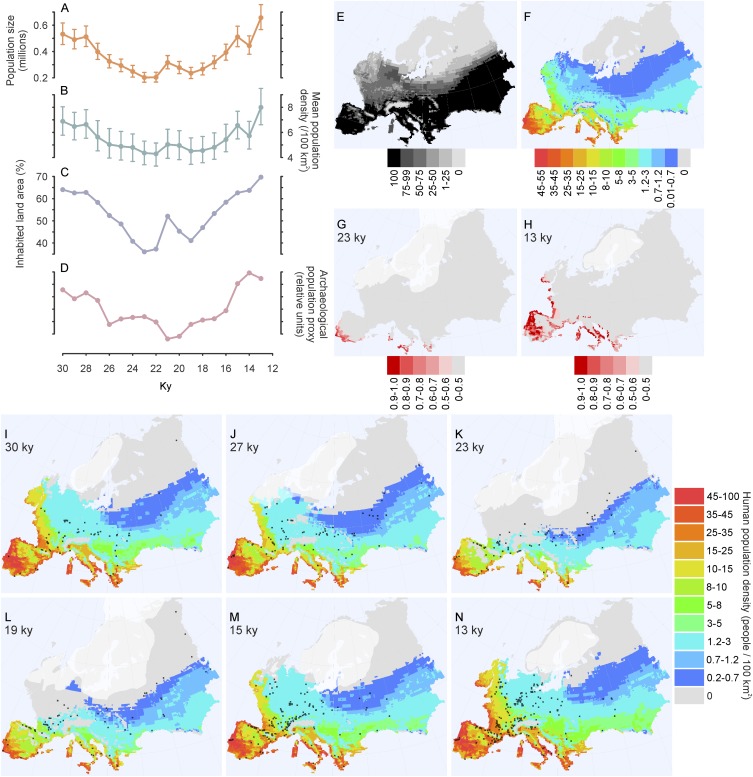
Fig. 1 shows that the temporal patterns in the simulated population size and archaeological population proxy are remarkably consistent (r_P = 0.84, P < 0.00002). Both show relatively high late-MIS-3 population size levels, a decline toward the Last Glacial Maximum (LGM) minimum, and a rapid growth during the Late Glacial. The simulation suggests that the human population size in Europe was about 330,000 at 30 ky ago, 130,000 during its minimum at 23 ky ago, and almost 410,000 at 13 ky ago, during the Greenland interstadial 1. The mean population density in the inhabited area varied between 2.8 and 5.1 persons per 100 km².

Fig. 1.

Comparisons between simulated hunter-gatherer population size and density, the archaeological population proxy, and paleoclimatic simulations between 30 and 13 ky ago in Europe. (A) Simulated human population size in Europe. Error bars show the resampling-based confidence limits (95%). (B) Simulated mean density in the inhabited area of Europe. Error bars show the resampling-based confidence limits (95%). (C) Archaeological population size proxy based on the taphonomically corrected number of dates. (D) European mean of simulated potential evapotranspiration. (E) European mean of simulated mean temperature of the coldest month. (F) European mean of simulated water balance. D–F are based on the downscaling from the CLIMBER-2 climate model.

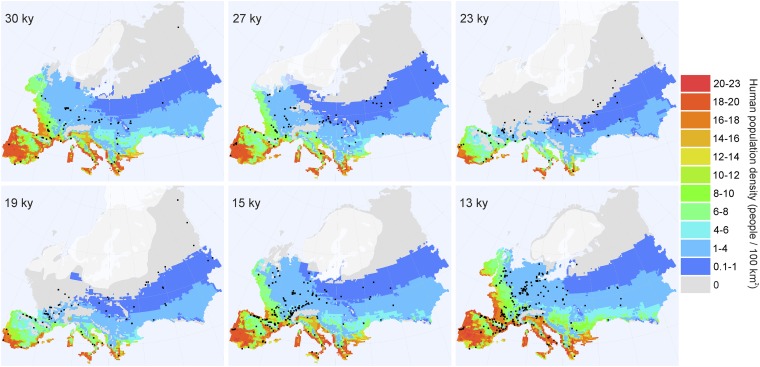
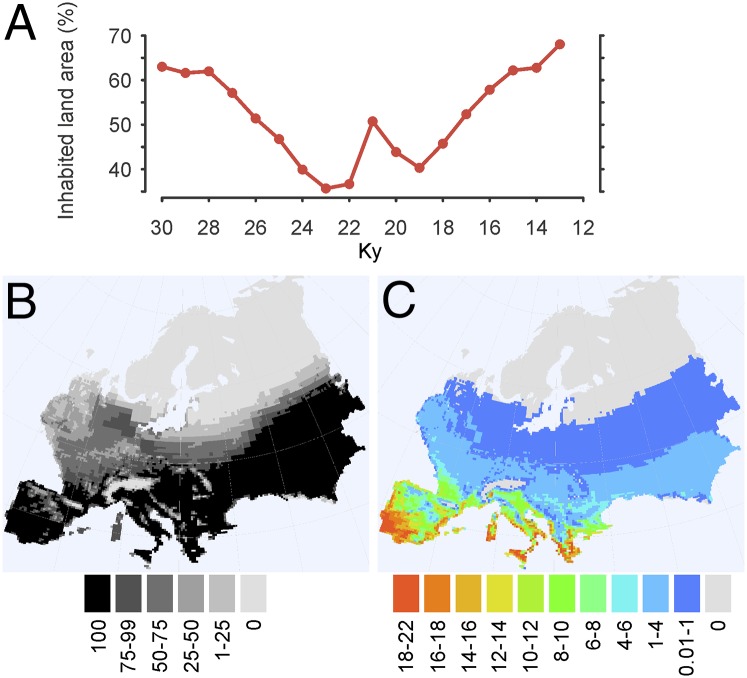
The simulated spatial pattern of human population (Figs. 2 and 3) indicates a population contraction starting in line with the ice sheet expansion at 27 ky ago. During the peak LGM, the northern limit of contiguous population in Europe extended from central France to lowlands in southern Germany and to the southern parts of modern Ukraine and European Russia (Fig. 2). Thus, there was an uninhabited zone about 500 km wide between the ice sheet and the northern limit of the human population. However, our simulation suggests that the continuously suitable and inhabited area between 30 and 13 ky ago covered 36% of the European land area even during the coldest LGM, stretching to the north of the Alps (Fig. 3), a result supported also by an emerging archaeological picture (33). In addition, the simulation shows a persistent southwest-northeast gradient of decreasing population densities, with the densest populations throughout the LGM in the Iberian Peninsula and the Mediterranean region (Figs. 2 and 3). The post-LGM recolonization of the continent began at 19 ky ago.

Fig. 2.

Simulated human population range and density compared with the spatial distribution of archaeological sites during six time intervals from 30 to 13 ky ago. Archaeological sites are indicated with black dots and in each time slice they represent sites dated within 1,000-y bins.

Fig. 3.

Climatic suitability of Europe for human population over the LGM according to the simulation. (A) Changes in the percentage of potentially inhabited land area in Europe. (B) Percentage of time the area has potentially been inhabited between 30 and 13 ky ago. (C) Mean population density (people/100 km²) between 30 and 13 ky ago.

These spatial dynamics concur with the archaeological data, although the latter show a spatially and temporally more sporadic pattern. Such a sparse pattern is most probably a result of a Wallacean shortfall-like effect of incomplete information on species distribution. Although Wallacean shortfall is true for current plant and animal species, paleontological and archaeological records provide obviously even more incomplete and coarse reflection of true ranges (23).

There are, nevertheless, two instances where the simulated range and density of the human population deviate from the distribution of archaeological data. First, in northern Russia, the archaeological record indicates occasional presence of humans much farther north than our simulation suggests. These anomalies may represent human populations whose climatic tolerance differed from that of the modern hunter-gatherer populations used in the calibration model, because it has been suggested that the archaeological lithic assemblage of Byzovaya site in the Polar Urals was produced by Neanderthals (34). The presence of Neanderthals is controversial (35), however, and the anomalies continue sporadically throughout the LGM, when Neanderthals are assumed to have already been extinct. Nonetheless, our results allow for the possibility that the late MIS-3 populations in northern Russia were biologically or behaviorally different from later humans.

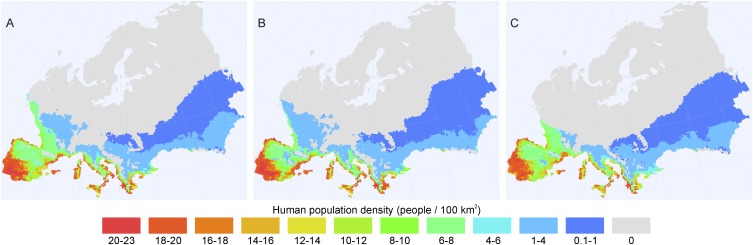
Second, whereas our model simulates high population densities in the Mediterranean region, the density of archaeological data in the region is relatively low throughout the study period. This difference does not relate to the properties of the climate data used in the simulation, because the LGM snapshot population simulations based on state-of-the-art general circulation model data (36–38) show the same pattern (Fig. S1). This similarity of the patterns strongly suggests that the Iberian Peninsula and the Mediterranean region have indeed been climatically the most suitable areas for hunter-gatherers throughout the LGM.

Fig. S1.

Population simulations based on LGM snapshot (∼21 ky) climate data downscaled from three different general circulation models. (A) Simulation based on the CCSM4 climate data (36). (B) Simulation based on the MPI-ESM climate data (37). (C) Simulation based on the MIROC-ESM climate data (38). Downscaled data were obtained from the WorldClim database (www.worldclim.org/). All three simulations show the pattern where the Iberian Peninsula and the Mediterranean region are climatically most suitable for hunter-gatherers.

It is possible that some nonclimatic factors made the region less suitable for humans, which would explain the difference between the simulation based on the hunter-gatherer climatic envelope and the archaeological data. For example, the climatically highly suitable, but relatively small, island of Sardinia may not have been attractive for terrestrially adapted hunter-gatherer groups of the LGM Europe. On a larger scale, however, the spatial distribution of archaeological data may not adequately reflect the distribution of human population, because of the systematic differences in taphonomic processes between different parts of Europe. Due to a combination of climatic and topographic features, erosion rates are higher in the Mediterranean region than in other parts of Europe (39, 40). The high erosion leads to loss or disturbance of the sediment layers containing archaeological material, which may explain the relatively low density of radiocarbon dated sites in the Mediterranean region. For example, in a sample of 164 Middle Paleolithic sites in southern Iberia, almost 80% of the sites were found to be clearly in a secondary context (41).

Research history may also play role in the spatial variability of archaeological data. In Portugal, for instance, there were only four Upper Paleolithic sites known in the early 1960s, and the region was considered largely uninhabited (42). Sensitivity of archaeological distributions to changes in research interests is reflected by the fact that in 50 y the number of sites has multiplied manifold with such discoveries as the Côa Valley dwelling and rock art sites (43, 44). However, relatively few of these new sites have been radiocarbon dated (44) and would not show up in our archaeological proxy. It is thus likely that the discrepancy between the simulated population densities and the spatial distribution of archaeological data in the Mediterranean region is a result of combined effect of research history and erosion-induced taphonomic loss and disturbance of archaeological material. In general, the archaeological data, nevertheless, fall within the simulated range area and the northern limits of the simulation and the archaeological data correspond to each other relatively well.

Discussion

The overall similarity of the simulated and archaeological population patterns supports our results about the European human population changes between 30 and 13 ky ago. However, the simulated population size in LGM Europe appears extremely high compared with the results of Bocquet-Appel et al. (45), who estimated the population size to be less than 6,000 persons. There are two main reasons that lead to these considerably smaller population size estimates. First, Bocquet-Appel et al. (45) estimate the human population range from the spatial distribution of archaeological data while assuming that it adequately reflects the true range of the human population. As discussed above, this assumption is probably not valid, because archaeological remains provide an incomplete and coarse reflection of past geographical distributions of human activity. Second, compared with ethnographically known hunter-gatherer populations (17, 24), Bocquet-Appel et al. (45) use extremely low population density estimates and, even more importantly, only single estimates for each period in question, which does not take into account geographical variability in climate and environment. As our simulation shows, this variability has a strong impact on human population densities and this result appears to be robust with respect to the choice of climate model simulation data (Fig. S1).

In addition, the simulated temporal pattern in population size and density differs from many previous reconstructions of Pleistocene dynamics of European populations, especially those based on DNA data (11–13), which show monotonic growth for the last 50 ky. However, the monotonic growth does not match the archaeological record, which shows substantial variations in human population size at high and low frequencies. These variations seem often to follow climatic variability and, as shown here, they are also simulated with the climate envelope modeling.

Our results have three important implications. First, we show that the range and size of prehistoric hunter-gatherer populations can be realistically modeled using information on modern hunter-gatherers and paleoclimatic simulations. This climate envelope modeling approach provides valuable insights into the patterns and causes of long-term human population dynamics and a necessary complement to archaeological and DNA-based methods when studying prehistoric human demography. Second, the consistency between the simulated patterns and the archaeological data are remarkable because it suggests that climatic conditions were crucial drivers of last glacial human population dynamics. This consistency also indicates that the climate envelope of the hunter-gatherers has remained relatively constant from the last glacial to present. Millennia of cultural evolution have not fundamentally changed constraints on terrestrially adapted hunter-gatherer populations posed by the climate. Third, even the harsh conditions of the LGM sustained a substantial human population in Europe, which was not fragmented to totally isolated refugia. The continuous range would have facilitated a flow of genes and cultural information between the western and eastern parts of the continent, which, in turn, has implications for understanding genetic diversity and cultural evolution in Europe.

Materials and Methods

Constructing the Calibration Model.

We used an ethnographic dataset (n = 339) of modern and recent historical hunter-gatherer populations (24) to extract calibration data to train the statistical models. This dataset is obviously geographically biased. The spatial distribution of ethnographically documented hunter-gatherers does not reflect the geographical area that is suitable for hunter-gatherers, because large areas previously occupied by foragers are dominated by agricultural populations from the Mid-Holocene onward. However, it has been shown that the ethnographic sample of hunter-gatherers is not biased in terms of their niche space (24). Therefore, these data are suitable for niche modeling including climate envelope modeling that are extrapolated to the geographical areas not recently occupied by hunter-gatherers.

For the calibration data, we excluded cases where subsistence is based on mutualistic relations with non–hunter-gatherers (SUBPOP = X). Because the isotope studies of human bone collagen indicate that the Pleistocene hunter-gatherers obtained, at most, 30% of their dietary protein from aquatic resources (46, 47), we also excluded populations whose main livelihood comes from aquatic resources (SUBSP = 3). In addition, we excluded populations that used horses (SYSTATE3 = 1), because mounted hunter-gatherers are unknown in the European Paleolithic record. To keep the simulated population densities conservative, we excluded populations that either move into and out of a central location that is maintained for more than 1 y or are completely sedentary (GRPPAT = 2). These groups usually live under high population densities. The exclusion means that the simulation assumes that the Pleistocene human populations in Europe were residentially mobile, an assumption commonly held by archaeologists. For a comparison, we present in SI Text and Fig. S2 a more relaxed simulation based on the calibration data that includes also semi- and fully sedentary groups.

Fig. S2.

Human population simulation in Europe based on the calibration data that includes also semi- and fully sedentary hunter-gatherer populations (GRPPAT = 2). (A) Simulated human population size in Europe. Error bars show the resampling-based confidence limits (95%). (B) Simulated mean density in the inhabited area of Europe. Error bars show the resampling-based confidence limits (95%). (C) Changes in the percentage of potentially inhabited land area in Europe. (D) Archaeological population size proxy based on the taphonomically corrected number of dates. (E) Percentage of time the area has potentially been inhabited between 30 and 13 ky ago. (F) Mean population density (people/100 km²) between 30 and 13 ky ago. (G and H) Probability of semi- or fully sedentary mobility patterns at two time slices. (I–N) Simulated human population range and density compared with the spatial distribution of archaeological sites during six time intervals from 30 to 13 ky ago. Archaeological sites are indicated with black dots and in each time slice they represent sites dated within 1,000-y bins.

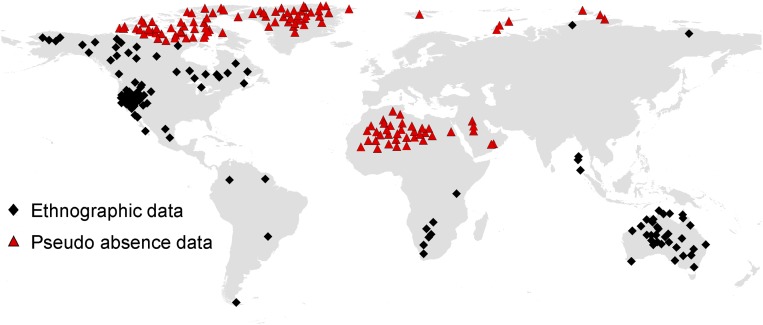
Altogether, the calibration data includes information on 127 hunter-gatherer populations. Because this dataset gives information only on environments where the hunter-gatherers have existed in recent historical times, we added 120 pseudo-absence data points to the climate space where terrestrially adapted hunter-gatherers have not recently existed (e.g., extremely cold and extremely hot and dry) to enhance the performance of the statistical models (Fig. S3 and Dataset S1). Pseudo-absence data have information on climatic conditions and the hunter-gatherer density for each point is zero. The climate data for these points were obtained from the WorldClim database (48). Addition of pseudo-absence data to presence-only data are a standard procedure in ecological modeling (49, 50).

Fig. S3.

The distribution of the calibration or training data.

We used potential evapotranspiration (PET), water balance (WAB), and mean temperature of the coldest month (MCM) as predictors of the density (DENSITY) and presence/absence (DENSITY > 0) of the human population. PET and MCM values are directly available from the ethnographic dataset. WAB values were calculated as the difference between annual precipitation and PET.

To model the distribution and density of the human population, we used two frameworks: one predicting the range (presence/absence) of the human population and the other predicting population density. The human population occurrence was modeled as a binary response variable and density as a continuous response variable. To take into account the fact that different modeling algorithms give diverse predictions, the following six alternative techniques were used to relate human presence/absence and density with the explanatory climatic variables: generalized linear modeling (GLM) (51), generalized additive modeling (GAM) (52), support vector machines (SVM) (53, 54), classification tree analysis (CTA) (55, 56), random forest (RF) (57, 58), and generalized boosting methods (GBM) (59, 60). All of the methods were implemented using R statistical software (61). A more detailed description of these techniques is given in the SI Text.

Predicted probabilities of occurrence were converted to presence/absence predictions using the threshold value maximizing the sum of sensitivity and specificity (62) (SI Text).

The ability of the models to predict human population occurrence and density was assessed using cross-validation (70% random sample for calibration and 30% for validation; 500 repeats). The predictive power of the binary models was determined by testing the accuracy of predictions made for the validation dataset by calculating the area under the curve of a receiver operating characteristic plot (AUC) and the true skill statistic (TSS) (63). For density models, mean R² values were calculated. Predictive accuracies of the six models based on three climate variables are summarized in Table S1.

Table S1.

Predictive accuracies of the six human occurrence and density models based on three climate variables

Modeling technique	AUC	TSS	R2
CTA	0.991	0.969	0.533
GAM	0.992	0.971	0.569
GBM	0.992	0.975	0.619
GLM	0.994	0.965	0.503
RF	0.996	0.962	0.614
SVM	0.995	0.954	0.543

Values are calculated from validation data. Calibration data were randomly split to training (70%) and validation (30%) sets. Models were built using training data, and their predictive abilities were assessed using new data (validation set). This was repeated 500 times, and the reported accuracies are mean values.

To further evaluate the ability of climate envelope modeling approach to correctly simulate hunter-gatherer populations, we simulated Australian hunter-gatherer population at 0.5 ky ago and compared the result to the historical, ethnographic, and archaeological estimates of population size at the European contact (64–66). This simulation is presented in the supplement (SI Text and Fig. S4).

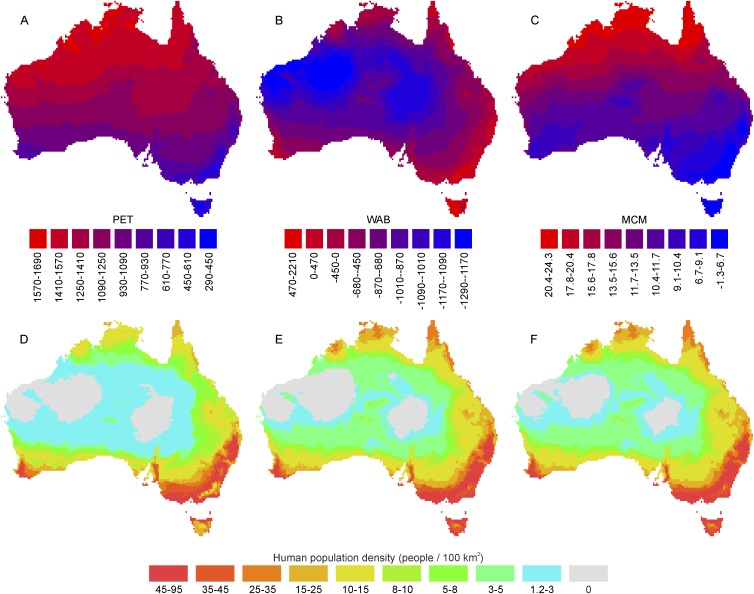
Fig. S4.

Climate variability and population simulation in Australia at 0.5 ky ago. (A) Potential evapotranspiration. (B) Water balance. (C) Mean temperature of the coldest month. (D) Population simulation using only terrestrial hunter-gatherers (SUBSP = 1 and 2) as calibration data (population size = 620,000). (E) Population simulation using terrestrial and aquatic hunter-gatherers as calibration data (population size = 780,000). (F) The same as E, but based on more relaxed optimal threshold value (population size = 800,000).

Climate Model.

The monthly average temperature and annual precipitation values for Europe were generated using a full last glacial cycle simulation (126 ky ago until the present day) with the CLIMBER-2-SICOPOLIS model system (27) that simulates climate at a temporal resolution of 1,000 y. Climate data were downscaled here to the resolution of 1.5° (longitude) × 0.75° (latitude) for a time slice of 30–13 ky ago using a GAM (52). The GAM used here was calibrated (28) using observations of the recent past climate (67, 68) and a short time slice simulation of the LGM (about 22 ky ago) using a relatively high-resolution general circulation model (CCSM4) (36). See SI Text for details. The temperature data at the spatial resolution of 1.5° × 0.75° were regridded to 0.375° × 0.250°. During the regridding process, monthly temperature values were lapsed by the pseudo adiabatic lapse rate (6.4 °C/km) to account for differences in average elevation between the fine-scale and coarse-scale grids (69) (Dataset S2). The problem with the climate model is that it cannot trace high-frequency climate variations. Therefore, for example, some of the cold events, such as Heinrich 1, do not show up in the model data.

Human Population Range and Density Model.

The range of the human population for every 1,000 y between 30 and 13 ky ago was simulated by predicting presence/absence of humans for every 0.375° × 0.25° cell containing land area. This simulation was done by using the above-mentioned calibration model algorithms and climate predictor values derived from the climate simulation. The climate simulation based monthly average temperature, and annual precipitation values were used to calculate PET and WAB values. WAB was calculated as the difference between precipitation and potential evapotranspiration. PET was calculated as (70, 71)

$$\text{PET}=58.93\times {\text{T}}_{\mathrm{above}\hspace{0.17em}\text{0}\hspace{0.17em}°\text{C}}$$

The results of different model algorithms were averaged by using ensemble averaging methods that have been shown to remarkably increase the robustness of forecasts (72). For binary models, majority vote was used. Majority vote is an ensemble forecasting method that assigns a presence prediction only when more than half of the models (i.e., >3) predicts a presence (73).

Next, population density was predicted for every 0.375° × 0.25° cell inside the modeled range. For density models, to average the results based on different algorithms, their median was calculated (consensus method) (72) for each cell.

To calculate the human population size in Europe every 1,000 y, we first calculated the land area of each cell. Here we took into account the systematic areal change of the 0.375° × 0.25° cells and the actual percentage of the land area in each cell. Next, we multiplied the predicted population density of the cell by the land area of the cell and summed these values to get the total population size.

To evaluate the uncertainty of population size estimates, we repeated the whole process from calibration model fitting to calculation of population size 500 times using each time a random sample (70%) of the training/calibration data. This procedure allowed us to calculate confidence limits for the simulated population size estimates. The set of modeling techniques and climate data were held constant throughout the process.

The changes in the percentage of inhabited land area in Europe between 30 and 13 ky ago were calculated by relating the summed land area of the inhabited cells to the total land area of the cells containing land (ice sheet included). To estimate the percentage of time the cell has been inhabited between 30 and 13 ky ago, we counted the number of 1,000-y intervals when the cell was inhabited (maximum 18) and related this to the total number of time intervals.

The ice sheets shown in Fig. 2 were drawn according to four sources (74–77). There is some overlap between the reconstructed ice sheets and the modeled population range, especially in the British Isles at 27 ky ago. This overlap may partly be due to the generalizing effect of using 1,000-y time intervals in climate and human population simulations and in the ice sheet reconstructions but may also reflect some inaccuracies in the modeled human populations ranges and/or ice sheet reconstructions.

We have taken into account eustatic changes in the sea level and the consequent changes in the land area of Europe by adjusting the sea level according to a global sea level change curve (78).

Archaeological Human Population Proxy.

Previous approaches of prehistoric human distribution and niche modeling have trained the predictive models using archaeological site distribution data (79–81). By keeping our calibration model independent from the archaeological data, we are able to test our simulation with the archaeological data.

To evaluate the simulated human population range and density, they were compared with the archaeological population proxy. The population proxy is based on ¹⁴C dates, and the dates extracted from the International Union for Quaternary Science (INQUA) Radiocarbon Paleolithic Europe Database v12 form the backbone of data (30). We also included several dates from other recently published sources. The reasoning behind such a dates-as-data approach is that reliable archaeological radiocarbon dates indicate human presence in the area and that the temporal variation in the frequencies of ¹⁴C dates reflects changes in prehistoric population size (8–10, 31, 32, 82).

The dataset was critically evaluated using the information given in the INQUA database. We excluded (i) all dates that were qualified as unreliable or contaminated, (ii) dates without coordinates or laboratory reference, (iii) duplicate dates, (iv) dates with SEs greater than 5% of the mean ¹⁴C age, (v) dates from gyttja, humus, peat, soil or soil organics, organic sediment, humic acid fraction of the sediment, and fossil timber, (vi) dates of marine origin, such as shell, marine shell, and molluscs, (vii) dates without a clear link to human activity, such as terminus ante and post quem, surface, above, up from, top, below and beneath of the cultural layer(s), minimum or maximum age of the layer, and beyond site, and (viii) dates of cave bear (Ursus spelaeus). In some cases, coordinates or even ages were corrected according to the original publication of the date. After the cleaning, the dataset contains 3,718 ¹⁴C dates from 895 sites (Dataset S3).

The dates were calibrated using the OxCal 4.2 calibration program (83) and IntCal13 calibration curve (84). In the analyses, we used the calibrated median dates. For comparisons between the model and archaeological data, median dates were grouped in intervals of 1,000 y so that the modeled human range at 30 ky was compared with the spatial distribution of dates between 30,499 and 29,500 cal BP, the modeled range at 29,000 cal BP to the distribution of dates between 29,499 and 28,500 cal BP, and so forth.

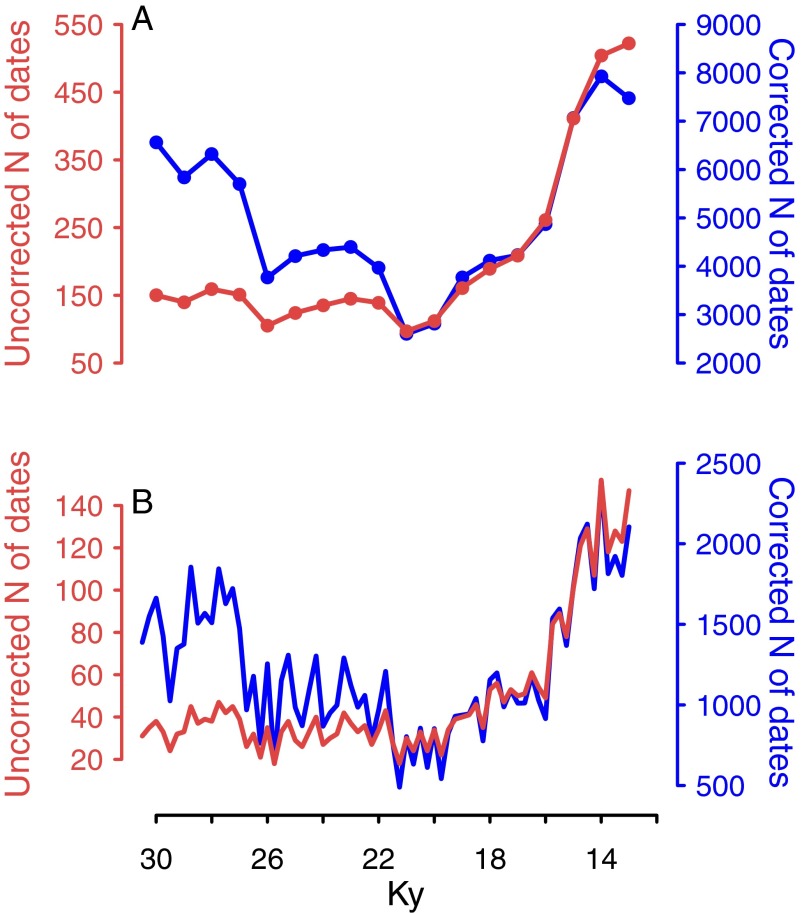
Surovell et al. (31) argued that the younger findings are overrepresented relative to older findings in the archaeological record due to the time-dependent influence of destructive processes such as erosion and weathering. Similar time-dependent loss processes seem to affect geological and palaentological data, as well as historical coin records (85, 86). Therefore, the temporal frequency distributions should be corrected for this taphonomic bias. Surovell et al. (31) proposed a model of taphonomic bias and suggested how to use it to correct the temporal frequency distributions. This method was evaluated, modified, and implemented in several subsequent studies (1, 32, 82, 86). Here, we used a taphonomic bias model modified by Williams (32). The temporal distribution of the taphonomically corrected number of dates was used as a proxy for relative changes in human population size between 30 and 13 ky ago, and this distribution was compared with the temporal distribution of modeled population sizes. See Fig. S5 for the comparison between raw temporal frequency distribution and the taphonomically corrected temporal frequency distribution of archaeological dates.

Fig. S5.

Taphonomically uncorrected and corrected temporal distributions of archaeological dates with bins of 1,000 (A) and 250 (B) y.

SI Text

Calibration Modeling Techniques.

• i)GLMs are mathematical extensions of linear models (51), which can handle nonlinear relationships and different types of statistical distributions characterizing spatial data and are technically closely related to traditional practices used in linear modeling and ANOVA. For the density model, linear and second- and third-order polynomial terms and, for the binary model, linear and second-order polynomial terms were computed with family specification = Poisson to provide the human population density and probability of human population occurrence in each grid square, as a response to the three climatic variables.
• ii)GAMs are nonparametric extensions of GLMs (52). GAMs provide a flexible data-driven class of models based on a cubic-spline smoother with 4 df that permit both linear and complex additive response shapes, as well as a combination of the two within the same model. The smooth functions are computed independently for each explanatory variable and added to construct the final model. GAM was implemented using the package mgcv (87) in R (61). The following smoothing parameters were used for the density model: k = 3 (MCM), k = 4 (PET), k = 4 (WAB). The following smoothing parameters were used for the binary model: k = 3 (MCM), k = 3 (PET), k = 3 (WAB). Family specification was set to Poisson.
• iii)SVM is a machine learning method able to deal with complex nonlinear relations between variables. The SVM constructs a hyperplane or set of hyperplanes in a high-dimensional space, which can be used for classification and regression (53, 54). The SVM transforms a nonlinear relationship to linear through its ability to map the problem into a higher dimension space using a kernel trick. The SVM was implemented using package e1071 (88). A radial basis kernel was used in both binary (C-classification) and density (eps-regression) models. Optimal values for gamma and cos parameters were searched using cross-validation using tune function. For binary model, values are gamma = 2 and cost = 8 and for the density model are gamma = 1 and cost = 1.
• iv)CTA is an alternative to regression techniques. It is based on classification trees (55) and uses recursive partitioning to split the data into progressively smaller, homogenous subsets until a termination is reached (56). The optimal length of the tree is selected by a procedure of 10 cross-validations. The advantage of CTA is that it allows the capturing of nonadditive behavior and complex interactions. CTA was implemented using the package rpart (89). Optimal values for the minimum number of observations that must exist in a node for a split to be attempted (minsplit) were searched using cross-validation. For the density model, the minsplit value was set to 20 and for the binary model was set to 50. Method was set to Poisson.
• v)RF is a machine learning method (57). RF generates hundreds of random trees. A selective algorithm limits the number of implemented parameters in each tree. A training set for each tree is chosen as many times as there are observations, among the whole set of observations. After the trees have been built, data are entered into them and each grid square is classified by all of the trees. At the end of the run, the classification given by each tree is considered as a “vote,” and the classification of a grid square corresponds to the majority vote among all trees (58). RF was implemented using the package randomForest v. 4.6–10 (90).
• vi)GBM is a machine learning method that estimates the relationship between a response variable and its predictors without a priori specification of a data model (59). Boosted regression trees (60), the GBM technique used here, is an advanced form of regression that automatically incorporates interactions between predictors and is capable of modeling complex nonlinear functions. Boosting is a numerical optimization technique for minimizing a loss function (such as deviance) by adding at each step a new tree that best reduces the loss function (59, 60). Here, GBM was implemented using the package gmb (91). The distribution parameter was set to Poisson. The total number of trees was set to 1,000, number of cross-validation folds to 4, shrinkage parameter to 0.005, and the maximum depth of variable interaction to 3. In addition, gbm.perf function was used to estimates the optimal number of boosting iterations.

Optimal Threshold Calculation.

Binary models were initially set to predict probabilities of occurrence. If the probability was higher than a certain threshold, the observation was classified as present (1) and otherwise as absent (0). A model-specific optimal threshold was calculated using calibration data so that the threshold would maximize the sum of the percentage of correctly identified occurrences (sensitivity) and absences (specificity). Calculation was performed using the optim.thresh function in the SDMTools package (92). This function often returns a range in thresholds that are equal for a given data and model. In such cases, the 95th percentile was selected as the threshold value, which means that our simulations of the human population range are relatively conservative.

Climate Model.

The climate predictors for Europe were generated using a full last glacial cycle simulation (126 ky ago until the present day) with the CLIMBER-2-SICOPOLIS model system (27). CLIMBER-2 is an Earth system model of intermediate complexity (EMIC). It includes model components for the atmosphere, ocean, sea ice, land surface, terrestrial vegetation, and ice sheets (93). The reason for using an EMIC instead of an Earth system model of full complexity (ESM) is that the time period considered is too long for ESM simulations with adequate spatial resolution. Therefore, downscaling the simulation results would have been necessary regardless of the choice of the simulation model. The resolution of the simulation data (10° in latitude and 51° in longitude in the atmospheric component) is very low but nevertheless sufficient for simulating the seasonal variability of many climate variables (93) and the climate response to changes in different types of forcing and boundary conditions within the range of ESM simulations (94). Of particular interest for us is the ability of this EMIC to simulate observed ice sheet evolution to obtain a more realistic climatology of temperature and precipitation in regions adjacent to land-ice masses. The CLIMBER-2 model has been coupled with a high-resolution 3D thermo-mechanical ice sheet model (SICOPOLIS) (95). The resolution of the ice sheet model is 1.5° × 0.75°, and the model domain covers the Northern Hemisphere from 21°N to 85.5°N. The atmosphere and ice sheets are coupled using a physically based energy and mass balance interface (SEMI) (96). The simulations were forced by the Earth’s orbital parameter variations (97), and atmospheric greenhouse gas concentrations were derived from the Vostok ice core. The modulating effect of atmospheric dust on radiative forcing was parameterized in proportion to the simulated global ice volume (98).

The annual mean temperature and total precipitation over Europe as simulated by CLIMBER-2 were downscaled here to resolution of 1.5° (longitude) by 0.75° (latitude) for a time slice of 30–13 ky ago using a GAM (52). The GAM used here was calibrated (28) using observations of the recent past climate (67, 68) and a short time-slice simulation of the LGM (about 21 ky ago) using a relatively high-resolution general circulation model (CCSM4) (36). The explanatory variables in the GAM were temperature and precipitation of CLIMBER-2, and elevation, distance to ice sheet, slope direction, and slope angle of the SICOPOLIS ice sheet model.

The mean temperature of the coldest month T_C(x,y,t) over Europe in each grid point (x,y) during the period 30–13 ky ago (t) with a time step of 1,000 y was computed as

$$T_C\left(x,y,t\right)=T_A\left(x,y,t\right)+\left[T_{Cp}\left(x,y\right)-T_{Ap}\left(x,y\right)\right]\times \left[1-\frac{\left|T_{EAp}-T_{EA}\left(t\right)\right|}{T_{EAp}-T_{EAL}}\right]+\left[T_{CL}\left(x,y\right)-T_{AL}\left(x,y\right)\right]\times \left[\frac{\left|T_{EAp}-T_{EA}\left(t\right)\right|}{T_{EAp}-T_{EAL}}\right],$$

where T_A(x,y,t) is the downscaled annual mean temperature, T_Cp(x,y) − TAp(x,y) is the difference between the mean temperature of the coldest month and the annual mean temperature in each grid in the observed recent past (67, 68), and T_CL(x,y) − TAL(x,y) is the corresponding difference in the general circulation model simulation of the LGM (36). T_EAL, T_EA(t), and T_EAp are the downscaled annual mean temperatures over Europe during the LGM, each millennium from 30 to 13 ky ago, and observed past, respectively.

Simulation of the Australian Hunter-Gatherer Population at 0.5 ky Ago.

To further evaluate the ability of the climate envelope modeling approach to simulate hunter-gatherer population densities, we simulated Australian population before the European contact at around 0.5 ky ago. The most recent estimates of Australian population size suggest that at the time of European contact (AD 1788), the hunter-gatherer population size was between 750,000 and 1.1 million and slightly higher at 0.5 ky ago (64–66). To simulate the Australian hunter-gatherer population, we extracted modern climate data from WorldClim database (48). As the Australian temperatures at 0.5 ky ago are estimated to be 0.5 °C lower than the current temperatures (99, 100), we subtracted 0.5 from all of the modern temperature values used in the simulation. Approximately similar climatic conditions prevailed also during the European contact in the 18th century, as the temperatures started to rise during the 19th and 20th century (99, 100).

We performed the Australian simulations using two different calibration sets. The first includes only terrestrially adapted groups. It also includes GRPPAT = 2; type hunter-gatherers as these are known in the Australian ethnographic record (24). Because the Australian ethnographic and historical record includes also aquatically adapted hunter-gatherers (24), whose population densities can be higher than the densities of terrestrially adapted populations living in similar climate, the simulation based on this kind of calibration data would underestimate Australian population size. Therefore, we performed the simulation also with the calibration data that also includes aquatically adapted hunter-gatherers (SUBSP = 3).

The results of these simulations are shown in Fig. S4. The simulation based on more realistic calibration data that also include aquatic foragers gives a precontact population size estimate of 780,000. This is within the suggested range at the time of the European contact, but slightly lower than the suggested population size of 1.2 million at 0.5 ky ago (66). The simulation suggests that areas in western and central Australia would have been uninhabited mainly due to the extremely negative water balance (Fig. S4). However, it is known that humans lived also in these areas. The reason for the simulated pattern relates to our selection of pseudo-absence data, which include locations in Africa and Arabian Peninsula, where the climate conditions resemble those of central Australia. Due to these pseudo-absence data points, the binary distribution model (humans present/absent) predicts uninhabited areas in Australia. When the selection of the optimal threshold value (see above) is relaxed from the 95th to the 5th percentile of the range of the optimal threshold values, population size increases to 800,000, and the uninhabited area decreases but does not disappear.

Despite the small discrepancy between the observed and simulated presence of humans, the simulated population size falls well within the range of historical and ethnographic estimates at the time of contact (64, 65) and is close to the size estimates based on archaeological and genetic data (66). Also the pattern in simulated population densities appears as expected and corresponds quite well the distribution archaeological data in Australia (66).

Simulation of the European Population 30–13 ky Ago Using Larger Ethnographic Calibration Data.

The European archaeological record may not totally exclude the possibility of semi- or fully sedentary populations. For example, substantial mammoth bone dwellings indicate that even in the Eastern European tundra-steppe zone, residential mobility was not very high (101) and in the more suitable region of the Mediterranean Greece, the characteristics of the bone assemblage of Klissoura Cave 1 allow for the possibility of year-round settlement during certain periods of the Paleolithic (102, 103). Therefore, we present here a simulation that is based on the ethnographic calibration data that also contain the semisedentary or sedentary groups (GRPPAT = 2). Such groups usually live under high population densities, and consequently, the simulation will yield higher population densities in the Pleistocene Europe than if these groups were excluded from the calibration data. Otherwise, the calibration data are the same as used in the primary simulation. One outlying GRPPAT = 2-type group, Clear Lake Pomo, was excluded from this calibration data because its density is exceptionally high. The results of the simulation are shown in Fig. S2.

This simulation suggests that the human population size in Europe was about 500,000 at 30 ky ago, 200,000 during its minimum at 23 ky ago, and almost 700,000 at 13 ky ago, during the Greenland interstadial 1. The mean population density in the inhabited area varied between 4.3 and 8.0 per 100 km².

As semisedentary or sedentary (GRPPAT = 2) groups are included in this calibration data, it is reasonable to ask to what extent the simulated population densities of the Pleistocene Europe would indicate at least a semisedentary mobility pattern. To illustrate this, we fitted a logistic regression model to the ethnographic data to explain the type of mobility pattern (mobile vs. semi- or full sedentary) with population density and PET that turned out to be the only statistically significant climate variable in this context.

Next, we used this model to hindcast occurrence probability of semi- or full sedentary mobility pattern over European land area at two time slices (23 and 13 ky ago). We used the simulated population density and the PET values from the downscaled CLIMBER-2 as predictor variables. The results of this simulation are shown in Fig. S2. They show that semi- or full sedentary mobility pattern would have occurred only in the climatically most suitable areas along the coasts.