Ongoing dynamics in large-scale functional connectivity predict perception

Significance

Most brain activity is not directly evoked by specific external events. This ongoing activity is correlated across distant brain regions within large-scale networks. This correlation or functional connectivity may reflect communication across brain regions. Strength and spatial organization of functional connectivity changes dynamically over seconds to minutes. Using functional MRI, we show that these ongoing changes correlate with behavior. The connectivity state before playback of a faint sound predicted whether the participant was going to perceive the sound on that trial. Connectivity states preceding missed sounds showed weakened modular structure, in which connectivity was more random and less organized across brain regions. These findings suggest that ongoing brain connectivity dynamics contribute to explaining behavioral variability.

Abstract

Most brain activity occurs in an ongoing manner not directly locked to external events or stimuli. Regional ongoing activity fluctuates in unison with some brain regions but not others, and the degree of long-range coupling is called functional connectivity, often measured with correlation. Strength and spatial distributions of functional connectivity dynamically change in an ongoing manner over seconds to minutes, even when the external environment is held constant. Direct evidence for any behavioral relevance of these continuous large-scale dynamics has been limited. Here, we investigated whether ongoing changes in baseline functional connectivity correlate with perception. In a continuous auditory detection task, participants perceived the target sound in roughly one-half of the trials. Very long (22–40 s) interstimulus intervals permitted investigation of baseline connectivity unaffected by preceding evoked responses. Using multivariate classification, we observed that functional connectivity before the target predicted whether it was heard or missed. Using graph theoretical measures, we characterized the difference in functional connectivity between states that lead to hits vs. misses. Before misses compared with hits and task-free rest, connectivity showed reduced modularity, a measure of integrity of modular network structure. This effect was strongest in the default mode and visual networks and caused by both reduced within-network connectivity and enhanced across-network connections before misses. The relation of behavior to prestimulus connectivity was dissociable from that of prestimulus activity amplitudes. In conclusion, moment to moment dynamic changes in baseline functional connectivity may shape subsequent behavioral performance. A highly modular network structure seems beneficial to perceptual efficiency.

The brain is highly active in a continuous manner, and much of neural activity is not directly locked to external events or stimuli. This continuous brain activity is spatiotemporally organized into a functional connectivity architecture that comprises several large-scale networks. Large-scale networks span different cerebral lobes and include subcortical structures (1). The regions comprised in such networks commonly coactivate together in response to task demands (2), but they also show correlated and spontaneous activity fluctuations when no changes occur in the external environment. The functional connectivity architecture ensuing from these activity cofluctuations largely persists across all mental states, including various tasks, resting wakefulness, and sleep, albeit showing some degree of modulation across these states (3, 4).

Strength and spatial distributions of functional connectivity within this architecture are not, however, stationary across time. At the spatial level of large-scale networks, functional connectivity shows prominent changes over the range of seconds to minutes (5). These so-called infraslow timescales and the spatial distribution of large-scale networks can be particularly well-investigated using functional MRI (fMRI). We refer to the nonstationarity of functional connectivity as ongoing dynamics. The notion of ongoing refers to dynamics that are not brought about by particular external events, such as stimuli or cues. Such large-scale ongoing network dynamics are thought to be crucial for the brain to explore a large space of dynamic functional capabilities (6). This potential functional importance has recently sparked interest in ongoing connectivity dynamics (5). The most common approach to studying ongoing dynamics in connectivity with fMRI has been to measure connectivity in time windows sliding through a prolonged task-free resting state (reviewed in ref. 5). These investigations have established the nonstationarity of large-scale functional connectivity that previously had been largely neglected. Some studies have shown characteristic changes of dynamic connectivity in different patient populations (7). However, none of these resting-state studies have directly investigated the functional consequences of ongoing dynamics during performance (in other words, how moment to moment changes in baseline functional connectivity relate to cognition and behavior). Furthermore, the ongoing dynamics of functional connectivity may be modulated by cognitive task context, further motivating investigation of the behavioral importance during task beyond the resting state.

Several lines of research call for a dedicated investigation of this question. Slow ongoing fluctuations in regional prestimulus baseline activity amplitudes (in fMRI or electrophysiological recordings) in task-relevant sensory or motor regions (8–12) as well as entire large-scale brain networks (12–14) correlate with evoked neural response strength and subsequent behavior. It is not clear whether, beyond fluctuations in regional ongoing activity amplitude, the correlation of such amplitude fluctuations across large-scale network regions (i.e., connectivity) relates to behavioral variability. Some prior work seems to suggest that ongoing connectivity dynamics between two task-relevant regions may turn behaviorally relevant (15). Also, in addition to these effects in infraslow timescales, some electrophysiological recordings indicate a behavioral relevance for phase synchrony between individual regions of interest and the rest of the brain at faster timescales (16). Building on this so-far rather sparse evidence, we here sought to investigate behavioral effects from ongoing dynamics in large-scale functional connectivity, calling on tools of multivariate classification for trial by trial prediction of behavior and graph theory for a more detailed and spatially comprehensive characterization.

We analyzed behavioral outcome on a trial by trial basis as a function of dynamic connectivity states before stimulus presentation. We tested whether large-scale functional connectivity states predict perception of a sparse and irregularly appearing stimulus. To investigate ongoing nontask-locked changes in baseline connectivity, we minimized contributions from stimulus-evoked activity. This study, therefore, extends beyond important previous investigations of connectivity dynamics that occur after changes in the external environment (such as stimulation, cues, instructions, or feedback) at infraslow (17–20) and fast electrophysiological timescales (21, 22). Specifically, we asked (i) whether ongoing dynamics of large-scale functional connectivity relate to perceptual performance and (ii) which properties of baseline functional connectivity distinguish brain states that support perceptual accuracy from those that do not.

Eleven blindfolded participants performed a detection task on an auditory broadband stimulus (500 ms). They pressed a button whenever they heard the sound during two to three 20-min-long fMRI runs. The stimulus was presented at the individually determined detection threshold and repeated very sparsely at highly variable interstimulus intervals ranging from 20 to 40 s (Fig. 1A). This dataset has previously been used to investigate behavioral correlates of baseline activity amplitudes and enables this investigation to directly compare effects from prestimulus activity amplitudes with those from prestimulus connectivity (12). The unusually long interstimulus interval design allowed us to focus all analyses on the prestimulus time after excluding the hemodynamic response evoked by the previous stimulus. To answer our first question of whether prestimulus baseline connectivity predicts behavior, we applied trial by trial classification of subsequent perceptual outcome based on patterns of functional connectivity before stimulus presentation. To address our second question and determine what characterizes the difference across these brain states, we modeled connectivity before hits and before misses as separate graphs using tools of complex network theory and compared graph metrics between these states.

Fig. 1.

(A) Experimental design of a threshold-level auditory stimulus presented on top of background scanner noise at very long, unpredictable interstimulus intervals (ISI, 20–40 s). Participants listened for the faint target sound continuously throughout 20-min runs and pressed a response button whenever they perceived the target. (B) Illustration of baseline time segments unaffected by evoked responses that were defined as appropriate for analysis of ongoing functional connectivity (marked in gray). The illustrated blood-oxygen-level-dependent (BOLD) hemodynamic response peaks at 6 s, reaches maximum poststimulus undershoot at 12 s, and returns to baseline before 16 s relative to stimulus onset according to finite impulse response estimation of the brain response to this stimulus in the same data in 10 bilateral brain areas (12). Baseline segments started after 16 s poststimulus and ended 1 s after the next stimulus onset. Baseline segments shorter than 6 s in length (interstimulus interval <22 s) were excluded. For classification analyses requiring trial by trial data, data were further restricted to baseline segments that were at least 15 s long (10 image volumes and interstimulus intervals ≥31 s). In this exemplary 2-min period of the task, four stimuli (marked as solid vertical lines) occur at interstimulus intervals of 40 (maximum in this design), 20 (minimum), and 32 s. Note that, for simplification, this illustration does not depict the spontaneous signal fluctuations during the baseline period and the ensuing variability in stimulus-evoked hemodynamic responses that are at the heart of this study.

Results

Overall, the threshold stimulus was detected in slightly more than one-half of the trials (62.2% ± 17% hits; defined as a button press within 1.5 s of stimulus onset). Perceptual outcome (hit vs. miss) was approximately stochastically distributed and independent of preceding interstimulus interval length (12).

Fig. 1 illustrates the selection of time segments of fMRI signal that were expected to be unaffected by any evoked activity. This procedure resulted in 26.5 ± 12.4 baseline segments (on average, 13.3 ± 2.25 volumes per segment) before hits and 15.6 ± 8.7 baseline segments (13.6 ± 2.56 volumes per segment) before misses per participant. For these time segments, we extracted fMRI signal from 24 regions of interest. These regions were defined on a participant by participant basis using seed-based resting-state functional connectivity on a task-free session (20 min) recorded on an earlier day and a passive functional auditory localizer. They were chosen in accord with our previous work on prestimulus activity, thereby making the investigations directly comparable (SI Text, section 1).

Prestimulus Baseline Connectivity Pattern.

To explore the difference in connectivity before hits (pre-hits) and before misses (pre-misses), prestimulus baseline segments (last four volumes) were concatenated across all hits and across all misses for each participant. The difference in within-network connectivity was investigated in the networks where we previously found behaviorally relevant differences in prestimulus activity amplitudes (12): auditory (AUD), cinguloopercular (CO), frontoparietal (FP), default mode (DM), and dorsal attention (DAT) networks. To this end, the correlations were averaged from all region pairs within each network and entered into a two-way ANOVA of network (AUD, CO, FP, DAT, and DM) and condition (pre-hits and pre-misses). These within-network average correlations showed a significant interaction (F_2.9,29.1 = 3.33, P = 0.034), and a two-sided posthoc t test was significant only in the DM network (stronger within-network connectivity for pre-hits t₁₀ = 3.72, P = 0.004).

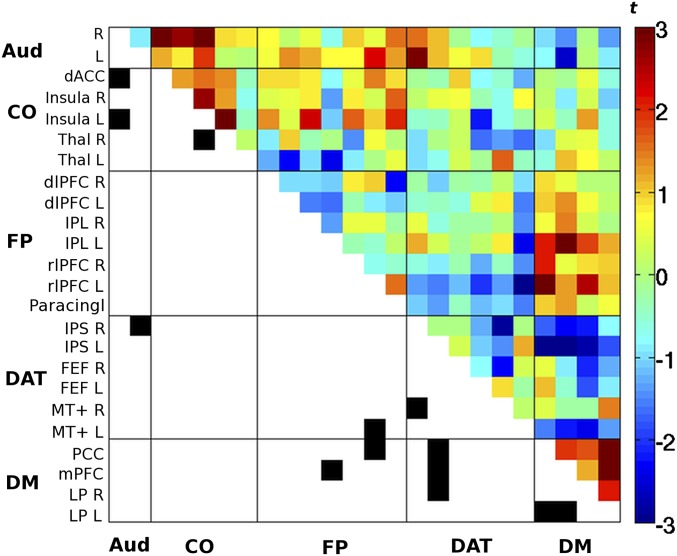
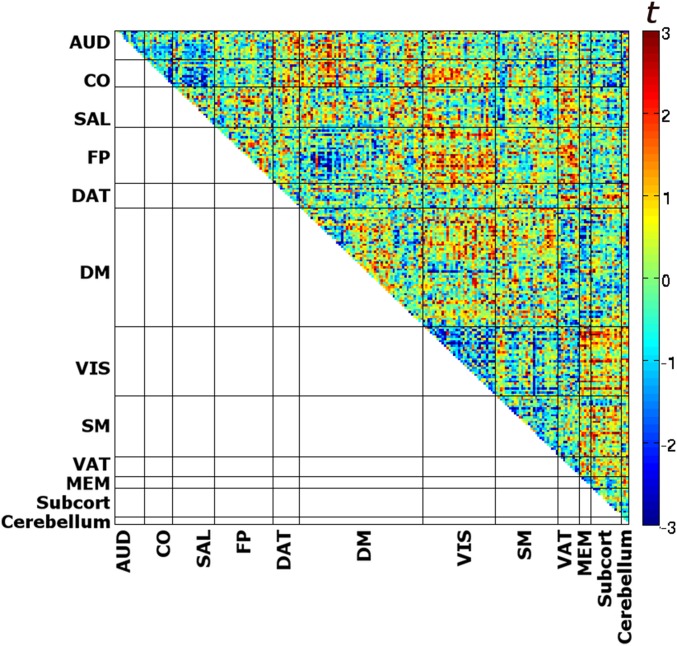
We further investigated whether coupling of the task-relevant AUD network with the other networks differed before hits and misses. Correlations were averaged across all of the respective region pairs. We found an interaction of condition (pre-hits and pre-misses) and network (CO, FP, DAT, and DM): F_2.6,26.2 = 4.31, P = 0.017. Two-sided posthoc t tests were significant for AUD–CO connectivity (t₁₀ = 3.01, P = 0.013) and AUD–DM connectivity (t₁₀ = −3.02, P = 0.013). Before hits, auditory cortex showed stronger coupling with the CO network but decreased coupling with the DM network. These effects persisted after equating the number of image volumes across pre-hits and pre-misses (SI Text, section 2 and Fig. S1). For a fine-grained visualization, the group-level contrast between the full 24 × 24 correlation matrices for pre-hits and pre-misses is shown in Fig. 2B. For comparison, we generated the equivalent figure after concatenating baseline segments according to the previous rather than the upcoming percept. This procedure resulted in a very distinct pattern (SI Text, section 3 and Fig. S2), indicating that the difference structure observed in Fig. 2B was not substantially driven by preceding evoked activity fluctuations.

Fig. S1.

Difference in cross-correlation for pre-hits > pre-misses. Each data point corresponds to a paired t test (uncorrected) between the two respective regions. Connections passing P < 0.02 (uncorrected) are marked in black in the lower triangle of the matrix (for visualization purposes only). This analysis corresponds to Fig. 2B after equating the number of image volumes for pre-hits and pre-misses. dACC, dorsal anterior cingulate cortex; dlPFC, dorsolateral prefrontal cortex; FEF, frontal eye fields; IPL, inferior parietal cortex; IPS, intraparietal sulcus; L, left; LP, posterior lateral parietal cortex; mPFC: medial prefrontal cortex; MT+: middle temporal area; Paracingl, paracingulate cortex; PCC, posterior cingulate/precuneus; R, right; rlPFC, rostrolateral prefrontal cortex; Thal, thalamus.

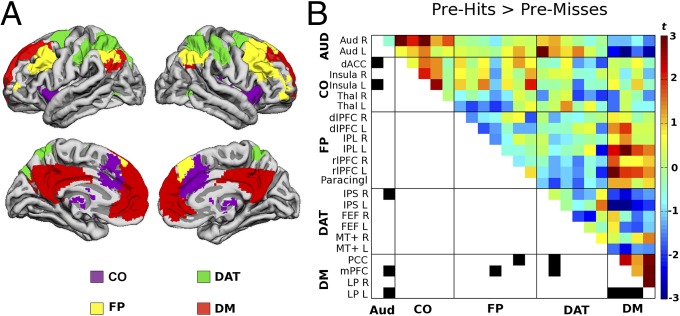
Fig. 2.

(A) Intrinsic functional connectivity networks derived from seed-based correlations in an independent resting-state session (12). (B) Difference in cross-correlation for pre-hits > pre-misses. Each data point corresponds to a paired t test (uncorrected) between the two respective regions. Connections passing P < 0.02 (uncorrected) are marked in black in the lower triangle of the matrix to exemplify the features used for subsequent classification analyses (from similar difference matrices leaving one trial out) (Methods). Of note, all 12 connections corresponded to connectivity with DM or AUD networks. dACC, dorsal anterior cingulate cortex; dlPFC, dorsolateral prefrontal cortex; FEF, frontal eye fields; IPL, inferior parietal cortex; IPS, intraparietal sulcus; L, left; LP, posterior lateral parietal cortex; mPFC: medial prefrontal cortex; MT+: middle temporal area; Paracingl, paracingulate cortex; PCC, posterior cingulate/precuneus; R, right; rlPFC, rostrolateral prefrontal cortex; Thal, thalamus.

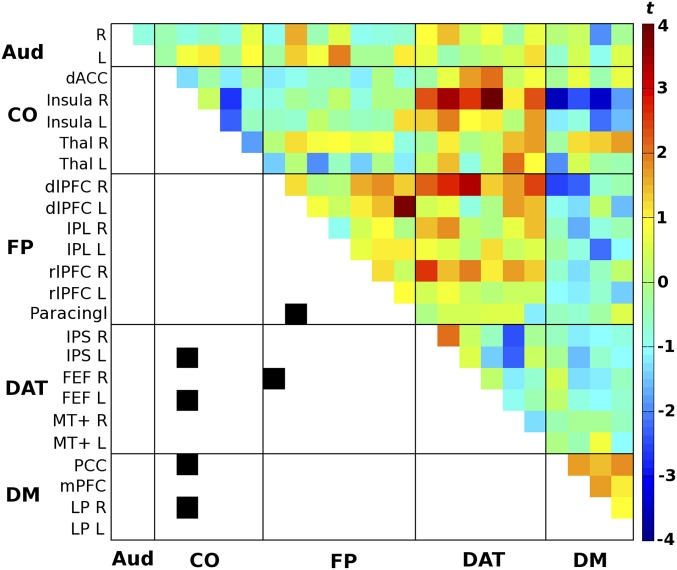
Fig. S2.

Difference in cross-correlation for posthits > postmisses. Each data point corresponds to a paired t test (uncorrected) between the two respective regions. In line with Fig. 2B, the black squares mark connections passing uncorrected P < 0.02 (for visualization purposes only). dACC, dorsal anterior cingulate cortex; dlPFC, dorsolateral prefrontal cortex; FEF, frontal eye fields; IPL, inferior parietal cortex; IPS, intraparietal sulcus; L, left; LP, posterior lateral parietal cortex; mPFC: medial prefrontal cortex; MT+: middle temporal area; Paracingl, paracingulate cortex; PCC, posterior cingulate/precuneus; R, right; rlPFC, rostrolateral prefrontal cortex; Thal, thalamus.

Classification of Upcoming Percept.

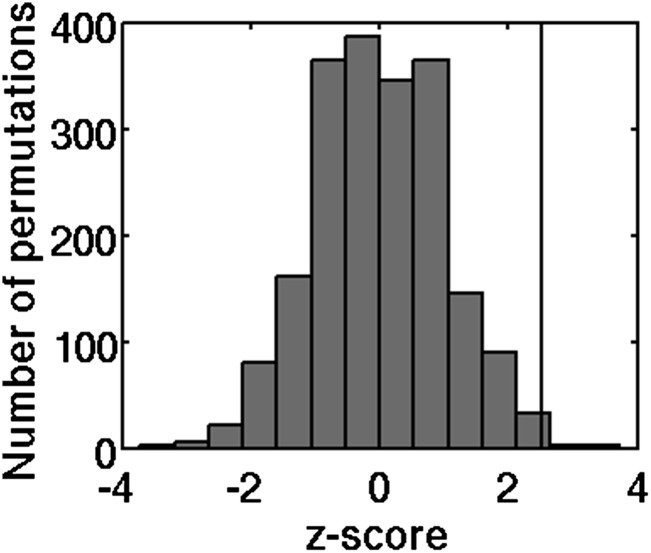
To address whether dynamic changes in ongoing functional connectivity influence perceptual decisions, we attempted to predict the upcoming percept from trial by trial prestimulus connectivity. The univariate contrast in prestimulus connectivity described above was used for feature selection in subsequent classification analyses (compare with Fig. 2B). A naïve Bayesian classifier predicted the upcoming percept significantly above permutation chance level (z = 2.30, P = 0.011; 62.5% correct) (Fig. 3A). Note that chance level was 58.6% rather than 50%, because Bayesian classifiers take advantage of the prior probability of hits being more common than misses. Using a linear classifier resulted in a 50.5% chance level and again, produced significant above-chance classification performance (56.0% correct; z = 2.36, P = 0.009). Training the naïve Bayesian classifier on upcoming percepts as described above but testing it on the previous rather than the next percept performed at chance level (P = 0.68), indicating that classification was not substantially driven by residual activity from the preceding trial.

Fig. 3.

Naïve Bayesian classifier performance (vertical line) and permutation distribution when trained on (A) prestimulus baseline connectivity, (B) prestimulus baseline activity amplitudes, and (C) the combination of prestimulus baseline activity amplitude and connectivity features. When trained on the combination of prestimulus activity and connectivity features, the classifier predicted the upcoming percepts with substantially higher precision than using prestimulus activity alone.

Next, we investigated whether prestimulus functional connectivity contains predictive information over and above that reflected in prestimulus regional activity amplitudes. In line with our previous observation of behavioral relevance of prestimulus activity amplitudes (12), Naïve Bayesian classification on baseline activity amplitudes successfully predicted the upcoming percept (z = 2.33, P = 0.010; 60.8% vs. chance 56.1%) (Fig. 3B). We next asked whether adding prestimulus connectivity features to this classifier would further improve classification performance. The performance of a classifier will not increase substantially if additional features are included that do not add new, nonredundant information, even if the added features on their own have discrimination power (SI Text, section 4 and Fig. S3). When trained on the combination of prestimulus activity amplitudes and connectivity features, the classifier predicted the upcoming perceptual decision with substantially higher precision of z = 3.87 (P = 0.00005; 63.6% vs. chance 55.4%) (Fig. 3C) than using prestimulus activity amplitudes alone. A power analysis of classification success (SI Text, section 5) found powers of 0.67 for prestimulus connectivity, 0.73 for prestimulus activity amplitudes, and 0.98 for combined activity amplitudes and connectivity. This improvement indicates that baseline connectivity is of relevance for perception over and above the effect of activity levels per se.

Fig. S3.

Bayesian classifier performance (vertical line) and permutation distribution when trained on prestimulus activity amplitudes, with duplication of the most discriminative 12 features.

Graph Theoretical Characterization of a Brain State Supporting Perceptual Accuracy.

After showing that functional connectivity differs before hits vs. misses, we next sought to identify characteristics of this difference. To quantify these characteristics at the whole-brain level, we applied complex network or graph theory. This approach models the brain as a graph, with regions represented as nodes and functional connections represented as edges between them. Functional brain networks emerge as modules of highly interconnected nodes, with relatively few long-distance edges integrating across modules. This topologically modular organization is characteristic of the brain and other complex systems and enables flexible behavior based on specialized processes in locally segregated modules as well as more globally integrated functions through fast communication across modules (23). The strength of modular organization can be quantified using the modularity metric. In a brain state with high modularity, many modules (networks) have a high number of within-module compared with between-module connections.

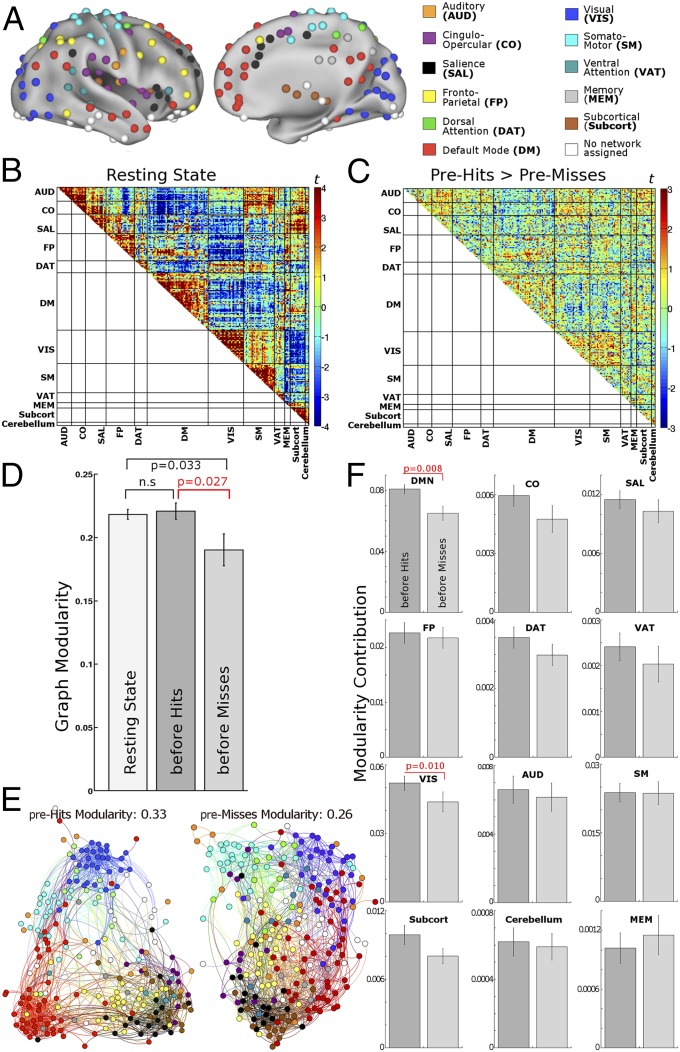
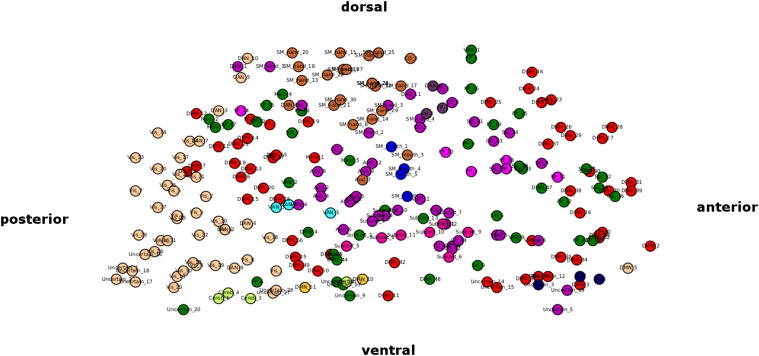
For this complex network analysis, we used a more comprehensive and fine-grained set of 238 atlas regions (Fig. 4A) (1), because the modularity metric is likely to be better estimated with a larger number of nodes. For each participant and condition (resting state, pre-hits, and pre-misses), a single 238 × 238 correlation matrix was generated from time courses concatenated across all respective baseline segments (last four volumes per segment). For the resting-state session, baseline segments were defined from pseudotrials generated according to the same timing parameters as the task session. Next, an adjacency matrix was derived by thresholding the correlation matrices, resulting in unweighted, undirected graphs.

Fig. 4.

Graph construction and graph modularity. (A) Nodes from a functional atlas defined on the combined basis of resting-state functional connectivity and a meta-analysis of cognitive tasks (1). (B) Resting-state correlation pattern across the nodes. This pattern with strong connectivity within the atlas modules shows that the predefined modular partition structure of the atlas reflects the data structure well. (C) Difference in functional connectivity of pre-hits baseline > pre-misses baseline (compare with Fig. 2B). Difference between task and resting state is in SI Text, section 7 and Fig. S5. (D) Graph modularity was reduced before misses compared with hits and task-free resting state. P values are Bonferroni-corrected. (E) A visual representation of the modularity difference before hits vs. misses for a representative individual participant (cost 0.05). This representation is generated by a force-field algorithm that treats nodes as magnets repulsing each other, whereas edges act as springs attracting the nodes that they connect (37). The configuration onto which these forces converge is visibly more modular before hits compared with misses. Networks (modules) are colored as in A. Most notably, DM (red) and VIS (dark blue) modules are less segregated from the rest of the graph before misses. (F) Contribution of individual modules to overall graph modularity. The strongest contribution to modularity difference was from DM and VIS networks. All error bars show SEMs. n.s., not significant.

In Fig. 2B, we had observed that, across pre-hits and pre-misses, connectivity changes more consistently within networks (modules) and across pairs of networks than across random pairs of regions, suggesting that dynamical shifts in the modular structure may relate to behavioral outcome. We chose Newman’s modularity (SI Text, section 8) to quantify such changes of modular integrity at the whole-brain level, because this metric provides a summary measure of within-module connectivity strength in relation to connectivity strength to other modules. In previous studies, modularity during the task-free resting state has been reported as a whole brain-level predictor for (offline) behavioral efficiency (24) and shown to describe modular network integrity in brain lesion patients (25). These observations of a role of modularity in interindividual variability further motivate investigation of this measure in intraindividual variability. In the first analysis, we assigned each node to one module according to the modular partition structure from ref. 1 as color-coded in Fig. 4A. We then tested for differences in modularity across conditions. Graph modularity was decreased before misses compared with hits (mean across costs: t = 2.84, P = 0.027 against permutation chance; Bonferroni-adjusted for three comparisons across condition pairs). This effect was also consistently observed for all individual costs (P < 0.05). Modularity before misses was likewise reduced compared with the task-free resting state (t = 2.41, P = 0.033, Bonferroni-adjusted). Conversely, pre-hits baseline showed no change in modularity compared with resting state (t = 0.35) (Fig. 4D). We replicated these effects after equating the number of imaging volumes across conditions (SI Text, section 2). Furthermore, we confirmed the modularity difference using a graph partition derived from the participants’ own resting-state data (SI Text, section 6 and Fig. S4). Finally, we investigated the most optimal modular partition structure as defined by maximizing modularity for each condition and participant separately. The spectral algorithm by Newman and Girvan (26) generated a modular partition for each graph as well as a modularity value for each graph (i.e., each participant and condition). This analysis confirmed a loss in modularity before misses compared with pre-hits (t = 3.01, P = 0.027) and the resting state (t = 3.93, P = 0.005). Pre-hits and resting state did not differ (t = 2.06; all Bonferroni-corrected for three comparisons). The number of modules showed no difference (pre-hits: 4.7 ± 0.8, pre-misses: 4.9 ± 0.7, and resting state: 4.7 ± 1).

Fig. S4.

Graph nodes (from the atlas in ref. 1) were partitioned into modules by applying the spectral algorithm by Newman and Girvan (26) that maximizes modularity onto resting-state data. Sagittal view. The DM network is depicted in red, and the VIS network is in beige. Network labels: AUD, auditory; CO, cingulo-opercular; SAL, salience; FP, fronto-parietal; DAT, dorsal attention; DM, default mode; VIS, visual; SM, somato-motor; VAT, ventral attention; MEM, memory; Subcort, subcortical.

Next, we investigated the contribution of each module to overall graph modularity, which is the sum of contributions from all individual modules. In a two-way ANOVA of modularity with factors condition (pre-hits and pre-misses) and module (12), a significant interaction (F = 9.84, P = 0.008) indicated that the modularity difference across perceptual outcomes differed across modules. Posthoc t tests were significant only in DM and visual (VIS) networks (t = 3.23, P = 0.008 and t = 2.77, P = 0.010), showing that the strongest contribution to the modularity difference across pre-hits vs. pre-misses originated from these networks (Fig. 4F). The observation in the DM network is in line with the significantly higher within-network connectivity during pre-hits baseline in this network (Fig. 2B).

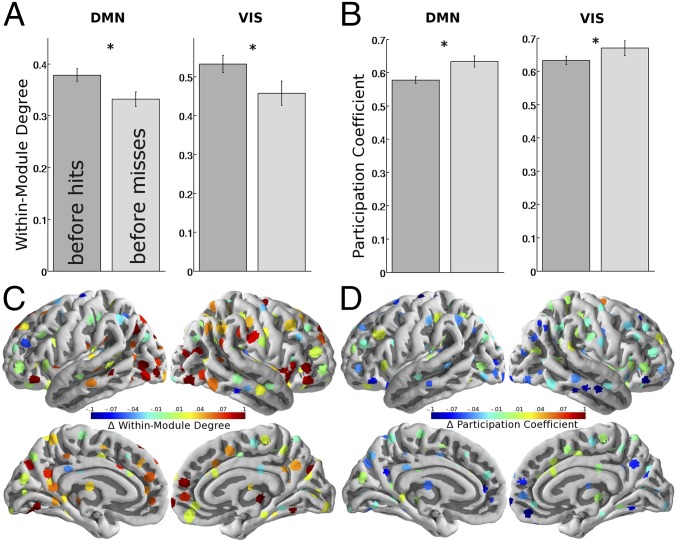
We investigated nodal graph metrics to answer whether the decrease in modularity before misses was driven by a decrease in within-module connectivity, an increase of connectivity to other modules, or both. Within-module degree measures how strongly each node is interconnected within its own module, and participation coefficient quantifies each node’s across-module connectivity (SI Text, section 8). We focused on DM and VIS networks, where the strongest modularity effect had been observed (Fig. 5 A and B). Within-module degree was significantly decreased before misses in both DM and VIS networks (average across the respective nodes and across five costs). This within-module degree decrease occurred across many but not all nodes of the graph (Fig. 5C), and the whole-brain average showed no significant difference (DM network: t = 2.88, P = 0.03; VIS network: t = 3.01, P = 0.015; whole brain: t = 1.96, not significant; P values Bonferroni-adjusted for three comparisons). Concurrently, participation coefficient was increased before misses in DM and VIS networks. Participation coefficient showed a universal pattern of decrease for pre-misses compared with pre-hits across the brain (Fig. 5D), and whole-brain average participation coefficient showed a significant effect (DM: t = 3.43, P = 0.014; VIS network: t = 2.55, P = 0.045; whole brain: t = 3.67, P = 0.005; Bonferroni-corrected for three comparisons). We replicated all within-module degree and participation coefficient results using the alternative graph partition that was derived from the participants’ own resting-state data (SI Text, section 6).

Fig. 5.

Nodal graph measures. In both the DM and VIS networks, the previously observed loss of modularity before misses was driven by both (A) a decrease in within-network connectivity as measured by within-module degree and (B) an increase in across-network connectivity as measured by participation coefficient. Across the whole brain, decreases in modularity before misses coincided with (C) decreased within-module degree in many but not all nodes and (D) a more global tendency toward increased participation coefficient. Error bars show SEMs. *Significant at P < 0.05 after Bonferroni correction.

Discussion

Our findings provide evidence that ongoing dynamic changes in the brain’s large-scale connectivity structure correlate with behavior. In a threshold detection task, where perception of an identical stimulus varied from trial to trial, we observed that prestimulus baseline connectivity differed between hits and misses. Most notably, before misses, functional connectivity was lower between task-relevant auditory cortices and the CO network involved in the maintenance of tonic alertness (27, 28). Conversely, connectivity before misses was higher between auditory cortices and the DM network often observed to activate when the brain disengages from external cognitive demands (29) or engages in internal mentation (30). Furthermore, the DM network showed decreased within-network connectivity before misses compared with hits. Using graph theory metrics, a combination of reduced within-network connectivity and stronger connectivity to other networks was observed foremost in the DM as well as VIS networks before misses. Both of these networks could be considered noncritical for the auditory detection task. These observations may, therefore, indicate a behavioral advantage from encapsulation of networks not critical for the task at hand.

On a trial by trial basis, prestimulus baseline connectivity was predictive of perceptual outcome on subsequent stimulation. We observed that functional connectivity across large-scale networks estimated in single-trial, short (15–25 s) baseline time windows was informative enough to allow some classification of the upcoming percept. Importantly, we made a particular effort to minimize the impact from evoked brain responses to the investigation of connectivity dynamics. Thus, our findings critically expand important previous fMRI investigations that used cue-evoked preparatory changes in connectivity for trial by trial prediction of behavior (17). Our results show that spontaneous, ongoing dynamics of brain connectivity are behaviorally relevant. Note that, in each classification cycle, all trials of all participants except for one trial entered the training set, and the classifier was tested on the left-out baseline segment. This procedure was chosen instead of the commonly used within-subject classification or leave one subject out procedures because of heterogeneity across participants and too few trials per participant (resulting from long interstimulus intervals). Because in general, the connectivity differences between individuals are much higher than between brain states within an individual, classifying across participants is difficult. However, our classifier’s above-chance prediction performance indicates that there are connectivity dynamics consistent enough across the participants of this study to yield an informative common pattern. Fig. 2B confirms such a common pattern.

Modeling whole-brain connectivity states using graph theory, we found that, in the context of a simple perceptual task, higher modularity characterized a more efficient brain state for stimulus detection. When the modular segregation weakened and widespread communication across modules increased, the target sound was more likely to go undetected. This effect was expressed in both decreased within-module degree (each node’s connectivity within its own module) in a variety of regions and widespread increase in across-module participation coefficient (each node’s connectivity to other modules) before misses. These whole-brain results expand previous observations in prestimulus functional connectivity confined to task-relevant regions (15) or networks (19).

Finally, our data suggest that the behavioral relevance of connectivity dynamics goes beyond the sum of distributed amplitude fluctuations of regional brain activity. Trial by trial prediction of subsequent percepts improved when the classifier additionally used baseline connectivity patterns compared with baseline activity amplitudes alone. This observation indicates that baseline connectivity provides additional information. Furthermore, investigation of baseline connectivity revealed a pattern diverging from and informing beyond that of baseline activity amplitudes. For example, baseline activity amplitudes and connectivity did not always change in the same direction; whereas higher baseline activity amplitude in the VIS network was biasing toward missing the subsequent stimulus (12), higher baseline connectivity in this network was predictive of successful stimulus detection. Conversely, in the DM network, both prestimulus baseline activity (12) and baseline connectivity were higher before hits compared with misses. In summary, not only activity amplitude fluctuations but also, their interplay across regions are relevant for behavior.

Our findings raise the fundamental question of why the brain’s processing architecture constantly undergoes such spatially extended modulations. In this auditory detection task, the behaviorally advantageous state showed only a limited and very specific increase of cross-module integration (e.g., between AUD and CO regions), whereas overall widespread integration was reduced. However, it is conceivable that, in more complex decision-making or working memory engagement, behavior would benefit from less modularity and hence, more widespread communication between task-relevant modules (e.g., see ref. 31 at much faster timescales). In other words, the brain may benefit from switching between states promoting locally integrated processing, e.g., for sensory perception, and states that integrate across modules to enable more complex cognition, albeit at the cost of modular tasks [see theoretical support for dynamic exploration of diverse intrinsic brain states (6) and the behavioral implications (32)]. In this context, it is important to note that ongoing dynamics in functional connectivity during cognitive task engagement may differ in strength and temporal and spatial characteristics from the dynamics during resting state, although both share the important property of occurring without direct dependence on changes in the external environment. Characterization of such differences is an important question that requires in-depth investigation in dedicated studies. Although this complex question is beyond the scope of this study, an initial comparison in this dataset is provided in SI Text, section 7 and Figs. S5 and S6.

Fig. S5.

Difference in cross-correlation for prestimulus task baseline > resting state. Each data point corresponds to a paired t test (uncorrected) between the two respective regions. No value passes FDR correction for multiple comparisons. Network labels: AUD, auditory; CO, cingulo-opercular; SAL, salience; FP, fronto-parietal; DAT, dorsal attention; DM, default mode; VIS, visual; SM, somato-motor; VAT, ventral attention; MEM, memory; Subcort, subcortical.

Fig. S6.

SD of Fisher-transformed Pearson correlations [SD(r)] measuring the ongoing dynamic change in functional connectivity during (A) baseline segments of the task and (B) the task-free resting state. C shows paired t tests (uncorrected) of their difference. No value passes FDR correction for multiple comparisons. Network labels: AUD, auditory; CO, cingulo-opercular; SAL, salience; FP, fronto-parietal; DAT, dorsal attention; DM, default mode; VIS, visual; SM, somato-motor; VAT, ventral attention; MEM, memory; Subcort, subcortical.

We conclude that spontaneous ongoing changes in baseline functional connectivity in and across large-scale brain networks correlate with perception and behavior. We found the dynamics in the strength of modular structure to be particularly important for behavior. Our analysis of large-scale connectivity captured functional connectivity dynamics occurring at infraslow timescales. Interestingly, behavioral performance when repeating the same task over and over again shows fluctuations with a qualitatively similar temporal profile as ongoing brain activity (i.e., high power at low frequencies; 1/frequency scale-free time history) (33). Although this temporal profile supports a strong relation between infraslow brain dynamics and behavioral variability, it likewise shows that behavior fluctuates as well at faster frequencies. The latter requires investigation of brain dynamics (in likely smaller networks) with methods allowing higher temporal resolution. Furthermore, our analyses could only capture dynamics that were consistent across trials of the same perceptual outcome (hits and misses) and across participants. However, functional connectivity dynamics are much more variable than observable in such dichotomous categorizations, with a wide-ranging repertoire of possible itinerant connectivity states. Importantly, however, in probing ongoing dynamic connectivity according to perceptual outcome, we were able to extract common characteristics of connectivity states that account for behavioral variability. Ongoing brain activity constitutes the vast majority of brain activity, and evoked responses add only a relatively small proportion (34). The findings obtained here, therefore, illustrate that any attempt to link behavior to brain function must conceptually integrate the role of ongoing brain activity and its connectivity dynamics.

Methods

For paradigm, behavior, and fMRI data acquisition (3 Tesla, repetition time = 1.5 s) see ref. 12. Regions of interest (ROI) definitions are in SI Text, section 1.

Preprocessing and Head Motion.

Standard preprocessing included realignment, coregistration, normalization and 5-mm FWHM spatial smoothing in SPM5. From each ROI’s linearly detrended signal time course, we regressed out the estimated evoked response up to 24 s poststimulus for hits, misses, and false alarms using stick functions from the previously reported finite impulse response deconvolution (12). We regressed out as nuisance regressors global gray matter, white matter, cerebrospinal fluid, out-of-brain signals, and six linear head motion parameters.

To investigate the potential nonlinear impact of head motion, we calculated the number of motion outlier volumes using the derivative root mean square method (35) implemented in FSL (FMRIB). After trial by trial segmentation of the time courses (see below), the numbers of motion outliers per experimental run before hits (1.18 ± 1.53) vs. misses (0.85 ± 1.65) did not differ from each other (P = 0.63). Furthermore, the difference of graph metrics across pre-hits and pre-misses did not correlate with the difference in the number of head motion outliers across pre-hits and pre-misses over the participant group (modularity: r² = 0.09, P = 0.37; within-module degree: r² = 0.1, P = 0.34; participation coefficient: r² = 0.002, P = 0.9).

Baseline Time Segments.

For classification analyses of activity amplitudes and connectivity requiring single-trial data, full baseline segments of 15 s or longer were used (292 hits and 172 misses across all participants) (Fig. 1). For all other analyses, only the last four volumes (6 s) before the next event were used from each segment of 6 s or longer, because the full baseline segment was not necessary for these analyses, and ongoing activity from the closest time points will have the strongest impact on the upcoming trial (cf. 12). These four-volume segments were concatenated across all hit trials (197 ± 71 volumes), all miss trials (129 ± 56.5), and all resting-state pseudotrials (160 volumes), yielding one correlation matrix per condition per participant.

Classification.

For each single prestimulus baseline segment, Pearson cross-correlations (baseline connectivity classification) or mean signal amplitudes (baseline activity classification) entered classification. In each classification cycle, all data of all participants (464 trials), except for a single baseline segment, entered feature selection and the training set. The classifier was then tested on the left-out baseline segment. For baseline connectivity feature selection, the strongest 12 connections were selected from a 24 × 24 matrix expressing the difference of pre-hits vs. pre-misses connectivity as t values similar to those in Fig. 2B but generated leaving out the trial to be tested. For baseline activity, all 24 ROIs were used. Mean value across both categories (pre-hits and pre-misses) was removed for each feature and participant; 2,000 × 464 permutations of the training data labels gave the chance distribution.

Graph construction.

Adjacency matrices were created for each participant from the Fisher-transformed Pearson cross-correlation matrices for pre-hits, pre-misses, and resting state thresholded at five cost values (fraction of strongest edges) to ensure that effects were not driven by particular connection density: 0.05, 0.1, 0.15, 0.2, and 0.25.

Graph metrics.

Equations for modularity (26), within-module degree, and participation coefficient (36) are in SI Text, section 8.

Statistical hypothesis testing on graph metrics.

Modularity, within-module degree, and participation coefficient cannot be assumed to be normally distributed. We, therefore, generated chance distributions for t and F values from 2,000 permutation cycles, where data from the different conditions (pre-hits and pre-misses) were randomized within each participant.

SI Text

Section 1: Regions of Interest.

The following two sets of regions of interest were used.

• i)Twenty-four regions as part of several well-known brain networks were defined on a participant by participant basis using seed-based resting-state functional connectivity and a functional auditory localizer. The task-free resting-state session (20 min) was recorded on a different day before the experiment. These regions were chosen as in our previous publication, thereby making this investigation of connectivity directly comparable with our previous report related to prestimulus activity (12). Seed-based maps were defined for each participant (P < 0.001, uncorrected) and further confined by group-level maps (P < 0.005, uncorrected) identical to the procedure and seed coordinate choice described in ref. 12. Each network was defined as the conjunction of two seed-based maps with the following seeds: posterior cingulate cortex/precuneus (−5, −49, and 40) and medial prefrontal cortex/ventral anterior cingulated cortex (−1, −47, and 4) for the DM network; right intraparietal sulcus (27, −58, and 49) and right frontal eye fields (24, −13, and 51) for the DAT network; right anterior insula (4, 16, 36) and right anterior thalamus (10, −15, and 8) for the CO network; and right and left dorsolateral prefrontal cortex (±43, 22, and 34) for the FP network. The resulting set of regions encompassed three task-positive networks and the DM network. In accord with well-known intrinsic network structure (1), the task-positive networks are the CO network comprised of the dorsal anterior cingulate cortex, the anterior insula/frontal operculum, and the anterior thalamus; the FP network comprised of the dorsolateral prefrontal cortex, the rostrolateral prefrontal cortex, the inferior parietal cortex, and the paracingulate cortex; and the DAT network comprised of the intraparietal sulcus, the frontal eye fields, and the middle temporal area. The DM network included posterior cingulate/precuneus, medial prefrontal cortex, and posterior lateral parietal cortex. Fig. 2A shows the group-level maps of these regions. Additionally, left and right stimulus-responsive AUD networks were defined participant by participant as auditory-responsive voxels selected from the contrast (hits and misses) > baseline masked by the auditory functional localizer (12).
• ii)Two hundred thirty-eight spheres of 6-mm radius from the functional atlas in the work by Power et al. (1) after excluding 26 atlas nodes that were not covered in all participants. The majority of exclusions were the most dorsal somatomotor nodes (8 nodes) and ventral or polar temporal nodes that the atlas does not assign to any partition (10 nodes labeled uncertain).

Section 2: Connectivity Pattern and Modularity After Equating Data Lengths.

Because across the group, more time points entered the generation of the correlation matrices and ensuing graphs for pre-hits baseline compared with pre-misses, we repeated the analyses of networkwise connectivity patterns and the calculation of graph modularity after equating the number of time points that entered the correlation matrices. To do so, the minimum total volume number m among the three mental conditions (pre-hits, pre-misses, and resting state) was determined for each participant. For each participant, each condition was then limited to a randomly chosen set of m volumes.

Networkwise connectivity effects remained statistically equivalent. The two-way ANOVA of network (AUD, CO, FP, DAT, and DM) and condition (pre-hits and pre-misses) showed a significant interaction (F_2.96,29.6 = 3.75, P = 0.022), and a two-sided posthoc t test was significant only in the DM network (stronger within-network connectivity for pre-hits: t₁₀ = 4.18, P = 0.002). For the coupling of the task-relevant AUD network with the other networks, we found an interaction of condition (pre-hits and pre-misses) and network (CO, FP, DAT, and DM): F_2.8,28.44 = 6.18, P = 0.003. Two-sided posthoc t tests were significant for AUD–CO connectivity (t₁₀ = 3.58, P = 0.005) and AUD–DM connectivity (t₁₀ = −3.22, P = 0.009). For a fine-grained visualization, the group-level contrast between the full 24 × 24 correlation matrices for pre-hits and pre-misses is shown in Fig. S1.

Likewise, for graph modularity, the effects remained statistically equivalent (mean across costs; pre-misses vs. pre-hits: t = 3.36, P = 0.003; pre-misses vs. resting state: t = 2.39, P = 0.0465; pre-hits vs. resting state: t = 0.81, not significant; all P values were adjusted using Bonferroni correction for three comparisons; P values were determined in a permutation procedure detailed in Methods).

Note that this control analysis was not necessary for classification analyses, because different amounts of data in each class would affect the permutation chance level equally.

Section 3: Comparing Cross-Correlations for Baseline Periods After Hits and Misses.

One concern might be whether the observed difference in connectivity pattern (Fig. 2B) reflects the residuals of the previous evoked response rather than ongoing (nonevoked) connectivity variations. We, therefore, generated the connectivity contrast after concatenating baseline segments according to the previous rather than the upcoming percept (Fig. S2). Note that the connectivity pattern in Fig. S2 differs considerably from the same data when they are ordered according to subsequent percepts instead of foregone percepts (compare with Fig. 2B).

Section 4: Classification with Redundant Features.

The performance of a classifier will not substantially increase if additional features are included that do not add new, nonredundant information, even if the added features on their own have discrimination power. To show this using our own data, classification of prestimulus activity amplitudes was repeated after duplication of the 12 most discriminative activity amplitude features for each trial. In other words, instead of adding the 12 most discriminative features from prestimulus connectivity (combined classification is given in the text), we added an identical set of 12 activity amplitude values using the same feature selection procedure as applied for connectivity (Fig. S3). The addition of even the most discriminative duplicate features caused only a minor change in classifier performance (z score = 2.53, P = 0.006, power = 0.76, 59.7% against chance level of 54.2%) compared with the strong increase that we observed when combining prestimulus connectivity features with activity features (z = 3.87, P = 0.00005, power = 0.98, 63.6% vs. 55.4%).

Section 5: Power Investigation of Classification Improvement from Combined Features.

To further quantify the improvement in classifier performance for the combined features, we computed the probability that the observed rate of classification (connectivity: 62.5%; activity: 60.8%; combined: 63.6%) is greater than the classifier rate at the 5% type I error observed in corresponding permutation null distributions. If we consider the classification significant when the observed classification rate is above the 5% threshold of the null distribution, then the described computation is the power analysis for classification success. The probability of the classifier rates is given by the binomial distribution with n = 464 trials and P = 0.625, 0.608, or 0.636 for connectivity, activity, and combined, respectively. The power (i.e., the cumulative probability of a classifier rate falling above the 5% type I error) was 0.67 for prestimulus connectivity, 0.73 for prestimulus activity amplitudes, and 0.98 for combined activity amplitudes and connectivity. The latter, thus, represents a marked improvement in classification performance compared with activity amplitudes or connectivity alone.

Section 6: Graph Metrics Using a Graph Partition Derived from the Resting State.

Analyses in the text used a partition of the graph according to the scheme provided in the atlas in the work by Power et al. (1) rather than partitions from our resting-state data. This allowed unbiased investigation of graph metrics from the resting state. Here, we repeated all graph analyses using a partition from the resting-state session of our own participants instead to ensure that results were not driven by the particular modular partition structure used. This modular partition was derived from a graph generated from an average correlation matrix across participants at a cost value of 0.05 using the spectral algorithm by Newman and Girvan (26) that maximizes modularity. It resulted in a partition of the graph into 13 modules (Fig. S4) comparable with the 12 modules provided by Power et al. (1).

Again, modularity differences across mental states were statistically significant (mean across costs; pre-misses vs. pre-hits: t = 3.28, P = 0.011; Bonferroni-corrected for three comparisons; permutation test as described in Methods). The pairwise comparisons with resting state remained likewise statistically significant, but note that these should be interpreted with caution, because the partition itself was derived from these resting-state data (pre-misses vs. resting state: t = 2.60, P = 0.024; pre-hits vs. resting state: t = 0.54, not significant; P values corrected).

Likewise, all of the nodal properties showed equivalent results using this partition scheme. We investigated within-module degree (average across five costs; DM network: t = 3.50, P = 0.006; VIS network: t = 3.52, P = 0.017; whole brain: t = 1.23, not significant; P values corrected) and participation coefficient (DM network: t = 4.13, P = 0.008; VIS network: t = 2.66, P = 0.044; whole brain: t = 3.64, P = 0.011; P values corrected). In summary, these analyses underline the robustness of global and nodal changes across mental conditions independent of the particular partition scheme.

Section 7: Comparing Cross-Correlation Structure and Dynamics for Task Baseline Vs. Resting State.

We compared the connectivity structure during all prestimulus baseline time windows of one task session with pseudotrial baseline time windows of the task-free, resting-state session (last four volumes) (compare with Methods). Here, baseline windows during task are concatenated irrespective of subsequent perceptual outcome of hits/misses. We used the functional atlas regions rather than seed-based regions, because the seed-based regions are defined from the resting-state session, which could bias the analysis. This analysis (Fig. S5) visualizes the change in connectivity structure caused by the constant and continuous task context compared with the absence of such task context. In contrast, the comparisons across pre-hit and pre-miss baseline windows in the text target the ongoing dynamic changes of connectivity occurring spontaneously during the task session.

Next, we compared the ongoing dynamic changes in functional connectivity during prestimulus baseline of task vs. task-free resting state. To this end, we calculated the SD of Pearson correlations across all respective time windows for each participant and region pair (Fig. S6 A and B). Because this analysis is based on single-window Pearson correlations, only baseline segments of >15 s were used (compare with the data used for trial by trial classification analysis). To make sure that the estimated variability of the SD was comparable between task and the resting-state session, we used baseline segments from a single task session only. We used the task session with the highest number of long (>15 s) baseline segments (18.1 ± 4.5) and limited the resting-state baseline segments to the same number for each participant. Fig. S6C shows group-level paired t tests contrasting the SD of correlations from task baseline vs. resting state. No clear network pattern is visually identifiable, and no t value passes false discovery rate (FDR) correction. We repeated the analysis using all baseline segments (41.5 ± 15.3 segments for task baseline collapsed over hits and misses and 23.1 ± 0.7 for resting state) and again, did not observe any significant changes at FDR-corrected level. These results need to be interpreted with caution, however, because the tests are performed in a univariate manner for each region pair rather than assessing changes in the overall pattern of connectivity. The latter requires the development of multivariate methods that appropriately deal with the complex, structured data dependencies in correlation matrices in dedicated future studies targeting the differences in ongoing activity dynamics across rest and task.

Section 8: Graph Metrics Definitions.

Modularity (26) was defined as

$$\text{modularity}={\displaystyle \sum _{u\in M}\left[e_{uu}-{\left({\displaystyle \sum _{v\in M}{e}_{uv}}\right)}^2\right]},$$ [S1]

where e_uu is the fraction of all edges that connect two nodes within a module u, e_uv is the fraction of all edges connecting nodes in module u with nodes in module v, and M is the total number of modules. The contribution of individual modules u to modularity is given as $\left[e_{uu}-{\left({\displaystyle {\sum }_{v\in M}{e}_{uv}}\right)}^2\right]$.

Within-module degree is calculated as

$$\text{within}‐\text{module}\hspace{0.17em}{\text{degree}}_i=\frac{k_i\left(m_i\right)}{n\left(m_i\right)},$$ [S2]

where m_i is the module containing node i, k_i(m_i) is the number of edges between node i and all other nodes in m_i, and n(m_i) is the number of nodes in module m_i. Note that this definition differs from the often used within-module degree z score, which defines a node’s within-module degree relative to that of other nodes in m_i (36).

Participation coefficient measures the number of intermodule connections for each node normalized by their expected value (36):

$$\text{participation}\hspace{0.17em}{\text{coefficient}}_i=1-{{\displaystyle \sum _{m\in M}\left(\frac{k_i\left(m\right)}{k_i}\right)}}^2,$$ [S3]

where k_i(m) is the number of edges between node i and all nodes within module m, and k_i is the total number of edges to node i across the entire graph.