A simple nutrient-dependence mechanism for predicting the stoichiometry of marine ecosystems

Significance

The elemental ratios of nitrogen, phosphorus, and carbon in marine phytoplankton can diverge significantly from the “Redfield ratio,” but the underlying reasons have been hard to elucidate. As a result, global biogeochemical models often ignore this stoichiometric variability. Here we show that, hidden within the noise of a large dataset of particulate measurements, a surprisingly consistent relationship exists between community P:C and dissolved phosphate concentrations. The plasticity of ecosystem stoichiometry in the face of nutrient scarcity, with greater plasticity for P relative to N, appears to explain the main divergences from the Redfield ratio. When included in a simple model, the relationship implies a more important role for low latitude nutrient cycling in the biological pump than is commonly assumed.

Abstract

It is widely recognized that the stoichiometry of nutrient elements in phytoplankton varies within the ocean. However, there are many conflicting mechanistic explanations for this variability, and it is often ignored in global biogeochemical models and carbon cycle simulations. Here we show that globally distributed particulate P:C varies as a linear function of ambient phosphate concentrations, whereas the N:C varies with ambient nitrate concentrations, but only when nitrate is most scarce. This observation is consistent with the adjustment of the phytoplankton community to local nutrient availability, with greater flexibility of phytoplankton P:C because P is a less abundant cellular component than N. This simple relationship is shown to predict the large-scale, long-term average composition of surface particles throughout large parts of the ocean remarkably well. The relationship implies that most of the observed variation in N:P actually arises from a greater plasticity in the cellular P:C content, relative to N:C, such that as overall macronutrient concentrations decrease, N:P rises. Although other mechanisms are certainly also relevant, this simple relationship can be applied as a first-order basis for predicting organic matter stoichiometry in large-scale biogeochemical models, as illustrated using a simple box model. The results show that including variable P:C makes atmospheric CO₂ more sensitive to changes in low latitude export and ocean circulation than a fixed-stoichiometry model. In addition, variable P:C weakens the relationship between preformed phosphate and atmospheric CO₂ while implying a more important role for the nitrogen cycle.

Nutrient elements are used by phytoplankton to synthesize molecules, in order to accomplish biochemical functions. Some of these molecules are absolutely necessary, and the nutrient elements have no substitutes. Examples are P in nucleic acids, N in amino acids, and Fe in the photosynthetic apparatus (1). However, there is a degree of plasticity in the molecular assemblage required per phytoplankton cell, which varies between species and between clades (2, 3). Furthermore, there is a capacity for plasticity in molecular composition of even a given species, as shown in culture experiments (4, 5). Such plasticity leads to variability in the elemental ratios of nutrients in marine phytoplankton, widely documented in laboratory and field measurements (2, 6, 7). Recent analyses of global nutrient and particulate observations have shown that N:P, the most commonly discussed ratio, varies regionally, including low N:P in the high-latitude Southern Ocean and high N:P in the oligotrophic regions (7–9). Explanations of high N:P in oligotrophic waters have often invoked an enhanced reliance on N-rich proteins for gathering scarce resources (1, 10), whereas low N:P in the Southern Ocean has been variously attributed to the abundance of P-rich molecules in cold, fast-growing plankton (11), or to the availability of Si, which supports P-rich diatom communities (8, 12).

Despite an abundant literature on stoichiometric variability and its potential causes, no simple predictive relationship has been widely adopted in global biogeochemical models. Instead, the vast majority of global biogeochemical models assumes fixed C:N:P in organic matter, including most participants in the recent Coupled Model Intercomparison Project, CMIP5 (13). Thus, the potential impact of changes in organic matter stoichiometry on ocean carbon storage and oxygen consumption remain largely unexplored. The neglect of stoichiometric variability is due, at least in part, to the lack of a clear predictive framework.

Here, it is argued that the concentration of a nutrient element in seawater can provide a suitable predictive framework, because it is a critical determinant of the rate at which that element will tend to be taken up by the organisms in the local community. This hypothesis builds on classic resource competition theory (14), which argues that if the concentration of an element is low, such that uptake is difficult, the community will be dominated by organisms that are well adapted to a low cellular quota of that nutrient (10). If, on the other hand, the concentration is high, facilitating high uptake rates, the community will be dominated by organisms that are capable of taking advantage of that nutrient to grow faster. This suggestion leads to clear predictions with significant biogeochemical consequences, as outlined below.

Observed Patterns

The cellular abundances of N and P are most often discussed in terms of the N:P ratio. However, carbon is by far the dominant element in biomass (not counting H and O, derived from water). It typically outweighs nitrogen by a factor of about seven, because of its central structural role in most organic molecules, and is thus the most logical normalizing factor for considering nutrient ratios. Relative to carbon, the ∼30 essential nutrient elements display a range of plasticities in their cellular requirements (15). Nitrogen tends to be the least plastic, varying in cellular N:C molar ratios from ∼1/5 to 1/10, a factor of two (2). The cellular P:C ratio is more variable, due to the ability of organisms to substitute phosphorus compounds such as phospholipids (16), and ranges from ∼1/50 to 1/500, or by about a factor of 10. Iron is even more variable, given the ability to substitute with other elements, such that Fe:C varies from about 1/1,000 to 1/1,000,000, or three orders of magnitude (17).

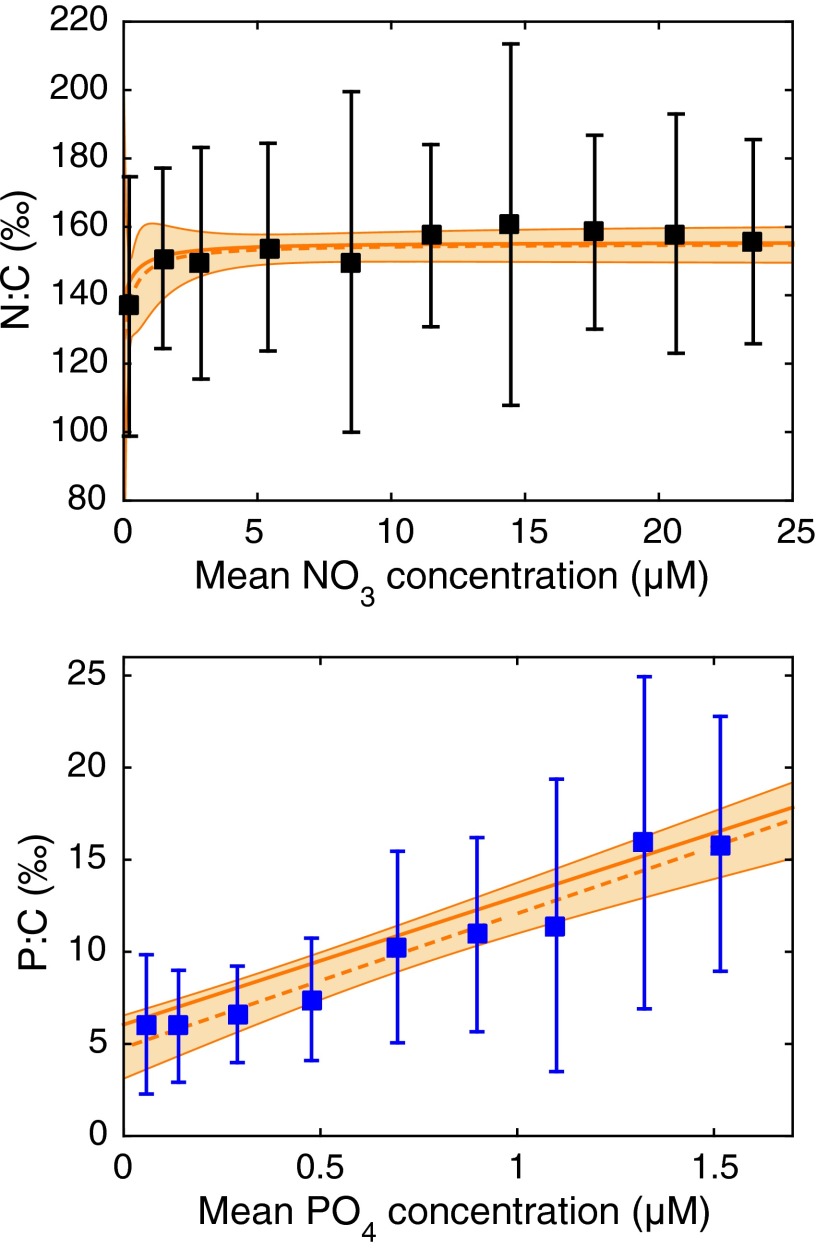
If we examine oceanographic data in terms of N:C and P:C, rather than the more commonly cited N:P ratio, some rather simple patterns emerge. Fig. 1 shows these ratios measured in hundreds of globally distributed organic particulate samples (locations shown in Fig. S1), binned by nutrient concentrations, and with the elemental ratios shown in permil units (‰) for ease of notation. As indicated by the large error bars, there is a broad range in the measured stoichiometry of particles found in waters of any given ambient nitrate or phosphate concentration, which partly reflects measurement error and the variable presence of nonliving detritus. Because these samples do not discriminate among particle types, they also include a significant fraction of heterotrophic plankton in addition to phytoplankton. However, the striking finding from this large dataset is that, despite wide variability among individual samples, the means of the bins display well-behaved trends with increasing ambient nutrient concentrations. The N:C increases by ∼20% over the range of 0–3 μM NO₃, and then remains relatively constant (Methods). Meanwhile, the P:C increases linearly across the observed range of PO₄ concentrations. These relationships are consistent with hyperbolic dynamics for the ratios of both elements as functions of the corresponding ambient nutrient concentrations, with saturation occurring for the N:C in nitrate-rich regions, but with all oceanic conditions falling below saturation for the P:C, so that the relationship of P:C vs. PO₄ is linear over the range of oceanic PO₄ concentrations sampled here. A linear regression of P:C vs. PO₄, using all available stations (Fig. S2), suggests that the relationship can be approximated as P:C = 6.9 ‰ μM⁻¹ × PO₄ + 6.0‰ (r² = 0.36, P < 10⁻⁶⁰). Binning and log-transforming the data leads to slight variations in the regression, with a similar slope but slightly lower intercept (Methods).

Fig. 1.

Observed elemental ratios of suspended particles at the ocean surface. Stations were binned according to the NO₃ concentration (Upper) and PO₄ concentration (Lower). Squares show the log-transformed mean of the elemental ratios of all measurements within each bin. Error bars show 1 SD of the elemental ratios of all measurements within each bin. The solid orange line in Upper shows a hyperbolic approximation to the variability in the mean, optimized from all data, whereas the dashed orange line is optimized from the binned, log-transformed means. The solid orange line in Lower shows a linear fit to all P:C data, referred to here as the Line of Frugality, whereas the dashed orange line shows an alternative linear fit using the means of the binned data. The orange-shaded regions in both panels show the combined 95% confidence interval spanning the binned and unbinned regressions.

These empirical relationships make sense. Nutrient elements exist at very low concentrations in the marine environment. Pumping them into the cell—and keeping them there—is a costly undertaking, and becomes diffusion-limited at low concentrations (18, 19). At very low concentrations, the benefit to be gained from having a bit more of an element within the cell could be easily negated by the high cost of bringing it into the cell. However, as the ambient concentration of the nutrient rises, it becomes much less costly to make it available, and therefore, the marginal increase in welfare to be gained from its use becomes worthwhile.

The existence of elemental plasticity can be conceptualized as the product of evolution under perennial nutrient scarcity in the ocean (20). A frugal phytoplankter carries out its tasks using smaller quantities of any molecules whose nutritive ingredients are scarce in the environment. Given millions of years of competition, the most frugal phytoplankton could be expected to have evolved to be very good at this, explaining the relatively high growth rates in nutrient-poor regions (21). An example of a frugal phytoplankter would be Prochlorococcus, with a high nutrient uptake capability despite a low cellular quota (22). On the other hand, less frugal phytoplankton, such as the diatoms that dominate eutrophic waters, have the genetic tools to construct a more diverse array of nutrient-rich molecules to accelerate their growth. There are rapidly diminishing returns on the benefits gleaned from these additional molecules, so that the average growth rates of a well fed, less frugal phytoplankton are only modestly elevated over those of the most frugal phytoplankton. However, it’s enough of a benefit that, under most conditions, given high nutrient concentrations and enough time, the community will tend to become dominated by the less frugal variety.

The robust linear correlation of P:C vs. PO₄ suggests that phosphorus frugality is an important consideration for phytoplankton everywhere in the ocean. Because this is an average expectation for the entire community, and because the samples probably include a significant fraction of heterotrophic biomass with less plastic stoichiometry (23), the underlying dependence of phytoplankton P:C on PO₄ may be stronger than implied by the empirical regression. This whole-community linear expectation could be locally modified by other factors such as water temperature and light intensity. Indeed, a regression of the P:C data vs. in situ temperature also shows a highly significant, although weaker, relationship (r² = 0.24), with a negative slope; part of this reflects the fact that cold waters typically have higher PO₄, but it has also been shown that more ribosomes are required to meet the same growth rate at low temperatures, exerting an additional effect on the P:C (11). Such modification could lead to small-scale spatiotemporal variability, or even cause large regions to diverge from the global “Line of Frugality.” However, the fact that the Line of Frugality explains 36% of the observed variability, despite measurement error, spatial and temporal patchiness, and non-steady-state conditions, suggests that the PO₄ concentration is a very important, and perhaps the most important single factor in determining community P:C at the ocean surface. In contrast, the absence of any dependence of N:C on NO₃ above a NO₃ concentration of ∼3 μM indicates that other environmental and ecological factors determine N:C at all but the lowest NO₃ concentrations. The saturation of average N:C at nitrate concentrations of about 3 μM does not indicate that nitrate is not limiting in the ocean. On the contrary, it is the most important limiting element, at least in a proximal sense, as clearly shown by nutrient assays everywhere outside of High Nitrate Low Chlorophyll (HNLC) regions (15). The observations here simply imply that higher N:C does not, on average, confer a consistent competitive advantage above a ratio of ∼155 ‰.

It follows that the common observation that N:P increases under oligotrophy would arise simply due to low N:C plasticity compared with P:C plasticity. The observed particulate data suggest that the average N:C of planktonic communities increases by less than 30% above its minimum value of ∼125 ‰ in response to an increase of NO₃, whereas community average P:C can increase by a factor of at least 3 above its minimum of ∼5 ‰ under increasing PO₄, exhibiting an order of magnitude more response to nutrient availability than the N:C. Thus, moving from eutrophic waters that are rich in both NO₃⁻ and PO₄^3- to oligotrophic waters that are poor in both NO₃⁻ and PO₄^3- involves a small decrease of N:C but a very large P:C decrease. As a result, nutrient-dependent stoichiometric plasticity would tend to drive high N:P in oligotrophic regions and low N:P in eutrophic regions. In agreement with the underlying dynamic of chemostat models (10, 19), this mechanism suggests that N:P in phytoplankton is determined by the absolute concentrations of NO₃⁻ and PO₄^3-, rather than their ratio, and explains why the NO₃:PO₄ ratio of ambient waters is a poor predictor of phytoplankton N:P (24).

Global Picture

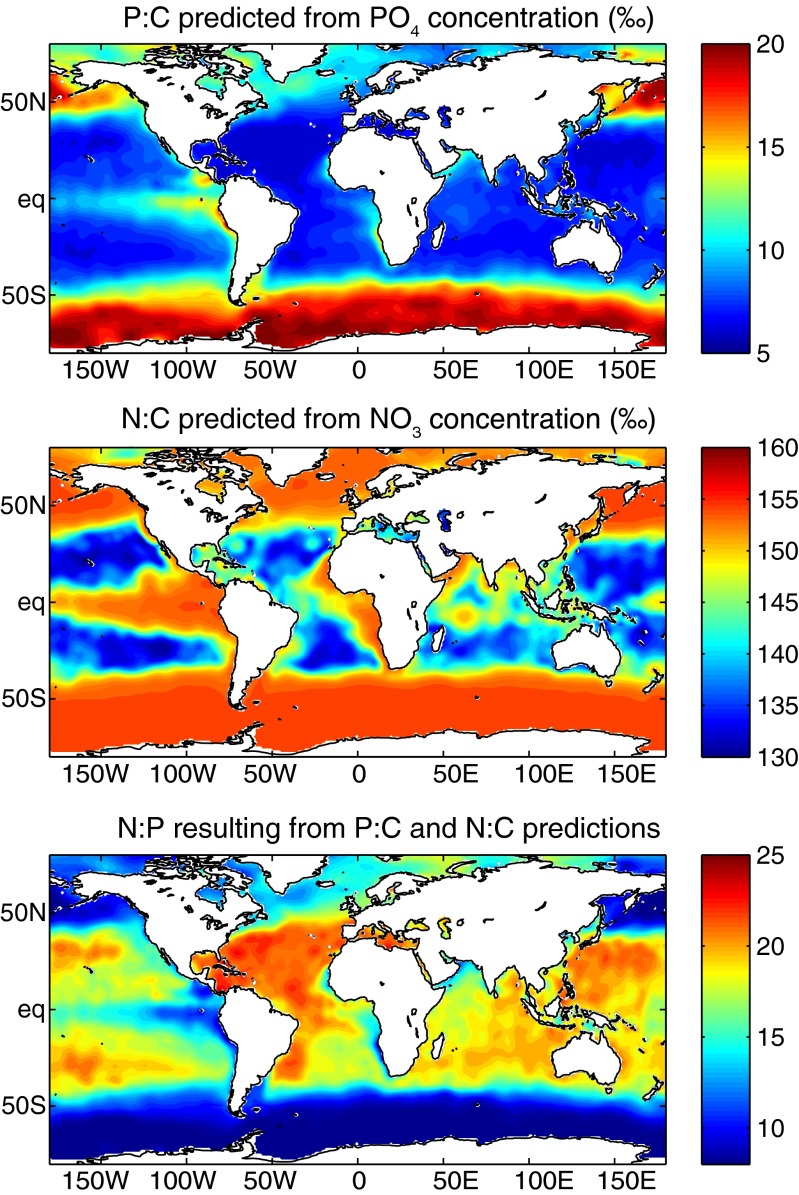
The simple predictive model proposed here can be used to generate global predictions of organic matter stoichiometry from observed surface nitrate and phosphate concentrations. The results are shown in Fig. 2. The predicted P:C agrees broadly with recent estimates from two global inverse models (Fig. S3), with the only significant discrepancy being that the inverse models suggest higher P:C in the subpolar North Atlantic than predicted here. The calculated N:C and P:C in Fig. 2 follow similar spatial patterns, given the strong correlation of NO₃ and PO₄ at the ocean surface. However, as expected from the reasoning laid out above, the N:P varies roughly inversely with the macronutrient concentrations, because N:C varies less than P:C. It should be emphasized that this result arises entirely from the elevated plasticity of P:C relative to N:C, and is not dependent on assumptions regarding the allocation of nutrient elements to cellular machinery or taxonomic groups.

Fig. 2.

Predicted elemental ratios at the ocean surface. The elemental ratios indicated are predicted from the Line of Frugality shown in Fig. 1, using the observed PO₄ and NO₃ concentrations from the upper 30 m in the World Ocean Atlas (45).

That is not to say that this simple mechanism is inconsistent with either of these other hypotheses. It is entirely possible that frugal phytoplankton do, in fact, produce more resource-gathering molecules relative to RNA (1). Similarly, the taxonomic composition of ecosystems in different parts of the ocean could reflect the fit between phytoplankton elemental compositions and the available nutrients (7). Diatoms with high P:C flourish in phosphate-rich regions (which also happen to be nitrate-rich), and therefore diatom-dominated communities have low N:P.

It is also important to emphasize that this prediction is suggested to hold only at large spatial and temporal scales, with important exceptions. Perhaps most importantly, Phaocystis, a prymnesiophyte that tends to have relatively low P:C, frequently blooms in the PO₄-rich Southern Ocean (12). The suggestion here would be that the success of Phaocystis reflects the relatively small advantage that less frugal phytoplankton gain by using more P such that, given other environmental factors (such as grazing pressures, temperature, light intensity, or iron availability), the more frugal Phaocystis can be very successful without taking full advantage of the abundant PO₄. This wrinkle would appear to be given additional weight by the analysis of DeVries and Deutsch (25), which suggests that the domains of polar oceans with seasonal sea ice may be typified by low P:C despite high phosphate concentrations. If it turns out that seasonal sea ice zones are indeed typified by anomalously low P:C, this could be an important consideration for carbon cycling during ice ages as well as in the future (8). At the same time, the availability of silicate could potentially expand the range of P-rich diatoms in the Southern Ocean northward into lower-PO₄ waters, driving relatively high P:C export at relatively low phosphate concentrations as proposed by Weber and Deutsch (8). For the time being, we assume these other factors to be stationary with respect to the distribution of phosphate, and explore the impact of changes in P:C driven exclusively by phosphate cycling on ocean carbon storage.

Implications for Carbon Export and Atmospheric CO₂

The global oceanic phosphorus inventory is determined by the balance between the supply rate, ultimately derived from the weathering of minerals on land, and the removal by burial in seafloor sediments (26). If the P:C of organic matter were fixed, the maximum amount of C that could be stored in the ocean interior by the biological pump would simply be equal to the P inventory divided the P:C ratio. This concept led to some early suggestions that glacial-interglacial changes in the global biological pump strength could have been caused by changes in either the global P inventory, or the P:C ratio (27). In addition, the use of preformed phosphate (i.e., phosphate that is transported physically to the ocean interior from phosphate-rich regions of the surface ocean, rather than being exported to the interior as a component of organic matter and subsequently remineralized) as a metric for the global strength of the biological pump is typically simplified to assume a constant P:C ratio, although the possibility that P:C varies is acknowledged (28–30). The theory associated with the concept of preformed phosphate suggests that the combined influences of ocean circulation and carbon export on atmospheric pCO₂ can be approximated quite well by the concentration of phosphate in the high-latitude regions that ventilate the deep ocean, most importantly the Southern Ocean.

The argument advanced here suggests that less-frugal phytoplankton in phosphate-rich regions actually use up P rapidly, without attaching much C_org to it. This profligate use of P makes for a relatively weak biological pump, for a given inventory of P. In contrast, more frugal phytoplankton attach a lot of C_org to every atom of P they export, storing a lot more respired carbon in the ocean interior per unit P exported. As such, in terms of carbon storage, not all use of a PO₄ molecule can be seen as equal.

We use a standard three-box ocean model coupled to a one-box atmosphere (Fig. S4), after Sarmiento and Toggweiler (31), to illustrate how P:C variability alters carbon export and atmospheric CO₂. Ref. 8 followed a similar approach to test the impact of a prescribed change in the P:C of export in the Southern Ocean. Although greatly simplified, the box model framework allows the rapid computation of a large number of experiments to plumb the main sensitivities of carbon storage to circulation and community export given different stoichiometries. The ocean boxes include a low-latitude surface box, high-latitude surface box, and a deep box, with realistic proportions (Methods). The box model predicts P:C as a function of PO₄ using the linear fit to the unbinned data shown by the solid line in Fig. 1. The model is then used to explore the impact of varying P:C, compared with fixed P:C, through a series of experiments. These experiments test the effect of variable high-latitude export Φ_h (which could vary due to iron supply to the Southern Ocean, or sea ice coverage), in combination with simultaneous changes in low-latitude phosphate concentration PO_4l (which might vary with changes in nitrogen fixation and denitrification rates), and the large-scale ocean circulation (varying the thermohaline overturning T and high-latitude vertical mixing f_hd).

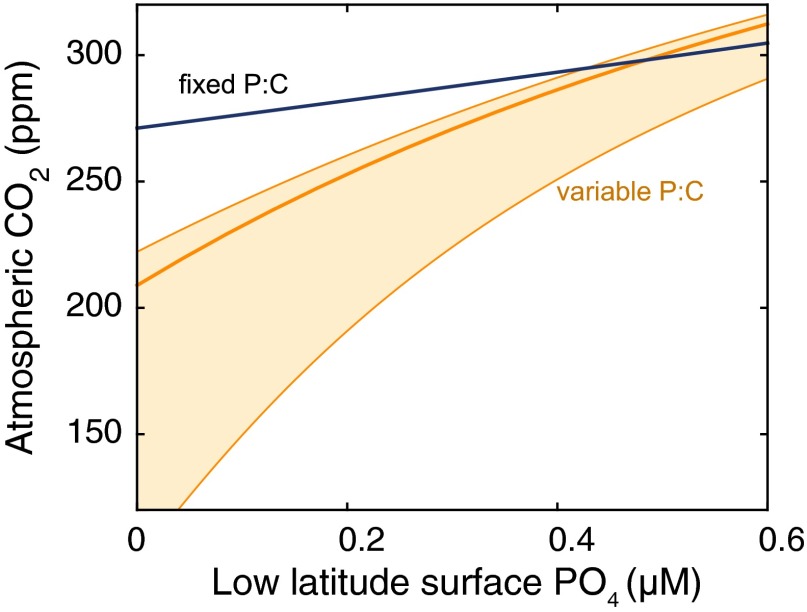
When the P:C is fixed, the prescribed changes modify atmospheric pCO₂ in a fairly strict relationship with preformed PO₄, as determined by the PO₄ concentration in the high-latitude box (Fig. 3) (31, 32). This strict relationship holds true over the range of changes in PO_4l, T, f_hd, and Φ_h, and indicates that in a world with fixed stoichiometry, it is hard to change the strength of the biological pump without changing preformed PO₄. However, when P:C is plastic, the effects of PO_4l and T can diverge significantly from the strict preformed-PO₄ relationship, producing a range of pCO₂ for a given preformed PO₄ concentration. This divergence is particularly pronounced for PO_4l, which has a far greater impact on pCO₂ under variable P:C than under fixed P:C (Fig. 4).

Fig. 3.

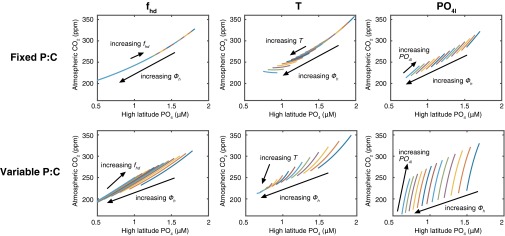
Relationship between preformed PO₄ and pCO₂ in box model simulations. Top panels show results with fixed P:C, bottom panels show variable P:C following the Line of Frugality illustrated in Fig. 1. Each panel shows the pCO₂ predicted by 100 model simulations that simultaneously vary the high-latitude export flux (Φ_h, each value of which is shown by a single color) along a range of values for the other variable as indicated (shown as a continuous line for each value of high-latitude export), where PO_4l is low-latitude PO₄, T is thermohaline overturning and f_hd is high-latitude vertical mixing. For example, for the variable P:C model, varying PO_4l over the full range of values produces pCO₂ changes of more than 70 ppm, with little effect on the preformed PO₄.

Fig. 4.

Relationship between low-latitude PO₄ and pCO₂ in box model simulations. High-latitude export Φ_h is held constant at an intermediate value for the simulations shown here. The variable P:C simulations (orange) show a much larger impact of low-latitude PO₄ on pCO₂ than the fixed P:C simulations (gray). The enhanced sensitivity of the variable P:C simulations arises from the greater carbon storage achieved by low-latitude export, per mol of P export, compared with high-latitude export. The range of possible CO₂, corresponding to the 95% confidence intervals of the Line of Frugality regression shown in Fig. 1, are indicated by the region of orange shading.

The reason for these divergences is fairly straightforward: when P:C varies, export that occurs under low PO₄ concentrations stores more C for the same P inventory, thereby lowering pCO₂. Because the low-latitude export flux (Φ_l) has a lower P:C than Φ_h, increasing the fraction of total export that occurs at low latitudes leads to lower pCO₂. In the model, Φ_l is simply equal to T(PO_4d − PO_4l), where PO_4d is the phosphate concentration in the deep box, which is essentially fixed by the total PO₄ inventory. Therefore, increasing T drives a linear increase of Φ_l, causing pCO₂ to decrease. Similarly, decreasing PO_4l increases Φ_l, an effect that is compounded by decreasing the P:C of Φ_l as the ambient PO₄ concentration becomes more scarce. Altogether, this could produce more than a 20 ppm difference in atmospheric CO₂ for a change in PO_4l of only 0.1 μM (Fig. 4), such as might occur given a change in nitrogen limitation at low latitudes. Thus, the export of low P:C organic matter at low latitudes could be a more significant player than often realized in determining the strength of the global soft tissue pump. Because PO_4l would be dependent on the availability of nitrogen in low-latitude surface waters, it would be expected to respond to changes in denitrification and N₂ fixation, emphasizing their importance to the carbon cycle (33).

Despite the reduced applicability of the preformed-PO₄ metric under variable P:C, the smaller variability of N:C would suggest that the relationship between remineralized NO₃ (i.e., the nonpreformed component of NO₃) and soft tissue pump carbon storage should be more robust. This general principle could make remineralized NO₃ a better monitor of changes in the biological pump, particularly given the fact that past changes in relative NO₃ consumption can be reconstructed using the stable isotopes of nitrogen recorded in marine sediments (34, 35). The difficulty in the use of remineralized NO₃ is the fact that denitrification can reduce NO₃ concentrations along circulation pathways, so that the nitrate concentration is less than the sum of the preformed and remineralized components. Furthermore, variability of N:C may be sufficient to cause a significant divergence of the soft tissue pump strength from remineralized nitrate, although this is difficult to judge without a better understanding of what controls the N:C (36).

Conclusions

The stoichiometric ratios P:C and N:C are usually held constant in global biogeochemical models, despite evidence for significant variability from field and laboratory studies. Based on global suspended particulate measurements, it would appear that the community-averaged N:C varies linearly with the dissolved concentrations of NO₃ over low NO₃ concentrations, and that the community-averaged P:C varies linearly with PO₄ across the range of modern ocean PO₄ concentrations. We suggest that this is because the phytoplankton community tends to adjust to the available nutrient concentrations, either by intraspecific plasticity of elemental composition (e.g., ref. 37), or by shifting the species assemblage. All else being equal, the most frugal phytoplankton—those with the lowest requirements for a nutrient—dominate when the concentrations of that nutrient are lowest, and therefore most difficult to obtain. Because N is an integral component of many organic molecules, the N:C varies by less than 30% in response to changes in NO₃, whereas P:C varies by a factor of three in response to changes in PO₄. As a corollary, changes in the N:P ratio of phytoplankton communities are mostly due to changes in the concentration of PO₄ in the ambient waters, with little dependence on the ambient ratio of NO₃:PO₄.

A simple model based on these observations predicts the P:C of export as a function of PO₄. When included in a classic box model, the flexible P:C model shows heightened sensitivity of atmospheric CO₂ to ocean circulation and the low-latitude PO₄ concentration. Significant variations in the P:C of sinking organic matter weaken the relationship between preformed PO₄ and CO₂ storage, suggesting that mechanisms of change in the biological pump could be better framed in terms of remineralized NO₃. The simple predictive model can be tested against future observations and laboratory study.

The large impacts of variable P:C on ocean carbon storage illustrated by the simple box model suggest that global biogeochemical models should place a high priority on resolving P:C plasticity, in order to improve the understanding of past and present variability, and to account for this important aspect of the marine ecosystem in future projections of N₂ fixation, denitrification, ocean carbon uptake and oxygen distributions.

Methods

Data Analysis.

The particulate data of ref. 7 is reanalyzed here as follows. For each station (i.e., geographic location at which samples were collected), all available measurements of particulate organic carbon (POC), particulate organic nitrogen (PON), particulate organic phosphorus (POP), nitrate, and phosphate within the upper 30 m of the water column were averaged. Wherever particulate data existed without corresponding nutrient measurements, the climatological nutrient concentration for the same location was taken from the monthly WOA climatology (7). The P:C and N:C were calculated for all stations at which the mean POP and PON concentrations were greater than 0.005 μmol l⁻¹. This selection process resulted in 610 stations with P:C and 4,064 stations with N:C data (Fig. S1).

A linear regression of P:C vs. PO₄ was calculated using all 610 (unbinned) data points, giving an intercept of 6.0 ± 0.2 ‰ and slope of 6.9 ± 0.4 ‰ μmol⁻¹ L as shown by the solid orange lines in Fig. 1 and Fig. S2, referred to as the Line of Frugality. The linear regression coefficient (r², Pearson) against all 610 data points is 0.36 (P < 10⁻⁶⁰). In addition, the log-transformed means of the binned data were used to generate an alternative linear regression, given that the log-transformed values within each bin showed a more normal distribution. The binned-lognormal mean regression gives a significantly lower intercept of 4.8 ± 0.5 ‰ and a slightly higher slope of 7.3 ± 0.6‰ μmol⁻¹ L, shown by the dashed orange lines in Fig. 1 and Fig. S2. The linear regression coefficient of the binned-lognormal mean regression line against the nine binned means is 0.95 (r², Pearson, P < 10⁻⁵). To illustrate the full uncertainty in the Line of Frugality, the combined range of the 95% confidence intervals for both regressions is shown by the shaded areas in Figs. 1 and 4.

A linear regression of N:C vs. NO₃ using all 4,064 stations shows a weak (0.8 ‰ μM⁻¹), but highly significant (P < 10⁻¹⁰) linear increase over the full range of NO₃ concentrations. However, if only the stations with >5 μM NO₃ are analyzed, the linear regression has a near-zero slope that is only weakly significant (P < 0.1), whereas a regression over the lowermost 3 μM NO₃ range shows a strong slope (11 ‰ μM⁻¹) with very high significance (P < 10⁻¹⁰). This rapid increase of N:C over low NO₃ concentrations, followed by negligible change, is consistent with a saturating hyperbolic relationship. An optimized fit using a Holling type 2 functional form is given by N:C = 125 ‰ + 30 ‰ × NO₃/(0.32 μM + NO₃), shown in Fig. 1 and Fig. S2 along with a shaded interval that spans the 95% confidence intervals of the nonlinear fit using both the full unbinned dataset as well as binned log-transformed means.

Model.

The biogeochemical model used here includes three ocean boxes and one atmospheric box, following ref. 31. The low-latitude surface PO₄ concentration is restored to a defined value, generating an export flux Φ_l that depends on the physical supply of PO₄ to the low latitudes by the thermohaline circulation T, whereas the high-latitude surface export flux Φ_h is imposed as an input parameter, representing iron-light-temperature-limited growth. A prescribed vertical mixing flux exchanges water between the high-latitude surface and the deep box, f_hd. Carbonate exported from the surface by calcifying organisms is set to 20% of the organic carbon export flux, within the observational range given by Berelson et al. (38). Within the surface boxes, the carbonate equilibria are solved as a function of Dissolved Inorganic Carbon (DIC) and alkalinity concentrations, to determine the saturation state of CO₂. Air–sea exchange is a linear function of CO₂ saturation state and a constant air sea exchange coefficient (the “piston velocity”), as described in ref. 39.

For the purposes at hand, we assume that the P:C of sinking particulate export follows the same relationship with surface phosphate as the measured surface particles. The real world is undoubtedly more complex, given preferential export by specific taxa (such as diatom aggregates) at particular times of year, and the consumption of phytoplankton by heterotrophs, producing rapidly sinking fecal pellets with P:C that differs from that of the food source (40). Additionally, it has been observed that P disappears more rapidly than C from sinking particles within the upper water column, implying preferential remineralization of P that would add a vertical dimension to differential P:C cycling (41–43). Nonetheless, two recent global inverse models incorporating ocean circulation and chemical data (25, 44) found a close match across ocean basins between the stoichiometry of net organic matter export and the suspended particulate data used here, as well as with the Line of Frugality prediction (Fig. S3). The good agreement between these alternative methods suggests that the Line of Frugality prediction captures the first order variability in P:C of exported organic matter.

The low-latitude PO₄ concentration PO_4l is restored to a prescribed value that is varied between 0–0.6 μM. The export flux of carbon from the high-latitude box Φ_h is prescribed to vary from 0.25 to 4 Pg C y⁻¹, as might occur under large changes of iron fertilization. The thermohaline overturning T is varied over a range of 10–45 Sv. The high-latitude vertical mixing f_hd is varied over a range of 30–130 Sv. Varying each of PO_4l, T, and f_hd over 10 values with simultaneous variations in Φ_h over 10 values results in a total of 300 simulations, each of which was repeated with both fixed and flexible P:C, run to equilibrium (20,000 y).