Synaptic clusters function as odor operators in the olfactory bulb

Significance

How the olfactory bulb organizes and processes odor inputs through fundamental operations of its microcircuits is still controversial. To reveal these operations we hypothesize that one of the key mechanisms underlying odor coding is the interaction among spatially restricted and well-defined clusters of potentiated mitral–granule cell synapses. These experimentally observed clusters selectively gate the propagation of neuronal activity within the olfactory bulb and extensively contribute to sculpting the mitral cell output to the cortex. We show and discuss how their interaction and computational roles can be described by a theoretical framework that can be used to derive, analyze, and predict the olfactory bulb network operations on an odor input.

Abstract

How the olfactory bulb organizes and processes odor inputs through fundamental operations of its microcircuits is largely unknown. To gain new insight we focus on odor-activated synaptic clusters related to individual glomeruli, which we call glomerular units. Using a 3D model of mitral and granule cell interactions supported by experimental findings, combined with a matrix-based representation of glomerular operations, we identify the mechanisms for forming one or more glomerular units in response to a given odor, how and to what extent the glomerular units interfere or interact with each other during learning, their computational role within the olfactory bulb microcircuit, and how their actions can be formalized into a theoretical framework in which the olfactory bulb can be considered to contain “odor operators” unique to each individual. The results provide new and specific theoretical and experimentally testable predictions.

The organization of olfactory bulb network elements and their synaptic connectivity has evolved to subserve special computational functions needed for odor detection and recognition (1–5). Key to this organization are the olfactory glomeruli, collecting input from olfactory receptor neuron subsets. These connect to the dendrites of mitral, tufted, and periglomerular cells, and the mitral and tufted cells in turn connect to granule cells. We term these interconnected cells a cluster, and a cluster related to a given glomerulus is a glomerular unit (GU), often visualized as a column of granule cell bodies located below a glomerulus (6, 7). The existence of such GUs has also been suggested from 2-deoxyglucose (8) and voltage-sensitive dye studies (9).

Understanding the neural basis of odor processing therefore requires understanding the computational functions and role of GUs. These issues, which are difficult or impossible in experiments, can be conveniently explored using realistic computational models, provided they are able to explain and reproduce crucial experimental findings on glomerular clusters or units.

Analyzing synaptic interactions between cells with overlapping dendrites requires modeling in real 3D space. Scaling up to the network level further requires scaling up realistic structural and functional properties to many thousands of cells (10). Building on this unique approach, we show that this model generates columnar clusters of cells related to individual glomeruli, as in the experiments, and further demonstrates mechanisms of odor processing within and between the GUs. Finally, interpreting this network activity requires a theoretical framework, incorporating distributed activated glomeruli within the global network, for which we introduce the concept of the odor operator. The results provide a basis for extension to the glomerular level on the one hand and interactions with olfactory cortex on the other.

Results

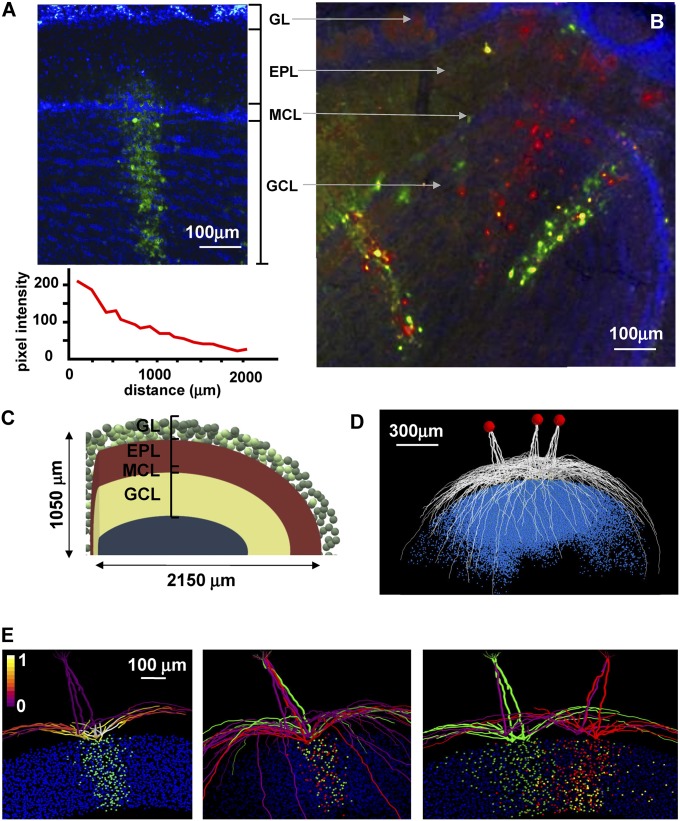
We began by identifying experimental findings as a basis for constructing and validating our theoretical model. Single clusters in the olfactory bulb, obtained from a pseudorabies virus staining pattern after a single injection (6), are illustrated in Fig. 1A. The entire cluster belongs to a GU. Because of its elongated form, we will term this type of experimentally observed cluster a column. The column can be distinguished by the green spots in the granule cell layer, and we assume that these indicate granule cells with active synapses on mitral cells at spatially segregated locations on their lateral dendrites. It has been observed that, on average, the number of GCs involved in a column varies with distance from its center (Fig. 1A, Bottom), and it was also demonstrated, using double injections (Fig. 1B, adapted from ref. 7), that mitral cells belonging to the same glomerulus form connections with different sets of GCs and make connections through their lateral dendrites with granule cells belonging to different GUs (yellow spots within columns in Fig. 1B).

Fig. 1.

A 3D model can reproduce single- and multicolumn formation, as observed in the experiments. (A and B) The main experimental results we used as a reference to study single- and multiple-column formation. A adapted from ref. 6. B adapted from ref. 7. (C) A schematic representation of the 3D model we used for all simulations. Adapted from ref. 10. (D) A model visualization of the mitral cells belonging to three different glomeruli; blue dots represent the soma of the granule connected to them. (E, Left) Typical findings for a single column; the picture shows the final weight configuration from a simulation in which glomerulus 37 was strongly activated with a peak individual synaptic conductance of 6.5 ± 1.95 nS; (Middle) the set of granule cells connected to the red and green mitral cells are distinct, whereas (Right) there are granule cells making synapses on MCs from different glomeruli (in yellow); for this simulation, glomeruli 37 and 123 were activated. The photos in A and B show coronal sections of the olfactory bulb, with labeling of columns of granule cells. EPL, external plexiform layer; GCL, granule cell layer; GL, glomerular layer; MCL, mitral cell layer. Mitral cell dendritic segments in the left plot are color coded according to the normalized peak inhibitory conductance they receive from the GCs, and green colored points below the mitral cells represent somas of granule cell in which at least one synapse was strongly potentiated (more than 95% of its peak value); in the middle and right panels, colors (red, green, and yellow) are used to distinguish cells belonging to different group.

To enable a precise comparison of our simulation findings with these experimental data, we used a recently implemented 3D model of the olfactory bulb network (10) (SI Appendix, Fig. S1 and Methods). The model structure is schematically represented in Fig. 1C, and a representative set of the mitral cells projecting to three glomeruli, with the corresponding cloud-like population of granule cells connected to them, is plotted in Fig. 1D. To validate the model against the experimental findings for a single column, we ran a simulation in which a relatively strong input was presented to one glomerulus (glomerulus 37) for a simulation time long enough to allow the synaptic weights to reach equilibrium values (7 s in this case). The final weight configuration is shown in Fig. 1E, Left. To make a clearer comparison with the experimental data of Fig. 1A, which are from a coronal section, we visualize the cells contained in a 200-μm-thick section centered on the glomerulus. Mitral cell lateral dendrite segments were color-coded for the peak (normalized) inhibitory inputs they receive from granule cells. Green-colored points represent granule cell somas in which at least one synapse was strongly potentiated more than 95% of its peak value. A clear column can be distinguished that is very similar to those observed experimentally (Fig. 1A), which also exhibit different widths and cell densities (6) (bottom plot of Fig. 1A). The model suggests that the balance between excitation and inhibition (in terms of the odor input and granule cell response, respectively) can underlie the experimentally observed variations in a column’s size and cell density (SI Appendix, Fig. S2). If we model a double injection in two of the mitral cells of the same glomerulus (red and green in Fig. 1E, Middle), we observe that they form connections with different sets of GCs (red and green dots below the glomerulus), as suggested by experiments (7). Finally, as shown in Fig. 1E, Right, a double injection in two different glomeruli, after a simulation activating two neighboring glomeruli, reveals the presence of lateral synaptic connections between mitral cells, through granule cells, belonging to different glomeruli (Fig. 1E, Right, yellow dots in the granule cell layer), a result that is again consistent with experimental findings (7) (Fig. 1B). These results show that the model can reproduce the basic experimental observations for single- and multiple-column formation.

The Functional Role of a Column Is to Regulate the Spread of Activity out of a Glomerulus.

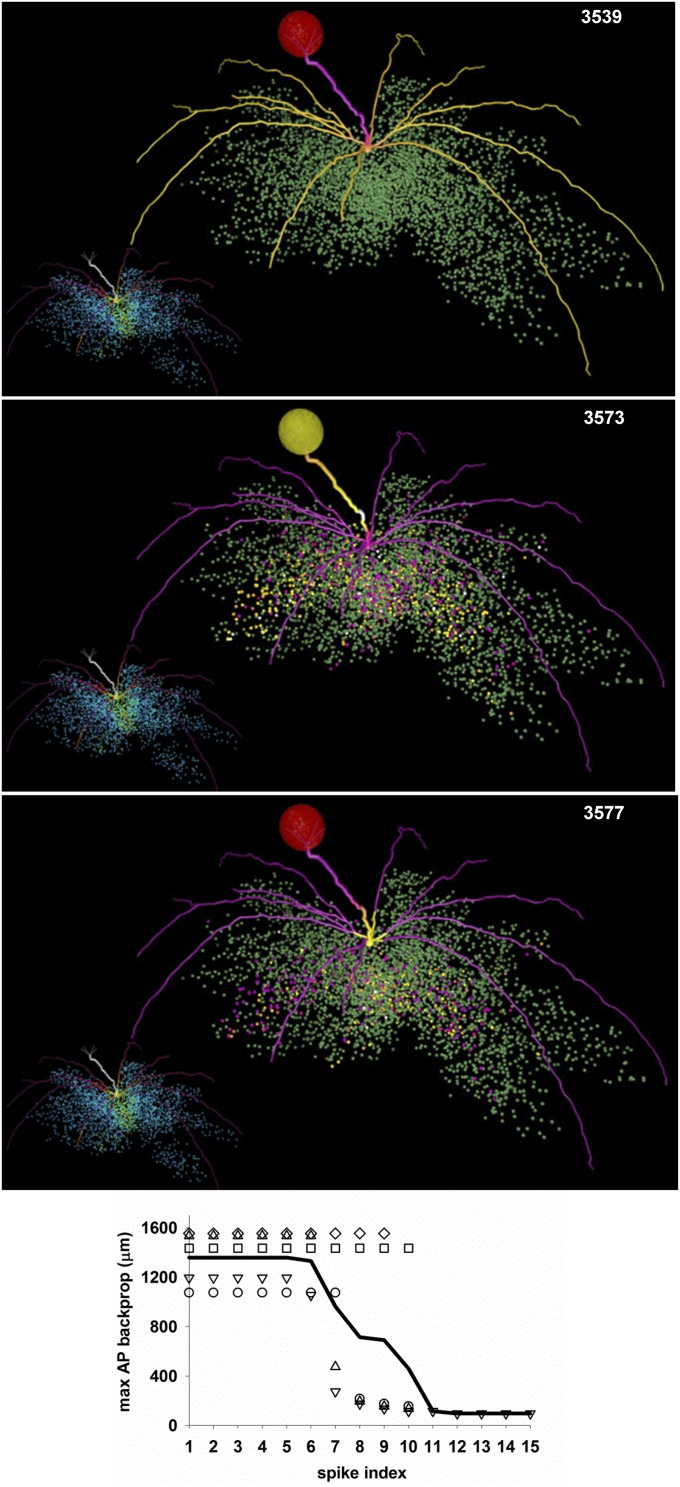
There must be a functional/computational reason for evolution to have developed an extremely robust way to form a spatially restricted region with a strong inhibitory action on any action potential (AP) crossing it. It has been shown experimentally in vitro (11, 12) and in a biophysically realistic model (13) that the local activation of GABA receptors on individual lateral mitral cell (MC) dendrites can be strong enough to block an otherwise normal backpropagating AP. To test how this relates to the functional role of a column, we carried out a simulation in which one glomerulus (glomerulus 37) was strongly activated. Three snapshots from the simulation are shown in Fig. 2 (Movie S1) and show the typical sequence of events revealing the effect of a column. The simulation started at t = 0, with all synapses set to 0, and the glomerulus was activated every 500 ms to simulate sniffing at a frequency low enough to allow the complete decay of inhibition between sniffs. After a few seconds of simulation time, a column was well formed (Fig. 2, red to yellow dots in inset of top image), and at the beginning of a sniff, APs backpropagated to the distal ends of all dendrites (Fig. 2, top plot). These initial APs activated all of the GCs with which their lateral dendrites formed reciprocal synapses (Fig. 2, middle plot, yellow dots below dendrites), but subsequent APs were unable to backpropagate more than ∼50 μm from the soma (Fig. 2, bottom plot). On average, it took approximately six spikes to activate GCs in such a way as to block AP backpropagation, as shown in the bottom plot in Fig. 2. With strong inputs, this corresponds to ∼50 ms, in agreement with experimental findings showing that this is the time to activate the maximal inhibitory response (14). This chain of events was robustly confirmed for all of the other glomeruli we tested. These results show that a column will block, within a relatively small time window, the entire activity fanning out from all dendrites of the mitral cells belonging to the same glomerulus.

Fig. 2.

Columns block AP backpropagation in mitral cell dendrites. Three selected snapshots from the simulation shown in Movie S1. The mitral cell dendrites are shown color-coded for membrane potential; inactive dendritic segments are shown in purple, APs in yellow. The glomerulus is colored according to the instantaneous spiking activity in the mitral cell tufts; red indicates no activity, yellow indicates spiking activity in any of the tuft dendrites. In the inset of each snapshot, the colored points represent granule cell somas color-coded according to the peak inhibitory conductance of their synapses on the mitral cells. A full high-definition movie can be downloaded from ModelDB. (Bottom) The max AP backpropagation as a function of the spike number; symbols represent each of the five MCs belonging to the glomerulus; the black line is the average.

GUs Positively or Negatively Interact with Each Other in a Distance-Dependent Way.

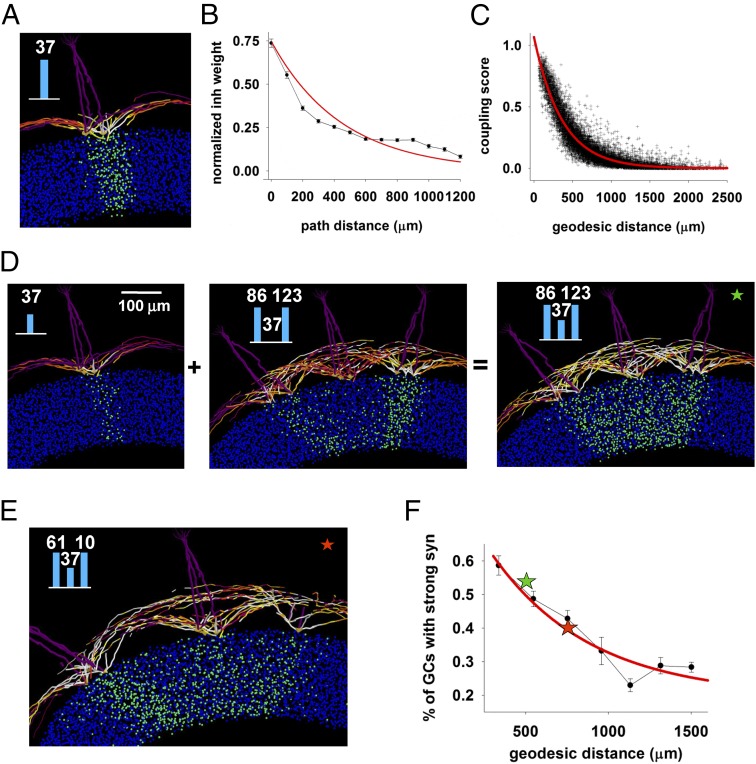
How do glomeruli affect each other’s activity through the inhibitory action generated by the columns? To investigate this issue, we first calculated the distance-dependent inhibition that a typical column (Fig. 3A) below a given glomerulus can exert on another column, assuming that this is proportional to the average inhibitory weight. This is shown in (Fig. 3B), where we plot the average normalized inhibitory weight of GC synapses versus the distance from the column center. Assuming that all glomeruli have the same type of column associated with them, it is possible to calculate theoretically a coupling score, defined as the extent to which two columns can interact through the GCs that make synapses on mitral cells belonging to both columns. The score was calculated as the normalized sum of the synaptic weights of the GCs in common found within a 50-μm rectangular box centered on each column. The distribution of the coupling score for all of the possible pairs of our 127 experimentally labeled glomeruli is shown in Fig. 3C as a function of the geodesic distance between their centers and implies that GCs in common between glomeruli can receive additional input that can act in a positive or negative way for column formation. It can be expected that most of this effect will be caused by the strongest synapses.

Fig. 3.

Columns interact in a predictable distance-dependent way. (A) Column formed under glomerulus 37 when activated alone, repeated here from Fig. 1E. (B) Normalized average inhibitory weight on MC dendrites as a function of distance from soma, from the simulation shown in A; the red line is a fitting of the data with an exponential function. (C) Coupling score between two glomeruli; the red line is a fit to an exponential. (D) Neighboring glomeruli can cooperate to promote formation of a column by a weakly activated glomerulus: (Left) column below glomerulus 37 formed during a weak input presentation; (Middle) activation of two neighboring glomeruli (86 and 123) did not generate any column below glomerulus 37; (Right) coactivation of all glomeruli resulted in a stronger column below glomerulus 37; bar plot in the inset represent glomerular input. (E) Coactivation of more distant glomeruli (61 and 10) resulted in a less pronounced increase of the column below glomerulus 37. (F) Simulation findings for the average interaction between glomerulus 37 and two other glomeruli at different average distance; for each bin, the average interaction was calculated as the percentage of strong GCs synapses inside a 50-μm rectangular box centered below glomerulus 37; colored stars represent the cases in E and F.

To test this hypothesis, we ran two simulations in which glomerulus 37 was weakly stimulated alone (Fig. 3D, Left) or together (Fig. 3D, Middle) with two other strongly activated neighboring glomeruli (glomerulus 86 and glomerulus 123). As can be easily seen in Fig. 3D, Right, the coupling with strongly active neighboring glomeruli promoted the formation of a better column by the weakly activated glomerulus 37. Coactivation of a more distant pair (glomeruli 61 and 10; Fig. 3E) resulted in a less pronounced increase of the column below glomerulus 37. We tested this mechanism for different combinations of two glomeruli at different distances from glomerulus 37, and the average (n = 9, ± SEM) proportion of GCs with strong synapses below glomerulus 37 is shown in Fig. 3F. A typical case in which the formation of a column can be hindered by activity in other glomeruli is shown in SI Appendix, Fig. S3.

Taken together, these results suggest that the sparse, distributed, and segregated columns of active GC synapses, as those observed experimentally, can interact in a way that can promote or hinder column formation on neighboring weakly activated glomeruli. In the Discussion, we suggest that this is an evolutionary reason for the existence of molecular-feature-activated clusters of glomeruli.

Odor Exposure Is a Noncommutative Operation.

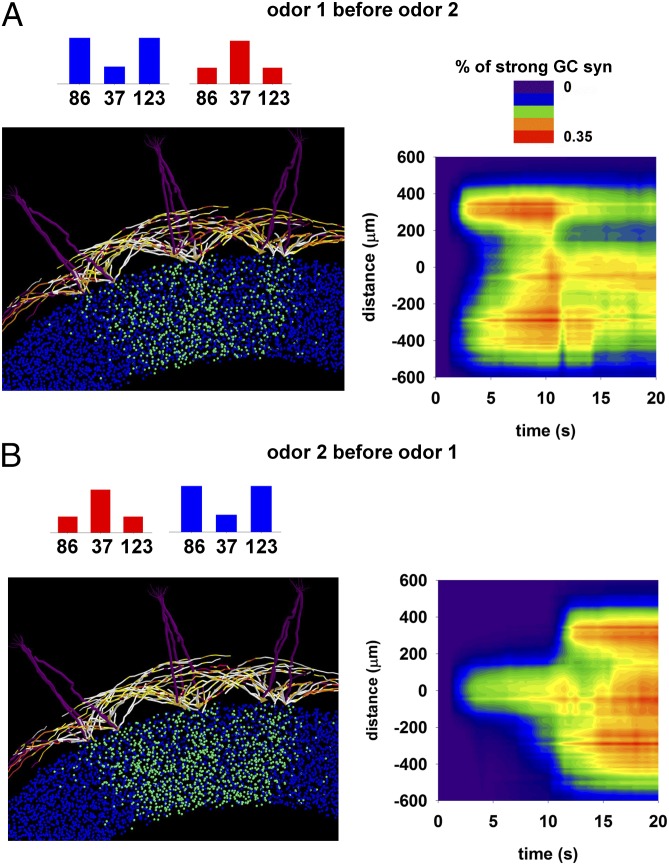
Another key point for understanding how olfactory bulb circuits work is the network reconfiguration (and thus odor representation) in the presence of different inputs. In terms of column operations, this is equivalent to studying how new inputs may change in a significant way the size and strength of any given column. In Fig. 4, we show what happens when the same two odors, activating the same neighboring glomeruli, are presented in a different sequence. This is important because although each individual may be exposed to similar odors during his or her life, the order in which odors are learned will be different. To explore this issue, we simulated the presentation of two odors in a different sequence. The final configuration of potentiated GC synapses in the two cases was significantly different (compare Fig. 4 A and B, Left), with a different dynamic (Fig. 4 A and B, Right). As also expected from the previous results, this effect depends on the relative distances between the glomeruli. These results suggest that the process of odor exposure is noncommutative. Each olfactory bulb at any given stage of its life thus contains a unique representation not only of the past odor learning episodes but also of the order in which they were learned. This is especially true for odors that activate neighboring glomeruli.

Fig. 4.

Odor exposure is a noncommutative operation. (A, Left) Final configuration the olfactory bulb network resulting from exposure to odor 1 and then odor 2. (Right) Temporal evolution of the proportion of potentiated GC synapses as a function of the distance from glomerulus 37. (B) Same as in A, but for presentation of odor 2 and then odor 1; note the different final state at the end of the simulation (t = 20 s).

Development of Odor Operators.

The previous results give insight into the interactions between mitral and granule cells within and between GUs. How can we summarize the general principles involved? As we have shown, once columns are formed according to a specific set of odor inputs presented in a specific sequence, a given input is processed in a specific way by the olfactory bulb network. How can this be reconciled with our everyday experience that many individuals can recognize the same odors even if their olfactory bulbs presumably have had (and continue to have) quite different experiences?

We propose that the main operations of the olfactory bulb mitral–granule circuit can be represented by an operator in the form of a square matrix OP, describing the overall inhibition on GU_i generated by activity in GU_k. The OP operator is the result of the past presentation history, hys, of a set of input vectors, INP^hys, and it operates a transformation in which to any INP $\in$ INP^hys is associated an output vector, OUT, in such a way that

$$INP\to OUT=\left(I-OP\right)INP,$$

where I is the identity matrix. Given the inhibitory action of the granule cells, this formulation simply implements the notion that any given input is reduced (in a potentially complex way) by the olfactory bulb. In general, we can assume that the interaction between GUs can be represented by the combination of the three matrices W^exc, W^inh, and H, where

$$W^{exc}=\left(w_{jk}^{exc}\right)\in M_{\left[GC\times GU\right]}$$

is the excitation on GC_j generated by GU_k,

$$W^{inh}=\left(w_{ij}^{inh}\right)\in M_{\left[GU\times GC\right]}$$

is the local inhibition on GU_i generated by GC_j, and

$$H=\left(h_{ij}(G{U}_i,G{C}_j)\right)\hspace{0.17em}\in \hspace{0.17em}{M}_{\left[GU\times GC\right]}$$

is the effective inhibitory action of GC_j on GU_i.

An element of OP, OP_i,k, will then be defined as

$$O{P}_{i,k}={\displaystyle \sum _{j=1}^{GC}\left(h_{ij}\times w_{ij}^{inh}\right)w_{jk}^{exc},}$$

where the symbol $\times$ represents element-by-element multiplication. The rationale for this choice is that it implements the classical sequence of steps in which an odor input generates an excitatory action on the granule cells (W^exc), which in turn generates an inhibitory action on the GUs (W^inh) that depends on the way in which they are connected (H). These results suggest a general strategy to study the olfactory bulb, which can be applied independent from any specific olfactory bulb size and connectivity.

Toward a Theory of Odor Operators.

To better illustrate the usefulness of this approach, we consider one of the simulation findings: that the presentation sequence of the learned odors affects the final network configuration (Fig. 5). This means that the olfactory bulb in each individual is different, implying that each individual would presumably transform the same input (say a rose odor) into different outputs. How can this be reconciled with the fact that most individuals, at different times of their life, are still able to recognize blindly the same odor even at very low concentrations, independent from their personal history of odor exposure?

Fig. 5.

There is a discrete number of operators that operate on a given input to give the same output. (Top) Normalized number of operators as a function of the number of GUs generated in the olfactory bulb by the past input history (GUs, x axis) when 5% of GUs are connected to r others (y axis). (Bottom) Relative change in the number of operators as a function of the connectivity among 100 GUs.

To answer this question, we use classical matrix operations. Let us indicate with OP_i the operator generated by the ${INP}^{{\mathit{h}\mathit{y}\mathit{s}}_{\mathit{i}}}$ set, and with OP_i(INP_h) the square matrix of order GL obtained by the usual row-by-column product between the matrix OP_i and the vector INP_h. The OP_i(INP_h) operates a transformation such that a unique vector $OU{T}_h^i$ will correspond to INP_h. A direct consequence of the way in which the elements of INP_h and OP_i can be combined to give the same OUT_h is that there can be two or more different classes of operators that result in the same output, OUT_h. This gives an explanation of how the olfactory bulbs of two or more individuals (i.e., two or more operators) can give the same output to the same input. Examples of different operators, resulting in the same output when presented with a given input, are shown in SI Appendix, Appendix S1 for an abstract numerical case and for a realistic model implementation.

The next step is to have an idea of how many different operators can exist. As shown in SI Appendix, Appendix S2 in the general case in which we can make the physiological reasonable assumption that only a given proportion, p, of GUs are involved in INP_h, and that each GU can be connected to at most r other GUs, the set of operators that transforms INP_h in OUT_h is

$${\displaystyle \sum _{\begin{array}{c}{k}_1+\mathrm{...}+k_r=1,\\ k_1+\mathrm{...}+k_r\le \lfloor pGU\rfloor \\ k_0=GU-\left(k_1+\mathrm{...}+k_r\right)\end{array}}^{\lfloor pGU\rfloor }\left[{\mathit{\Omega }}_{GU}^r{\displaystyle \prod _{j=1}^r{\left(\begin{array}{c}\lfloor pGU\rfloor \\ j\end{array}\right)}^{k_j}}\right]},$$

where $\mathrm{\lfloor }.\mathrm{\rfloor }$ indicates the floor function,

$${\mathit{\Omega }}_{GU}^r=\left(\begin{array}{c}GU\\ k_0\end{array}\right)\left(\begin{array}{c}GU-k0\\ k_1\end{array}\right)\left(\begin{array}{c}GU-k_0-k_1\\ k_2\end{array}\right)\dots \left(\begin{array}{c}GU-{\displaystyle \sum _{i=0}^{r-2}{k}_i}\\ k_{r-1}\end{array}\right),$$

and $r\le \mathrm{\lfloor }pGU\mathrm{\rfloor }$.

If $r={\displaystyle {\sum }_{i=0}^r{k}_i}=\lfloor pGU\rfloor ,$ that is, all of the involved GUs are fully connected according to the equation provided earlier, the number of operators becomes $2^{\mathrm{\lfloor }pGU\mathrm{\rfloor }2}$. It is important to stress that these formulas give the maximum theoretical number of operators for a particular pair of two nonzero vectors INP_h and OUT_h. Here we have shown only the most relevant equations. A complete mathematical formulation is reported in SI Appendix, Appendix S2.

The number of operators, in general, changes as a function of the parameters within physiological plausible ranges. For this purpose, in Fig. 5, we show the normalized number of operators as a function of the number of involved GUs (and thus in the inputs that generated the operator) and the degree of connectivity between them. In this case, we assumed an olfactory bulb composed of 1,000 GUs. As can be expected, the number of operators increases with the number of GUs involved in the operator, but it can increase or decrease with their connectivity (Fig. 5, Top). However, there is a specific combination of size and connectivity for which the number of operators is higher. This optimal number can further increase or decrease with the number of GUs connected to others (Fig. 5, Bottom). It should be stressed that the actual number of operators will depend on the values of the parameters, such as the number of GUs (which affects the size of the operator) and the connectivity properties (which affect the way in which nonzero elements are distributed in the operator). In SI Appendix, Appendix S2 (Eqs. S23–S27), we discuss a few specific numerical examples. Taken together, these results suggest that the number of different olfactory bulbs able to give the same output in the presence of a given input is a complex but analytical function of both the number of involved GUs and how they are connected; many GUs, highly or loosely connected, would not be the optimal choice if the best coding strategy requires maximizing the number of ways in which a given input is transformed to a given output.

Discussion

This study focused on two main points directly related to the network mechanisms underlying the input/output (I/O) computational properties of the olfactory bulb: the dynamic formation, interaction, and computational role of sparse and spatially segregated clusters of granule cell synapses on mitral cells, in relation to given glomeruli that we term GUs, and the development of a theoretical framework to analyze the olfactory bulb network in terms of interactions between GUs.

GUs: Functions and Interactions.

The model gives new insight into the neural basis of the experimental findings on variations in a column’s size, connectivity, and cell density. This in turn suggests specific theoretical and experimentally testable predictions:

• i)Column formation and interaction is a dynamic process that depends in a predictable way on the concurrent activity of different GUs, their respective locations, and past odor inputs in such a way as to promote or hinder column formation on neighboring GUs. This supports and gives a physiological plausible explanation for the hypothesis and the experimental suggestions (reviewed in ref. 15) of the existence of molecular-feature-activated clusters of glomeruli. Column formation can be experimentally tested by examining changes in the activity of the same set of GCs belonging to a glomerulus before and after delivering different stimulation protocols to the glomerulus.
• ii)The main computational role of a column is to limit the interaction of its GU to a restricted spatial region, thus affecting a relatively small number of other GUs. The overall picture emerging from this prediction is one in which, after a silent period at the end of a respiratory cycle, inhalation (and a physiologically relevant odor input) starts to generate a powerful mitral cell activity, and the first few APs fully backpropagate into distal dendrites and activate all granule cells they are connected to, setting the stage for the rest of the network operation, and from then on the local activity involves only feedback and lateral connections within the spatial range of the each column that sculpts a GU-specific pattern of spikes that project to the cortex for odor recognition. This sequence is consistent with experimental findings suggesting that granule cells are normally silent and need a powerful MC input to be activated (16);
• iii)Each olfactory bulb at any given stage of its life contains a unique representation not only of the past odor learning episodes but also of the order in which they were learned. In principle, this effect can be experimentally tested by training different animals to the same or different sequences of the same odors, and then analyzing the spatial distribution of the columns formed in their olfactory bulb: individuals trained with the same odor sequence should show fewer differences among column size and distribution.

Odor Operators.

A theory based on experiments is necessary to gain insight into a complex system such as the mitral–granule cell network. The mathematical framework introduced in this work illustrates how the transformation of an input into a specific output can be described by a square matrix defining an operator corresponding to a specific olfactory bulb glomerular network at any given instant of its life. Operators are commonly used to describe input/output transformation of neuronal signals. Typical examples are those used to model the receptive field of retinal ganglion cells (17), representation of time (18), auditory stimuli (19), and extracellular neural signals (20). In our case, this seems to be a promising approach that allows one to make general predictions about the properties, number, and structure of the operators representing the odor stimuli. This appears to be the first time to our knowledge that the operations of the olfactory bulb are represented in this way, with the notable exception of Urban (21), who discussed the role of lateral inhibition using the simplifying assumption of considering the olfactory bulb circuitry as implementing a simple 2D filter. General computational models of the olfactory bulb operations (reviewed in ref. 22) are usually implemented using a pattern recognition approach with artificial or single-point neuron networks, built from scratch according to the kind of problems/hypotheses to investigate. In this article, we were instead interested in obtaining an abstract representation of the olfactory bulb that nevertheless retained a direct link with its physiological components, structure, and properties at the single-cell level.

The odor operator concept thus provides a framework for understanding how the glomerular-based connectivity of the olfactory bulb can mediate noncommutative learning experiences in different individuals that nonetheless can give rise to similar odor perceptions. The degree of similarity can be seen to be a complex but analytical function of both the number of involved GUs and how they are connected. A next step will be to adapt the odor operator approach to the processing that takes place at the glomerular level (5) to achieve a full model of olfactory bulb processing. Further development of this approach should lead toward insight into the optimal balance between numbers and sizes of GUs and the uniqueness of individual odor learning experiences.

Materials and Methods

For all simulations, we used a model of the olfactory bulb (10), which implemented the natural 3D layout of mitral and granule cells, using the reported spatial distribution of 128 glomeruli distributed in ∼2 mm² of the dorsal area and activated by natural odors (SI Appendix, Fig. S1). The layout was composed of 635 MCs (five for each glomerulus) and 97,017 GCs. Simulation files specifically used for this work are available for public download under the ModelDB section of the SenseLab database suite (senselab.med.yale.edu; accession no. 168591). For additional implementation details see SI Appendix, Methods.