Abstract
Respondent-Driven Sampling (RDS) is n approach to sampling design and inference in hard-to-reach human populations. It is often used in situations where the target population is rare and/or stigmatized in the larger population, so that it is prohibitively expensive to contact them through the available frames. Common examples include injecting drug users, men who have sex with men, and female sex workers. Most analysis of RDS data has focused on estimating aggregate characteristics, such as disease prevalence. However, RDS is often conducted in settings where the population size is unknown and of great independent interest. This paper presents an approach to estimating the size of a target population based on data collected through RDS.
The proposed approach uses a successive sampling approximation to RDS to leverage information in the ordered sequence of observed personal network sizes. The inference uses the Bayesian framework, allowing for the incorporation of prior knowledge. A flexible class of priors for the population size is used that aids elicitation. An extensive simulation study provides insight into the performance of the method for estimating population size under a broad range of conditions. A further study shows the approach also improves estimation of aggregate characteristics. Finally, the method demonstrates sensible results when used to estimate the size of known networked populations from the National Longitudinal Study of Adolescent Health, and when used to estimate the size of a hard-to-reach population at high risk for HIV.
Keywords and phrases: Hard-to-reach population sampling, network sampling, social networks, successive sampling, model-based survey sampling
1. Introduction
Respondent-Driven Sampling (RDS, introduced by Heckathorn 1997) is an approach to sampling from hard-to-reach human populations in the interest of conducting statistical inference, typically on population proportions. In such hard-to-reach populations, a sampling frame for the target population is not available, and members are difficult to identify or recruit from broader sampling frames. In public health, RDS is often used in studies of high-risk populations such as injecting drug users, men who have sex with men, and female sex workers. RDS has been used in hundreds of studies in over 30 countries worldwide, mostly to arrive at estimates for UNAIDS (Johnston et al., 2008). It is also widely used in the US, especially by public health departments as part of CDC-led monitoring surveys for HIV and other STIs. In these studies, epidemiological characteristics such as the number of people at risk for infection and the infection prevalence are of primary interest. RDS has also been used in other populations such as jazz musicians (Heckathorn and Jeffri, 2001) and demographic studies of unregulated workers (Bernhardt et al., 2009).
RDS is a form of link-tracing network sampling, in which subsequent sample members are selected from among the social relations of current sample members. Unlike most link-tracing designs, respondent-driven sampling relies on study respondents to choose which of their contacts will be sampled next. Each respondent is given a small number of uniquely identified coupons to distribute among their contacts in the target population. Contacts receiving coupons become eligible for the study.
1.1. An illustration of Respondent-Driven Sampling
To illuminate this process, and later to demonstrate the effectiveness of our methods, we introduce an example using a known networked population. Note that in practice RDS is most often used in high-risk hard-to-reach populations, such as people who inject drugs, for whom actual population sizes are rarely available for validation. We therefore first consider a known real networked population within which we can both apply and evaluate the performance of our proposed method.
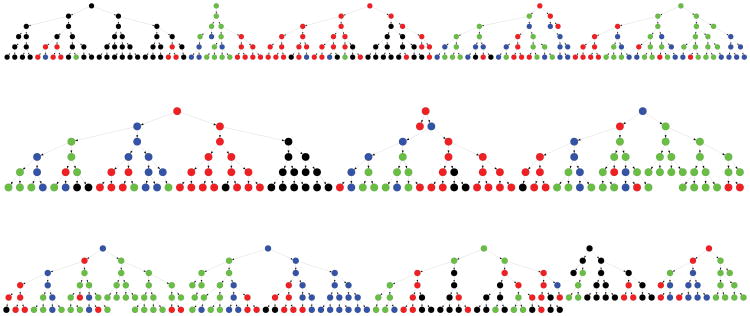
Suppose we wished to survey the population of students within a high-school but did not have a roster to sample them from. We could use the friendship relations among the students to obtain a sample. Specifically, we consider a high-school of 1,249 students for which complete network information was collected as part of the National Longitudinal Study of Adolescent Health (Add Health; Udry, 2003). All students in the school were asked to report on their friendship relations. We simulated an RDS sample by starting with 12 randomly chosen “seed” students. Each seed was allowed to recruit two friends into the sample, and each of these was able to recruit two more, and so on. The cohort of seeds comprised “wave”, their recruits wave 1, and so on. The survey continued until wave 5, with 143 students recruited in wave 4 and 201 in wave 5. The total number of students surveyed was 500. A graph of the recruitment is given in Figure 1. The tendency of students to have friends within their own grade is apparent from the patterns in the recruitment chains. We will return to this illustration in depth in Section 3.
Fig 1.
Graphical representation of the recruitment tree for the sampling of students in the school. The nodes are the respondents and the wave number increases as you go down the page (within each seed). The node color corresponds to the grade of the student (black=9, red=10, blue=11, green=12). Note the “clustering” effect of homophily but also the cross-grade recruitment.
1.2. Estimation of the size of population from RDS data
Most existing estimators from RDS data attempt to estimate population proportions (Gile, 2011; Gile and Handcock, 2014; Heckathorn, 1997, 2002; Salganik and Heckathorn, 2004; Volz and Heckathorn, 2008). Population size estimation based on RDS data is also of interest for three reasons: First, these data are often collected in precisely the populations in which there is interest in population size. In fact, RDS-based prevalence estimates are often used in the Estimation and Projection Package (EPP) model used by UNAIDS (UNAIDS, 2009). For concentrated epidemics, EPP estimates national HIV rates based on both prevalence and population size estimates for several high-risk populations. The resulting estimates of the numbers of infections are used in decisions about resource allocation, research design and intervention planning (UNAIDS and World Health Organization, 2010). Second, new prevalence estimators for RDS (Gile, 2011; Gile and Handcock, 2014) require estimates of the size of the population. And finally, because the information in the sequence of RDS samples has not yet been exploited to estimate population size, this approach introduces a new source of information on the size of the hard-to-reach population.
There are many approaches to estimating the size of a hard-to-reach human population (Bao, Raftery and Reddy, 2010; Berchenko and Frost, 2011; Paz-Bailey et al., 2011; UNAIDS and World Health Organization, 2010), including a few that use link-tracing samples similar to RDS (Felix-Medina and Thompson, 2004; Frank and Snijders, 1994). The validity of these approaches typically rests on strong assumptions about the populations and adherence to sampling designs. A common approach is to use capture-recapture sampling (Fienberg, Johnson and Junker, 1999; Paz-Bailey et al., 2011; Rocchetti, Bunge and Böhning, 2011), which estimates population size based on the overlap between two or more captures of population members. In particular, Fienberg, Johnson and Junker (1999) present a general approach to population size estimation using multiple-recapture data and develop a sophisticated Bayesian estimation approach for it. Related approaches include the (network) scale-up or multiplier methods. In these, one or more of the captures may be from enumerations or convenience samples, rather than from probability samples. All methods using RDS data are of this type. The accuracy of such multiplier methods varies with the quality of the captures data (Salganik et al., 2011; UNAIDS and World Health Organization, 2010).
Because they are based on multiple captures, to date, all methods that use RDS data require additional data collected by mechanisms other than RDS (Bernard et al., 2010; Johnston et al., 2011; Niccolai et al., 2010; Salganik et al., 2011).
1.3. Overview of this paper
The primary contribution of this paper is to introduce an estimator of population size based solely on RDS data. This approach is also novel in that the population size estimates are based on information in the sample sequences, exploiting the dependence in the sampling process. In contrast, most inference from sampled data relies directly on the sampled values and treats dependence in the sample as a nuisance. The proposed estimator can also be combined with estimates based on other approaches to produce improved inference about the population size.
The approach is founded on the successive sampling approximation to the RDS process introduced in Gile (2011). It extends the approach developed by West (1996) for ecological applications (e.g., estimating the number of oil fields based on the sizes of the known fields). Under successive sampling, larger units have higher probabilities of being sampled at any stage, so tend to be sampled earlier, then no longer be available at later stages of sampling. This approach leverages the information in the decreasing size of sampled units (a function of oil reserve magnitude for West's application, and social connectedness for RDS) over time to make inference about population size. Like West, it uses a super-population model-based formulation within a Bayesian inferential framework by positing a prior distribution over population size. It differs from that of West in three key ways: First, the unit sizes are modeled as discrete rather than continuous. Second, the branching and network nature of the RDS sample may reduce or confound the information in the ordering of the sample. Third, the sample sizes of RDS samples are typically larger, and with a different range of unit sizes than in the data available in ecological applications such as oil fields.
The next section (Section 2) develops the inferential framework and suggests a flexible class of priors for the population size. Section 3 applies the methodology to a known networked population from the National Longitudinal Study of Adolescent Health. To complete a broader assessment of the methodology, Section 4 reports on an extensive simulation study of the Frequentist performance of the population size estimator as well as the performance of a prevalence estimator derived from it. Section 5 then presents an application in a truly hard-to-reach population, using the method to estimate the number of injecting drug users that share needles in Colorado Springs (Potterat et al., 2004). Finally, Section 6 concludes the paper with a broader discussion.
2. Bayesian inference for the population size
The goal here is to make inference for population size N. The approach taken is Bayesian, treating N as an unknown parameter. This requires a probability model for the observed data given N, as well as a prior for N. Most information about the population size is drawn from the pattern in the sampling process. In particular, this sampling model is non-amenable to the model (Handcock and Gile, 2010), also see Appendix A. For this reason, the probability model must represent both the sampling structure, and a superpopulation model.
The distribution of the sampling process of the units is modeled as a function of their unit sizes. The sampling model, described in Section 2.2 below, follows Gile (2011) and is based on a successive sampling approximation to the RDS process. The super-population model for these unit sizes is given in Section 2.5. A likelihood function for N can be computed from these two models and then combined with a prior to make inference for N.
The inferential frame is described as follows: Section 2.1 introduces the form of the likelihood. Section 2.2 adds the particular form of the sampling distribution based on successive sampling. Section 2.3 introduces the Bayesian frame for inference for the parameter of the unit size distribution, which is extended in Section 2.4 to inference for N. Section 2.5 presents the parametric model for the unit size distribution. Finally, Section 2.6 presents the forms of the prior distributions for the super-population model and the population size.
2.1. Likelihood for the super-population parameter
Consider a population of N units, denoted by indices 1,…, N with an associated variable unit size represented by U1, U2,…, UN. For RDS, unit sizes are often the numbers of network connections, also known as personal network sizes or degrees, but they can be any function of individual unit variables. The unit sizes are treated as an i.i.d. sample of size N generated from a super-population model based on some (unknown) distribution. For simplicity of presentation, the unit sizes are presumed to have the natural numbers as their support (e.g., degrees). Specifically: where f(·|η) is a probability mass function (PMF) with support 1,…, and η is a parameter. In most situations of interest, the population size N is unknown and also treated as a parameter.
Consider first a general ordered sampling design. The random indices of the sequentially sampled units are denoted by the tuple G = (G1, …, Gn), with realization g = (g1, …, gn). Let (gn+1, gn+2,…, gN) be the ordered values in the set {1,…, N}\{g1, …, gn}, representing the ordered indices of the unsampled population units. Let Uobs = (Ug1, Ug2, …, Ugn), the random tuple of observed unit sizes (in sampling order), with values uobs = (ug1, …, ugn). Similarly, let Uunobs = (Ugn+1, Ugn+2, …, UgN) and uunobs = (ugn+1, ugn+2, …, ugN) represent the random and possible values of the unit sizes of the unobserved units, respectively. Let U = (U1, …, UN), u = (u1, …, uN). Note that U and Uunobs are ordered according to the unknown, fixed, but arbitrary population labeling, while the first n elements of Uobs are in the order of observation. The tuple G maps between the two orderings. The full observed data is uobs.
Inference for N and η should be based on all the available observed data including the sampling sequence information. The likelihood is any function of N and η proportional to p(Uobs|η, N), which can be computed by summing over all sets of u and g consistent with uobs:
| (2.1) |
where
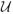 (uobs, N) = {(υg1,…, υgN): ∃υ1, …, υN, g1, …, gN s.t. (υg1, …, υgn) = uobs and (gn+1, …, gN) are the ordered va lues of the set {1, …, N}\{ g1, …, gn} }.
(uobs, N) = {(υg1,…, υgN): ∃υ1, …, υN, g1, …, gN s.t. (υg1, …, υgn) = uobs and (gn+1, …, gN) are the ordered va lues of the set {1, …, N}\{ g1, …, gn} }.
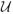 (uobs, N) is the set of equivalence classes of unit sizes possible for the N units given that the sequence of sampled unit sizes was uobs. Because the likelihood is equivalent for different values of g so long as they are consistent with u and uobs, we index the sample by g = (1, …, n) and apply the factor outside the sum to account for the number of sequences of n indices chosen from the N possible for each u (See, also, Nair and Wang, 1989, equation 3.2). Typically
(uobs, N) is the set of equivalence classes of unit sizes possible for the N units given that the sequence of sampled unit sizes was uobs. Because the likelihood is equivalent for different values of g so long as they are consistent with u and uobs, we index the sample by g = (1, …, n) and apply the factor outside the sum to account for the number of sequences of n indices chosen from the N possible for each u (See, also, Nair and Wang, 1989, equation 3.2). Typically
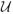 (uobs, N) will be the N – n product support of f(·|η). Thus, the likelihood involves the sampling design, p(G = g|U = u), as well as the super-population model.
(uobs, N) will be the N – n product support of f(·|η). Thus, the likelihood involves the sampling design, p(G = g|U = u), as well as the super-population model.
2.2. Modeling the RDS process
The RDS process is complex as it both depends on the structure of the networked population and is not completely under the control of the surveyors. As such there is not an unambiguous statistical representation of RDS sampling. Various representations of the process have been studied (Gile, 2008, 2011; Heckathorn, 1997; Volz and Heckathorn, 2008). Gile (2008) modeled the RDS process as a successive sampling (SS) process. Gile (2008) and Gile (2011) provide extensive theoretical and empirical justification for approximating RDS data via SS. Following Gile (2011), the RDS sampling is approximated as a successive sampling process. Gile argues that this model approximates a without-replacement random walk on the network, and demonstrates that using this model can reduce finite population biases for RDS estimates of population characteristics. This sampling scheme is also known as probability proportional to size without replacement (PPSWOR) sampling, and is treated in the survey sampling and ecological literature (Andreatta and Kaufman, 1986; Bickel, Nair and Wang, 1992; Nair and Wang, 1989). The Successive Sampling (SS) sampling procedure is defined as follows:
Sample the first unit from the full population {1,…, N} with probability proportional to unit size ui, i = 1, …, N: .
Select each subsequent unit with probability proportional to unit size from among the remaining units, such that
| (2.2) |
The probability of the observed sequence g for a given population of unit sizes is:
where
| (2.3) |
so that the full likelihood (2.1) is:
| (2.4) |
This likelihood can be the basis of maximum likelihood estimation for η and N. In general, this sum will be very difficult to compute because of the N – n embedded sums over typically infinite supports of f(·|η).
Note that this likelihood involves models for both the sampling design and the super-population, necessary because the design is not amenable to the model (See Appendix A for details). Intuitively, ignoring the sampling distribution would likely result in positive bias in inference about unit sizes as the larger-sized units will tend to be sampled first.
2.3. Bayesian inference for the unit size distribution
This section develops inference for the unit size distribution, conditional on known N. In this case, the posterior is:
where π(η) is a prior for the unit size distribution parameter.
Because of the complexity of computing the likelihood (2.4), West (1996) suggests using the relatively simple
| (2.5) |
and a two component Gibbs sampler with p(η|Uunobs = uunobs, Uobs = uobs) and p(U = u|η, Uobs = uobs). The current paper uses a variant of this approach for discrete unit size distributions.
From (2.5),
| (2.6) |
As the rk are hard to deal with, West (1996) notes that,
where ψk has exponential distribution with rate parameter rk. That is,
| (2.7) |
He augments the data with Ψ = (ψ1, …, ψn) where the components are drawn (conditionally) independently so that
and from (2.3),
| (2.8) |
Hence the elements of Uunobs are conditionally an i.i.d. sample from the unnormalized PMF , and are, in fact, conditionally independent of Uobs = uobs.
The augmented posterior:
| (2.9) |
can then be easily computed via a three component Gibbs sampler. Details of this and an explicit statement of the MCMC algorithm are given in Appendix B.
The algorithm produces samples from p(η|Uobs = uobs) and from the posterior predictive distribution for the unobserved unit sizes: p(Uunobs = uunobs|Uobs = uobs). These in turn enable inference for such quantities as the mean unit size, the unit size distribution, etc.
2.4. Estimating the size of the hidden population
When N is unknown, it becomes an additional parameter to be estimated. For simplicity, specify that N and η are a priori independent so that π(N, η) = π(N)·π(η). A variant of the approach in the last section allows draws from the joint posterior
| (2.10) |
This change requires p(N, η, Ψ|Uobs = uobs). Using (2.5) and (2.7),
| (2.11) |
| (2.12) |
The full-conditional for N is
| (2.13) |
The other full-conditionals are unchanged. This leads to a four component Gibbs sampler, the details of which are given in the Appendix B. The algorithm can be run to produce a large sample from the augmented posterior: p(N, η, Uunobs = uunobs, Ψ|Uobs = uobs). This can then be marginalized to produce samples from p(N|Uobs = uobs), p(η|Uobs = uobs), and the posterior predictive distribution of the unobserved unit sizes, p(Uunobs = uunobs|Uobs = uobs). Hence it produces posterior predictive distributions of the full population of unit sizes (ui, i = 1, …, N). These posteriors enable inference for such quantities as the population size, the mean unit size, the unit size distribution, etc.
2.5. Models for the unit size distribution
The methods in this paper require a parametric model for the super-population draws of the unit sizes. Although our approach is general with respect to the parametric distribution of unit sizes, the case where the unit sizes are degrees is focused on here.
There is a substantial literature on models for the degree distributions of social networks (Handcock and Jones, 2004, 2006; Jones and Handcock, 2003a,b). The naive models for these distributions include the Poisson and the Negative binomial (to allow Gamma over-dispersion relative to the Poisson). However, degree distribution tend to be long-tailed, suggesting alternatives such as the Yule and the Waring distributions (Jones and Handcock, 2003a), which allow power-law over-dispersion. Another in this class is the Poisson-log-normal, allowing log-normal over-dispersion (Perline, 2005). This allows longer-tails than the Negative Binomial but less than the power-law models. These models are unable to represent under-dispersion of the degree counts. The Conway-Maxwell-Poisson distribution allows both under-dispersion and over dispersion with a single additional parameter over a Poisson (Shmueli et al., 2005). It is possible to augment these distributions by directly parameterizing the lower-tail or upper-tail (e.g., ). This can improve the fit. Each of these options was considered in the studies in this paper and are also available in the R package degreenet on CRAN (Handcock, 2003; R Development Core Team, 2011).
Because of its flexibility, the parametric class of Conway-Maxwell-Poisson distributions is used in the applications in this paper.
2.6. Prior specification
2.6.1. Prior for the unit size distribution model
While the model for the unit size distribution can be arbitrary, in many applications it is helpful to focus on two-parameter models which enable separate specification of the location and spread of the degree distribution (with the shape a feature of the model). Each two-parameter unit size distribution considered above, including the Conway-Maxwell-Poisson, can be parameterized in terms of its mean and standard deviation.
For specificity, here we use the prior where the mean given the standard deviation is normal and the variance is a scaled inverse Chi-squared:
In the applications in this paper, we choose an equivalent sample size of dfmean = 1 for the mean of the unit size distribution and dfsigma = 5 for the variance of the unit size distribution. In practice, we find our results to be quite insensitive to the prior mean chosen for this distribution.
2.6.2. Prior for the population size
The model allows for an arbitrary prior distribution over the population size (N). In addition, the algorithms can easily incorporate them with little computational or programming burden. In this sub-section we suggest possible choices for the prior that may aid elicitation from substance area experts or encapsulate concomitant sources of information about the population size. They may also be used as reference priors in a sensitivity analysis.
The models in Section 2.6.1 are natural classes for priors, albeit with much higher means than that for the units sizes. In addition it may be desired to have greater dispersion. To complement the standard distributions we suggest distributions that place non-negligible mass on large N. The first is a prior that is constant over the range where the likelihood is non-negligible:
| (2.14) |
where Nmax covers the range where the likelihood is non-negligible. An alternative was suggested by Fienberg, Johnson and Junker (1999):
| (2.15) |
For their applications they choose their Jeffrey's prior l = 1, π(N) ∝ 1/N, n < N < Nmax. In addition to these possibilities, we consider a two-parameter class of priors that is in the same spirit as (2.15) and does not require the specification of an upper bound. The density function on N (considered as a continuous variable) is:
| (2.16) |
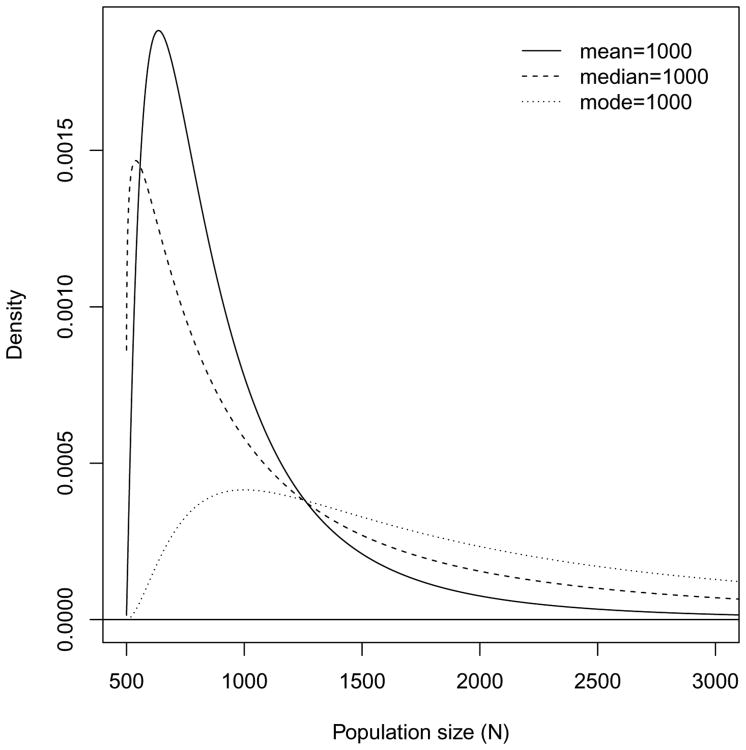
This class was proposed in Handcock, Gile and Mar (2014) and can be motivated as specifying knowledge about the sample proportion (i.e. n/N) as a Beta(α, β) distribution. Figure 2 presents three different versions of this prior, corresponding to a prior mean, median and mode of 1000. In applications such as those in Handcock, Gile and Mar (2014) the prior was flexible enough to capture both the possibility of quite large values of the population size while maintaining coverage around the values thought most likely. This class of priors for the population size was chosen after careful consultation with field researchers who choose n and implement the RDS surveys. The sample size is usually fixed in advance (based on cost and logistic considerations). Often a sampling “budget” is allocated across locations based on rough assumptions about the population sizes in each area. The prior class reflects this. Additional details on this prior are given in Appendix C.
Fig 2.
Three example prior distributions for the population size (N). They correspond to α = 1 and β = 1.55, 1.16 and 3.
3. Application to the National Longitudinal Study of Adolescent Health
In this section we return to the analysis of the population of a large high-school introduced in Section 1.1. The primary purpose is to elucidate the ideas in Section 2 via a specific example. Complete network data on the school was collected as part of the National Longitudinal Study of Adolescent Health (Add Health; Udry, 2003). The school has students from grades 9 though 12. All students were asked to report up to five male and up to five female friends. The same data were used to evaluate RDS in Goel and Salganik (2010). Like Goel and Salganik, we clean the data by first making them symmetrical and second treating the largest connected component. We symmeterize the networks by considering any reported friendship in either direction as a bi-directional friendship, rather than considering only mutual ties. The ultimate size of the population is N = 1249 students.
A common feature of networked populations is that social ties are often more likely to occur between people who have similar attributes than those who do not, a tendency called homophily by attributes (Freeman, 1996; Lazarsfeld and Merton, 1954; McPherson, Smith-Lovin and Cook, 2001). Population homophily leads to a clustering of the attribute values in the RDS. We chose this school as it exhibits strong homophily of friendship based on grade. As a measure of population homophily we use the ratio, H, of the expected number of discordant-grade ties absent homophily to the expected number of discordant-grade ties with the homophily:
| (3.1) |
so that larger values of H indicate more homophily. For this school the homophily, H, is approximately 5.74, indicating that individuals are almost six times less likely to have friendships outside their grade than we would expect at random.
As noted in the introduction, we simulated an RDS sample with 12 seeds selected with probability proportional to degree. Each seed distributed up to two virtual coupons, as did all recruits. A graph of the recruitment process through its completion in wave 5 is given in Figure 1. The homophily is apparent in the figure where we see the tendency for the grade of those recruited to be similar to their recruiters. However, there is also evidence of cross-grade recruitment, indicating that the successive waves do break out of the grade of the seeds. Such homophily or “clustering” could have an impact on the procedure and so we will also assess how it works in this school.
In this case, the units are the students and the unit sizes are their degrees. The class of distributions used for the units sizes was the Conway-Maxwell-Poisson distribution for its flexibility in capturing the over/under-dispersion. The hyperparameters for the mean and standard deviation of the unit size distributions are μ0 = 10, σ0 = 3 with an equivalent sample size of dfmean = 1 and dfsigma = 5, respectively.
The MCMC was run with a burn-in of 10000 and a interval of 1000. Analysis of the samples using standard MCMC diagnostics suggested little evidence of lack of convergence or lack of mixing (Plummer et al., 2006).
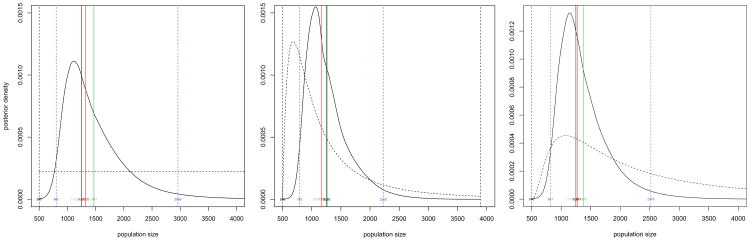
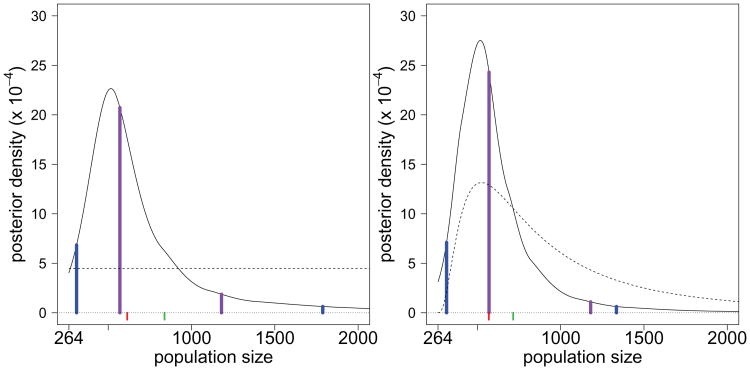
We consider three specifications of prior knowledge about the population size N. The first prior is constant over the range of population sizes where the likelihood is non-negligible (2.14). The first panel of Figure 3 plots both the prior and posterior distributions. The peakedness of the posterior shape indicates that there is information in the data about the population size, with a mode of 1122 students. The true value of N = 1249 also falls within the 95% HPD interval of 806 to 2914 students (blue lines). Overall, the posterior distribution is well centered about the true population size.
Fig 3.
Posterior distributions for the number of students in the school based on three prior distributions for the population size: flat, a prior median of 1000, and a prior median of 2000. The prior is dashed. The red mark is at the posterior median. The green mark is at the posterior mean. The blue lines are at the lower and upper bounds of the 95% highest-probability-density interval.
The second prior specifies a low prior median of 1000 students. This corresponds to a prior mode of 680 students. The second panel of Figure 3 plots this prior and the resulting posterior. The mean, median and mode of the posterior again fall close the true value and the posterior is centered about the truth. Finally the third prior over-specifies the prior median as 2000, corresponding to a prior mean of 2825. The third panel of Figure 3 plots this prior and the resulting posterior. While the prior is clearly up-shifted relative to the second prior the overall impact is small with the posterior again centered about the true value and the 95% HPD interval of 821 to 2519 students is not dramatically effected.
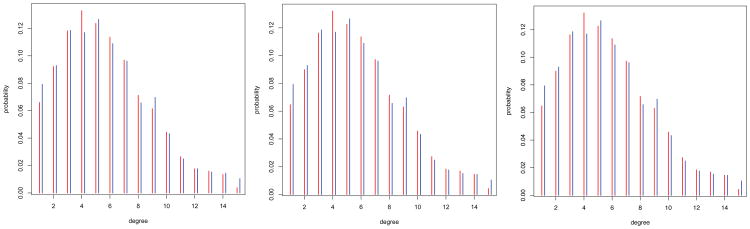
In this case, we can also consider other diagnostics of the model. Figure 4 presents the posterior means of the population degree distributions. These can be computed as the sample means of the posterior draws of the unit size distributions. The first panel presents the posterior based on the flat prior for the population size (red bars). We see that the modal degree is four friends. The posterior mean degree is 5.63, which is below the prior value (10), but very close to the true value for the school (5.68). The blue bars represent the actual degree distribution for the school. We see that the model very closely reproduce the population degree distribution.
Fig 4.
Posterior mean of the population degree distribution compared to the known population distribution for three prior specifications. The red bars represent the posterior mean proportions and the blue the actual proportions. The results indicate the model is capturing the degree distributions accurately.
The second and third panels present a similar analysis for the alternative priors, the first under-specifying the population size and the second over-specifying it. As we see, in both cases the models reproduces the degree distribution accurately.
4. A simulation study to assess frequentist properties
The primary focus of the simulation study is to evaluate the Frequentist performance of the proposed estimator for population size, including point estimation, interval estimation, and sensitivity to prior specification. Of secondary interest, is the use of these estimates to inform the estimation of population proportions using the estimator introduced in Gile (2011). In keeping with the applications typically of interest, we will create populations that are compatible with populations at high risk for HIV/STI infection. The parameters of the study are largely chosen for consistency with the simulation studies of RDS-based estimators of population proportions in Gile and Handcock (2010), Gile (2011), and Tomas and Gile (2011), although with a greater range of population sizes. As in these studies, to increase the realism of the study, parameters match the characteristics of the pilot data from the CDC surveillance program (Abdul-Quader et al., 2006) whenever possible. The general procedure is: (1) 200 Networks are simulated under each test condition; (2) An RDS sample is simulated from each sampled network; (3) Point and interval estimators of population size are computed from each sample.
For the simulation, all samples are of size 500, and the population mean degree is fixed at 7. A discoverable class, referred to as “infection status,” is assigned to each member of the population such that each population has prevalence 20%.
The varying characteristics of the synthetic populations are also chosen to represent those expected in the real world. These characteristics include population size (i.e., the number of nodes), tendency for individuals to preferentially form relations with others of the same infection status (that is, homophily), and different rates of network connectivity by infection status (referred to as differential activity).
Population network structures are modeled using Exponential family Random Graph Models (ERGM) (Snijders et al., 2006). That is, the N × N binary matrix of relations, y, is represented as a realization of the random variable Y with distribution:
| (4.1) |
where x are covariates, g(y, x) is a p-vector of network statistics, η ∈ ℝp is the parameter vector,
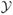 is the set of all possible undirected graphs, and exp{κ(η, x)} = Σu∈
is the set of all possible undirected graphs, and exp{κ(η, x)} = Σu∈
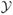 exp{η·g(u, x)} is the normalizing constant (Barndorff-Nielsen, 1978).
exp{η·g(u, x)} is the normalizing constant (Barndorff-Nielsen, 1978).
This modeling framework can represent a very wide range of populations, with the particular structures determined by the choice of g(y, x). Here, differential activity is parameterized as the ratio, DA, of the mean degree of infected nodes to the mean degree of uninfected nodes, where DA = 1 represents the absence of differential activity. While homophily can and will occur on multiple variables, any of them may have similar effects on population size estimation, and the most impactful type for proportion estimation is that on infection status. As defined in Section 3, homophily is parameterized, for fixed mean degree of each group, as the ratio, H, of the expected number of discordant-infection-status ties absent homophily to the expected number of discordant-infection-status ties with the homophily:
| (4.2) |
so that larger values of H indicate more homophily. This measure is meaningful across different levels of differential activity. Note that this parameterization of homophily is different from that in earlier studies (e.g. Gile and Handcock, 2010).
These features are represented in the ERGM by choosing network statistics to represent the mean degree, the relative activity levels of the two groups, and homophily. The binary nodal covariate xi represents infection status, such that xi = 1 indicates infection. These three parameters then map to the expected cell counts of the mixing matrix on infection status. Our networks are thus simulated from an ERGM with
The range of population characteristics modeled is (a) population size: N ∈ {5000, 1500, 1000, 750, 555}; (b) differential activity: DA ∈ {0.5, 1, 2}; and (c) homophily: H ∈ {1, 1.8}. The η parameter of the ERGM is chosen so the expected values of the statistics are equal to the values given above, and the simulated networks are generated from the resulting model, as in van Duijn, Handcock and Gile (2009). This was implemented using the R package statnet (Handcock et al., 2003).
Subsequent sample waves are selected without-replacement by sampling two nodes (where possible) at random from among the unsampled alters of each sampled node. This typically resulted in four complete waves and part of a fifth wave, stopping at sample size 500.
Throughout the simulations, unit sizes are modeled with a Conway-Maxwell-Poisson distribution with diffuse priors (hyper parameters μ0 = 7, dfmean = 1, σ0 = 3, dfsigma = 5). The prior for the population size is a Beta distribution with α = 1 as describe in (2.16). Sensitivity of the method to incorrect priors is tested with priors based on three different prior means: equal to the true population size, N, a high estimate equal to 2N, and a low estimate halfway between N and the sample size n: (N + n)/2.
Results from each simulation are summarized using the posterior mean as a point estimate, and the 95% highest posterior density region as an interval estimate.
4.1. Point and interval estimation of population size
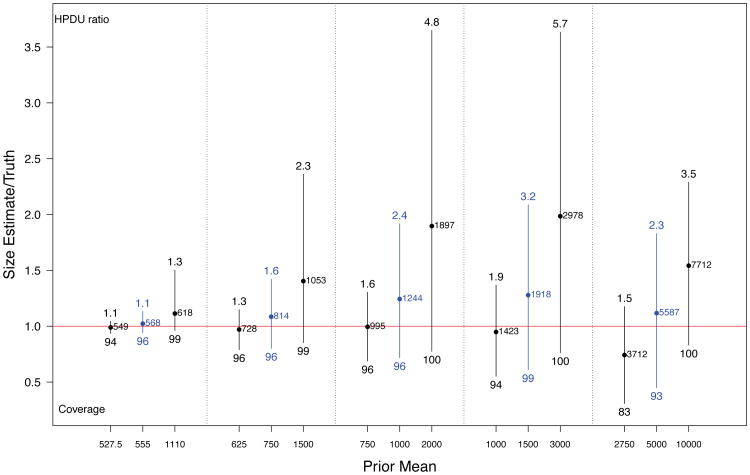
Figure 5 summarizes population size estimates based on simple network structures with no homophily (H = 1) or differential activity (DA = 1) for all five population sizes (corresponding to different sample fractions), and low, accurate, and high prior estimates of population size.
Fig 5.
Spread of central 95% of simulated population size estimates (posterior means) for 5 population sizes for low, accurate, and high priors. Dots represent means. Estimates are represented as multiples of the true population size (red line at 1 indicates true population size). Numbers below the bars are coverage rates of 95% HPD intervals, numbers above the bars indicate the widths of these intervals (ratio of median upper bound to truth).
When the prior is correct (blue lines), average point estimates are reasonably close in all cases. There is a small amount of positive bias. This is because of the successive sampling (SS) approximation to the true link-tracing network sampling process. In SS, the next unit sampled would be chosen with probability proportional to unit size from among all unsampled units. In RDS, the network structure constrains the selection of each subsequent unit, with the effect that the decrease in sampled unit sizes over time is less sharp than in successive sampling, leading to a slight positive bias in the population size estimates. The coverage rates of nominal 95% credible intervals are about right in the case of accurate prior information.
Because there is limited information regarding population size in the RDS samples, results are affected by the choice of prior mean, with greater impact for smaller sample fractions. This is because smaller sample fractions entail less exhaustion of the target population and therefore less information in the data about population size.
The coverage rates for the 95% HPD regions for cases of prior mis-specification range from 83% to 100%, with higher coverage rates for higher prior means. These intervals can be quite wide. Because of the lower bound induced by the sample size, interval width is largely determined by the upper limits. The numbers above the bars in Figure 5 represent the median across each set of 200 simulations of the upper limit of the HPD intervals, represented as a multiple of the true population size. When the population size is close to the sample size, intervals are quite tight, while smaller sample fractions yield intervals that are often very large, with median upper point 3.2 times the true population size for N = 1500, and
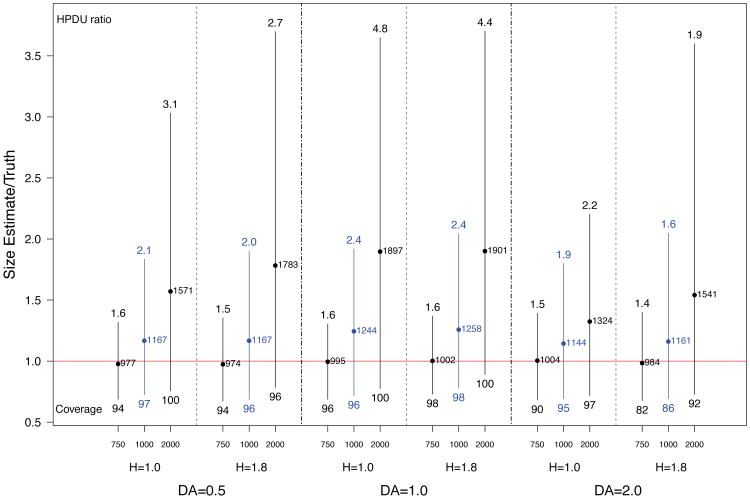
4.2. Impact of network structure
Figure 6 summarizes the results of varying the levels of homophily and differential activity, for varying prior specifications, all for populations of size 1000. Each pair of columns provides comparison across two levels of homophily (H). The paired columns are very similar, in both point and interval estimates, and across all levels of differential activity. This suggests that under a broad range of circumstances, homophily does not have a strong first-order impact.
Fig 6.
Spread of central 95% of simulated population size estimates (posterior means) for population size 1000 for low, accurate, and high priors, with varying levels of homophily (H) and differential activity (DA). The legend is the same as Figure 2.
There does appear, however, to be a first order impact of differential activity (DA = 0.5 and DA = 2), across levels of homophily. By systematically varying mean degree across infection groups, differential activity increases the variation in the unit size distribution, increasing the rate of decline in sampled unit sizes, and therefore providing more information about population size, resulting in better point estimates. Note how the prior mean 2000 cases have point estimates far closer to the truth when DA = 2 as compared to DA = 1. The credible intervals (HPDU ratios) are also typically smaller for DA ≠ 1 cases, without substantial reduction in the coverage rates.
4.3. Estimation of population proportions
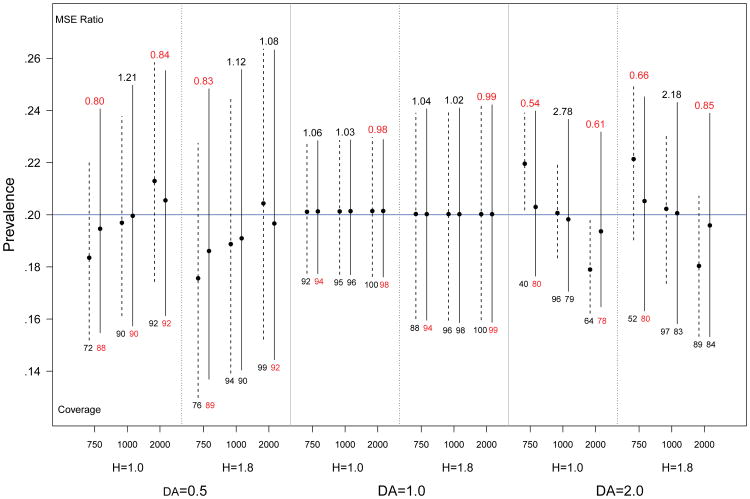
RDS is typically conducted in the interest of estimating population features such as population proportions. Earlier estimators based on RDS data assumed the population size was very large with respect to the sample size, so that finite population effects could be ignored. The more recent estimator which introduces the successive sampling (SS) approximation on which this paper is based (Gile, 2011), however, includes a finite population adjustment, but assumes that the population size is known. It is natural, therefore, to use the approach to population size estimation introduced in this paper to provide a population size estimate for use in the prevalence estimator in Gile (2011). Hence this section considers estimates of infection prevalence using the SS estimator. This section compares results using the prior mean as the population size to results using the posterior mean.
Figure 7 shows the SS results for the same simulation conditions as Figure 6. Absent differential activity (Figure 7, middle 2 columns), there is little difference between results using the prior and posterior means. This is because the SS estimator re-weights the sample based on unit sizes (degrees) and the assumed population size. Absent differential activity, the infected and uninfected subsamples will have similar degree distributions, and therefore be similarly affected by any aberrations in the unit weights.
Fig 7.
Spread of central 95% of simulated prevalence estimates for population size 1000, with varying levels of homophily (H) and differential activity (DA). Solid lines represent prevalence estimates based on the posterior mean, dashed lines represent comparable estimates using the prior mean. Relative efficiency (MSE posterior/MSE prior) is given above each bar, and the coverage of nominal 95% confidence intervals is below each bar. The true prevalence is 0.2 (blue line).
In the presence of differential activity, inaccurate population size estimates introduce bias in the point estimates given by the successive sampling estimator (see Gile, 2011). The first and last two columns of Figure 7 compare prevalence estimates based on the prior and posterior means for cases with strong differential activity. Consistent with Gile (2011), the dashed bars, corresponding to estimates using the prior mean, show substantial bias when the population size is inaccurate. This is due to imperfect adjustment for finite population effects. The primary advantage of estimates based on the posterior mean is the reduction of this dramatic bias. The cost of this reduction, however, is increased variance of the estimator, resulting in higher MSE in cases with small finite population biases, such as when the prior mean is correct. Note that because the bootstrap standard error estimator associated with the successive sampling estimator does not account for uncertainty in the population size, coverage rates can be dramatically low, especially for the estimator based on the prior mean.
5. Estimating the number of injecting drug users that share needles in Colorado Springs
In the interest of demonstrating the method in a hard-to-reach high-risk population, in this section we use the methodology to estimate the size of a sub-population of those at high-risk for HIV in a moderate-sized city (Colorado Springs, El Paso County, CO). The data are a product of epidemiological study of high-risk individuals to better understand factors affecting the transmission of a variety of pathogens, including HIV (Rothenberg et al., 1995), and have been used in the evaluation of RDS prevalence estimators (Goel and Salganik, 2010). The study focused on sub-groups thought to be most at risk: prostitutes, injecting drug users (IDU) and their sex partners. As this was a hard-to-reach population, for which a standard sampling frame was not available, they were enrolled through clinic and “outreach” activities and through a form of network sampling. Specifically, respondents were asked for a complete enumeration of their close personal contacts of various types. Persons named by two or more respondents were also sought as participants. Hence, the final sample was a combination of peer recruitment and direct enrollment.
We will focus on a sub-population at very high-risk for HIV: those injecting drug users that share needles with other IDU. The number of IDU who shared needles was unknown. To apply the methodology, we approximate the sampling process by successive sampling proportional to size. The IDU respondents were asked the number of people they have taken drugs with or shared needles with in the last 6 months. We will use this as the measure of size, approximating their visibility within the population. The sequence order of the 264 people who shared needles in the sample was determined from their interview date. These choices illustrate the use of the methodology when only sequence order and relative measures of visibility are available, demonstrating that a full RDS design is not necessary. They also highlight that subsamples of successive samples are also successive samples, enabling sub-population estimation within a broader sampling scheme.
We consider two prior specifications. First we consider a prior for the population size that is constant over the range of population sizes where the likelihood is non-negligible.
The first panel of Figure 8 plots both the prior and posterior distributions in this case. The posterior mass ranges from the sample size (267) up to about 2500. The peakedness of the posterior shape indicates that there is information in the data about the population size, with a mode of around 450 IDU. The posterior mean is about 820 IDU. The lower blue line is at the 2.5% quantile of the posterior the upper blue line is at the 97.5% quantile (310 and 1800, respectively).
Fig 8.
Posterior distribution for the number of needle sharing IDU in El Paso County based on two prior distributions for the population size: flat and matching the 1992 consensus. The prior is dashed. The red mark is at the posterior median. The green mark is at the posterior mean. The blue lines are at the lower and upper bounds of the 95% highest-probability-density interval. The purple lines demark the lower and upper quartiles of the 2004 guidelines.
The second prior we consider uses a guideline available to the researchers at the time of the study (1988–1992). We consider as a guideline the consensus figure for the whole U.S. of 1 per 725 persons (Anderson and May, 1992). Using the 1988 population of El Paso county (394,000) produces a population size of 525 needle sharing IDU. We use this value to determine a prior as described in Section 2.6.2 and Appendix C. Specifically, we choose the prior mode to be 525 and choose α = 1 in equation (2.16). The right panel of Figure 8 plots this prior and the resulting posterior. The posterior median and mean are in the range of 600–700.
As a further assessment of the estimates, we consider the guidelines provided by Friedman et al. (2004). They compute estimates for the U.S. and give a range of values for metropolitan areas. While El Paso County is not explicitly included, extrapolating the rate for Denver gives 960. The quartiles of rates in all metropolitan areas (SMSA) in the U.S. project to a range of 570 to 1180 people. While there is much ambiguity about these figures, we can consider them as alternative benchmark figures and have included them in Figure 8. The lower purple line is the lower quartile and the upper purple line is at the upper quartile. For the flat reference prior (left-hand panel), the benchmarks fall in the mid to upper part of the posterior distribution and are broadly consistent with it. The same is true for the prior based on the 1992 guidelines (right-hand panel), For both prior distributions, the benchmarks also fall within the 95% HPD interval (blue lines).
6. Discussion
The primary contribution of this paper is a method to estimate population size from RDS data alone. All existing methods require at least two data sources, and strong assumptions about their dependence structure. Intuitively, when unit sizes are associated with sampling probability, a systematic decline in observed unit sizes over time is indicative of the depletion of the available population. As described in this paper, a successive sampling (SS) approximation to the RDS process leverages this change in observed sizes to estimate the size of the hidden population. These data were previously unexploited in the estimation of the size of hard-to-reach human populations. Because RDS is designed for inference in hard-to-reach populations, such data often exist in precisely the populations where population size is both unknown and great interest. Thus this method provides additional important information, that is, an estimate of population size, at no extra cost. Furthermore, the Bayesian framework of this work allows for easy incorporation of informative prior information or data from other sources.
We note that in a companion paper (Handcock, Gile and Mar, 2014), we present an application of the proposed method to RDS samples from hard-to-reach populations in El Salvador. In that paper, we also present additional nuance concerning the practical details of the application of the method.
Here, the methodology is applied to a known networked school population from the National Longitudinal Study of Adolescent Health. In this case the population size and network structure are known, and the student social network is very clustered by grade. The approach accurately estimates the population size and measures the certainty in the knowledge about it. Further, we illustrate that the population unit size distribution can also be estimated accurately, indicating that the approach can be used to estimate other population characteristics in addition to the overall size.
The simulation study of the Frequentist performance of the population size estimator reported in Section 4 indicates good results can be obtained. A further insight is that the SS approximation to RDS balances realism with the limitation of the available information. If the representation of the sampling design relies on unknown quantities its value is limited as a model. Hence a primary motivation of the SS approximation is parsimony. Conceptually, it has appeal to capture the primary feature used in current RDS methodology (i.e., that the probability of being sampled at a given point in the survey is proportional to the unit size). The empirical performance of the procedure in the simulation study indicates that the SS approximation can be good enough to quantify the major sources of uncertainty.
The main limitation of the proposed method is the small amount of information on population size available in many RDS samples, with less information available in smaller sample fractions. In cases with little information, this method results in very large interval estimates in order to obtain reasonable Frequentist coverage properties. However, existing methods are also subject to great uncertainty, even though they typically require additional data collection. Often these methods lead to apparently conflicting results because they poorly estimate measures of uncertainty (Salganik et al., 2011). The advantage of the proposed method is that it uses existing data and accurately assesses the degree of uncertainty in N over a wide range of practical situations. Results from the analysis of the complete network data collected as part of the National Longitudinal Study of Adolescent Health indicate it can accurately estimate both the population size and degree distribution.
This method is also useful for estimators of population characteristics that require an estimate of the population size. The simulation study demonstrates that using population size estimates from the proposed method in the SS estimator (Gile, 2011) works well and is particularly helpful in conditions of strong differential activity and larger sample fractions.
The framework developed in this paper is designed to be a foundation upon which other approaches to population size estimation can build. In particular, it is designed to facilitate combination with data from multiple methods (e.g., direct surveys, capture-recapture, network scale-up and multiplier). The posterior from the approach in this paper can be used as a prior for combination with information from these alternative methods. Thus this methodology will lead to coherent inference that can be incrementally improved in a constructive way.
While the methods in this paper have been applied to data collected via RDS, we note that the approach is general and applies to data collected via successive sampling. Hence the method has broad applicability (Andreatta and Kaufman, 1986; Bickel, Nair and Wang, 1992; Nair and Wang, 1989). The application in Section 5 provides one example of this, as it is based on a sample only partially collected through link-tracing but approximated as successive sampling based on a proxy for visibility. The resulting inference is credible and consistent with expectations based on other sources of information. In general, the approach can be applied when the data collection mechanism can be credibly approximated by a successive sampling mechanism. However, in all situations the quality of this approximation should be assessed through sensitivity analyses.
The R package implementing the methods developed in this paper (Handcock, 2011) will be available on CRAN (R Development Core Team, 2011).
Acknowledgments
The project described was supported by grant numbers 1R21HD063000 and 5R21HD075714-02 from NICHD, grant number N00014-08-1-1015 from ONR, grant numbers MMS-0851555 MMS-1357619 from NSF, and grant number SES-1230081 from NSF, including support from the National Agricultural Statistics Service. We are grateful to the California Center for Population Research at UCLA (CCPR) for general support. CCPR receives population research infrastructure funding (R24-HD041022) from the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD). Partial support for this research came from a Eunice Kennedy Shriver National Institute of Child Health and Human Development research infrastructure grant, R24 HD042828, to the Center for Studies in Demography & Ecology at the University of Washington. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the Demographic & Behavioral Sciences (DBS) Branch, the National Science Foundation, the Office of Navel Research, or the National Agricultural Statistics Service. The authors would like to thank Michael L. Lavine and the members of the Hard-to-Reach Population Research Group (hpmrg.org), especially Lisa G. Johnston, for their helpful input.
Appendix A: RDS is not amenable to the model
The RDS design is not amenable to the modeling framework used in this paper, and here we explain why. In Section 2.2, modeling the sampling design along with the resulting data structure adds a great deal of complexity (see, e.g., (2.1)). It is natural to ask when we might consider the simpler face-value likelihood,
| (A.1) |
which ignores the sampling design.
The sampling design is amenable, in the sense of Handcock and Gile (2010), if:
In this case:
so that the sampling design is ignorable in the sense that the resulting likelihoods are proportional (Little and Rubin, 2002). When this condition is satisfied likelihood-based inference for η and N, as proposed here, is unaffected by the (possibly unknown) sampling design.
However, based on equation (2.2), the successive sampling design is clearly not amenable. Likelihood inference should be based on the full likelihood given by equation (2.1).
Appendix B: Algorithmic details
This section details the algorithm used to compute the joint posterior for the population size, the super-population parameter η and the unobserved population sizes Uunobs. It is based on that developed by West (1996).
First consider the case in Section 2.3 where the population size N is assumed known. The augmented posterior:
| (B.1) |
can be computed via a three component Gibbs sampler. Explicitly, the steps are:
Initialize uunobs at a set of unit sizes.
-
Sample η from
(B.2) Sample Ψ from p(ψj = ψ|η, Uunobs = uunobs, Uobs = uobs) in equation (2.7).
Sample Uunobs from p(Uunobs = uunobs|Ψ, η, Uobs = uobs) in equation (2.8).
Repeat steps (2) through (4) until convergence.
The MCMC should be run until burn-in and then sampled after an interval of iterations to produce a large sample from the augmented posterior (B.1). Standard MCMC diagnostics can be applied to assess convergence (Gilks, Richardson and Spiegelhalter, 1996). In our experience, the procedure is well behaved and converges quickly. The augmented posterior can be marginalized to produce samples from p(η|Uobs = uobs) and from the posterior predictive distribution for the unobserved unit sizes: p(Uunobs = uunobs|Uobs = uobs).
These in turn enable inference for such quantities as the mean unit size, the unit size distribution, etc.
We make the following step-by-step remarks on the algorithm:
uunobs ∼ f(·|η0), where η0 is a specified starting value.
This is done with a Metropolis-Hastings algorithm with Gaussian proposal for the mean size and a inverse χ for the standard deviation of the size.
These are independent standard Exponential draws.
- This is done with a rejection algorithm (West, 1996). For each element of uunobs:
- Draw d ∼ f(·|η) and independently, u ∼ U(0, 1).
- If log(u) > –d then reject d and return to (a); otherwise save d as the element of uunobs and return to (a) for the next element.
In the situation in Section 2.4 where N is not known, we need to extend the above algorithm to sample from the joint posterior p(N, η, Uunobs, Ψ|Uobs = uobs).
The algorithm is:
Initialize N at a point estimate and uunobs at a set of unit sizes.
-
Sample η from
(B.3) Sample Ψ from p(ψj = ψ|η, Uunobs = uunobs, Uobs = uobs, N) in equation (2.7).
Sample N from p(N|η, Ψ, Uobs = uobs) in equation (2.13).
Sample Uunobs from p(Uunobs = uunobs|Ψ, η, Uobs = uobs, N) in equation (2.8).
Repeat steps (2) through (5) until convergence.
As before, this expanded MCMC can be run to produce a large sample from the augmented posterior:
| (B.4) |
This can then be marginalized to produce samples from p(N|Uobs = uobs), p(η|Uobs = uobs) and the posterior predictive distribution of the unobserved unit sizes, p(Uunobs = uunobs|Uobs = uobs). Hence it produces posterior predictive distributions of the full population of unit sizes (ui, i = 1,…, N).
The step-by-step remarks are the same as before. For step 4, the complete PMF is discrete and is computed directly from (2.13) and hence sampled from directly.
Both these algorithms have been implemented at the C level in the R package size (Handcock, 2011; R Development Core Team, 2011). They are accessible via a user-friendly front-end. It includes a range of unit size distribution models, each of which is parametrized in terms of the mean and standard deviation of the distribution.
Appendix C: Prior for the population size
This section contains additional aspects to those considered in Section 2.6.1 of the paper. Note that the data effectively truncates the prior below the sample size n. In addition to the uniform prior, there are natural classes of parametric models for counts considered for the unit sizes in Section 2.6.1 (e.g., Negative Binomial, Poisson-log-normal, Conway-Maxwell-Poisson).
The novel class of priors proposed in Handcock, Gile and Mar (2014), Section 2.6.2, and used in the application and simulation study can be motivated as an elicitation of knowledge about the sample proportion (i.e. n/N). Specifically, it represents n/N as a Beta(α, β) distribution. This is based on the idea that the sample size may not be chosen separately from the population size but is often chosen in relation to it. So a simple prior is a uniform prior on the sampling proportion (i.e. the proportion of the population in the sample). This translates to a closed form for the prior on N which has infinite mean (and higher moments) and allows for very large population sizes. To allow a more flexible prior, we specify a Beta(α, β) distribution on the sample proportion. This is translated to a prior on the discrete support of n/N by assigning the probability mass to the closest discrete value.
When α = l – 1 > 0, this class is similar to the class in (2.15) as proposed by Fienberg, Johnson and Junker (1999).
A uniform distribution on the sample proportion corresponds to a median of twice the sample size. While the mapping from the mean to β does not have a closed from (for general β) it can be easily computed numerically. We have found the sub-class with α = 1 to be the most useful. For these the mode of the prior is at 0.5n(β + 1) and the median is given by n/(1 − (1/2)1/β).
These choices and more are available for selection in the software.
Contributor Information
Mark S. Handcock, Email: handcock@stat.ucla.edu, Department of Statistics, University of California, Los Angeles, Los Angeles CA 90095-1554, USA, url: http://www.stat.ucla.edu/∼handcock.
Krista J. Gile, Email: gile@math.umass.edu, Department of Mathematics and Statistics, University of Massachusetts, Amherst, Amherst, MA 01003-9305, USA, url: http://www.math.umass.edu/∼gile.
Corinne M. Mar, Email: cmmar@uw.edu, Center for Studies in Demography and Ecology, University of Washington, Seattle, WA 98195-1554, url: http://www.csde.washington.edu.
References
- Abdul-Quader AS, Heckathorn DD, McKnight C, Bramson H, Nemeth C, Sabin K, Gallagher K, Jarlais DCD. Effectiveness of Respondent-Driven Sampling for recruiting drug users in New York City: findings from a pilot study. Journal of Urban Health. 2006;83:459–476. doi: 10.1007/s11524-006-9052-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson RM, May RM. Understanding the AIDS pandemic. Scientific American. 1992;266:58–66. doi: 10.1038/scientificamerican0592-58. [DOI] [PubMed] [Google Scholar]
- Andreatta G, Kaufman GM. Estimation of finite population properties when sampling is without replacement and proportional to magnitude. Journal of the American Statistical Association. 1986;81:657–666. MR0860497. [Google Scholar]
- Bao L, Raftery AE, Reddy A. Estimating the Size of Populations at High Risk of HIV in Bangladesh Using a Bayesian Hierarchical Model. Department of Statistics Technical Report number 573; University of Washington; 2010. [Google Scholar]
- Barndorff-Nielsen OE. Information and Exponential Families in Statistical Theory. Wiley; New York: 1978. MR0489333. [Google Scholar]
- Berchenko Y, Frost SDW. Capture-recapture methods and Respondent-Driven Sampling: their potential and limitations. Sexually Transmitted Infections. 2011;87:267–268. doi: 10.1136/sti.2011.049171. [DOI] [PubMed] [Google Scholar]
- Bernard HR, Hallett T, Iovita A, Johnsen EC, Lyerla R, McCarty C, Mahy M, Salganik MJ, Saliuk T, Scutelniciuc O, Shelley GA, Sirinirund P, Weir S, Stroup DF. Counting hard-to-count populations: the network scale-up method for public health. Sexually Transmitted Infections. 2010;86:ii11–ii15. doi: 10.1136/sti.2010.044446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernhardt A, Milkman R, Theodore N, Heckathorn D, Auer M, DeFilippis J, Gonzalez AL, Narro V, Perelshteyn J, Polson D, Spiller M. Broken Laws, Unprotected Workers: Violations of Employment and Labor Laws in America's Cities, Report, National Employment Law Project. New York, NY 10038: 2009. [Google Scholar]
- Bickel PJ, Nair VN, Wang PCC. Nonparametric inference under biased sampling from a finite population. The Annals of Statistics. 1992;20:853–878. MR1165596. [Google Scholar]
- Felix-Medina MH, Thompson SK. Combining link-tracing sampling and cluster sampling to estimate the size of hidden populations. Journal of Official Statistics. 2004;20:19–38. [Google Scholar]
- Fienberg SE, Johnson MS, Junker BW. Classical multilevel and Bayesian approaches to population size estimation using multiple lists. Journal of the Royal Statistical Society: Series A (Statistics in Society) 1999;162:383–405. [Google Scholar]
- Frank O, Snijders TAB. Estimating the size of hidden populations using snowball sampling. Journal of Official Statistics. 1994;10:53–67. [Google Scholar]
- Freeman LC. Some antecedents of social network analysis. Connections. 1996;19:39–42. [Google Scholar]
- Friedman S, Tempalski B, Cooper H, Perlis T, Keem M, Friedman R, Flom P. Estimating numbers of injecting drug users in metropolitan areas for structural analyses of community vulnerability and for assessing relative degrees of service provision for injecting drug users. Journal of Urban Health. 2004;81:377–400. doi: 10.1093/jurban/jth125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gile KJ. Inference from Partially-Observed Network Data PhD in Statistics, University of Washington Advisor: Mark S Handcock. 2008 MR2717562. [Google Scholar]
- Gile KJ. Improved inference for Respondent-Driven Sampling data with application to HIV prevalence estimation. Journal of the American Statistical Association. 2011;106:135–146. MR2816708. [Google Scholar]
- Gile KJ, Handcock MS. Respondent-Driven Sampling: an assessment of current methodology. Sociological Methodology. 2010;40:285–327. doi: 10.1111/j.1467-9531.2010.01223.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gile KJ, Handcock MS. Network model-assisted inference from Respondent-Driven Sampling data. Journal of the Royal Statistical Society: Series A (Statistics in Society) 2014 doi: 10.1111/rssa.12091. Forthcoming. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilks WR, Richardson S, Spiegelhalter DJ. Markov Chain Monte Carlo in Practice. Chapman and Hall; London: 1996. MR1397966. [Google Scholar]
- Goel S, Salganik MJ. Assessing Respondent-Driven Sampling. Proceedings of the National Academy of Science, USA. 2010;107:6743–6747. doi: 10.1073/pnas.1000261107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Handcock MS. degreenet: Models for Skewed Count Distributions Relevant to Networks, Statnet Project, Seattle, WA Version 1.0 2003 [Google Scholar]
- Handcock MS. size: Estimating Population Size from Discovery Models using Successive Sampling Data, Hard-to-Reach Population Methods Research Group, Los Angeles, CA R package version 0.20 2011 [Google Scholar]
- Handcock MS, Gile KJ. Modeling networks from sampled data. Annals of Applied Statistics. 2010;272:383–426. doi: 10.1214/08-AOAS221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Handcock MS, Gile KJ, Mar CM. Estimating the size of populations at high risk for HIV using Respondent-Driven Sampling data. Biometrics. 2014 doi: 10.1111/biom.12255. Forthcoming. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Handcock MS, Jones JH. Likelihood-based inference for stochastic models of sexual network formation. Theoretical Population Biology. 2004;65:413–422. doi: 10.1016/j.tpb.2003.09.006. [DOI] [PubMed] [Google Scholar]
- Handcock MS, Jones JH. Interval estimates for epidemic thresholds in two-sex network models. Theoretical Population Biology. 2006;70:125–134. doi: 10.1016/j.tpb.2006.02.004. [DOI] [PubMed] [Google Scholar]
- Handcock MS, Hunter DR, Butts CT, Goodreau SM, Morris M. statnet: Software Tools for the Statistical Modeling of Network Data, Statnet Project. Seattle, WA: 2003. http://statnet.org/ R package version 2.0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckathorn DD. Respondent-Driven Sampling: a new approach to the study of hidden populations. Social Problems. 1997;44:174–199. [Google Scholar]
- Heckathorn DD. Respondent-Driven Sampling II: deriving valid population estimates from chain-referral samples of hidden populations. Social Problems. 2002;49:11–34. [Google Scholar]
- Heckathorn DD, Jeffri J. Finding the beat: using Respondent-Driven Sampling to study jazz musicians. Poetics. 2001;28:307–329. [Google Scholar]
- Johnston LG, Malekinejad M, Kendall C, Iuppa IM, Rutherford GW. Implementation challenges to using Respondent-Driven Sampling methodology for HIV biological and behavioral surveillance: field experiences in international settings. AIDS and Behavior. 2008;12:131–141. doi: 10.1007/s10461-008-9413-1. [DOI] [PubMed] [Google Scholar]
- Johnston LG, Prybylski D, Raymond HF, Mirzazadeh A, Manopaiboon C, McFarland1 W. Unpublished manuscript. University of California; San Francisco: 2011. Incorporating the service multiplier method in respondent driven sampling surveys to estimate the size of hidden and hard-to-reach populations: Case studies from around the world. [DOI] [PubMed] [Google Scholar]
- Jones JH, Handcock MS. An assessment of preferential attachment as a mechanism for human sexual network formation. Proceedings of the Royal Society of London, B. 2003a;270:1123–1128. doi: 10.1098/rspb.2003.2369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones JH, Handcock MS. Sexual contacts and epidemic thresholds. Nature. 2003b;423:605–606. doi: 10.1038/423605a. [DOI] [PubMed] [Google Scholar]
- Lazarsfeld P, Merton R. Friendship as social process: a substantive and methodological analysis. In: Berger M, Abel T, Page CH, editors. Freedom and Control in Modern Society. Van Nostrand; New York: 1954. pp. 18–66. [Google Scholar]
- Little RJA, Rubin DB. Statistical Analysis with Missing Data. 2nd. John Wiley & Sons, Inc.; Hoboken, New Jersey: 2002. MR1925014. [Google Scholar]
- McPherson M, Smith-Lovin L, Cook JM. Birds of a feather: homophily in social networks. Annual Review of Sociology. 2001;27:415–444. [Google Scholar]
- Nair VN, Wang PCC. Maximum likelihood estimation under a successive sampling discovery model. Technometrics. 1989;31:423–436. MR1041563. [Google Scholar]
- Niccolai LM, Verevochkin SV, Toussova OV, White E, Barbour R, Kozlov AP, Heimer R. Estimates of HIV incidence among drug users in St. Petersburg, Russia: continued growth of a rapidly expanding epidemic. The European Journal of Public Health. 2010 doi: 10.1093/eurpub/ckq115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paz-Bailey G, Jacobson JO, Guardado ME, Hernandez FM, Nieto AI, Estrada M, Creswell J. How many men who have sex with men and female sex workers live in El Salvador? Using respondent-driven sampling and capture-recapture to estimate population sizes. Sexually Transmitted Infections. 2011;87:279–282. doi: 10.1136/sti.2010.045633. [DOI] [PubMed] [Google Scholar]
- Perline R. Strong, weak and false inverse power laws. Statistical Science. 2005;20:68–88. MR2182988. [Google Scholar]
- Plummer M, Best N, Cowles K, Vines K. CODA: convergence diagnosis and output analysis for MCMC. R News. 2006;6:7–11. [Google Scholar]
- Potterat JJ, Woodhouse DE, Muth SQ, Rothenberg RB, Darrow WW, Klovdahl AS, Muth JB. Network dynamism: history and lessons of the Colorado Springs study. In: Morris M, editor. Network Epidemiology: A Handbook for Survey Design and Data Collection. Oxford University Press; 2004. International Studies in Demography Series 87 – 114. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2011. Version 2.14. [Google Scholar]
- Rocchetti I, Bunge J, Böhning D. Population size estimation based upon ratios of recapture probabilities. Annals of Applied Statistics. 2011;5:1512–1533. MR2849784. [Google Scholar]
- Rothenberg RB, Woodhouse DE, Potterat JJ, Muth SQ, Darrow WW, Klovdahl AS. Social networks in disease transmission: the Colorado Springs study. NIDA. 1995;1995:3–19. [PubMed] [Google Scholar]
- Salganik MJ, Heckathorn DD. Sampling and estimation in hidden populations using Respondent-Driven Sampling. Sociological Methodology. 2004;34:193–239. [Google Scholar]
- Salganik MJ, Fazito D, Bertoni N, Abdo AH, Mello MB, Bastos FI. Assessing network scale-up estimates for groups most at risk of HIV/AIDS: evidence from a multiple-method study of heavy drug users in Curitiba, Brazil. American Journal of Epidemiology. 2011;174:1190–1196. doi: 10.1093/aje/kwr246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shmueli G, Minka TP, Kadane JB, Borle S, Boatwright P. A useful distribution for fitting discrete data: revival of the Conway-Maxwell-Poisson distribution. Journal of the Royal Statistical Society: Series C (Applied Statistics) 2005;54:127–142. MR2134602. [Google Scholar]
- Snijders TAB, Pattison P, Robins GL, Handcock MS. New specifications for exponential random graph models. Sociological Methodology. 2006;36:99–153. [Google Scholar]
- Tomas A, Gile KJ. The effect of differential recruitment, non-response and non-recruitment on estimators for Respondent-Driven Sampling. Electronic Journal of Statistics. 2011;5:899–934. MR2831520. [Google Scholar]
- Udry JR. The National Longitudinal Study of Adolescent Health (Add Health), Waves I & II, 1994–1996; Wave III, 2001–2002 [machine-readable data file and documentation], Technical Report. Carolina Population Center, University of North Carolina; Chapel Hill: 2003. [Google Scholar]
- UNAIDS. Estimating National Adult Prevalence of HIV-1 in Concentrated Epidemics, Technical Report. UNAIDS – Joint United Nations Programme on HIV/AIDS; 2009. [Google Scholar]
- UNAIDS and World Health Organization. Guidelines on estimating the size of populations most at risk to HIV, Technical Report No UNAIDS/00.03E. UNAIDS – Joint United Nations Programme on HIV/AIDS; 2010. [Google Scholar]
- van Duijn MAJ, Handcock MS, Gile KJ. A framework for the comparison of maximum pseudo likelihood and maximum likelihood estimation of exponential family random graph models. Social Networks. 2009;31:52–62. doi: 10.1016/j.socnet.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volz E, Heckathorn DD. Probability based estimation theory for Respondent Driven Sampling. Journal of Official Statistics. 2008;24:79–97. [Google Scholar]
- West M. Inference in successive sampling discovery models. Journal of Econometrics. 1996;75:217–238. [Google Scholar]