Abstract
Electron paramagnetic resonance imaging (EPRI) provides 3D images of absolute oxygen concentration (pO2) in vivo with excellent spatial and pO2 resolution. When investigating such physiologic parameters in living animals, the situation is inherently dynamic. Improvements in temporal resolution and experimental versatility are necessary to properly study such a system. Uniformly distributed projections result in efficient use of data for image reconstruction. This has dictated current methods such as equal-solid-angle (ESA) spacing of projections. However, acquisition sequencing must still be optimized to achieve uniformity throughout imaging. An object-independent method for uniform acquisition of projections, using the ESA uniform distribution for the final set of projections, is presented. Each successive projection maximizes the distance in the gradient space between itself and prior projections. This maximally spaced projection sequencing (MSPS) method improves image quality for intermediate images reconstructed from incomplete projection sets, enabling useful real-time reconstruction. This method also provides improved experimental versatility, reduced artifacts, and the ability to adjust temporal resolution post factum to best fit the data and its application. The MSPS method in EPRI provides the improvements necessary to more appropriately study a dynamic system.
INTRODUCTION
The oxygenation status of tumors has been known to have important prognostic implications for decades (1). Low oxygen concentration (pO2), or hypoxia, causes cancer cells to have greater resistance to radiation therapy (2,3) and a strong correlation has been established between electrode measurements of low pO2 and radiotherapy treatment failure in humans (4). Hypoxic tumors are more resistant to chemotherapy as well (5). Hypoxia also leads to faster tumor growth due to abnormal proliferation (6), and increases the potential for metastatic progression (7).
These implications have led to increased interest in methods for probing and, a fortiori, imaging pO2 deep in tissues. Advances in methods to investigate/image pO2 in tissue have been detailed in the literature (8–11). In particular, electron paramagnetic resonance imaging (EPRI) has proven to be a robust modality for measuring tissue pO2. EPRI noninvasively acquires highly-resolved, both spatially (~1mm3 voxels) and in pO2 (1–3 torr), 3D images of in vivo pO2 (12–16). The low electromagnetic wave excitation frequencies used in EPRI (comparable to that of 6T MRI) penetrate deep in tissue (>7 cm). EPR pO2 images use an intravenously injected, non-toxic spin probe, which distributes in the extracellular compartment of tumors, to report local pO2 (17).
EPRI as described in this paper is a projection based imaging modality. Projections are acquired using fixed stepped linear magnetic field gradients for spatial encoding of the concentration of exogenous spin probe within the object. Projections are acquired in a spherical geometry and thus projection directions can be considered as points on the unit sphere. Uniform distribution of these projection points results in better image quality and less artifacts (18, 19). According to the Nyquist sampling theorem, more uniform and/or dense radial sampling of k-space affects the size of the artifact free FOV, as described previously (20). This has led to the previous efforts to achieve a uniform distribution of projection points for the final EPRI image. Equal linear angle (ELA) spacing of projections was used for increased reconstruction speed using a multi-stage reconstruction (21), but this scheme resulted in gradient oversampling near the poles of the unit sphere. Currently, our standard images use equal solid angle (ESA) spacing of projections, which provides approximate uniformity (22,23). More complicated methods, such as quasi Monte Carlo based techniques (18) and Fekete distributions (19), have been investigated and found to give slight improvements in reconstruction quality.
While the uniformity of the distribution of projection points for the final image has been extensively studied, projection acquisition sequencing (i.e. uniformity of the distribution of projections throughout imaging) for EPRI has not been investigated. Most previous studies considered only images reconstructed from all acquired projections and did not consider images reconstructed from subsets of the acquired projections. The current polar-azimuthal raster method (used to minimize gradient changes) is highly non-uniform throughout image acquisition. Other groups have investigated the use of adaptive acquisition techniques, where projections are acquired based on the assumed information content of a projection using either entropy (24–26) or mean-square amplitude (27,28) to measure the information content. The merit of these adaptive acquisition techniques is object-dependent and they are only useful assuming the object is highly anisotropic and unchanging in time. Alternatively, an object-independent method for maximally spaced projection sequencing is necessary when imaging a dynamic object of unknown shape, which is often the case. The method presented in this paper is a novel approach to solving the problem of 3D radial sampling with approximately uniform sampling, or uniform distribution of projection points, throughout acquisition. The issue of distributing points uniformly on a sphere has been studied for over a century and is sometimes called Thomson’s problem, referring to Thomson’s plum-pudding model of atomic structure (29). Since the formulation of this problem, various solutions have been devised. The most common approach involves considering the points as point charges and minimizing the potential energy of the system (30–36). The resulting solution is sometimes referred to as Fekete points. For any substantial number of points, these solutions tend to become complex. However, the uniformity of our ESA distribution of points for the final image is acceptable and need not change. Therefore, determining approximate Fekete points as successive projections are acquired, while restricting the projections to the final set of ESA projections, allows for approximately uniform distributions of projection points throughout the image acquisition, maintains the standard uniformly distributed ESA projections for the final complete image, and is not computationally intensive. This will be the basis for the maximally spaced projection sequencing (MSPS) method presented here.
This paper will discuss how to achieve maximally spaced projection sequencing of projection data as well as the potential applications and benefits of its implementation.
METHODS
Pulsed EPRI Imaging Model
The pulsed imaging methods developed in our laboratory have been detailed elsewhere, starting with T2-imaging (37) and, more recently, T1-imaging, which reduces confounding spin probe concentration dependent self-broadening and provides a near absolute pO2 image (38). Signal for these EPRI techniques comes from an exogenous spin probe (trityl) (16,39) with an unpaired electron that is remarkably difficult to reduce, particularly in the in vivo environment. Both T2 and T1 report on the local environment of the unpaired electron. The electron relaxation rates (R2 = 1/T2 and R1 = 1/T1) are proportional to pO2 and therefore directly report local pO2. To transition from spectroscopy to imaging, linear magnetic gradients are applied to spatially encode an object. The magnetic gradients are applied along different directions in a spherical geometry to obtain radial projections in k-space, which can be Fourier transformed to produce spatial projections. An inverse radon transform (e.g., filtered backprojection (FBP)) of many spatial projections from different views is used to reconstruct a 3D image of spin-density. A series of such 3D images is acquired to give the average relaxation rate of each image voxel, giving a 3D parametric image with a measure of pO2 at each voxel.
Maximally Spaced Projection Sequencing Algorithm
Until now, we have acquired EPRI projections using a polar-azimuthal raster (PAR) method. This projection acquisition order was chosen to minimize the distance between successive projections, and therefore gradient change magnitude, but is highly non-uniform. With our current equipment, minimizing gradient changes is no longer necessary (with the necessary gradient changes, settling time will not exceed 10ms, which is ~1–2% or less of the standard projection acquisition time). Since this is no longer a restriction, a maximally spaced projection sequencing (MSPS) method should be used rather than the suboptimal PAR method.
The projection directions for an EPR image can be represented as points on the unit sphere. Subsequently, the idea of uniformly acquiring projections can be reformulated as an issue of picking the projection points so that, throughout imaging, the points are always approximately uniformly distributed on the unit sphere. In other words, the points should be chosen in such an order so that each successive point is added to the set of total acquired points so that this new set of points will be maximally spaced from one another. As mentioned previously, the current ESA spacing of points for the complete image is essentially uniform and thus we do not wish to change the final distribution. Therefore, a constraint that points must be chosen from the final ESA set of points will be applied. It should also be noted that our final ESA spaced set of points is distributed on the unit hemisphere (rather than the full sphere) due to data redundancy provided by the symmetry of the radon transform, which is the continuous mathematical representation of the acquisition of an EPRI projection.
The algorithm for achieving MSPS will treat the projection points as point charges. Points from the final ESA set of points will be divided into subsets A and B, acquired points and not yet acquired points, respectively. The first point (same as that for the PAR method) is added to subset A. Next, each point from subset B is individually and temporarily included in subset A. Electrostatic potential energy, U, of the system of point charges in subset A is then calculated using equation (1). Because all points from both subsets are only on the positive hemisphere, points are mirrored onto the negative hemisphere as well when calculating U. This process is done using each point from subset B, and whichever point results in the smallest value for U is selected as the next point and moved from subset B, to be included as the next entry in subset A. This procedure is repeated until all points from subset B have been incorporated into subset A. This algorithm will be referred to as the MSPS method.
| (1) |
Simulations
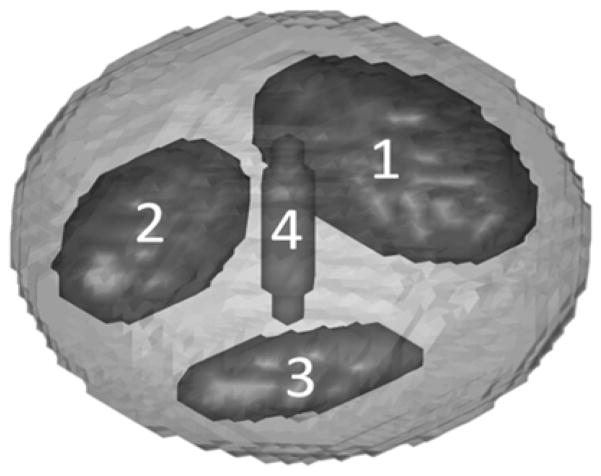
Simulated EPRI studies were used to investigate the effects of using the MSPS method as well as its applications and advantages over the PAR method. Simulations allow comparison of images for data acquired using the two methods with or without added noise, where the truth is known. Matlab (MathWorks, Massachusetts, USA) simulations were written locally. The digital phantom consisted of a main ellipsoid body and four interior ellipsoid sub-volumes varying in spatial orientation and size (figure 1). The phantom was discretized to be a 64×64×64 voxel matrix. The ellipsoid sub-volumes 1–4 were 8.92%, 4.88%, 1.54%, and 0.06% of the entire phantom volume respectively. The pO2 for each sub-volume could be individually adjusted as necessary and could be made to vary in time with any desired arbitrary temporal pattern. The range of pO2 values used for this phantom was chosen to reflect those observed in vivo (0–60 torr). A forward projection algorithm simulated projection acquisition with our laboratory’s EPRI technology. These simulated projections were then reconstructed according to standard protocol using a single-stage reconstruction developed in our laboratory (40). For this reconstruction, to properly weight each projection in order to account for non-uniformities in the distributions of projections, the area on the unit sphere of the Voronoi cell is computed for each projection point and used as the relative weigh for the projection. For a given set of points on the unit sphere, P = [P1, P2,…Pn], where n is the total number of points, the corresponding Voronoi cells (Vk) are a measure of what portion of the surface of the sphere is closer to a particular point than any of the other points. In other words, Vk is the set of points contained on the surface of the unit sphere with dk ≤ dj, for all j ≠ k, where di is the Euclidean distance to Pi (18).
Figure 1.
Discretized ellipsoid phantom used for digital simulations of EPR imaging of pO2 with labeled sub-volumes. The pO2 in any region of the phantom can be made to vary in time with an arbitrary pattern.
Figures of Merit
The standard deviation of the Voronoi weights (σv) for the projection points is used as a metric of the uniformity of the distribution of points on the unit sphere. Perfectly uniform points should be evenly spaced from one another and therefore occupy equal portions of the surface of the unit sphere. The corresponding Voronoi weights for such points are equal and the standard deviation of these weights will be zero. Therefore, the closer σv is to zero, the closer the distribution of projection points is to absolute uniformity.
For simulated data, mean squared error (MSE) is used as a measure of image accuracy by quantifying the fidelity for an image reconstructed using some given projection sampling scheme to an ideal image. For comparison of intermediate images reconstructed from incomplete projection sets, the ideal image is the final image reconstructed from the complete set of projections. For comparison of images reconstructed using different sampling schemes and data of varying noise level, the ideal image is an oversampled noiseless image (3304 projections). MSE is defined by equation (2), where is the ith voxel in the non-ideal image, Ii is the ith voxel in the ideal image, and V is the number of voxels in each image.
| (2) |
Mouse Imaging
A dynamic EPRI study with a live, tumor bearing mouse was used to demonstrate the post factum temporal resolution enhancement enabled by the MSPS method. The pulsed imaging spectrometer used has been described previously (13). The images from this study were 64×64×64 voxels3, with a voxel size of (0.66 mm)3. The EPR images were registered with a spin-echo weighted MRI image, using methods described previously (41), providing the anatomic information that EPRI lacks.
A female C3H type mouse (Harlan Sprague Dawley Inc., Indianapolis, IN) with human mammary tumor cells, MCA4 F6m (M. D. Anderson Hospital, Houston, TX), implanted and grown subcutaneously in the mid-distal hind leg was used. Once the tumor was an appreciable size (~450μL) the mouse was imaged. The mouse weighed 22.2g. To prevent motion during imaging, the animal was immobilized using a soft elastic vinyl polysiloxane dental mold material (GC America Inc., Alsip, IL) and anesthetized with 1–2% isoflurane. Respiration frequency and depth during imaging were monitored continuously. A 24 gauge angiocath was used to cannulate the mouse tail vein for i.v. injection of the spin probe. A digital needle probe thermometer (Physitemp, Clifton, NJ) monitored skin temperature, which was maintained at ~37° C using adjustable opposed heating lamps.
A single 36 minute, 828 projection image using the MSPS method was acquired. Halfway through imaging, a forced increase in the mouse’s tissue pO2 was produced by adjusting the fraction of inspired oxygen (FiO2) for the anesthetized mouse by having it initially breathe air (21% O2) and then having it breathe carbogen (95% O2 and 5% CO2) for the second half of the image.
These animal experiments were performed according to the US Public Health Service “Policy on Humane Care and Use of Laboratory Animals” and the protocols were approved by the University of Chicago Institutional Animal Care and Use Committee (ACUP No. 71697). The University of Chicago Animal Resources Center is an AALAC approved animal care facility.
RESULTS
Uniform Distribution of Projections Throughout Acquisition
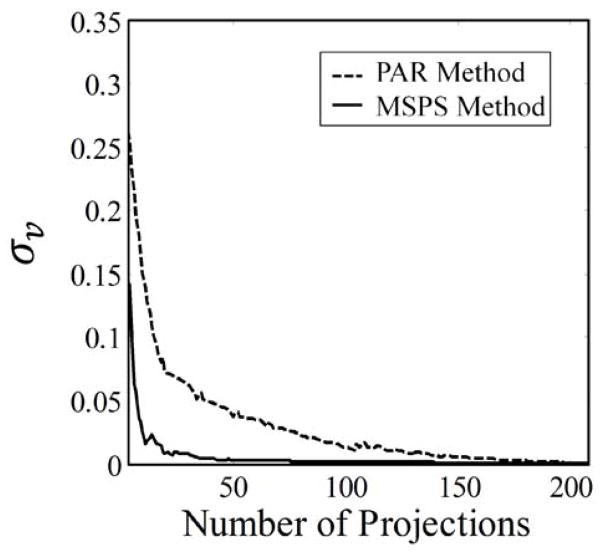
The current PAR acquisition method results in non-uniform projection sampling for intermediate images throughout imaging. The MSPS acquisition method fixes this. In other words, the distribution of acquired projections converges to uniformity far faster as projections are acquired for the MSPS method, when compared to the PAR method. This is demonstrated in figure 2, where the distributions of projection points at intermediate steps throughout imaging for both methods are compared. This convergence to uniformity can also be seen in the rate of convergence to zero of σv for the MSPS method as compared to that for the PAR method (figure 3). This uniformity in the distribution of projections throughout imaging has many potential benefits and applications, which will be discussed next.
Figure 2.
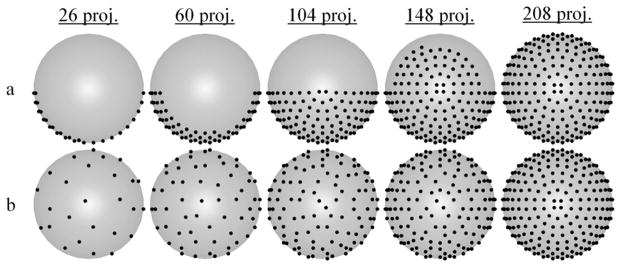
Comparison of the distributions of projection points at intermediate steps throughout imaging for both a) the PAR acquisition method and b) the MSPS acquisition method as viewed from above the unit hemisphere. The final full set of 208 ESA projection points is the same for both methods, but the distribution of acquired points at intermediate steps approaches uniformity more quickly for the MSPS method.
Figure 3.
Faster convergence of σv illustrates the improvement in projection distribution convergence to uniformity throughout image acquisition with the MSPS method compared to that with the PAR method.
Real-time Reconstruction
The non-uniform sampling at intermediate steps throughout imaging when using the PAR acquisition method leads to essentially meaningless intermediate images until imaging is nearly finished. The MSPS method produces approximately uniform sampling of projections at intermediate steps throughout imaging, which therefore provides useful intermediate images that converge to the final image faster. The ability to reconstruct meaningful images from incomplete projection sets enables useful real-time reconstruction, where a new image is produced as each successive projection is acquired. Noiseless simulations using the phantom described in the methods section were used to demonstrate this. Figure 4 compares slices from intermediate 3D images of the phantom reconstructed using different portions of the full projection set for qualitative comparison. It can be seen in Fig. 4 that when using the PAR method, the intermediate images reconstructed from incomplete projection sets do not accurately represent the final image until imaging is nearly complete. On the other hand, when using the MSPS method, the intermediate images begin to resemble the final image very quickly. An image reconstructed after only 1/36th of the total imaging time has passed (23/828 projections), already begins to approximate the final image and after 1/9th of the projections have been collected (92/828 projections), most significant artifacts seem to have been eliminated. The MSPS method allows for the implementation of a system in which one can watch the buildup of an image while acquiring new projection data, i.e. real-time reconstruction.
Figure 4.
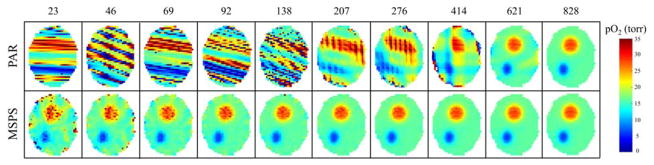
A slice from a 3D EPRI image reconstructed from different numbers of projections acquired using either the PAR or the MSPS method. The numbers above the images are the number of projections used for image reconstruction. This is a demonstration of how acquiring an image using the MSPS method enables useful real-time reconstruction, allowing for the visualization of the buildup of an image by reconstructing subsequent intermediate images as more projections are acquired.
Experimental Versatility
Standard experimental procedure uses the PAR method and predetermines the number of projections to acquire prior to imaging (usually 208 ESA projections). To increase temporal resolution and obtain short (temporally) images, with a fixed number of projections, signal averaging for each projection must be decreased by some factor, which decreases the signal-to-noise ratio (SNR) by the square root of that factor. Following a multi-image experiment, a higher SNR image can be obtained post factum by averaging the short images. However, this image will have unimproved projection sampling density and, of course, decreased temporal resolution.
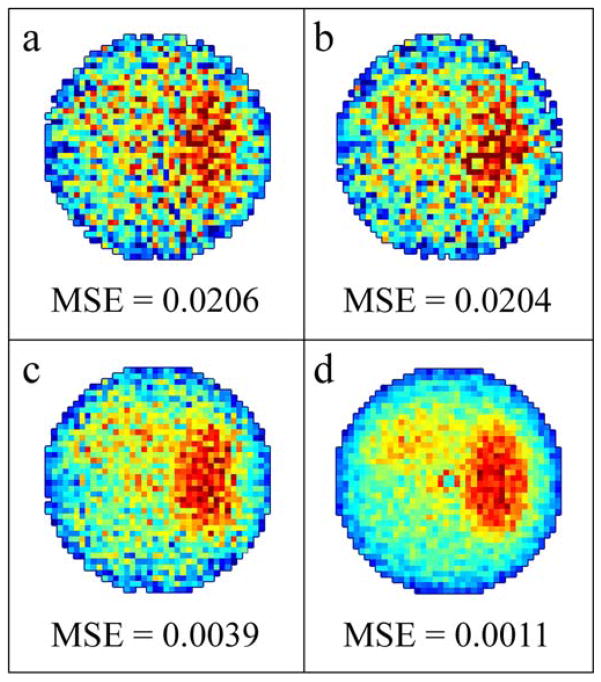
The MSPS method allows for a different experimental paradigm. For a multi-image experiment, a highly-sampled, long image is acquired and short intermediate images are reconstructed from approximately uniformly sampled intermediate divisions of the full set of projections. In this manner, the MSPS short intermediate images (figure 5(b)) and PAR short full images of equivalent imaging time (figure 5(a)) will be equally accurate and have approximately the same projection sampling density and uniformity. The MSPS long image not only has better SNR (due to increased signal averaging from increased number of projections) than the short images, but also increased density of projection sampling. MSPS long images (figure 5(d)) therefore have higher image quality and less sampling artifacts than PAR long images (figure 5(c)). Additionally, the number of projections for each MSPS short image can be adjusted to any fraction of the total number of projections for the long image, which is less restrictive than the PAR methodology.
Figure 5.
Simulated noisy a) full short 42 projection PAR image; b) intermediate short 46 projection (1/18th of a full 828 projection image) MSPS image with the same imaging time as (a); c) a full long 42 projection PAR image obtained by averaging 18 full short 42 projection PAR images; d) a full long 828 projections MSPS image with the same imaging time as (c). MSE when compared to an ideal oversampled noiseless image reconstructed from 3304 projections is used as a measure of accuracy and is 0.0206 for (a), 0.0204 for (b), 0.0039 for (c), and 0.0011 for (d).
The MSPS method allows for adjusting of images from long to short rather than short to long, providing more experimental versatility. With the MSPS methodology, multiple experiments (lower image quality/higher temporal resolution versus higher image quality/lower temporal resolution) can be performed simultaneously on a single subject.
Artifact Reduction
Highly non-maximally spaced projection sequencing, such as the PAR method, propagates localized changes during imaging throughout the entire image, which can result in significant distortions. The MSPS method helps to ameliorate this because at intermediate steps throughout imaging, the state of the object at a particular time is captured more accurately due to the uniformity in the distribution of projections at those intermediate steps. To demonstrate this, a noiseless simulation was done using the phantom described in the methods section. The largest sub-volume ellipsoid in the dynamic phantom had pO2 oscillating sinusoidally from 20 torr to 40 torr (representing reasonable physiologic tissue pO2 changes, see figure 7) with a period equal to acquisition time. Figure 6 shows the results of this simulation. Figure 6(a) shows a slice from the image of the constant phantom with the sub-volume having constant pO2 equal to the average pO2 of the sinusoidally varying pO2 in the dynamic phantom, representing the ideal case (no artifacts due to pO2 fluctuations during imaging) for comparison. Figure 6(b) shows the same slice from the PAR image of the dynamic phantom. The localized temporal pO2 changes are spatially smeared out into a swirling pattern due to the non-maximally spaced projection sequencing. The fidelity between the PAR image and the ideal constant image is very low (MSE = 6.44). Figure 6(c) shows the same slice from the MSPS image of the dynamic phantom. The artifacts seen in the PAR image are no longer present in the MSPS image. The fidelity between the MSPS image and the ideal constant image is over two orders of magnitude better (MSE = 0.02). The imaging of living animals presents an inherently dynamic situation and therefore the MSPS method of acquiring projection data is needed to avoid the artifacts resulting from misrepresentation of localized changes (Fig. 6).
Figure 7.
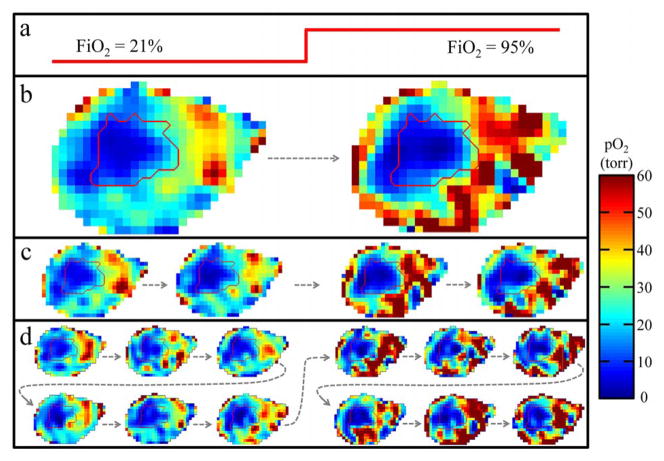
Images with increasingly higher temporal resolution resulting from division of projection data and subsequent reconstruction of intermediate images for the full 36 minute, 828 projection MSPS image with the mouse breathing air (21% O2) for 18 minutes, then breathing carbogen (95% O2) for 18 minutes. a) Diagram of the breathing gas changing with time. b) Division of the full image into two 18 minute, 414 projection images, c) four 9 minute, 207 projection images, and d) twelve 3 minute, 69 projection images. The dashed arrows show the temporal order of the images. The tumor outline is contoured in red.
Figure 6.
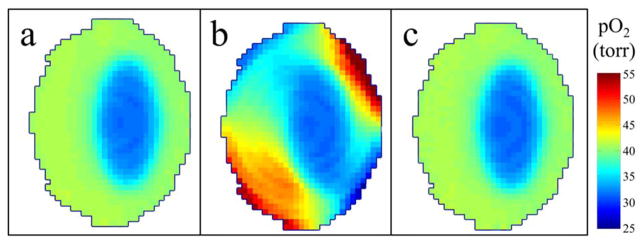
(a) Ideal image acquired with no temporal changes. (b) Image acquired using the PAR method with the ellipsoid sub-volume sinusoidally varying during image acquisition and the resulting artifacts. (c) Image acquired using the MSPS method with the ellipsoid sub-volume sinusoidally varying during image acquisition, no longer containing artifacts due to non-uniform projection sampling throughout imaging.
Post Factum Temporal Resolution Enhancement
There is no way of going back after an experiment has been completed to investigate changes in the imaged object during imaging when using the PAR method because intermediate images reconstructed from incomplete projection sets are inaccurate and hard to interpret. With the MSPS method, these intermediate images become useful, allowing for post factum temporal resolution enhancement, with a tradeoff in image quality (spatial resolution, SNR, artifacts) (20), so that important dynamic properties of the imaged object can be resolved and studied.
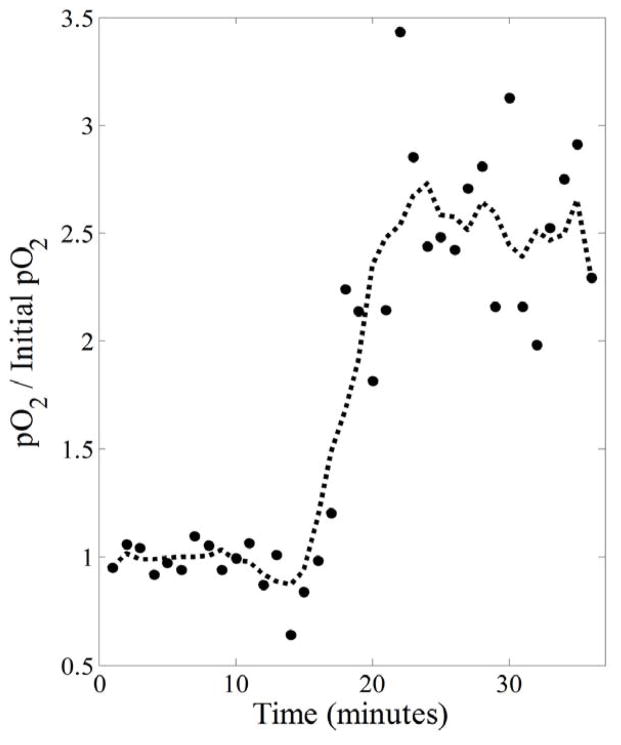
This was demonstrated using a dynamic EPRI experiment on a live mouse bearing a tumor on its hind leg. A 36 minute, 828 projection MSPS image of the mouse was acquired. Halfway through imaging, the breathing gas was switched from normoxic (medical grade air: 21% O2) to hyperoxic (carbogen: 95% O2 and 5% CO2). After acquiring the data, temporal resolution was enhanced post factum with a tradeoff in image quality by reconstructing intermediate images from consecutive partial projection sets to observe the response to the change in FiO2 (figure 7). Figure 7(b) shows the images resulting from dividing the original 36 minute image into two 18 minute images that already begin to show responsive regions of the mouse’s leg increasing in pO2 with the change in FiO2. Figure 7(c) shows the result of dividing those two images in half to obtain four 9 minute images, and figure 7(d) shows the result of dividing each of those four images further into thirds to obtain twelve 3 minute images. Figure 8 shows the result of increasing the temporal resolution by a factor of 36, allowing for the change in tissue pO2, averaged over responsive regions, to be clearly seen to occur approximately halfway through imaging as expected. Regions responding to the change in FiO2 were determined by correlating the temporal changes in each voxel to the FiO2 step function and finding voxels with r ≥ 0.4 (400 of 5682 voxels, ~7%). The plotted points in figure 8 are the actual values resulting from this averaging and the dashed line shows the result of filtering these points with a 5-point moving average smoothing to illustrate that, on average, the pO2 in responsive regions increases by a factor of ~2.5 when the mouse is switched to breathing hyperoxic gas. It should be noted that, while the presented data demonstrates the ability to enhance temporal resolution post-factum, due to shortcomings in the ability of current image reconstruction methods to handle sparsely sampled projections, it is hard to separate high frequency pO2 fluctuations caused by physiologic changes from those caused by image reconstruction artifacts and decreased SNR. Future improvements to image reconstruction algorithms will help to separate these effects.
Figure 8.
Temporal resolution of the 36 minute image is enhanced by a factor of 36 to produce 36 one minute images. For this series of images, voxels responding to the change in FiO2 (those having a temporal pattern with r ≥ 0.4 when correlated with the FiO2 step function) are averaged over to produce the overall temporal response (dots). A 5-point running average smoothed temporal response (dashed line) clearly shows that the average increase in tissue pO2 for responsive regions is by a factor of ~2.5 and occurs about halfway through imaging as expected.
DISCUSSION
EPRI is a particularly useful imaging modality for determining static local distributions of pO2 in vivo. However, when imaging living animals, the situation is inherently dynamic. There may be movement such as repositioning, breathing, heartbeat, etc., and there may be physiological changes such as cycling hypoxia. In this paper, a method for maximally spaced projection sequencing for EPRI is presented. This MSPS method is easily implemented and the resulting improvements over the previously used PAR method, as well as its applications, are necessary to appropriately study such intrinsically dynamic systems. It should be noted that while the ESA distribution was used for the final set of points in this paper to demonstrate the MSPS method, the algorithm for implementing the MSPS method and the advantages of using the MSPS method hold for final sets of points that have been distributed using other methods. Therefore, other methods that result in more uniform distribution of the final set of points may help to further improve the usefulness of the MSPS method.
One advantage of the MSPS method presented over the PAR method previously used for our EPRI is that it allows useful real-time reconstruction. Currently, image reconstruction is computationally intensive and therefore reconstruction on the fly, as projections are collected, is not feasible. However, computing capability is constantly improving and we are moving toward GPU accelerated reconstruction techniques. Therefore, we will eventually be able to implement the real-time reconstruction made possible by the MSPS method (40). This real-time reconstruction will have many uses. For instance, when imaging living animals (particularly in the patient setting), the situation is often time sensitive. Real-time reconstruction will allow the user to resolve certain issues early and avoid wasted time. During imaging, an image may become corrupted (e.g. the subject and/or the imaging equipment may have been setup improperly, the subject may move, imaging equipment may fail, etc.) and, because imaging can require significant time, the ability to visualize any such errors without having to wait for completion of the scan would be advantageous. Real-time reconstruction can also allow the user to save time in identifying a region of interest (ROI) by locating it earlier in a lower quality image, reconstructed before all projections have been collected (Note, such intermediate images reconstructed during acquisition will allow more rapid visualization of low spatial frequency content but may not help to visualize high spatial frequency content until imaging is nearly complete).
The MSPS method helps to reduce artifacts present in data collected using non-maximally spaced projection sequencing due to the resulting propagation of localized temporal changes throughout the entire image. MSPS essentially fixes these issues because, for any given unit of time during image acquisition, the projections acquired in this time will capture the state of the entire object at that time more accurately. This is demonstrated for a simple situation in figure 6, but holds true in general.
Current standard procedures for imaging are logistically restrictive because temporal resolution of a study must be decided beforehand, forcing one to acquire short images and then average to obtain an equivalently sampled longer image with higher SNR but unchanged resolution and sampling artifacts. MSPS provides more experimental versatility by allowing for the acquisition of highly-sampled longer images, which can be subdivided to obtain shorter images. This is logistically advantageous as it allows for multiple studies to be performed simultaneously, making good use of resources as well as making the best use of the data. If one study is interested in features requiring high SNR and good spatial resolution and one study is interested in features requiring higher temporal resolution but lower SNR and spatial resolution can suffice, one experiment can produce data for both. The MSPS method is also useful if an in depth study with longer images is performed and, at a later time, it is determined that data with high temporal resolution is needed, one can make use of previously acquired data without needing to perform new experiments and waste time and resources. These benefits come at no cost because the MSPS short images are as accurate as the PAR short images, and there is even an improvement in the MSPS long images compared to the PAR long images, as shown in the results section.
The advantages of the MSPS method regarding improved experimental versatility discussed in the previous paragraph can be considered from a technological/scientific point of view as well as a logistical point of view. MSPS data can be used to resolve or investigate interesting physiological aspects that may not have been possible using other experimental methodologies. If an image is acquired and there is reason to believe that changes of interest are occurring on a shorter time scale (e.g., changes in pO2 or object shape/position), with the current PAR method, the experiment would have to be repeated and there is no guarantee the same conditions and results will be reproducible. The MSPS method allows for post factum enhancement of temporal resolution by dividing the full image projection data set into temporally subsequent subsets and then reconstructing a set of intermediate images from these partial projection sets. Therefore, if there are changes of interest too rapid to be resolved with the initial experiment, the temporal resolution can be adjusted as needed, with a tradeoff in image SNR and quality. Future studies will work to quantify this tradeoff. An example of interesting physiology that can be more effectively studied in this way is the interplay between chronic hypoxia and acute hypoxia by acquiring simultaneous images of both (higher image quality/lower temporal resolution and lower image quality/higher temporal resolution images respectively) in the same animal.
Our original PAR method was chosen to minimize the necessary gradient changes. While there appear to be no effects on image quality due to the significant gradient changes required for the MSPS method, as imaging times decrease (as projection acquisition times approach maximum gradient settling time of 10ms, i.e., sub-minute images), the effects of induced eddy currents in the spectrometer from the gradient changes may begin to affect the reconstructed images and therefore limit the benefits of using the MSPS method. Most of the benefits and applications of the MSPS method discussed above are limited by SNR of the imaging system and sub-optimal handling of sparsely sampled data with current reconstruction methods. However, we are constantly improving the SNR of our imaging system by improving the imaging equipment and techniques, as well as our data processing and filtering (42). Additionally, the reconstruction techniques for EPRI are rapidly developing to more appropriately handle sparsely sampled data. For FBP reconstruction we can use different interpolation methods to try to alleviate issues of undersampling. Furthermore, the fields of MRI (43) and CT (44) have made great strides with optimization-based iterative reconstruction of sparsely sampled data (sometimes referred to as compressed sensing) and we are working to implement similar techniques. As both the SNR and reconstruction algorithms continue to improve, the usefulness of acquiring images with the MSPS method will continue to increase.
Similar issues related to more efficient projection-based or radial sampling trajectories have been considered for MRI. One particularly relevant solution is golden ratio based sampling. This solution uses a constant angular increment based on the golden ratio to ensure approximately uniform distributions of projections throughout image acquisition for any arbitrary number of projections (45). This method was found to result in an optimal projection ordering in 2D (46) and was then applied to 3D MRI k-space sampling by simply stacking 2D planes (47,48). However, the problem of radial sampling or projection acquisition, such that projections are relatively uniform throughout acquisition becomes far more complicated in 3D. The golden ratio has been expanded to higher dimensions (49) and applied to 3D MRI k-space sampling (50,51). The golden ratio sampling method is particularly suited for the case where there are an unknown arbitrary number of projections to be acquired. However, the distribution of acquired projections will never reach uniformity. The MSPS method is advantageous when the final distribution and number of projections is predetermined and they are as uniformly spaced as possible (e.g., using the ESA distribution). While the golden ratio based sampling and MSPS method are similar, each has their own advantages and disadvantages. Therefore a more rigorous comparison between the two methods may be useful.
CONCLUSIONS
The MSPS method described herein is a novel approach for acquiring EPRI projection data that results in more uniform distributions of projections throughout image acquisition. The MSPS method provides many benefits and advantages over the previously used PAR method, such as useful real-time reconstruction, improved experimental versatility, a reduction in potential image artifacts, and the ability to arbitrarily adjust temporal resolution post factum to best fit the acquired data and its application. These improvements provided by the MSPS method are necessary to more appropriately study physiologic changes in a dynamic system.
Acknowledgments
This work was supported by grants from the NIH (P41 EB002034 and R01 CA98575).
Contributor Information
Gage Redler, Email: gage@uchicago.edu.
Howard J. Halpern, Email: h-halpern@uchicago.edu.
References
- 1.Overgaard J. Hypoxic radiosensitization: adored and ignored. J Clin Oncol. 2007;25(26):4066–4074. doi: 10.1200/JCO.2007.12.7878. [DOI] [PubMed] [Google Scholar]
- 2.Schwarz G. Uber Desensibilisierung gegen Rontgen- und Radiumstrahlen. Munchner Medizinische Wochenschrift. 1909;56:1217–1218. [Google Scholar]
- 3.Hall EJ. Radiobiology for the Radiologist. 5. Philadelphia: Lippincott Williams & Wilkins; 2000. [Google Scholar]
- 4.Hockel M, Schlenger K, Aral B, Mitze M, Schaffer U, Vaupel P. Association between tumor hypoxia and malignant progression in advanced cancer of the uterine cervix. Cancer Res. 1996;56(19):4509–4515. [PubMed] [Google Scholar]
- 5.Shannon AM, Bouchier-Hayes DJ, Condron CM, Toomey D. Tumour hypoxia, chemotherapeutic resistance and hypoxia-related therapies. Cancer Treat Rev 2003. 2003;29(4):297–307. doi: 10.1016/s0305-7372(03)00003-3. [DOI] [PubMed] [Google Scholar]
- 6.Carmeliet P, Dor Y, Herbert JM, Fukumura D, Brusselmans K, Dewerchin M, Neeman M, Bono F, Abramovitch R, Maxwell P, Koch CJ, Ratcliffe P, Moons L, Jain RK, Collen D, Keshert E, Keshet E. Role of HIF-1alpha in hypoxia-mediated apoptosis, cell proliferation and tumour angiogenesis. Nature. 1998;394(6692):485–490. doi: 10.1038/28867. [DOI] [PubMed] [Google Scholar]
- 7.Rofstad EK. Microenvironment-induced cancer metastasis. Int J Radiat Biol. 2000;76(5):589–605. doi: 10.1080/095530000138259. [DOI] [PubMed] [Google Scholar]
- 8.Dewhirst MW, Klitzman B, Braun RD, Brizel DM, Haroon ZA, Secomb TW. Review of methods used to study oxygen transport at the microcirculatory level. Int J Cancer. 2000;90(5):237–255. [PubMed] [Google Scholar]
- 9.Zhao DW, Jiang L, Mason RP. Measuring changes in tumor oxygenation. Methods Enzymol. 2004;386:378–418. doi: 10.1016/S0076-6879(04)86018-X. [DOI] [PubMed] [Google Scholar]
- 10.Tatum JL. Hypoxia: Importance in tumor biology, noninvasive measurement by imaging, and value of its measurement in the management of cancer therapy. Int J Rad Biol. 2006;82(10):699–757. doi: 10.1080/09553000601002324. [DOI] [PubMed] [Google Scholar]
- 11.Bayer C, Vaupel P. Acute versus chronic hypoxia in tumors: Controversial data concerning time frames and biological consequences. Strahlenther Onkol. 2012;188(7):616–627. doi: 10.1007/s00066-012-0085-4. [DOI] [PubMed] [Google Scholar]
- 12.Elas M, Ahn KH, Parasca A, Barth ED, Lee D, Haney C, Halpern HJ. Electron paramagnetic resonance oxygen images correlate spatially and quantitatively with Oxylite oxygen measurements. Clin Cancer Res. 2006;12(14 Pt 1):4209–4217. doi: 10.1158/1078-0432.CCR-05-0446. [DOI] [PubMed] [Google Scholar]
- 13.Epel B, Sundramoorthy SV, Mailer C, Halpern HJ. A versatile high speed 250-MHz pulse imager for biomedical applications. Concept Magn Reson B Magn Reson Eng. 2008;33B(3):163–176. doi: 10.1002/cmr.b.20119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Epel B, Sundramoorthy SV, Barth ED, Mailer C, Halpern HJ. Comparison of 250 MHz electron spin echo and continuous wave oxygen EPR imaging methods for in vivo applications. Med Phys. 2011;38(4):2045–2052. doi: 10.1118/1.3555297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Epel B, Haney CR, Hleihel D, Wardrip C, Barth ED, Halpern HJ. Electron paramagnetic resonance oxygen imaging of a rabbit tumor using localized spin probe delivery. Med Phys. 2010;37(6):2553–2559. doi: 10.1118/1.3425787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Elas M, Williams BB, Parasca A, Mailer C, Pelizzari CA, Lewis MA, River JN, Karczmar GS, Barth ED, Halpern HJ. Quantitative tumor oxymetric images from 4D electron paramagnetic resonance imaging (EPRI): Methodology and comparison with blood oxygen level-dependent (BOLD) MRI. Magn Reson Med. 2003;49(4):682–691. doi: 10.1002/mrm.10408. [DOI] [PubMed] [Google Scholar]
- 17.Golman K, Petersson JS, Ardenkjaer-Larsen JH, Leunbach I, Wistrand LG, Ehnholm G, Liu KC. Dynamic in vivo oxymetry using Overhauser enhanced MR imaging. J Magn Reson Imaging. 2000;12(6):929–938. doi: 10.1002/1522-2586(200012)12:6<929::aid-jmri17>3.0.co;2-j. [DOI] [PubMed] [Google Scholar]
- 18.Ahmad R, Deng YM, Vikram DS, Clymer B, Srinivasan P, Zweier JL, Kuppusamy P. Quasi Monte Carlo-based isotropic distribution of gradient directions for improved reconstruction quality of 3D EPR imaging. J Magn Reson. 2007;184(2):236–245. doi: 10.1016/j.jmr.2006.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ahmad R, Vikram DS, Clymer B, Potter LC, Deng YM, Srinivasan P, Zweier JL, Kuppusamy P. Uniform distribution of projection data for improved reconstruction quality of 4D EPR imaging. J Magn Reson. 2007;187(2):277–287. doi: 10.1016/j.jmr.2007.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Scheffler K, Hennig J. Reduced circular field-of-view imaging. Magn Reson Med. 1998;40(3):474–480. doi: 10.1002/mrm.1910400319. [DOI] [PubMed] [Google Scholar]
- 21.Hyslop WB, Woods RK, Lauterbur PC. Four-dimensional spectral-spatial imaging using projection reconstruction. IEEE Trans Med Imaging. 1995;14(2):374–383. doi: 10.1109/42.387718. [DOI] [PubMed] [Google Scholar]
- 22.Lai CM, Lauterbur PC. A gradient control device for complete 3-dimensional nuclear magnetic resonance zeugmatographic imaging. J Phys E Sci Instrum. 1980;13(7):747–750. [Google Scholar]
- 23.Ahn KH, Halpern HJ. Spatially uniform sampling in 4-D EPR spectral-spatial imaging. J Magn Reson. 2007;185(1):152–158. doi: 10.1016/j.jmr.2006.12.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Placidi G, Alecci M, Sotgiu A. Theory of adaptive acquisition method for image reconstruction from projections and application to EPR imaging. J Magn Reson. 1995;B108:50–57. [Google Scholar]
- 25.Placidi G, Alecci M, Sotgiu A. Angular space-domain interpolation for filtered back projection applied to regular and adaptively measured projections. J Magn Reson. 1996;B110(1):75–79. [Google Scholar]
- 26.Placidi G, Alecci M, Sotgiu A. Omega-space adaptive acquisition technique for magnetic resonance imaging from projections. J Magn Reson. 2000;143(1):197–207. doi: 10.1006/jmre.1999.1966. [DOI] [PubMed] [Google Scholar]
- 27.Deng Y, Kuppusamy P, Zweier JL. Progressive EPR imaging with adaptive projection acquisition. J Magn Reson. 2005;174(2):177–187. doi: 10.1016/j.jmr.2005.01.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ahmad R, Clymer B, Deng Y, He G, Vikram D, Kuppusamy P, Zweier JL. Optimization of data acquisition for EPR imaging. J Magn Reson. 2006;179(2):263–272. doi: 10.1016/j.jmr.2005.12.013. [DOI] [PubMed] [Google Scholar]
- 29.Thomson JJ. On the structure of the atom: an investigation of the stability and periods of oscillation of a number of corpuscles arranged at equal intervals around the circumference of a circle; with application of the results to the theory of atomic structure. Philos Mag. 1904;7(39):237–265. [Google Scholar]
- 30.Edmundson JR. The distribution of point charges on the surface of a sphere. Acta Crystallogr A. 1992;48:60–69. [Google Scholar]
- 31.Glasser L, Every AG. Energies and spacings of point charges on a sphere. J Phys A: Math Gen. 1992;25(9):2473–2482. [Google Scholar]
- 32.Altschuler EL, Williams TJ, Ratner ER, Dowla F, Wooten F. Method of constrained global optimization. Phys Rev Lett. 1994;72(17):2671–2674. doi: 10.1103/PhysRevLett.72.2671. [DOI] [PubMed] [Google Scholar]
- 33.Morris JR, Deaven DM, Ho KM. Genetic-algorithm energy minimization for point charges on a sphere. Phys Rev B Condens Matter. 1996;53(4):R1740–R1743. doi: 10.1103/physrevb.53.r1740. [DOI] [PubMed] [Google Scholar]
- 34.Saff EB, Kuijlaars ABJ. Distributing many points on a sphere. Math Intell. 1997;19(1):5–11. [Google Scholar]
- 35.Hannay JH, Nye JF. Fibonacci numerical integration on a sphere. J Phys A: Math Gen. 2004;37(48):11591–11601. [Google Scholar]
- 36.Bendito E, Carmona A, Encinas AM, Gesto JM. Estimation of Fekete points. J Comput Phys. 2007;225(2):2354–2376. [Google Scholar]
- 37.Mailer C, Sundramoorthy SV, Pelizzari CA, Halpern HJ. Spin echo spectroscopic electron paramagnetic resonance imaging. Magn Reson Med. 2006;55(4):904–912. doi: 10.1002/mrm.20849. [DOI] [PubMed] [Google Scholar]
- 38.Epel B, Bowman MK, Mailer C, Halpern HJ. Absolute oxygen R1e imaging in vivo with pulse electron paramagnetic resonance. Magn Reson Med. 2014;72(2):362–368. doi: 10.1002/mrm.24926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ardenkjaer-Larsen JH, Laursen I, Leunbach I, Ehnholm G, Wistrand LG, Petersson JS, Golman K. EPR and DNP properties of certain novel single electron contrast agents intended for oximetric imaging. J Magn Reson. 1998;133(1):1–12. doi: 10.1006/jmre.1998.1438. [DOI] [PubMed] [Google Scholar]
- 40.Redler G, Qiao Z, Epel B, Halpern HJ. Real-time image reconstruction for pulse EPR oxygen imaging using a GPU and lookup table paramter fitting. Concepts Magn Reson Part B Magn Reson Eng. 2015 doi: 10.1002/cmr.b.21281. In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Haney CR, Fan X, Parasca AD, Karczmar GS, Halpern HJ, Pelizzari CA. Immobilization using dental material casts facilitates accurate serial and multimodality small animal imaging. Concept Magn Reson B Magn Reson Eng. 2008;33B(2):138–144. doi: 10.1002/cmr.b.20108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Redler G, Epel B, Halpern HJ. Principal component analysis enhances snr for dynamic electron paramagnetic resonance oxygen imaging of cycling hypoxia in vivo. Magn Reson Med. 2014;71(1):440–450. doi: 10.1002/mrm.24631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Huang YX, Wright GA. Time-resolved MR angiography with limited projections. Magn Reson Med. 2007;58(2):316–325. doi: 10.1002/mrm.21312. [DOI] [PubMed] [Google Scholar]
- 44.Chen GH, Tang J, Leng SH. Prior image constrained compressed sensing (PICCS): A method to accurately reconstruct dynamic CT images from highly undersampled projection data sets. Med Phys. 2008;35(2):660–663. doi: 10.1118/1.2836423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Koehler T. A projection access scheme for iterative reconstruction based on the golden section. IEEE Nuclear Science Symposium Conference Record. 2004;6:3961–3965. [Google Scholar]
- 46.Kasantsev IG, Matej S, Lewitt RM. Optimal ordering of projections using permutation matrices and angles between projection subspaces. Electron Notes Descrete Math. 2005;20:205–216. [Google Scholar]
- 47.Song H, Lin W, Dougherty L, Schnall MD. A 3D golden-angle projection reconstruction technique for dynamic contrast-enhanced MRI. Proc Intl Soc Mag Reson Med. 2006;14:3364. [Google Scholar]
- 48.Winkelmann S, Schaeffter T, Koehler T, Eggers H, Doessel O. An optimal radial profile order based on the golden ratio for time-resolved MRI. IEEE T Med Imaging. 2007;26(1):68–76. doi: 10.1109/TMI.2006.885337. [DOI] [PubMed] [Google Scholar]
- 49.Anderson PG. Multidimensional golden means. Applications of Fibonacci Numbers. 1993;5:1–9. [Google Scholar]
- 50.Doneva M, Eggers H, Rahmer J, Bornert P, Mertins A. Highly undersampled 3D golden ratio radial imaging with iterative reconstruction. Proc Intl Soc Mag Reson Med. 2008;16:336. [Google Scholar]
- 51.Chan RW, Ramsay EA, Cunningham CH, Plewes DB. Temporal stability of adaptive 3D radial MRI using multidimensional golden means. Magn Reson Med. 2009;61(2):354–363. doi: 10.1002/mrm.21837. [DOI] [PubMed] [Google Scholar]