Abstract
New and important separations capabilities are being enabled by utilizing other electric field-induced forces besides electrophoresis, among these is dielectrophoresis. Recent works have used experimentally simple insulator-based systems that induce field gradients creating dielectrophoretic force in useful formats. Among these, juxtaposing forces can generate gradient-based steady-state separations schemes globally similar to isoelectric focusing. The system of interest is termed gradient insulator-based dielectrophoresis and can create extremely high resolution steady-state separations for particles four nanometers to ten micrometers in diameter, including nearly all important bioparticles (large proteins, protein aggregates, polynucleotides viruses, organelles, cells, bacteria, etc.). A theoretical underpinning is developed here to understand the relationship between experimental parameters and resolution and to identify the best expected resolution possible. According to the results, differences in particles (and bioparticles) as small as one part in 104 for diameter (sub-nanometer resolution for a one micrometer particle), one part in 108 for dielectrophoretic parameters (dielectrophoretic mobility, Clausius-Mossotti factor), and one part in 105 for electrophoretic mobility can be resolved. These figures of merit are generally better than any competing technique, in some cases by orders of magnitude. This performance is enabled by very strong focusing forces associated with localized gradients.
Keywords: dielectrophoresis, electrophoresis, resolution, bioparticles, electrokinetics
1 Introduction
Effective control over the selective transport of biological material lies at the heart of medical, pharmaceutical, and environmental analytical strategies. Many existing methodologies, such as those used in clinical diagnosis are quite limited in their capabilities, at least relative to the bioanalytical challenges of modern personalized medicine. Developments of new separatory tools are needed to meet these challenges of medical diagnostics and environmental monitoring.
In many analytical separations, components become segregated as they move along a linear axis at different rates. Chromatography and zone electrophoresis serve as examples of this paradigm [1, 2]. Such methods are ultimately limited by band broadening from dispersive effects, which decrease analyte concentration throughout the process. This limits subsequent analyte detection and multi-dimensional analysis. Steady-state separation schemes, such as equilibrium-gradient techniques, employ competing forces to simultaneously concentrate and fractionate analytes. Each unique species is focused to a distinctive zero-velocity location, where the concentration distribution about that point reflects the interplay between focusing and dispersive forces. Isoelectric focusing [3], density gradient sedimentation [4], and electric field gradient focusing [5] serve as paradigmatic examples.
The quality of any separation is described in terms of resolution, an expression that specifies separation of the centroid of the analyte concentration profiles versus the spreading of each band. Most separatory systems have been thoroughly explored theoretically and experimentally including chromatography [6, 7], capillary electrophoresis [8], isoelectric focusing [9], and electric field gradient focusing [10].
The current work is focused on developing a theoretical basis of resolution for gradient insulator-based dielectrophoresis (g-iDEP). This area of research was initiated in 2007, when Pysher and Hayes introduced a novel microfluidic approach to bioparticle separation [11]. It was built upon prior developments in insulator-based dielectrophoresis (iDEP) [12–16]. Additional significant contributions have been made in this arena since then, primarily aimed at single-target analysis [17], sample bifurcation [18, 19], or multiple-outlet diversion strategies [20–22]. The scheme discussed here is an amalgam of iDEP and traditional linear separation science, which represents a new approach to equilibrium-gradient separations conducive to use with any analyte from ~4 nm to 10 μm diameter and is especially useful for a large portion of, if not all bioparticulates (viruses, organelles, cells, lysosomes, vesicles, etc.). This technique, while employing local-gradient, steady-state focused bands of material, differs significantly from true global gradient techniques in that it is directional; the analytes/targets must be introduced from a single side of the device. There is no mechanism to refocus materials once past their first focus or balance point. This is an important distinction for classification of separations science and will affect certain operating paradigms, but the general advantages of gradient techniques are true for this strategy also. This technique has already demonstrated isolation and concentration of a wide range of particles, including bacteria, polystyrene spheres, red blood cells, and amyloid fibrils [11, 23–26].
Within g-iDEP, a combination of dielectrophoretic (DEP), electrophoretic (EP), and electroosmotic flow (EOF) forces are used to transport, separate, and concentrate particles within a channel. This technique utilizes a continuous microchannel patterned with sequentially changing, constrictive insulating features. These constrictions, referred to as gates, create a series of DEP-inducing electric field non-uniformities. The specific geometry of the channel yields increasingly strong DEP forces along the channel. Particles traveling through the microchannel are propelled by a combination of EP and EOF forces. Since DEP forces scale differently with the channel’s cross-sectional area than do EP and EOF forces, unique traps are formed at each gate as they become sequentially narrower. This causes physically distinct particles to settle into discrete zones near different gates. Thus, they assume unique positions along the channel’s separatory axis based on their electrophoretic and dielectrophoretic mobilities (Figure 1). Considered together, a particle’s electrophoretic and dielectrophoretic mobilities reflect an array of properties including size, charge, polarizability, shape, and heterogeneity. Interrogating all these properties together yields a separatory scheme that can be fine-tuned for high-resolution capture and concentration of analytes. This work will allow the estimation of the smallest change in electrokinetic or dielectrophoretic properties that can be uniquely differentiated by g-iDEP.
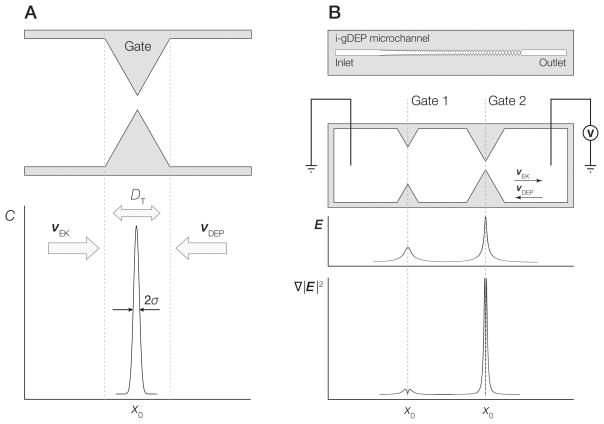
Figure 1.
A) Diagram depicting concentration of analyte at a gate structure within a g-iDEP microchannel. Peak width is a function of focusing factors associated with electrophoretic velocity (νEK) and dielectrophoretic velocity (νDEP) balanced with dispersive forces including diffusion (Ddiff). B) (upper image): Schematic representation of an entire g-iDEP device. (lower three panels): Detail of two gates within a g-iDEP microchannel. Below the gates are representations of the absolute magnitude of the centerline electric field strength and ∇|E|2. The device shown here serves only illustrative purposes. Specific implementation and geometry of gates are flexible, and may be altered significantly depending on the desired application. Gates may also be operated in parallel, attaining the same resolution as expressed in this document.
Using common experimental values for field strength, gradient and particle properties, these calculations suggest that separation of targets based on 15-nm differences in 1-μm diameter particles is possible (one part in 102) and the smallest resolvable difference in dielectrophoretic mobility is 10−23 m4/V2s (one part in 104) and the smallest resolvable change in Clausius–Mossotti factor is 10−5. When the highest experimentally available values are used, the smallest resolvable difference for these physical parameters are 500 pm for radius, 10−26 m4/V2s (one part in 107) for dielectrophoretic mobility, and 10−8 for the Clausius–Mossotti factor (all for a nominal one-micrometer diameter particle). This suggests that the technique promises to be an ultra-high resolution separation scheme for molecules and particles ranging from 4 nm to 10 μm in diameter.
2 Theory
2.1 Analyte behavior, transport and capture zones
Particle motion within a g-iDEP channel results from a superposition of forces induced by the applied electric field (Figures 1 and 2). These forces vary predictably with the electric field and depend on electro-physical properties of the analyte. As a result, a particle’s translational velocity in an electric field is described by electrokinetic mobilities intrinsic to that particle. Electrophoretic and electroosmotic forces are both proportional in magnitude and directionally coincident to the electric field and these two terms are included in an electrokinetic mobility (μEK).
Figure 2.
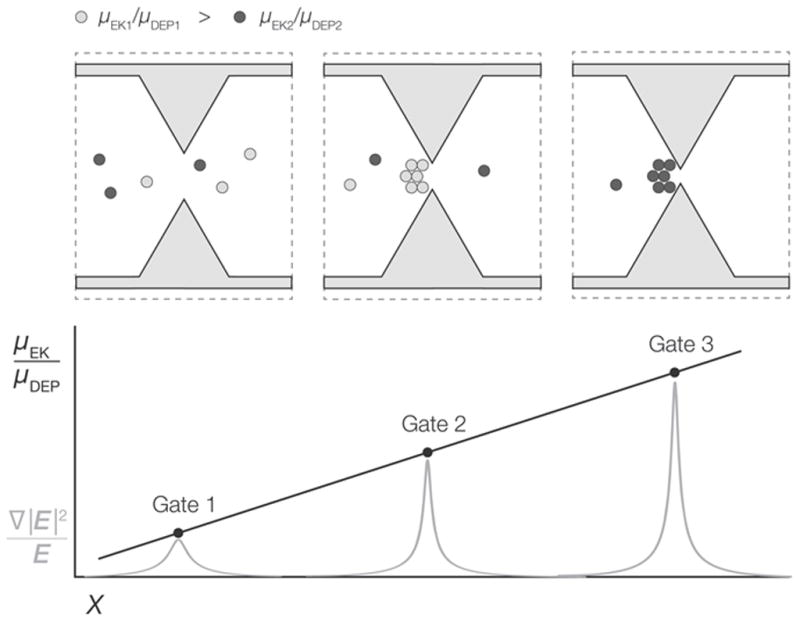
(Top) Illustration of three adjacent gates within a hypothetical g-iDEP channel. One of two target analytes is selectively captured and concentrated at the center gate. The other target analyte is captured at the gate to the right. (Bottom) Since gate pitch decreases along the channel in a determinate manner, distance is used to relate the resolvability of two target species. Note capture zones are of finite width, indicating dispersive effects including diffusion, field inhomogeneity, electrothermal effects, diffusion and particle-particle interaction.
| (1) |
The third electrokinetic force to consider is dielectrophoresis, characterized by dielectrophoretic mobility (μDEP). The dielectrophoretic mobility is a function of the permittivity of the solution (εf), particle radius (r), Clausius-Mossotti factor (fCM) and solution viscosity (η) according to μDEP = εfr2fCM/3η [27].
In order to represent the transport of target analyte along the centerline of the system, conventions provided by Giddings are used [28]. These state that transport (w) is the sum of field-induced analyte velocity (u) and pressure-driven fluid flow velocity (b).
| (2) |
No pressure-driven flow exists, so we consider only field-induced analyte motion. Transport or net velocity is the sum of component electrokinetic and dielectrophoretic velocity vectors for the analyte:
| (3) |
The component electrokinetic and dielectrophoretic velocity vectors can be expressed in the following terms, which derive from the respective force equations (not shown):
| (4) |
| (5) |
Each of two analytes can be assigned an electrokinetic mobility (μEK1 and μEK2) and dielectrophoretic mobility (μDEP1 and μDEP2). For further discussion of analyte separation, we will also consider the average of the two species’ electrokinetic or dielectrophoretic mobilities:
| (6) |
Since transport velocity is dependent on the position of the analyte along the separatory axis, equations (3) and (4) can be written as functions of x:
| (7) |
| (8) |
These equations hold true for any physical position along the centerline of the channel’s separatory axis.
While the field and gradient are continuous throughout the system, the areas near the points of closest approach (gates) define the resolution-limiting conditions (Figures 1 and 2). The width of these zones and the intervening minimum gradient zones are discussed below, but these factors do not need to be considered to develop this approach. At or near one of these gates, for a specific analyte, a balance point is induced and a zone forms about this zero velocity crossover. The width of the zone will directly impact the ability to keep that material trapped at a single gate and prevent some material from moving to the next gate. The variable, x0, is set at the center of the local capture zone. The forces and resulting velocity are conveniently related to the distance from the balance point for a particular analyte.
| (9) |
The slope a represents the intensity of the local restoring forces. The a term may be treated as linear, either by assuming very small values of x − x0, or by using the first non-zero factor in a Taylor series expansion about x0 (in some cases the factor treated as linear from a Taylor series expansion is u; instead a is utilized here to avoid confusion with the velocity term expressed above). This focusing effect generates a steady-state Gaussian concentration profile around the force balance point. The characteristic width and properties of this distribution define the concentration profile for a band of material.
| (10) |
Furthermore, Giddings showed that the characteristic variance profile for this type of system is [28]:
| (11) |
In this case, the term DT represents the sum of all dispersive forces, including those resulting from diffusion (Ddiff), flow-based effects, solution heating, particle-particle interactions, and heterogeneous fields (Figure 2). Substituting equation 10 for a and solving for σ yields the standard deviation:
| (12) |
This expression provides a measure for the peak width of captured analyte. This construct is virtually identical to that of isoelectric focusing, adapted to the focusing forces present in g-iDEP.
2.2 Assigning distance between concentration centroids
Spatial segregation of two similar analytes is designated as resolution of the analytes. This is defined by the distance between the centroids of two separated species (ΔX), and their degree of spreading (σ) [29].
| (13) |
The definition of the smallest difference in analytes that can be separated on a g-iDEP device is similar to traditional techniques. There are still slightly overlapping peaks, with R > 1.5, but each peak is collected at separate, nearest neighbor gates (Figure 2). Just to emphasize this point, the resolution of two species is defined as collection of one species at one gate and the other species at the next gate. A finite distance separates these gates. This distance is used to assign differences in the maximum field and gradient at those gates, allowing for calculation in Eulerian space (focusing on static space instead of time or moving coordinates).
For any two arbitrary neighboring gates, the local maxima are defined as E1 and E2. The average of these two local maxima is Eave. The change between successive pairs of gates is ΔEmax = E2 − E1. The local maximum gradient terms are defined as ∇|E|21 and ∇|E|22. The average of these values is ∇|E|2ave. The difference in this parameter between successive pairs of neighboring gates or capture zones is expressed as Δ(∇|E|2)max = ∇|E|22 − ∇|E|21.
Within this context, ΔX represents the distance between capture zones of two analytes along the projected continuum of gates. This concept facilitates determination of the minimum difference in the maximum field strength and the gradient term between two gates required for analyte separation. The term Δv represents the difference in instantaneous net velocity of analytes 1 and 2 at their balance point at adjoining gates. The expression du/dx represents the rate at which the field and gradient terms change along the channel from gate to gate.
| (14) |
where:
| (15) |
| (16) |
Combining these yields a complete expression for ΔX:
| (17) |
An equation for resolution may be expressed by incorporating equations 17 and 12 (and 13) for ΔX and combined zone width:
| (18) |
In order to achieve baseline separation, by setting R greater than or equal to 1.5 the equation can be rearranged to solve for the minimum differences between two analytes that can still be separated.
| (19) |
Assume there is no change in DEP forces to calculate minimum resolvable differences in electrokinetic effects:
| (20) |
Similarly, setting the EK forces to a constant value allows the minimum resolvable differences in dielectrophoretic effects:
| (21) |
By assigning any changes in dielectrophoretic mobility to altered radius, a minimum value of resolvable particle diameter can be calculated according to:
| (22) |
A similar approach allows solving equation 21 for minimum resolvable differences in fCM:
| (23) |
3 Results
In the following section, two scenarios will be addressed. In the first, the relationships described above are explored using typical field and gradient values achieved in published works. In the second scenario, resolution capabilities will be explored at the extent of highest reasonably achievable values (these values are limited by complicating factors such as heating or material breakdown). The values used for these two categories are listed in Table 1. They reflect numbers reported from experiments as well as those calculated via multi-physics modeling software (COMSOL) for existing g-iDEP designs. Note that most of the common values are within two orders of magnitude of the maximum values and extremely high-resolution separations have already been accomplished with this strategy.
Table 1.
Common and maximum experimental values. A typical particle diameter is one micrometer for many dielectrophoretic experiments. Geometric factors (insulator-based dielectrophoresis) include gate-widths between 100 nm and 30 mm, global applied fields of 104 V/m. These two factors and ranges therein allow for all calculated values.
| Eave(V/m) | ∇|E|2ave(V2/m3) | dE/dxave(V/m2) | d∇|E|2/dxave(V2/m4) | ΔEmax/dx(V/m2) | Δ(∇|E|2max/dx)(V2/m4) |
|---|---|---|---|---|---|
| Common input values | |||||
| 1.4 × 105 | 9 × 1014 | −3.5 × 109 | 3.1 × 1019 | 1.3 × 107 | 2.5 × 1017 |
| Highest experimentally accessible values | |||||
| 5.0 × 106 | 1.0 × 1018 | 3.5 × 1011 | 3.1 × 1020 | 1.6 × 108 | 1.1 × 1017 |
3.1 Calculated values under common and best case conditions
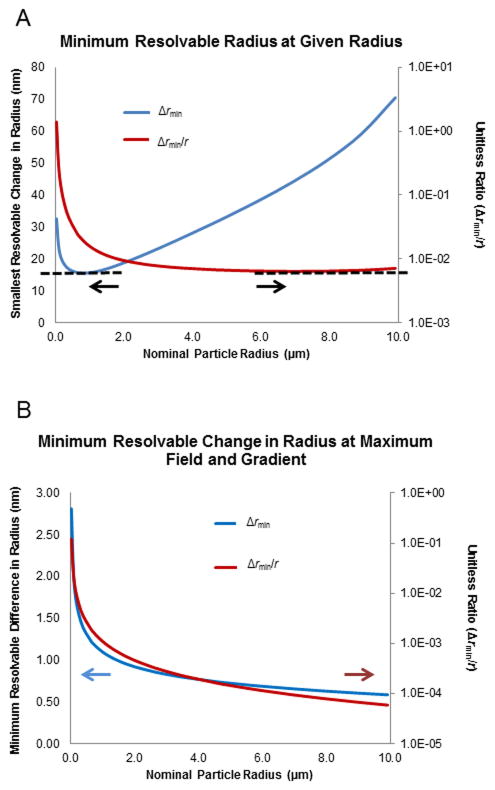
Equation 22 can be used to estimate the smallest resolvable difference in radius for a given nominal radius (Figure 3A). This calculation includes an estimate of the diffusion coefficient (Ddiff) as a function of radius, according to the Einstein equation (Ddiff = RT/6πηr). The results indicate that the smallest resolvable difference at any radius is about 15 nm, and may be achieved when the nominal particle radius is approximately 1 μm. By dividing the smallest differentiable radius by the nominal radius, the relative resolving power can be estimated across a range of particle sizes. The result is approximately one part in 100. This proportionality is fairly consistent across particles ranging from one to ten micrometers in diameter. For a one-micrometer particle, the expected radius-based resolution should reach to ±10 nanometers.
Figure 3.
A) Plot showing the smallest change in radius (blue line) that can be resolved as a function of the nominal radius of a particle using experimentally common field and gradient values (see Table 1). Also plotted is the normalized ratio of smallest resolvable difference divided by the nominal radius (red line). Arrows emphasize axis associated with each plot line. Note smallest value is ~15 nm at ~1 μm diameter and about 1:102 can be separated. B) Plot showing the smallest change in radius (blue line) that can be resolved as a function of the nominal radius of a particle using maximum experimentally accessible field and gradient values (Table 1). Also plotted is the normalized ratio of smallest resolvable difference divided by the nominal radius (red line). Arrows emphasize axis associated with each plot line. Note smallest value is ~500 pm at ~1 μm diameter and about 1:104 can be separated.
Using the above equations with higher field strengths or a redesigned microchannel would result in improved resolution. This would yield smaller minimum differentiable variations in analytes. The increased electric field values considered here were the highest noted occurrences in our models as well as in the literature (Table 1). These values are currently limited by experimental considerations such as solution or materials breakdown. Improved power supplies or other trivial strategies cannot functionally improve values beyond what is considered here. At these higher field and gradient values, the smallest resolvable change in radius is reduced to approximately 500 pm for nearly all particles in the range investigated (Figure 3B).
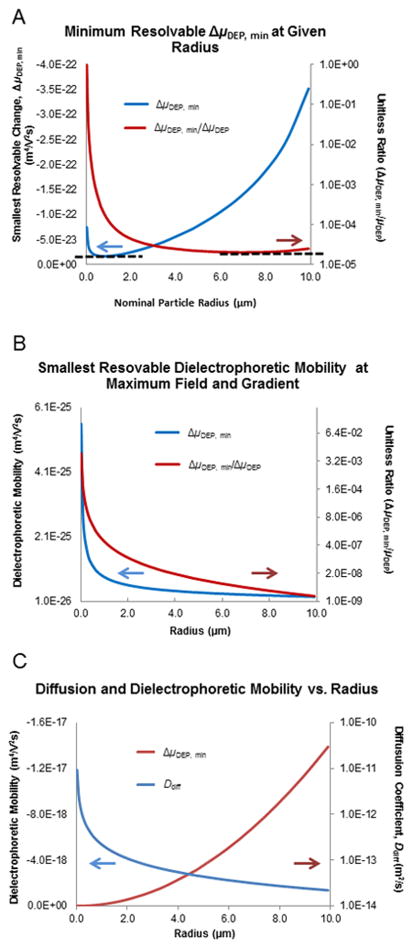
Considering a particle with a diameter slightly less than one micrometer, for typical absolute magnitudes of operating fields and gradients, the minimum resolvable difference in dielectrophoretic mobility from equation 21 is about 10−23 m4/V2s for a particle with a nominal mobility of 10−19 m4/V2s (μDEP = εfr2fCM/3η, εf = 10−9 F/m, r = 10−6 m, fCM = −0.3, η = 10−3 Ns/m2, Figure 4A). This relationship also displays a fairly constant relative resolving power at around 1:104 or 0.01% of the dielectrophoretic mobility. The minimum resolvable change in dielectrophoretic mobility is reduced to 10−26 m4/V2s with a relative resolution of about 1:108, for maximized field and gradient strengths—some four orders of magnitude higher than the common experimental values (Figure 4B).
Figure 4.
A) Examination of smallest difference in dielectrophoretic mobility (ΔμDEP.min) that is calculated to be resolvable using experimentally common values of electric field strength and gradient. Absolute values (blue line, left axis) and the ratio of the minimum resolvable value divided by the nominal dielectrophoretic mobility (red line, right axis) are shown. Arrows emphasize axis associated with each plot line. Note the smallest absolute value is about 10−23 m4/V2s and relative values of about 1:104 can be separated. B) Examination of smallest difference in dielectrophoretic mobility (ΔμDEP.min) that is calculated to be resolvable using maximum experimentally accessible values of electric field strength and gradient. Absolute values (blue line, left axis) and the ratio of the minimum resolvable value divided by the nominal dielectrophoretic mobility (red line, right axis—note: logarithmic) are shown. Arrows emphasize the axis associated with each plot line. Note the smallest absolute value is about 10−26 m4/V2s and about 1:107 can be separated. C) Plots of two of the most influential factors defining the minimum resolvable physical properties of particles via g-iDEP: average dielectrophoretic mobility (μDEP,ave) and diffusion coefficient (Ddiff). Arrows emphasize the axis associated with each plot line. Note the diffusion coefficient becomes quite large at small particle diameters and the dielectrophoretic mobility becomes larger with increasing diameter.
Two factors that chiefly influence the profile of these relationships are the diffusion coefficient and the dielectrophoretic mobility (Figure 4C). 1) The diffusion coefficient becomes large and an important factor at small radii. It effectively increases dispersion at small radii, increasing the variance (σ2) and broadening the collected concentration profile. 2) The dielectrophoretic mobility ranges over several orders of magnitude, from 10−23 to 10−17 m4/V2s over the 20-nm to 10-μm range of this study. For larger DEP mobilities, the magnitude of the minimum resolvable value increases. However, comparing minimum to nominal values acts as a normalizing factor leaving the relative resolving power approximately constant across the range.
Similar calculations were performed to determine the minimum resolvable difference in Clausius-Mossotti factor. The result is approximately one part in 105 (Figure 5, red line) under standard conditions. The assessment of the Clausius-Mossotti factor under optimal or maximum conditions results in a similar plot (Figure 5, blue line), but with the resolving power increasing to 1:108.
Figure 5.
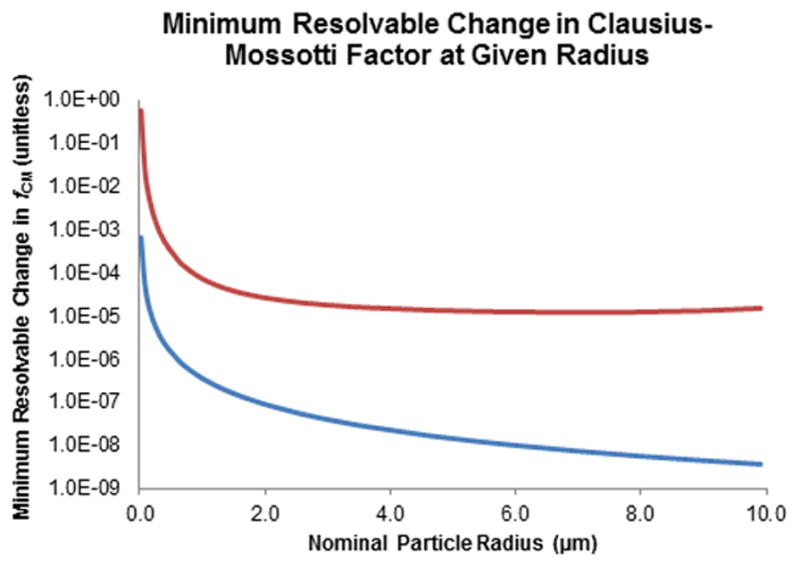
Red line: Plot of smallest change in Clausius-Mossotti factor (fCM) that can be separated versus particle diameter. Note that fCM is unitless and that this plots suggests that relative values of approximately 1:105 can be resolved under experimentally common values of electric field strength and gradient. Blue line: Plot of smallest change in fCM (unitless) that can be separated versus particle diameter, for maximum experimentally accessible values of electric field strength and gradient. This suggests that differences as small as approximately 1:108 can be resolved.
4 Discussion
The equations developed above suggest that a limited number of factors affect the resolution of a g-iDEP separation, including field strength (Eave and indirectly ∇|E|2ave), the local slope of the electric field at each gate (dE/dx and d(∇|E|2)/dx), dispersive effects (DT, including diffusion Ddiff), and the gate-to-gate step-wise increase in (dEmax/dx and d(∇|E|2max)/dx). Each of these factors can be manipulated by adjusting channel geometry and applied potential. In general, increasing local field gradients (dE/dx and d(∇|E|2)/dx), and decreasing gate-to-gate variation (dEmax/dx and d(∇|E|2max)/dx) will improve resolution (Table 2). We note the maximum experimental values demonstrated in condensed phase aqueous solution are about 106 V/m for Eave and 1018 V2/m3 for ∇|E|2ave [30]. We also note that other related forces can be harnessed to create a local trap, including electrothermal effects, while understanding that this effect may also add to dispersion.
Table 2.
Maximizing resolution. Since diffusion (Ddiff) and average dielectrophoretic mobility (μ̄DEP) are a function of radius and influence resolution, these variables interact to give a minimum in Δrmin.
| Minimize | Maximize | Minimal, arbitrary, or not adjustable |
|---|---|---|
| dEmax/dx | Eave | ΔμEK, min |
| d(∇|E|2max)/dx | ∇|E|2ave | μEK |
| dE/dx | ΔμDEP, min | |
| d(∇|E|2)/dx | ΔμDEP | |
| DT |
There are some subtle issues, which must be addressed when executing these calculations. For any given specific gate, and true for all of these calculations, the forces (velocities) must balance (μEK * Eave + μDEP * ∇|E|2ave = 0). Generally, electrokinetic mobility was used as an adjustable parameter, keeping well within ranges of known values from a very rich data set, captured over decades via capillary electrophoresis, as reflected in the literature. In some cases, the electric field (Eave) was adjusted. The dielectrophoretic mobility was not adjusted, since it was calculated from fundamental factors (radius, permittivity, etc.). In general, these values corresponded reasonably with real-world expectations. For instance, for a balanced target . Real values of μDEP can differ significantly from the simple Clausius-Mossotti factor-based calculations, but this is relatively unimportant to the development of this theory [27, 31]. The actual values are bracketed in practice and these remain within reasonable values of the juxtaposing μEK * Eave product. Using modeled values and multiplying the ratio of by ∇|E|2ave yields 106 V/m. An Eave maximum value is approximately 106 V/m before materials begin to break down.
The Clausius-Mossotti factor (fCM) was set at −0.3, which is a reasonable value and results in a negative dielectrophoretic force. Mathematically and theoretically this factor only accounts for the polarizability of the particle, but in practice this factor turns into the catchall for differences in behaviors of otherwise-identical particle populations. The real physical origins of the forces on the particles arise from a diverse range of features, including size, shape, roughness, heterogeneity, internal structures, internal charge distribution, fluidity of internal structures, deformability, charge mobility, and interactions with local environment, all of which may or may not directly influence polarizability. Any difference in any of these features may result in a separation, although none of them are analytically accounted for in the theory underlying fCM.
Noting that for a given capture or balance point, the focusing can be maintained while minimizing Eave. This suggests that dynamic range can be extended with lower applied voltage for capture, avoiding limitations in power supplies or physical breakdown of materials. However, this extension is juxtaposed by a decrease in resolution with lower Eave.
The derivation presented herein ties the change in maximum local gradient between gates (dEmax/dx and d(∇|E|2max)/dx) to the specific gate position along the channel (x). Conceptually, as the gate-to-gate separation approaches zero, the capture regions become arbitrarily close to each other and thus the continuous analysis is valid [10, 32]. One way our approach may be considered is to examine continuous functions which are sampled in either time or space and then analyzed and processed in sampled-data systems. Subsequently, the processed samples are used to reconstruct a continuous waveform [33]. Sampled data methods are not explored here, but serve to illustrate that such treatment is not unprecedented. Treating these values as continuous variables of x simplifies the derivation, but brings up a noteworthy caveat. In actuality, the local maxima which comprise dEmax/dx and d(∇|E|2max)/dx must occur at successive gates with a finite, non-zero x-axis separation. Physical implementation of arbitrarily-close gates is not realizable. As the distance between gates becomes very small, the necessary local field maxima, Emax and ∇|E|2max, decrease and eventually collapse into a smooth global gradient. Since each gate creates a local disruption/maximum in the field, sufficient space is required for the field to return to its relaxed or average value before a new disruption/maximum can be created with an even higher value of ∇|E|2 Furthermore, gates must be separated by a distance greater than the characteristic variance of a captured analyte. This distance may be estimated from the predicted peak width of a target population. As long as the physical separation between gates is several times the width of collected targets, the system is reasonable.
This system can be operated with gates in parallel as well as in series with the same or similar results, and the derivation could be reconstructed to reflect such a design. A similar construct has been used to examine electrophoretic exclusion [34]. Relevant field maxima at each parallel gate element would need to be designed with sufficiently different values to capture non-mixed analyte populations. The work by Kenyon et al., utilized alongside the approach developed here would elucidate these values.
A practical and important metric of resolution is ΔμEK,min and ΔμDEP,min. These two values allow direct comparison with other electrokinetic and dielectrophoretic techniques. In general, two scenarios are considered when assessing the theoretical resolution. Under common experimental values, ΔμEK,min = 2 × 10−12 m2/Vs (equation 20) and ΔμDEP,min = 10−23 m4/V2s (see Figure 4A). Current and past literature contains many examples of minimum resolvable electrokinetic values; this number is demonstrably better than any reported [34]. Such values are rarely reported for DC dielectrophoresis and thus cases for comparison are limited. For the ‘best case’ scenario, limited by breakdown voltages for materials and maximal gradients, these become ΔμEK,min = 2 × 10−14 m2/Vs and ΔμDEP,min = 10−26 m4/ V2s. One limitation for the high-resolution capabilities of electrokinetic effects is that the targets need appreciable dielectrophoretic force and therefore traditional targets smaller than 20 nm in diameter are not accessible.
No quantitative studies have been published examining the peak width and resolution of g-iDEP, or any iDEP device for that matter. One major limitation is the lack of accepted standard materials of known dielectrophoretic properties. However, there are many clues suggesting the calculated bandwidths are reasonable and that the technique offers high-resolution separations. In the work of Staton et al. [23], 200 nm particles were focused into a band approximately three micrometers wide (Figure 2 in reference). Under the conditions of the experiment, the calculated bandwidth using the derivation here is one micrometer. This result is reasonable since there may be many sources of dispersion not explicitly included in this model for this study. Other experiments using iDEP show bandwidths for targets ranging from large molecules to 5-μm diameter particles in the range of 1–10 μm [35, 36]. The simple reason for these narrow peaks is that the focusing slopes for this strategy are very large compared to other techniques. The ‘a’ factor (slope of restoring force) for focusing can reach 103 s−1 whereas traditional techniques (IEF, gradient field systems) range from 10−4 to 10 s−1. Since our model does not yet include the dispersive effects of particle-particle interactions and lateral heterogeneity of the gate gradient, these results again suggest that the theory presented is reasonable.
5 Conclusions
The derivation presented here suggests that extremely high-resolution separations are possible for particles from 20 nm to 10 μm in diameter. These separations may reflect very subtle differences in the target particles. In fact, specific strains of bacteria have already shown significant differentiation using these forces [26, 37]. Used as ultimate benchmarks, the best case suggests that one part in 103 differences in diameter (1 nm for a 1-μm particle) can be isolated, one part in approximately 108 can be separated as measured by ΔfCM or ΔμDEP,min. Compared with competing separations or analysis techniques, these offer orders of magnitude improvements.
Abbreviations
- g-iDEP
gradient insulator-based dielectrophoresis
- iDEP
insulator-based dielectrophoresis
- DEP
dielectrophoresis
- EP
electrophoresis
- EOF
electro-osmotic flow
- μEK
electrokinetic mobility
- μEP
electrophoretic mobility
- μEOF
electroosmotic mobility
- μDEP
dielectrophoretic mobility
- fCM
Clausius-Mossotti factor
- w
total transport velocity
- u
field-induced analyte velocity
- εf
solution permittivity
- η
solution viscosity
- b
pressure-driven fluid flow velocity
- DT
total dispersive forces
- Ddiff
diffusion constant
- νEK
electrophoretic velocity
- νDEP
dielectrophoretic velocity
- E
electric field strength
- ∇|E|2
dielectrophoretic gradient factor
- μ̄
average mobility
- a
slope of velocity change
- σ2
variance of final peak
slope of electric field
slope of dielectrophoretic gradient factor
- R
resolution
References
- 1.Giddings JC, Eyring H. Journal of Physical Chemistry. 1955;59(5):416–421. [Google Scholar]
- 2.Jorgenson JW, Lukacs KD. Anal Chem. 1981;53:1298–1302. [Google Scholar]
- 3.Kolin A. Journal of Chemical Physics. 1954;22(9):1628–1629. [Google Scholar]
- 4.Brakke MK. Journal Of The American Chemical Society. 1951;73(4):1847–1848. [Google Scholar]
- 5.Koegler WS, Ivory CF. Journal of Chromatography A. 1996;726(1–2):229–236. [Google Scholar]
- 6.Keller RA, Giddings JC. Journal of Chromatography. 1960;3(3):205–220. [Google Scholar]
- 7.Giddings JC. Analytical Chemistry. 1963;35(13):1999–2002. [Google Scholar]
- 8.Foret F, Fanali S, Ossicini L, Bocek P. J Chromatogr. 1989;470:299–308. [Google Scholar]
- 9.Giddings JC, Dahlgren K. Separation Science. 1971;6(3):345–356. [Google Scholar]
- 10.Kelly RT, Woolley AT. Journal of Separation Science. 2005;28(15):1985–1993. doi: 10.1002/jssc.200500228. [DOI] [PubMed] [Google Scholar]
- 11.Pysher MD, Hayes MA. Analytical Chemistry. 2007;79(12):4552–4557. doi: 10.1021/ac070534j. [DOI] [PubMed] [Google Scholar]
- 12.Chou CF, Tegenfeldt JO, Bakajin O, Chan SS, Cox EC, Darnton N, Austin RH. Biophys J. 2002;83:2170–2179. doi: 10.1016/S0006-3495(02)73977-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cummings EB, Singh AK. Anal Chem. 2003;75:4724–4731. doi: 10.1021/ac0340612. [DOI] [PubMed] [Google Scholar]
- 14.Suehiro J, Zhou GB, Imamura M, Hara M. IEEE Transactions On Industry Applications. 2003;39(5):1514–1521. [Google Scholar]
- 15.Lapizco-Encinas BH, Simmons BA, Cummings EB, Fintschenko Y. Electrophoresis. 2004;25:1695–1704. doi: 10.1002/elps.200405899. [DOI] [PubMed] [Google Scholar]
- 16.Barrett LM, Skulan AJ, Singh AK, Cummings EB, Fiechtner GJ. Analytical Chemistry. 2005;77(21):6798–6804. doi: 10.1021/ac0507791. [DOI] [PubMed] [Google Scholar]
- 17.Bhattacharya S, Chao TC, Ros A. Electrophoresis. 2011;32(18):2550–2558. doi: 10.1002/elps.201100066. [DOI] [PubMed] [Google Scholar]
- 18.Lapizco-Encinas BH, Davalos RV, Simmons BA, Cummings EB, Fintschenko Y. Journal of Microbiological Methods. 2005;62(3):317–326. doi: 10.1016/j.mimet.2005.04.027. [DOI] [PubMed] [Google Scholar]
- 19.Kang Y, Li D, Kalams SA. Biomed Microdev. 2008;10:243–249. doi: 10.1007/s10544-007-9130-y. [DOI] [PubMed] [Google Scholar]
- 20.Srivastava SK, Artemiou A, Minerick AR. Electrophoresis. 2011;32(18):2530–2540. doi: 10.1002/elps.201100089. [DOI] [PubMed] [Google Scholar]
- 21.Srivastava SK, Baylon-Cardiel JI, Lapizco-Encinas BH, Minerick AR. Journal Of Chromatography A. 2011;1218(13):1780–1789. doi: 10.1016/j.chroma.2011.01.082. [DOI] [PubMed] [Google Scholar]
- 22.Abdallah BG, Chao TC, Kupitz C, Fromme P, Ros A. ACS Nano. 2013;7(10):9129–9137. doi: 10.1021/nn403760q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Staton SJR, Chen KP, Taylor TJ, Pacheco JR, Hayes MA. Electrophoresis. 2010;31:3634–3641. doi: 10.1002/elps.201000438. [DOI] [PubMed] [Google Scholar]
- 24.Jones PV, Staton SJR, Hayes MA. Analytical and Bioanalytical Chemistry. 2011;401:2103–2111. doi: 10.1007/s00216-011-5284-9. [DOI] [PubMed] [Google Scholar]
- 25.Staton SJR, Jones PV, Ku G, Gilman SD, Kheterpal I, Hayes MA. Analyst. 2012;137(14):3227–3229. doi: 10.1039/c2an35138b. [DOI] [PubMed] [Google Scholar]
- 26.Jones PV, DeMichele AF, Kemp L, Hayes MA. Analytical and Bioanalytical Chemistry. 2014;406(1):183–192. doi: 10.1007/s00216-013-7437-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Weiss NG, Jones PV, Mahanti P, Chen KP, Taylor TJ, Hayes MA. Electrophoresis. 2011;32(17):2292–2297. doi: 10.1002/elps.201100034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Giddings JC. Unified Separation Science. New York: John Wiley and Sons; 1991. [Google Scholar]
- 29.Giddings JC. Dynamics of Chromatography. Vol. 1. New York: M. Dekker; 1965. [Google Scholar]
- 30.Jacobson SC, Culbertson CT, Daler JE, Ramsey JM. Anal Chem. 1998;70:3476–3480. [Google Scholar]
- 31.Kang KH, Xuan XC, Kang YJ, Li DQ. Journal Of Applied Physics. 2006;99(6):art. numb. 064702. [Google Scholar]
- 32.Tolley HD, Wang QG, LeFebre DA, Lee ML. Analytical Chemistry. 2002;74(17):4456–4463. doi: 10.1021/ac020027w. [DOI] [PubMed] [Google Scholar]
- 33.Shannon CE. Proceedings of the Institute of Radio Engineers. 1949;37(1):10–21. [Google Scholar]
- 34.Kenyon SM, Keebaugh MW, Hayes MA. Electrophoresis. 2014;35:2551–2559. doi: 10.1002/elps.201300572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.LaLonde A, Gencoglu A, Romero-Creel MF, Koppula KS, Lapizco-Encinas BH. Journal Of Chromatography A. 2014;1344:99–108. doi: 10.1016/j.chroma.2014.03.083. [DOI] [PubMed] [Google Scholar]
- 36.Liao KT, Tsegaye M, Chaurey V, Chou CF, Swami NS. Electrophoresis. 2012;33(13):1958–1966. doi: 10.1002/elps.201100707. [DOI] [PubMed] [Google Scholar]
- 37.Braff WA, Willner D, Hugenholtz P, Rabaey K, Buie CR. PLoS One. 2013;8(10):art. numb. e76751. doi: 10.1371/journal.pone.0076751. [DOI] [PMC free article] [PubMed] [Google Scholar]