Abstract
The ability to predict and reason about other people's choices is fundamental to social interaction. We propose that people reason about other people's choices using mental models that are similar to decision networks. Decision networks are extensions of Bayesian networks that incorporate the idea that choices are made in order to achieve goals. In our first experiment, we explore how people predict the choices of others. Our remaining three experiments explore how people infer the goals and knowledge of others by observing the choices that they make. We show that decision networks account for our data better than alternative computational accounts that do not incorporate the notion of goal-directed choice or that do not rely on probabilistic inference.
People tend to assume that other people's behavior results from their conscious choices—for example, choices about what outfit to wear, what movie to watch, or how to respond to a question (Ross, 1977; Gilbert & Malone, 1995). Reasoning about choices like these requires an understanding of how they are motivated by mental states, such as what others know and want. Even though mental states are abstract entities and are inaccessible to other people, most people find it natural to make predictions about what others will choose and infer why they made the choices they did. In this paper, we explore the computational principles that support such inferences.
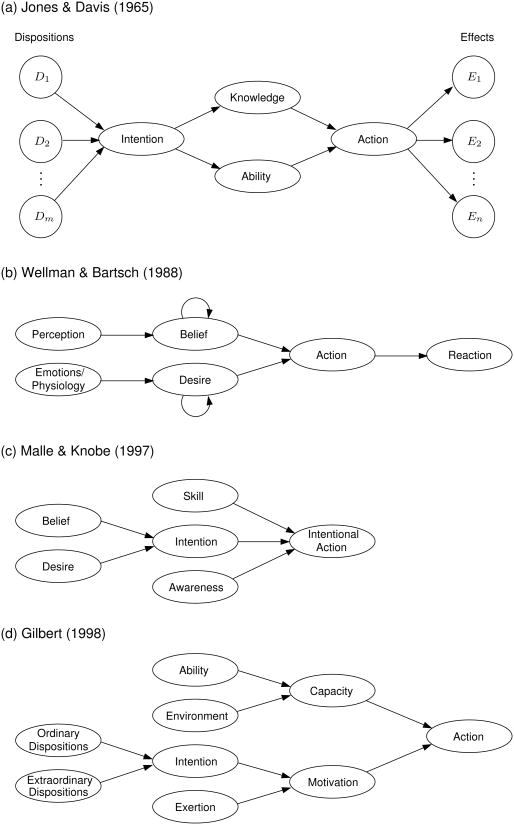
Several models of how people reason about others' actions have been proposed by social and developmental psychologists (e.g., Jones & Davis, 1965; Wellman & Bartsch, 1988; Malle & Knobe, 1997; Gilbert, 1998). Four examples are shown in Figure 1. For instance, Figure 1a shows a model of how people reason about others' actions. According to this model, a person's dispositional characteristics combine to produce an intention to take an action. Then, if that person has the necessary knowledge and ability to carry out the action, he or she takes the action, producing a set of effects. The other three models in Figure 1 take into account additional variables such as belief and motivation. For example, Figure 1b proposes that people take actions that they believe will satisfy their desires. The models in Figure 1 are not computational models, but they highlight the importance of structured causal representations for reasoning about choices and actions. We show how representations like these can serve as the foundation for a computational account of social reasoning.
Figure 1.
Qualitative models of how people reason about other people's actions and behaviors, drawn from research on attribution theory and theory of mind. These models are reproductions of figures found in (a) Jones & Davis (1965), (b) Wellman & Bartsch (1988), (c) Malle & Knobe (1997) and (d) Gilbert (1998).
Our account draws on two general themes from the psychological literature. First, people tend to assume that choices, unlike world events, are goal-directed (Baker, Saxe, & Tenenbaum, 2009; Csibra & Gergely, 1998, 2007; Goodman, Baker, & Tenenbaum, 2009; Shafto, Goodman, & Frank, 2012). We refer to this assumption as the principle of goal-directed action, although it has also been called the intentional stance (Dennett, 1987) and the principle of rational action (Csibra & Gergely, 1998, 2007). Second, we propose that human reasoning relies on probabilistic inference. Recent work on inductive reasoning has emphasized the idea that probabilistic inference can be carried out over structured causal representations (Griffiths, Chater, Kemp, Perfors, & Tenenbaum, 2010; Tenenbaum, Kemp, Griffiths, & Goodman, 2011; Griffiths & Tenenbaum, 2005), and our account relies on probabilistic inference over representations similar to those in Figure 1.
Our account is related to previous work on Bayes nets (short for Bayesian networks; Pearl, 2000), which have been widely used to account for causal reasoning (Gopnik et al., 2004; Sloman, 2005). Bayes nets rely on probabilistic inference over structured causal representations, but they do not capture the principle of goal-directed choice. In this paper, we present an extension of Bayes nets called decision networks1 (Howard & Matheson, 2005; Russell & Norvig, 2010, ch. 16) that naturally captures the principle of goal-directed choice. We propose that people reason about choice behavior by constructing mental models of other people's choices that are similar to decision networks and then performing probabilistic inference over these mental models. Decision networks may therefore provide some computational substance to qualitative models like the ones in Figure 1.
Our decision network account of reasoning about choices builds on previous approaches, including the theory theory of conceptual structure. The theory theory proposes that children learn and reason about the world by constructing scientific-like theories that are testable and subject to revision on the basis of evidence (Gopnik & Wellman, 1992). These theories can exist at different levels of abstraction. Framework theories capture fundamental principles that are expected to apply across an entire domain, and these framework theories provide a basis for constructing specific theories of concrete situations (see Wellman & Gelman, 1992). The decision network account can be viewed as a framework theory that captures the idea that choices are made in order to achieve goals, whereas individual decision networks can be viewed as specific theories. Gopnik and Wellman (2012) argue that Bayes nets provide a way to formalize the central ideas of the theory theory, and their reasons apply equally well to decision networks. For example, decision networks can be used to construct abstract causal representations of the world, to predict what will happen next, or to infer unobserved causes.
Although decision networks have not been previously explored as psychological models, they have been used by artificial intelligence researchers to create intelligent agents in multi-player games (Gal & Pfeffer, 2008; Koller & Milch, 2003; Suryadi & Gmytrasiewicz, 1999). In the psychological literature there are a number of computational accounts of reasoning about behavior (Bello & Cassimatis, 2006; Bonnefon, 2009; Bonnefon & Sloman, 2013; Hedden & Zhang, 2002; Oztop, Wolpert, & Kawato, 2005; Shultz, 1988; Van Overwalle, 2010; Wahl & Spada, 2000), and some of these accounts rely on Bayes nets (Goodman et al., 2006; Hagmayer & Osman, 2012; Hagmayer & Sloman, 2009; Sloman, Fernbach, & Ewing, 2012; Sloman & Hagmayer, 2006). However, our work is most closely related to accounts that extend the framework of Bayes nets to include the principle of goal-directed action (Baker, Goodman, & Tenenbaum, 2008; Baker et al., 2009; Baker, Saxe, & Tenenbaum, 2011; Baker & Tenenbaum, 2014; Doshi, Qu, Goodie, & Young, 2010; Goodman et al., 2009; Jara-Ettinger, Baker, & Tenenbaum, 2012; Pantelis et al., 2014; Pynadath & Marsella, 2005; Tauber & Steyvers, 2011; Ullman et al., 2009). Much of this work uses a computational framework called Markov decision processes (MDPs; Baker et al., 2009; Baker & Tenenbaum, 2014).
In the next section, we describe the decision network framework in detail and explain how it is related to the Bayes net and MDP frameworks. We then present four experiments that test predictions of the decision network framework as an account of how people reason about choice behavior. Our first two experiments are specifically designed to highlight unique predictions of decision networks that distinguish them from an account based on standard Bayes nets. Our second two experiments focus on inferences about mental states. Experiment 3 focuses on inferences about what someone else knows and Experiment 4 focuses on inferences about what someone else's goals are.
Decision networks
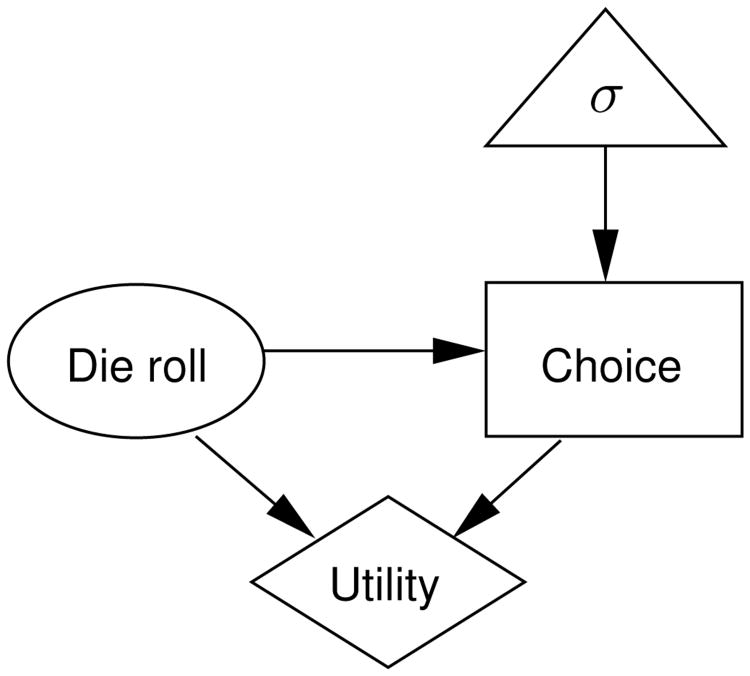
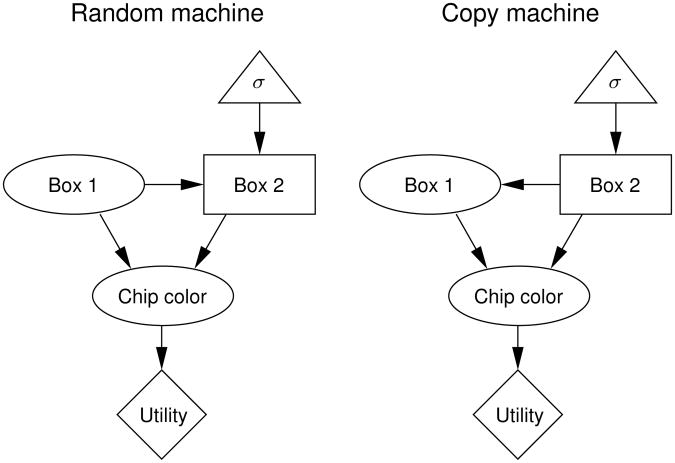
We will introduce the details of decision networks (decision nets for short) with the following running example. Suppose Alice is playing a game. In the game, a two-colored die is rolled, and if Alice chooses the color of the rolled die, she earns a reward. Suppose further that Alice is able to see the outcome of the rolled die before making her choice. This situation can be represented using the decision net in Figure 2.
Figure 2.
A decision network representing Alice's choice in the die-rolling game.
Decision nets distinguish between four different kinds of variables: world events, choices, utilities, and choice functions. In Figure 2, these different variables are represented using nodes of different shapes. World event variables are depicted by ovals and represent probabilistic events like the outcome of the die roll. Choice variables are depicted by rectangles and represent intentional choices like Alice's choice of color. Utility variables are depicted by diamonds and represent the decision maker's utility. Choice functions are depicted by triangles and specify the function that the decision maker applies to make the choice. Choice functions allow decision nets to capture the principle of goal-directed choice. Specifically, the choice function can be chosen to reflect the assumption that the decision maker chooses optimally. For example, the choice function σ in Figure 2 might specify that Alice will make her choice in order to maximize her expected reward.
The edges that define the graph structure of the decision net capture relationships between the nodes. Incoming edges to choice nodes represent information available to the decision maker when making the choice. Therefore, we will refer to these edges as knowledge edges. Because Alice is able to see the outcome of the die roll before making her choice, there is a knowledge edge leading from the die roll to Alice's choice. If Alice were unable to see the outcome of the die roll before making her choice, this knowledge edge would be removed. Edges leading from choice functions to choice nodes indicate that the choice is made by applying the specified choice function. In this example, regardless of whether Alice is able to see the outcome of the die roll, her choice would be driven by the goal of maximizing her expected reward. Incoming edges to utility nodes represent the information that is relevant to the decision maker's utility. Therefore, we will refer to these edges as value edges. In Figure 2, there are value edges leading from both the choice node and the die roll node, representing the fact that Alice's reward depends on both her choice and the outcome of the die roll. Incoming edges to world event nodes represent causal dependencies. Therefore, we will refer to these edges as causal edges. There are no causal edges in Figure 2, but if the situation were different such that the die were simply placed on the table to match Alice's chosen color, the knowledge edge in Figure 2 would be replaced by a causal edge leading from Alice's choice to the outcome of the die roll.
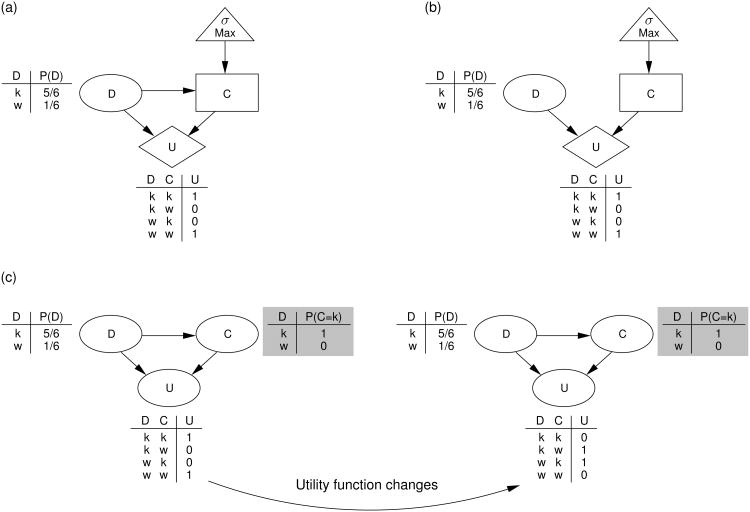
In addition to a graph structure, a full specification of a decision net includes a choice function, a conditional probability distribution (CPD) for each world event node, and a utility function that specifies how the value of each utility node is determined by the values of its parent nodes. A fully specified decision net for the die-rolling example is shown in Figure 3a. We have relabeled the nodes using a single letter for each node: D = die roll, C = choice, U = utility. The CPDs and utility functions are shown using tables. The CPD for the D node indicates that the color black (denoted by k) on the die is more probable than the color white (w). The choice function σ indicates that Alice makes the choice that maximizes her expected utility. The utility function for the U node indicates that Alice receives a reward only when her chosen color matches the rolled color.
Figure 3.
(a) A decision net for a case in which Alice's choice C is made after observing the value of the die roll event D. (b) A decision net for a case in which Alice's choice C is made without knowing the value of the die roll event D. (c) A Bayes net representation of the decision net in panel b. When the utility function changes, the Bayes net incorrectly predicts that Alice will continue to match the rolled color (see the shaded CPD for choice node C).
Once a utility function is specified, the expected utility, EU, for each of the decision maker's possible choices ci can be computed by summing over the unknown variables. For example, suppose Alice is unable to see the outcome d of the roll before making her choice. This situation is captured by the decision net in Figure 3b, where the knowledge edge from D to C has been removed. In this case, the expected utility associated with choosing black is EU(k)=Σd∈{k, w}u(k, d)P(d), where u(·, ·) is the utility function shown in the table in the figure, and P(·) is the CPD for the D node in the figure. If we assume that Alice is able to see the outcome of the roll before making her choice, as in Figure 3a, there is no uncertainty in the expected utility computation: EU(k) = u(k, d).
The choice function σ specifies the probability of making choice ci as a function of the expected utility of each possible choice. An optimal decision maker will use a utility-maximizing choice function:
| (1) |
If the die in our example has five black sides and one white side and Alice maximizes her utility, she will choose black if she cannot see the outcome of the roll. Under some conditions, however, people's behavior is more consistent with probability matching than maximizing (Vulkan, 2002).
Thus, another reasonable choice function is a utility-matching function:
| (2) |
Later, we will compare people's inferences about other people's choices to predictions made by both of these choice functions.
Reasoning about other people's choices
Decision nets were originally developed as tools for computing optimal decisions under uncertain conditions (Howard & Matheson, 2005). For this purpose, the “user” of a decision net might be both the designer of the decision net as well as the decision maker represented in it. In this paper, however, we use decision nets to capture the mental models that people use to reason about other people's choices. Suppose, for example, that Bob is observing Alice play the die-rolling game. We propose that Bob reasons about Alice using a mental model that is similar to the decision net in Figure 3a. All aspects of this decision net represent Bob's beliefs about Alice. For example, the value edge from D to U indicates that Bob believes that Alice's utility depends on the outcome of the die roll, the knowledge edge from D to C indicates that Bob believes that Alice observes the die roll before making her choice, and the utility function for node U captures Bob's beliefs about Alice's utility. Bob's beliefs about Alice may not be accurate, but our goal is not to predict Alice's choices. Rather, our goal is to predict the inferences that Bob will make about Alice, and Bob's inferences will depend on his (possibly false) beliefs about Alice. This perspective allows decision nets to straightforwardly capture reasoning about false beliefs. Even if Alice has a false belief about the game, as long as Bob's beliefs about Alice are accurate, his mental model of Alice's choice will take her false belief into account. A corresponding decision net would therefore make accurate inferences about Alice's choices.
When reasoning about other people's choices, people are capable of many types of inferences. We have already mentioned two such inferences: predicting someone's choice and inferring the mental states that motivated an observed choice. In both cases, an observer has incomplete information about someone's choice and must infer the missing information. Decision nets can be used to enumerate the possible inferences about others that result from withholding a piece of information about someone else's choice. Table 1 lists these inferences. Each row of the table contains an inference someone might draw by reasoning about someone's choice behavior and its decision net analogue. The experiments in this paper address four of the inferences in Table 1: predicting someone's choice (Experiment 1), learning what someone believes about about causal dependencies in the world (Experiment 2), learning whether someone can observe a state of the world (Experiment 3), and learning what factors someone cares about (Experiment 4).
Table 1.
Types of inferences people are capable of making about other people and their analogous decision net inferences. Inferences marked with an asterisk (*) are explored in the experiments reported in this paper.
| Inference | Decision net analogue | |
|---|---|---|
| * | Predicting someone's choice | Inferring the value of a choice node |
| Predicting how satisfied someone will be | Inferring the value of a utility node | |
| Learning what someone believes about a state of the world | Inferring the value of a world event node | |
| * | Learning whether someone can observe a state of the world | Inferring which knowledge edges exist |
| * | Learning what factors someone cares about | Inferring which value edges exist |
| * | Learning what someone believes about causal dependencies in the world | Inferring which causal edges exist |
| Learning what someone believes about the strength of causal dependencies in the world | Inferring the parameters of a CPD | |
| Learning how someone weights different factors when making choices | Inferring the parameters of a utility function |
Related computational frameworks
As we noted earlier, decision nets are related to several other computational frameworks that have been used by psychologists to account for reasoning about behavior. First, decision nets extend Bayes nets by adding a notion of goal-directed choice that captures the relationship between choice variables and utility variables. Second, decision nets are related to Markov decision processes (MPDs), which extend a class of models called Markov models in the same way that decision nets extend Bayes nets. We now examine the similarities and differences between decision nets and both Bayes nets and MDPs and discuss how all of these computational frameworks are related to one another.
Bayes nets
Like decision nets, Bayes nets are probabilistic models defined over directed graphs. The key difference is that Bayes nets do not explicitly capture the notion of goal-directed choice. Bayes nets include only one type of node, and do not distinguish between choices and world events. Each node in a Bayes net is associated with a conditional probability distribution (CPD) that captures how it is influenced by its parents in the network. Bayes nets are therefore compatible with the idea that choices have causes, but do not highlight the idea that choices are made in order to achieve goals.
Several authors have used Bayes nets to account for reasoning about choices (Goodman et al., 2006; Hagmayer & Osman, 2012; Hagmayer & Sloman, 2009; Sloman et al., 2012; Sloman & Hagmayer, 2006). For example, Sloman and Hagmayer (2006) discuss a Bayes net account of reasoning that combines causal reasoning with decision making. Given these applications of the Bayes net framework, it is important to consider whether decision nets offer any advantages that are not equally well supported by Bayes nets.
Any decision net can be “compiled” into a Bayes net that is equivalent in some respects. The compilation is carried out by discarding the choice function, replacing all remaining nodes with world event nodes and choosing CPDs that are consistent with the decision net's choice function. For example, the Bayes net on the left of Figure 3c is a compiled version of the decision net in Figure 3a. The two networks are equivalent in the sense that they capture the same distribution over events, choices and utilities. For example, both networks capture the idea that black is rolled 5/6 of the time, and that on every such occasion, Alice chooses black and receives a reward. A critical difference between the two, however, is that only the decision net acknowledges that Alice's choices are made in order to achieve her goals. This notion of goal-directed choice is a critical element of the compilation process that produced the Bayes net, but is absent from the Bayes net that is the outcome of the process.
Explicitly representing the connection between choices and goals leads to a number of advantages. First, this connection means that choices can be explained by reference to the goals that they achieve. For example, the most natural explanation for why Alice chose black in the die-rolling game is that Alice wanted the reward and chose the color that earned her the reward (see Malle, 1999, 2004). This explanation can be formulated in terms of the choice function of the decision net in Figure 3a. Specifically, the decision net transparently represents that Alice's utility depends on the outcome of the die roll and her choice (the value edges), that Alice is able to see the die roll before making her choice (the knowledge edge), and that Alice will make the choice that maximizes her utility (the choice function). By examining the corresponding Bayes net on the left of Figure 3c, however, one can only conclude (from the CPD for choice node C) that Alice chose black because she always chooses black when the die roll comes up black. Without a choice function, one cannot explain why the choice node has a particular CPD.
Second, the connection between choices and goals supports inferences about how choices will change when goals are altered. For example, suppose that the rules of the game change, and that Alice is now rewarded for choosing the opposite of the rolled color. This change is naturally accommodated by updating the utility function of the decision net. After making this single change, the decision net now predicts that Alice will choose the color that was not rolled. Figure 3c shows, however, that updating the CPD for the utility node U of the Bayes net leaves the CPD for the choice node C unchanged. The resulting Bayes net incorrectly predicts that Alice will continue to match the rolled color. To update the Bayes net in a way that matches the decision net account, the CPDs for nodes U and C must both be changed. From the perspective of a Bayes net account, the CPDs for these nodes are coupled in a way that violates the fact that Bayes nets are modular representations. That is, Bayes nets capture joint distributions over multiple variables by specifying local relationships between related variables. The modularity of Bayes nets implies that changing the CPD of one node should not affect the CPDs for other nodes. We explore this issue further in Experiment 1.
Third, the connection between choices and goals allows known goals to support inferences about the causal structure of a choice situation. For example, suppose that there are two possible relationships between the die and Alice's choice: either the die is rolled before Alice makes her choice, or the die is simply set to match the color Alice chooses. In other words, the knowledge edge leading from D to C in Figure 3b might instead be a causal edge leading from C to D. You observe the final outcome of the game, but do not see how this outcome was generated. If the rules of the game state that Alice is only rewarded for choosing the opposite of the die's color, but Alice's chosen color matched the die's color, a decision net approach will be able to infer that there is likely a causal edge from C to D—in other words, that the die was simply set to match Alice's choice. This inference follows from the assumption that Alice chooses to maximize her reward, which implies that she would have chosen not to match the die's color had there been an edge from D to C. In contrast, a standard Bayes net approach cannot use the information in the CPD for node U to infer the direction of the edge between C and D. This again follows from the modularity of Bayes nets: the CPD for one node cannot provide information about other nodes in the network that are not directly connected to it. We explore this issue further in Experiment 2.
Fourth, the connection between choices and goals allows observed choices to support inferences about unobserved goals. Imagine that the structure of the decision net in Figure 3a is known but that the utility function is not. A learner repeatedly observes trials in which Alice chooses a color that matches the rolled die, but the reward that Alice receives on each trial is not observed. A decision net model of this situation will be able to infer that Alice receives greater utility when the colors match than when they do not, because this kind of utility function makes the observed data most probable. In contrast, consider the corresponding situation in which the structure of the compiled Bayes net is known but the CPD for node U is not. In the absence of direct observations of U, a standard Bayes net approach will be unable to learn the CPD for this node. We explore this issue further in Experiment 4.
Even though decision nets can be compiled into Bayes nets, the examples just described suggest that decision nets offer several distinct advantages as accounts of reasoning about choice. All of these examples rely on the idea that decision nets go beyond Bayes nets by explicitly capturing the notion of goal-directed choice. Our experiments are specifically designed to explore some of the issues mentioned in this section, and we will apply both decision net models and Bayes net models to all of our experiments.
Markov decision processes
Markov decision processes (MDPs), like decision nets, use structured representations and incorporate the principles of goal-directed choice and probabilistic inference. MDPs have been used to model situations in which an agent navigates through a state space and chooses an action in each state (Baker et al., 2008, 2009, 2011; Baker & Tenenbaum, 2014; Doshi et al., 2010; Jara-Ettinger et al., 2012; Pynadath & Marsella, 2005; Tauber & Steyvers, 2011; Ullman et al., 2009). For example, Baker et al. (2009) used MDPs to model people's inferences about an agent's goal after people observed the agent move through a simple spatial environment. At each time step, the agent could move in at most four directions, constrained by obstacles in the environment. The best action available to an agent was the one that best served its goal. If the agent's goal was to reach a particular destination, the best action in most cases was the one that brought the agent closer to the destination. In some cases, however, it was necessary to move away from the destination, in order to navigate around obstacles. Baker et al. (2009) inverted this MDP action-planning model in order to make inferences about the agent's goals.
Although decision nets and MDPs are similar, they make different representational assumptions and are therefore each best suited for different types of reasoning problems. Standard MDPs use a state-based representation in which many features of the world and their relations to one another are captured by a single state variable. By contrast, decision nets use a feature-based representation in which all of the features of the world and their relations to one another are represented explicitly by separate variables in a decision net (Boutilier, Dean, & Hanks, 1999; Boutilier, Dearden, & Goldszmidt, 2000; Poole & Mackworth, 2010). For this reason, Koller and Friedman (2009) write that decision nets are best suited for modeling situations with only a few decisions in a rich environment with many causal dependencies and that MDPs are best suited for modeling situations involving sequences of decisions, possibly of indefinite length, in a relatively simple state space.
The feature-based representation of decision nets permits questions about what a decision maker knew, or what factors a decision maker cared about when making a choice, to be formulated in terms of whether certain edges in a decision net are present or absent (see Table 1). In Experiments 3 and 4, we asked people to make inferences about what a decision maker knew or cared about, and we contend that a feature-based representation best reflects people's mental representations in our tasks. It is possible to develop equivalent MDP models of these tasks, and we discuss one such model at the end of this paper. However, for an MDP, information about knowledge and goals must be implicitly captured by the values of state variables, rather than the structure of the network itself. We will therefore suggest that the feature-based representation used by decision nets captures the inferences people made in our experiments more transparently than the state-based representation used by MDPs.
Relationships between computational frameworks
The computational frameworks of decision nets, Bayes nets, and MDPs can be classified along two dimensions: the types of variables they represent and whether or not they represent a sequence. Table 2 is organized around these dimensions, and includes a fourth computational framework that is not directly related to decision nets: Markov models. Markov models are useful for reasoning about extended sequences of events and can be viewed as Bayes nets in which the variables capture states of a system and the edges capture transitions between these states. Markov models are best known as simple models of language (Shannon, 1948), but these models have also been explored as psychological models of causal reasoning (Rottman & Keil, 2012), memory (Kintsch & Morris, 1965; Körding et al., 2007) and sequential choice behavior (Gray, 2002).
Table 2.
Computational frameworks that differ in the types of variables they represent and whether or not they represent a sequence of events or choices. Three of the cells cite previous researchers who have used these frameworks to model aspects of cognition. Although Bayes nets, Markov models, and Markov decision processes have been used by psychologists, decision nets have not yet been explored as psychological models.
| Variables | ||
|---|---|---|
|
|
||
| Sequence | World events | World events, choices, utilities |
| No | Bayes netsGopnik et al. (2004) Griffiths & Tenenbaum (2005) Rehder & Kim (2006) Sloman (2005) |
Decision nets |
| Yes | Markov models Kintsch & Morris (1965) Körding, Tenenbaum, & Shadmehr (2007) Rottman & Keil (2012) Wolpert, Ghahramani, & Jordan (1995) |
Markov decision processes Baker et al. (2009) Tauber & Steyvers (2011) Ullman et al. (2009) |
Table 2 shows that decision nets differ from MDPs in the same way that Bayes nets differ from Markov models. Both Bayes nets and Markov models have been usefully applied to psychological problems, and it is difficult to argue that one of these approaches should subsume the other. Similarly, working with both MDPs and decision nets may help us to understand a broader class of problems than would be possible by concentrating on only one of these two frameworks. Therefore, decision nets and MDPs are best viewed as complementary rather than competing frameworks.
The logit model of preference learning
Before turning to our experiments, we will address one additional computational model that has been previously used to explain how people reason about choices. The logit model, also known as the multinomial logit model, has been used to explain how people infer other people's preferences after observing their choices (Lucas et al., 2014; Bergen, Evans, & Tenenbaum, 2010; Jern, Lucas, & Kemp, 2011). The model makes some basic assumptions about how preferences lead to choices, and works backward from an observed choice to infer the preferences that likely motivated it.
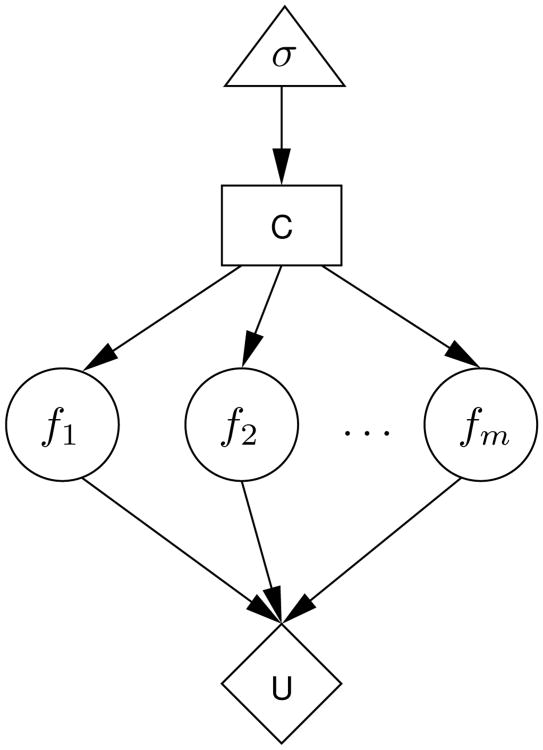
Although the logit model has not been expressed graphically by previous authors, Figure 4 shows how it can be formulated as a special case of a decision net. The model assumes that the decision maker makes a choice between multiple options, each of which produces one or more effects from the set {f1, f2, …, fm}. In Figure 4, the causal edges from the choice C to the effects fi illustrate that the choice determines which effects are produced. Figure 4 also illustrates that the decision maker's utility depends on which effects are produced. Using the logit model to infer the decision maker's preferences corresponds to inferring the parameters of the decision net's utility function. As shown in Table 2, this kind of inference is only one of many that are possible with decision nets. As a result, the decision net framework subsumes and is more general than the logit model of preference learning.
Figure 4.
The logit model of preference learning represented as a decision net. The choice C is between options that produce multiple effects fi.
Overview of experiments
We conducted four experiments to evaluate how well the decision net framework accounts for people's inferences about choice behavior. Our first two experiments were designed to directly compare decision nets with Bayes nets that do not contain a notion of goal-directed choice. Experiment 1 focuses on predicting choices after a utility function changes, and Experiment 2 focuses on using observed choices to make causal inferences. Our second two experiments examine how people make inferences about what other people know or value by observing their choices. Experiment 3 focuses on inferring what someone knows and Experiment 4 focuses on inferring someone's goal.
Experiment 1: Predicting other people's choices
Given that it is possible to compile any decision net into a Bayes net that makes identical choice predictions, it is important to ask whether the decision net is a better psychological model than the compiled Bayes net version of the same network. Earlier, we argued that one advantage of a decision net over a Bayes net is that a decision net can naturally accommodate changes to the utility function. When the utility function of a decision net changes, the decision net predicts that the decision maker will change her choice in order to maximize her rewards with respect to the new utility function. By contrast, as illustrated in Figure 3c, changing the CPD for the utility node of a Bayes net will not result in any change to the CPD for the choice node. Experiment 1 explores this difference between the accounts by asking people to predict someone's choice in a simple game, both before and after the payouts of the game change. We hypothesized that people's predictions would match the decision net account, which says that the player's choice will change when the payouts change.
The cruise ship game
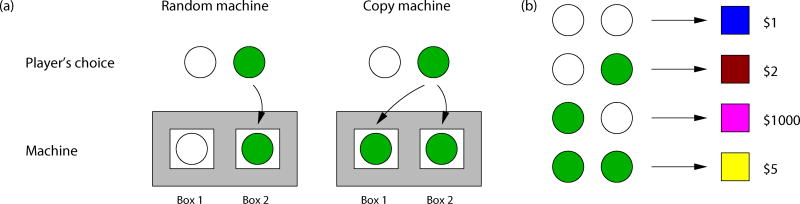
Participants in the experiment were told about a simple game played on cruise ships. We will refer to this game as the cruise ship game. The cruise ship game consists of a machine with two boxes, Box 1 and Box 2, that display pictures. There are two different versions of the cruise ship game: one uses a “random machine” and one uses a “copy machine.” When playing with the random machine, the machine fills Box 1 with a randomly chosen picture and then the player chooses a picture to fill Box 2. When playing with the copy machine, both boxes are initially empty and the picture that the player chooses fills both Box 1 and Box 2. The operation of both machines is illustrated in Figure 5a. Every cruise ship game has only two pictures. Therefore, there are at most four different pairs of pictures that may be displayed on a given machine. However, when playing with the copy machine, only two of these pairs—in which both boxes contain the same picture—are actually possible.
Figure 5.
The cruise ship game from Experiments 1 and 2. (a) When playing with the random machine, the machine randomly selects a picture for Box 1 and then the player chooses a picture for Box 2. When playing with the copy machine, the player's chosen picture is copied into both Box 1 and Box 2. The colored circles shown here are for illustrative purposes. In the experiment, participants saw pictures of different fruits and vegetables. (b) Every cruise ship has its own payout table that is shown to the player during the game. For each pair of pictures, the machine dispenses a different colored chip, which may be redeemed for cash.
After the player makes a choice, the machine dispenses a colored chip based on which two pictures are shown on the machine. Each pair of pictures is associated with a different color chip. These colored chips may be redeemed for a cash reward and each color has a different value: $1, $2, $5, or $1000. The payouts are different on each cruise ship and there is no consistent goal, such as choosing a matching picture, across cruise ships. An example payout table is shown in Figure 5b.
Models
Decision net model
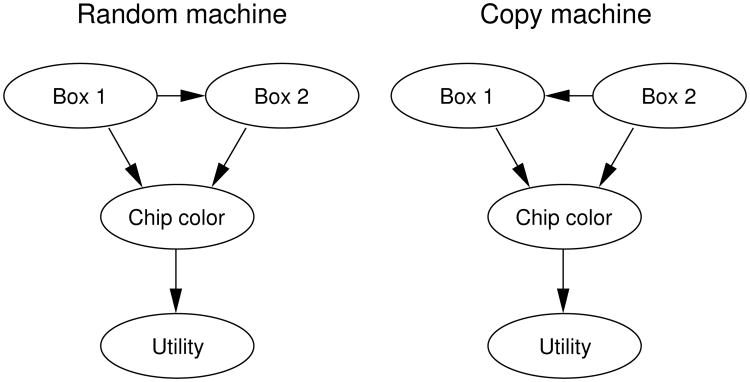
Figure 6 shows how the two different versions of the cruise ship game can be represented by decision nets. In these decision nets, the player's choice for Box 2 is represented by a choice node, the contents of Box 1 and the color of the dispensed chips are represented by world event nodes, and the cash reward is represented by a utility node. The causal edges leading from the nodes for Box 1 and Box 2 to the chip color node indicate that the color of the chip is determined by the contents of both boxes, and the value edge leading from the chip color node to the utility node indicates that the cash reward depends only on the chip color. The two decision nets differ only in the direction of the edge between the nodes for Box 1 and Box 2. For the random machine, the edge is a knowledge edge leading from Box 1 to Box 2, indicating that the contents of Box 1 are random and that the player knows what is in Box 1 before making a choice. For the copy machine, the edge is a causal edge leading from Box 2 to Box 1, indicating that the player's choice for Box 2 is copied into Box 1. The decision net in Figure 6 for the copy machine is equivalent to a decision net in which the player makes a choice that is copied into both Box 1 and Box 2.
Figure 6.
Decision nets representing the two versions of the cruise ship game in Experiments 1 and 2.
The utility functions and CPDs for the chip color nodes have been omitted from the decision nets in Figure 6 because these details varied across different cruise ships in the experiment. Once these details are specified, however, the choice function can be used to predict what a player will choose for Box 2 for a given machine. In this experiment, we assumed that the player uses the utility-maximizing choice function in Equation 1. Later, in Experiments 3 and 4, we consider alternative choice functions.
To predict a player's choice in the cruise ship game using a decision net, one must use the decision net from Figure 6 corresponding to the appropriate version of the game. Then, given the current game's payout table and the shape chosen by the machine for Box 1 (for the random machine), it is possible to compute the expected utility of the player's two options. Because we assumed a utility-maximizing choice function, the decision net model predicts that the player will choose the option with the greater expected utility.
Bayes net model
We created Bayes net models by compiling the decision nets in Figure 6 into equivalent Bayes nets. Recall that compiling a decision net into a Bayes net requires discarding the choice function, replacing all nodes with world event nodes and encoding the decision net's choice function into the CPD for the choice node in the Bayes net. Consistent with Figure 3c, we assumed that only the CPD for the utility node will change when the cruise ship game's payouts change; the CPD for the choice node will remain unchanged.
Method
Participants
Forty-two Carnegie Mellon University undergraduates completed the experiment for course credit.
Design and materials
All of the information was presented to participants on a computer. The pictures in the game were different fruits and vegetables. There were two within-subjects conditions, one for each type of machine: a random condition and a copy condition. In the random condition, participants were asked to predict what a player using the random machine would choose. Similarly, in the copy condition, participants were asked to predict what a player using the copy machine would choose.
Procedure
Participants were first introduced to the cruise ship game by playing two rounds of the game with each machine. Participants were told that each round they played was with a machine on a different cruise ship. The chip colors, chip values, and pictures on the machines changed in each round. For each machine, participants played one round in which the $1000 chip was dispensed for two matching pictures and one round in which the $1000 chip was dispensed for two mismatching pictures. These payouts were selected in order to dispel any notion that there was a consistent pattern to the payout structure. Participants completed the four practice rounds in a random order. In each round, after choosing a picture, the corresponding chip color and its dollar value appeared on the screen until the participant pressed a button.
The two conditions were presented in a random order. In each condition, participants saw a payout table, like the one in Figure 5b, indicating the values of all the colored chips. The four chip values were randomly assigned to the four picture pairs.
In the first phase of each condition, participants were told about another player of the game who had access to all of the same information as the participants, including the payout table. Participants were asked to predict for six rounds which picture the player would choose. They were given feedback (correct or incorrect) for each round. The feedback was based on the assumption that the player played optimally and did not make mistakes. In the random condition, the machine showed one of the two pictures on half of the rounds and showed the other picture on the other rounds.
In the second phase of each condition, the values of the chips changed, but everything else (the player, pictures, and chip colors) remained the same. Participants were told that the player knew what the new chip values were. Participants were asked to predict what the player would do for two rounds. The new chip values were manipulated so that the player's best choice in every circumstance was the opposite picture from the one he or she would have chosen before the chip values changed. In the random condition, the machine showed a different picture in each of the two rounds. Participants did not receive feedback for these two predictions.
After participants finished one condition, they were told that they would now see someone else play on a different cruise ship. The pictures, chip colors, and the name of the player changed for the second condition.
All participants completed Experiment 2, described later, before Experiment 1. It is unlikely that completing Experiment 2 before Experiment 1 biased participants' judgments for Experiment 1 because Experiment 2 did not require participants to make any predictions about player's choices and participants were never told that the players were making choices to earn the largest rewards.
Model predictions
The model predictions, shown in Figure 7b, are straightforward. When the payouts change, the decision net model is adjusted by changing the utility function, and the adjusted model predicts that the player will now make the opposite choice. The Bayes net model is adjusted by changing the CPD for the utility node. The CPD for the choice node, however, is unchanged, which means that the Bayes net model predicts that players will continue to make the same choices after the payouts change.
Figure 7.
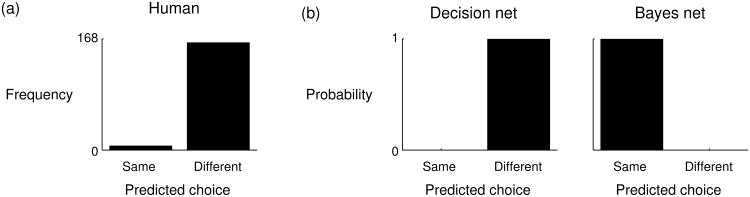
Experiment 1 results. (a) The number of times participants predicted that a player would make the same or a different choice after the payouts changed. (b) Decision net and Bayes net model predictions.
Results and discussion
Of the 168 predictions made by 42 participants in the second phase of the experiment, 162 (96%) were consistent with the decision net model's prediction, a proportion significantly higher than the chance level of 50%, Binomial test, p < .001. That is, participants predicted in nearly every case that the player would choose the opposite picture than the one he or she had chosen before, consistent with the decision net model.
The results in Figure 7a are not surprising, but they do have some theoretical implications. Compiling a decision net into a Bayes net may produce a model that captures the same distribution over world events and choices, but the two models are not completely equivalent. The decision net incorporates the notion of goal-directed choice, and can therefore make sensible predictions when the utility function changes. The Bayes net does not incorporate this notion, and therefore does not naturally handle changes in the utility function.
Decision nets are designed for computing choices, so it may not be surprising that they can be used to predict what choices others will make. Decision nets, however, can also be applied to many other tasks where participants are not required to make predictions about choices. To test the generality of the decision net framework, the remaining experiments explore three of these tasks.
Experiment 2: Reasoning about goal-directed choices
The purpose of Experiment 2 was to explore whether people rely on the assumption of goal-directed choice even when they are not asked to make direct judgments about others' choices. We asked participants to make a causal inference that was informed by someone's choice. Specifically, we asked participants to observe another person play a single round of the cruise ship game and then infer which machine the player was using. Such inferences are possible by considering how much money a player could have earned on a round and determining whether the player made the best possible choice given each of the two machines. However, these inferences would not be possible without information about the values of the chips. In other words, an understanding that people's choices are directed toward the goal of maximizing rewards supports a causal inference that would not otherwise be possible. We predicted that people would have no difficulty drawing these inferences when the payouts were known because they naturally think of people's choices as goal-directed.
Models
Decision net model
Inferring what version of the game a person was playing can be framed as a model selection problem in which the models are the decision nets in Figure 6 corresponding to the two versions of the game. Observers see a player's choice c ∈ {Picture 1, Picture 2}. We then use Bayes' rule to compute the probability of each decision net given choice c. For a decision net Nj,
| (3) |
where σ is the choice function for decision net Nj. We assumed a uniform prior distribution P(Nj), reflecting the fact that both versions of the machine are equally probable.
Bayes net model
In order to test whether the goal-directed choice assumption is necessary to account for people's inferences, we compared the decision net model to a Bayes net model without this assumption. Multiple authors have previously used Bayes nets to account for causal structure learning (Steyvers, Tenenbaum, Wagenmakers, & Blum, 2003; Griffiths & Tenenbaum, 2005; Deverett & Kemp, 2012) and the model we considered is a standard structure learning algorithms from this literature (Heckerman, Geiger, & Chickering, 1995).
The Bayes nets we used are shown in Figure 8. As with the decision net model, we treated the inference about what version of the game a person was playing as a model selection problem with these Bayes nets. For a Bayes net Nj,
Figure 8.
Bayes nets representing the two versions of the cruise ship game in Experiment 2.
| (4) |
Unlike the Bayes net model in Experiment 1, we did not create the Bayes net model by compiling the decision nets in Figure 6 into Bayes nets. As discussed earlier, compiled Bayes nets rely on the assumption of goal-directed choice, because the CPDs for the choice nodes are computed by the choice functions of the corresponding decision nets. Because the purpose of the current experiment was to test whether the goal-directed choice assumption is needed to account for people's inferences, we instead assumed that the CPDs for all nodes in the Bayes nets, except the choice node, were known. We used a uniform prior distribution over each row of the CPD for the choice node so that the model does not incorporate any a priori assumptions about how choices are made. In order to compute P(c|Nj), we averaged over all possible parameters of the CPD for the choice node. Once again, we assumed a uniform prior distribution P(Nj).
Method
Participants
The same 42 participants from Experiment 1 also participated in Experiment 2. All participants completed Experiment 2 first.
Design and materials
There were three within-subjects conditions: the random condition, the copy condition, and the uncertain condition. In each condition, participants observed one round of a player's gameplay. Participants were shown the two pictures in the machine but were not told what type of machine the player used. Let A and B denote the two pictures used in a given game. In all conditions, the observed round was a pair of matching pictures: AA.
In the random condition, participants were told that outcome BB dispensed a chip worth $1000. The values of the rest of the chips were not provided, but participants knew, from playing the game themselves beforehand, that $1000 was the highest possible payout. In this condition, if a player had been using the copy machine, he or she could have selected picture B to obtain the $1000 chip. Instead, the outcome on the machine was AA, strongly suggesting that the player was using the random machine with the picture in Box 1 randomly chosen to be picture A. In the copy condition, participants were told only that outcome AB dispensed a chip worth $1000. In this case, if the player had been using the random machine, he or she could have selected picture B to obtain the $1000 chip. Instead the outcome on the machine was AA, strongly suggesting that the player was using the copy machine and therefore could not produce an outcome with mismatching pictures. Finally, in the uncertain condition, participants were given no information about the chip values. In this case, it is impossible to know whether the AA outcome was good or bad for the player and no strong inferences can be drawn.
All of the information was presented to participants using on a computer. The outcome of each round was shown as a machine with two boxes, each filled with a picture. The chip values were indicated by a payout table in the upper-left of the screen that showed all four possible pairs of pictures, the color of the chip that was dispensed for each, and the corresponding dollar values (see Figure 5b). For chips with unknown values, the dollar value was replaced with a question mark.
Procedure
Participants were told that they would see three choices made by three different players on three different cruise ships, but they would not know what machine each player was using or what all of the chip values were. Each round constituted one of the three conditions. The three rounds were shown in a random order.
For each round, participants were asked to make three judgments. First, they were asked, “Would [the player's] choice make sense if the machine on this ship was a random machine?” They were then asked the same question about a copy machine. In both cases, they responded on a scale from 1 (“Definitely not”) to 7 (“Definitely yes”). The order of these two questions was randomized. The purpose of asking these questions was to encourage participants to explicitly consider both possible explanations for the player's choice as well as to provide an additional opportunity to test our models. Participants were then asked, “Based on [the player's] choice and the chip values you know, which type of machine do you think is on this ship?” They responded on a scale from 1 (“Definitely a random machine”) to 7 (“Definitely a copy machine”). The polarity of the scale was randomized.
Model predictions
Decision net model
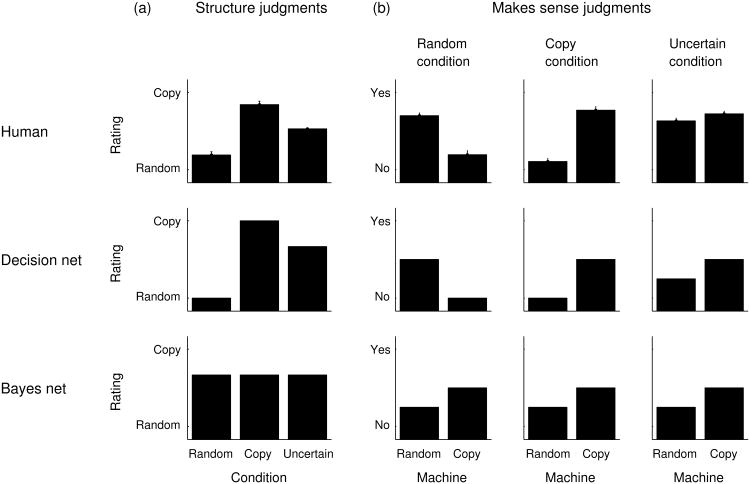
Predictions for the decision net model are shown in the second row of Figure 9. Figure 9a shows causal structure predictions for the three conditions. Because the model uses a utility-maximizing choice function, it makes certain causal structure judgments in the random and copy conditions. Because matching pictures are more likely with the copy machine than the random machine, the model slightly favors the copy machine in the uncertain condition.
Figure 9.
Experiment 2 results and model predictions. (a) Judgments about how probable the two machines were in the three conditions. (b) Judgments from each condition about whether the observed choice made sense given each of the two machines.
Figure 9b show the model's predictions for the “makes sense” judgments for each condition. These predictions were generated by computing the probability that the outcome would occur given each of the two machines. The model predicts that the outcome in the random condition does not make sense with a copy machine. Similarly, it predicts that the outcome in the copy condition does not make sense with a random machine. The model's predictions for the random machine in the random condition and the copy machine in the copy condition are not at ceiling because, in both conditions, the observed outcome is not the only possibility. In the uncertain condition, the model predicts that the outcome makes more sense with the copy machine than the random machine, because matching shapes are more common with the copy machine, but the predicted difference is smaller than in the other conditions.
Bayes net model
Predictions for the Bayes net model are shown in the third row of Figure 9. Just as for the decision net model, the Bayes net model predictions for the “makes sense” judgments were generated by computing the probability of the observed outcome given each of the two machines. Without an assumption that choices are goal-directed, the values of the chips contribute no information that could be used to learn the structure of the game. As a result, the model makes the same inferences in all three conditions. Just like the decision net model in the uncertain condition, the Bayes net model predicts that the observed outcome makes more sense with the copy machine than with the random machine. However, the Bayes net model makes this prediction in all three conditions.
As explained earlier, the behavior of the Bayes net model is a consequence of the fact that Bayes nets are modular representations that specify local relationships between related variables. As a result, learning something about the CPD for one node cannot provide information about other nodes in the network that are not directly connected to it. This point is made especially clear in Figure 8, where the utility node is separated from the Box 1 and Box 2 nodes by the chip color node. That is, the values of Box 1 and Box 2 are conditionally independent of the utility given the chip color. This conditional independence property means that observing the utility cannot provide information about the relationship between Box 1 and Box 2 if the chip color is already observed.
Decision nets are also modular representations, but the modularity of decision nets has very different consequences. In decision nets, the choice function requires that choices are motivated by all of their anticipated consequences in the network. As a result, when choices are involved, information about variables at the bottom of a decision net can inform inferences about variables at the top even if intermediary variables are observed.
Results and discussion
Mean human judgments are shown in the first row of Figure 9. As predicted by the decision net model, participants judged the random machine to be more probable in the random condition, the copy machine to be more probable in the copy condition, and gave more uncertain ratings in the uncertain condition. Participants gave significantly lower ratings—indicating more certainty about the random machine—in the random condition (M = 2.1, SD = 1.6) than in the uncertain condition (M = 4.2, SD = 0.5), t(41) = -8.36, p < .001. Participants gave significantly higher ratings— indicating more certainty about the copy machine—in the copy condition (M = 6.0, SD = 1.7) than in the uncertain condition, t(41) = 7.18, p < .001. We also looked at participants' individual ratings to see if they followed this same overall pattern. We found that 86% of participants matched the predictions of the decision net model by giving the copy machine the highest rating in the copy condition and giving the random machine the highest rating in the random condition.
We now consider participants' responses to the “makes sense” questions in Figure 9b. In the random condition, participants gave significantly higher ratings when asked if the observed round made sense if the player had been using a random machine (M = 5.2, SD = 1.4) than if the player had been using a copy machine (M = 2.2, SD = 2.0), t(41) = 7.03, p < .001. This pattern was reversed in the copy condition, with participants giving significantly higher ratings when asked about the copy machine (M = 5.6, SD = 1.7) than when asked about the random machine (M = 1.6, SD = 1.5), t(41) = 10.25, p < .001. Finally, in the uncertain condition, participants gave significantly higher ratings when asked about the copy machine (M = 5.3, SD = 1.3) than when asked about the random machine (M = 4.8, SD = 1.4), t(41) = 2.88, p < .01. However, consistent with the decision net model, this difference was not as large as in the copy condition.
The results of Experiments 1 and 2 support the idea that the assumption of goal-directed choice is essential for capturing how people reason about choice behavior. Whereas Experiment 1 focused directly on predicting people's choices, Experiment 2 did not involve predictions or judgments about choices. In both cases, participants' judgments were more consistent with a decision net model than a Bayes net model without the goal-directed choice assumption.
Experiment 3: Inferring what other people know
We have hypothesized that people reason about other people's choices by constructing mental models of those choices and that these mental models are similar to decision nets. Our second two experiments further test this hypothesis by focusing on two more inferences from Table 1 that are related to choice behavior. In particular, Experiments 3 and 4 focus on inferences about mental states. Mental state inferences are common in social interactions. For example, when you see a man gossiping about a person who is standing behind him, you can infer that he does not know the person can hear what he is saying. Or when someone at the dinner table asks you to pass the salt, you can infer that she wants to salt her food. In the first case, you can infer what the gossiper knows; in the second case, you can infer what the dinner guest wants.
Recall that edges leading to choice nodes in a decision net are called knowledge edges because they indicate what information is available to a decision maker when making the choice. Consequently, as indicated in Table 1, inferences about what someone knows (i.e., inferences about whether someone can observe a state of the world) correspond to inferences about which knowledge edges are present in a decision net representing that person's choice. If people's mental models are similar to decision nets, their inferences about what a person knows should be well predicted by a model that learns which knowledge edges are present in a decision net. Experiment 3 focuses on this type of inference. Experiment 4 focuses on inferring someone else's goal, which corresponds to learning which value edges are present in a decision net.
The shape game
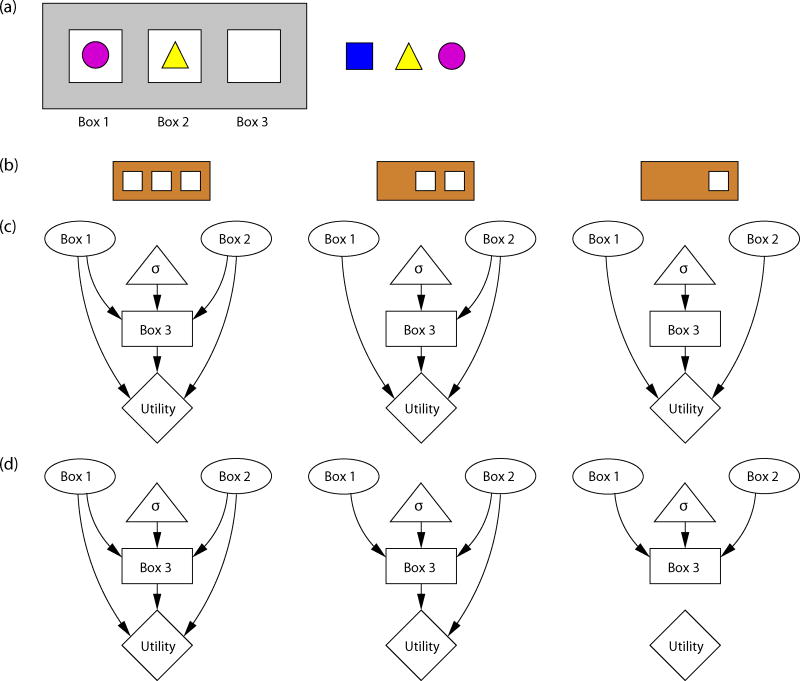
We used a modified version of the cruise ship game from Experiments 1 and 2 to create a simple setting that would allow us to study inferences about what someone knows. We will call this modified game the shape game because it uses pictures of shapes. The shape game consists of two components. The first component (Figure 10a) is a machine with three boxes. In each round of the game, the machine randomly selects two different shapes from the set of three shown in the figure and displays them in Box 1 and Box 2. The player then chooses one of the three shapes to display in Box 3. The second component of the game (Figure 10b) is a filter that may cover up some of the boxes of the machine. We call this the “information filter” because it is placed over the machine at the beginning of the round and therefore determines how much information about the machine's shapes is available to the player. There are three different filters: one filter covers Box 1 and Box 2 of the machine, one filter covers just Box 1, and one filter covers no boxes. Thus, the amount of information available to the player depends on which filter the player is required to use.
Figure 10.
The shape game from Experiments 3 and 4. (a) The machine and the three shapes the player may choose from in the shape game. (b) The three different filters in the game. (c) Decision nets representing a player's choice for each filter in Experiment 3. (d) Decision nets representing a player's choice for each filter in Experiment 4.
The goal of the game is to pick a shape that is different from the shapes picked by the machine. Players are awarded 10 points for each of the machine's shapes that is different from the player's shape. Because the machine's two shapes are always different, the minimum number of points a player can receive is 10 and the maximum is 20. The more information a player has about the machine's shapes, the greater advantage the player has in the game.
In the inference task, an observer is shown a record of 10 rounds from another player. The record for each round shows the three shapes but not the filter. The observer is told that the same filter was used in all 10 rounds. The observer's task is to infer from the player's gameplay record which filter was used in the game.
Decision net models
Figure 10c shows how the shape game can be represented by a set of decision nets, each one corresponding to a different information filter. In these decision nets, the contents of Box 1 and Box 2 are represented by world event nodes, the player's choice for the shape in Box 3 is represented by a choice node, and the awarded points are represented by a utility node. The value edges leading to the utility node from the nodes for the three boxes indicate that the player's reward always depends on the contents of all three boxes. The three decision nets differ only in the presence of knowledge edges because the different filters only affect what the player is able to see when making his or her choice. For example, the middle decision net in Figure 10c does not have a knowledge edge leading from Box 1 to Box 3 because the filter prevents the player from knowing the shape in Box 1 before making a choice for Box 3.
Inferring what a player knew in the game may now be framed as a model selection problem, like in Experiment 2. This time, observers see n rounds of gameplay from each player. Let the choices made for each round be denoted by c = (c1, …,cn), where each choice ci ∈ {square, triangle, circle}. We use Bayes' rule to compute the probability of each decision net given a set of observed decisions. For a decision net Nj,
| (5) |
We assumed a uniform prior distribution P(Nj) because all information filters are equally probable.
Choice function
In Experiments 1 and 2, we only considered a utility-maximizing choice function. Here we consider three different choice functions, each of which represents a different expectation an observer might have about a player's behavior. Identifying the choice function that best explains people's mental state inferences will provide further insight into how people reason about others' choices. For example, a utility-maximizing choice function is consistent with optimal behavior. Given that people do not always behave optimally, people may not adopt this assumption when reasoning about others' choices.
The first two models we considered were based on the utility-maximizing and utility-matching choice functions in Equations 1 and 2. Correspondingly, we will refer to these models as the utility-maximizing decision net model and the utility-matching decision net model. The utility-matching decision net model assumes that players make choices in proportion to their expected point rewards. We also considered a third choice function that assumes that players will usually behave optimally (i.e., as prescribed by the utility-maximizing choice function) but may sometimes make a “mistake,” which we define as a random choice among the non-optimal options, with some probability e. This choice function can be expressed as follows:
| (6) |
where k is the number of options (for the shape game, k = 3). We will refer to the model based on this choice function as the near-optimal decision net model. When e = 0, the near-optimal model is identical to the utility-maximizing model. The rounds of the shape game are independent. Therefore, all three models assume that for a given decision net Nj, σ(c|Nj) = Πi σ(ci|Nj).
Because the shape game is relatively simple and participants were given the opportunity to play the game themselves before observing another player's gameplay, we predicted that they would expect other players to play nearly optimally. That is, we predicted that the utility-maximizing or the near-optimal decision net model would account best for people's judgments.
Comparison models
The decision net models just described all incorporate the principles of goal-directed choice and probabilistic inference, which we have argued are essential for capturing how people reason about choices. To test whether both assumptions are truly essential, we designed two additional comparison models that each include only one of these assumptions.
Bayes net model
We wished to test whether a Bayes net structure learning model could account for our results without relying on the assumption of goal-directed choice. Thus, rather than compile the decision nets in Figure 10c into Bayes nets, we treated the graphs in Figure 10c as four-node Bayes nets with known CPDs for the utility nodes and applied the same Bayesian structure learning procedure that we used for the Bayes net model in Experiment 2. Unlike in Experiment 2, the inference task in the current experiment involves multiple observations of all variables. Consequently, a Bayes net structure learning model should be able to draw causal structure inferences in this task. For example, if the probability distribution for the shape chosen for Box 3 changes as a function of the shape in Box 1, the Bayes net model can conclude that there is an edge between Box 1 and Box 3.
Logical model
The decision net model selection account depends fundamentally on probabilistic inference. By contrast, previous authors (Bello & Cassimatis, 2006; Shultz, 1988; Wahl & Spada, 2000) have explored primarily logical accounts of mental state reasoning. In order to evaluate the importance of probabilistic inference, we implemented a strictly logical model.
The logical model treats all information filters that are logically consistent with the observed rounds as equally probable. For example, if a player chooses a shape that matches the shape in Box 1, the logical model would rule out the filter that covers up no boxes but treat the remaining two filters as equally probable. As a consequence of this approach, the logical model is not sensitive to the number of times an outcome occurs, and would, for instance, judge all three filters to be equally probable after observing a sequence of any length consisting only of outcomes in which all the shapes are different. By contrast, our decision net models take into account the fact that a player would need to be exceptionally lucky to repeatedly choose a shape that is different from the machine's shapes if he or she were playing with the filter that covers up Box 1 and Box 2. Consequently, the decision net models increasingly favor the three-hole filter after observing a series of outcomes in which all the shapes are different.
Method
Participants
Fifteen Carnegie Mellon University undergraduates completed the experiment for course credit.
Design and materials
There are three qualitatively different outcomes that might be observed in each round: all different shapes (outcome D), matching shapes in Box 1 and Box 3 (outcome M1), or matching shapes in Box 2 and Box 3 (outcome M2). These are the only possible outcomes because the machine always picks two different shapes to fill Box 1 and Box 2.
Participants saw the three gameplay records shown in Table 3. These records were used to create three conditions. The sequences were designed to instill some uncertainty in the earlier rounds about which filter was being used, but to provide strong evidence for one of the three filters by the end of the sequence. For example, in the first sequence consisting entirely of D outcomes, it is possible for a player who cannot see Box 1 or Box 2 to choose a mismatching shape by chance every time, but this outcome becomes less likely as the length of the sequence increases. In the third sequence, there is increasingly strong evidence that the player was using the two-hole filter until the M2 round, when the one-hole filter seems more likely.
Table 3.
Gameplay records used in the three conditions of Experiments 1 and 2. D: A round in which all three shapes were different. M1: A round in which the same shape appeared in Box 1 and Box 3. M2: A round in which the same shape appeared in Box 2 and Box 3. The condition column indicates the filter that the corresponding gameplay record is most consistent with.
| Round | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
||||||||||
| Condition | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
D | D | D | D | D | D | D | D | D | D |

|
D | D | D | M1 | D | M1 | M1 | M1 | D | D |

|
D | D | D | M1 | D | M1 | M1 | M2 | D | D |
Participants completed the experiment on a computer, with a display similar to the one used in Experiment 2. The outcome of each round was shown as a machine like the one in Figure 10a with all three boxes filled with a shape.
Procedure
Participants were first introduced to the shape game by playing six rounds with each of the three filters. After playing each version of the game, the experimenter asked if they understood the rules and addressed any misconceptions before they continued. In the subsequent inference task, the sequences of rounds were displayed one at a time with all previous rounds remaining on the screen. The specific shapes that appeared in each round of the gameplay records in Table 3 were randomly generated for each participant. After viewing each round, participants were asked to judge how likely it was that the player had been using each of the three filters for the entire sequence of gameplay. They made their judgments for each filter on a scale from 1 (very unlikely) to 7 (very likely). They were also asked to give a brief explanation for their judgments.
Model predictions
Decision net models
Here we discuss the predictions of the utility-maximizing and utility-matching decision net models. We will consider the near-optimal model when we discuss the human data below.
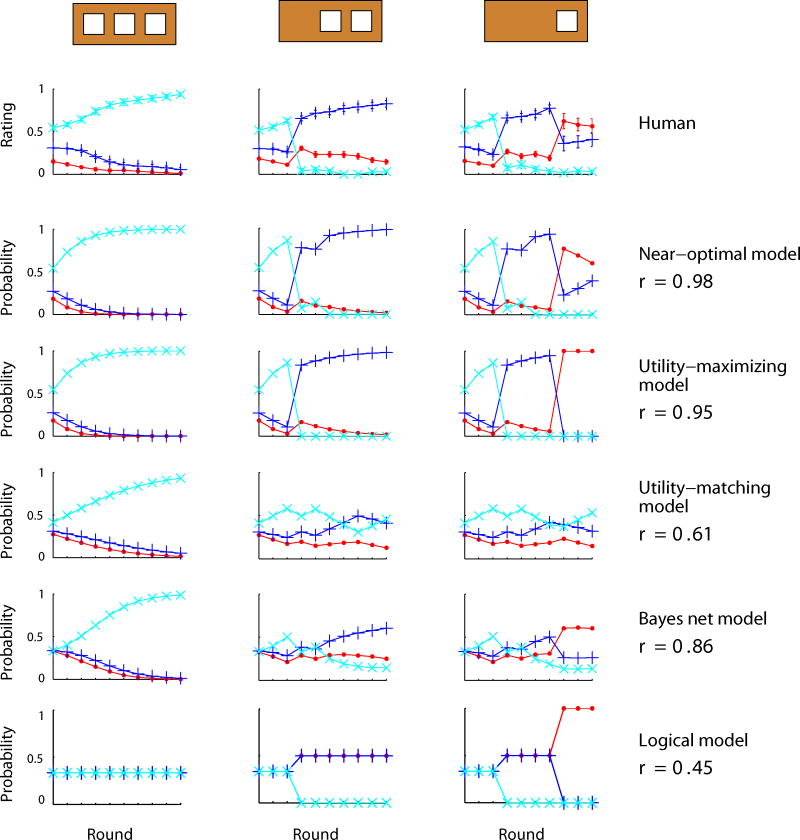
Predictions for the utility-maximizing model are shown in the third row of Figure 11. In all conditions, after observing all ten rounds, the utility-maximizing model predicts a near certain inference about the player's filter. In the three-hole filter condition, the model becomes more certain about the three-hole filter after observing each round. In the two-hole filter condition, the model initially judges the three-hole filter to be most probable, but dramatically changes its judgments in favor of the two-hole filter after observing the first M1 outcome in Round 4. Recall that an M1 outcome is one in which the shapes in Box 1 and Box 3 match. If a player were using the three-hole filter, he or she would have known what shape was in Box 1 when choosing a shape for Box 3, and choosing a matching shape in Box 3 would reduce the number of points the player earned. Thus, if the player is choosing optimally with the three-hole filter, an M1 outcome should not occur. Finally, in the one-hole filter condition, the model's predictions are identical to those in the two-hole filter condition until Round 8, when the first M2 outcome is observed. At this point, the model becomes certain that the player is using the one-hole filter. To understand why this occurs, first recall that an M2 outcome is one in which the shapes in Box 2 and Box 3 match. Observing an M2 outcome indicates that an optimal player was not able to see the shape in Box 2. Because the M2 outcome comes after several M1 outcomes, which already suggested that the player could not see the shape in Box 1, the only remaining explanation is that the player could not see the shapes in either Box 1 or Box 2 and was using the one-hole filter.
Figure 11.
Experiment 3 results and model predictions for the three conditions. In all plots, the cyan line (× markers) corresponds to the three-hole information filter, the blue line (+) corresponds to the two-hole information filter, and the red line (·) corresponds to the one-hole information filter. The error bars in the human plots are standard errors. For the models, r is the correlation coefficient between the model's predictions and the human judgments.
Predictions for the utility-matching model are shown in the fourth row of Figure 11. This model does not assume optimal choices and therefore does not achieve the same level of certainty as the utility-maximizing model in any of the three conditions. Because the utility-matching model assumes that choices are made in proportion to their expected point values, and no choice of shape ever results in zero points, the model judges any outcome to be fairly consistent with any of the three filters. As a result, the model does not draw strong inferences in the two-hole filter and one-hole filter conditions.
Comparison models
The Bayes net model predictions are shown in the fifth row of Figure 11. These predictions are averages of predictions for 5000 randomly sampled data sequences that were consistent with the outcomes in Table 3. In all conditions, after observing all ten rounds, the Bayes net model predicts that the intended filter is the most probable. However, the model makes considerably less certain inferences than the utility-maximizing decision net model. This effect is evident in the Bayes net model's predictions after observing the first round: the model assigns equal probability to all three filters. Without an expectation about how the choice for Box 3 is made, a single round provides insufficient covariation information to draw an inference about the causal relationships between the boxes. In contrast, the decision net models assign a higher probability to the three-hole filter than the other two filters after observing the first round. The decision net models assume that players' choices are directed toward the goal of choosing a shape for Box 3 that is different from the shapes in both Box 1 and Box 2. Observing even a single round in which this goal is achieved provides evidence that the player was able to see what was in Box 1 and Box 2.
The logical model predictions are shown in the sixth row of Figure 11. As explained earlier, the logical model's predictions do not change after repeated observations of the same outcome because the model does not take probabilistic information into account. This is best illustrated in the logical model's predictions for the three-hole filter condition, consisting of all D outcomes (leftmost plot). In this case, the logical model predicts that all three filters are equally likely throughout the entire sequence. As the model's predictions for the other two conditions show, only outcomes that have not been previously observed cause the model to adjust its predictions.
Results and discussion
Participants' mean judgments are shown in the first row of Figure 11. In order to convert participants' judgments on the 1 to 7 scale to approximate probabilities, the ratings in each round were first decremented by 1 to make 0 the lowest value. The ratings were then normalized by dividing by their sum to obtain ratings that summed to 1. The error bars are standard errors and were approximated using a statistical bootstrap with 10,000 samples.
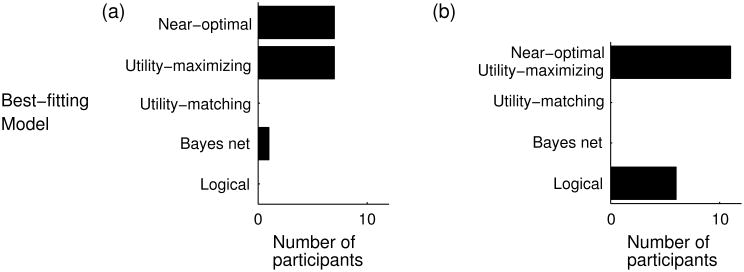
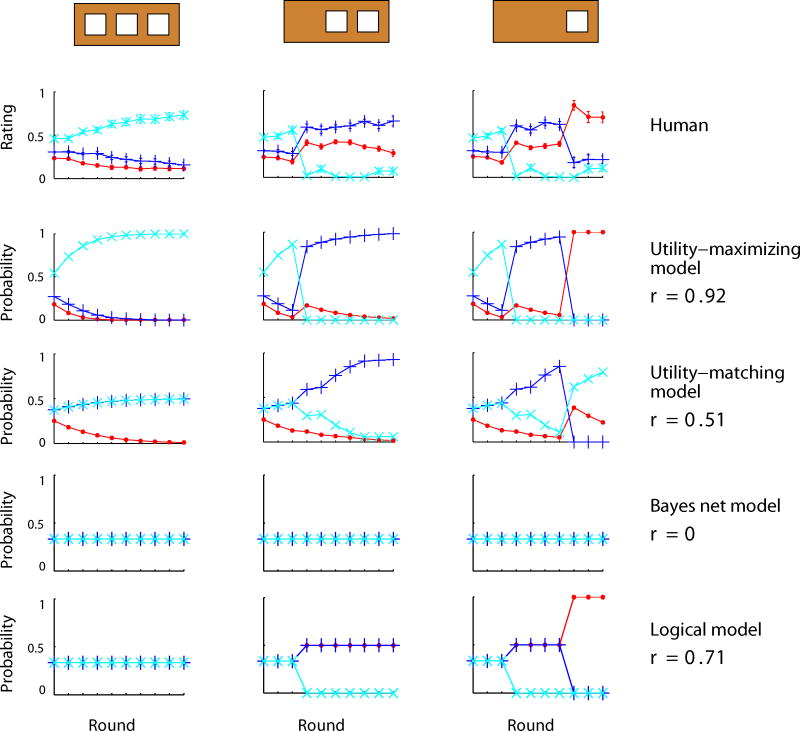
Participants' judgments exhibit two key features predicted by the utility-maximizing decision net model. First, participants changed their judgments dramatically after observing the M1 and M2 outcomes, unlike the predictions of the utility-matching decision net model or the Bayes net model. Second, participants tended to become more certain after observing the same outcome in multiple rounds, unlike the predictions of the logical model. Accordingly, participants' mean judgments across conditions correlated most highly with the predictions of the utility-maximizing decision net model (r = 0.95), compared with the utility-matching decision net model (r = 0.61), the Bayes net model (r = 0.86), or the logical model (r = 0.45).
There are still some qualitative differences between participants' judgments and the predictions of the utility-maximizing decision net model. For instance, consider the one-hole filter condition. In Round 4, the first M1 outcome is observed, and in Round 5, a D outcome is observed. The utility-maximizing model completely rules out the three-hole filter after observing the M1 outcome because it assumes that players will not make mistakes. By contrast, participants briefly increased their ratings for the three-hole filter after observing the D outcome in Round 5. Similarly, after Round 8, when the first M2 outcome is observed, the utility-maximizing model completely rules out the two-hole filter, but participants did not.
In light of these differences, we now consider the near-optimal decision net model. The predictions for the near-optimal model, shown in the second row of Figure 11, were obtained by fitting the e parameter to the mean human data in order to obtain the highest correlation coefficient. The best-fitting value was e = 0.007, which corresponds to an expectation that players will make a mistake 0.7% of the time. In other words, participants expected other players to exhibit close to optimal behavior. Because the near-optimal model maintains a small probability of a mistake, it does not definitively rule out the three-hole filter after the first M1 outcome or the two-hole filter after the first M2 outcome in the one-hole filter condition. Consequently, the model achieves the best fit to the human data of all the models we considered (r = 0.98).
Individual differences
The correlations shown in Figure 7 are based on participants' mean judgments. In order to evaluate whether the the decision nets account well for individuals' judgments, we compared model fits for all five models (with e fixed to its best-fitting value of 0.007 for the near-optimal model) to each participant's ratings. The number of participants that were best fit by each model are shown in Figure 12a. As the figure shows, 14 out of 15 participants were best fit by the near-optimal or the utility-maximizing decision net models, suggesting that the decision net approach provides a good account of people's inferences about other people's knowledge.
Figure 12.
Number of participants that were best fit by each model in (a) Experiment 3 and (b) Experiment 4. For Experiment 4, the near-optimal and utility-maximizing models were identical and are therefore represented by a single bar.
Experiment 4: Inferring other people's goals
Experiment 3 showed that performing model selection over decision nets accounted well for people's inferences about what someone else knows. The purpose of Experiment 4 was to apply this same account to a situation in which people must infer someone else's goals.
Revised shape game
In Experiment 3, there was a single payout function and the player's goal in the shape game was always to maximize the score. For Experiment 4, we modified the shape game in order to create a game in which players could have different goals.
Previously, the information filters were placed over the machine at the beginning of the round. This time, the filters—which we now call “payout filters”—are not placed over the machine until the end of each round. Thus, when playing the payout filter variation of the game, players are able to see the shapes in all boxes when choosing their own shape. The payout filter determines how the score for each round is computed: only the boxes not covered by the filter are counted. Thus, when the payout filter covers Box 1, the maximum number of points is 10, which is achieved when the player's shape in Box 3 is different from the shape in Box 2. When the payout filter covers Boxes 1 and 2, there are no shapes to mismatch and 10 points are awarded no matter what shape the player picks.
Decision net models
Figure 10d shows how this variation of the shape game can be represented by a set of decision nets, each one corresponding to a different payout filter. The player always gets to see the shapes in Box 1 and Box 2, which is why there are knowledge edges leading from Box 1 and Box 2 to Box 3 in all three decision nets. However, the points the player receives may not depend on the contents of all of the boxes. Thus, the decision nets differ only in the presence of value edges. The decision net representing the one-hole payout filter version of the game has no value edges because players receive 10 points no matter what they choose in this case.
Inferring what a player's goal was—that is, which payout filter the player was using— corresponds to an inference about what value edges are present in the player's decision net. Once again, we modeled this inference as model selection among the three decision nets. The remaining details of the model were identical to those for the model in Experiment 3. We implemented utility-maximizing, utility-matching, and near-optimal versions of the decision net model for this task and, once again, hypothesized that people's inferences would be best accounted for by either the near-optimal or utility-maximizing model.
Comparison models
For comparison, we again implemented the Bayes net and logical models described in Experiment 3.
Method
All of the participants from Experiment 3 also participated in Experiment 4. Participants completed the two experiments in a random order. There were two additional participants in the current experiment because their data for Experiment 3 were lost due to a programming error (total N = 17). Experiment 4 was identical to Experiment 3 except that participants made judgments about the payout filter version of the shape game.
Model predictions
Decision net models
Predictions for the decision net models are shown in the second and third rows of Figure 13. Predictions from the near-optimal model are omitted because the best-fitting near-optimal model was equivalent to the utility-maximizing model. In other words, people were best fit by a decision net model that assumed other players behaved optimally (e = 0).
Figure 13.
Experiment 4 results and model predictions for the three conditions. In all plots, the cyan line (× markers) corresponds to the three-hole payout filter, the blue line (+) corresponds to the two-hole payout filter, and the red line (·) corresponds to the one-hole payout filter. The error bars in the human plots are standard errors. For the models, r is the correlation coefficient between the model's predictions and the human judgments.
The utility-maximizing model makes identical predictions for both Experiments 3 and 4. From the perspective of the model, the optimal choices in the game are the same whether a player is playing the information filter shape game and does not know what is in a box, or if the player is playing the payout filter shape game and does not care what is in that box.
The utility-matching model's predictions, however, depart notably from its predictions for Experiment 3. The differences result from the different payout functions for the two variants of the shape game. In the information filter shape game, the maximum reward is always 20 points, but in the payout filter shape game, the maximum reward is sometimes 20 points and sometimes 10 points, depending on the payout filter. The utility-matching model assumes that choices are made in proportion to their expected scores, and because these scores differ between the two experiments, the model makes different predictions.
Comparison models
The Bayes net model predictions are shown in the fourth row of Figure 13. As the figure shows, the Bayes net model is unable to make any inferences in the payout filter shape game. This result is a direct consequence of the fact that the model does not assume any particular (e.g., goal-directed) relationship between choices and utilities. To provide some intuition for this result, imagine an M1 outcome is observed: the shape in Box 3 matches the shape in Box 1. The goal is to infer which boxes contribute to the value of the utility node, which is never observed. By assuming that choices are goal-directed, the shape in Box 3 provides some information about edges leading to the utility node because the shape in Box 3 was intentionally chosen to maximize expected utility. Namely, one might infer that Box 1 does not contribute to utility, otherwise the player would have chosen a different shape for Box 3. The Bayes net model, however, does not assume a relationship between Box 3 and utility and therefore cannot conclude anything about the edges leading to the utility node.
The logical model predictions, shown in the last row of Figure 13, are identical to the logical model predictions for Experiment 3.
Results and discussion
Participants' mean judgments are shown in the first row of Figure 13. Once again, the ratings were normalized to convert them into probabilities and the standard error bars were approximated using a statistical bootstrap with 10,000 samples. People's inferences were qualitatively similar to the inferences from Experiment 3, consistent with the utility-maximizing decision net model (r = 0.92) but not the utility-matching decision net model (r = 0.51) or the Bayes net model (r = 0). The logical model provides a better account of people's judgments (r = 0.71) than it did for Experiment 3, but not better than the utility-maximizing decision net model.
Individual differences
Once again, we tested whether the decision net approach accounted well for individuals' judgments by comparing model fits for all of the models to each participant's ratings. The results of this analysis are shown in Figure 12b. The figure shows that the majority of participants were best fit by the utility-maximizing decision net model and the remaining participants were best fit by the logical model.
The larger number of participants best fit by the logical model might be due to a key difference between the payout filter and information filter variations of the shape game. In the information filter shape game, the filter covers up the machine before the shapes are revealed. This means that for some information filters, players will not know all of the machine shapes and must make an educated guess when choosing a shape. In the payout filter game, however, all shapes are visible when the player makes a choice, even though some of the shapes may not matter for some payout filters. Nevertheless, the payout structure ensures that players always receive the maximum number of points if they pick a shape that is different from both of the machine shapes. If a player adopted this strategy, observing a round in which all three shapes are different would not provide any information about the payout filter being used because the player's behavior is consistent with any filter. As mentioned earlier, the logical model makes the exact same inference.
General discussion
We proposed that decision networks can help to understand how people reason about the choices of others. Decision nets are extensions of Bayes nets, and the critical difference between the two is that decision nets incorporate the assumption of goal-directed choice. The results of our first two experiments suggested that people make use of this assumption when reasoning about other people's choices. Experiment 1 showed that this assumption allows people to quickly adjust their predictions about other people's choices when rewards change. Experiment 2 showed that this assumption allows people to draw stronger causal inferences in situations involving observed choices. In both experiments, standard Bayes nets without a goal-directed choice assumption were unable to account for participants' judgments.
Experiments 3 and 4 showed that decision nets can account for other kinds of inferences that people can make after observing others' choices. Experiment 3 focused on inferences about what someone else knows and Experiment 4 focused on inferences about someone else's goals. In both experiments, participants' judgments exhibited two key features that were predicted by the decision net account. First, participants' judgments changed dramatically after key observations. Second, participants' judgments changed gradually in response to probabilistic information, such that participants became more certain after repeated observations. In both experiments, decision nets provided a good quantitative account of human judgments. In particular, we found that the decision net approach accounted for people's inferences better than a standard Bayes net approach, and better than an approach that relies on logical rather than probabilistic reasoning.
The value of decision networks
We believe that decision nets can make several practical and theoretical contributions to the study of human reasoning. First, just as Bayes nets have been valuable for understanding how people reason about causes and effects, decision nets are valuable for understanding how people reason about choices. Part of the value of Bayes nets as a theoretical framework is that they can be used to capture, clearly and graphically, the features of a causal reasoning problem (Gopnik & Tenenbaum, 2007). Because decision nets build on Bayes nets, they retain all of the appealing properties of Bayes nets. In addition, decision nets allow for the clear representation of goal-directed choices. Decision nets not only capture the key computational principles that appear to be central for reasoning about choices, but also provide a simple and powerful graphical language from which both computational and non-computational researchers may derive insights.
Decision nets also build on earlier lines of research in constructive ways. For example, a number of models of interpersonal attribution have emphasized how prior knowledge about other people combines with observations through probabilistic inference (Ajzen & Fishbein, 1975; Ajzen & Holmes, 1976; Medcof, 1990; Trope, 1974; Trope & Liberman, 1993). However, these models have generally considered fairly simple kinds of prior knowledge, whereas the prior knowledge that describes how behaviors and dispositions are related can be relatively complex. The models in Figure 1 illustrate this point by capturing some of the rich theory-based knowledge that supports inferences about other people's behavior. These models, however, are qualitative, and do not provide a computational account of human inference. In contrast, decision nets combine the expressive graphical language of structured causal representations with probabilistic inference.
As a result, decision nets might be used to develop formalized versions of previous ideas in the attribution literature. For example, the goal-directed choice assumption captured by the choice function in decision nets neatly captures the notion of equifinality discussed by Heider (1958, ch. 4). Equifinality describes the phenomenon whereby a goal-directed decision maker will choose different actions in different circumstances to achieve the same goal. In the decision net representation of a person's choice, the preferred action will depend on the outcomes of the various world event variables, but the goal always remains the same (e.g., to maximize utility). Using decision nets to develop formal treatments of earlier ideas can also provide new insights. For example, Jern and Kemp (2011) show how the logit model of preference learning can provide an explanation for an empirical result that an early model of attribution (Jones & Davis, 1965) could not explain (Newtson, 1974). As explained earlier in the paper, the logit model can be viewed as an instance of the decision net framework.
As discussed earlier, decision nets can be compiled into Bayes nets. It is possible to use these compiled Bayes nets to generate predictions that are identical to the predictions of our decision net models. In Experiment 1, the decision net predictions could be replicated by using two compiled Bayes nets, one before and one after the utility function changes. In Experiments 2, 3, and 4, the decision net predictions could be replicated by performing model selection over compiled Bayes net versions of the decision net models. In all cases, however, constructing the compiled Bayes nets relies on the assumption that choices are goal-directed. In other words, the compiled Bayes nets do not rely on fewer assumptions than the decision net models that they are based on. In addition, by no longer including an explicit choice function, the compiled Bayes nets hide the key principle that explains why a particular choice was made. We have argued that the assumption of goal-directed choice is essential to how people reason about choices and therefore should be explicitly represented in a computational account.
A second possible approach is to work with Bayes nets that explicitly represent beliefs and goals as parents of a choice node. The probability distribution associated with the choice node can capture the idea that someone will make choices that will likely increase his or her utility, given his or her beliefs about the situation. This approach seems adequate in some simple situations. For example, the decision net in Figure 2 can be replaced with a four-node network in which the choice variable has three parents: one that specifies beliefs about the die roll, a second that specifies beliefs about the utility function, and a third that specifies the goal of maximizing utility. In more complex situations, however, Bayes nets of this sort quickly become unwieldy. In general, the belief nodes will need to capture a complex system of beliefs about causal relationships and utility functions. For example, consider the cruise ship game used in Experiments 1 and 2. This game is still relatively simple, but the belief nodes in a Bayes net representation of the game would need to capture a system of beliefs about the causal structure of the machine, including beliefs about the direction of the causal link between Box 1 and Box 2, and beliefs about the CPT that captures how chip color depends on Box 1 and Box 2. In principle, all of these beliefs about the machine could be represented by a single belief node, but each possible value of this belief node would have to correspond to an entire Bayes net. Decision nets avoid this problem because the decision maker's beliefs can be captured by edges and CPTs in addition to values of nodes, which allows for modular representations of complex systems of belief.
Comparison of decision nets to previous Bayes net accounts
Bayes nets have previously been used to account for several kinds of inferences about choice behavior, and this line of research has been pursued most extensively by Sloman and colleagues (Hagmayer & Sloman, 2009; Sloman & Hagmayer, 2006; Sloman et al., 2012). For instance, Hagmayer and Sloman (2009) focus on how decision makers think of their own choices, but the part of their work that is most relevant to our own proposes that observers understand the choices of others by constructing Bayes net models of these choices. Hagmayer and Sloman provide an example model in which the choice node has a parent labeled “decision-making process.” Although we apgree that choices are the outcomes of decision-making processes, the Bayes net that Hagmayer and Sloman propose does not characterize these processes in detail, and additional work is needed to specify exactly what the “decision-making process” might entail. For example, the Bayes net includes a downstream node labeled “consequences,” but the Bayes net itself does not explicitly capture the idea that decisions are made in anticipation of expected consequences. In contrast, decision nets make a concrete proposal about how choices are made: choices result from using the choice function to select among the available options on the basis of their expected utilities. We believe that decision nets are not necessarily incompatible with the Bayes nets described by Hagmayer and Sloman, but are best viewed as models that flesh out some aspects of decision making that are left unspecified by these Bayes nets.
Comparison of decision nets to previous Markov decision process accounts
Earlier we argued that although decision nets and Markov decision processes (MDPs) are similar and related, they are best suited to different types of reasoning problems because they make different representational assumptions. Namely, decision nets use a feature-based representation and MDPs use a a state-based representation (Boutilier et al., 1999, 2000; Poole & Mackworth, 2010). Here we make this distinction concrete by describing how MDPs might be used to develop an account of Experiments 3 and 4.
MDPs typically represent features of the world and their relations to one another using a single world event variable. An MDP account of social reasoning might also include separate variables for a decision maker's beliefs or goals (Baker & Tenenbaum, 2014). All of these variables are time-dependent and may vary from one time step to the next. Figure 14a shows how this general approach can be applied to the knowledge inference task of Experiment 3. In this model, there is a single state node that encapsulates what shapes are present on the machine and which shapes are visible. The player's choice of shape is influenced by the current state of the world and his or her goal. After choosing a shape, the state of the world is updated to include the chosen shape and to reveal all hidden shapes. As the figure indicates, from the observer's perspective, the final state and the player's choice and goal are all known, but the initial state (i.e., which shapes were present and visible) is unknown and must be inferred. Figure 14b shows how this model can be applied to the goal inference task of Experiment 4. In this case, the state of the world is always known to the observer, as well as the player's choice, but the goal is unknown and must be inferred.
Figure 14.
MDP accounts of the reasoning tasks in (a) Experiment 3 and (b) Experiment 4.
Both MDPs and decision nets incorporate the key principles of goal-directed choice and probabilistic inference. As a result, there are versions of the MDPs in Figure 14 that make predictions identical to our decision net models of Experiments 3 and 4. However, comparing Figure 14 to the decision nets in Figures 10c and 10d helps to reveal why the feature-based representation of decision nets is preferable in cases like the ones that we have studied. In Experiment 3, inferring what a player knew neatly corresponds to an inference about the presence or absence of a knowledge edge in the decision net representation. In the MDP, however, what a player knew is “hidden” within the state node. In Experiment 4, inferring what factors the player cared about in the game neatly corresponds to an inference about which nodes have value edges leading to the utility node in the decision net. In the MDP, however, the factors the player cared about are encoded within the single goal state node.
Although we have argued that decision nets are more natural accounts of the mental state reasoning involved in our experiments, MDPs provide more natural accounts of the reasoning involved in other tasks. For example, MDPs have been successfully applied to inferences about agents' actions as they move through a state space (Baker et al., 2009, 2011; Ullman et al., 2009). Because MDPs represent sequences of actions, they are better suited than decision nets for modeling these sorts of tasks (see Table 2). For this reason, MDPs should be viewed as models that complement rather than compete with decision nets.
Making choices versus reasoning about other people's choices
The results of our experiments suggested that participants expected others to make optimal or nearly optimal choices. This result may seem surprising given the many studies that show that people often do not make optimal choices. In particular, people tend to probability match when making predictions about a probabilistic event (Vulkan, 2002). For example, in one study, when one of two events had a 67% probability and the other had a 33% probability, people tended to predict the more probable event on about 67% of trials, even though predicting the more probable event on every trial would maximize overall prediction accuracy (Neimark & Shuford, 1959).
There is a key difference, however, between our experiments and the sorts of probabilistic prediction tasks that have been used to demonstrate probability matching. In tasks that produce probability matching, one could potentially perform better on a single trial by making a suboptimal choice and predicting the less probable response. By contrast, in the shape game, there was no potential for achieving a greater reward by making a suboptimal choice. To see why, consider the shape game with information filters from Experiment 3. Suppose a player is using the filter that conceals the contents of Box 1 of the machine, but the player can see that Box 2 contains a triangle. The optimal choice in this case is a square or a circle. The least number of points one could earn by choosing one of these shapes is 10. The greatest number of points a player could earn by making a suboptimal choice (a triangle) is only 10. Therefore, there is no potential advantage to making anything other than the optimal choice on a single trial.
Because our tasks were simple enough that it was easy to determine the optimal choice on a given trial, it is likely that probability matching would not have been observed when participants were playing the shape game for themselves. Thus, participants' expectations about other players may simply have been a reflection of how they themselves would have behaved. If the games were designed to be more like the tasks typically used in the probability matching literature, participants may have expected other players to adopt more probability matching behavior just as they themselves likely would have. Future research can use the decision net framework to explore in more detail the extent to which people's own behavior aligns with their expectations about others' behavior.
Theories of theory of mind
In the Introduction, we suggested that the decision net account is related to the theory theory of conceptual structure. The theory theory has often been applied to theory of mind by suggesting that people have explicit theories of behavior that they use to predict and reason about others' behavior. An alternative approach is known as simulation theory (Goldman, 1992; Harris, 1992). Simulation theory proposes that people do not rely on explicit theories of behavior, but instead predict others' behavior by imagining how they themselves would behave under similar circumstances. The key claim of simulation theory is that people possess a behavior “module” that is normally used for choosing actions, but that can also be used to simulate the actions of others if the “inputs” to the module are adjusted to reflect the different beliefs, desires, or circumstances of others.
The decision net account hypothesizes that people create mental models of others' choices and then perform inference over these models. The account can therefore be viewed as a formal instantiation of the theory theory. It is possible, however, that simulation theory could also account for our results. In Experiment 1, participants could have predicted what choices players would make in the cruise ship game by imagining that they were playing the game themselves. In Experiments 2 through 4, participants were required to choose among different explanations for the data that they observed, and we formalized this choice using probabilistic model selection. Model selection can be achieved using a process that might be called “simulate and evaluate.” For each possible explanation (i.e., for each causal model in Experiment 2, and for each filter in Experiments 3 and 4), participants might have simulated how they would have behaved if that explanation were correct, and then evaluated how well the observed choices matched the outcomes of these simulations. In order to turn this proposal into a fully specified computational account, it would be necessary to specify how each simulation is carried out—in other words, to specify computationally how people decide which actions they would have taken under various circumstances. To our knowledge, no existing version of simulation theory achieves this level of specificity, but it may be possible to develop a simulation-based account that meets this requirement.
Toward a complete account of social reasoning
We found that decision nets accounted well for people's inferences in our experiments. Many real-world situations, however, are richer and more complex than the simple games we considered. This section considers some aspects of social reasoning that we did not address and suggests how our approach might be extended to provide a more complete account of social reasoning.
A richer concept of choice
The decision net models in this paper worked with a simple notion of choice, and treated choices as identical to observed actions. In some situations, however, it is important to treat a choice as an unobservable mental event that causes an observable action (Kushnir, 2012; Malle, 1999; Monroe & Malle, 2010). This view is consistent with the idea that it is possible to choose an action but fail to carry it out as intended. Although we did not consider this possibility, future research can explore the conceptual distinction between choices and actions using the decision net framework. For example, when specifying the decision net representation of someone's choice, the choice node can be treated as a representation of the person's private unobserved choice. A separate world event node can be used to represent the corresponding observable action, with a causal edge leading from the choice node to the action node. The CPD for the action node will then capture how closely the action is expected to align with the internal choice.
The simple games in our experiments highlight the idea that choices are shaped in part by what people know and what they value. Decision nets, however, can capture additional variables that influence people's choices. For example, several of the models in Figure 1 include an ability, or skill, variable. These variables capture the idea that people's actions are influenced not only by their intentions or desires, but also by their knowledge about their own level of ability. For example, someone playing darts may know that the area of the board worth the most points is the “triple 20,” worth 60 points, but lack the ability to reliably hit that space. As a result, the player might instead aim for the larger area worth only 20 points. A decision net can capture cases like this by including a world event node that represents ability, along with a knowledge edge leading from the ability node to the choice node.
Utility
Our experiments explored games in which choices led directly to rewards, and in which players attempted to maximize these rewards. In some settings, however, people make goal-directed choices that do not maximize direct rewards. Some choices are driven by the anticipation of future rewards. For example, someone might turn down a paying job in favor of an unpaid internship with the expectation that the internship will lead to better job opportunities in the future. Some choices involve competing utilities at different levels. For example, someone might get more direct pleasure or utility from eating cake than from eating a salad, but might still choose to eat a salad because of a higher-order weight-loss goal (see Stanovich, 2010, ch. 6). Finally, some choices are motivated by altruism. For example, a person may donate money with the goal of helping others.
Decision nets are capable of capturing cases like these. Recall that we have treated decision nets as mental models of the factors that influence another person's choice. As a result, the utility function in a decision net should incorporate any beliefs that the observer might have about the goals of the decision maker. For example, if the observer knows that the decision maker has the goal of losing weight, then the utility function can assign higher value to choices that are consistent with that goal than choices that are not. Similarly, if the observer knows that the decision maker is altruistic, then the utility function can assign high value to choices that help many others even if these choices provide no direct reward to the decision maker.
Although decision nets can accommodate many different beliefs about the utility function of the decision maker, this flexibility raises an important question for future research to pursue. When constructing a mental model of the decision maker, an observer needs to make some assumptions about the kinds of goals that the decision maker is attempting to achieve. These assumptions may later need to be revised—for example, an observer who initially believes that a decision maker is primarily motivated by direct rewards may adjust this belief upon learning that she donated a kidney to a stranger. Future research can explore the assumptions and inferences that people tend to make about the utility functions of others.
Social choices
In our experiments, participants made judgments about a single person's choices. Sometimes, however, people's choices take place in a social context (Jern & Kemp, 2014). For instance, whether Alice chooses to increase the price of her products will depend in part on how she expects her customers to respond. In general, a social situation may involve multiple choices made by different people, and these choices may in turn affect multiple people.
Several authors (Baker et al., 2008; Pynadath & Marsella, 2005; Ullman et al., 2009) have used MDPs to study these types of problems. A similar extension of decision nets called multi-agent influence diagrams2 (MAIDs) can also capture social choice problems. MAIDs have been used by artificial intelligence researchers to model the behavior of agents in competitive games (Koller & Milch, 2003; Pfeffer & Gal, 2007; Suryadi & Gmytrasiewicz, 1999), but they have not been used as psychological models of how people reason about others' choices. Just as MDPs have provided good accounts of how people reason about groups of people with social goals navigating through state spaces, future research might explore MAIDs as a framework for accounting for how people reason about social choices.
Recursive reasoning
Reasoning about social choices can become further complicated by the fact that decision makers are themselves reasoning about other people's choices in a recursive fashion. This type of situation is relatively common in competitive situations. For example, two opponents may both aim to choose strategies that the other person is unprepared for, but each person's choice of strategy will depend on the other's choice. MDP accounts of reasoning about social behavior have dealt with this issue by assuming that this recursive reasoning terminates after a finite number of steps (Baker et al., 2008; Ullman et al., 2009).
Another approach from the artificial intelligence literature is based on the idea that agents represent multiple MAIDs for a given situation and maintain uncertainty about which MAID best captures the current state of the world. This set of MAIDs can be represented hierarchically as its own network of influence diagrams (NIDs). Gal and Pfeffer (2008) show that NIDs can be used to represent recursive beliefs and that computing equilibrium solutions in such cases does not depend on an assumption of terminating recursion. Future research can explore NIDs in more detail as an account of how people reason recursively about others' choices.
Process models of social reasoning
In this paper, we focused on decision nets as an account of the computational principles that underlie social reasoning. We have not, however, provided an account of the cognitive processes that are used to carry out computations over decision nets. For example, we have not characterized the process that is used to compute the expected utility associated with each possible action. Computer scientists and engineers have developed several different algorithms for performing computations over decision nets (Jensen, Jensen, & Dittmer, 1994; Shachter, 1986; Zhang, 1998), and future work can explore whether these algorithms provide insight into cognitive processing.
Developing process models of how people perform probabilistic inference is an area of ongoing work (Griffiths, Vul, & Sanborn, 2012). A common theme in the literature is that people make inferences by sampling from probabilistic models (Fiser, Berkes, Orb´an, & Lengyel, 2010; Jern & Kemp, 2013; Shi & Griffiths, 2009). Sampling is a general-purpose algorithmic strategy that can be applied to many different probabilistic models, including the decision net models evaluated in this paper. For example, the “simulate and evaluate” approach mentioned earlier could be converted into a sampling-based process model. When applied to Experiments 3 and 4, this model would first construct decision networks corresponding to the three filters. The model would then use sampling to draw a set of possible choices for each network, and would choose the network that generated the samples that matched the observed choices most closely.
The literature on mental models (Byrne, 2002; Garnham, 1987; Johnson-Laird, 1980, 1983) is also relevant to the goal of developing a process-level decision net account. Our central claim in this paper is that people reason about other people's choices by constructing mental models of those choices. As a general principle, reasoning is likely to be difficult to the extent that multiple mental models must be maintained, and to the extent that each of these mental models is complex. Previous versions of mental model theory have used principles like these to make successful empirical predictions (Johnson-Laird, Byrne, & Schaeken, 1992; Johnson-Laird, 2006), and similar principles are likely to apply to social reasoning. For instance, previous research has shown that people are more prone to social reasoning errors when a problem includes more possible states of affairs (Birch & Bloom, 2007).
Conclusion
We presented a computational framework for reasoning about choices. We proposed that people reason about other people's choices by constructing mental models that are similar to decision nets. Decision nets use structured causal representations and incorporate two key computational principles: goal-directed choice and probabilistic inference. Decision net models can be used to make predictions and inferences about other people's choices, and we described four experiments in which decision nets provided a strong quantitative account of human inferences.
Decision nets and Bayes nets are closely related, but we have argued that decision nets are better able to support inferences about goal-directed choices. Over the past two decades, Bayes nets have been widely used by psychologists and have been especially valuable in helping to explain how people reason about causal relationships. It is possible that decision nets will turn out to be equally valuable in helping to explain how people reason about choices.
Paper highlights.
People can predict what others will choose and infer what others know and want.
Decision networks help to explain how people make inferences like these.
Decision networks extend Bayes nets by adding a notion of goal-directed choice.
In four experiments, people's inferences were best predicted by decision networks.
Acknowledgments
We thank Jessica Lee for helping to collect the data for Experiments 1 and 2. We thank David Danks for feedback on the development of this work, and Jean-Francois Bonnefon, Mark Steyvers, and two anonymous reviewers for feedback on the manuscript. This work was supported by the Pittsburgh Life Sciences Greenhouse Opportunity Fund and by NSF Grant CDI-0835797. Alan Jern was supported in part by NIMH Training Grant T32MH019983.
Footnotes
Data from Experiments 3 and 4 were presented at the 33rd Annual Conference of the Cognitive Science Society.
Decision networks are sometimes called influence diagrams.
Recall that decision nets are also sometimes called influence diagrams.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Alan Jern, Department of Humanities and Social Sciences, Rose-Hulman Institute of Technology.
Charles Kemp, Department of Psychology, Carnegie Mellon University.
References
- Ajzen I, Fishbein M. A Bayesian analysis of attribution processes. Psychological Bulletin. 1975;82(2):261–277. [Google Scholar]
- Ajzen I, Holmes WH. Uniqueness of behavioral effects in causal attribution. Journal of Personality. 1976;44(1):98–108. [Google Scholar]
- Baker CL, Goodman ND, Tenenbaum JB. Theory-based social goal inference. Proceedings of the 30th Annual Conference of the Cognitive Science Society 2008 [Google Scholar]
- Baker CL, Saxe R, Tenenbaum JB. Action understanding as inverse planning. Cognition. 2009;113:329–349. doi: 10.1016/j.cognition.2009.07.005. [DOI] [PubMed] [Google Scholar]
- Baker CL, Saxe RR, Tenenbaum JB. Bayesian theory of mind: Modeling joint belief-desire attribution. Proceedings of the 33rd Annual Conference of the Cognitive Science Society 2011 [Google Scholar]
- Baker CL, Tenenbaum JB. Modeling human plan recognition using Bayesian theory of mind. In: Sukthankar G, Goldman RP, Geib C, Pynadath D, Bui H, editors. Plan, activity and intent recognition: Theory and practice. Morgan Kaufmann; 2014. [Google Scholar]
- Bello P, Cassimatis N. Developmental accounts of theory-of-mind acquisition: Achieving clarity via computational cognitive modeling. Proceedings of the 28th Annual Meeting of the Cognitive Science Society 2006 [Google Scholar]
- Bergen L, Evans OR, Tenenbaum JB. Learning structured preferences. Proceedings of the 32nd Annual Conference of the Cognitive Science Society 2010 [Google Scholar]
- Birch SAJ, Bloom P. The curse of knowledge in reasoning about false belief. Psychological Science. 2007;18(8):382–386. doi: 10.1111/j.1467-9280.2007.01909.x. [DOI] [PubMed] [Google Scholar]
- Bonnefon JF. A theory of utility conditions: Paralogical reasoning from decision-theoretic leakage. Psychological Review. 2009;116:888–907. doi: 10.1037/a0017186. [DOI] [PubMed] [Google Scholar]
- Bonnefon JF, Sloman SA. The causal structure of utility conditionals. Cognitive Science. 2013;37(1):193–209. doi: 10.1111/cogs.12014. [DOI] [PubMed] [Google Scholar]
- Boutilier C, Dean T, Hanks S. Decision-theoretic planning: Structural assumptions and computational leverage. Journal of Artificial Intelligence Research. 1999;11:1–94. [Google Scholar]
- Boutilier C, Dearden R, Goldszmidt M. Stochastic dynamic programming with factored representations. Artificial Intelligence. 2000;121(1):49–107. [Google Scholar]
- Byrne RMJ. Mental models and counterfactual thoughts about what might have been. Trends in Cognitive Sciences. 2002;6(10):426–431. doi: 10.1016/s1364-6613(02)01974-5. [DOI] [PubMed] [Google Scholar]
- Csibra G, Gergely G. The teleological origins of mentalistic action explanations: A developmental hypothesis. Developmental Science. 1998;1(2):255–259. [Google Scholar]
- Csibra G, Gergely G. ‘Obsessed with goals’: Functions and mechanisms of teleological interpretation of actions in humans. Acta Psychologica. 2007;124:60–78. doi: 10.1016/j.actpsy.2006.09.007. [DOI] [PubMed] [Google Scholar]
- Dennett DC. The intentional stance. Cambridge, MA: MIT Press; 1987. [Google Scholar]
- Deverett B, Kemp C. Learning deterministic causal networks from observational data. Proceedings of the 34th Annual Conference of the Cognitive Science Society 2012 [Google Scholar]
- Doshi P, Qu X, Goodie A, Young D. Modeling recursive reasoning in humans using empirically informed interactive POMDPs. Proceedings of 9th International Joint Conference on Autonomous Agents and Multiagent Systems 2010 [Google Scholar]
- Fiser J, Berkes P, Orb´an G, Lengyel M. Statistically optimal perception and learning: from behavior to neural representations. Trends in Cognitive Sciences. 2010;14:119–130. doi: 10.1016/j.tics.2010.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gal Y, Pfeffer A. Networks of influence diagrams: A formalism for representing agents' beliefs and decision-making processes. Journal of Artificial Intelligence Research. 2008;33(1):109–147. [Google Scholar]
- Garnham A. Mental models as representations of discourse and text. Chichester, UK: Ellis Horwood Publishers; 1987. [Google Scholar]
- Gilbert DT. Ordinary personology. In: Gilbert DT, Fiske ST, Lindzey G, editors. The handbook of social psychology. Vol. 1. New York: Oxford University Press; 1998. [Google Scholar]
- Gilbert DT, Malone PS. The correspondence bias. Psychological Bulletin. 1995;117(1):21–38. doi: 10.1037/0033-2909.117.1.21. [DOI] [PubMed] [Google Scholar]
- Goldman AI. In defense of simulation theory. Mind & Language. 1992;7(1–2):104–119. [Google Scholar]
- Goodman ND, Baker CL, Bonawitz EB, Mansighka VK, Gopnik A, Wellman H, et al. Tenenbaum JB. Intuitive theories of mind: A rational approach to false belief. Proceedings of the 28th Annual Meeting of the Cognitive Science Society 2006 [Google Scholar]
- Goodman ND, Baker CL, Tenenbaum JB. Cause and intent: Social reasoning in causal learning. Proceedings of the 31st Annual Conference of the Cognitive Science Society 2009 [Google Scholar]
- Gopnik A, Glymour C, Sobel DM, Schulz LE, Kushnir T, Danks D. A theory of causal learning in children: Causal maps and Bayes nets. Psychological Review. 2004;111(1):3–32. doi: 10.1037/0033-295X.111.1.3. [DOI] [PubMed] [Google Scholar]
- Gopnik A, Tenenbaum JB. Bayesian networks, Bayesian learning and cognitive development. Developmental Science. 2007;10(3):281–287. doi: 10.1111/j.1467-7687.2007.00584.x. [DOI] [PubMed] [Google Scholar]
- Gopnik A, Wellman HM. Why the child's theory of mind really is a theory. Mind & Language. 1992;7(1–2):145–171. [Google Scholar]
- Gopnik A, Wellman HM. Reconstructing constructivism: Causal models, Bayesian learning mechanisms and the theory theory. Psychological Bulletin. 2012;138(6):1085–1108. doi: 10.1037/a0028044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gray R. “Markov at the bat”: A model of cognitive processing in baseball batters. Psychological Science. 2002;13(6):542–547. doi: 10.1111/1467-9280.00495. [DOI] [PubMed] [Google Scholar]
- Griffiths TL, Chater N, Kemp C, Perfors A, Tenenbaum JB. Probabilistic models of cognition: Exploring representations and inductive biases. Trends in Cognitive Sciences. 2010;14(8):357–364. doi: 10.1016/j.tics.2010.05.004. [DOI] [PubMed] [Google Scholar]
- Griffiths TL, Tenenbaum JB. Structure and strength in causal induction. Cognitive Psychology. 2005;51:354–384. doi: 10.1016/j.cogpsych.2005.05.004. [DOI] [PubMed] [Google Scholar]
- Griffiths TL, Vul E, Sanborn AN. Bridging levels of analysis for probabilistic models of cognition. Current Directions in Psychological Science. 2012;21(4):263–268. [Google Scholar]
- Hagmayer Y, Osman M. From colliding billiard balls to colluding desperate housewives: Causal Bayes nets as rational models of everyday reasoning. Synthese. 2012;189:17–28. [Google Scholar]
- Hagmayer Y, Sloman SA. Decision makers conceive of their choices as interventions. Journal of Experimental Psychology: General. 2009;138(1):22–38. doi: 10.1037/a0014585. [DOI] [PubMed] [Google Scholar]
- Harris PL. From simulation to folk psychology: The case for development. Mind & Language. 1992;7(1–2):120–144. [Google Scholar]
- Heckerman D, Geiger D, Chickering DM. Learning Bayesian networks: The combination of knowledge and statistical data. Machine Learning. 1995;20:197–243. [Google Scholar]
- Hedden T, Zhang J. What do you think I think you think?: Strategic reasoning in matrix games. Cognition. 2002;85:1–36. doi: 10.1016/s0010-0277(02)00054-9. [DOI] [PubMed] [Google Scholar]
- Heider F. The psychology of interpersonal relations. Hillsdale, NJ: Lawrence Erlbaum Associates, Inc; 1958. [Google Scholar]
- Howard RA, Matheson JE. Influence diagrams. Decision Analysis. 2005;2(3):127–143. [Google Scholar]
- Jara-Ettinger J, Baker CL, Tenenbaum JB. Learning what is where from social observations. Proceedings of the 34th Annual Conference of the Cognitive Science Society 2012 [Google Scholar]
- Jensen F, Jensen FV, Dittmer SL. Proceedings of the 10th International Conference on Uncertainty in Artificial Intelligence. San Francisco, CA: Morgan Kaufmann Publishers Inc; 1994. From influence diagrams to junction trees; pp. 367–373. [Google Scholar]
- Jern A, Kemp C. Decision factors that support preference learning. Proceedings of the 33rd Annual Conference of the Cognitive Science Society 2011 [Google Scholar]
- Jern A, Kemp C. A probabilistic account of exemplar and category generation. Cognitive Psychology. 2013;66(1):85–125. doi: 10.1016/j.cogpsych.2012.09.003. [DOI] [PubMed] [Google Scholar]
- Jern A, Kemp C. Reasoning about social choices and social relationships. Proceedings of the 36th Annual Conference of the Cognitive Science Society 2014 [Google Scholar]
- Jern A, Lucas CG, Kemp C. Evaluating the inverse decision-making approach to preference learning. Advances in Neural Information Processing Systems. 2011;24 [Google Scholar]
- Johnson-Laird PN. Mental models in cognitive science. Cognitive Science. 1980;4:71–115. [Google Scholar]
- Johnson-Laird PN. Mental models: Towards a cognitive science of language, inference, and consciousness. Cambridge, MA: Harvard University Press; 1983. [Google Scholar]
- Johnson-Laird PN. How we reason. New York, NY: Oxford University Press; 2006. [Google Scholar]
- Johnson-Laird PN, Byrne RMJ, Schaeken W. Propositional reasoning by model. Psychological Review. 1992;99(3):418–439. doi: 10.1037/0033-295x.99.3.418. [DOI] [PubMed] [Google Scholar]
- Jones EE, Davis KE. From acts to dispositions: The attribution process in person perception. In: Berkowitz L, editor. Advances in experimental social psychology. Vol. 2. New York: Academic Press; 1965. [Google Scholar]
- Kintsch W, Morris CJ. Application of a Markov model to free recall and recognition. Journal of Experimental Psychology. 1965;69(2):200–206. doi: 10.1037/h0021588. [DOI] [PubMed] [Google Scholar]
- Koller D, Friedman N. Probabilistic graphical models: Principles and techniques. Cambridge, MA: MIT Press; 2009. [Google Scholar]
- Koller D, Milch B. Multi-agent influence diagrams for representing and solving games. Games and Economic Behavior. 2003;45(1):181–221. [Google Scholar]
- Körding KP, Tenenbaum JB, Shadmehr R. The dynamics of memory as a consequence of optimal adaptation to a changing body. Nature Neuroscience. 2007;10(6):779–786. doi: 10.1038/nn1901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kushnir T. Developing a concept of choice. In: Liben LS, Bigler RS, editors. Advances in child development and behavior. Vol. 43. Elsevier Inc; 2012. pp. 193–218. [DOI] [PubMed] [Google Scholar]
- Lucas CG, Griffiths TL, Xu F, Fawcett C, Gopnik A, Kushnir T, et al. Hu J. The child as econometrician: A rational model of preference understanding in children. PLoS ONE. 2014;9(3):e92160. doi: 10.1371/journal.pone.0092160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malle BF. How people explain behavior: A new theoretical framework. Personality and Social Psychology Review. 1999;3(1):23–48. doi: 10.1207/s15327957pspr0301_2. [DOI] [PubMed] [Google Scholar]
- Malle BF. How the mind explains behavior: Folk explanations, meaning, and social interaction. Cambridge, MA: MIT Press; 2004. [Google Scholar]
- Malle BF, Knobe J. The folk concept of intentionality. Journal of Experimental Social Psychology. 1997;33:101–121. [Google Scholar]
- Medcof JW. PEAT: An integrative model of attribution processes. In: Zanna MP, editor. Advances in experimental social psychology. Vol. 23. New York, NY: Academic Press; 1990. pp. 111–210. [Google Scholar]
- Monroe AE, Malle BF. From uncaused will to conscious choice: The need to study, not speculate about, people's folk concept of free will. Review of Philosophy and Psychology. 2010;1:211–224. [Google Scholar]
- Neimark ED, Shuford EH. Comparison of predictions and estimates in a probability learning situation. Journal of Experimental Psychology. 1959;57:294–298. doi: 10.1037/h0043064. [DOI] [PubMed] [Google Scholar]
- Newtson D. Dispositional inference from effects of actions: Effects chosen and effects forgone. Journal of Experimental Social Psychology. 1974;10:489–496. [Google Scholar]
- Oztop E, Wolpert D, Kawato M. Mental state inference using visual control parameters. Cognitive Brain Research. 2005;22:129–151. doi: 10.1016/j.cogbrainres.2004.08.004. [DOI] [PubMed] [Google Scholar]
- Pantelis PC, Baker CL, Cholewiak SA, Sanik K, Weinstein A, Wu CC, et al. Feldman J. Inferring the intentional states of autonomous virtual agents. Cognition. 2014;130:360–379. doi: 10.1016/j.cognition.2013.11.011. [DOI] [PubMed] [Google Scholar]
- Pearl J. Causality: models, reasoning, and inference. New York, NY: Cambridge University Press; 2000. [Google Scholar]
- Pfeffer A, Gal Y. On the reasoning patterns of agents in games. Proceedings of the 22nd AAAI Conference on Artificial Intelligence 2007 [Google Scholar]
- Poole DL, Mackworth AK. Artificial intelligence: Foundations of computational agents. New York, NY: Cambridge University Press; 2010. [Google Scholar]
- Pynadath DV, Marsella SC. PsychSim: Modeling theory of mind with decision-theoretic agents. Proceedings of the 19th International Joint Conference on Artificial Intelligence 2005 [Google Scholar]
- Rehder B, Kim S. How causal knowledge affects classification: A generative theory of categorization. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2006;34:3–16. doi: 10.1037/0278-7393.32.4.659. [DOI] [PubMed] [Google Scholar]
- Ross L. The intuitive psychologist and his shortcomings: Distortions in the attribution process. In: Berkowitz L, editor. Advances in experimental social psychology. Vol. 10. Orlando, FL: Academic Press; 1977. pp. 173–220. [Google Scholar]
- Rottman BM, Keil FC. Causal structure learning over time: Observations and interventions. Cognitive Psychology. 2012;64:93–125. doi: 10.1016/j.cogpsych.2011.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell SJ, Norvig P. Artificial intelligence: A modern approach. Upper Saddle River, NJ: Prentice Hall; 2010. [Google Scholar]
- Shachter RD. Evaluating influence diagrams. Operations Research. 1986;34(6):871–882. [Google Scholar]
- Shafto P, Goodman ND, Frank MC. Learning from others: The consequences of psychological reasoning for human learning. Perspectives on Psychological Science. 2012;7(4):341–351. doi: 10.1177/1745691612448481. [DOI] [PubMed] [Google Scholar]
- Shannon CE. A mathematical theory of communication. The Bell System Technical Journal. 1948;27(3):379–423. [Google Scholar]
- Shi L, Griffiths TL. Neural implementation of Bayesian inference by importance sampling. Proceedings of Neural Information Processing Systems. 2009;22 [Google Scholar]
- Shultz TR. Assessing intention: A computational model. In: Astington JW, Harris PL, Olson DR, editors. Developing theories of mind. New York: Cambridge University Press; 1988. [Google Scholar]
- Sloman SA. Causal models: How people think about the world and its alternatives. New York, NY: Oxford University Press; 2005. [Google Scholar]
- Sloman SA, Fernbach PM, Ewing S. A causal model of intentionality judgment. Mind & Language. 2012;27(2):154–180. [Google Scholar]
- Sloman SA, Hagmayer Y. The causal psycho-logic of choice. Trends in Cognitive Sciences. 2006;10(9):407–412. doi: 10.1016/j.tics.2006.07.001. [DOI] [PubMed] [Google Scholar]
- Stanovich KE. Decision making and rationality in the modern world. New York: Oxford University Press; 2010. [Google Scholar]
- Steyvers M, Tenenbaum JB, Wagenmakers EJ, Blum B. Inferring causal networks from observations and interventions. Cognitive Science. 2003;27:453–489. [Google Scholar]
- Suryadi D, Gmytrasiewicz PJ. Learning models of other agents using influence diagrams. Proceedings of the 7th International Conference on User Modeling 1999 [Google Scholar]
- Tauber S, Steyvers M. Using inverse planning and theory of mind for social goal inference. Proceedings of the 33rd Annual Conference of the Cognitive Science Society 2011 [Google Scholar]
- Tenenbaum JB, Kemp C, Griffiths TL, Goodman ND. How to grow a mind: Statistics, structure and abstraction. Science. 2011;331(6022):1279–1285. doi: 10.1126/science.1192788. [DOI] [PubMed] [Google Scholar]
- Trope Y. Inferential processes in the forced compliance situation: A Bayesian analysis. Journal of Experimental Social Psychology. 1974;10:1–16. [Google Scholar]
- Trope Y, Liberman A. The use of trait conceptions to identify other people's behavior and to draw inferences about their personalities. Personality and Social Psychology Bulletin. 1993;19(5):553–562. [Google Scholar]
- Ullman TD, Baker CL, Macindoe O, Evans O, Goodman ND, Tenenbaum JB. Help or hinder: Bayesian models of social goal inference. Advances in Neural Information Processing Systems. 2009;22 [Google Scholar]
- Van Overwalle F. Infants' teleological and belief inference: A recurrent connectionist approach to their minimal representational and computational requirements. NeuroImage. 2010;52:1095–1108. doi: 10.1016/j.neuroimage.2010.05.028. [DOI] [PubMed] [Google Scholar]
- Vulkan N. An economist's perspective on probability matching. Journal of Economic Surveys. 2002;14(1):101–118. [Google Scholar]
- Wahl S, Spada H. Children's reasoning about intentions, beliefs, and behaviour. Cognitive Science Quarterly. 2000;1:5–34. [Google Scholar]
- Wellman HM, Bartsch K. Young children's reasoning about beliefs. Cognition. 1988;30(3):239–277. doi: 10.1016/0010-0277(88)90021-2. [DOI] [PubMed] [Google Scholar]
- Wellman HM, Gelman SA. Cognitive development: Foundational theories of core domains. Annual Review of Psychology. 1992;43:337–375. doi: 10.1146/annurev.ps.43.020192.002005. [DOI] [PubMed] [Google Scholar]
- Wolpert DM, Ghahramani Z, Jordan MI. An internal model for sensorimotor integration. Science. 1995;269(5232):1880–1882. doi: 10.1126/science.7569931. [DOI] [PubMed] [Google Scholar]
- Zhang NL. Probabilistic inference in inuence diagrams. Computational Intelligence. 1998;14(4):475–497. [Google Scholar]