Abstract
Cognitive control allows us to follow abstract rules in order to choose appropriate responses given our desired outcomes. Cognitive control is often conceptualized as a hierarchical decision process, wherein decisions made at higher, more abstract levels of control asymmetrically influence lower-level decisions. These influences could evolve sequentially across multiple levels of a hierarchical decision, consistent with much prior evidence for central bottlenecks and seriality in decision-making processes. However, here, we show that multiple levels of hierarchical cognitive control are processed primarily in parallel. Human participants selected responses to stimuli using a complex, multiply contingent (third order) rule structure. A response deadline procedure allowed assessment of the accuracy and timing of decisions made at each level of the hierarchy. In contrast to a serial decision process, error rates across levels of the decision mostly declined simultaneously and at identical rates, with only a slight tendency to complete the highest level decision first. Simulations with a biologically plausible neural network model demonstrate how such parallel processing could emerge from a previously developed hierarchically nested frontostriatal architecture. Our results support a parallel processing model of cognitive control, in which uncertainty on multiple levels of a decision is reduced simultaneously.
Keywords: serial vs. parallel, executive function, computational model, prefrontal cortex, basal ganglia
1. Introduction
In complex environments, adaptive behavior can involve rule-like dependencies on numerous conditions. Behavior in such domains relies on a capacity known as cognitive control – i.e., the use of knowledge, perception, and goals to guide action selection (Badre & Wagner, 2004; Bunge, 2004; Miller & Cohen, 2001; O'Reilly & Frank, 2006). Cognitive control is often conceptualized as having a hierarchical architecture, such that the way that contexts are interpreted in order to select a specific action can be contingent on more abstract, superordinate policies or goals (e.g., Badre & D'Esposito, 2007; Koechlin, Ody, & Kouneiher, 2003).
The game of chess provides a colloquial example of this hierarchical dynamic. Moving a chess piece involves a decision that is, at its simplest level, a motor process that displaces an object. However, the choice of move also derives from more abstract considerations, such as the rules of the game, the state of the board, the player's prior experiences, and a prevailing strategy. Similar hierarchical abstractions likely constrain many real world behaviors.
Traditionally, action selection on the basis of rules has been conceptualized as just such a hierarchical, multi-step process, with early perceptual stages giving way to a stimulus-to-response (S-R) mapping stage, which then determines the final motor action that is executed in a terminal response stage (Biederman, 1972; Braverman, Berger, & Meiran, 2014; Rubinstein, Meyer, & Evans, 2001). The traversal of more abstract rules (rules that select other rules) would presumably transpire during the S-R stage of this classical single-channel model. However it remains unknown whether the addition of these higher-order contingencies results in the addition of new S-R stages (with new bottlenecks), corresponding to each rule, or rather is accomplished in parallel within a single S-R mapping stage.
In the laboratory, hierarchical control is often studied using rules with multiple levels of contingency. Decision trees, in which some rules are contingent on others, create multiple orders of policy abstraction. Policy is the mapping between a state, an action, and an anticipated outcome, and policy abstraction is the extent to which a rule determines an action. A rule that maps a stimulus directly to a response is a first-order policy (e.g. if the shape is a square, press 1). A second-order policy is a more abstract rule that maps a stimulus to a first-order rule (e.g. if the color is red, use the shape rules), and so forth.
In recent years, cognitive neuroscience has leveraged this logic to provide new insights into the processing architecture that might support hierarchical decisions. Most notably, there has been evidence that the functional organization of frontal cortex may support hierarchical control by allowing a physical separation between decisions at each level of contingency, as a function of rule abstraction. A range of studies suggests that frontal cortical areas that are more rostral process the most abstract aspects of decision-making (Badre & D'Esposito, 2007; Badre, Hoffman, Cooney, & D'Esposito, 2009; Christoff & Gabrieli, 2000; Christoff, Keramatian, Gordon, Smith, & Mädler, 2009; Koechlin et al., 2003; Koechlin & Summerfield, 2007; O'Reilly, Noelle, Braver, & Cohen, 2002).
These data have been cited in support of models of hierarchical cognitive control wherein multi-level rules are executed via spatially separate but interacting neural circuits. For example, the cascade model of Koechlin et al. (2003) conceptualizes hierarchical control as emerging from a series of uncertainty-reducing steps progressing from rostral to caudal frontal cortex. Though these steps do not map directly onto different levels of contingency, uncertainty reduction is serial from rostral to caudal frontal cortex. Evidence of this priority of processing was supported by directional interactions from front to back within frontal cortex, as estimated through fMRI effective connectivity analysis.
A separate model from Frank and Badre (2012) conceptualizes hierarchical control as arising from multiple interacting frontostriatal loops. In this model, separate frontal areas support different levels of a decision, with striatally-mediated “gates” acting as the interface for this communication (Badre & Frank, 2012; Collins & Frank, 2013; Frank & Badre, 2012; see also Kriete, Noelle, Cohen, & O'Reilly, 2013). Information related to higher-level decisions is maintained in rostral frontal cortex, and it influences more caudal sectors of prefrontal cortex via corticostriatal interactions. This allows for a gating dynamic by which more caudal areas of frontal cortex can be selectively modulated given the more abstract constraints represented rostrally.
Importantly, however, models like the ones noted above raise new questions about the temporal dynamics of hierarchical decision-making that have received comparatively scant attention. In particular, it is unclear whether the physical separation of circuits processing different levels of abstraction also requires serial decision-making during hierarchical control. That is, it is unknown whether lower-level decisions start only when higher-level decisions have completed (a serial model), or whether different levels of the decision are processed simultaneously, with higher levels continuously constraining lower levels (a parallel model).
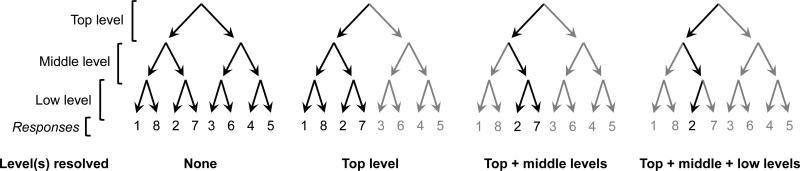
Both systems could be adaptive. Given a large enough capacity, parallel processing can result in time savings, as progress is made on all decisions simultaneously. However, in such a system, energy may be inefficiently spent making decisions about features that will ultimately prove irrelevant to response selection. Alternatively, a serial model may be less time-efficient and more energy-efficient: as decisions at higher levels are made, the number of decisions that must be considered at lower levels is systematically reduced (Figure 1). Thus, decisions among higher-level processors reduce demands on capacity-limited lower-level processors, an adaptive feature of hierarchical architectures.
Figure 1. Serial reduction of uncertainty.
When each level of a hierarchical decision is resolved, it reduces uncertainty on all lower levels. In the three-level binary decision tree shown, solving a level reduces the number of relevant items on all lower levels by half. Potentially relevant paths are shown in black for each stage of the serial decision, while irrelevant paths are gray.
Though the parallel versus serial nature of choice during multiply contingent hierarchical rules has not been investigated systematically, evidence for at least some degree of seriality comes from the rich literature on the “central processing bottleneck” during response selection (Dux, Ivanoff, Asplund, & Marois, 2006; Gottsdanker & Stelmach, 1971; Levy, Pashler, & Boer, 2006; Pashler, 1994; Welford, 1952). These studies have suggested that processing of stimulus-response mappings is highly capacity limited and must occur one at a time, enforcing serial processing when multiple such mappings must be processed (though see Meyer and Kieras, 1997).
However, many of the paradigms that support these inferences (including the psychological refractory period paradigm) involve asynchronous presentation of stimuli and two independent tasks. This is in contrast to the multiple levels of contingency required by hierarchical control problems, wherein decisions are interdependent on one another in a ranked way. This aspect of prior work raises the possibility that more parallel cognitive processing might be observed when the structure of the task better affords it: for example, when stimuli are presented simultaneously and pertain to the same rule structure. Indeed, Schumacher et al. (2001) demonstrated that the psychological refractory period disappears when the two independent tasks are presented simultaneously.
The study of task switching – when cues are used to select between two or more stimulus dimensions and associated rule sets for behavior – has provided evidence that people can process decisions at “task” (usually 2nd order) and “response” (1st order) levels separately. For example, evidence of advance preparation effects (e.g., endogenous versus exogenous switch costs; Rogers & Monsell, 1995; Monsell, 2003; De Jong, 2000) and within-trial preparation effects (Braverman & Meiran, 2010; Goldfarb & Henik, 2007) indicate that people can make task-level decisions separately in time from response-level decisions. Similarly, there is evidence for putatively higher order switching effects that are behaviorally separable from a local task-level switch, such as with mixing costs (Mayr, 2001) and task sequence-level costs (Schneider & Logan, 2006). Moreover, the study of multi-level switching has shown asymmetries wherein behavior costs incurred by higher order switches are inherited by lower order decisions but not vice versa (Kleinsorge & Heuer, 1999). This type of asymmetry is consistent with the hypothesis that participants represent the task as a hierarchical structure. Thus, the study of task switching provides evidence consistent with the hypothesis that people structure tasks in terms of separate multi-level decisions and can order them as hierarchical structures.
Nevertheless, these studies have provided few insights into the temporal dynamics of these decisions. The observation of preparation effects might be suggestive of serial processing, but most studies that demonstrate these effects do so in tasks where cues and other stimulus elements are themselves presented serially. As such, these studies leave open whether people would separate these decision stages in time when they have the opportunity to process everything in parallel.
Neuroscience data have similarly contributed little to the question of temporal dynamics during hierarchical control. However, a recent EEG study supported a serial model of decision-making (Braverman et al., 2014). The authors manipulated task conflict (an S-R stage manipulation) and response conflict (a response stage manipulation) independently in their paradigm, which involved simultaneous presentation of all aspects of the stimulus. Examining the timing of ERPs for high-conflict vs. low-conflict trials, they found that the task conflict effect was evident significantly earlier than the response conflict effect. They suggested that this showed that the task-processing, i.e. the S-R stage, was temporally distinct from the response stage. However, these results did not reveal temporal patterns within the S-R phase. In other words, they did not address how a complex hierarchical rule structure with multiple contingencies is traversed.
The present study seeks to test the hypothesis that decisions required by multiply contingent rules are processed serially. Specifically, we used a hierarchical decision task that requires traversal of a three-level decision tree to make a response. A response deadline procedure was used that allowed us to assess the accuracy and timing of decisions made at each level of abstraction independently from the other levels. This approach provides conjoint measures of the accuracy and speed of processing. It has been used effectively to estimate the time course by which information becomes available to response systems for a wide range of cognitive processes (Benjamin & Bjork, 2000; Hintzman & Curran, 1994; McElree & Dosher, 1989; Öztekin, Güngör, & Badre, 2012; Öztekin & McElree, 2007, 2010; Wickelgren, Corbett, & Dosher, 1980). In the present task, information pertaining to all levels of the hierarchical decision was presented simultaneously, and the task was designed such that parallel and serial processing would produce distinct trajectories of error rates across sampled deadlines.
Our results are inconsistent with strong serial processing hypothesis, providing evidence of primarily parallel processing within the S-R stage in complex, hierarchical decision-making. We also demonstrate that a previously developed model of response selection that has an underlying hierarchical architecture with physically separated corticostriatal decision-making circuits can explain the sources of the temporal dynamics evident in our behavioral results. These empirical and computational analyses converge to suggest that hierarchical decision-making within the S-R stage can be processed in a parallel manner.
2. Experiment 1 – Behavioral Task
2.1 Methods
2.1.1 Participants
Twenty-three participants (mean 22.1 years, range 18-28, 12 female) were recruited from the Providence, RI area to participate in a behavioral task performed on a computer. All participants were right-handed, had normal or corrected-to-normal vision, and reported that they were free of neurological or psychiatric disorders. They had all completed at least 12 years of education. Data from an additional eightparticipants were excluded for reasons of poor accuracy (<65%) at long intervals during the practice or experimental phase. An additional participant was excluded for failing to comply with task instructions: they responded to fewer than half of the experimental trials. Informed consent was obtained from all participants, and they received payment for their time.
2.1.2 Task design
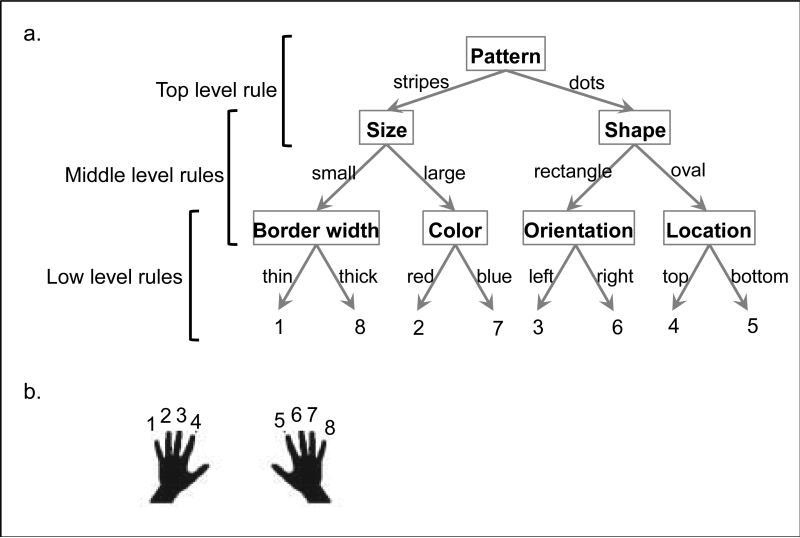
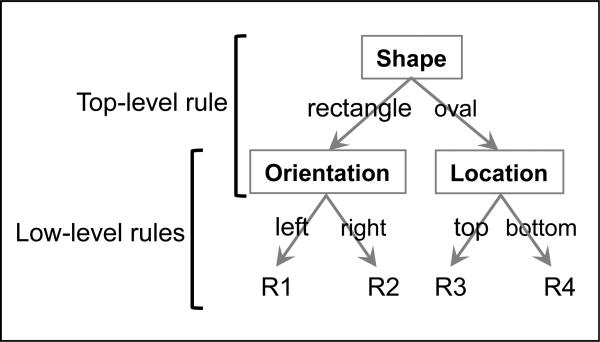
The basic task involved response selection based on a complex set of rules. On each trial, participants pressed one of eight buttons in response to a stimulus that varied trial-to-trial along seven independent dimensions (shape, pattern, location, orientation, color, border width, and size). Each dimension was binary (e.g. the color was either red or blue). To select a response, participants were trained to use a hierarchically structured, third-order set of rules that mapped combinations of features to each button (Figure 2). The experiment was divided into three parts: a rule-learning phase, a response deadline practice phase, and the experimental phase.
Figure 2. Experimental task.
(a) The experiment involved a stimulus-response task with rules that were structured hierarchically. The three levels of hierarchy are labeled in this figure (top, middle, and low). The stimuli for the task had seven dimensions, named in boxes. Each dimension had two variants (e.g. stripes and patterns), which either indicated which lower-level dimension was relevant, or mapped directly to a response. The responses are numbered 1-8 at the bottom of the tree and correspond to buttons pressed using the fingers shown in (b).
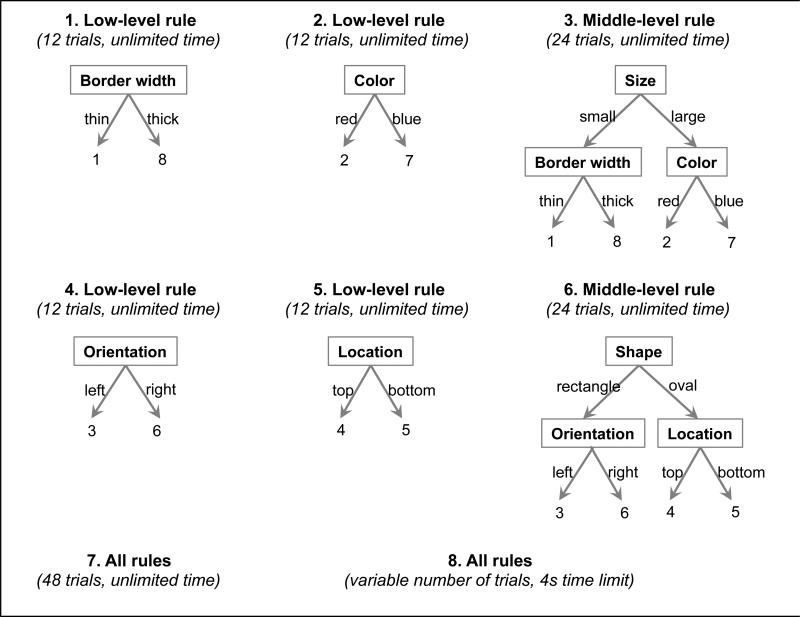
2.1.2.1 Rule-learning phase
In the first phase, participants learned and practiced the hierarchical rules they would use to make a response, with auditory feedback after each trial. All participants were taught the rules in the same order (Figure 3). Comparing error rates for each of the low- and middle-level rules did not reveal any significant effects due to the order of rule learning (see Appendix A).
Figure 3. Order of rule learning.
Participants learned and practiced the rule set incrementally and in a prescribed order.
Participants first learned two of the low-level rules, practicing each rule on its own for 12 trials. Next, they were taught the middle-level rule that combined those two low-level rules, with 24 practice trials. Then they learned the other two low-level rules and the middle-level rule that combined them in the same way. Finally, participants were taught the top-level rule that combined all of the other rules. At this point, in addition to verbal instructions, the experimenter showed the participant a visual representation of the rules (similar to Figure 2a). The participant practiced using all of the rules for a minimum of 48 trials, repeating this practice block as needed (mean number of trials=75.1, SD=35.0). The block was repeated until participants reached at least 65% accuracy in the second half of the block (mean=87.5%, SD=8.8%), and they reported that they felt comfortable continuing. Then they practiced responding to a stimulus within a 4-second deadline. They practiced this for at least 24 trials until they successfully responded to at least two thirds of the trials, with additional practice as needed (mean number of trials=32.3, SD=11.7).
2.1.2.2 Response deadline practice phase
Participants then proceeded to the response deadline practice phase. On every trial, a stimulus appeared, and then a tone was played when the deadline for that trial was reached. Participants were instructed to make a response as soon as possible after the deadline, even if they were unsure of the correct answer. They were encouraged to respond on every trial, even if they felt they were guessing randomly. There was no auditory feedback in this phase.
Deadlines were drawn from a discrete set with a range from 50ms to 3500ms, with most of the deadlines less than 2000ms. The set of deadlines was adjusted several times throughout data collection (Appendix B). Deadlines were adjusted in an effort to gain as many observations as possible. In particular, we wanted most of the trials to occur before participants had completed the decision. Analysis of preliminary results suggested that many responses were occurring after error rates had reached an asymptote, and we adjusted the set of deadlines accordingly. Deadline presentation was randomized.
Participants were informed that trials must meet the following criteria in order to be included in analysis: (a) there must be a button press, (b) the response must come after the trial's tone, and (c) the time between the tone and the response (“response delay”) must be less than 600ms. Participants practiced using the rules with the new timing. A screen displayed the latency between the response cue and the response after each trial. At the end of every block (64 trials), there was a summary of the participant's performance in that section, consisting of their mean response delay and the number of “no response” trials. This phase of the experiment was stopped when participants were responding promptly to approximately 80% of the trials, and when they indicated that they were comfortable with the procedure. Participants completed one to three blocks of the response deadline practice phase (mean number of trials=114.8, SD=29.8).
2.1.2.3 Experimental phase
Finally, participants began the experimental phase of the task. This phase was nearly identical to the response deadline practice phase, except that participants were not informed of their response delay after every trial. All participants completed at least six blocks of task (384 trials). A subset of 17 participants performed an additional two blocks for a total of 512 trials. Trials were added to the paradigm partway through data collection because we felt that participants could continue the experiment without losing focus.
Following the task, participants completed a post-task questionnaire that asked them to produce as many of the rules as they could remember and rate their attention and performance during the task.
2.1.3 Apparatus
All experimental scripts were programmed and run on a Macintosh computer using MATLAB with the Psychophysics Toolbox (www.psychtoolbox.org). Participants responded to each stimulus by pressing one of eight keys on a keyboard. The keys used were in the “home row” of the keyboard, with index fingers positioned on the “f” and “j” keys. The response keys were labeled 1 through 8. Participants were instructed to have all of their fingertips touching the keys at all times. Auditory feedback was presented through the built-in computer speakers.
2.1.4 Data trimming and preprocessing
Following conventional response deadline procedures, trials were excluded from analysis if (a) there was no response, (b) the response occurred before the response deadline, or (c) the response came more than 600ms after the deadline. In addition, 10 trials were excluded across all participants because of a technical error. On average, participants met the criteria in 82.4% (SD=11.4%) of their trials, or 396 trials per participant (SD=75).
2.1.5 Error rate calculations
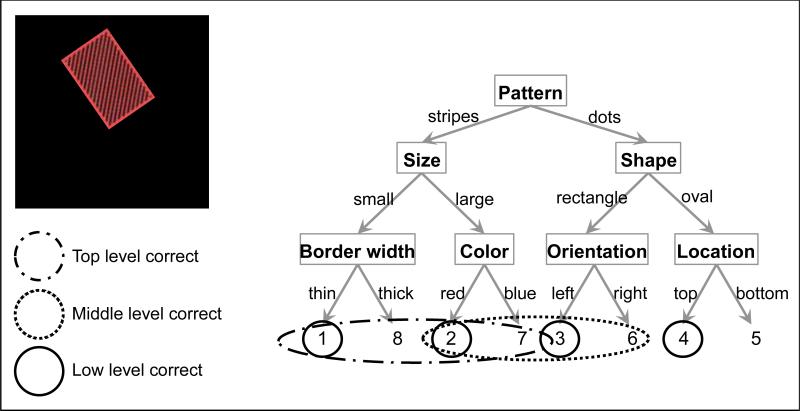
Trials were binned by the time of the response deadline, and error rates for each level of the hierarchy were calculated within each bin. For any given stimulus, each specific combination of correct and incorrect decisions on the three levels of the rule structure would result in a unique button press (Figure 4). Thus, each response was classified as being independently correct or incorrect for each of the three levels. Error rates were calculated as the proportion of the trials in which the response violated the feature(s) for a single level of the hierarchy. This allows for one response to be classified as an error on multiple levels of the hierarchy. For example, consider a response that was correct given the top-level feature, but incorrect given the middle-level feature and incorrect given the low-level feature (e.g. response “8” in Figure 4). This response would be considered both a middle-level error and a low-level error. Defining errors as such equates the level of chance for all levels of the hierarchy – given random responding, a participant would be likely to make each error type 50% of the time (though the level of chance for overall accuracy would be 12.5%).
Figure 4.
Each level of the decision, examined independently from the others, reduces the number of responses that are potentially correct (from eight to four). In this figure, the responses that are consistent with each level of the hierarchy are circled (for the example stimulus, pictured on a black background). Only one of the eight responses is consistent with all three levels of the rule set (button 2): this is the correct response.
2.1.6 Statistical modeling
To characterize the temporal dynamics of decision-making in this task, three parameters were estimated for each level of the decision tree based on the error rates at each time bin. The first parameter, start, was defined as the point in time at which participants first began responding in a manner that was consistent with an ascent from chance performance in applying a particular rule. Three such “start” parameters were estimated, one for each level of the rule hierarchy (top, middle, and low). Thus, start-top was an estimate of the earliest time at which participants were more likely to press one of the four buttons that would be consistent with the top-level feature of the stimulus than any of the four buttons that were inconsistent with it. Similarly, start-middle was an estimate of the earliest time at which participants were more likely to press one of the buttons consistent with the middle-level features of the stimulus than one of the buttons that would violate the middle-level rules. Finally, start-low was an estimate of the earliest time at which participants were more likely to press the buttons that matched the low-level features than the buttons that did not.
The second parameter, asymptote, was an estimate of the asymptotic probability that a participant would make an error for a given level of the hierarchy. This parameter was based on the assumption that at some point during the trial, presumably when participants finish making the decision, the error rates should stabilize at some (possibly non-zero) value. The asymptote parameter thus allowed for the likely possibility that participants would make mistakes even without the response deadline procedure. Three such parameters were estimated, one for each level of the rule hierarchy. Asymptote-top was the asymptotic error rate for the top-level rule, asymptote-middle was the asymptotic error rate for the two middle-level rules, and asymptote-low was the asymptotic error rate for the four low-level rules.
The third parameter, end, was the time at which the error rate reached the asymptote. Like the other types of parameters, three end parameters were estimated. Endtop was the time when asymptote-top was reached, end-middle was the time when asymptote-middle was reached, and end-low was the time when asymptote-low was reached.
A hierarchical Bayesian model was established using the three parameters to calculate the error rate on a single level of the hierarchy at time t:
| (1) |
Parameters were estimated using a Markov chain Monte Carlo simulation with Gibbs sampling. The analysis script was written and run in R64 (version 2.15.1) communicating with the program JAGS (Just Another Gibbs Sampler, version 3.1.0). The model was hierarchical: distributions of the parameters were estimated for the entire group of participants, assuming a normal distribution. Individual participant parameters were drawn from these distributions.
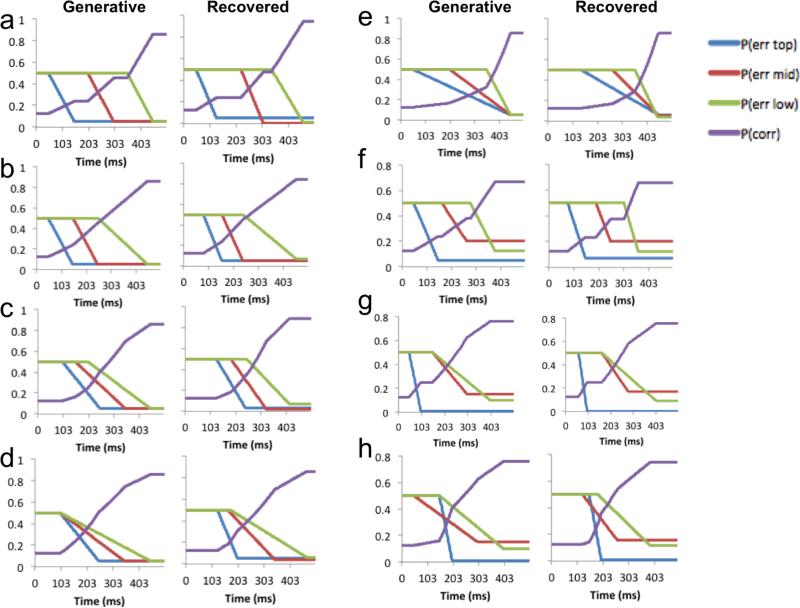
A large range of simulations of our model, using different underlying decision dynamics, revealed that it is capable of recovering the parameters of interest and distinguishing between a parallel and serial decision process. Simulation analyses are detailed in Appendix C.
For any given stimulus, each specific combination of correct and incorrect decisions on the three levels of the rule structure would result in a unique button press. Responses were thus classified into one of eight categories according to their accuracy on all levels of the rule structure. The parameters were estimated using the reaction time and this classification of the response. Estimation was conducted on included trials from all 23 subjects.
The probability that a participant would make an error on each of the levels of the rule structure was assumed to decline linearly between the start and the end times, decreasing from chance level (50%) to the asymptote. We tested several variations on this model. In one such variant, uncertainty declined according to a sigmoidal rather than linear function. In another variant, the start for any given level was constrained to be later than start for any of the higher levels (i.e., start-top < start-middle < start-low). A “robust” version of this model was also tested, using group parameters sampled from t-distributions, rather than normal distributions. Another model allowed for the possibility of two different “modes” of decision-making within a trial, with hysteresis between them (as in Dutilh, Wagenmakers, Visser, & van derMaas, 2011). In the first part of the trial, the fast guess mode, responses would be made randomly (i.e. all error rates would be at chance). Then, there would be a transition to stimulus-controlled responses, with a period of hysteresis, such that in the transition, uncertainty could instantaneously decrease from chance (to some lower but variable value). Results from these alternative models were qualitatively identical to the results of the simpler model reported here and so are not discussed further.
2.2 Results
2.2.1 Model free analysis
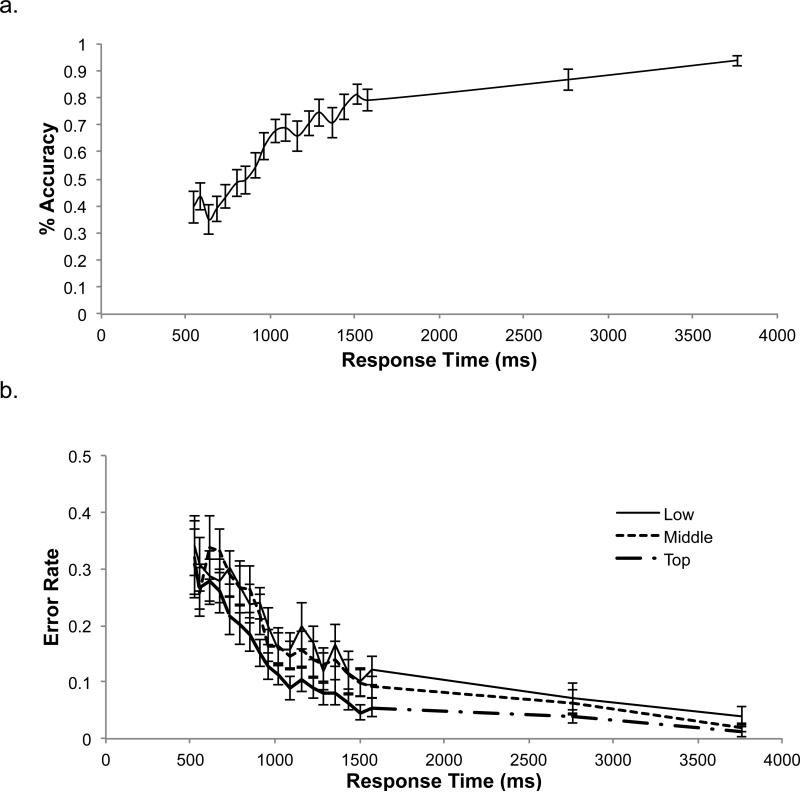
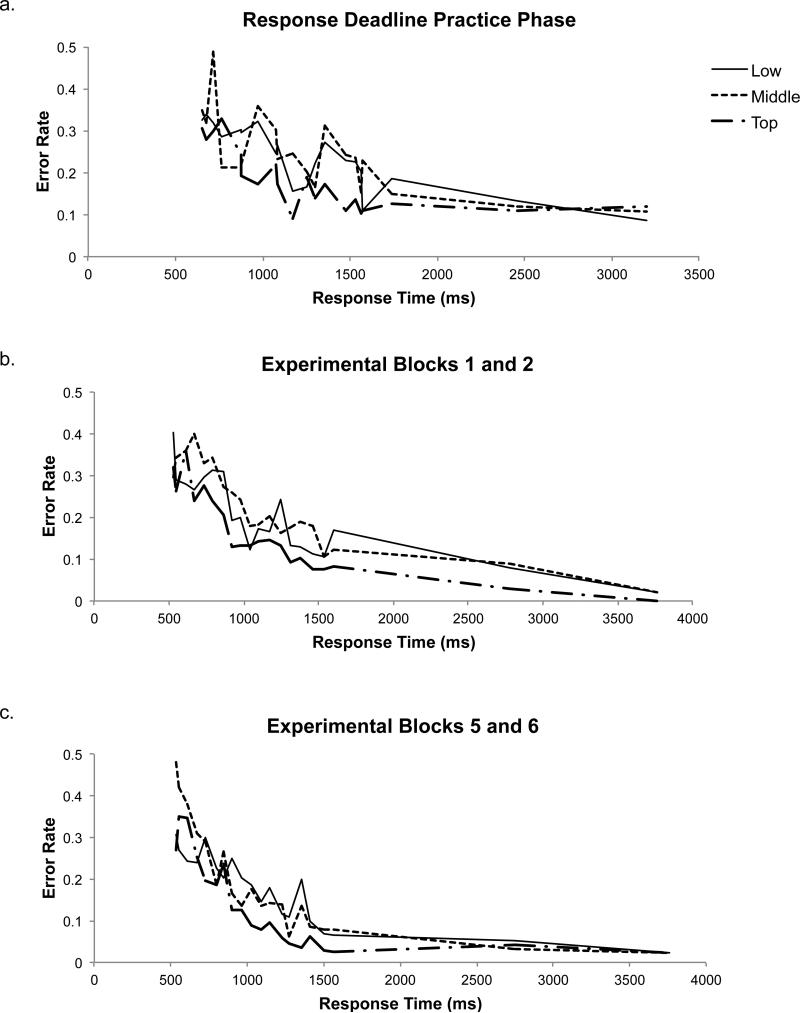
Our data indicate that our response deadline manipulation was successful. As response times (RT) increased, so did overall accuracy (Figure 5a). Thus, participants tended to obey the deadline and were increasingly successful at determining the correct response when given more time to make their decision. The average accuracy over all trials was 65.1% (SD=16.2%), but for trials with a response time over 2600ms, the average accuracy was 89.9% (SD=10.5%). These error rates were similar to those observed during a pilot study in which responses times were unconstrained (mean accuracy 87.7%; SD=8.7%; t(26)=3.01, p<0.01 ). Thus, the window of time sampled by the response deadline procedure was sufficient for participants to reach an asymptotic level of accuracy in some trials. Finally, participants generally responded promptly to the deadlines, with an average delay between the deadline and the committed response of 331.6ms (SD=33.1ms). Altogether, these results confirm the success of our response deadline manipulation.
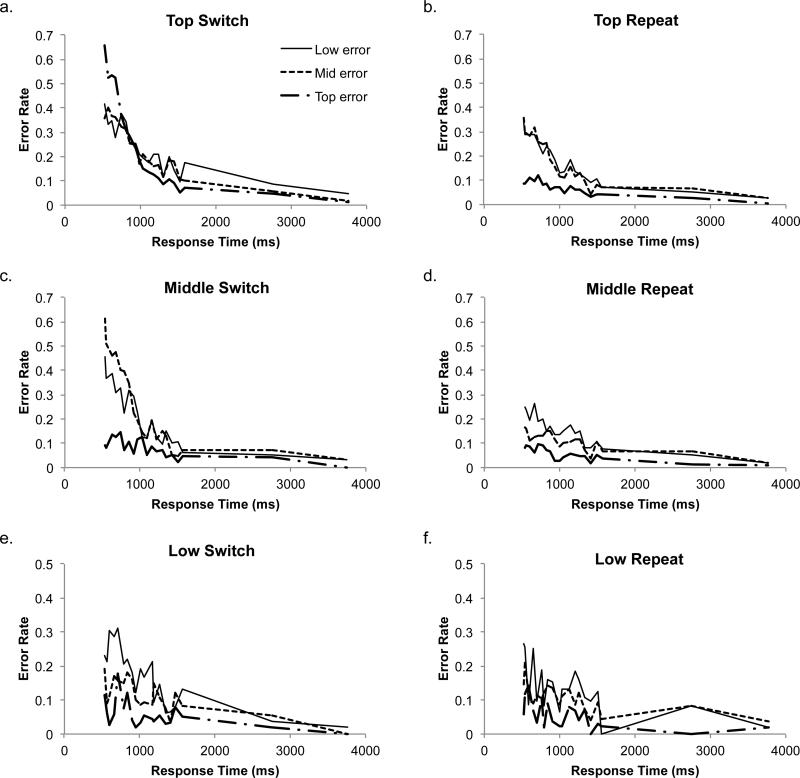
Figure 5.
These plots show how (a) accuracy and (b) error rates for each policy level change over the window of time sampled. These analyses only include the 18 participants who were presented with the final set of deadlines. In both graphs, responses are binned by deadline and plotted by average response time (measured from the onset of the stimulus). Error bars show standard error.
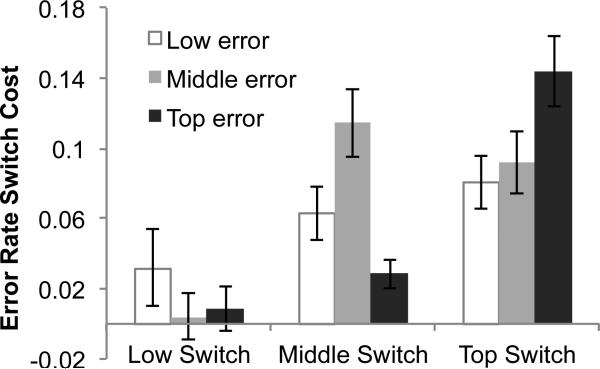
In contrast to predictions of the serial hypothesis, the decreases in overall error rates with increasing deadlines reflected roughly equivalent changes in accuracy at each level of the hierarchy (Figure 5b). These error rates were changing in an approximately parallel pattern: uncertainty at all three levels of the decision appears to have been resolved in tandem. This is unlike what would be expected from a fully serial model, in which the error rate at one level of the hierarchy would decrease before the others deviated from chance. However, these results are noisy because the response deadline procedure only sparsely samples the time span in question, and because this analysis necessitated the binning of trials.
We also conducted similar analyses to examine how various factors may have affected the temporal dynamics of the decision, including the effects of gaining experience with the rules over the course of the experiment (Appendix D) and task-switching effects (Appendix E). Though both of these factors influenced the evolution of error rates over time, the analyses reinforce the robustness of the parallel pattern of decision making.
2.2.2 Statistical modeling
To better parse the temporal dynamics of the different levels of policy, we turned to a hierarchical Bayesian modeling approach for estimating three types of parameters related to the temporal dynamics of hierarchical control. As laid out in the methods section, for each of the three levels of the hierarchical rule, we estimated the following three parameters: the time at which uncertainty started to decrease (start-top, start-middle, start-low), the time at which uncertainty stopped decreasing (end-top, end-middle, end-low), and the asymptotic error rate reached at the end time point (asymptote-top, asymptote-middle, asymptote-low).
In support of the good fit of our model, the fitted asymptote parameter estimates were highly correlated to asymptotic accuracy as calculated on the raw data. Specifically, the estimated asymptotes for errors on each level were used to calculate an overall accuracy rate, in order to compare it to accuracy rates calculated directly from the data. The accuracy rate for each participant, based on the estimated parameters, was calculated using the formula:
Participant-specific accuracy rates were calculated from the behavioral data using all trials with reaction times greater than 1428ms (equal to the last end parameter estimated). These accuracy values were highly correlated with those calculated from the asymptote parameter (r=0.97) (Figure 6). This correlation supports the efficacy of the modeling approach, and suggests that the parameter values are representative of the underlying temporal patterns.
Figure 6.
The asymptotic accuracy calculated from the model results was highly correlated to the asymptotic accuracy calculated from the raw behavioral data (r=0.97).
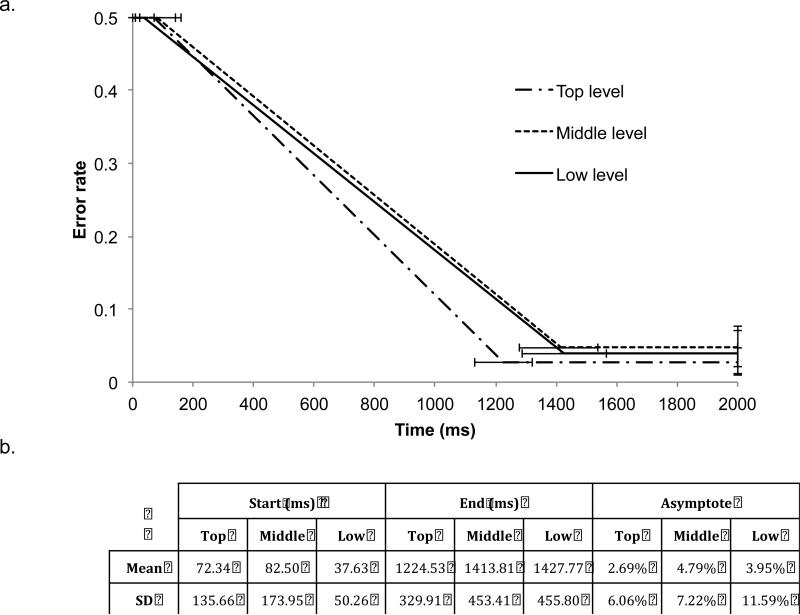
The parameters recovered are consistent with a primarily parallel model, in which all of the levels of the decision are resolved at the same time (Figure 7). All of the start parameters for the group distributions were approximately equal (start-top=72.3ms, SD=135.66ms; start-middle=82.5ms, SD=173.95ms; start-low=37.63ms, SD=50.26ms). Using the posterior density of the estimated group parameters, all of the start parameters fell well within the 95% credibility intervals of each other.
Figure 7. Results from MCMC modeling.
The mean and standard deviation of the distributions for the group parameters are shown above, represented graphically (a) and in a table (b).
We also found highly similar end parameters across levels of the hierarchy (endtop=1224.5ms, SD=329.91ms; end-middle=1413.8ms, SD=453.41ms; end-low=1427.8ms, SD=455.80ms). End-top was slightly lower than end-middle and end-low, suggesting that participants resolved the top level of the decision a little earlier than the middle and low levels. The posterior density of the group mean for end-top was outside the 95% credibility interval of the other two end parameters. In addition, using the participant-specific estimates from the model, a paired t-test of end-top and end-middle was significant (t(22)=2.76, p<0.05), and the paired t-test of end-top and end-low showed the same trend, although it was not significant (t(22)=2.00, p=0.06). No significant difference was found between end-middle and end-low, using the participant-specific estimates or the mean group estimate.
The entire time frame for the decision (i.e. the start and end parameters) estimated by the model was also consistent with the pattern seen in the binned error rates, based on visual inspection.
2.3 Discussion
Our results are inconsistent with a fully serial S-R stage during hierarchical control. Rather, though there are small differences in end times between the top-level decisions and the lower-order decisions, the change in error rates over time suggests a mostly parallel process of decision-making toward a response. This conclusion is supported by both the change in error rates over time and from the start and end times estimated from the Bayesian model. Specifically, error rates on all three levels of the decision appeared to start declining simultaneously, and they reached an asymptote at roughly the same time for the low and middle levels of the hierarchical decision. These results support a primarily parallel processing model of the complex hierarchical decision.
It is important to emphasize that we observed this largely parallel dynamic during a very complex decision, involving third-order policy abstraction. There were seven varying dimensions to track, three levels of contingency to traverse, and eight competing responses to consider. Despite the load that this task would place on capacity limited working memory and decision-making systems, performance nevertheless reflected a high degree of parallelism.
At the same time, our results do not indicate that the various levels of this hierarchical decision were carried out in a wholly undifferentiated manner. Specifically, the error rate for the top level of the decision was estimated to start with the lower levels of the decision, but reached asymptote at a slightly, but significantly earlier time point than the other two levels. This observation argues against a fully undifferentiated or “flat” form of processing of the various levels of our task, a point we elaborate in the General Discussion.
3. Experiment 2 – Neural Network Modeling
The existence of such highly parallelized temporal dynamics could be seen to challenge the neurocognitive architectures such as a cascade of a decision processes that have been proposed in prior work to capture hierarchical cognitive control (Collins & Frank, 2013; Frank & Badre, 2012; Koechlin et al., 2003). For example, the interacting corticostriatal loops model proposes that interactions across frontal regions are not completely continuous in time, but are instead punctuated by an emergent gating function arising from cortico-striato-thalamo-cortical connectivity and reinforcement learning processes (see also Chatham et al., 2011; Hazy, Frank, & O'Reilly, 2007; Kriete et al., 2013; O'Reilly & Frank, 2006).
To understand our behavioral results within the context of frontostriatal gating accounts, we attempted to capture our results using a previously developed multiple-loop neural network architecture (Collins and Frank, 2013). Counter-intuitively, we find that this frontostriatal gating model could naturally account for parallel-like processing, despite the operation of discrete, punctate gating dynamics. Our analysis further indicates how this parallel dynamic might arise in the brain, and what factors determine the degree to which some decisions (e.g., the top-level) might partially precede the lower ones, as observed in the behavioral data.
3.1 Methods
3.1.1 Model architecture and dynamics
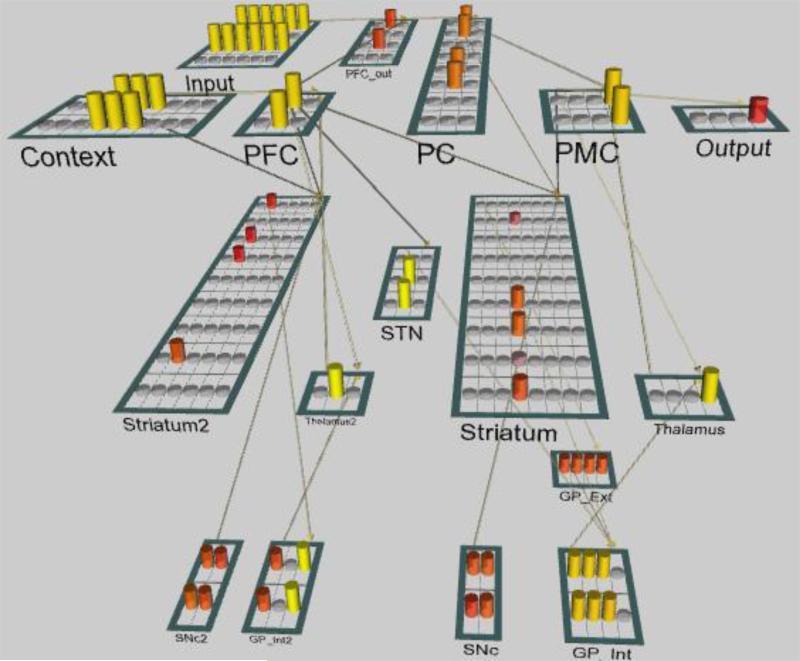
In order to investigate the temporal patterns of decision-making that can emerge from a hierarchically structured neural network, we simulated task performance using a modified version of a neural network architecture with multiple, nested corticostriatal loops from Collins and Frank (2013) that was implemented in the Emergent neural simulation software (Aisa, Mingus, and O'Reilly, 2008; Figure 8). The neurobiologically realistic model simulates the frontal-striatal interactions that are thought to be integral for hierarchical cognitive control, and it can learn and perform a two-level hierarchical stimulus-response task analogous to the third-order task used in Experiment 1.
Figure 8. Emergent network.
Modified version of the basal ganglia loop model from Collins & Frank (2013), shown in an exemplar state of activity. Layers are labeled and represented as bordered rectangles containing circular units. Cylinders indicate the strength of a unit's activity at a particular moment. Our model manipulations affected the strength of the connection from PFC to Striatum and the connection from PC to Striatum. PC: Parietal cortex; PFC: Prefrontal cortex; PMC: Premotor cortex; SNc: Substancia nigra pars compacta; STN: Subthalamic nucleus; GP_Int: globus pallidus internal segment; GP_Ext: globus pallidus external segment. Layers labeled “2” indicate the higher-order loop.
Collins and Frank explored their model in the context of acquiring hierarchical rule structures, considering task-switching costs, learning speeds, and task-set clustering. The model captured behavioral effects both in reaction times within a trial and over longer time scales. These effects were robust across variations in the model's parameter settings. In addition, the structure of the model is in line with research that shows that striatum is instrumental in such high level executive functions as task-switching (van Schouwenburg, den Ouden, & Cools, 2010; Moustafa, Sherman, & Frank, 2008) and working memory (O'Reilly & Frank, 2006; Cools, Sheridan, Jacobs, & D'Esposito, 2007; Baier et al., 2010).
Our implementation of the model was mostly unchanged from that of Collins and Frank (2013), with minor exceptions. Specifically, in order to accommodate the structure of our hierarchical task, two rows of units were added to the layers Input, PFC_out, and PC (see architecture description below, as well as Collins & Frank, 2013 for more details). However, the patterns of connectivity between these layers were preserved, and thus the network was largely the same as the original. This was intentional. In this way, we did not iteratively adjust the model to capture our behavioral results, but rather report results from simulations run on a multiple corticostriatal loop model that had been developed independently to capture other data.
The network has two nested corticostriatal loops, each of which involves connectivity between a cortical layer and a striatal layer. The loops are structured hierarchically, simulating the rostro-caudal organization of the frontal lobe, and the network learns stimulus-response mappings through reinforcement learning. The network receives stimulus input into two different layers: Context, which represents information relevant to the higher-level decision, and Input, which represents information relevant to the lower-level decision. Each of these layers has distinct groups of units that are active for each feature variant.
Context units project to the prefrontal cortex layer (PFC), which is the cortical layer involved in the higher-level corticostriatal loop. Input projects to a layer called PFC_out, which sends activity only to parietal cortex (PC), the cortical layer involved in the lower-level loop. Contextual information from the higher-level loop reaches the lower-level loop through cortico-cortical projections between PFC and PFC_out, as well as through a diagonal projection from PFC to Striatum, the striatal area in the lower-level loop. Once the network has accumulated enough evidence for a particular response in the premotor cortex layer (PMC), it selects that response by activating one of the units in the Output layer.
In the lower-level loop, PMC has a pair of units for each of the four responses, and it projects directly to the layer where the network outputs responses (Output). Lateral inhibition within PMC creates competition between the responses. When the network is presented with a stimulus, if it does not have a strong mapping to a response, activity in PMC is noisy and does not produce a response. PMC has bidirectional connectivity with the Thalamus layer, which also has units corresponding to each response. When a stripe of thalamic units becomes active, it provides a strong excitatory boost to the corresponding motor units in PMC, and the other responses are inhibited through lateral inhibition. The network's ability to gate out a single response relies on this connectivity.
Thalamic units are normally inhibited by high tonic rates of activity in the globus pallidus internal segment (GP_Int). The Striatum layer has both Go and NoGo units for each response, which cause the corresponding thalamic units to be disinhibited and inhibited respectively, via connectivity through GP_Int and the globus pallidus external segment (GP_Ext). Therefore, the activation of striatal Go and NoGo units for each response relative to the others reflects the probability that that response will be gated out. Striatum receives input from PC, the cortical layer involved in the lower loop, as well as from the higher loop's cortical area, PFC, via a diagonal projection between the nested loops.
The structure of the higher-level loop is similar to that of the lower-level loop, with the cortical layer PFC processing higher-level information about the stimulus and passing it to the lower loop via connectivity to Striatum2 and PFC_out.
As an explanation of hierarchical control, the Collins and Frank (2013) model extends and generalizes previous related corticostriatal gating models of hierarchical control, such as Frank and Badre (2012). Nevertheless, the core components of this prior theory of hierarchical control are included in this more general model. First, the model separates higher versus lower order selection between two corticostriatal loops. Thus, the PMC and PFC in the model correspond to the dorsal premotor cortex (PMd) and anterior premotor cortex (prePMd) layers in Frank and Badre (2012), respectively. Importantly, just as in Frank and Badre (2012), selection occurs through an output gating process of selection from within working memory, and diagonal connections allow the higher order loop to influence output gating by the lower order loop. Thus, though more up to date and general, Collins and Frank (2013) shares the same core account of hierarchical control in terms of separate corticostriatal interactions along the rostro-caudal axis of the frontal lobe. As such, we sought to test this more current model in the present work.
3.1.2 Basic model training and simulation procedures
The simulations were run in order to determine how the network's support for each possible response to a stimulus evolved over time, as well as how those temporal patterns were affected by changing the strength of various connections in the network. The network performed a two-level hierarchical task, structured like a single top-level branch of the behavioral paradigm (Figure 9). There were eight possible stimuli, spanning all possible combinations of the two variants of three dimensions (called, for convenience: shape, orientation, and location). The shape, which guided the top-level rule, was presented to Context. The conjunction of the orientation and location, the two low-level dimensions, was presented to Input.
Figure 9. Task for Emergent simulations.
A schematic of the task that the network learned, with two levels of hierarchy (top and low), three features (shape, orientation, and location) and four possible responses (R1-R4).
The network was trained on the task solely on the basis of reinforcement learning (as in Collins & Frank, 2013). The training phase was terminated once the network had performed without error for five epochs in a row (40 trials). At this point, the connection weights that the network had learned were saved. In each trial of the testing phase, the network selected a response to a stimulus, and activity was recorded from the units in Striatum throughout the entirety of each trial. The weights that had been learned were reloaded before each test trial. This effectively reset any activity that would produce switch effects between trials, which is different from the behavioral paradigm. However, the aim was to examine the dynamics of hierarchical decisions without necessarily including switch effects, particularly given that switch effects do not appear to have influenced the temporal pattern of decision making across levels in the behavioral experiment (Appendix E).
3.1.3 Model manipulations
The entire training and testing procedure was run multiple times under specific modifications to the relative weights of connections to Striatum from PFC and PC. As described above, striatal Go and NoGo activity is critical for thalamic units to become disinhibited, which is necessary for the network to gate out a response. Therefore, Go and NoGo activity reflects the likelihood that the network will produce each of the responses. Striatum receives information about the stimulus from PFC and PC. PFC receives a projection directly from Context, and it is part of the higher-level loop. PC is part of the lower-level loop. It receives projections from PFC_out, which is influenced both by Input (low-level features) as well PFC (and thus indirectly, Context). Therefore, the balance between the influences of these two layers (PFC and PC) on Striatum determines which responses are supported and suppressed by striatal Go and NoGo units, and thus how the hierarchical decision proceeds over time. The relative balance of the projections is set by a relative weight parameter (wt_scale.rel), a scaling factor that determines how much a layer is influenced by each projection that leads to it without altering the total amount of input to the layer. For any two projections that go to the same layer, the ratio of their input strengths is equal to the ratio of their relative weight parameters. We tested separate simulations of the model across systematic manipulations of the relative weightings of PFC and PC to Striatum.
For each setting of the relative weight parameters, the network was initialized five times with random weights and trained, and each trained network was given five testing epochs. Therefore, each setting of the projection was recorded for 25 total epochs (200 trials). The wt_scale.rel values tested for the projection between PFC and Striatum were 0.75 (the default), 0.5, 0.3, and 1.25. Other inputs to Striatum, which remained at default, include PC (wt_scale.rel=1.25) and SNc (wt_scale.rel=2). One additional parameter setting was tested, in which the relative weights of the projections from PFC and PC to Striatum were reversed (PC to Striatum wt_scale.rel=0.75, and PFC to Striatum wt_scale.rel=1.25).
3.1.4 Measurement of response representations over time
Activity in Striatum, the lower-order striatal layer, was recorded because it is updated continuously as higher cortical levels process information, and it is closely connected to Output. Striatum has two columns corresponding to each response: one with Go units, which have the net effect of disinhibiting that response, and the other with NoGo units, which have the net effect of inhibiting the response. The patterns of Go and NoGo activity for each response provide insight into when, during the course of a trial, the network makes certain parts of the decision. Solving part of the decision can be conceptualized as using the presented information to eliminate some responses, while keeping others in contention, with the goal of eventually choosing the single appropriate response. Therefore, if the network has Go activity for a certain incorrect response, it has not yet resolved the part of the decision that would eliminate that response. This logic mirrors that targeted in human behavior by the response deadline procedure, but as we have access to the internal representational states of the model, this recording more directly assesses which responses remain candidates throughout the trial.
Thus, striatal Go and NoGo activity was used as a measure of how much support the network had for each response at any given time in a trial, with activation in that response's Go column (Goa, for response a) increasing support for it and activation in the NoGo column (NoGoa, for response a) decreasing support. Therefore,
is the net striatal activity in support of response a (“response support”). In order to compare the strength of activity between responses at a particular time point, a normalizing factor was applied:
| (2) |
The denominator incorporates Go and NoGo activity over all the responses, and thus it is the same for all responses at a single time point. The absolute value is necessary to avoid scaling issues when there is approximately equal Go and NoGo activation across the entire layer. This is not a calculation of probability, but it incorporates both Go and NoGo activation, and the normalizing factor allows for comparison of response activations within a time point. Thus, it is an appropriate and interpretable measure for comparison with estimates of human behavior from our statistical model.
For each trial, the trajectory of striatal support for each response was classified by error type, as in the analysis of the behavioral task. That is, the response corresponding to correct usage of both the top- and low-level rules was classified as the correct response. The response corresponding to the correct use of the top-level rule but incorrect use of the appropriate low-level rule was classified as a low-level error. The other two responses were classified as top-level errors. One such top-level error response was inconsistent with the top-level rule only (termed top error/low correct), while the other response was incorrect according to both the top- and low-level rule (termed top error/low error).
3.2 Results
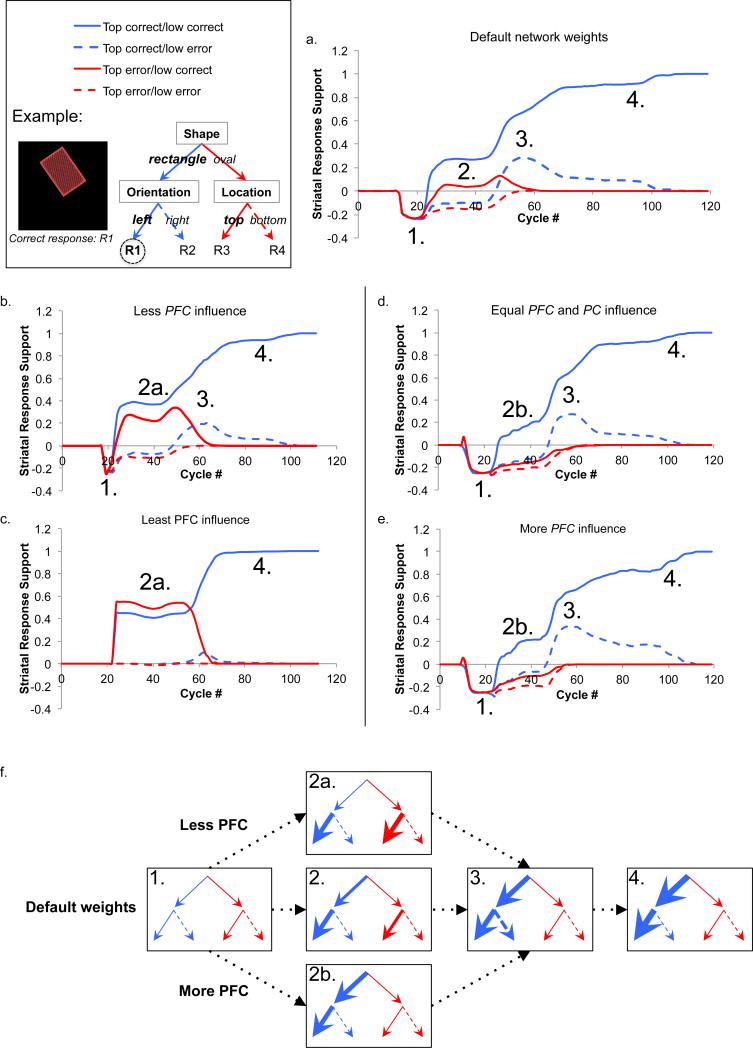
3.2.1 Default network weights
In the network's default settings, the strength of the projection from PFC to Striatum (wt_scale.rel=0.75) is less than the strength of the projection from PC to Striatum (wt_scale.rel=1.25). As can be seen in Figure 10a, initially, there was no net activity supporting or inhibiting any of the responses, due to net inhibition of all responses early in the trial (i.e. more NoGo than Go activity). After the initial dip, the correct response started to obtain more net Go activity than any of the others, becoming disinhibited almost immediately. Thus, early in the trial, information from both PC and PFC accumulated in Striatum, such that the responses inconsistent with lower- or higher-order policy received less conjunctive support than the single correct response. In a corresponding behavioral paradigm, this would be akin to a participant appearing to solve two levels of the decision at the same time (i.e., parallel processing).
Figure 10. Emergent results plotted as trajectories of each response type.
Support for each response was calculated from striatal Go and NoGo activity (see equation 2) averaged over five runs of the network (i.e. five initializations of the weights). Each run consisted of five epochs (40 trials). Inset illustrates what each response trajectory would correspond to on a decision tree for an example trial of the experiment. (a) Trajectory of response support over time using the default network weights. In the default settings, the weight of the connection from PFC to Striatum was less than the weight of the projection from PC to Striatum. (b) Trajectory of response support over time when there is less influence of PFC on Striatum. The relative weight of the projection from PFC to Striatum was decreased from 0.75 to 0.5, while the relative weight of the projection from PC to Striatum remained at the default level of 1.25. (c) Trajectory of response support over time when there is the least influence of PFC on Striatum. The relative weight of the projection from PFC to Striatum was decreased to 0.3, while the relative weight of the projection from PC to Striatum was kept at the default level of 1.25. (d) Trajectory of response support over time when there is equal PFC and PC influence on Striatum. The relative weight of PFC on Striatum was increased from the default, so that it had an equal influence on Striatum as the PC layer. (e) Trajectory of response support over time when there is more influence of PFC than PC. The default relative weights of the PFC and PC projections were reversed, so that the PFC projection on Striatum had a higher relative weight (1.25) than the PC projection to Striatum (0.75). (f) Evolution of response support from each model manipulation (labeled in a-e) is represented using a tree structure, with thicker lines indicating more support for a particular branch. The four highlighted phases are as follows: 1. All responses are inhibited. 2. The responses that are correct on the low level (solid lines) have more support. The response correct on both levels has the most support. With less influence of PFC on Striatum (2a), support for the two responses correct on the low level are similarly supported. With more influence of PFC on Striatum (2b), the correct response has more support than all others. 3. Both responses correct on the top level (blue lines) get a late boost of support, while support for the top-level errors (red lines) goes to zero. 4. Support for the top correct/low error response decreases, and support for the response correct on both levels increases until the end of the trial.
Support for the correct response continued to increase throughout the trial, though not monotonically, until sufficient evidence accumulated for the network to output a response. In the middle of the trial, at around cycle 45, a transient increase in the amount of support for the top correct/low error response coincided with a decrease in the amount of support for the top error/low correct response. Although information from the higher-level loop influenced striatal activity earlier in the trial, as the single correct response was supported above the other options, additional evidence about the higher-level decision appears to have reached Striatum at this time: net support for the top-level errors went to zero, while the two responses consistent with the top-level feature received more support. After this boost in evidence, support for the correct response continued to increase while net support for the others settled to zero, until the network output the correct response, ending the trial.
3.2.2 Less relative influence of PFC on Striatum
To decrease the direct influence of PFC on Striatum, the relative weight of that projection was reduced to 0.5 while keeping the relative weight of the PC to Striatum projection constant (wt_scale.rel=1.25). As can be seen in Figure 10b and similar to the default setting, all responses were inhibited at around cycle 20, although this dip was less pronounced in this network configuration. Then, evidence increased for both the correct response and the top error/low correct response, reaching a temporary plateau of positive net Go activation. Unlike the default, however, there was no significant difference between these two response probabilities (paired t-tests: df=4, p>0.05 until cycle 48). Thus at this point in time, Striatum had equal support for both responses consistent with the low-level input, while the two responses that violated the lower-order policy were inhibited. In a behavioral experiment, the participant would appear to have solved only the low level of the decision at this time.
At around cycle 45, the net positive activation for the correct response began to increase again, and it also increased transiently for the top correct/low error response. The two responses that received a boost at this point in the trial were consistent with the higher-order policy, while support for the top error/low correct response decreased. This would be the point in time when the participant appeared to solve the top level of the decision. For the remainder of the trial, the correct response had increasingly more support than all of the incorrect responses.
When the relative weight of PFC on Striatum was decreased further (wt_scale.rel=0.3) while maintaining the default setting for the PC to Striatum projection (wt_scale.rel=1.25), depicted in Figure 10c, the first change in net support for any of the responses occurred at around 20 cycles. At that time, support for the correct response and the top error/low correct response increased rapidly to a plateau, while the other two responses continued to have approximately equal Go and NoGo activity. As in the previous settings, at this point Striatum had equal support for the two responses consistent with the lower-order policy, above the two responses that violated that level of the decision. For approximately 40 cycles, the response probabilities did not change, and there was no significant difference between the correct response and the top error/low correct response (paired t-tests: df=4, p>0.05 until cycle 58) or the top correct/low error response and the top error/low error response (paired t-tests: df=4, p>0.05 until cycle 55). Again, in a behavioral paradigm, the subject would appear to have solved only the low level of the decision at this time.
Then, at around 55 cycles, the probability of the correct response increased while the probability of the top error/low correct response decreased. At this point, the Striatum was accumulating support for the single response consistent with both orders of policy: in other words, resolving uncertainty for the top level of the decision. There was also a small transient increase in the probability of the top correct/low error response, but it was far less pronounced than the two previously described parameter settings. This indicates that a weaker relative influence of PFC compared to PC prevents Striatum from accumulating support for the response that violates the low-level information, even though it is consistent with top-level information.
3.2.3 More relative influence of PFC on Striatum
The relative weight of the projection from PFC was increased such that Striatum received equal input from PC and PFC (wt_scale.rel=1.25 for both projections). As shown in Figure 10d, the initial dip of support for the four responses began earlier and lasted slightly longer for this configuration than it did for any of the previous settings. When support for all responses first began to increase, only the correct response was differentiated from the others and had net positive support. This suggests that both higher- and lower-order information was influencing activity in Striatum, as the correct response was the only one consistent with both orders of policy. In a behavioral task, this would appear as though the subject were solving both levels of the decision simultaneously. At cycle 45, the correct response probability increased more rapidly, and there was also a sizable boost in the support for the top correct/low error response: i.e., the two responses consistent with the top-level information received a boost in support. The increase in support for the top correct/low error response was transient, as in the default setting, while support for the correct response continued to increase until the network output the response.
Finally, the relative weights of PFC and PC were reversed from the default, so that PFC had more influence on the Striatum layer than PC did (PFC wt_scale.rel =1.25, PC wt_scale.rel =0.75). The pattern of activity shown in Figure 10e is nearly identical to the pattern when PFC and PC had equal influence on Striatum, but the late boost in support for the top correct/low error was even more pronounced, and it decreased more slowly. This supports the idea that a stronger relative influence of PC is what prevents Striatum from accumulating support for the response that violates the low-order policy but is consistent with the top-level information.
3.3 Discussion
The neural network simulations suggest that a hierarchical frontostriatal architecture can indeed support parallel processing of a decision. In the default settings of the model, it was apparent that the network favored only the correct response as soon as accumulating evidence showed any difference between the four options. In order for this to occur, there must have been information from both levels of the rule structure influencing striatal Go and NoGo activity. Had only one level of the decision been influencing striatal activity at a time (i.e. serial processing), the network would have supported half of the responses at first, and then the correct response would have gained all of the support at a later time point.
Interestingly, a more serial pattern in early decision stages was observed only when the connection from PFC to Striatum was weakened (and thus the PC to Striatum connection relatively strengthened). As soon as striatal activity differentiated the responses, the two responses consistent with the low-level rule had the greatest support. This suggests that the network used the low-level features of the stimulus to eliminate half of the responses, even though information about the top-level decision had not yet influenced striatal activity. At a later time point, all of the activity favored the single response that was consistent with both top- and low-level features of the stimulus, indicating that both levels of the decision had been solved. Thus, temporally distinct stages of the onset of the decision were clear when the PFC to Striatum connection was weakened.
Conversely, when the PFC to Striatum projection was given greater relative weight than in the default settings, the temporal pattern was more parallel in the early phase of the decision, akin the behavioral results. Evidence for the correct response accumulated more quickly, and the difference between the correct response and the three errors was even more pronounced.
The amount of support given to the incorrect responses is also important for interpretation of the neural network results. In the default settings, support for the two top-level errors decreased to zero in the middle of the trial, as support for the other two responses (including the correct response) received a sizable boost. In the behavioral paradigm, this would be the time when the participant appeared to solve the top level of the decision (i.e. eliminating responses inconsistent with top-level information). Critically, this boost of top-level correct responses included an increase in support for a response that was incorrect on the low level. In the behavioral task, this dynamic would yield responses that appear as though the participant had not yet finished solving the low level of the decision. This pattern is consistent with the earlier end time for the top level of the decision compared to the lower two levels in Experiment 1. This feature of the temporal pattern was present when the connection from PFC to Striatum was at default levels or stronger, and it became less pronounced when that connection was weakened. Thus, just as it resulted in a more parallel dynamic early in the decision, the strength of the PFC-Striatum connection also supports the slightly earlier end point of the top-level decision in the behavioral results.
4. General Discussion
Our results suggest that when traversing multiple contingencies, hierarchical decision-making within the S-R stage is strikingly parallel. Behavioral results from Experiment 1 indicate that participants were processing all levels of the hierarchical rule structure at roughly the same time, although they completed the top level of the decision slightly earlier than the others. The simulations of Experiment 2 suggest that this parallel processing is consistent with the frontostriatal connectivity thought to underlie cognitive control. In the default settings of the neural network (derived from simulating an independent task), the processing of a two-level hierarchical decision occurred in parallel, causing the correct response to be supported more than all the others from an early time point in the trial. The neural network results also provided a potential mechanism by which a lower level of the decision might finish later than the top level, as observed in Experiment 1. In the network settings that produced parallel processing, resolution of the top level of the decision coincided with a transient boost in support for an error on the low level (the response that was also consistent with top-level information). At that time, the correct response was supported more than all of the others, indicating parallel processing, but the low level of the decision was not complete until later in the trial, when support for the low-level error disappeared. Thus, the top level of the decision was solved slightly earlier. Importantly, model manipulations associated both of these features – parallel early decision evolution and differentiated decision resolution – with greater PFC to striatum influence.
Our results support a parallel processing system, but they certainly do not rule out the prospect of serial processing or a bottleneck in decision-making. First, though our task requires resolving a considerable amount of uncertainty —27 possible stimuli mapping to eight responses—each dimension-based rule was only a binary choice. It seems reasonable to assume that there is some limit at which parallel processing would be overly costly and more clearly maladaptive. For example, if a higher-level decision could significantly decrease the amount of uncertainty on a lower level, it would be more efficient to delay processing of the lower level of the decision until the higher level had been resolved. This would lessen demands for the lower level of the decision, making the problem more tractable. Thus, there could be situations where serial processing is adaptive, and in these situations, the system (as with any parallel architecture) may strategically or by necessity exhibit a serial processing dynamic.
Second, our results do not necessarily contradict the conventional multi-stage model of response selection that posits serial perceptual, S-R, and response stages. Indeed, there may still be a basic separation between the decisions made during the S-R stage and their motor implementation at response (e.g., Braverman et al., 2014). In our model, this distinction is reflected, to some degree, in the difference between the evolution of the decision in striatum, and the actual output of the response in the model's motor cortex. Rather, what our results indicate is that within the S-R stage, multiple contingent decisions can be managed in parallel rather than strictly in series.
The temporal patterns evident in our results imply that the distinct frontal areas implicated in prior studies of hierarchical cognitive control (Badre & D'Esposito, 2007; Badre et al., 2009; Christoff & Gabrieli, 2000; Christoff et al., 2009; Koechlin et al., 2003;O'Reilly et al., 2002) may process information simultaneously. Such parallel processing is possible in our task because each stimulus contained information relevant to every level of the decision. By this hypothesis, one rostral frontal area may use the top-level feature to select the relevant middle-level feature, while a more caudal frontal area uses the middle-level features to select relevant low-level features. Likewise, a still more caudal frontal area could use these low-level features to select a set of viable responses. To settle on a single response, as demanded by our task, information must still be combined across these different levels.
The neural network model sheds light on this conundrum, as well as illuminating how a few key connections may influence the temporal pattern of a decision. We used an independently developed and tested model, in order to test whether existing theory captures the essential patterns from the behavioral results. The model's task had two orders of policy, unlike the three levels of the behavioral paradigm, because that was the degree of abstraction that the model was originally built to accommodate. Thus, though there were small changes to the model, the essential structure and connectivity was preserved. The simulations demonstrate that a hierarchical network can represent and process a multi-level rule structure in parallel.
In principle, a simple three-layer neural network could also perform the behavioral task, simply by representing a “flattened” version of the rules: complex feature conjunctions, rather than hierarchical contingencies, can also uniquely map stimuli to responses in our task. Notably, this flattened rule structure would make similar behavioral predictions as a hierarchical decision that is solved in parallel. That is, the behavioral results that suggest that three levels of hierarchical rules are resolved simultaneously would also result if the task were represented with a single level rule structure. The significant difference between end-top and the other end parameters argues against the use of such a flat representation by our participants, as described above. It remains possible that participants used a partially flattened hierarchy, separating the top level, but combining the middle and low levels using feature conjunctions. However, separable effects of middle-level switches and low-level switches suggest that this is not the case (Appendix E). While prior models predict flattening will occur with extended practice of hierarchical control tasks (Frank & Badre, 2012), the possibility for progressive flattening is an important direction for future work.
Future work should also explore further predictions of our model for the temporal dynamics of cognitive control. First, our model suggests that the strength of PFC to striatal projections impacts the temporal dynamics of decision-making during hierarchical control. To the degree that “connection strength” can be measured (an admittedly assumption-laden prospect with current technologies), this hypothesis leads to straightforward predictions about the impact of these connections on performance during the task we test here.
There are a number of possible biological mechanisms that could alter the strength of connectivity between PFC and striatum, and thus modulate the degree to which decisions are performed in parallel. Several dynamic state changes could result in individual flexibility on a short-term basis, including metabolic state (e.g. recent glucose consumption) or greater spine densities on the afferent connections in striatum, which can undergo relatively rapid changes in response to synaptic activity (Yagishita et al., 2014; Oh, Hill, & Zito, 2013; Matsuzaki et al., 2004). Similarly, individual differences in connectivity or influence might map onto differences in decision-making performance. There are several more static traits that could account for heterogeneity between individuals, such as the degree of myelination or the efficiency of NMDA/AMPA signaling (e.g. genetic polymorphisms in glutamate receptors). To the degree that this top down influence is dynamic and under control of the brain, it could provide a potential mechanism by which serial versus parallel decision-making can be dynamically regulated based on task demands and strategy.
Broadly consistent with the present results and modeling, prior research has provided evidence for a model in which a finite central capacity can be shared between multiple tasks (Logan & Gordon, 2001; Navon & Miller, 2002; Tombu & Jolicoeur, 2003, 2005). This capacity sharing model allows for the possibility of simultaneous performance of multiple tasks. However, it can also behave as a bottleneck if one task is prioritized such that it consumes the entire central capacity. In fact, some of the literature supporting this possibility of parallel processing maintains that serial processing is often more strategic (Logan & Gordon, 2001; Meyer & Kieras, 1997a, 1997b). This framework appears broadly consistent with the present computational model in which top down signals from PFC to striatum can have the consequence of making the decision more or less serial. Moreover, our results motivate the further hypothesis that these corticostriatal dynamics might be a means by which allocation of central capacity among one or more tasks is allocated. Such a hypothesis would be important to test in future research.
A second prediction from our model is that upon being given a response deadline, participants rapidly utilize information from separate frontal regions to help select a specific response. Recently a specific kind of frontostriatal gating has been implicated in such hierarchical modulations – a stochastically time-consuming process known as “output gating” (Chatham, Frank, & Badre, 2014). One clear prediction is that similar sluggishness and variability should be visible in the latency of responses relative to the deadline. Furthermore, this sluggishness and variability should scale with the depth of the hierarchical rule being used. That is, in a task with a less abstract rule structure, the average delay between deadline and response should be both shorter and less variable.
A third, related prediction motivated by our model is that without top-down control, such as through output gating across the putative frontal hierarchy, response selection processes should predominantly reflect the information that is represented in cortical areas most proximal to motor cortex. In trials with very short deadlines, it is possible that not all of the frontostriatal circuits successfully underwent the time-consuming output gating process in time for the response. As a result, these trials may contain a somewhat larger proportion of top- and middle-level errors.
This last prediction is broadly consistent with research on hierarchical control in patients with frontal lobe damage. Two studies have shown deficits in hierarchical control at policy levels that were higher, but not lower, than the level directly affected by the lesion along the rostro-caudal axis of lateral frontal cortex (Badre et al., 2009; Azuar et al., 2014). Thus, to the degree that one must rely on output gating of higher order information, a lesion to more rostral frontal cortex would disrupt performance. This would be akin to a loss of top down, “diagonal influence” from rostral PFC to caudal striatum. As such, the lesion would be an extreme of the model manipulation that weakened the diagonal connection between PFC and striatum. Thus, under such conditions, the model predicts that the responses themselves would be dominated by lower-order information. In the patients tested by Badre et al. (2009), the response mappings overlapped across feature sets, and so this prediction could not be tested. However, if response mappings were separated or if asymmetries in feature salience were manipulated, the model predicts that patients will show biases in their errors reflecting an overreliance on lower order information. These predictions are also broadly consistent with the general vulnerability of frontal lobe patients to prepotent response pathways.
It is notable that our neural network simulations revealed non-monotonic features not apparent in the experimental data (see Figure 10). As we can directly measure the internal components of the model, the model provides better resolution in time than behavior, as well as a more precise way of interpreting the trajectories themselves (as evidence for each response). The overall parallel evolution of these decisions captures the essential findings of the behavior, but the enhanced resolution and specificity of these measures reveals new complexities in the time-courses of evidence for each decision within striatum that are not available in behavior. In some sense, these changes constitute additional novel predictions of the model. Testing such predictions would need to focus on striatal measures specifically and could be conducted through neuroimaging, like EEG (e.g. Borst & Anderson, 2015) or combined EEG/fMRI (Frank et al., 2015) or even direct striatal recordings.
Another difference between the model and the behavioral data is the manner in which the rules were learned: the model learned the rule set via reinforcement learning, whereas the human participants learned through explicit instruction. At a high level, this difference reflects a commonly cited limitation of computational modeling: namely, models often require different training procedures than human beings. A common response to this point is that the learning in the model mirrors – albeit in a simplified form – the acquisition of control policies that a human experiences over a lifetime spent behaving in the real world before entering the lab. Thus, by the time a human adult participant does a task, the instructions merely draw on already learned policies for cognitive control via some process of analogy, and thus mirror the test phase of the model. A similar point applies in the present case, wherein we examined the performance of both the model and the human participants during the test phase. Nevertheless, the specific rules were novel for humans, and so a form of explicit learning took place during the training phase to map these rules to existing policies, and this process was not captured in the model.
However, there are two factors that mitigate concern over this potential difference. First, using only a second order rule, at least one prior study (Badre, Kayser, & D'Esposito, 2010) has shown that hierarchical rules acquired through pure reinforcement learning exhibit similar patterns of frontal activity during performance as those acquired through explicit instruction. Second, even though it was explicit, our participants learned the rules in a progressive training procedure, practicing one rule at a time and combining them incrementally. Thus, if anything, the training procedure would have encouraged a serial type of representation in the human participants. However, such serial processing was not evident, even when analysis was restricted to the practice phase or early in the test phase (Appendix D). Hence, the observed similarities between the model and the behavioral data are all the more striking, given the potential differences in training.
Another important consideration is whether the effects observed here could be attributed to a perceptual stage rather than the S-R stage. It is certainly the case that abstract rules can affect perceptual processes. Indeed, evidence of preparation effects in the traditional task switching literature may be partially attributable to the construction of such an advance attentional set. Similarly, in the theoretical framework we use in this paper, this process might correspond to an “input gate”, whereby a cue would indicate what other stimulus information to allow into working memory to influence responding (Frank et al., 2001; Hazy et al., 2007). Just as with output gating, input gating can be driven by higher order rules. For example, Chatham et al. (2014) used a serial stimulus ordering manipulation during a 2nd order rule task to separately test input versus output gating of working memory. This study found that both types of gating make use of similar corticostriatal systems that are central to the present model.
Nevertheless, we are doubtful that perceptual attentional selection or an input gating process is driving the effects in the present study. First, as noted previously, most task switching studies showing preparation effects use serial stimulus presentation, providing cues in advance of target stimuli. Chatham et al. (2014) similarly encouraged input gating by providing higher order contextual cues in advance of lower order cues. However, when stimulus information is presented simultaneously as we did in this study, there is evidence that people tend to encode task-irrelevant information into visual working memory (Marshall and Bays, 2013; Shen, Tang, Wu, Shui, & Gao, 2013) and filter after the fact; a process akin to output gating.
Second, the present results are themselves inconsistent with filtering of irrelevant dimensions, as the initiation time for each level of the decision was simultaneous. The top-level rule indicated which middle-level feature was relevant for a particular stimulus. Thus, if an input gating/attentional selection strategy were being used, solving the higher level first would allow for early attentional resources to be directed toward the relevant middle-level feature and away from the irrelevant middle-level feature. However, the middle-level error rate appeared to start declining just as early as the top-level feature. In other words, not only was the middle-level decision in process before the top-level rule completed, but this suggests that attention could not have been biased toward either of the middle-level features initially. The same reasoning follows for the middle-level rules biasing perception of the low-level features. Thus, it seems likely that these effects are occurring at the S-R stage, and moreover, it is output gating, rather than input gating, that is the process being governed by the higher order rule in this task. Nevertheless, this does not rule out the possibility that people can make use of input gating strategies in other contexts. The process by which people choose to strategically input or output gate is a topic for future research.
Finally, some aspects of our results might reflect characteristics of hierarchical rules rather than hierarchical decision-making per se. For example, the earlier top-end time could arise because top-level rules are more frequently relevant than any given lower-level rule. This differential exposure might contribute to the faster resolution or prioritization of that level of the hierarchy. Thus, future study will be required to determine whether the parallel dynamic observed here might also apply in other hierarchical control settings without the specific concrete features of this design.
In summary, the results from our response deadline experiment support a parallel S-R stage, wherein multiple contingent decisions are made roughly in parallel, though with the top-level decision resolving slightly earlier than the lower-order decisions. Simulations with a neural network that implements a hierarchical multiple frontostriatal gating loop architecture also produced evidence of parallel evolution of decisions at all levels of contingency. Interestingly, this model suggests that the top down influence of PFC on striatum may result in both dynamics observed in behavior. A greater influence of PFC resulted in a more parallel initiation of the decision, overcoming a bottom-up bias toward decisions proximate to the response, and a differentiation of the resolution of the decision, with the higher level resolving first and so influencing the lower decision. These results are consistent with theories proposing a dynamic cognitive control system that leverages frontostriatal circuits for solving complex tasks.
Acknowledgements
This research was supported by a grant from the National Institute of Neurological Disease and Stroke (R01 NS065046) to D.B, research awards from the Alfred P. Sloan Foundation and the James S. McDonnell Foundation to D.B., and a Karen T. Romer Undergraduate Teaching and Research Award from Brown University to C.R. We are grateful to Ilke Öztekin for helpful advice during early stages of this project, Anne Collins and Michael Frank for advice regarding the neural network modeling, and Kieran Alessi for assistance with data collection.
Appendix A: Rule Learning Order Effects
We compared error rates for different rules in the hierarchy, in order to explore how the temporal ordering of the rule-learning procedure may have impacted results. All participants learned and practiced the rules in the same order (Figure 3). We looked at the average error rates for the two middle-level rules and the four low-level rules. All participants were included in this analysis.
There was no significant difference in the average number of errors between the two middle-level rules (paired t-test: t(22)=1.18, p=0.25) (Figure A.1a). Thus, the order in which subjects learned the middle-level rules seems to have had little effect on their performance.
Examining the number of errors for each of the low-level rules revealed minor differences (Figure A.1b). Low-level rules were taught in pairs, followed by a middle-level rule that combined them. Thus, participants learned the border thickness rule (low level), followed by the color rule (low level), and then the size rule (middle level, combining the previous two). Next, they learned the orientation rule (low level), followed by the location rule (low level), and then the shape rule (middle level, combining the previous two). There was no significant difference between the number of errors made for the first pair of low-level rules compared to the second pair (paired t-test: t(22)=1.64, p>0.05).
However, the low-level rules taught first within their pair (i.e., border thickness and orientation) had fewer errors than the rules taught second within each pair (color and location, respectively). These effects were significant, assessed via paired t-tests (border thickness (1st) vs. color (2nd): t(22)=3.04, p<0.01; orientation (3rd) vs. location (4th): t(22)=7.99, p<0.01).
Despite differences in the number of errors made for each of the low-level rules, these effects do not appear to have emerged from the overall order in which participants learned the rules, per se. In addition, our analyses collapse across each level of the hierarchy. Though these differences may have increased the variance in our sample, this variability does not account for the observation that participants performed the decision across levels in parallel.
Figure A.1. Order of rule learning.
Average number of errors made for individual rules on (a) the middle level of the hierarchy and (b) the low level of the hierarchy. Error bars depict standard error.
Appendix B: Deadlines for the Response Deadline Procedure
Appendix B.
Deadlines for the Response Deadline Procedure
| Set 1 (n=1) [ms] | Set 2 (n=2) [ms] | Set 3 (n=2) [ms] | Set 4 (n=18) [ms] |
|---|---|---|---|
| 50 | 50 | 50 | 50 |
| 200 | 200 | 100 | 100 |
| 350 | 300 | 185 | 175 |
| 500 | 400 | 270 | 250 |
| 650 | 500 | 355 | 325 |
| 800 | 600 | 440 | 400 |
| 950 | 700 | 525 | 475 |
| 1100 | 800 | 610 | 550 |
| 1250 | 900 | 695 | 625 |
| 1400 | 1000 | 780 | 700 |
| 1550 | 1100 | 865 | 775 |
| 1700 | 1200 | 950 | 850 |
| 1850 | 1300 | 1035 | 925 |
| 2000 | 1400 | 1120 | 1000 |
| 2150 | 1500 | 1205 | 1075 |
| 2300 | 1750 | 1290 | 1150 |
| 2450 | 2000 | 1375 | 1225 |
| 2600 | 2250 | 1460 | 1300 |
| 3000 | 3000 | 2500 | 2500 |
| 3500 | 3500 | 3500 | 3500 |
Table B.1: The set of deadlines for the response deadline procedure was adjusted several times throughout data collection. Four different sets of deadlines were used in total: each set had 20 deadlines ranging from 50ms to 3500ms. The deadlines that participants actually experienced varied slightly from these times, because of hardware delays. The number of participants for each set is presented in the table.
Appendix C: Parameter Recovery Tests
Simulations were run in order to verify the ability to recover parameters in the hierarchical Bayesian model from the data collected in the behavioral experiment. For each simulation, a mock data set was generated, with trials from a number of “subjects.” A temporal pattern for each data set was set by selecting values for each of the nine parameters that the model would estimate (start, end, and asymptote values for the three levels of the hierarchy). A mean and standard deviation were chosen for the distribution of each parameter among the entire group. Subject-specific values for each parameter were drawn using a normal distribution with the group mean and standard deviation. Each subject had a set of several hundred trials, with “reaction times” that spanned the length of the experimental trial (<4s).
For each trial, the probability of making an error was calculated separately for each level (top, middle, and low), using the subject-specific parameters and the “reaction time.” The error rate on each level was set to decrease linearly from chance (50%) at the start time to the asymptote level at the end time, as implemented in Equation 1. Using these error rates for each level, a response was probabilistically chosen for each trial. Finally, the Bayesian model was used to estimate the parameters from the mock data set (which included subject numbers, reaction times, and response types). The parameters that were estimated were compared to the values that were originally assigned to the data set. This procedure was repeated for data sets that had a variety of temporal patterns, and the model was consistently able to recover the parameters accurately (Figure C.1).
Figure C.1. Model simulations.
The model successfully recovered the parameters underlying the mock data sets, for a variety of temporal patterns, some of which are pictured here. The graphs above illustrate the parameters that were selected to create the mock data sets (in the “Generative” column), as well as the parameters that were recovered by the model (in the “Recovered” column). Each graph shows how the probability of making an error on each level of the decision changes across time in a trial, as well as the changing probability of making a correct response. Some of the temporal patterns tested include: (a & b) serial: error rates decrease for one level at a time, (c) partially parallel: each level has a different start and end, but there is some overlap in the resolution of uncertainty, (d) equal start: error rates for all levels start to decrease at the same time, (e) equal end: error rates on all levels reach asymptote at the same time, (f) asymptotic differences: error rates are different between levels at the end of the trial, (g) partially parallel: the top level resolves before the middle and low levels, which have the same start time, and (h) middle before top: the error rate for the middle level of the decision starts to decrease first.
Appendix D: Experiential Effects
We explored the possibility that experience with the task in Experiment 1 may have affected the temporal pattern of the decision by examining error rates in three different subsections of the experiment: the response deadline practice phase, the first two blocks of the experimental phase, and the fifth and sixth blocks of the experimental phase. For each phase, we plotted how error rates on each level of the decision changed over the trial period, mirroring the standard analysis carried out over the whole session (see Figure 5b). However, because these analyses relied on a fraction of the trials used for full session analysis, there was insufficient data to generate estimates of each individual's error rates for each of the 20 response deadlines. Thus, we pooled data across participants and examined how group-level error rates changed over the course of the trial period.
First, we examined error rates during the response deadline practice phase (Figure D.1a), which was the earliest time in the experiment when participants were behaving according to the complete rule structure. In order to include as much data as possible, we included trials where the response delay was more than 600ms, which was one of the exclusion criteria for experimental trials. We also compared error rates in the first two experimental blocks (Figure D.1b) to error rates in the fifth and sixth experimental blocks (Figure D.1c).
Figure D.1. Experiential effects on group-level error rates.
These plots show how error rates for each policy level change over the window of time sampled in three subsections of the experiment: (a) the response deadline practice phase, (b) the first two experimental blocks, and (c) the fifth and sixth experimental blocks. All participants were included in this analysis, and trials were pooled between individuals (i.e., error rates are on the group level). Responses are binned by deadline and plotted by average response time (measured from the onset of the stimulus).
All three subsections of the experiment show the same general trend as seen in Figure 5b: error rates on all levels of the decision appear to decline in parallel. At the earliest time point available, the error rates are under the level of chance (50%) and generally continue to decline over the course of the trial. The top-level error rate also follows the same trend in all subsections: it appears to decline slightly faster than error rates for the other two levels. In addition, the time frame over which the error rates are declining does not appear to shift substantially over the course of the experiment: most of the decline occurs before 1500ms.
However, the asymptotic error rate does seem to have been affected by familiarity with the task. Early in the experiment, in both the response deadline practice phase and the first two experimental blocks, the error rates do not appear to reach an asymptote by the longest deadline. Error rates continue to decline after 1500ms until the end of the trial period, although the rate of decline is much slower. In contrast, the error rates seem to have reached a relatively stable low by the same time in the fifth and sixth blocks.
This practice effect was evident in the average accuracy rates within the last four response deadline bins. Average accuracy was 67.5% (SD = 22.3%) in the response deadline learning practice phase, 80.5% (SD = 14.5%) in experimental blocks 1 and 2, and 87.3% (SD = 14.8%) in experimental blocks 5 and 6. Paired t-tests between the accuracy for longer trials showed a significant difference between the response deadline practice phase and the first two experimental blocks (t(17)=2.88, p=0.01), as well as the practice phase and the fifth and sixth experimental blocks (t(17)=3.66, p<0.01). There was a trending difference between the first two experimental blocks and the later experimental blocks (t(17)=1.93 p=0.07). These changes are consistent with an overall performance improvement across all levels of the decision with practice.
Overall, we do not find evidence for an experience-dependent flattening of the rule structure. Of course, the earliest point in the experiment when we can examine the timing of the decision is the response deadline practice phase, which follows a lengthy rule-learning phase. It is possible that subjects had already learned to collapse the low- and middle-level rules by that phase. However, the consistency of the general parallel trend across different subsections of the experiment suggests that participants may also have been solving the middle- and low-level rules simultaneously, rather than learning over time to respond to feature conjunctions. Familiarity with the rules seems to have primarily affected the speed at which participants completed all levels of the decision, rather than the relative timing of each level.
Appendix E: Switch Effects
Task-switching is a critical factor to consider in the results from the behavioral paradigm. Due to the structure of the rules, switches occurred at different frequencies for each level of the policy. Thus, the slightly earlier end-time of the top-level decision may have been a result of more frequent rule repetition. In order to explore such effects, we conducted analyses of task switching at different levels of the rule structure.
We assigned a switch to a given level based on the highest level at which a switch occurred between trials. Thus, we defined a switch on the middle- or low-levels as occurring only if the relevant higher-level features repeated. This labeling followed from the logic of the present design, which required that a switch at a given level always entailed switching at all lower levels. Therefore, it was not possible to code switch and repeat across levels as a fully factorial crossing. First, we tested how each type of rule switch affected error rates, comparing switch trials to trials where all the rules repeated (Figure E.1).
Across levels, a switch on any given level of the hierarchy resulted in an increased average error rate for that level relative to repeat trials. This effect was significant for the middle-level error rate in middle-level switch vs. repeat trials (paired t-test: t(17)=6.01, p<0.001), as well as the top-level error rate in top-level switch vs. repeat trials (paired t-test: t(17)=7.19, p<0.001). The effect was not significant for the low-level switch cost (paired t-test: t(17)=1.47, p>0.05).
Figure E.1. Error rate switch cost.
Switch costs were calculated by subtracting the error rate in a repeat trial (all rules repeat) from the error rate in each type of switch trial. Error bars depict standard error.
A switch on any given level also resulted in a switch cost for error rates on lower levels of the hierarchy. This follows naturally from the fact that a higher order rule switch also resulted in a switch of all lower level rules. These observations are supported statistically. There was a switch cost on the low-level error rate when the middle level rule switched (paired t-test: t(17)=4.19, p<0.001), as well as when the top-level rule switched (paired t-test: t(17)=5.34, p<0.001). There was also a significant switch cost on the middle-level error rate when the top-level rule switched (paired t-test: t(17)=5.21, p<0.001).
Notably, switching at a given level did not consistently impact likelihood of an error at a higher level. In other words, we compared the repeat conditions at higher levels with and without a lower level switch. When the low level rule switched, there was not a significant switch cost apparent in middle level error rates (paired t-test: t(17)=0.32, p>0.05) or top-level error rates (paired t-test: t(17)=0.68, p>0.05). When the middle-level rule switched, there was a slightly higher rate of top level errors (paired t-test: t(17)=3.44, p<0.01). However, the switch cost on top-level error rates was higher when the top-level rule was switching, compared to middle-level switches (paired t-test: t(17)=6.48, p<0.001). Note that the significance levels for these paired t-tests were Bonferroni corrected.
To summarize this initial analysis, we found that switching made individual levels of the decision more difficult and had an asymmetrically greater effect on error rates at lower but not higher levels, consistent with the hierarchical structure of the task. This is consistent with prior work that has examined effects of multi-level task switching (Kleinsorge & Heuer, 1999). Moreover, the observation of distinct switching effects at the middle and low level suggests that participants may not have employed a partially flattened task structure that combined the middle and lower levels.
Next, we examined how the timing of the decision may have been affected by top-level rule-switches vs. rule-repetitions (Figure E.2a-b). Unsurprisingly, there was a switch cost on the initiation point when the top-level rule switched and a pronounced benefit when the top-level rule repeated. The middle- and low-level error rates began at very similar levels in both types of trials, although they were slightly lower when the top-level rule repeated.
Despite these initial differences, the time frame over which the error rates declined looked to be largely the same across switch and repeat: error rates reached a stable low at around 1500ms in both the switch and the repeat trials. Strikingly, the top-level error rate was numerically less than the other error rates by this point in both the switch and the repeat trials, consistent with the faster resolution of the top-level decision seen in the full data set. This pattern suggests that the top level of the decision was being resolved earlier than the middle and low levels, even when the top-level rule switched. This is evidence that the top-level timing differences that we report are not an artifact of task-switching, per se. The parallel pattern was also observed for both switch and repeat trials for both middle and low levels of decision, as well (Figure E.2c-f).
The cost of switching a rule appears to affect the initial error rate, but not the parallel nature of the decision or the time at which error rates reach a relatively stable low. This analysis revealed effects of switching at each level, but it was not the case that the top level's earlier end time could be accounted for based on frequency of switching. Moreover, the evidence of separable effects of switching between the low and middle levels may suggest that participants did treat these separately, as opposed to a partially flattened structure.
Figure E.2. Rule-switching effects on group-level error rates.
This analysis includes the 18 participants who were presented with the final set of deadlines. Responses were pooled across the group, binned by deadline, and plotted by average response time (measured from the onset of the stimulus).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aisa B, Mingus B, O'Reilly R. The emergent neural modeling system. Neural networks: the official journal of the International Neural Network Society. 2008;21(8):1146–1152. doi: 10.1016/j.neunet.2008.06.016. doi:10.1016/j.neunet.2008.06.016. [DOI] [PubMed] [Google Scholar]
- Azuar C, Reyes P, Slachevsky A, Volle E, Kinkingnehun S, Kouneiher F, Bravo E, Dubois B, Koechlin E, Levy R. Testing the model of caudo-rostral organization of cognitive control in the human with frontal lesions. NeuroImage. 2014;84(1):1053–1060. doi: 10.1016/j.neuroimage.2013.09.031. doi:10.1016/j.neuroimage.2013.09.031. [DOI] [PubMed] [Google Scholar]
- Badre D, D'Esposito M. Functional magnetic resonance imaging evidence for a hierarchical organization of the prefrontal cortex. Journal of Cognitive Neuroscience. 2007;19(12):2082–2099. doi: 10.1162/jocn.2007.19.12.2082. doi:10.1162/jocn.2007.19.12.2082. [DOI] [PubMed] [Google Scholar]
- Badre D, Frank MJ. Mechanisms of hierarchical reinforcement learning in corticostriatal circuits 2: evidence from fMRI. Cerebral Cortex. 2012;22(3):527–536. doi: 10.1093/cercor/bhr117. doi:10.1093/cercor/bhr117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badre D, Hoffman J, Cooney JW, D'Esposito M. Hierarchical cognitive control deficits following damage to the human frontal lobe. Nature Neuroscience. 2009;12(4):515–522. doi: 10.1038/nn.2277. doi:10.1038/nn.2277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badre D, Kayser AS, D'Esposito M. Frontal cortex and the discovery of abstract action rules. Neuron. 2010;66(2):315–26. doi: 10.1016/j.neuron.2010.03.025. doi:10.1016/j.neuron.2010.03.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badre D, Wagner AD. Selection, integration, and conflict monitoring: assessing the nature and generality of prefrontal cognitive control mechanisms. Neuron. 2004;41:473–487. doi: 10.1016/s0896-6273(03)00851-1. doi:10.1016/S0896-6273(03)00851-1. [DOI] [PubMed] [Google Scholar]
- Benjamin AS, Bjork RA. On the relationship between recognition speed and accuracy for words rehearsed via rote versus elaborative rehearsal. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2000;26(3):638–648. doi: 10.1037//0278-7393.26.3.638. doi:10.1037/0278-7393.26.3.638. [DOI] [PubMed] [Google Scholar]
- Baier B, Karnath HO, Dieterich M, Birklein F, Heinze C, Muller NG. Keeping memory clear and stable – the contribution of human basal ganglia and prefrontal cortex to working memory. Journal of Neuroscience. 2010;30(29):9788–9792. doi: 10.1523/JNEUROSCI.1513-10.2010. doi:10.1523/JNEUROSCI.1513-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biederman I. Human performance in contingent information-processing tasks. Journal of Experimental Psychology. 1972;93(2):219–238. doi: 10.1037/h0032511. doi:10.1037/h0032511. [DOI] [PubMed] [Google Scholar]
- Borst JP, Anderson JR. The discovery of processing stages: Analyzing EEG data with hidden semi-Markov models. NeuroImage. 2015;108:60–73. doi: 10.1016/j.neuroimage.2014.12.029. doi:10.1016/j.neuroimage.2014.12.029. [DOI] [PubMed] [Google Scholar]
- Braverman A, Berger A, Meiran N. The hierarchy of task decisions and response selection: A task-switching event related potentials study. Brain and Cognition. 2014;88:35–42. doi: 10.1016/j.bandc.2014.04.006. doi:10.1016/j.bandc.2014.04.006. [DOI] [PubMed] [Google Scholar]
- Braverman A, Mieran N. Task conflict effect in task switching. Psychological Research. 2010;74(6):568–78. doi: 10.1007/s00426-010-0279-2. doi:10.1007/s00426-010-0279-2. [DOI] [PubMed] [Google Scholar]
- Bunge SA. How we use rules to select actions: A review of evidence from cognitive neuroscience. Cognitive, Affective, & Behavioral Neuroscience. 2004;4:564–579. doi: 10.3758/cabn.4.4.564. doi:10.3758/CABN.4.4.564. [DOI] [PubMed] [Google Scholar]
- Chatham CH, Frank MJ, Badre D. Corticostriatal output gating during selection from working memory. Neuron. 2014;81(4):930–942. doi: 10.1016/j.neuron.2014.01.002. doi:10.1016/j.neuron.2014.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatham CH, Herd SA, Brant AM, Hazy TE, Miyake A, O'Reilly R, Friedman NP. From an executive network to executive control: A computational model of the n-back task. Journal of Cognitive Neuroscience. 2011;23(11):3598–3619. doi: 10.1162/jocn_a_00047. doi:10.1162/jocn_a_00047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christoff K, Gabrieli JDE. The frontopolar cortex and human cognition: Evidence for a rostrocaudal hierarchical organization within the human prefrontal cortex. Psychobiology. 2000;28:168–186. [Google Scholar]
- Christoff K, Keramatian K, Gordon AM, Smith R, Mädler B. Prefrontal organization of cognitive control according to levels of abstraction. Brain Research. 2009;1286:94–105. doi: 10.1016/j.brainres.2009.05.096. doi:10.1016/j.brainres.2009.05.096. [DOI] [PubMed] [Google Scholar]
- Collins AGE, Frank MJ. Cognitive control over learning: Creating, clustering, and generalizing task-set structure. Psychological Review. 2013;120(1):190–229. doi: 10.1037/a0030852. doi:10.1037/a0030852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cools R, Sheridan M, Jacobs E, D'Esposito M. Impulsive personality predicts dopamine-dependent changes in frontostriatal activity during component processes of working memory. The Journal of Neuroscience: the official journal of the Society for Neuroscience. 2007;27(20):5506–14. doi: 10.1523/JNEUROSCI.0601-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Jong R. An intention-activation account of residual switch costs. In: Monsell S, Driver J, editors. Control of cognitive processes: Attention and performance XVIII. MIT Press; Cambridge, MA: 2000. pp. 357–376. [Google Scholar]
- Dutilh G, Wagenmakers E, Visser I, van der Maas HLJ. A Phase transition model for the speed-accuracy trade-off in response time experiments. Cognitive Science. 2011;35:211–250. doi: 10.1111/j.1551-6709.2010.01147.x. doi:10.1111/j.1551-6709.2010.01147.x. [DOI] [PubMed] [Google Scholar]
- Dux PE, Ivanoff J, Asplund CL, Marois R. Isolation of a central bottleneck of information processing with time-resolved fMRI. Neuron. 2006;52:1109–1120. doi: 10.1016/j.neuron.2006.11.009. doi:10.1016/j.neuron.2006.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank MJ, Badre D. Mechanisms of hierarchical reinforcement learning in corticostriatal circuits 1: Computational analysis. Cerebral Cortex. 2012;22(3):509–526. doi: 10.1093/cercor/bhr114. doi:10.1093/cercor/bhr114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank MJ, Gagne C, Nyhus E, Masters S, Wiecki TV, Cavanagh JF, Badre D. fMRI and EEG predictors of dynamic decision parameters during human reinforcement learning. Journal of Neuroscience. 2015;35:484–494. doi: 10.1523/JNEUROSCI.2036-14.2015. doi:10.1523/JNEUROSCI.2036-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank MJ, Loughry B, O'Reilly RC. Interactions between the frontal cortex and basal ganglia in working memory: A computational model. Cognitive, Affective, and Behavioral Neuroscience. 2001;1:137–160. doi: 10.3758/cabn.1.2.137. [DOI] [PubMed] [Google Scholar]
- Goldfarb L, Henik A. Evidence for task conflict in the Stroop effect. Journal of Experimental Psychology – Human Perception and Performance. 2007;33(5):1170–76. doi: 10.1037/0096-1523.33.5.1170. [DOI] [PubMed] [Google Scholar]
- Gottsdanker R, Stelmach GE. The persistence of psychological refractoriness. Journal of Motor Behaviors. 1971;3:301–312. doi: 10.1080/00222895.1971.10734910. doi:10.1080/00222895.1971.10734910. [DOI] [PubMed] [Google Scholar]
- Hazy TE, Frank MJ, O'Reilly RC. Towards an executive without a homunculus: Computational models of the prefrontal cortex/basal ganglia system. Philosophical Transactions of the Royal Society B. 2007;362:1601–1613. doi: 10.1098/rstb.2007.2055. doi:10.1098/rstb.2007.2055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hintzman DL, Curran T. Retrieval dynamics of recognition and frequency judgments: Evidence for separate processes of familiarity and recall. Journal of Memory and Language. 1994;33:1–18. doi:10.1006/jmla.1994.1001. [Google Scholar]
- Kleinsorge T, Heuer H. Hierarchical switching in a multi-dimensional task space. Psychological Research. 1999;62:300–312. [Google Scholar]
- Koechlin E, Ody C, Kouneiher F. The architecture of cognitive control in the human prefrontal cortex. Science. 2003;302:1181–1185. doi: 10.1126/science.1088545. doi:10.1126/science.1088545. [DOI] [PubMed] [Google Scholar]
- Koechlin E, Summerfield C. An information theoretical approach to prefrontal executive function. Trends in Cognitive Sciences. 2007;11:229–235. doi: 10.1016/j.tics.2007.04.005. doi:10.1016/j.tics.2007.04.005. [DOI] [PubMed] [Google Scholar]
- Kriete T, Noelle DC, Cohen JD, O'Reilly RC. Indirection and symbol-like processing in the prefrontal cortex and basal ganglia. Proceedings of the National Academy of Sciences. 2013;110(41):16390–16395. doi: 10.1073/pnas.1303547110. doi:10.1073/pnas.1303547110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy J, Pashler H, Boer E. Central interference in driving: Is there any stopping the psychological refractory period?. Psychological Science. 2006;17:228–235. doi: 10.1111/j.1467-9280.2006.01690.x. doi:10.1111/j.1467-9280.2006.01690.x. [DOI] [PubMed] [Google Scholar]
- Logan GD, Gordon RD. Executive control of visual attention in dual-task situations. Psychological Review. 2001;108:393–434. doi: 10.1037/0033-295x.108.2.393. [DOI] [PubMed] [Google Scholar]
- Marshall L, Bays PM. Obligatory encoding of task-irrelevant features depletes working memory resources. Journal of Vision. 2013;13(2):1–13. doi: 10.1167/13.2.21. doi:10.1167/13.2.21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin AD, Quinn KM, Park JH. MCMCpack: Markov Chain Monte Carlo in R. Journal of Statistical Software. 2011;42(9):1–21. URL http://www.jstatsoft.org/v42/i09/ [Google Scholar]
- Matsuzaki M, Honkura N, Ellis-Davies GCR, Kasai H. Structural basis of long-term potentiation in single dendritic spines. Nature. 2004;429:761–766. doi: 10.1038/nature02617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayr U. Age differences in the selection of mental sets: the role of inhibition, stimulus ambiguity, and response-set overlap. Psychology and Aging. 2001;16:96–109. doi: 10.1037/0882-7974.16.1.96. [DOI] [PubMed] [Google Scholar]
- McElree B, Dosher BA. Serial position and set size in short-term memory: Time course of recognition. Journal of Experimental Psychology: General. 1989;18:346–373. doi:10.1037/0096-3445.118.4.346. [Google Scholar]
- Meyer D, Kieras D. A computational theory of executive cognitive processes and multiple-task performance: Part 1. Basic mechanisms. Psychological Review. 1997a;104:3–65. doi: 10.1037/0033-295x.104.1.3. doi:10.1037/0033-295X.104.1.3. [DOI] [PubMed] [Google Scholar]
- Meyer D, Kieras D. A computational theory of executive cognitive processes and multiple-task performance: Part 2. Accounts of a psychological refractory-period phenomena. Psychological Review. 1997b;104:749–791. doi: 10.1037/0033-295x.104.1.3. [DOI] [PubMed] [Google Scholar]
- Miller EK, Cohen JD. An integrative theory of prefrontal cortex function. Annual Review of Neuroscience. 2001;24:167–202. doi: 10.1146/annurev.neuro.24.1.167. doi:10.1146/annurev.neuro.24.1.167. [DOI] [PubMed] [Google Scholar]
- Monsell S. Task switching. Trends in Cognitive Sciences. 2003;7(3):134–140. doi: 10.1016/s1364-6613(03)00028-7. [DOI] [PubMed] [Google Scholar]
- Moustafa AA, Sherman SJ, Frank MJ. A dopaminergic basis for working memory, learning and attentional shifting in Parkinsonism. Neuropsychologia. 2008;46(13):3144–56. doi: 10.1016/j.neuropsychologia.2008.07.011. doi:10.1016/j.neuropsychologia.2008.07.011. [DOI] [PubMed] [Google Scholar]
- Navon D, Miller J. Queuing or sharing? A critical evaluation of the single-bottleneck notion. Cognitive Psychology. 2002;44:193–251. doi: 10.1006/cogp.2001.0767. [DOI] [PubMed] [Google Scholar]
- Oh WC, Hill TC, Zito K. Synapse-specific and size-dependent mechanisms of spine structural plasticity accompanying synaptic weakening. PNAS. 2013;110(4):E305–E312. doi: 10.1073/pnas.1214705110. doi:10.1073/pnas.1214705110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Reilly RC, Frank MJ. Making working memory work: A computational model of learning in the prefrontal cortex and basal ganglia. Neural Computation. 2006;18:283–328. doi: 10.1162/089976606775093909. doi:10.1162/089976606775093909. [DOI] [PubMed] [Google Scholar]
- O'Reilly RC, Noelle DC, Braver TS, Cohen JD. Prefrontal cortex and dynamic categorization tasks: Representational organization and neuromodulatory control. Cerebral Cortex. 2002;12:246–257. doi: 10.1093/cercor/12.3.246. doi:10.1093/cercor/12.3.246. [DOI] [PubMed] [Google Scholar]
- Öztekin I, Güngör NZ, Badre D. Impact of aging on the dynamics of short-term memory retrieval: A time-course analysis. Journal of Memory and Language. 2012;67:285–294. doi: 10.1016/j.jml.2012.05.003. doi:10.1016/j.jml.2012.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Öztekin I, McElree B. Proactive interference slows recognition by eliminating fast assessments of familiarity. Journal of Memory and Language. 2007;57:126–149. doi:10.1016/j.jml.2006.08.011. [Google Scholar]
- Öztekin I, McElree B. Relationship between measures of working memory capacity and the time course of short-term memory retrieval and interference resolution. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2010;36(2):383–397. doi: 10.1037/a0018029. doi:10.1037/a0018029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pashler H. Dual-task interference in simple tasks: Data and theory. Psychological Bulletin. 1994;116:220–244. doi: 10.1037/0033-2909.116.2.220. doi:10.1037/0033-2909.116.2.220. [DOI] [PubMed] [Google Scholar]
- Plummer M. rjags: Bayesian graphical models using MCMC. R package version 3-5. 2011 URL http://CRAN.R-project.org/package=rjags.
- R Core Team . R: A language and environment for statistical computing. R Foundation for Statistical Computing; Vienna, Austria: 2012. ISBN 3-900051-07-0, URL http://www.R-project.org/ [Google Scholar]
- Rogers RD, Monsell S. Costs of a predictable switch between simple cognitive tasks. Journal of Experimental Psychology. 1995;124(2):207–231. [Google Scholar]
- Rubinstein JS, Meyer DE, Evans JE. Executive control of cognitive processes in task switching. Journal of Experimental Psychology: Human Perception and Performance. 2001;27(4):763–797. doi: 10.1037//0096-1523.27.4.763. doi:10.1037/0096-1523.27.4.763. [DOI] [PubMed] [Google Scholar]
- Schneider DW, Logan GD. Hierarchical control of cognitive processes: Switching tasks in sequences. Journal of Experimental Psychology. 2006;135(4):623–640. doi: 10.1037/0096-3445.135.4.623. [DOI] [PubMed] [Google Scholar]
- Schumacher EH, Seymour TL, Glass JM, Fencsik DE, Lauber EJ, Kieras DE, Meyer DE. Virtually perfect time sharing in dual-task performance: Uncorking the central cognitive bottleneck. Psychological Science. 2001;12(2):101–108. doi: 10.1111/1467-9280.00318. doi:10.1111/1467-9280.00318. [DOI] [PubMed] [Google Scholar]
- Shen M, Tang N, Wu F, Shui R, Gao Z. Robust object-based encoding in visual working memory. Journal of Vision. 2013;13(2):1–11. doi: 10.1167/13.2.1. doi:10.1167/13.2.1. [DOI] [PubMed] [Google Scholar]
- Tombu M, Jolicoeur P. A central capacity sharing model of dual task performance. Journal of Experimental Psychology: Human Perception and Performance. 2003;29:3–18. doi: 10.1037//0096-1523.29.1.3. [DOI] [PubMed] [Google Scholar]
- Tombu M, Jolicoeur P. Testing the predictions of the central capacity sharing model. Journal of Experimental Psychology: Human Perception and Performance. 2005;31:790–802. doi: 10.1037/0096-1523.31.4.790. [DOI] [PubMed] [Google Scholar]
- van Schouwenburg MR, den Ouden HEM, Cools R. The human basal ganglia modulate frontal-posterior connectivity during attention shifting. The Journal of Neuroscience: the official journal of the Society for Neuroscience. 2010;30(29):9910–8. doi: 10.1523/JNEUROSCI.1111-10.2010. doi:10.1523/JNEUROSCI.1111-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welford AT. The ‘psychological refractory period’ and the timing of high-speed performance – A review and a theory. British Journal of Psychology. 1952;43:2–19. [Google Scholar]
- Wickelgren WA, Corbett AT, Dosher BA. Priming and retrieval from short-term memory. Journal of Verbal Learning and Verbal Behavior. 1980;19:387–404. doi:10.1016/S0022-5371(80)90276-5. [Google Scholar]
- Yagishita S, Hayashi-Takagi A, Ellis-Davies GCR, Urakubo H, Shin I, Kasai H. A critical time window for dopamine actions on the structural plasticity of dendritic spines. Science. 2014;345(6204):1616–1620. doi: 10.1126/science.1255514. doi:10.1126/science.1255514. [DOI] [PMC free article] [PubMed] [Google Scholar]