Staged Inertial Microfluidic Focusing for Complex Fluid Enrichment

Abstract

Microfluidic inertial focusing reliably and passively aligns small particles and cells through a combination of competing inertial fluid forces. The equilibrium behavior of inertially focused particles in straight channels has been extensively characterized and has been shown to be a strong function of channel size, geometry and particle size. We demonstrate that channels of varying geometry may be combined to produce a staged device capable of high throughput particle and cell concentration and efficient single pass complex fluid enrichment. Straight and asymmetrically curved microchannels were combined in series to accelerate focusing dynamics and improve concentration efficiency. We have investigated single and multiple pass concentration efficiency and results indicate that these devices are appropriate for routine cell handling operations, including buffer exchange. We demonstrate the utility of these devices by performing a ubiquitous fluorescence staining assay on-chip while sacrificing very little sample or processing time relative to centrifugation. Staged concentration is particularly desirable for point of care settings in which more conventional instrumentation is impractical or cost-prohibitive.

Introduction

Inertial microfluidic focusing is a passive, high-throughput particle and cell focusing technique with diverse applications in particle and cell sample filtration^1–3, encapsulation^4–6, separation^7–13 and flow cytometry^{14, 15}. This unique microfluidic phenomenon passively aligns microparticles and cells to well-defined lateral and longitudinal locations without the need for external actuation^16–19. Inertial focusing is the product of a force balance between opposing inertial lift forces and occurs under flow conditions characterized by Reynolds numbers that approach or exceed a value of one^{19, 20}. In straight channels, these hydrodynamic lift forces arise from interactions between particles, fluids and surfaces, combining to produce well-defined, predictable equilibrium focusing behavior^21–25. Initially observed in a cylindrical tube¹⁶, inertial lift forces confine dispersed particles to narrow equilibrium focusing positions within microchannels, where the number and orientation of focusing positions is dictated by microchannel geometry^{16, 26–28}.

At high flow rates, asymmetrically curved microchannels induce a secondary recirculating (Dean) flow perpendicular to the primary flow direction²⁹. This secondary recirculating flow arises from the gradient in fluid velocity between the center and top and bottom walls of the curved channel. Inertia carries the fluid in the channel center toward the outer side wall of the curve, where mass conservation establishes two counter-rotating vortices. Inertially focused particles are subjected to these secondary flows, referred to as “Dean flows”, and experience a drag force that displaces them from their straight channel equilibrium positions toward the inside of the focusing curve. The biasing of these particles from their straight channel equilibrium positions results in lateral repositioning that is, in turn, balanced by the lift force induced by the inner wall. Previously, the offsetting of particles by curved channels has been used in staged inertial focusing channels¹⁵ to generate focused streams of single particles.

There has been considerable effort focused upon the development of compact, lightweight and cost-effective laboratory equipment for point-of-care (POC) applications^30–32, which are particularly desirable for settings in which conventional instrumentation is impractical or cost-prohibitive. POC technologies based upon microfluidic inertial focusing for the passive handling, concentrating, and sorting of complex biological suspensions are particularly attractive^33–36. Numerous other reports have demonstrated the ability to concentrate particles^{37, 38} some using dielectrophoresis^39–41, magnetophoresis^{13, 42, 43} or acoustophoresis^{44, 45} for microfluidic bioassays, but these techniques are lower throughput or require external hardware and actuation. We have developed a staged inertial focusing approach that is passive, high throughput and robust. We examine the relationship between geometry and particle focusing for the development of an autonomous staged microfluidic device capable of efficiently simplifying sample handling procedures. We show that staged inertial focusing can be applied effectively to concentrate particle suspensions with very high throughput and single pass efficiency. Despite this being a microfluidic approach, a single channel may process milliliters of fluid per minute and channels may be easily parallelized for even higher throughput. In this work, the equilibrium behavior of inertial focused channels has been extensively characterized and the constitutive phenomena described empirically. In POC scenarios, these devices may be readily substituted for centrifugation, which is energy-intensive and can result in significant sample loss.

Materials and Methods

Standard soft lithography methods were used to fabricate and replicate microfluidic devices in polydimethylsiloxane (PDMS)^{46, 47} (Sylgard 184. Dow Corning). PDMS microchannel replicas were bonded to clean glass slides following exposure to oxygen plasma. Microparticle suspensions were pumped with a syringe pump (neMESYS, cetoni GmbH) into microchannels from a 5 mL plastic syringe via Tygon tubing (0.01″ ID). Long exposure imaging was used to capture streaks from particle ensembles in channel expansions using fluorescence microscopy (Olympus IX71 inverted microscope and a VisionResearch Phantom v310 camera). One-dimensional fluorescent intensity profiles perpendicular to the flow direction were acquired and normalized using image processing and analysis software (ImageJ64, National Institutes of Health).

Polystyrene bead solutions were prepared from green fluorescent polystyrene microparticle stock solutions (Thermo Scientific) with an aqueous suspension of 1% solids, a density of ρ=1.05 g/cm³, and a diameter of a=9.9 μm. Microparticles were dispersed into deionized water and iodixanol (OptiPrep, Sigma Aldrich) to final solution concentrations. To prepare neutrally buoyant solutions, fluid density was modified with OptiPep to match the density of the polystyrene microparticles.

Particle suspensions with an initial concentration of 2×10⁶ beads/mL were loaded into a 5mL syringe, and injected into microfluidic devices at a velocity of 0.5 m/s. The device contained 3 outlets: concentrator outlet 1 (fraction 1), concentrator overflow outlet 2 (fraction 2) and bulk fluid outlet 3 (fraction 3). Each output solution was collected separately, and outlets 1 and 2 were recombined prior to analysis. A hemocytometer was used to calculate the concentration of effluent particle solutions. The combined solution (fractions 1 and 2) from the first pass was then re-injected into the same device and collection and analysis was repeated for the second pass. This protocol was repeated for a total of four passes.

Cell suspensions were prepared using A431 cell lines maintained in Dulbecco’s Modified Eagle Medium (Lonza) supplemented with 10% fetal bovine serum (ATCC) and 1% penicillin/streptomycin (Millipore) at 37°C and 5% CO₂. Cells were grown to confluence, trypsinized with a 0.25% trypsin solution, labeled with CellTracker Blue CMAC (Life Technologies), and resuspended at a concentration of 2×10⁶ cells/mL in 16% OptiPrep in PBS. Eosin Y (Sigma) was added to the cell suspension to achieve a final concentration of 25 μM.

All microfluidic channels were primed with a 0.01% Tween 20 solution to prevent cell aggregation. The cell suspension was loaded into a 5 mL syringe and passed through the channel at a velocity of u=0.5 m/s. The same enrichment protocol was followed for fluorescent polystyrene microparticles and cells. A total of four passes were performed, provided sufficient sample was collected from the previous pass. Experiments at each condition were performed in triplicate. Following the third and fourth passes, the final combined output of fractions 1 and 2 were diluted to the original cell concentration (2×10⁶ cells/mL) with 16% OptiPrep in PBS. In order to demonstrate complete removal of the eosin dye from the cell suspension, the concentration of eosin in this diluted sample was measured based on the absorbance at 525 nm (extinction coefficient=89,313 M-1cm-1) using a TECAN Microplate Reader. The concentration of eosin in the bulk fluid output (fraction 3) collected from the third pass of outlet 3 was also measured. A cell suspension at a concentration of 2×10⁶ cells/mL in 16% OptiPrep in PBS (no eosin) was used as a blank for the diluted sample.

Results and Discussion

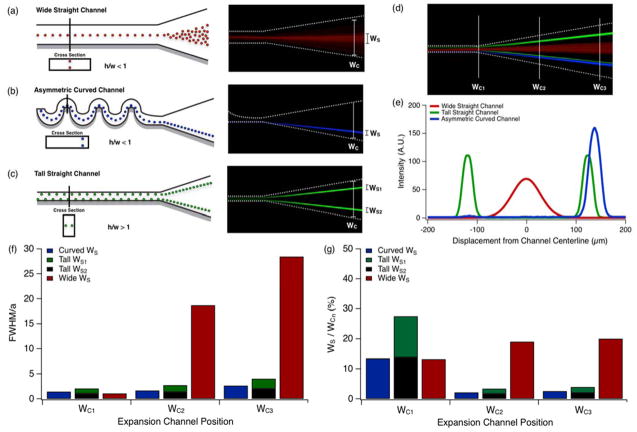
It has been well documented that inertial focusing can be used to concentrate solutions of cell or particles. Even under optimal conditions, however, channel geometry imposes physical constraints upon the efficiency of particle concentration by inertial focusing^48–50. Interacting Stokes’ wakes produce long-range interparticle separations²² that reduce the effective particle concentration within a given collectible fraction, resulting in excess fluid being drawn off with the particles. It is therefore desirable to minimize the fluid volume-to-particle ratio in order to maximize concentration efficiency. As seen in Figure 1, inertial focusing behavior was observed from below using long-exposure fluorescent imaging, and aggregate particle positions were visualized as “streaks”. We define a device’s concentration efficiency as α = 1-W_S/W_C, where W_S is the width of the particle streak and W_C is the width of the channel in which the streak was measured. This ratio provides a partial measure of a channel’s concentration efficiency.

Figure 1.

Inertial focusing behavior in select channel geometries, terminating in expansions, is visualized schematically and by long exposure fluorescent imaging. Focusing performance was observed in channel expansions following: a) a horizontal (h/w < 1) high aspect ratio channel, b) an asymmetrically curved microchannel and c) a vertical (h/w > 1) high aspect ratio channel. d) Collage of long exposure particle streak images overlaying (a)–(c) at positions corresponding to increasing expansion channel width, W_C1, W_C2 and W_C3. e) One dimensional intensity profile of long-exposure particle streak images for (a)–(c). f) Width of particle streak in the channel expansion at positions W_C1, W_C2 and W_C3. g) Percent of channel area occupied by particles for each geometry shown in (e). Particle solutions with a concentration of 2×10⁶ beads/mL were flowed through channels at a constant Re_p=1.5.

To increase the concentration efficiency of inertially focused particles, the interparticle spacing must also be decreased without increasing the relative particle streak-width to channel-width ratio. As previously demonstrated³, channel expansions can be a useful tool to reduce interparticle spacing. As a microfluidic channel expands, the average fluid velocity decreases. While inertial forces dissipate quickly due to a decrease in the particle Reynolds number (Re_p)⁷, corresponding to the fluid velocity, the particles maintain a uniform relative lateral position that is dependent on their initial position as they enter the expansion (Figure 1a–c). As the channel expands the drop in fluid velocity is uniform, except very near the channel side-walls. As stream lines diverge along the expansion section of the channel, imperceptible variations in particle position become amplified. The decreasing fluid velocity also reduces that magnitude of the viscous dissipation that constrains interparticle spacing. In turn, interparticle spacing is reduced, resulting in a concentration efficiency increase. The increase in efficiency is linear with decreasing velocity until the point at which interparticle collisions begin to occur, which manifests in a broadening of the streak width as particles become deflected off-axis. With a minimization of particle stream broadening and interparticle spacing in the expansion, staged inertial focusing devices with expansions are capable of significantly higher concentration efficiencies and collection yields than inertial focusing devices without expansion sections.

A particle’s equilibrium focusing position dictates its position as it enters the expansion, which can be manipulated by channel geometry. Straight, high aspect ratio channels (h/w < 1, Figure 1a) produce two equilibrium focusing positions, one at each channel face, centered on the channel’s longitudinal centerline. Short channel faces are unpopulated as no shear gradient exists in the lateral dimension. Focusing depletes the entire fluid volume of particles across the remainder of the channel. Asymmetrically curved channels were fabricated with cross sections similar to straight, wide high aspect ratio channels, and produce similar focusing behavior. However, they also posses asymmetrical curvature which induces a secondary, orthogonally unidirectional Dean flow that shifts equilibrium focusing positions to the inside channel edge^{7, 22, 28, 29}, reducing the number of focusing positions from two to one as demonstrated by the blue particle streak in Figure 1b and Figure 2a. Straight, high aspect ratio channels (h/w > 1) contain two visible focusing positions, one at each channel face, centered on the channel’s vertical centerline. These two focusing positions are visualized by the two green streaks in Figure 1c. While particles are tightly focused by this geometry, concentration efficiency is confounded by the presence of two lateral particle positions. To most effectively concentrate and collect particles, therefore, a single, tightly focused stream is desired. Particle stream broadening was assessed for each of these three channel geometries by observing particle behavior in the expansion section. Fluorescence intensity was measured at the beginning (W_C1), middle (W_C2) and end (W_C3) of the expansion using long-exposure fluorescent microscopy (Figure 1d). Figure 1e shows one dimensional intensity profiles for each geometry considered in Figure 1a–c at W_C3. The width of the particle streak is expressed as the full width-half maximum (FWHM) of the fitted gaussian distribution for each intensity profile. Theoretically, the FWHM of an optimal particle focusing streak should be equivalent to the FWHM measured from the intensity profile of a single fluorescent particle. Consequently, measured FWHM values were normalized by dividing the streak FWHM by the FWHM measured from a single particle of diameter a=9.9 μm. Therefore, optimum equilibrium focusing behavior should converge to a value of FWHM/a = 1. Values greater than 1 indicate sub-optimal focusing or particle stream broadening. Figure 1f illustrates the effects of channel geometry on particle stream broadening in the expansion section for straight high aspect ratio (h/w > 1, width w=20μm, height h=35μm; h/w < 1, width w=60μm, height h=35μm) and curved microchannels (width w=60 μm, height h=35μm) with similar geometric aspect ratios. Straight, wide high aspect ratio channels (h/w < 1) produced the most particle stream broadening, whereas tall high aspect ratio channels showed the least amount of particle steam broadening. Figure 1g demonstrates the functional outcome of channel geometry on the relative amount of the expansion populated by particles for W_C1, W_C2 and W_C3. Curved channel geometries preformed the best overall, with less than 2% channel consumption by the effluent particle stream, while straight wide high aspect ratio channels (h/w <1) preformed the worst with over 20% particle stream channel consumption at position W_C3.

Figure 2.

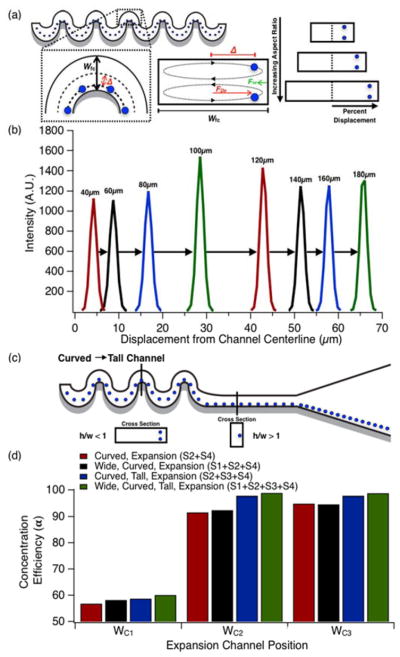
Focusing position biasing efficiency. a) Schematic representation of effects of focusing curve width on lateral particle displacement for increasing focusing curve widths. b) Fluorescent intensity profiles in curved channels with focusing curves of increasing widths. c) Schematic overview of staging curved and tall channels to aligning particles to a uniform lateral streamline position. d) Concentration efficiency of particles in expansion sections W_C1, W_C2 and W_C3 from Fig. 1d for each staged geometry considered. Particle solutions with a concentration of 2×10⁶ beads/mL flowed through 35 μm deep channels at a constant Re_p=1.5. Pre-focusing was performed in horizontally-oriented straight channels with widths, w=80 μm.

The improvement in concentration efficiency between curved channels and tall, high aspect ratio channels is due solely to the number of lateral focusing positions (one vs. two, respectively). It was therefore anticipated that tall, high aspect ratio concentration efficiency would be improved by eliminating one of the two lateral equilibrium focusing positions. As previously demonstrated¹⁵, and shown in Figure 2c, this can be achieved by biasing particles to one side of the channel with a staged asymmetrically curved/straight channel configuration. To examine the limitations of biasing via asymmetrically curved microchannels we evaluated a series of eight channels with increasingly wider focusing curves. Focusing curve widths ranged from w=40 μm to w=180 μm in increments of Δw=20 μm and a channel height of h=35 μm. The fluid velocity was u=0.5 m/s in the smallest channel, and scaled with geometry to maintain constant Re_p number over the range of channel widths. In curved channels, relative particle focusing position changes with focusing curve width as illustrated schematically in Figure 2a. Figure 2b illustrates this shift as one-dimensional intensity profiles taken from long-exposure streak images for increasing focusing curve widths. Figure 2b shows that an increase in focusing curve width results in an increase in particle displacement from the channel centerline. Because the particles’ new equilibrium position is defined by the balance of drag experienced by a particle within a Dean flow and the wall induced lift force, wider channels will necessarily produce greater deviations from the centerline.

While asymmetrically curved channels can both focus and bias particles, it was speculated that their focusing performance was poor relative to their straight, high aspect ratio analogs. To investigate this performance, particles were pre-focused within a straight wide high aspect ratio channel (h/w < 1) before being fed to an asymmetrically curved channel. Two sets of eight channels with varying focusing curve widths and an expansion section downstream of the curvature were examined. One set of eight channels had a straight, wide high aspect ratio channel with a width of w=80 μm and a height of h=35 μm leading into the curved section, while the other set did not. Focusing curve geometries and flow conditions were identical to previous experiments. Intensity profile data was collected at the focusing curve farthest downstream prior to the expansion. Black bars in Figure 2d displays the concentration efficiency for this device configuration.

Next, focused, biased particles exiting the asymmetric curvature were fed directly into a straight vertically-oriented (h/w > 1) high aspect ratio section. This final section aligned focused particles along a uniform lateral streamline near the channel wall before being introduced into the expansion. Particles also assumed uniform longitudinal spacing, which is greater than the mean spacing imposed by curved channels¹⁵ as illustrated schematically in Figure 2c. Green bars in Figure 2d indicate the concentration efficiency for this four stage focusing device.

In comparison to other previously described channel geometry combinations, the four stage focusing device appeared to yield the greatest concentration efficiency at widths W_C1, W_C2 and W_C3 in the expansion. The combined effect of staging can be explained by considering the function of each channel section. Section 1 fully focuses particles to the centerline, at a higher yield than a curved channel alone. This is supported by the observation of a small, but present, particle peak mirroring the primary peak in the asymmetrically curved channel results of Figure 1e. Section 2 efficiently biased the focused particle stream to one half of the channel. Section 3 laterally re-focused and longitudinally spaced the focused and biased particles. Section 4 compacted particle trains⁵¹ to minimize interparticle separation. The net result of these four processing steps was not only optimal concentration efficiency, but also maximum collection yield.

To validate device characterization, particle concentration experiments were performed in each of the geometries examined in Figures 3b–c. First, a feed solution of 2×10⁶ beads/mL was injected into devices and all 3 outlet fractions were collected separately. Post collection concentrated outlets 1 and 2 were then combined and mixed thoroughly prior to analysis. The concentrated solution of combined fractions 1 and 2 from the first pass were then re-injected into the same device and output collection and analysis was repeated for the second pass concentrated and bulk solutions. This protocol was repeated for a total of four passes. Figure 3b displays the particle collection yield in beads/mL as a function of pass number for each of the channel configurations examined previously. Figure 3c shows the fold increase of the concentrated samples for the geometries depicted in Figure 3b as a function of pass number. All measurements for Figures 3b–c were conducted in various channel configurations with a horizontally-oriented channel (w=80μm), focusing curve (w=120 μm), vertically-oriented channel (w=20 μm, h=35μm) and a constant fluid velocity of u=0.5 m/s.

Figure 3.

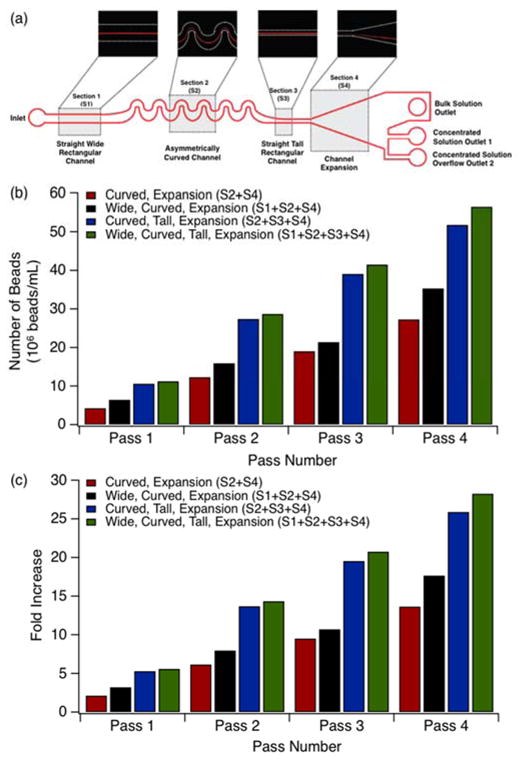
Effects of channel geometry on particle concentration performance: a) Schematic representation of final microfluidic concentrator device design. b) Collection yield for device configurations considered. c) Fold increase in collection yield data illustrated in (b). Particle solutions with a concentration of 2×10⁶ beads/mL flowed through 35 μm deep channels at a constant Re_p=1.5 for all data shown. Pre-focusing horizontally-oriented straight channel width w=80 μm. Focusing curve channel width w=120 μm. Post-focusing vertically-oriented straight channel width w=30 μm.

Each of these three optimized sections were combined into a single four-stage focusing device for final analysis (Figure 3a). Based upon our analysis above, we determined that an optimal staged concentrator device would consist of an inlet, a straight horizontally-oriented (h/w <1) high aspect ratio channel (width w=80 μm), a series of asymmetric curves (focusing curve width w=120 μm), a short straight vertically-oriented (h/w >1) high aspect ratio channel and an expansion section leading into a single bulk solution outlet and two concentrated stream outlets as the schematic in Figure 3a illustrates. Two concentrated solution outlets were included in this design because concentrator outlet 2 acts as an overflow outlet for higher pass numbers where the highly concentrated particle stream exceeds the collection capacity of concentrator outlet 1. The second outlet not only captures overflow particles, but also buffers fluctuations in collection position, making the overall device performance more robust.

Having determined that the four-stage inertial focusing device was optimally suited for particle concentration efficiency and yield, multi-pass particle separations were performed and analyzed. Identical protocol were used for these experiments as those described in Figures 3. A total of three trials were conducted using this protocol. Figure 4a is a micrograph of the concentrator outlet stream in the expansion section of the channel. Figure 4a also shows equal volumes of the initial solution and fractions collected after each pass. Results for this concentration experiment are summarized in Figures 4b–c. Figure 4b displays the number of beads collected in bulk and concentrated fractions following each pass. With increasing passes, the number of beads collected in concentrated fractions 1 and 2 increases. Figure 4c corresponds to Figure 4b and represents the fold increase as a function of pass number. The average fold increase for passes 1 through 4 were determined to be, 4, 13, 20 and 28, respectively. It is noted that higher pass numbers produce a slight increase in occurrence of beads in the bulk solution indicating the performance threshold of the device. Following inertial focusing, the majority of the collection channel is unpopulated with particles, which are concentrated to a narrow streamline. At high initial particle concentrations, therefore, the carrying capacity of the focusing streamline is exceeded and streak broadening occurs as particles interact⁵⁰. As such, the number of passes used depends upon the desired concentration factor and the acceptable degree of particle loss. This tradeoff will likely be based upon application.

Figure 4.

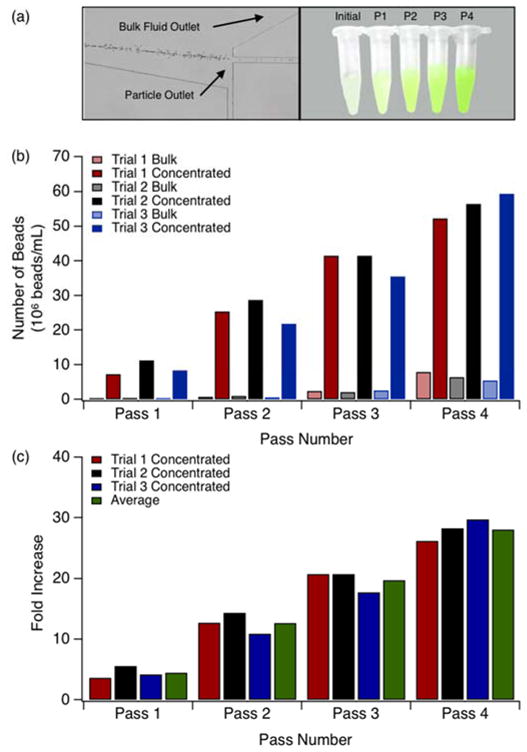
Particle collection yield from a four stage inertial focusing device. a) Visualization of concentrated stream outlet in expansion section (left). Initial solution and fractions collected after each pass (right). b) Particle concentration of concentrated and bulk fractions from the initial suspension and concentrated fractions after each pass. c) Particle concentration fold increase per pass. Particle solutions with a concentration of 2×10⁶ beads/mL flowed through 35 μm deep channels at a constant Re_p=1.5 for all data shown. Pre-focusing horizontally-oriented straight channel width w=80 μm. Focusing curve channel width w=120 μm. Post-focusing vertically-oriented straight channel width w=30 μm.

Concentration of Cells for Solution Exchange

Inertial focusing devices represent an alternative to centrifugation for point-of-care settings and for samples requiring more delicate handling. The passive nature of inertial focusing allows for gentle cell handling that increases cell viability in biological sample processing^{7, 13}. Centrifuges are commonly used to exchange media or to remove excess unbound molecules following a staining or binding protocol (e.g. binding an antibody-fluorophore conjugate to cell surfaces). To demonstrate the applicability of inertial focusing devices to the removal of unbound molecules, we prepared cell suspensions with Eosin Y dye, and subsequently quantified the reduction in the dye concentration following sequential passages. Eosin Y was used as a representative dye in part due to its frequent use as a cellular stain.

Figure 5a presents the relative reduction in eosin concentration once the cells are resuspended to their original concentration following the third and fourth passes. Demonstrating the potential of these devices to be used in place of centrifugation for rinsing cells after labeling, more than 88% of the eosin was removed with the bulk fluid following the third pass for each of the three trials. Figure 5b shows the cell density in the concentrated (fractions 1 and 2) and bulk fluid (fraction 3) for each pass for the three trials performed. As observed with fluorescent microparticles, the concentration of cells from each outlet increased as the concentrated output (fractions 1 and 2) was repeatedly passed through the optimized microfluidic concentrator device. Figure 5c illustrates the fold increase for concentrated suspensions represented in Figure 5b. The average concentration fold increase observed for cell suspensions of passes 1 through 4 were 2, 4, 10, and 15, respectively. This represents a slight reduction in performance relative to tests conducted with polystyrene beads, but this is expected since the cells used were somewhat larger and heterogeneous in size. As demonstrated by the successful processing of both cells and particles, this technology is well suited for high-yield, efficient biological sample processing.

Figure 5.

Concentrator device performance with biological suspensions. a) Percent reduction in eosin concentration. b) Cell density in concentrated and bulk fractions collected in passes 1–4. c) Concentration fold increase per pass. Cell solutions with a concentration of 2×10⁶ cells/mL flowed through 35 μm deep channels at a constant Re_p=1.5 for all data shown. Pre-focusing horizontally-oriented straight channel width w=80 μm. Focusing curve channel width w=120 μm. Post-focusing vertically-oriented straight channel width w=30 μm.

Conclusion

We have used inertial microfluidic focusing to develop a staged microfluidic separation device capable of effective, high-throughput complex fluid enrichment. We have investigated the influence of geometry on particle enrichment and found relationships between overall device performance and channel geometry. Geometric improvements were made to generate a high-yield, tightly focused single stream of particles, which minimizes particle-to-buffer ratio in the effluent stream. We have found that four-staged inertial focusing devices provide the highest per pass concentration efficiency. We have investigated the performance of this concentration device, and have demonstrated its overall effectiveness with bead and cell suspensions. Single and multiple pass concentration efficiencies were demonstrated to be sufficient for routine and complex tasks, alike, including media exchange or the removal of unbound antibodies or fluorophores during assays. This technology has the capability to enable simple, autonomous sample handling for diagnostic and other clinical operations at the point-of-care.