Bleed-through correction for rendering and correlation analysis in multi-colour localization microscopy

Abstract

Multi-colour localization microscopy has enabled sub-diffraction studies of colocalization between multiple biological species and quantification of their correlation at length scales previously inaccessible with conventional fluorescence microscopy. However, bleed-through, or misidentification of probe species, creates false colocalization and artificially increases certain types of correlation between two imaged species, affecting the reliability of information provided by colocalization and quantified correlation. Despite the potential risk of these artefacts of bleed-through, neither the effect of bleed-through on correlation nor methods of its correction in correlation analyses has been systematically studied at typical rates of bleed-through reported to affect multi-colour imaging. Here, we present a reliable method of bleed-through correction applicable to image rendering and correlation analysis of multi-colour localization microscopy. Application of our bleed-through correction shows our method accurately corrects the artificial increase in both types of correlations studied (Pearson coefficient and pair correlation), at all rates of bleed-through tested, in all types of correlations examined. In particular, anti-correlation could not be quantified without our bleed-through correction, even at rates of bleed-through as low as 2%. Demonstrated with dichroic-based multi-colour FPALM here, our presented method of bleed-through correction can be applied to all types of localization microscopy (PALM, STORM, dSTORM, GSDIM, etc.), including both simultaneous and sequential multi-colour modalities, provided the rate of bleed-through can be reliably determined.

1. Introduction

The resolution limit (~200nm) imposed by diffraction for far-field fluorescence microscopy [1] has been recently overcome with the advent of a group of localization-based super-resolution microscopy techniques, including fluorescence photoactivation localization microscopy (FPALM) [2], photoactivated localization microscopy (PALM) [3], stochastic optical reconstruction microscopy (STORM) [4], direct STORM (dSTORM) [5], and ground state depletion microscopy followed by individual molecule return (GSDIM) [6]. By utilizing the probe photophysics to ensure only optically resolvable sparse subsets of fluorophores are visible at any given moment, these techniques localize the diffraction-limited point spread function (PSF) of each emitter with near-molecular precision [7] and reconstruct the final image with localized coordinates. In this way, these techniques have allowed sub-diffraction imaging with resolution of tens of nanometers or better in both fixed and living cells, 10–30nm laterally and ~10–75nm axially [8–11].

Multi-colour imaging with localization microscopy has been demonstrated in different modalities. Thus far, the different modalities of multi-colour imaging can be largely classified as either sequential or simultaneous. The sequential methods utilize spectrally distinct fluorophores and optics for selective and sequential excitation [12, 13] and/or activation [14], and the type of fluorophore visualized at a given time is determined by a particular combination of lasers and/or filter sets used. Conversely, dichroic-based simultaneous imaging simultaneously acquires fluorescence from different probe species excited at the same time, typically with a single excitation laser line capable of exciting all probe types used. The fluorescence of each emitter is then split by a dichroic in the detection path to yield two channels, the transmitted (T) and reflected (R), which are imaged simultaneously by the camera, and which monitor different spectral ranges. The ratio of the PSF intensities in each channel (I_T and I_R) is then used to discriminate the probe species of each molecule in a ratiometric manner [15]. Determined by the emission spectrum of each fluorophore and the transmission profile of the dichroic used, each fluorophore has its own ratio distribution; these methods have been used in simultaneous imaging modalities to discriminate 3–4 probes with even highly overlapping emission spectra [16, 17].

Even though colocalization analysis with multi-colour imaging has become an important tool to elucidate possible molecular interactions at previously inaccessible length scales, bleed-through, which is the improper assignment of probe species, can strongly affect the reliability of information provided by colocalization and subsequent quantification of correlation between species. In sequential methods, nonspecific activation and/or excitation can lead to large bleed-through rates (~35%) [14, 18]. In dichroic-based simultaneous imaging, photon collection statistics and potentially other factors governing I_T and I_R measurements lead to uncertainties in the spectral ratios, causing them to have a distribution, rather than a single value, for each species. Overlap between the distributions of individual species leads to ambiguity and errors in their identification and hence bleed-through. Molecules with measured ratios within the region of distribution overlap can be discarded to keep bleed-through rates as low as ~10% [17] or ~5% [16]. Even though simultaneous imaging with organic dyes has been recently done under a single excitation laser with bleed-through rates as low as 2% [19] and 0.04% [20], these relied on the wide spectral separation (~60nm and ~100nm) of two dyes, while the details of dichroic-based multi-colour imaging had been unchanged. Because of the limited number of dyes that can be excited by a single laser and still have wide spectral separation, and because of the limited number of photons that can be extracted from even the best available fluorophores, bleed-through is expected to remain a major consideration in the application of localization microscopy to the imaging of multiple fluorescent probes.

While conventional microscopy provides a rasterized image with diffraction-limited resolution, the outcome of localization microscopy is the coordinates of localized molecules, and this has naturally led to coordinate-based correlation analyses to quantify the degree of colocalization in multi-colour localization microscopy [16, 21–23]. However, the bleed-through affecting multi-colour localization microscopy interchanges molecules between two crosstalking channels and artificially increases the correlation between the corresponding molecular species. Although stochastic methods of bleed-through correction have previously been used in rendering multi-colour localization microscopy images [14], neither the effect of bleed-through on different correlation functions nor methods of its correction in correlation analyses has been systematically studied at the typical rates of bleed-through reported to affect multi-colour imaging.

Here we present a reliable method of bleed-through correction applicable to the rendering and correlation analysis of multi-colour localization microscopy images. In contrast to the stochastic method mentioned above, our method of bleed-through correction relies on obtaining correct numbers of each species within a sufficiently large area (i.e. within pixels of order tens of nanometers in size), given the rates of bleed-through are provided. We used the Pearson correlation coefficient as a measure of the correction accuracy, and compared its pre- and post-correction values to determine the accuracy and applicability of our bleed-through correction. In addition, we developed a novel method of calculating the Pearson correlation coefficient which yields reliable values unaffected by uncertainties associated with the grid position. Furthermore, we also present a grid-based method of pair correlation calculation which is compatible with our bleed-through correction and yields pair correlation values corrected for artefacts resulting from the bleed-through. Application of our correction method on simulated data shows our method accurately corrects for the artificial increase in the correlation induced by bleed-through and restores the correct value of correlation in both types of above correlation functions, at all rates of bleed-through tested, in all types of correlations examined. Furthermore, a rate of bleed-through as small as 2% reported for certain previous multi-colour imaging [19] with organic dyes was enough to destroy anti-correlation, which was only revealed by using our method of bleed-through correction.

Our presented method of bleed-through correction can be applied to any other dichroic-based modality of multi-colour localization microscopy with dSTORM and GSDIM, and even to sequential multi-colour imaging with PALM or STORM, given that the rates of bleed-through can be determined. Furthermore, apart from the bleed-through correction, our phase-averaging method of Pearson coefficient calculation can also be applied to the analysis of confocal images. Because of the desire for quantification of the interactions between biological species, and because of the sensitivity of these quantifications to bleed-through, this bleed-through correction method is expected to form an important resource for users of localization-based super-resolution microscopy.

2. Methods

2.1. Multi-colour FPALM Setup

Multi-colour FPALM imaging was performed on a setup similar to what was previously described [16], using an inverted-type Olympus IX-71 microscope equipped with 60×1.45-NA TIRF oil-immersion objective lens. Collinear beams from 556nm (readout) and 405nm (activation) diode lasers passed through a +350mm lens to form a focus at approximately the back focal plane of the objective lens, resulting in an illumination area of 1/e² radius of 11 μm at the sample. Fluorescence from the sample was collected by the same objective lens, separated from the lasers with dichroic Z565LP (Chroma, Bellows Falls, VT), and filtered with a long-pass emission filter (LP02-561RU-25, Semrock, Rochester, NY) and a 405nm notch filter (NF03-405E-25, Semrock, Rochester, NY). The single-molecule fluorescence was split by dichroic Z585RDC (Bellows Falls, VT) into transmitted (T) and reflected channels (R), which were filtered, respectively, using FF01-630-92 and FF01-585-40 (Semrock, Rochester, NY), before being projected side-by-side onto an electron-multiplying charge coupled device (EMCCD) camera (iXon DU-897D-CS0-#BV, Andor Technology, South Windsor, CT).

2.2. Image acquisition and analysis

By applying ~15mW (7.3 kW/cm² at the peak) of 556nm laser and varying power of 405nm laser simultaneously onto the sample, a 10,000-frame movie (stack) of the transmitted and reflected channel images was taken for each FPALM image. Frames were acquired at a frequency of 31.5Hz using a high EM gain (200) yielding 34.0 pixel counts per photon. Typically, to account for the photobleaching of molecules, the 405nm laser power was gradually increased from ~0.1 μW to ~100 μW (roughly equivalent to ~0.05 to 50 W/cm²) to keep the number of activated fluorophores to 20–40 in each frame. Analysis of the FPALM image stacks was performed as described previously [16] with custom-written MATLAB scripts. Briefly, the images of the transmitted and reflected channels were combined according to the experimentally-determined channel correlation transformation [24], and the PSFs of activated fluorophores were identified in this combined image (with pixel values above certain threshold, typically equal to 5–10 times the background noise per pixel). Identified fluorophores were then localized by a 2D-Gaussian fit after subtraction of region-specific background using the rolling-ball algorithm [25]. The sample drift was corrected by the cross-correlation method [26]. The α value (spectral ratio) of each localized molecule was determined by evaluating the following ratio using the PSF intensities in the reflected (I_T) and transmitted (I_T) channels:

$$\alpha =I_T/(I_T+I_R).$$ (2.1)

The identity of each species of molecule was assigned based on a range of α values, such that all molecules with α values between ${\alpha }_{\mathrm{A}}^1$ and ${\alpha }_{\mathrm{A}}^2$ were assigned to species A, for example.

2.3. Determination of bleed-through rates

The bleed-through rate k_AB of species A into the channel of another species B is defined as the fraction of species A misidentified as species B and determined from the α-value histogram of species A alone by evaluating the following integral:

$$k_{AB}=\underset{{\alpha }_{\mathrm{B}}^1}{\overset{{\alpha }_{\mathrm{B}}^2}{\int }}{G}_{\mathrm{A}}(\alpha ){\mathrm{d}}^{\alpha }$$ (2.2)

where G_A(α) is the normalized α value histogram of species A, and ${\alpha }_{\mathrm{B}}^1$ and ${\alpha }_{\mathrm{B}}^2$ are the lower and upper limits of the α range specified for B, respectively. The α-value histogram of each fluorescent species was obtained by imaging a single-species sample transfected with only one type of probe construct, imaged with the same multi-colour setup on the same day as multi-colour imaging.

2.4. Phase-averaged Pearson coefficient calculation

The Pearson coefficient measures the correlation between two functions (here, numbers of molecular species A and B as a function of position) in terms of the product of the fluctuations of the two functions about their respective means; a value of 1 indicates perfect correlation, −1 indicates perfect anti-correlation, and 0 indicates no correlation. To restrict Pearson coefficient analysis to the region of interest within the cell, a mask was drawn manually. The binary mask was evaluated with a pixel size d_mask = 50nm small enough to describe the desired contour, with a value of 1 if enclosed or 0 otherwise.

For phase averaging, the grid spacing d_calc used for Pearson coefficient calculation was divided into n equally-spaced values for lateral displacements. These n values were rounded to a nearest integer multiple of the mask pixel size so that the displacement of the image could always be accompanied by the exact same displacement of the mask along with the image. Using two nested for loops in MATLAB, the x and y coordinates of the localized molecules were displaced by each combination of x and y displacements with values determined as above. For each species, these displaced molecule coordinates were then projected onto a grid of spacing d_calc to obtain a density-plot for each of the species, whose pixel values equal the number of localized molecules within the respective grid element (pixel). When desired, the density-plots for each species were then corrected for the bleed-through using (2.6) and (2.7). After correction of bleed-through, the Pearson coefficient between two species A and B for a given displacement was calculated only over the grid elements completely contained by the displaced mask using the following equation:

$${\rho }_{\text{AB}}=\frac{\frac{1}{N_{\text{in}}}{\displaystyle \sum _{x,y}}\left[n_{\mathrm{A}}(x,y)-{\overline{n}}_{\mathrm{A}}\right]·\left[n_{\mathrm{B}}(x,y)-{\overline{n}}_{\mathrm{B}}\right]}{{\sigma }_{\mathrm{A}}{\sigma }_{\mathrm{B}}},$$ (2.3)

where the sum is over all pixels (x,y) enclosed by the mask, N_in is the number of density-plot pixels enclosed by the mask, n_A(x,y) and n_B(x,y) are the pixel value of the density plot of species A and B, n̄_A and n̄_B are the average pixel value of density plot of species A and B within the mask, and σ_A and σ_B are the standard deviation of the pixel values of the density plot of species A and B within the mask, respectively. The Pearson coefficient at a particular grid spacing was reported to be the average of ρ_AB evaluated for the n² displacements, with their standard deviation used for indicating an error bar. We used n = 10 for our calculations.

In practice, this calculation was done by logically indexing the 2D density-plot elements by the binary mask in MATLAB to obtain one dimensional column arrays containing only elements contained within the mask. Multiplication of respective grid elements in the two 2D density plots was done by multiplying the elements of these column arrays having the same index, while N_in is simply the length of these column arrays.

2.5. Pair correlation calculation

The pair (cross) correlation g_AB (r) between molecules of species A and B is typically calculated with coordinates of molecules using the following equation:

$$g_{\text{AB}}(r)=\frac{{\displaystyle \sum _i^{N_{\mathrm{A}}}}{n}_{\mathrm{B}}(r)/A(r){\rho }_{\mathrm{B}}}{N_{\mathrm{A}}},$$ (2.4)

where i is the index running over all molecules of species A (typically within a certain mask), N_A is the total number of molecules of species A, n_B (r) is the number of molecules of species B within r ± Δr/2 of i^th molecule of species A, A(r) is the area of the circular shell within which the molecules of species B were counted, and ρ_B is the average density of molecules of species B. The two-species pair correlation g_AB (r) describes the relative probability (compared to a uniform distribution) of a molecule of species B being found at a distance r away from molecules of species A; values of g(r) >1, 0, and <1 indicate correlation, no correlation, and anti-correlation, respectively. This same quantity can be computed on a grid with an analogous procedure described below.

For the grid-based computation of g_AB (r) between molecules of species A and B, the area over which g_AB (r) will be calculated was specified by drawing a mask as above. To minimize edge effects, this mask was eroded by a distance r_max to yield an eroded mask for selection of inner molecules of species A, which ensures that molecules of species A used in the calculation are at least a distance r_max away from the edge of the region of interest. Localized molecules of species A and B, within the eroded and original masks, respectively, were projected onto a grid of spacing d_pair to yield density plots for each of the species. These density plots were then corrected for the bleed-through using (2.6) and (2.7). When desired, more complete bleed-through correction was achieved by using corrected bleed-through rates (figure B1; see Appendix A.3). For each non-zero pixel n_A (x,y) in the density plot of species A after the bleed-through correction, the sum of the pixel values in the density plot of species B was calculated for all B pixels whose centres were within a radius r ± Δr/2 of that given A pixel, divided by the area of all of those pixels within r ± Δr/2 of that given A pixel, and then multiplied by the pixel value n_A (x,y). The grid-based pair correlation g_AB (r) is then:

$$g_{\text{AB}}(r)=\frac{{\displaystyle \sum _{i=1}^{N_{\mathrm{A}}}}{n}_A(x_i,y_i)\left[{\displaystyle \sum _{j=1}^{N_B}}{n}_B(x_j,y_j)/A(r){\rho }_{\mathrm{B}}\right]}{{\displaystyle \sum _{i=1}^{N_A}}{n}_{\mathrm{A}}(i)}$$ (2.5)

where i is the index running over all pixels enclosed by the eroded mask in the density plot of species A; n_A(x_i,y_i) is the i^th pixel value of the density plot of species A; j is the index that runs over all pixels whose centres are within r ± Δr/2 of n_A(x_i,y_i); N_A is the number of pixels enclosed by the eroded mask in the density plot of species A, N_B is the number of pixels whose centres are within r ± Δr/2 of n_A (i), A(r) is the sum of areas of all pixels that have centres within r ± Δr/2 of n_A(x_i,y_i); and ρ_B is the density of species B within the original mask, calculated by summing all species-B density-plot pixel values within the mask and dividing it by the area of the mask. This method of pair correlation calculation is equivalent to the calculation using the standard definition for pair-correlation (2.4), but is done on the basis of grid elements that allow correction of bleed-through. For our calculations, we used a grid spacing of d_pair = 0.01μm and a binning width of Δr = 0.01μm.

2.6. Bleed-through correction

For Pearson coefficient and g(r) calculations above, the density plots of species A and B corrected for bleed-through ( $n_{\mathrm{A}}^{\text{corr}}$ and $n_{\mathrm{B}}^{\text{corr}}$, respectively) were obtained from the original (or measured) density plots before the bleed-through correction ( $n_{\mathrm{A}}^{\text{meas}}$ and $n_{\mathrm{B}}^{\text{meas}}$, respectively) using the following equations:

$$n_{\mathrm{A}}^{\text{corr}}=\frac{n_{\mathrm{A}}^{\text{meas}}-k_{\text{BA}}{n}_{\mathrm{A}}^{\text{meas}}-k_{\text{BA}}{n}_{\mathrm{B}}^{\text{meas}}}{1-k_{\text{AB}}-k_{\text{BA}}}$$ (2.6)

$$n_{\mathrm{B}}^{\text{corr}}=\frac{n_{\mathrm{B}}^{\text{meas}}-k_{\text{AB}}{n}_{\mathrm{A}}^{\text{meas}}-k_{\text{AB}}{n}_{\mathrm{B}}^{\text{meas}}}{1-k_{\text{AB}}-k_{\text{BA}}},$$ (2.7)

which can be obtained by solving the following equations

$$n_{\mathrm{A}}^{\text{meas}}=n_{\mathrm{A}}^{\text{corr}}-k_{\text{AB}}{n}_{\mathrm{A}}^{\text{corr}}+k_{\text{BA}}{n}_{\mathrm{B}}^{\text{corr}}$$ (2.8)

$$n_{\mathrm{B}}^{\text{meas}}=n_{\mathrm{B}}^{\text{corr}}-k_{\text{BA}}{n}_{\mathrm{B}}^{\text{corr}}+k_{\text{AB}}{n}_{\mathrm{A}}^{\text{corr}},$$ (2.9)

where k_AB is the bleed-through rate of species A into the channel of species B, and k_BA is the bleed-through rate of species B into the channel of species A. Equations (2.8) and (2.9) state that the observed number of molecules of a certain species within a grid element is the true number of molecules minus what bled through to the other channel plus what bled through from that channel. Equations (2.8) and (2.9), together with the measured bleed-through rates, yield the corrected number of molecules of each species within experimental uncertainty. Bleed-through correction becomes more accurate with larger grid spacings, which minimize the effect of counting statistics.

2.7. Density-plot image rendering

The density plots resulting from the above bleed-through correction were assigned with a grayscale pixel intensity proportional to the number of molecules within that pixel. The grayscale images for species A and B were assigned to the green and red channels, respectively, of a single RGB image to form the merged image. For two-colour experimental images with Dendra2 and PAmCherry, the density-plots of Dendra2 and PAmCherry were assigned as the green and red channels, respectively.

3. Results

3.1. Validation of bleed-through correction on simulated data

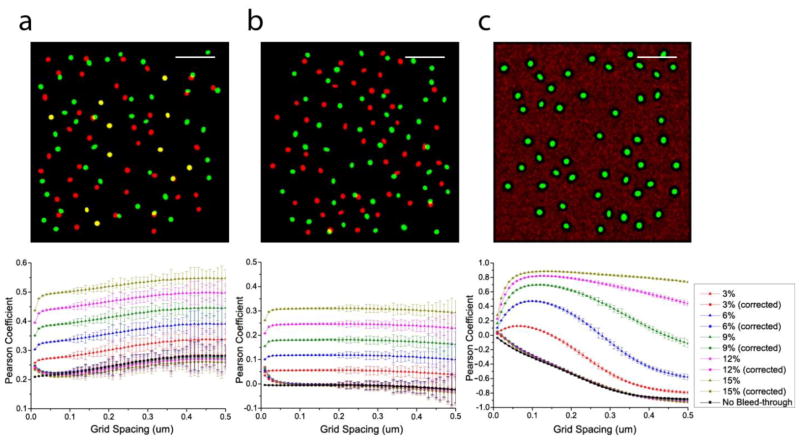
We first confirmed the accuracy and applicability of our bleed-through correction on simulated data before demonstrating its application on experimentally obtained images. In order to test the accuracy of bleed-through correction presented here ((2.6) and (2.7)), we applied the bleed-through correction on simulated two-colour data of three different colocalization patterns (correlation, no correlation, and anti-correlation, shown in figure 1(a), 1(b), and 1(c), respectively) and determined the accuracy of the correction in these simulated data at various bleed-through rates. We used the phase-averaged Pearson coefficient ρ̄_AB (see Appendix B.2) as a measure of the accuracy of correction and compared the pre- and post-correction ρ̄_AB values to determine the applicability of this correction method. The images in figure 1, generated as described in Appendix A.4, were applied with various rates of bleed-through indicated in figure 1 by randomly assigning the indicated fractions of the green molecules into the red channel and vice versa. ρ̄_AB (bottom row, figure 1) were calculated for these three images at those bleed-through rates before and after bleed-through correction, along with the original values in the absence of bleed-through.

Figure 1.

Pearson coefficient as a function of grid spacing before and after the correction of various bleed-through rates in simulated two-colour images of different colocalization patterns. (a) correlation. (b) no correlation. (c) anti-correlation. Scale bar, 2μm.

The bleed-through uncorrected values of ρ̄_AB for these images show that the effect of bleed-through on the Pearson coefficient is to artificially increase the correlation between the two channels with a magnitude that depends on the rates of bleed-through present (figure 1). In all cases, our grid-based correction of bleed-through using (2.6) and (2.7) restores ρ̄_AB close to its value in the absence of bleed-through, correcting 94.3%–99.6% correction of error in these examples (as measured by ρ̄_AB at 0.2 μm).

While ρ_AB is often calculated with a grid spacing equal to the camera pixel size [27, 28], we find that ρ̄_AB may depend significantly on the grid spacing compared to the size of the imaged structure. Figure 1 shows that the values of ρ̄_AB change substantially until the grid spacing becomes as large as the imaged structures (in this case, the clusters of molecules). Beyond this point, larger grid spacings do not affect ρ̄_AB as strongly. Correlation or anti-correlation typically disappears at grid spacings much larger than the size of the correlated structures. In the case of the correlated example, ρ̄_AB values increase rapidly until the grid spacing reaches 0.2μm, which is approximately the diameter of the clusters in the image, beyond which ρ̄_AB changes less rapidly, then reaches a plateau, and finally diminishes as the grid spacing progressively increases. In the anti-correlated example shown in figure 1(c), ρ̄_AB reaches the minimum at a grid spacing of ~0.5μm, which is the length scale of the exclusion of the red molecules from the green structure, and persists until the grid spacing becomes too large to capture the anti-correlation.

3.2. Bleed-through correction in grid-based pair correlation calculations

We next examined the applicability of the grid-based bleed-through correction in the calculation of the pair correlation function g(r), and our ability to obtain correct g(r) values in the presence of bleed-through. The grid-based bleed-through correction method presented here ((2.6) and (2.7)) uses known or estimated rates of bleed-through to correct the number of each species within a sufficiently large area (grid element) that the correction is not substantially affected by counting statistics. Since this grid-based method cannot be directly combined with the standard method of pair correlation calculation based on molecule coordinates (2.4), we introduced a grid-based method of calculating pair correlation (2.5).

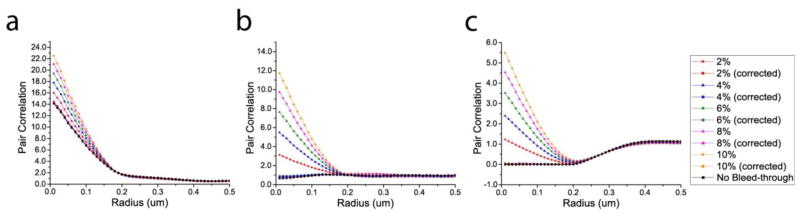
To test our methods for bleed-through correction of g(r), we used the same images shown in figure 1 with various rates of bleed-through applied. Using grid-based methods of bleed-through correction ((2.6) and (2.7)) and of g(r) calculation (2.5), the g(r) was computed before and after bleed-through correction and is shown in figures 2 and B3. As with the above example of the Pearson coefficient, increasing bleed-through rates artificially increased g(r). This artificial increase, however, was restricted to correlations at small radii (r < ~0.2 μm), while g(r) at large radii was less affected by bleed-through. This result is expected from the clustered pattern of the tested structures and the local nature of bleed-through: interchanging species within a cluster makes a misidentified molecule correlate with the immediate neighbours within the cluster, resulting in high correlation at short length scales.

Figure 2.

Pair correlation before and after the correction of various bleed-through rates in the simulated images of different colocalization patterns shown in figure 1 (with the use of the calibration curve). The g(r) curves after the bleed-through correction are mostly hidden behind the black curve showing g(r) values in the absence of bleed-through. (a) correlation. (b) no correlation. (c) anti-correlation.

Application of the above methods resulted in g(r) values close to those obtained in the absence of bleed-through, correcting 78.2–98.1% of error under different bleed-through rates, as measured by g(r) values at r = 10nm (figure B3). Although the agreement between the corrected values and the original g(r) values was satisfactory for small rates of bleed-through (≤ 4% ), there was a general pattern of over-correction, which was pronounced especially at higher rates of bleed-through. While the large values of g(r) in the correlated case were less susceptible to such over-correction (figure B3(a)), the disagreement was more pronounced for the uncorrelated example with small values of g(r) (figure B3(b)) and for the perfectly anti-correlated example with zero values of g(r) (figure B3(c)), leading to negative values of g(r) in some cases (figure B3(b) and figure B3(c)). In order to improve the correction accuracy, we determined the effective bleed-through rate k_eff which resulted in the original values of g(r) when used for correction of the applied bleed-through rate k_app (see Appendix A.3). The values of k_eff as a function of k_app serve as a calibration curve shown in figure B1 and table b1. The calibration curve obtained from the anti-correlated data was used for calculations of g(r) for all three images of different correlation types shown in figure 1, and the g(r) values computed this way are shown in figure 2.

Figure 2 shows the use of the calibration curve obtained from the anti-correlated data yields a good agreement between the corrected and original g(r) values, in all three cases (correlation, no correlation, and anti-correlation), at all rates of bleed-through shown in figure 2. On the average, our method corrected 96.2%, 97.8%, and 99.0% of the error in the examples of correlation, no correlation, and anti-correlation shown in figure 2(a), 2(b), and 2(c), respectively (as measured by g(r) values at r = 10nm). The absence of over-correction and the agreement between the corrected and original g(r) values suggests the calibration curve appears to be applicable to all types of correlation, and the same calibration curve in figure B1 was used for subsequent validation with the simulated data below and for g(r) calculations of experimental data.

3.3. Bleed-through corrected correlation analysis and rendering of a simulated FPALM Image

3.3.1. Application of bleed-through correction on image rendering

We next examined the applicability of the bleed-through correction on the phase-averaged Pearson coefficient analysis and the grid-based pair correlation calculations with a more realistic simulated FPALM image, rather than the previous simulated data artificially constructed with controlled structures and parameters. We also demonstrated bleed-through corrected rendering to show the effects of bleed-through and its correction on a rendered FPALM image. It would be ideal to demonstrate the applicability and accuracy of the bleed-through correction analysis on an actual multi-colour FPALM image acquired from a real sample. However, some degree of bleed-through is usually present in actual multi-colour localization microscopy images, either due to the overlap of the spectral ratio in simultaneous methods or to the overlap of absorption and/or emission spectra of probes in sequential methods. Consequently, there is often no data available for the case of no bleed-through, which must be compared against the pre- and post-correction values in the process of this validation. Therefore, we constructed an FPALM image with no bleed-through by independently acquiring hemagglutinin (HA) and β-actin images (each acquired separately as a single species imaged in two different cells) and merging the two images into a single image, with all of the localized HA and β-actin molecules assigned into the green and red channels, respectively. This yields an effective two-colour FPALM image with molecule numbers and structures typical of actual FPALM images obtained from cells but devoid of any bleed-through. Bleed-through was then applied to the composite HA and β-actin image with rates of 3%, 6%, 9%, 12%, and 15% between the two channels. Such an image, constructed with its two channels taken from two different cells is expected to have little co-localization except for random overlap, and hence little correlation between the two channels.

Using the bleed-through correction and the density-plot rendering described in Methods, the simulated 2-colour image of HA and β-actin was rendered and is shown in figure 3 before (figure 3(a–c)) and after (figure 3(d–f)) bleed-through correction. The composite image before bleed-through correction (figure 3(a)) is characterized by a markedly larger number of yellow pixels throughout the image, compared to its post-correction counterpart (figure 3(d)) in which the pixels making up the HA clusters are almost exclusively green. By comparing the composite channels of the pre- and post-correction images, it is clear that the effect of bleed-through is to create more “yellows” in the bleed-through uncorrected image that signify false co-localization between the two structures. When corrected for bleed-through using the grid-based correction procedure, these false colocalizations disappear completely as the composite channel of the post-correction image shows HA molecules consisting almost exclusively of green pixels. This is the expected result since the actin molecules in the red channel and the HA molecules in the green channel are obtained from two different cells and have no spatial correlation between them.

Figure 3.

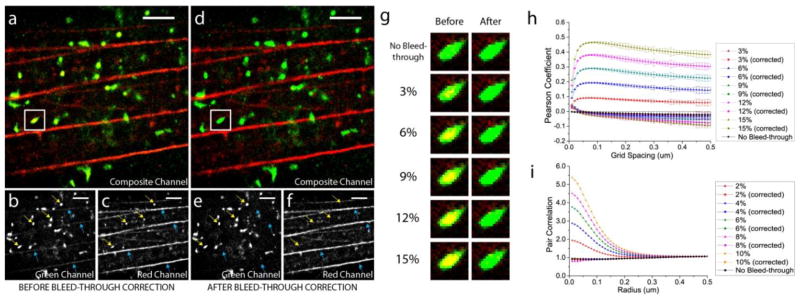
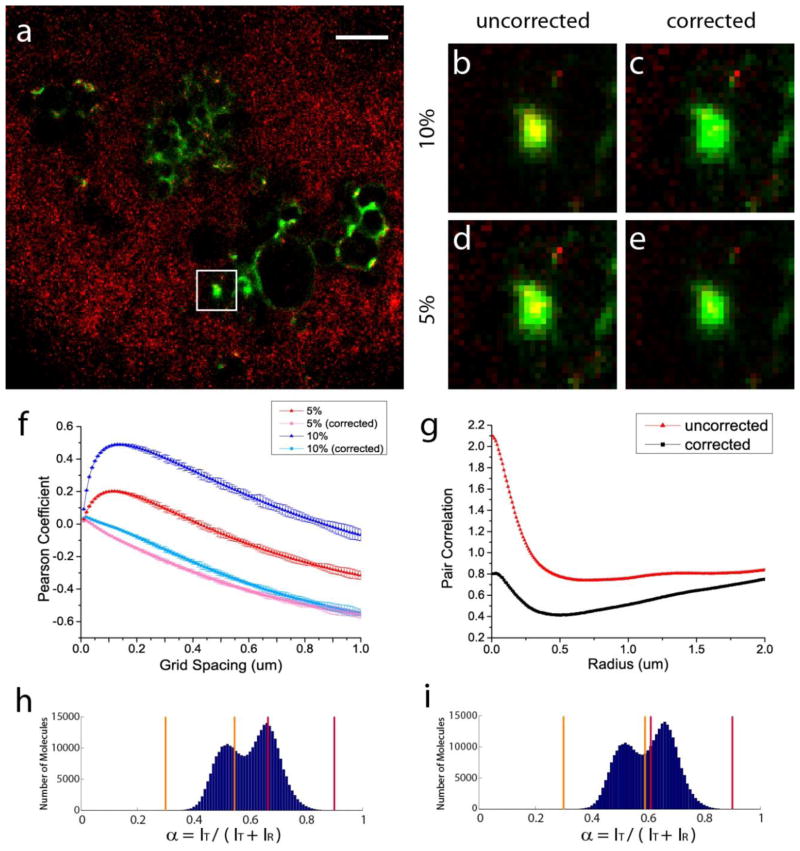
Demonstration of bleed-through correction on a simulated two-colour FPLM image of HA (green) and actin (red). (a) Composite channel of the image before the bleed-through correction, with its green (b) and red (c) channels. (d) Composite channel of the image after the bleed-through correction, with its green (e) and red (f) channels. Scale bar, 2μm. Width of the box, 0.75μm. (g) HA cluster enclosed in the white box rendered before and after the correction of various bleed-through rates. (h) Pearson coefficient between HA and actin as a function of grid spacing before and after the bleed-through correction. (i) Pair correlation between HA and actin molecules before and after the bleed-through correction (with the use of the calibration curve).

The effects of bleed-through and its correction become more apparent when the red and green channels of the pre- and post-correction images are shown separately. The green channel of the HA-actin image before the bleed-through correction (figure 3(b)) shows a number of circular HA clusters, some of which are indicated by yellow arrows. When uncorrected for the simulated bleed-through, these HA clusters originally in the green channel also appear in the corresponding red channel as similar bright clusters (see figure 3(c)), despite the absence of correlation between the two channels due to the controlled merging described above. This artefact of bleed-through can be falsely interpreted as co-localization of the two imaged species if the effect of bleed-through is underestimated or uncorrected. Likewise, the actin stress fibres indicated by blue arrows in the red channel (see figure 3(c)) appear in the corresponding green channel of the uncorrected image (figure 3(b)). However, when the bleed-through is corrected, these same stress fibres are not visible in the green channel, as indicated by the absence of these stress fibres at the same locations indicated by blue arrows in figure 3(e). Similarly, the correction of bleed-through effectively eliminates the HA clusters originally appearing in the red channel in the presence of bleed-through from appearing in the red channel of the corrected image (figure 3(f)), at the locations indicated by the yellow arrows.

The HA cluster enclosed by the white box appearing in figure 3(a) and figure 3(d) is shown in figure 3(g) before and after the correction of the various rates of bleed-through indicated above. As expected from the pre-correction Pearson coefficient values in figure 3(h), an increasing rate of bleed-through entails an increasing false co-localization as shown by an increasing number of yellows pixels for higher rates of bleed-through. However, regardless of the rates of bleed-through applied to our simulated HA-actin image, our method of bleed-through correction can successfully reconstruct the original image without bleed-through (figure 3(g)). Therefore, these examples of simulated images before and after the correction of various bleed-through rates show that our correction method minimizes the artefacts of bleed-through in rendered localization microscopy images.

3.3.2. Application of bleed-through on quantification of correlations

We next compared the Pearson coefficient values ρ̄_AB before and after the bleed-through correction to statistically determine the correlation in the pre- and post-correction images and the accuracy of the bleed-through correction on this simulated HA-actin FPALM image. Figure 3(h) shows that ρ̄_AB for the case of no bleed-through stays close to zero at all grid spacings used, reflecting the fact that there is no correlation between the HA clusters in the green channel and the actin fibres in the red channel. This confirms our earlier statement that we expect no correlation between the two since these are structures imaged from two different cells but simply merged to yield one image. As in the previous simulated examples, the ρ̄_AB values become artificially elevated and reflect different degrees of positive correlation in the presence of bleed-through of varying rates (see figure 3(h)). When corrected for the bleed-through, these elevated Pearson coefficients collapse to values close to the original ρ̄_AB for the case of no bleed-through. Therefore, we have confirmed this bleed-through correction analysis not only yields an image with pixel values satisfactorily close to the original pixel values for the purpose of the bleed-through corrected rendering, but also quantitatively removes the bias introduced by bleed-through, as is reflected by the closeness of the corrected ρ̄_AB to the original.

Finally, the pair correlation g(r) values for HA and actin molecules in this image was computed and is shown in figure 3(i) before and after the bleed-through correction using the calibration curve discussed above (see figure B1). The application of bleed-through in this simulated HA-actin image shows the same general trends we have observed previously: higher rates of bleed-through artificially increase the correlation, particularly at short length scales. Furthermore, in parallel with the near-zero values of bleed-through corrected ρ̄_AB shown in figure 3(h), g(r) values before the application of bleed-through stay very close to 1, indicating no correlation between the two channels. More importantly, the corrected values of g(r) are in very good agreement with the original values of g(r) of no bleed-through. This result indicates that our grid-based methods of pair correlation calculation and bleed-through correction can yield correct g(r) values even in a simulated two-colour FPALM image with parameters and structures typical of experimental FPALM images, and that the calibration curve obtained from the above anti-correlated example of simulated data works well for other types of structures with parameters typical of experimental images.

3.4. Experimental example of anti-correlation: Dendra2-HA and PAmCherry-Cofilin

We next demonstrate the above bleed-through correction on correlation functions and rendering of multi-colour FPALM images obtained from mouse HAb2 fibroblasts [29] expressing two fluorescent probes. With multi-colour FPALM, we imaged the distribution of influenza A virus hemagglutinin (HA; Strain A/X-31(H3N2), 1961, Aichi) and human non-muscle cofilin 1, genetically fused to photoswitchable proteins Dendra2 and PAmCherry, respectively, at the coverslip-proximal membrane of mouse fibroblast HAb2 cells.

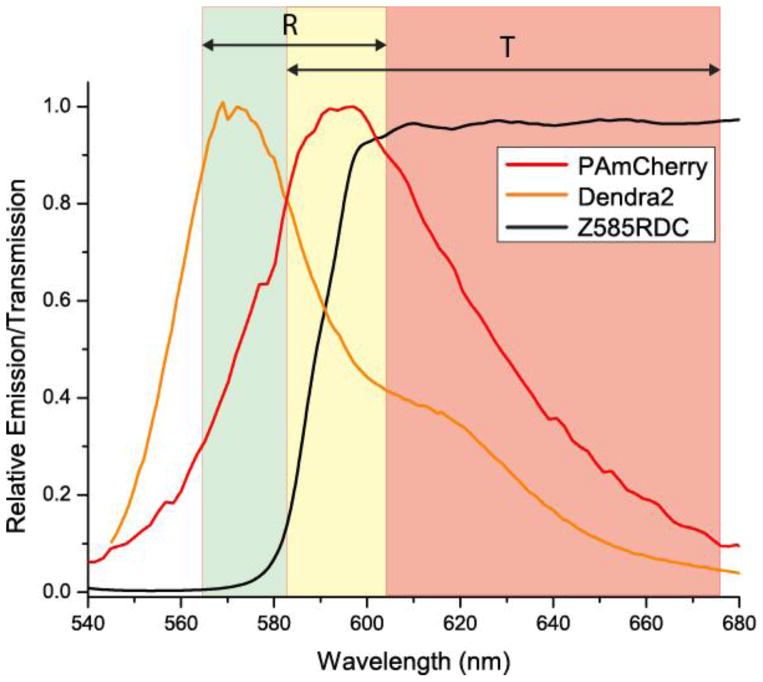
Despite the highly overlapping emission spectra shown in figure A1, Dendra2 and PAmCherry can be distinguished by the dichroic-based method of multi-colour imaging [15, 16]. The rate of bleed-through of a particular probe into the detection channel of another probe can be accurately determined from the single-species distributions of α values using (2.1) [16].

Two-colour FPALM images of Dendra2-HA and PAmCherry-Cofilin show strong exclusion of cofilin molecules from HA clusters (see figure 4(a)). HA molecules often formed dense clusters at the membrane, in various shapes ranging from circular and ring-like to long and linear structures. In contrast, most of the cofilin molecules were diffusely distributed without forming a particular structure, except for the striking exclusion of cofilin molecules from HA clusters even at distances 0.5–1 μm radially beyond the edge of the HA clusters. This strong exclusion between the two imaged species suggests there is an anti-correlation in their spatial distribution. If correlation between the two species were calculated for the image shown in figure 4(a), one would expect a significant negative value for the Pearson coefficient and g(r) significantly below 1, signifying an anti-correlation between them.

Figure 4.

Demonstration of bleed-through correction on experimental images of Dendra2-HA (green) and PAmCherry-cofilin (red) as an anti-correlated example. (a) Two-colour FPALM image of Dendra2-HA and PAmCherry-cofilin (shown after the bleed-through correction). Scale bar, 2μm. (b–e) HA cluster enclosed in the white box rendered before and after the correction of 5% and 10% bleed-through. Rate of bleed-through from Dendra2 (A) into the PAmCherry channel (B) and the rate of bleed-through from PAmCherry (B) into the Dendra2 channel (A) are equal in both cases: k_AB = k_BA. (f) Pearson coefficient as a function of grid spacing before and after the correction of 5% and 10% bleed-through rates. (g) Pair correlation between HA and cofilin molecules with and without the bleed-through correction, for k_AB = k_BA= 0.10. α-value (spectral ratio) ranges used for (h) 5% and (i) 10% bleed-through rates.

The Pearson correlation coefficient was calculated for the molecules shown in this image by selecting the two sets of α-value ranges for Dendra2 and PAmCherry that result in 5% and 10% bleed-through rates (figure 4(h) and figure 4(i), respectively). When the Pearson coefficient was calculated without the bleed-through correction, the correlation between HA and cofilin for this image was in fact positive (figure 4(f)), with values that peak at the grid spacing of ~0.1 μm at both bleed-through rates. These peak positive correlation values in the absence of bleed-through correction were dependent on the rates of bleed-through, and the degree of this positive correlation can be made stronger by choosing non-conservative bins that allowed greater rates of bleed-through between the two species (top blue curve in figure 4(f)). The dependence of the correlation on the selected α-value ranges and hence rates of bleed-through indicates that this positive correlation is an artificial result of the bleed-through, not a characteristic of the image itself.

The Pearson coefficient between HA and cofilin in this image was calculated again with the bleed-through correction for the same bleed-through rates as above. When the bleed-through correction was applied, the correlation coefficient showed negative (anti-)correlation, as indicated by negative values of the Pearson coefficient at nearly all grid spacings (bottom two lines in figure 4(f)). Furthermore, these Pearson coefficients corrected for the two different rates of bleed-through reflect a similar degree of anti-correlation at all grid spacings, unlike the uncorrected values whose magnitude of false correlation depends on the rates of bleed-through present in the data. Therefore, these results indicate the bleed-through correction analysis described here is able to correct for the bleed-through present in actual multi-colour localization microscopy images of biological structures and provide Pearson correlation coefficient values unaffected by the bleed-through of fluorescent probes used. Without the bleed-through correction analysis, such negative correlation could not be quantified in the presence of even a small bleed-through rate (e.g. 5%).

The pair correlation g(r) between the HA and cofilin molecules was computed for this image and is shown with and without the bleed-through correction in figure 4(g). The g(r) without the bleed-through correction was able to quantify long-range anti-correlation at r > 0.25 μm as slight anti-correlation, but showed a positive correlation at short length scales (r < 0.25 μm). Application of bleed-through correction, however, eliminated the short-range positive correlation and further reinforced the long-range anti-correlation, indicating anti-correlation at all length scales examined. Again, without the bleed-through correction, the above positive correlation at short length scale could be falsely interpreted as short-range correlation between HA and cofilin molecules, and such anti-correlation at the short length scale could not have been revealed in the pair correlation without the bleed-through correction.

Figure 4(b–e) shows the HA cluster enclosed in the white box in figure 4(a) rendered as a density plot at 5% and 10% bleed-through rates before and after the bleed-through correction. The images before the bleed-through correction are characterized by pixels with non-zero intensity in both red and green channels, many appearing as yellow, suggesting colocalization between the two species. A higher degree of apparent colocalization is observed at higher rates of bleed-through. After the correction of bleed-through, however, those yellow pixels are largely eliminated in figure 4(c) and figure 4(e), indicating the observed colocalization was false and in fact due to the bleed-through present. At both rates of bleed-through, the corrected images, regardless of the bleed-through rate corrected, consistently show the absence of the artificial colocalizations observed in their pre-correction counterparts. The above results together confirm that the bleed-through correction method not only successfully restores the correct pixel values devoid of bleed-through but also produces accurate and consistent correlation values.

3.5. Experimental example of correlation: Dendra2-actin and PAmCherry-Tm4

As an example of two spatially correlated biomolecules, we imaged Dendra2-tagged β-actin (Dendra2-actin) and PAmCherry-tagged tropomyosin 4 (PAmCherry-Tm4) in NIH-3T3 cells with multi-colour FPALM. Tropomyosins are actin associated proteins; the tropomyosin isoform Tm4 forms a polymer along the length of actin filaments and aids in their stabilization [30]. Based on the previously reported strong spatial association between these two protein species [30, 31], actin and Tm4 were here chosen as examples of correlated species.

In the actin-Tm4 image shown in figure 5(a), a large number of Tm4 molecules (red) were found to colocalize with the stress fibres of actin (green), leading to large portions of the stress fibres in the cell being rendered as yellow pixels as shown. Observed colocalizations, in principle, could disappear after a correction of bleed-through, and these colocalizations cannot be conclusively determined as real unless confirmed by the bleed-through correction analysis.

Figure 5.

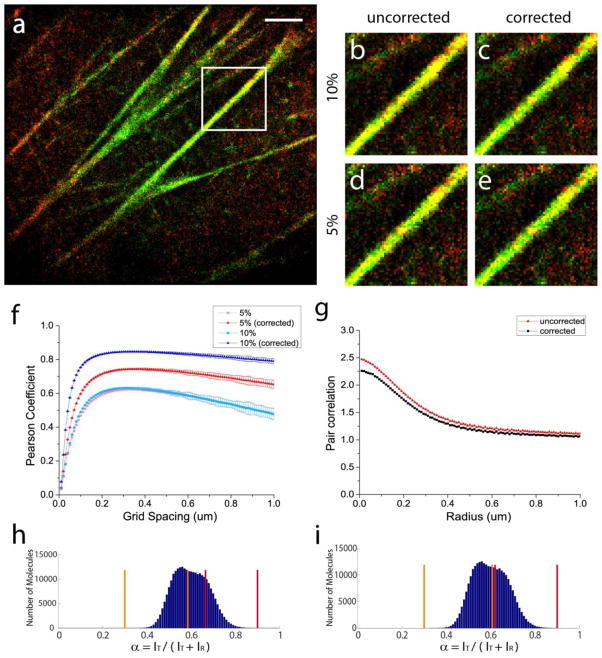
Demonstration of bleed-through correction on experimental images of Dendra2-actin (green) and PAmCherry-Tm4 (red) as a correlated example. (a) Two-colour FPALM image of Dendra2-actin and PAmCherry-Tm4 (shown before the bleed-through correction). Scale bar, 2μm. (b–e) Portion of the stress fibre enclosed in the white box rendered before and after the correction of 5% and 10% bleed-through. Rate of bleed-through from Dendra2 (A) into the PAmCherry channel (B) and the rate of bleed-through from PAmCherry (B) into the Dendra2 channel (A) are equal in both cases: k_AB = k_BA. (f) Pearson coefficient as a function of grid spacing before and after the correction of 5% and 10% bleed-through rates. (g) Pair correlation between HA and cofilin molecules with and without the bleed-through correction, for k_AB = k_BA= 0.10. α-value (spectral ratio) ranges used for (h) 5% and (i) 10% bleed-through rates.

Figure 5(b–e) shows the stress fibre enclosed in the white box in figure 5(a) rendered before and after the correction of 5% and 10% bleed-through rates. Unlike the anti-correlated case of HA and cofilin (figure 4), where the bleed-through correction made a significant difference between corrected and uncorrected images, images of correlated structures like actin and Tm4 were not significantly affected by the correction of bleed-through. Comparison of uncorrected and corrected images shows much of the colocalization indicated by the yellow pixels is preserved after the bleed-through correction.

The Pearson coefficient was calculated on this image before and after the correction of the above bleed-through rates and is shown in figure 5(f). Consistent with previous examples of correlated distributions, correction of bleed-through in this correlated example of actin and Tm4 did not produce a dramatic difference in the Pearson correlation, although higher rates of bleed-through resulted in more artificial increase in the correlation. After the correction of bleed-through, however, the Pearson coefficient values corrected for two different rates of bleed-through (5% and 10%) resulting from different α value ranges for the two species (figure 5(h) and figure 5(i)) agreed with each other within the uncertainty indicated by the error bars (± one standard deviation), indicating our bleed-through correction produces consistent values of correlation independent of the rates of bleed-through corrected. Furthermore, g(r) values shown in figure 5(g) before and after bleed-through correction indicate that the short-range correlation between actin and Tm4 is preserved after the correction. As with other examples of correlation, this example further demonstrates that the bleed-through correction in the presence of genuine correlation produces slightly decreased values of short-range correlation without substantially affecting the overall shape of the g(r) curve.

The bleed-through-corrected Pearson coefficients shown in figure 5(f) rapidly increase at very small grid spacings, and reach the peak value of 0.60 at the grid spacing of approximately 0.2μm, which is approximately the thickness of the imaged stress fibres. The correlation value stays relatively constant for somewhat larger grid spacings until its value slowly decreases for grid spacings much larger than the imaged structures. The maximum Pearson coefficient (ρ̄_AB = 0.60) was obtained for a grid spacing of 0.2μm, indicating a correlation between these two proteins for this particular image. If the Pearson coefficient is to be reported at a single choice of grid spacing, such choice should be guided by the length scales of interest.

4. Discussion

Multi-colour imaging of distinctly labelled biomolecules has become an important tool to answer a variety of biological questions in many types of fluorescence microscopy. Quantification of nanoscale codistribution can provide valuable information about possible molecular interactions [32, 33]. Established correlation functions applied to imaged biomolecules can provide objective and quantitative methods to characterize the type, degree, and spatial dependence of correlation; localization microscopy offers an invaluable advantage by allowing coordinate-based correlation analysis [16, 21, 22] and quantification of correlation at length scales previously inaccessible with conventional forms of fluorescence microscopy. To obtain correct colocalization and correlation between two species of biological molecules, accurate labelling and imaging of each species followed by correction for any misidentification are crucial for correct interpretation of correlation analysis.

The results of our bleed-through correction analysis clearly show that quantification of correlation is very sensitive to bleed-through and that certain types of correlations cannot be quantified even at a bleed-through rate as small as 2%, which is far lower than the rates of bleed-through reported for previous demonstrations of multi-colour imaging, including 5% used for Dendra2/PAmCherry combination in FPALM [16], <10% for Alexa488/Alexa514/Rhodamine3c/Cy3 combination in GSDIM [17], and 25–35% for Cy2/Cy3 activator combination in STORM [14, 18]. Because different modalities of multi-colour imaging can be easily affected by bleed-through for a variety of reasons, ranging from the overlap of spectral histograms in simultaneous imaging modalities [15–17, 19, 20] to non-specific activation/excitation [14, 18] of different probes in laser-specific or sequential methods [13, 21], the presence and extent of bleed-through must be carefully examined and quantified, even if the fluorescent probes used to label different biomolecules appear to have spectra widely separated enough to produce seemingly negligible bleed-through. The extreme sensitivity of correlation to bleed-through also suggests that the bleed-through correction must be used in correlation analyses if there is any rate of bleed-through, even if the bleed-through rate appears to be small enough to produce a visually imperceptible difference in the rendered images. Furthermore, because bleed-through always tends to increase the correlation, any observed correlation between two species of biomolecules [16, 21, 22] must be carefully scrutinized with a bleed-through correction analysis by obtaining single-species data using the same experimental multi-colour setup and estimating the rate of bleed-through using the equations analogous to (2.2).

Our method of bleed-through correction is useful for rendering and correlation analysis with any type of multi-colour imaging modality (simultaneous or sequential, localization-based or conventional). However, when used with the dichroic-based simultaneous method of multi-colour localization microscopy [15–17, 19, 20], it is especially useful in the case of unbalanced distributions of overlapping spectral histograms: for example, when the number of localized molecules of one species tends to dominate that of another species. In such cases of unequal amplitudes, the dominating species tends to leak into the channel assigned for the most spectrally similar probe, resulting in a large number of bled-through molecules and significantly inflated correlation coefficients.

One of the strengths of this bleed-through correction methodology is the fact that it relies on the rates of bleed-through, defined as the fraction of one species being misidentified as another species, rather than the rates of misidentification, defined as the fraction of misidentified molecules compared to the total number of molecules identified (including the bleed-through) for one species. In contrast to the bleed-through rate, the misidentification rate depends not only on the number of bled-through molecules but also the number of molecules correctly identified for that species. Whereas the rate of misidentification is sensitive to the relative amplitudes of spectral histograms of imaged species, the rate of bleed-through is a constant for a fixed choice of probes and α-value ranges assigned for each probe, provided that imaging conditions are unchanged. Its independence from the relative amplitudes of different species makes the bleed-through correction presented here a powerful method unaffected by the number of molecules acquired for each species (which varies from cell to cell depending on the transfection or staining efficiency) and being especially useful in the cases of unequal amplitudes of spectrally similar species.

The Pearson coefficient, also called Pearson product moment coefficient, is a widely used method to quantify co-distribution of two species. Although Pearson coefficient analysis can be done with any type of multi-colour imaging technique, this is most commonly done with the prevalent confocal microscopy, with the image pixel being the natural choice of the grid used for Pearson coefficient calculations [27, 28]. By calculating the Pearson coefficient with the image pixels as the grid, the outcome of this analysis is a single number for the Pearson coefficient between −1 and +1, and this single value of Pearson coefficient is reported to be the correlation between two species analyzed. In localization-based microscopies, where the experimental outcome is a list of localized molecule coordinates, there is no pre-defined choice of pixel or grid spacing to be used for the rendered image. This difference raised the question of what grid spacing should be used to analyze a localization microscopy image for Pearson coefficient calculations, and provided a motivation to calculate the Pearson coefficients over a range of grid spacings as done in this study.

The various simulated and experimental examples above show that the Pearson coefficient values change significantly when computed as a function of the grid spacing, signifying the importance of the grid spacing when computing correlation values. The correlated examples in figure 1 and figure 5 show that the Pearson coefficient values increase dramatically at short grid spacings, reach a plateau approximately at a grid spacing comparable to the size of the imaged structure, and gradually diminish for larger grid spacings. In the anti-correlated examples in figure 1 and figure 4, the Pearson coefficient values decrease rapidly at short grid spacings and reach a minimum at grid spacings comparable to the length scale of the exclusion between the imaged species. Typically, the magnitude of correlation or anti-correlation is maximized by a Pearson coefficient calculated at a grid spacing comparable to the length scale of the correlation or anti-correlation being investigated. In this study, we computed the Pearson coefficients over a wide range of grid spacings to show its behaviour as a function of grid spacing. However, in practice, a single value of the Pearson coefficient could be reported for the optimal grid spacing, if the length scale of the structure or (anti-)correlation is a priori approximately known. The dependence of the Pearson coefficient on the grid spacing suggests that the use of image pixels as the grid for Pearson coefficient calculations in confocal microscopy may not give the maximum magnitude of Pearson coefficient reflecting the degree of (anti-) correlation present in the image. Rather, it is often useful to calculate the Pearson coefficient for a grid spacing comparable to the length scale of the correlation or the size of the structure of interest.

The choice of grid spacing used in bleed-through correction must be made with careful consideration in order to have enough molecules within grid elements to allow correction which is not substantially affected by counting statistics. In our demonstrations of bleed-through correction on various examples above, we observed the convergence of corrected values with the original values of no bleed-through for grid spacings larger than 50nm (figure 1). For this reason, the density-plot images were rendered with the grid spacing of 50nm, which is effectively a lower limit for the grid spacing that can be used while having accurate bleed-through correction in our cases. Larger grid spacings can also be used, although use of large grid spacing limits the resolution of rendered images.

In the bleed-through correction analysis, it should be noted that random errors (with zero net sum) in the pixel values can lead to systematic errors in the Pearson coefficient. This phenomenon can be explained in terms of the conservation of molecules within each grid element. As the addition of (2.8) and (2.9) yields $n_{\mathrm{A}}^{\text{meas}}+n_{\mathrm{B}}^{\text{meas}}=n_{\mathrm{A}}^{\text{corr}}+n_{\mathrm{n}}^{\text{corr}}$, there is a conservation of molecules before and after the bleed-through correction within each grid element. Thus, an increase in one channel is accompanied by a decrease in the other channel, and will therefore cause a trend toward reduced correlation (increased anti-correlation). This is not the same as systematic correction error since the error in the corrected values of the density-plot elements themselves fluctuate about zero. However, for the number and density of molecules typical of usual FPALM images, it has been shown in the many examples above that the correction of various rates of bleed-through yields corrected correlation values in agreement with each other, implying our correction method produces accurate values of the correlation between the imaged species.

Demonstrated with a discrete Fast Fourier Transform (FFT) method previously [23] and with a brute-force method here, the grid-based method of pair correlation has the spacing of data points determined by the binning width Δr during the binning process (see Methods). When made equal to the binning width as done here, the grid spacing used for the bleed-through correction determines the spacing of data points in g(r) graphs and must be made small enough to allow fine enough spacing of data points in g(r). Even though 50nm was proposed above as the lower limit on the grid spacing for proper bleed-through correction, our grid-based method of pair correlation in combination with bleed-through correction was done with 10nm of grid spacing to allow fine resolution because the error of correction fluctuates about zero and the pair correlation calculation directly counts and adds molecule numbers during the computation, cancelling the fluctuating noise during the computation to yield a value with relatively low uncertainty and good convergence toward the ensemble value. This is not the case with the Pearson coefficient calculation, where the product of respective grid elements from two channels is used and any error of correction accumulates as an anti-correlation. For this reason, the over correction observed for higher rates of bleed-through without using the calibration curve (figure B1) is not eliminated by using larger grid spacing for bleed-through correction and g(r) calculation, and the g(r) values calculated with larger grid spacings yielded the same values calculated with small grid spacing we used in our study. Therefore, in grid-based pair correlation calculations, the grid spacing for projection of molecules and the binning width Δr can be made small enough to match the desired resolution of g(r) graphs.

Although demonstrated with a multi-colour FPALM based on dichroic-based simultaneous imaging, this grid-based bleed-through correction method can be applied to other multi-colour localization microscopy methods, including dichroic-based simultaneous imaging with GSDIM or dSTORM and sequential or laser-specific methods of multi-colour imaging with PALM, STORM, or dSTORM, as long as the rate of bleed-through can be determined. In addition, despite its demonstration for the case of two-colour imaging here, this bleed-through correction can be extended to multi-colour imaging with an arbitrary number of probes by directly generalizing (2.6) and (2.7) to the desired number of species. Furthermore, apart from the grid-based bleed-through correction, the phase-averaged Pearson coefficient analysis presented here can be applied even to the analysis of confocal imaging.

Appendix A. Supplementary methods

A.1. Plasmid construction

To construct the plasmid coding for PAmCherry-tagged cofilin (PAmCherry-cofilin), the coding DNA sequence for human non-muscle cofilin 1 (NCBI Accession: BC018256.2) was PCR-amplified and inserted between BamHI and AgeI restriction sites in the Multiple Cloning Site (MCS) of PAmCherry-N1 vector, which was created by replacing EGFP in the pEGFP-N1 vector (Clontech, Mountain View, CA) with the coding sequence of PAmCherry [34].

The construct coding for PAmCherry-tagged tropomyosin 4 (PAmCherry-Tm4) was made by replacing EYFP in the pEYFP-C1 vector (Clontech, Mountain View, CA) with PCR-amplified coding DNA of PAmCherry [34] between NheI and BsrGI restriction sites, and inserting the coding sequence of rat tropomyosin 4 (Tm4; NCBI Accession: NM_012678.2) between BspEI and SalI restriction sites, and C-terminal to the PAmCherry cDNA. Dendra2-HA and Dendra2-actin were the same constructs as those described previously [24].

A.2. Sample preparation

HAb2 [29] or NIH-3T3 cells were cultured, transfected, and prepared for multi-colour imaging as previously described [16] in 8-well chambers with a #1.5 coverslip bottom (155409, Nalge Nunc, Rochester, NY). For transient transfection, we used the following amounts of DNA (per well): 1.0μg of Dendra2-HA and 0.3μg of PAmCherry-cofilin for two-colour HA/cofilin imaging, 0.5μg of Dendra2-actin and 1.0μg of PAmCherry-Tm4 for two-colour actin/Tm4 imaging, and 1.0μg for any single-species imaging. A prepared sample was typically imaged on the same day as fixation to reduce background autofluorescence.

A.3. Calibration of bleed-through corrections to g(r)

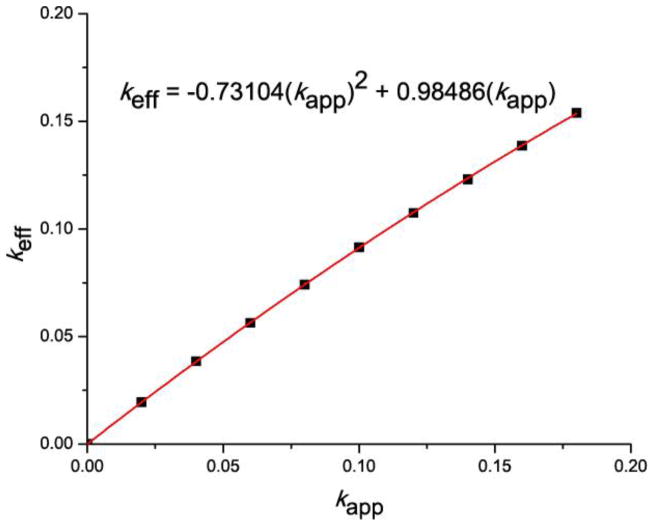
In some cases, particularly for high rates of bleed-through, the standard correction for bleed-through was found to overcorrect. In order to account for these overcorrections, we introduced an effective bleed-through rate k_eff, which yields the proper amount of correction, and is thus used for bleed-through correction of g(r). For obtaining the value of k_eff for a given applied rate of bleed-through k_app, we used the anti-correlated image shown in figure 1(c), which showed the highest sensitivity to bleed-through among the three simulated images. We focused on the g(r) value at 10nm, which has a known value of zero in this case, and is thus particularly sensitive to bleed-through. Bleed-through was applied to this anti-correlated image with various rates k_app ranging from 0% to 18%, in increments of 2%. For a given value of k_app, the value of g(r) at 10nm was evaluated for several rates of bleed-through correction k_eval, in increments of 0.1%. The value of g(r = 10nm) as a function of k_eval was then fitted with a linear function to determine the x-intercept, namely the effective bleed-through rate k_eff needed to produce the correct value (zero) for g(r = 10nm) when used for bleed-through correction. The values of k_eff versus k_app (table B1) were fitted with a 2nd-order polynomial that passes through the origin to yield the calibration curve shown in figure B1.

A.4. Generation of simulated images

The green channel in each of the correlated, non-correlated, and anti-correlated images in figure 1 contains 100,000 molecules consisting of 50 clusters of 2000 molecules each. In order to avoid artefacts that can arise from the periodicity in position or the similarity in simulated cluster shape, these clusters were assigned centre positions randomly scattered across the image, were given the shape of an ellipse with the values of major and minor axis randomly drawn from a Gaussian distribution with a mean of 0.1μm, and were rotated by a random angle. The red channel in the correlated and non-correlated images also consists of 100,000 molecules of 50 clusters of 2000 molecules generated from the same random profile described above, but in the correlated image, ten of the red clusters shared identical centre coordinates with the green clusters so that these overlapping cluster coordinates gave rise to correlation between the two channels. Finally, in the anti-correlated image, in addition to the 100,000 green molecules consisting of 50 clusters of 2,000 molecules as above, 100,000 red molecules were scattered randomly across the image, and were forced to be at least 0.2μm away from the centre coordinate of any green cluster, so that the exclusion of the red molecules from zones with a certain distance of the green clusters yielded anti-correlation between the two channels.

A.5. Emission spectra, dichroic, and filters used in multi-colour images shown

Figure A1.

Emission spectrum of Dendra2 and PAmCherry, and dichroic and filters used in multi-colour FPALM. Dendra2 and PAmCherry have highly overlapping spectra with emission peaks at 573nm and 595nm, respectively. The dichoric Z585RDC separates the fluorescence of Dendra2 and PAmCherry into reflected (R) and transmitted (T) channels, which are filtered with emission filters FF01-630-92 and FF01-585-40, respectively (ranges indicated by double arrows).

Appendix B. Supplementary results

B.1. Calibration curve

The calibration curve which yields the effective bleed-through rate k_eff to be used for correction of a given applied bleed-through rate k_app was determined as described in Appendix A.3 and is shown below. The numerical values fitted to yield the equation shown in figure B1 is tabulated in table B1.

Figure B1.

Calibration curve used for bleed-through correction in pair correlation calculations.

Table B1.

Values of k_eff versus k_app for obtaining the calibration curve.

keff	kapp
0.02	0.01957
0.04	0.03857
0.06	0.05634
0.08	0.07412
0.10	0.09155
0.12	0.10742
0.14	0.12310
0.16	0.13875
0.18	0.15394

B.2. Phase-averaged Pearson coefficient calculation

Determination of co-distribution using Pearson coefficient analysis requires projection of molecule coordinates onto a grid of a defined size (bold black lines in figure B2(a)). The size of an original image (bold blue lines in figure B2(a)) is not in general an integer multiple of the chosen grid spacing. As a result, projection of molecules always leaves grid elements with partially empty areas in the last row and column (fourth column and row in figure B2(a)) such that those grid elements are partially contained by the original image. To avoid artefacts resulting from empty grid elements, it is important to exclude the grid elements not fully contained by the image (or mask of the image). Otherwise, these grid elements can give rise to false correlation and elevated Pearson coefficient values (ρ_AB) that vary with the amount of empty area. For the diagram shown in figure B2(a), the area fully enclosed by the image and thus used for this example of Pearson coefficient calculation is the upper-left 3×3 bold black grid.

A distinct feature of our method of Pearson coefficient analysis is the use of “phase,” namely evenly spaced lateral displacements of the grid relative to the molecular coordinates, to average out the uncertainties associated with the position of the grid relative to the structures being quantified. The initial relative position of the grid with respect to the sample (figure B2(a)) is generally arbitrary, since molecular coordinates are not measured with respect to an absolute reference; thus, one can displace the grid relative to the molecules, and obtain a value for the Pearson coefficient for each displacement. The average of these values (ρ̄_AB ), is not biased as a result of using one particular position of the grid. For example, the cluster circled by the red dashed circle in figure B2(a) is split in half between two grid elements, but would be contained in the same grid element if the grid was slightly displaced to the right. This cluster would then make a strong contribution towards a positive Pearson coefficient when contained within the same grid element, whereas its contribution is diminished when split between two grid elements. These examples demonstrate the variability of the Pearson coefficient associated with the relative position of the grid with respect to the imaged structure.

In order to obtain Pearson coefficient values unaffected by this variability, we subdivide the original grid (bold black lines, figure B2(a)) into n-by-n smaller squares uniformly spaced horizontally and vertically (dashed lines, figure B2(a)). The Pearson coefficient (ρ_AB) is then calculated with the grid at each of these n² positions (“phases”). The value of ρ̄_AB reported is then the average of these n² values, plus or minus the standard deviation of the same values. Since it is the relative position between the image and the grid is that is physically relevant, we effectively realized these phase displacements of the grid by subtracting the desired displacement from the molecule coordinates before being projected on the grid. Figure B2(b) shows that using phase averaging of the Pearson coefficient reduces uncertainty due to the arbitrary position of the grid relative to the imaged structure.

Figure B2.

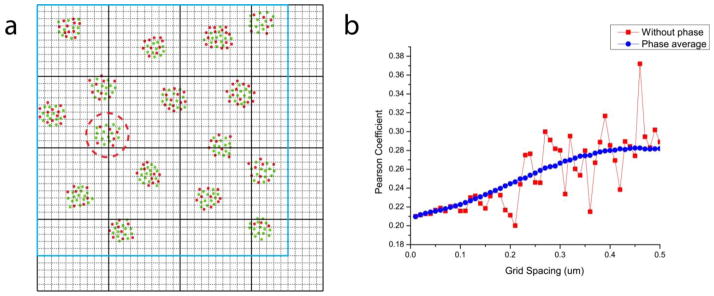
Phase-averaged Pearson coefficient calculation. (a) A schematic diagram showing the (phase) displacement of the calculation grid in Pearson coefficient (ρ_AB) calculations. The grid for ρ_AB calculation (black bold lines) is moved to each of the n² positions defined by the dotted black lines, which divides the calculation grid spacing into n equally spaced intervals (shown for n = 10). The Pearson coefficient was calculated only over the area fully contained by the image (defined by blue bold lines) at each grid position. For example, the cluster within the dashed red circle contributes different degrees of correlation between the green and red species, depending on whether it is split between different grid elements (as shown) or contained within the same element, under different grid positions. (b) Pearson coefficient calculated with (blue circles) and without (red squares) the phase-averaging method.

B.3. Pair correlation calculation without calibration curve

Figure B3.

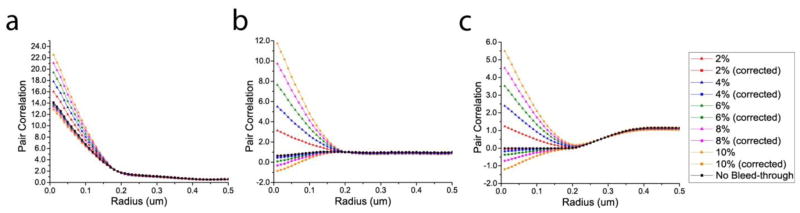
Pair correlation before and after the correction of various bleed-through rates in the simulated images of different colocalization patterns shown in figure 1 (without the use of the calibration curve). (a) correlation. (b) no correlation. (c) anti-correlation.