Hierarchical architecture influences calcium dynamics in engineered cardiac muscle

Abstract

Changes in myocyte cell shape and tissue structure are concurrent with changes in electromechanical function in both the developing and diseased heart. While the anisotropic architecture of cardiac tissue is known to influence the propagation of the action potential, the influence of tissue architecture and its potential role in regulating excitation–contraction coupling (ECC) are less well defined. We hypothesized that changes in the shape and the orientation of cardiac myocytes induced by spatial arrangement of the extracellular matrix (ECM) affects ECC. To test this hypothesis, we isolated and cultured neonatal rat ventricular cardiac myocytes on various micropatterns of fibronectin where they self-organized into tissues with varying degrees of anisotropy. We then measured the morphological features of these engineered myocardial tissues across several hierarchical dimensions by measuring cellular aspect ratio, myocyte area, nuclear density and the degree of cytoskeletal F-actin alignment. We found that when compared with isotropic tissues, anisotropic tissues have increased cellular aspect ratios, increased nuclear densities, decreased myocyte cell areas and smaller variances in actin alignment. To understand how tissue architecture influences cardiac function, we studied the role of anisotropy on intracellular calcium ([Ca²⁺]_i) dynamics by characterizing the [Ca²⁺]_i –frequency relationship of electrically paced tissues. When compared with isotropic tissues, anisotropic tissues displayed significant differences in [Ca²⁺]_i transients, decreased diastolic baseline [Ca²⁺]_i levels and greater [Ca ²⁺]_i influx per cardiac cycle. These results suggest that ECM cues influence tissue structure at cellular and subcellular levels and regulate ECC.

Introduction

The adult heart is characterized by aligned cylindrical muscle cells that facilitate the propagation of electrical signals in directions parallel to the long axis of myocardial fibers.^{1 –3} Within the cardiac tissue microenvironment, a variety of factors, such as the distribution of connexin proteins,^{4 –6} cell shape and size⁷ and the functional integration of myogenic progenitors,⁸ can affect excitation–contraction coupling (ECC). Parsing the sensitivities of ECC to these parameters has proven difficult because of a lack of techniques that facilitate controlled experimental intervention.

Intracellular calcium ([Ca²⁺]_i) dynamics are tightly regulated in the heart and the loss of this regulation marks cardiac pathogenesis.^{9– 11} In vitro studies suggest that changes in myocyte shape,¹² stretch,^13,14 substrate topography and matrix proteins, and exogenous mechanical forces broadly affect cardiac function and can specifically regulate Ca^2+.15,16 We recently showed that geometric cues in the extracellular matrix (ECM) drive unique myofibrillar patterning within isolated ventricular myocytes.^17,18 Given these reports and our own previous work, we hypothesized that the shape and the orientation of cardiac myocytes induced by altered geometry of the ECM might influence Ca²⁺ handling in cardiac tissues.

To test our hypothesis, we used soft lithographic techniques to build two-dimensional (2D) myocardial constructs from ventricular myocytes, permitting control of myocyte shape, architecture and tissue anisotropy on the substrate surface. We quantified the tissue architectures that resulted from the self-organization of the myocytes to the ECM at the subcellular, cellular and tissue levels. Using ratiometric [Ca²⁺]_i imaging, we found that cell and tissue architecture were associated with unique Ca²⁺ dynamics. Our results suggest that tissue structure is an additional regulatory mechanism in cardiac ECC and complements the more commonly investigated contributions of soluble mitogens.

Materials and methods

Myocyte isolation and culture

All experiments were conducted in accordance with the guidelines of the Institutional Animal Care and Use Committee of Harvard University. The isolation of neonatal rat ventricular myocytes has been previously described in detail.^18,19 Ventricular tissue from the hearts of two-day-old Sprague-Dawley rats (Charles River Laboratories, Wilmington, MA, USA) were excised and enzymatically dissociated in 0.1% trypsin and collagenase type 2. Isolated myocytes were suspended in culture medium consisting of Medium 199 (Invitrogen, Carlsbad, CA, USA) supplemented with 10% fetal bovine serum (Invitrogen), 10 mmol/L HEPES buffer (Invitrogen), MEM non-essential amino acids (Invitrogen), 3.5 g/L, glucose, 2 mmol/L l-glutamine, 2 mg/L vitamin B₁₂ and 50 U/mL of penicillin. The fetal bovine serum concentration of the culture medium was reduced to 2% from the second day of culture forward. No streptomycin was used during the isolation and culture of myocytes due to its known inhibitory effects on stretch-activated ion channels.^20,21

Microcontact printing to control tissue structure

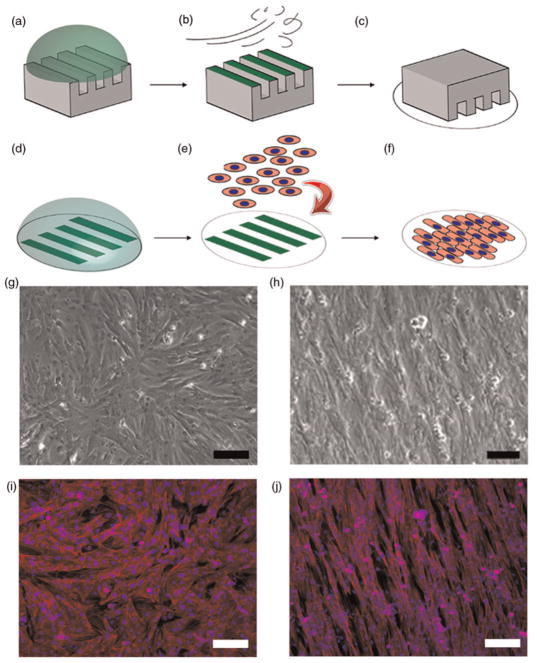
Cardiac tissues with defined architectural anisotropy were engineered by microcontact printing of the ECM protein fibronectin (FN, Invitrogen) onto Sylgard 184 polydimethyl-siloxane (PDMS, Dow Corning, Midland, MI, USA)-coated glass coverslips. Microcontact printing was performed based on previously published methods.²² In this process, 2D photolithographic masks were designed using AutoCAD (Autodesk, San Rafeal, CA, USA), consisting of 20 μm wide lines with 20 μm spaces between them (20 μm × 20 μm) and 10 μm wide lines with 10 μm spaces (10 μm × 10 μm) to pattern anisotropic tissues. Line widths were chosen in an attempt to coax the neonate myocytes to assume shapes in the plane of the culture surface that were within the range of spatial dimensions observed in vivo.²³ A schematic of the microcontact printing procedure is depicted in Figure 1 (panels a–f). First, the PDMS stamps were incubated with 25 μg/mL drops of FN for one hour and dried with a nitrogen gun (Figures 1a and b). The FN pattern was transferred onto the PDMS-coated coverslip surface by bringing the surface of the dry stamp in contact with the ultraviolet ozone (UVO)-treated coverslip (Figure 1c). Following the first printing of FN protein, a background application of 2.5 μg/mL FN was added directly onto of the existing coverslips (Figure 1d). The printing of high concentration FN protein lines on a background of lower density FN provided regular patterning of differential ECM concentrations that potentiated myocyte alignment and fusion into a continuous 2D tissue. Isotropic tissues on uniform ECM density were achieved by incubating UVO-treated coverslips with 25 μg/mL FN for one hour followed by rinsing and storage in PBS. Coverslips were seeded with 1 × 10⁶ cells at a concentration of 5 × 10⁵ cells per mL (Figure 1e). Myocytes formed a continuous syncytium by the third day (Figure 1f) and contracted in a synchronous fashion.²⁴

Figure 1.

Schematic of microcontact printing technique to control tissue architecture. The alignment of 2D myocardial tissues was engineered via printing of fibronectin (FN) protein onto polydimethylsiloxane (PDMS) substrates. (a) High concentration incubation of FN on PDMS stamp. (b) Removal of excess FN by nitrogen gas. (c) Transfer of FN onto UV-treated hydrophilic PDMS surface. (d) Secondary incubation with low-concentration FN. (e) Seeding of prepared cover-slips with primary cell myocytes. (f) Myocytes adhere to geometric FN cues and form a continuous syncytium by day 3. (g and i) Phase contrast and immuno-fluorescence staining of nuclei (blue) and F-actin (green) in isotropic tissues. (h and j) Patterning of high- and low-concentration FN produced aligned anisotropic myocardial tissues. Scale bar = 100 μm

Three tissues architectures were analyzed for cell aspect ratio, cell area, nuclear density and angular myofibril orientation: unpatterned isotropic tissues and anisotropic tissues patterned 20 μm lines with 20 μm spacing (20 × 20) and 10 μm lines with 10 μm spacing (10 × 10). Isotropic and anisotropic myocardial tissues possessed distinctly different tissue architectures when viewed with both phase contrast and immunofluorescence imaging. Upon patterning, the underlying FN matrix provided geometric cues for myo-cytes to spread and align so that they assembled into ordered tissues (Figures 1h and j). Isotropic tissues cultured on uniform ECM density (Figure 1g) were characterized by the unorganized alignment of actin myofibrils (Figure 1i).

Fura-2 measurement of [Ca²⁺]_i

We measured [Ca²⁺]_i-transients in the engineered tissues using high-speed ratiometric [Ca²⁺]_i imaging as previously described.²⁵ Unlike single-wavelength probes, using the ratio-metric dye Fura-2 allows estimation of [Ca²⁺]_i independent of dye concentration, dye leakage, optical path length and instrument sensitivity.²⁶ Measurements of [Ca²⁺]_i-transients were performed on days 3 and 4 after cell seeding. Fura-2 acetoxymethyl cell permeant dye (5 μmol/L final concentration; Molecular Probes, Carlsbad, CA, USA) was added to myocytes in 2 mL of culture medium and incubated for 20 min at 37°C in the dark. The coverslip was then loaded onto a custom-built microscope chamber with integrated platinum electrodes for field stimulation and perfused with oxygenated Tyrode’s solution at 35±2°C. The solution contained (in mmol/L): 1.8 CaCl₂, 5 C₆H₁₂O₆, 5 HEPES, 1 MgCl₂, 5.4 KCl, 135 NaCl, 0.33 NaH₂PO₄. The pH was adjusted to 7.4 using NaOH. Samples were imaged using a Leica IRB inverted microscope with a ×40 NA 1.4 plan-apochromat oil objective. The excitation wavelength was switched between 340 and 380 nm using a galvo-driven mirror at 500 Hz. Fluorescence emission was passed through a 510/40 nm band-pass filter and measured using a photomultiplier detector (Ionoptix, Milton, MA, USA). Anisotropic tissues were oriented so that the major cell axis was perpendicular to the electric field and measurement of Fura-2 was conducted in regions away from the field electrodes. Tissues were field stimulated at frequencies between 1 and 5 Hz using 5 ms long biphasic pulses with an amplitude set to ~10% above the excitation threshold. Fluorescent data were collected from regions of interest 160 × 120 μm² in area.

The calibration of indicator fluorescence was determined at the end of each experiment by measuring the minimum and maximum fluorescent intensity levels as outlined by Grynkiewicz et al.²⁶ Tissue nuclear density was characterized using live 4′,6-diamidino-2-phenylindole staining over a fixed region of interest (160 × 120 μm²). Measurements of [Ca²⁺] were analyzed with customized Matlab (Natick, MA, USA) programs and the maximum return velocity is defined as the maximum derivative from the peak to diastolic baseline of the [Ca²⁺] transient.

Tissue structure quantification

Myocyte morphology was quantified from images of anisotropic and isotropic tissue. The membrane-binding dye di-8-ANEPPS (Invitrogen) was added to culture medium M199 + 2% fetal bovine serum at a concentration of 8 μmol/L for 10 min in order to mark the cell membrane, permitting the area of individual cells to be calculated. Marked cells were imaged on a Leica DM IRB inverted fluorescence microscope (Leica, Wetzlar, Germany) and captured on a EMCCD camera (Cascade 512B Coolsnap; Roper Scientific, Tucson, AZ, USA). Images were analyzed in IPLab (BD Biosciences, Rockville, MD, USA) using image frames selected within the diastolic phase of contraction. Due to high fluorescence signal-to-noise ratio, individual myocytes were randomly selected from each sample image and manually outlined to analyze the cell length, width and area. The cell length was defined as the longest cross-section parallel with the longitudinal axis of the myocyte; the cell width was measured as the length perpendicular to the longitudinal axis through the middle of the cell. The corresponding aspect ratio for each myocyte was calculated as cell length divided by cell width. Tissue anisotropy was characterized by analysis of the intra-cellular myofibril network obtained from fixed and stained tissue cultures¹⁸ via staining of the actin cytoskeleton (AlexaFluor 488 Phalloidin; Invitrogen).

Characterization of actin filaments was performed on the immunofluorescence images using previously described feature enhancement procedures.^27,28 Briefly, grayscale images of actin networks were normalized by their mean and variance to reduce intensity variations. The normalized images were processed to create an orientation image by calculating the local orientation of elongated regions of high fluorescence relative to background, in this case the phalloidin-labeled actin. Frequency image estimation was then conducted in order to identify the distribution and frequency of polymer-ized actin. These images served to initialize Gabor filters that were applied to the normalized image to produce an enhanced actin ridge image, which was then skeletonized to yield line segments identifying individual myofibrils. The angular orientation data of all identified myofibrils were collected and used to characterize the degree of tissue anisotropy for each image as a measure of the angular distribution. Statistical significance was assessed by analysis of variance combined with Wilcoxon’s rank sum test.

Results

Cell shapes in isotropic and anisotropic monolayers

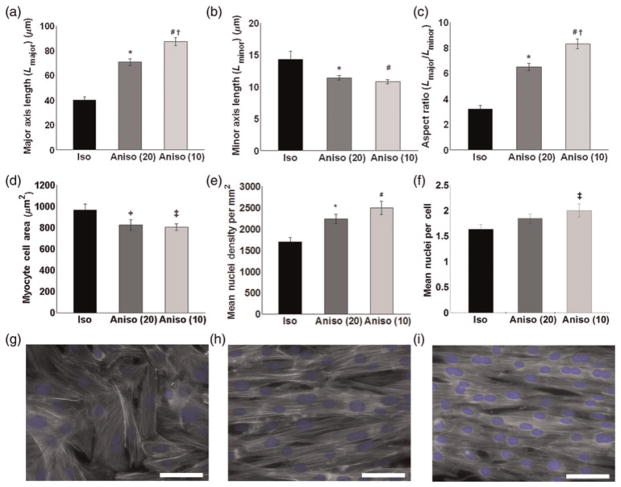
We analyzed cell shapes in our engineered tissues to understand how the cardiac myocytes adapted to the geometrical constraints of the ECM substrate. Cells cultured on FN lines formed anisotropic tissues and were elongated, with a longer major axis and a shorter minor axis (Figures 2a and b) compared with isotropic tissues. The mean cellular aspect ratio was larger in cultures that had thinner lines, i.e. 6:1 for 20 × 20 and 8:1 for 10 × 10 patterns. In contrast, isotropic tissues had a significantly smaller mean aspect ratio of 3:1 (Figure 2c). Anisotropic patterning significantly reduced myocyte area in both anisotropic groups (Figure 2d). We found that the most anisotropic tissues had significantly more nuclei per unit area when compared with isotropic tissues (Figure 2e), where statistical analysis of tissues revealed that 10 × 10 μm anisotropic tissues had significantly more nuclei per cell than isotropic cultures (Figure 2f). These data suggest that binucleation in cardiac myocytes can be induced by cellular elongation within a confluent monolayer (Figures 2g–i).

Figure 2.

Characterization of myocardial tissue architecture. Individual cells organized within isotropic and anisotropic tissues were characterized for cell shape, cell area and nuclear properties. Engineered anisotropic tissues display elongated cell shapes illustrated by increased major axis length (a), decreased minor axis length (b) as well as greater cellular aspect ratios (c). Anisotropic patterning significantly regulates myocyte cell area (d). Myocardial tissues were characterized for nuclear density per region of interest (160 × 120 μm²) (e) and the mean number of nuclei per cell (f). The 20 × 20 and 10 × 10 tissues possessed higher nuclear densities per region of interest when compared with isotropic tissues. The patterning of isotropic (g), 20 × 20 anisotropic (h) and 10 × 10 anisotropic tissues (i). Values are expressed as mean ±SE. ^{*, #}P < 0.01 versus isotropic, ^{+, ‡}P < 0.05 versus isotropic, ^†P < 0.01 versus anisotropic (20 × 20). Isotropic (n = 24), 10 × 10 anisotropic (n = 21) and 20 × 20 anisotropic (n = 30)

Quantification of architectural anisotropy

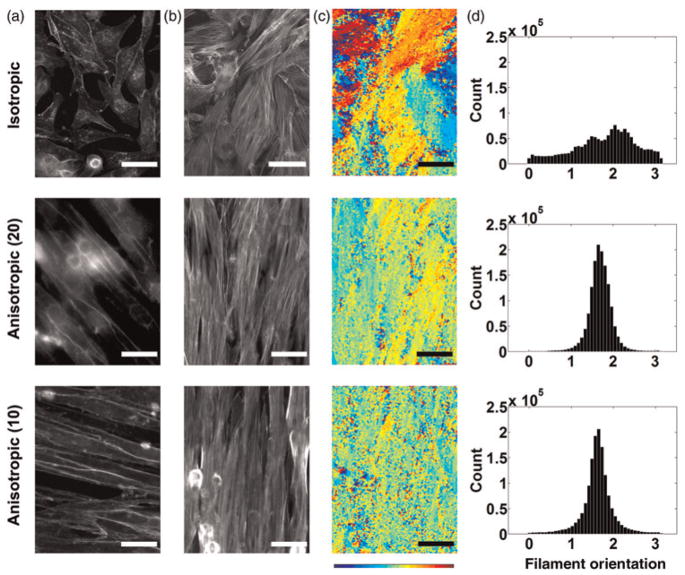
We reasoned that myofibrils represent an accurate measure of tissue anisotropy because myofibrils align in parallel with the principal axis of the cell.²⁹ Flourescent microscopy of tissues with stained cell membranes (Figure 3a) and F-actin (Figure 3b) confirmed that the myofibrils were generally aligned with the long axis of the myocyte. Isotropic tissues displayed localized regions of alignment, but none in the aggregate (Figure 3a, top panel) while anisotropic tissues consistently displayed uni-axial alignment (Figure 3a, middle and bottom panels). Compared with the isotropic, the 10 × 10 and 20 × 20 anisotropic tissues showed more organized alignment of myocyte cell membranes. Corresponding F-actin stains revealed that the polymerized F-actin aligned with the long axis of the myocyte (Figure 3b).

Figure 3.

Quantification of tissue anisotropy via angular orientation analysis. The staining for plasma cell membrane and F-actin revealed co-alignment of actin myofibrils with cell membrane orientation; immunofluorescence of plasma membrane (a) and F-actin (b). Isotropic tissues (top row) adopt disorganized tissue structures with minimal alignment of adjacent myocytes. The 20 × 20 (middle row) and 10 × 10 (bottom row) anisotropic tissues align to form much more homogeneous structures. (c) Actin alignment quantified with angular mapping; the angular orientation of actin myofibrils is color-coded. Evaluation of color homogeneity provides a measure of overall tissue alignment. (d) Angular histogram showing the distribution of actin orientation; the standard deviation is a measure of the angular spread (n = 7 for isotropic, n = 7 for 20 × 20 anisotropic and n = 5 for 10 × 10 anisotropic)

We quantified tissue anisotropy by measuring myofibril orientation in individual samples and constructed color-coded angular maps (Figure 3c) and orientation histograms (Figure 3d). As expected, angular maps for isotropic tissues (Figures 3c and d, top panel) displayed more heterogeneity in the orientation of actin myofibrils than anisotropic tissues (Figures 3c and d, middle and bottom panels). In contrast, angular maps for anisotropic tissues displayed in Figures 3c and d (middle and bottom panel) were characterized by more homogeneous angular measures, indicating that actin filaments were more organized and aligned in the same direction.

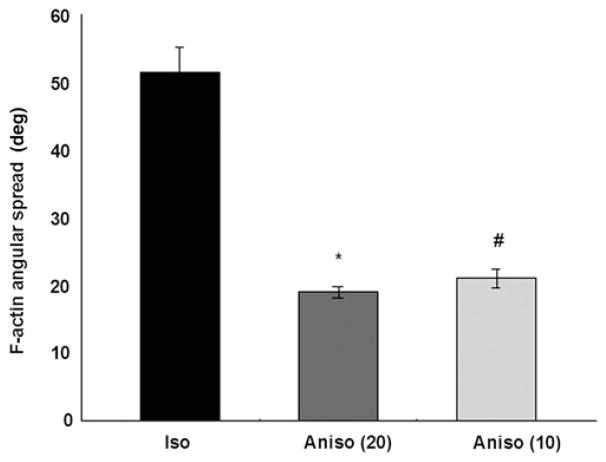
To investigate the statistical distributions of actin alignment, we condensed the 2D orientation data from our angular maps into histograms of angular distribution; the standard deviation of the angular data provides a single value describing an aggregate measure of tissue anisotropy. The mean myofibrillar angular spread (defined as the standard deviation of the angular distribution) of isotropic tissues was significantly larger than both anisotropic groups (P < 0.01) while there was no significant angular difference between 20 × 20 and 10 × 10 anisotropic tissues (Figure 4). Isotropic cell networks possess wider angular distributions because their myofibril structures are characterized by greater disorganization and more variance in myofibril orientation. Thus, the more aligned a tissue, the lower the angular spread of the fibril orientation angles, and the higher the anisotropy.¹⁸ These data suggest that geometric patterning of cardiac myocytes causes polarization of the actin cytoskeleton, as indicated by a decrease in the angular spread of the actin myofibrils.

Figure 4.

Angular spread of F-actin in cardiac tissues. The 20 × 20 and 10 × 10 anisotropic tissues were characterized by significantly lower standard deviations in F-actin angular spread than isotropic tissues. Values are expressed as mean±SE. ^*, ^#P < 0.01 versus isotropic

Tissue anisotropy affects Ca²⁺ dynamics

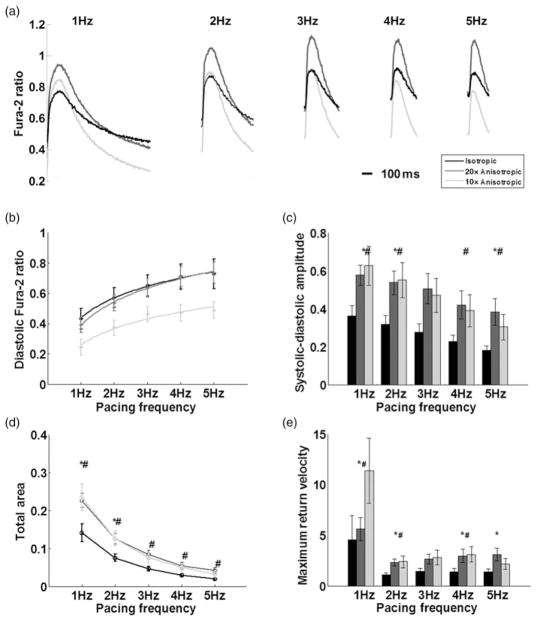
Previous work by Entcheva and colleagues³⁰ showed that when cardiac myocytes are grown on microgrooved substrata, myocytes showed increased diastolic and systolic [Ca²⁺]_i during pacing. In addition, work by Walsh and Parks¹² showed increased voltage-gated currents, including Ca²⁺ in ventricular myocytes cultured in aligned collagen, resulting in elongated cell shapes. Given the results of these studies and our morphometric measurements, we hypothesized that the anisotropic cellular arrangement in our engineered tissue would affect [Ca²⁺]_i. To test this, we measured [Ca²⁺]_i-transients in isotropic and anisotropic tissue cultures during field stimulation. Example [Ca²⁺]_i-transients averaged over 10 consecutive beats and a comparison between isotropic, 20 × 20 and 10 × 10 anisotropic tissues are shown in Figure 5a. All three groups displayed a positive [Ca²⁺]_i –frequency relationship,31 i.e. an increase of the diastolic baseline [Ca²⁺]_i with increasing frequency.

Figure 5.

Functional evaluation of Ca²⁺ dynamics with respect to tissue architecture. Isotropic (black, n = 9), 20 × 20 anisotropic (dark gray, n = 9) and 10 × 10 anisotropic (light gray, n = 9). (a) Example Ca²⁺ transients waveforms obtained by averaging 10 consecutive Ca²⁺ transients. Tissues were electrically stimulated between 1 and 5 Hz with Ca²⁺ levels measured by the ratiometric Ca²⁺ indicator Fura-2. (b) Frequency-dependent sensitivity of diastolic Ca²⁺ levels, 10 × 10 anisotropic tissues were characterized by lower diastolic baseline levels. (c) More Ca²⁺ is cycled into cells during each contraction in anisotropic tissues as evidenced by the systolic–diastolic amplitude in Ca²⁺ intensity. (d) Integrated total area is significantly higher in anisotropic tissues, indicative of more Ca²⁺ cycled into myocytes per contraction. (e) Decay phase Ca²⁺ removal kinetics. Maximum return velocity (Fura-2 ratio, R/s) of transient decay from peak to baseline. Bars represent mean ±SE (^#significant difference between isotropic and 10 × 10 tissues, ^#significant difference between isotropic and 20 × 20 tissues, P < 0.05)

We quantified the frequency response of the diastolic [Ca²⁺]_i in tissues stimulated between 1 and 5 Hz (Figure 5a). The diastolic [Ca²⁺]_i rose as a function of pacing frequency in all tissue constructs, with consistently lower diastolic [Ca²⁺]_i in 10 × 10 μm anisotropic tissues versus 20 × 20 anisotropic and isotropic tissues (Figure 5b). The systolic–diastolic amplitude (peak [Ca²⁺] – diastolic baseline [Ca²⁺]), the change in cytoplasmic Ca²⁺ during the cardiac cycle, was significantly larger in both anisotropic groups (Figure 5c), indicating that more Ca²⁺ was cycled into the cytoplasm per contraction in anisotropic tissues. The total area under the Ca²⁺ transients (Fura-2 concentration multiplied by the duration of the waveform) provides a measure of the total available cytoplasmic Ca²⁺ for contraction.³⁰ We found the total available Ca²⁺ in 20 × 20 and 10 × 10 anisotropic tissues to be signifi-cantly larger (Figure 5d). In order to characterize the kinetics of Ca²⁺ removal from the cytoplasm, we calculated the transient decay time (time from peak time to 50% baseline) and the maximum return velocity of the decay phase of the transient (Figure 5e). All three groups possessed similar decay times, but the anisotropic tissues demonstrated a sig-nificant trend towards faster Ca²⁺ removal kinetics where the maximum return velocity was overall faster in the anisotropic groups. Taken together, these results suggest that higher levels of tissue anisotropy contribute to decreased diastolic [Ca²⁺]_i and increased Ca2+ influx at all frequencies.

Discussion

We report that anisotropic patterning of FN results in cyto-skeletal remodeling, i.e. the functional alignment of actin within the sarcomeres with the underlying, patterned FN and that the resulting subcellular, cellular and tissue architecture are correlated with unique Ca²⁺ handling. Tissue anisotropy is characterized by lower variances in the angular spread of actin myofibril alignment and a signifi-cantly greater probability of binucleation. Thus, physical restrictions in the form of geometrically patterned ECM results in tissues that possess distinct, hierarchically aligned, architecture.

Cytoskeletal reorganization with respect to external geometric cues in the ECM has been reported in a variety of cell types, including cardiac myocytes cultured on individual ECM islands.^{15,18,22,32,33} Studies of non-myocyte cell pairs cultured on patterned islands suggest that the actin cytoskeleton reorganizes as cells dynamically reconfigure their internal architecture with respect to the boundary conditions represented by both the ECM and adjacent and adjoining cells.^34,35 In the case of capillary endothelial cells and fibroblasts, these reports demonstrated that the motile characteristics are an important mechanism in this process. For less motile cardiac myocytes, cytoskeletal remodeling is considerably slower. The reassembly of the actin network, cell–cell adhesion and gap junction coupling of myocytes is formed over the course of days in culture,^15,18 while endothelial cells reorganize on the timescale of minutes to hours.^34,35 These reports suggest that the longer periods of time required to polarize the contractile apparatus in a striated muscle cell reflect more complex self-organizing processes than in non-striated cells.

Previously, we reported changes in nuclear shape as a function of cytoskeletal organization in engineered myo-cytes and tissues, suggesting mechanical coupling of the nucleus to the contractile cytoskeleton.³⁶ Anisotropic tissue constructs cultured on similarly patterned FN lines possessed a high degree of nuclear alignment similar to that found in vivo; nuclei in isotropic tissues were polymorphic and not aligned. Nuclear eccentricity was also higher in anisotropic tissues, suggesting that following cytoskeletal reorganization with respect to external cues, intracellular stresses deform the nucleus. In the same study, systolic deformation of the nuclei was measured during high-speed fluorescence microscopy, revealing that the nuclei deformed anisotropically in the aligned tissues. In the current study, anisotropic tissues possessed significantly higher nuclear densities when compared with isotropic tissues, suggesting that as the myocytes elongated, aligned myofibrils increased the intracellular stresses, and thus contributed to binucleation.

Binucleation may be a contributor to the altered Ca²⁺ dynamics that we report, as a number of reports suggest that nuclear Ca²⁺ diffusion during contraction is an important contributor in ECC³⁷ and more recent evidence shows that nuclear Ca²⁺ signals actively regulate myocardial tissue function and excitability.^38,39 To date, spatiotemporal correlation of Ca²⁺ sparks throughout the intracellular space has been hindered by a lack of appropriate image acquisition and analysis techniques;⁴⁰ however, new experimental techniques may enable future investigations on this topic.⁴¹ Future work should address the differences in gene expression that may characterize tissue architecture and their role in regulating Ca²⁺ in heart muscle.

In conclusion, extracellular cues regulate the architecture of myocytes across multiple hierarchical length scales including cytoskeletal myofibrillogenesis, cellular morphology, cell area and nuclear density. In addition, variations in these structural parameters correlate with functional differences in Ca²⁺ handling between anisotropic and isotropic myocardial tissues. Future studies may explore how tissue architecture affects the expression of Ca²⁺ channel and exchanger expression and proteins involved in Ca²⁺ handling in the sarcoplasmic reticulum. In vitro tissue engineering provides a robust platform for future investigation of how adaptive and maladaptive ventricular remodeling can affect cardiac electrophysiology and contractility. Systematic investigation of cell size, morphology, orientation and anisotropy may prove to be a powerful experimental assay in modeling cardiovascular development and pathophysiology.