Initial Stability of Subtrochanteric Oblique Osteotomy in Uncemented Total Hip Arthroplasty: A Preliminary Finite Element Study

Abstract

Background

Subtrochanteric oblique osteotomy (SOO) has been widely used to reconstruct highly dislocated hips in uncemented total hip arthroplasty. The occurrence of complications can be attributed to the instability of the osteotomy region. The aim of this study was to evaluate the initial stability of SOO in uncemented total hip arthroplasty.

Material/Methods

A 3-dimensional finite element femur-stem model was created, and a virtual SOO was performed at 4 oblique angles: 30°, 45°, 60°, and 90°. The von Mises stress distribution in the femur-stem complex and the displacement under different oblique angles were evaluated in the SOO models, in comparison with that of the intact model.

Results

The study demonstrated that the distal fragment of the femur bore more stresses than the proximal fragment, and the maximum stress was concentrated in the femoral neck and the cortical bone, which contacted with the distal end of the stem. SOO increased the stress of both the femur and the stem, and fractures may occur in the stress concentration sites. Additionally, comparing the displacement at different oblique angles, the lateral region was larger than that of the medial region on the subtrochanteric osteotomy plane. The minimum micromotion on the osteotomy plane was obtained when the oblique angle was 45°.

Conclusions

The fit and fill of the distal fragment of the femur and the stem is essential for the stability of the subtrochanteric osteotomy region. The optimal oblique angle for SOO appears to be 45°.

Background

Total hip arthroplasty (THA) has been recognized as one of the most effective orthopedic procedures to treat end-stage hip disorders, such as osteoarthritis, rheumatoid arthritis, and hip dislocation [1]. Although wear of the femoral components at the articular interface still occurs and wear debris-induced bone resorption is a matter of concern, the overall success of THA has been generally satisfactory [2]. However, a number of anatomical deformities derived from highly dislocated femur make specific THA particularly demanding for patients who require this operation [3]. Hip dislocation can be caused by various disease conditions such as hip dysplasia, trauma, and infection, and over the past few years strenuous attempts have been made to improve the outcome of THA in patients with highly dislocated hip [4,5]. Initially, the acetabular component is placed at the “high hip center”. However, this kind of surgery is associated with an increased failure rate of the acetabular component, which can be attributed to abnormal hip biomechanics [6]; therefore, an increasing number of researchers recommend positioning the cup at the true acetabular center to restore the normal rotational center and the typical loading transfer [7]. However, when the anatomical hip center is restored, it is difficult to reset the femur toward the level of anatomical acetabulum due to the constraints of soft tissue. In addition, the risk of nerve traction injury due to lengthening of affected lower extremity is also increased [3]. Consequently, femur-shortening osteotomy has been introduced to facilitate the pulling down of the femur and to reduce the risk of nerve injury, and it has become an integral part of THA to treat those patients with dislocated femur.

Recently, a variety of osteotomy techniques for achieving femur shortening have been reported in clinical studies, including intertrochanteric, subtrochanteric, and supracondylar osteotomy [8–10]. At the subtrochanteric level, different subtrochanteric osteotomy geometries, including transverse [11,12], oblique [13], Z [14], and chevron [15] shapes, are available to stabilize the osteotomy. Among these approaches, subtrochanteric oblique osteotomy (SOO) is preferred because it is convenient to reconstruct the normal femur anatomy as much as possible, while at the same time preserving the proximal femur bone mass [3,16]. In spite of the advantages, complications associated with this procedure remain a major issue. For example, the rate of fracture and nonunion has been reported to range from 5% to 22% and 8% to 29%, respectively [17]. Therefore, it is of great importance to further improve the outcome of THA associated with SOO.

It has been well accepted that biomechanical factors play a fundamental role in bone healing following osteotomy, and the rigidity of the fixation can affect the type of healing because a relative micromotion in the osteotomy plane may result in the development of cartilaginous callus or even nonunion [18]. However, to the best of our knowledge, little attention has been paid to the biomechanical properties of subtrochanteric shortening osteotomy. It is therefore crucial to gain insight into the biomechanical pattern of the subtrochanteric osteotomy region so that the surgeons can make better choices to improve the performance of this procedure. In recent decades, finite element (FE) modeling has been used as a powerful tool to simulate and analyze the stress and displacement characteristics under specific load in order to obtain information that is impossible to measure in vivo. In the present study, we developed a 3-dimensional (3D) FE model to evaluate the initial stability of SOO, based on the analysis of von Mises stress in the femur-stem complex and displacement under different oblique angles.

Material and Methods

Development of FE model of SOO

Two types of models were developed in order to investigate the biomechanical profiles of SOO. For the first type, the femur was kept intact, and for the second type subtrochanteric oblique osteotomy was performed using the same femur but with different oblique angles set at 30°, 45°, 60°, and 90°.

The numerical data of the femur were based on a middle-aged male volunteer without any hip disease. Computed tomography (CT) scanning of the volunteer’s left femur by the Siemens Dual-Source CT scanner (Siemens Medical Solutions, Germany) was performed to generate a meshed, solid model using 4-node tetrahedral elements. Only the proximal femur was scanned at 0.5 mm intervals from the top of the femoral head to the level 20 cm below the lesser trochanter. Then, a 3D FE model of the femur was established using the computer-assisted design software, MIMICS (Materialise, Leuven, Belgium). In addition, a 3D FE model of the S-ROM stem (DePuy, Inc, Raynham, Massachusetts) was created using the SolidWorks software (SolidWorks Corporation, Concord, MA, USA), which was identical in size to the actual femoral stem and used for implantation into the femur.

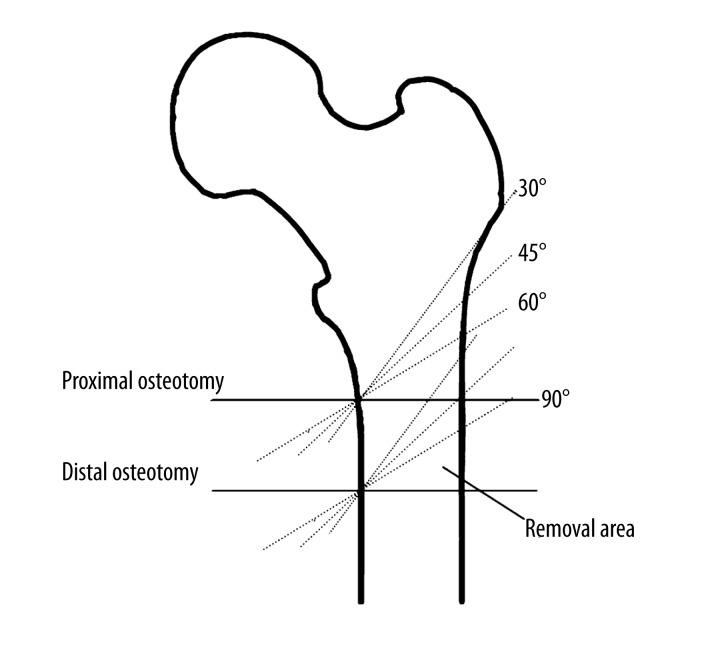
On the basis of the femur model developed as indicated above, subtrochanteric shortening osteotomy was performed, as shown in Figure 1. Perpendicular to the axis of the femoral shaft, the level 3 cm below the lesser trochanter was assigned as the proximal osteotomy plane at the oblique angle of 90° – the horizontal plane. Similarly, the distal osteotomy plane was defined, which was 3 cm below and parallel to the proximal osteotomy plane. The segments between these 2 planes were removed to simulate the shortening length in the operation. Afterwards, the remaining 2 parts of femur were put together maintaining the consistency of the axis of the femoral shaft to generate the femur model with SOO at 90°. Likewise, the oblique angles of 30°, 45°, and 60° were determined with fixation of the medial point, and the femur models with SOO at these angles were constructed. Finally, the femoral head was removed according to the standard osteotomy technique, and the simulation of the stem insertion into the femoral canal was completed with alignment of the axes of the stem and the femur. The models were named “intact”, “SOO30”, “SOO45”, “SOO60”, and “SOO90”, respectively.

Figure 1.

Schematic graph showing subtrochanteric shortening osteotomy performed at different oblique angles.

Meshing, material property, loading and contact condition

Meshing was generated automatically using four-node tetrahedral element for all the models by ABAQUS software (ABAQUS Inc., Providence, USA). Extensive meshing refinement was performed in order to provide a satisfactory balance between accuracy and computing resources. The final configuration was comprised of more than 300 000 elements.

The material properties applied were as follows. Young’s modulus of the titanium alloy stem (Ti6Al4V) was set 110 GPa [19], and Young’s modulus of the bone was coupled with the apparent bone density (ABD) using a function described by Lerch et al. [20]. Specifically, ABD was calculated based on the CT Hounsfield (HU) values and using the equation: ρ (g/cm³)=0.0008*HU+0.04. The relationship between elastic constants and density was described by E (MPa)=10200 ρ^2.01. Poisson’s ratio was set at 0.3 for all materials [19]. All the materials were considered as linear, elastic, and isotropic.

The single-leg stance loading condition was used in the FE model of the femur-stem structure, as the axial loading of the hip joint was prominent for the load transfer mechanism during postoperative rehabilitation activities. To make the results more realistic and accurate, a loading program which included the muscle force was adopted as described previously [21]. The direction and magnitude of the hip force during a normal walking cycle were based on the data displayed in Table 1. In this analysis, the distal end of the femur was completely constrained.

Table 1.

Force components at the hip joint used in the study.

Muscle name and hip of force	Force components (N)
	X	Y	Z
Piriformis	−99.9	52.57	31.97
Gluteus maximus	−197.33	75.93	260.9
Gluteus medius	−51.43	2.23	96.23
	−68.77	6.83	84.9
	−75.23	14.43	78.23
Gluteus minimus	−19.27	−5.43	39.4
	−23.3	5.13	37.17
	−33.43	9.63	27.43
Psoas	−1.0	77.37	73.1
Adductor magnus	−8.03	2.3	13.57
	−6.77	2.2	14.23
	−5.93	2.03	14.63
	−5.27	1.87	14.93
Adductor minimus	−5.7	−1.43	1.47
	−5.3	−1.07	2.7
	−4.7	−0.83	3.7
	−4.1	0.63	4.4
Hip joint contact force	777.43	219.53	−2216.03

Different friction coefficients were assigned to the femur-stem interface to simulate the frictional effect of different prosthetic surfaces [19,22]. In this study, a friction coefficient of 0.51 was used between the sleeve-bone interface, and the other parts of the femur-stem were given a frictional coefficient of 0.32. In addition, the coefficient of friction for the frictional contacts between the 2 subtrochanteric osteotomy planes was 0.46. In the sleeve region where osseointegration was expected to occur, we considered immediate post-operative condition without ingrowth of any tissue.

Data analysis

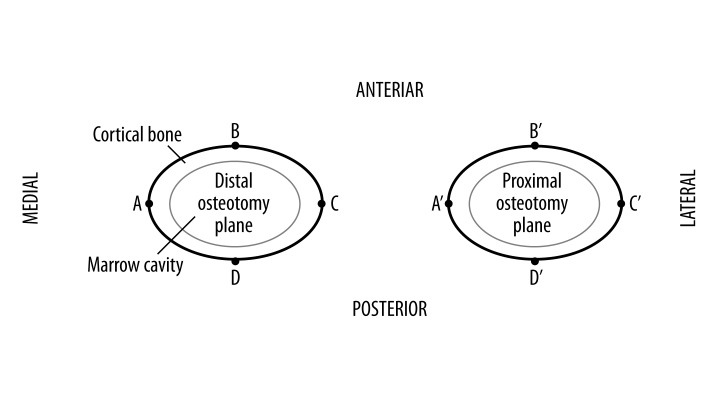
For each model, the distribution of von Mises stresses and displacements in the femur-stem complex was analyzed, which was obtained by ABAQUS software automatically. Four nodes – A, B, C, and D – on the external edge of the distal osteotomy plane were selected to represent the medial, anterior, lateral, posterior region, respectively, (Figure 2). Similarly, the corresponding points in the proximal osteotomy planes were assigned to A′, B′, C′, and D′. The values of von Mises stress and displacement in those nodes were examined. All the relative displacements and their components (1 component on the horizontal plane and the other along the longitudinal axis of the femur) of AA′, BB′, CC′, and DD′ were also calculated by computer. For each model, the average relative displacement of the 4 pairs of corresponding points was regarded as the relative displacement of the whole osteotomy plane.

Figure 2.

The SOO45 model showing the proximal osteotomy plane, the distal osteotomy plane, and the selected nodes.

Results

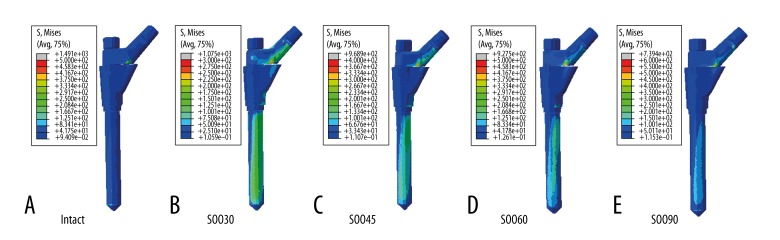
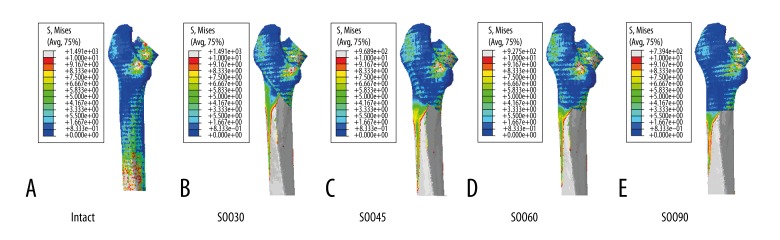
Stress distribution maps were created to reflect the von Mises stresses experienced by the femoral stem (Figure 3) and the femur (Figure 4). The grey, red, and orange colors represented regions of greater stress, which were more evident on the distal fragment of the femur. These results indicated that SOO technique changed the stress distribution in the femur-stem complex in comparison with the intact model. However, the stress distribution was almost similar among the SOO models, which were primarily concentrated in the posterior region of the femoral neck and the medial-posterior region from the subtrochanteric osteotomy plane to the distal end of the stem. The maximum stress values of the stem, the medial nodes of stem in the osteotomy plane, the proximal and distal fragment of the femur and the selected nodes (A, B, C, D, A′, B′, C′, and D′) are shown in Table 2. For the femoral stem, the maximum stresses were all located in the junction between the sleeve and the stem. The highest stress values of the SOO models were all larger than that of the intact model, and increased with the change of the oblique angles from 90° to 30°. In the osteotomy plane, the stress of the medial nodes of the stem showed no significant difference for the oblique angles from 30° to 60°, but it decreased markedly at 90°. In contrast, the stress distribution of the femur was more complicated. For the proximal fragment of the femur, the maximum stress occurred in the posterior region of the femoral neck, and the highest stress values of the SOO30, SOO45, SOO60, and SOO90 model increased by 176%, 211%, 216%, and 30% in comparison with the intact model, respectively. For the distal fragment of the femur, the maximum stress occurred in the cortical bone adjacent to the distal end of the stem, and the stress values of the SOO30, SOO45, SOO60, and SOO90 models increased by 673%, 467%, 451%, and 435% in comparison with the intact model, respectively. With regard to the osteotomy plane, the stress of the nodes B, B′, C and C′ increased while the stress of the nodes A, A′, D and D′ decreased when the oblique angles changed from 30º to 60º. The stress values for the selected nodes of the SOO30, SOO45, and SOO60 models, i.e. A, B, C, D, A′, B′, C′, and D′, were all larger than that of the corresponding nodes of the SOO90 model.

Figure 3.

Stress distribution in the femoral stem: (A) intact; (B) SOO30; (C) SOO45; (D) SOO60; and (E) SOO90.

Figure 4.

Stress distribution in the femur: (A) intact; (B) SOO30; (C) SOO45; (D) SOO60; and (E) SOO90.

Table 2.

Maximum stress values of various femur-stem models and selected nodes.

Model	von Mises stress (MPa)
	Stem	The medial node on stem in SOO plane	The proximal fragment of femur	The distal fragment of femur	A	A′	B	B′	C	C′	D	D′
SOO30	1075	160	395	286	73	28	35	3	1.9	1.5	50	35
SOO45	968	164	446	210	68	20	42	15	5	4.6	25	22
SOO60	927	161	452	204	38	12	47	31	9	4.9	17	10
SOO90	739	126	186	198	6.2	6	2.8	2.3	0.4	0.1	5.5	2
Intact	230	–	–	–	–	–	–	–	–	–	–	–

The displacements of various femur-stem models and the micromotion in the osteotomy plane are shown in Table 3. For all the nodes, the maximum spatial displacements of the SOO models decreased from 30º to 90º, but were all higher than that of the intact model. The relative displacement in the osteotomy plane for each SOO model was another important parameter in our study. In general, the relative displacement of CC′ in each SOO model showed the largest spatial displacement, followed by BB′, DD′, and AA′, respectively. In terms of relative displacement of the whole osteotomy plane, it was the minimum for the SOO45 model, and the values of the SOO60, SOO30, and SOO90 models increased by 13.6%, 131%, and 184%, respectively. The component of the relative displacement on the horizontal plane increased when the oblique angle varied from 30° to 90°, whereas the component of relative displacement on the longitudinal axis of the femur showed the opposite trend.

Table 3.

Displacement of various femur-stem models and micromotion in the osteotomy plane.

	Displacement (mm)									Micromotion in osteotomy plane (μm)
	Maximum	The distal fragment of femur				The proximal fragment of femur				The relative displacement	Component in the horizontal plane	Component along the longitudinal axis of femur
		A	B	C	D	A′	B′	C′	D′	–	–	–
SOO30	5.53	2.22	2.52	2.74	2.51	2.17	2.51	2.84	2.53	129	7	128
SOO45	4.67	1.7	1.77	1.87	1.77	1.69	1.87	1.91	1.85	38	12	36
SOO60	4.77	1.76	1.79	1.82	1.78	1.74	1.84	1.84	1.81	57	39	33
SOO90	4.69	1.56	1.62	1.69	1.64	1.69	1.65	1.56	1.62	141	139	23
Intact	3.15	–	–	–	–	–	–	–	–	–	–	–

Discussion

The technique of subtrochanteric shortening osteotomy has been used to correct proximal femoral deformity. Among the osteotomy methods, Z and chevron shapes have been abandoned by some surgeons due to the complexity of the surgery and the requirement for experience obtained from long-term training [16]. Modular stem prosthesis with metaphyseal sleeve allows the oblique osteotomy to be used in a simplified surgical procedure with reduced operation time [23]. Therefore, the SOO technique, which can preserve proximal femur bone mass and adjust the anteversion, has been widely used. While this technique makes THA available for the patients with high dislocation of the hip, clinical studies have reported some complications associated with this procedure, such as delayed nonunion or nonunion. These complications, which may be attributed to lack of stability, can eventually affect the longevity of the hip prosthesis [3]. Consequently, a fixation operation or even revision of THA is required for these patients [6,24].

Mechanical behaviors of biological systems can be investigated through FE modeling more accurately and sensitively as a result of precise control over the experimental design [25]. In the present study, we established an FE model to investigate the biomechanical behaviors of SOO and to optimize this technique by examining the stress distribution in the femur-stem complex and the displacement at different oblique angles. To the best of our knowledge, this is the first FE model of SOO to assess the initial stability of this osteotomy technique.

The results show that the SOO affects the stress distribution in both the femur and the stem. Specifically, the distal fragment of the femur bears most of the stresses, and plays a key role in the initial stability of the stem. In those patients with high hip dislocation, the femur canal is usually narrow and straight [26]. Consequently, the implant shape determines cortical contact and initial stability. Porous-coated proximally, long femoral prosthesis with cylindrical shape seems to be appropriate for this purpose. The S-ROM stem, acting as an intramedullary nail, can be fixed to both the proximal and distal parts of the femur individually with a porous-coated stepped proximal sleeve and polished distal flutes and fins, providing rotational stability and compression pressure at the osteotomy site [27]. This is the main reason for choosing the S-ROM stem in our study. In addition, the results also imply that strong fixation in the distal fragment of the femur is more important compared to the proximal fragment of the femur when an intraoperative cleavage fracture occurs during insertion of the femoral component. The stress concentration regions hint at the potential site where a fracture may occur during postoperative rehabilitation programs.

With regard to displacement, looking separately from the horizontal and axial directions, the SOO30 and SOO90 models demonstrate the highest rotational and axial stability, respectively. This indicates that, with the reduction in the oblique angle, the rotational stability of the osteotomy plane increases while the axial stability decreases, and vice versa. Overall, the SOO45 model yielded the minimum relative displacement value, meaning that SOO at 45° strikes a balance between rotational stability and axial stability among those specific angles. The initial stability appears to be the primary cause of the union and is a crucial factor in the short-term and long-term clinical success of total hip arthroplasty [3]. From this viewpoint, although the SOO90 model gives the minimum stress on the osteotomy region, the results of the present study suggest that a 45º oblique angle may be the optimal choice for this technique.

There are some inherent limitations in the present study. Firstly, the effect of biological difference between individual subjects, including the deformity of the proximal femur, was not considered. Therefore, the influence of different femur morphologies on stress distribution cannot be predicted. However, because the severities of deformity of the proximal femur in highly dislocated hips in clinical settings are various, and the S-ROM stem can adapt to different forms of abnormal femurs, we believe that adoption of a healthy femur is reasonable as it eliminates the influence of other variables. In addition, the FE model is only concerned with immediate initial stability of the osteotomy region but cannot predict the long-term outcome of the SOO technique, which can be influenced by other factors (apart from biomechanics). Simplifications are also introduced into the specification of material properties. The femoral bone is set as an isotropic material, and the femur-stem interface is assumed as a perfectly matching fit. Furthermore, the use of physiological load may be overestimated for the early stage of the SOO healing, because after surgery the treated leg is often partially loaded by using a crutch or a walker. But if a shorter period of bed-rest is desired, this study can provide the worst-case scenario in the context of full body weight. Further research will include modeling of different loading patterns to reflect distinctive activities.

Conclusions

The parameters in the FE analysis and loading conditions are based on published reports, so these mechanical characteristics revealed in the present study are probably reliable. However, further experimental and clinical studies may be required to confirm the results obtained from the FE model.