Tailoring plasmonic properties of gold nanohole arrays for surface-enhanced Raman scattering

Abstract

The wide plasmonic tuning range of nanotriangle and nanohole array patterns fabricated by nanosphere lithography makes them promising in surface-enhanced Raman scattering (SERS) sensors. Unfortunately, it is challenging to optimize these patterns for SERS sensing because their optical response is a complex mixture of localized and propagating surface plasmons. In this paper, transmission and reflection measurements are combined with finite difference time domain simulations to identify and separate each plasmonic mode, discerning which resonance leads to the electromagnetic field enhancement. The SERS enhancement is found to be dominated by the absorption, which is shifted from the transmission and reflection dips usually used as tuning points, and by the ‘gap’ defects formed within the pattern. These effects have different spectral and geometric dependences, forming two optimization curves which can be used to predict the best performance for a given excitation wavelength. The developed model is verified with experimental SERS measurements for several nanohole sizes and periodicities, and then used to give optimal fabrication parameters for a range of measurement conditions. The results will promote the application of two-dimensional plasmonic nanoarrays in SERS sensors.

Introduction

SERS has become ubiquitous for chemical and biological detection because of its molecular fingerprinting and point-of-care abilities.^1-4 SERS originates from chemical and electromagnetic (EM) enhancement of the otherwise small Raman scattering cross section, of which the EM field enhancement is usually dominant.^5-7 In SERS sensors, colloidal plasmonic nanoparticles are often employed to create strong “hot spots” necessary to increase the Raman signal.^8-11 Unfortunately, colloidal sensors suffer from aggregation and instability issues, as well as being difficult to re-use and incorporate in detection schemes like microfluidics.⁴ To overcome this, two-dimensional (2D) plasmonic solid-state patterns have been developed with high hot spot densities, ranging from random, annealed Ag films¹ to ordered nanoarrays.^12,13 Patterns made by nanosphere lithography (NSL) stand out as particularly suitable for commercialized designs because NSL is a high throughput and low cost manufacturing method. In the most popular photomask based implementation, the polystyrene (PS) sphere template is etched for various times, reducing the sphere diameters, and allowing creation of nanotriangle or nanohole based arrays after deposition of a metal.^14-17 Alternatively, a metal can be directly deposited on the PS spheres to make a film-over-nanosphere (FON) structure.^18,19

Among the patterns created by NSL,^20-36 Au nanohole arrays have the most versatility, supporting both localized and propagating surface plasmons resonances. The two optical modes can be tuned spectrally, as well as in their relative strengths, across the visible to near-infrared range by changing the periodicity, size of the hole, and metal used.³⁶ The localized surface plasmon resonance (LSPR) mode leads to focusing of the incident field with a decay length of ∼10-30 nm; and the surface plasmon polariton (SPP) mode leads to enhanced transmission through the nanohole array and evanescent fields that decay over ∼100 nm.^1,4 While the flexibility is ultimately beneficial for designing a sensor, the large range of tuning parameters and complex optical response makes it difficult to optimize the array pattern for SERS sensing, especially when choosing between the full set of nanotriangle to nanohole based patterns. For example, while an optimal hole to periodicity ratio was measured, its origin is not completely known.²⁸

Therefore, this study aims to investigate the correlation of the optical properties of 2D NSL-formed nano-arrays with the underlying EM field enhancement, giving optimal SERS tuning curves for any measurement wavelength across the nanotriangle to nanohole array transition. The origins of the LSPR and SPP peaks are discerned by comparing the measured transmission, reflection, and absorption to the spectrally resolved local field calculated by finite difference time domain simulations (FDTD). This reveals the transmission or reflection spectrum alone cannot be used to optimize the patterns for SERS. Instead, the EM field best correlates with the absorption, being maximized for a certain ratio of hole size to periodicity. Additionally, the role of defects is analyzed, and found to contribute independent of the measured absorbance. The defect EM field enhancement is maximized with a geometric condition that increases the formation of gap ‘hot spots’ between hole arrays. The LSPR is also found to give a larger SERS enhancement than the SPP in a reflection based measurement. These findings are confirmed by accurately predicting the measured SERS performance of the nanohole arrays with different periodicities across a range of nanohole sizes. Further, tuning curves are given, allowing optimal nanoarray fabrication parameters to be chosen for any excitation or scattered wavelength. The results given in this paper will provide the guidelines for design of 2D NSL-based plasmonic architectures for SERS sensors.

Experimental section

Fabrication of Au nanohole arrays

The protocol for Au nanohole array fabrication using nanosphere lithography is shown in Figure 1.¹⁷ Quartz slides (AdValue Technology) were cut into pieces (1 cm × 1.5 cm), then washed by immersing into piranha base (H₂SO₄:H₂O₂=3:1 at 90 °C (caution must be taken when using piranha solution) for two hours, followed by sonication in acetone, methanol, and D.I. water for 15 min each. Next, polystyrene (PS) microspheres with a diameter of 500 nm were drop-coated on the cleaned quartz slides to form a monolayer PS sphere template. After natural drying, the coated quartz slides were put under oxygen plasma etching for various durations (from 0 min to 10.5 min with a step of 1.5 min) to change the underlying pattern from triangles to holes of different sizes. E-beam evaporation was used to deposit a layer of Ti (5 nm in thickness) to enhance the adhesion between the quartz substrate and deposited Au layer (45 nm). Finally, the PS microspheres were removed by sonication in methanol. The Au nanohole layer thickness was chosen to facilitate easy removal of the PS sphere mask. As later discussed, and shown in Figure S10, the chosen thickness was in a region where optical properties were robust against changes in metal thickness. The as-prepared Au nanohole arrays were rinsed with D.I. water and dried by compressed nitrogen gas. Polystyrene microspheres, glycerine, thiophenol (TP) were purchased from Alfa Aesar. Deionized (D.I.) water was produced by the Milli-Q Integral 3/5/10/15 system (18.2 MΩ·cm, Millipore Corp., USA).

Figure 1. Protocol for nanosphere lithography.

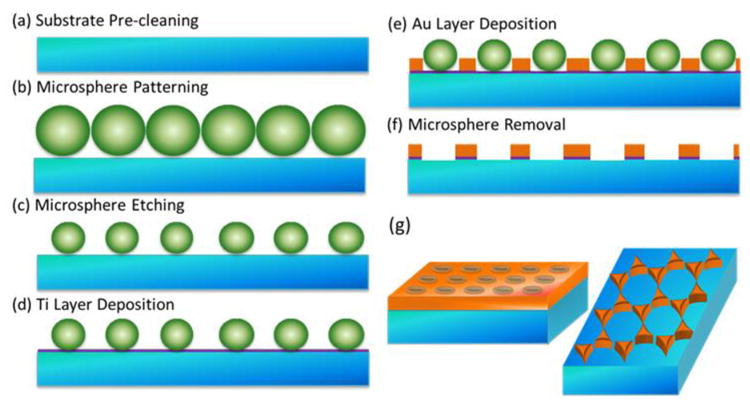
(a) Substrate (quartz slides) cleaning in an acid piranha bath at 90 °C for 2 h and sonication in acetone, methanol, and deionized water; (b) deposition of a monolayer of polystyrene spheres on the cleaned substrates; (c) polystyrene sphere etching using an oxygen plasma asher; (d) 5 nm thick titanium adhesion layer deposition; (e) 45 nm thick Au layer deposition; (f) polystyrene sphere removal by sonication in methanol; (g) nanohole or nanotriangle arrays formed depending on time of sphere-etching.

Characterization

Au nanotriangle arrays and Au nanohole arrays were characterized under a JEOL JSM-7600F scanning electron microscope (SEM). The full set of SEM images is shown in Figure S1 and S2 for the 500 nm and 600 nm periodicities, respectively. An Ocean Optics USB 4000 spectrometer and DT-MINI-2-GS were used to acquire the transmission and reflection spectra of the fabricated Au nanotriangle and nanohole arrays. Reflection was measured normal to the surface using an Ocean Optics Reflection Probe. Raman spectra were acquired with an Inspector Series, DeltaNu spectrometer with an excitation laser wavelength of 785 nm.

Refractive index sensitivity

To measure the refractive index sensitivity, glycerine-water mixtures were prepared to make a series of solutions with refractive indices ranging from 1.33333 (only water) to 1.41299 (60% glycerine in glycerine-water mixture). The shift in the resonance peaks of the Au nanohole arrays was measured using a UV-Vis spectrometer for each refractive index solution in a transmission geometry. The resonance peak scaled linearly with the refractive index. The refractive index sensitivity for each Au nanohole array was defined as the ratio of the peak shift to the refractive index change.

SERS measurement

Thiophenol (TP) has four prominent Raman peaks at 997 cm^-1, 1020 cm^-1, 1071 cm^-1, and 1571 cm^-1, which were used to study the SERS response of the as-prepared Au nanoarrays. To coat a uniform layer of TP molecules on the surface of the Au nanoarrays, TP stock solution was prepared in ethanol with a concentration of 3 mM. Au nanoarrays were immersed in 3 mM TP ethanolic solution for two days. TP-functionalized Au nanoarrays were washed by ethanol and dried under compressed nitrogen gas prior to Raman measurements. Quartz slides were used to suppress the background signals in Raman measurement. The measurement was repeated three times to create the error bars shown throughout the manuscript.

FDTD simulation

Finite Difference Time Domain (FDTD) simulation was used to calculate the transmission and reflection spectra by the commercially available Optiwave software. The simulation cell with a grid size of 3 nm was constructed to match the Au nanoarrays fabricated. A plane wave input source of 500 nm to 1200 nm was used. The refractive indices of Au and titanium were taken from the data of Palik⁴². The quartz slides were given a refractive index of 1.53. Both linearly polarized in x and y plane waves were checked, with the maximum EM field contribution used. All simulation used periodic boundary conditions to replicate the periodic Au nanoarrays.

Results and discussions

Evolution of Optical Modes

Figure 2 shows the SEM and corresponding transmission spectrum for a range of nanotriangle to nanohole arrays created by etching the PS sphere diameter before metal deposition. Without etching, a nanotriangle array was formed, which only supported a LSPR mode. The LSPR mode led to a dip in the transmission, either from absorption or reflection of light by the plasmon. As the PS sphere was etched for the fixed 500 nm periodicity, the metal was increasingly deposited between the spheres, connecting the nanotriangles into nanoholes.

Figure 2. Correlation of optical and geometrical properties.

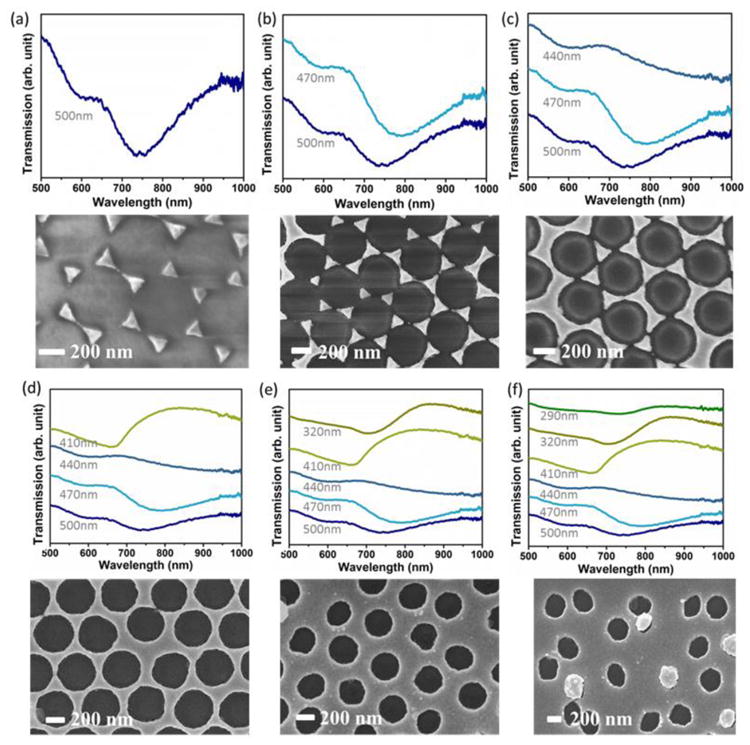
(a-f) The transmission and corresponding SEM image are shown for a nanohole array with periodicity of 500 nm and various etching times which cover the range of nanotriangle to nanohole to defect ridden pattern. The hole diameters from (a-f): 500 nm, 470 nm, 440 nm, 410 nm, 320 nm, and 290 nm. The defective pattern still has sufficient periodicity to support SPP and LSPR, albeit with a weakened response.

The LSPR initially red-shifted as the size of the nanotriangle increased. However, after further etching, the nanotriangles joined, causing two abrupt changes in the optical properties. First, the LSPR dip blue-shifted drastically. The estimated peak positions are shown in Figure 3, along with an expanded set of etched hole sizes for fixed periodicity. The blue-shift can be understood as the optical response of the nanohole being the opposite of a nanosphere of similar size, related by ${\mathit{\omega }}_{\mathit{\text{hole}}}^{\mathbf{2}}+{\mathit{\omega }}_{\mathit{\text{particle}}}^{\mathbf{2}}={\mathbf{\omega }}_{\mathit{p}}^{\mathbf{2}}$.³⁷ In this formula, ω_hole is the LSPR frequency of the nanohole. ω_particle is the LSPR frequency of the nanoparticle that has the same shape as the nanohole. ω_p is the bulk plasma frequency. When the Au nanohole arrays were just formed, the nanohole corresponded to a large nanoparticle with a redshifted frequency, so the Au nanohole resonance must blue-shift.

Figure 3. Change in optical modes at transition region.

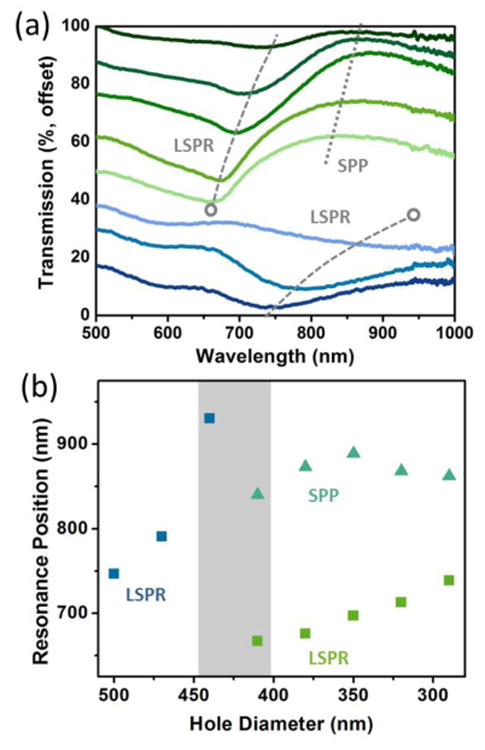
(a) The transmission is shown for an expanded set of hole sizes from Figure 2, covering 500 nm to 290 nm in 30 nm intervals from bottom to top. (b) The estimated peak position of the LSPR and SPP for each hole diameter with a fixed periodicity of 500 nm. The LSPR peak jumps drastically in the transition region from nanotriangle to nanohole array around 425 nm, while the SPP only exists after the conversion to nanoholes has occurred.

Second, sufficient periodicity existed to allow incident light to excite the propagating surface plasmon polariton (SPP) modes, with the grating like nature of the hole array, providing the extra momentum needed for free space coupling.^1,4 While the LSPR was characterized by a dip in the transmission, the SPP led to extraordinary optical transmission (EOT).²¹ EOT occurs when the SPP modes on the two sides of the hole array connect, re-radiating the incident field even if the hole is smaller than the wavelength of light, increasing the transmission.^32-35

After the transition region between the nanotriangle and nanohole array, further etching just reduced the size of the nanohole, continually red-shifting the LSPR and SPP modes. However, the limit to which the PS spheres can be etched was eventually reached, destroying the long range periodicity of the lattice and creating dimer and trimer hole groups, which weakened the optical response. At this point, sufficient periodicity still existed to support the SPP and LSPR modes, significantly reducing the strength of the transmission peak and dip. The measured trends for 500 nm periodicity were consistent with those of a 600 nm periodicity pattern as the nanohole size is tuned (Figure S3), only the peak positions and transition region positions shifted.

Connection with maximum SERS enhancement

The optical response shown in Figure 3 and Figure S3 is quite complex, making optimization of the corresponding LSPR and SPP modes difficult. First, the peaks and dips must be assigned as either localized SPR or propagating SPP modes. One method to achieve this is to check the change in the transmission with angle. As the input angle is changed, the diffraction condition, which matches the momentum of the SPP mode to free space also changes, shifting the resonance wavelength (Figure S4). The LSPR mode should remain relatively unchanged. A simpler method, since an angle-resolved setup was not available, was to measure the reflection and transmission at normal incidence, as shown in Figure 4. It was seen that if LSPR existed, a peak in the reflection and dip in the transmission co-existed, while for the SPP a peak in the transmission and dip in the reflection co-existed. This relationship originates in that the SPP leads to EOT at resonance, while the LSPR leads to scattering or absorption.

Figure 4. Comparison of optical modes and resulting EM field enhancement for 500 nm periodicity.

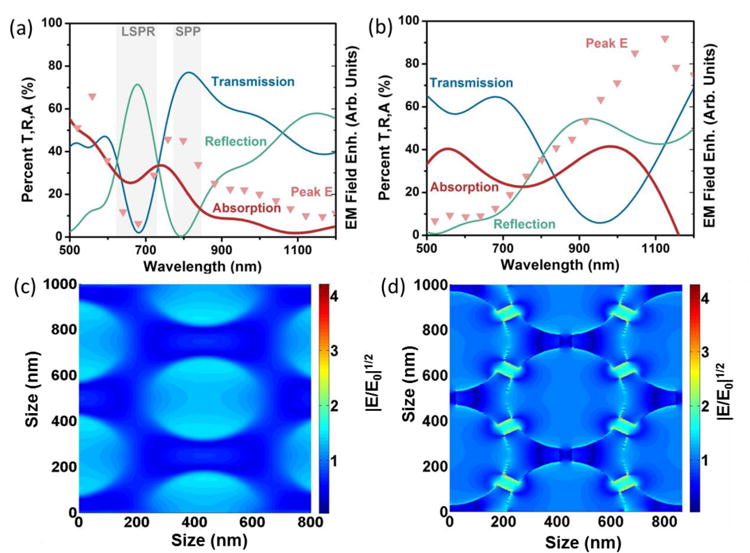
The transmission (T), reflection (R), and absorption (A=1-T-R) is compared to the peak EM field enhancement for an (a) ordered and (b) ‘gap’ defective pattern. For the ‘gap’ defect, the EM field from an ordered and defective pattern of the same hole size are shown for comparison. The absorption and EM field are similar for the ordered pattern, with the local field (c) focused on the nanohole walls, but differ (d) for the defective pattern, with the local field focused within and at the ‘gap’ defect edges. (a) and (c) are the data of ordered Au nanohole array with a periodicity or 500 nm, a hole diameter of 350 nm, and a film thickness of 50 nm; (b) and (d) are the data of Au nanohole array of the same parameter as (a) and (c) but with 50 nm ‘gap’ defects.

The nature of each mode must be understood more in-depth before optimization of SERS is possible. For the SPP, the local EM field enhancement is weaker and extends with a decay length of ∼100 nm.^1,4 While the EM field enhancement is smaller, if the increased transmission at the SPP resonance is taken advantage of by measuring in a transmission SERS geometry, this enhancement can still be useful. However, for a reflection based portable SERS instrument, as used in this study and necessitated for point-of-care applications, the SPP is not ideal because it increases transmission instead of reflection and has a smaller local field. Instead, the intense LSPR of the plasmon must be utilized. In LSPR, after light is incident on the plasmon, two decay routes can exist: (i) the energy of the field can be re-radiated as scattering for the large nanotriangles (Figure 3); and (ii) the energy will be trapped in the local field until the collective electron oscillations decay into phonons through electron-electron, electron-phonon, and finally phonon-phonon scattering.³⁸ This second process leads to a large EM field, and corresponds to an absorption in the spectral response. The balance between absorption and scattering can be controlled through geometry and size, generally with smaller nanoparticles absorbing light and larger nanoparticles scattering the incident light.^1,39

Therefore, to find the optimal geometry for the nanotriangle-nanohole array, the absorption was measured using both the reflection and transmission at normal incidence (Figure 4a). The corresponding EM field enhancement is also shown as calculated by FDTD. The EM field was closely correlated with the absorption peak, being red-shifted from the reflection and blue-shifted from the transmission. This proved that for the nanohole array, both reflection and transmission must be measured when tuning the spectral response for SERS enhancement if the local EM field is wished to be known. At the absorption peak, the local EM field was found to be concentrated at the edge of the nanohole array (Figure 4c). The peak EM field, which relates the largest electric field enhancement (E/E₀)², is reported in Figure 4. However, the average EM field over the nanohole array area had the same spectral form. It is important both average and peak contributions are considered, as a combination of high strength hot spots and distributed field density will give the best overall SERS signal.^13,14 The similarity between the average and peak EM field in the nanohole array therefore indicated a balance of high field intensity and spatial extent was achieved in these modes. A similar study was repeated for a 600 nm periodicity hole array, and the same correlation was found (Figure S5). The absorption increased as the hole size was reduced and the nanohole array can no longer efficiently re-radiate absorbed energy (Figure S6b).

If the nanoarray had perfect periodicity, the local EM field at the absorption peak would be the only effect considered in finding the optimal SERS enhancements. While defects may not greatly affect the optical response, the ‘hot spots’ formed create a large local field enhancement, meaning fabrication defects in NSL can be beneficial. Figure 2 shows defects existed in hole arrays with two origins. First were the dimer and trimer groups that formed due to sphere dislocation (Figure 2f). Interestingly, these defects spectrally gave a similar EM field enhancement as the ordered hole array. The total EM field contribution, however, was small compared to the ordered hole array, so the impact of these defects was judged minimal in increasing SERS. The role of the dimer and trimer based defects was therefore only to weaken the optical response and EM field at the absorption peak, although enough periodicity was usually maintained to support LSPR and SPP modes.

Second, the existence of ‘gaps’ between nanotriangles in the nanohole transition was considered. The ‘gap’ defects will form modes independent on the LSPR and SPP of the ordered array. However, they are hallmark of high local field enhancement, and therefore could have a larger effect than the dislocation related defects. The nature of ‘gap’ defects is seen in Figure 4b, wherein the peak local field enhancement from the ‘gap’ defects is compared to the ordered EM field, as well as the reflection, transmission, and absorption. The ordered pattern EM field in Figure 4b followed the absorption similar to the response calculated in Figure 4a, while the defect originated EM field did not. Instead, the peak EM field from 50 nm ‘gap’ defects was correlated better with the absorption of the nanotriangle arrays, as seen in Figure S5b for small etching times. The EM field enhancement was still strong off-resonance at 785 nm, with this mode corresponding to focusing of light at the edges of the gap between the nanotriangles instead of the rim of the nanohole, Figure 4d.

The ‘gap’ defects were replicated in FDTD simulations by taking the 440 nm hole size array and placing 50 nm gaps between the nanotriangle sites, breaking their connection, in correspondence with Figure 2c. The size of the nanogap to be tested was chosen by calculating the field verse gap thickness for a 785 nm excitation (Figure S6a). The gaps formed ‘hot spots’ at small distances, while tuning the nanotriangle response to be resonant with the excitation laser at larger distances, with both effects increasing the local field. The EM field of the maximal gap enhancement in Figure 4d was concentrated at the edges and between the defects. The ‘gap’-based defects had a spectral response different from the LSPR and SPP modes, and therefore represent a second tuning parameter which must be taken into account in addition to the absorption. However, the ‘gap’-based defects do not have a signature optical trait like the absorption of the ordered mode, with the largest enhancement occurring when the geometric parameters of pattern formation allowed breaks in the connection between nanotriangles, approximately at hole size of the periodicity minus ∼40-80 nm. The same trends were present when ‘gap’ defects were tested for a 600 nm periodicity (Figure S5b). The relative percentage of defects for the 500 nm periodicity and 600 nm periodicity hole arrays at this conditions was ∼50% and ∼85% from the SEM images (Figure S1 and Figure S2).

Prediction of SERS Enhancement

The contributions of both the ordered and defect modes were combined to predict the Raman response of hole arrays with periodicities of 500 nm and 600 nm for varying hole sizes (Figure 5). The Raman enhancement was measured at 1071 cm^-1, with the individual curves shown in Figure S7. For both the 500 nm and 600 nm periodicities, the Raman intensity has been normalized by the same peak value, allowing comparisons of their enhancements. Without the Au nanohole array, no SERS was measurable, preventing normalization by this method. Instead, the concentration of Raman reporter, laser intensity, and integration time were kept constant to ensure that the comparison is repeatable.

Figure 5. Origin of EM field enhancement.

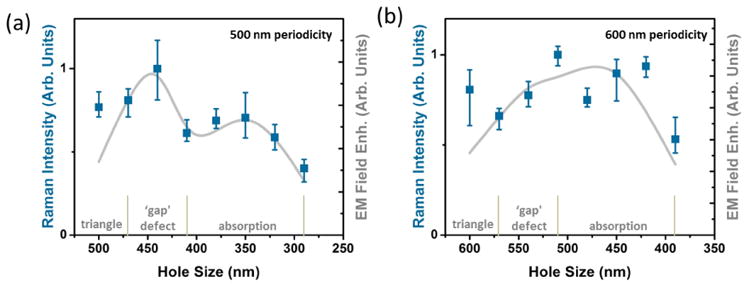
The combined EM field enhancement for the ordered and defective EM field enhancement mechanisms are compared to the measured Raman response for a (a) 500 nm periodicity and (b) a 600 nm periodicity pattern as the hole size is varied. The region where each contribution dominates is shown, with the ‘gap’ defects enhancing over a range given by the formation of gaps between nanoholes in the transition from triangles, the ordered pattern contribution corresponding to the peak absorption when there are only nanoholes. The range where only nanotriangles exist is shown for comparison.

To determine if the absorption and ‘gap’ defect EM fields could completely determine the Raman enhancement across the range of pattern parameters, the fields were output at the excitation wavelength laser (785 nm) as well as the Raman peak at 1071 cm^-1. For the 500 nm periodicity, the excitation and scattered enhancements were identical, allowing the overall EM field enhancement |E_inc|²|E_out|² to be calculated as |E_inc|⁴.^1-4 This simplification is reflected in Figure 4a, where the absorption peak and EM field were seen to cover the spectral range of excitation and Raman peak. For the 600 nm periodicity, this case was not true, Figure S5, and contributions from both the excitation and emission enhancements were included.

The contribution of the ‘gap’ defects was considered using the peak EM field enhancement at the optimized gap thickness and hole size, and then applying a Gaussian broadening for the range of film thicknesses which guaranteed gap formation. This was combined linearly with the enhancement predicted from the absorption, giving the overall EM enhancement verse hole size for both periodicities (Figure 5).

Figure 5a shows that these two contributions can accurately predict the SERS signal, with two unique enhancement regions. First, when the hole size was between 40-80 nm less than the periodicity, a large number of ‘gap’ defects were formed, increasing the enhancement. The geometric region this corresponds to was the transition region shown in Figure 3 and Figure S3 where the triangles became nanoholes. The strong contribution of these defects was originated in the EM field being focused at the gap between nanotriangles and the nanotriangle edges.

Second, at a hole to periodicity ratio of ∼0.6-0.8, the absorption of the hole array became maximum leading to a second enhancement peak. As the hole array size was reduced, radiative efficiencies decreased and the electron scattering losses increased, leading to more light being absorbed (Figure S6b). While this would seem to predict the smaller nanohole sizes as giving higher SERS enhancements, if the PS sphere hole size was etched too far, a large amount of trimer and dimer defects were introduced and the pattern was distorted. The defects weakened the optical properties, placing a limit on the minimum size achievable with a high field enhancement, and leading to the maximization ratio of hole size, equaling ∼0.6-0.8 times the periodicity.

It is interesting to note that for the 500 nm periodicity, the ‘gap’ enhancement was much larger than that from the ordered hole array absorption; but at 600 nm periodicity, the enhancements were roughly equal, both between the two mechanisms and to the ‘gap’ enhancement in the 500 nm periodicity. This can be explained as at 600 nm periodicity the absorption enhancement overlapped well with the excitation laser (785 nm) and the Raman peak at 1071 cm^-1, giving the maximum combination of excitation and emission enhancements, and increasing the relative contribution of this effect.

A third region is marked on Figure 5, which corresponds to where nanotriangles exist. The combined EM field mechanism does not completely account for this region, because the enhancement mainly lies in pattern defects and roughening which are difficult to replicate in FDTD simulations. This conclusion can be safely drawn because the absorption of the nanotriangle array at these sizes was at ∼1100 nm (Figure S6b), much higher than the excitation or Raman peak. The enhanced signal therefore must come from ‘hot spots’ instead of the LSPR. While the nanotriangle region is useful, fabrication limits of small PS spheres make it difficult to tune the LSPR to the desired resonance range while maintaining enough order for a large SERS signal. Instead, the formation of ‘hot spots’ must be relied on, which are difficult to optimize since unlike the ‘gap’ defects they do not have a clear geometric formation condition, and will lead to more variations between samples. Given that the enhancement from the triangle region is similar for both periodicities to the other more tunable enhancement mechanisms, this area was not further considered. For comparison, the effect of the defect regions on refractive index sensitivity is shown in Figure S7.

Guidelines for optimization

Since the two main contributions to SERS in a 2D nanoarray fabricated by NSL were identified, and correlated with measured Raman data, tuning guidelines can be developed for optimal enhancement with any excitation source (Figure 6). The first plot in Figure 6a shows the maximum absorption for a given periodicity hole ratio of 0.7 as the periodicity was changed, the ratio found experimentally to lead to the largest enhancement from this effect, in agreement with previous work.²² The absorption peak scaled linearly with increase in periodicity for a constant hole size to periodicity ratio. The EM field was found to be redshifted from the peak absorption by ∼50-100 nm, which given the broad absorption peak, allows this quantity to be used to tune the strength of the ordered pattern EM field contribution. Alternatively, the EM field can be used directly to pick the pattern parameters, as plotted in Figure S9a.

Figure 6. Optimization of pattern for SERS.

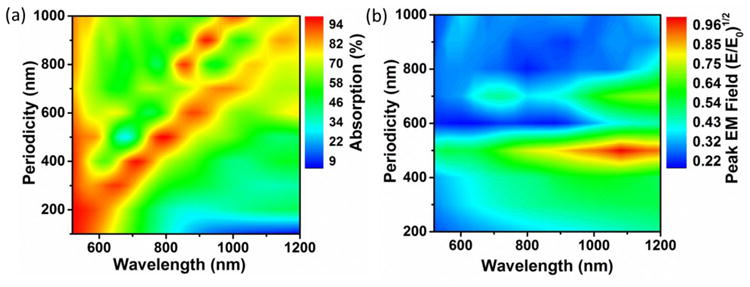
(a) The absorption peak position for a fixed hole to periodicity ratio of 0.7 at which the ordered EM field contribution was found to be maximal. The peak EM field is slightly red shifted from the absorption peak position. (b) The ‘gap’ defect EM field enhancement peaks for a periodicity of 400∼500 nm and a hole size of ∼40-80 nm less than the periodicity. These two curves can be used independently, or in combination, to find the best patterning parameters for a given excitation or Raman peak.

The absorption was also chosen to be shown in Figure 6 instead of the local EM field since it is an easily measurable lab quantity when the arrays are fabricated. In situations for which the reflection and transmission cannot both be measured, the general guideline found in this paper is that the max EM field enhancement will be slightly redshifted from the LSPR peak (dip in transmission and peak in reflection) or blue-shifted from the SPP peak (peak in transmission and dip in reflection). The origin of this trend is that the scattering and absorption are offset by frequency factors from the underlying dipole moment.⁴⁰ Therefore, the measured optical properties do not directly correlate to the best SERS enhancement, but some spectrally shifted wavelength will. The dimer and trimer defects act spectrally similar to the absorption shown in Figure 6a, and do not need to be accounted for separately.

The second plot in Figure 6b shows the contribution from the ‘gap’ defects for different periodicities with a hole size 60 nm less than the periodicity. These are general parameters, but the gap modes can exist within a range around this guideline, depending on the fabrication and deposition used. From the fitting to the measured SERS spectrum, the gap enhancement occurred for hole sizes between ∼40-80 nm less than the periodicity for a 50 nm metal thickness. Given that the absorption of the defects is difficult to measure directly, the maximum EM field verse wavelength must be used for optimization instead. Fortunately, the spectral range over which defects can enhance the SERS signal is broad, meaning that the introduction of ‘gap’ like defects will almost always be beneficial to the Raman enhancement.

What is most important to notice in Figure 6b is that, whereas the absorption scaled linearly with periodicity changes, the ‘gap’ defect mode does not have a general trend. This is because the ordered absorption in Figure 6b is based on a ratio of periodicity to nanohole size, and the solutions scale accordingly in Maxwell's equations, giving a linear dependence on periodicity. The ‘gap’ based defect is based on a geometric condition which does not scale, instead it is at an offset hole size per periodicity. Therefore, the peak EM field only occurred when the ‘gap’ defect was tuned to hybridize with the resonance of the nanotriangles and nanohole (Figure 6b), which occurred around a 500 nm periodicity. At larger and smaller periodicities, the gap had little effect on the possible resonances, and instead the nanotriangle or nanohole resonances dominated. Figure 6b is normalized globally to show where the ‘gap’ defects are most important, however to aide in tuning, the EM field from the ‘gap’ defect is shown normalized individually in Figure S9b.

The film thickness was also tuned to see its possible effect on the two contributions to the EM field enhancement (Figure S10). For thick films, little change in the absorption occurred. When the Au film thickness decreased below 40 nm, the SPP modes on the two opposite sides of the Au nanohole arrays could interact, splitting the 800 nm mode into a low frequency mode (symmetric) at 1000 nm and a high frequency mode (anti-symmetric) at 600 nm.⁴¹ At thinner film thicknesses, the absorption was seen to increase, which may be helpful for increasing the effects of the ordered and defect originating enhancements.

Conclusions

Overall, the optical modes of 2D nano-array patterns ranging from nanotriangle to nanohole arrays have been identified, with those relevant to SERS enhancement being singled out, and optimization curves given. The Au nanohole arrays provide a versatile platform for SERS enhancement, whether used in a reflective or transmission based geometry. The importance of measuring the transmission and reflection to get the absorption when planning a SERS substrate was shown. If this is not done, the maximum EM field enhancement can be missed, as the maximum EM field is offset from these quantities. Even though the EM field was slightly offset from the absorption in the 2D nanoarrays measured, it was found to be the best guideline for optimization. As well, the continued importance of defects in plasmonic patterns was shown, encouragingly proving that even though ordered 2D nanoarrays are needed, defects in fabrication are equally important to obtaining large field enhancements. Therefore quality considerations may be relaxed while still creating higher SERS enhancements. The results give promise to application of cost-effective plasmonic nano-array patterns in SERS sensing.