MAPPING BRAIN ANATOMICAL CONNECTIVITY USING WHITE MATTER TRACTOGRAPHY

Abstract

Integration of the neural processes in the human brain is realized through interconnections that exist between different neural centers. These interconnections take place through white matter pathways. White matter tractography is currently the only available technique for reconstructing the anatomical connectivity in the human brain non-invasively and in-vivo. The trajectory and terminations of white matter pathways are estimated from local orientations of nerve bundles. These orientations are obtained using measurements of water diffusion in the brain. In this paper, the techniques for estimating fiber directions from diffusion measurements in the human brain are reviewed. Methods of white matter tractography are described along with the current limitations of the technique including sensitivity to image noise and partial voluming. We discuss the white matter tractography applications for topographical characterization of the white matter connections and the segmentation of specific white matter pathways and corresponding functional units of gray matter. In this context, we describe the potential impact of white matter tractography in mapping the functional systems and sub-systems in the human brain and their interrelations. Finally, we discuss white matter tractography applications to the study of brain disorders, including fiber tracts localization in brains affected by tumors and identifying impaired connectivity routes in neurologic and neuropsychiatric diseases.

Graphical Abstract

White Matter Tractography techniques have undergone extensive development in the last several years and have proved the potential to reveal new and important information regarding brain organization. This manuscript reviews the latest developments in this field.

INTRODUCTION

Brain-mapping imaging techniques have tremendously contributed in the last decade to our understanding of the brain organization and function. The opportunity to conduct in-vivo, non-invasive studies has led to characterization of structure and function on individual subject bases. It also allowed the study of multiple subjects and the mapping of the brain natural anatomical variability through probabilistic brain atlases. Functional imaging techniques have opened a new era by mapping the brain regions involved in specific tasks, thus associating function to structure. Furthermore, identification of brain regions that work in synchrony when performing specific tasks led to maps of the brain functional integration (1). Functional integration of brain regions is conditioned by the physical or anatomical connectivity defined by their associated white matter pathways. It is well recognized that higher order brain functions involve complex interactions between different brain regions. Thus, knowledge of the organization and integrity of the underlying white matter circuitry is essential in understanding brain normal function as well as the causes of some of the brain pathologies.

Until recently, structural imaging techniques were reduced to the gross assessment of white matter extent in an individual’s brain and did not allow differentiation of fiber structures or of brain connectivity. Most of the present knowledge of the fiber systems organization in the brain has come from fiber dissection of post-mortem material, indirect assessment of tracts’ functional associations from studies of functional impairments in trauma patients, or was inferred from invasive tracer studies in primates (2, 3).

The limitations in imaging the white matter specific structures were overcome by the advent of diffusion imaging and white matter tractography (WMT) techniques (4–9). Diffusion imaging estimates white matter local direction from measurements of water diffusion. White matter tractography pieces together this information to infer long-range connectivity patterns between distant brain regions. Consequently, white matter tractography offers unique avenues for the study of brain connectivity in both normal and pathological brain. Integration of WMT with functional mapping techniques such as functional MRI, transcranial magnetic stimulation, or electroencephalography has the potential to contribute to our understanding of brain functional integration.

In this paper we will present white matter tractography methods and white matter tractography potential applications. White Matter Tractography results are highly dependent on the quality of the underlying diffusion measurements and image processing techniques. With this consideration in mind, we will review the diffusion imaging techniques, their current technical limitations, and how these limitations may affect the accuracy of the WMT results.

ESTIMATING FIBER DIRECTIONALITY: DIFFUSION IMAGING

Diffusion imaging estimates the orientation of white matter pathways from estimates of water diffusion profile in each brain voxel. In tissues, the water molecules collide with one another and with the surrounding medium during their movements. Microscopic barriers such as cell membranes and macromolecules restrict and hinder molecules’ motion and thereby modify both their rate of diffusion and the shape of the diffusion profile. As a result, diffusion reflects microscopic characteristics of the medium. In fibrous tissues, such as brain white matter, water molecules diffuse faster along the fibers’ direction than perpendicular to it. This directional heterogeneity is termed diffusion anisotropy. Diffusion anisotropy provides a contrast mechanism that allows the estimation of the white matter bundles’ orientation by the directions of the peaks in diffusion profile.

The non-invasive measurement of diffusion by Magnetic Resonance Imaging is based on the early observation that spin diffusion reduces the magnitude of the MR signal. The signal attenuation E(q,t) in a PGSE experiment (10) that uses diffusion gradients to increase the signal’s sensitivity to spin diffusion is given by the Fourier transform of the spin displacement probability density function (PDF), P(s,t):

$$E(\mathbf{q},t)=S(\mathbf{q},t)/S_0=\int d^{3}sP(\mathbf{s},t)e^{2\pi i\mathbf{q}·\mathbf{s}}$$ [1]

where S(q,t) is the MR signal corresponding to the diffusion wavevector, q, and diffusion time, t, and S₀ is the MR signal when no diffusion weighting is applied. The spin displacement PDF describes the probability of a spin originally at the origin to be at position s after a diffusion time t; it is also referred to as the ensemble-average diffusion propagator. The diffusion wavevector is a function of the magnitude, orientation, and duration (δ) of the diffusion gradients, g: q=γδg (where γ is the gyromagnetic ratio). The direction of the diffusion gradient is often referred to as the diffusion encoding direction. The diffusion weighting of the MR signal may also be expressed by using a different parameter, the b value, where b = (2πq)²t.

In homogeneous white matter regions, where fibers have preponderantly the same orientation, a direction of fastest diffusivity may be defined. Fiber orientations in these regions may be described using the diffusion tensor model (DT). DT approximates the probability distribution function of the diffusing water molecules by a three-dimensional multivariate Gaussian distribution (4, 5). Mathematically, this distribution is described by a second-order symmetrical tensor, with 6 independent elements (4). For a Gaussian PDF, the signal attenuation due to diffusion is given by:

$$S(b)\cong S_0·\text{exp}(-b{\mathbf{ĝ}}^T\mathbf{D}\mathbf{ĝ})$$ [2]

where ĝ is the unit vector indicating the diffusion gradient orientation, D is the diffusion tensor, and the MR signal is expressed as a function of the b value.

The displacement profile of the Gaussian distribution has an ellipsoidal shape; as a result the DT is easily visualized using the so-called diffusion ellipsoid (Fig. 1). The orientation of the tensor’s major eigenvector, which aligns with the ellipsoid major axis (or the direction of fastest diffusivity), is used to estimate the orientation of white matter tracts and to map their course by DTI-based white matter tractography techniques.

Figure 1.

(a) The diffusion tensor may be visualized using the diffusion ellipsoid, which has the direction of its main axis (the direction of the fastest diffusivity, λ₁) given by the DT major eigenvector, e₁. The two other eigenvectors, e₂ and e₃, give the orientation of the ellipsoid’s medium and minor axes. Their corresponding eigenvalues, λ₂ and λ₃, relate to the ellipsoid magnitude along these axes. The relative magnitudes of the three eigenvalues determine the ellipsoidal shape which varies for brain voxels from prolate to spherical (b), with the oblate and spherical shapes being assumed to characterize crossing fiber regions (see also Fig. 2). For tractography applications, the diffusion tensor (c) and major eigenvector (d) are calculated at each brain voxel.

DTI allows the estimation of the preponderant diffusion direction using a relatively small number of measurements (6–30 diffusion encoding directions) and low b-values (b ~ 1000s/mm²). Whereas only 6 encoding directions are needed to estimate DT’s elements, a larger number of spatially uniformly distributed encoding directions is usually acquired to mitigate the noise effects on the DT derived parameters (11, 12). Current advances in the imaging hardware allow acquisitions of diffusion imaging data with resolution of 2–2.5 mm cubic voxels in clinically feasible times (8–15 minutes). One major limitation of DTI is its inability to describe fiber directionality in regions where two or more fiber populations with different orientations are present (e.g., crossing fiber regions). This limitation has led to the introduction of new techniques that try to estimate the component fibers either discretely or as a fiber orientation distribution (FOD) using multi-tensor approaches, spherical deconvolution, or from the angular dependence of the diffusion profile. Different functions have been proposed to express this angular dependence, including the Orientational Distribution Function (ODF, (13)), the Persistent Angular Structure (PAS, (14)), or the PDF itself at a fixed radius (15). In the following, we will describe some of these techniques in more detail.

ADVANCED DIFFUSION IMAGING METHODS

Multi-Tensor and Deconvolution Methods

A first approach in trying to describe regions with multiple intravoxel fiber orientations is to fit the diffusion signal to a combination of diffusion tensors (16–20), with each diffusion tensor describing structures with different orientations and properties:

$$S\cong S_0·\sum _{n=1}^N{f}_n·\text{exp}(-b{\mathbf{ĝ}}^T{\mathbf{D}}_n\mathbf{ĝ})$$ [3]

where N is the total number of components and D_n and f_n are the diffusion tensor and the volume fraction, respectively, of each of the components, with $\sum _{n=1}^N{f}_n=1$. In general, simplifying assumptions are used for the properties of the component fibers in order to reduce the number of unknowns to be fitted by the model and to stabilize the fitting algorithm (e.g., the component fibers are most often assumed axially symmetrical or individual tensors are assumed to have a predetermined shape). Behrens et al. (17) fit the diffusion signal to a combination of “sticks” and “balls”, with the sticks representing fibers of different orientation with infinite anisotropy, and the “balls” the isotropic components of the diffusion at a voxel.

One of the limitations of the multi-tensor model is the need to correctly estimate the number of fiber components to be fitted in a voxel. This number is not known a priori and its misestimation may lead to erroneous fiber estimates (e.g., if a two-tensor model is fitted in a voxel with a single fiber, fiber directionality will not be correctly described). Different criteria (e.g., the goodness of fit of the measured diffusion signal to the signal predicted by the model, bayesian approaches) are used to estimate N value at each voxel (17–20).

A different approach to overcome this limitation is to use a distribution to describe the fiber orientations (21–25). The diffusion signal is considered to be given by the convolution of the fiber orientation distribution (FOD) with a response (kernel) function:

$$S(\theta ,\phi )/S_0=F(\theta ,\phi )\otimes R(\theta )$$ [4]

where F(θ,φ) is the FOD and R(θ) is the kernel (or response) function in spherical coordinates. Tournier et al. (21, 23) and Anderson (22) use spherical harmonics as basis functions for the FOD, whereas Jian and Vemuri (24) use a Wishart basis function. The use of basis functions reduces Eq. [4] to a linear problem. The kernel function may be estimated using a mixture of Gaussian functions (22, 24, 25) or from a known configuration (i.e., a single tensor model in voxels with high anisotropies) (21). Deconvolution methods are noise-sensitive and regularization methods are usually employed to improve their performance (23, 24).

Multi-tensor and deconvolution methods customarily employ a High Angular Resolution Diffusion Imaging (HARDI) acquisition, where diffusion weighted images are obtained for a large number of different encoding direction (spatially uniformly distributed) at a single b-value. Thus HARDI data is acquired on a spherical shell in the diffusion space (i.e., the q-space). With both approaches higher b-values (b~3000s/mm²) and a larger number of encoding directions (N_enc > 60) than customarily used for DTI improve the ability to resolve fiber orientation in voxels where more than one fiber population is present (17, 23). The higher b-values increase the contrast between different orientations resulting in better performance of the algorithms for fiber orientation estimation and less sensitivity to noise. Nevertheless, lower b-value data is often used with these methods and appears to improve upon single tensor fiber orientation estimation – however the intravoxel orientation detection in these cases is limited to at most two fiber components (17, 20).

Diffusion Spectrum Imaging (DSI)

Diffusion Spectrum Imaging employs the relationship reciprocal to Eq. [1] to estimate the diffusion PDF from the diffusion MR signal (26):

$$P(\mathbf{s},t)=\frac{1}{S_0}\int d^{3}qS(q,t)e^{-2\pi i\mathbf{q}·\mathbf{s}}$$ [5]

Diffusion-weighted MR data is acquired for a large number of encoding directions and diffusion weightings in order to obtain a good coverage of the q-space. Current protocols implemented on clinical scanners customarily acquire between 129 (27) and 515 (26) q-space data points, for q corresponding to b values of up to 12000s/mm² (26–28). The PDF is obtained by using the 3D Fourier transform of the q-space data (Eq. [5]).

To estimate the component fiber directions, an ODF function is derived by projecting the PDF in the radial direction, ŝ,:

$$\mathrm{O}\mathrm{D}\mathrm{F}(\mathbf{ŝ})=\int ds·s^{2}P(s,t)$$ [6]

Local maxima in the ODF are used to estimate the component fiber directions.

Since a large number of data points in the q-space are acquired, DSI is associated with long imaging times. The large gradients needed to obtain diffusion data for large b values result in images with low signal to noise ratio (SNR). Current studies are trying to optimize DSI acquisitions by reducing the number the q-space data points acquired (28).

Q-ball Imaging (QBI)

Q-ball imaging (13) estimates a diffusion ODF defined customarily in a slightly different manner than in Eq. [6]:

$$\mathrm{O}\mathrm{D}\mathrm{F}(\mathbf{ŝ})=\int ds·P(s,t)$$ [7]

from HARDI data using the Funk transform (13). The Funk transform reduces the calculation of the ODF value along a direction ŝ to an integration of the signal values on the perpendicularly oriented great circle:

$$\mathrm{O}\mathrm{D}\mathrm{F}(\mathbf{ŝ})\cong \underset{\mathbf{q}\perp \mathbf{ŝ}}{\int }E(\mathbf{q})d\mathbf{q}$$ [8]

QBI was shown to resolve fiber crossings if q is sufficiently large (13). Different QBI implementations have used either the spherical radial functions (13) or the spherical harmonics as basis functions for the ODF (29, 30), thus reducing the QBI calculations to a linear matrix formulation. QBI algorithms employ interpolation and regularization procedures in order to improve ODF reconstructions which are relatively noisy when only raw data are used (13).

As it only needs diffusion-weighted data for a single spherical shell in the q-space, the QBI acquisition is less demanding than that of DSI.

Diffusional Kurtosis Imaging ODF (DK-ODF)

Lazar et al. have shown recently that the ODF (Eq. [7]) may be also estimated using the diffusional kurtosis (DK) approximation of the diffusion signal (31). DKI characterizes the departure from Gaussian diffusion using a fourth order tensor, the kurtosis tensor (32–34).

Similar to Q-ball Imaging, the ODF value along a direction ŝ may be obtained from the integration of the signal values on the perpendicularly oriented great circle. When ŝ coincides with the ẑ coordinate axis the ODF may be approximated as:

$$ODF\cong \frac{MD}{6\pi }·\underset{0}{\overset{2\pi }{\int }}d\phi \frac{3+K(\theta ,\phi )}{D(\theta ,\phi )}{|}_{\theta =\pi /2}$$ [9]

where D and K are the are the diffusion and kurtosis coefficients, θ and φ are the polar and the azimuthal angles with respect to ẑ, and MD is the mean diffusivity. The DKI-based ODF approximation may be decomposed into two components representing the Gaussian and non-Gaussian diffusion contributions, respectively:

$$\psi (\mathbf{ẑ})\approx {\psi }_{\mathrm{D}\mathrm{K}}(\mathbf{ẑ})=\frac{MD}{6\pi }·\underset{0}{\overset{2\pi }{\int }}d\phi \frac{3}{D(\theta ,\phi )}{|}_{\theta =\pi /2}+\frac{MD}{6\pi }·\underset{0}{\overset{2\pi }{\int }}d\phi \frac{K(\theta ,\phi )}{D(\theta ,\phi )}{|}_{\theta =\pi /2}$$ [10]

DKI requires only a relatively limited number of diffusion measurements and, for the brain, b values no higher than 2500 s/mm² (32, 34). These requirements result in diffusion-weighted images with relatively higher signal to noise ratio compared to the signal-to-noise ratio of images used by some of other advanced diffusion imaging techniques. The DK approximation includes only the lower moments of the water diffusion distribution, thus retaining only the low frequency components of the ODF spherical harmonic spectrum. Consequently, the reconstructed ODFs are inherently smooth and do not require further regularization. A potential disadvantage of the DK-ODF approach is that it may not be able to resolve fiber crossing configurations described by ODFs with high frequency components.

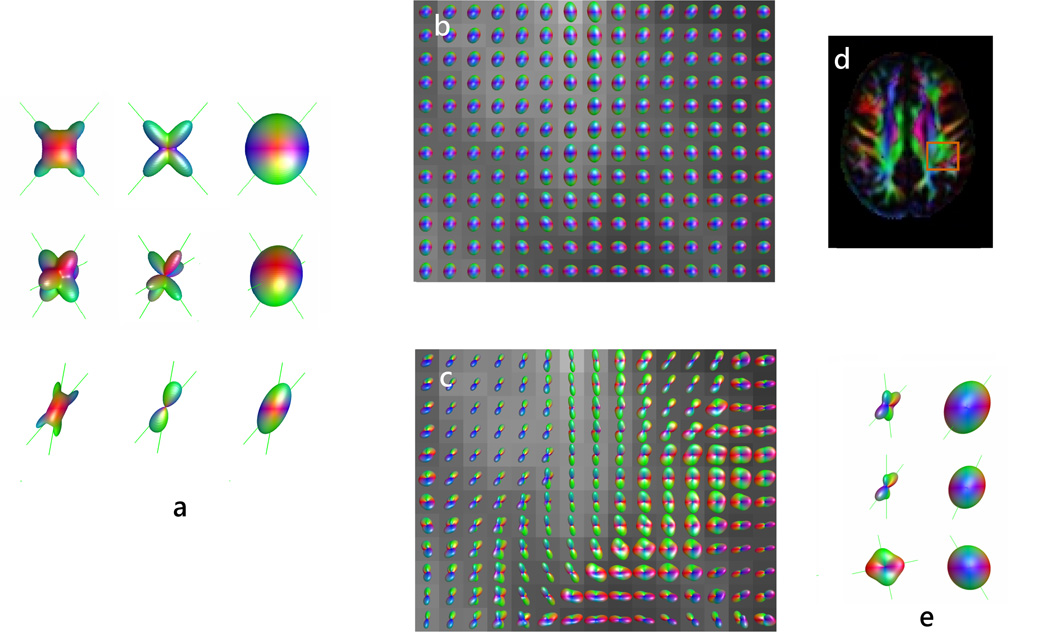
Fig. 2 presents ODF reconstructions using QBI and DK-ODF methods for different fiber configurations. Simulations of fiber crossings have shown that the ODF methods give good estimates of the fiber directionality when fibers are crossing at large angles (31, 35). However, as the crossing angle decreases, the ODF peaks become offset with respect to the true fiber directions (35). For small angles, the component fibers may not be resolved (31).

Figure 2.

(a) ODF reconstructions of two and three simulated fibers crossing at large angle (top two rows) and of fibers crossing at 30 degrees (bottom row) using DK-ODF, Q-ball, and DT methods (from left to right). The original fiber directions are indicated by lines. Note that the ODF methods are able to resolve the fibers, with better accuracy for large angle crossings. (b) DT and (c) DK-ODF maps of the intersection between posterior corona radiata, superior longitudinal fasciculus, and short association fibers. The position of the mapped area is shown in (d). Several of the voxels with apparent crossing fibers are detailed in (e), using both DK-ODF and the diffusion ellipsoid. Fiber estimates (given by the ODF and diffusion ellipsoid peaks) are indicated by lines.

Adapted by permission from Lazar et al (31).

WHITE MATTER TRACTOGRAPHY (WMT)

White Matter Tractography techniques estimate the connectivity patterns between different brain regions from the continuity in the local estimates of fiber direction at each voxel. To date, a large number of WMT algorithms have been proposed. These algorithms include as a first step the selection of a starting point or seed, which may be either a voxel or a precise location defined by Cartesian coordinates in the brain space. WMT algorithms can be classified largely in deterministic, probabilistic, and global optimization algorithms. The deterministic algorithms construct a unique trajectory for each seed point (5–9). The result is a path that connects two discrete regions of the brain. The probabilistic algorithms generate multiple possible trajectories for a seed point using either propagation fronts or Monte Carlo techniques (36–43). These algorithms connect the seed with a set of voxels or brain locations using weights defining the relative connectivity. Global optimization algorithms (44–47) generate the most optimal path between two brain regions by minimizing a cost function that usually describes the smoothness of the path and the goodness of fit of the path configuration to the underlying diffusion signal. Some of the early WMT algorithms have been previously reviewed in by Mori and van Zijl (48).

Deterministic White Matter Tractography Algorithms

Deterministic WMT algorithms involve several common steps including seed selection, fiber trajectory termination, and fiber selection strategies (6–9, 48). A trajectory is initiated at the seed point in both forward and reverse directions of fiber orientation field in a stepwise fashion (Fig. 3). At each step the trajectory is advanced along an estimated tract direction. The fiber trajectory is propagated until some stopping criterion is met. Stopping criteria include exiting the brain space, intersection with voxels characterized by low anisotropy values, or large local curvature of the trajectory (6–9, 48). The low anisotropy criterion, which is more common for DTI-based WMT techniques, stops the propagation of the computed tract when it reaches regions where a fastest diffusivity direction is not well defined (e.g., gray matter or cerebro-spinal fluid). The curvature criterion is based on the assumption that white matter bundles follow smooth paths and aims to stop trajectories from following unlikely routes.

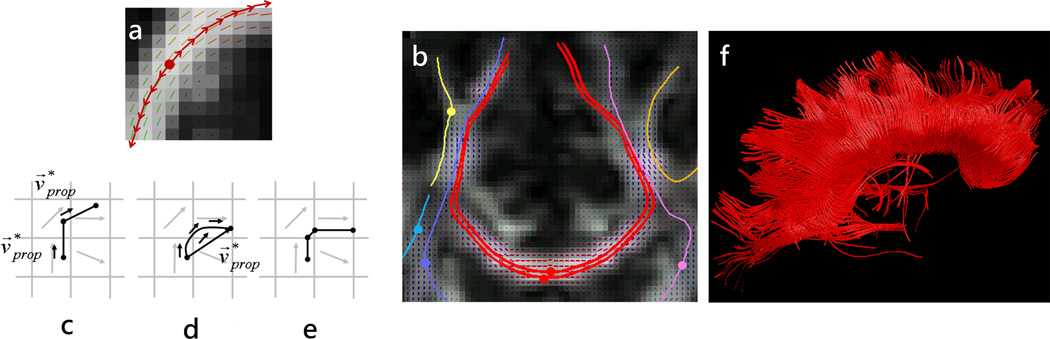
Figure 3.

(a) and (b): Fiber trajectories are obtained by following fiber direction estimates from voxel to voxel; the trajectory is initiated in both forward and backwards vector field directions starting at a “seed” point (indicated by a dot) ; (c)–(e) Several strategies may be used to step along the trajectory including a constant step size with the propagation direction estimated at the beginning of the step (Euler, (c)) or along the step (Runge-Kutta, (d)), or a variable step size (FACT, (e)); (f) Tractography reconstruction of the corpus callosum obtained from seeds situated in the mid-sagittal region of the tract.

The fiber trajectory, r⃗(t), can be described using a differential equation (8):

$$\frac{d\overrightarrow{r}(t)}{dt}={\overrightarrow{v}}_{\mathit{\text{prop}}}(t)$$ [11]

where V⃗_prop is the estimate of the pathway direction at position t. The fiber propagation involves two steps: 1) estimation of V⃗_prop, and 2) derivation of the trajectory by integrating Eq. [11] with the initial conditions given by specified seed position. By solving Eq. [11], the trajectory is advanced from a position, r⃗_old, to a new position, r⃗_new, by stepping along a direction, V⃗_prop, for a distance Δp, which is called the step size:

$${\overrightarrow{r}}_{\mathit{\text{new}}}={\overrightarrow{r}}_{\mathit{\text{old}}}+\mathrm{\Delta }p·{\overrightarrow{v}}_{\mathit{\text{prop}}}^{*}$$ [12]

With DTI, the basic method to approximate V⃗_prop is to use the major eigenvector of the diffusion tensor: V⃗_prop = e⃗ (6–8). This approach, generally called streamlines algorithm (STR), works well in regions of high anisotropy where the direction of fastest diffusivity is well defined. An alternative to the streamline algorithm in the DTI framework is to use the entire tensor information to estimate the local tract direction (9). The tensor deflection algorithm (TEND) estimates the propagation direction at each step using the full diffusion tensor to deflect the propagation direction from the previous propagation step: V⃗_out = D · V⃗_in, where the incoming vector (V⃗_in) represents the propagation direction from the previous integration step (9). Generally, TEND limits the curvature of the deflection, and results in smoother tract reconstructions.

With more complex imaging methods, using a deterministic approach, V⃗_prop is chosen (26, 49) in voxels with multiple orientations as the orientation that provides the smoothest path for the trajectory (i.e., the orientation that has the smallest angle with the incoming trajectory direction). Several studies have shown that tracing based on advanced diffusion models improved the reconstruction of fiber trajectories in region of fiber crossings (26, 49). For example, these methods appear to reconstruct the lateral fibers of the cortico-spinal tract and corpus callosum, which are known to exist from anatomical studies but have been poorly reconstructed by the DTI-based tractography methods. Fig. 4 shows tractography results in a crossing fiber region. Of note here is that whereas more advanced diffusion imaging methods may identify the presence of multiple intravoxel orientations, they do not offer sufficient information to distinguish between multiple possible configurations, such as as crossing, kissing, or bending fibers (50). These configurations may potentially be resolved using either directionality information in a neighborhood of the voxels of interest or a priori anatomical knowledge.

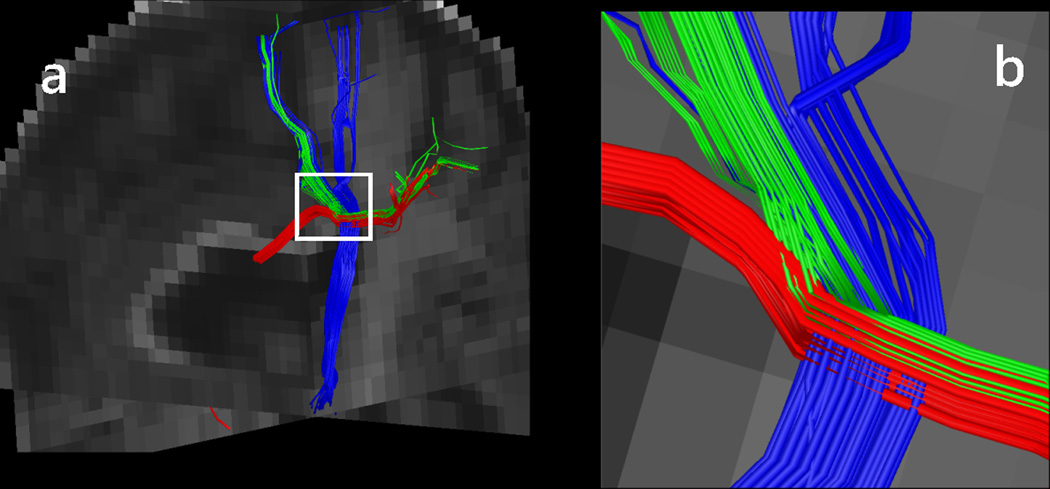
Figure 4.

(a) Intersection of a callosal (red) and a short association (green) fiber bundle with the projection fibers of the corona radiata (blue). Fiber directionality was estimated using the DK-ODF method; (b) Detailed view of the crossing region highlighted in (a).

The value of ${\overrightarrow{v}}_{\mathit{\text{prop}}}^{*}$ in Eq. [12] can be calculated either at r⃗_old (using either interpolation of the neighboring data or the data from the closest voxel (the Euler integration method)) or at an intermediate position between r⃗_old and r⃗_new (the Runge-Kutta method). The Euler and Runge-Kutta methods are using a constant step size, usually smaller than the voxel size (Fig. 3). An alternative to these methods is the FACT algorithm (Fiber Assignment by Continuous Tracking, (7)), that does not employ interpolation and uses a variable step size from voxel to voxel, with the direction of propagation changing at the voxel boundaries (Fig. 3).

Fiber Trajectories Selection – Reconstructing Specific White Matter Pathways

In order to reconstruct specific white matter structures different approaches can be used. One approach consists in generating fiber trajectories by seeding specified tract regions that are identified using anatomical maps and following them until termination. An alternative is to seed large regions of the brain. With both approaches, region of interests (ROIs) may be used to subsequently select the tract of interest by retaining only those trajectories that intersect the specified ROIs (6–9, 51, 52). One or multiple selection ROIs may be used for either including trajectories or excluding trajectories that are not part of the group of interest (52). It has been shown that by using well-designed fiber selection protocols (52) the major white matter brain tracts can be reconstructed with high inter-user reproducibility.

As ROI based approached may be time consuming, new algorithms that automate fiber clustering have emerged (53–56). These algorithms cluster fiber trajectories based on their properties such as length and curvature profile (53–56) or by comparison with fiber tracts atlases (56).

With both manual and automatic approaches, one issue to address is the presence of spurious fiber trajectories (erroneous trajectories due to noise and partial volume averaging, such as a trajectory jumping from a tract to another) that are often obtained in particular when using DTI-based deterministic tractography. In general a “NOT” operation (52) is employed in order to remove these trajectories from the group of fibers of interest. Improved diffusion imaging methods are likely to greatly minimize generation of erroneous trajectories.

Deterministic algorithms have been used to reconstruct the major white matter structures of the brain with results that are in good agreement with known anatomy (5–9,50,52,57, 58).

Accuracy and Precision of White Matter Tractography

The noise associated with the diffusion imaging data leads to uncertainty in the estimates of fiber directions. A question that arose early on in the WMT field was how can one determine the accuracy and precision of white matter tractography algorithms and define measures of confidence for specific tractography results. Several studies have tried to address this question using Monte Carlo simulations of synthetic diffusion tensor fields (12, 59, 60). It was found that, the precision of a tract trajectory is influenced by both tract properties, such as anisotropy, geometry, and properties of the surrounding structures, as well as data acquisition characteristics such as diffusion direction encoding, acquisition resolution, and image SNR (12, 59, 60). The choice of the fiber tracking algorithm may also affect white matter tractography results.

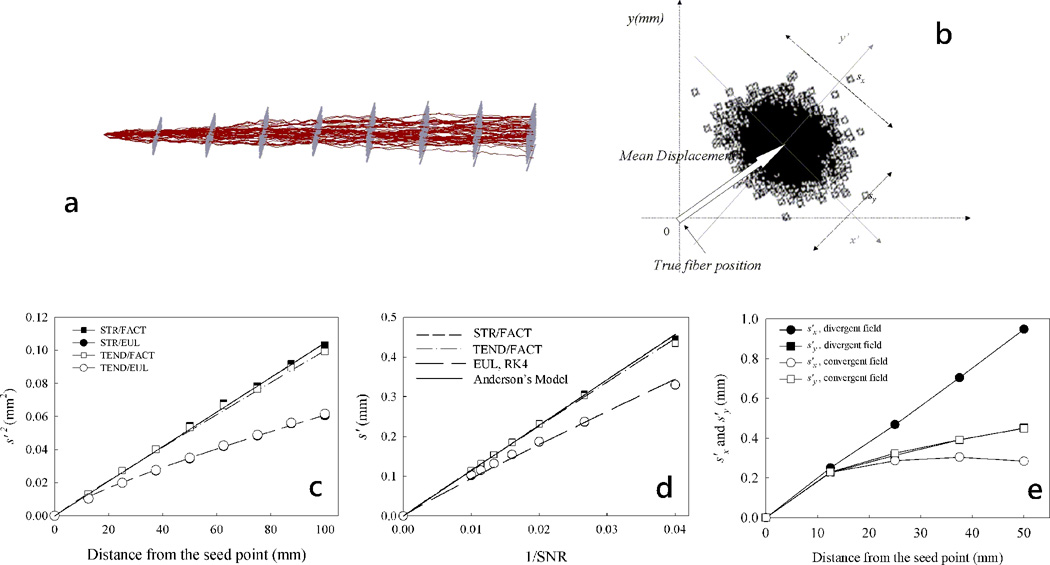
To analyze the accuracy and precision of a single fiber trajectory Lazar et al. have performed a comprehensive study of the factors that influence them using Monte Carlo simulations (12). Monte Carlo fiber tracking experiments were performed using synthetic homogeneous tensor fields of simple geometry (linear, circular, and radial) and constant anisotropy and SNR. Additional investigated geometries were the divergent and convergent fields - with fibers spreading (gathering) along the bundle length (12). For all the simulations, the noise was assumed to be normally distributed and independent between voxels and different measurements. For each ideal trajectory in the noise-free diffusion tensor field a distribution of noisy trajectories was obtained using fields with different noise realizations (Fig. 5a). The distribution of trajectories was characterized at different distances from the seed point in planes orthogonal to the ideal trajectory direction (Fig. 5b).

Figure 5.

Image noise and tensor field characteristics affect the accuracy and precision of the tractography methods; consequently reconstructed pathways may deviate from the true trajectory. (a) An example of fiber tract dispersion due to noise in a linear tensor field. (b) Tract error was characterized using the standard deviations of the two-dimensional distribution of fibers in planes perpendicular to the true trajectory at different distances from the seed point and the displacement of the mean trajectory position relative to the true trajectory position. The tractography error increases with the distance from the seed point (c), decreasing SNR (d) and increased tensor field convergence (e). The error decreases in regions of field convergence (e).

Reproduced with permission from Lazar and Alexander (12).

The results showed that the precision of the tractography algorithms decreases with the decreasing image SNR and tensor anisotropy, and increasing distance from the seed point (i.e., tractography error is cumulative, increasing as the trajectory grows, Figs. 5c–e). Tract precision also depends on the diffusion encoding direction set, and the fiber geometry characteristics such as divergence and tensor field homogeneity. For algorithms based on Euler integration or TEND propagation algorithm, the tract accuracy decreased with increasing curvature of the circular field. Interpolation-based path integration methods (Euler and Runge-Kutta) yielded the lowest tract dispersion. However, the precision of the interpolated integration methods was more sensitive to divergent and convergent field effects compared with FACT method (Fig. 5e). For all algorithms, the divergent fields increased the tract dispersion, whereas the convergent fields decreased it.

Based on the numerical results obtained from the Monte Carlo simulations and previous theoretical models of tract dispersion (61), Lazar et al. (12, 39) developed numerical analytical models to describe tract precision in homogeneous fields of zero-divergence. Tract dispersion can be described by:

$$s_j\cong \alpha ·w·\frac{{\left(\sqrt{N_v}\right)}^a}{SN{R}^b·\mathrm{\Delta }{\lambda }_j^c}·\sqrt{{ẽ}_j}$$ [13]

where s₂ and s₃ are estimates of the tract dispersion standard deviations along the median and minor tensor eigenvectors, e₂ and e₃, respectively, in the plane perpendicular to the tract, w is the voxel width, N_V the number of voxels crossed by the fiber trajectory (and relates to the trajectory length). Δλ_j represent the eigenvalue contrasts between the first and the second and third eigenvalues, respectively (Δλ_j = λ₁ − λ_j, j=2,3) and are measures of the DT field degree of anisotropy. The factors ẽ_j describe the intercorrelated dependences of tract dispersion onto the encoding directions and tensor orientation (12, 61). The parameters, a, b, and c modulate tract dispersion dependence on N_V, SNR, and Δλ_j, and α is a proportionality parameter. The values of these parameters are algorithm specific, with all of them being close to 1 for algorithms that do not use interpolation, and having values slightly lower than 1 for interpolating algorithms (12).

Fig. 5 shows the expected tractography error for different tensor fields configurations. Should be noted here that tract dispersion of non-divergent fibers with high anisotropy was observed to be generally, less than one voxel (Figs. 5c–d), even for long trajectories. As the anisotropy in the central region of the most white matter tracts is relatively large, most tractography methods should be able to reconstruct this region with relatively high precision. Low anisotropy may be encountered in regions of fiber crossing, bending, or divergence at the intravoxel level. Consequently, in these regions the inability of the tensor model to describe this complex anatomy is reflected as an increase in the tractography uncertainty. Most fiber structures diverge as they reach the cortex. Thus, tractography methods will be less precise in the cortical terminal regions of the white matter tracts. Tractography accuracy of a fiber tract is also highly affected by an anisotropic surrounding or neighboring medium. That is, once a fiber trajectory jumps from the true path to an adjacent white matter structure, it is highly unlikely to return to the original tract.

In real human brain DTI data the tensor eigenvalues as well as the voxel width vary along the trajectory. The SNR may also vary spatially due to coil sensitivity, physiological noise and other factors and its distribution may be different from normal. A discrete generalization of the Eq. [13] for variable tract characteristics can be approximated by (39):

$$s_j^2(i)\approx {\alpha }^2·N_v^a·\sum _{i=1}^{N_v}\frac{1}{N_v}·\frac{w^2(i)}{SN{R}^{2b}(i)·\mathrm{\Delta }{\lambda }_j^{2c}(i)}·{ẽ}_j(i)\approx {\alpha }^2·N_v^{a-1}·\sum _{i=1}^{N_v}\frac{w^2(i)}{SN{R}^{2b}(i)·\mathrm{\Delta }{\lambda }_j^{2c}(i)}·{ẽ}_j(i)$$ [14]

where i is the voxel index along the fiber trajectory. In Eq. [14] the variances of the two-dimensional distribution are approximated by summing independently over the values corresponding to the local directions e₂ and e₃. This approximation gives only the upper and lower bound of the tract error estimates in both directions (39). In brain DTI data, the tensor frame (as defined by e₂ and e₃) may vary along the fiber tract, leading to errors that are mixtures of the two different components. Moreover, axial asymmetry of the diffusion tensor (λ₂ ≠ λ₃) may lead to an “asymmetrical” dispersion pattern of a tractography result (62). Tracking errors are expected to be elliptical in this case (63, 64), with the major axis of the ellipse parallel to the tensor’s median eigenvector. Eq. [14] may be used to derive the degree of confidence in a fiber tractography result and was found to give a good approximation of the tractography dispersion in the homogeneous structures with low divergence (39). A limitation of this model is that it does not describe tract behavior in divergent fields or mixed fields that contain structures of different orientation or anisotropy.

Whereas tractography error in this section is discussed in the context of the DT model, the results described here can be in part extrapolated to WMT based on more advanced methods, as large portions of the large tracts are homogeneous and thus fiber directionality is well described by the DT model. With a better estimation of the underlying fiber structure, the tractography accuracy is expected to increase and the uncertainty to decrease in regions of fiber crossing.

Probabilistic White Matter Tractography Algorithms

The deterministic fiber tracking techniques infer white matter connectivity by assuming a unique fiber direction estimate in a voxel. As discussed above, the precision and accuracy of this estimate can be influenced by acquisition-related parameters, diffusion tensor field properties, and the choice of the tractography algorithm. To characterize the uncertainty in fiber path estimation, probabilistic algorithms have been proposed that generate a set of possible propagation directions for a given voxel. For each seed point, a set of possible trajectories is obtained (Fig. 6c). Each trajectory is generated in a streamline fashion, with the propagation direction at each step being chosen at random from the distribution of directions available at the step’s corresponding voxel. In the following sections different types of probabilistic algorithms are described.

Figure 6.

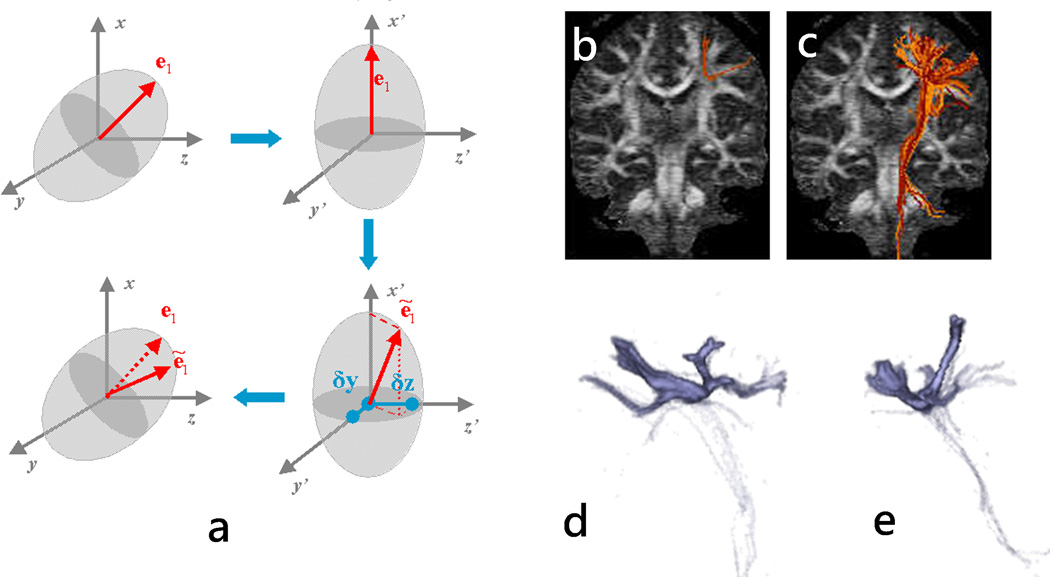
(a) RAVE method involves the DT transformation in its reference frame, the perturbation of the major eigenvector, and the rotation of the perturbed eigenvector back into the laboratory frame. (b) and (c): Fiber trajectories obtained for the same seed point using deterministic streamline(b) and RAVE(c) algorithms. Three-dimensional renderings of the fiber density for the trajectories depicted in (c) are shown in (d) and (e) using a sagittal and coronal view, respectively.

Model-Based Probabilistic Algorithms

Model-based (or parametric) probabilistic algorithms use a distribution of possible propagation directions at each step along the trajectory, with distributions generally being defined based on the diffusion tensor model and derived parameters (36–43). Fiber distributions are obtained by perturbing the tensor major eigenvector (38), or by deflecting a set of directions uniformly distributed onto a sphere using the tensor operator (41), similar to TEND algorithm (9). In the latest approach, the larger deflection toward the tensor major eigenvector for more anisotropic tensors results in a more focused distribution of directions. A similar approach is used in reference (37), where the focused set of directions is used to define the extent of a propagation front. An alternative to these approaches is a Bayesian approach where a likelihood function is usually defined using tensor or multi-tensor based descriptions of the diffusion signal (42, 43) and a priori considerations are included as priors (e.g., positivity of the diffusion coefficients, smoothness of the tensor field). The likelihood function also includes an estimation of the noise distribution (e.g., Gaussian, Rician). The final distribution (the posterior distribution) is calculated from the likelihood function and the prior distribution using the Bayes theorem (42, 43).

Here we use for illustration the Random Vector Propagation (RAVE) algorithm (38) due to its simplicity, with the other probabilistic model-based algorithm being relatively similar. With RAVE, the tensor in the measurement frame, D, is diagonalized into the tensor frame, D₀. In this frame, the major eigenvector e₁, is oriented along the x axis (Fig. 6a) and consequently does not have components along the y and z directions. A perturbed direction e₁ is obtained by randomly generating normally distributed y and z offsets with mean zero and standard deviation proportional to ratio of the ellipsoid length along the corresponding axes and the length along the x axis: $\delta y=N(0,\alpha ·\sqrt{{\lambda }_2}/\sqrt{{\lambda }_1})$ and $\delta z=N(0,\alpha ·\sqrt{{\lambda }_3}/\sqrt{{\lambda }_1})$, where α is a proportionality factor that is chosen by the user. This method allows the degree of perturbation to be proportional to the tensor degree of anisotropy and also accounts for cases where λ₂ and λ₃ have different magnitudes. Alternatively, eigenvector perturbation along low anisotropy directions (described by higher $\sqrt{{\lambda }_{2,3}}/\sqrt{{\lambda }_1}$ ratios) can be weighted more by using a power function rather than a linear dependence of the standard deviation on these ratios: $y=N(0,\alpha ·{(\sqrt{{\lambda }_2}/\sqrt{{\lambda }_1})}^n)$ and $z=N(0,\alpha ·{(\sqrt{{\lambda }_3}/\sqrt{{\lambda }_1})}^n)$, with n > 1. The perturbed vector is rotated back to the measurement frame and used as the local propagation direction by the fiber-tracking algorithm. Multiple streamlines are obtained for each seed point, with each trajectory being obtained using a randomly perturbed major eigenvector at each step. Probabilistic algorithms usually maintain the curvature smoothness criterion for the individual streamlines, but relax the anisotropy threshold for terminating trajectories, in order to potentially capture tract information in regions of fiber crossing. Figs. 6c–e present tract reconstructions obtained using RAVE method, which generates a more extended network of pathways compared to the streamline deterministic approach. There are several limitations of the RAVE and other similar algorithms: 1) they are not correctly describing fiber distribution in regions were noise structure is different than Gaussian (or other assumed distributions); 2) they require a calibration factor (e.g., α for RAVE) that will influence the results, but its optimal value may vary even within the same data set; 3) they are tensor-based, so they only address the crossing fibers issue marginally (as increased dispersion) when used with a single tensor model, although they can be used in combination with multi-tensor approaches.

Probabilistic algorithms generate multiple pathways to construct a distribution of trajectories for a seed point. A probability of connection between the seed voxel and other voxels or regions of the brain is usually defined as the density of the trajectories that connect them, where the density is calculated as the number of connecting trajectories normalized by the total number of trajectories (with higher densities indicating higher probability of connection). The connectivity in this case reflects the degree of confidence in a particular connection obtained using WMT, given the acquired data (and should not be seen as a measure of brain anatomical or functional connectivity). To map the extent of a tract, connectivity maps are thresholded such as voxels with low-probability of connection are not included in the estimated tract volume (20).

Bootstrap Tractography

An alternative approach for estimating the inherent variability of the diffusion measurements is to use bootstrap statistical techniques. Bootstrapping is a non-parametric procedure for evaluating the distributional properties of a statistic from a limited number of measurement samples, without making prior assumptions about its distribution. With regular bootstrapping, a pool of diffusion weighted measurements is obtained for each configuration of interest (e.g., defined by specific diffusion encoding direction, b-value, etc.) by repeating the experiment. A distribution of the statistic of interest is obtained from repeated random sampling of the original pool of measurements. Regular bootstrap techniques have been first used in diffusion imaging to characterize the DTI parameters (e.g., eigenvalues) within a single brain voxel and within a region of interest (65) and to estimate the dispersion of the tensor major eigenvector (11).

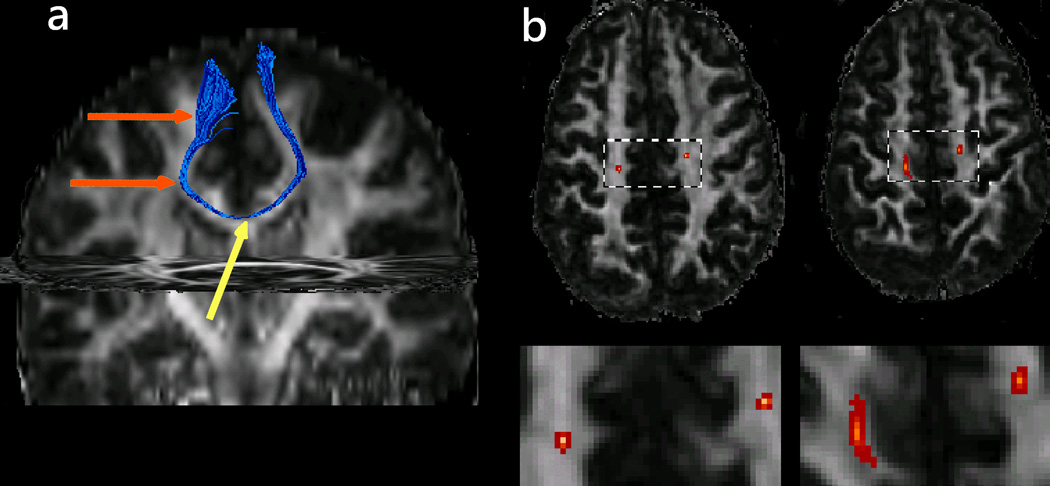
The technique may be also used to generate a distribution of trajectories for a seed point (39, 66, 67). In this approach, a set of multiple repeated measurements of the diffusion-weighted signal is obtained for all the brain voxels and for all the encoding directions. One volume sample of the signal bootstrap distribution is obtained by drawing a random number of samples (N_s) with replacement from the original pool of independent diffusion acquisitions. The replacement implies that multiple drawings of the same independent measurement are allowed (i.e., one measurement may be included in the number of samples N_s more than once). The signal is then calculated as the average of the N_s randomly selected samples. This signal is used to estimate the fiber orientation (e.g., major eigenvector of the diffusion tensor, ODF, etc.) at each voxel in the brain’s volume. For each volume sample, a bootstrap trajectory is obtained for the seeds of interest using a deterministic algorithm. By repeating this procedure multiple times a distribution of trajectories is obtained for each seed. An example of DTI-based bootstrap tractography is presented in Fig. 7 for a seed situated in the midline region of the corpus callosum.

Figure 7.

(a) Bootstrap tractography for a seed point situated near the corpus callosum’s midline (yellow arrow). In this example, one thousand trajectories were generated to construct the bootstrap fiber distribution for the seed. Other bootstrap parameters included a pool size of eight independent measurements (N_s=8). (b) Corresponding density maps shown for two different slices (top, full slice, and bottom magnified ROI) demonstrate increased fiber dispersion as the distance from the seed point increases.

Reproduced with permission from Lazar and Alexander (39).

As opposed to the model-based approaches, the bootstrap probabilistic tractography does not assume any inherent noise distribution in the data. In cases where the noise does not obey a specific model, bootstrap methods will provide a more accurate representation of the data variation than the model-driven approaches.

A limitation of the regular bootstrap techniques is the long imaging time needed to obtain the repeated data samples. Recently, two new bootstrap methods that are not repetition based have been employed to characterize uncertainty in the diffusion data, the wild and residual bootstrap (66–69). The wild and residual bootstrap methods estimate the signal distribution by resampling not the signal, but the residuals obtained by fitting the signal to a model. The resampled residual distributions are used to generate signal distributions. The wild bootstrap is based on the assumption that the residual distributions are symmetrical and resample by randomly changing the signs of the residuals (69). The residual bootstrap assume that the residuals are independent and identically distributed (i.i.d.) and resample the distributions by freely interchanging the different residuals. These approaches are easily implemented for the DT-based models, where a scaling procedure is usually employed for the residual bootstrap to enforce i.i.d. error terms (70).

Both repetition and model-based bootstrap methods are easily extended to describe higher order diffusion imaging data. Residual bootstrap has been used to estimate the uncertainty associated with Q-ball and spherical deconvolution based tractography methods (66–68), with residuals obtained by fitting the signal to either a multi-tensor model or to a spherical harmonics series. Comparisons of the wild or the residual bootstrap with repetition based bootstrap tractography have shown that similar results are obtained using the different approaches (66, 68).

Global Optimization Algorithms

Global Optimization Algorithms reconstruct the most probable paths in the brain space such that path configurations are consistent with the underlying diffusion data and satisfy specified constraints. They work by optimizing global parameters that are calculated at the path level (e.g., minimizing a cost function or maximizing a posterior probability). A first constraint is to consider path optimization between two regions, a seed and a target region (44, 46). Optimization of the whole brain tractography has also been proposed (45). Most often, path smoothness is used as an additional constraint to the optimal trajectories.

Global optimization algorithms are less affected by the cumulative error effect characteristic of the deterministic (and probabilistic) algorithms. They are also less likely to be influenced by local irregularities in the diffusion data. One disadvantage of the global optimization algorithms is that they are generally computationally intensive.

APPLICATIONS

Mapping Specific White Matter Pathways

WMT has been extensively used to demonstrate the in vivo mapping of the white matter pathways of the brain (6–9,51,52,57,58,71–76). First WMT studies had focused on replicating the course of the major fiber structures known from classical anatomy. Structures such as the corpus callosum, superior longitudinal fasciculus, fibers of the corona radiata, and fronto-occipital fasciculus were easily identified using WMT. Whereas not a direct validation, the similarity of the WMT fiber reconstructions to the known anatomy was a first confirmation of the WMT potential for the non-invasive mapping of distinct white matter structures. Postmortem, invasive anatomical techniques, such as fiber dissections and fiber tracing techniques allow very few structures to be traced for a specimen (since unveiling a structure of interest involves a specific sequence of dissection steps, which render unusable the specimen for future investigations). As a three-dimensional computerized technique WMT has the advantage of allowing an infinite number of “in vivo” dissections (73) procedures of a single data set.

More recently, tractography studies have generated new information regarding brain organization and development. WMT improved current understanding of the organization of the association fibers such as the language pathways (20, 74) and the U-fibers (75) and have shown for the first time the existence of a pathway system interconnecting the mid-fusiform gyrus with the amygdala and hippocampus (76).

White Matter Parcellation

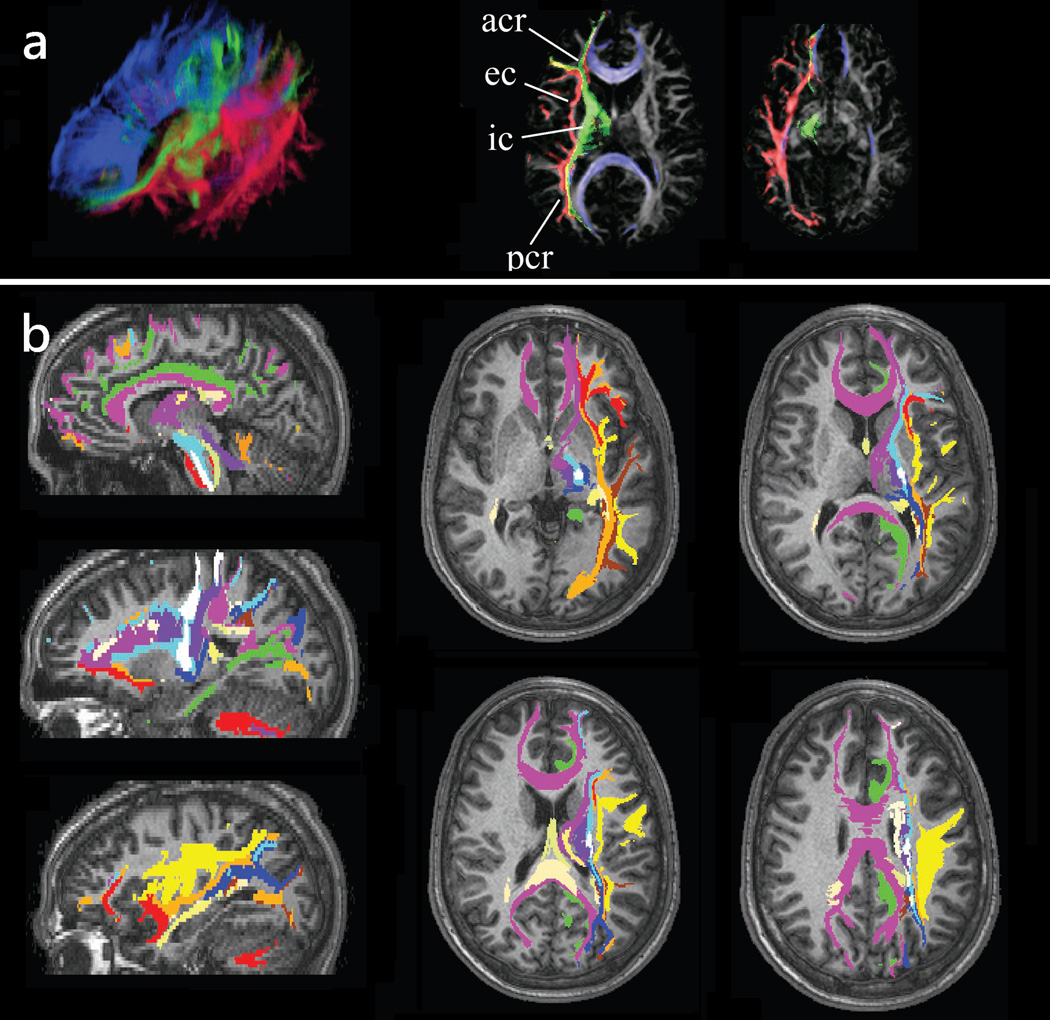
Since WMT can identify specific white matter tracts it may be used to segment out the brain volume occupied by these tracts. Thus, WMT allows parcellation of the WM in regions corresponding to different structures. This information is not possible to obtain with any other imaging technique. The segmented tracts can be used for morphometric analyses (e.g., volumetric, cross-sectional area, etc.) or as regions of interest for quantitative analyses of anisotropy and diffusivity data, or data originating from other imaging modalities. Fig. 8 shows an example of white matter segmentation based on the constituent structures.

Figure 8.

White matter tractography may be used to label brain voxels according to the white matter structure they are part of. (a) Image tractograms of the projection (green), association (red), and callosal (blue) fibers are mapped into the brain space indicating their position with respect to other brain regions. (b) A similar procedure has been used to label various white matter tracts including the corpus callosum (purple), superior longitudinal fasciculus (yellow), cingullum (green), uncinate fasciculus (dark red), inferior occipito-frontal fasciculus (orange), inferior longitudinal fasciculus (brown), cortico-bulbar tract (light blue), cortico-spinal tract (white), fornix and stria terminalis (light yellow). Tract positions are shown in several sagittal and axial slices.

Adapted by permission from Wakana et al. (51).

Recently, this approach has been applied widely to investigate the integrity of white matter in a variety of brain disorders. Several examples include segmentation of the tracts of the frontal and limbic lobes in schizophrenic (77) and temporal epilepsy (78) patients, fronto-striato-thalamic connections in Tourette syndrome (79), and hypoccampo- and amygdalo-fusiform pathways in autism (80). The segmented volumes were used as regions of interest to characterize tract-specific differences in anisotropy and diffusivity between different populations and to characterize the developmental aspects of white matter microstructure in both control and patient populations.

Gray Matter Parcellation

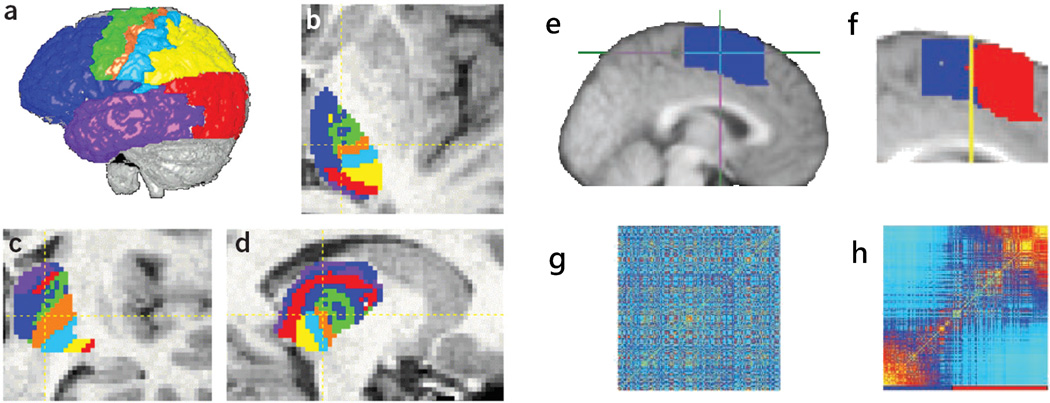
Connectivity maps of the neural connections in primates suggested that distinct functional regions of the brain are characterized by distinct connectivity patterns (81). Based on this idea, WMT has been used to segment gray matter regions based on their connectivity patterns (81, 82). In a first approach (82) the thalamus was subdivided based on its connectivity with distinct cortical regions (Figs. 9a–d). In a second approach (81), clustering based on distinct patterns of distributed connectivity all over the brain has been used to separate supplementary motor area (SMA) and pre-SMA regions of the premotor cortex (Figs. 9e–h). These approaches have been used subsequently to segment other gray matter regions, including the parietal cortex (83), the Broca’s area (84), and the cingulate gyrus (85).

Figure 9.

(a)–(d) Segmentation of the thalamus based on its cortical connectivity; each thalamic voxel is labeled according to its predominant cortical projection (e.g., blue-prefrontal, red-occipital, etc.). (e)–(f) Segmentation of the pre-SMA and SMA based on their connectivity patterns is obtained by first constructing a connectivity matrix (g) from the tractography data of the entire pre-motor region (e); this matrix is then reordered (h) to segregate voxels with different connectivity. The voxels separated using the connectivity matrices are then mapped back into the space brain (f) to reveal two contiguous and distinct regions.

(a–d) Reproduced with permission from Behrens et al (82).

(e–f) Reproduced with permission from Johansen-Berg et al. (82). Copyright (2004) National Academy of Sciences, U.S.A.

Brain Connectivity

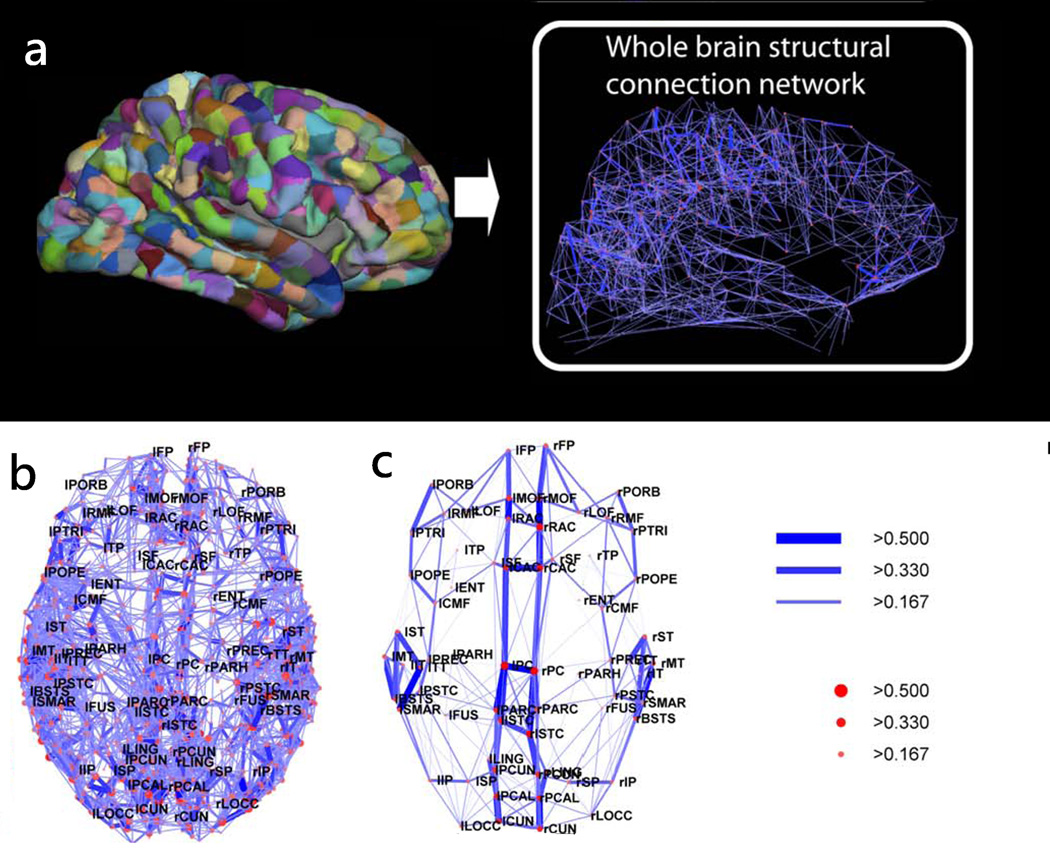
WMT has also been used recently to generate connectivity matrices of the entire brain and to study brain structure at the network level (27). In this approach, WMT derived trajectories are used to define the properties of the connections (or edges) between different nodes of the brain network (such as weight and length, where the weight is usually defined in terms of the number of trajectories between two regions/nodes) and node properties such as degree (the number of independent connections) and strength (a measure of how strong are the connections of a node). These local network properties are integrated to globally characterize the network organization and to identify relevant network sub-structures and their interrelations. In a recent study, Hagmann et al. (27) have used this approach to show the existence of a structural core within posterior medial and parietal cerebral cortex and in several temporal and frontal modules (Fig. 10).

Figure 10.

Whole brain tractography was used to generate connections between the different cortical regions obtained by parcellating the cortex into1000 regions of interest. The cortical regions and resulting connectivity graph are shown for one subject in (a). The connectivity backbone, indicating regions highly connected and highly central, is shown in (b) for one subject and in (c) averaged across five subjects. The edges and nodes of the network are labeled according to their connection weight and strength. The connection weight of an edge is given by the number of trajectories connecting its end nodes, normalized by the connection length and total surface area of the connected cortical regions. The node strength gives a measure of the extent to which a node is connected to the rest of the network.

Adapted from Hagmann et al. (27).

Recent work has suggested that neurogenerative disorders are characterized by specific atrophy patterns that correspond closely to specific functional networks in the brain (86). It has also been shown that the brain is affected at the network level in neuropsychiatric disorders such as schizophrenia (87). Thus mapping of the brain networks and their microstructural properties (through WMT and quantitative measures derived using diffusion imaging) and complementary imaging methods (such as resting state functional MRI) may be instrumental in understanding the causes and evolution of these disorders. Measures describing brain network properties may potentially be useful biomarkers for characterizing different brain disorders as well as brain development in both normal and pathological brain.

Clinical Applications: Presurgical Planning

The major clinical application of WMT has been the reconstruction of relevant fiber tracts in patients undergoing brain surgery (88–92) including patients that present with brain neoplasms and space occupying lesions. In many of these patients, white matter tracts are often distorted or displaced by the mass effect of the tumors or lesions (Figs. 11 and 12) and microstructurally altered by pathology (e.g., tumor infiltration, edema). Since white matter tractography indicates both the courses and the cortical regions the tracts connect it may be used to identify pathways that are related to vital neural functions and thus are essential to be preserved by surgical procedures. The applications for both pre-surgical and intra-operative mapping are obvious. To date, WMT feasibility to map the effect of brain tumors on white matter anatomy was investigated by many studies (90–92). Comparative studies between tractography derived tract courses and intra-operative cortical stimulation in cortical regions relevant for motor and language functions have shown a good correspondence between the locations of tracts identified through the two different methods (92, 93). Tractography becomes less reliable in regions that are highly affected by increased partial voluming (due to the mass effect of the lesions) or regions that have their diffusion characteristics modified by pathology (92).

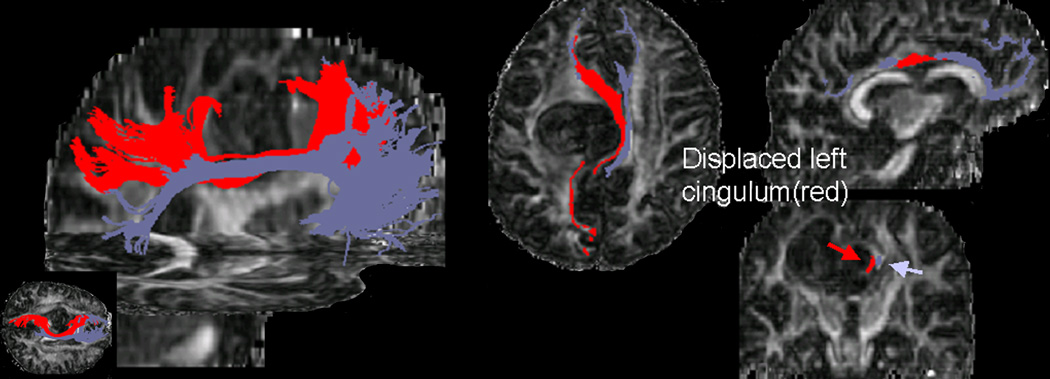
Figure 11.

Cingulum displacement due to tumor-mass effect in a patient with a grade III astrocytoma situated in the superior medial region of the left frontal lobe. The tractograms were generated from a set of seeds placed in the anterior region of the tract. The relative positions of the ipsilateral (red) and contralateral (purple) bundles are labeled onto axial, sagittal, and coronal fractional anisotropy maps.

Adapted by permission from Lazar et al. (91).

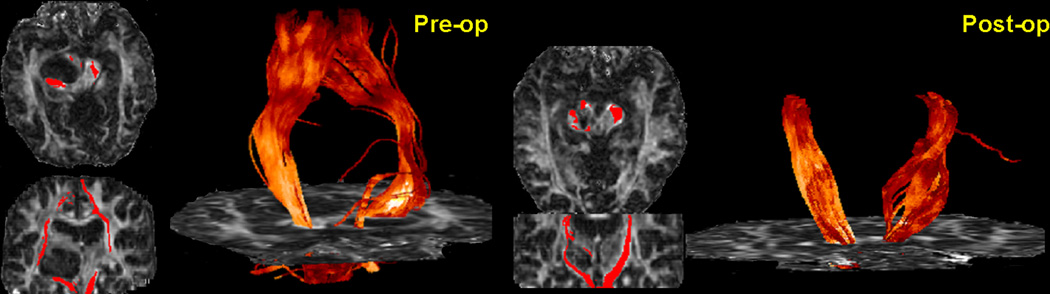
Figure 12.

Tractograms of the cortico-spinal tracts superimposed onto preoperative (left) and postoperative (right) fractional anisotropy maps in a patient with a ganglioglioma involving left cerebral peduncle and deviating in a splaying fashion the fibers of the right cortico-spinal tract anteromedially and posterolaterally. Postoperatively, the ipsilateral tract appears preserved after the surgery and positioned closer to normal anatomical position, except in the immediate vicinity of the resection.

Adapted by permission from Lazar et al. (91).

SUMMARY AND FUTURE DIRECTIONS

In this paper we reviewed current white matter tractography methods and presented some of the white matter tractography applications. Until recently many of the white matter tractography studies attempted to reconstruct fiber tracts that were already known from classical anatomy. As the technique starts to be widely applied to multiple subject studies, and with increasing image quality and improved diffusion imaging methods, it has the potential to uncover connectivity patterns that were previously unknown and to map the human connectome and its variations within and across populations.

In particular, higher image resolution (conditioned by the image signal-to-noise ratio, which has the potential to improve with better coils and gradient systems, and providing technological advancements, with higher magnetic fields) should allow for detection of finer tracts that are not detectable at current voxel sizes (94). Improved acquisition and analysis methods of the higher order diffusion imaging data should allow for better angular resolution of the estimated crossing fibers (i.e., better detection of fibers crossing at small angles) further increasing the accuracy of the fiber tracking results. A challenging issue remains the differentiation among crossing, kissing, and bending fibers configurations (8, 13) as they all lead to similar diffusion profiles. Incorrect assignment of the “crossing” patterns was shown to affect the tractography results (95). Finally, essential to the large-scale application of the HARDI and DSI techniques is the development of optimal protocols that will allow the acquisition of the needed data in clinically feasible times.

WMT generates a wealth of data for even a single subject, with most of it not even explored as the smaller (i.e., either shorter or containing fewer trajectories) tracts have received little attention to date (with several notable exceptions (e.g., (75))) or have been analyzed along larger tracts in a non-differential fashion. One of the future challenges for tractography applications is to devise adequate methods for extracting the relevant information from the extremely large amounts of data they may generate. One may envision the creation of databases to store the information gained from different studies in a manner that will allow meaningful comparisons and integration of the differently estimated connections. Perhaps, the previous development of brain databases (such as CoCoMac (96)) may serve as a starting point for such endeavors. Detailed fiber tract atlases obtained for high quality data may potentially be used as references for tractography studies based on lower-resolution or employing more basic diffusion imaging methodologies.

WMT is anticipated to be a powerful technique for studying anatomical connectivity in both normal cases and brains affected by different pathologies. Of great interest is applying white matter tractography techniques to study disorders that are assumed to involve affected brain circuitry such as schizophrenia and autism.

Abbreviations

CSF

Cerebro-Spinal Fluid

DKI

Diffusional Kurtosis Imaging

DK-ODF

Diffusional Kurtosis Imaging ODF

DT

Diffusion Tensor

DSI

Diffusion Spectrum Imaging

DTI

Diffusion Tensor Imaging

FACT

Fiber Assignment by Continuous Tracking

FOD

Fiber Orientation Distribution

HARDI

High Angular Resolution Diffusion Imaging

i.i.d.

Independent and Identically Distributed

MD

Mean Diffusivity

ODF

Orientation Distribution Function

PAS

Persistent Angular Structure

PDF

Probability Distribution Function

PGSE

Pulsed Gradient Spin-Echo

QBI

Q-ball Imaging

RAVE

Random Vector Propagation Algorithm

ROI

Region of Interest

SNR

Signal to Noise Ratio

STR

Streamline Algorithm

TEND

Tensorline Algorithm

WMT

White Matter Tractography