Deconvolution filters to enhance resolution of dense time-of-flight survey spectra in the time-lag optimization range

Abstract

By applying time-domain filters to time-of-flight (TOF) mass spectrometry signals, we have simultaneously smoothed and narrowed spectra resulting in improved resolution and increased signal-to-noise ratios. This filtering procedure has an advantage over detailed curve fitting of spectra in the case of large dense spectra, when neither the location nor the number of mass peaks is known a priori. This time series method is directly applicable in the time lag optimization range, where point density per peak is constant. We present a systematic methodology to optimize the filters according to any desired figure of merit, illustrating the procedure by optimizing the signal-to-noise per unit bandwidth of matrix-assisted laser desorption/ionization (MALDI) data. We also introduce a nonlinear filter that reduces the spurious structure that often accompanies deconvolution filters. The net result of the application of these filters is that we can identify new structures in dense MALDI-TOF data, clearly showing small adducts to heavy biomolecules.

Matrix-assisted laser desorption/ionization time-of-flight mass spectrometry (MALDI-TOFMS) has become one of the preferred techniques for proteomics analysis of complex biological mixtures because it is capable of producing very high mass biomolecular ions with relatively little fragmentation during the ionization process.^1,2 Moreover, linear TOF instruments can provide an immense mass range, high sensitivity to minute (femtomole-attomole) sample amounts, operational simplicity, and low cost.^3–6 These characteristics have given linear TOF instruments an advantage in detection efficiency for biological and medical researchers performing high-throughput survey experiments in biological mixtures, e.g., for disease classification.^7–11 Although MALDI-TOF techniques can achieve very high mass resolution in a restricted mass range by using nonlinear mass focusing devices,^12,13 survey studies that record a wide range of ion masses in the linear mode usually reduce this resolution from its optimal value.^5,14 Moreover, these spectra are typically generated at low repetition rates, with high signal levels that require analog signal detection. The net result is a dense, low-resolution spectrum with a relatively high noise level compared to that produced by ion-counting instruments.¹⁵

In any one region, a portion of the linear TOF spectrum could be fit to a sum of individual lines, as long as the instrumental line shape is understood sufficiently well, but this process would be onerous for a large survey spectrum with hundreds of lines. Instead, we have introduced¹⁶ a filtering procedure that maps the original TOF signal onto an improved version that preserves the position of the individual lines, while simultaneously reducing the line widths and the noise. This time series filtering procedure works in the time-lag optimization range for linear TOF instruments, where the spectral lines have constant point density in the time domain. Here, we illustrate a systematic procedure to choose parameters for this deconvolution filter so that signal-to-noise ratio (SNR) enhancement and line width reduction are balanced according to any desired figure of merit. This method relies on the peak shape model. We characterize analytical and numerical errors associated with the deconvolution formalism and computational precision, and set corresponding thresholds for signal detection. We continue development of the nonlinear filtering process, introduced in our previous report,¹⁶ to produce narrower individual lines with fewer and smaller deconvolution artifacts. We provide guidelines to determine length of the filter, target wavelet model, noise weighting parameters, and thresholds for subsequent peak detection.

Several previous attempts have been made to use time series filtering techniques on mass spectrometry data.^4,17–23 These approaches have been oriented mostly at smoothing the data by suppressing high-frequency noise. As smoothing is equivalent to application of a low-pass filter, the net effect of such filters is always to broaden the signal, and decrease the resolution. Any smoothing operation will also require setting the band-width for noise suppression, and this is generally mass-dependent. Matrix convolution and bandpass filters do not make assumptions about peak shape. They have the benefit of a wide mass extrapolation range, and have been successfully applied to suppress chemical noise and backgrounds arising from specific ionization mechanisms.^18,22 These methods, however, are not generally suitable for spectral deconvolution because they smooth the spectrum rather than enhance its resolution.

Other researchers have used matched filters for random noise suppression in the Fourier domain conjugate to time.^17,20,23 As with all smoothing techniques, matched filters tend to broaden the data up to 40%, and thus decrease the resolution. In order to limit excessive broadening, these methods have either been limited to small mass ranges^17,20 or have employed subjective thresholds^20,23 and time-consuming iterations.²⁰ These methods have not been extrapolated from the narrow mass range to the wider ranges typical for TOF survey spectra. Maximum likelihood (ML) (autoregressive) smoothing methods,^4,21 which rely on peak and noise models, offer better potential for automatic noise suppression. However, these methods generally suffer from distorted relative peak magnitudes in the filtered spectrum.^21,24 Similar to matched filters, they also suffer from over smoothing.^4,21 When peak densities are high compared to the mass record length, which is frequently the case with TOFMS survey data, it might not be possible to automate ML techniques.²¹

For both matched and ML filtering, spectrum deconvolution can be performed after noise suppression by modeling the instrumental function (assuming peak shape) and correcting for its convolution with an observed ‘true’ signal.^14,17,20,22 However, errors during the noise suppression step frequently enhance artifacts during deconvolution of the instrumental function.^20,22 None of the above-cited approaches has fully addressed the problem of characterizing filtering artifacts in MS data and setting the corresponding thresholds for peak detection, nor have they suggested techniques for optimizing the corresponding filtering parameters over the broad range of dense TOF data to suppress such artifacts and enhance the true signal.

In the Experimental section of this paper, we give a brief description of each step in the filtering process that we used for the results presented here. In the Results and Discussion section, we describe and explain the motivation for our various design choices so that the method can be extended to other work. We also illustrate the systematic procedure using deconvolution filters to balance SNR enhancement per unit line width. Finally, we show that a nonlinear filtering process produces even narrower individual lines with fewer and smaller deconvolution artifacts. We illustrate this by deconvolution of model data and experimental MALDI-TOF data from pooled serum to resolve adducts and neutral losses.

EXPERIMENTAL

Mass spectrometry data

The mass spectra of the pooled serum reported here were acquired at the Eastern Virginia Medical School (EVMS), using a SELDI PBS II instrument with an IMAC-Cu affinity capture chip (Ciphergen, Inc.). The protocols for the serum preparation and acquisition of the mass spectra have been described in detail previously.^7,16 The pooled serum samples are currently used to monitor and enhance the reproducibility of data generated by linear TOF survey instruments in multiple clinical research laboratories.^25,26 During our studies we examined about 300 spectra generated by five different TOF instruments in the linear TOF mode, including the Ultraflex (Bruker). The linear TOF spectra from PBS instruments were recorded by an 8-bit analog-to-digital converter (ADC) sampling at 250 MHz. The Ultraflex instrument allowed the sampling frequency to be set at 500 MHz, or 1 and 2 GHz. The average mass resolution of the spectra in the time-lag focusing range was $\frac{m}{\mathrm{\Delta }m}=450-500$,⁷ as specified by the manufacturers. The actual resolution of the spectra varied with mass as expected for time-lag focusing conditions.¹⁵ The optimal resolution of nearly 700 was achieved for masses between 10 and 11 kDa. In contrast to the mass resolution, the measured point density per peak (HWFM) in time was constant for the TOF signals that arrived earlier than the optimum¹⁶ (extraction delay of 900 ns). Although we show an example of a single TOF spectrum in the discussion below, all 300 studied spectra showed a constant point density over the time-lag optimization range. The Ultraflex data taken at different sampling rates with the same extraction delay exhibited no change in the range of constant peak width, while the number of points per peak scaled consistent with the increase in the sampling rate. Time-lag, or delayed extraction, mass-focusing compensates for an initial spread of kinetic energies to optimize the resolution at a specific mass value,⁵ but the spread in time also varies because time and mass are related quadratically. This means that for TOF instruments in linear mode, in general, there will be a region before the optimal mass resolution, where all peaks will have the same number of time points per peak width.

Prior to filtering, we removed a slowly varying baseline using a charge accumulation model,¹⁶ although any method that removes a smooth background would suffice. We modeled our experimental peak shape as a truncated, asymmetrical shape with a Gaussian leading edge and a Lorentzian trailing edge, so that for a peak at i = i₀:

$$S=\{\begin{array}{ll}{e}^{-{\left(i-i_0\right)}^2/2{\mathrm{\Gamma }}_{\mathit{in}}^2}\hfill & i<i_0\hfill \\ \frac{1}{1+\frac{{\left(i-i_0\right)}^2}{{\mathrm{\Gamma }}_{in}^2}}\hfill & i>i_0\hfill \end{array}$$ (1)

We used the same line shape (in time) for all peaks with Γ_in = 8.5 because there is a constant point density per peak over the mass-focusing range between 5000 and 12000 TOF points (m/z = 2–11 kDa).¹⁶ General considerations due to the Jacobian that governs the transformation of the ion flux as it passes through the field-free TOF region will lead to an asymmetric lineshape that extends further on the later arrival time side. We have examined multiple spectra on different affinity surfaces, and found that the width parameters and asymmetry of the line shape are sensitive to the ionization and focusing conditions, including time-lag, laser intensity and surface chemistry of the source. Nevertheless, this asymmetric model has performed well. We performed all filtering in the time domain and then converted to the mass domain using the quadratic conversion equation provided by the manufacturer:

$$\frac{m}{z}=5.159{\left(t-0.255\right)}^2+11.6$$ (2)

where time is measured in μs and m/z is in atomic mass units divided by the electron elementary charge, a unit that is sometimes called the Thomson. For singly charged species, Eqn. (2) simply indicates the mass of the species in Daltons. The parameters in the equation were determined by least-squares fit for the calibration mixture of seven peptides: Arg-8-vasopressin (1084 Da), somatostatin (1637 Da), dynorphin (2145 Da), ACTH (1–24) (2933 Da), porcine insulin β-chain (3495 Da), human insulin (5807), and hirudin (7033 Da). The instrument was calibrated the same week as the pooled serum spectra were acquired, and the manufacturer’s software performed the fit. We believe that the time-offset parameter reflects any time delay between the laser firing and the digitization start; the coefficient of the quadratic term depends primarily on the ratio of the TOF length to the accelerating potential.⁵ The constant offset results from the manufacturer’s three-parameter quadratic fit to calibration peaks.

In other studies, we have observed that data from different instruments taken 2 years apart can be aligned by small adjustments of the offset and the quadratic coefficient, suggesting that the manufacturer’s equation in its current form might be over-parameterized. However, we used the manufacturer’s equation, just as we expect general users will do. Since our filtering is done in the time domain prior to conversion, it is not susceptible to any errors in the calibration equation. Further, we applied Eqn. (1) globally to the acquired TOF spectra up to 12 kDa, although part of the data fell above the mass of the heaviest calibrant used (7 kDa–hirudin). We did not attempt any mass recalibration using the deconvolved spectra after filtering. We deconvolved purely in the time domain, improving our ability to measure splittings in time but we have not yet attempted to extend this to improvements in mass calibration.

The mass eventually increases as the square of the measured TOF arrival time and this leads to a decreasing sample density per unit mass because the instrument samples at a constant rate of every 4 ns. With fewer points per unit mass, a high mass peak will appear compressed in the time domain as compared to a low mass peak of the same width.

Deconvolution filtering

We filtered each spectrum three times using three different filtering techniques: (1) a conventional matched filter that produces the highest SNR at the maximum of a mass peak; (2) an optimized linear filter that simultaneously smoothes and narrows to produce the largest SNR per unit line width; and (3) a nonlinear filter that further narrows the spectrum, enhancing the SNR per unit bandwidth and suppressing deconvolution artifacts.

Each shaping filter creates a filtered output, by summing over the current and later input values weighted by the M filter coefficients. For a time series of N input signal values of x_k, this filter will produce output signal values, y_k, according to:

$$y_k={\displaystyle \sum _{j=1}^M{a}_j{x}_{k+j},}1<k<N-M,$$ (3)

where a_j are the M filter coefficients. In the following, all sums are to be truncated whenever an index falls outside of its allowable range. According to Eqn. (3), the filtered signal is a weighted sum of all data at or after a specific time point. This choice of a filtering algorithm will lead to a constant shift forwards in time that will then be removed, so that each filtered data point then includes data before and after the output point. If we require this filter to minimize the least-squares difference between the narrow (predicted) target and the actual signal wavelet,^27,28 and assume that the noise is stationary and additive to the signal, then the minimization procedure results in the system of M equations for the filter coefficients, a_k:

$${\displaystyle \sum _{k=1}^M{a}_k\left(r_{ki}+v{\lambda }_0{\delta }_{ki}\right)}={\displaystyle \sum _{j=1}^M{d}_{j-i}{b}_j,}1<i<M,$$ (4)

where b_k is the expected input wave shape and d_k is the desired target shape (both having M points); $r_{ik}={\displaystyle {\sum }_{j=1}^M{b}_j{b}_{j+i-k}}$ are the elements of a matrix formed from the autocorrelation of the input wave; δ_ik is the Kronecker delta; v is a parameter that weights the importance of noise smoothing (high v values) to signal shaping (low v values), and λ₀ is the sum of any row or column of r_ik. The autocorrelation matrix is a Toeplitz matrix whose elements only depend on the difference between the row index and the column index.

We used the same asymmetric half Gaussian/half Lorentzian of Eqn. (1) for both input and target shapes, truncated to zero for values below 0.2% of their maximum value, as described in the Discussion section. We used a filter length of 451 points, and we shifted our target shape by 200 points, so that the cross-correlation between the input wavelet and the target wavelet (the right-hand side of Eqn. (4)) begins and ends at zero. This shift of the target removes the causality of the filter, making its coefficients depend on data both before and after signal arrival time. Since this filtering is not performed in real time, there is no a priori reason to require causality. After solving Eqn. (4), we also truncated the filter coefficients before the secondary maximum produced by the wavelet truncation, thereby reducing the number of non-zero filter coefficients to 171. The shift and truncation help reduce numerical artifacts from solving Eqn. (4). The criteria for the choices of shifts and truncations are described in more detail in the Discussion section on spectral analysis of deconvolution filters.

The matched filter, which produces the largest SNR at the maximum of a peak, has filter coefficients equal to the input wave shape.^27,28 Alternatively, Eqn. (4) can be solved for the matched filter in the limit of a single point target shape and values of v approaching infinity, or for v = 0, with the target shape being the autocorrelation of the input wave.

We determined the optimal single filter, which produces the largest SNR per unit line width, by solving Eqn. (4) with v = 0.01 and a target shape reduced from the input shape to 80%. This filter process then creates a signal with a width of 90% of the original width (Γ_f = 0.9Γ_in), but less noise.

For the nonlinear filter, we created three linear filters by solving Eqn. (4) for v = 10⁻², 10⁻³ and 10⁻⁴ with target widths Γ_t = 0.2Γ_in, 0.2Γ_in and 0.5Γ_in to preserve the desired narrowing of 40–50%. Then, we created the point-wise geometric mean of those three filtered spectra to produce the nonlinear filter result.

RESULTS AND DISCUSSION

In the following discussion, we present an overview of the characteristics of a linear deconvolution filter and then illustrate how to optimize the parameters of a single linear filter according to a desired figure of merit that depends on the filtered SNR enhancement and on the line narrowing. Following that, we describe how to construct a nonlinear filter to enhance the narrowing and suppress the deconvolution artifacts, and finally present results of filtered MALDI data.

Spectral analysis of deconvolution filters

Convolution and correlation filters were originally introduced for time-series analysis of seismic and RADAR data.^27,28 These filters do not separate deconvolution and noise smoothing into sequential steps, but they use a parameter that balances the relative importance of noise smoothing versus deconvolution shaping. Essentially, these filters attempt to transform the input shape into the desired shape, while the additional parameter forces a high frequency roll-off that smoothes noise but also broadens the output. Such a filter becomes a matched filter in either of two extreme cases: (a) a single time-point target shape with maximal smoothing, or (b) an output shape equal to the autocorrelation of the input shape, with no smoothing at all. Spectral analysis of shaping and smoothing filters helps make intelligent choice of roll-off parameters to achieve desired narrowing and minimize filtering artifacts.

Specifically, the shaping filter creates a filtered output, by summing over the current and later input values weighted by the M filter coefficients according to Eqn. (3). Note that the last M mass values cannot be filtered. By minimizing the least-squares difference between a noisy input signal after filtering and the desired signal shape (as in Robinson and Treitel²⁸), it is straightforward to derive a set of equations, similar to Eqn. (4), that determine the filter coefficients as:

$${\displaystyle \sum _{k=1}^M{a}_k\left(r_{ik}+v{q}_{ik}\right)}={\displaystyle \sum _{j=0}^M{d}_{j-i}{b}_j}$$ (5)

where q_ik are elements of a Toeplitz matrix formed from the autocorrelation of the noise.

Equation (5) has a particularly simple form, because both of the matrices on the left-hand side are Toeplitz matrices. This means that, if the input signal and the noise signal were both periodic, there would be no effect at all from simultaneous shift of any row and column on the matrices. Therefore, the eigenvectors of the two matrices would be the same as the eigenvectors of the shift operations. These eigenvectors are the Fourier basis vectors with two degenerate sets formed by $V_j^k=\cos \frac{2\pi k}{M}j$ and $W_j^k=\sin \frac{2\pi k}{M}j$, where k labels the eigenvector and j enumerates the components of that vector. In the nonperiodic case, the matrices can be written as a periodic matrix plus a correction term that only affects the upper right-hand and lower left-hand corners. This perturbation forces a specific choice of the phase of the Fourier basis eigenvectors so that $V_j^k=\cos \frac{\pi k}{M}\left(2j-1\right)$ and $W_j^k=\sin \frac{\pi k}{M}\left(2j-1\right)$, and it breaks the degeneracy between V^k and W^k. For the matrices in question, which have large values only near the main diagonal, any higher order effects are small. Thus, a standard Fourier analysis of the frequency components of the signal and the filter will provide guidance for the filter performance.

For example, since the sums in Eqns. (3) and (5) are discrete convolutions, they become products under a Fourier transformation. So, when v is small enough to ignore the second term of the left-hand side of Eqn. (5), the Fourier transform of the filter coefficients becomes the ratio of the target Fourier components to the input Fourier components, and exactly transform the input wavelet into the target wavelet. When n is large, so that one can ignore the first term of the left-hand side of Eqn. (5), then the Fourier transform of the filter coefficients become the product of the target Fourier components and the input Fourier components. This will usually have a narrower spectrum, so that in the time domain the filtered output has a broader shape. To generalize the n parameter, we have scaled the noise autocorrelation matrix by the maximum eigenvalue of the signal autocorrelation matrix, λ₀ (which, as the zero frequency eigenvalue, is just the sum of the autocorrelation of the input signal).

For TOF signals, there is usually almost no structure to the noise autocorrelation because most instruments are designed to ensure that the value at one time point is statistically independent of the value at any other time point. This is the definition of white noise, so we have found that it is sufficient to use the identity matrix instead of a measured noise autocorrelation matrix. To normalize it so that the parameter n is most meaningful, we have multiplied the identity matrix by the maximum eigenvalue of r_ik, so that q_ik = λ₀λ_ik, as in Eqn. (4). This makes the structure of the solutions independent of the normalization of the input, or target wavelets. With the λ₀ scaling, the smoothing parameter must be small, v < 1, to achieve any substantial width reduction. How small will depend on the frequency spectrum of the input and target wavelets. For example, to decrease a Gaussian line width by a factor of 2, v < e⁻⁴, because the high frequency components must be amplified from the original to produce a narrow time shape.

To create a filter, one needs to choose the input wavelet model, the target wavelet model, the filter length M, and the smoothing parameter v. The input wavelet should be a good representation of a data peak. The best output wavelet is usually a reduced-width version of the input wavelet, since this minimizes misshaping artifacts. We truncated both shapes to zero for values less than 1/512 of their maximum value, in accordance with the limitation of the ADC of our detector. This truncation introduces high frequency components and increases the smallest values of the eigenvalues of the signal autocorrelation matrix. In a typical case without truncation, these eigenvalues span more than 25 orders of magnitude, making the equations difficult to solve numerically unless n is set to a high value. After truncation, any numerical method simply solves the filter equation. The filter length, M, depends on the input and target wavelets widths as described below.

To create a filter that only depends on the future points, Eqn. (4) requires that the cross-correlation between the input and target shapes begins and ends at zero. Accordingly, we shifted the target wavelet into the future by enough points so that the input and target wave have no overlap initially, and then chose the length of the filter, M, sufficiently large that the target wavelet is zero by the end of the filter. After applying this filter, we shifted the output backward by the same amount as the forward shift of the target wavelet. This deviation from causality for our filter is useful for elimination of numerical artifacts. The length of the filter is then a small fraction of the full TOF record length.

The choice of the smoothing parameter depends on the desired characteristics of the final output. We illustrate potential choices here, by designing three filters: two linear filters, and a nonlinear composite filter formed from a series of three linear filters. A well-designed TOF instrument will strongly localize the signal wave, making its frequency spectrum broad. For our first example, we used symmetric Gaussian waves, which are strongly localized in time and frequency. A solution of Eqn. (4) for filter coefficients will span the entire M points. The filter coefficients that are far away essentially represent a way of modeling the noise to smooth it out. To eliminate secondary maximum artifacts in filter coefficients produced by the wavelet truncation, we have also truncated the filter coefficients before this maximum, thereby reducing the number of non-zero filter coefficients to M/3.

The net result of the truncations and of the nonperiodic nature of the wavelets is that this target filtering will introduce artifacts or spurious peaks in the filtered signal that become more intense if the filter substantially narrows the input waveform. Increasing the smoothing parameter, v, reduces these artifacts and also reduces the noise amplitude. However, this increased smoothing broadens the filtered shape. Figure 1 shows the interplay between smoothing and narrowing for the case of Gaussian input and output waves. Figure 1 is a contour plot of the ratio of the filtered output width to input width as a function of the ratio of the target width to input width and the smoothing parameter v. Plotting dimensionless ratios reflects the fact that these contours are independent of absolute peak width (point density). Clearly, if v is small enough, then the output width equals the target width. But, for large v > 1, the resulting signal’s width no longer depends on the width of the target, but rapidly approaches the matched filter width.

Figure 1.

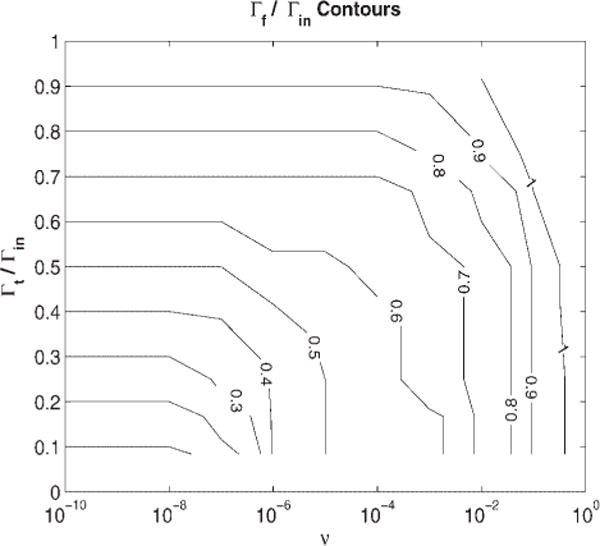
Contours of constant final filtered signal width for various filter parameters, using an input Gaussian signal.

Optimal single filter construction

To filter a TOF signal to distinguish important features, one will generally want to smooth the noise and narrow the signal shape simultaneously. In Fig. 2, we show a surface plot of a combined figure of merit (the SNR increase divided by the reduction in filtered line width) to determine an optimal filter. For the case of Gaussian input and output waves, the restricted frequency spectrum makes it difficult to substantially narrow an input wave without seriously reducing the SNR. The filter works by amplifying the high frequencies, and a Gaussian pulse has very little power in the frequencies higher than the inverse of the FWHM. Figure 2 shows that the optimal filter parameters lie on a ridge where the net linewidth reduction, Γ_f/Γ_in, is only 10%, but that the SNR is enhanced by a factor of 5. The coordinates of the merit surface maximum (target width is 50% of the input width, v = 0.1) define our optimal single filter. The SNR enhancement is almost as good as the matched filter (SNR enhancement of 6), but without the 40% increase in width. This figure of merit landscape is insensitive to the choice of point density, although the improved SNR increases as the square root of the number of points within the line shape.

Figure 2.

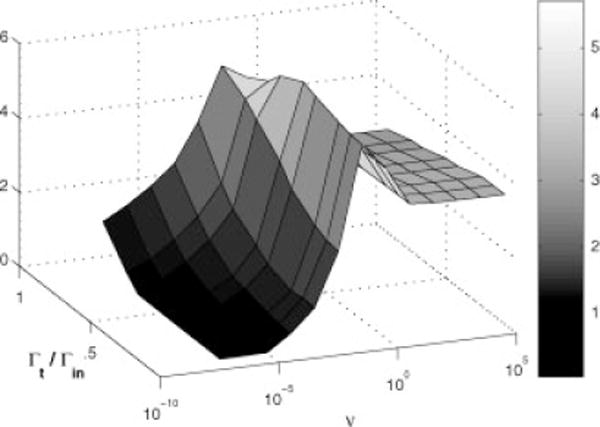
Signal-to-noise enhancement per unit bandwidth following filtering. The maximum ridge is relatively independent of the target width for v between 0.01 and 0.1.

Because any shaping filter that narrows a waveform must amplify higher frequencies, it will necessarily increase some noise components, possibly shifting the location of the filtered peak centroid, as determined by downstream peak detection. These shifts are caused by the random nature of the local noise which will not average to zero for a finite filter length. Since increasing the filter length is impractical because it enhances numerical artifacts and includes contributions from other peaks, we will characterize the shifts for the ensemble of noise samples within the finite filter width to set thresholds for peak detection. When these shifts are larger than the filtered line width, the errors from the narrowing process will reduce the accuracy of peak location below that for broadened unfiltered data. Although enhanced resolution may still be desirable for detection of peak splitting, the errors in peak location need to be estimated to set the limits on data interpretation. Accurately detected splittings, consistent with predictions, e.g., for adducts and neutral loss species, may be used for recalibration of the mass axis.²⁹ Thus, it is important to predict the SNR thresholds at which deconvolution filtering (signal narrowing) is meaningful for downstream data analysis and interpretation. Below these thresholds data smoothing might be more beneficial than narrowing.

In general, the noise-induced shift can be modeled as the shift of a line centroid, and so it will be inversely proportional to the SNR. In Fig. 3, we show the threshold SNR that produces an average centroid shift of one final half width. Peaks in an input spectrum must be above this threshold for the peak centroid to be within a HWHM of its true position. Note that, since target filter deconvolution by design produces reduction in the final half-width (Γ_f/Γ_in < 1), the associated HWFM uncertainty in peak location will be smaller than for any smoothing, which necessarily broadens the signal (Γ_f/Γ_in > 1). However, as expected, the SNR thresholds for detection of narrower peaks with meaningful uncertainty in peak location are higher than for smoothed data. Even without filtering, input noise will produce some shift in the centroid of a peak (Fig. 3, Γ_f/Γ_in = 1). This shift will also be inversely proportional to the SNR, requiring a higher peak detection threshold than for smoothed data.

Figure 3.

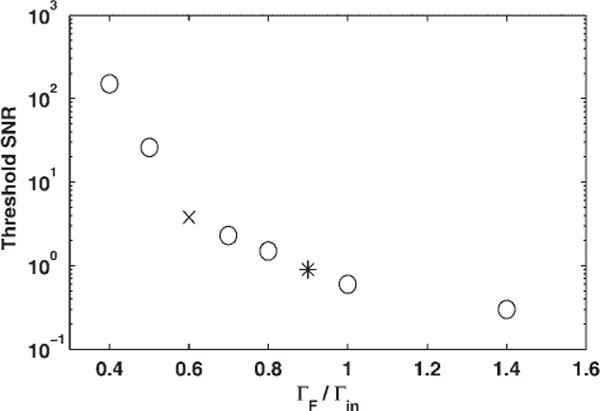
Required SNR for input signals as a function of the width reduction to insure that the centroid uncertainty is less than the final half width. The asterisk marks the coordinates of the optimal single filter, and the × marks the coordinates for the 40% reduction.

For Gaussian wavelet models, strongly localized in time and frequency, we expect deconvolution to be extremely sensitive to input noise and to produce large uncertainties if too much narrowing is attempted. Indeed, a jump in the threshold SNR is visible in Fig. 3 for final widths less than 60% of the original width (marked by an × in Fig. 3). To achieve more than 40% narrowing with a single filter, the input SNR should be more than 25. Such a large threshold may not be practical for some TOF peaks with limited signal-to-noise; therefore, the best narrowing that can usually be achieved by a single linear target filter will be 40% for peaks with input SNR > 4. Note that the optimal single filter, producing ~10% narrowing (marked by an asterisk in Fig. 3), has a threshold SNR = 0.9 for an uncertainty in peak position equal to the half-width of the filtered line. For input signals larger than the threshold in Fig. 3, the centroid uncertainty will be reduced proportionately resulting in better precision for peak location. Thus, for peaks with an original SNR > 10 and HWFM of 5 points, the 40% reduction in width results in a centroid uncertainty of less than a single time tick, while the unfiltered data would have the same one-tick uncertainty for input data with SNR > 4. Note that an optimal linear filter would produce the same one-tick uncertainty with input SNR > 4.1.

Nonlinear filter construction and use

In a dense spectrum, the deconvolution filter can introduce spurious extra features, which are oscillations at time locations slightly displaced from the true peak, as opposed to amplified noise signal. However, the locations of these artifacts depend on the specific choice of target waveform and smoothing parameter v, while the true peak positions are insensitive to these choices. Moreover, an ideal TOF signal is positive definite, riding on a zero background, at least after correcting for any ADC produced offset. Consequently, we have found that if we create several different filters, designed to produce almost the same final shape, and then use the geometric mean of these signals, we can eliminate most of the artifacts that are reflections of the main peak. This nonlinear filtering introduces frequency mixing in just such a way to reduce the final signal amplitude at any locations where any single filter result would have a small value. This is much more efficient at reducing signal in the wings of a peak than an arithmetic mean. An arithmetic mean, because it is still a linear operation, cannot improve on the result obtained from the generalized linear filter optimization method shown above. So, for example, no arithmetic mean of linear filters could produce a higher SNR per unit bandwidth than our optimal linear filter.

Geometric averaging has two undesired side effects: (1) spurious noise shots that look like signal are shaped to appear clearly as signal, and (2) the relative intensities of overlapping peaks are not always accurately reproduced due to biased suppression of small signals in the vicinity of large peaks. We have found that both of these difficulties are minor, compared to advantages of the enhanced resolution, when we are analyzing TOF spectra. Because we typically analyze our filtered spectra with an automated peak detection routine, we can avoid small noise peaks by setting our threshold for peak detection sufficiently high. Furthermore, once our peak detection routine has identified multiple peaks separated by the filtering process, we use standard curve fitting algorithms to accurately reproduce the positions and amplitudes of the lines. However, having these limitations in mind, we present our preliminary results here as one of the possible solutions and acknowledge the possibility of better venues. We have not yet developed a complete mathematical analysis of this technique; however, we have studied it using both simulated and experimental data, and we have developed a prescription for its use that results in substantial improvements.

In our prescription, we created three filters by letting n vary in steps of one order of magnitude while adjusting the target to maintain the desired narrowing. Specifically, we used target widths of 2, 2, and 5 and v = 10⁻², 10⁻³, and 10⁻⁴ for an input width of 10.2. After filtering the spectra by each of these three filters, we generated a new spectrum from the cube root of the absolute value of the point-wise product of the three spectra, choosing the sign of the root to match the sign of the initial product. This procedure eliminates negative products under the root and helps avoid imaginary intensities. Figure 4 shows the result of applying this nonlinear filtering process to the simulated data. The top curve shows the simulated Gaussian doublet with noise. The middle curve shows the signal after application of a single linear filter designed to narrow the spectrum by 40%. Note that the filtered noise now appears as a coherent oscillation. The lower curve shows the result of using the geometric mean of three filters. This has produced the desired narrowing while suppressing the noise.

Figure 4.

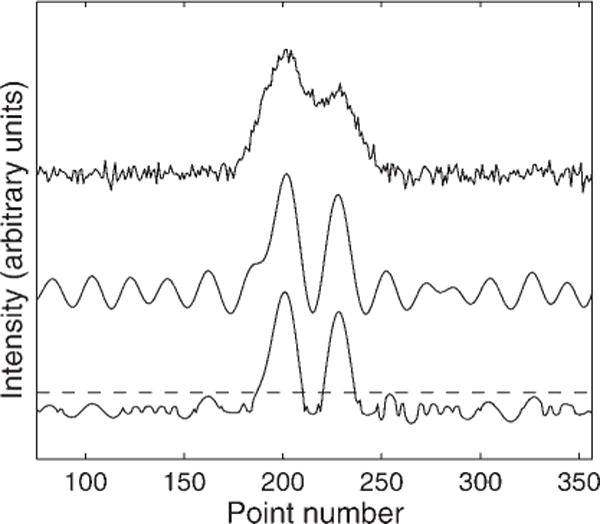
Comparison of a simulated Gaussian doublet with noise (top), to the output of a single 40%-narrowing target filter (middle), and the geometric average of three filters (bottom). The dashed horizontal line shows the SNR threshold for peak detection.

The nonlinear filter produces a noise-dependent centroid shift that is essentially the average of the shifts created by each linear component. Therefore, the input SNR thresholds for peak detection calculated for linear filters (Fig. 3) also serves for nonlinear filters. Of course, some of the residual noise features look like the signal, so it is imperative to require all detected peaks to be above the detection threshold, shown as a dashed line in Fig. 4. For this nonlinear filter, we have found that the remaining artifacts are grouped within three final half-widths of the real signal and are smaller than 5% of the real peak for a noise-free input. When noise is present, a single filter can transform the noise into a long coherent wave, as in the middle curve of Fig. 4 and the geometric average of multiple filters may not be as effective in eliminating the ‘remote’ noise ringing as in eliminating the artifacts in the vicinity of signal. The lower curve of Fig. 4 clearly shows a small noise signal ringing near 320 time points, but below the peak detection threshold. This oscillating signal is clearly different from the true signal, so it may be possible to reduce it further by building a nonlinear filter with more than three components.

If a signal has a large baseline present, then the leading term of the geometric mean will simply be the arithmetic average. Thus, these nonlinear filters cannot work properly with large baselines. However, we have found that a baseline as large as 10% of the peak height does not appreciably deteriorate the performance of these filters. Moreover, the noise also creates a variation in the amplitude of any filtered peak, but only by 1/SNR (input) as with a single, linear filter.

Application to experimental MALDI-TOF data

We have applied these optimal linear and nonlinear filters to data obtained from a PBS II Ciphergen linear TOF spectrometer. To create a filter, we first modeled the input signal using the low mass (m/z = 23) monoisotopic sodium ionic peak, although any other single peak between 2 and 11 kDa could be used as a model. As explained in the Experimental section, the measured point density per peak remained constant until approximately 11 000 time ticks. The top trace in Fig. 5 shows a portion of the spectrum around m/z 5500, with our modeled waveform superimposed as ‘crosses’. This illustrates that the model fits the data at high masses well, even though it was developed at m/z = 23. This asymmetric model used a Gaussian shape on the rising edge, and a Lorentzian shape on the falling edge, with Γ_in = 8.5. The middle trace shows the result of filtering with a matched filter, using the model lineshape, which produces about 40% broadening, as expected. The lower trace in Fig. 5 shows the results of applying our single optimal linear filter, which was constructed from a target with Γ_t = 6.8 and v = 0.01.

Figure 5.

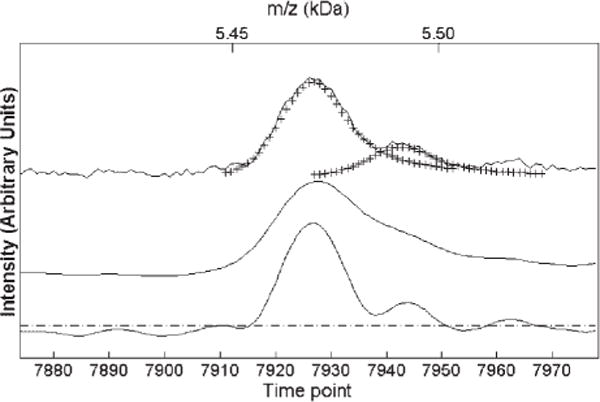
Experimental SELDI data (top) compared to the output of a matched filter (middle) and a single optimal linear filter (bottom, Γ_t 6.8, Γ_in 8.5 and v = 0.01) The input wavelet model is plotted as crosses on top of the experimental data. The dashed line shows the SNR threshold for peak detection.

To create deconvolution filters, we used the same model for the target shape with reduced line widths. With the combined Gaussian/Lorentzian model, the linear filter was able to reduce the line width more than 40%, without the large noise-induced variation in the centroid (unlike Fig. 3 for the symmetric Gaussian shape). This is presumably because the Lorentzian part of the model extended the signal waveform to higher frequencies. This allowed more narrowing, but at a cost of less effective noise removal than in the pure Gaussian case. We created a figure of merit landscape similar to Fig. 2 for these line shapes and determined that the optimal linear filter (Γ_t = 0.8, Γ_in, v = 0.01) would again reduce the linewidth by 10% while enhancing the SNR, but only to a value of 3.5 (compared to 4.5 for the matched filter).

Figure 6 shows the results of constructing a geometric mean of the signals from three (nonlinear) flters similar to the Gaussian case shown in Fig. 4. These spectra were then converted to the m/z domain using external calibration from the seven-peptide mixture (see Experimental section) after the filtering process was complete in time. Note the considerable resolution enhancement (peak narrowing) over a wide range of masses. With this enhanced resolution, we can assign the mass differences between close peaks above the uncertainty threshold (dashed line) to an accuracy of better than ±2 Da, and identify mass shifts consistent with sodium adducts (Na: ±22 Da) and neutral losses (H₂O: −18 Da, CO₂: −44 Da). Such adducts and losses have been previously observed in high-resolution MALDI-MS.^4,15 We have also routinely observed similar adduct and neutral loss structures in the TOF spectra of the seven-peptide calibration mixture, which consists of known peptides from 1 to 7 kDa (see Experimental section). Most of these features are already visible in the original, unfiltered data, which is the thin line in Fig. 6. However, the filtering will make automatic peak detection much easier. Some new structures, such as the triplet near 8.7 kDa, appear only after deconvolution filtering. We verified the accuracy of this deconvolution by constructing a semi-simulated spectrum by shifting and scaling the experimental spectrum of Fig. 6 to generate a new triplet near 5.7 kDa with the same shifts and amplitude as that near 8.7 kDa. This shifted spectrum consists of real data, with its true instrumental profile and noise. The deconvolution results were consistent with our input shifts, and confirmed that triplet structures resolved after filtering in Fig. 6 are not due to artifacts from deconvolution. We also observed consistent results from filtering more than 300 serum spectra from five different linear TOF instruments, after automating the procedures that are described here.

Figure 6.

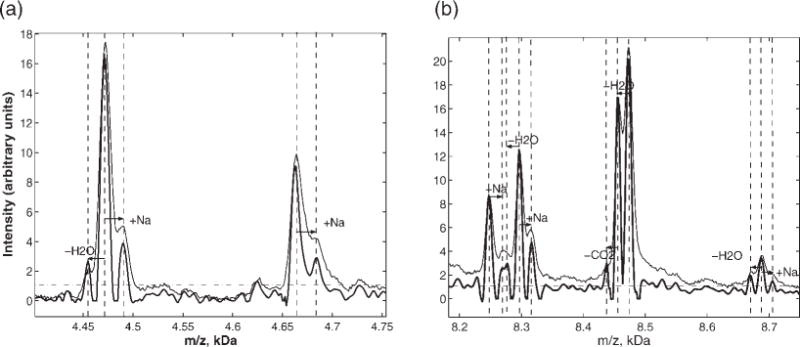
SELDI spectra for pooled serum (thin line), and resolution-enhanced filtered data near 4 and 8 kDa. The filtered signal is the geometric average of three filters (Γ_t 0.2Γ_in, v = 0.01; Γ_t = 0.2Γ_in, v = 0.001; Γ_t = 0.5Γ_in, v = 0.0001;). The horizontal dashed line shows the SNR threshold for peak detection. The mass differences for the deconvolved peaks suggest sodium adducts and neutral losses as indicated by dashed lines and arrows.

This is precisely the type of information that is crucial to understanding a dense survey spectrum. For instance, if an adduct peak shows more discriminating power for a disease diagnostic than its corresponding parent, subtle peptide modifications, such as chemical affinity changes or topology changes, may be an outcome of a disease. It may also be that a disease marker is itself a fragment of an altered enzyme or metabolite involved in the disease.³⁰ The detected splitting for the abundant ions may be used as internal standards for better m/z recalibration.²⁹ This increased resolution may also be a useful prerequisite for deconvolving adducts and multiply charged ions into precursor ion intensities to increase SNR, and ultimately for the identification of parent peptides. Filtering with a single optimal filter for noise suppression preserving the experimental resolution may also be useful for peak detection, when more narrowing is not desired. The suppressed, but visible, artifacts suggest that a uniform threshold can be introduced for peak detection. In Fig. 6, we have represented the appropriate peak detection threshold by a dashed horizontal line at 1.1 units. Target filter deconvolution almost doubled the effective resolution of our linear TOF spectra, from 540 to 910 at 8 kDa. The uncertainties in peak position in time after nonlinear filtering for all signals above the threshold of SNR = 4 are less than 2.5 time points, the half-width of the filtered peaks.

CONCLUSIONS

Our results prescribe a simple methodology to optimize deconvolution filters to simultaneously enhance the SNR and to improve the resolution of dense TOF survey spectra up to the 11 000 m/z range. We have characterized and optimized the filtering parameters for both simulated and experimental TOF data with invariant peak shape. The optimal single filter produces a 10% width reduction and a 4-fold increase in the SNR for linear MALDI-TOF data. We have shown that a geometric mean of multiple filtered signals efficiently suppresses filter artifacts, random noise, and improves the signal resolution by a factor of 1.7, reducing the width to 60% of its initial value. The narrow, filtered signals maintain their detected peak centroid position to better than a final half-linewidth for all peak signals with an input SNR in excess of 4.

These time-domain filters eliminate the need for deconvolution of individual peaks, or the fitting of individual peaks, and streamline the processing of the full TOF record. Our findings are general for linear TOF techniques for peptide analysis in the range where the point density per peak is constant, since the methods that we apply are time-series filtering. Application of the target filtering to TOFMS data for peptide expression profiling will give an immediate benefit of increased resolution with preserved sensitivity and attenuation of stationary white noise. Applying this target filtering technique to the experimental data for pooled serum, we have been able to deconvolve peak splittings consistent with the chemical adducts and neutral losses from parent peptide peaks, and suppress the noise in the range from 2 to 11 kDa, where the number of time points per peak is constant. This is not a fundamental constraint, and we plan to show extrapolation of these techniques to the full range of the TOF data record in our future work. This enhanced resolution, with uncertainty estimates for peak positions and intensities, will facilitate peak detection and alignment for multiple records, and provides a prerequisite for adduct deconvolution^23,31 and peak assignment to individual biological species.