Abstract
For two-stage randomized experiments assuming partial interference, exact confidence intervals are proposed for treatment effects on a binary outcome. Empirical studies demonstrate the new intervals have narrower width than previously proposed exact intervals based on the Hoeffding inequality.
Keywords: Causal Inference, Exact Confidence Interval, Interference, Randomization Inference
1. Introduction
In a randomized experiment, it is commonly assumed that an individual only has two potential outcomes: an outcome on control, and an outcome on treatment. That an individual has only two potential outcomes assumes no interference (Cox, 1958) between individuals, i.e., an individual’s potential outcomes are unaffected by the treatment assignment of any other individual in the study. There are many settings where this assumption of no interference is clearly violated (Hong and Raudenbush, 2006; Sobel, 2006; Rosenbaum, 2007).
Partial interference holds when individuals can be partitioned into groups such that there is no interference between individuals in different groups. In settings where partial interference holds, two-stage randomized experiments have been suggested as a study design for drawing inference about treatment (i.e., causal) effects. Two-stage randomized experiments proceed by (i) randomizing groups to treatment strategies and (ii) randomizing individuals within groups to different treatments based on the treatment strategy assigned to their group in stage (i). Two-stage randomized experiments are found in many fields of study, e.g., infectious diseases (Baird et al., 2012), medicine (Borm et al., 2005), economics (Duflo and Saez, 2003), and political science (Ichino and Schündeln, 2012; Sinclair et al., 2012). Building upon ideas in Halloran et al. (1991), Hudgens and Halloran (2008) defined and derived unbiased estimators for the direct, indirect, total, and overall effects of treatment in a two-stage randomized experiment assuming partial interference. Liu and Hudgens (2014) showed that Wald-type confidence intervals based on these estimators perform well when the number of groups is large; however, often the number of groups may not be large enough. For example, Moulton et al. (2001) describe a group-randomized vaccine trial involving approximately 9,000 individuals but only 38 groups. Tchetgen Tchetgen and VanderWeele (2012), henceforth TV, proposed exact confidence intervals using the Hoeffding inequality for these four effects in a two-stage randomized experiment with partial interference. Unfortunately, as will be shown below, the TV intervals can be very wide and conservative.
In this paper, we propose different exact confidence intervals based on inverting exact hypothesis tests that tend to be less conservative than TV. The remainder of the paper is organized as follows. In §2, treatment effects in the presence of interference are defined and existing inferential results are reviewed. In §3, the assumption of stratified interference is presented and bounds are derived for the causal effects under this assumption. In §4 the proposed new exact confidence intervals are described by inverting certain permutation tests. In §5 a simulation study is conducted comparing the TV, asymptotic, and new exact confidence intervals. §6 concludes with a discussion. An R package is available implementing the proposed confidence intervals.
2. Preliminaries
2.1. Estimands
Consider a finite population of N individuals partitioned into k groups with ni individuals in group i for i = 1, …, k. Assume partial interference, i.e., there is no interference between individuals in different groups. Consider a two-stage randomized experiment wherein h of k groups are assigned to strategy α1 and k–h are assigned to α0 in the first stage, where strategy αs specifies that of ni individuals will receive treatment. For example, strategy α0 might entail assigning (approximately) 1/3 of individuals within a group to treatment whereas strategy α1 might entail assigning (approximately) 2/3 of individuals within a group to treatment (see TV for further discussion about different types of treatment allocation strategies). Let Si = 1 if group i is randomized to α1 and 0 otherwise so that Pr[Si = 1] = h/k. In the second stage, individuals will be randomized to treatment conditional on group assignment in the first stage. Let Zij = 1 if individual j in group i is assigned treatment and 0 otherwise. Let Zi = (Zi1, …, Zini) be the random vector of treatment assignments for group i taking on values , the set of all vectors of length ni composed of elements equal to 1 and elements equal to 0. Additionally, let Zi(j) denote the random vector of treatment assignments in group i excluding individual j taking on values .
Let yij(zi) be the binary potential outcome for individual j in group i when group i receives treatment vector zi. A randomization inference framework is adopted wherein potential outcomes are fixed features of the finite population of N individuals and only treatment assignments S and Z are random (as in Sobel (2006); Rosenbaum (2007); Hudgens and Halloran (2008)). Define the average potential outcome for individual j in group i on treatment z = 0, 1 under strategy αs as
| (1) |
where . Henceforth, let and . For treatment z under strategy αs define the group average potential outcome as , and the population average potential outcome as ȳ(z; αs) ≡ k−1 Σi ȳi(z; αs). Define the average potential outcome for individual j in group i under strategy αs as
| (2) |
the group average potential outcome as , and the population average potential outcome as . Define the direct effect of treatment for strategy αs as DE(αs) = ȳ(0; αs) − ȳ(1; αs), the indirect effect of α0 versus α1 as IE(α0, α1) = ȳ(0; α0) − ȳ(0; α1), the total effect as TE(α0, α1) = ȳ(0; α0) − ȳ(1; α1), and the overall effect of α0 versus α1 as OE(α0, α1) = ȳ(α0) − ȳ(α1); see Hudgens and Halloran (2008) and TV for additional discussion regarding these effects.
2.2. Existing Inferential Results
Hudgens and Halloran (2008) derived unbiased estimators for all population average potential outcomes, and thus for the four causal effects. Noting that Pr[Si = s] and Pr[Zij = z|Si = s] are known by design, the estimator
| (3) |
where is unbiased for ȳ(z; αs). Additionally, the estimator
| (4) |
is unbiased for ȳ(αs). Unbiased estimators for the effects of interest follow immediately: , and .
TV proposed exact confidence intervals based on the Hoeffding inequality for the effects of interest in a two-stage randomized experiment where partial interference is assumed. In particular, for any γ ∈ {0, 1}, is a 1 − γ exact confidence interval for DE(αs) where is given in equation (17) of TV for s = 0, 1. Additionally, , and are all 1 − γ exact confidence intervals for their target parameters where ε*(γ, α0, q0, α1, q1, k) is given in Theorem 3 of TV.
Liu and Hudgens (2014) examined conditions under which Wald-type intervals and Chebyshev-type intervals are valid, large sample confidence intervals for DE(αs), where z(1−γ/2) is the 1 − γ/2 quantile for the standard normal distribution and is an estimator of the variance of for s = 0, 1. They also considered Wald and Chebyshev-type confidence intervals for the indirect, total, and overall effects.
3. Bounds Under Stratified Interference
Exact randomization based inference about the four effects is challenging without further assumptions as the experiment reveals only N of the total potential outcomes. One such additional assumption is stratified interference (Hudgens and Halloran, 2008), which assumes that individual j in group i has the same potential outcome when assigned control or treatment as long as a fixed number of other individuals in group i are assigned treatment, i.e.,
| (5) |
Under (5), individual j in group i only has four potential outcomes, which we denote by yij(z; αs) for z, s = 0, 1, so that the experiment reveals the observed outcome Yij = Σz,s=0,1 1{Zij = z; Si = s}yij(z; αs) for each individual and thus N of the 4N total potential outcomes. Furthermore, (5) implies that ȳij(z; αs) = yij(z; αs), and that where .
Under (5), the observed data form bounded sets for all effects contained in the interval [−1, 1]. The bounded sets have widths less than two where here and in the sequel the width of a set is defined to be the difference between its maximum and minimum values. Consider for illustration. For the Σi Σj(1 − Si)(1 − Zij) individuals with Si = Zij = 0, yij(0; α0) is revealed; however, for the N − Σi Σj(1 − Si)(1 − Zij) individuals with Si = 1 or Zij = 1, yij(0; α0) is missing and only known to be 0 or 1. Let y⃗(z; αs) be the N-dimensional vector of potential outcomes for treatment z under strategy αs. Under (5), a lower bound for DE(α0) is found by filling in all missing potential outcomes in y⃗(0; α0) as 0 and all missing potential outcomes in y⃗(1; α0) as 1. An upper bound for DE(α0) is found by filling in all missing potential outcomes in y⃗(0; α0) as 1 and all missing potential outcomes in y⃗(1; α0) as 0. Simple algebra shows that width of the bounded set for DE(α0) is equal to 2 − (k − h)/k. The width of this bounded set approaches 1 as (k − h)/k → 1, i.e., as more groups are randomized to α0.
Similar logic leads to bounds for the other effects. The width of the bounded set for DE(α1) is equal to 2 − h/k which approaches 1 as h/k → 1. The width of the bounded set for IE(α0, α1) is equal to which approaches 1 as the proportion of individuals assigned Zij = 0 approaches 1. The width of the bounded set for TE(α0, α1) is equal to which approaches 1 as the proportion of individuals with Si = Zij = 0 or Si = Zij = 1 approaches 1. Lower and upper bounds for OE(α0, α1) can be derived similarly but the corresponding width does not have a simple closed form.
4. EIT Confidence Intervals
In addition to leading to unbiased estimators and bounds, the observed data can be used to form 1 − γ confidence sets for the four effects. The confidence sets are formed by inverting hypothesis tests about the potential outcomes that define the effect of interest. This section is divided into two parts: §4.1 outlines how the confidence sets are formed and §4.2 presents a computationally feasible algorithm for constructing an interval that contains the exact confidence set. Henceforth this interval is referred to as the exact inverted test (EIT).
4.1. An Exact Confidence Set
The methods to follow can be generalized to any effect, so consider DE(α0). Inference about DE(α0) concerns the vectors y⃗(0; α0) and y⃗(1; α0), which are partially revealed by the experiment. A hypothesis about these vectors is considered sharp if it completely fills in the potential outcomes not revealed by the experiment. A sharp null H0 : y⃗(0; α0) = y⃗0(0; α0), y⃗(1; α0) = y⃗0(1; α0) maps to a value of DE(α0), which we denote DE0(α0). Only sharp null hypotheses that are compatible with the observed data need to be tested as other sharp nulls can be rejected with zero probability of making a type I error. Thus for each sharp null to be tested, the implied null value DE0(α0) will be a member of the bounded set derived in §3. There are B1 = 2Σi(1−Si)ni4ΣiSini sharp null hypotheses to test, as individuals with Si = 0 have only one missing potential outcome with two possible values {0, 1}, and individuals with Si = 1 have two missing potential outcomes with four possible values {0, 1} × {0, 1}.
After filling in the missing potential outcomes under H0, the null distribution of the test statistic
can be found by computing the statistic, denoted by
, for each of the c = 1, …, C1 possible experiments under H0, where
and
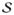 is the set of all possible values of the vector S such that
. A two-sided p-value to test H0 is given by
. If p0 < γ, H0 is rejected. Note p0 is a function of the null hypothesis vectors y⃗0(0; α0) and y⃗0(1; α0). Let p(DE0(α0)) denote the set of all p0 which are functions of compatible vectors y⃗0(0; α0) and y⃗0(1; α0) that map to DE0(α0). A 1 − γ confidence set for DE(α0) is {DE0(α0) : max{p(DE0(α0))} ≥ γ}. P-values, and thus confidence sets, can be found in an analogous manner for the other effects.
is the set of all possible values of the vector S such that
. A two-sided p-value to test H0 is given by
. If p0 < γ, H0 is rejected. Note p0 is a function of the null hypothesis vectors y⃗0(0; α0) and y⃗0(1; α0). Let p(DE0(α0)) denote the set of all p0 which are functions of compatible vectors y⃗0(0; α0) and y⃗0(1; α0) that map to DE0(α0). A 1 − γ confidence set for DE(α0) is {DE0(α0) : max{p(DE0(α0))} ≥ γ}. P-values, and thus confidence sets, can be found in an analogous manner for the other effects.
4.2. A Computationally Feasible Algorithm
Finding the exact confidence set for DE(α0) described above entails testing B1 hypotheses, where each hypothesis test involves C1 randomizations. As N becomes large, the computational time necessary to perform B1×C1 operations grows exponentially. For illustration of the problem, consider two examples in which h = 1 of k = 1 groups are assigned α0, in which of n1 = 20 individuals are randomized to treatment such that B1 = 220 and . Suppose there are two cases of observed data: (a) 5 of 10 unexposed experienced an event, and 5 of 10 exposed experienced an event, and (b) 8 of 10 unexposed experienced an event and 2 of 10 exposed experienced an event. Figure 1 displays a plot of DE0(α0) versus p(DE0(α0)) for both examples. The bounded set and 95% exact confidence set for DE0(α0) are, respectively, {−0.5, −0.45, …, 0.45, 0.5} and {−0.35, −0.3, …, 0.3, 0.35} in (a) and {−0.2, −0.15, …, 0.75, 0.8} and {0.15, 0.2, …, 0.75, 0.8} in (b).
Figure 1.
Plot of DE(α0) versus p(DE(α0)) for examples (a) and (b) as outlined in §4.2.
A computationally feasible algorithm is given below for approximating the confidence sets. The algorithm entails testing a targeted random sample of B2 of the B1 total sharp null hypotheses, and computing p-values for each sampled sharp null based on a random sample of C2 of the C1 possible randomizations. The set of computed p-values are then used to approximate the confidence set endpoints using local linear interpolation. For intuition underlying the interpolation step, consider the piecewise linear function that connects the maximum p-values for each compatible value of DE(α0) in Figure 1. Finding the x-coordinates for the intersection points of this function and a horizontal line at γ will conservatively approximate the lower and upper 1 − γ confidence limits for DE(α0). This suggests the following targeted, local linear interpolation algorithm for estimating the lower bound of a confidence set for DE(α0). An analogous algorithm can be used to target the upper limit of the confidence set for DE(α0).
Let denote the lower bound for DE(α0), and ŷ(z; α0)l and ŷ(z; α0)u denote the lower and upper bounds, respectively, for ȳ(z; α0).
Test the unique sharp null about y⃗(0; α0) and y⃗(1; α0) that maps to . If the corresponding p-value p0 ≥ γ, let be the lower limit of the confidence set and do not proceed. Otherwise, let and let pl = 1 − 1/B2. Let and
 = {p0}.
= {p0}.Fill in the missingness in y⃗(0; α0) with samples from a Bernoulli distribution with mean and fill in the missingness in y⃗(1; α0) with samples from a Bernoulli distribution with mean where qp(a, b) = (1 − p)a + pb, and f(x) = x if 0 ≤ x ≤ 1, f(x) = 0 if x < 0, and f(x) = 1 if x > 1.
-
If the sampled sharp null maps to a value , add DE0(α0) to the set
 , add the corresponding p0 to
, add the corresponding p0 to
 , and if p0 ≥ γ then update l to equal DE0(α0). Otherwise, do not compute a p-value corresponding to the sampled sharp null and let pl = pl − 1/B2.
, and if p0 ≥ γ then update l to equal DE0(α0). Otherwise, do not compute a p-value corresponding to the sampled sharp null and let pl = pl − 1/B2.Repeat Steps 2 and 3 B2/2 − 1 times.
Let t be the function from
 to
to
 that maps each p-value p0 in
that maps each p-value p0 in
 to the null value of DE0(α0) in
to the null value of DE0(α0) in
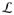 which corresponds to the sharp null hypothesis which generated p0. Let
which corresponds to the sharp null hypothesis which generated p0. Let
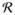 = {max{p ∈
= {max{p ∈
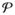 : t(p) = l} : l ∈
: t(p) = l} : l ∈
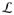 }. Let r1 = min{r ∈
}. Let r1 = min{r ∈
 : r ≥ γ} and let r2 = max{r ∈
: r ≥ γ} and let r2 = max{r ∈
 : r < γ}. Let li = t(ri) for i = 1, 2. The lower limit of the confidence set l* is found by local linear interpolation by finding the x-coordinate for the point at which a line drawn from (l2, r2) to (l1, r1) intersects a horizontal line at γ, i.e., l* = l2+(γ−r2)(l2−l1)/(r2−r1). The upper limit u* is found analogously. As B2 → B1 and C2 → C1, the interval [l*, u*] will contain the exact confidence set described in §4.1 with probability approaching 1.
: r < γ}. Let li = t(ri) for i = 1, 2. The lower limit of the confidence set l* is found by local linear interpolation by finding the x-coordinate for the point at which a line drawn from (l2, r2) to (l1, r1) intersects a horizontal line at γ, i.e., l* = l2+(γ−r2)(l2−l1)/(r2−r1). The upper limit u* is found analogously. As B2 → B1 and C2 → C1, the interval [l*, u*] will contain the exact confidence set described in §4.1 with probability approaching 1.
The algorithms for approximating confidence sets for IE(α0, α1) and TE(α0, α1) are analogous. For OE(α0, α1) the algorithm is modified slightly as it involves all four vectors y⃗(z; αs), z, s = 0, 1. Let ŷ(αs)l and y⃗(αs)u be the lower and upper limits, respectively, for ȳ(αs) under (5). If p0 < γ for OE(α0, α1)l, set and fill in the missingness in y⃗(0; α0) and y⃗(1; α0) with samples from a Bernoulli distribution with mean where pl = 1 − 1/B2. A p-value is computed if and if not pl = pl − 1/B2. If p0 ≥ γ for OE(α0, α1)l, l is set to equal OE0(α0, α1). The upper endpoint can be approximated using an analogous approach.
The R package interferenceCI is available on CRAN (Rigdon, 2015) for computing EIT confidence intervals via this algorithm for the four effects assuming stratified interference when the outcome is binary. The Wald, Chebyshev, and TV intervals are also computed in the package.
5. Comparisons Via Simulation
A simulation study was carried out to compare the asymptotic, TV, and EIT confidence intervals. The simulation proceeded as follows for fixed values of α0, α1, DE(α0), DE(α1), IE(α0, α1), k, ni = n for i = 1, …, k such that N = kn:
-
0
Potential outcomes were generated by first fixing the vectors y⃗(z; αs) for z, s = 0, 1 to be length N vectors of all 0s. Group membership was assigned by letting elements n(i − 1) + 1, …, ni of each vector belong to group i = 1, …, k. Then, N(0.5+DE(α0)/2) elements in y⃗(0; α0) were randomly set to equal 1 and N(0.5−DE(α0)/2) elements in y⃗(1; α0) were randomly set to equal 1. Then, N(0.5 + DE(α0)/2 − IE(α0, α1)) elements in y⃗(0; α1) were randomly set to equal 1. Finally, N(0.5 + DE(α0)/2 − IE(α0, α1) − DE(α1)) elements in y⃗(1; α1) were randomly set to equal 1.
-
1
Observed data were generated by (i) randomly assigning h of k groups to strategy α1 and (ii) randomly assigning of n individuals per group to treatment for s = 0, 1. Observed outcomes followed based on these treatment assignments and the potential outcomes from step 0.
-
2
For each effect, 95% confidence intervals were computed using the observed data generated in step 1.
-
3
Steps 1–2 were repeated 1000 times.
In the simulation we let k = n = 10 or k = n = 20 with h = k/2, under α0, under α1, DE(α0) = 0.95, DE(α1) = 0.3, and IE(α0, α1) = 0.5 (such that TE(α0, α1) = 0.8 and OE(α0, α1) = 0.395). In the targeted sampling algorithm, B2 = C2 = 100 such that B2/B1 and C2/C1 were less than 10−20 for all effects. Table 1 displays average widths and coverages for Wald, EIT, Chebyshev, and TV. Wald and Chebyshev fail to achieve nominal coverage for DE(α0) when k = n = 10 and Wald additionally fails to cover for DE(α0) when k = n = 20 and for IE(α0, α1) and TE(α0, α1) when k = n = 10. As guaranteed by their respective constructions, EIT and TV achieve nominal coverage for all setups; however, EIT has narrower width than TV in all setups. In fact, EIT is an order of magnitude narrower than TV in three instances: DE(α0), TE(α0, α1), and OE(α0, α1) when k = n = 20.
Table 1.
Empirical width [coverage] of Wald (W), exact inverted test (EIT), Chebyshev (C), and TV 95% CIs for simulation study discussed in §5.
| n | k | DE(α0) | DE(α1) | IE(α0, α1) | TE(α0, α1) | OE(α0, α1) | |
|---|---|---|---|---|---|---|---|
| W | 10 | 10 | 0.13 [0.84] | 0.51 [0.96] | 0.39 [0.93] | 0.30 [0.93] | 0.24 [0.94] |
| 20 | 20 | 0.09 [0.89] | 0.26 [0.96] | 0.21 [0.95] | 0.14 [0.98] | 0.11 [0.97] | |
| EIT | 10 | 10 | 0.28 [0.98] | 0.52 [0.98] | 0.47 [0.99] | 0.31 [0.98] | 0.36 [1.00] |
| 20 | 20 | 0.12 [0.98] | 0.27 [0.98] | 0.24 [0.98] | 0.14 [0.98] | 0.18 [1.00] | |
| C | 10 | 10 | 0.22 [0.84] | 1.15 [1.00] | 0.84 [1.00] | 0.54 [1.00] | 0.54 [1.00] |
| 20 | 20 | 0.15 [0.99] | 0.59 [1.00] | 0.49 [1.00] | 0.32 [1.00] | 0.26 [1.00] | |
| TV | 10 | 10 | 1.95 [1.00] | 2.00 [1.00] | 2.00 [1.00] | 2.00 [1.00] | 2.00 [1.00] |
| 20 | 20 | 1.41 [1.00] | 2.00 [1.00] | 1.86 [1.00] | 1.56 [1.00] | 1.96 [1.00] |
6. Discussion
In this paper new exact confidence intervals have been proposed for causal effects in the presence of partial interference. The new intervals are constructed by inverting permutation based hypothesis tests. These intervals do not rely on any parametric assumptions and require no assumptions about random sampling from a larger population. The confidence intervals are exact in the sense that the probability of containing the true treatment effects is at least the nominal level. As there may be many vectors of potential outcomes that map to one value of the causal estimand, a computationally feasible algorithm was proposed in §4.2 to approximate the exact confidence intervals. Empirical studies demonstrate the new exact intervals have narrower width than previously proposed exact intervals based on the Hoeffding inequality. Nonetheless, the empirical coverage of the proposed intervals still tends to exceed the nominal level, suggesting one possible future avenue of research would be to develop alternative intervals which are less conservative and narrower but maintain nominal coverage.
Acknowledgments
This research was supported by the National Institutes of Health. The content is solely the responsibility of the authors and does not necessarily represent the official views of the the NIH. The authors thank Mark Weaver for helpful comments.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Joseph Rigdon, Email: jrigdon@stanford.edu, Quantitative Sciences Unit, Stanford University, Palo Alto, California 94304, U.S.A.
Michael G. Hudgens, Email: mhudgens@bios.unc.edu, Department of Biostatistics, CB 7420, University of North Carolina, Chapel Hill, North Carolina 27516, U.S.A
References
- Baird S, Garfein R, McIntosh C, Özler B. Effect of a cash transfer programme for schooling on prevalence of HIV and herpes simplex type 2 in Malawi: a cluster randomised trial. The Lancet. 2012;379:1320–1329. doi: 10.1016/S0140-6736(11)61709-1. [DOI] [PubMed] [Google Scholar]
- Borm G, Melis R, Teerenstra S, Peer P. Pseudo cluster randomization: a treatment allocation method to minimize contamination and selection bias. Statistics in Medicine. 2005;24:3535–3547. doi: 10.1002/sim.2200. [DOI] [PubMed] [Google Scholar]
- Cox D. Planning of Experiments. Wiley; New York, NY: 1958. [Google Scholar]
- Duflo E, Saez E. The role of information and social interactions in retirement plan decisions: Evidence from a randomized experiment. The Quarterly Journal of Economics. 2003;118:815–842. [Google Scholar]
- Halloran M, Haber M, Longini I, Struchiner C. Direct and indirect effects in vaccine efficacy and effectiveness. American Journal of Epidemiology. 1991;133:323–331. doi: 10.1093/oxfordjournals.aje.a115884. [DOI] [PubMed] [Google Scholar]
- Hong G, Raudenbush S. Evaluating kindergarten retention policy: A case study of causal inference for multi-level observational data. Journal of the American Statistical Association. 2006;101:901–910. [Google Scholar]
- Hudgens M, Halloran M. Toward causal inference with interference. Journal of the American Statistical Association. 2008;103:832–842. doi: 10.1198/016214508000000292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ichino N, Schündeln M. Deterring or displacing electoral irregularities? Spillover effects of observers in a randomized field experiment in ghana. The Journal of Politics. 2012;74:292–307. [Google Scholar]
- Liu L, Hudgens M. Large sample randomization inference of causal effects in the presence of interference. Journal of the American Statistical Association. 2014;109:288–301. doi: 10.1080/01621459.2013.844698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moulton L, O’Brien K, Kohberger R, Chang I, Reid R, Weatherholtz R, Hackell J, Siber G, Santosham M. Design of a group-randomized Streptococcus pneumoniae vaccine trial. Controlled Clinical Trials. 2001;22:438–452. doi: 10.1016/s0197-2456(01)00132-5. [DOI] [PubMed] [Google Scholar]
- Rigdon J. interferenceCI: Exact Confidence Intervals in the Presence of Interference. R package version 1.1. 2015 doi: 10.1016/j.spl.2015.06.011. http://CRAN.R-project.org/package=interferenceCI. [DOI] [PMC free article] [PubMed]
- Rosenbaum P. Interference between unites in randomized experiments. Journal of the Americal Statistical Association. 2007;102:191–200. [Google Scholar]
- Sinclair B, McConnell M, Green D. Detecting spillover effects: Design and analysis of multilevel experiments. American Journal of Political Science. 2012;56:1055–1069. [Google Scholar]
- Sobel M. What do randomized studies of housing mobility demonstrate?: Causal inference in the face of interference. Journal of the Americal Statistical Association. 2006;101:1398–1407. [Google Scholar]
- Tchetgen Tchetgen E, VanderWeele T. On causal inference in the presence of interference. Statistical Methods in Medical Research. 2012;21:55–75. doi: 10.1177/0962280210386779. [DOI] [PMC free article] [PubMed] [Google Scholar]


