Black–white asymmetry in visual perception

Abstract

With eleven different types of stimuli that exercise a wide gamut of spatial and temporal visual processes, negative perturbations from mean luminance are found to be typically 25% more effective visually than positive perturbations of the same magnitude (range 8–67%). In Experiment 12, the magnitude of the black–white asymmetry is shown to be a saturating function of stimulus contrast. Experiment 13 shows black–white asymmetry primarily involves a nonlinearity in the visual representation of decrements. Black–white asymmetry in early visual processing produces even-harmonic distortion frequencies in all ordinary stimuli and in illusions such as the perceived asymmetry of optically perfect sine wave gratings. In stimuli intended to stimulate exclusively second-order processing in which motion or shape are defined not by luminance differences but by differences in texture contrast, the black–white asymmetry typically generates artifactual luminance (first-order) motion and shape components. Because black–white asymmetry pervades psychophysical and neurophysiological procedures that utilize spatial or temporal variations of luminance, it frequently needs to be considered in the design and evaluation of experiments that involve visual stimuli. Simple procedures to compensate for black–white asymmetry are proposed.

Introduction

Luminance increments on a uniform background appear lighter than the background. Luminance decrements appear darker than the background or even black, depending on the magnitude of the decrement. In psychophysical models, it has generally been taken for granted that the physiological responses to small luminance increments and to small luminance decrements also would be quite symmetric (Burr & Morrone, 1994; Chey, Grossberg, & Mingolla, 1998; Chubb & Sperling, 1989; Graham & Sutter, 1998; Marr, 1982; Morgan & Watt, 1997; Sperling, 1989). However, black–white asymmetries have been noted frequently (Bowen, Pokorny, & Smith, 1989; Bowen, Pokorny, Smith, & Fowler, 1992; Boynton, Ikeda, & Stiles, 1964; Cao, Zele, & Pokorny, 2007; Chubb & Nam, 2000; Cohn, 1974; Cohn & Lasley, 1975; Dannemiller & Stephens, 2001; DeMarco, Hughes, & Purkiss, 2000; He & MacLeod, 1998; Henning, Hertz, & Broadbent, 1975; Herrick, 1956; Kelly & Savoie, 1978; Komban, Alonso, & Zaidi, 2011; Legge & Foley, 1980; Levinson, 1960; Levinson & Harmon, 1961; MacLeod, Williams, & Makous, 1992; Patel & Jones, 1968; Rashbass, 1970; Roufs, 1974; Scott-Samuel & Georgeson, 1999; Short, 1966; Solomon & Sperling, 1994; Vingrys & Mahon, 1998; Watson, 1986; Wolfson & Graham, 2001; but see Alexander, Xie, & Derlacki, 1993). By black–white asymmetry we mean that to obtain equal psychophysical responses, increment and decrements must be consistently different in magnitude (Sperling & Lu, 1999). In virtually all asymmetric cases, it was found that a black (decremental) stimulus is more effective than an equal magnitude white (incremental) stimulus, i.e., decrements are represented in the visual system by a larger magnitude than increments that have an equal-magnitude deviation from the background.

Sometimes black–white asymmetry has indeed come into prominence as, for example, in the argument that the detection of texture-defined motion (second-order motion) is mediated by luminance (first-order) contamination in the second-order motion stimuli (Smith & Ledgeway, 1997). When there is black–white asymmetry in early visual processing, unless this asymmetry is recognized and compensated, incidental stimulation of the first-order motion system (first-order contamination) is likely (Lu & Sperling, 2001a; Scott-Samuel & Georgeson, 1999; Sperling & Lu, 1998) in stimuli intended to stimulate only higher-order motion and texture systems.

Because most studies of black–white asymmetry have dealt only with threshold increments and decrements, and because they generally have been confined to a single type of stimulus, the significance of black–white asymmetry for perception in general (not merely for motion perception) has been largely overlooked. Here we investigate a large number of stimuli with similar apparatus and observers to compare black–white asymmetry in a wide range of conditions. The issue here is not whether distortion produced by black–white asymmetry exists but what its magnitude is and how it affects the conclusions that can be made when uncompensated stimuli are used. Among the questions we propose to answer are: In what paradigms does one find black–white asymmetry? What is the magnitude of the distortion produced by black–white asymmetry? What is its origin? And how can it best be cancelled or avoided?

This paper is divided into three sections. In section I, we demonstrate the existence and measure the magnitude of black–white asymmetry with eleven different types of stimuli that exercise a wide gamut of spatial and temporal visual processes. Negative perturbations from mean luminance are found to be typically 25% (range 8–67%) more effective visually than positive perturbations of the same magnitude, and the magnitude of the asymmetry varies significantly among individuals. In section II, we measure and model the functional relationship between black–white asymmetry and stimulus contrast. We derive a computational rule for the magnitude of black–white asymmetry. We also investigate the nonlinear properties of the internal representation of stimulus contrast in the perceptual system. In section III, we consider the origins of the black–white asymmetry.

Black–white asymmetry in a range of visual tasks

The current experiments investigate the generality of black–white asymmetry in visual perception and offer a simple procedure for canceling the asymmetry. Three previous paradigms are repeated and seven new experiments are performed to demonstrate black–white asymmetry in a wide range of perceptual tasks, including incremental and decremental thresholds, flicker fusion, first- and second-order motion, texture slant, Gestalt grouping, and object perception, all with the same group of observers. In all cases, there is black–white asymmetry.

We summarize all the asymmetric phenomena in the first eleven experiments with a single parameter α: The internal representation of the contrast of areas of a stimulus that are below the mean luminance is α times larger than the internal representation of equivalent areas that are greater than the mean luminance. Specifically, if ΔL_w is a luminance increment (white), and ΔL_b is a luminance decrement (black) then, to produce internal representations of equal magnitude for subsequent visual processing,

This piecewise linear approximation to the black–white luminance nonlinearity is refined in Experiments 12 and 13, in which α is shown to be a saturating function of contrast c and to involve a nonlinearity in representation of decrements. However, the linear approximation of Equation 1 used in the first 11 experiments is adequate to quantify and to compensate for the aggregate effect of the black–white luminance nonlinearity.

In the present experiments, conducted with the same observers, α typically is in the neighborhood of 1.25, although it varies from about 1.08 to 1.67 depending on the observer and the task. One advantage of formulating the black–white asymmetry as a ratio is that it suggests a simple means of canceling black–white asymmetry and thereby of producing stimuli that have a more nearly symmetric black–white representation after the early stages of visual processing.

General methods

Eleven stimulus types were investigated. These are designated, for short, as first-order and second-order. First-order stimuli refers to stimuli in which detection is based on luminance directly, i.e., on whether the luminance in the test area differs from the luminance of the background. Second-order stimuli is an abbreviation that refers to stimuli in which detection is intended to be based on the variance of luminance; e.g., on whether the texture-contrast in the test area differs from the texture-contrast in the background. In uncompensated second-order stimuli, the physical difference between the mean luminance of the test and the background areas is either zero or random—that is, these stimuli would be uninformative for a physical luminance-based system. In second-order stimuli in which black–white asymmetry has been compensated, the effective intensity of the neural input to first-order processes is uninformative because the neural difference in mean intensity between test and background is either zero or random with an expected value of zero. In all experiments, viewing was binocular.

Displays

Additionally, two different display devices with different calibration procedures were used to provide a crosscheck within the experiments. Specifically, Experiments 1, 2, 4, 8, and 11 were implemented on an achromatic Nanao Technology FlexScan 6600 monitor. Experiments 5, 6, 7, 9, and 10 were implemented using a Proxima DLP-4200 projector. The three experiments that are related to prior observations are reported first. (They were carried out so that all the procedures could be compared in the same observers under similar conditions.) The eleven experiments involve many thousands of trials, but the results can be reported very simply.

Observers

The first author and two UCI graduate students participated in all the experiments. The second author and two other observers participated in some of the experiments. All observers had corrected-to-normal vision and provided informed consent.

Apparatus

An achromatic 19” Nanao FlexScan 6600 monitor was driven by an internal video card in a 7500/100 Power PC Macintosh at 120 frames/s using a C++ version of Video Toolbox (Brainard, 1997; Pelli, 1997). A special circuit (Pelli & Zhang, 1991) was used to combine two 8-bit output channels of the video card to produce 6144 distinct voltage levels (12.6 bits). A psychophysical procedure was used to generate a linear lookup table to divide the entire dynamic range of the monitor (from 1 cd/m² to 53 cd/m²) into 256 equally-spaced levels. The background luminance was set at 27 cd/m². Viewing was binocular at a distance of 1.0 m.

The Proxima DLP-4200 projector was set at its achromatic mode with a refresh rate of 67 frames/s. The gamma of the projector was reset to 1.0 using a proprietary program. The voltage-luminance response of the reset DLP-4200 is linear within measurement error. In the chromatic mode, each RGB channel of the projector could produce 256 (8-bit) color levels. In the achromatic mode, the projector could produce 768 evenly spaced gray levels. Light from the projector was reflected to the observer using a white screen. The dynamic range of the projection system was 10.3 to 151.6 cd/m². The background luminance was set at 81.0 cd/m². The psychophysical calibration was verified with the Tektronics J18 photometer. Viewing was binocular at a distance of 2.0 m.

Calibration procedure

The aim of a calibration procedure is to determine the lookup table value so that a requested intensity is accurately produced by the graphics display hardware. The calibration procedure determines which subset of the 6144 available luminance levels will produce the 256 most evenly spaced values. The procedure for producing such a linear lookup table involves creating in one area of the viewing surface, as uniform-as-possible a mixture (in space and time) of equal quantities of zero and full-intensity pixels flickering at 30 Hz and determining the lookup table value of pixels in an adjacent homogeneous area (in which all pixels have the same intensity) that produces a psychophysical match to the luminance of the mixed-pixel area (Lu & Sperling, 1999; Li & Lu, 2012). The calibration stimuli are either viewed from a sufficient distance so that the grating is not resolvable or are blurred by a superimposed milk-glass filter.

The first calibration match determines the lookup table value for 0.5 of maximum luminance. A mixture of 0.5 and 1.0 pixels is used to determine the 3/4 value, and this procedure is repeated until seven values from 1/8 to 7/8 have been determined. These matches are repeated, and various checks for consistency are made, such as verifying that a mixture of 3/4 and 1/4 matches 0.5. The remaining lookup table values are derived from the first nine values by fitting a power function to the nine initial values and interpolating. Parts of the calibration procedure are repeated at regular intervals to ensure that calibration remains valid. Colombo and Derrington (2001) showed that such visual calibration is equivalent to that obtained from photometer measurements. The psychophysical calibration was confirmed with a Tektronics J18 photometer. Any psychophysically observed black–white asymmetry was not due to equipment calibration issues.

Procedures and results

Experiment 1. First-order luminance increment versus decrement thresholds

There is an inherent arbitrariness in the definition of increments and decrements because it requires the specification of a background or reference from which there is a deviation. While this may be obvious in simple cases where the background is absolutely uniform everywhere except in a tiny patch (the increment or decrement), the specification of the reference is problematical, for example, in texture stimuli where luminance may be almost any function of (x, y). The approach we take here is to consider stimuli L(x, y) that are composed of a luminance L₀ that is constant over the entire stimulus except for a modulation of that luminance ΔL(x, y) in a localized test area (Figure 1):

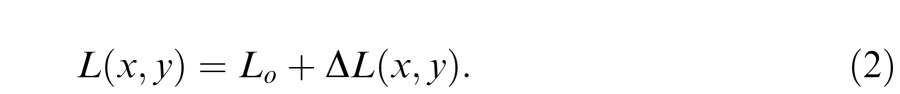Positive values of ΔL(x, y) are referred to as “increments” or “white”; negative values are “decrements” or “black.”

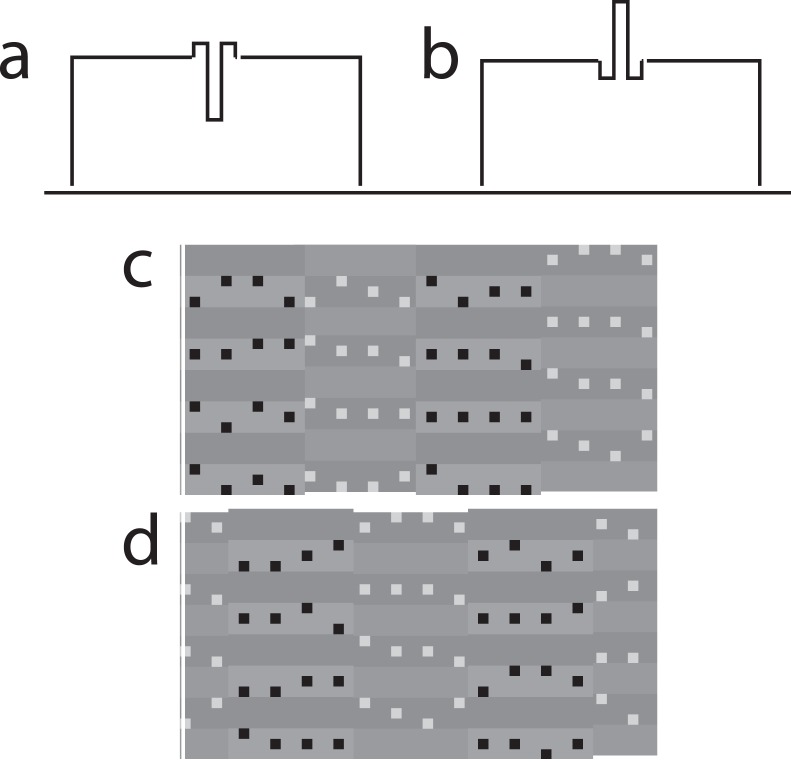
Figure 1.

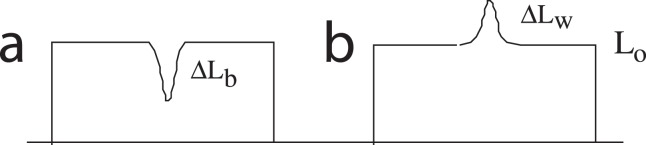
Increment (white) and decrement (black) Gaussian blob stimuli for Experiment 1. (a) Intensity profile of a luminance decrement ΔL_b, (b) a luminance increment ΔL_w.

Procedure:

In Experiment 1, the increments and decrements are Gaussian blobs, ΔL(x, y):

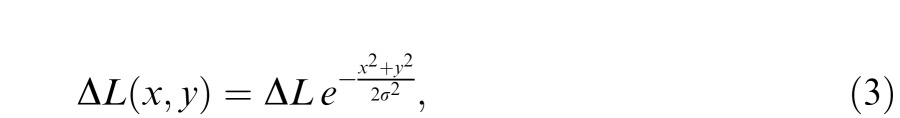on a large, uniform background (21 × 17°). The blob width was σ = 0.88°; the exposure duration was 50 ms. The Gaussian blob was either a decrement ΔL_b or an increment ΔL_w from the background. The stimulus is first-order because it involves directly detecting a luminance variation, not some more complex stimulus attribute. It is a pure first-order stimulus because it directly involves detecting minimal luminance increments or decrements that are unlikely to stimulate any higher-order processes.

A two-interval forced-choice procedure was used to determine the luminance deviation ΔL that can be detected with 75% accuracy. There were seven values of the increment, 40 trials for each observer with each value; the 75% point was determined by extrapolation from the psychometric function [percent correct versus ΔL(x, y)].

Results:

For the three observers, the white-to-black threshold ratios α = ΔL_w/ΔL_b were 1.07, 1.09, and 1.14, with an average of 1.10. An increment threshold 10% greater than the decrement threshold is consistent with previous reports (e.g., Boynton et al., 1964; Patel & Jones, 1968; Short, 1966).

Experiment 2. Black-centered versus white-centered hats: Second-order texture processing

Experiment 2 measures perceptual black–white asymmetry in stimuli in which the expected mean luminance is the same everywhere and in which only the variance between areas varies. To accomplish this, Experiment 2 uses stimulus elements (Mexican hats) that are perfectly luminance balanced. A white hat is a micropattern consisting of a 3 × 3 pixel array (0.11 × 0.11 °/pixel) in which the center pixel is w percent lighter than the background and the surrounding eight pixels are ⅛w percent darker than the background so that the mean luminance of the entire micropattern is the same as the background. In a black hat, the center pixel is b percent darker than the background, etc.¹

Method:

A texture grating was constructed of stripes composed entirely of columns of white hats alternating with stripes composed entirely of columns of black hats (Figure 2). These hats are all well above threshold and easily visible. The black-hat and white-hat stripes were calibrated for first-order equivalence by viewing at a distance at which the hats were unresolvable, ensuring that the stripe pattern was invisible. Between successive frames, the black-hat/white-hat stripe pattern was moved 90° (half a stripe width) consistently in one direction. After each movement, new random positions were chosen for the hats within a stripe. From trial-to-trial, the motion direction was determined randomly. The task of the observer was to report the perceived motion direction.

Figure 2.

Stimuli for Experiment 2: Cross-section intensity profile of a hat decrement (a) and a hat increment (b). (c, d) Sections of two consecutive frames showing four vertical black-dot and white-dot stripes of the hat stimulus. The black and white centers were jittered within each stripe of the stimulus. For illustrative purposes, the contrast in c and d is much larger than in the actual displays.

According to Chubb and Sperling (1988), first- and second-order processing differ only in the preprocessing prior to the motion or pattern computation. First-order motion processes take photons (local mean luminance) directly as their input; second-order motion processes take activity (local luminance variance) as their input. Activity is computed by texture grabbers, spatio-temporal filters whose output is rectified (absolute value or square) so that only the amount of output at a location is reported, not the sign (+/−). If the stripes filled with black hats and the stripes filled with white-hats had different mean luminance, the stimulus would be a first-order stimulus. However, the stripes were calibrated to have the precisely same mean luminance in all stripes. Insofar as the black-hat stripes and white-hat stripes have different variances (expected deviations of points in a stripe from the mean luminance of the stripe), it is a second-order stimulus, i.e., a stimulus in which stripes are defined by different variances with mean luminance equated in all stripes. The empirically measured value of α measures the effectiveness of the variance of black-hat stripes versus the variance of white hat stripes.

Experiment 2 fixed the white hat magnitude at 10% (of maximum possible) and determined the black hat magnitude that minimized apparent motion. That is, the black-hat and white-hat stripes were matched in overall physical luminance and only the variance (the hat magnitude) was varied. Insofar as these black-hat and white-hat textures produce equal neural luminance and equal neural variance at the points in the visual system where first-order and second-order motion is computed, detecting motion would require abstraction of higher-order texture properties, i.e., third-order motion processes (Lu & Sperling, 1995). In this case, the minimum-motion texture grating could activate only the third-order motion system insofar as it activated any motion system. If there was a significant nonlinearity in the representation of increments and/or decrements, there might be a small residual first-order motion contamination. In either case, the black/white (b/w) ratio at minimum-motion represents primarily the relative efficiency of white hats versus black hats in exciting the variance-detecting component in the second-order motion system.

Procedure:

Three observers viewed stimuli of five consecutive frames, with a frame time of 66.7 ms (3.75 Hz), a spatial frequency of 0.2 c/deg, and an overall size of 10 × 5°. They made left–right motion judgments in a method of constant stimuli in which b/w ratio took one of nine values.

Results:

At the b/w ratio that yielded minimum-motion, direction discrimination was reduced almost to chance. We interpret this result to indicate that the second-order components were truly canceled, and that any residual first- or third-order motion components in these stimuli were extremely weak. For the three observers the measured b/w ratios at minimum-motion were 1.39, 1.20, and 1.14 (mean = 1.24), indicating a mean greater efficiency for black over white of 24% in exciting second-order texture processes (for these observers). This is consistent with Solomon and Sperling (1994), who found ratios ranging from 1.08 to 1.37 (mean = 1.20) for their observers.

Experiment 3. cos(2πft) + cos(4πft) versus cos(2πft) − cos(4πft) flicker fusion: First-order temporal processing

To measure black–white asymmetry in flicker detection, Experiment 3 compares flicker detection in stimuli that have large positive peaks with stimuli that have large negative peaks (valleys). This experiment was originally performed by Levinson (1960) and Levinson and Harmon (1961) to demonstrate black–white asymmetry in temporal vision. Our digital display system cannot produce these stimuli as well as Levinson's analog equipment, so we report here his original observations. Two sinusoidally flickering stimuli with equal amplitude, one at frequency f Hz, and the other at 2f Hz, were superimposed in two different relative phases (Figure 3). In cos(2πft) + cos(4πft), the positive peaks of the two sine waves add; in cos(2πft) − cos(4πft), the negative peaks (valleys) of the two sine waves add. The stimuli were disks, 1° in diameter with an average luminance of 686 cd/m² against a background of 137 cd/m². Flicker fusion thresholds, that is, the threshold modulation amplitudes m_b (valleys add) and m_w (peaks add) were determined by the method of adjustment. Each of the five observers made 20 adjustments at each of the frequencies tested. For f = 10 Hz, the average threshold ratio m_w/m_b was 1.28; for f = 20 Hz, the threshold ratio was 1.16 (Levinson, 1960; Levinson & Harmon, 1961). These ratios indicate a significant relative advantage of black (valleys add) over white (peaks add) in flicker perception.

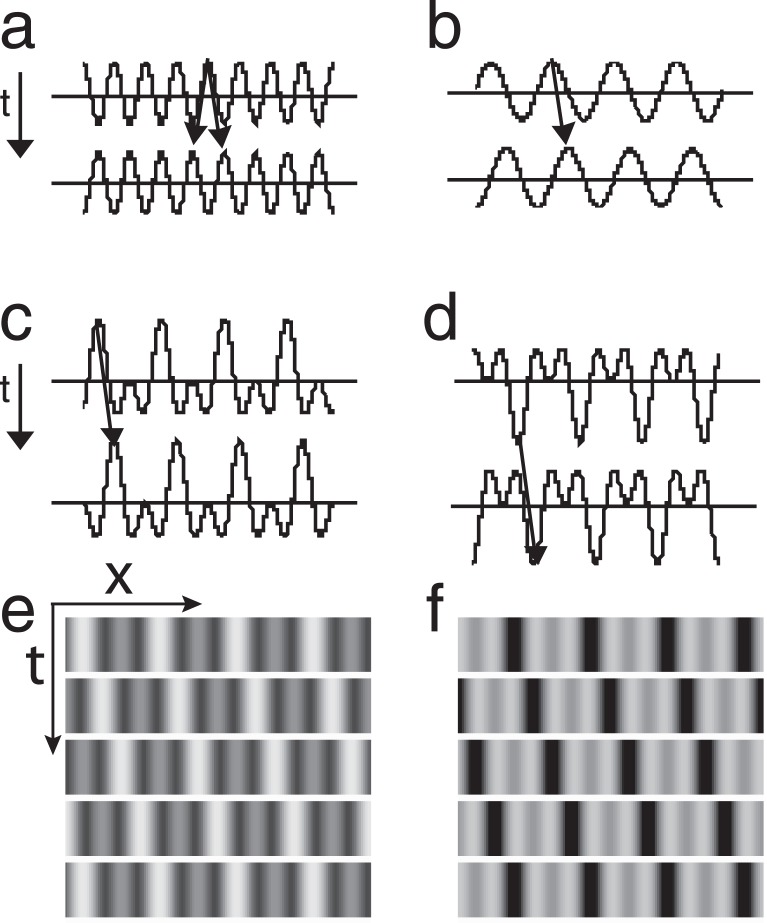
Figure 3.

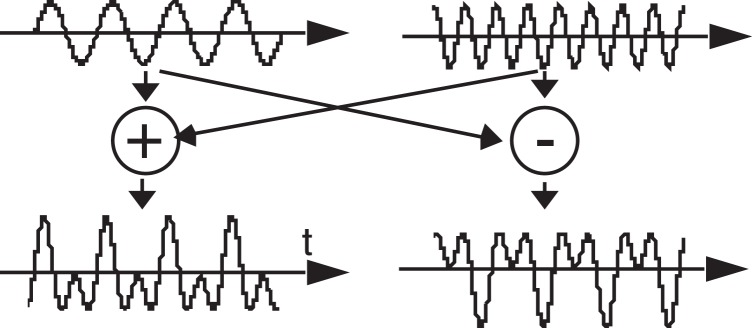
Stimuli for Experiment 3: Two luminance sine waves with temporal frequencies f and 2f added or subtracted to produce peaks-add (left) and valleys-add (right) waveforms that are tested for flicker detection.

Experiment 4. (f_x, f_t) + (2f_x, 2f_t) versus (f_x, f_t − (2f_x, 2f_t): First-order motion perception

To measure black–white asymmetry in first-order motion perception, Experiment 4 compares motion perception of stimuli that have large positive peaks with stimuli that have large negative peaks (valleys). Let (f_x, f_t) represent a sine wave grating with spatial frequency f_x that moves 90° in a consistent direction between successive frames so that it translates f_t full cycles per second (Figure 4a, right). The sideways stepping grating (f_x, f_t) is an extensively-analyzed apparent-motion display (Adelson & Bergen, 1985; van Santen & Sperling, 1984; Watson & Ahumada, 1985). Let (2f_x, 2f_t) be a grating of double spatial and temporal frequencies that moves the same physical distance as (f_x, f_t) between frames (Figure 4a, left). Then (2f_x, 2f_t) moves 180° between frames, so it is a counter-phase flickering stimulus without any motion information. (2f_x, 2f_t) is superimposed on (added to) (f_x, f_t) with two different relative phases. In (f_x, f_t) + (2f_x, 2f_t), the negative peaks (valleys) of the two sine waves add (Figure 4, right column); in (f_x, f_t) − (2f_x, 2f_t), the positive peaks of the two sine waves add (Figure 4, left column).

Figure 4.

Stimuli for Experiment 4: Two luminance sine waves with spatial and temporal frequencies (f_x, f_t) and (2f_x, 2f_t) are added or subtracted to produce peaks-add or valleys-add waveforms that are tested for motion-direction perception. (a, b) Two consecutive frames of spatial sine waves of frequencies 2f_x and f_x. (b) The sine wave f_x is shifted 90° rightward in Frame 2 as indicated by the arrow. (a) The 2f_x sine wave is shifted the same physical amount as f_x but this is now 180°, so the direction of shift is ambiguous, as indicated by the two arrows. (c) Two successive frames of f_x + 2f_x (as above) in peaks-add configuration (left), (d) valleys-add configuration. The arrow (t) indicates the direction of time, the horizontal arrows indicate the direction of motion. (e) Five frames of a motion stimulus illustrating left-to-right movement (from top to bottom) of peaks-add (left) and (f) valleys-add (right) configurations.

Procedure:

The motion stimuli (f_x, f_t) ± (2f_x, 2f_t) were instantiated in a rectangular region (14 × 8°) with f_x = 0.3 c/deg and f_t = 15 Hz. The modulation amplitudes m_b (valleys add) and m_w (peaks add) for correctly discriminating motion direction were determined using the method of constant stimuli as in Experiment 2.

Results:

For three observers, the ratio of the 75%-correct threshold m_w/m_b was 1.32, 1.14, and 1.12 (mean = 1.19). This indicates 19% greater effectiveness of black versus white in this particular first-order motion stimulus.

Experiment 5. First-order contamination in second-order stimuli with a static carrier

Square-wave texture-contrast gratings were created by modulating the contrast of binary random pixel noise. In the high contrast regions, the pixels take contrasts ±0.75 with equal probability; in the low contrast regions, the pixels take contrast ±0.25 with equal probability (Figures 5a and b). A display consisting of five frames of such a contrast-modulated texture with 90° phase shift between successive frames produces vivid apparent motion. The display is a conventional second-order stimulus with a static carrier (Cavanagh & Mather, 1989; Chubb & Sperling, 1989). The stimulus is not first-order because the mean luminance of the high-contrast and of the low-contrast regions is identical. Perception of stimulus motion requires a second-order system (Chubb & Sperling, 1989) that rectifies the stimulus contrast prior to motion computation (e.g., second-order system utilizes local luminance variance, first-order uses local mean luminance to compute motion) or a third-order system that computes motion from salience maps by attending to the dark or light regions (Lu & Sperling, 1995, 2001a). To reduce or eliminate contributions from the third-order system, we performed the experiment at a high temporal frequency (7.5 Hz) at which the third-order system is ineffective.

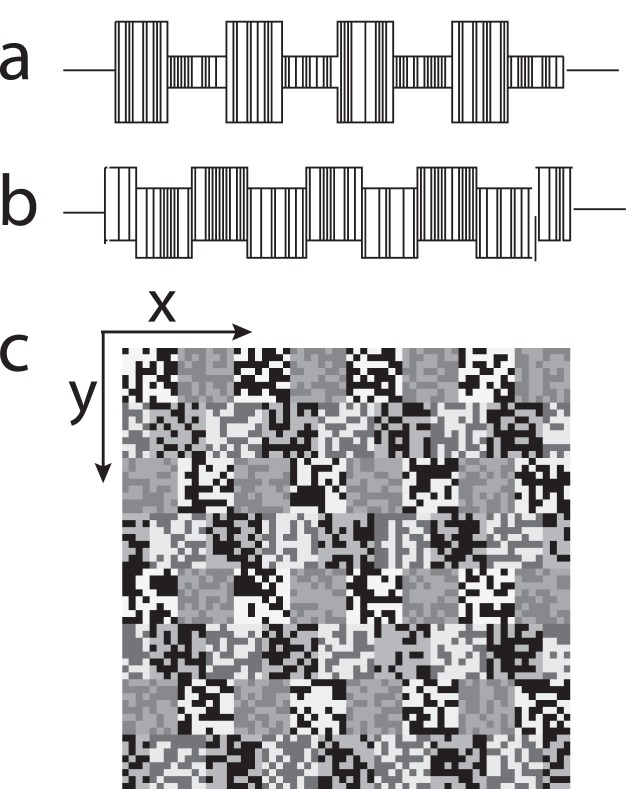
Figure 5.

Stimuli for Experiment 5: Contrast-modulation motion with a static random texture carrier. (a) Intensity profile of one row of a contrast modulated texture. In alternate vertical stripes within a stimulus frame, binary random noise (−1, +1) is multiplied by 0.25 and 0.75 to produce a 50% contrast modulation. (b) Intensity profile of one row of a luminance-modulated texture. In alternate vertical stripes, either 0.25 or −0.25 was added to each pixel intensity. (c) Five frames of a static texture-modulated (second-order) motion stimulus. In a static texture-modulation motion stimulus, the texture pattern remains the same from frame to frame, the imposed 0.25–0.75 contrast modulation translates 90° to the right in successive frames. (d) Five frames of a sandwich stimulus in which the odd frames are made of contrast modulated texture, and the even frames are made of luminance modulated texture.

There is a potential problem of first-order luminance contamination in this class of contrast-modulated stimuli (Lu & Sperling, 2001b; Scott-Samuel & Georgeson, 1999; Smith & Ledgeway, 1997). That is, such a stimulus, even though constructed in a way that theoretically negates the possibility of useful motion information from the first-order (luminance based) visual motion system (Chubb & Sperling, 1989) might nevertheless contain useful first-order information because of nonlinearities in early visual processing. To reveal such first-order luminance contamination, we replaced the even frames of the five-frame texture sequence (Figure 5c) with luminance modulation (Figure 5b). If there was no luminance contamination, one would not perceive linear directional motion in such a display because within the odd frames alone (binary texture) the phase shift is 180°, which is motion-ambiguous. Similarly, within the even frames alone (uniform luminance stripes) the phase shift also is 180°. However, if there was luminance contamination in the texture frames due to a greater representation of black than white, then consistent first-order motion would be perceived (to the right in Figure 5c) because all frames would contain a luminance stimulus; i.e., the 75% contrast stripes would have lower effective luminance than the 25% contrast stripes. Conversely, if white elements of the texture had a greater representation than black elements, leftward motion would be perceived.

Procedure:

To eliminate the visual system's black–white luminance distortion in the texture frames, the luminances are transformed as follows: Let ΔL(x, y) be the original luminance modulation of pixel (x, y) (Equation 2); Δ′L(x, y) is the transformed luminance modulation. For ΔL(x, y) < 0, Δ′L(x, y) = (1/α)ΔL(x, y), 0 < (1/α) < 1. That is, pixels with luminance less than the mean luminance have their difference from the mean reduced by 1/α. The luminance of pixels with luminance equal to or greater than the mean is unchanged. The operation was applied in all the frames. The goal is to determine a critical α_c that eliminates perceived motion, i.e., makes the perceived motion direction ambiguous. α_c is the relative effectiveness of black versus white in first-order motion.

The motion display was instantiated with a pixel size of 8.4 min in a rectangular display of 9.0 × 9.0°, a modulator frequency of 0.45 c/deg, and a temporal frequency of 7.5 Hz. In the candidate second-order frames, binary random noise (−1, +1) was multiplied by 0.25 and 0.75 to produce a 50% contrast modulation in alternate vertical stripes. In the luminance frames, either 0.25 or −0.25 was added to each pixel intensity in alternate vertical stripes. The five rows in Figure 5c illustrate the five frames of such a display. Using Figure 5c as an example, when motion is perceived to the right (slant from upper left to lower right in the figure) it means that α is too small; a sufficiently large α would produce apparent motion in the opposite direction, and vice versa. The critical α for motion ambiguity α_c was determined by the method of constant stimuli. Four observers viewed the displays.

Results:

For all observers, it was possible to completely eliminate consistent directional apparent motion in these displays by suitable choice of α_c. The measured α_c were 1.32, 1.39, 1.47, and 1.54 (mean = 1.43), indicating that, in the average, black is represented with 1.43 times the magnitude of white for these stimuli.

Obviously, there is very considerable black–white asymmetry in the stimuli (e.g., Figure 5b) used to demonstrate second-order motion. Surprisingly, in stimuli that are near threshold for second-order motion, the first-order contamination is below the first-order motion threshold (Lu & Sperling, 2001a), i.e., it is invisible. However, in suprathreshold second-order stimuli, first-order contamination can be very substantial.

Experiment 6. First-order contamination in second-order stimuli with dynamic carriers

The procedure in Experiment 6 is identical to that of Experiment 5 except that each new frame has a new, independent random binary texture.

Results:

For four observers, it was possible to completely cancel apparent motion with appropriate α_c of 1.28, 1.32, 1.38, and 1.59 (mean = 1.39). It had been argued that there are no “first-order artefacts in second-order motion” with a dynamic carrier (Smith & Ledgeway, 1997, p. 45). However, in Experiment 6, within measurement error, the contribution of the first-order motion system due to uncorrected black–white imbalance was the same in both static and dynamic stimuli. Again, with a relative black/white ratio of 1.39, the first-order contamination in near threshold second-order stimuli would be below first-order threshold (Lu & Sperling, 2001a). In suprathreshold second-order stimuli, first-order contamination could be substantial.

Experiment 7. First-order contamination in texture slant

To measure black–white asymmetry in a static texture image, Experiment 7 uses an ambiguous texture-slant paradigm, in which the perceived slant direction indicates the nature of the distortion. The texture stimulus is basically a variation in x, y space of the x, y, t motion stimuli of Experiment 6. A large square filled with binary texture of medium contrast is divided into eight rows (Figure 6c). Odd number rows have a square-wave texture-contrast modulation imposed. That is, they are divided into eight squares alternating between high and low contrast, all squares having the same average luminance. In even rows, the texture-contrast is the same throughout but the squares alternate between higher and lower luminance. The phase shift between successive rows is 90°, so that the phase-shift between successive odd rows or between successive even rows is 180°. By analogy to Experiments 5 and 6, if black and white were represented with equal magnitude in the visual system, texture slant would be perceived at +63° and −63° with equal likelihood. However, if there was black–white asymmetry, there would be consistent bias in judging texture slant. (Note: The bias in viewing a printed version of Figure 6c results from a combination of printing and visual distortions. The printing distortion can be judged by viewing Figure 6 at such a distance that the individual pixels can no longer be resolved. With undistorted printing, slants of +63 and −63° would have equal perceptual strength. Any change in perceived slant upon closer viewing is due to visual biases.)

Figure 6.

An ambiguous random texture stimulus for testing first-order contamination in second-order texture stimulus with a dynamic random texture carrier (Experiment 6). (a) Intensity profile of one row in a random-pixel stimulus with pure contrast modulation. In alternate blocks, binary random noise (−1, +1) was multiplied by 0.25 and 0.75 to produce a 50% contrast modulation. (b) Intensity profile of one row of a with added luminance modulation. In alternate blocks, either 0.25 or −0.25 was added to each pixel intensity. Blocks of higher and lower (average) luminance alternate, but the absolute contrast variation is the same throughout. (c) Five frames of a motion display; even-numbered frames are of type (a), odd-numbered frames are of type (b). Every row contains a different random texture. The five rows represent the five frames of the test stimulus for determining first-order contamination in dynamic-noise, second-order motion. As in Figure 5, the apparent slant (+ or −63°) represents a printing plus intrinsic visual system bias.

Procedure:

To measure black–white asymmetry in the stimulus of Figure 6c, the contrast of all black pixels is multiplied by 1/α and observers report the direction of apparent slant (+ or −63°). A method of constant stimuli was used to determine the value of α_c for which the perceived texture slant was ambiguous. The spatial dimensions of the display were identical to those of the motion displays of Experiment 5 and the exposure duration was 200 ms.

Results:

For three observers, the values of α_c were 1.32, 1.39, and 1.39 (mean = 1.36).

Experiment 8. Gestalt grouping

To measure the influence of perceptual black–white asymmetry on perceptual grouping, Experiment 8 uses an ambiguous slant paradigm. Gestalt psychologists (Wertheimer, 1912) studied how the perceptual system groups elements into a coherent percept of a whole (a Gestalt). Figure 7 depicts a pattern composed of black and white diamonds on a neutral background. The black diamonds form −45° stripes, the white diamonds +45° stripes. The question is which set of stripes (black or white) dominates the percept? This paradigm is based on a classic Gestalt paradigm that has been analyzed extensively in the motion domain by Burt and Sperling (1981) and in the spatial domain by Kubovy, Holcombe, and Wagemans (1998). When black decrements and white increments are of the same physical magnitude (contrast is ±75%), the black lines clearly dominate the percept. The psychophysical measurement procedure used the method of constant stimuli to determine the values of α for which slant was completely ambiguous (balanced). The size of the stimulus was 6 × 6° with each black/white dot subtending 0.4 × 0.4°. The duration of the stimulus was 200 ms.

Figure 7.

Stimulus for Experiment 8: An ambiguous pattern for Gestalt grouping. When printed correctly with equal luminance increments and decrements, the visual black–white asymmetry causes the black diamonds, which form −45° stripes, to have greater strength than the white dots at +45°.

Results:

For three observers the values of α were 1.11, 1.19, and 1.67 (mean is 1.32). That is, the contrast of black diamonds (relative to white diamonds) must be divided by 1.32 to make the black and white stripes equally salient.

Experiment 9. Perfect sine waves

Following the discovery of visual channels (Campbell & Robson, 1968; Kuffler, 1953) and the advent of linear systems theories of early vision, sine wave gratings have become the most important stimuli in visual psychophysics and neurophysiology (Figure 8). Conventionally, a luminance sine wave grating is defined in physical terms, i.e., the black valleys and white peaks are equally different from the mean luminance level but have opposite signs. Experiment 9 asks if there is there a black–white asymmetry that must be overcome to produce a perceptually symmetric sine wave grating.

Figure 8.

A stimulus for Experiment 9: A physically perfect sine wave grating. When printed correctly, the black stripes are perceived to be obviously wider than the white stripes.

Procedure:

To produce a perceptually symmetric sine wave grating, we begin with a physically perfect vertically oriented sine wave grating of contrast 0.47 and a spatial frequency of 0.45 c/deg, viewed in a window 9 × 9° of visual angle. Different distortions of the physically perfect sine wave were produced by multiplying the contrast of all the black pixels by a factor 1/α. The method of constant stimuli was used with α taking 20 values ranging from 0.71 to 1.67. Each presentation had a randomly chosen α and lasted 300 ms. The observer judges whether or not the white stripes are narrower than the black stripes (relative to an ideal, symmetrical sine wave). The α_c value corresponding to 50% judgments on the psychometric function is defined as the α_c that produces a perceptually symmetric sine wave grating.

Results:

For our four observers, the values of α were 1.18, 1.22, 1.25, and 1.28 (mean = 1.23): To produce a perceptually perfect sine wave grating, the contrast of the black portion had to be reduced by a factor of 0.81 (1/1.23).

Experiment 10. Second harmonics in imperfect sine waves

To measure consequences of perceptual black–white asymmetry in a physically perfect sine wave grating (other than merely appearance), Experiment 10 investigates the influence of black–white distortion on motion perception. The perceptual distortion of sine waves caused by black–white asymmetry is equivalent, in a Fourier series representation, to adding even harmonics to the original sine wave. That is, when the original sine wave frequency is f_x, the black–white asymmetry produces waveform that, in addition to f_x, contains diminishing amounts of frequencies 2f_x, 4f_x, 6f_x, .... The magnitude of these distortion-produced sine waves is predicted from the black–white asymmetry.

We tested for the presence of the 2f_x distortion product in an f_x sine wave by means of a three-frame motion sequence (Figure 9). Frame 1 is a 2f_x spatial sine wave, Frame 3 is its negative. These frames alone are motion-ambiguous. Frame 2 contains an f_x sine wave of intermediate phase. When the f_x sine wave contains a 2f_x distortion product, motion will be seen in the rightward direction if black has a bigger representation than white, and in the leftward direction otherwise. If there was no distortion product, there would be no common frequencies and therefore no apparent motion.

Figure 9.

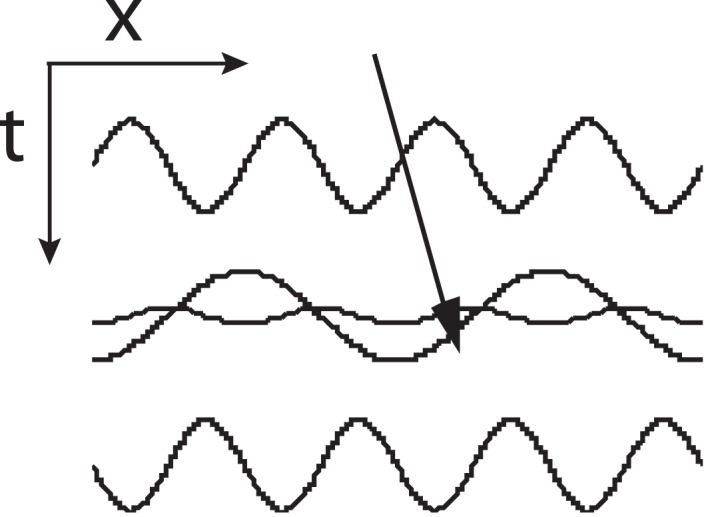
Stimulus for Experiment 10: A three frame display for demonstrating perceptual distortion in the second frame. Frames 1 and 3 contain only 2f_x and −2f_x, respectively. By themselves, they cannot produce motion. Frame 2 contains a physically perfect sine wave f_x offset by 90° relative to Frame 1. When f_x is perceptually distorted by perceptual black–white asymmetry in early visual processing, it will acquire a second harmonic, 2f_x (indicated by dotted line) which, in subsequent motion processing, produces apparent motion in combination with Frames 1 and 3.

Procedure:

In Experiment 9, the judgments of perfect sine wave were made at a sine wave contrast of 47%. This is too large a contrast for easy motion judgments, so the contrast of the f_x sine wave in Frame 2 was reduced to 4.0% and that of 2f_x in Frames 1 and 3 was 4.0%. The spatial frequency of the sine wave (f_x) was 0.45 c/deg, the viewing window was 9 × 9°, and the duration of each frame of the three successive frames was 33.3 ms. The full presentation was equivalent to 3/4 of a cycle of a 7.5 Hz motion stimulus.

Three observers viewed the test stimulus (Figure 9). As before, the magnitude of the black-attenuation was varied to determine the point of minimum motion—i.e., where the observer's internal representation of black was of the same magnitude as that of white. All even harmonics higher than 2f_x are irrelevant in this paradigm because they would have phase shifts of 180 or 360°.

Results:

For three observers, the point of minimum motion corresponded to attenuations of 0.75, 0.72, and 0.70 (average 72%), equivalent to values of α of 1.33, 1.39, and 1.43 (mean = 1.38).

For the two observers who also judged the perfect static sine wave in Experiment 9, the motion procedure indicated a slightly larger motion black–white asymmetry in Experiment 10 than static black–white asymmetry in Experiment 9. We expect black–white asymmetry to be smaller for the 4% contrast stimulus of Experiment 10 (motion) than for the 47% contrast static sine wave of Experiment 9 because α is a monotonically increasing function of stimulus contrast (Experiment 12). For these observers, the difference in their average canceling-attenuation (83%, 72%) in Experiments 9 (sine contrast 47%) and 10 (sine contrast 4%) is unexpected, and suggests that different perceptual processes may be operating in the two experiments. All in all, the presence of the 2f components indicates that predictions based on the black–white asymmetry, such as the distortion-induced Fourier components, do indeed occur.

Experiment 11. Differential intensity thresholds: First-order intensity discrimination

Experiment 1 measured detection thresholds for a single increment or decrement Gaussian blob flashed against a uniform background. Experiment 11 measures the ability of observers to discriminate the flash of a fairly high contrast blob from an even higher contrast blob flashed successively on a uniform background (Figure 10).

Figure 10.

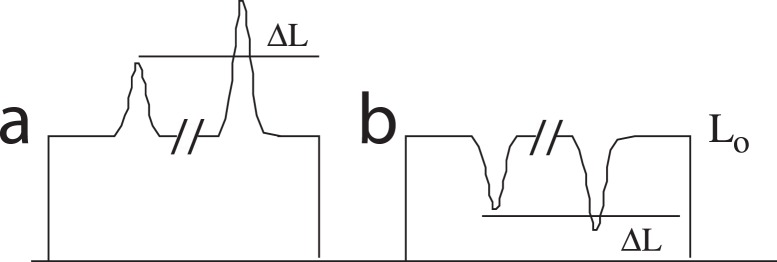
Stimuli for Experiment 11: Testing discrimination between two decrement Gaussian-windowed flashes (a) and between two increment flashes (b).

Procedure:

Except for the fact that there are two, not one, stimulus flashes on each trail, the stimulus conditions are the same as in Experiment 1. The two flashes are separated by 0.5 s. Here we also use a different definition of the various luminance levels: The maximum attainable luminance is designated as 2.0, the minimum light level as 0, and the mean light level is 1.0. A light flash is a Gaussian-windowed 50 ms increment of a spatial Gaussian blob which produces an intensity of 1.75 or to 1.75 + Δ_w (light flash). The visual angle subtended by the flash was σ = 0.88° and the overall viewing area was 21 × 17°. Flashes of 1.75 and 1.75 + Δ_w were presented in random order in a two-interval forced choice paradigm. The observer's task was to say which interval of the pair contained the more intense flash. A method of constant stimuli was used to find the value of Δ_w that yielded 75% correct responses. A similar experiment was conducted with dark flashes of 0.25 and 0.25 − Δ_b.

Results:

For three observers, the average Δ_w = 0.061 and Δ_b = 0.018. Δ_w/Δ_b is about 3.23 (2.38, 3.13, and 5.00). The huge Δ_w/Δ_b asymmetry (3.23) is much larger than the other black–white asymmetries observed so far (typically 1.28). It indicates that two decrements were enormously more discriminable than two equal-size increments. It is similar to a related asymmetry observed by Kingdom and Whittle (1996) with low-frequency, but not high-frequency, spatial sine wave displays. The previous experiments involved differences between effectiveness of increments and decrements relative to the same background luminance for each. In Experiment 11, the luminance of the reference stimulus for increment discrimination was seven times higher than for decrement discrimination (1.75 versus 0.25).

Summary and discussion

Ten widely different testing procedures, spanning a large range of perceptual processes, show that when black stimuli have equal energy deviations from the background as white stimuli, the black stimuli are represented with a larger magnitude in the visual system, typically a factor of 1.28 (Table 1). We proposed a one-parameter summary of each observation. Assume that the magnitudes of the internal representations of white areas of a stimulus (areas with luminance greater than the mean) are represented accurately, output = input, then the internal representation of a black areas (areas with luminance less than the mean) is output = α × input, where α typically is about 1.28 but varies from 1.08 to 1.67 depending on experimental conditions and observers. The black–white asymmetry with α = 1.28 is not a major distortion, but it was easily demonstrated for every observer in every psychophysical procedure we tried.

Table 1.

Summary table of estimated values of α. Notes: ^a observer 5; ^b observer 6. Lum: Luminance; incr: increment; decr: decrement; Mex: Mexican.

Experiment	Contrast	S1	S2	S3	S4	Mean
1. Lum incr vs. decr	0.02	1.08	1.10	1.14		1.10
2. Mex hats	0.10	1.39	1.14	1.19		1.24
3. Flicker cos(2nft) + cos(4nft)
4. Motion sin(2nfx) + sin(4nfx)	0.02	1.12	1.14	1.32		1.19
5. Second motion static	0.75	1.32	1.47	1.39	1.54	1.43
6. Second motion dynamic	0.75	1.39	1.32	1.28	1.59	1.39
7. Second texture slant	0.75	1.39	1.32	1.39		1.36
8. Gestalt grouping	0.75	1.67	1.11	1.19		1.32
9. Static sine wave	0.47	1.22	1.18	1.25	1.28a	1.22
10. Sin x + sin 2x motion	0.040		1.33	1.43	1.39b	1.38
Mean		1.32	1.23	1.29		1.28

To cancel the black–white asymmetry, we divide the contrast of the black pixels by α. A candidate stimulus is generated, and the deviation from the mean luminance of pixels with amplitudes less than the mean was reduced by 1/α, where the value of α is the experimentally determined value that equalizes the effectiveness of black and white pixels.

The existence of a 28% black–white asymmetry in visual perception has pervasive consequences, as it invades nearly every psychophysical or neurophysiological procedure in which intensity is involved. For example, when a sine wave of frequency f_x and amplitude A is subjected to the 28% distortion, it generates a series of distortion-product sine waves beginning with frequency 2f_x with amplitude 0.14A, as well as a mean level reduced by 0.14A. Whether or not these distortion by-products are critical depends on the particular experiment. For example, with regard to the current debate on first-order contamination in second-order stimuli, the computational rule (and data) implies that there is indeed first-order contamination in all uncorrected second-order stimuli.

Previous parametric studies of the black–white asymmetry have been conducted mainly with the paradigm of Experiment 1, first-order detection of circular flashes. The magnitude of the black–white asymmetry diminishes with increasing background illumination (Patel & Jones, 1968; Short, 1966). At the minimum luminance at which it can be measured (when completely turning off the background intensity produces a threshold decrement) the black/white effectiveness ratio α is 2.4 (Short, 1966) and 2.2 (Patel & Jones, 1968). At high luminance, α(c) asymptotes at values greater than 1.2 (Short, 1966), 1.2 (Patel & Jones, 1968), and 1.1 (Legge & Kersten, 1983). The greater the maximum flash excursion away from background intensity, the greater the black–white asymmetry. Thus, the asymmetry is greater in a detection procedure using brief and/or small-area flashes than in detection of long-duration or large-area flashes. However, because contrast threshold amplitude is confounded with mean luminance level, we can't simply attribute changes in α to changes in mean luminance. Occasionally, investigators have reported in their conclusions or summary that no black–white asymmetry exists (Herrick, 1956; Rashbass, 1970; Roufs, 1974). In cases where the experimental data are actually presented, it appears to us that a black–white asymmetry actually exists, merely that was smaller than other effects of interest to the author and therefore neglected (Herrick, 1956; Roufs, 1974). Finally, there are occasional reports of isolated observers who appear to have a very slightly reversed black/white asymmetry in a particular condition. Selective attention to different colors (e.g., black or white) in a display may also alter their relative salience in visual processing (Blaser, Sperling, & Lu, 1999; Lu & Sperling, 1995).

Two experiments to investigate the nature of the black–white computation

How does black–white asymmetry, i.e., α, depend on stimulus contrast? Is black–white asymmetry a consequence of greater internal representation of black or less internal representation of white in the visual system? In this section, we derive a computational rule of black–white asymmetry in answering these questions. Both Experiments 12 and 13 were run on the Nanao monitor.

Experiment 12. Black–white asymmetry as a function of stimulus contrast

In Experiment 12, we use an ambiguous second-order motion stimulus to measure α as a function of stimulus contrast. The paradigm is similar to that of Experiment 6 (dynamic carrier).

Procedure

As shown in Figures 11a and b, square-wave texture-contrast gratings were created by modulating the contrast of binary random pixel noise in odd frames. In the high contrast regions, the pixels take contrast ±c with equal probability; in the low contrast regions, the pixels take contrast 0. The contrast c took one of the values of 0.03, 0.06, 0.12, 0.24, 0.48, and 0.96 in different conditions. These texture frames were sandwiched with luminance gratings of 8% modulation in even frames. In different trials, the gratings shift either +90° or −90° between successive frames.

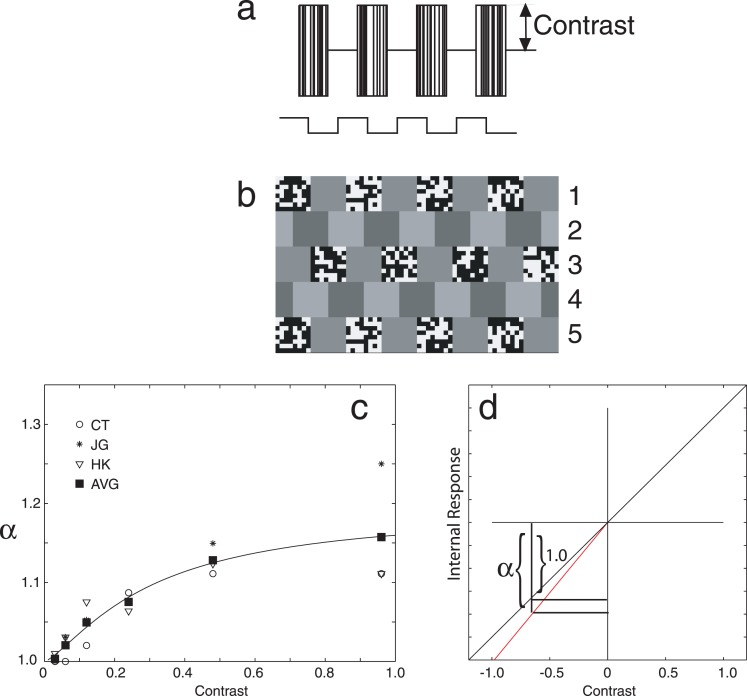
Figure 11.

Measuring perceptual black–white asymmetry α as a function of stimulus contrast. (a) Intensity profiles of one texture frame and one luminance frame of the motion stimulus. (b) Slices of five consecutive frames of the motion stimulus. (c) The data of Experiment 12 and the continuous derived function α_c(c) as a function of stimulus contrast. (d) A possible internal representation of contrast that is consistent with α_c(c).

As discussed in Experiment 6, if there was no luminance distortion in the texture frames, one would not perceive linear motion in a display like Figure 11b because, within the odd frames alone (binary texture), the phase shift is 180°, which is motion-ambiguous. Similarly, within the even frames alone (uniform luminance stripes) the phase shift is also 180°. However, if there was a luminance distortion product in the texture frames due to a greater representation of black than white, then consistent first-order motion would be perceived because all frames would contain luminance modulation.

To eliminate the luminance distortion component in a texture frame, the contrasts are transformed. Let c(x, y) be the original contrast modulation of pixel x, y (Equation 2); c′(x, y) is the transformed contrast modulation. For c(x, y) < 0, c′(x, y) = (1/α) × c(x, y), 0 < (1/α) < 1 . That is, pixels with negative contrast, have their contrast reduced by (1/α). The contrast of pixels with zero or positive contrast is unchanged. The goal is to determine critical α_cs that eliminate perceived motion as a function of contrast c.

The motion display was instantiated with a pixel size of 3.75 × 3.75 min in a rectangular display of 4.0 × 8.0°, a modulator frequency of 0.5 c/deg, and a temporal frequency of 10 Hz. The five rows in Figure 11b illustrate the five frames of such a display. Three observers viewed the displays, and α_c (critical α for motion ambiguity) was determined by the method of constant stimuli for each of the six stimulus contrast used, using the same procedure as in Experiment 5. All experimental conditions were interleaved.

Figure 11c plots α_c as a function of stimulus contrast for all the observers and their average. The following function:

was fit to the average data. The best fitting function has the following parameters: α₀ = 0.19, c₀ = 0.30, and η = 1.33, with r² = 0.9940. In other words, for the average of the three observers, and for these stimuli, α_c is 1 for very small contrasts, α_c asymptotes at 1.19 for very large contrasts, and α_c reaches half of its asymptotic value when c = 0.30.

Equation 4 provides a good description of α_c(c) as a function of c. This implies that α_c is a saturating function of stimulus contrast. The functional form (Equation 4) provides a computational rule for the perceptual black–white asymmetry produced by this particular stimulus.

Experiment 13. Histogram analysis of black–white asymmetry

In Experiment 13, we varied pixel contrast histograms in texture-modulation gratings to investigate a functional property of internal representation of black and white: Is there expansive black representation or compressive white representation, or both?

Procedure

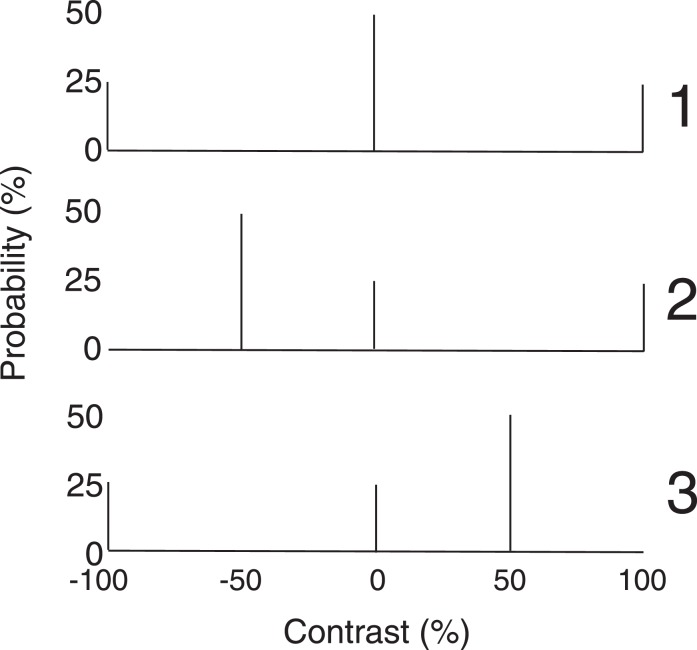
The experimental procedure was identical to that of Experiment 12 except that one of three different pixel contrast histograms was used for the texture region in different conditions (Figure 12). Every texture histogram was composed of pixels with just three contrasts chosen with one of the probability distributions described in Table 2.

Figure 12.

Three histograms for investigating the linearity of the internal representation of contrast. In the experimental displays, the negative contrasts were divided by α_ci, α_c2, or α_c3 in order to determine the α_ci value that maximized slant ambiguity.

Table 2.

Probabilities of pixel contrasts in Experiment 13 in the textured areas of the three ambiguous motion stimuli of Figure 12; decrement contrasts were divided by α_c1, α_c2, and α_c3.

Stimulus	Pixel Contrast
	−0.96	−0.48	0	0.48	0.96
1	0.25		0.50		0.25
2		0.50	0.25		0.25
3	0.25		0.25	0.50

The method of constant stimuli was used to estimate the critical α_c that eliminated perceived motion from the stimuli α_c1, α_c2, and α_c3 in all three experimental conditions. Four observers participated in this experiment.

Deriving the functional form f(c) of the internal representation of contrast

Let the internal representation of stimulus contrast used by the first-order motion system be f(c). That no motion was perceived at critical α_c, implies that the texture-modulation gratings did not contain any luminance modulation—the internal representation of the mixture of the pixels in the texture regions averaged to zero. Therefore:

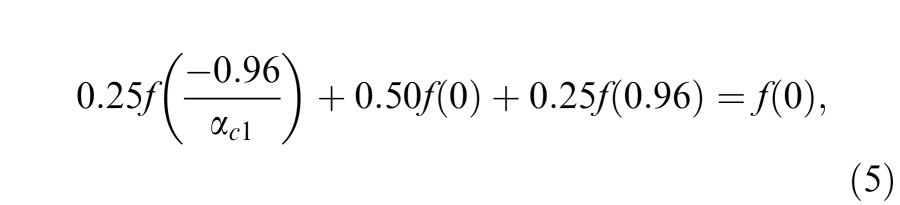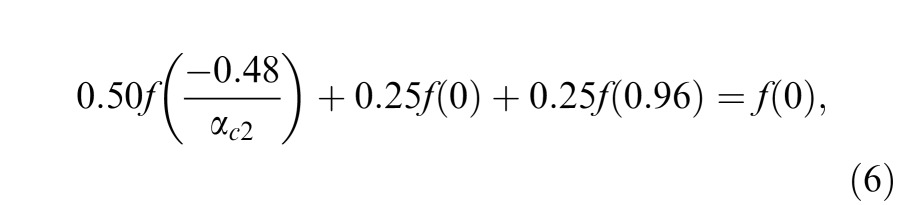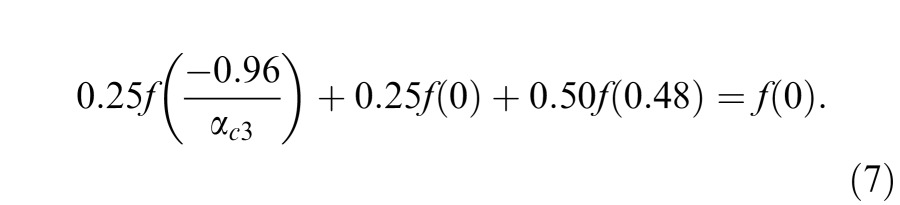Because f(0) = 0 by definition, Equations 5–7 reduce to:

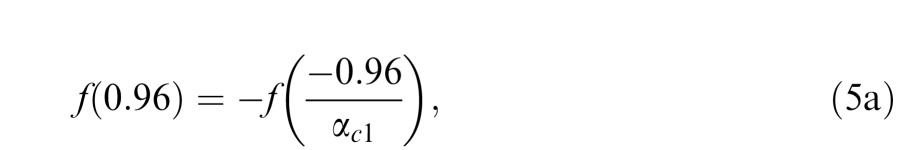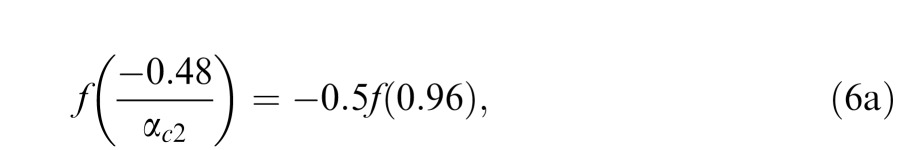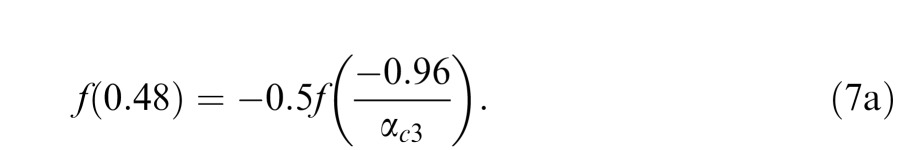Combining Equations 5a and 7a, we have:

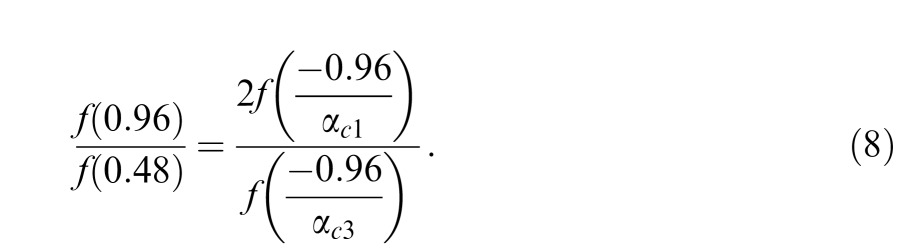Combining Equations 5a and 6a, we have:

The estimates of α_c1, α_c2, and α_c3 indicate the curvature of f(c).

Results

Table 3 shows the critical αs for the three observers. For all the observers, α_c1 is the same as α_c3 within measurement error. If we take α_c1 and α_c3 as identical, Equation 8 leads to the conclusion that f(0.96)/f(0.48) = 2.0. In other words, the function f(c) is approximately linear for c > 0—the magnitude of the internal representation of contrast 0.96 is twice that of contrast 0.48.

Table 3.

Black–white asymmetries for both black and white extreme contrasts α_c1, for extreme white contrasts only α_c2, and for extreme black contrasts only α_c3.

Observer	αc 1	αc 2	αc 3
CT	1.08	1.00	1.11
JG	1.22	1.11	1.25
HK	1.21	1.09	1.25

On the other hand, for all the observers, α_c2 is significantly less than α_c1 [t(2) = 6.008, p < 0.015]. Because f(−0.96/α_c1)/f(−0.48/α_c2) = 2 (Equation 9), this implies f(−0.96/α_c1)/f(−0.48/α_c1) > 2. In other words, the function f(c) is expansive when c < 0—the magnitude of the internal representation of contrast −0.96 is more than twice that of contrast −0.48. We conclude that the black–white asymmetry is due to a nonlinear concave-down internal representation of black whereas, following the same reasoning, the internal representation of white would be slightly compressive, but linear within measurement error.

General discussion

The ubiquity of black–white asymmetry suggests it occurs early in visual processing, i.e., before the visual processing of motion, flicker, slant orientation, grouping, brightness, and the other processes investigated here that exhibited black–white asymmetry. We consider multiple possible origins, and divide them into two classes (a) within retinal cones and (b) in subsequent stages that have ON- and OFF-center neurons (Kuffler, 1953; Schiller, 1992).

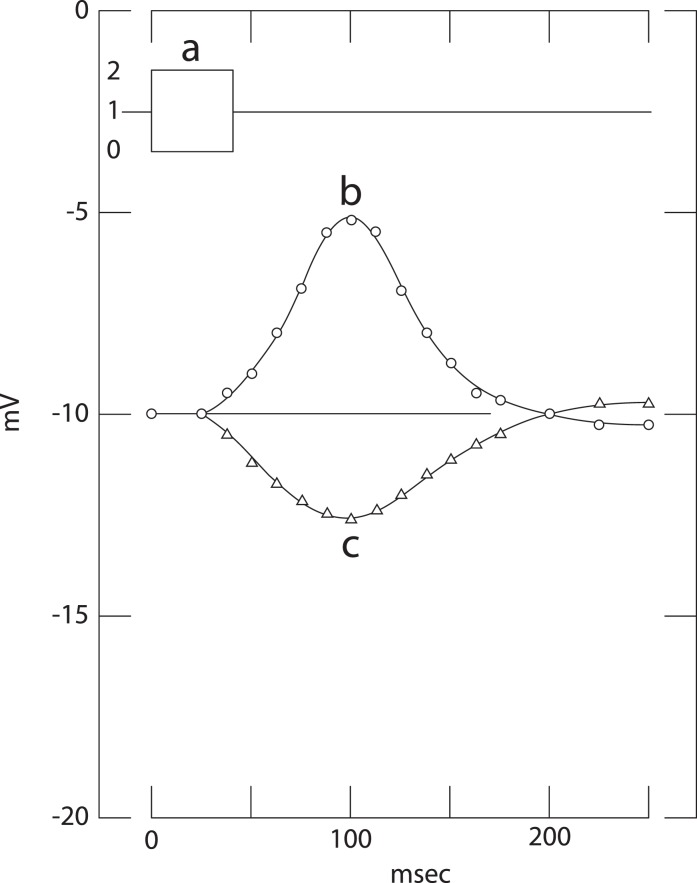
Evidence for a cone origin

Classical electrical recordings of cone responses in the turtle retina found that “the depolarization resulting from the gap of darkness is much larger than the hyperpolarization resulting from the [equal amount of] added light” (Baylor, Hodgkin, & Lamb, 1974a, p. 714). This is illustrated in Figure 13. If retinal cones were to respond asymmetrically to increments and decrements, then one would expect black–white asymmetry to be universal.

Figure 13.

Effects of interrupting or brightening a steady light on membrane potential in turtle long-wavelength cones. The cones were stimulated with a steady light of intensity equivalent to 3.74 × 10⁴ photons μm⁻²s⁻¹ at the optimum wavelength of 644 nm. (a) The steady light was turned off for 40 ms or the intensity was doubled for 40 ms. The resulting changes in membrane potential were averaged in a few frames and plotted (continuous lines, open symbols), (b) decrement, (c) increment. (Adapted from Figure 14, Baylor, Hodgkin, & Lamb, 1974a, p. 714).

He and MacLeod (1998) suggested that black–white asymmetry in human vision originated in an early stage of visual processing that had at least the resolution of cones. They used lasers to project extremely high spatial frequency gratings on their observers' retinas. Although the gratings were too fine to be perceptually resolved, the perceived brightness of an area covered by the grating was lower than the brightness of an equal luminance background. Further, grating brightness diminished in proportion to increases in grating contrast. He and MacLeod (1998) observed that the induced brightness change, measured in terms of grating contrast (i.e., normalized brightness change), was independent of the grating's mean luminance over the range of 200–20,000 td.

He and MacLeod (1998) attributed their black–white asymmetry to early visual stages with cone resolution because, according to their assumptions, the high spatial frequency grating could not be resolved by later stages in the visual system. Their phenomenon is similar to the black–white asymmetries reported here except that He and MacLeod's observers judged the zero-frequency (so called “DC”) spatial frequency component—the overall brightness—versus our observers who judged aspects of the display such as slant or direction of motion that correspond to fundamental frequency components.

He and MacLeod (1998) propose a theory based on feed-forward gain control (Sperling & Sondhi, 1968), quite similar in concept to the theory originally proposed by Baylor, Hodgkin, and Lamb (1974b) to account for their turtle cone observations. In the He and MacLeod theory, the gain control has a time constant of 10 ms. These assumptions lead to the peculiar property that the model's response to a spatially varying pattern would have diminished to 0.050 of its initial value in 30 ms and to 0.007 in 50 ms. In the He and MacLeod theory, output of the model to impulse flashes and to long duration stimuli is virtually indistinguishable; how this can be made consistent with visual experience is an unanswered challenge.

Application of the He–MacLeod theory to the present experiments

The essence of He and MacLeod's (1998) theory (feed-forward gain control) is captured by their equation:

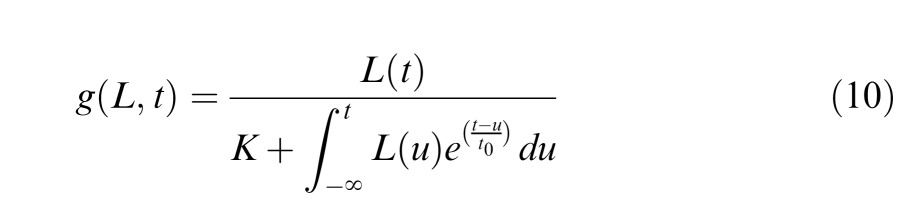where L(t) is stimulus luminance as a function of time t, g(L, t) is the internal representation of luminance, K is a constant, and t₀ is the time constant of the exponential decay of luminance persistence. In order to determine whether the He–McLeod theory was compatible with our data, we applied their theory to the procedures of Experiment 12 to generate a prediction relating our parameter α to stimulus contrast.

In Experiment 12, observers eliminated perceived motion from the displays by reducing the modulation amplitude of the black pixels, thereby canceling the luminance distortion product that produced first-order motion perception in these texture grating sequences. In this procedure, when motion perception has been eliminated, white pixels differ from the mean luminance by ΔL but black pixels differ from the mean by only ΔL/α_c, α_c > 1. Motion is eliminated when the motion system's perceived luminance g(L) of the untextured stripes composed of gray pixels equals the perceived average luminance of the textured stripes composed of white and black pixels:

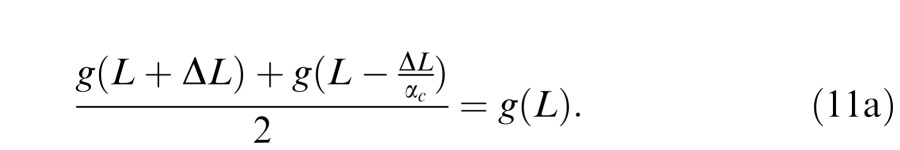Substituting g(.) from Equation 10 into Equation 11 yields:

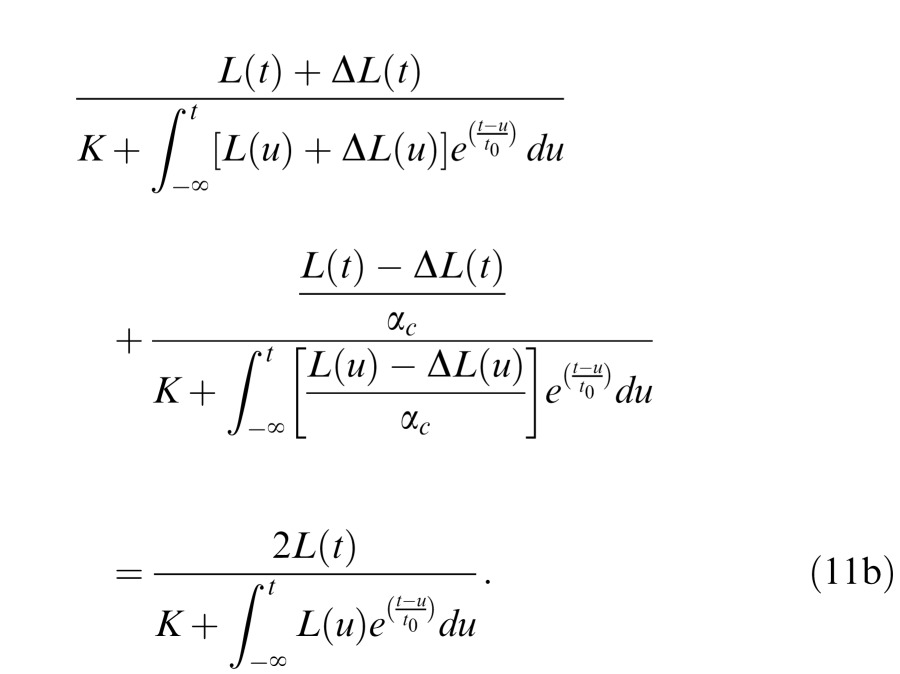Algebraic simplification of Equation 11a leads to:²

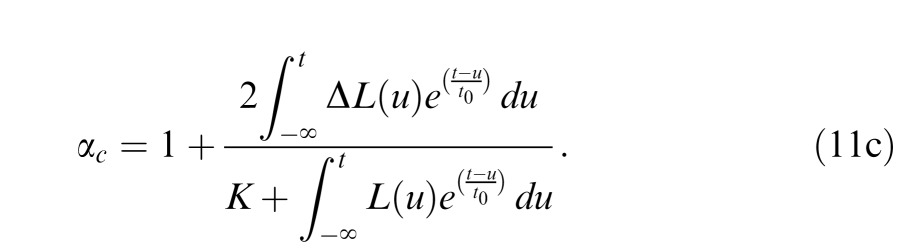For L ≫ K,

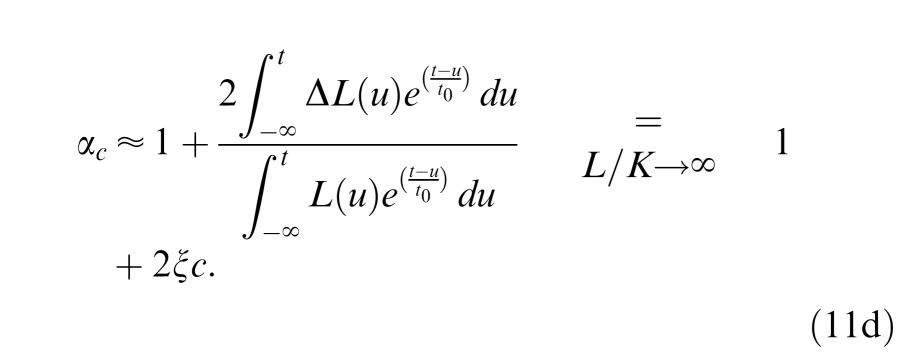The constant ξ is defined by Equation 11e:

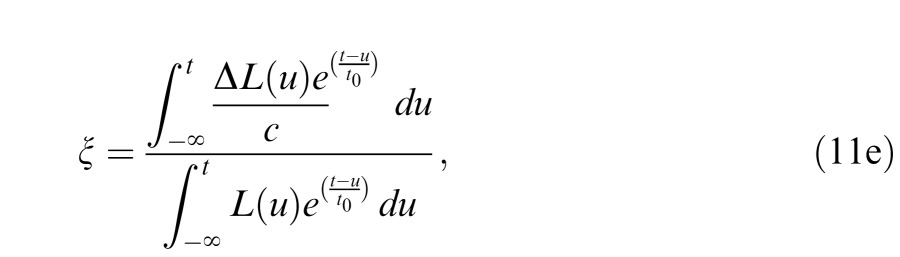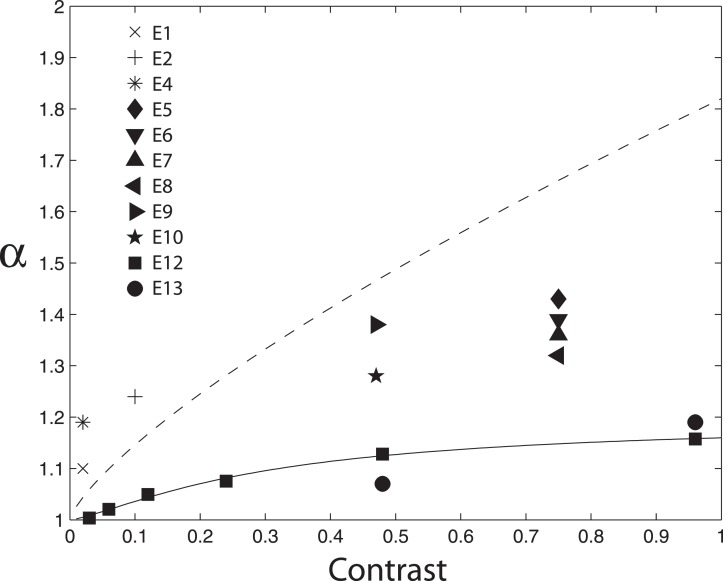
which for the 15 Hz stimulus and 10 ms theoretical receptor feed-forward time constant has the value ξ = 0.48. The theoretical linear relation of α with contrast c in Equation 11d that we derived from He and MacLeod's retinal model is at odds with their empirical observations (He & MacLeod, 1998, Figure 5) which can be expressed as α = 1 + 0.82c^0.75. Additionally, in their empirical observations when c ≈ 0, α ≈ 1.0; when c = 1.0, α = 1.82. This variation of α with stimulus contrast that we derive from He and MacLeod's data is much greater than the variation in our observed α values in Experiments 1–10 (Figure 14). The obvious conclusion of this exercise is that there is black–white asymmetry both in our experiments and in He and MacLeod's (1998) experiment, but these asymmetries are governed by different rules or parameters.

Figure 14.

Estimated α values versus stimulus contrast in the twelve experiments. Each plotted data point is the mean α value for all the observers in the particular experiment. The solid curve represents Equation 4, an empirical fit to the data of Experiment 12. The dotted curve represents the power-law relationship between α and contrast derived for the data of He and MacLeod (1998).

Black–white asymmetry in stages beyond the retinal cones

Single-channel versus dual-channel representations

The output of visual receptors, indeed nearly all receptors, is not a linear function over wide ranges of the input but necessarily is concave down, i.e., the receptor output at first saturates slightly and ultimately completely for sufficiently large inputs. From a concave-down input-output function, it follows that negative perturbations in the input will inevitably produce a bigger perturbation in the output than equal magnitude positive perturbations. In the visual system, negative perturbations in output are subsequently recognized as darkening or black and positive perturbations as white. Immediately subsequent to receptors, however, negative and positive perturbations from the local mean input intensity are represented in different neurons that function like half-wave rectifiers. Negative perturbations from mean intensity are represented in so-called OFF-center neurons (negative half-wave rectifiers), whereas positive perturbations are represented in ON-center neurons (positive half-wave rectifiers) (Kuffler, 1953; Schiller, 1992) and recognized as white. The advantage of the dual channel ON–OFF system of representation versus the single-channel receptor representation is that in the dual channel representation only deviations from the local mean luminance are represented, and little or no energy is consumed in representing the mean luminance. Because neural firing rate is inherently a positive number, representing both positive and negative excursions in a single neuron would require representing them as deviations from a nonzero mean output level. Therefore, in single-channel receptors, representing the mean luminance wastes considerable energy resources.

Retinal ON-center and OFF-center neurons have radially-symmetric center-surround receptive fields. This easily recognizable dual-channel half-wave organization of neural signals into two parallel pathways, an OFF system for black and an ON system for white, is exclusively maintained through four successive stages of neural processing: retinal bipolar cells, retinal ganglion cells, lateral geniculate neurons, and input neurons in cortical area V1 (layers 4cα and elsewhere). Many psychophysics experiments have suggested separate on and off pathways for processing luminance increments and decrements (Bowen, 1995; Chichilnisky & Wandell, 1996; Tyler, Chan, & Liu, 1992).

ON-center and OFF-center channels are not perfect mirrors of each other

While the strength of signal representation is monotonic with input strength in the ON and OFF systems, the two input-output functions need not be—indeed cannot be—exactly equal. A priori, depending on the particular subset of neurons involved in principally conveying information from a particular stimulus, the post-receptor black–white asymmetry could favor either black or white and it could be greater or smaller than receptor black–white asymmetry and it could have a different functional form. The saturating curve of α as function of contrast in Experiment 12 demonstrated that the functional form of receptor-plus-post-receptor black–white asymmetry differs in form from the He–MacLeod black–white receptor asymmetry in which α varies linearly with contrast.

Although there is inevitably some black–white asymmetry in the post-receptor channels, this does not rule out more complex processes in the cones themselves, i.e., cone outputs that depend on spatial interactions or black–white asymmetries that depend on temporal dynamics of the input. The values of α in the 10 of our 13 experiments that use suprathreshold stimuli are generally smaller than the α values we derived from the He–MacLeod (1998) receptor data. This would require either positive black–white asymmetry in post receptor changes (white represented more strongly than black) or, more likely, different αs in the receptors themselves depending on the stimuli used.

Scott-Samuel and Georgeson (1999) used a nulling procedure similar to Experiments 5 and 6 to measure luminance distortion in contrast-modulated (CM) patterns, formed by modulating contrast variations on higher-frequency carriers. They found that the amplitude of the distortion product increased with the temporal frequency of the motion stimuli and with the contrast of the CM patterns. In log-log plots, the slope of the amplitude of the distortion product versus CM contrast function is 1.7. This translates into the following relationship: α = 1 + kc^0.7, where k ranges from 0.01 to 0.05 in different temporal frequency conditions. The maximum amplitude of α is lower in Scott-Samuel and Georgeson (1999) compared to the data in Figure 14, probably due to the different spatial frequency of the carrier used in their study.

Following the prodding of an anonymous referee, we derived the relationship between α and c from the Naka–Rushton equation (Naka & Rushton, 1966):

where L is the input luminance, R_max is the maximum response, and S is the saturation point. Going through similar derivation steps starting from Equation 11a, we derived the following relationship (Appendix B):

where L₀ is the mean luminance and c is the stimulus contrast. In other words, the Naka–Rushton equation predicts that α is a linear function of c, similar to the He–MacLeod theory but inconsistent with our (and their) data: Fitting a linear model to the data in Figure 11 resulted in an r² of 0.8006, significantly lower than r² = 0.9940 from the nonlinear model (Equation 4); A nested model tests rejected the linear model (F[2, 9] = 145.05, p < 0.00001).

Summary and conclusions

The visual effectiveness of areas of a stimulus that are darker than the mean luminance (decrements, black) was compared to the effectiveness of areas lighter than the mean luminance (increments, white) in 10 experiments involving different stimuli and responses. In all experiments, the magnitudes of the stimulus decrements were divided by a factor α, relative to the magnitudes of the increments. In each experiment i and for each observer j a value α_i,j was determined that produced equal effectiveness for black and white. The following types of responses and stimuli were tested: detection of luminance increments versus decrements, detection of motion from movement of stimuli made of center-black versus center-white Mexican hats, first-order motion-direction discrimination for stimuli composed of different sine wave combinations, texture slant discriminations for static and dynamic second-order textures, Gestalt groupings of blacks versus whites, and the apparent width of black versus white areas. Levinson (1960) provided flicker detection data for sin(x) + sin(2x) in different phases. Although α_i,j was found to vary among experimental condition, contrast, and observers, in all experiments and for all observers, α_i,j was greater than 1. The average α was 1.28 (range 1.08 to 1.67) indicating that blacks were 28% more effective that whites in controlling visual responses. The universality of black–white asymmetry suggests that it needs to be taken into account more often than it has in visual experiments and theories.

Three additional experiments were conducted to determine the basis of black–white asymmetry. Just noticeable differences (JNDs) between two luminance decrements were found to be much smaller than JNDs between two luminance increments. Experiments 12 and 13 varied contrasts within moving texture patterns and determined that the magnitude of α itself was an increasing, concave down function of the contrasts of the black and white areas. Values of α greater than one imply a concave representation of stimulus contrast (from negative to positive). The variation of α values (all were greater than one) with stimulus contrast was determined to be primarily due to a nonlinear concave-down internal representation of black. Following the same reasoning, the internal representation of white would also be compressive, but it was found to be linear within measurement error.

Previous measurements (He & MacLeod, 1998) of black–white asymmetry in human visual receptors were recomputed to enable comparison to the present data. Their receptor αs are generally larger and change in a somewhat different way with contrast than the αs measured in the present experiments.

In the receptors, luminance increments and decrements are represented as variations around the mean output. Given the extremely wide range of light inputs, receptor output as a function of input intensity is necessarily concave downward, from which it follows that decrements will produce greater changes in output than equal magnitude increments. Immediately after the receptors, however, blacks and whites are represented in separate channels composed of ON-center and OFF-center neurons. This has the advantage that, after the receptors, no energy is wasted conveying the local mean luminance level as it is in receptors. Dual-channels (versus single-channel representations) also mean that the amount of post-receptor black–white asymmetry is unconstrained and can vary depending on the particular subset of neurons involved in the particular task. As is typical in biology, black–white asymmetry is complex and has multiple origins.

Appendix A: Derivation of α from Scott-Samuel and Georgeson (1999)

Scott-Samuel and Georgeson (1999) found that in log-log plots, the slope of the amplitude of the distortion product versus CM contrast function is 1.7. In the terminology of this paper, the magnitude of the internal representation of an increment c is c; the magnitude of a decrement −c is −αc. We can express Scott-Samuel and Georgeson's empirical finding as:

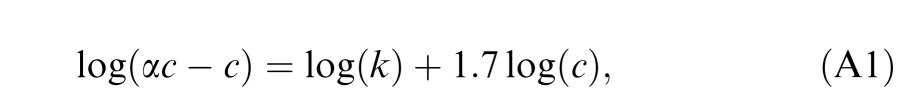where log(k) is the intercept of the empirical functions measured by Scott-Samuel and Georgeson (1999).

From Equation A1, we have:

This translates into the following relationship: α = 1 + kc^0.7, where k ranges from 0.01 to 0.05 in different temporal frequency conditions. The maximum amplitude of α is lower in Scott-Samuel and Georgeson (1999) compared to the data in Figure 14, probably due to the different spatial frequency of the carrier used in their study.

Appendix B: Derivation of α from Naka–Rushton equation

In the Naka–Rushton equation (Naka & Rushton, 1966), the neural response R(L) to luminance L is expressed as:

where R_max is the maximum response, and S is the saturation point.

When neural responses to black and white increments are balanced, we have:

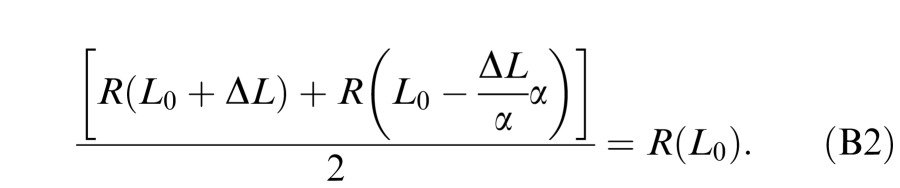Substituting B1 into B2 gives us:

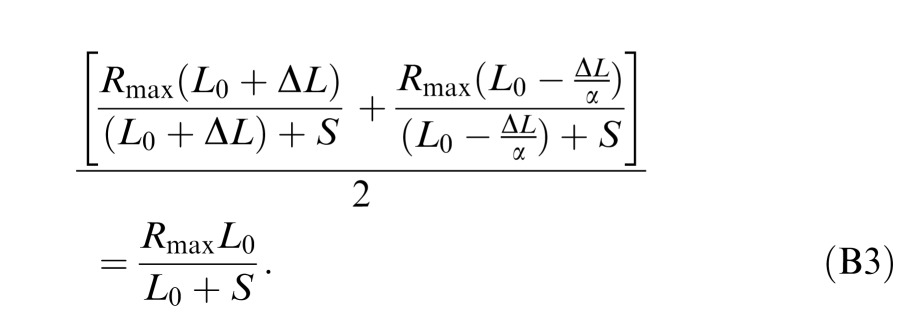Defining c = ΔL/L₀. and algebraic simplification of Equation B3 leads to: