Multiple risk factors predict recurrence of major depressive disorder in women

Abstract

Background

It is difficult to predict recurrence of depressive episodes in patients with major depression (MD): evidence for many risk factors is inconsistent and general prediction algorithms are lacking. The aim of this study was to develop a prediction model for recurrence of depressive episodes in women using improved methodology.

Methods

We used prospective data from a general population sample of female twins with a last-year MD episode (n=194). A rich set of baseline predictors was analyzed with Cox proportional hazards regression subject to elastic net regularization to find a model predicting recurrence of depressive episodes. Prediction accuracy of the model was assessed in an independent test sample (n=133), which was limited by the unavailability of a number of key predictors.

Results

A wide variety of risk factors predicted recurrence of depressive episodes in women: depressive and anxiety symptoms during the index episode, the level of symptoms at the moment of interview, psychiatric and family history, early and recent adverse life events, being unmarried, and problems with friends and finances. Kaplan Meier estimated survival curves showed that the model differentiated between patients at higher and lower risk for recurrence; estimated areas under the curve were in the range of 0.61-0.79.

Limitations

Despite our rich set of predictors, certain potentially relevant variables were not available, such as biological measures, chronic somatic diseases, and treatment status.

Conclusions

Recurrence of episodes of MD in women is highly multifactorial. Future studies should take this into account for the development of clinically useful prediction algorithms.

Introduction

Patients with major depression (MD) differ considerably in their course of illness: most patients have recurrent episodes, but others suffer only one single depressive episode during their lifetime(Eaton, et al, 2008; Hardeveld, et al, 2010; Solomon, et al, 2000). These course differences complicate clinical decisions concerning monitoring and long-term treatment, and can result in both under- and overtreatment of patients(Patten, 2013).

In order to differentiate between MD patients with distinct course types, a number of prior studies have sought to identify predictors of relapse and recurrence. Although some predictors have been found to consistently increase the risk of recurrence – the number of previous episodes, the level of residual symptoms, and childhood maltreatment (Hardeveld, et al, 2010; Nanni, et al, 2012) – evidence for other predictors is inconsistent (Hardeveld, et al, 2010). Moreover, general prediction algorithms, which quantify risk for recurrence based on a combination of risk factors that can be applied in clinical practice, are lacking (Hardeveld, et al, 2010; Patten, 2013). Such instruments might guide clinical decision making, comparable to instruments in for instance cardiology (Antman, et al, 2000; Granger, et al, 2003). This makes it difficult to discriminate between patients with a benign course versus those with recurrent episodes (Hardeveld, et al, 2010; Monroe and Harkness, 2011; Mueller, et al, 1999), and personalize treatments in order to prevent future episodes.

However, research on prediction algorithms for psychiatry is growing. Several recent studies have investigated multivariate prediction algorithms for MD onset (King, et al, 2008; Wang, et al, 2013), MD treatment resistance (Perils, 2013), suicide (Kessler, et al, 2015; Tran, et al, 2014), and persistence and severity of course of MD (van Loo, et al, 2014; Wardenaar, et al, 2014). One study developed a multivariate prediction model for recurrence of MD, which resulted in an algorithm with 19 unique factors and a C-statistics of 0.72 in independent test data (Wang, et al, 2014). Our aim was to contribute to the development of prediction algorithms by studying recurrence of MD in a female sample from the general population. We did this from a novel perspective using a rich set of predictors in a regularized multivariate prospective design, focusing on maximizing prediction accuracy in cross-validation instead of model fit, and testing our model in an independent validation sample.

Methods

Samples

The data for this study consisted of subsamples of female-female twin pairs from the Virginia Adult Twin Study of Psychiatric and Substance Use Disorders (VATSPSUD), a population-based longitudinal study of Caucasian twins (for details, see(Kendler and Prescott, 2006). We studied female-female twin pairs because their follow up included four interview waves. Moreover, studying females and males separately might lead to more accurate prediction models because risk factors can be sex-dependent, which has been shown for episodes of MD (Kendler and Gardner, 2014). Female-female twin pairs born during 1933–1972 were initially contacted by a mailed questionnaire, the response to which was 64% (n=2,435). Participants were then interviewed face-to-face in 1988–1989 (FF1 interview), at which time the refusal rate was 12%. These twins completed three more telephone interviews in 1990–1991 (FF2), 1992–1994 (FF3), and 1995–1997 (FF4), with cooperation rates ranging from 85%–93%. All participants provided written informed consent for face-to-face interviews and verbal consent prior to all telephone interviews; the study was approved by the Office of Research Subjects Protection at Virginia Commonwealth University.

For this report, we used two independent samples from the full dataset to find an optimal prediction model (training sample – model selection) and to evaluate its performance (test sample – model assessment). The goal was to obtain estimates of prediction accuracy: if a prediction model is overfitting the training data (i.e. the modeling process capitalizes on “noise” in the training data), the training data will give an overly optimistic estimate of prediction accuracy. Thus, new data are needed to get an estimate of the prediction accuracy and generalizability of the model(Hastie, et al, 2009; James, et al, 2013).

The training sample – used for model selection – included 194 twins who reported a DSM-III MD episode in the year prior to FF1 interview and who completed at least the subsequent FF2 interview. To minimize recall bias, we used twin reports of a depressive episode in the last year rather than those reported for a lifetime episode. Of 2163 twins interviewed at FF1, 217 females reported a MD-episode in the year prior to FF1, of whom 196 completed at least the subsequent FF2 interview. In addition, we excluded two twins who reported a chronic episode lasting from the year prior to FF1 up to the first follow up interview (FF2), so as to focus on the prediction of MD recurrence instead of chronicity. Thus, all 194 twins included in our training sample had a depression-free period between the first episode in the year prior to FF1 and the interview at FF2.

The independent test sample – used for model assessment – included 133 twins who reported a DSM-III MD episode in the year prior to FF2 interview, and who completed at least the subsequent FF3 interview. Of 2002 twins interviewed at the subsequent FF2 interview, 200 females reported a MD-episode in the year prior to FF2, of whom 182 completed at least the subsequent FF3 interview. A female who had not recovered from this episode at the time of the FF3 interview was excluded, again to focus on MD recurrence instead of chronicity. From this sample of 181 twins, we excluded 48 additional twins who also reported an episode at FF1 interview to keep the training sample independent. Due to this selection procedure, all subjects in the test sample were by definition depression-free for a period (i.e., the year preceding FF1) unlike the training sample. We were unable to draw two random mixed samples from the total 327 females because the design of the FF1 and FF2 interview diverged too much: many relevant predictors that were expected to be predictors of recurrence of MD were not assessed at the FF2 interview, as this interview focused more on parent-child relationships. A flow chart of the selection of both samples is presented in additional table 1.

Table 1. Baseline characteristics.

	Mean training data (n=194)	(SD)	Mean test data (n=133)	(SD)	t-testa	P-value
Demographics
Age at interview (years)	30.7	(7.1)	32.4	(7.1)	-2.1	0.04
Unmarried	53%		47%		1.06	0.29
Number of years of education	13.2	(1.9)	13.5	(2.2)	-1.28	0.20
Psychiatric history
Age at MD onset (years)	22.1	(9.4)	26.1	(9.5)	-3.74	0.00
History of MD	63%		44%		3.34	0.00
Number of episodes (if history of MD is present)	10.1	(20.0)	5.1	(9.1)	2.33	0.02
History of early anxiety	58%		53%		0.87	0.39
Episode prior to FF1 (training data)/FF2 (test data)
Sum of 9 MD criteria	6.3	(1.2)	6.4	(1.1)	-0.95	0.34
Duration of longest episode previous (months)	2.7	(3.0)	2.7	(2.8)	0.19	0.85
Number of episodes in year prior to interview	2.3	(2.0)	2.4	(2.3)	-0.47	0.64
Adverse life events (early and recent)
Number of lifetime traumas	2.3	(1.8)	2.0	(1.6)	1.81	0.07
Number of stressful life events past year	4.0	(2.4)	2.7	(2.0)	5.16	0.00

^aWelch's t-test

Assessment of Major Depression

At all interview waves, participants were asked about all the depressive symptoms in the 12 months prior to interview by a structured psychiatric interview based on the Structured Clinical Interview for DSM-III-R (SCID) (Spitzer and Williams, 1985). If depressive symptoms occurred, respondents were asked if they clustered together temporally into a syndrome and then when they occurred and the months of their onset and remission. The diagnosis of major depression was based on the DSM-III-R criteria, which had to be present for at least 2 weeks, with the exception of criterion B2 (which excludes depressive syndromes considered to be “uncomplicated bereavement”). Recurrence of a depressive episode was defined as the first episode meeting DSM-III-R criteria after a period of not meeting the criteria (remission or recovery) for at least 4 months. Time to recurrence was the number of months elapsed since the inclusion interview (i.e. FF1 for the training sample, FF2 for the test sample). Almost all participants completed two follow up interviews (90.7% and 92.5% for the training and test sample); the majority of the training sample completed all three waves (79.4%). Data were right censored for subjects not reporting a recurrence during the year prior to the last follow-up interview (FF4), and for subjects that were lost to follow up at FF3 or FF4. Median follow up time was 5.5 years for the training sample (interquartile range (IQR) 2.9), and 6.1 years (IQR 2.6) for the test sample. In some cases, the scheduling of follow-up interviews exceeded one year, resulting in periods of time that may not have been reported on if the twin accurately followed instructions to report on only their experiences over the prior year. The interval between baseline and FF2 was slightly longer than one year (median 16, IQR 4 months), so a median of 4 months was not covered by the FF2 interview. The intervals between FF2-FF3 and FF3-FF4 were longer which resulted in longer periods of missing information (median 31, IQR 4 months between FF2-FF3; median 19, IQR 9 months between FF3-FF4).

Predictor variables

We included 81 putative predictor variables covering eight major risk domains:

1. Characteristics of the depressive episode in the 12 months prior to FF1 included information on the symptoms, duration, and severity of the index depressive episode. In total we included 20 symptom predictors: 16 depressive symptoms of MD (representing the nine aggregated symptoms of criterion A for MD in DSM-III-R (American Psychiatric Association, 1987); 2 symptoms of generalized anxiety (feeling anxious, nervous, worried or tense and shaky) and 2 symptoms of panic (unexpected attacks of feeling frightened or physical experiences of panic such as palpitations or shortness of breath). In addition, we included a count variable of the positively endorsed aggregated MD symptoms as a measure of episode severity. Other severity measures included the duration of the longest episode and the number of depressive episodes lasting at least 5 days in the past year (note that only for this predictor variable we used a shorter duration criterion than the 14 days indicated by the DSM-III-R). Finally, we included the degree to which the episode interfered with work, social and leisure time activities.

2. Current state included age at the time of the initial interview (after the index episode) and the current level of internalizing symptoms (past 30 days) to account for residual symptoms (Fava, et al, 2007; Hardeveld, et al, 2010). The latter variable was operationalized as the first principal component of depression and anxiety scales of the Symptom Checklist in the past 30 days (Derogatis, et al, 1973).

3. Psychiatric history involved both a lifetime history of MD as well as other psychiatric disorders. Predictors included the age at the first MD episode, the number of episodes prior to the index episode, and the duration of the most severe lifetime episode. Other predictors concerned a lifetime history of generalized anxiety disorder, alcohol dependence, and bulimia, all according to DSM-III-R criteria (American Psychiatric Association, 1987). Furthermore, early-onset anxiety was included as a binary predictor, indicating the onset of generalized anxiety disorder, panic or phobia before the age of 18 years.

4. Family history was made up of six separate predictors for a history of MD or GAD in cotwin, mother or father. Family history diagnoses were assessed using the Family-History Research Diagnostic Criteria (Endicott, et al, 1975).

5. Personality included measures of neuroticism and extraversion based on the short version of the Eysenck Personality Questionnaire (Eysenck, et al, 1985).

6. Early adverse life events consisted of childhood adversity and distal traumas. Predictors included disturbed family environment (measured by 14 items chosen from the Family Environment Scale) (Moos and Moos, 1986), low parental warmth (measured with a modified version of the Parental Bonding Instrument) (Parker, et al, 1979), and parental loss during childhood or adolescence (parent left the home due to death, divorce, or parental separation before the age of 17). Childhood sexual abuse was included as an ordinal predictor variable defined as unwanted sexual contact before the age of 16 with an older individual. The variable was categorized as no abuse, moderate abuse (physical contact without attempted intercourse), and severe abuse (attempted or completed intercourse), as previous study showed that the severest class was at highest risk for MD (Kendler, et al, 2000). Other distal life events were measured by the number of 10 possible lifetime traumas including life-threatening accidents or illnesses, the unexpected death of a loved one, and sexual or physical assault.

7. Recent adverse life events included a history of divorce and the number of stressful life events in the past year, such as life-threatening illness or death of a close relative, interpersonal conflicts, or legal problems.

8. Current social and economic environment included marital status and satisfaction; number of confidants; support from or problems with friends or relatives; and the frequency of meetings with friends or clubs. Also, this domain included the numbers of years of education and financial problems (problems affording food, clothes or leisure activities).

All predictors of the training sample were measured utilizing a face-to-face interview and questionnaire at baseline (FF1), except parental warmth and disturbed family environment (FF2) and childhood abuse (self-report FF4). Predictors were categorized to minimize the impact of non-normal distributions or when cross tabulations of raw data indicated possible non-linear relationships with recurrence of depression.

Model selection

Elastic net penalized regression was used to find a sparse prediction model in the training sample. Penalized linear regression methods include a penalty for model complexity resulting in the selection of variables and shrinkage of beta-coefficients. The aim of these methods is to increase prediction accuracy and model interpretation by reducing overfitting, which makes them more appropriate for studies among large numbers of predictors such as in the current study(Hastie, et al, 2009; James, et al, 2013), or in genome wide association studies (Wu, et al, 2009). One of the advantages of regularized methods is that these models are likely less variable than those based on subset selection because the selection process is continuous instead of discrete (Tibshirani, 1996). Different types of penalties can be included. Since some predictors were highly inter-correlated (e.g., 0.7 for appetite and weight loss), we used the elastic net penalty – a mixture of the lasso and ridge penalty – as it can improve prediction accuracy variables by encouraging a grouping effect among collinear variables (i.e., highly correlated variables tend to be dropped or retained in the model together) (Zou and Hastie, 2005).

All statistical analyses were performed in R(R Core Team, 2014). Elastic net regression analyses were performed with R-package glmnet for Cox's proportional hazard models, which fits penalized cox models for a range of low to high penalties for model complexity (version 1.9-5) (Friedman, et al, 2010; Simon, et al, 2011). Higher penalties resulted in more predictors driven to zero and a sparser prediction model. The optimal type (alpha) and overall strength (lambda) of the penalty were selected that minimized prediction error. Prediction error was defined in terms of average partial likelihood deviance in 100 runs of 10-fold cross-validation; the cross-validation was repeated to diminish the influence of random folds. All predictors were standardized; dummy variables were created for different levels of categorical variables.

Model assessment

Performance of a prediction model can be assessed by estimating model discrimination (do patients with recurrent MD have higher risk predictions than those who have no recurrent MD?), and calibration (do about × of 100 patients with a risk prediction of ×% report MD recurrence?) (Royston and Altman, 2013; Steyerberg, et al, 2010). Discrimination of the selected multivariate model was first assessed by averaging areas under the receiving operating characteristic-curve (AUC) for a range of different time points in the training and test data (R package survivalROC, Kaplan Meier method, time points included all months in the interquartile range of follow up, Heagerty and Saha-Chaudhuri, 2013). Second, Kaplan Meier survival curves were used to assess cumulative recurrence estimates for different tertile risk groups based on linear predictor scores of the selected prediction model to get a general impression of both model calibration and discrimination (Royston and Altman, 2013) (R packages survival, Thernau, 2014; GGally, Schloerke, et al, 2014).

Due to different research goals for that phase of the project, the FF2 interview lacked predictors such as social support, marital satisfaction, and financial problems. In case of missing information at FF2, values of FF1 were used for the calculation of a risk score (linear predictor), which would be expected to result in substantial reduction in estimated prediction accuracy. The aim of the model assessment in the test data was therefore not to achieve precise estimates of prediction accuracy, but to get an impression of the expected range of prediction accuracy (the actual accuracy is expected to lie somewhere in between estimates in the training and test data).

Results

Recurrence of depression

The participants in the training sample – females who reported a depressive episode in the year prior to FF1, and who completed at least the FF2 interview – had a mean age of 30.7 years at FF1 interview (Table 1). The mean duration of their longest episode in the 12 months prior to the FF1 interview was 2.7 months. Most females reported a history of MD previous to the index episode (62.9%) with a median of 3 prior episodes (mean=10.1). Kaplan Meier cumulative recurrence estimates were 26.8% (95% confidence interval (CI) 20.3-32.8), 43.1% (CI 35.5-49.8), and 52.3% (CI 44.3-59.2) in the years prior to FF2, FF3, and FF4 respectively (Figure la).

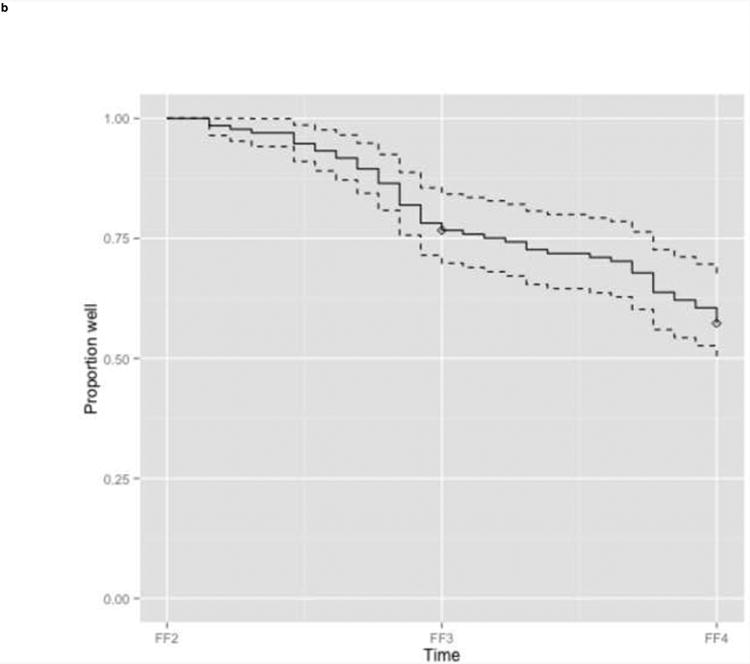
Figure 1. Recurrence of MD in the years preceding the follow up interviews.

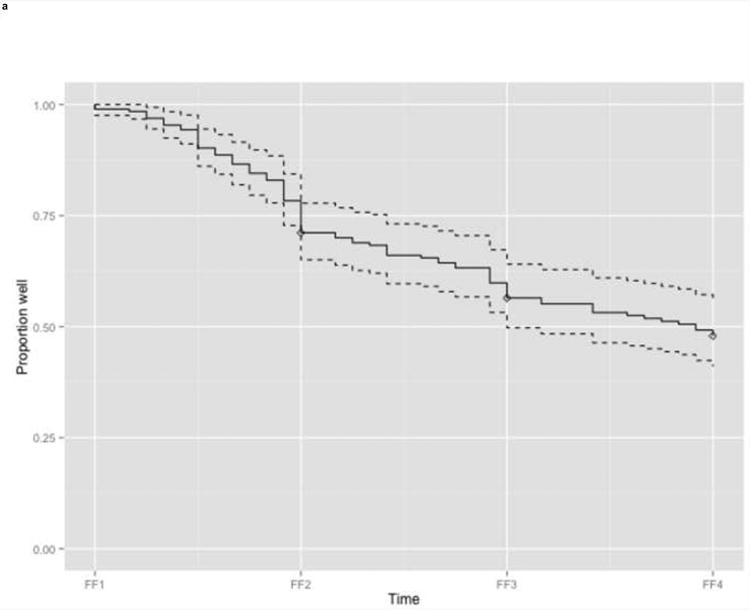
a. Training sample (n=194)

b. Test sample (n=133)

Legend: Kaplan Meier estimated proportion of subjects without recurrence (solid line) with 95% confidence interval band (dashed lines). Diamonds indicate censored subjects.

FF1, interview wave 1 (1988-1989); FF2, interview wave 2 (1990-1991); FF3, interview wave 3 (1992-1994); FF4, interview wave 4 (1995-1997)

The participants in the independent test sample – females who reported a depressive episode in the year prior to FF2, but not in the year prior to FF1, and who completed at least the FF3 interview – had a higher mean age at interview (32.4 years) and a milder depression history than the training sample: their average age at depression onset was higher, and a smaller proportion of females reported a history of prior MD (44.4%), in which case they reported fewer episodes (median 2; mean 5.1). Also the numbers of early and recent adverse life events were lower in the test sample (Table 1). Despite these baseline differences, cumulative recurrence estimates were relatively similar to these in the training data: 23.3% (CI 15.8-30.2), and 42.7% (CI 33.4-50.7) in the years prior to FF3, and FF4, respectively (Figure lb).

Predictors of recurrence

In the training sample, a wide and diverse set of variables contributed to the prediction of recurrence of MD in the best prediction model. From each domain at least one predictor ended up being retained in the best predictive model (Table 2). In total, 26 different predictors out of 81 (dummy) variables were part of this model, of which 24 increased the risk for rapid recurrence. Effect sizes for these 24 risk factors were generally small and comparable, with an average penalized HR of 1.05. The strongest predictors came from four different domains: the depressive symptom loss of interest (HR 1.10), severe financial problems (HR 1.15), number of recent life events, and the level of residual symptoms (HR's of 1.03 per unit increase). Two predictors reduced recurrence risk, viz., weight gain and a modest duration of the most severe lifetime episode (as opposed to the reference class without lifetime episodes or long lasting lifetime episodes), but effect sizes were small (HR's of 0.99 and 0.98).

Table 2. Predictors of recurrence in penalized multivariate Cox model.

I) Recent depressive episodea	HRb
Loss of interest	1.10
Appetite loss	1.02
Weight loss	1.05
Weight gain	0.99
Insomnia	1.07
Concentration difficulties	1.07
Feeling anxious, nervous, worried	1.03
Feeling tense, jumpy, shaky	1.06
Sum of9MD criteria	1.02
II) Current state
SCL past 30 daysc	1.03
III) Psychiatric history (lifetime)d
Age at first depressive MD episode (<=15 years)	1.06
Number of MD episodes (≥6)	1.05
Duration of most severe MD episode (1-3 months)	0.98
Duration of most severe MD episode (≥3 months)	1.03
Early anxiety	1.06
IV) Family history
GAD cotwin	1.06
V) Personality
Extraversion	1.02
VI) Adverse life events (early)
Parental loss childhood/adolescence	1.03
Disturbed family environment	1.02
Sum of lifetime traumas (3-4)	1.06
Childhood sexual abuse (severe)	1.04
VII) Adverse life events (recent)
Number of stressful life events in past year	1.03
VIII) Social and economic environment
Marital status (never married)	1.03
Low marital satisfaction (not married)	1.04
Problems with relatives	1.02
Financial problems (severe)	1.15

GAD, generalized anxiety disorder; HR, hazard ratio; MD, major depression; SCL, Symptom Checklist

^aCharacteristics of episode in the year prior to FF1 interview.

^bPenalized hazard ratios of all predictors with effect sizes ≤0.99 or ≥1.01 based on elastic net regression including all 81 (dummy) variables in the training sample (n=194).

^c1st principal component of depression and anxiety scales of the Symptom Checklist past 30 days.

^dLifetime: prior to last year (≥ 1 year ago).

Prominent predictor variables retained in the final prediction model included depressive symptoms, anxiety, lifetime history of MD and trauma's or stressful life events. Certain symptoms used to define the index episode (e.g. interest loss, weight loss, insomnia, concentration problems), and the level of (residual) symptoms predicted a rapid recurrence. In addition, four predictors related to anxiety were included in the prediction model: two symptoms of GAD present during the index episode (feeling anxious, nervous, or worrisome and feeling tense, jumpy, shaky), a history of early anxiety (the onset of GAD, panic or phobia before age 18) and a history of GAD in the cotwin. Other prominent predictors were related to a more severe lifetime history of MD (early onset of MD, longer lifetime episode, and more lifetime episodes) and both past and recent adversity (parental loss, disturbed family environment, childhood sexual abuse, the number of lifetime traumas and recent life events).

Prediction accuracy

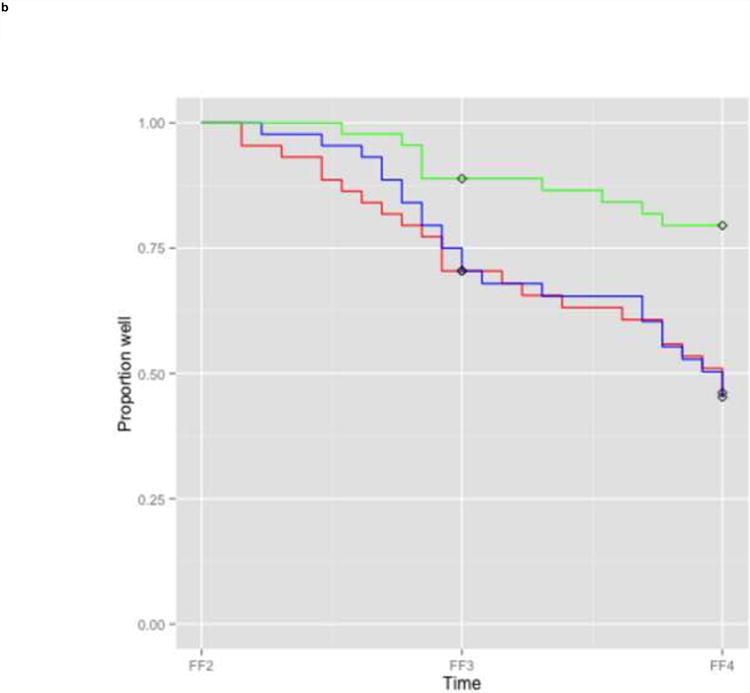
We then examined the performance of the best model in the training and test sample to get an impression of its performance. Kaplan Meier survival curves showed that higher risk scores were associated with more recurrences in both data sets, but more so in the training data (Figure 2). In the training data, all three risk groups based on tertiles of linear predictor scores had different estimates of recurrence (Figure 2a). After two interview waves (i.e. FF3), the lowest risk group had a cumulative recurrence estimate of 16.4% (CI 6.6-25.3), the intermediate risk group of 39.2% (CI 25.6-50.4) and the highest risk group of 73.6% (CI 60.0-82.5). In the test data, the lowest risk group suffered fewer recurrences than the higher two risk groups, which had similar recurrence estimates (Figure 2b). After two interview waves (i.e. FF4) the lowest risk group had a cumulative recurrence estimate of 20.5% (CI 7.6-31.6), whereas the intermediate and highest risk group had equal recurrence estimates: 53.8% (CI 36.0-66.7) and 54.7% (CI 36.6-67.6), respectively. The comparable KM-curves for the two lower risk groups in both datasets suggest that the model is well-calibrated for patients with a lower risk of recurrence. However, the KM-curves differed for the highest risk groups: more recurrences occurred in the training data than in the test data. This suggests that the model is less well-calibrated and might overpredict risk of recurrence in high risk patients.

Figure 2. Survival curves for different tertile risk groups.

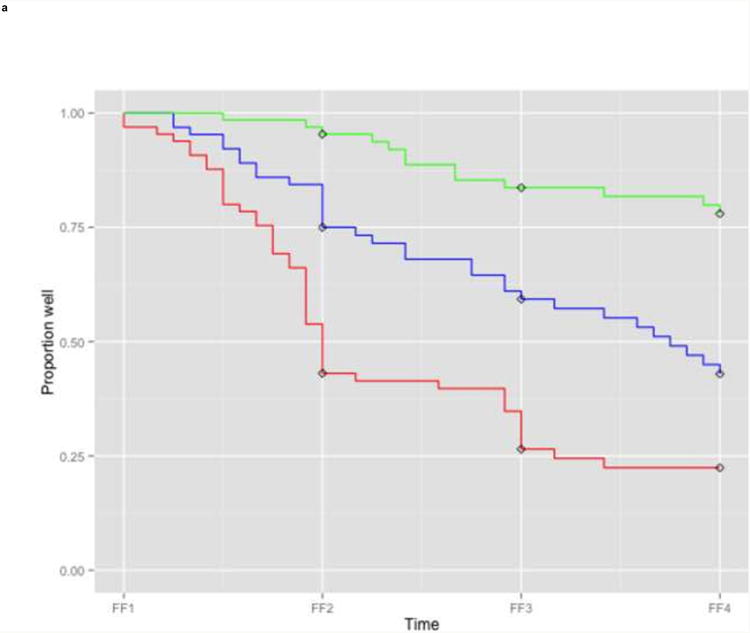
a: Training sample (n=194)

b: Test sample (n=133)

Legend: Kaplan Meier survival curves for subjects in the lowest one third (green), intermediate one third (blue), and highest one third risk group (red) based on linear predictor scores derived from the full prediction model. In case of missing information on predictors at FF2, FF1 information was used for the linear predictor score of the test sample. Diamonds indicate censored subjects.

FF1, interview wave 1 (1988-1989); FF2, interview wave 2 (1990-1991); FF3, interview wave 3 (1992-1994); FF4, interview wave 4 (1995-1997)

The widely separated Kaplan Meier curves indicated good discrimination in the training data, and good discrimination between the lowest and two higher risk groups in the test data, but poorer discrimination was evident between the two higher risk groups in the test data. As expected, estimates of discrimination accuracy were higher in the training sample (AUC 0.79) than in the test sample (AUC 0.61), suggesting that the actual model accuracy can be anticipated to lie somewhere in the range between these values.

Discussion

A broad range of risk factors predicted recurrence of MD in females: depressive and anxiety symptoms during the index episode, the level of internalizing symptoms at the time of interview, psychiatric and family history, personality, early and recent adverse life events, marital status and problems with friends and finances. Our best prediction model showed that recurrence of depression depends on the combination of many risk factors, each having a small effect.

Estimates of prediction accuracy in the training and test sample were found to differ: the model discriminated well between the different risk groups in the training data, but more poorly between patients with intermediate or high risk of recurrence in the test data. We attribute this difference partly to data restrictions in the test sample, and partly to overfitting in the training data. The model's accuracy in the test sample was likely underestimated for several reasons. In order to obtain an independent test set, we excluded females with a depressive episode in the year prior to FF1 interview from the test sample, which resulted in a necessary ‘depression-free’ interval of at least one year. As a consequence, the independent test sample was less severely affected than the training sample, with fewer subjects reporting a history of MD or a young age of onset. This might have biased the estimates of prediction accuracy downwards and might explain why fewer events were observed especially in the highest risk group. Furthermore, due to missing data at FF2 interview, we used older FF1 values to calculate risk scores for the test sample for over 40% of the predictors (11 of 26) included in the model. The use of FF1 values for time-dependent variables (such as financial problems, problems with relatives, and current level of symptoms), might also have led to lower accuracy estimates in the test data than if current values, assessed at the FF2 interview, could have been used. Then, the difference between model performance in training and test set could suggest that the use of penalized regression did not entirely prevent overfitting. Therefore, we expect the actual performance of the model to lie somewhere in between the estimates in the training and test set, i.e., an AUC within the range of 0.61-0.79. These estimates are similar to AUC's of prediction models, identified with similar statistical methods, for different aspects of course of illness of MD in a large general population study (AUC's 0.62-0.73 in training data) (Wardenaar, et al, 2014) and somewhat lower than AUC estimates in the most comparable study, specifically for the test data (AUC's of 0.72-0.75 in test and training data) (Wang, et al, 2014). We will compare our studies in further detail below.

Relation to previous studies

Although many studies have focused on predictors of MD recurrence, only one previous study - similar to this study – attempted to develop and validate a multivariate prediction algorithm in order to calculate individuals' risk of developing recurrent MD. The study by Wang et al. used a sample of 1,518 subjects with current or lifetime MD of the National Epidemiological Survey on Alcohol and Related Condition dataset to develop a prediction algorithm (Wang, et al, 2014). Similar to our study, Wang et al. investigated a large number of potential predictors and validated their model in an independent test sample from the same dataset. The general results of both studies are comparable: large numbers of variables from different risk domains were included in the final prediction models (31 and 26 coefficients in Wang et al.'s and this study). Similar to this study, Wang et al.'s model included risk factors from different domains with relatively small (penalized) effect sizes, such as marital status, number of previous episodes, childhood adversities, and concentration difficulties).

However, some risk factors were included in our model but not in Wang et al.'s model (MD onset before the age of 15, family history of anxiety, recent adverse life events), and vice versa (e.g. discrimination, race). Some differences might have arisen because of sample characteristics: we studied a smaller sample of Caucasian females who reported a MD episode in the past year, whereas Wang et al. studied a larger multiracial male and female sample with a current or lifetime depressive episode. Hence Wang et al.'s data might be more representative of a broader population, but our data are probably more reliable because of the shorter recall period (e.g., more reliable reports of depressive and anxiety symptoms). Second, some of the differences between the models might be due to different statistical methodology: this study used regularized Cox proportional hazards modeling, whereas Wang et al. used stepwise logistic regression modeling. The latter method is expected to show more variability in the resulting models because of the discrete selection process of relevant predictors (Tibshirani 1996). Furthermore, as noted above, the estimates of prediction accuracy of Wang et al.'s model in their test data were higher than estimates of our model in the test data, which might be due to the aforementioned limitations of our test data.

Compared with other previous studies, both our and Wang et al.'s studies consistently found a larger number of risk factors contributing to prediction of recurrence in a multivariate context. Some of the predictors – a large number of episodes, residual symptoms, traumas including childhood adversity and abuse – have been consistently found by previous studies to recurrence of depression (Fava, et al, 2007; Hardeveld, et al, 2010; Hardeveld, et al, 2013; Nanni, et al, 2012; Patten, et al, 2010). Also comorbid anxiety symptoms and a history of (early) anxiety were associated with a severe course of depression with frequent and long-lasting episodes (RW.ERROR - Unable to find reference:590; van Loo, et al, 2014; Wardenaar, et al, 2014). The contribution of other predictors, however, is less consistent in previous studies: associations were significant in some studies, but insignificant in others (such as age of onset, marital status) (Hardeveld, et al, 2010). There are several possible explanations for why our study and Wang et al. found a wider variety of risk factors than those reported in previous studies, and why we believe this multifactorial model provides a more realistic picture of risk prediction for women with MD.

First, the set of predictors was larger than used previously, involving many domains usually assessed in a thorough clinical evaluation. Previous studies have tested up to 45 predictors in univariate analyses (Holma, et al, 2008; Melartin, et al, 2004), but usually the number of investigated predictors was much lower and few broad sets of predictors have been investigated in a multivariate context (e.g. in the range of 6-19) (Eaton, et al, 2008; Hardeveld, et al, 2013; Hardeveld, et al, 2013).

Second, instead of studying both sexes, we studied females only. This might have influenced the prediction model because of sex differences, such as they have been demonstrated for the onset of MD (Kendler and Gardner, 2014).

Third, in this study we presented all variables that were part of the best prediction model, instead of only significant predictors. Whether a predictor is significant – i.e. the probability (p-value) of getting the observed result is small, assumed that the predictor's effect is zero – is a different question than whether a variable contributes to predicting an outcome in a multivariate context. Moreover, p-values can be unstable especially when samples and effect sizes are small(Cumming, 2008).

Strengths and limitations

The results of this study should be considered within the context of five limitations. First, the follow up interviews instructed twins to report on recurrences in the year prior to interview as opposed to recurrences over the entire period between each successive interview. Due to this design and variation in scheduling of interviews, there may have been periods that were unreported on for recurrences for some twins. This might have resulted in an underestimation of the time to recurrence, despite our overall recurrence rates exceed previous estimates in the general population(Eaton, et al, 2008; Hardeveld, et al, 2013; Mattisson, et al, 2007; Patten, et al, 2010). Since this source of missing data was most likely the result of unsystematic features of the interview scheduling process of the study – as opposed to being dependent on subject characteristics – it is unlikely that the periods of missing data affected the prediction model to a large extent, although this should be demonstrated in follow-up studies. In addition, the strength of this design is that it involved short one-year recall periods so that reports of MD are more reliable than if longer recall periods were used.

Second, we studied a relatively small heterogeneous group of female twins with regard to their longitudinal history of depression: some females reported a first episode, but most had a more extensive history of depression. Analyzing these subgroups might lead to more accurate prediction models if risk factors are different for patients with a first episode than for patients with an extensive depression history(Boschloo, et al, 2014; Kendler, et al, 2000). Larger prospective samples of patients with first episodes would be needed to explore this. In general, larger study samples would be expected to result in more stable and generalizable prediction models.

Third, despite our rich set of predictors, certain potentially relevant predictors were not available, such as biological variables, chronic somatic diseases (Gerrits, et al, 2013), information on current treatment and prior treatment response (Gopinath, et al, 2007), and workload and stress (Wang, et al, 2012).

Fourth, as described in the foregoing, our model validation procedure was limited because of data restrictions of the test sample. This could have biased the estimates of prediction accuracy in the test data downwards.

Fifth, the identified model was relatively complex containing many predictors with small effects, which can complicate attempts to translate these findings into clinical practice. However, progress in computerized data collection and computation offer opportunities to use more complex prediction models in clinical practice. For example, a complex risk algorithm could be implemented as software that automatically calculates risk scores for each patient combining large numbers of variables. Thus, we believe that the greatest benefits will come from improving the accuracy of prediction models instead of focusing on reducing their complexity.

Beside these limitations, this study improves on previous studies of recurrence of depression by combining a very rich and diverse set of predictors in multivariate analyses aimed at maximizing prediction accuracy in a general population sample, with only a one year recall period. We used statistical methods which are specifically developed to deal with large sets of predictors and we tested our prediction model in independent test data.

Multifactorial nature of MD recurrence

In this study, the best prediction model consisted of diverse, relatively small sized, predictors drawn from different risk domains. The model suggests that the course of MD is multifactorial, involving many risk factors and in this sense is similar to predictive models for the onset of MD (Kendler, et al, 2002; Kendler, et al, 2006). Thus, risk assessment presumably improves when a diverse set of predictors representing various domains is taken into account. In addition, the wide variety of risk factors supports the idea that the development and course of MD depends upon a complex interplay between biological, psychological, and environmental factors (Kendler, 2014; Machamer, et al, 2000), although caution is advised regarding causal inference based on statistical results in observational data.

While part of the limited predictive accuracy of the best model in the test data is probably due to data restrictions and overfitting in the training sample, another relevant consideration is related to the complexity of all factors associated with the course of MD, such as life events, social and economic circumstances, which can be highly personal (certain events might be traumatic for some individuals, but not for others), subject to change, and in itself difficult to predict.

For clinical practice, this study implies that it is preferable to base risk assessment on an extensive set of predictors from multiple domains, and that – even with a rich set of baseline information – prediction of the course of illness over several years can be challenging. Given that some risk factors vary over time, risk estimation in individual patients will probably be more accurate when changes over time are taken into account, such as when patients experience life events or changes in their social and economic situation.

Future research

This study has implications for future studies aimed at developing accurate and sparse prediction models to differentiate between patients with high and low risk for MD recurrence in clinical practice. First, prediction models based on a broad set of biological, psychological and environmental predictors will probably outperform models including only a few predictors from a narrow set of domains. Second, the time-dependency of risk factors related to recurrence suggests that longitudinal data collection and analysis should benefit prediction models, as recently illustrated in prediction of treatment remission status in MD (Liu, et al, 2014). Third, another opportunity to improve prediction accuracy would be to find prediction models for more homogeneous subgroups of MD patients: patients with a first episode versus patients with a history of MD, male versus female patients, patients with a younger versus older age of onset (Kendler and Gardner, 2014; Monroe and Harkness, 2011). Fourth, to get an impression of the actual performance, prediction models need to be cross-validated in new data, as good model performance in the training data does not guarantee generalizability to future data (Hastie, et al, 2009). Fifth, a future study in a male sample could clarify whether sex dependent variations in predictors of MD are present, which have been shown for the onset of MD (Kendler and Gardner, 2014).

Conclusion

The results of our study suggest that many different types of risk factors contribute to predicting recurrence of depressive episodes in women. These identified predictors can serve as a starting-point for future studies aiming to identify clinically useful prediction models.