Biodiversity comparison among phylogenetic diversity metrics and between three North American prairies

Abstract

Protection of Earth’s ecosystems requires identification of geographical areas of greatest biodiversity. Assessment of biodiversity begins with knowledge of the evolutionary histories of species in a geographic area. Multiple phylogenetic diversity (PD) metrics have been developed to describe biodiversity beyond species counts, but sufficient empirical studies, particularly at fine phylogenetic scales, have not been conducted to provide conservation planners with evidence for incorporating PD metrics into selection of priority regions. We review notable studies that are contributing to a growing database of empirical results, we report on the effect of using high-throughput sequencing to estimate the phylogenies used to calculate PD metrics, and we discuss difficulties in selecting appropriate diversity indices. We focused on two of the most speciose angiosperm families in prairies—Asteraceae and Fabaceae—and compared 12 PD metrics and four traditional measures of biodiversity between three North American prairie sites. The varying results from the literature and from the current data reveal the wide range of applications of PD metrics and the necessity for many more empirical studies. The accumulation of results from further investigations will eventually lead to a scientific understanding upon which conservation planners can make informed decisions about where to apply limited preservation funds.

Worldwide budgets for ecosystem and species protection are limited, and for many years, scientists, conservation planners, and policy makers have agreed that science should inform how those limited funds are used to support the preservation of Earth’s biodiversity (Vane-Wright et al., 1991; Vane-Wright, 1996; Crozier, 1997; Sechrest et al., 2002; Steele and Pires, 2011). Biodiversity assessment tools vary, and species richness and endemicity often serve as the primary metrics (e.g., Mittermeier et al., 2011). Researchers agree that considering evolutionary history for conservation prioritization is an important way to preserve biodiversity (Naeem et al., 2012), but few studies have demonstrated the best means of measuring this community feature.

Scientists from North America and Europe met to discuss phylogenies in conservation, and they concluded that the use of phylogenetic approaches is very promising, but more research is required that provides concrete recommendations to conservation planners (Rolland et al., 2012). In 1992, E. O. Wilson noted that as the cost of DNA sequencing decreased and became routine, scientists would be fully prepared to address the question of how much biodiversity exists on Earth. With advances in high-throughput DNA sequencing, we are now prepared to live up to Wilson’s (1992) prediction and to provide the much-needed conservation guidance.

As ecosystems and communities change due to anthropogenic activities, the conservation of evolutionary histories may be an effective way to prioritize potential conservation sites because evolutionary diversification has led to the broad range of attributes and functions contributing to biodiversity (Barker, 2002; Forest et al., 2007). Although in some studies species richness (S) has been a good indicator of phylogenetic variation (Barker, 2002; Rodrigues and Gaston, 2002; Schipper et al., 2008), other studies show no relationship between the two (Forest et al., 2007; Devictor et al., 2010). Maximizing phylogenetic diversity is regarded as the best bet-hedging strategy (Forest et al., 2007); i.e., preserving sites with the greatest amount of phylogenetic variation will, in turn, protect the greatest variation in organismal features and functions, thus ensuring the greatest chance that ecosystems continue to persist and provide services regardless of future environmental changes. Despite strong arguments for incorporating evolutionary history into conservation strategies, it has not yet been adopted universally by conservation planners, due, in part, to a scarcity of broad-scale empirical studies, particularly at fine or low taxonomic levels.

A strategy for quantifying biodiversity is to assess phylogenetic diversity (PD) between organisms in a community; i.e., measuring the evolutionary history (or branch lengths) between taxa (Forest et al., 2007; Winter et al., 2013). The original PD metric (PD_Faith) measures the total evolutionary distances among taxa in a community (Faith, 1992). Since the introduction of the initial PD metrics over 20 yr ago (e.g., May, 1990; Vane-Wright et al., 1991; Faith, 1992; Nixon and Wheeler, 1992), multiple indices have been developed (common metrics described in Table 1). Some metrics have been reviewed in attempts to distinguish them and their applications (Webb et al., 2002; Vellend et al., 2011; Winter et al., 2013), but they have not all been applied in an empirical comparative study such that the differences between them can be detected.

Table 1.

Twelve common PD metrics that were compared in this study, citations and descriptions of each, and the R algorithm used to calculate each metric.

Metric	Definition	Citations	How calculated; indication (interpretation of values)a	R algorithmb
PDFaith	Original phylogenetic diversity metric	Faith, 1992	Sum of all branch lengths connecting the species in the community; overall diversity (diversity increases as the value increases)	pd
PDSES	Standardized effect size of PDFaith	Webb et al., 2008	Compares PDFaith to null communities; phylogenetic structure (+ values = PO; – values = PC)	ses.pd
MPD	Mean pairwise distance	Webb, 2000	Average evolutionary distance between all pairwise species; relatedness of species deep in the tree (higher values = more species with above-average branch lengths)	mpd
MNTD	Mean nearest taxon distance	Webb et al., 2002	Average branch lengths connecting each species to its nearest relative; relatedness near branch tips (lower values = compact topology and higher values = some taxa with branches much longer than average)	mntd
NRI	Net relatedness index	Webb, 2000	Compares MPD to null communities; phylogenetic structure (+ values = PC; – values = PO)	ses.mpd
NTI	Nearest taxon index	Webb, 2000	Compares MNTD to null communities; phylogenetic structure (+ values = PC; – values = PO)	ses.mntd
SPD	Sum of phylogenetic distances	Crozier, 1997	MPD multiplied by number of species pairs; overall tree topology (lower values = compact; higher values = sprawling)	mpd * #sp.pairs
PSV	Phylogenetic species variability	Helmus et al., 2007	Compares variance in tree estimated from data to variance under a star phylogeny; degree of relatedness between taxa in the tree (values range asymptotically from 0 = increased relatedness to 1 = decreased relatedness)	psv
PSR	Phylogenetic species richness	Helmus et al., 2007	PSV multiplied by S; species richness after discounting species relatedness (values range asymptotically from 0 = increased relatedness to S = decreased relatedness)	psr
PSC	Phylogenetic species clustering	Helmus et al., 2007	Modified PSV; branch tip clustering (values range asymptotically from 0 = increased relatedness to 1 = decreased relatedness)	psc
IST	Local phylogenetic similarity excess	Hardy and Senterre, 2007; Hardy and Jost, 2008	Average among-community diversity / total diversity across all samples; amount of pairwise differentiation between communities (high values = high differentiation)	raoD
SEH	Species evolutionary history	Redding and Mooers, 2006	Portion of phylogenetic tree attributable to a species; evolutionary distinctiveness for every species in the tree (value increases as a species distinctiveness increases in a particular data set)	evol.distinct

^aPO = phylogenetic overdispersion or evenness; PC = phylogenetic clustering.

^bMetrics were calculated in R (R Core Team, 2013) using the Picante package (Kembel et al., 2010) and the R function listed.

PD_SES, NRI, and NTI (PD metric abbreviations are defined in Table 1) compare the phylogenetic diversity in the data set to a randomly generated data set, or null model, from the regional species pool, revealing either phylogenetic overdispersion or evenness (co-occurring species more distantly related than expected by chance) or phylogenetic clustering (species more closely related than expected by chance) (Cavender-Bares et al., 2004). PSV compares the variance of a hypothetical neutral trait evolving randomly to the variance expected under a star phylogeny (with all branch lengths = 1), and PSR is PSV multiplied by S; therefore, it is comparable to S (Helmus et al., 2007). PD_Faith is compared between sites to reveal total diversity, MPD reveals relatedness of species deep in the tree, and MNTD reveals relatedness near branch tips.

Examples of recent investigations comparing PD metrics include those that assessed phylogenetic structure of hummingbird community assemblages along an elevational gradient (NRI, NTI, PSV, and PSC; González-Caro et al., 2012), explored diversity patterns in a grassland community (PD_Faith plus various abundance metrics; Cadotte et al., 2010), evaluated relative PD and endemism in Australian Acacia (Mishler et al., 2014), and examined fern diversity and determined the environmental predictors of diversity metrics across Australia (Nagalingum et al., 2015). Some studies assessing PD have used simulated data (taxonomic distinctiveness metrics; Schweiger et al., 2008), supertrees (NRI and NTI across rainforest trees [Webb, 2000]; PD_Faith plus various abundance metrics in New Zealand birds [Barker, 2002]; PD_Faith in carnivores and primates [Sechrest et al., 2002]; and PSV and PSR in Wisconsin lake fish [Helmus et al., 2007]), or trees estimated from a few gene sequences downloaded from GenBank (PD_Faith, MPD, and MNTD with and without abundance; Cadotte et al., 2012). PD_Faith has also been compared with other biodiversity assessment tools such as S (Forest et al., 2007; Davies and Buckley, 2011) and taxonomic and functional diversity (Devictor et al., 2010; Flynn et al., 2011).

Most investigations that compared PD with S found that these two measurements often do not lead to the same conclusions for conservation (e.g., Tucker et al., 2012). Rapid species radiations and imbalanced phylogenies, high temporal turnover of lineages, and rare dispersal events can result in large variations between S and PD (Davies and Buckley, 2011; Tucker and Cadotte, 2013). Additionally, most studies infer phylogenies from few genetic markers, resulting in poorly resolved phylogenies or resolved phylogenies with weak support for clades, and they calculate PD metrics across very deep phylogenies (i.e., phylogenies that extend back hundreds of millions of years). Estimating phylogenies from many genetic markers almost always results in well-supported evolutionary relationships that may not be possible with fewer DNA characters, but how do trees estimated with varying quantities of DNA characters affect PD metrics? We present results of a study in which we used high-throughput DNA sequencing to estimate phylogenies from nearly all the genes in the plastid genomes and compared 12 PD metrics to the four most common traditional biodiversity indices (i.e., those diversity metrics that do not incorporate phylogenetic information) across three North American prairie preserves. With examples from the literature, we discuss the following questions: (1) How do PD metrics compare to each other and with traditional measures of biodiversity? (2) How do PD metrics vary among similar communities? and (3) How do PD metrics calculated from multigene phylogenies compare to those that were calculated from single- or dual-gene phylogenies?

METHODS

Study sites

The research sites consisted of three North American prairie preserves: (1) Tucker Prairie Natural Area (Tucker), (2) Nine-Mile Prairie (NMP), and (3) Niobrara Valley Preserve (NVP). Prairies are among the most biologically productive of all communities (Williams and Diebel, 1996), and yet the decline of native prairies since 1830 has exceeded that of any other ecosystem in North America (Samson and Knopf, 1994). These three sites were selected because they are relict prairies that have never been plowed, and they have similar abiotic conditions (i.e., temperature, rainfall, number of daylight hours, etc.) but somewhat differing plant composition (i.e., species present). Across these sites, we expected PD to be similar but with some variation attributed to differences in plant composition. Our sampling covered the entire areas at Tucker and NMP (both tallgrass communities) but only about 1/10 of NVP (various grass communities). Our application of PD metrics serves as an example of the types of comparisons that may be made by conservation planners.

Tucker is a University of Missouri research facility and a remnant tallgrass prairie located in Calloway County, 25 km east of Columbia, Missouri. The 59-ha site has been owned and managed by the university for over 50 yr; it has been the site of controlled burns and restoration and has been designated as a Registered National Landmark by the U.S. National Park Service. Flowering plants at the site include 239 species in 52 families (R. Kennedy, personal communication).

NMP is a 93-ha tallgrass prairie owned by the University of Nebraska Foundation, where 392 vascular plant species have been observed. Because this prairie has never been plowed or grazed, it is used as a seed source of local genotypes of grasses and wildflowers for use in prairie restoration efforts in the region (University of Nebraska–Lincoln, School of Natural Resources, 2015).

NVP, owned by The Nature Conservancy, is a unique region of mixed grass, tallgrass, and sandhills prairie in north-central Nebraska where six major ecosystems converge due to unique geology and geography (The Nature Conservancy, n.d., para. 1). NVP, at nearly 23,000 ha, is one of the largest Conservancy preserves in the United States and is a model for grassland management using bison, cattle, and fire. We sampled approximately 2100 ha, consisting primarily of sandhills and mixed grass communities that vary in soil composition from clay-like to sandy loam. Five hundred eighty-one plant species have been recorded at the site (Churchill et al., 1988).

Taxon sampling

To assess PD in a community, ideally, all of the organisms present would be considered; however, this technique is not practical due to time and monetary constraints. To address the research questions while conforming to a practical budget, we sampled a subset of the flowering plants present in each community. Flowering plants are major components defining ecosystems, and species composition varies between communities as biotic associations and abiotic conditions vary. Studies have shown that the evolutionary histories making up the plant community strongly affect diversity and abundance of other organisms in the community, such as arthropods (Dinnage et al., 2012). Therefore, plant diversity serves as a surrogate for the biodiversity of all organisms in the community.

Although grasses comprise the greatest biomass in prairies, forbs contribute the greatest diversity (Turner and Knapp, 1996). Asteraceae (sunflowers) and Fabaceae (legumes) are two of the three largest flowering plant families (Poaceae [grasses] being the third) in North American prairies. Our taxon sampling spanned the morphological breadth and habitat range of species in these two families, including 29 Asteraceae and 20 Fabaceae (Appendix 1). We collected silica-dried leaf tissue from multiple individuals in the population, masking genetic variation between individuals.

DNA extraction and sequencing

We extracted total genomic DNA from 49 species with either the IBI Mini Genomic DNA Kit (IBI Scientific, Peosta, Iowa, USA) or QIAGEN DNeasy Plant Mini Kit (QIAGEN, Germantown, Maryland, USA). We conducted extractions multiple times from the same sample to obtain approximately 12 μg of DNA. For samples collected at Tucker, we performed end repair on sheared genomic DNA prior to ligating barcoding adapters for multiplexing using NEB Prep kit E600L (New England Biolabs, Ipswich, Massachusetts, USA). We size-selected samples for ∼300 bp and used PCR to enrich fragments. We sent final products to the University of Missouri (MU) DNA Core Facility for quantitation, fragment size verification, and sequencing on the Illumina GAIIx Genome Analyzer (San Diego, California, USA). We ran Tucker samples at six samples per lane with single-end, 80- or 120-bp reads. For samples collected at NMP and NVP, core staff made sequencing libraries and conducted sequencing at the University of Nebraska Medical Center (UNMC) Next Generation Sequencing Core Facility on the Illumina HiSeq 2000. All Nebraska samples ran at 14 samples per lane with paired-end 120-bp reads.

Sequence assembly, annotation, and alignment

We assembled Illumina reads, identified and extracted plastid genes, and concatenated and aligned genes in preparation for phylogenetic analysis as follows. We downloaded Illumina reads for each sample from sequencing-facility servers to a desktop computer where we assembled reads in Geneious (version 6.1.7; Biomatters [www.geneious.com]) by mapping reads to various, previously assembled plastid genomes (per methods by Steele et al., 2012). We identified and annotated plastid genes in Geneious, and then concatenated genes that were recovered consistently for each plant family into a single sequence. To align concatenated sequences for each plant family, in Geneious, we used the sequence alignment tool MAFFT (v. 7.017; with default algorithm, scoring matrix: 200PAM / k = 2, gap open penalty: 1.53, and offset value 0.123; Katoh et al., 2002). We uploaded sequence alignments to the Dryad Digital Repository (http://dx.doi.org/10.5061/dryad.7s4h1; Kellar et al., 2015) and all gene sequences used for phylogenetic analyses to GenBank (Benson et al., 2005; Appendix S1 ^{(95.7KB, docx)} ).

Phylogenetic analyses

We conducted maximum likelihood (ML) analyses for each plant family on the complete concatenated data sets and, for comparison, on data sets including only one or two genes. Estimation of phylogenies from few to several DNA regions has become routine, and the most common plastid genes used for phylogenetic inference are matK and rbcL. Phylogenetic inference on the basis of many genes or complete plastid genomes is becoming more common (e.g., Jansen et al., 2007; Moore et al., 2010) as these data-heavy phylogenies often result in well-supported evolutionary relationships that may not be possible with fewer DNA characters. Therefore, we estimated phylogenies and compared PD metrics calculated from multigene data sets (>70 genes) and from single/dual-gene data sets as follows: (1) matK only, (2) rbcL only, and (3) matK + rbcL.

For phylogenetic analyses, we used Garli v0.951 (Zwickl, 2006; www.bio.utexas.edu/faculty/antisense/garli/Garli.html), accessed through the online CIPRES Science Gateway (www.phylo.org), with the default model of evolution (GTR + I + Γ). We rooted trees with the most distinct taxon, noted in tree figure legends (below). ML analyses used the automated stopping criterion, terminating a search when the likelihood score remained constant for 20,000 consecutive generations. We calculated likelihood scores of the optimal tree generated by Garli in PAUP* (Swofford, 2003), which better optimizes branch lengths (Zwickl, 2006). We performed ML bootstrap analyses in Garli on 1000 replicates using an automated stopping criterion set at 20,000 generations.

We did not fossil-calibrate the resulting phylogenies. For calculating PD metrics, some published studies have used ultrametric or rate-smoothed phylogenies (e.g., Purschke et al., 2013). However, there are equally as many studies that have not used calibrated trees (e.g., Lessard et al., 2009; Mishler et al., 2014; Schmidt-Lebuhn et al., 2015), and tree calibration is not necessary to obtain valid results. There are multiple published examples that have assessed the importance of rate-smoothing trees for phylogenetic diversity estimates, and they show relatively minor influences of subtle branch length transformations (Cadotte et al., 2008, 2009).

PD metrics and traditional measures of biodiversity

We calculated 12 PD metrics (Table 1) using various functions in the Picante package (Kembel et al., 2010) within R statistical software (R Core Team, 2013) for each plant family at each site. Also in R, we assessed the statistical significance of the PD results by comparing each observed value to a null distribution generated from 10,000 randomizations of the phylogeny. For statistical comparisons between values, we used SAS 9 (SAS Institute, Cary, North Carolina, USA), a Mann-Whitney U Test (Mann and Whitney, 1947), a Kruskal–Wallis test (Kruskal and Wallis, 1952), and a one-way ANOVA to compare PD metrics between study sites and between different data sets.

We calculated traditional descriptors of species diversity, including S, or the total number of species in a sample (Gotelli and Chao, 2013), as well as the effective number of species (ENS), which normalizes S for comparisons between sites. ENS is calculated by taking the exponential of the Shannon–Wiener index (H′), which quantifies the entropy in a set of samples (Shannon, 1948). ENS reveals the number of equally frequent species in a simulated community that would produce the calculated H′ (Jost, 2006). When more diversity exists than is expected, ENS > S, and when less diversity exists, ENS < S. We calculated ENS in EstimateS (version 9; Colwell, 2013).

To compare biotic similarity between two communities or geographic sites, we calculated the Jaccard index (S_J; Jaccard, 1912) and the Sørensen index (S_S; Sørensen, 1948), both of which use presence/absence data, but S_S applies weight to species that are common to both sites over those found at only one site. These indices reveal similarities between sites based on species incidence data (e.g., Hastings and Rothenberger, 2013). We compared these traditional biodiversity indices to I_ST (Hardy and Senterre, 2007), which incorporates phylogeny and measures differences between sites. We calculated S_J and S_S in EstimateS (version 9; Colwell, 2013) and I_ST in R (R Core Team, 2013). Higher values of S_J and S_S indicate increased site similarity, whereas higher values of I_ST indicate greater difference between sites. We calculated six pairwise values (across two plant families and three sites) for each index (S_J, S_S, and I_ST).

We compared three PD metrics (PD_Faith, MPD, and MNTD) between sites using both the multigene phylogeny and the single/dual-gene phylogenies. We selected only these three metrics, because they are the most common and easily differentiated PD metrics. We used Tukey’s honestly significant difference (HSD) tests to determine significant differences between means.

RESULTS

Plastid gene assembly and sequence alignment

We recovered the majority of the ca. 81 plastid genes (Jansen et al., 2007) in each family—76 plastid genes for 29 species of Asteraceae and 71 plastid genes for 20 species of Fabaceae (Appendix 2). Alignments for concatenated multigene and single/dual-gene data sets varied in length (Table 2). The depth of Illumina sequence coverage for assemblies ranged from 11× to 1896× in Asteraceae and 62× to 3027× in Fabaceae (Appendix 1). We uploaded all gene sequences to GenBank (Appendix S1 ^{(95.7KB, docx)} ).

Table 2.

Alignment lengths and maximum likelihood tree statistics for all data sets.

Data seta	No. of taxa	Gene(s)	Aligned length (bp)	ML tree score (-lnL)
Asteraceae	29	76 plastid genesb	54,786	137,611.954
Fabaceae	20	71 plastid genesb	53,699	182,497.596
Asteraceae	29	matK	1542	5165.388
Fabaceae	20	matK	1608	6959.812
Asteraceae	29	rbcL	1458	4285.702
Fabaceae	20	rbcL	1428	4649.922
Asteraceae	29	matK + rbcL	3000	9604.216
Fabaceae	20	matK + rbcL	3036	11,795.693

Note: bp = nucleotide base pairs; ML = maximum likelihood.

^aSequence alignments available from the Dryad Digital Repository (http://dx.doi.org/10.5061/dryad.7s4h1; Kellar et al., 2015).

^bSee Appendix 2 for the list of genes.

We recovered all genes completely with both start and stop codons without ambiguities or missing data, with a few exceptions. The following genes were complete except for a small number of unknown bases, which we coded as missing data in phylogenetic analyses as follows (bp = number of unknown nucleotide bases): Asteraceae—matK (15 bp), ndhG (28 bp), and ndhF (21 bp) in Helianthus mollis, rbcL (7 bp) in Tragopogon dubius, and atpB (6 bp) in Gutierrezia sarothrae; Fabaceae—rpl33 (4 bp) in Strophostyles leiosperma. Also, for rpl33 in S. leiosperma, we did not identify start and stop codons.

Phylogenetic analyses

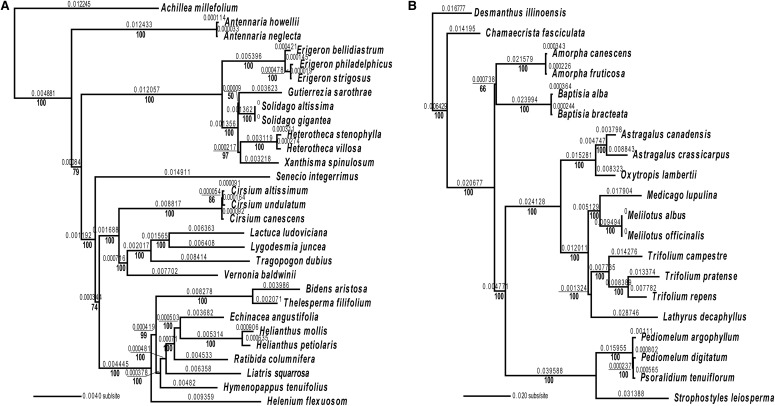
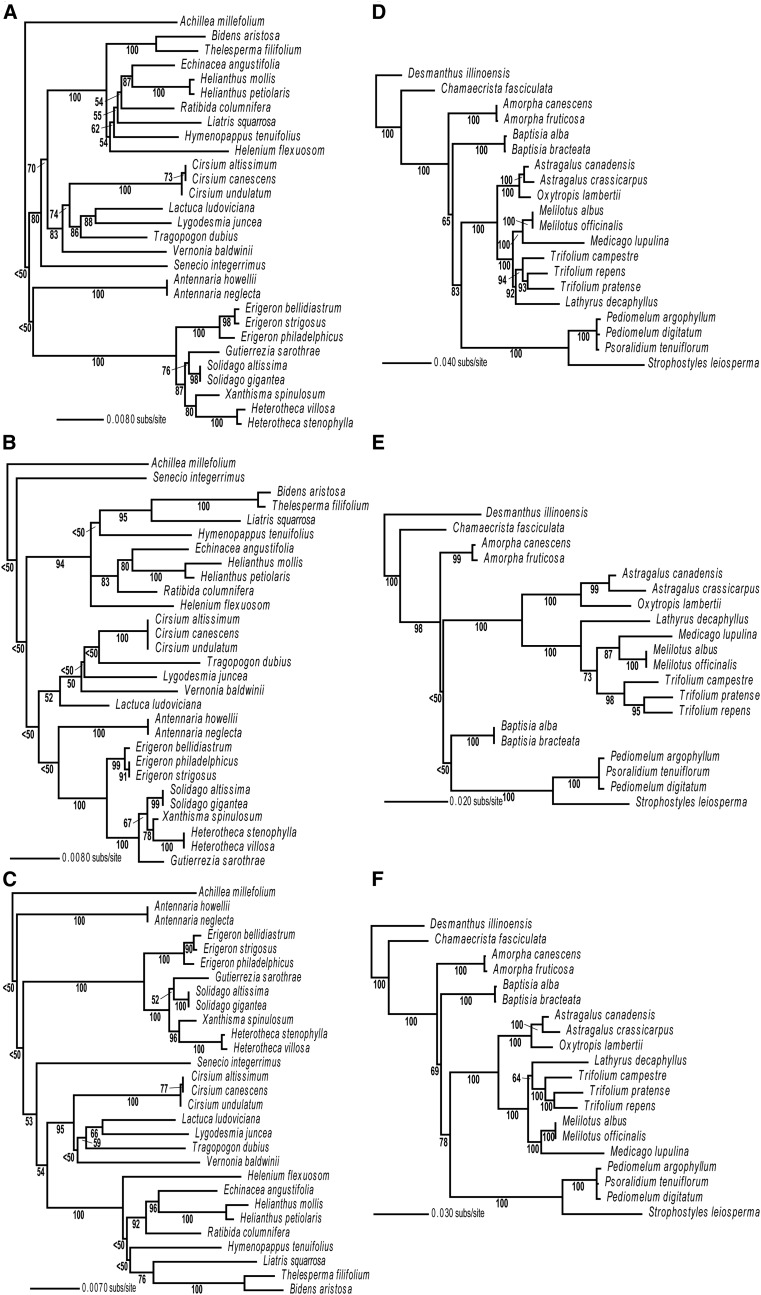
We estimated ML trees for Asteraceae and Fabaceae from multigene data sets (Fig. 1), single-gene data sets (Fig. 2A, B, D, and E), and dual-gene data sets (Fig. 2C and F). Many nodes with high bootstrap support in the multigene trees were not well supported in the single/dual-gene trees. For example, in the Asteraceae multigene tree (Fig. 1A), most branches had bootstrap values of 100, and all but one branch in the Fabaceae multigene tree (Fig. 1B) had bootstrap values of 100. Topologies in the single/dual-gene trees (Fig. 2) and the multigene trees (Fig. 1) showed similarities in clades but also contained incongruent species relationships between the trees. In single/dual-gene trees (Fig. 2), many branches received weak (<50) bootstrap support.

Fig. 1.

Maximum likelihood (ML) trees inferred from the concatenated set of (A) 76 plastid genes for 29 species of Asteraceae with Achillea millefolium as the outgroup, and (B) 71 plastid genes for 20 species of Fabaceae with Desmanthus illinoensis as the outgroup. Numbers above branches indicate branch lengths used in the calculations of phylogenetic diversity (PD) metrics; numbers below the branches indicate ML bootstrap support values resulting from 1000 bootstrap replicates.

Fig. 2.

Maximum likelihood (ML) trees inferred in Asteraceae from (A) matK, (B) rbcL, and (C) matK + rbcL genes with Achillea millefolium as the outgroup, and in Fabaceae from (D) matK, (E) rbcL, and (F) matK + rbcL genes with Desmanthus illinoensis as the outgroup. Numbers below the branches indicate ML bootstrap support values resulting from 1000 bootstrap replicates.

PD metrics and traditional measures of biodiversity

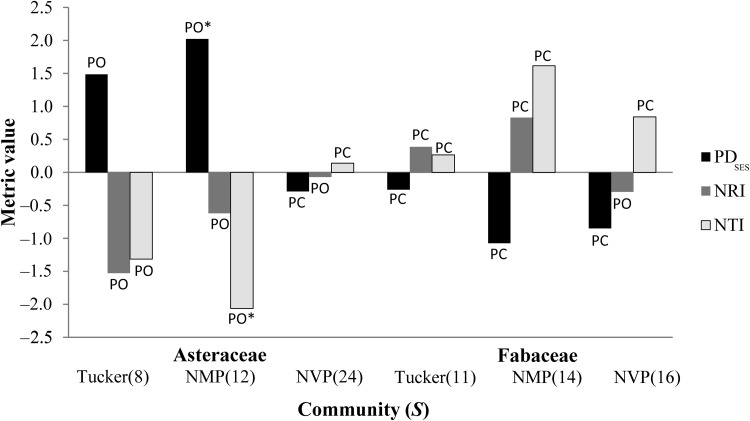
We calculated traditional biodiversity indices, and we used the multigene data sets to calculate all 12 PD metrics (Table 3 and Appendix S2 ^{(382.7KB, pdf)} ). Those values found to be significantly different from random are marked with an asterisk. Figure 3 reveals which of the community assembly metrics (PD_SES, NRI, and NTI) indicate phylogenetic evenness or clustering of species in our data sets. Only two of these values were statistically significant; therefore, the other values indicate random assembly.

Table 3.

Eleven^a PD metrics (in boldface) calculated from multigene phylogenies of two angiosperm families (Asteraceae [Fig. 1A] and Fabaceae [Fig. 1B]) and four traditional measures of biodiversity, among three North American prairies.^b

	Asteraceae			Fabaceae
Metric	Tucker	NMP	NVP	Tucker	NMP	NVP	F statistic (P value)c
PDFaith	0.094	0.127	0.158	0.285	0.307	0.338	0.10 (0.91)
PDSES	1.489	2.026*	−0.288	−0.262	−1.073	−0.848	—
MPD	0.028	0.026	0.025	0.079	0.078	0.082	0.00 (0.99)
MNTD	0.017	0.016	0.007	0.051	0.032	0.017*	1.52 (0.35)
NRI	−1.527	−0.618	−0.070	0.387	0.832	−0.295	—
NTI	−1.314	−2.062*	0.140	0.265	1.616	0.843	—
SPD	0.777	1.702	6.928	6.560	9.996	9.784	2.26 (0.25)
PSV	0.648	0.608	0.550*	0.592	0.563	0.511	—
PSR	5.181	7.293	13.201	6.517	7.885	8.173	—
PSC	0.590	0.619	0.824	0.722	0.812	0.869	2.01 (0.28)
IST	Tucker:NMP = 0.032	NMP:NVP = 0.011	Tucker:NVP = 0.026	Tucker:NMP = 0.015	NMP:NVP = 0.007	Tucker:NVP = 0.019	2.22 (0.25)
S	8	12	24	11	14	16	4.45 (0.13)
ENS	24.8	20.3	12.8	18.67	17.31	13.56	4.82 (0.12)
SJ	Tucker:NMP = 0.25	NMP:NVP = 0.35	Tucker:NVP = 0.08	Tucker:NMP = 0.47	NMP:NVP = 0.67	Tucker:NVP = 0.35	1.15 (0.43)
SS	Tucker:NMP = 0.40	NMP:NVP = 0.52	Tucker:NVP = 0.15	Tucker:NMP = 0.64	NMP:NVP = 0.80	Tucker:NVP = 0.52	1.17 (0.42)

*Indicates a statistically significant result; metrics are defined in Table 1.

^aThe SEH metric results in a vector of distinctiveness for every species in the tree for each site (Appendix S2 ^{(382.7KB, pdf)} ); therefore, it is not shown here.

^bTucker = Tucker Prairie Natural Area, Missouri; NMP = Nine-Mile Prairie, Nebraska; NVP = Niobrara Valley Preserve, Nebraska.

^cStatistical comparison among the three sites, with two data points (Asteraceae and Fabaceae) at each site.

Fig. 3.

PD_SES, NRI, and NTI across the species gradient in two plant families and three prairies. For NRI and NTI, statistically significant negative values indicate phylogenetic overdispersion or evenness (PO) and positive values indicate phylogenetic clustering (PC), whereas for PD_SES, negative values indicate PC, and positive values indicate PO. However, values that were not statistically significant indicate random community assembly. * = statistically significant; Tucker = Tucker Prairie, Missouri; NMP = Nine-Mile Prairie, northwest of Lincoln, Nebraska; NVP = Niobrara Valley Preserve in north-central Nebraska.

Across two plant families and three sites, we made six pairwise comparisons using S_J, S_S, and I_ST (Table 3). As expected, S_J tends to increase as S_S increases, and I_ST decreases to some extent with increased S_S and S_J. We calculated SEH for each species at each site. Calculations resulted in distinctiveness values (i.e., portion of the phylogeny attributable to each species, based on branch lengths, where shared branches are divided equally among descendant lineages) for each taxon relative to the other species present at the site. Because not all species occur at every site, SEH values vary for each taxon at each site. In our data set, excluding the outgroup, the most distinct taxon in each community was as follows: Asteraceae—Tucker (Bidens aristosa), NMP and NVP (Antennaria neglecta); Fabaceae—Tucker (Strophostyles leiosperma), NMP (Baptisia bracteata and Chamaecrista fasciculata are equally distinct), NVP (S. leiosperma and Lathyrus decaphyllus are equally distinct) (Appendix S2 ^{(382.7KB, pdf)} ). ENS values (>S) for Tucker and NMP in both plant families indicated higher diversity than expected, but both ENS values (<S) for NVP indicated lower diversity than expected (Table 3).

Overall, results revealed variation among PD metrics at the different sites (Table 3); however, the one-way ANOVA revealed no differences that were statistically significant (Table 3). Therefore, we ranked the diversity values (low to high) at each site (Table 4), and then performed Kruskal–Wallis tests (between three sites) and Mann–Whitney tests (for pairwise comparisons). Results were statistically significant and revealed the tendency for Tucker to rank lowest in diversity and NVP to rank highest across metrics. However, pairwise comparisons of ranked diversity between sites revealed that NMP and Tucker are both less diverse than NVP, but Tucker is not significantly less diverse than NMP (significance values shown in Table 4).

Table 4.

Diversity rank (1 = lowest to 3 = highest) for seven^a biodiversity metrics in two plant families between three North American prairies.^b,c

Metric	Tucker	NMP	NVP
Asteraceae
PDFaith	1	2	3
MPDc	2	2	2
MNTD	3	2	1
SPD	1	2	3
PSC	1	2	3
S	1	2	3
ENS	3	2	1
Fabaceae
PDFaith	1	2	3
MPD	1	2	3
MNTD	3	1	2
SPD	1	2	3
PSC	1	2	3
S	1	2	3
ENS	3	2	1
Average rank	1.64	1.93	2.43

^aPD metrics not included here have normalized values based on comparisons with null models or hypothetical data sets.

^bTucker = Tucker Prairie Natural Area, Missouri; NMP = Nine-Mile Prairie, Nebraska; NVP = Niobrara Valley Preserve, Nebraska.

^cSite comparison statistics were calculated using a Kruskal–Wallis test or Mann–Whitney U test: Tucker:NMP:NVP (F₂ = 6.984, P = 0.03); Tucker:NMP (U₁ = 2.296, P = 0.13); NMP:NVP (U₁ = 5.155, P = 0.02); Tucker:NVP (U₁ = 4.645, P = 0.031).

^cMetric value was equivalent across sites, so all were ranked “2.”

One-way ANOVA tests indicated no significant difference between PD_Faith (Asteraceae) values or MNTD (Asteraceae and Fabaceae) values calculated from multigene phylogenies and single/dual-gene phylogenies (Table 5; “—” in HSD column). However, there was significant difference between PD_Faith (Fabaceae) values and between MPD (Asteraceae and Fabaceae) values calculated from the different data sets (Table 5; letters A–H in the HSD column indicate values that were significantly different from each other). In Asteraceae, MPD calculated from the multigene phylogeny (Table 5, A) was significantly different from MPD calculated from the other three data sets (Table 5, B). In Fabaceae, PD_Faith and MPD calculated from the multigene and rbcL phylogenies (Table 5, E and H for PD_Faith and MPD, respectively) were significantly different from those calculated from the other two data sets, which were also significantly different from each other (see Table 5).

Table 5.

Comparison of three PD metrics from phylogenies of two flowering plant families across three North American prairies,^a estimated from data sets containing varying quantities of plastid DNA characters.

		Asteraceae				Fabaceae
Metric	Genes included	Tucker (S = 8)	NMP (S = 12)	NVP (S = 24)	Tukey’s HSDb	Tucker (S = 11)	NMP (S = 14)	NVP (S = 16)	Tukey’s HSDb
PDFaith	>70 genesc	0.094	0.127	0.158	—	0.285	0.307	0.338	E
	matK	0.178	0.232	0.291	—	0.487	0.518	0.557	C
	rbcL	0.163	0.193	0.258	—	0.258	0.299	0.334	E
	matK + rbcL	0.171	0.217	0.278	—	0.376	0.411	0.447	D
MPD	>70 genesc	0.028	0.026	0.025	A	0.079	0.078	0.082	H
	matK	0.054	0.047	0.048	B	0.125	0.125	0.131	F
	rbcL	0.048	0.040	0.040	B	0.075	0.079	0.084	H
	matK + rbcL	0.051	0.044	0.044	B	0.100	0.101	0.107	G
MNTD	>70 genesc	0.017	0.016	0.007	—	0.051	0.032	0.017	—
	matK	0.033	0.029	0.014	—	0.050	0.028	0.028	—
	rbcL	0.030	0.024	0.013	—	0.023	0.015	0.017	—
	matK + rbcL	0.032	0.028	0.014	—	0.037	0.022	0.022	—

Note: PD_Faith = phylogenetic diversity (Faith, 1992); MPD = mean pairwise distance (Webb et al., 2002; Kembel et al., 2010); MNTD = mean nearest taxon distance (Webb et al., 2002; Kembel et al., 2010); S = species richness.

^aTucker = Tucker Prairie Natural Area, Missouri; NMP = Nine-Mile Prairie, Nebraska; NVP = Niobrara Valley Preserve, Nebraska.

^bTukey’s honestly significant difference (HSD) tests were conducted for each metric and each plant family separately. Letters A–H indicate values that were significantly different from each other. Values with the same letter are not significantly different at alpha = 0.05; — indicates that there were no statistically significant differences between values of that metric between the various data sets.

^cSeventy-six plastid genes included for Asteraceae; 71 plastid genes included for Fabaceae (see Appendix 2 text for the list of genes).

DISCUSSION

In this review, we highlight the 12 most common PD metrics found in the literature (Table 1) and report results from a study focused on two major angiosperm families found in prairies. We compared these 12 metrics with traditional diversity indices and compared among values from phylogenetic alignments varying from few to many plastid genes generated with high-throughput sequencing. Our phylogenies were inferred from genes from only one organelle, and a majority of our resulting PD metric values were not significantly different from random (Table 3); therefore, we cannot make concrete recommendations for conservation planners based on our results. However, our results contribute to a growing database of phylogenies and PD metric evaluations that reveal a means to inform conservation decision makers, given more empirical studies. Biodiversity metrics are calculated in distinct ways, leading to varying results and differing interpretations of biodiversity in a region, and individual conservation/research goals vary from project to project; therefore, we describe how the results of each metric may be interpreted (Table 1; “interpretation of values”), so the conservation planner, community ecologist, or other investigator can select the best metric for his/her application. Below, we discuss the results of our study, results from other notable PD investigations, provide a list of the metrics with their potential uses by practitioners, and make suggestions for future applications of PD metrics to conservation questions.

How do PD metrics compare to each other and with traditional measures of biodiversity, and how do they vary among similar communities?

Computer modeling studies have shown varying results from regression analyses between S (species richness) and the different PD metrics (Cadotte et al., 2010; Tucker and Cadotte, 2013). In our study, in data sets with greater S, PD_Faith was higher (Table 3) for both angiosperm families. This was expected as modeling has shown a strong correlation between S and PD_Faith when the species pool contains less than 80 taxa (Tucker and Cadotte, 2013). PD_Faith was the first biodiversity metric to incorporate phylogeny (Faith, 1992). It reveals overall diversity resulting from evolutionary history, i.e., higher values indicate a greater range of phylogenetic variation across the taxa in a tree, but PD_Faith does not reveal anything about tree topology or the source of diversity within the data set. However, it is the metric that is easiest to describe and understand; therefore, it is the one that has been calculated and discussed most often in the literature. Multiple studies have compared changes in PD_Faith with changes in S, with mixed results.

Cadotte et al. (2010) compared phylogenetic structure between native and exotic plant communities using PD_Faith and various metrics incorporating abundance, and found PD_Faith to increase with community richness. Rodrigues and Gaston (2002) found equally effective results in selecting complementary sets of sites using South African bird data, when they maximized for S and PD_Faith separately. However, in a complementarity study using 735 species of angiosperms across the Cape of South Africa, Forest et al. (2007) showed S to be dissociated from PD_Faith. The modeling results of Tucker and Cadotte (2013) may explain both the Cape angiosperm results (Forest et al., 2007) that included 735 species and did not show a relationship between PD_Faith and S and our data that included only 49 species and showed an increase in PD_Faith with increased S (Table 3).

Species richness is also expected to correlate with both SPD and PSR because their calculations incorporate S. SPD reveals overall tree topology (Crozier, 1997), and PSR reveals species richness after discounting relatedness (Helmus et al., 2007). Although we have results from only three prairie sites, our data reveal the tendency for both SPD and PSR to increase with increased S (Table 3). Based on these results and the PD_Faith correlations discussed above, conservation planners may use S as a predictor of overall phylogenetic diversity in communities with low species richness.

MPD and MNTD are both averages and reveal relatedness of co-occurring species within a community. Across our data (Table 3), MNTD values were lower than MPD values. This was expected since MNTD is the average of only the nearest neighbor distances, whereas MPD is the average of all pairwise species. Higher MPD values indicate relatedness deep in the tree (i.e., older lineage splitting); higher MNTD values indicate species relatedness at branch tips (i.e., more recent lineage splitting). MPD is not expected to change as S changes, but MNTD is expected to decrease with increased S (Cadotte et al., 2010). We did not conduct regressions with these data because we only had three data points for each plant family; however, as expected, MNTD values decreased with increased S and MPD did not change with S (Table 3) in either plant family. When MPD and MNTD metric values do not follow this trend, it may indicate a nonrandom change in species relatedness as S changes, leading a practitioner to conclude that there are phylogenetically unique species in the community.

Like MPD and MNTD, PSV and PSC reveal phylogenetic relatedness of species in a data set, but to calculate PSV and PSC, all branch lengths are proportioned such that the total length of all branches from the root to each species tip equals 1 (Helmus et al., 2007). Higher values of both PSV and PSC indicate decreased relatedness among species or higher diversity in the community. As with MPD, our data reveal no change in PSV as S changes, and PSC increases with increased S, both as expected. PSV and PSC do not reveal community characteristics or species content beyond the PD metrics described above, but calculating these metrics can provide support to (or show conflict with) results of MPD and MNTD values.

PD_SES, NRI, and NTI compare observed values of PD_Faith, MPD, and MNTD, respectively, to null communities, randomly generated from the same data set. As in the hummingbird data set (González-Caro et al., 2012), our data showed mixed results (Table 3, Fig. 3). With only two exceptions (PD_SES and NTI in NMP for Asteraceae), none of our results were statistically significant; therefore, we can only conclude that the communities assembled randomly. When the values of PD_SES, NRI, and NTI are significantly different from random, researchers can draw one of two conclusions: (1) communities that show phylogenetic overdispersion or evenness likely assembled via competitive exclusion, or (2) communities that show phylogenetic clustering likely assembled via environmental filtering (Cavender-Bares et al., 2004). Additionally, with statistically significant results, conservation practitioners may conclude that there is greater diversity in phylogenetically overdispersed communities than in phylogenetically clustered communities.

SEH (Appendix S2 ^{(382.7KB, pdf)} ) values reveal the most distinct species, which vary between data sets as the plant composition changes. These values can help conservation planners identify unique taxa in various communities.

Despite the fact that traditional measures of biodiversity do not include information about evolutionary history, they can provide supporting data to ecological and conservation investigations into diversity. ENS indicates the number of equally frequent species in a simulated community that would produce the Shannon–Wiener index (Jost, 2006). Knowing S, practitioners can calculate ENS to determine if a community has higher or lower diversity than expected.

Traditional diversity indices, S_J (Jaccard, 1912) and S_S (Sørensen, 1948), reveal relative diversity between two sites and may be compared with I_ST (Hardy and Senterre, 2007), a similar metric that incorporates phylogeny. Higher values of S_J and S_S indicate increased similarity between sites, whereas higher values of I_ST indicate greater differences between sites. Therefore, across pairwise comparisons of communities, as S_J and S_S increase, I_ST is expected to decrease. Our data showed this trend, but only moderately. When comparing multiple communities, practitioners can use these metrics to determine relative diversity between sites.

Conservation biologists, ecologists, and other researchers and practitioners may calculate any or all of these metrics, depending on their goals or the focus of their study, and then draw conclusions when metrics agree or disagree. Following is a list of the potential applications for all metrics discussed in this study:

• • S may be used as a predictor of overall phylogenetic diversity (PD_Faith, SPD, and PSR) for data sets with less than 80 samples.

• • MPD and MNTD can be used to discover relatedness between species either deep in the tree (MPD) or near branch tips (MNTD). PSV and PSC reveal similar phylogenetic characteristics.

• • PD_SES, NRI, and NTI can be used to determine if a community is phylogenetically even (overdispersed), indicating greater diversity than expected, or is phylogenetically clustered, indicating lower diversity than expected.

• • SEH can be used to identify unique taxa.

• • ENS may be used to determine if a community has higher or lower diversity than expected from the number of species.

• • S_J, S_S, and I_ST can be used to compare relative diversity between sites.

The most challenging task in calculating PD metrics may be the acquisition of a phylogeny for the taxa present; however, once a phylogeny is obtained, it is fairly simple to calculate all of the metrics, thanks to various functions in the Picante package (Kembel et al., 2010), for use in R and EstimateS (version 9; Colwell, 2013). For the most comprehensive picture of diversity at a site or between sites, we recommend calculating all of these metrics. As described above, various combinations of these metrics should give similar indications about diversity. If great biodiversity exists in a community or in comparisons between communities, then the metrics should agree, and the conclusions will be supported by multiple results. If the metrics do not agree, one can draw conclusions about the source of variation from the descriptions of the metrics above. If results are not statistically significant, then a nonparametric rank test, such as a Kruskal–Wallis test (Kruskal and Wallis, 1952), can provide an indication of biodiversity.

How do PD metrics calculated from multigene phylogenies compare to those that were calculated from single- or dual-gene phylogenies?

The different data sets led to varying tree topologies (Figs. 1, 2), resulting in varied PD metric values (Table 5). The PD metrics calculated from multigene phylogenies were, in all cases, lower than the PD metrics from single- or dual-gene phylogenies (Table 5). This was expected because branch lengths (i.e., phylogenetic distances between taxa) are measured in average nucleotide substitutions per site, and the multigene data set contains some relatively slowly evolving coding regions. In contrast, rbcL and matK are relatively faster-evolving (compared to other plastid genes), which is why they are the most common plastid markers used in systematics. The total quantities of phylogenetically informative sites in the multigene data sets are much higher than those in the single- or dual-gene data sets, leading to greater support for clades (though not necessarily leading to greater confidence in relationships, since only plastid genes were used).

Based on Tukey’s HSD tests, some of the PD metrics were significantly different between data sets (Fabaceae: PD_Faith and MPD; Asteraceae: MPD; Table 5). These mixed results hint at the possibility that data sets of varying sequence content may result in different interpretations of biodiversity; however, they do not present a clear indication as to whether the expense of generating the multigene data set is warranted. More empirical studies with larger data sets are required to draw strong conclusions.

As reported above, not all PD metric values were significantly different from random; therefore, results must be interpreted with caution. First, the differences in PD metrics calculated from the various data sets were not consistent, revealing that the cases in which the multigene metrics will differ from the single- or dual-gene metrics may not be predictable. Second, even when PD metrics calculated from various data sets result in similar relative diversity values between geographic sites, the single- and dual-gene phylogenies had varying topologies and did not contain strong or even moderate support for relationships across all branches (Fig. 2). Third, our results show that it will be vital to compare PD metrics calculated from phylogenies estimated from comparable character matrices.

Conclusions

For conservation planners to incorporate evolutionary history into priority region selection, they must have empirical evidence from studies that replicate the challenges they face, such as limited funds and use of surrogate organisms. Simulated data can aid in determining certain behaviors of PD metrics given particular assumptions, but our study may reflect well the true scope of decision making by land managers. As more sequence data are generated from high-throughput sequencing and more phylogenies are published across the tree of life, the time and expense of calculating multiple, reliable biodiversity metrics will become routine. Additionally, decision makers must trust the accuracy of metric values and understand distinctions between the many PD equations now available. The results of our study begin to address these criteria by demonstrating how PD metrics compare with traditional measures of biodiversity and between similar communities, but many more empirical studies are needed. Based on our recommendations, practitioners can use multiple PD metrics and traditional diversity indices to build a picture of diversity at a site or between sites.

Many researchers now agree that including evolutionary history into biodiversity assessment is important. Calculating and comparing several PD metrics can provide multiple lines of support to characterize the source of biodiversity or reveal communities with conflicting phylogenetic structure. Our results suggest that it is vital to compare PD metrics based on comparable data sets. However, further investigations are needed that: (1) include additional DNA sequence data available from high-throughput DNA sequencing from other cellular compartments such as mitochondrial and nuclear genomes, to add evidence for relationships; (2) expand data sets to include larger numbers of taxa (>80) and greater breadth of organisms; (3) compare PD metrics from phylogenies estimated with three to many genes to determine the data set size by which PD metric values are not affected; (4) compare PD metrics between contrasting geographic sites; (5) include PD metrics that account for abundance of species; (6) compare PD metrics calculated from phylogenies estimated using alternative algorithms, such as Bayesian; and (7) compare PD metrics calculated from empirical data to simulated data sets under the same parameters to assess the accuracy, consistency, and efficiency of indices. It is with empirical data that conservation planners and decision makers will have the information needed to select the best sites for preservation.

Appendix 1.

Flowering plant species included in phylogenetic trees and in calculations of PD metrics, the study sites at which each species occurs, and the average depth of sequence coverage across the complete set of genes.

						Presence at study sitesc
Family	Genus	Specific epithet	Scientific authoritya	Voucher no.	Herbariumb	Tucker	NMP	NVP	Average Illumina sequence coveraged
Asteraceae	Achillea	millefolium	L.	Steele 1317	OMA	Yes	Yes	Yes	100×
Asteraceae	Antennaria	howellii	Greene	Steele 1262	OMA	No	No	Yes	127×
Asteraceae	Antennaria	neglecta	Greene	Steele 1258	OMA	No	Yes	Yes	353×
Asteraceae	Bidens	aristosa	(Michx.) Britton	Steele 1224	UMO	Yes	No	No	296×
Asteraceae	Cirsium	altissimum	(L.) Spreng.	Steele 1219	UMO	Yes	Yes	Yes	160×
Asteraceae	Cirsium	canescens	Nutt.	Steele 1302	OMA	No	No	Yes	294×
Asteraceae	Cirsium	undulatum	(Nutt.) Spreng.	Steele 1355	OMA	No	No	Yes	214×
Asteraceae	Echinacea	angustifolia	DC.	Steele 1365	OMA	No	Yes	Yes	103×
Asteraceae	Erigeron	bellidiastrum	Nutt.	Steele 1299	OMA	No	No	Yes	1489×
Asteraceae	Erigeron	philadelphicus	L.	Steele 1323	OMA	No	No	Yes	171×
Asteraceae	Erigeron	strigosus	Muhl. ex Willd.	Steele 1357	OMA	Yes	Yes	Yes	946×
Asteraceae	Gutierrezia	sarothrae	(Pursh) Britton & Rusby	Steele 1360	OMA	No	No	Yes	100×
Asteraceae	Helenium	flexuosum	Raf.	Steele 1209	UMO	Yes	No	No	51×
Asteraceae	Helianthus	mollis	Lam.	Steele 1202	UMO	Yes	No	No	11×
Asteraceae	Helianthus	petiolaris	Nutt.	Steele 1366	OMA	No	No	Yes	275×
Asteraceae	Heterotheca	stenophylla	(A. Gray) Shinners	Steele 1350	OMA	No	No	Yes	210×
Asteraceae	Heterotheca	villosa	(Pursh) Shinners	Kellar 1379	OMA	No	No	Yes	617×
Asteraceae	Hymenopappus	tenuifolius	Pursh	Steele 1325	OMA	No	No	Yes	547×
Asteraceae	Lactuca	ludoviciana	(Nutt.) Riddell	Kellar 1383	OMA	No	Yes	Yes	87×
Asteraceae	Liatris	squarrosa	(L.) Michx.	Steele 1347	OMA	No	No	Yes	231×
Asteraceae	Lygodesmia	juncea	(Pursh) D. Don ex Hook.	Steele 1362	OMA	No	Yes	Yes	229×
Asteraceae	Ratibida	columnifera	(Nutt.) Wooton & Standl.	Steele 1354	OMA	No	Yes	Yes	118×
Asteraceae	Senecio	integerrimus	Nutt.	Steele 1274	OMA	No	Yes	Yes	93×
Asteraceae	Solidago	altissima	L.	Steele 1216	UMO	Yes	No	No	47×
Asteraceae	Solidago	gigantea	Aiton	Kellar 1389	OMA	No	Yes	Yes	839×
Asteraceae	Thelesperma	filifolium	(Hook.) A. Gray	Steele 1308	OMA	No	No	Yes	1896×
Asteraceae	Tragopogon	dubius	Scop.	Steele 1291	OMA	No	Yes	Yes	403×
Asteraceae	Vernonia	baldwinii	Torr.	Steele 1200	UMO	Yes	Yes	No	99×
Asteraceae	Xanthisma	spinulosum	(Pursh) D. R. Morgan & R. L. Hartm.	Steele 1352	OMA	No	No	Yes	145×
Fabaceae	Amorpha	canescens	Pursh	Jones 1024	OMA	Yes	Yes	Yes	325×
Fabaceae	Amorpha	fruticosa	L.	Jones 1023	OMA	No	Yes	Yes	1603×
Fabaceae	Astragalus	canadensis	L.	Jones 1030	OMA	No	Yes	Yes	526×
Fabaceae	Astragalus	crassicarpus	Nutt.	Jones 1003	OMA	No	Yes	Yes	1727×
Fabaceae	Baptisia	alba	(L.) R. Br.	Steele 1119	UMO	Yes	No	No	62×
Fabaceae	Baptisia	bracteata	Muhl. ex Elliott	Steele 1107	UMO	Yes	Yes	No	250×
Fabaceae	Chamaecrista	fasciculata	(Michx.) Greene	Steele 1206	UMO	Yes	Yes	No	163×
Fabaceae	Desmanthus	illinoensis	(Michx.) MacMill. ex B. L. Rob. & Fernald	Steele 1151	UMO	Yes	Yes	Yes	176×
Fabaceae	Lathyrus	decaphyllus	Pursh	Jones 1001	OMA	No	No	Yes	676×
Fabaceae	Medicago	lupulina	L.	Jones 1020	OMA	No	Yes	Yes	1292×
Fabaceae	Melilotus	albus	Medik.	Jones 1031	OMA	Yes	Yes	Yes	494×
Fabaceae	Melilotus	officinalis	(L.) Lam.	Jones 1016	OMA	Yes	Yes	Yes	3027×
Fabaceae	Oxytropis	lambertii	Pursh	Jones 1009	OMA	No	No	Yes	1131×
Fabaceae	Pediomelum	argophyllum	(Pursh) J. W. Grimes	Jones 1027	OMA	No	Yes	Yes	580×
Fabaceae	Pediomelum	digitatum	(Nutt. ex Torr. & A. Gray) Isely	Jones 1029	OMA	No	No	Yes	1957×
Fabaceae	Psoralidium	tenuiflorum	(Pursh) Rydb.	Jones 1026	OMA	No	Yes	Yes	1417×
Fabaceae	Strophostyles	leiosperma	(Torr. & A. Gray) Piper	Steele 1225	UMO	Yes	No	Yes	324×
Fabaceae	Trifolium	campestre	Schreb.	Steele 1126	UMO	Yes	No	No	312×
Fabaceae	Trifolium	pratense	L.	Steele 1112	UMO	Yes	Yes	Yes	353×
Fabaceae	Trifolium	repens	L.	Steele 1113	UMO	Yes	Yes	Yes	69×

^aScientific authorities are per the International Plant Names Index (www.ipni.org) and Tropicos (http://www.tropicos.org/).

^bOMA = Herbarium at the University of Nebraska at Omaha, Omaha, Nebraska; UMO = Herbarium at the University of Missouri, Columbia, Missouri.

^cTucker = Tucker Prairie, Missouri; NMP = Nine-Mile Prairie, northwest of Lincoln, Nebraska; NVP = Niobrara Valley Preserve in north-central Nebraska.

^dAsteraceae average coverage = 353× ± 81×, median = 210×; Fabaceae average coverage = 23× ± 176×, median = 510×.

Appendix 2.

Plastid genes concatenated and aligned for Asteraceae (76 genes) and Fabaceae (71 genes) phylogenetic analyses.

Gene	Asteraceae	Fabaceae		Gene	Asteraceae	Fabaceae
atpA	X	X		psbF	X	X
atpB	X	X		psbH	X	X
atpE	X	X		psbI	X	X
atpF	X	X		psbJ	X	X
atpH	X	X		psbK	X	X
atpI	X	X		psbL	X	X
ccsA	X	X		psbM	X	X
cemA	X	X		psbN	X	X
clpP	X	X		psbT	X	X
infA	X	—		psbZ	X	X
matK	X	X		rbcL	X	X
ndhA	X	X		rpl14	X	X
ndhB	X	X		rpl16	X	X
ndhC	X	X		rpl2	X	X
ndhD	X	X		rpl20	X	X
ndhE	X	X		rpl22	X	—
ndhF	X	X		rpl23	X	X
ndhG	X	X		rpl32	X	X
ndhH	X	X		rpl33	X	X
ndhI	X	X		rpl36	X	X
ndhJ	X	X		rpoA	X	X
ndhK	X	X		rpoB	X	X
petA	X	X		rpoC1	X	X
petB	X	X		rpoC2	X	X
petD	X	X		rps11	X	X
petG	X	X		rps12	X	X
petL	X	X		rps14	X	X
petN	X	X		rps15	X	X
psaA	X	X		rps16	X	—
psaB	X	X		rps18	X	—
psaC	X	X		rps19	X	X
psaI	X	X		rps2	X	X
psaJ	X	X		rps3	X	X
psbA	X	X		rps4	X	X
psbB	X	X		rps7	X	X
psbC	X	X		rps8	X	X
psbD	X	X		ycf3	X	X
psbE	X	X		ycf4	X	—

Note: “X” indicates inclusion of the gene; “—” indicates exclusion of the gene.