Predicting the Metabolic Cost of Incline Walking from Muscle Activity and Walking Mechanics

Abstract

The goal of this study was to identify which muscle activation patterns and gait features best predict the metabolic cost of inclined walking. We measured muscle activation patterns, joint kinematics and kinetics, and metabolic cost in sixteen subjects during treadmill walking at inclines of 0%, 5%, and 10%. Multivariate regression models were developed to predict the net metabolic cost from selected groups of the measured variables. A linear regression model including incline and the squared integrated electromyographic signals of the soleus and vastus lateralis explained 96% of the variance in metabolic cost, suggesting that the activation patterns of these large muscles have a high predictive value for metabolic cost. A regression model including only the peak knee flexion angle during stance phase, peak knee extension moment, peak ankle plantarflexion moment, and peak hip flexion moment explained 89% of the variance in metabolic cost; this finding indicates that kinematics and kinetics alone can predict metabolic cost during incline walking. The ability of these models to predict metabolic cost from muscle activation patterns and gait features points the way toward future work aimed at predicting metabolic cost when gait is altered by changes in neuromuscular control or the use of an assistive technology.

INTRODUCTION

Walking up an incline requires adjustments of muscle activations and increases metabolic cost, compared to walking on flat terrain (Duggan and Haisman, 1992; Hortobagyi et al., 2011; Kang et al., 2002; Pandolf et al., 1977). Pandolf et al. (1977) introduced a model that predicts the metabolic cost of walking up an incline from three easily measured variables: subject mass, walking velocity, and incline. This model is valuable, but like other models (Duggan and Haisman, 1992; van der Walt and Wyndham, 1973), it does not account for variations in muscle activations, body composition, or gait features, all of which can influence the metabolic cost of walking. As a result, the model described by Pandolf et al. (1977) is unlikely to accurately predict metabolic cost for a subject walking at a constant velocity and incline, but with muscle activation patterns that are altered as a result of using an assistive technology, such as an active orthosis. In such cases, muscle forces and activations may change, thereby altering metabolic cost. Models that account for variations in muscle activation patterns and gait features may provide more accurate predictions of metabolic cost in some cases.

Muscle activation patterns are associated with metabolic cost during walking (Hortobagyi et al., 2011). The magnitude and duration of muscle activity increases when subjects walk up an incline (Franz and Kram, 2011; Hortobagyi et al., 2011; Lay et al., 2007), suggesting that muscle activation patterns may help predict the increase in metabolic cost associated with inclined walking. Musculoskeletal simulations often estimate muscle activation patterns during walking using an objective function that minimizes the sum of squared simulated muscle activations (Anderson and Pandy, 2001; Thelen et al., 2003), which is thought to be related to metabolic cost; however, this relationship has not been rigorously tested.

Percent body fat also affects the metabolic cost of inclined walking (Kang et al., 2002) and level gait (Browning et al., 2006). Compared to healthy normal weight adults, obese subjects and normal weight subjects with a relatively high percent body fat have a higher mass-specific metabolic cost of walking (Browning et al., 2006; Kang et al., 2002). Percent body fat is not generally included predictive models (Duggan and Haisman, 1992; Hall et al., 2004; Pandolf et al., 1977; van der Walt and Wyndham, 1973), but may improve predictive accuracy.

Gait features, such as changing preferred step width (Donelan et al., 2002), eliminating arm swing (Umberger, 2008), and walking with flexed knees (Waters and Mulroy, 1999) can increase the metabolic cost of level walking. Thus, it seems likely that biomechanical changes in gait brought about by walking on an incline may also help to predict the increase in metabolic cost of incline walking.

The goal of this study was to determine which muscle activation patterns, physical characteristics, and gait features best predict metabolic cost during inclined walking. We hypothesized that the sum of squared integrated electromyographic (EMG) signals from lower limb muscles would be correlated with net metabolic cost. Further, because incline is a strong predictor of metabolic cost (Pandolf et al., 1977) and because certain muscles contribute more to metabolic cost than others, we hypothesized that incline and the squared integrated EMG signals from a subset of muscles would have better predictive capabilities than the sum of squared integrated EMG signals from all muscles. We also hypothesized that the predictive accuracy of the model described by Pandolf et al. (1977) could be improved by including percent body fat and fat distribution in place of total body mass. Finally, we hypothesized that kinematic and kinetic gait variables could predict metabolic cost, independent of incline. In addition to testing these hypotheses, this study provides a comprehensive description of the changes in metabolic cost, lower limb joint kinematics and kinetics, and muscle activation patterns during inclined walking.

METHODS

Equations placed in the text did not convert into pdf format properly. Certain instances of VO₂ and VCO₂ should have a superscript dot to indicate rate. The VO and VCO did not convert, so they appear in the text as “ ₂”

Sixteen subjects (10M, 6F; 33±8y; 68±11kg; 1.77±0.09m) provided informed consent to participate in this study, according to a protocol approved by the Stanford University Institutional Review Board. None of the subjects had current or previous lower limb or back injury, pain during walking, or illness within the past four-weeks, and all were able to run continuously for 60 minutes.

Body Composition and Metabolic Data

We measured each subject’s body composition using whole body dual-energy x-ray absorptiometry (iDXA; GE Healthcare, Waukesha, WI, USA). The scanner and software measured total mass, fat mass, and lean tissue mass of the full body, trunk, arms, and lower limbs as well as estimated percent android and gynoid fat. Android fat was estimated from the lower abdomen region, and gynoid fat was estimated from the upper thigh and gluteal region.

Standing metabolic cost (mean±SD: 1.29±0.30W/kg) was obtained by measuring oxygen consumption (V̇O₂, ml of O₂ per second) and carbon dioxide output (VĊO₂, ml of CO₂ per second) for a minimum of five minutes (Quark b², Cosmed, Italy). Prior to further testing, each subject chose a preferred walking velocity (1.29±0.11m/s) on a nearby treadmill that allowed the subject to manually choose a walking velocity (model ELG, Woodway Inc., Waukesha, WI, USA). Subjects were then familiarized with walking on a split belt instrumented treadmill, which was used for the remainder of testing (model TMO8I with incline, Bertec Corporation; Columbus, OH, USA). The test consisted of 15 minutes of continuous treadmill walking without rest periods: five minutes each at 0%, 5%, and 10% inclines. Average V̇O₂ and VĊO₂ were calculated during the final minute of each five minute period after subjects reached steady state (i.e. no significant increase in V̇O₂ and respiratory exchange ratio <1.0). Gross metabolic cost was estimated during standing and walking trials using Brockway’s equation (Brockway, 1987). The net normalized metabolic cost was estimated by subtracting standing metabolic cost from walking metabolic cost and dividing by body mass.

Spatiotemporal, Kinematic, and Kinetic Data

During each walking trial, whole body motion was tracked using 21 retroreflective markers placed on identifiable landmarks and 19 additional markers that aided in segment tracking (Cappozzo et al., 1995). Marker data were collected at 100Hz using an eight camera motion capture system (Vicon, Oxford Metrics Group, Oxford, UK). Ground reaction forces and moments measured from the treadmill were recorded at 2000Hz and defined using a coordinate system orthogonal to the walking surface. Motion, forces, and EMG data were collected for ~20s during the final minute of each trial. Five successive left limb gait cycles were chosen for analysis (Altman et al., 2012) during which the subject did not cross the center line of the split-belt instrumented treadmill. A scaled, 29 degree-of-freedom, 12 segment model was used to represent the torso, arms, pelvis, and lower extremity of each subject (Delp et al., 1990). The pelvis was the base segment and had six degrees-of-freedom, the hip was represented as a spherical joint and had three degrees-of-freedom, the knee was represented as a one degree-of-freedom joint in which non-sagittal rotations and tibiofemoral and patellofemoral translations were computed as a function of the sagittal knee angle (Walker et al., 1988), and the ankle and subtalar joints were represented as pin joints aligned with anatomical axes (Delp et al., 1990). A functional hip joint center identification algorithm (Piazza et al., 2004) was implemented using pelvis and thigh marker motion from trials in which the subject circumducted their right and left hips; this was used with a static standing calibration trial to define body segment coordinate systems and segment lengths. Pelvis position, pelvis orientation, and lower extremity joint angles were computed using a global optimization inverse kinematics routine (Lu and O’Connor, 1999). Inverse dynamics was conducted using body segment kinematics, anthropometric properties (de Leva, 1996), and treadmill forces. Dynamics Pipeline (Motion Analysis Corp, Santa Rosa, CA, USA, Delp and Loan, 2000) was used with SD/FAST (Parametric Technology Corporation, Waltham, MA, USA) to perform the inverse kinematics and inverse dynamics analyses. Joint works were calculated during select phases of the gait cycle by integrating the power curves over time. Step length (half the distance traveled between two successive left heel contacts), cadence (number of steps taken per minute), and percent stance phase (percentage of one gait cycle the left foot was in contact with the ground) were calculated.

Electromyography (EMG)

Muscle activity was monitored using surface electrodes placed on eight left lower limb muscles: soleus, medial gastrocnemius, tibialis anterior, medial hamstrings, lateral hamstrings, vastus medialis, vastus lateralis, and rectus femoris. EMG signals were recorded at 2000Hz using pre-amplified single differential electrodes with 10mm inter-electrode distance (DE-2.1, DelSys, Inc, Boston, MA, USA). Data were processed with a 30–500Hz sixth order bandpass Butterworth filter and full wave rectified. The Teager-Kaiser energy operator was then applied (Li and Aruin, 2005) and data were re-rectified. An average signal for each subject and incline was obtained by averaging across the same five gait cycles as the motion data. The onset, offset, and duration of muscle activity, relative to a gait cycle, was then manually determined (Li and Aruin, 2005). The integrated EMG signals were calculated by low-pass filtering the un-averaged data at 30Hz, averaging across five gait cycles, and normalizing to the maximum low-pass filtered signal for each muscle during level walking.

Statistical Analysis

To test our hypotheses, we built linear regression models to predict the net normalized metabolic cost (W/kg) from select measured variables. Simple linear regression was used to test our first hypothesis that the sum of squared integrated EMG signals would be correlated with net normalized metabolic cost. To test our hypothesis that incline and the squared integrated EMG signals from a subset of muscles would have better predictive capabilities than the sum of squared integrated EMG signals from all muscles, a multivariate regression model was generated using incline and the squared integrated EMG signals from the eight measured muscles as candidate predictor variables. To test our hypothesis that the predictive capabilities of the Pandolf model (Pandolf et al., 1977) could be improved by including percent body fat and fat distribution in place of total body mass, a multivariate regression model was generated that included walking velocity, incline, percent body fat, and a measure of fat mass distribution obtained from the iDXA. To compare the accuracy of this model to the one described by Pandolf et al. (1977), we created a comparative model using the same predictor variables as the Pandolf model: subject mass, walking velocity, and incline. A final multivariate regression model was created to test the hypothesis that kinematic and kinetic gait variables could predict metabolic cost, independent of incline; variables included for consideration in this model were: spatiotemporal, kinematic, and kinetic measures. All of the regression models were developed using the following general form:

$$Y=\sum {\beta }_i{x}_i$$ Eq. 1

where Y is the net normalized metabolic cost, β are the linear weighting coefficients, and x are the standardized predictive variables (non-standardized values reported in Tables 2 and 3). All data considered for the models were standardized by subtracting the mean and dividing by the standard deviation. Akaike’s Information Criterion (AIC) was first used to determine the best combination of variables to be included in each model (Akaike, 1974). AIC represents the goodness of fit of a regression model by accounting for the interaction between model accuracy and complexity. Pearson’s correlation was then used to check for multicolinearity among the AIC chosen variables. Finally, stepwise forward linear regression was used to determine the final set of variables to be included in each model.

Table 2.

Mean (standard deviation) spatiotemporal measures and peak ground reaction forces, normal to the walking surface.

	0%	5%	10%	p-value
Spatiotemporal
Step Length (normalized to height)	0.40 (0.03)	0.40 (0.03)	0.40 (0.03)	0.12
Cadence (steps/min)	110 (6)	109 (6)	110 (6)	0.15
Stance Phase (%)	59 (2)	61 (3)	61 (4)	0.03c
Peak Normal Force (normalized to body weight)
Loading	1.16 (0.06)	1.08 (0.09)	0.99 (0.21)	0.96
Pushoff	1.08 (0.05)	1.10 (0.10)	1.05 (0.23)	0.20

^a0≠5%,

^b5≠10%,

^c0≠10%

Table 3.

Mean (standard deviation) peak joint kinematics and kinetics for the three inclines tested.

	0%	5%	10%	p-value
Peak Joint Angles
Hip
Flexion	29 (6)	35 (5)	43 (6)	<0.01a,b,c
Extension	−15 (9)	−15 (9)	−15 (9)	0.58
Knee
Flexion - Stance	21 (6)	25 (7)	34 (8)	<0.01a,b,c
Flexion - Swing	69 (7)	67 (7)	68 (7)	<0.01a,c
Ankle
Dorsiflexion	10 (7)	11 (7)	14 (8)	<0.01b,c
Plantarflexion	−14 (7)	−15 (8)	−15 (7)	0.67
Peak Joint Moments (Nm/kg)
Hip
Flexion	0.58 (0.18)	0.49 (0.28)	0.34 (0.50)	0.08
Extension	−0.93 (0.23)	−1.22 (0.25)	−1.70 (0.32)	<0.01a,b,c
Knee
Flexion	0.44 (0.19)	0.68 (0.21)	1.03 (0.24)	<0.01a,b,c
Extension	−0.94 (0.24)	−0.67 (0.27)	−0.36 (0.25)	<0.01a,b,c
Ankle
Plantarflexion	−1.62 (0.17)	−1.87 (0.14)	−2.16 (0.29)	<0.01a,b,c
Peak Joint Powers (W/kg)
Hip
Generation (1st peak)	1.20 (0.36)	1.78 (0.53)	3.15 (0.91)	<0.01a,b,c
Absorption	−0.49 (0.23)	−0.35 (0.25)	−0.02 (0.28)	<0.01b,c
Generation (2nd peak)	0.94 (0.29)	1.09 (0.34)	1.06 (0.37)	0.20
Ankle
Generation	2.00 (0.51)	2.52 (0.49)	3.35 (0.75)	<0.01b,c
Joint Works (J/kg)
Hip
Positive (1st peak)	0.20 (0.06)	0.37 (0.10)	0.73 (0.19)	<0.01a,b,c
Negative	−0.06 (0.03)	−0.03 (0.03)	0.00 (0.01)	<0.01a,b,c
Positive (2nd peak)	0.13 (0.03)	0.15 (0.04)	0.16 (0.05)	0.06
Ankle
Positive	0.21 (0.06)	0.28 (0.08)	0.38 (0.11)	<0.01a,b,c

^a0≠5%,

^b5≠10%,

^c0≠10%

Repeated measures ANOVA (STATISTICA 6.0, StatSoft, Inc., Rulsa, OK, USA) was used to test the effect of incline on the following gait features: step length, cadence, percent stance phase, integrated muscle activities, muscle activation timing, and peak lower extremity joint kinematics and kinetics. Post-hoc analyses of main effects were investigated using Tukey’s Honestly Significant Difference (HSD). Significance for all analyses was set at p<0.05.

RESULTS

Metabolic Cost

The net normalized metabolic cost of level walking was 3.3±0.6W/kg. Metabolic cost increased 52±17% above level walking at 5% incline and increased 113±32% above level walking at 10% incline.

Muscle Activity

The sum of squared integrated EMG signals was correlated with the normalized net metabolic cost (R²=0.40). A linear regression model containing incline and the squared integrated EMG signals from the soleus and vastus lateralis resulted in an R² value of 0.96 (Table 1).

Table 1.

Standardized multivariate linear regression was used to investigate the relationship between three groups of measured variables and the net metabolic cost normalized to body mass.

	β	t-value	p-value
1. Squared Integrated Electromyographic Signals (iEMG2), R2 = 0.96
Incline	0.88	9.34	<0.01
Soleus iEMG2	0.37	4.94	<0.01
Vastus Lateralis iEMG2	−0.20	−2.26	0.05
2. Physical and Physiological Characteristics, R2 = 0.85
Incline	1.78	15.41	<0.01
Walking Velocity	0.05	0.51	0.61
Percent Body Fat	−0.29	−2.04	0.03
Percent Gynoid Fat	−0.29	2.20	0.04
3. Kinematic and Kinetic Variables, R2 = 0.89
Peak Knee Flexion – Stance	0.72	6.23	<0.01
Peak Knee Extension Moment	1.10	10.60	<0.01
Peak Ankle Plantarflexion Moment	−0.36	−3.00	<0.01
Peak Hip Flexion Moment	0.18	1.90	0.07

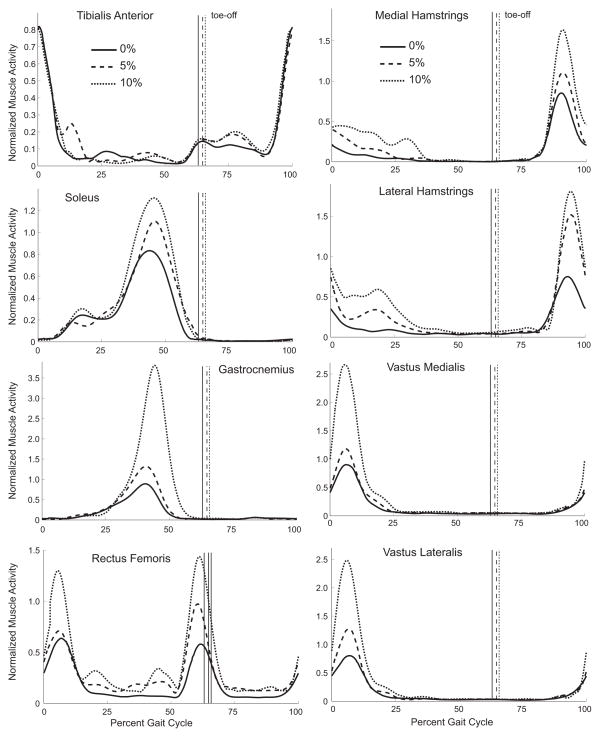
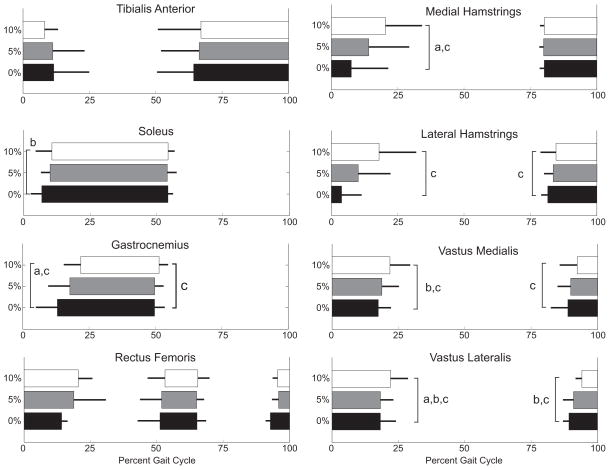
Integrated EMG activity of all but the tibialis anterior increased with incline (Fig. 1) (p<0.05). The timing of muscle activity was also affected by incline for all muscles except the tibialis anterior and rectus femoris (Fig. 2). As incline increased, the onset of soleus (p=0.04) and gastrocnemius (p<0.01) activity occurred later in stance phase. The gastrocnemius remained active for a shorter duration at incline, compared to level walking (p<0.01). The duration of activity increased for both the medial (p<0.01) and lateral (p=0.01) hamstrings, primarily as a result of these muscles turning off at a later time (p<0.01). Although the duration of vastus medialis and lateralis activity did not significantly change across inclines, the onset and offset of activity occurred later in the gait cycle (p<0.05).

Figure 1.

Ensemble averaged low-pass filtered muscle activity averaged across the same five gait cycles as the motion data. The signals from each subject and muscle were normalized to the maximum low-pass filtered signal of that muscle during level walking.

Figure 2.

Mean and standard deviation of muscle activation timing averaged across the same five gait cycles as the motion data. Thick bars represent when each muscle is active, and thin bars represent the standard deviation across all subjects tested.

^a0≠5%, ^b5≠10%, ^c0≠10%

Body Composition

A regression model that included incline, walking velocity, percent body fat, and percent gynoid fat explained 85% of the variance in metabolic cost; this was only marginally better than the model that included the same variables as the Pandolf model: incline, walking velocity, and body mass (R²=0.84) (Table 1). Mean body composition measures from the iDXA scan were: body fat, 16.9±6.4% (range, 7.2–32.0%); android fat 15.1±6.5% (range, 4.0–25.3%); gynoid fat 20.6±8.7% (range, 7.3–43.9%); legs/total fat mass ratio, 0.38±0.07 (range, 0.25–0.49); trunk/total fat mass ratio, 0.43±0.09 (range, 0.30–0.59); and the (arms+legs)/trunk fat mass ratio, 1.20±0.40 (range, 0.56–1.93).

Gait Features

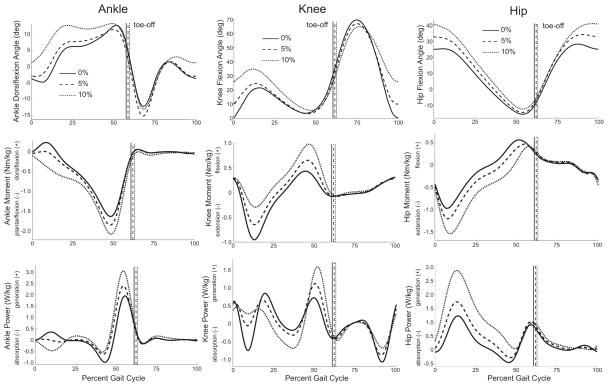
A regression model using only kinematic and kinetic variables resulted in an R² value of 0.89. Predictive variables in this model included two features from the first half of stance phase (peak knee flexion angle and peak knee extension moment) and two features from the second half of stance phase (peak ankle plantarflexion moment and peak hip flexion moment). The only spatiotemporal measure altered by incline was the duration of stance phase, which increased with incline (p=0.03) (Table 2). Peak hip flexion angle, peak stance phase knee flexion angle, and peak ankle dorsiflexion angle all increased with incline (Fig. 3, Table 3) (p<0.01). With the exception of the hip moment, power, and work associated with hip power generation during late stance and early swing phase, all peak joint moments, powers, and work were affected by incline (p<0.01) (Fig. 3, Table 3).

Figure 3.

Ensemble averaged lower extremity sagittal plane joint angles, moments and powers averaged across five gait cycles for walking on a level surface and up inclines of 5% and 10%.

DISCUSSION

The goal of this study was to determine which muscle activation patterns, physical characteristics, and gait features best predict metabolic cost during inclined walking. In achieving this goal, we provide a comprehensive description of lower extremity kinematics, kinetics, and muscle activation patterns during treadmill walking at inclines of 0%, 5%, and 10%. In support of our first hypothesis, the sum of squared integrated muscle activations from the eight lower extremity muscles measured in this study was correlated with net metabolic cost (R²=0.40). The sum of squared simulated muscle activations is a commonly used optimization function in musculoskeletal simulations to predict muscle activity during walking, and is thought be related to metabolic cost (Anderson and Pandy, 2001; Thelen et al., 2003). Our findings support this idea.

In support of our second hypothesis, a regression model containing only incline and the squared integrated EMG signals of soleus and vastus lateralis explained 96% of the variance in metabolic cost (Table 1). The improved predictive capability of this model likely arises for two reasons. First, incline is a strong predictor of metabolic cost (Pandolf et al., 1977) and was included in this model. Second, individual muscles contribute differently to metabolic cost. The soleus and vasti are the muscles with the two largest physiological cross-sectional areas in the lower limb (Arnold et al., 2010; Ward et al., 2009) and their activations increase significantly with incline (Fig. 1); thus, they likely contribute substantially to changes in metabolic cost with incline. The ability of muscle activations to predict metabolic cost may provide a rationale for predicting the metabolic cost of incline walking from muscle activation patterns derived from musculoskeletal simulations.

A commonly used model to predict metabolic cost during inclined walking does so using only subject mass, walking velocity, and incline (Pandolf et al., 1977). We hypothesized that the predictive capabilities of this model could be improved by including percent body fat and fat distribution in place of total body mass. Our analysis did not support this hypothesis. A linear regression model containing incline, walking velocity, percent body fat, and percent gynoid fat resulted in an R² value of 0.85, which is similar to the model containing body mass, incline, and walking velocity (R²=0.84). We recruited subjects with a range of fat distribution (e.g. percent gynoid fat range, 4.0–25.3%), but all of our subjects were physically fit. A model including mass distribution may be better applied to a group of subjects with more diverse body composition.

We hypothesized that kinematic and kinetic measurements alone could predict metabolic cost, independent of incline. Indeed, 89% of the variance in metabolic cost was explained using two features from the first half of stance phase (peak knee flexion angle, peak knee extension moment) and two features from the second half of stance phase (peak ankle plantarflexion moment, peak hip flexion moment). Because biomechanical gait patterns are commonly measured, a model such as this may be valuable when metabolic or EMG measurements are not available.

During the first half of stance phase, incline necessitated an increase in peak hip, knee, and ankle flexion angles (Fig. 3), which has been observed by others (Lay et al., 2006; McIntosh et al., 2006). The largest change in gait dynamics with incline was the stance phase hip power generation, which increased an average of 163% between 0% and 10% incline (Fig. 3). During this time, muscle activity from gluteus maximus, a powerful hip extensor, also increases (Franz and Kram, 2011; Lay et al., 2007; McIntosh et al., 2006). Although we did not measure gluteus maximus activity, we observed increased activity in the hamstrings, rectus femoris, and vasti (Fig. 1) along with a longer activation in the bi-articular hamstrings and vasti (Fig. 2).

The second half of stance phase was characterized by an increase in plantarflexor power generation with incline (Fig. 3); this is consistent with others (DeVita et al., 2007; Lay et al., 2006). Similar to Litchwark and Wilson (2006) and Wall-Scheffler et al. (2010), we also observed an increase in gastrocnemius activity with incline (Fig. 1).

Each subject in our study walked at their preferred level walking velocity at all inclines. This enabled us to evaluate changes in gait features across incline irrespective of speed but made comparisons with previous studies difficult, because some studies allowed subjects to walk at different preferred speeds at each incline (i.e., slower up incline than level walking) (Kawamura et al., 1991; McIntosh et al., 2006; Sun et al., 1996).

Our goal was to determine which measured variables best predict metabolic cost, not to determine the direct relationship between each measured variable and metabolic cost. Developing regression models this way yields beta coefficients that are not intuitive, such as the negative coefficient associated with vastus lateralis activity (Table 1). Although we ensured that no multicolinearity existed between the predictive variables included in each model, numerous correlations did exist between the predictor variables and the remaining variables not included in the models. This yielded beta coefficients that may not represent a direct relationship with net metabolic cost.

The regression models presented here have other limitations. For example, the model that used EMG to predict metabolic cost was developed using activation patterns from only eight muscles. Given that the peak hip extension moment and hip power generation increased significantly with incline (Fig. 3, Table 4), it is possible that including gluteus maximus activity might have improved the predictions of metabolic cost from EMG. Further, the models using EMG cannot explicitly account for factors that influence muscle energetics, such as the volume of muscle activated, fiber type, and contraction velocity.

This study provides a description of muscle activation patterns, joint kinematics and kinetics, and metabolic cost during inclined walking. Regression models using these data predict net metabolic cost well, suggesting that muscle activities and biomechanical gait patterns may predict metabolic cost during other gait patterns of healthy adults walking with flexed knees (e.g. crouch), while carrying loads, or at various speeds. This motivates future studies to predict the metabolic cost of walking when gait is altered by changes in neuromuscular control or while using an assistive technology.