Abstract
Research on emotion and decision-making has suggested that arousal mediates risky decisions (e.g., Bechara et al., 1997), but several distinct and often confounded processes drive such choices. Here, we used econometric modeling to separate and quantify the unique contributions of loss aversion, risk sensitivity and choice consistency to risky decision-making. We administered the beta-blocker propranolol in a double-blind, placebo-controlled within-subjects study, targeting the neurohormonal basis of physiological arousal. Matching our intervention’s pharmacological specificity with a quantitative model delineating decision-making components allowed us to identify the causal relationships between arousal and decision-making that do and do not exist. Propranolol selectively reduced loss aversion in a baseline- and dose-dependent manner (i.e. as a function of initial loss aversion and body-mass index), and did not affect risk sensitivity or choice consistency. These findings provide evidence for a specific, modulatory, and causal relationship between precise components of both emotion and risky decision-making.
Keywords: decision making, emotion, propranolol, loss aversion, risk attitudes
Introduction
One of the ways emotion has been suggested to influence decision-making is by modulating the evaluation of risk (Bechara, Damasio, Tranel, & Damasio, 1997), a link established by studies manipulating (Dunn et al., 2010; Lerner & Keltner, 2001; Porcelli & Delgado, 2009) or measuring (Bechara, et al., 1997; Lo & Repin, 2002) components of emotion during risky decision tasks. However, our understanding of the ways in which emotion does and does not shape risky decisions remains unclear, in part because risky decision-making is the result of not one but multiple distinct processes. Just as various component processes contribute to emotion (Scherer, 2005), decision-making also results from dissociable processes. For example, someone may be uninterested in playing a gamble equally like to yield a gain or a loss because she dislikes the element of chance or risk, or because she weighs the potential loss more heavily than the potential gain. These processes are termed risk attitudes and loss aversion respectively. They are definitionally independent, but often confounded in decision-making tasks (see Methods; Phelps, Lempert, & Sokol-Hessner, 2014). Because not all decision processes may be related to a given emotional component, we must separately examine the processes underlying both decision-making and emotion to identify which relationships do and do not exist.
Recent studies dissociating risky decision-making processes found that loss aversion (and not risk attitudes or consistency) correlated both with physiological arousal responses to losses versus gains (Sokol-Hessner et al., 2009) and amygdala hemodynamic responses to losses versus gains (Sokol-Hessner, Camerer, & Phelps, 2013), and was reduced in case studies of patients with amygdala damage (De Martino, Camerer, & Adolphs, 2010). As the amygdala mediates the effects of arousal in other cognitive domains (Garavan, Pendergrass, Ross, Stein, & Risinger, 2001; Glascher & Adolphs, 2003), these studies are consistent with a selective relationship between amygdala-mediated arousal responses and loss aversion, to the exclusion of risk attitudes and consistency.
Studies from two other domains align with this hypothesized selective relationship. First, in rodents, the amygdala drives avoidance actions during fear learning through striatal projections (LeDoux, 2000). In human decision-making, loss aversion is by definition avoidant, characterizing the tendency to avoid monetary loss in choices, an action also linked to striatal activity (Sokol-Hessner, et al., 2013; Tom, Fox, Trepel, & Poldrack, 2007). Second, a large body of work has shown that propranolol – a beta-blocker that crosses the blood-brain-barrier and interferes with the neurohormonal basis of autonomic arousal – attenuates arousal’s effect on memory systems including the striatum by diminishing the amygdala’s influence (McGaugh, 2002, 2004). The hypothesis most consistent with findings linking arousal, the amygdala, and the striatum to loss aversion (De Martino, et al., 2010; Sokol-Hessner, et al., 2013; Sokol-Hessner, et al., 2009) and identifying amygdala/striatal modulatory circuits as necessary for avoidance actions (LeDoux, 2000) and supported by adrenergic signaling (McGaugh, 2002, 2004), is that of a general modulatory relationship (Phelps, et al., 2014) in which amygdala and arousal responses drive avoidant behavior, including loss aversion.
Here, we use propranolol to pharmacologically interfere during risky decision-making with the hypothesized mechanism of loss aversion: the neurohormonal system underlying autonomic arousal. We combine that precise manipulation with a similarly precise monetary decision task and accompanying econometric model of value and decision processes. Together, this task and model allow us to reliably separate and quantify three decision processes for each individual (loss aversion, risk attitudes, and choice consistency; see Methods) and examine how propranolol affects each process. We predict that if amygdala-based arousal responses causally drive loss aversion, then propranolol should selectively blunt loss aversion, but because neither risk attitudes nor consistency have been linked to the hypothesized modulatory circuit, we predict they will be unaffected. Finding such a specific effect of propranolol would also more generally provide causal evidence for a precise role of one neurohormonal system in risky decision-making.
Methods
Participants
Fifty participants passed the medical screening (see Supplementary Materials), and forty seven completed the study. Of the 3 participants who passed the screening and began but did not complete the study, one did not show up for their second appointment, and two had “adverse events”. One experienced a sensation of warmth in their left leg accompanied by tingling (similar to the phenomenon of a limb “falling asleep”), and the other reported feeling lightheaded for roughly one hour during the experiment (though she did not mention it until the end of the session, as she attributed it to not having her morning coffee). Both events took place during the first visit. Neither participant was asked to return for their second test day, as they might have perceived the blind to have been broken. No other side effects were reported by any of the 47 remaining participants (22 females; mean age of 26.6 ±5.1 years) who completed the double-blind, two-test-day design (Figure 1). The sample size goal of 50 was conservatively selected based on previous findings of within-subject changes in loss aversion due to emotion regulation identified in samples roughly half that size (Sokol-Hessner, et al., 2013; Sokol-Hessner, et al., 2009).
Fig. 1.
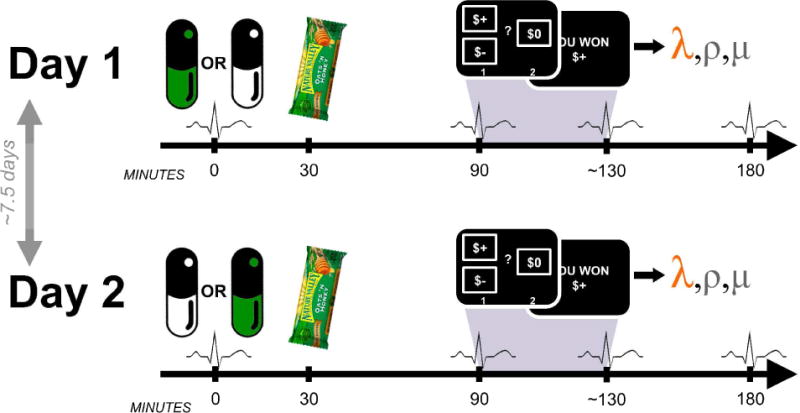
Task structure. Days were identical except for the order in which propranolol and placebo were received. Participants ate a standard meal to aid propranolol absorption. Blood pressure and heart rate were assessed four times each day.
Test Visits
The two test days were separated by an average of 7.5 days (5–14 days). Each day was identical, except that all participants received an orally-administered propranolol pill (80mg) on one, and a matched placebo pill on the other, with the order counterbalanced (see below).
Prior to test visits, participants were asked to refrain from eating for three hours prior to each session and 30 minutes following drug administration, in an attempt to standardize the propranolol dose.
Each day began with pill administration followed 30 minutes later by consumption of a standard meal (a granola bar) in order to increase the plasma concentration of propranolol. Participants were on average blind to propranolol-placebo treatment order (overall explicit guess accuracy at the end of the study = 47%; chance = 50%). The task began 90 minutes after medication administration, and concluded within approximately 40 minutes, including task instructions, a brief comprehension quiz, practice trials, and the gamble task itself. Participants left after 180 minutes. As part of the safety protocol, blood pressure (BP) and heart rate (HR) were assessed four times: at medication administration (0 min), before the task (90 min), after the task (~130 min), and 180 minutes post-medication administration. All measurements were either taken by a registered nurse (RN) or were taken by the experimenter and checked with an RN to ensure participants’ vital signs were within the medical safety monitoring bounds (see Supplementary Methods). To ensure the specific experimenter administering the task was blind to the medication condition, the experimenter only took the BP/HR measurements at 90 and 130 minutes. Without knowing the BP/HR values at 0 or 180 minutes (which the RN took), they could not ascertain whether participants were on propranolol or placebo, and as such, their blind was maintained throughout and between participants and sessions.
Participants made 150 choices/day between risky gambles and guaranteed alternatives (Sokol-Hessner, et al., 2013; Sokol-Hessner, Hartley, Hamilton, & Phelps, 2014; Sokol-Hessner, et al., 2009). At the end of each test day, participants were paid the actual value of a randomly selected subset of the trials (10% of all trials, or 15 trials), relative to a $30 endowment. Participants’ endowments changed by an average of $28.17 on the first day (i.e. they won $28 in addition to the endowment), and $26.66 on the second day. There was no significant difference across the two days (p = 0.82). Participants were fully informed about all contingencies and probabilities in the task, and as mentioned above, were quizzed on them to ensure comprehension. Participants found the task to be easy (mean rating of 1.8 (SE = 0.14) on a scale from 1 = very easy to 7 = very difficult; rating taken at the end of Day 1’s testing), a fact reflected in the number of missed trials (a mean of 0.9±1.4 trials on Day 1, and 0.6±1.0 trials on Day 2). The gamble amounts were identical to those specified previously (Sokol-Hessner, et al., 2013). Briefly, 120 choices were between gain-loss gambles, in which participants chose between a gamble with positive and negative possible outcomes, and a guaranteed alternative of $0. The remaining 30 gain-only trials entailed choices between gambles with positive and zero possible outcomes, and a positive guaranteed alternative. The probabilities associated with the gamble outcomes were always p = 0.5. All test visits began during the morning and an effort was made to schedule sessions at the same time across days for each participant (mean time of pill administration on Day 1 = 9:49AM; mean time on Day 2 = 9:54AM).
Propranolol and Dose Dependence
Propranolol’s ability to act within the central nervous system is due to its high lipophilicity (Woods & Robinson, 1981), meaning that it easily dissolves through and into lipids, including the blood-brain barrier and peripheral adipose cells. Because of this property, propranolol has dose dependent pharmacokinetics (Borgström, Johansson, Larsson, & Lenander, 1981). Individuals with a high body mass index (BMI; [weight in kilograms]/[height in meters]2) experience lower peak concentrations and a greater medication “volume of distribution” (Bowman, Hudson, Simpson, Munro, & Clements, 1986), which therefore leads to a lower concentration in any one location (including the brain). In other words, propranolol’s pharmacokinetics indicate that the medication’s effects should be stronger in smaller versus larger individuals. To address this, we used the median participant BMI (median=25.8; range: 16.4–39.1) to split participants into Low and High BMI groups (an approach that does not involve likely incorrect assumptions of linearity in dose-dependence), and included this grouping in our regressions.
Behavioral Modeling
We modeled participants’ behavior using maximum likelihood estimation as implemented in MATLAB (Mathworks, Natick, MA) to fit a prospect-theory-inspired model (Tversky & Kahneman, 1992) to choices, identical to that used in previous studies (Sokol-Hessner, et al., 2013; Sokol-Hessner, et al., 2014; Sokol-Hessner, et al., 2009).
| (eq. 1) |
| (eq. 2) |
| (eq. 3) |
Equations 1 and 2 calculate the utility of gains and losses respectively. These are used to compute the utility of the gamble and the guaranteed alternative, which are then converted into a probability of choosing the gamble using the softmax in Equation 3. The model’s parameters quantify loss aversion (λ, the relative multiplicative weight placed on losses compared to gains), risk attitudes (ρ, feelings about chance/diminishing marginal sensitivity to value), and choice consistency (μ, noisiness in choices, also called the softmax temperature). All analyses of loss aversion used log(λ); the logarithm is commonly used since λ is positively skewed.
This task has the ability to separate changes in loss aversion from those in risk attitudes by including both gain-loss and gain-only trial types. Gain-loss trials consist of a gamble with positive and negative possible outcomes, and a guaranteed alternative of zero. Choices in these trials reflect both risk attitudes (because the gamble is risky) and loss aversion (because losses are being evaluated). Gain-only trials consist of a gamble with possible outcomes of a large positive amount or zero, and a guaranteed alternative of a small positive amount. In these trials, risk attitudes affect behavior (because the gamble is still risky), but loss aversion does not (because there are no losses). When gain-loss and gain-only trials are simultaneously fit, risk attitudes are estimated that account for behavior across all trials, while loss aversion accounts for the remainder of gain-loss gambling behavior not explained by risk attitudes. In studies that only include gain-loss trial types, it is impossible to identify to what extent loss aversion or risk aversion is driving behavior because both processes are present and have similar gross effects on behavior (increasing or decreasing gambling). Both gain-loss and gain-only trial types are necessary to separately identify risk attitudes and loss aversion.
To analyze changes in choice behavior, we first regressed the change in log(λ) across days on Day (the constant), Medication (−1 placebo to propranolol; +1 propranolol to placebo), BMI group (+1 Low BMI group; −1 High BMI group), and the interaction between Medication and BMI group. We also did this exact regression using risk attitudes (ρ) and choice consistency (μ) instead of log(λ). To clarify the effect of the interaction, we subtracted the strong Day effect from the change in log(λ) leaving the residual change in loss aversion (ΔλR) due to propranolol. The resulting values were still in “Day” space (i.e. reflecting changes from Day 1 to Day 2), so we flipped the sign of the values corresponding to individuals who received placebo on Day 1 so that all values were in a “Medication” space (reflecting propranolol-to-placebo changes). We called this ΔλR as it reflected the residual change in loss aversion due to propranolol, and performed subsequent analyses on these residuals.
We think it likely that there is some more continuous relationship between BMI and a constant 80mg dose of propranolol. However, this relationship is certainly non-linear, characterized by both ceiling effects (in which 80mg of propranolol has a constant, maximal effect below some BMI) and floor effects (in which 80 mg of propranolol has no observable effect above a particular BMI). To avoid arbitrary assumptions of functional forms, and allow our data to shape the monotonic transformation of BMI, we used nonlinear curve fitting procedures in MATLAB (NonLinearModel.fit) to fit a model based on the following two equations:
| (eq. 4) |
| (eq. 5) |
in which z() indicates the use of z-scoring. This regression is identical to that described earlier, except instead of a median split on BMI, we allowed the modified softmax function (Equation 4, parameterized by α and γ) to transform BMI into tBMI as best fit the change in loss aversion. This transformation function avoids arbitrary assumptions as it can approximate a wide variety of possible monotonic relationships including linear, sigmoidal, curvilinear, or step functions, and is thus capable of modeling both ceiling and floor effects. For analyses using BMI as a strictly linear covariate, see Supplementary Materials, though note non-linearity caveats above.
Results
We fit a prospect theory inspired (Tversky & Kahneman, 1992) model to each participant’s choices on each day. This model quantified three distinct processes: loss aversion (λ), risk attitudes (ρ), and choice consistency (μ), and we analyzed the change in these parameter values across days, using linear regression.
We regressed individuals’ change in log loss aversion (log(λDay 2) − log(λDay 1)) on the following factors: Day, Medication, BMI group, and the interaction between Medication and BMI group (see Methods). We identified a strong effect of Day (β = 0.20, p = 0.0002, 95% CI = [0.10 0.29]; Figure 2A), illustrating that participants were generally more loss averse on Day 2. The effect of Medication was in the expected direction, but not significant on its own (propranolol reduced loss aversion: β = 0.05, p = 0.34, 95% CI = [−0.05 0.14]). BMI group was also not significant (β = 0.04, p = 0.42, 95% CI = [−0.06 0.13]). However, as expected given the dose-dependent pharmacokinetics of propranolol (Borgström, et al., 1981) and the variation in propranolol concentrations as a function of BMI (Bowman, et al., 1986), the interaction of BMI and Medication was significant (β = 0.11, p = 0.03, 95% CI = [0.01 0.20]). In other words, propranolol interacted with BMI to reduce loss aversion in a dose-dependent manner. Because the regression was performed on the change in log(λ), the effect of these coefficients on λ can be understood in terms of the percentage change in λ value: Day, 22%; Medication, 5%; BMI group, 4%; and Medication × BMI group, 11%. No significant effects were identified performing the same regression on risk attitudes or choice consistency (risk attitudes, ρ; effect of Day, β = −0.06, p = 0.21, 95% CI = [−0.14 0.03]; Medication −0.05, β = −0.05, p = 0.31, 95% CI = [−0.13 0.04]; BMI group, β = 0.06, p = 0.21, 95% CI = [−0.03 0.14]; Medication × BMI group, β = −0.01, p = 0.74, 95% CI = [−0.10 0.07]; choice consistency, μ, using log(μ); effect of Day, β = 0.26, p = 0.11, 95% CI = [−0.06 0.59], 30%; Medication, β = −0.03, p = 0.87, 95% CI = [−0.35 0.30], −3%; BMI group, β = −0.29, p = 0.09, 95% CI = [−0.61 0.04], −25%; Medication × BMI group, β = 0.12, p = 0.46, 95% CI = [−0.20 0.45], 13%).
Fig. 2.
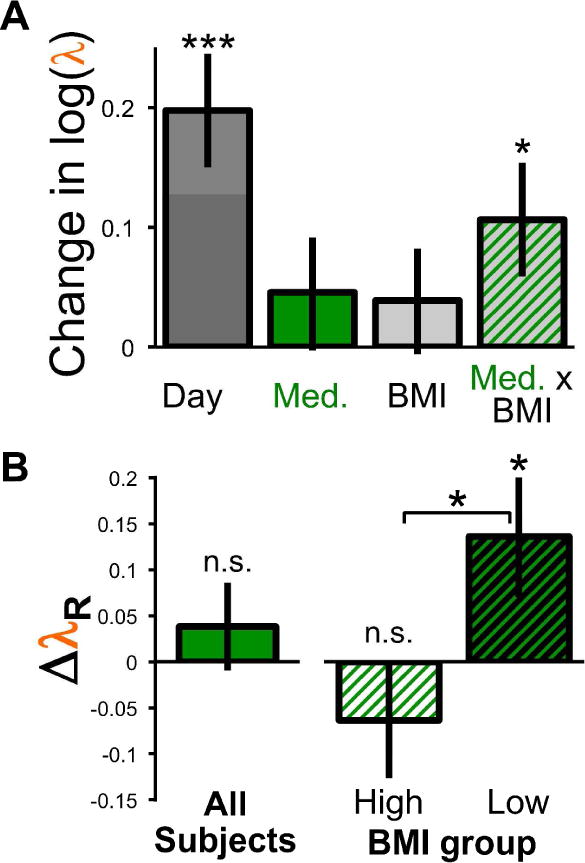
The effect of propranolol on loss aversion as identified by (A) regression coefficients, and (b) separated into the average effect of propranolol overall, and in the low- and high-BMI groups separately. Error bars are standard error of the mean, asterisks indicate one-sample t-tests against zero in all cases except the two-sample t-test examining differences between BMI groups (* = p < 0.05, *** = p < 0.001).
To clarify the interaction, we removed the strong effect of Day from the change in log(λ) using the estimated regression coefficients, yielding the residual change in loss aversion (ΔλR) due to propranolol. The overall average ΔλR is not significantly different from zero (t(46) = 0.81, p = 0.42, Cohen’s dz = 0.11; Figure 2B), replicating the average effect of Medication in the regression. However, examining the BMI groups separately, we see no significant effect of propranolol for High BMI participants (t(22) = −1.09, p = 0.29, Cohen’s dz = 0.23), whereas Low BMI participants were significantly less loss averse with propranolol (t(23) = 2.17, p = 0.04, Cohen’s dz = 0.44). All of these results replicated with non-parametric tests, demonstrating their robustness (Wilcoxon signed rank tests: Average ΔλR vs. 0, z = 0.69, p = 0.49; High BMI ΔλR vs. 0, z = −0.97, p = 0.33; Low BMI ΔλR vs. 0, z = 2.17, p = 0.03; Wilcoxon rank sum test: High vs. Low BMI ΔλR, z = 2.07, p = 0.04).
While there may be a more continuous relationship between BMI and an 80mg dose of propranolol, it is certainly nonlinear, characterized by lower and upper bounds. That is, whatever the effects of propranolol, we expect them to disappear entirely at very high BMIs and be constant and maximal at very low BMIs. Therefore, to avoid arbitrarily assuming a functional form for this relationship, we used nonlinear regression to estimate transformed BMI values (“tBMI”) simultaneously with the interaction with propranolol. The transformation function we fit as part of this regression (see Eq. 4; parameterized with α and γ) allowed BMI values to be transformed into a variety of monotonic shapes (e.g. linear, curvilinear, sigmoidal, or step functions), and could thus capture both ceiling and floor effects. These transformed values were then used in place of the BMI group term in the regression. The best fitting transformation of BMI was effectively a step function (α = 155 and γ = 422; see Figure S1 and Supplementary Materials) splitting individuals into low- and high-BMI groups with an intermediate point (~25.0 kg/m2) extremely close to the median BMI (25.8 kg/m2) used before. The other estimated parameters were nearly identical, identifying a strong effect of Day (β = 0.19, p = 0.0002, 95% CI = [0.10 0.29]), a non-significant effect of Medication in the expected direction (β = 0.047, p = 0.32, 95% CI = [−0.05 0.14]), no effect of tBMI (β = 0.05, p = 0.28, 95% CI = [−0.04 0.15]), but a significant Medication × tBMI interaction (β = 0.12, p = 0.02, 95% CI = [0.02 0.21]). Though we believe the relationship is ultimately more likely to be sigmoidal, these findings nevertheless empirically support the existence of a threshold BMI value, above which there is no reduction in loss aversion, and below which there is a constant effect.
Finally, we examined whether propranolol’s effect was related to the initial level of loss aversion. Because correlating the change in loss aversion with its initial level is statistically biased (Tu, Bælum, & Gilthorpe, 2005), we used an accepted, alternative test to examine whether the variance of loss aversion on propranolol is different from that on placebo (Tu & Gilthorpe, 2007). If the medication effect is independent of initial loss aversion, variance should not change; but, if there is baseline dependency, the range of loss aversion will either compress or expand. The test of equality of correlated variances (Tu & Gilthorpe, 2007) was significant (t(45) = 2.50, p = 0.016), suggesting that propranolol’s effect depended on the initial level of loss aversion. As the variance in log(λ) was lower on propranolol (0.17) than on placebo (0.28), it shows that higher values were reduced more than smaller values, i.e. that the effect of propranolol in reducing loss aversion was greater in those with initially higher levels of loss aversion. This is the definition of baseline-dependence, and is consistent with a hypothesis that propranolol operates on a modulatory mechanism – the greater the initial modulatory signal, the more of an effect propranolol will have.
Discussion
Propranolol’s reduction of loss aversion constitutes causal evidence that adrenergic responses drive the avoidance of monetary losses in risky decision-making. Though other studies have linked risky decisions to arousal (Bechara, et al., 1997; Lo & Repin, 2002) and shown effects of propranolol (Rogers, Lancaster, Wakeley, & Bhagwagar, 2004), these failed to differentiate the contributions of loss aversion, risk attitudes, and consistency. Because all of these processes contribute to risky choices, prior studies were limited to the broad conclusion that arousal and the adrenergic system were related to risky decision-making. Here we show that pharmacologically manipulating the neurohormonal basis of arousal alters only loss aversion (other affective components may be related to other decision-making processes, e.g. mood changes risk sensitivity by altering appraisals; Lerner & Keltner, 2001). This corroborates and builds on studies selectively linking loss aversion to arousal (Sokol-Hessner, et al., 2009), the amygdala (De Martino, et al., 2010; Sokol-Hessner, et al., 2013), and PET assays of noradrenergic activity (Takahashi et al., 2013), and converges with findings from other domains identifying an amygdala-based, adrenergically-mediated system modulating avoidance actions (LeDoux, 2000; McGaugh, 2002, 2004).
Propranolol’s high lipophilicity and pharmacology (Borgström, et al., 1981; Bowman, et al., 1986) indicate its effects should be functionally dose-dependent, i.e. greater in smaller versus larger individuals, as we find here. The fact that many studies using propranolol in humans have not discussed interactions between dose size and body mass could reflect the predominance of smaller subject pools containing younger, lower-BMI participants (with little variation in BMI to observe dose-dependence), or could simply be because dose size/body mass interactions were not examined at all (see Table S1 and Supplementary Analyses). This approach in the human literature sharply contrasts with the use of propranolol in non-human animals, where it is standard to titrate doses by body weight, implicitly anticipating and correcting for dose-dependence. In addition to more directly testing dose-dependence, we hope future studies might examine other limitations of this work, including testing whether propranolol’s effect is mediated by the amygdala as predicted using neuroimaging or non-centrally-acting beta-blockers, and allowing risk attitudes to vary across the gain and loss domains.
Identifying relationships between emotions and choices begins by measuring and correlating specific processes underlying both, and separating those from others that may appear superficially similar, despite being fundamentally different. However, this important first step must be followed by direct manipulation to establish causality. In doing so here, we have empirically demonstrated that precise components of our emotions can have very specific, causal effects on precise components of decision-making.
Supplementary Material
Acknowledgments
This work was supported by the National Institutes of Health (AG039283 to EAP).
Footnotes
Author Contributions:
PSH designed the study with the assistance of BLL and EAP. SFL and RHT collected the data, and PSH, SFL, and RHT analyzed the data. All authors contributed to the drafting, editing and development of the manuscript.
References
- Bechara A, Damasio H, Tranel D, Damasio AR. Deciding advantageously before knowing the advantageous strategy. Science. 1997;275(5304):1293–1295. doi: 10.1126/science.275.5304.1293. [DOI] [PubMed] [Google Scholar]
- Borgström L, Johansson CG, Larsson H, Lenander R. Pharmacokinetics of propranolol. Journal of pharmacokinetics and Biopharmaceutics. 1981;9(4):419–429. doi: 10.1007/BF01060886. [DOI] [PubMed] [Google Scholar]
- Bowman S, Hudson S, Simpson G, Munro J, Clements J. A comparison of the pharmacokinetics of propranolol in obese and normal volunteers. British Journal of Clinical Pharmacology. 1986;21:529–532. doi: 10.1111/j.1365-2125.1986.tb02837.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Martino B, Camerer CF, Adolphs R. Amygdala damage eliminates monetary loss aversion. Proceedings of the National Academy of Sciences. 2010;107:3788–3792. doi: 10.1073/pnas.0910230107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunn B, Galton H, Morgan R, Evans D, Oliver C, Meyer M, Dalgleish T. Listening to Your Heart: How Interoception Shapes Emotion Experience and Intuitive Decision Making. Psychological Science. 2010;21(12):1835–1844. doi: 10.1177/0956797610389191. [10.1177/0956797610389191] [DOI] [PubMed] [Google Scholar]
- Garavan H, Pendergrass JC, Ross TJ, Stein EA, Risinger RC. Amygdala response to both positively and negatively valenced stimuli. Neuroreport. 2001;12(12):2779–2783. doi: 10.1097/00001756-200108280-00036. [DOI] [PubMed] [Google Scholar]
- Glascher J, Adolphs R. Processing of the arousal of subliminal and supraliminal emotional stimuli by the human amygdala. The Journal of Neuroscience. 2003;23(32):10274–10282. doi: 10.1523/JNEUROSCI.23-32-10274.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LeDoux JE. Emotion circuits in the brain. Annu Rev Neurosci. 2000;23:155–184. doi: 10.1146/annurev.neuro.23.1.155. [DOI] [PubMed] [Google Scholar]
- Lerner JS, Keltner D. Fear, anger, and risk. Journal of Personality and Social Psychology. 2001;81(1):146–159. doi: 10.1037//0022-3514.81.1.146. [DOI] [PubMed] [Google Scholar]
- Lo AW, Repin DV. The Psychophysiology of Real-Time Financial Risk Processing. J Cognit Neurosci. 2002;14(3):323–339. doi: 10.1162/089892902317361877. [DOI] [PubMed] [Google Scholar]
- McGaugh JL. Amygdala Modulation of Memory Consolidation: Interaction with Other Brain Systems. Neurobiology of Learning and Memory. 2002;78(3):539–552. doi: 10.1006/nlme.2002.4082. [DOI] [PubMed] [Google Scholar]
- McGaugh JL. The amygdala modulates the consolidation of memories of emotionally arousing experiences. Annu Rev Neurosci. 2004;27(1):1–28. doi: 10.1146/annurev.neuro.27.070203.144157. [DOI] [PubMed] [Google Scholar]
- Phelps EA, Lempert KM, Sokol-Hessner P. Emotion and decision making: Multiple modulatory neural circuits. Annu Rev Neurosci. 2014;37:263–287. doi: 10.1146/annurev-neuro-071013-014119. [DOI] [PubMed] [Google Scholar]
- Porcelli AJ, Delgado MR. Acute stress modulates risk taking in financial decision making. Psychol Sci. 2009;20(3):278–283. doi: 10.1111/j.1467-9280.2009.02288.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogers RD, Lancaster M, Wakeley J, Bhagwagar Z. Effects of beta-adrenoceptor blockade on components of human decision-making. Psychopharmacology. 2004;172(2):157–164. doi: 10.1007/s00213-003-1641-5. [DOI] [PubMed] [Google Scholar]
- Scherer KR. What are emotions? And how can they be measured? Social Science Information. 2005;44(4):695–729. doi: 10.1177/0539018405058216. [DOI] [Google Scholar]
- Sokol-Hessner P, Camerer CF, Phelps EA. Emotion Regulation Reduces Loss Aversion and Decreases Amygdala Responses to Losses. Social Cognitive and Affective Neuroscience. 2013;8:341–350. doi: 10.1093/scan/nss002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokol-Hessner P, Hartley CA, Hamilton JR, Phelps EA. Interoceptive ability predicts aversion to losses. Cognition & Emotion. 2014 doi: 10.1080/02699931.2014.925426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokol-Hessner P, Hsu M, Curley NG, Delgado MR, Camerer CF, Phelps EA. Thinking like a trader selectively reduces individuals’ loss aversion. PNAS. 2009;106(13):5035–5040. doi: 10.1073/pnas.0806761106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi H, Fujie S, Camerer CF, Arakawa R, Takano H, Kodaka F, Suhara T. Norepinephrine in the brain is associated with aversion to financial loss. Molecular Psychiatry. 2013;18:3–4. doi: 10.1038/mp.2012.7. [DOI] [PubMed] [Google Scholar]
- Tom SM, Fox CR, Trepel C, Poldrack RA. The Neural Basis of Loss Aversion in Decision-Making Under Risk. Science. 2007;315:515–518. doi: 10.1126/science.1134239. [DOI] [PubMed] [Google Scholar]
- Tu YK, Bælum V, Gilthorpe MS. The relationship between baseline value and its change: problems in categorization and the proposal of a new method. European Journal of Oral Sciences. 2005;113:279–288. doi: 10.1111/j.1600-0722.2005.00229.x. [DOI] [PubMed] [Google Scholar]
- Tu YK, Gilthorpe MS. Revisiting the relation between change and initial value: a review and evaluation. Statist Med. 2007;26(2):443–457. doi: 10.1002/sim.2538. [DOI] [PubMed] [Google Scholar]
- Tversky A, Kahneman D. Advances in Prospect-Theory – Cumulative Representation of Uncertainty. Journal of Risk and Uncertainty. 1992;5(4):297–323. doi: 10.1007/BF00122574. [DOI] [Google Scholar]
- Woods P, Robinson M. An investigation of the comparative liposolubilities of beta-adrenoceptor blocking agents. Journal of Pharmacy and Pharmacology. 1981;33:172–173. doi: 10.1111/j.2042-7158.1981.tb13743.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


