Abstract
The concept of synergy provides a theoretical framework for movement stability resulting from the neural organization of multiple elements (digits, muscles, etc.) that all contribute to salient performance variables. Although stability of performance is obviously important for steady-state tasks leading to high synergy indices, a feed-forward drop in synergy indices is seen in preparation to a quick action (i.e., anticipatory synergy adjustments, ASAs). We review recent studies of multi-finger and multi-muscle synergies that show decreased indices of synergies and ASAs in patients with Parkinson’s disease (PD) or multisystem atrophy. In PD, the impairments in synergies and ASAs are partially reversed by dopaminergic drugs, and changes in synergy indices are present even in PD patients at earliest diagnosis. Taken together, these results point at subcortical structures that are crucial for proper control of movement stability. It is timely to introduce the concept of impaired control of stability as an objective, quantifiable, and theory-based clinical descriptor of movement disorders that can increase our understanding of the neural control of movement with all of its implications for clinical practice.
Keywords: stability, synergy, anticipatory synergy adjustments, Parkinson’s disease, multisystem atrophy, stroke, movement disorders
1. Introduction
Perturbation of neural processes that modulate the coordinated movement of healthy people results in a variety of clinical presentations united under the label of movement disorders. Clinically, movement disorders have been described generally based on their phenomenology: excessive movement (hyperkinesia or dyskinesia); movement poverty (hypokinesia or bradykinesia); presence of involuntary rhythmic movements (tremor vs. clonus vs. chorea vs. tics); presence of atypical postures (dystonic vs. non-dystonic); etc. These phenomenological descriptions have been useful for clinical differential diagnosis and localization of lesions in the central and peripheral nervous system, yet they are limited in their contribution to understanding the fundamental origins of abnormal movements. This knowledge gap translates into the overall lack of objective, quantitative measures for many movement disorders, that in turn limits our ability to detect movement disorders earlier and track progression sensitively. We review the basic concept of movement stability and propose its utility as a new dimension to quantify abnormalities common to a variety of movement disorders. In addition, we discuss the theoretical background of the concept of movement stability, and the clinical and scientific data that support its usage.
1.1. Impaired control of movement stability – a common feature of movement disorders
Stability refers to an ability of a system (e.g., the human motor system or its parts) to return to a certain state or trajectory after small, transient perturbations. Since all natural human movements are performed in a poorly predictable environment and involve varying internal states, movement stability is crucial for successful everyday motor performance. For example, holding a cup of water steady requires stability of the integrated contribution of the many involved joints and muscles, all of which may vary their state.
The concept of stability has been explored during multi-effector actions within the dynamic systems approach to motor control (reviewed in Kelso, 1995). In those studies, stability of the relative phase between actions of two (or more) effectors has been typically studied during both rhythmical and discrete actions. Neurological patients show impaired stability of relative phase and delayed switching time when the task requires a shift in the relative phase (Creath et al., 2008; Brown and Almeida, 2011).
Another approach to multi-joint coordination and its impairment in neurological patients have been based on analysis of joint torques during multi-joint movements. Several studies documented atypical movement patterns associated with an impaired ability of neurological patients to predict and compensate for joint torque components due to movement of other joints of the limb (interaction torques). Such impairments have been reported for patients with cerebellar disorders (Bastian et al., 1996) and with large-fiber peripheral neuropathy (Sainburg et al., 1995).
The mentioned impairments may lead to compensatory changes in muscle activation strategies. In particular, a number of populations characterized by impaired motor coordination use increased levels of co-activation within agonist-antagonist muscle pairs. This may be considered as a method of decreasing joint deviations (increasing stability) under the action of poorly predictable torques (Woollacott and Shumway-Cook, 1990; Horak et al., 1992; Horak and Diener, 1994). Within this review, our goal is to introduce a more general approach to movement stability that is applicable across tasks and effector systems.
Recently, an important concept of task-specific stability has been introduced (Schöner, 1995). This concept implies that the same set of elements (muscles, joints, digits, etc.) can be organized by the central nervous system to stabilize different task-specific performance variables. For example, the joints of an arm can be organized to stabilize orientation of a hand-held object as, for example, in such tasks as using a pointer, or walking while holding a cup of coffee. In other tasks, however, the same joints can be organized to stabilize location of the hand either with respect to the body (e.g., when cutting one’s nails or applying make-up) or with respect to an external object (e.g., when trying to pet a dog or pick a morsel of food from the plate).
Loss of stability of motor performance may cause water spills, falls, dropped objects, illegible writing, stuttering, etc. The above examples are extreme and obvious; but loss of movement stability may also be subtle, not observable with the naked eye. As we describe in detail later, loss of movement stability is a common consequence of many states of human health. These include aging, atypical development (e.g., Down syndrome), and a variety of neurological disorders. There are well-known examples from the field of movement disorders, such as ataxia and certain types of tremor typically associated with cerebellar disorders. The loss of stability, however, is also seen in conditions that are not directly linked to identifiable disorders of the cerebellum.
Maintenance of stability of movement is crucial, yet it is equally important for movement agility; paradoxically, this requires controlled loss of stability. Thus, “too much stability” may lead to such consequences as rigidity and freezing of gait. These features are traditionally associated with disorders of the basal ganglia, although other brain structures may also be involved. Taken together, these examples suggest that controlled stability is a crucial feature of normal functional movements.
One of the most commonly quantified aspects of motor behavior related to movement stability is co-contraction of agonist-antagonist muscle pairs. Excessive co-contraction has been reported for many populations and interpreted as adaptive to loss of stability. Indeed, increased co-contraction is seen in healthy persons in challenging tasks (Slijper and Latash, 2000). It is typical of performance across a variety of postural and movement tasks in the healthy elderly, in people with Down syndrome, and in neurological patients (Abbruzzese, 2002; Gibo et al., 2013; Gontijo et al., 2008). Increased muscle co-contraction has been proposed as the means of increasing the apparent stiffness of joints, thereby reducing joint deviations in response to unexpected external perturbations of movement (Nielsen et al., 1994; Fraklin et al., 2003; Heitmann et al., 2012). Increased co-contraction, however, may be both energetically wasteful and inefficient, in particular if the source of instability is internal.
Until recently, there were no methods to quantify aspects of motor function related to movement stability across the repertoire of everyday actions that involve multi-digit object manipulation, multi-joint reaching, and whole-body actions (although important advances have been made in the field of non-linear time series analysis, see Stergiou, 2004). As summarized in the next section, new methods have been developed based on the principle of abundance (Gelfand and Latash, 1998; Latash, 2012) and the uncontrolled manifold hypothesis (Scholz and Schöner, 1999). Both of these theoretical constructs have been crucial for the development of the theory of motor synergies and its application to disordered movements (reviewed in Latash, 2008; Latash et al., 2010).
2. The application of the concept of motor synergies to quantify stability
2.1. Stability, redundancy, and abundance
All major functions of the human body that involve interaction with the environment are characterized by redundancy, that is, an excess of elements that allow numerous solutions for typical problems (Bernstein, 1967). In the motor domain, the term redundancy implies that, at any level of description of human movements, there are more elements (such as muscles, digits, joints, etc.) than minimally necessary to perform typical tasks. As examples, one can place the index fingertip into a point in space with an infinite number of joint configurations, or one can hold a glass of water with an infinite number of digit forces and moments of force.
Recently, the problem of redundancy has been re-assessed based on the principle of abundance (Gelfand and Latash, 1998; Latash, 2012). Although this principle can be applied to various functions of the human body, we now focus on motor function. The principle of abundance differs from traditional methods (e.g., optimization; reviewed in Prilutsky and Zatsiorsky, 2002) of addressing the problems of motor redundancy by conceptualizing the apparently redundant design of the human body not as a source of computational problems for the brain, but as a rich apparatus that ensures the proper stability of actions in combination with the possibility of performing several actions with the same set of elements. For example, according to the principle of abundance, when the central nervous system organizes an action (e.g., reaching for an object with an arm), it does not select a unique optimal pattern of joint rotations, but rather facilitates a family of joint trajectories that are equally able to solve the task.
Thus, in repetitive attempts at the same task, numerous different trajectories are observed because of the unpredictable internal and environmental processes that can affect performance. This feature of natural movements has been demonstrated in many studies beginning with the classical experiment of Bernstein (1930) who observed families of joint trajectories during repetitive movements by professional blacksmiths using a hammer to hit a chisel. The principle of abundance led to the development of a theory of synergies reviewed briefly in the next section.
2.2. Synergies, uncontrolled manifold, and action stability
Synergy is a commonly used term both in the fields of movement science and movement disorders, yet it has had at least three different connotations. In most contemporary clinical papers, the word “synergy” has a strong negative connotation and is used to describe stereotypical patterns of muscle activation seen in some neurological patients, in particular after cortical stroke (Bobath, 1978; DeWald et al., 1995). Such patterns frequently lead to activation of a combination of predominantly flexor muscles (flexor synergy) or extensor muscles (extensor synergy) in an affected limb interfering with voluntary movements that may require different, more flexible, patterns of muscle activation.
A second definition comes from studies that have explored changes in large sets of kinematic, kinetic, and electromyographic variables during the execution of natural actions and also across trials where task parameters were varied. Different methods have been applied to extract groups within the original (elemental) set of variables that tended to show parallel changes in the magnitudes of those variables, as for example, in sets of muscles with parallel scaling of their activation levels (d’Avella et al., 2003; Krishnamoorthy et al., 2003; Ivanenko et al., 2004; Ting and Macpherson, 2005). Such groups also have been addressed as “synergies” (d’Avella et al., 2003; Ting and Macpherson, 2005) or “modes” (Krishnamoorthy et al., 2003). The organization of the original variables into groups has been assumed to alleviate the problem of motor redundancy. The number of such groups is, however, still larger than the number of constraints associated with typical tasks, and as a result, the problem of redundancy is not eliminated.
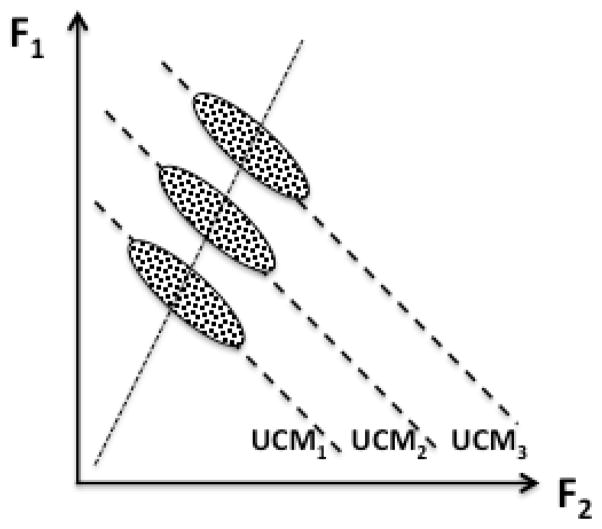
Finally, the definition we prefer links the notion of synergy to stability of performance (reviewed in Latash et al., 2007). According to this definition, synergies are neural organizations that ensure stability of task-specific salient performance variables. If a system stabilizes a performance variable, its inter-trial deviations in directions that lead to changes in that variable are expected to be low as compared to directions that keep the variable unchanged. Hence, quantifying inter-trial variance in different directions within the space of elemental variables can potentially produce indices reflecting task-specific stability. For example, if a person tries to produce a certain value of total force while pressing with two fingers (Fig. 1), there is an infinite number of solutions corresponding to a line with a negative slope on the force-force plane (dashed lines in Figure 1). If the person is asked to perform this task many times, the cloud of data points on the plane may be expected to form an ellipse elongated along the dashed line and variance along that line is expected to be higher than variance in the orthogonal direction. This line is the uncontrolled manifold (UCM – Scholz and Schöner, 1999) for this task – a sub-space where the central nervous system theoretically does not have to exercise control over the performance. This is true, however, only if achieving accurate performance in the explicit task is the only goal and no other constraints are present. Typically this is not the case and, as a result, only a range of solutions within the UCM is explored, possibly reflecting additional constraints, for example associated with optimization of a particular cost function (e.g., Park et al., 2010).
Figure 1.
An illustration of possible data distributions in a task of accurate total force production while pressing with two fingers: F1 + F2 = C. For any value of C, there are an infinite number of solutions corresponding to a line with a negative slope on the force-force plane (dashed lines, UCM1, UCM2, and UCM3). If the person is asked to perform this task many times, the cloud of data points on the plane is expected to form an ellipse elongated along the dashed line and variance along that line is expected to be higher than in the orthogonal direction.
2.3. Analysis of synergies based on the uncontrolled manifold (UCM) hypothesis
The UCM hypothesis permits the introduction of a quantitative measure for use of flexible solutions for a task. It does this by comparing the amounts of the total variance of elemental variables per degree-of-freedom within the UCM (VUCM) with that orthogonal to the UCM (VORT). This method has been developed for analysis of various actions, both steady-state and quick, including multi-digit pressing and prehension, multi-joint reaching, and whole-body standing, swaying, and stepping (reviewed in Latash, 2008). Depending on the task, analysis is performed in different spaces of elemental variables, digit forces/moments for prehension, joint rotations for reaching, and muscle modes for whole-body tasks. Note that the UCM in many tasks is non-linear (unlike the simple example in Figure 1). In such cases, the UCM is approximated by a linear sub-space and the analysis of variance is performed within that sub-space.
Frequently, the two variance indices are reduced to a single metric reflecting the relative amount of VUCM within the total variance (Latash et al., 2010). This allows computing an index of synergy, ΔV = (VUCM − VORT)/VTOT, where VTOT stands for total variance and all variance indices are quantified per dimension in the corresponding sub-spaces. Positive ΔV values are interpreted as corresponding to a synergy stabilizing the performance variable, with respect to which the analysis has been performed. Larger positive ΔV values correspond to stronger synergies. Non-positive ΔV values correspond to no synergy stabilizing the performance variable, whereas large negative values may be interpreted as pointing at loss of stability of that performance variable. The method of ΔV computation places limitations on its values depending on the dimensionality of the involved sub-spaces. To overcome this problem, a modified Fischer’s z-transformation is commonly used to normalize the index’s distribution (e.g., Solnik et al., 2013).
2.4. Anticipatory synergy adjustments
Although movement stability is crucial in most tasks, sometimes it actually may be counter-productive. For example, if a person wants to change a variable quickly, having a strong synergy ensuring high stability of that variable would be unwise. There is an inherent trade-off between stability and agility exemplified by the fact that all passenger airplanes have a vertical rudder whereas no bird has one. Obviously, within the evolutionary context, the stability ensured by the rudder has been less important for birds than ability to change the flight direction quickly. Depending on the context, high stability of biological movement may be beneficial (for example, during steady-state tasks) or detrimental (for example, during very fast actions). Recently, an ability of the central nervous system to adjust stability properties of an ongoing action has been discovered: Several studies have shown that humans have an ability to adjust their synergies in preparation for a quick action (Olafsdottir et al., 2005; Shim et al., 2005; Zhou et al., 2013). Such anticipatory synergy adjustments (ASAs) are seen as a drop in the synergy index (relative amount of VUCM in the total variance) 200–300 ms prior to the initiation of a quick action.
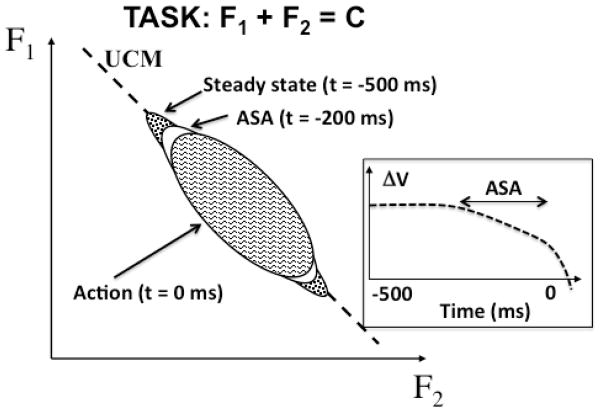
Figure 2 illustrates typical changes in the shape of data point clouds and the time profile of the corresponding synergy index for the task of producing a quick force pulse by four fingers pressing in parallel. In such studies, the subjects place their fingers on top of the force sensors, one for each finger. They are asked to follow a task line shown on the monitor with a signal representing the total pressing force of the four fingers. The task requires constant force production with a natural sharing of the total force among the fingers, and then the subjects are required to produce, in a self-paced manner, a very quick force pulse such that force peak lands within a target window. During steady-state portion of the task, strong synergies stabilizing total force (VUCM ≫ VORT) are seen. These synergies become attenuated prior to the force pulse initiation. ASAs represent an important component of feed-forward control of fast actions seen across tasks. In particular, ASAs are seen during postural tasks in preparation to an action (Klous et al., 2011; Krishnan et al., 2011) prior to the classical anticipatory postural adjustments (reviewed in Massion, 1992).
Figure 2.
When a person prepares to produce a quick force pulse from a steady-state force production, the shape of data point clouds changes as illustrated in the graph: The data point cloud becomes less and less elongated along the corresponding UCM: Three such clouds are illustrated for steady state − 500 ms prior to force pulse initiation, for 200 ms prior to the force pulse initiation, and at the moment of force pulse initiation (t = 0). The time profile of the corresponding synergy index (ΔV) in shown in the insert. The drop in ΔV prior to t = 0 is the anticipatory synergy adjustment (ASA).
3. Changes in stability of action in healthy elderly
A series of studies have shown that impaired control of action stability may be a component of healthy aging (Shinohara et al., 2004; Olafsdottir et al., 2007a,b). Those studies tested healthy elderly subjects (70–85 years of age) and documented a reduction in the synergy index in multi-digit pressing and prehensile tasks as well as reduced indices of ASAs. Two studies have shown that exercise may lead to a significant improvement in the synergy index in older adults. One of those studies (Olafsdottir et al., 2008) explored effects of a strength training exercise of the hand, and showed an improvement in the index of multi-digit synergies stabilizing total force produced by the four fingers; this correlated with the improvement of performance in a dexterity Pegboard test. The other study (Wu et al., 2013) used a specially designed exercise with adjustable instability during accurate four-finger force production tasks. That study showed a significant increase in VUCM accompanied by a drop in VORT in both young and older subjects within a 40-min practice session.
4. Movement disorders with impaired stability of action
Impaired stability is a common feature of many neurological disorders. In this section, we review a few recent applications of the aforementioned approach to a few cases of movement disorders and its potential for other neurological disorders.
4.1. Parkinson’s disease
Impaired motor stability is not typically mentioned as a clinical problem in early-stage Parkinson’s disease (PD), yet it is obvious at later stages when it leads to postural instability, falls, mishandling of everyday objects, etc. Several recent studies have shown, however, that impaired motor synergies during multi-finger action may be one of the earliest detectable motor dysfunctions of PD, seen in Hoehn-Yahr stage I and II patients, even in the apparently unaffected (subclinical) side of the body of stage I patients (Park et al., 2012, 2013a, 2014).
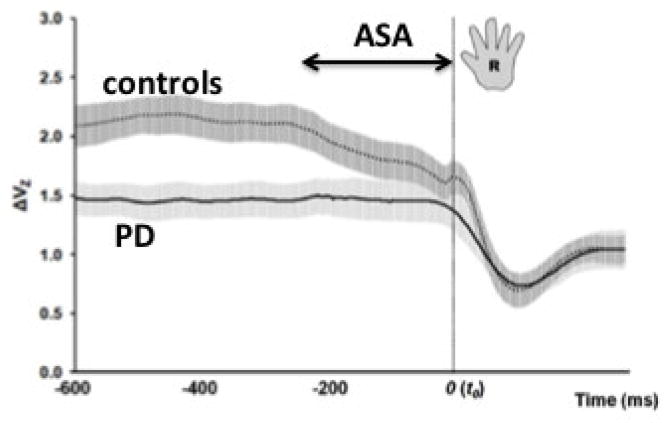
Figure 3 illustrates the time profiles of the synergy index (ΔV, reflecting the relative amount of VUCM in the total inter-trial variance) in groups of early-stage PD patients and age-matched controls. The PD patients were tested on their optimal medication as defined by their neurologist. The subjects pressed on individual force sensors with the fingers of a hand, and performed a task of accurate total force production followed by a quick force pulse into the target. Two major group differences are obvious in Figure 3. First, during the steady-state phase of the task, the control group showed a significantly higher synergy index as compared to the PD group. Second, the control group shows a clear ASA starting about 250 ms prior to the time of force pulse initiation. Much smaller and much later ASA is seen in the PD group.
Figure 3.
Averaged across subjects time profiles of the index of synergy (log-transformed, ΔVZ, with standard error shades) are shown for a group of patients with Parkinson’s disease (solid line) and for a group of healthy controls (dotted line). The control group shows higher ΔV during the steady state and an earlier and larger drop in ΔV (larger ASA) in preparation to the force pulse, which started at time t = 0. Reproduced by permission from Park et al., 2012.
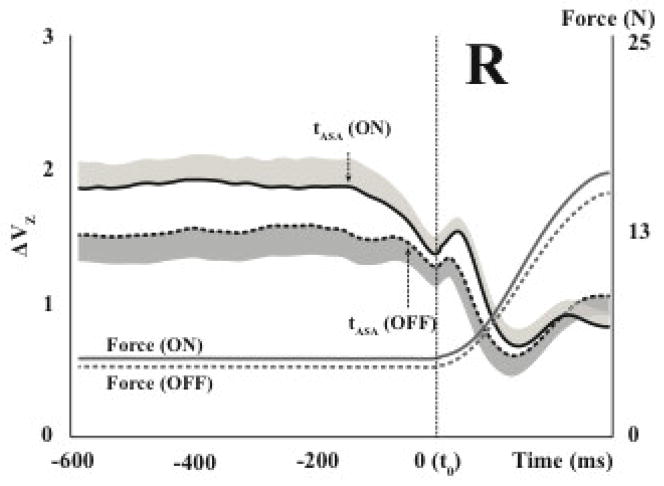
A follow-up study explored the effects of dopamine-replacement drugs on the synergy indices (Park et al., 2014). A group of PD patients were tested off their drugs (early in the morning) and on the drugs (40 min following the first morning dose of the medication). The patients demonstrated significantly lower synergy indices and significantly shorter and smaller ASAs off the drugs suggesting that both indices (ΔV and ASA) reflect functioning of neural pathway affected by dopaminergic mechanisms. These results are illustrated in Figure 4.
Figure 4.
Averaged across subjects time profiles of the index of synergy (log-transformed, ΔVZ, with standard error shades) are shown for a group of patients with Parkinson’s disease on their dopamine-replacement mediation (“on-drug”, solid line) and off the mediation (dashed line). Note the higher ΔV during the steady state and an earlier and larger drop in ΔV (larger ASA) in preparation to the force pulse for the “on-drug” test. The initiation of ASA is shown with the arrows and tASA label. Reproduced by permission from Park et al., 2014.
The data illustrated in Figures 3 and 4 suggest that PD is associated with two problems of synergic control. First, during steady-state tasks, the PD patients have an impaired ability to organize the elements in a task-specific way so that their combined action stabilizes an important performance variable (total pressing force in Figure 3). Second, when the task requires changing the performance variable, the PD patients show an impaired ability to attenuate the corresponding synergy; as a result, their intended action is opposed by their own preexistent synergy. These are the two major components of the Impaired Control of Stability (ICS), and these components are present across a variety of clinical populations as we illustrate below.
We would like to emphasize that the decreased ASAs in PD patients may have significant clinical implications. The impaired ability to start turning-off a synergy stabilizing a performance variable in anticipation of its planned quick change may lead to problems with the initiation of next action. This may be particularly pronounced with respect to actions starting from a state that requires high stability of performance variables, for example actions initiated from a standing posture. This makes delayed ASAs potential contributors to episodes of freezing, a major disabling feature in later stages of PD.
Problems with multi-finger synergies in PD are not limited to pressing tasks that might be considered artificial and static. For example, a prehensile task designed to simulate the natural movement of taking a sip from a glass demonstrated that there were low synergy indices among the fingers, as well as between the fingers and the thumb (Jo et al., 2015). In that study, indices of ASAs correlated significantly with the score in a functional hand task involving quick movement across a sequence of targets of the glass filled with water. The score in that task represented the movement time normalized by the amount of spilled water. Neither the synergy indices nor the functional hand test score, however, correlated with the UPDRS (Unified PD Rating Scale), possibly because of the very narrow range of the UPDRS scores in this particular group with early-stage PD subjects.
ICS has several potential consequences for motor behavior. First, the low synergy index reflects the impaired stability of the action. This means that a change in the external conditions (a perturbation) is more likely to lead to destruction of the ongoing action as compared to persons without ICS. Second, a person with ICS may have problems initiating an action from a steady state, for example initiating a step from a standing posture, or initiating a turn from an ongoing rhythmical walking pattern. This makes the feature of ICS reflected in reduced ASAs potentially related to one of the most disabling features of PD, namely episodes of freezing.
4.2. Multisystem atrophy
Patients with multisystem atrophy with cerebellar involvement (known also as olivo-ponto-cerebellar atrophy) show a mixture of cerebellar and parkinsonian signs and symptoms reflecting the involvement of several subcortical loops. These patients also show signs of ICS similar to the one described in the previous section for PD. In particular, they also show reduced indices of multi-finger synergies and reduced ASAs (Park et al., 2013b). As can be seen in Figure 5A, the synergy index is decreased during the steady-state phase of the task, and the ASAs delayed and decreased in patients compared to the controls. This same study (Park et al., 2013b) showed that patients had a wide range of functional involvement and a correspondingly wide range of UPDRS scores. As a result, there were strong correlations between the synergy index and UPDRS score illustrated in Figure 5B.
Figure 5.
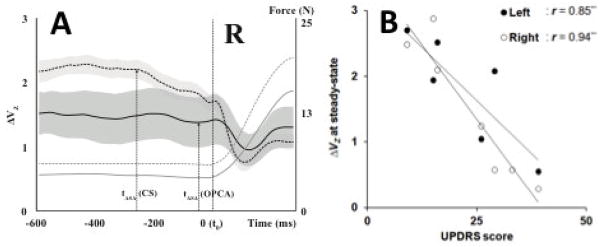
A: Averaged across subjects time profiles of the index of synergy (log-transformed, ΔVZ, with standard error shades) are shown for a group of patients with multiple brain atrophy (solid line) and for a group of healthy controls (dotted line). The control group shows higher ΔV during the steady state and an earlier and larger drop in ΔV (larger ASA) in preparation to the force pulse, which started at time t = 0. B: The UPDRS scores and ΔVZ during steady state correlated significantly in this group. Modified by permission from Park et al., 2013.
5. Examples of impaired coordination in other populations
5.1. Down syndrome
A study of multi-finger coordination in young adults with Down syndrome documented significantly reduced indices of multi-finger synergies (Latash et al., 2002; Scholz et al., 2003). During accurate pressing tasks, these persons used their hand as a fork turned upside down, pressing more strongly or weakly with all four fingers, causing positive co-variation of finger forces and poor performance accuracy. Although these people showed clear signs of ICS, two days of practice allowed them to improve the indices of finger synergies significantly, suggesting that control of stability can be recovered with an appropriately designed practice schedule. A number of more recent studies have documented significant improvements in synergy indices with specialized training in both young and older healthy adults (reviewed in Wu and Latash 2014). Taken together, these observations carry an optimistic message that ICS may be reversible with properly designed exercise.
5.2. Cortical stroke
Although the mentioned studies of patients with PD and multisystem atrophy show significant changes in indices of synergic control even in patients with mild symptoms, in other patient groups much stronger motor impairments may not be associated with consistent ICS. Reisman and Scholz (2003) studied reaching movements in eight stroke survivors, 60.6 ± 4.7 years of age, who had had a single cortical or subcortical stroke leading to a moderate impairment in the arm function. They reported similar indices of multi-joint synergies in the ipsilesional and contralesional arms despite the major differences in the overall movement patterns. This result suggests that problems with movement stability are not linked in an obligatory fashion to problems with overall movement patterns. These observations justify separation of ICS as a separate clinical denomination reflecting specific impairments in the neural control of movement stability.
Consistent with the above notion, our recent studies of multi-finger interaction similar to the ones described earlier (currently unpublished) have confirmed the cited observations of Reisman and Scholz. Only twelve stroke patients have been tested so far (aged 64.5 ±4 years) with single cortical stroke leading to mild arm/hand impairment. The patients showed no differences in the synergy indices measured during pressing tasks in the ipsilesional and contralesional hands; the magnitude of these indices was very close to the magnitudes observed in age-matched healthy controls. On the other hand, those participants showed significantly delayed ASAs supporting the notion that ICS may have two components, low synergy indices and reduced/delayed ASAs. Although the sample sizes for both studies are small, the potential of different components of ICS informing on abnormalities in different neurophysiological loops is exciting and shall be explored further.
6. The role of central nervous system in ICS
The association of ICS with disorders having known impairment of subcortical structures, such as the basal ganglia (e.g., PD) and the cerebellum (e.g., MSA-OCPA), fits well Houk’s theory (Houk, 2005) of the brain control of movements with distributed processing modules (DPMs). Within that scheme, two major anatomically defined DPMs (neuronal structures united into loops) have been proposed to be responsible for the selection and initiation of action (loops through the basal ganglia), and the amplification and refinement of action (loops involving the cerebellum). Note that several recent brain-imaging studies have suggested cerebellar involvement in PD (Lewis et al., 2007, 2011; Yu et al., 2007; Wu et al., 2011). In particular, weakened striatum-cerebellar connections have been documented (Wu et al., 2011), possibly related to problems with action initiation. It is feasible that some of the reviewed changes typical of ICS reflect changes involving both the basal ganglia and the cerebellum.
A number of earlier studies linked activity of the basal ganglia and cerebellum to synergies. In particular, the basal ganglia have been implicated in uniting the postural and locomotor synergies (Mori, 1987) and in the grasp-lift synergy (Forssberg et al., 1999). In those studies, however, synergies were defined as proportional changes within a set of elemental variables, not related to movement stability. Studies on monkeys have suggested that signals from the dentate nuclei are more closely related to control of muscle synergies rather than being prime movers of the explicitly required action (Thach et al., 1992; also see Rispal-Padel et al., 1981). One of the studies performed principal component analysis of the activity patterns of a large set of neurons within the dorsal spinocerebellar tract during hindlimb motion simulating walking (Bosco and Poppele, 2002). The two principal components that accounted for most of the variance of the neuronal activity were related not to individual joint movements, but to the whole limb length and orientation changes during the leg movement cycle. The limb length and orientation can be considered important performance variables for locomotion stabilized by co-varied joint rotations.
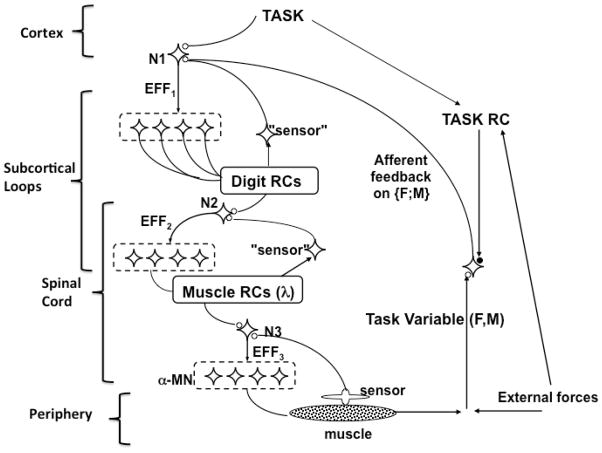
Figure 6 illustrates a multi-level scheme of hierarchical control of a natural action modified from an earlier paper. Within this scheme, it is assumed that, at each level, neural control signals define referent spatial coordinates for elemental variables salient for that level (Feldman and Levin, 1995; Latash, 2010). Figure 6 suggests tentative associations of different levels with structures within the central nervous system. The task is formed at cortical levels while the few-to-many mappings rely significantly on subcortical structures. These may involve the spinal cord as suggested by recent observations of multi-joint synergies stabilizing paw trajectory during locomotion of intact cats and induced locomotion in spinalized cats (Klishko et al., 2014a,b). Future systematic studies of the neural control of movement stability in animal models, healthy humans, and different neurological disorders may help us to understand the neural substrates of ICS, assist the lesion localization, and development of treatment strategies.
Figure 6.
A multi-level scheme of hierarchical control of a natural action. The scheme involves a chain of few-to-many mappings organized in a synergic way. Tentative association of different levels with structures within the central nervous system is suggested. The task is formed at cortical levels while the few-to-many mappings rely significantly on subcortical structures. Modified by permission from Latash, 2010.
7. Summary – ICS as a new dimension of neurological disorders
The evidence presented in this review has led to several main conclusions. First, ICS is commonly seen in persons with impaired motor function including those with disorders involving subcortical brain structures. Significant changes in indices of movement stability are seen even at subclinical stages of the disease and/or in tasks where traditional clinical examination fails to show any impairment. This feature of ICS potentially makes it a powerful tool for early detection of emergence of motor symptoms.
Second, signs of ICS can also be seen in otherwise healthy older adults who show a drop in the synergy indices and reduced ASAs (Shinohara et al., 2004; Olafsdottir et al., 2007a,b).
Third, ICS includes at least two distinct components. One of them reflects low stability, even of slow movements. It is reflected in reduced synergy indices. It is possible that this component is an important contributor to such motor impairments as ataxia. The other component reflects reduced ability to adjust (reduce) stability of a performance variable in preparation to an action that requires its quick change. It is reflected in delayed and reduced ASAs. The inability to modify movement stability in an appropriate and timely fashion may be central to motor signs such as “freezing of gait” in PD.
Finally, changes in motor synergies are treatable. They change with medication treatment as illustrated by the effects of dopamine replacement therapy in PD and also with an appropriately designed practice. A central element of the exercise leading to a quick improvement in synergy indices is the element of instability artificially introduced into the task (e.g., using virtual reality as in Wu et al., 2013).
Thus, we conclude that it is timely to introduce ICS as an objective, quantifiable, and theory-based clinical descriptor of movement disorders. It will allow integrating the recent progress in understanding the neural control of movement to improve diagnosis, treatment and clinical research of a range of neurological diseases. ICS has a great deal of potential as a very useful behavioral biomarker of significant motor changes in patients who otherwise display no clinically identifiable symptoms in the tested parts of the body and within the explored range of tasks. While, to date, this feature of ICS has been shown in PD patients only, these promising early results suggest that in a near future more examples of such high sensitivity of ICS indices to early stages of neurological movement disorders will be documented.
Recent studies of people with neurological disease have contributed significantly to the progress in understanding the neurophysiological mechanisms of movement stability. In particular, the contrast between ICS in even early-stage subcortical disorders versus no signs of ICS in even more involved cortical stroke survivors points to subcortical loops as being crucial for the proper control of movement stability. In fact, proper control of stability is not limited to the realm of movements (reviewed in Latash, 2008). It is crucial for any functions based on proper coordination of multiple elements. Examples include creation of a single coherent picture of the world based on sensory signals of different modalities, expression of thoughts and emotions using redundant sets of words during speech, and even organization of cognitive processes based on multiple (abundant) sources of information.
Highlights.
Synergies are neural mechanisms ensuring task-specific movement stability;
Anticipatory synergy adjustments (ASA) reduce stability in preparation to quick actions;
Impaired control of stability (ICS) is an objective descriptor of movement disorders;
Subcortical structures are crucial for control of movement stability.
Acknowledgments
Study funding
The preparation of the manuscript was supported in part by grants from the National Institutes of Health NS060722, NS035032, ES019672, and NS082151. The funding source had no involvement in any stage of work on the paper.
We are very much grateful to our colleagues and students who took part in the clinical studies reviewed in this paper: Hang Jin Jo, Mechelle Lewis, Jaebum Park, and Yen-Hsun Wu. We are grateful to Dr. Richard Mailman for his thoughtful input during the preparation of the manuscript.
Footnotes
Conflict of Interest
Drs. Latash and Huang declare no conflict of interest.
Role of Authors
Dr. Latash and Dr. Huang contributed equally to all the steps of conceiving, writing, and finalizing this manuscript.
Full financial disclosure for the previous 12 months:
This study was supported by NIH grants NS060722, NS035032, ES019672, and NS082151
Dr. Latash reports no other disclosures
Dr. Huang reports no other disclosures.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Abbruzzese G. The medical management of spasticity. Eur J Neurol. 2002;9(Suppl 1):30–34. doi: 10.1046/j.1468-1331.2002.0090s1030.x. discussion 53–61. [DOI] [PubMed] [Google Scholar]
- Bastian AJ, Martin TA, Keating JG, Thach WT. Cerebellar ataxia: abnormal control of interaction torques across multiple joints. J Neurophysiol. 1996;76:492–509. doi: 10.1152/jn.1996.76.1.492. [DOI] [PubMed] [Google Scholar]
- Bernstein NA. A new method of mirror cyclographie and its application towards the study of labor movements during work on a workbench. Hygiene, Safety and Pathology of Labor. 1930;56:3–9. 3–11. (in Russian) [Google Scholar]
- Bernstein NA. The Co-ordination and Regulation of Movements. Oxford: Pergamon Press; 1967. [Google Scholar]
- Bobath B. Adult Hemiplegia: Evaluation and Treatment. William Heinemann; London: 1978. [Google Scholar]
- Bosco G, Poppele RE. Encoding of hindlimb kinematics by spinocerebellar circuitry. Arch Ital Biol. 2002;140:185–192. [PubMed] [Google Scholar]
- Brown MJ, Almeida QJ. Evaluating dopaminergic system contributions to cued pattern switching during bimanual coordination. Eur J Neurosci. 2011;34:632–640. doi: 10.1111/j.1460-9568.2011.07773.x. [DOI] [PubMed] [Google Scholar]
- Creath R, Kiemel T, Horak F, Jeka JJ. The role of vestibular and somatosensory systems in intersegmental control of upright stance. J Vestib Res. 2008;18:39–49. [PMC free article] [PubMed] [Google Scholar]
- d’Avella A, Saltiel P, Bizzi E. Combinations of muscle synergies in the construction of a natural motor behavior. Nat Neurosci. 2003;6:300–308. doi: 10.1038/nn1010. [DOI] [PubMed] [Google Scholar]
- DeWald JP, Pope PS, Given JD, Buchanan TS, Rymer WZ. Abnormal muscle coactivation patterns during isometric torque generation at the elbow and shoulder in hemiparetic subjects. Brain. 1995;118:495–510. doi: 10.1093/brain/118.2.495. [DOI] [PubMed] [Google Scholar]
- Feldman AG, Levin MF. Positional frames of reference in motor control: their origin and use. Behav Brain Sci. 1995;18:723–806. [Google Scholar]
- Forssberg H, Eliasson AC, Redon-Zouitenn C, Mercuri E, Dubowitz L. Impaired grip-lift synergy in children with unilateral brain lesions. Brain. 1999;122:1157–1168. doi: 10.1093/brain/122.6.1157. [DOI] [PubMed] [Google Scholar]
- Franklin DW, Milner TE. Adaptive control of stiffness to stabilize hand position with large loads. Exp Brain Res. 2003;152:211–220. doi: 10.1007/s00221-003-1540-3. [DOI] [PubMed] [Google Scholar]
- Gelfand IM, Latash ML. On the problem of adequate language in movement science. Motor Control. 1998;2:306–313. doi: 10.1123/mcj.2.4.306. [DOI] [PubMed] [Google Scholar]
- Gibo TL, Bastian AJ, Okamura AM. Effect of age on stiffness modulation during postural maintenance of the arm. IEEE Int Conf Rehabil Robot. 2013 Jun;:6650395. doi: 10.1109/ICORR.2013.6650395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gontijo AP, Mancini MC, Silva PL, Chagas PS, Sampaio RF, Luz RE, Fonseca ST. Changes in lower limb co-contraction and stiffness by toddlers with Down syndrome and toddlers with typical development during the acquisition of independent gait. Hum Mov Sci. 2008;27:610–621. doi: 10.1016/j.humov.2008.01.003. [DOI] [PubMed] [Google Scholar]
- Heitmann S, Ferns N, Breakspear M. Muscle co-contraction modulates damping and joint stability in a three-link biomechanical limb. Front Neurorobot. 2012;5:5. doi: 10.3389/fnbot.2011.00005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horak FB, Diener HC. Cerebellar control of postural scaling and central set in stance. J Neurophysiol. 1994;72:479–93. doi: 10.1152/jn.1994.72.2.479. [DOI] [PubMed] [Google Scholar]
- Horak FB, Nutt JG, Nashner LM. Postural inflexibility in parkinsonian subjects. J Neurol Sci. 1992;111:46–58. doi: 10.1016/0022-510x(92)90111-w. [DOI] [PubMed] [Google Scholar]
- Houk JC. Agents of the mind. Biol Cybern. 2005;92:427–437. doi: 10.1007/s00422-005-0569-8. [DOI] [PubMed] [Google Scholar]
- Ivanenko YP, Poppele RE, Lacquaniti F. Five basic muscle activation patterns account for muscle activity during human locomotion. J Physiol. 2004;556:267–282. doi: 10.1113/jphysiol.2003.057174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jo HJ, Park J, Lewis MM, Huang X, Latash ML. Prehension synergies and hand function in early-stage Parkinson’s disease. Exp Brain Res. 2015;233:425–440. doi: 10.1007/s00221-014-4130-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelso JAS. Dynamic patterns: The self-organization of brain and behavior. Cambridge: MIT Press; 1995. [Google Scholar]
- Klishko AN, Farrell BJ, Beloozerova IN, Latash ML, Prilutsky BI. Stabilization of cat paw trajectory during locomotion. J Neurophysiol. 2014a;112:1376–1391. doi: 10.1152/jn.00663.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klishko AN, Lemay MA, Latash ML, Prilutsky BI. Multi-joint kinematic synergies stabilize hindlimb length and paw vertical coordinate during walking in the chronic spinal cat. Abstr Soc Neurosci 44-th Ann Meet, 732.28/MM17; Washington, DC. November 15–19, 2014.2014b. [Google Scholar]
- Klous M, Mikulic P, Latash ML. Two aspects of feed-forward postural control: Anticipatory postural adjustments and anticipatory synergy adjustments. J Neurophysiol. 2011;105:2275–2288. doi: 10.1152/jn.00665.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnamoorthy V, Latash ML, Scholz JP, Zatsiorsky VM. Muscle synergies during shifts of the center of pressure by standing persons. Exp Brain Res. 2003;152:281–292. doi: 10.1007/s00221-003-1574-6. [DOI] [PubMed] [Google Scholar]
- Krishnan V, Aruin AS, Latash ML. Two stages and three components of postural preparation to action. Exp Brain Res. 2011;212:47–63. doi: 10.1007/s00221-011-2694-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML. Synergy. Oxford University Press; New York: 2008. [Google Scholar]
- Latash ML. Motor synergies and the equilibrium-point hypothesis. Motor Control. 2010;14:294–322. doi: 10.1123/mcj.14.3.294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML. The bliss (not the problem) of motor abundance (not redundancy) Exp Brain Res. 2012;217:1–5. doi: 10.1007/s00221-012-3000-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Kang N, Patterson D. Finger coordination in persons with Down syndrome: Atypical patterns of coordination and the effects of practice. Exp Brain Res. 2002;146:345–355. doi: 10.1007/s00221-002-1189-3. [DOI] [PubMed] [Google Scholar]
- Latash ML, Levin MF, Scholz JP, Schöner G. Motor control theories and their applications. Medicina. 2010;46:382–392. [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Scholz JP, Schöner G. Toward a new theory of motor synergies. Motor Control. 2007;11:276–308. doi: 10.1123/mcj.11.3.276. [DOI] [PubMed] [Google Scholar]
- Lewis MM, Du G, Sen S, Kawaguchi A, Truong Y, Lee S, Mailman RB, Huang X. Differential involvement of striato- and cerebello-thalamo-cortical pathways in tremor- and akinetic/rigid-predominant Parkinson’s disease. Neurosci. 2011;177:230–239. doi: 10.1016/j.neuroscience.2010.12.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Massion J. Movement, posture and equilibrium – interaction and coordination. Prog Neurobiol. 1992;38:35–56. doi: 10.1016/0301-0082(92)90034-c. [DOI] [PubMed] [Google Scholar]
- Mori S. Integration of posture and locomotion in acute decerebrate cats and in awake, freely moving cats. Prog Neurobiol. 1987;28:161–195. doi: 10.1016/0301-0082(87)90010-4. [DOI] [PubMed] [Google Scholar]
- Nielsen J, Sinkjaer T, Toft E, Kagamihara Y. Segmental reflexes and ankle joint stiffness during co-contraction of antagonistic ankle muscles in man. Exp Brain Res. 1994;102:350–358. doi: 10.1007/BF00227521. [DOI] [PubMed] [Google Scholar]
- Olafsdottir H, Yoshida N, Zatsiorsky VM, Latash ML. Anticipatory covariation of finger forces during self-paced and reaction time force production. Neurosci Lett. 2005;381:92–96. doi: 10.1016/j.neulet.2005.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olafsdottir H, Yoshida N, Zatsiorsky VM, Latash ML. Elderly show decreased adjustments of motor synergies in preparation to action. Clin Biomech. 2007a;22:44–51. doi: 10.1016/j.clinbiomech.2006.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olafsdottir HB, Zatsiorsky VM, Latash ML. The effects of strength training on finger strength and hand dexterity in healthy elderly individuals. J Appl Physiol. 2008;105:1166–1178. doi: 10.1152/japplphysiol.00054.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olafsdottir H, Zhang W, Zatsiorsky VM, Latash ML. Age related changes in multi-finger synergies in accurate moment of force production tasks. J Appl Physiol. 2007b;102:1490–1501. doi: 10.1152/japplphysiol.00966.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J, Jo HJ, Lewis MM, Huang X, Latash ML. Effects of Parkinson’s disease on optimization and structure of variance in multi-finger tasks. Exp Brain Res. 2013a;231:51–63. doi: 10.1007/s00221-013-3665-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J, Lewis MM, Huang X, Latash ML. Effects of olivo-ponto-cerebellar atrophy (OPCA) on finger interaction and coordination. Clin Neurophysiol. 2013b;124:991–998. doi: 10.1016/j.clinph.2012.10.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J, Lewis MM, Huang X, Latash ML. Dopaminergic modulation of motor coordination in Parkinson’s disease. Parkinsonism Rel Disord. 2014;20:64–68. doi: 10.1016/j.parkreldis.2013.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J, Wu Y-H, Lewis MM, Huang X, Latash ML. Changes in multi-finger interaction and coordination in Parkinson’s disease. J Neurophysiol. 2012;108:915–924. doi: 10.1152/jn.00043.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J, Zatsiorsky VM, Latash ML. Optimality vs. variability: An example of multi-finger redundant tasks. Exp Brain Res. 2010;207:119–132. doi: 10.1007/s00221-010-2440-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prilutsky BI, Zatsiorsky VM. Optimization-based models of muscle coordination. Exer Sport Sci Rev. 2002;30:32–38. doi: 10.1097/00003677-200201000-00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reisman D, Scholz JP. Aspects of joint coordination are preserved during pointing in persons with post-stroke hemiparesis. Brain. 2003;126:2510–2527. doi: 10.1093/brain/awg246. [DOI] [PubMed] [Google Scholar]
- Rispal-Padel L, Cicirata F, Pons C. Contribution of the dentato-thalamo-cortical system to control of motor synergy. Neurosci Lett. 1981;22:137–144. doi: 10.1016/0304-3940(81)90077-x. [DOI] [PubMed] [Google Scholar]
- Sainburg RL, Ghilardi MF, Poizner H, Ghez C. Control of limb dynamics in normal subjects and patients without proprioception. J Neurophysiol. 1995;73:820–835. doi: 10.1152/jn.1995.73.2.820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scholz JP, Kang N, Patterson D, Latash ML. Uncontrolled manifold analysis of single trials during multi-finger force production by persons with and without Down syndrome. Exp Brain Res. 2003;153:45–58. doi: 10.1007/s00221-003-1580-8. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Schöner G. The uncontrolled manifold concept: Identifying control variables for a functional task. Exp Brain Res. 1999;126:289–306. doi: 10.1007/s002210050738. [DOI] [PubMed] [Google Scholar]
- Schöner G. Recent developments and problems in human movement science and their conceptual implications. Ecol Psychol. 1995;8:291–314. [Google Scholar]
- Shim JK, Olafsdottir H, Zatsiorsky VM, Latash ML. The emergence and disappearance of multi-digit synergies during force production tasks. Exp Brain Res. 2005;164:260–270. doi: 10.1007/s00221-005-2248-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shinohara M, Scholz JP, Zatsiorsky VM, Latash ML. Finger interaction during accurate multi-finger force production tasks in young and elderly persons. Exp Brain Res. 2004;156:282–292. doi: 10.1007/s00221-003-1786-9. [DOI] [PubMed] [Google Scholar]
- Slijper H, Latash ML. The effects of instability and additional hand support on anticipatory postural adjustments in leg, trunk, and arm muscles during standing. Exp Brain Res. 2000;135:81–93. doi: 10.1007/s002210000492. [DOI] [PubMed] [Google Scholar]
- Solnik S, Pazin N, Coelho C, Rosenbaum DA, Scholz JP, Zatsiorsky VM, Latash ML. End-state comfort and joint configuration variance during reaching. Exp Brain Res. 2013;225:431–442. doi: 10.1007/s00221-012-3383-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stergiou N, editor. Innovative analyses of human movement. Human Kinetics; Urbana, IL: 2004. [Google Scholar]
- Thach WT, Goodkin HG, Keating JG. Cerebellum and the adaptive coordination of movement. Ann Rev Neurosci. 1992;15:403–442. doi: 10.1146/annurev.ne.15.030192.002155. [DOI] [PubMed] [Google Scholar]
- Ting LH, Macpherson JM. A limited set of muscle synergies for force control during a postural task. J Neurophysiol. 2005;93:609–613. doi: 10.1152/jn.00681.2004. [DOI] [PubMed] [Google Scholar]
- Woollacott MH, Shumway-Cook A. Changes in posture control across the life span--a systems approach. Phys Ther. 1990;70:799–807. doi: 10.1093/ptj/70.12.799. [DOI] [PubMed] [Google Scholar]
- Wu Y-H, Latash ML. The effects of practice on coordination. Exer Sport Sci Rev. 2014;42:37–42. doi: 10.1249/JES.0000000000000002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Y-H, Pazin N, Zatsiorsky VM, Latash ML. Improving finger coordination in young and elderly persons. Exp Brain Res. 2013;226:273–283. doi: 10.1007/s00221-013-3433-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu T, Wang L, Hallett M, Chen Y, Li K, Chan P. Effective connectivity of brain networks during self-initiated movement in Parkinson’s disease. Neuroimage. 2011;55:204–15. doi: 10.1016/j.neuroimage.2010.11.074. [DOI] [PubMed] [Google Scholar]
- Yu H, Sternad D, Corcos DM, Vaillancourt DE. Role of hyperactive cerebellum and motor cortex in Parkinson’s disease. Neuroimage. 2007;35:222–33. doi: 10.1016/j.neuroimage.2006.11.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou T, Wu Y-H, Bartsch A, Cuadra C, Zatsiorsky VM, Latash ML. Anticipatory synergy adjustments: Preparing a quick action in an unknown direction. Exp Brain Res. 2013;226:565–573. doi: 10.1007/s00221-013-3469-5. [DOI] [PMC free article] [PubMed] [Google Scholar]