Hepatic insulin sensitivity in healthy and prediabetic subjects: from a dual- to a single-tracer oral minimal model

Abstract

Recently, a model was proposed to assess hepatic insulin sensitivity during a meal, i.e., the ability of insulin to suppress glucose production (EGP), S_I^P. The model was developed on EGP data obtained from a triple-tracer meal and the tracer-to-tracee clamp technique and validated against the euglycemic hyperinsulinemic clamp. The aim of this study was to assess whether S_I^P can be obtained from plasma concentrations measured after a single-tracer meal by incorporating the above EGP model into the oral glucose minimal model by describing both glucose production and disposal (OMM^PD). Triple-tracer meal data of two databases (20 healthy and 60 healthy and prediabetic subjects) were used. Virtually model-independent EGP estimates were calculated. OMM^PD was identified on exogenous and endogenous glucose concentrations, providing indices of S_I^P, disposal insulin sensitivity (S_I^D), and EGP. The model fitted the data well, and S_I^P and S_I^D were estimated with precision in both databases (S_I^P = 5.48 ± 0.54 10⁻⁴ dl·kg⁻¹·min⁻¹ per μU/ml and S_I^D = 9.93 ± 2.18 10⁻⁴ dl·kg⁻¹·min⁻¹ per μU/ml in healthy; S_I^P = 5.41 ± 3.55 10⁻⁴ dl·kg⁻¹·min⁻¹ per μU/ml and S_I^D = 5.34 ± 6.17 10⁻⁴ dl·kg⁻¹·min⁻¹ per μU/ml, in healthy and prediabetic subjects). Estimated S_I^P and that derived from the triple-tracer EGP model were very similar on average. Moreover, the time course of EGP normalized to basal EGP (EGP_b), and EGP/EGP_b agreed with the results obtained using the triple-tracer method. In this study, we have demonstrated that S_I^P, S_I^D, and EGP/EGP_b time course can be estimated reliably from a single-tracer meal protocol in both healthy and prediabetic subjects.

the primary source of endogenous glucose production (EGP) in the body is the liver, which modulates glucose release into the circulation influenced by prevailing glucose, insulin, glucagon, and other hormone concentrations. In a healthy subject, when plasma glucose and insulin concentrations rise, e.g., after a meal, EGP is suppressed, whereas if plasma glucose and insulin concentrations decrease below a given threshold (such as during prolonged fasting), more glucose is delivered to avoid potentially dangerous hypoglycemia. In pathological situations, such as type 2 diabetes, insulin regulation of EGP is altered (17). Thus, quantifying the effect of insulin in suppressing EGP [hepatic insulin sensitivity (S_I^P)] could be a useful tool for studying the pathophysiology of metabolic disorders, including various stages of diabetes and efficacy of therapeutic approaches.

Among the methods proposed in the literature to estimate S_I^P in vivo, the labeled euglycemic hyperinsulinemic clamp (16), and surrogate indices of hepatic insulin resistance (1) have been used. However, both methods suffer from important limitations. Briefly, the clamp method calculates S_I^P as the difference between net (derived from steady-state glucose infusion rate, plasma glucose, and insulin concentrations) and disposal insulin sensitivity (derived from steady-state tracer infusion rate, plasma glucose, tracer glucose, and insulin concentrations). Its main drawbacks are that it is labor intensive and nonphysiological. The index proposed by Abdul-Ghani et al. (1) is the product of the area under glucose and insulin concentrations measured in the first 30 min of an oral glucose tolerance test (OGTT). It utilizes a simpler method and is more physiological. However, it is based on the erroneous assumptions that glucose utilization minimally increases during the initial 30 min after food ingestion and that glucose rate of appearance in the first 30 min is zero.

An important step forward was a model-based method to estimate S_I^P during a meal (14). The model was fitted against model-independent estimates of EGP from the triple-tracer meal protocol (4) and has recently been validated against the labeled euglycemic hyperinsulinemic clamp (13). Of note, only two of the three tracers available in Basu et al. (4) were used to reconstruct the EGP time course, i.e., one oral to segregate the endogenous from the exogenous source of glucose and the other intravenous to mimic the expected EGP pattern, keeping the tracer-to-tracee (TTR) ratio constant (5). Thus, the state-of-the-art method to estimate S_I^P during a meal uses a dual-tracer approach.

However, a less labor-intensive method that is able to provide an estimation of S_I^P would be particularly appealing for large-scale studies. One possibility could be to derive S_I^P as the difference between net (S_I) and disposal insulin sensitivity (S_I^D) derived from the labeled oral glucose minimal model (12), but, as already pointed out in Dalla Man et al. (12), this would lead to a nonphysiological result in a not insignificant percentage of the subjects (19% of them showed net insulin sensitivity lower than disposal insulin sensitivity), as shown in Fig. 7 in Ref. 9. This was proven to be due largely to a suboptimal description of EGP in the minimal model (14).

The aim of this study was to combine the EGP model proposed by Dalla Man et al. (14) with the oral minimal model (12) to enable an accurate estimation of the S_I^P index from a single-tracer meal protocol. First, we identified and validated the model on healthy subjects, and then we evaluated the performance of the method in prediabetes.

MATERIALS AND METHODS

Subjects and Protocols

In this analysis, two different databases were used. The first database (healthy) was employed to build and validate the new oral minimal model. It consisted of 20 healthy subjects (age = 32 ± 4 yr, BMI = 25 ± 1 kg/m²), already described in Dalla Man et al. (14), who received a triple-tracer mixed meal (10 kcal/kg: 45% carbohydrate, 15% protein, 40% fat) containing 1.00 ± 0.02 g/kg glucose (4). [1-¹³C]glucose was administered orally together with the meal, and [6,6-²H₂]glucose and [6-³H]glucose were infused intravenously, as described below. Blood samples were drawn frequently to measure plasma glucose (G), insulin (I), and tracer concentrations, as reported previously (4). In particular, labeling the meal with [1-¹³C]glucose (G*) allowed for deriving the exogenous, i.e., coming from the meal, glucose (G_exo) concentration as

$${\text{G}}_{\text{exo}}={\text{G}}^{\ast }\cdot \left[1+\frac{1}{{\text{z}}_{\text{meal}}}\right]$$ (1)

with z_meal denoting the TTR ratio in the meal. Endogenous glucose (G_end) was then calculated as difference between G, G_exo, and the intravenously infused tracer [6,6-²H₂]glucose (G_D2):

$${\text{G}}_{\text{end}}=\text{G}-{\text{G}}_{\text{exo}}-{\text{G}}_{\text{D2}}$$ (2)

It is worth noting that, in the case of a single-tracer protocol, G_D2 in Eq. 2 is zero.

The [6-³H]glucose and [6,6-D₂]glucose tracers were infused intravenously at variable rates, to clamp, respectively, the specific activity, i.e., the ratio between [6-³H]glucose and [1-¹³C]glucose, and the TTR, i.e., the ratio between [6.6-²H₂]glucose and G_end. More details on the experimental protocol can be found in Basu et al. (4). Thanks to this protocol, it was possible to simultaneously estimate both EGP and meal glucose rate of appearance (R_{a meal}) using Radziuk's model (18) by minimizing the non-steady-state model error.

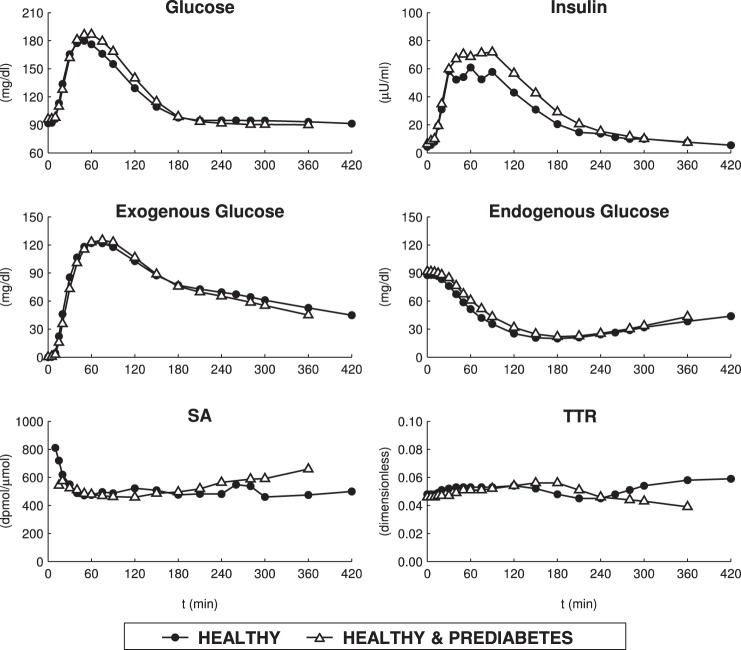
The second database (healthy and prediabetic subjects) was used to test the new method in prediabetes. In particular, this database consisted of 32 subjects (age = 54 ± 1 yr, BMI = 31 ± 1 kg/m²) with impaired fasting glucose (IFG) and 28 subjects (age = 51 ± 2 yr; BMI = 28 ± 1 kg/m²) with normal fasting glucose (NFG) (6) classified in subgroups on the basis of their glucose tolerance, i.e., 16 NFG subjects (age = 50 ± 2 yr, BMI = 27 ± 1 kg/m²) with normal glucose tolerance (NFG/NGT), 12 NFG subjects (age = 53 ± 3 yr, BMI = 30 ± 1 kg/m²) with impaired glucose tolerance (NFG/IGT), seven IFG subjects (age = 53 ± 3 yr, BMI = 31 ± 2 kg/m²) with normal glucose tolerance (IFG/NGT), 17 IFG subjects (age = 54 ± 2 yr, BMI = 31 ± 1 kg/m²) with impaired glucose tolerance (IFG/IGT), and eight IFG subjects (age = 54 ± 2 yr, BMI = 32 ± 1 kg/m²) with diabetes (IFG/DM). These subjects underwent the same triple-tracer mixed meal protocol described above, except for the glucose amount, fixed here at 75 g. Average time courses of G, I, G_exo, G_end, SA and TTR are shown in Fig. 1 for both databases. For more details on protocol we refer to Bock et al. (6).

Fig. 1.

Mean concentrations of plasma glucose and insulin (top), exogenous and endogenous glucose (middle), and specific activity (SA) and clamped tracer-to-tracee ratio (TTR) (bottom) in healthy database (n = 20) and healthy and prediabetes database (n = 60).

A Production and Disposal Minimal Model

A production and disposal oral minimal model (OMM^PD) is presented, which permits description of G, G_exo, and G_end using a single, orally administered tracer. The model, shown in Fig. 2, is built on the mass balance principle

$$\dot{\text{G}}\left(t\right)=\frac{\text{EGP}\left(t\right)+{\text{R}}_{\text{a}\hspace{0.17em}\text{D2}}\left(t\right)+{\text{R}}_{\text{a}\hspace{0.17em}\hspace{0.17em}\text{meal}}\left(t\right)-{\text{R}}_{\text{d}}\left(t\right)}{\text{V}}\hspace{0.17em}\text{G}\left(0\right)={\text{G}}_{\text{b}}$$ (3)

Fig. 2.

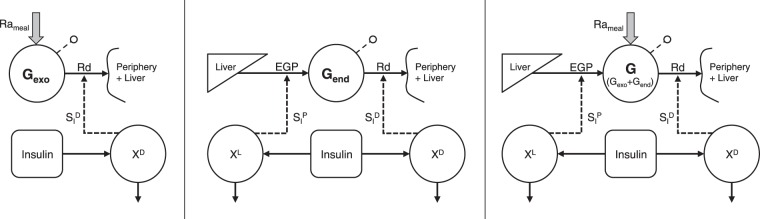
Scheme of the production and disposal oral minimal model (OMM^PD). Left: submodel of exogenous glucose (G_exo). Middle: submodel of endogenous glucose (G_end). Right: submodel of total glucose (G = G_exo + G_end).

where G_b is basal glucose, V is the distribution volume, EGP is the endogenous glucose production, R_{a D2} is the [6,6-²H₂]glucose rate of appearance, R_{a meal} is the meal glucose rate of appearance, and R_d is the rate of glucose disposal. It is of note that, in the case of single-tracer approach, R_{a D2} is zero and Eq. 3 becomes

$$\dot{\text{G}}\left(t\right)=\frac{\text{EGP}\left(t\right)+{\text{R}}_{\text{a}\hspace{0.17em}\text{meal}}\left(t\right)-{\text{R}}_{\text{d}}\left(t\right)}{\text{V}}\hspace{0.17em}\text{G}\left(0\right)={\text{G}}_{\text{b}}$$ (4)

Since Eq. 2 holds, Eq. 3 can be split to distinguish the exogenous and endogenous components

$${\dot{\text{G}}}_{\text{exo}}\left(t\right)=\frac{{\text{R}}_{\text{a}\hspace{0.17em}\text{meal}}\left(t\right)-{\text{R}}_{\text{d}\hspace{0.17em}\text{exo}}\left(t\right)}{\text{V}}\hspace{0.17em}{\text{G}}_{\text{exo}}\left(0\right)=\text{0}$$

$${\dot{\text{G}}}_{\text{end}}\left(t\right)=\frac{\text{EGP}\left(t\right)-{\text{R}}_{\text{d}\hspace{0.17em}\text{end}}\left(t\right)}{\text{V}}\hspace{0.17em}{\text{G}}_{\text{end}}\left(0\right)={\text{G}}_{\text{endb}}$$ (5)

with G_endb the basal endogenous glucose and R_{d exo} and R_{d end} the disposal rates of G_exo and G_end, respectively. Like in Cobelli et al. (9) and Dalla Man et al. (12), OMM^PD assumes that R_{a meal} is described by a piecewise-linear function with known break points t_i and unknown amplitudes α_i

$${\text{R}}_{\text{a}\hspace{0.17em}\text{meal}}\left(\alpha ,t\right)=\{\begin{array}{ll}{\alpha }_{\text{i}-1}+\frac{{\alpha }_{\text{i}}-{\alpha }_{\text{i}-1}}{t_{\text{i}}-t_{\text{i}-1}}\cdot \left(t-t_{\text{i}-1}\right)\hfill & \text{for}{t}_{\text{i}-1}\le t\le t_{\text{i}},i=1,\dots ,8\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (6)

and R_d is linearly dependent on G and controlled by insulin in a remote compartment:

$$\{\begin{array}{l}{\text{R}}_{\text{d}}\left(t\right)=\text{V}\cdot \left[{\text{S}}_{\text{G}}^{\text{D}}+{\text{X}}^{\text{D}}\left(t\right)\right]\cdot \text{G}\left(t\right)\hfill \\ {\dot{\text{X}}}^{\text{D}}\left(t\right)=-k_1^{\text{D}}\cdot \left[{\text{X}}^{\text{D}}\left(t\right)-k_2^{\text{D}}\cdot \left(\text{I}\left(t\right)-{\text{I}}_{\text{b}}\right)\right]\hspace{0.17em}{\text{X}}^{\text{D}}\left(0\right)=0\hfill \end{array}$$ (7)

where S_G^D is the fractional (i.e., per unit distribution volume) disposal glucose effectiveness (GE^D), I is the plasma insulin concentration (with I_b its basal value), and X^D is the insulin action on glucose disposal, and k₁^D and k₂^D are rate constants describing its dynamics and magnitude. Similarly, R_{d exo} and R_{d end} are defined as in Eq. 7, substituting G with G_exo and G_end, respectively.

In addition, OMM^PD incorporates the EGP description proposed in Dalla Man et al. (14), which is based on the assumption that EGP is suppressed by plasma glucose and a delayed insulin action, and it is also promptly inhibited by portal insulin. In particular, portal insulin is substituted with insulin secretion rate, which can be modeled as the sum of two components, i.e., one proportional to the glucose rate of change (which takes into account of the newly secreted insulin) and one to the above-basal glucose concentration. Therefore, EGP suppression is described by three components: one proportional to glucose rate of change (through k_GR), one proportional to glucose concentration (through k_G), and a delayed insulin action (X^P):

$$\{\begin{array}{ll}\text{EGP}\text{(}t\text{)}={\text{EGP}}_{\text{b}}-k_{\text{G}}\cdot \left[G(t)-{\text{G}}_{\text{b}}\right]-{\text{X}}^{\text{P}}\text{(}t\text{)}-{\text{X}}^{\text{Der}}\text{(}t\text{)}\hfill & \text{EGP}\left(0\right)={\text{EGP}}_{\text{b}}\hfill \\ {\dot{\text{X}}}^{\text{P}}\left(t\right)=-k_1^{\text{P}}\cdot \left[{\text{X}}^{\text{P}}\left(t\right)-{\text{X}}_1\left(t\right)\right]\hfill & {\text{X}}^{\text{P}}\left(0\right)=0\hfill \\ {\dot{\text{X}}}_1\left(t\right)=-k_1^{\text{P}}\cdot \left[{\text{X}}_1\left(t\right)-k_2^{\text{P}}\cdot \left(\text{I}\left(t\right)-{\text{I}}_{\text{b}}\right)\right]\hfill & {\text{X}}_{\text{1}}\left(0\right)=0\hfill \end{array}$$ (8)

with

$${\text{X}}^{\text{Der}}\left(t\right)=\{\begin{array}{ll}{k}_{\text{GR}}\cdot \frac{\text{dG}\left(t\right)}{\text{d}t}\hfill & \text{if}\hspace{0.17em}\frac{\text{dG}\left(t\right)}{\text{d}t}\ge 0\hfill \\ 0\hfill & \text{if}\frac{\text{dG}\left(t\right)}{\text{d}t}<0\hfill \end{array}$$ (9)

and EGP_b related to the other model parameters through the steady-state constraint

$${\text{EGP}}_{\text{b}}=\text{V}\cdot {\mathrm{S}}_{\mathrm{G}}^{\text{D}}\cdot {\mathrm{G}}_{\text{b}}-{\text{R}}_{\text{a}\hspace{0.17em}\text{D}2}\left(0\right)$$ (10)

Hence, OMM^PD is described by Eqs. 3 and 5-10. The production and disposal components of the insulin sensitivity indices (S_I^P, S_I^D) and glucose effectiveness (GE^P, GE^D) are derived from steady-state model equations as follows:

$${\text{GE}}^{\text{D}}=\frac{{\partial \text{R}}_{\text{d}}}{\partial \text{G}}{|}_{\text{ss}}={\text{S}}_{\text{G}}^{\text{D}}\cdot \text{V}$$ (11)

$${\text{S}}_{\text{I}}^{\text{D}}=\frac{{{\partial }^2\text{R}}_{\text{d}}}{\partial \text{G}\partial \text{I}}{|}_{\text{ss}}=k_{\text{2}}^{\text{D}}\cdot \text{V}$$ (12)

$${\text{GE}}^{\text{P}}=\frac{\partial \text{EGP}}{\partial \text{G}}{|}_{\text{ss}}=k_G+k_{\text{GR}}\cdot \frac{{\text{G}}_{\max }-{\text{G}}_{\text{b}}}{{\text{AUC}}_{\text{G}}}$$ (13)

$${\text{S}}_{\text{I}}^{\text{P}}=\frac{\partial \text{EGP}}{\partial \text{I}}{|}_{\text{ss}}\cdot \frac{1}{{\text{G}}_{\text{b}}}=\frac{k_2^{\text{P}}}{{\text{G}}_{\text{b}}}$$ (14)

where AUC_G is the area under plasma glucose curve.

Model Identification

Identifiability.

OMM^PD is a priori nonidentifiable; in particular, parameter V is not identifiable and parameter S_G^D is not uniquely identifiable. The a priori knowledge required for model identification was obtained paralleling that done in Dalla Man et al. (12). The model of Eqs. 3, 5, and 7-10 was identified using R_{a meal} as known input (available from the triple-tracer protocol), and parameter V and S_G^D were estimated in each subject. Then, to identify the OMM^PD, V and S_G^D were fixed to their respective mean values in the population (V = 1.61 ± 0.06 dl/kg, S_G^D = 0.0115 ± 0.0007 min), and the constraint

$${\displaystyle {\int }_0^{\infty }}{\text{R}}_{\text{a}\hspace{0.17em}\text{meal}}\left(t\right)\text{d}t=\frac{\text{D}\cdot \text{f}}{\text{BW}}$$ (15)

was imposed to the area under estimated R_{a meal}, where D is the dose of ingested glucose, f is the fraction of absorbed glucose, and BW is the body weight of the subject. However, due to Eq. 10, fixing both V and S_G^D would make it impossible to individualize EGP_b in a given subject. Hence, GE^D (and thus S_G^D) was decomposed into its insulin-independent [i.e., glucose effectiveness on glucose disposal at zero insulin (GEZI^D)] and insulin-dependent components (3):

$${\text{GE}}^{\text{D}}={\text{GEZI}}^{\text{D}}+{\mathrm{S}}_{\mathrm{I}}^{\mathrm{D}}\cdot {\mathrm{I}}_{\mathrm{b}}\cdot \text{V}$$ (16)

$${\mathrm{S}}_{\mathrm{G}}^{\mathrm{D}}={\text{GEZI}}^{\text{D}}/\text{V}+{\mathrm{S}}_{\mathrm{I}}^{\mathrm{D}}\cdot {\mathrm{I}}_{\mathrm{b}}$$ (17)

By fixing GEZI^D to its mean value (GEZI^D = 0.021 ± 0.001 dl·kg⁻¹·min⁻¹ in healthy, GEZI^D = 0.017 ± 0.001 dl·kg⁻¹·min⁻¹ in healthy and prediabetic subjects), estimated with an approach similar to that presented in Dalla Man et al. (12), we were able to ensure a certain degree of freedom for S_G^D (S_I^D is derived from k₂^D in Eq. 12), therefore providing an estimation of EGP_b for each subject. It is worth noting that the steady-state plasma clearance rate results were underestimated using a single compartment (7); as a consequence, the estimated EGP_b, and thus also the estimation of absolute EGP, is partially incorrect. However, to overcome this drawback, one can consider the EGP/EGP_b ratio, which is more robust (see results).

Parameter estimation.

The model was numerically identified on G_exo and G_end by nonlinear least squares (8, 10), as implemented in SAAM II (2). Measurement errors on exogenous and endogenous glucose were assumed to be independent, Gaussian, with zero mean and known standard deviations calculated by error propagation from primary measurements. Plasma insulin concentration was the model-forcing function and was assumed to be known without error.

Model Validation

As already pointed out in Subjects and Protocols, the healthy database used for model identification is the same as that employed in Dalla Man et al. (14). Therefore, in addition to assessing model performance in terms of ability to fit the data and provide precise parameter estimates, it has been possible to validate OMM^PD in normal subjects by comparing the estimated S_I^P with that provided in Dalla Man et al. (14). Moreover, the comparison between the estimated EGP time course and that obtained with the triple-tracer method provided a further validation of OMM^PD.

To evaluate the performance OMM^PD in healthy and prediabetic subjects, S_I^P and S_I^D were compared with those presented in Bock et al. (6). The EGP was compared in terms of prediction of time course and by calculating a suppression index S_%, defined as

$${\text{S}}_{\%}=\frac{{\displaystyle {\int }_0^{\infty }}\left({\text{EGP}}_{\text{b}}-\text{EGP}\left(t\right)\right)\text{d}t}{{\displaystyle {\int }_0^{\infty }{\text{EGP}}_{\text{b}}\text{d}t}}$$ (18)

Statistical Analysis

Data are presented as means ± SE. Two sample comparisons were done by Wilcoxon signed-rank test, and Shapiro-Wilk test was used to verify whether parameters are normally distributed (significance level set to 5%). Pearson's correlation was used to evaluate univariate correlation. Two-way ANOVA, including both the main effects and a term for interaction, was used to assess difference in prediabetes between type of data (triple-tracer estimates vs. OMM^PD predictions) among the subgroups (NFG/NGT, NFG/IGT, IFG/NGT, IFG/IGT, and IFG/DM). In particular, we focused on the significance of the interaction term, indicating whether the differences among the subgroups were affected or not by the factor “type of data” (significance level set to 5%).

RESULTS

Model Fit and Indices in Healthy Subjects

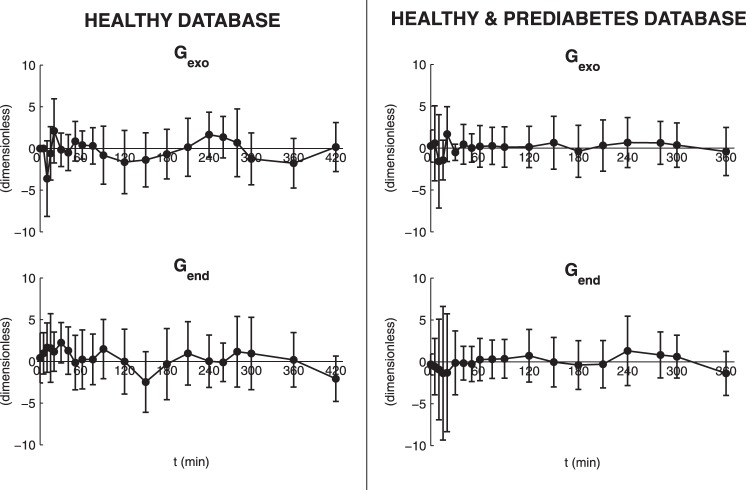
The OMM^PD provided a good fit of the data, as demonstrated by the weighted residual time courses shown in Fig. 3, left. Parameters were estimated with precision: S_G^D = 0.0151 ± 0.0003 min [coefficient of variation (CV) = 1.1 ± 0.4%], k₁^D = 0.0248 ± 0.0062 min (CV = 40.5 ± 9.4%), k₂^D = 0.0006 ± 0.0001 min·μU⁻¹·ml⁻¹ (CV = 8.4 ± 2.7%), k_G = 0.0174 ± 0.0033 dl·kg⁻¹·min⁻¹ (CV = 9.5 ± 1.1%), k_GR = 0.1210 ± 0.0426 dl/kg (CV = 28.1 ± 6.5%), k₁^P = 0.0199 ± 0. 0017 min (CV = 5.1 ± 0.6%), k₂^P = 0.0469 ± 0.0045 mg·kg⁻¹·min⁻¹ per μU/ml (CV = 3.4 ± 0.8%), EGP_b = 2.01 ± 0.05 mg·kg⁻¹·min⁻¹ (CV = 1.1 ± 0.5%), GE^P = 0.019 ± 0.003 dl·kg⁻¹·min⁻¹ (CV = 10.6 ± 2.6%), GE^D = 0.024 ± 0.001 dl·kg⁻¹·min⁻¹ (CV = 1.1 ± 0.4%), S_I^P = 5.48 ± 0.54 10⁻⁴ dl·kg⁻¹·min⁻¹ per μU/ml (CV = 3.4 ± 0.8%), and S_I^D = 9.93 ± 2.18 10⁻⁴ dl·kg⁻¹·min⁻¹ per μU/ml (CV = 8.4 ± 2.7%).

Fig. 3.

Weighted residuals (vertical bars represent SD) of OMM^PD fit on G_exo and G_end. Left: results in healthy database (n = 20). Right: results in healthy and prediabetes database (n = 60).

It is worth noting that GE^P and GE^D account for 44 and 56% of total glucose effectiveness, respectively, whereas S_I^P and S_I^D account for 36 and 64% of total insulin sensitivity, respectively.

Model Validation

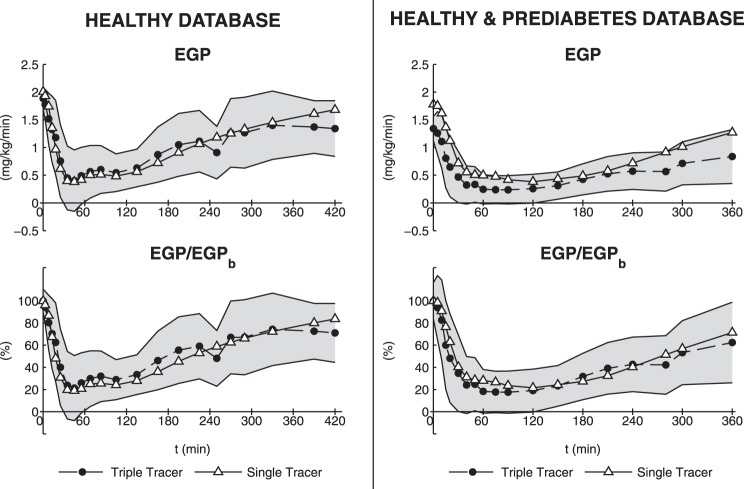
The comparison between S_I^P estimated with OMM^PD and that estimated in Dalla Man et al. (14) using triple-tracer-derived EGP is reported in Fig. 4; mean values are very similar (5.34 ± 0.47 vs. 5.48 ± 0.54 10⁻⁴ dl·kg⁻¹·min⁻¹ per μU/ml), and correlation is very good (r = 0.87, P < 0.0001). Furthermore, percentages of production and disposal S_I are in agreement with those presented in Dalla Man et al. (14). Moreover, the time course of EGP derived with OMM^PD is reproduced reliably with that obtained by the triple-tracer method (Fig. 5, top left), except for EGP_b (2.01 ± 0.05 vs. 1.88 ± 0.04 mg·kg⁻¹·min⁻¹). On the other hand, if EGP/EGP_b (%) is considered, the comparison between single-tracer model-based predictions and triple-tracer estimates is satisfactory (Fig. 5, bottom left).

Fig. 4.

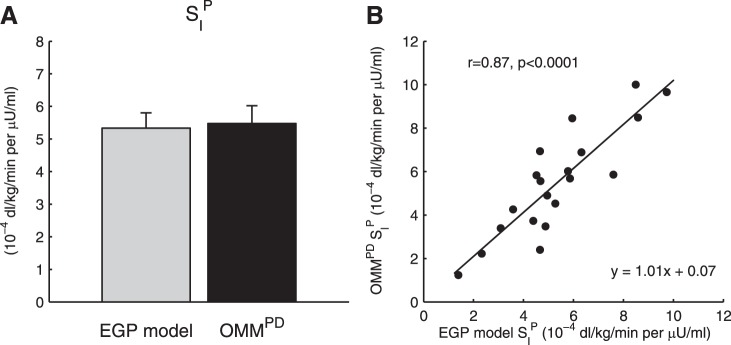
A: comparison between hepatic insulin sensitivity (S_I^P) estimated from OMM^PD (black bar) and endogenous glocose production (EGP) model of Dalla Man et al. (14) (gray bar) in the healthy database (n = 20). B: correlation plot.

Fig. 5.

OMM^PD predictions (solid line and △) vs. triple-tracer estimates (dashed line and ●) with SD variability range (gray region). Left: absolute EGP and EGP normalized to basal EGP (EGP_b) in healthy database (n = 20). Right: absolute EGP and EGP normalized to EGP_b in healthy and prediabetes database (n = 60).

Model Fit and Indices in Prediabetes

The results of OMM^PD identification were satisfactory also in prediabetes, providing good fit of the data (Fig. 3, right). Parameters were estimated with precision: S_G^D = 0.0117 ± 0.0021 min (CV = 1.0 ± 1.9%), k₁^D = 0.0283 ± 0.0365 min (CV = 51.5 ± 40.7%), k₂^D = 0.0003 ± 0.0004 min·μU⁻¹·ml⁻¹ (CV = 3.3 ± 2.7%), k_G = 0.0116 ± 0.0081 dl·kg⁻¹·min⁻¹ (CV = 13.3 ± 15.2%), k_GR = 0.1046 ± 0.1327 dl/kg (CV = 29.7 ± 29.6%), k₁^P = 0.0177 ± 0.0090 min (CV = 5.3 ± 3.3%), k₂^P = 0.0515 ± 0.0337 mg·kg⁻¹·min⁻¹ per μU/ml (CV = 3.3 ± 2.7%), EGP_b = 1.75 ± 0.34 mg·kg⁻¹·min⁻¹ (CV = 1.1 ± 2.0%), GE^P = 0.013 ± 0.008 dl·kg⁻¹·min⁻¹ (CV = 11.3 ± 12.6%), GE^D = 0.019 ± 0.003 dl·kg⁻¹·min⁻¹ (CV = 1.0 ± 1.9%), S_I^P = 5.41 ± 3.55 10⁻⁴ dl·kg⁻¹·min⁻¹ per μU/ml (CV = 3.3 ± 2.7%), and S_I^D = 5.34 ± 6.17 10⁻⁴ dl·kg⁻¹·min⁻¹ per μU/ml (CV = 12.2 ± 20.6%). Figure 6 shows the average S_I^P and S_I^D obtained for each subgroup. In particular, the distributions of S_I^P and S_I^D reflected those presented in Bock et al. (6), with both S_I^P and S_I^D significantly lower (P < 0.05) in the IFG group in IFG/IGT and IFG/DM compared with NFG/NGT. On the other hand, S_I^P and S_I^D in NFG/IGT and IFG/NGT were lower than NFG/NGT, but not significantly. In terms of model fit, exogenous and endogenous glucose profiles were predicted well, but the EGP time course was overestimated if compared with the triple-tracer estimate (Fig. 5, top right), similar to what was found in the 20 healthy subjects. Conversely, also in this case the EGP/EGP_b time course was similar to that obtained from the triple-tracer protocol (Fig. 5, bottom right). S_% obtained with OMM^PD was 54.4 ± 2.7 (NFG/NGT), 56.1 ± 2.8 (NFG/IGT), 55.7 ± 5.2 (IFG/NGT), 62.7 ± 2.7 (IFG/IGT), and 62.8 ± 2.4% (IFG/DM), and S_% derived from the triple-tracer data was 56.7 ± 5.7 (NFG/NGT), 61.0 ± 2.7 (NFG/IGT), 61.0 ± 4.4 (IFG/NGT), 65.2 ± 2.2 (IFG/IGT), and 60.6 ± 5.9% (IFG/DM). S_% from OMM^PD was identical to that derived from the triple-tracer data in all of the subgroups.

Fig. 6.

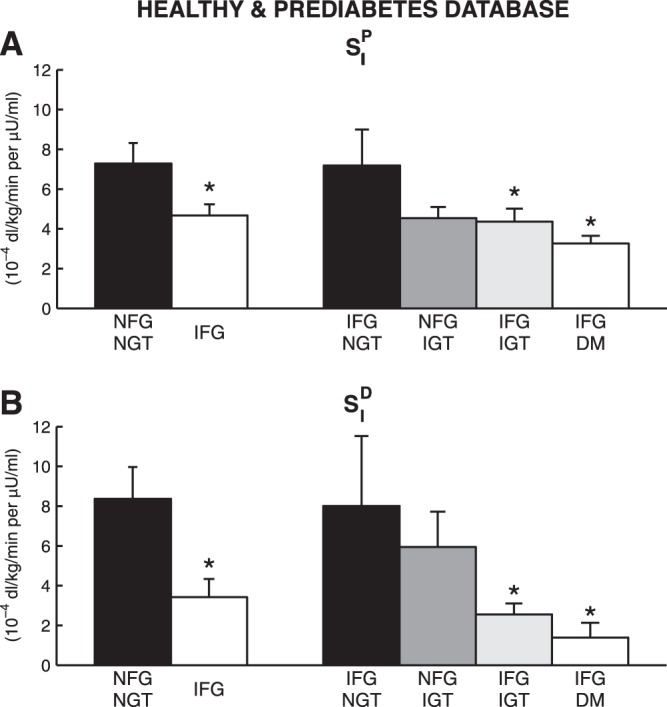
S_I^P (A) and disposal insulin sensitivity (S_I^D) (B) estimated with OMM^PD in healthy and prediabetes database, i.e., subjects with normal fasting glucose/normal glucose tolerance (NFG/NGT; n = 16), impaired fasting glucose (IFG; n = 32), IFG/NGT (n = 7), NFG/impaired glucose tolerance (IGT) (n = 12), IFG/IGT (n = 17), and IFG/DM (n = 8). *P < 0.05 vs. NFG/NGT.

DISCUSSION

The labeled euglycemic hyperinsulinemic clamp is the gold standard method to measure S_I^P in humans. However, this procedure is laborious, thus precluding its use in large-scale studies. In addition, during a clamp the liver is exposed to a nonphysiological glucose and insulin milieu. Conversely, the oral tests (OGTT and meal), besides being easier to perform, better reproduce physiological conditions and are thus potentially usable to assess S_I^P index in vivo. Currently, the state-of-the-art method to estimate S_I^P during a meal employs a dual-tracer approach. The first tracer, ingested with the meal, allows the segregation of plasma glucose into its endogenous and exogenous components; the second tracer, infused intravenously, mimics EGP time course and allows EGP estimation in a model-independent way (5). The EGP is then used to identify a mathematical model [recently validated against clamp (13)], providing an estimate of S_I^P. This technique requires the use of two isotopes. Moreover, achieving a quasi-constant TTR, thus obtaining a model-independent estimate of EGP, is not an easy task. Hence, an alternative, less labor-intensive method to assess insulin action on EGP is highly desirable.

Thus the purpose of this study was to develop a method to estimate S_I^P from a single-tracer oral test (OMM^PD). To do so, we incorporated the EGP model of Dalla Man et al. (14) into the oral minimal model (12) and identified it on the data of 20 healthy subjects studied with a triple-tracer mixed meal (4). The model fitted the data well, and its parameters were estimated with good precision. Furthermore, S_I^P obtained with OMM^PD from a single-tracer meal performed well against that estimated with a dual-tracer method and the EGP model (Fig. 4).

The performance of OMM^PD was also judged in terms of EGP prediction; the comparison of model-derived EGP with that derived from triple-tracer was satisfactory despite EGP_b being slightly overestimated from the model (Fig. 5, top left), as expected. This is likely due to the inability of a single-compartment model to correctly measure the steady-state plasma clearance rate, and certainly it represents a limitation of the OMM^PD. Nevertheless, the comparison with the model-independent profiles definitely improved if one looks at the EGP/EGP_b time course (Fig. 5, bottom left).

To test the performance of OMM^PD also in subjects with quite varying stages of prediabetes into type 2 diabetes, we applied OMM^PD on a population of IFG and NFG subjects, classified on the basis of their glucose tolerance, i.e., normal (NGT), impaired (IGT), or diabetes (DM) (6). For all of these subjects, GEZI^D was available from the analysis performed by Bock et al. (6). Hence, it was considered as appropriate to apply OMM^PD on this population, setting GEZI^D at the respective average value (GEZI^D = 0.017 ± 0.001 dl·kg⁻¹·min⁻¹). It is of note that, even if GEZI^D distributes among the subjects with a certain degree of variability, the use of the parameter mean value is sufficient to have a satisfactory model performance. In fact, S_I^P and S_I^D estimates in the subgroups reflected the pattern observed by Bock et al. (6) (Fig. 6). In particular, whole body S_I obtained with OMM^PD, derived as S_I = S_I^P + S_I^D, was higher than the triple-tracer-related values, as expected, due to the significant contribution of S_I^P.

Moreover, similarly to what was observed in the healthy subjects, OMM^PD predicted the EGP/EGP_b time course well (Fig. 5, bottom right) and provided values of EGP suppression (S_%), which were identical to those derived from the triple-tracer data. Therefore, using the more appropriate GEZI^D value, we were able to successfully apply OMM^PD on different populations.

Despite the satisfactory results, the proposed method has limitations. First of all, the prediction of EGP suffers from the EGP_b overestimation. As a consequence, the R_d also is partially incorrect, since it consists of its endogenous (R_{d end}) and exogenous (R_{d exo}) components. To have good estimation of EGP, an intravenous tracer needs to be infused to extract the individual EGP_b, or regression models could be used to derive EGP_b on the basis of patient's characteristics (basal concentrations, anthropometric measurements, etc.). However, most of the clinical studies are focused on quantifying the EGP suppression, and thus the provided EGP/EGP_b could be sufficient for this purpose. However, this limitation does not affect the estimation of either S_I^P, which was proven to be in agreement with that of Dalla Man et al. (14), or S_I^D, which was independent of EGP_b, as derived from R_{d exo}.

It is important to point out that the proposed model assumes that EGP depends on plasma glucose and a delayed insulin action but does not account for a direct effect of plasma insulin. As discussed in Dalla Man et al. (14), given the similarity between patterns of portal insulin and plasma glucose, a model that includes direct effect of both plasma insulin and glucose is not identifiable; i.e., it is unable to distinguish the two components of glucose effectiveness on the liver. On the other hand, considering plasma glucose also as a surrogate of portal insulin allows a better description of EGP suppression, particularly in the last portion of the meal. Moreover, the EGP model assumes that both the direct control of plasma glucose and the indirect control of portal insulin on EGP suppression are regulated by the same parameter, i.e., k_G. However, this problem can be overcome by interpreting the parameter GE^P as an overall measure of the ability of glucose to inhibit EGP both directly and indirectly. It is also important to underline that, in calling S_I^P as index of hepatic insulin sensitivity, a strong correlation between portal insulin action and S_I^P itself is implied. To support this assumption, we compared S_I^P with portal insulin action (i.e., parameter k₃ of Eq. 12 reported in Ref. 14), and indeed, a good correlation between the two was found (r = 0.85, P < 0.0001).

Another limitation concerning the minimal model is that the distribution volume (V) needs to be fixed. Therefore, error in the assumed V might introduce error in estimation of R_{a meal} and R_d, as already stated in Basu et al. (5). However, such methods represent the state of the art for the estimation of postprandial glucose fluxes, and a previous work revealed that V can be fixed to the population average without introducing appreciable bias (15).

Finally, the model requires an observation interval of ≥240 min. To apply OMM^PD on shorter protocols, such as the reduced OGTT (120 min), we would need to modify the description of R_{a meal}, as described previously (11). Moreover, prior studies have shown that fixing first-pass hepatic extraction of glucose absorption may affect whole body insulin sensitivity. However, as shown in Fig. 4, S_I^P estimated with the model compares well with that estimated from EGP model presented in Dalla Man et al. (14), which is independent from the first-pass hepatic extraction.

In conclusion, we have presented a model capable of reliably estimating both production and disposal contribution of insulin sensitivity index from a single-tracer meal (or OGTT) protocol in both normal individuals and individuals with prediabetes. The single-tracer approach, being less complex than the dual-tracer meal and labeled euglycemic hyperinsulinemic clamp methods, is a candidate as the method of choice to measure the index S_I^P in clinical studies.

GRANTS

This study was supported by National Institute of Diabetes and Digestive and Kidney Diseases Grant DK-29953 and Italian Ministero dell'Università e della Ricerca, FIRB 2008.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

R.V., C.D.M., and C.C. conception and design of research; R.V. analyzed data; R.V. prepared figures; R.V. and C.D.M. drafted manuscript; R.V., C.D.M., R.B., A.B., R.A.R., and C.C. edited and revised manuscript; R.V., C.D.M., R.B., A.B., R.A.R., and C.C. approved final version of manuscript; R.B. and A.B. performed experiments.