Role of Dynamics in the Autoinhibition and Activation of the Hyperpolarization-activated Cyclic Nucleotide-modulated (HCN) Ion Channels^,

Background: Hyperpolarization-activated cyclic nucleotide-modulated (HCN) ion channels control rhythmicity in neurons and cardiomyocytes, but their regulatory mechanism is not fully understood.

Results: Both tetramerization and cAMP binding reduce dynamics in the HCN intracellular region.

Conclusion: Intracellular HCN dynamics are crucial for HCN autoinhibition and cAMP modulation.

Significance: A full map of the changes in dynamics coupled to HCN gating is necessary to understand HCN regulation by cAMP.

Abstract

The hyperpolarization-activated cyclic nucleotide-modulated (HCN) ion channels control rhythmicity in neurons and cardiomyocytes. Cyclic AMP allosterically modulates HCN through the cAMP-dependent formation of a tetrameric gating ring spanning the intracellular region (IR) of HCN, to which cAMP binds. Although the apo versus holo conformational changes of the cAMP-binding domain (CBD) have been previously mapped, only limited information is currently available on the HCN IR dynamics, which have been hypothesized to play a critical role in the cAMP-dependent gating of HCN. Here, using molecular dynamics simulations validated and complemented by experimental NMR and CD data, we comparatively analyze HCN IR dynamics in the four states of the thermodynamic cycle arising from the coupling between cAMP binding and tetramerization equilibria. This extensive set of molecular dynamics trajectories captures the active-to-inactive transition that had remained elusive for other CBDs, and it provides unprecedented insight on the role of IR dynamics in HCN autoinhibition and its release by cAMP. Specifically, the IR tetramerization domain becomes more flexible in the monomeric states, removing steric clashes that the apo-CDB structure would otherwise impose. Furthermore, the simulations reveal that the active/inactive structural transition for the apo-monomeric CBD occurs through a manifold of pathways that are more divergent than previously anticipated. Upon cAMP binding, these pathways become disallowed, pre-confining the CBD conformational ensemble to a tetramer-compatible state. This conformational confinement primes the IR for tetramerization and thus provides a model of how cAMP controls HCN channel gating.

Introduction

The hyperpolarization-activated cyclic nucleotide-modulated (HCN)² ion channels are key determinants of nerve impulse transmission and heart rate modulation in neuronal and cardiac cells, respectively (1–12). The HCN channels exist in four known isoforms, HCN1–4, of which HCN2 and HCN4 are the isoforms most significantly regulated by cAMP (1, 2, 5, 7, 9, 10, 13). All isoforms contain an N-terminal trans-membrane region (TM), which assembles as a tetramer harboring the ion pore, and a C-terminal intracellular region (IR), which confers channel regulation by cAMP (Fig. 1, a and b) (1, 2, 5, 7, 9, 10). The cAMP-induced up-regulation of ion channel opening has been suggested to be closely linked to tetramerization of the HCN IR monomers in response to cAMP binding. However, it is currently not fully understood how cAMP promotes tetramerization of the HCN IR (3, 14–16).

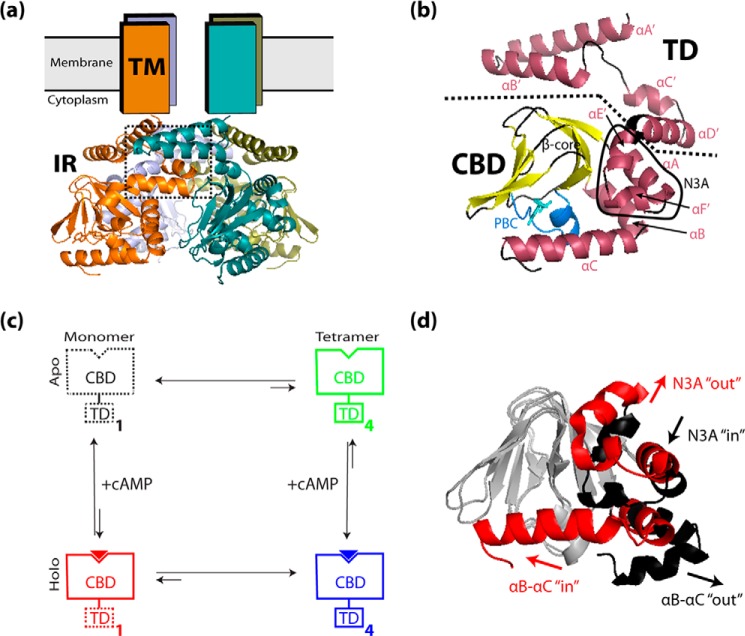
FIGURE 1.

a and b, overview of the HCN architecture. a, active tetrameric structure of HCN4, based on the structure of the HCN4 IR bound to cAMP (RCSB Protein Data Bank code 3OTF), viewed parallel to the plane of the cell membrane. The four HCN4 monomers are indicated in orange, olive green, blue-gray, and teal, and the tetramerization interface between the C-linkers of neighboring monomers is indicated (dotted rectangle). The four N-terminal transmembrane (TM) regions, whose atomic resolution structure is currently unknown, are indicated as rectangles, while the four C-terminal intracellular regions (IR) are shown as ribbon structures. b, structural details of the HCN4 intracellular region for a single protomer illustrated as a ribbon structure, with α-helices indicated in maroon, β-strands in yellow, and bound cAMP as cyan sticks. Boundaries between major structural regions are delineated by dotted lines, and key structural elements are indicated. The αA′–αD′ helices of the C-linker form the TD of the IR. The αA helix N-terminal to the β-subdomain, together with the αE′ and αF′ C-linker helices, forms the N-terminal “N3A” motif of the cAMP-binding domain (CBD). The phosphate-binding cassette (PBC), where cAMP binds, is indicated in light blue. c, outline of the thermodynamic cycle for the coupling between cAMP binding and tetramerization of the HCN intracellular region. The TD and CBD regions are schematically indicated as rectangles, and bound cAMP is indicated as a solid triangle. Solid contour lines indicate domain states with structures similar to the 3OTF x-ray structure, and dashed contour lines indicate domain states with structures that are possibly different from the 3OTF x-ray structure. The subscripts 1 and 4 refer to the number of protomers within each state. d, overlay of the 3OTF (red ribbon) and average 2MNG (black ribbon) structures (overlaid at their β-cores), illustrating the conformational changes that occur within the CBD α-subdomain during cAMP-associated activation. Upon cAMP binding, the αB–αC region shifts from an out position to an in position, and the N3A shifts from an in position to an out position. For clarity, the β-cores of both structures are shown in gray, and the bound cAMP and αA′–αD′ helices are omitted. All ribbon structures were generated using PyMOL (Schrödinger, LLC).

The HCN IR tetramer adopts an “elbow-shoulder” topology (3) involving four contiguous α-helices (αA′–αD′) at the IR N terminus, which are referred to as the tetramerization domain (TD) (Fig. 1, a and b). The TD is followed by a C-terminal cAMP-binding domain (CBD), which allosterically controls the self-association of the TD. In the absence of cAMP, the TD tetramer is unstable, whereas in the presence of cAMP, the TD tetramerizes (3). In a recent study performed by Akimoto et al. (17), the apo-state structure of the HCN4 CBD was solved by NMR, and it was found to differ from the structure of the cAMP-bound CBD (5) by a rearrangement of the CBD α-helical structure elements similar to that observed for CBDs of other eukaryotic cAMP receptors (18–26). The study proposed a model of HCN4 allostery in which the apo-state CBD conformation destabilizes the tetramer through steric clashes with the TD, arising from the incompatibility of the apo-state CBD conformation with the tight packing imposed by the tetramer assembly (17). It has been hypothesized that the CBD/TD steric clashes are released through an increase in TD structural dynamics occurring upon dissociation of the tetramer (17). This hypothetical dynamics-based model provides a simple and effective mechanism to explain how cAMP controls IR tetramerization and contributes to ion channel gating. Nevertheless, only limited information is currently available on the TD dynamics and on the inactive/active transition within the CBD, even though such attributes play a critical role in the proposed model.

Monomer TD dynamics are not easily experimentally assessed in the currently available HCN IR monomer constructs, because the αA′–αB′ helices were deleted to stabilize the monomeric state, and the αC′–αD′ helices are possibly affected by the construct's N-terminal truncation as well as by line broadening in the NMR spectra (17). Furthermore, although the cAMP-bound and apo CBD structures of the HCN4 IR were experimentally determined, providing the start and end points of the active/inactive transition, the pathways and structural variations that occur between these structures have eluded experimental analysis so far.

Here, we examine the structural dynamics of the HCN4 intracellular region through molecular dynamics (MD) simulations in explicit solvent. Multiple MD trajectories were simulated for each of the four states of the thermodynamic cycle describing the coupling between cAMP binding and tetramerization of the HCN4 intracellular region (i.e. the apo-monomer or inactive state, the apo-tetramer, the holo-monomer, and the holo-tetramer or active state; Fig. 1c), resulting in a total of 1.2 μs of simulated trajectory time (Table 1). The comparative analysis of these four sets of MD simulations provides unprecedented opportunities to dissect the distinct contributions of cAMP binding and tetramerization to the structural dynamics of the HCN IR and its domains (i.e. TD and CBD). In addition, we show that our MD simulations capture the active-to-inactive CBD conformational transition, which occurs in the sub-microsecond time scale for the apo-monomeric HCN IR, but had remained elusive for other eukaryotic CBDs (27). Our results on HCN reveal that CBDs sample a manifold of active/inactive pathways that are significantly more divergent than previously anticipated. The occurrence of the active-to-inactive conversion in our MD trajectories is also critical to probe the TD dynamics in the inactive form of the auto-inhibitory apo-monomer HCN IR. The MD simulations were validated and complemented by experimental NMR and CD data and reveal that dynamics play a pivotal role in the allosteric coupling between cAMP binding to the CBD and self-association of the TD.

TABLE 1.

Summary of the MD simulations performed for the HCN4 IR

Simulated IR statea	No. of HCN4 IR protomers	Contains bound cAMP (yes/no)?	Simulation length per replicate	No. of simulation replicates executed	No. of CPUs used
			ns
Apo-monomer	1	No	100.0	3	64
Apo-tetramer	4	No	100.0	3	64
Holo-monomer	1	Yes	100.0	3	64
Holo-tetramer	4	Yes	100.0	3	64

^a The initial structures for all states were obtained from the x-ray crystal structure of the cAMP-bound intracellular region of human HCN4 (PDB code 3OTF).

Experimental Procedures

Overview

Molecular dynamics (MD) simulations were performed for a protein construct spanning residues 521–717 of the intracellular region of human HCN4 (referred to herein as “HCN4 IR”), which contains the full TD and CBD regions of the HCN4 intracellular region (Fig. 1b). Although the intact HCN4 IR construct also contains an additional segment C-terminal to the CBD (a segment absent from the x-ray structure), previous functional data suggest that deletion of this C-terminal segment has a negligible effect on the function of the intact HCN protein (28). Initial structures for the simulations of all four states in the thermodynamic cycle of Fig. 1c were constructed based on the x-ray crystal structure of the cAMP-bound intracellular region (PDB code 3OTF) (5). Hence, the simulations for the apo-monomer HCN IR state were initiated from a nonequilibrium state, i.e. the active HCN IR protomer conformation. Details about the preparation of the initial structures as well as the MD simulation protocols, analyses, and validation by experimental data are described below.

Molecular Dynamics Simulation Protocol

Initial Structure Preparation

The HCN4 IR construct spanning residues 521–717 of the HCN4 intracellular region was used for all MD simulations. The initial structure for the holo-monomer state (Fig. 1c) was obtained from the x-ray crystal structure of the cAMP-bound intracellular region (PDB code 3OTF) (5) by deleting all water molecules from the structure and using SwissPDB Viewer (29) to reconstruct partially missing side chains on the protein surface. The initial structure for the apo-monomer state (Fig. 1c) was obtained from the initial structure for the holo-monomer state simply by deleting the bound cAMP. The initial structures for the apo-tetramer and holo-tetramer states (Fig. 1c) were obtained from the initial structures for the apo-monomer and holo-monomer states, respectively, by using the SwissPDB Viewer (29) to generate four copies of the monomer structure by applying “BIOMT” rotation/translation structure transformations specified in the header lines of the 3OTF PBD text file.

MD Simulation Protocol

All MD simulations were performed using the NAMD 2.8 software (30) on the Shared Hierarchical Academic Research Computing Network (SHARCNET). The CHARMM27 force field with CMAP correction (32–35) was implemented for all simulations, and the simulations were set up to mimic the following experimental conditions: pH of 7.0; explicit water (with periodic boundary conditions) with a 50 mm concentration of NaCl; a constant temperature of 34 °C (307 K); and a constant external pressure of 1 atm. Protein structure coordinate and parameter files with hydrogen atoms for the HCN4 IR structures were constructed using the “Psfgen” module of VMD 1.8.6 (36). Parameters for cAMP were constructed from the parameters for the adenine ribonucleotide (“ADE” in the CHARMM force field) by applying the force field's intrinsic “CY35” patch function (32). To mimic a pH of 7.0, hydrogen atoms were added such that all His side chains were in their un-ionized τ-state, and the N/C termini and all Asp, Glu, Arg and Lys side chains were in their ionized states. The structures were then immersed in a cubic box of TIP3P water molecules (with box dimensions of 90 Å for monomers or 120 Å for tetramers) using the Solvate module of VMD 1.8.6 (36), such that there was a minimum distance of 12 Å between the protein and the edge of the solvent box. Salt ions (Na⁺ and Cl⁻) were added to the solvent box using the Autoionize module of VMD 1.8.6 (36), such that the system was neutralized and the number of ions corresponded to a NaCl concentration of 50 mm.

Initial energy minimizations were performed using the conjugate gradient algorithm of NAMD. Minimization was performed for 5000 steps with harmonic position restraints on the protein backbone (force constant of 300.0 kcal/mol·Å²), followed by an additional 2000 steps without restraints. During minimization, a cutoff of 15 Å was utilized for all nonbonded energy calculations. Electrostatic interactions beyond the cutoff distance were computed using the Particle Mesh Ewald algorithm (37), with a tolerance of 10⁻⁶ and a maximum grid spacing of 1.0 Å. Molecular dynamics simulations were then performed under cubic periodic boundary conditions, beginning from the energy-minimized initial structures. A time step of 1.0 fs was implemented throughout the simulations. All water molecules were constrained to their equilibrium geometries using the SETTLE algorithm (38), and all covalent bonds to hydrogen were constrained using the SHAKE algorithm (39). A cutoff of 12 Å with Particle Mesh Ewald implementation was utilized for nonbonded energy calculations during the simulations. Short range nonbonded and long range electrostatic interactions were evaluated every 2.0 and 4.0 fs, respectively, using the RESPA multiple time step integrator (40). All minimizations and simulations were executed on a 2.83-GHz octuple-core Xeon cluster, using 64 CPUs per run.

The structures were heated linearly from 0 to 307 K over 200 ps at a constant volume, using the velocity reassignment protocol of NAMD. The heated structures were then simulated at 307 K and constant volume (NVE ensemble) for another 1.0 ns, to allow a period of temperature equilibration prior to introducing pressure regulation. Next, the structures were simulated at a constant temperature and pressure (NPT ensemble) for 1.0 ns, to allow a period of temperature and pressure equilibration prior to the NPT production run. A constant temperature of 307 K was maintained using the Langevin dynamics algorithm (41) with a Langevin damping coefficient of 1.0 ps⁻¹. A constant pressure of 1 atm (1.01325 bar) was maintained using the Nosé-Hoover Langevin piston method (30), with a barostat oscillation period of 200.0 fs and a barostat damping time scale of 100.0 fs. Throughout the heating and equilibration runs, harmonic position restraints were imposed on the protein backbone (force constant of 5.0 kcal/mol·Å²) to permit equilibration of the protein side chains and solvent without altering the protein backbone. Finally, production-run simulations were performed at a constant temperature and pressure (NPT ensemble) without restraints. These runs were executed for 120 ns to obtain a 100-ns trajectory for analysis, while allowing for a final unrestrained equilibration period of 20 ns before the 100-ns trajectory, and were performed at constant temperature and pressure using the NPT protocol described above. The simulations of all four states were performed in triplicate, and during the production runs, structures were saved every 10,000 time steps (i.e. every 10.0 ps) for subsequent analysis. A summary of the MD simulations performed for the HCN4 IR construct is given in Table 1.

Analysis of HCN4 IR Structural Dynamics

Backbone Root-Mean-Square Deviations

As an assessment of HCN4 IR structural propensities within the simulations, root-mean-square deviations (r.m.s.d.) from the initial “3OTF” monomer structure were computed for the constituent HCN4 IR protomers within each simulation, as well as for selected highly dynamic structural regions within each protomer (Fig. 1b) as follows: the CBD; the tetramerization domain (i.e. αA′–αD′ region); the N3A (i.e. αE′-αA region); the PBC; and the αB–αC region. The root-mean-square deviations for the tetramerization domain, N3A, PBC, and αB–αC regions were computed via a protomer backbone overlay onto the 3OTF protomer reference structure at the β-core, to permit examination of the movement of these regions relative to the central scaffold of the CBD (i.e. the β-core). The root-mean-square deviations for the full-length protomer and CBD were computed via a protomer backbone overlay onto the 3OTF protomer reference structure at the region under examination, to permit examination of the structural variation within that region. In addition, r.m.s.d. calculations were performed for the N3A and αB–αC regions using the average atomic coordinates for the previously solved apo HCN4 CBD structure ensemble (solved by NMR; i.e. the average structure derived from PDB entry 2MNG) (17) as a reference structure, to assess the extent of tendency toward the inactive-state CBD structure that was exhibited by these regions during the simulations.

Root-Mean-Square Deviation-based Structural Distributions to Map the Pathways of Active/Inactive Transition in the CBD of HCN4

To further assess CBD structural propensities within the simulations, r.m.s.d.-based structure similarity measures were computed for the constituent HCN4 IR protomers within each simulation. First, the root-mean-square deviations of the N3A and αB–αC regions from both the 3OTF and 2MNG protomer reference structures were computed as described above. Then, the r.m.s.d.-based similarity measure for the N3A in any given structure (“SM_N3A”) was computed from the r.m.s.d. values for each constituent protomer as shown in Equation 1,

with RA denoting the N3A r.m.s.d. between the given structure and the active-state structure (i.e. 3OTF); RI denoting the N3A r.m.s.d. between the given structure and the inactive-state structure (i.e. average structure from 2MNG); and R_ref denoting the N3A r.m.s.d. between the active- and inactive-state structures. For comparison, the SM_N3A values for the individual structures from the 2MNG ensemble were also computed. Similar definitions were used to compute the corresponding similarity measures for the αB–αC region (“SM_αB–αC”). Two-dimensional plots of the computed similarity measures were then constructed to examine how concertedly the similarities for the N3A and αB–αC regions vary.

Backbone N-H Order Parameters: Local Dynamics and Comparison with NMR Data

To quantify the amplitudes of local structural fluctuations and to permit a validation of the simulations against NMR data available for the HCN4 CBD, an analysis of backbone N-H order parameters (S²) was performed for the constituent HCN4 IR protomers within each simulation. First, the generated structures of each constituent protomer were optimally superimposed onto the initial protomer structure based on α-carbon coordinates, using the “orient” module of CHARMM 31.1 (42). Then, calculation of the S² order parameters across the simulation trajectory was performed using the “NMR” module of CHARMM 31.1 (42). During the calculation, the NMR magnetic field strength parameter (“hfield”) was set to a value of 16.44 tesla, in accordance with the magnetic field strength of the NMR spectrometer utilized in the NMR experiments. In addition, the characteristic correlation time of overall protein tumbling (“rtumbl”) was set to a value of 12310.0 ps. This value of rtumbl was calculated based on the 3OTF protomer x-ray structure using the HYDRONMR 7c software (43). In the HYDRONMR calculation, the temperature was set to 307 K, and the magnetic field strength to 16.44 tesla.

To assess whether key CBD dynamic features were successfully captured by the simulations, the CBD order parameters computed from the holo-monomer simulations were compared with a corresponding set of experimentally derived order parameters (S²) obtained for the cAMP-bound monomeric CBD, because in both cases the CBD was expected to exist predominantly in its active-state conformation. The experimentally derived order parameters were computed from experimentally measured ¹³Cα, ¹³Cβ, ¹³CO, ¹H, and ¹⁵N chemical shifts for the cAMP-bound HCN4 IR-ΔA′B′ construct (which is monomeric due to deletion of the αA′–αB′ segment of the TD) using the RCI algorithm (44). The RCI-based order parameters do not rely on specific models of overall rotation and therefore are ideally suited for constructs with extensive flexible regions that may affect the rate and anisotropy of the overall tumbling, such as the HCN4 IR and HCN4 IR-ΔA′B′ constructs.

Backbone Root-Mean-Square Fluctuations (RMSFs)

To further assess structural fluctuations with residue resolution, an analysis of RMSFs was performed for the constituent HCN4 IR protomers within each simulation. In this analysis, the generated structures of each constituent protomer were first optimally superimposed onto the initial protomer structure based on α-carbon coordinates. The RMSF calculation was subsequently performed by first computing the average Cartesian coordinates of the α-carbon atoms over all structures in each overlaid structure set. Then, the RMSFs around the average coordinates of each structure set were calculated as shown in Equation 2,

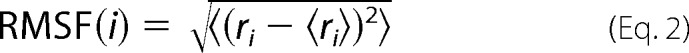where “RMSF(i)” denotes the RMSF describing the fluctuations of residue i, and “r_i” denotes the Cartesian coordinates of the α-carbon atom of residue i for a given structure; “〈r_i〉” denotes the average Cartesian coordinates of the α-carbon atom of residue i, computed over the whole structure set; and the angle brackets denote averages computed over the whole structure set. This process was performed with all structure overlays done at the β-core, to permit examination of residue-specific movements relative to the central scaffold of the CBD (i.e. the β-core).

Circular Dichroism

CD spectra were recorded using an AVIV spectrometer model 215. All measurements were taken in a 1-mm quartz cuvette using a slit width of 1.053 cm. The CD spectra were measured at 25 °C for solutions of the HCN4 αA′–αB′ (521–562) and αC′–αD′ (566–588) peptides (GenScript USA Inc.) at a 0.1 mg/ml concentration in a 10 mm potassium phosphate buffer (pH 6.5) with and without 40% TFE. The estimated percentage of helical structure was calculated from the [θ]₂₂₂. Each point in the CD spectra was corrected for background reading using a blank buffer solution.

Results

Overall IR Dynamics

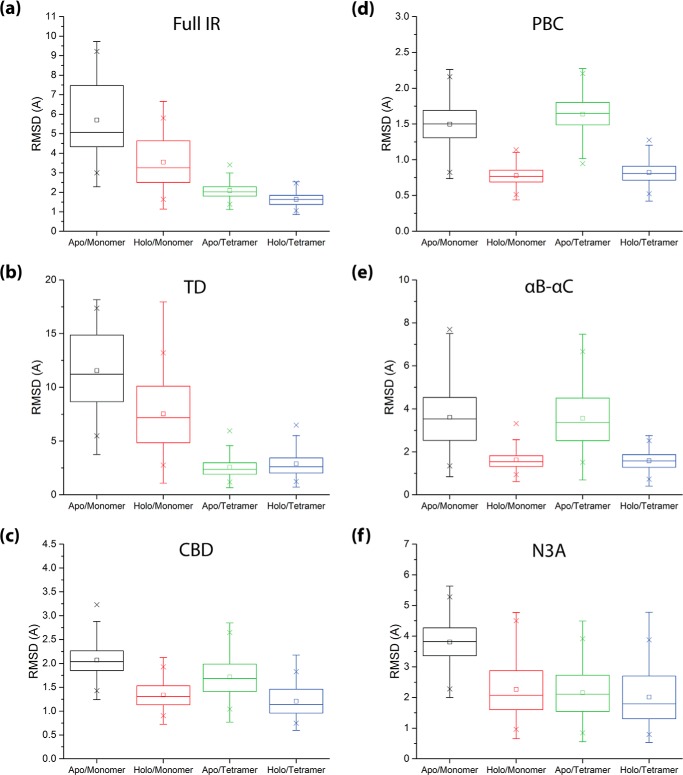
As an initial assessment of the IR structural dynamics, root-mean-square deviations of the full IR and its constituent domains (i.e. the TD and CBD; Fig. 1, a and b) were computed from the cAMP-bound structure, which is assumed to represent the active-state IR (3, 5, 45). All r.m.s.d. calculations were performed for the constituent protomers of all four simulated states (Fig. 2). To obtain insight on how these states vary across the thermodynamic cycle of Fig. 1c, we mapped the r.m.s.d. distributions within each set of simulations (Fig. 3). The r.m.s.d. values for the full IR exhibit a trend of progressive decrease in the order apo-monomer > holo-monomer > apo-tetramer > holo-tetramer (Fig. 3a), suggesting that stabilization of the overall active-state IR structure involves contributions from both cAMP binding and IR tetramerization. However, the degrees of contribution by cAMP binding and tetramerization were found to vary significantly between the TD and CBD regions (Fig. 3, b and c). For the TD, the r.m.s.d. values of the monomers generally exceed those of the tetramers, irrespective of whether they are apo or holo (Fig. 3b), suggesting that the active-state TD configuration is stabilized primarily by tetramerization. For the CBD, a different pattern is observed (Fig. 3c). The CBD root-mean-square deviations from the active-state structure are only marginally reduced in each tetramer state relative to its respective monomer state (Fig. 3c), suggesting that unlike the TD, the main determinant of active-state CBD structure stabilization is not tetramerization.

FIGURE 2.

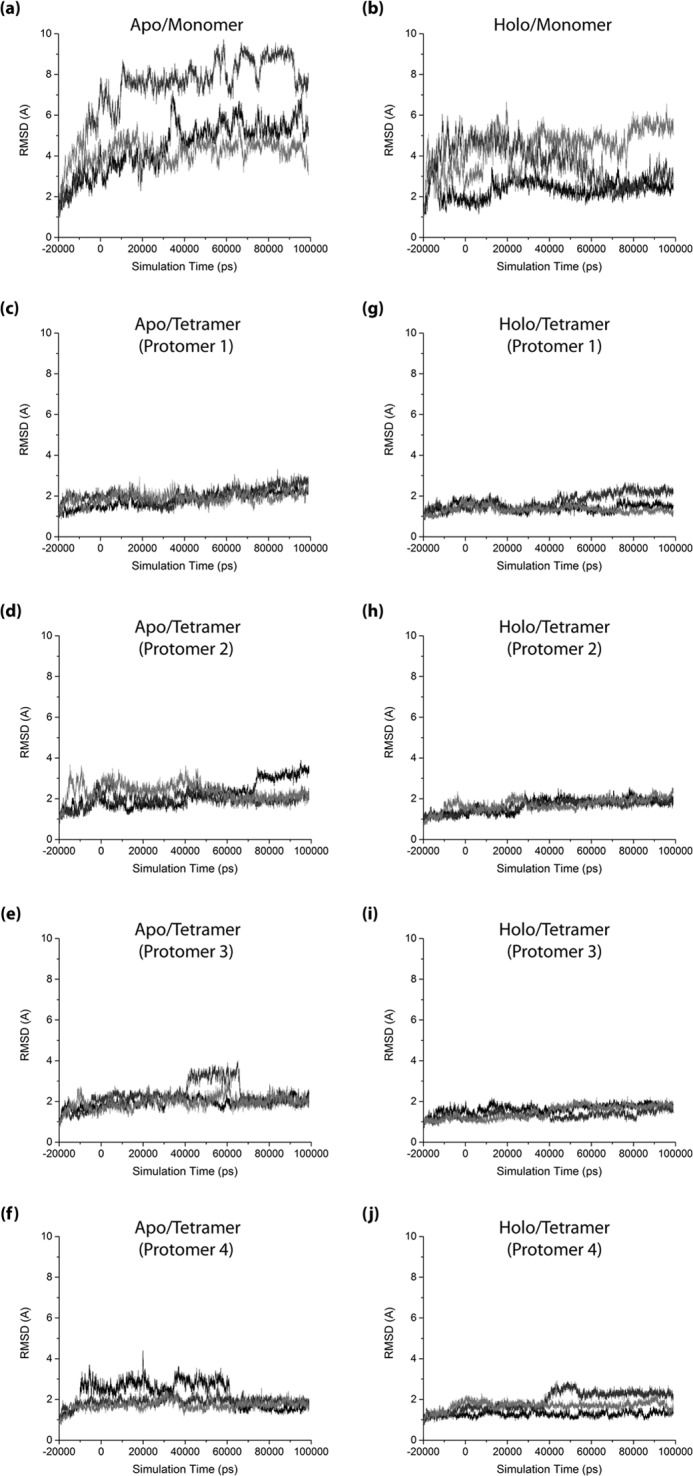
Root-mean-square deviations from the initial 3OTF structure computed for each HCN4 IR protomer over the course of the respective HCN4 IR simulations. a, apo-monomer state; b, holo-monomer state; c–f, apo-tetramer state; and g–j, holo-tetramer state. r.m.s.d. trajectories are shown for all individual protomers (individual panels) and replicates (black, dark gray, and light gray plots in each panel) for the respective states. The initial equilibration period of each simulation is indicated as negative times, and the production run used in the other analyses is indicated as positive times.

FIGURE 3.

Distribution of backbone root-mean-square deviations of the major protomer structural regions from their configurations in the initial 3OTF structure, as observed in the context of the apo-monomer (black), holo-monomer (red), apo-tetramer (green), and holo-tetramer (blue) states of the HCN4 IR. a, root-mean-square deviations for the entire HCN4 IR; b, root-mean-square deviations for the tetramerization domain (TD), computed with structure overlay at the β-core; c, root-mean-square deviations for the CBD. d–f, distributions of root-mean-square deviations from the initial 3OTF structure computed for the major CBD α-subdomain structural regions: d, the PBC; e, the αB–αC region; and f, the N3A (i.e. αE′–αA region); all computed with structure overlay at the β-core. The color code is as in Fig. 1c. All boxplots were constructed using Origin 9.1 (OriginLab Corp.), based on the r.m.s.d. data from all protomers and replicates for the respective states. The statistics reported in each boxplot are as follows: the middle, bottom, and top lines of the central box represent the median, 25th percentile, and 75th percentile of the data set, respectively; the whiskers represent additional data falling within 1.5*IQR above the 75th percentile or below the 25th percentile (where IQR is the difference between the 75th and 25th percentiles); □ represents the mean of the data set; and the two × symbols represent the 1st and 99th percentiles of the data set.

CBD Dynamics

To further examine the CBD structural dynamics, root-mean-square deviations of the major CBD α-helical structural elements (i.e. the PBC, αB–αC, and N3A; Fig. 1b) relative to the β-core were computed (Fig. 3, d–f). The root-mean-square deviations for both the PBC and αB–αC elements demonstrated a reduction in the extent of deviation from their active-state configurations only in the two holo states (Fig. 3, d and e), suggesting that the active-state configurations of these elements are stabilized mainly by cAMP binding, with little contribution from tetramerization. In marked contrast with the PBC and αB–αC regions, the N3A demonstrated an enhancement in its extent of deviation from the active structure only in the apo-monomer state, while the other three states all exhibit similarly quenched dynamics (Fig. 3f). This result suggests that the stabilization of the N3A active-state configuration is strongly influenced by both cAMP binding and tetramerization.

To assess the extent to which the CBD structural dynamics span active-to-inactive conformational transitions, active versus inactive similarity measures (SM) were defined according to Equation 1 (see under “Experimental Procedures”) based on the root-mean-square deviations from both the experimental active and inactive conformations for two key CBD elements involved in the transition, i.e. the αB–αC helices and the N3A. When the SM approaches a value of 1 (−1), the CBD element for which the SM was computed adopts a conformation similar to the active (inactive) state. In the active CBD conformation, the αB–αC helices are proximal to the β-barrel, whereas the N3A moves away from it (i.e. αB–αC in/N3A out topology, or “in-out” for short; Fig. 1d). In the inactive CBD conformation, however, the reverse CBD topology prevails, with the αB–αC helices moving away from the β-barrel, and the N3A residing near it (i.e. αB–αC out/N3A in topology, denoted as “out-in”; Fig. 1d).

The active versus inactive structure similarity measures were computed for the αB–αC helices and N3A in each frame of the simulated trajectories and compiled as two-dimensional plots (Fig. 4). Each two-dimensional plot is composed of four quadrants corresponding to the αB–αC in/out and N3A in/out-independent combinations. The αB–αC in/N3A out topology of the active CBD conformation falls in the top-right quadrant (i.e. SM(αB–αC) > 0 and SM(N3A) > 0), whereas the αB–αC out/N3A in topology of the inactive CBD conformation falls in the bottom-left quadrant (i.e. SM(αB–αC) < 0 and SM(N3A) < 0; Fig. 4). The other two quadrants correspond to mixed “out/out” and “in/in” CBD topologies (i.e. SM(αB–αC) < 0 and SM(N3A) > 0, or SM(αB–αC) > 0 and SM(N3A) < 0; Fig. 4).

FIGURE 4.

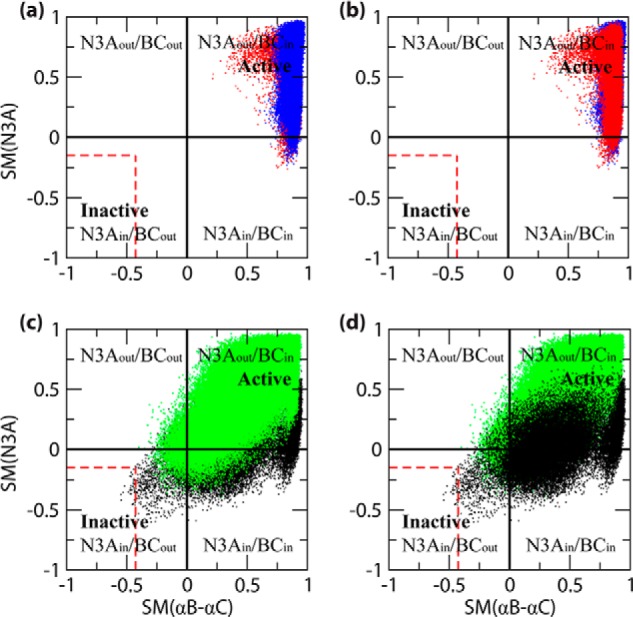
Two-dimensional plots of the computed active versus inactive structure similarity measures (SM) for the N3A (i.e. αE′-αA) and αB–αC regions, as observed in the context of the four states of the HCN4 IR. The SM values were computed based on Equation 1 under “Experimental Procedures.” a and b, holo-monomer (red) and holo-tetramer (blue); c and d, apo-monomer (black) and apo-tetramer (green). Note that each top panel (i.e. a and b) includes both holo simulation data, but with a different order of front versus back layers. Similarly, each bottom panel (i.e. c and d) includes both apo simulation data, again with different orders of front versus back layers. The color code is as in Fig. 1c, and the N3A and αB–αC structural topologies (i.e. in versus out, and “Inactive” versus “Active”) represented by the quadrants of each graph are indicated. For comparison, the boundaries of the range of similarity measure values computed from the individual structures of the inactive-state NMR structure ensemble (i.e. 2MNG) are also indicated (red dashed lines). Details of the similarity calculations are provided under “Experimental Procedures” (Equation 1).

The two-dimensional plots of active versus inactive structure similarity measures were constructed for each state of the thermodynamic cycle of cAMP-dependent tetramerization (Fig. 1c) as shown in Fig. 4, a–d, using the same color code as in Fig. 1c. It should be noted that both a and b of Fig. 4 include the two-dimensional SM plots for the holo states, but in Fig. 4a, the plot for the holo-tetramer is in the front layer, and in Fig. 4b, it is the plot for the holo-monomer that is in the front layer. Similarly, both c and d in Fig. 4 display the two-dimensional SM plots for the apo states, but with different superimposition orders.

Fig. 4, a and b, shows that both holo states (i.e. the holo-monomer and holo-tetramer) are confined primarily to the active CBD quadrant, consistent with the experimental evidence that cAMP stabilizes the active CBD conformation irrespective of the IR oligomerization state (17). However, marked and unanticipated differences exist between the similarity distributions of the αB–αC and N3A elements. Specifically, although the αB–αC similarity distributions are narrow and entirely confined to the active CBD quadrant, the N3A distributions are significantly broader and partially exit from the active CBD quadrant (Fig. 4, a and b). These distribution patterns change dramatically in the apo states (i.e. the apo-monomer and apo-tetramer), as shown in Fig. 4, c and d.

Both apo states exhibit an αB–αC distribution significantly broader than that of the holo states (Fig. 4). Unlike the holo states, the apo states span both in and out αB–αC orientations relative to the β-core, with the latter orientation sampled slightly more in the apo-monomer than the apo-tetramer simulations (Fig. 4, c and d). In addition, the apo-monomer and apo-tetramer differ in terms of the N3A distributions. In the apo-tetramer, the range of N3A similarity measures (Fig. 4, c and d) remains confined to values comparable with those observed for the two holo states (Fig. 4, a and b). In the apo-monomer, however, the N3A distribution shifts to lower values, suggesting a further transition toward the inactive CBD conformation (Fig. 4, c and d). Indeed, the simulated ensemble generated for the apo-monomer includes a sub-set of conformations exhibiting the inactive out-in topology, with multiple conformations approaching or falling within the range of similarity measures calculated for the experimental inactive-state CBD NMR structure ensemble (17) (dashed red lines in Fig. 4, c and d). This observation is significant because the MD trajectories started from the opposite topology (active in-out) and suggests that the active-to-inactive transition was captured by the simulations, in agreement with the experimental observation that the inactive CBD state is the most stable conformation in the apo-monomeric IR (17).

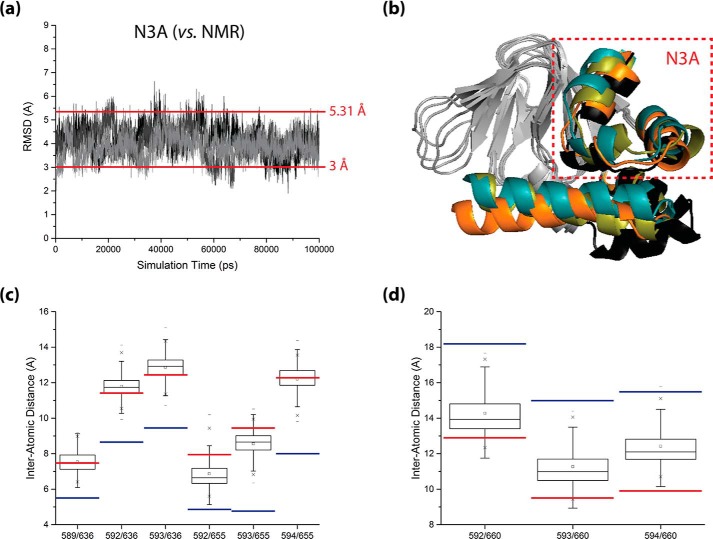
To confirm that inactive-state-like CBD configurations were being explored within the apo-monomer HCN4 IR simulations, frames exhibiting minimal N3A root-mean-square deviations (i.e. <3 Å) from the average apo-monomer CBD structure previously solved by NMR (2MNG) were selected for further assessment (Fig. 5a). The N3A root-mean-square deviations were used as a selection criterion because the orientation of the N3A relative to the β-core in the CBD is a key determinant of the inactive/active conformational shift, as noted previously (17), while the inherent apo-state flexibility in the αB–αC region could bias the selection. Once the inactive-state-like structures from each apo-monomer simulation were selected, the structures exhibiting the smallest, median, and largest N3A root-mean-square deviations out of all of the selected inactive-state-like structures were overlaid onto the average 2MNG structure to assess their extent of similarity to the average 2MNG CBD conformation (Fig. 5b). In addition, inter-α-carbon contact distances were computed for selected pairs of residues that bridge the interface between the N3A and β-core, to further confirm whether the selected structures exhibited N3A/β-core relative orientations close to or approaching that of the average 2MNG structure (Fig. 5, c and d). To properly assess the N3A movement, the contact distance analysis was performed for representative residue pairs that are farther apart in the 2MNG structure than in the 3OTF structure, as well as representative residue pairs that are closer together in the 2MNG structure than in the 3OTF structure (Fig. 5, c and d). Overall, the results of Fig. 5 confirm the occurrence of active-to-inactive CBD conversion in our apo-monomer simulations as also suggested by Fig. 4, c and d, and hence, the two-dimensional plots in Fig. 4, c and d, provide invaluable clues about the pathways for the active-inactive CBD transition of the apo-monomeric HCN IR.

FIGURE 5.

Sampling of inactive-state-like CBD topologies within the apo-monomer HCN4 IR simulations. a, backbone root-mean-square deviation trajectories of the N3A (i.e. αE′-αA region) from its configuration in the average apo-state NMR structure of the HCN4 CBD (i.e. the average structure derived from RCSB PDB entry 2MNG), as observed in each of the three replicate apo-monomer HCN4 IR simulations (black, dark gray, and light gray plots, respectively). All root-mean-square deviations were computed with structure overlay at the β-core. The threshold r.m.s.d. value used for selecting inactive-state-like structures for further assessment (i.e. 3 Å) and the r.m.s.d. between the 3OTF and average 2MNG structures (i.e. 5.31 Å), are indicated by horizontal lines. b, ribbon structure illustration of the selected inactive-state-like structures exhibiting the smallest (orange ribbon), median (olive green ribbon), and largest (teal ribbon) N3A root-mean-square deviations from the average 2MNG structure, overlaid at their β-cores onto the average 2MNG structure (black ribbon). For clarity, the β-cores of all structures are shown in gray, and the αA′–αD′ helices of all structures are omitted. c and d, boxplots of inter-α-carbon distances for selected pairs of residues that bridge the interface between the N3A and β-core, as observed for the selected ensemble of inactive-state-like structures. Residue pairs that are farther apart in the average 2MNG structure (c) and residue pairs that are closer together in the average 2MNG structure (d) were considered. All boxplots were constructed using Origin 9.1 (OriginLab Corp.), and for reference, the corresponding distance values observed in the 3OTF structure (blue lines) and in the average 2MNG structure (red lines) are indicated for all plots.

Fig. 4, c and d, shows that the active versus inactive similarity measures for the N3A and αB–αC elements in the apo-monomer trajectories are significantly less correlated than expected for a fully concerted in-out to out-in transition (Fig. 4, c and d). The N3A and αB–αC SM distributions sample a wide range of values, indicating the existence of a manifold of pathways for the transition between active-like and inactive-like structures within the apo-monomer ensemble and suggesting that the apo-monomer CBD also transiently samples noncanonical mixed CBD topologies (e.g. in-in and, to a smaller extent, out-out topologies; Fig. 4, c and d).

TD Dynamics

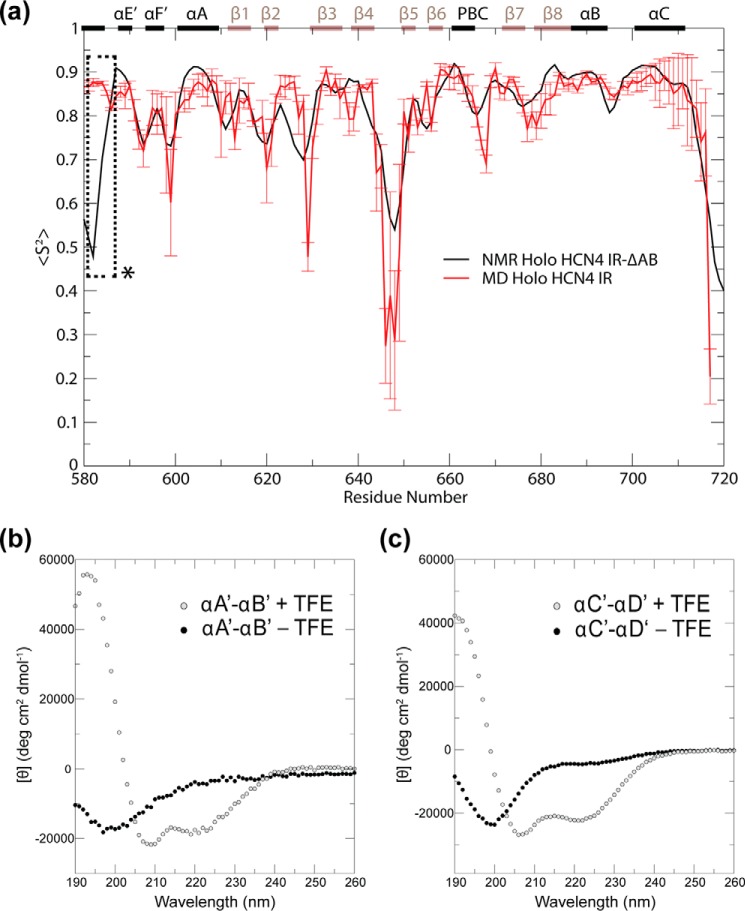
To further assess the internal TD structural dynamics, backbone N-H order parameters (S²; Fig. 6a) and root-mean-square fluctuations (RMSFs; Fig. 6b) were computed for the constituent protomers of all four simulated states. The S² and RMSF profiles in Fig. 6 are validated by their agreement with the experimentally observed quenching of dynamics observed for the αB–αC regions upon cAMP binding in both monomeric and tetrameric states (17, 45). As an additional means of validating the simulations, backbone N-H order parameters (S²) computed for the CBD from the holo-monomer simulations were compared with order parameters determined experimentally for the cAMP-bound monomeric state (Fig. 7a). In this state, the CBD is expected to exist predominantly in its active-state structure, which is represented by the initial simulation structure for this state (Fig. 1). Comparison of the two S² data sets revealed that the trends in CBD local dynamics computed from the simulations were comparable with the trends observed from experiment (Fig. 7a). This observation suggests that key CBD dynamic features were successfully captured by the simulations, thus lending further credibility to the MD trajectories.

FIGURE 6.

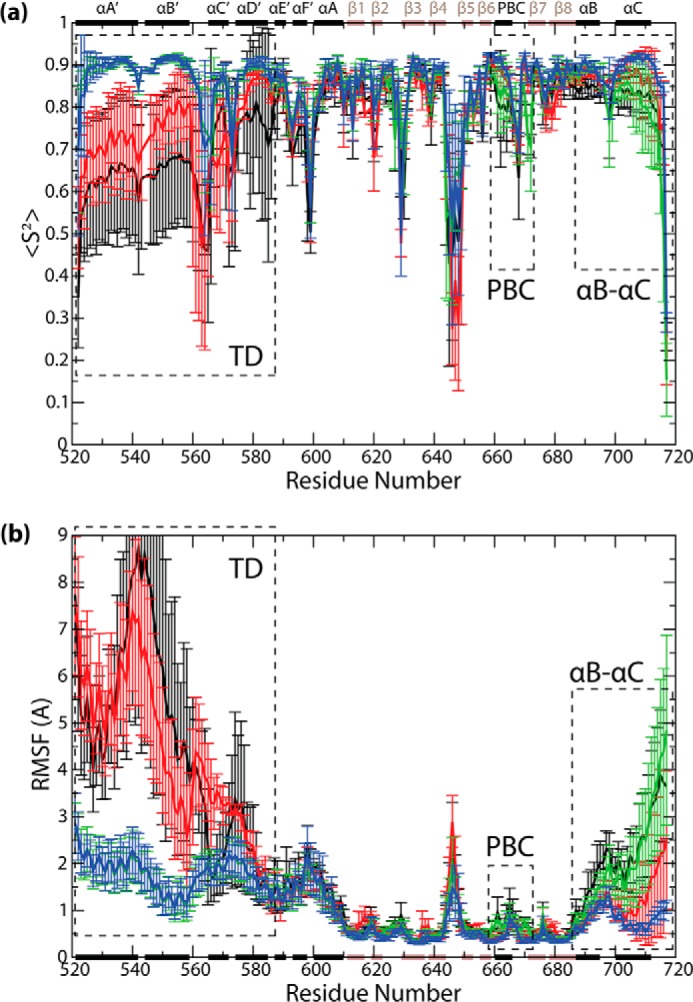
a, backbone N-H order parameters (S²), and b, RMSFs versus residue number plots, computed with structure overlay at the β-core, and averaged across all protomers and replicates for the respective states. The secondary structure elements are indicated along the horizontal dimensions of both graphs (black bars, α-helices; brown bars, β-strands), and structural regions exhibiting notable differences among states are indicated (dotted rectangles).

FIGURE 7.

Experimental data supporting the MD simulations of HCN4. a, comparison of the CBD region backbone N-H order parameters (S²) obtained for the monomeric, cAMP-bound HCN4 intracellular region from NMR (black plot) and from MD (red plot). The secondary structure elements are indicated along the top of the graph (black bars, α-helices; brown bars, β-strands). The dashed box marked with an asterisk signifies that the experimental S² values for the αD′ helix are not reliable due to lack of assignment in this region, in which multiple residues are subject to broadening beyond detection. b and c, CD spectra of synthetic peptides spanning the HCN4 αA′–αB′ (b) and αC′–αD′ (c) helices in 10 mm potassium phosphate buffer (pH 6.5) in the presence (open circles) and absence (solid circles) of 40% TFE.

The S² and RMSF plots (Fig. 6) are not only in agreement with the available experimental data, but they also reveal new dynamic attributes that are currently not fully accessible to experiments. For example, the S² values in the TD region (i.e. αA′–αD′) are consistently lower in the monomeric states than in the tetrameric states (Fig. 6a). A distinct monomer versus tetramer difference is also observed for the RMSF values in the TD region (Fig. 6b). These observations point to an enhancement of TD dynamics in the monomeric states irrespective of whether they are apo or holo (Fig. 6), in agreement with the trends observed in Fig. 3b for the whole-TD root-mean-square deviations. The monomer versus tetramer increase in TD flexibility suggests that the former is significantly less structured than the latter. To gauge the degree of unstructuring of the monomeric TD region, we acquired CD spectra of two peptides spanning the αA′–αB′ and αC′–αD′ helices, which constitute the TD region. Two separate αA′–αB′ and αC′–αD′ peptides (as opposed to a single αA′–αD′ peptide) were utilized to circumvent tetramer formation and better probe the monomeric state. The CD spectra of both peptides show only marginal helical content in the absence of helix inducers such as TFE (Fig. 7, b and c, and Table 2). Although the αA′–αB′ and αC′–αD′ peptides may not retain the same degree of structuring as the full αA′–αD′ TD region, these results suggest that in the absence of tertiary interactions between the αA′–αB′ and αC′–αD′ segments of the TD, the helical secondary structure of the TD is to a large extent lost (Fig. 7, b and c, and Table 2).

TABLE 2.

Helical content (%)

	0% TFE	40% TFE
HCN4 αA′–αB′a	6%	46%
HCN4 αC′–αD′a	7%	66%

^a The peptide concentration was 0.1 mg/ml. The estimated percentage of helical structure was calculated from the [θ]₂₂₂ in Fig. 7, b and c.

Discussion

We have examined how HCN4 IR dynamics vary along the thermodynamic cycle arising from the coupling between the cAMP binding and tetramerization equilibria (Fig. 1c). The key results are summarized in Table 3 and Fig. 8. The reliability of these results is supported by the fact that several changes in the simulated dynamics are in agreement with previous experimental observations. For instance, our MD simulations correctly capture the quenching of dynamics of the C-terminal CBD αB–αC helices upon cAMP binding to either the monomeric or tetrameric IR (Table 3 and Fig. 8), as determined previously by NMR, DEER, and fluorescence spectroscopy (17, 45–47). Furthermore, our MD simulations correctly predict that the N3A topology in the apo-monomer IR undergoes a transition from the “out” to the “in” orientation, in agreement with the recently solved NMR structure of the apo-monomeric CBD (17). Our MD simulations are also corroborated by the fact that they reproduce the order parameter (S²) trends derived from the NMR data for the holo-monomeric CBD. Overall, our MD-based results appear in agreement with the available experimental information on the HCN4 IR dynamics, lending credibility to our simulations.

TABLE 3.

Summary of dynamic changes along the thermodynamic cycle for the coupling between tetramerization and cAMP binding to the HCN4 IR

Simulated IR states		TD (αA′–αD′)	CBD
			N3A (αE′–αA)	αB–αC
Apo-monomer	IR1	Higha	In/outa	High,a in/outb
Apo-tetramer	IR4	Lowa	Out (in)c	High,a in/outb
Holo-monomer	IR1:cAMP1	Higha	Out (in)c	Low,a inb
Holo-tetramer	IR4:cAMP4	Lowa	Out (in)c	Low,a inb

^a “High”/“low” refers to enhanced/quenched internal dynamics as quantified by r.m.s.d., S², and RMSF changes in Figs. 3 and 6.

^b “In” refers to the in-topology whereby the αB–αC helices are oriented toward the CBD β-barrel (Fig. 1d). “Out” refers to the out topology whereby they are oriented away from the CBD β-barrel (Fig. 1d). “In/out” indicates that both topologies are sampled by the αB–αC helices, as shown in Fig. 4.

^c “In” refers to the in-topology whereby the N3A is oriented toward the CBD β-barrel (Fig. 1d). “Out” refers to the out topology whereby the N3A is oriented away from the CBD β-barrel (Fig. 1d). The topology in parentheses is less populated than the one without parentheses, but it is still sampled by the N3A as shown in Fig. 4.

FIGURE 8.

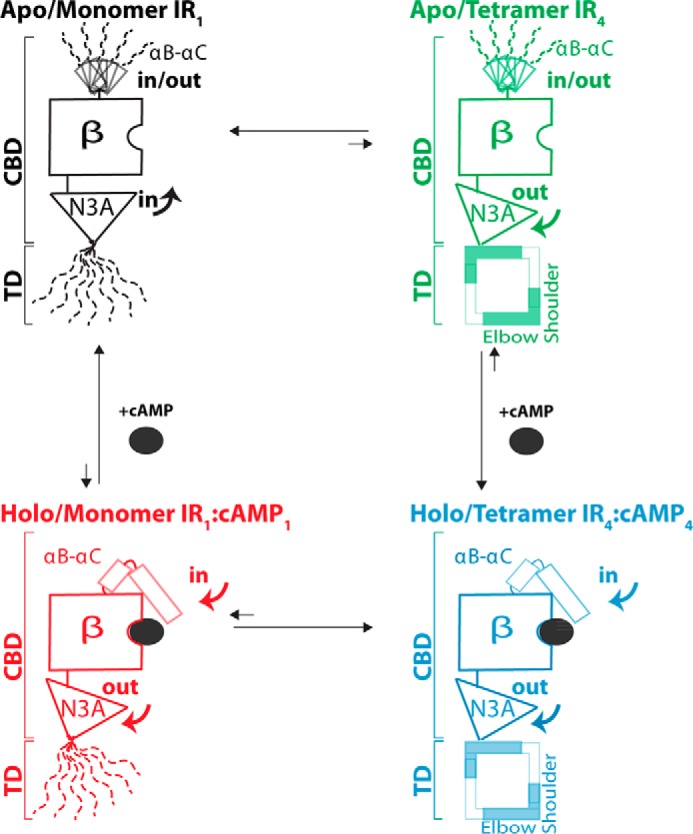
Scheme summarizing the dynamic changes in the HCN4 IR that occur along the thermodynamic cycle for the coupling between tetramerization and cAMP binding (Fig. 1c). Dashed lines denote segments that are at least partially unstructured and highly dynamic. The β-subdomain is denoted as “β” and remains largely invariant across the thermodynamic cycle. For the sake of clarity, only the most populated in/out topologies are shown for the N3A motif. Further details are available in Table 3.

The MD simulations presented here are not only supported by previous measurements, but they also reveal several functionally relevant dynamic attributes of the HCN4 IR that have so far remained elusive to experimental approaches. First, the MD trajectories of the inactive apo-monomeric IR clearly indicate that the TD is highly dynamic (Fig. 6). The TD flexibility in the apo-monomer plays a central role in stabilizing the monomeric form of the apo IR, because it effectively removes the steric hindrance that would otherwise arise between the αA′–αB′ helices and the β-subdomain of the inactive-state CBD. Hence, the TD dynamics is critical to explain how cAMP binding and IR tetramerization are coupled.

Second, the MD simulations show that, overall, the active holo-tetrameric IR is less dynamic than the inactive apo-monomeric state (Figs. 3, 6, and 8; Table 3). Both cAMP binding and tetramerization contribute to the quenching of IR dynamics that occurs upon activation. However, the extent of influence by cAMP binding versus tetramerization varies between structural regions within the IR, as revealed by the comparative analysis of the dynamic profiles for the four states of the thermodynamic cycle in Fig. 1c (Table 3 and Fig. 8). The TD structural dynamics are influenced primarily by tetramerization, while the CBD structural dynamics are influenced mainly by cAMP binding, with a lesser contribution from tetramerization (Table 3 and Fig. 8). In particular, closer examination of the CBD revealed that the PBC and αB–αC helices are influenced primarily by cAMP binding, but the N3A motif is influenced by both cAMP binding and tetramerization. The latter observation suggests that the N3A may play a critical allosteric role in the synergistic coupling between cAMP binding and tetramerization, whereby perturbation of the N3A upon cAMP binding may facilitate tetramerization and vice versa.

Third, our MD simulations reveal that the transition between the inactive (i.e. N3A in/αB–αC out) and active (i.e. N3A out/αB–αC in) CBD topologies occurs through a manifold of divergent pathways (Fig. 4, c and d, and Table 3). The active-to-inactive transitions captured by our HCN simulations could not be detected in previous simulations of other CBDs (27, 48) and indicate that the conversion between the in/out and out/in CBD topologies is significantly less concerted than previously anticipated (49). Our results clearly show that transient exploration of noncanonical mixed topologies is possible for the apo CBD (Fig. 4, c and d). Notably, although the noncanonical CBD topologies appear accessible to both apo-monomers and apo-tetramers, in the former the in N3A topology is more populated than in the latter, i.e. tetramerization of the apo IR causes a shift to a preferred out N3A topology. In fact, the apo-tetramer distribution of N3A orientations is similar to that observed for the holo IR states, despite the absence of cAMP (Figs. 4 and 8; Table 3). The preference for the out N3A topology in the apo-tetramer is explained by the reduction in TD dynamics that occurs upon TD self-association (Figs. 4 and 8; Table 3), which in turn destabilizes the in N3A topology due to intra- and intermolecular steric clashes between the TD and the CBD β-barrel.

The preference of the apo-tetramers for the out N3A topology revealed by our simulations rationalizes why the relative N3A/β-barrel orientation remains virtually unaffected irrespective of whether the HCN IR tetramer is crystallized in the presence or absence of cAMP (45). This prior observation based on x-ray crystallography was puzzling given the markedly different functional gating properties of the apo- and holo-HCN IR, but it is well explained in light of our MD results. Furthermore, our simulations reveal that although minor populations of the two holo ensembles still sample the N3A in topology preferred by the apo-monomer, the ranges of possible conformations for the two holo states exhibit a greater degree of overlap than is observed for the two apo states (Fig. 4 and Table 3). These findings suggest that cAMP binding selectively stabilizes the CBD into tetramer-compatible configurations, thereby priming the IR for tetramerization and providing a viable mechanism for the cAMP-dependent gating of HCN ion channels.

In conclusion, this study provides an unprecedented view of TD and CBD structural dynamics within the HCN IR and their role in promoting HCN channel gating through tetramerization. First, the TD is dynamic in the monomeric states but becomes structured in the tetrameric states. The TD flexibility in the monomeric states removes the steric clashes that the structure of the apo CBD would otherwise impose, explaining the autoinhibitory role of the apo IR. Second, the apo CBD undergoes an active/inactive transition through a manifold of pathways. These pathways are more divergent than previously anticipated and involve a combinatorial array of in/out topologies for the orientation of the N- and C-terminal CBD α-helices relative to the β-subdomain. Third, the conformational ensemble accessible to the apo CBD is confined in the tetrameric state due to steric constraints imposed by the tetramer, which prevents a complete active-to-inactive transition. The binding of cAMP pre-confines the CBD conformational ensemble to a tetramer-compatible state, thereby priming the IR for tetramerization and providing an explanation for how cAMP controls HCN channel gating through IR tetramerization. We anticipate that the concepts proposed here may be of general applicability for gating rings controlled by allosteric effectors as well as for multidomain signaling systems (31, 50–62).