Dynamic heart rate measurements from video sequences

Abstract

This paper shows how dynamic heart rate measurements that are typically obtained from sensors mounted near to the heart can also be obtained from video sequences. In this study, two experiments are carried out where a video camera captures the facial images of the seven subjects. The first experiment involves the measurement of subjects’ increasing heart rates (79 to 150 beats per minute (BPM)) while cycling whereas the second involves falling heart beats (153 to 88 BPM). In this study, independent component analysis (ICA) is combined with mutual information to ensure accuracy is not compromised in the use of short video duration. While both experiments are going on measures of heartbeat using the Polar heart rate monitor is also taken to compare with the findings of the proposed method. Overall experimental results show the proposed method can be used to measure dynamic heart rates where the root mean square error (RMSE) and the correlation coefficient are 1.88 BPM and 0.99 respectively.

1. Introduction

Heart rates and heart rate variations are widely analysed especially in sports and medicines [1,2]. Electrocardiography (ECG) signals from ECG based machine are extracted to monitor human’s physiological signals including heart rate (HR) and heart rate variability (HRV) [3–5]. There are some other methods used to estimate the heart rates, as described in [6–8]. However, these methods generally require expensive specialized machines.

Human heart rate can also be estimated from the plethysmographic signals since the heart rate has the same frequency as the cardiac cycle. Previous studies [9,10] showed the relationship of the intensity of the reflected light from the trans-illuminated tissue and the change in blood volume. This measurement of blood volume pulses (BVP) through reflected light intensity variations is known as photoplethysmography (PPG).

Similarly, BVP can also be obtained from video sequences. Poh et al. developed a method for measuring multiple physiological parameters using a basic webcam [11,12]. The blood volume pulse (BVP) signals were recovered from the facial region of the subjects. Independent component analysis (ICA) was used to separate the sources from the colour channels in the video recordings. In contrast to correlation-based transformation such as Principal Component Analysis (PCA), ICA does not only de-correlate the signals, but also reduces higher-order statistical dependencies [13,14]. The red, green, and blue (RGB) components in the video recordings are actually the sensors or mixture of the reflected plethysmographic signals and other sources (as well as the artefacts).

For the video-based heart rate measurements and monitoring, the BVP is the independent source signal of interest. The colour components of the facial images captured by the video recorder, particularly, the RGB, vary in accordance to the heart rate variation, since the changes in blood volume alter the light intensity reflected from facial tissue. Hence, heart rate readings can be estimated from the video sequences.

In addition to the method using ICA, Pursche et al. concluded that centre of the face region provides better information compared to the other parts of the face region [15]. They concluded that the power-spectrum-analysis algorithm can also give similar results compared to the peak-detection algorithm.

On the other hand, Xu et al. [16] designed a simplified mathematical model for images of human skin to obtain the BVP signals. They developed a model for pigment concentration in human skin, and used it to estimate the heart rate. They computed the heart rate readings from video recordings lasting from 45s to 90s. The subjects are required to keep still during the recording. Their heart rates do not vary much.

Previous works focus more on the heart rate computation from longer video duration which is reliable for heart rates that do not vary much. However, for heart rates of subjects that vary while not at rest, then the techniques used in [11,12] need to be changed. We have developed a technique that reflects the dynamic heart rate variations using short time Fourier transform [17] and filter bank [18]. The methods developed in [17] and [18] require a longer video duration for accurate readings, which is not practical in many situations where short video duration is required to give heart rate readings.

In the previous research [12,16], the focus was not on dynamic heart rate measurements and hence the need did not arise in their work to get the shortest video duration. However, in applications that need dynamic heart rates, it is then essential to use the shortest video duration that gives accurate heart rate readings. Hence, two conditions have to be satisfied for dynamic heart rate measurements: minimum video duration and accurate heart rate estimation.

In this paper, a method is proposed to measure instantaneous heart rate that varies dynamically from short video sequences. The challenge in using short video sequences is that the ICA sources may not have sufficient independence among them. Without determining the independence of the sources, there is a possibility of the heart rate signal combining with other signals to render an inaccurate reading. Hence in this paper, mutual information [19] is used to determine the independence of the sources to obtain an accurate reading. It is found that the value of mutual information of the ICA sources will be converging when the ICA sources are sufficiently independent. Beyond this video duration, any further computation of mutual information does not change the accuracy of the heart rate readings. Hence, the earliest point of mutual information value for the video duration is identified when it begins converging.

In Section 2, the related works of Poh et al. and Xu et al. in estimating the heart rate from video sequences is reviewed. The proposed method comprising ICA and mutual information for estimating the dynamic heart rates from video sequences is presented in Section 3. The results obtained from the proposed method for dynamic heart rate variations of subjects performing cycling activity are shown and analysed in Section 4. Section 5 gives the conclusion of the study.

2. Related works

There are several approaches used in determining the heart rates from video sequences. This section deals in detail with two studies we deem to be of particular relevance to our own study. Poh et al. [12] exploit the relationship between pixel intensities and heart rates by recovering the BVP signals from the RGB components. On the other hand, Xu et al. [16] designed a model for images of facial skin, without any blind source separation algorithm, to exploit the relationship between pixel intensities and heart rate pulses. Both methods are tested on subjects who keep still during the video recordings causing the heart rates not to vary much.

2.1 BVP recovery using blind source separation

In [11] and [12], blind source separation (BSS) is used to recover the independent source signals (including BVP signal) from a set of sensor observations (RGB pixel intensities). Independent Component Analysis (ICA) is used to recover the BVP signals.

This is how the method works. Assume that there are n linear mixtures (sensors) x₁, …, x_n of n independent components

$$x_j=a_{j1}{s}_1+a_{j2}{s}_2+\mathrm{...}+a_{jn}{s}_n,\hspace{0.17em}\text{for all}j,$$ (1)

and each mixture x_j as well as the independent component s_k is a random variable, instead of a proper time signal. Let x denotes the mixture x₁, …, x_n, s denotes s₁, …, s_n, and A denotes the a_ij, then Eq. (1) can be written as

$$x=As.$$ (2)

The statistical model in Eq. (2) is known as independent component analysis. It describes how the observed sensors x_i are generated by a process of mixing the components s_i. The mixing matrix A is unknown but can be estimated. The independent components can be obtained by the computing the inverse of mixing matrix A, denoted by W. Hence,

$$s=Wx$$ (3)

Using this method, ICA sources were recovered from the RGB components obtained from 60-second video intervals. The source with the highest peak in the frequency domain was selected as the BVP signal. Next from the selected source, the inter-beat intervals (IBI) which were the intervals between two subsequent BVP peaks were obtained from 60-second video interval. The mean of the inter-beat intervals ($\overline{IBI}$) was calculated and the heart rate (HR) for the particular video interval was computed using

$$HR=60/\overline{IBI}$$ (4)

2.2 Estimation of heart rate pulses from video

Unlike the method used in [11,12], Xu et al. developed a simplified mathematical model to predict human heart rates from video frames based on the absorbance of the lights by the skin. The skin absorbance A at wavelength λ, as in defined in [16] is

$$A(\lambda )=v_m(\lambda )c_m+v_h(\lambda )c_h+A_0(\lambda ),$$ (5)

where c_m and c_h represent the pigment concentration for melanin and hemoglobin respectively, v is the product of pigment extinction coefficient and the mean path length of photons in the skin layer. A₀ denotes the baseline skin absorbance and the residual pigment contribution.

Since the spectral function of the camera sensor can be considered as a delta function [20,21], the colour components can be then expressed in log space as

$$\begin{array}{l}\log P_R=-\{v_m(R)c_m+v_h(R)c_h+A_0(R)\}+\log kE(R),\\ \log P_G=-\{v_m(G)c_m+v_h(G)c_h+A_0(G)\}+\log kE(G),\end{array}$$ (6)

where R and G represent the red and green components of the image. k is a constant for the camera gain while E is the power of the transmitted light and incident light respectively.

A series of signals that can be used for the heart rate estimation is formed as:

$$y(n)=[\log (\frac{P_R^2·P_G^1}{P_R^1·P_G^2}),...,\log (\frac{P_R^n·P_G^{n-1}}{P_R^{n-1}·P_G^n})].$$ (7)

To obtain the heart rate, Eq. (7) is transformed into frequency domain, and the highest peak in the frequency domain is selected as the corresponding heart rate for the selected video interval.

3. Proposed method

In this section, the proposed model to estimate the dynamic heart rate measurements is discussed together with how the independence of the ICA sources is established. The earliest sign of the independence of the ICA sources determined from the mutual information establishes the minimum video duration which gives the most accurate heart rate estimation is elaborated. The significance of the video duration and its relationship to the accuracy of the heart rate estimation is also discussed.

3.1 Workflow of the proposed method

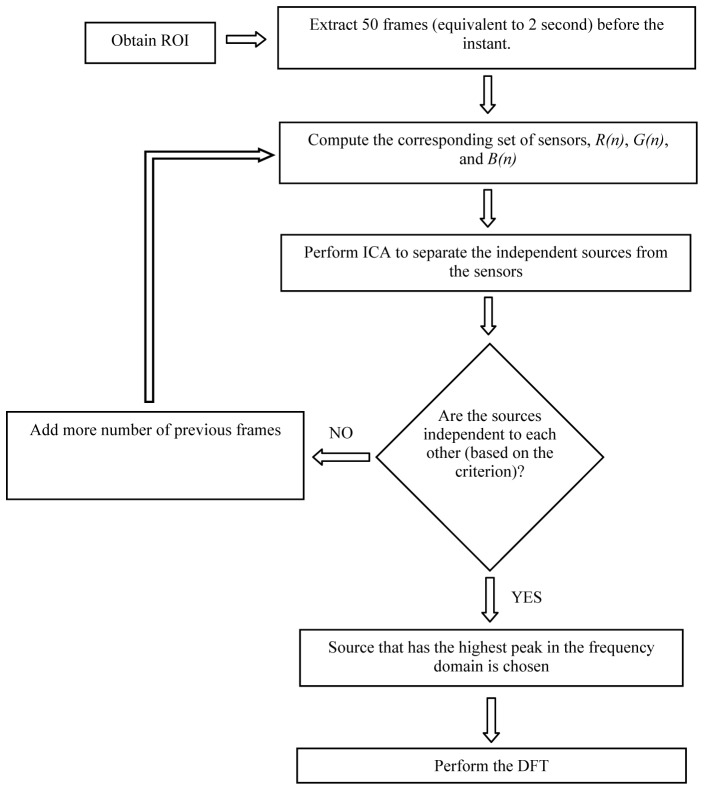
In order to compute the instantaneous heart rate of a subject at n-th second instant, 50 frames of raw images (equivalent to 2 seconds) before the instant were used. The block diagram of the proposed model for dynamic heart rate measurement is illustrated in Fig. 1.

Fig. 1.

Flow chart of the proposed method.

After the ROI of each frame was identified, the mean of pixel values for red (R), green (G) and blue (B) components were computed separately, where

• µ_R: the mean of all pixel values for R component

• µ_G: the mean of all pixel values for G component

• µ_B: the mean of all pixel values for B component

The respective µ_R, µ_G, and µ_B of all these 50 continuous frames were calculated. Therefore, at n-th second instant, a set of three raw sensors R(n), G(n), B(n) were formed. Each raw sensor consisted of 50 elements. The set of raw sensors were then detrended using algorithm developed by Tarvainen et al. [22]. The ICA model developed by Cardosa and Souloumiac [23,24] was then used to separate one set of 3 independent sources from the set of sensors. The set of ICA sources were bandpass filtered (128-point Hamming window, 0.6-4 Hz), and the mutual information was applied to obtain the independence of the ICA sources.

The entire process was repeated by increasing the number of previous frames, one-by-one until it fulfilled the criterion. The criterion was based on the convergence of the curve fitting coefficients. It is described in details in Section 3.2.

Once it fulfilled the criterion, the process was stopped. The number of frames (or video duration) at this point was chosen as the video duration needed for computing the instantaneous heart rate reading n-th second time instant. The respective sources were considered independent to each other. The source that had the highest peak in the frequency domain was chosen as the BVP or heart rate sources. The corresponding frequency was considered as the instantaneous heart rate at n-th second time instant.

3.2 Criterion determining the independence of the ICA sources

One of the criteria or requirements to use the ICA is that the sources must be independent of each other. ICA itself will separate the sources by maximizing the statistical independence among the given sensor signals. In this paper, mutual information is used to measure the mutual dependence (and independence) of the ICA sources.

In this study, three ICA sources, i.e. S₁, S₂, and S₃, are separated from each set of Red(R), Blue(B) and Green(G) sensors. The normalized mutual information of any two source S_p and S_q, I_n (S_p ;S_q) is expressed as

$$I_n(S_p;S_q)=\frac{I(S_p;S_q)}{\sqrt{H(S_p)H(S_q)}},$$ (8)

where I(S_p; S_q) is the mutual information of the sources S_p and S_q while H(S_p) and H(S_q) are the respective entropies of the sources S_p and S_q.

The mutual information I(S_p; S_q) can be expressed in terms of their entropy:

$$I(S_p;S_q)=H(S_p)+H(S_q)-H(S_p,S_q).$$ (9)

The entropy H(S) of a source S can be computed from

$$H(S)=-{\displaystyle \sum _{s\in S}p(s)\log p(s)},$$ (10)

while the joint entropy H(S_p,S_q) of the sources S_p and S_q can be computed from

$$H(S_p,S_q)=-{\displaystyle \sum _{s_p\in S_p}{\displaystyle \sum _{s_q\in S_q}p(s_p,s_q)\log p(s_p,s_q)}},$$ (11)

where p(s_p,s_q) is the joint probability density function of the sources S_p and S_q.

The normalized mutual information gives zero if both sources are totally independent of each other and unity if both sources are totally dependent on each other. Since there are three ICA sources, hence their normalized mutual information is averaged and it is expressed as

$$C(S_1;S_2;S_3)=\frac{I_n(S_1;S_2)+I_n(S_1;S_3)+I_n(S_2;S_3)}{3}.$$ (12)

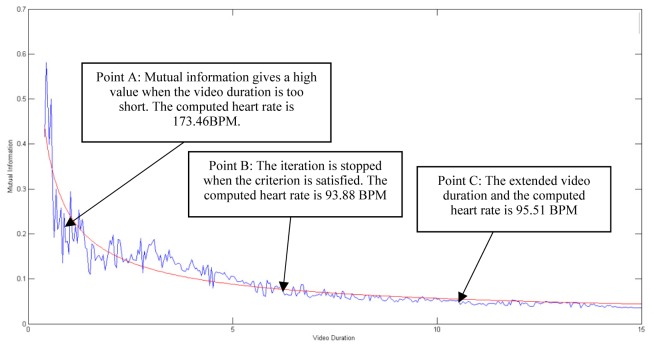
The relationship of C(S₁;S₂;S₃) and video duration for estimating the instantaneous heart rate reading at a particular instant is shown in Fig. 2. It indicates that the value of C(S₁;S₂;S₃) decreases as the video duration (or number of video frames) increases. A best fit curve is used to represent the function C(S₁;S₂;S₃). In this study, the best fit curve to represent the function of mutual information with the video duration is given as

$$C_t(S_1;S_2;S_3)=a{t}^b,$$ (13)

where t is the video duration used, a and b are the coefficients of the function.

Fig. 2.

The relationship between the averaged normalized mutual information C(S₁;S₂;S₃) and the video duration and the respective computed heart rates. The actual heart rate is 93 BPM.

The confident intervals for the fitted coefficients are set at 95%. The coefficients change drastically at the beginning, but remain almost constant when the video duration exceeds a specific duration and the mutual information value changes very little after this duration. The stopping criterion is set as when the difference of coefficient values for 2 continuous video frames is smaller than 2 × 10⁻⁴. Once the stopping criterion is met, the corresponding video duration is identified as the video duration to compute the instantaneous heart rate at that particular instant.

As an example, Fig. 2 shows that different time intervals give different value mutual information and hence different heart rate readings. In this case, the actual heart rate reading of the subject obtained from Polar Heart Rate Monitor is 93 BPM. Now consider point A in Fig. 2 which indicates the corresponding value of C(S₁;S₂;S₃) when the video duration is 2.2 seconds. Notice at this point, the mutual information gives a high value indicating the ICA sources are not independent. The heart rate computed based on these ICA sources is 173.46 BPM. As the video duration increases, correspondingly C(S₁;S₂;S₃) too decreases. This trend continues till the stopping criterion is met. As can be seen in Fig. 2, the criterion is satisfied at point B (video duration for this case is 6.88s). The heart rate reading computed at this point is 93.88 BPM, which is closer to the actual reading. Even if the video duration is extended longer than the necessary duration, the C(S₁;S₂;S₃) doesn’t vary much. However, the heart rate accuracy drops further if longer video duration is taken after the stopping criterion is met. For example, consider point C where the video duration is 10.8 seconds and the ICA sources are still independent to each other but it gives a less accurate heart rate reading when compared to point B. The computed heart rate is 95.51 BPM. The details of the heart rate accuracies at different points (hence different durations) are discussed in Section 3.3.

3.3 Significance of the minimum video duration

In this sub-section, the significance of the video duration and its relationship to the accuracy of the heart rate estimation is presented. The significance of the independent sources and how they relate to the accuracy of the heart rates is shown in Fig. 3, Fig. 4 and Fig. 5. Figure 3 shows the separated ICA sources for point A (at 2.2 s) in the frequency domain. As can be seen in Fig. 3, the highest peak is observed at S₃ and the corresponding frequency is 173.46 BPM. The actual heart rate reading obtained from the Polar heart rate monitor for the particular instant discussed in Fig. 2 is 93 BPM. As pointed out earlier in Section 3.2, the ICA sources are not independent and hence the computed heart rate reading is inaccurate.

Fig. 3.

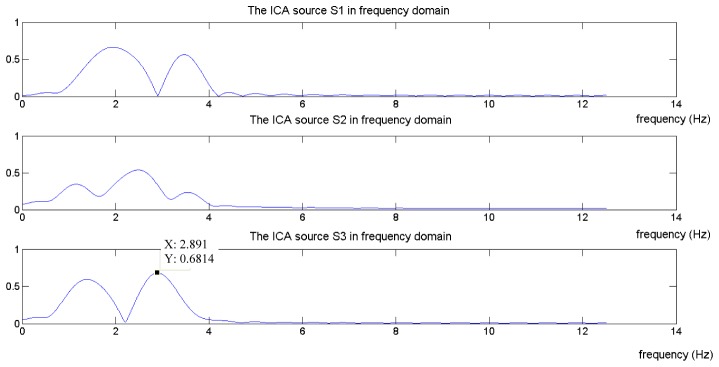
The frequency domain of the ICA sources when video duration at point A is selected.

Fig. 4.

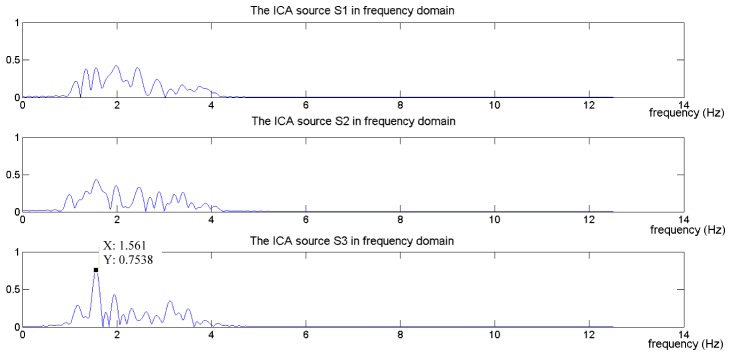
The frequency domain of the ICA sources when video duration at point B is selected.

Fig. 5.

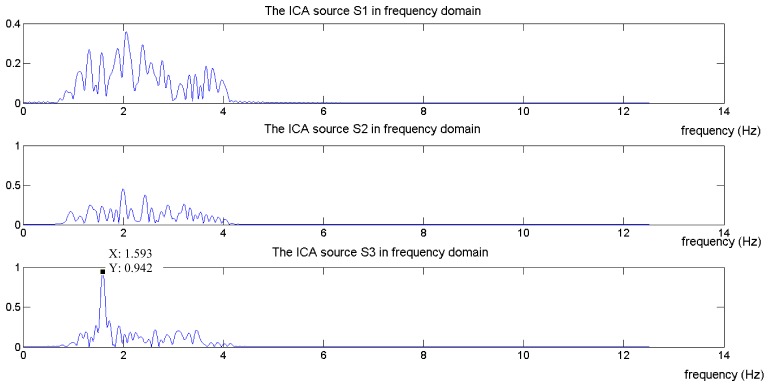
The frequency domain of the ICA sources when video duration at point C is selected.

Figure 4 shows the separated ICA sources for point B (at 6.88 s) in frequency domain. At this point, the stopping criterion is met. As shown in Fig. 4, the highest peak is significantly seen at S₃ and the corresponding frequency is 93.88 BPM. The computed reading is closer to the actual heart rate reading. For the video duration that is beyond point B, the accuracy of the computed heart rate readings decreases. This is shown in Fig. 5. In this figure, point C (10.8 s), the highest peak in the frequency domain is observed at S₃ and the corresponding frequency is 95.51 BPM. For dynamic heart rate measurements, a shorter video duration is preferred as it would allow a more frequent update of heart rate measurements.

Figure 6 shows how the errors of the computed heart rate readings vary at different video intervals. It shows the error bars of the heart rate errors for subjects tested in the experiments. As can be seen from Fig. 6, the error rates are considerably high if the video duration is less than 4 seconds. Even though the mean errors from 4 seconds to 5.5 seconds are relatively as close to the mean error of the proposed method, however, the standard deviation of the errors for the proposed method is much smaller when compared with those from 4.5 seconds to 5.5 seconds. This explains the need to determine the earliest sign of the independence of the ICA sources which corresponds to the minimum video duration that gives accurate heart rate estimation for all readings. Table 1 summarizes the video durations for all readings to estimate the heart rates of each subject using the proposed method.

Fig. 6.

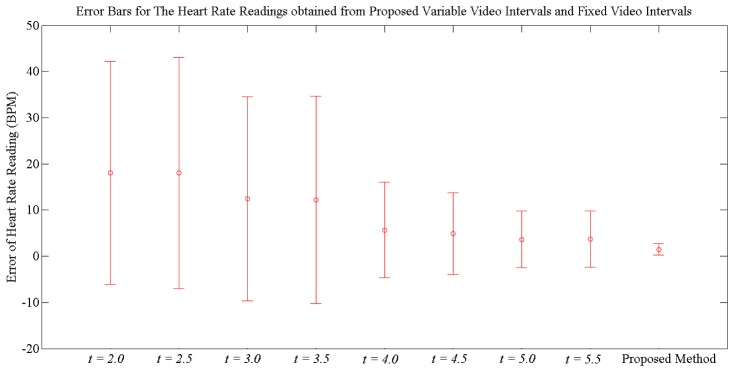
Comparison of the mean square and standard deviation of the heart rate errors for the proposed variable video intervals and fixed video intervals. t represents the video interval.

Table 1. Summary of the video durations for all heart rate readings of each subject using the proposed method.

Experiment	Subject	Video Duration (sec)		Mean (sec)	Standard Deviation (sec)
		Minimum	Maximum
1	1	3.88	7.52	5.35	0.83
	2	3.76	7.56	5.56	0.91
	3	3.76	6.80	5.47	0.68
	4	3.80	7.32	5.63	0.90
	5	3.64	7.36	5.37	0.85
	6	3.76	7.48	5.26	0.89
	7	3.72	7.32	5.49	0.88
2	1	3.76	7.56	5.51	0.91
	2	3.72	6.80	5.17	0.68
	3	3.60	7.12	5.45	0.80
	4	3.64	7.16	5.29	0.78
	5	3.84	7.56	5.47	0.80
	6	3.96	7.20	5.42	0.76
	7	3.52	7.04	5.42	0.78

4. Experimental study

In this section, the experimental setup and two experiments that relate to dynamic heart rate variation are discussed. Heart rate variation can be either increasing or decreasing. This study consists of both cases. In the first experiment, the heart rates of the subjects were increasing, ranging from 79 to 150 BPM, while in the second experiment, the heart rates of the subjects are decreasing, ranging from 153 to 88 BPM. In addition to the dynamic heart rate experiments, a sub-section is included to show that the proposed method can also be used for subjects while at rest.

4.1 Experimental setup

All experiments were set up under office fluorescent lights with indirect sunlight as the source of illumination. The lighting background was homogeneous and had no significant changes or variation. All the data were processed and analyzed offline using MATLAB R2013a.

A Handycam Camcorder (Sony HDR-PJ580V) with resolution of 1440 × 1080 pixels was used with 25 frames were sampled every second for video recording purpose. All videos were recorded in 24-bit RGB (with 8 bits per channel). The video camera was fixed at a position with a distance of about 0.60 m from the subject’s face. In this paper, the Region of Interest (ROI) is fixed at the area below eyes and above the upper lip of mouth in a video frame. As what concluded by Pursche et al. [15], this region gives better accuracy compared to other facial regions. The face region was detected by using the model described in [25,26].

All subjects were asked to wear the Polar chest strap before doing the experiments. In the first experiment, seven subjects were asked to cycle at different speeds for three minutes and significant changes of the subjects’ heart rates were observed after the first two minutes. The heart rate readings were taken in the last one minute for every subject. An increasing heart rate variation was observed for every subject. Video was recorded while the subjects were cycling where their faces had minimum movement.

In the second experiment, seven subjects were asked to cycle at fast speed to raise their heart rates to a certain high level. Once this was achieved, then the subjects were asked to rest for one minute and their heart rates were observed and computed from video recorded during this rest period. The subjects did not move during the video recording. 60 consecutive heart rate readings (sampled at each second) were computed for every subject.

The instantaneous heart rates of all subjects for both experiments were computed based on the detailed algorithm proposed in Section 3. For reference, all instantaneous heart rates of the subjects were measured using Polar Heart Rate Monitor – Polar Team² Pro. Polar Team² transmitter set records and transmits the subjects’ ECG signals to its base station. The heart rate was sampled and computed by measuring at least one ECG signal waveform, as described in the patents described in [27,28]. A comparative study was done between the actual readings obtained from Polar Team² Pro and those computed readings from the proposed method.

4.2 First experiment: observed heart rates varying from low to high

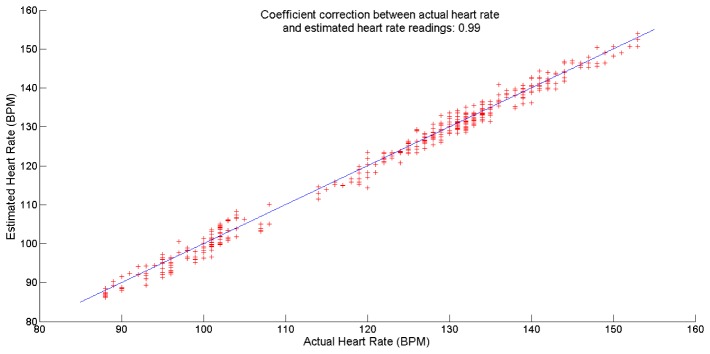
In the first experiment, seven subjects’ heart rates were measured while cycling and they varied from 79 BPM to 150 BPM. The video duration needed for each instantaneous heart rate reading computed using the proposed method varied from 3.64 to 7.52 seconds with a mean value of 5.45 seconds. A total of 420 instantaneous heart rate readings were obtained from the experiment. A comparison of the computed and actual readings of the subjects in this experiment is shown in Fig. 7. The root mean square error is 1.97 BPM while the Pearson correlation coefficient is 0.99.

Fig. 7.

Comparison of actual heart rate readings and computer heart rate readings in the first experiment.

The details of the heart rate variations of the seven subjects and their corresponding RMSE are shown in Table 2. From Table 2, the highest and lowest RMS errors are 2.92 and 1.64 BPM respectively. In addition to this, the performance of the proposed algorithm is evaluated using the Bland Altman plot, as shown in Fig. 8. The Bland Altman plot is used to quantify the agreement between two methods of measurements [29]. The 95% limits of agreement, estimated by mean difference ± 1.96 standard deviation of the difference, provide an interval within which 95% of the differences between the measurements by the two methods. It can be seen from Fig. 8 that the Bland Altman plot quantifies the agreement between the actual heart rate readings obtained from the Polar Heart Rate Monitor and the computed heart rate readings using the proposed method. As can be seen, most of the computed readings are located inside the blue boundary lines that satisfying the 95% limits of agreement. However, there are some readings located out of the boundary lines and this is probably due to some motion artifacts.

Table 2. Summary of heart rate readings results in the second experiment.

Subject	Heart Rate Readings(BPM)		RMSE (BPM)
	Highest	Lowest
1	91	104		2.01
2	101	136		1.76
3	104	120		2.03
4	93	150		1.64
5	110	129		1.67
6	110	140		2.33
7	79	96		2.28

Fig. 8.

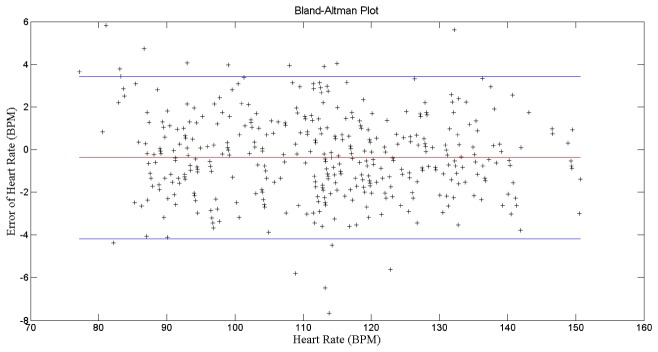
Bland-Altman Plot for all computed heart rate readings for the first experiments.

4.3 Second experiment: observed heart rates varying from high to low

In the second experiment, the seven subjects’ heart rates varied from 153 BPM to 88 BPM. A total of 420 instantaneous heart rate readings were obtained from this experiment. The video duration needed for each instantaneous heart rate reading computed using the proposed method varied from 3.52 to 7.56 seconds with a mean value of 5.39 seconds. Figure 9 shows the comparison of the computed and actual heart rate readings of the seven subjects. The root mean square error is 1.77 BPM while the Pearson correlation coefficient is 0.99. Table 3 shows the details of the heart rate variations of the seven subjects and their corresponding RMSE. Just as in the first experiment, the highest and the lowest high rate RMS errors are less than 3 BPM.

Fig. 9.

Comparison of actual heart rate readings and computer heart rate readings in the second experiment.

Table 3. Summary of heart rate readings results in the second experiment.

Subject	Heart Rate Readings(BPM)		RMSE (BPM)
	Highest	Lowest
1	108	88		1.97
2	150	114		1.49
3	105	98		2.14
4	153	119		1.73
5	153	127		1.58
6	141	127		1.57
7	146	129		1.82

The Bland Altman plot as shown in Fig. 10 indicates that a smaller number of computed heart rate readings are located outside the 95% limit of agreement interval. The accuracy of computed heart rate readings in this experiment is better than the accuracy of the readings in the first experiment. This may be because the subjects in the second experiment did not move as they were not cycling.

Fig. 10.

Bland-Altman Plot for all computed heart rate readings for the second experiments.

4.4 Heart rates estimation for subjects at rest using proposed method

In addition to the dynamic heart rate measurements, the proposed method can also be used for subjects whose heart rates are almost constant (non-dynamic). To do that, subjects were at rest for one minute and their measured and computed heart rate readings are shown in Fig. 11. The root mean square error is 1.54 BPM while the Pearson correlation coefficient is 0.98.

Fig. 11.

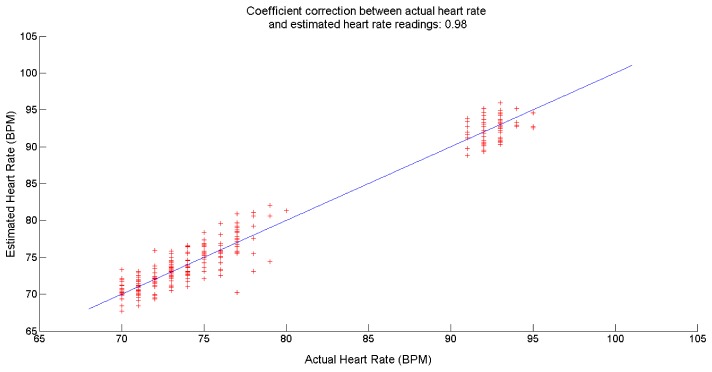
Comparison of actual heart rate readings and computer heart rate readings for subjects at rest.

5. Conclusion

A new method of computing dynamic heart rate involving the use of short video clips has been proposed in this paper. Video clips are far easier to obtain and cheaper than the existing invasive or in-contact methods of obtaining the heart rates. In this study, it is observed that close to accurate readings can be obtained if the three ICA sources are independent of each other. The independence of the ICA sources needs to be established to ensure the reliability of the findings. For this, mutual information developed earlier was used. Two experiments were done to corroborate the validity of the proposed method and the accuracy of its findings. These experiments show that the findings of this method agree with the findings of the established, and therefore accepted, method. The Bland-Altman plot shows that most of the findings of this study fall within the boundaries set for 95% limit of agreement interval. The RMSE in both experiments is less than 3 BPM.