Flux or speed? Examining speckle contrast imaging of vascular flows

Abstract

Speckle contrast imaging enables rapid mapping of relative blood flow distributions using camera detection of back-scattered laser light. However, speckle derived flow measures deviate from direct measurements of erythrocyte speeds by 47 ± 15% (n = 13 mice) in vessels of various calibers. Alternatively, deviations with estimates of volumetric flux are on average 91 ± 43%. We highlight and attempt to alleviate this discrepancy by accounting for the effects of multiple dynamic scattering with speckle imaging of microfluidic channels of varying sizes and then with red blood cell (RBC) tracking correlated speckle imaging of vascular flows in the cerebral cortex. By revisiting the governing dynamic light scattering models, we test the ability to predict the degree of multiple dynamic scattering across vessels in order to correct for the observed discrepancies between relative RBC speeds and multi-exposure speckle imaging estimates of inverse correlation times. The analysis reveals that traditional speckle contrast imagery of vascular flows is neither a measure of volumetric flux nor particle speed, but rather the product of speed and vessel diameter. The corrected speckle estimates of the relative RBC speeds have an average 10 ± 3% deviation in vivo with those obtained from RBC tracking.

1. Introduction

Laser speckle contrast imaging (LSCI) utilizes widefield laser illumination and camera acquisition, achieving millisecond order temporal resolution and spatial resolution on the order of tens of microns for full-field imaging of specimen motion, such as blood flows. LSCI has been predominantly adopted for imaging cerebral blood flow (CBF) dynamics in small animals [1–3] and clinically during intra-operative neurosurgery [4–6]. Beyond CBF dynamics, LSCI has applications in dermal [7] and retinal [8–10] perfusion imaging.

Specifically, dynamic scattering of coherent light introduces temporal fluctuations in the observed speckles, which manifests as a blurring of the speckle pattern imaged over a fixed exposure duration [8]. The degree of blurring can be quantified by computing the local spatial contrast:$K\left(T\right)={\sigma }_s\left(T\right)/\langle I\rangle$, defined as the standard deviation over the mean pixel intensities within a small spatial window in the image taken over the camera exposure duration, T. Since Fercher and Briers [8], models relating speckle contrast to exposure time have been developed to decouple the flow contribution from the speckle contrast measurements by extracting the characteristic temporal autocorrelation decay time of the speckles [11]. From dynamic light scattering (DLS) theory, this speckle correlation time has been posed to be inversely proportional to the speed of the scatterers [12] but also weighted by the number of dynamic scattering events in the multiple scattering limit [13,14].

Microvascular calibers (i.e. 10 - 200 µm) are predominantly greater than the intravascular scattering mean free path (i.e. 10 - 12 µm). Therefore, photon paths through superficial vessels may encounter multiple moving particles before termination at their respective camera imaging pixels. While the effects of sequential intravascular scattering may be more readily recognized for applications and geometries used in diffuse correlation spectroscopy (DCS) [15–18], the applicability to exposed microvascular flows needs further examination. The results of a recent photon migration study of laser speckle imaging highlight that multiple dynamic scattering is occurring from pixels imaging both resolvable vessels and parenchymal regions of the tissue [19]. Particularly, pixels imaging resolvable vessels sampled dynamic scattering interactions localized largely within the individual vessels of interest. Vessels of varying sizes may be associated with disparate amounts of dynamic scattering and therefore may provide misleading estimates of flow, both absolute and relative, if not correctly estimated. These effects are now evaluated empirically using Multi-Exposure Speckle Imaging (MESI) by initially examining controlled flows in microfluidic channels of varying sizes. Subsequently, the DLS assumptions in the underlying form of the autocorrelation function used for estimating the speckle decorrelations are revisited in light of the effects of multiple dynamic scattering. Finally, the effect of the flow estimates garnered from regions of interests spanning single superficial microvessels in mice are compared against the red blood cell (RBC) speeds obtained from high speed reflectance imaging.

2. Theory

Although speckle contrast values are indicative of motion within the specimen in the form of speed or flow, the relationship is nonlinear. A common practice of dynamic light scattering inversion techniques is to relate the physically measureable normalized intensity autocorrelation function, $g_2(\tau )$, to the normalized electric field autocorrelation function,$g_1(\tau )$, by using the Siegert relationship, g₂(τ) = 1 + β|g₁(τ)|², where β accounts for polarization effects and speckle sampling. By taking the second moment of the intensity autocorrelation function and incorporating the Siegert relationship, the speckle variance [8,11] can be expressed as

$${\upsilon }_2(T)=\frac{2\beta }{T}{\displaystyle {\int }_0^T\left(1-\frac{t}{T}\right){\left[g_1(t)\right]}^{2}dt},$$ (1)

where T is the camera exposure duration. The form of g₁ is traditionally based on assumptions of Brownian motion of scatterers and single dynamic scattering contributions to the imaged speckles and thus is often approximated by the Lorentzian profile of g₁(τ) = exp(-τ). After evaluating Eq. (1) and equating the square root of the observed speckle variance to the speckle contrast (K), the correlation time can be extracted from:

$$K(T,{\tau }_c)={\left(\beta \frac{e^{-2x}-1+2x}{2x^2}\right)}^{1/2}$$ (2)

where $x=\frac{T}{{\tau }_c}$ and ${\tau }_c$ is the speckle correlation time. This simplified model has been demonstrated to be fairly accurate in its ability to predict relatively modest, or under 50% change, in blood flow acutely with proper selection of camera exposure duration [17] and has been adopted for a wide range of applications.

The development of a multi-exposure speckle visibility expression followed the derivation begun by Fercher and Briers [8] and expanded by Bandyopadhyay et al. [11], but mapped the speckle variance to a range of exposure times to achieve a more quantitative set of flow metrics [20–22]. The Multi-Exposure Speckle Imaging (MESI) model includes accounting of i) dynamic and static scattering contributions through a modified Siegert relationship, ii) the inherent non-ergodicity in the spatial contrast measurements of temporal fluctuations and iii) exposure-independent noise [20]. Specifically, the modified Siegert relationship can be expressed as:

$$g_2^h(\tau )=1+\beta {\rho }^2{\left|g_1(\tau )\right|}^2+2\beta \rho (1-\rho )\left|g_1(\tau )\right|+\beta {(1-\rho )}^2,$$ (3)

where $\rho =\frac{I_f^{}}{(I_f+I_s)}$. I_s and I_f are the intensity contributions from the statically and dynamically scattered light, respectively. After taking the second central moment of the intensity autocorrelation function while assuming single dynamic scattering and diffusional particle dynamics (e.g. Brownian motion), the following multi-exposure expression [2,20] is obtained:

$$K(T,{\tau }_c)={\left\{\beta {\rho }^2\frac{e^{-2x}-1+2x}{2x^2}+4\beta \rho \left(1-\rho \right)\frac{e^{-x}-1+x}{x^2}+\beta {\left(1-\rho \right)}^2+v_{noise}\right\}}^{1/2},$$ (4)

where again $x=\frac{T}{{\tau }_c}$ and β is a normalization factor to account for speckle sampling. ρ is the fraction of light dynamically scattered, and ν_noise is exposure independent instrument noise [20]. In vivo studies have shown that single exposure LSCI measurements Eq. (2) underestimate large flow changes [21], while MESI Eq. (4) can substantially improve the accuracy of measured flow dynamics resulting from global and local flow obstructions in both acute and chronic settings [22].

3. Methods

3.1 Multi-exposure specking imaging (MESI) of blood flow

The instrumentation for MESI image acquisition, although similar to traditional LSCI implementations, requires synchronous control over both the camera exposure duration and the laser intensity. A laser diode (λ = 660nm, Micro Laser Systems, Garden Grove, CA) illuminated the sample while the computer triggers 15 camera (A602f, Basler Vision Technologies, Germany) exposures from 0.05 to 80 msec. Simultaneously, the amplitude of the laser light in each exposure was adjusted through an acousto-optic modulator (Fig. 1(a)). The selected exposures (Fig. 2(b)) attempted to capture the full speckle decorrelation (e.g. speckle image blurring) associated with cortical microcirculatory flows in mice by sampling a range of relatively high to low speckle visibility [23]. Remitted light was collected by an objective (10X, 0.25NA) and imaged onto the camera. A 7x7 pixel window was utilized to convert the raw frames to speckle contrast images [24]. The 15 single exposure frames comprise one MESI computed frame (Fig. 2(a)) of inverse correlation time using Eq. (4). The exposure range may be expanded or contracted to sample the specimen specific perfusion levels of interest. By holding the total amount of laser light in each image constant, variations in illumination (i.e. shot noise) are minimized. Thus signal-to-noise stability was maintained across exposures, necessary for keeping the speckle statistics (i.e. speckle contrast) sensitive to the specimen dynamics. An alternative MESI acquisition scheme that uses the longest selected camera exposure for imaging and varies exposure solely with illumination time may better control for factors such as camera readout noise at the expense of temporal resolution. Camera noises contribute relatively more to degrading the signal- or contrast-to-noise at shorter exposures. However, by keeping the integrated intensity in each exposure constant, variations in the readout noise should have limited impact on the overall contrast-to-noise. This scheme was avoided due to the remnant detection period of no illumination during the shorter exposures, which can be susceptible to integrating varying levels of background light that has interacted with the sample.

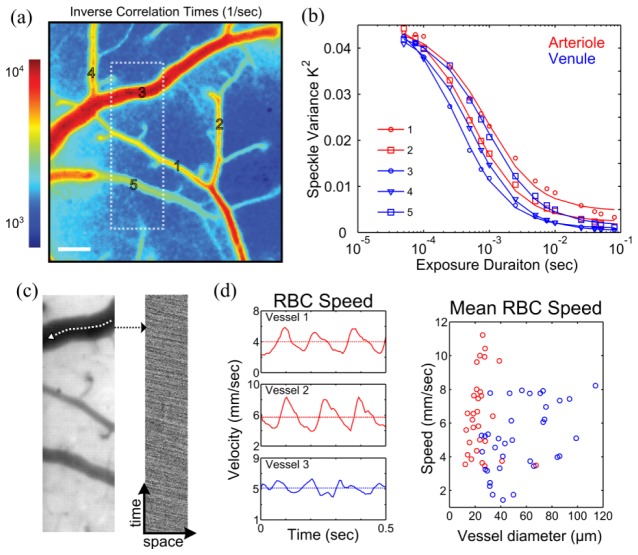
Fig. 1.

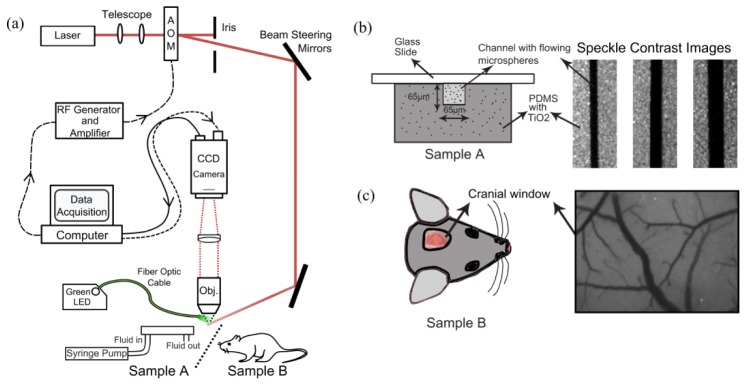
(a) Schematic of combined Multi-Exposure Speckle & RBC Reflectance Imaging. Pixel size in the object plane was 2.13 μm, which approximates to 3 pixels per erythrocyte. (b) Microfluidic sample cross-section highlighting a square channel embedded in scattering PDMS along with speckle contrast images of three calibers of flowing channels (65, 115, and 175 μm). (c) Typical cranial window location and speckle contrast image at 5ms exposure.

Fig. 2.

(a) Inverse correlation time map (Scale bar = 100µm). (b) Speckle variance curves from arterioles (red) and venules (blue) labeled in (a). (c) Green reflectance field (left) from region outlined in (a) used for high frame rate (495 fps) imaging to track red blood cells (RBCs). Spatio-temporal composite (right) of red blood cells observed as negative contrast down the selected vessel centerline. d) Extracted temporal profile of RBC speeds (left) highlighting pronounced pulsatile flow in arterioles (red) versus venules (blue). Time-averaged RBC speeds depicted with dashed line and also versus microvessel diameter (right) from all animals (n = 13, one minute averaged) examined in this study.

The MESI computed correlation times enable mapping of the flow dynamics by analyzing the characteristics of the shape of the speckle visibility curve (Fig. 2(b)). Comparisons between regional changes in inverse correlation time (1/τ_c) are tested against centerline speed dynamics in single vessels obtained by RBC tracking within resolvable surface microvasculature. Regions of interest of approximately 100 x 1 pixel² in size were placed within the vascular lumens of the speckle images (Fig. 2(a)-2(b)) to distinguish centerline and neighboring flows, which were also RBC tracked over a comparable displacement.

3.2 Red blood cell (RBC) tracking

High speed reflectance imagery was used for determining RBC velocities [22,25–27]. A fiber coupled green light-emitting-diode (MSB-RGB, Dicon LED, Richmond, CA) illuminated the cranial windows. Absorption contrast between hemoglobin in RBCs and blood plasma enabled tracking of RBC displacement in space and time (Fig. 2(c)). A graphical user interface was used to manually select the centerline profile, which followed the vascular curvature, as shown in Fig. 2(c). This profile was then extracted from a set of repeating green reflectance images to track RBCs, which appear as negative contrast in a space-time composite (Fig. 2(c)), similar to linescans in laser scanning microscopy. The cortical surface of the mouse was imaged using the same collection optics (e.g. magnification and numerical aperture) and camera (Fig. 1(a)) as were used for speckle imaging but operated at 495 frames per second (camera frame rate limit) through reduced area readout, typically a quarter of the area (2.13 µm/pixel, Fig. 2(c)) of the full field image. This enabled approximately 2-3 pixels per rodent RBC and a 2 msec camera exposure. Over a moving 24 msec temporal window with a 6 msec overlap, the Radon transform was used to determine the inclination angle of the streaks in the linescan from which velocity estimates were calculated [28], as the frame rate and spatial length scales were known. A maximum single-to-noise ratio (SNR) of 14 for velocity determination, typical for a 20 µm diameter vessel, and minimum of 3.5 for a 120 µm vessel, were observed following the algorithm and definitions of Drew et. al [28] for pulsatile flow characterization.

Increasing the camera frame rate to 495 frames per second lessened the restriction of the available in-plane length of the surface vessel needed for accurate RBC speed sampling. Spatio-temporal sampling of RBCs was optimized to obtain absolute centerline velocities (Fig. 2(d)) in selected vasculature with a maximum sampling uncertainty of 10% in the velocity estimates, as has been suggested for optimal camera based RBC tracking [26]. This uncertainty would be below or comparable to typical physiological variations, such as from vasomotion [29]. Detailed interpretation of the maximum uncertainty into minimum spatial and temporal samples has been provided by Duncan et. al [26]. At 10% uncertainty, maintaining a minimum of 100 spatial samples (i.e. pixels) and 100 sequential images enabled RBC speeds from 10⁻² to 10² mm/sec to be accurately sampled, well beyond the range of mean and time-varying RBC speeds reported and expected [25,30–32] for rodent cortical microvasculature with diameters ≤ 150µm.

3.3 Animal preparation

The sterile animal preparation protocol utilized has been detailed elsewhere [22]. Briefly, mice (n = 13, male CD-1 and C57, 25-30 g, Charles River) were anesthetized with vaporized isoflurane (2-3%) in medical air through a nose-cone. Temperature was maintained at 37°C with a feedback heat pad (DC Temperature Controller, FHC, Inc., Bowdoin, ME). Heart-rate and arterial oxygen saturation were monitored via pulse oximetry (MouseOx, Starr Life Sciences Corp., Oakmont, PA). The scalp was shaved and resected to expose skull between bregma and lambda cranial sutures. A 2 to 3 mm diameter portion of skull was removed with a dental drill (Ideal Microdrill, 0.8mm burr, Fine Science Tools, Foster City, CA) with constant ACSF (buffered pH 7.4) perfusion. Cyanoacrylate (Vetbond, 3M, St. Paul, MN) was added to exposed skull areas to facilitate dental cement adhesion. A 5 to 8 mm round coverglass (#1.5, World Precision Instruments, Sarasota, FL) was placed on the brain with ACSF perfusion between the exposed brain and the glass. Dental cement mixture was used to seal the glass to the surrounding skull, while retaining gentle pressure on the coverslip to keep an air-tight seal for sterility and to restore intra-cranial pressure after craniotomy. A layer of cyanoacrylate was applied over the dental cement to fill porous regions and further seal the cranial window. Animals were allowed to recover from anesthesia and monitored for behavior normality before imaging as in vivo data also used as part of a related chronic study [22]. C57 strain mice exhibited less dural expansion and skull regrowth than CD-1 mice and thus retained better optical clarity of the cranial window.

3.4 Microfluidic phantom preparation

Microfluidics molds were fabricated using photo-lithographically patterned photoresist (SU-8 2000, Microchem, Newton, MA) spin coated on silicon wafers to attain the desired channel thickness. The molds were designed with square cross sections (1:1 aspect ratio) in order to better resemble vascular geometries. A mixture comprised of 1.8 mg of TiO₂ per gram of polydimethylsiloxane (PDMS) was used to mimic reduced tissue scattering (µ_s^’ ≈8/cm). The completed mixture was poured onto the silicon molds, cured at 70°C for approximately 30 minutes, and detached from the mold to form the microfluidic channel structures. Inlet and outlet holes were blunt needle-punched and the exposed facets of the PDMS channels were oxygen plasma bonded to glass slides. Inlet and outlet tubing was inserted and secured to the underside of the phantom with room temperature vulcanizing (RTV) silicone. Phantom cross-section is shown in Fig. 1(b). PDMS thickness of each phantom was ~1.5 cm.

3.5 Photon scattering simulations

Heterogeneous geometries [33,34] mimicking the microfluidic phantoms were generated for photon migration simulations in a three dimensional Monte Carlo model, as has been done in a similar laser speckle contrast imaging simulation for in vivo geometries [19]. Widefield illumination at a wavelength of 660 nm was approximated with a sight divergence (NA = 0.01) incident and centered on the channel surface with a spot diameter of 1600 µm. Approximately 10¹¹ photons were launched and the photon scattering angle was determined by the Henyey-Greenstein phase function [35]. Every scattering event was recorded for photons exiting the surface of the sample (i.e. remitted photons).

Exiting photons were further sifted by retaining those with angles falling within the specified numerical aperture (NA) of the collection optics, namely the objective lens, for imaging by a detection region of interest centered over the surface of the channel. The detector size was approximated as the product of a 2.13 x 2.13 µm² object plane pixel area with a 7x7 speckle contrast kernel, resulting in a 15 x 15 µm² effective collection region. A distribution of dynamic scattering was formed by the normalized number of intra-channel scattering events encountered by each photon reaching the detector (Fig. 4(a)), equivalently the distribution of dynamic scattering pathlengths taken by the detected photons. The average number of dynamic scattering events from the perspective of the camera was quantified as the expectation of this distribution for each channel size. Different intra-channel scattering coefficients were also incorporated to simulate hematocrit variations, while keeping optical properties of static elements (i.e. PDMS) fixed.

3.6 Experiment protocol

A syringe pump provided controlled flow rates, encompassing microcirculatory flow ranges (Fig. 2(d)) observed in mice [22,25,30,36], through microfluidics of 65, 115, and 175 µm feature sizes. Three distinct concentrations of 1 µm polystyrene beads were utilized with the intermediate dilution (µ_s = 25/mm, g = 0.92) having a reduced scattering coefficient comparable to whole blood at the interrogating wavelength (µ_s’ ≈2.0/mm). In addition to blood mimicking scatterers, data using human blood flowing through the 175 µm channel was collected to test hematocrit dependence.

Cranial window implanted mice were anesthetized and affixed to stereotaxic frame at least 24 hours after initial surgery to reduce post-surgical physiological instability. Arterial oxygen saturation and heart-rate from pulse oximetry were recorded and temperature was maintained via feedback. First, speckle contrast imaging was performed, followed by RBC reflectance tracking over multiple regions with the same optical configuration. Best plane of focus was achieved for imaging with both techniques and their respective illumination wavelengths by slight translation of the fixed camera and optical assembly in z-direction between techniques. Variations in depths of field with wavelength were theoretically a maximum of 7 µm between the two techniques. A maximum heart rate variation of 10% was tolerated between the two optical imaging techniques and maintained with pro re nata adjustments to anesthesia in order to prevent drift in cardiac output (e.g. systemic blood flow). Data utilized for speckle imaging and RBC tracking each spanned a period of approximately 1 minute.

All experiments were approved by the Institutional Animal Care and Use Committee (IACUC) at The University of Texas at Austin under guidelines and regulations consistent with the Guide for the Care and Use of Laboratory Animals, the Public Health Service Policy on Humane Care and Use of Laboratory Animals (PHS Policy) and the Animal Welfare Act and Animal Welfare Regulations.

4. Results

We begin with imaging microfluidic flow phantoms for evaluating the scattering regime interpretations of the outputs of the speckle inverse models and then test the revised interpretations on imagery of neurovascular flows in vivo.

4.1 Calibrations in controlled flow microfluidics

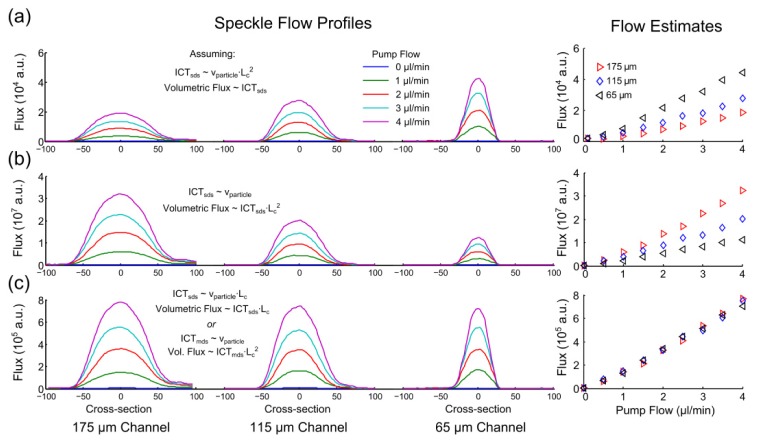
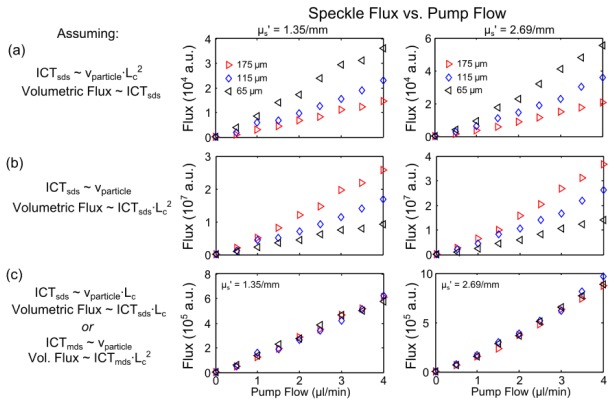
Speckle flow profiles through three channels (65, 115, and 175 µm feature sizes) are compared in Fig. 3(a)-3(c) along with their centerline flow estimates under varying assumptions and interpretations of the inverse correlation times with the physical flow index. A syringe pump conserves flow or volumetric flux through all channels (Fig. 3, x-axis). When inverse correlation times are interpreted as directly proportional to volumetric flux, the resulting speckle predicted flow magnitudes (Fig. 3(a), y-axis) depict a substantial discrepancy across the disparately sized channels.

Fig. 3.

Inverse correlation time (ICT) derived spatial flow profiles (left) and extracted centerline flow magnitudes (right) of volumetric flows as a function of controlled pump flow in three separate channels from Multi-Exposure Speckle Imaging. Single dynamic scattering (SDS) model derived ICTs are assumed proportional to (a) volumetric flux (particle speed - channel area product, p<0.09 ANOVA repeated measures), (b) particle speed alone (p<0.07) and (c) speed-channel feature size product (p>0.95). The multiple dynamic scattering (MDS) interpretation of (c) can be made equivalently by estimating N_d to be proportional to channel feature size L_c (see Tables 1 and 2). Comparisons were made at a fixed µ_s^’ = 2.03 /mm of 1 µm polystyrene beads in water (λ = 660 nm) as well as two other fluid scattering coefficients (Appendix A.1).

Traditionally, speckle visibility expressions have relied on the assumption that inverse correlation times are an estimate of particle speed. Noting that increasingly higher volumetric flows are predicted as the channel size decreases (Fig. 3(a)) also suggests a sensitivity to speed. However, the relative discrepancy in flow magnitudes across channels in Fig. 3(a) remains substantial even after the correlation times are assumed to be approximating the relative particle speeds (Fig. 3(b)). Under this assumption, the ICTs have been scaled by the respective square cross-sections to estimate the conserved pump flows across the channels. Such scaling can overestimate Poiseulle flow magnitudes when channel feature sizes approach the flowing particle sizes [37,38], as with channel feature sizes under 15 µm for 1 µm particles, which is well below the size of the selected channels. Additionally, the observed inter-channel discrepancies in Figs. 3(a)-3(b) are also observed across a wide range of reduced scattering coefficients of flowing particles solutions (Fig. 8, Appendix A.1), encompassing the reduced scattering range (µ_s,blood’ = 1.6-2.1/mm) reported of whole blood [39–41]. Figure 3(c) attempts to rectify the observed inter-channel discrepancy by assuming that ICT is instead proportional to the product of speed and channel feature size, L_c, motivated by the scattering simulations and speckle model revisions to follow.

4.2 Scattering regime simulation

As speckle imaging is reliant on dynamic light scatting, we examine the scattering variations encountered within the disparately sized channels through photon migratory modeling. Square microfluidic channels of three sizes were fabricated and therefore are the geometry utilized for the 3D Monte Carlo simulations. Predictions on the number of scattering events in the microchannels with widefield illumination followed by camera detection with various objective numerical apertures (NA) at a fixed magnification are shown for an interrogating wavelength of 660 nm (Fig. 4(a)). The reduced scattering coefficient of the fluid is approximated to that of whole blood (µ_s’ ≈2.0/mm).

Fig. 4.

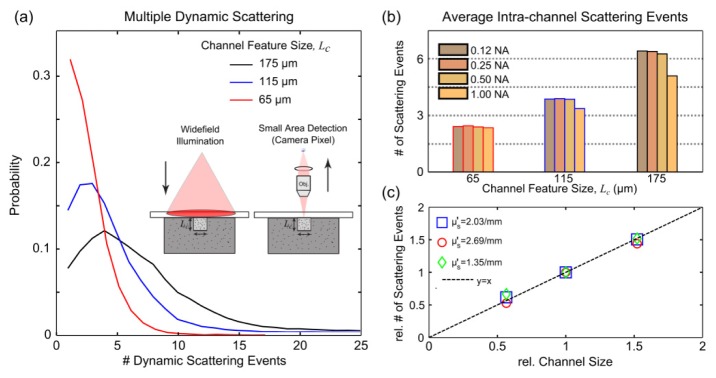
Monte Carlo simulation of scattering within microfluidic flow channels of three feature sizes, L_c, assuming a camera pixel imaging geometry with widefield illumination. (a) Probability of encountering n-number (horizontal axis) of dynamic scattering events in square channels of 65, 115, and 175 µm feature dimension from the perspective of a 15 µm square detector after magnification by a 0.25NA objective. Average number of dynamic scattering events given varying collection numerical apertures (b) and scattering coefficients (Appendix A.1). (c) Observed relative dynamic scattering versus channel size (normalized to 115 µm channel) at varying microsphere scattering coefficients (particle dilutions, Mie theory).

Within the channels, the distribution of intra-channel (e.g. dynamic) scattering events indicates that multiple scattering events are encountered by the light arriving at the detector (Fig. 4(a)). Additionally, as the channel feature size varies so does the distribution of dynamic scattering events (Fig. 4(a)-4(b)). The NA dependence of any single channel shows that the relative degree of dynamic scattering encountered is similar for a particular channel of the selected sizes until an NA of 1.00 where a reduction in observed dynamic scattering is apparent in the larger channels. This reduction is likely attributable to a substantial reduction of the depth of field, resulting in a greater mismatch between the scattering photon paths sampled and the absolute channel size, and may account for the more pronounced reduction in dynamic scattering in the largest channel with increasing NA. For any given NA, the amount of dynamic scattering between channels in particular appears dependent on the feature size (Fig. 4(b)-4(c)).

Additionally, as the reduced scattering coefficient in any given channel increases (Fig. 9, Appendix A.1), the number of scattering events encountered in the photon migration simulation proportionately increase as well. Holding scatterer concentrations fixed, the relative number of scattering events continues to directly scale with the channel feature size with a nearly one-to-one correspondence between the relative measures (Fig. 4(c)). Ultimately, the simulated photon pathlengths and trajectories through the microchannel geometries suggest that remitted photons from the observation point of the imaging detector are i) undergoing a moderate amount of multiple scattering and ii) experiencing scattering that is scaling by the channel or vessel caliber (Fig. 4). While the former is governed by the scattering properties relative to the feature sizes, the latter is likely attributable to the high scattering anisotropy at the interrogating wavelength.

4.3 Revised speckle visibility expression

The expressions in Table 1 attempt to model the decorrelation of the speckles by selecting an appropriate form of the field autocorrelation function, g₁(τ), where q is the difference in wavevectors between the incident and scattered fields, k_o is the wavenumber,$\langle \Delta r^2\left(\tau \right)\rangle$ is the mean squared displacement of scatterers, D_b is the Brownian diffusion coefficient of the scatterers,$\langle V^2\rangle$is the mean squared speed of the scatterers, τ_c is the correlation time of the speckles, and N_d is proportional to the number of dynamic scattering events. Case 1A highlights the most common expression utilized for derivation of speckle visibility expression Eqs. (2) and (4) and has fit the empirical data well. Case 1A-B assume that the interfering fields encountered a single dynamic scattering event, and therefore its inverse correlation times have been interpreted as directly proportional to particle speed. Recognizing that multiple dynamic scattering events are likely occurring for typical in vivo blood flow imaging applications (Section 4.2), selection of the appropriate statistical model for the expected sample dynamics and scattering regime is necessary.

Table 1. Scattering regime and sample dynamics dependent normalized field autocorrelation functions.

Case	Dynamic Scattering regime	g1(τ), backscattering expressions	Sample dynamics (Velocity distribution)	Simplified g1(x), x = τ/ τc and Nd = $\langle S\rangle$/lt	Ref.
1A	Single	${}^{\exp \left[-\frac{1}{6}{q}^2\langle \Delta r^2\left(\tau \right)\rangle \right]}$	Diffusion (Lorentzian) $\Delta r^2\left(\tau \right)=6D_b\tau$	${}^{\exp \left(-x\right)}$	[8,12]
1B	Single	${}^{\exp \left[-\frac{1}{6}{q}^2\langle \Delta r^2\left(\tau \right)\rangle \right]}$	Bulk Flow (Gaussian) $\Delta r^2\left(\tau \right)=\langle V^2\rangle {\tau }^2$	${}^{\exp \left(-x^2\right)}$	[11]
2A	Multiple	$\exp \left[-\sqrt{k_o{}^2\langle \Delta r^2\left(\tau \right)\rangle }\frac{\langle S\rangle }{l_t}\right]$	Diffusion (Lorentzian) $\Delta r^2\left(\tau \right)=6D_b\tau$	${}^{\exp \left(-N_d\sqrt{x}\right)}$	[13,42]
2B	Multiple	$\exp \left[-\sqrt{k_o{}^2\langle \Delta r^2\left(\tau \right)\rangle }\frac{\langle S\rangle }{l_t}\right]$	Bulk Flow (Gaussian) $\Delta r^2\left(\tau \right)=\langle V^2\rangle {\tau }^2$	${}^{\exp \left(-N_{d}x\right)}$	[13,42]

The multiple dynamic scattering approximation of the field autocorrelation function can be derived from modeling correlation transport under diffusive approximations [13,16]. Within dynamic light scattering, diffusive-wave spectroscopy (DWS) is an approach applicable to dense scattering media (e.g multiple scattering) and has been applicable for both particle sizing and motion measurements [13,14,42]. DWS models the total phase change of the field as a summation over successive dynamic scattering events as seen from the perspective of the detector. Therefore, the field autocorrelation function can be expressed for a single photon pathlength, s, and the transport mean free path as,

$$g_1^s(\tau )=\exp \left(-\frac{1}{3}{k}_o^2\hspace{0.17em}\langle \Delta r^2(\tau )\rangle \frac{s}{l_t}\right)$$ (5)

The expectation over all photon pathlengths describes the general DWS formulation of $g_1(\tau )={\displaystyle \int P(s)g_1^s(\tau )ds}$ [13,42–44]. This function highlights that the full distribution of pathlengths, P(s), contributes to g₁(τ), which can be solved for different imaging geometries, particularly with the aid of Monte Carlo simulations [13]. Solutions for a backscattering geometry (Table 1, Case 2A-B) result in notable formulaic differences with single dynamic scattering (SDS) model (Table 1, Case 1A-B). These differences include the power on the mean-squared-displacement,$\langle \Delta r^2\left(\tau \right)\rangle$, and inclusion of an average pathlength factor,$\langle S\rangle$. The average pathlength is of photons undergoing dynamic scattering during their propagation into and out of the tissue. Therefore when normalized by the transport mean free path, l_t, the pathlength factor estimates the average number of dynamic scattering events, N_d = $\langle S\rangle$/l_t. Hence the integral for the expected form of g₁(τ) can be equivalently expressed as a discretized summation over scattering events [43].

In a typical imaging geometry, pixels are largely either sampling scattering from within single microvessels when registered over surface vessels larger than a pixel, or integrating flows from a host of unresolvable depth-distributed microvasculature (i.e. parenchymal perfusion). Given these imaging conditions, the assumption that encountered dynamic scatterers from any given photon path will collectively exhibit Gaussian velocity distributions, akin to bulk flows, is more appropriate than assumptions of Brownian motion [45].

From Table 1, we can re-derive the corresponding speckle visibility expression, K(T, τ_c), for the multiple dynamic scattering and Gaussian velocity distribution. Again, by taking the second moment Eq. (1) of the intensity autocorrelation function, approximated from the normalized field autocorrelation function by the heterodyne mixing Siegert relationship Eq. (3), and equating the square root of the speckle variance with the spatial contrast we arrive at the visibility expression in Table 2. The traditional formulation, assuming single dynamic scattering and a Lorentzian velocity (Brownian kinetics) distribution [20], is presented for comparison as well. The two expressions differ in the added dynamic scattering weighting factor on the ratio of exposure duration and correlation time, x, for the multiple scattering formulation. Particularly, in the limiting case where the number of dynamic scattering events reduces to one (N_d = 1) or is identical for cross-regional comparisons (N_d,i/ N_d,j = 1), the multiple scattering and bulk flow based expression is equivalent to the one assuming single dynamic scattering and Brownian particle kinetics. This limiting case would be appropriate physically, but likely only valid when imaging a single isolated capillary vessel or making comparisons across parenchymal regions or similarly sized vessels.

Table 2. Speckle visibility expressions relating speckle contrast (K) to camera exposure (T), correlation time (τ_c), instrumentation factor (β), fraction of light dynamically scattered (ρ), lumped noise term (ν_noise), and number of dynamic scattering events (N_d) where appropriate.

Scattering regime	Velocity distribution	Speckle Visibility Expression, where x = T/ τc
Single	Lorentzian	$K(T,{\tau }_c)={\left\{\beta {\rho }^2\frac{e^{-2x}-1+2x}{2x^2}+4\beta \rho \left(1-\rho \right)\frac{e^{-x}-1+x}{x^2}+\beta {\left(1-\rho \right)}^2+v_{noise}\right\}}^{1/2}$
Multiple	Gaussian	$K(T,{\tau }_c)={\left\{\beta {\rho }^2\frac{e^{-2N_{d}x}-1+2N_{d}x}{2N_d^2{x}^2}+4\beta \rho \left(1-\rho \right)\frac{e^{-N_{d}x}-1+N_{d}x}{N_d^2{x}^2}+\beta {\left(1-\rho \right)}^2+v_{noise}\right\}}^{1/2}$

The multiple dynamic scattering (and bulk flow) based visibility expression (Table 2) can now be used to estimate the correlation times of flows in the microfluidic channels of varying sizes. From analysis of the photon scattering simulations (Section 4.2), the dynamic scattering factor can be assumed proportional to the channel feature size. The inverse correlation times from the revised model can then be reconciled to estimating particle speed by the inclusion of the dynamic scattering factor to account for the channel dependent variations in encountered dynamic scattering. The conserved volumetric flux across each channel is again estimated by the product of the ICTs and the channel cross-sectional area in Fig. 3(c), similar to Fig. 3(b). However, now an improved correspondence is observed in terms of conservation of estimated flows across the varying sized microfluidic channels (Fig. 3(c)) and at varying dilutions of scatterers (Fig. 8, Appendix A.1). In Fig. 3(c) the feature size was measured in units of pixels. The multiple dynamic scattering (MDS) visibility expression appears to better decouple the ICT proportionality to the average particle speed, as observed by the conservation of flow or flux predicted by speckle imaging across the channels. These results suggest that the number of dynamic scattering events ($N_d=\langle S\rangle /l_t$) for both absolute and relative flow assessments could be approximated by the vessel caliber, where $\langle S\rangle \propto d_{vessel}\to N_d\propto d_{vessel}$. The mean free path (l_t) would be of blood (i.e. intravascular scattering) and assumed relatively invariant.

The similarity in the visibility expressions in Table 2 enables correlation times originally derived with the single (or identical) dynamic scattering visibility expression (${\tau }_c^{sds}$) to be converted to correlation times from the multiple (or variable) dynamic scattering model (i.e.${\tau }_c^{sds}={\tau }_c^{mds}/N_d$) provided that the vascular calibers are known or can be estimated. The improved cross-channel flow correspondence achieved by estimating the dynamic scattering variations (Figs. 3(c) and 8(c), Appendix A.1) suggests potential for robust vascular flow comparisons. However, for in vivo assessments a validation technique was necessary.

4.3 In vivo calibration and assessment

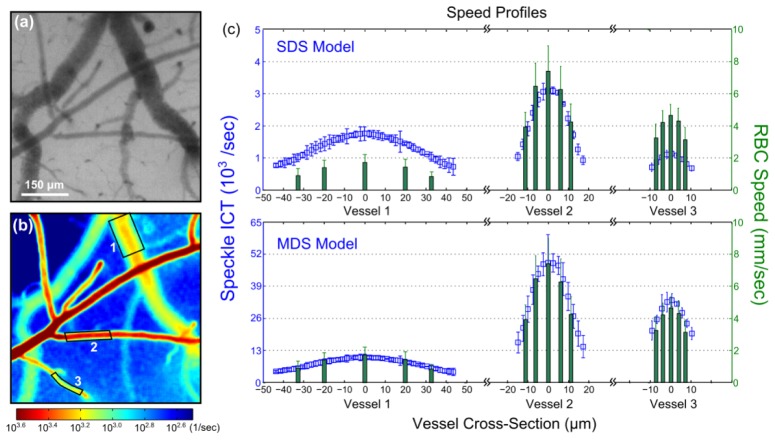
In speckle imaging of the cortical microcirculation, the intravascular multiple scattering effects are examined by relating the ICTs to a measure of erythrocyte velocity. This is performed for resolvable surface vessels (Fig. 5(a)-5(b)) visible in both green reflectance and speckle imagery. High speed reflectance imaging under green light illumination (Figs. 2(c)-2(d) and 5(a)) enabled RBC tracking along the vascular centerlines as well as at ± 25% and ± 10% of each vessel’s radial cross-section about the centerline. In Fig. 5(c), the absolute RBC speed spatial profiles from three vessels are examined against the speckle ICTs using the single (SDS) and multiple dynamic scattering (MDS) models (Table 2), respectively. A comparison of the relative magnitudes of the speed profiles between modalities suggests substantial discrepancies between the ICTs and a consistent estimate of the relative RBC speeds across the three vessels under the SDS model (Eq. (4) and Table 2). Speckle over predicts the speed profile in Vessel 1, slightly under predicts in Vessel 2, and substantially under predicts in Vessel 3.

Fig. 5.

(a) Green LED illuminated reflectance image of the mouse cortex. (b) Speckle inverse correlation time (ICT) map of the cortical perfusion computed indiscriminately at each pixel using the single dynamic scattering MESI visibility expression. (c) Time-averaged RBC speeds from three surface microvessels labeled in (b) at centerline, ± 25% and ± 10% of vessel diameter about the centerline. Also shown are the corresponding temporally and spatially averaged speckle ICT vascular cross-sections over the vessel sections labeled in (b) assuming single or identical dynamic scattering (SDS) indiscriminate of the vessel sizes and alternatively multiple dynamic scattering (MDS) incorporating vessel calibers normalized by transport mean free path of 0.5 mm for blood. Specifically, ICT_mds = ICT_sds / N_d, where N_d = d_vessel / l_t and l_t ≈0.5 mm to retain ICT_mds units of inverse seconds. Errorbars represent mean + std. dev.

Given the observed disparity in vessel calibers, varying degrees of dynamic scattering are likely incorporated in the speckle predicted speeds from each vessel. To estimate the relative number of dynamic scattering events, the dynamic scattering parameter, N_d, from Table 2 was estimated by each vessel’s diameter normalized by an estimate of whole blood’s reduced scattering properties (Fig. 5(c)). Upon multiple scattering correction of the inverse correlation times (ICT_mds = ICT_sds / N_d, Table 2), speckle predicted speed profiles for the three vessels exhibit improved cross-vascular consistency (Fig. 5(c) bottom). Any residual variation in the relative speed profile magnitudes falls within the reported uncertainty of each technique’s measurements. Additionally, this improvement appears to be retained across the entire cross-section of the vessel, suggesting limited intravascular variation in dynamic scattering. Nonetheless, the dynamic scattering corrections necessitated continued examination.

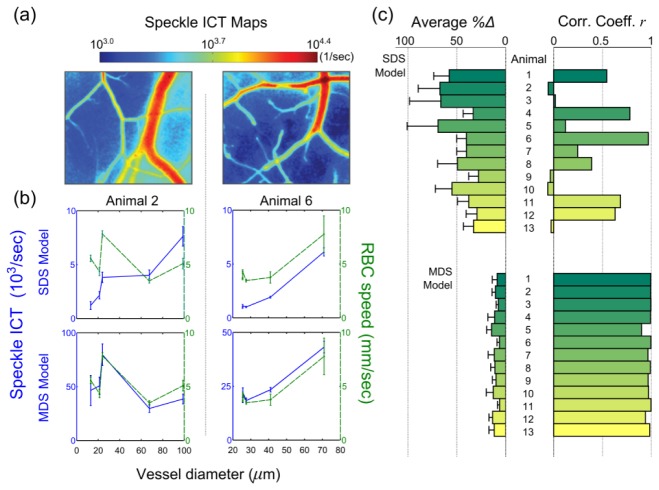
Figure 6(a) depicts the absolute perfusion in terms of the corresponding speckle inverse correlation time maps from two animals, each image employing the traditional SDS model definitions (Eq. (4) and Table 2) at each pixel. Five vessels sampling the range of blood vessel calibers within each animal’s field of view are selected for comparison against time-averaged centerline RBC speeds estimated from high speed reflectance imaging. The selected vessels retained sufficient SNR for RBC tracking and are presented with the single and multiple scattering corrected speckle ICTs sorted by the respective vessel diameters in Fig. 6(b). In Animal 2 there is a both a lack of positive correlation and substantial deviations between the RBC speeds and speckle ICTs from the SDS model. Driving this anti-correlation is the observance of higher RBC speed in a smaller vessel. This particular vessel is a surface supply arteriole, confirmed by direction of flow from RBC tracking, while the larger vessels with lower speeds are draining venules. Alternatively, Animal 6 exhibits strong positive correlation, likely due to the bimodal cluster of similar speeds and a large outlier vessel, but still has substantial deviations with RBC tracking. Employing the dynamic scattering revisions by correction of the speckle ICTs by the vessel diameter factor, as described for Animal 1 in Fig. 5, cross-modality speed estimates in both animals improve in terms of higher correlation and decreasing deviation (Fig. 6(b), MDS model).

Fig. 6.

(a) Speckle inverse correlation time (ICT) maps of the cortical perfusion in two animals computed using the single dynamic scattering MESI visibility expression. (b) Average centerline RBC speeds and average speckle inverse correlation times from individual surface microvessels sorted by vessel diameter assuming single dynamic scattering (ICT_sds, top row, indiscriminate of vessel size) and multiple dynamic scattering regime (ICT_mds, bottom row, incorporating normalized vessel diameters). Lines between measurements have been included to guide the reader. ICT_mds = ICT_sds / N_d (Table 2), where N_d = d_vessel / l_t and l_t ≈0.5 mm. Average percent deviation between normalized MESI ICTs and RBC speeds and correlations coefficients between absolute MESI ICTs and RBC speeds across 5 vessels centerlines (c) and vascular edges (Appendix A.2) from each animal and model. Errorbars represent mean + std. dev.

Percent deviations, each averaged across 5 vessels, and correlation coefficients are presented for all animals in Fig. 6(c). To facilitate calculation of a cross-modality deviation, flow measures were normalized by the average speed or ICT across the selected vasculature in each animal. The first set of metrics (Fig. 6(c), upper set) assume single dynamic scattering (Eq. (4) and Table 2) while the lower set have been re-evaluated for each animal in keeping with the multiple dynamic scattering MESI visibility expression (Table 2). Across all animals, there is an average of 47 ± 15% cross-modality difference between the relative speeds and the SDS model derived ICTs (i.e.${\text{N}}_{\text{d}}=1\hspace{0.17em}or{N}_{d,i}/N_{d,j}=1$) with cross-modality correlations of r = 0.32 ± 0.36 versus deviations of 10 ± 3% and correlations of r = 0.98 ± 0.03 with the MDS model (Table 2, ${\text{N}}_{\text{d}}\propto d_{vessel}$). The units of the revised speckle ICTs can either be arbitrary or remain absolutely in inverse seconds, such as by normalizing the diameters by an estimate of the transport mean free path of blood, as in Figs. 5(c) and 6(b).

Assumptions of more isotropic intravascular dynamic scattering and therefore sensitivity to volumetric flux (${\text{N}}_{\text{d}}\propto d_{vessel}^2$) demonstrated the greatest deviations of 91 +/− 43% (Fig. 10, Appendix A.2) but retained a strong positive correlation (r = 0.91 ± 0.13), highlighting the utility of including a vessel caliber related dynamic scattering factor. Similar vessel caliber dependence was observed for speckle ICTs and RBC speeds measured closer to the vessel walls across all animals, as initially examined in Fig. 5(c) and expanded on in Appendix A.2 (Fig. 11) along with vessel diameter and RBC speed distributions in each animal. Specifically, the SDS model percent deviations slightly improve (Fig. 6(c), Animals 9, 11-13) when vessel diameter distributions are smaller (Fig. 12(a), Appendix A.2). Therefore, the relative multiple scattering weighting factor would be more comparable and equally impactful on the measured correlation times across the selected vasculature. It follows that the observed single dynamic scattering deviations are greatest (Fig. 6(c)) when the vessel diameter spread is widest (Animals 1-3, 5, and 8, Fig. 12(a)). Some comparisons (Fig. 6(c), Animals 4, 6, 11 and 12) retain positive correlation between the SDS model and RBC tracking when the spread in velocity magnitudes were large and uneven (Fig. 12(b)), resulting in comparable flow trends accentuated by the extrema. Finally, RBC speeds are regressed against the ICTs from the MDS (Fig. 7(a)) and SDS (Fig. 7(b)) speckle models across all vasculature and animals (n = 65 vessels). Speckle ICT predictions de-weighted by the vessel diameter dependence (i.e. ICT_mds) exhibit stronger correspondence (r = 0.88 vs. 0.50) than those irrespective (i.e. ICT_sds) of multiple or variable dynamic scattering.

Fig. 7.

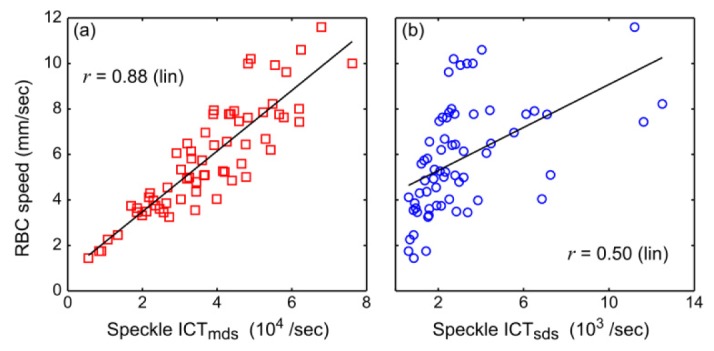
Regression plots with the (a) multiple/variable and (b) single/identical dynamic scattering speckle models. Data is comprised of 65 vessels from a total of 13 animals.

5. Discussion

Direct comparisons of the spatially-integrated speckle flow measures with the absolute erythrocyte speeds would demand spatial decoupling and specificity of the dynamic light scattering technique, which traditionally would comprise an ill-posed inverse problem. However, administration of such analyses was necessary to examine the relationship between the speckle inverse correlation times (ICTs) from selected vascular regions with the magnitude of RBC velocities in order to assess the degree and manner of the spatial integration.

With the reformulation of the speckle visibility expressions under the new assumptions of multiple dynamic scattering and bulk flow distributions, the average percent deviation of intravascular erythrocyte speed estimates reduced to 10 +/− 3% from the 47 +/− 15% achieved with the original assumptions of single dynamic scattering and Brownian motion. Correspondingly, a three-fold improvement in correlation of flow trends between RBC tracking and speckle imaging was observed on average from r = 0.32 ± 0.36 to 0.98 ± 0.03. The improved accuracy is afforded by estimating the variations in intravascular scattering by the channel feature size or vessel caliber.

5.1 Implications for speckle flowmetry

While a multi-exposure implementation was used for greater sensitivity to specimen flows by better sampling flow magnitudes and better decoupling of the motion contributions in the imaged speckles [20,23], single exposure implementations Eq. (2) may be similarly revisited. In fact, the expressions in Table 1 approximate to their single exposure variants in the limit of no static scattering (ρ→1) contributions. A consequence of the multiple scattering re-derivations is the similarity of the new formulation to the prevailing visibility expression (Table 2), which can facilitate computational processing of flow imagery indiscriminately prior to estimating and correcting for multiple scattering effects, as was done routinely in this paper.

If the effects of multiple dynamic scattering are not estimated for single exposure LSCI, a single contrast value, and consequently a single autocorrelation decay time, may be equivalent to multiple flow levels even when the exposure selected is optimal for sensitivity to the sample flow distributions. By extension, in a multiple exposure imaging paradigm a single visibility curve (Fig. 2(b)) and its extracted correlation time may correspond to multiple flow levels if the variations in dynamic scattering are not estimated. LSCI applications that quantify volumetric blood flows in resolvable vasculature by vessel cross-section scaling [46,47] are best served by the multiple scattering corrections posed in this study, as the ICT relationship with particle speed will then be conserved.

In this paper, fields-of-view (FOV) sufficient for rodent cortical imaging were utilized and comprise the higher end of magnification typically used in LSCI applications. Microvessels ranged up to 120 µm in diameter, given the specimen, magnification and selected optics for combined RBC tracking and speckle imaging. As the speckle imaging FOV is scaled larger, i) the spread in resolvable vessel caliber will be extended to include larger microvasculature, while smaller vessels may become less resolvable and ii) the collection optics will ultimately govern the absolute photon paths sampled and degree of spatial integration. Consequently, the relative variation in dynamic scattering encountered by the interfering fields at the camera pixel will scale commensurately and therefore is expected to be more of a concern, especially for comparisons across more disparate vessel sizes with inclusion of larger micro- and macro-vasculature (i.e. diameters above 150 µm). The maximum vessel size that can be interrogated is dependent on the scattering properties and imaging depth and can be estimated through photon migration simulations [19].

5.2 Cross-regional dynamics (spatial comparisons)

Speckle contrast imaging is ideally performed at wavelengths that maximize scattering contributions. The absolute number of dynamic scattering events experienced by detected photons suggests an intermediate scattering regime beyond that of single scattering but below what is typically associated with photon diffusion and has also been noted elsewhere [19]. Nevertheless, variations in dynamic scattering across the imaging field of view are not negligible. Consequently, the manner in which speckle contrast imagery is analyzed, calibrated, and simply interpreted must be revisited. To facilitate analysis, the interpretation of the speckle imagery may be better served by image segmentation into resolvable vascular and parenchymal regions. The physics of parenchymal regions is beyond the empirical scope of this study, as the parenchyma is not avascular but rather highly multi-vascular [2,19]. Therefore the number of dynamic scattering interactions may still be of concern along with spatial integration (i.e. photon paths and their lengths) recorded by a pixel. The geometric correction employed for single vascular flows essentially enable comparisons with similar regions of interest (i.e. other resolvable vasculature).

5.3 Hematocrit variations (scatterer concentration dependence)

Spatial variations in blood hematocrit may also be of concern when comparing flows between vessels. The number of dynamic scattering events will be directly influenced by the resulting variations in the intravascular scattering properties, as per the definitions in Section 4.3. While the hematocrit may vary greatly when comparing capillaries and macro-vasculature, the nearly three-fold range from 15% Hct (capillary) to 42% Hct (systemic) results in a more nominal scattering coefficient variation of 40% [41]. Furthermore, the dynamic scattering corrections identified in this paper are relegated to superficial arterioles and venules, where hematocrit only varies between 36 and 33% (Δµ_s = 4%, Δµ_s^’ = 8%), as observed in rodents [48]. The effects of these variations are examined with hemodilutions of whole human blood in speckle imaging of controlled microfluidic flows (Fig. 13, Appendix A.3). The relative dynamic scattering variations (Table 1) are accounted for in the visibility expression (Table 2) by estimating the different transport mean free paths of whole blood and its saline dilutions, as determined by Meinke et al. [41]. However, regional hematocrit variation cannot be estimated for practical speckle flowmetry and ultimately remains a quantitative limitation dependent on the magnitude of the regional discrepancy.

5.4 Within region comparisons (temporal dynamics)

Building on the slightly better correspondence observed between vessels of similar size without accounting for variations in multiple scattering (Fig. 6 and Appendix A.2), there is the limiting case of following speckle dynamics within the same vessel or region of interest over time. Such measurements would likely not be subject to appreciable variations in dynamic scattering. Hematocrit variations would also be limited and less consequential within the same vasculature over time. Therefore, as long as cross-regional measurements are not of interest, intra-regional dynamics should be well-estimated irrespective of the multiple scattering corrections. In this case, both speckle visibility expressions in Table 2 would be formulaically identical. However, with induced flow alterations (i.e. occlusions, stenosis, constrictions, and dilations) associated with physiological perturbations and disease models, vessel calibers may change routinely, unpredictably and appreciably [22]. In summary, within region temporal comparisons may be accurate as long as lumenal area is conserved, as the degree of dynamic scattering will be similar.

6. Conclusions

Speckle contrast imagery of resolvable vascular perfusion does not appear to be a measure of RBC speed nor volumetric flux in the traditional sense, but rather the product of speed and a uni-dimensional pathlength factor proportional to the vessel diameter. These empirically observed caliber dependent variations agreed well with photon migration modeling, which is a function of the imaging geometry and the sample scattering properties, and were physically rationalized through revised inversion models. Prevalent concerns of the accuracy of speckle flowmetry have been these specific discrepancies in the derivational assumptions with the physical realities of the imaging paradigm and specimen properties [45,49], which are now better conforming.

Appendix A: Explanatory figures and equations

A.1 Dynamic scattering and microfluidic channels

The feature size dependence on speckle inverse correlation times was initially observed with controlled flow microfluidic imaging in Fig. 3 and now further in Fig. 8

Fig. 8.

Speckle predicted flows derived from inverse correlation times (ICT) over typical physiological flow rates. Assumptions of traditional single dynamic scattering ICT proportionality to (a) volumetric flux, (b) particle speed, and (c) speed – channel feature size product are presented over various flowing scatterer dilutions to simulate a large range of reduced scattering inclusive of what is expected for whole blood.

over flowing scatterer concentrations collectively covering reduced scattering (µ_s^’) coefficients of 1.35/mm and 2.69/mm. The reduced scattering coefficient range of whole blood is expected between 1.6-2.1/mm [39–41].

Figure 9

Fig. 9.

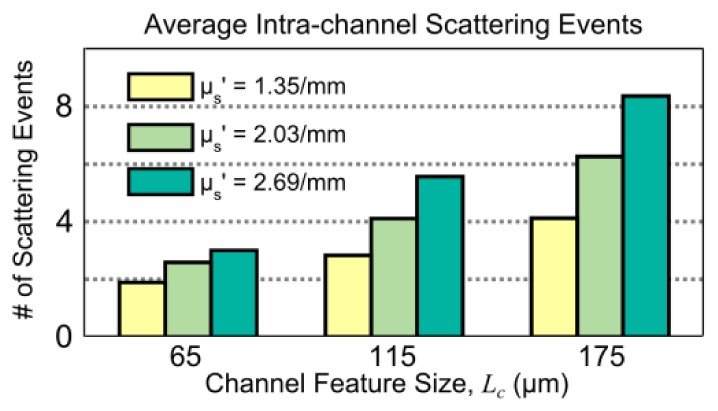
Average number of dynamic scattering events (Monte Carlo simulated) within microfluidic flow channels of three sizes, assuming a camera pixel imaging geometry with widefield illumination. Varying channel feature sizes are simulated along with varying scatterer concentrations of polystyrene microspheres, reported in terms of the respective reduced scattering coefficients from Mie theory.

further highlights the dynamic scattering dependence on channel feature sizes and scatterer concentration simulated from the perspective of the imaging geometry.

A.2 Cross-modality deviations

The cross-modality percent deviation for each vascular region, i, is calculated as follows:

$${\Delta }_i(\%)=\left|\frac{IC{T}_{i,MESI}\frac{1}{5}{\displaystyle \sum _{i=1}^{5}RB{C}_{i,speed}}}{RB{C}_{i,speed}\frac{1}{5}{\displaystyle \sum _{i=1}^{5}IC{T}_{i,MESI}}}-1\right|\times 100$$ (6)

The average percent deviation between MESI inverse correlation times and volumetric flux approximated by the product of the centerline RBC speed (v) and the vessel cross-sectional area $\left(d_{vessel}^2\right)$, each normalized by their means (Eq. (6)), across five vessels in each animal is shown in Fig. 10

Fig. 10.

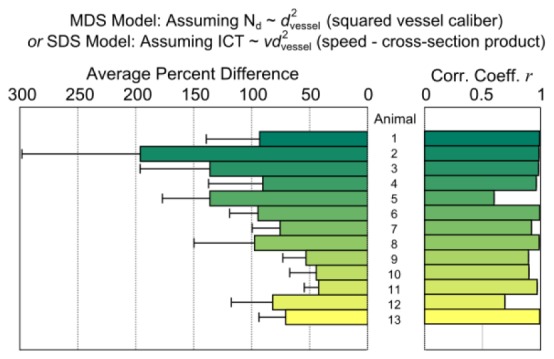
Average percent deviation and correlation between normalized MESI ICTs and cross-sectional area-speed product $\left(v{d}_{vessel}^2\right)$ from each animal, postulating isotropic multiple scattering.

.

Near the vessel edge, the relative percent deviations (Fig. 11

Fig. 11.

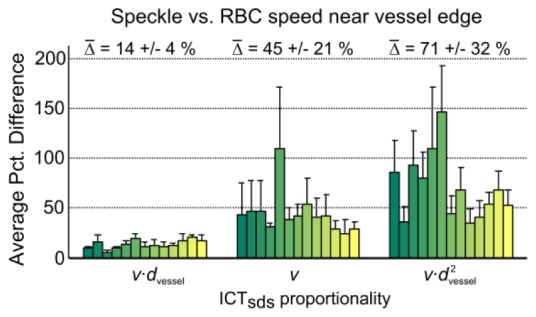
Average percent deviation between single or identical dynamic scattering ICTs and RBC speed (v) - vessel diameter product (d_vessel), RBC speed alone, and RBC speed – vessel cross-section product from 130 comparisons sampled at ± 10% of vessel diameter (about the centerline) away from the vessel edge obtained from 13 animals.

) between MESI inverse correlation times and speed-diameter product ($v{d}_{vessel}^{}$), speed alone ($v$), and volumetric flux ($v{d}_{vessel}^2$) are 14 ± 4% (r = 0.94 ± 0.06), 45 ± 21% (r = 0.50 ± 0.34) and 71 ± 32% (r = 0.83 ± 0.13), respectively, averaged over 2 edges across 5 vessels in each animal totaling 130 measurements.

The distribution of vessel diameters and centerline RBC speeds for each animal are presented in Fig. 12

Fig. 12.

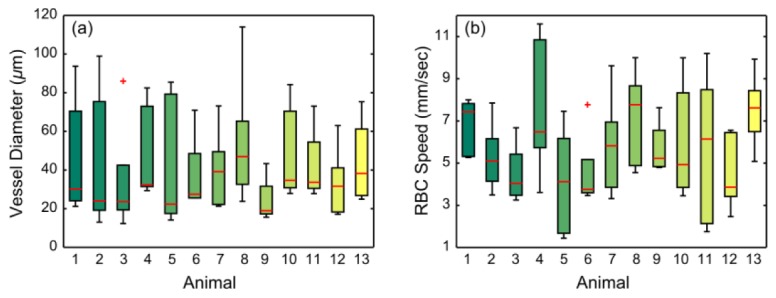
RBC speed (a) and diameter (b) distributions of 5 micro-vessels from each animal. Red central mark is the median, edges of the box are the 25th and 75th percentiles, whiskers extend to the most extreme values, and outlying values are denoted individually with red crosses.

.

A.3 Hematocrit variations

Speckle inverse correlation times assuming single and multiple dynamic scattering using the MESI visibility expressions in Table 2 are shown for microchannel flows of whole blood and two saline dilutions performed in the largest channel (L_c =175 µm) to facilitate blood flow integrity ex vivo.

Fig. 13.

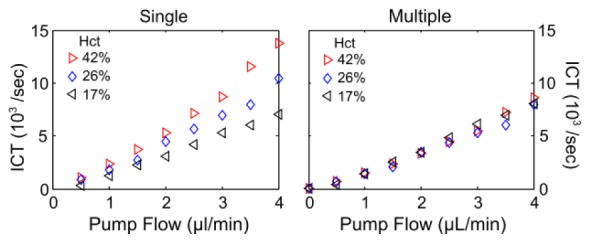
Speckle inverse correlation time (ICT) versus particle speed in L_c = 175 µm channel using the single (p<0.3, ANOVA repeated measures) and multiple (p>0.9, ANOVA repeated measures) dynamic scattering MESI visibility expressions (Table 2). Measurements were made with whole human blood and two dilutions denoted by the respective hematocrits at λ = 660nm. The multiple scattering model incorporates the channel feature size and the varying µ_s’ (from Meinke et al. [41]) for the respective hematocrits and saline dilutions to obtain an estimate of the varying dynamic scattering (N_d = L_c µ_s’).