Abstract
X-ray luminescence computed tomography (XLCT) has become a promising imaging technology for biological application based on phosphor nanoparticles. There are mainly three kinds of XLCT imaging systems: pencil beam XLCT, narrow beam XLCT and cone beam XLCT. Narrow beam XLCT can be regarded as a balance between the pencil beam mode and the cone-beam mode in terms of imaging efficiency and image quality. The collimated X-ray beams are assumed to be parallel ones in the traditional narrow beam XLCT. However, we observe that the cone beam X-rays are collimated into X-ray beams with fan-shaped broadening instead of parallel ones in our prototype narrow beam XLCT. Hence we incorporate the distribution of the X-ray beams in the physical model and collected the optical data from only two perpendicular directions to further speed up the scanning time. Meanwhile we propose a depth related adaptive regularized split Bregman (DARSB) method in reconstruction. The simulation experiments show that the proposed physical model and method can achieve better results in the location error, dice coefficient, mean square error and the intensity error than the traditional split Bregman method and validate the feasibility of method. The phantom experiment can obtain the location error less than 1.1 mm and validate that the incorporation of fan-shaped X-ray beams in our model can achieve better results than the parallel X-rays.
OCIS codes: (110.3010) Image reconstruction techniques, (340.7440) X-ray imaging
1. Introduction
Since the 1970s, the rare earth phosphors, especially the oxysulfide phosphors, due to its advantages such as high luminescence efficiency and innocuity, etc., have caused great attention as the host materials of X-ray phosphors [1]. While radioluminescence of phosphor material has long been used in radiation detectors, the use of nanophosphors in biological contexts is just beginning to be explored [2]. Among these applications, X-ray luminescence computed tomography (XLCT) is one of the newly-developed and most attractive imaging modality, which has been demonstrated by in vitro imaging of nanoparticles in tissue phantoms for oxysulfides (Gd2O2S: Eu) [3]. The combination of insignificant scattering of X-rays in tissues, and the high tissue penetration of near-infrared (NIR) optical photons emitted from appropriate phosphors, opens up the possibility of achieving deep tissue optical imaging in vivo with unprecedented spatial resolution [4]. Meanwhile researchers have synthesized potentially less toxic particles recently [5, 6]. This can overcome the limitation of phosphor nanoparticle synthesis of XLCT molecular probes and further promote its future application.
Based on the promising nanophosphors and its attractive imaging principles, many researchers have studied and developed X-ray luminescence computed tomography (XLCT) these years. To take advantage of linear propagation of the X-rays, Xing et. al. proposed the narrow beam X-ray excitation technology known as XLCT in their papers [7]. Then, Li et. al. used a collimated pencil beam X-ray with a beam size of 1 mm diameter to more selectively excite deep targets [8]. However, since the scanning area of the collimated pencil beam X-ray is smaller than narrow beam XLCT, this technology demands relatively longer scanning time under X-ray exposure which limits its application in biology processes. In order to overcome this issue, a cone beam XLCT imaging system was designed by our group [9] to improve scanning speed, and was applied to small animal experiments by Liu et. al. [10]. Nevertheless, the introduction of cone beam XLCT may cause limited spatial resolution for deep targets due to light scatter, which is similar to fluorescence molecular tomography (FMT) and bioluminescence tomography (BLT) [8]. Wang et. al. also analyzed that the cone beam scanning mode does not sufficiently utilize the primary benefit of XLCT in terms of a reduced permissible source region and presented a fan-beam stimulation scheme for XLCT, which can be regarded as one transformation of narrow beam XLCT [11]. Hence, among these XLCT imaging strategies, narrow beam XLCT can be regarded as an optimal balance between the pencil beam mode and the cone-beam mode in terms of imaging efficiency and image quality.
In the traditional narrow beam XLCT, the collimated X-ray beams are modeled as parallel ones [7]. However, in our prototype narrow beam XLCT system, we observed that the X-rays were collimated into fan-shaped X-ray beams instead of parallel X-rays, which was different from traditional narrow beam XLCT. The description of precise X-rays distribution can contribute to the XLCT imaging quality. Hence we first established the X-ray distribution model through our experiment and applied it in our propagation model. Meanwhile to further speed up the scanning time, we collected the optical data from only two perpendicular directions. In order to recover the distribution of the nanophosphors within such limited information, we also proposed a depth related adaptive regularized split Bregman (DARSB) method to overcome the ill-posedness of our reconstruction problem.
The remaining sections are organized as follows. Section 2 describes the photon propagation model and reconstruction method in our system. In Section 3, the numerical simulation with different phantoms is conducted as well as the phantom experiment. Finally, the conclusion and discussion are given in Section 4.
2. Method
2.1. Imaging System
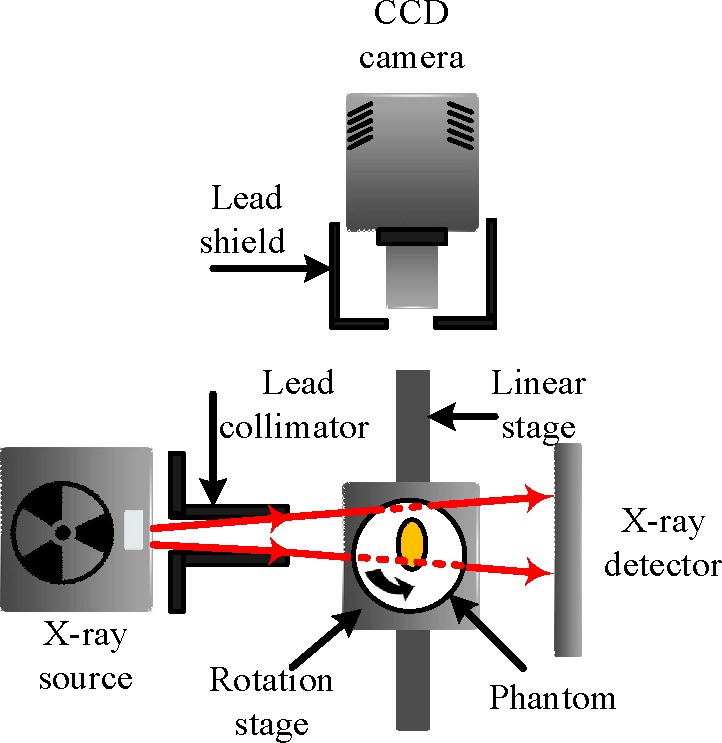
A prototype XLCT system is built in our laboratory with the configuration shown in Fig. 1. The system can perform conventional computed tomography (CT) imaging with a microfocus X-ray source (Apogee, Oxford Instruments, USA) and an X-ray flat panel detector (C7921CA-02, Hamamatsu, Japan). Meanwhile, the X-ray beam is collimated with the X-ray collimator made up of two L-shaped lead shields to excite the nanophosphors. A liquid-cooled back illuminated CCD camera (PIXIS 2048B, Princeton Instruments, USA) with a focus lens (Micro-Nikkor 55 mm f/2.8, Nikon, Japan) is positioned to capture the emitted light for the X-ray luminescence imaging. The phantom is placed on a motorized rotation stage which is mounted on a motorized linear stage to realize the scanning of the object with selectable step interval at selectable directions. A lead made X-ray shield is placed between the camera and the phantom to reduce x-ray radiation on the CCD.
Fig. 1. An overview of the system.
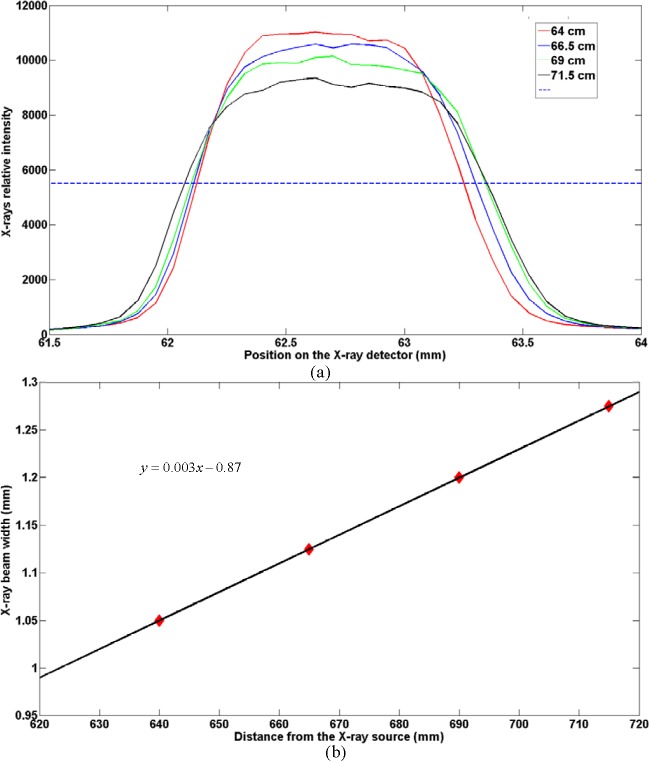
It is necessary to perform a fundamental assessment after building our experiment system. We collect the X-ray data from the X-ray detector with the collimator positioned in front of the X-ray source. First we adjusted the collimator with the motorized linear stage to align the X-ray beam with the X-ray source focus spot, which was realized by comparing the maximum of the X-ray data on the X-ray detector for every movement. Then we adjusted the X-ray detector with different distances from the X-ray source (715 cm, 690 cm, 665 cm, and 640 cm) and obtained corresponding X-ray data. The width of X-ray beam was measured by selecting the full width at half maxima (FWHM) of the average value of the columns in the X-ray data and multiplying the pixel of the detector as shown in Fig. 2(a). The widths of the X-ray were 1.275, 1.2, 1.125, and 1.05 mm at the corresponding position. The experiment shows that the width of the X-ray beam is linearly changing with the position of the detector as shown in Fig. 2(b). It can be concluded that the profile of the X-ray after the collimator is fan-shaped broadening at the plane of the stage. Meanwhile, based on the relationship between the X-ray beam width and the distances from the X-ray source, the X-ray beam was 0.6 mm at the end of the collimator. Based on the X-ray distribution model and the widths of X-ray beams obtained on the X-ray detector, we can calculate the width of the X-ray beam at any distance between the collimator and the X-ray detector, which can be applied to establish the accurate fan-shaped X-ray distribution model in the following photon propagation model.
Fig. 2.
(a)Data analysis of the X-ray detection with different distances from the X-ray source (71.5 cm, 69 cm, 66.5 cm, and 64 cm). (b)Relationship between the X-ray beam width and the distances from the X-ray source
2.2. Photon propagation model
In XLCT imaging process, the imaging model involves the following three steps: First, the X-rays are emitted from the X-ray source and suffer from attenuation through the tissues or the phantoms as follows:
| (1) |
where X0 is the X-ray source intensity with the initial position r0, and µt(τ) is the X-ray attenuation coefficient at position τ; Second, once the nanophosphors are excited by the X-rays, they will emit NIR light, which follows linear relationship with the nanophosphor density and the X-ray intensity as follows:
| (2) |
where S(r) is the light source, X(r) is the X-ray intensity, ρ(r) is the nanophosphor density at position r and ε is the light yield; Last, the NIR light will transport to the surface of the biological tissues and be captured by our CCD camera which can be accurately modeled by the radiative transfer equation (RTE) or diffusion approximation [12] and expressed as:
| (3) |
where r is the position vector, Ω is the domain under consideration, D(r) is the diffusion coefficient, Φ(r) is the photon flux density and S(r) is the source.
Based on the finite element method (FEM), the above model can be converted into the following matrix between the nanophosphor concentration ρ and the NIR measurement Φ, whose details can be found in [9]:
| (4) |
where , . is the system matrix constructed with FEM, ⊛ represents the operation that removes rows in matrix corresponding with the zero-elements in columns vector while is a columns vector composed of zero or unity elements and defined by the specific X-rays distribution as follows:
| (5) |
Our above fundamental assessment convealed that the cone beam X-rays became X-ray beams with fan-shaped broadening after collimation. Based on the X-ray distribution model and the widths of X-ray beams obtained on the X-ray detector, we can establish the accurate fan-shaped distribution model using Eq. (5).
2.3. Reconstruction Method
The solution to the above linear inverse problem in Eq. (4) can be tackled as the recovery of the nanophosphor concentration ρ from the measured luminescent boundary data Φ. The inverse reconstruction problem suffers from ill-posedness because of the high scattering of light in biological tissues, the limited optical measurements and the other experiment conditions. This ill-posed problem can be addressed by means of implicit regularization and skillful iterative methods like the algebraic reconstruction technique [13], unconstrained optimization methods based on l2-regularization [14] or l1-regularization [15] and even lp-regularization [16]. Meanwhile, the priori information such as the permissible region strategy [17] and multispec-tral method [18] are also commonly applied in optical imaging and have also been applied in XLCT [19].
Compared with these advanced methods, the methods based on Bregman iteration transform the optimization problem to an equivalent constrained problem with the concept of Bregman distance [20]. Among these methods, the split Bregman (SB) method addresses the optimization problem by analyzing it into several functions and minimizing them separately on an efficient and simple way [21, 22]. For instance, for l1-constraints such as the total variation (TV), the SB method decouples l1-functionals and l2-functionals, and minimizes them separately, the l2-part by using conventional methods, and the l1-part by straightforward shrinkage formulas [23]. The SB method has been widely applied in image denoising and magnetic resonance imaging [20, 21, 24]. Recently, it has also been extended to the application of fluorescence diffuse optical tomography and bioluminescence tomography [23, 25]. The problem is converted into the following unconstrained optimization problem by the Lagrangian method [26]:
| (6) |
In reconstruction, there are some problems that the reconstructed sources tend to become superficial while the localization errors are increasing particularly for deep sources [27]. Here we fully utilized the X-ray attenuation information as a related depth weighting factor and introduced two auxiliary variables when referring to the variable splitting technique. Hence, we apply the X-ray attenuation information as a related depth weighting factor to modify the l1-norm part of Eq. (6) as follows:
| (7) |
where in which Π is the vector that reflects the corresponding X-ray relative attenuation value at each vertex and ·* represents the product of corresponding elements of the vectors Π and ρ. The corresponding X-ray relative attenuation value at each vertex is estimated by accumulating the attenuation value on the voxel data of CT reconstruction.
Then we decouple it into two subproblems to minimize over ρ with dk fixed and next minimize over d with ρk+1 fixed alternately [28], in which λ and θ are the regularization coefficient and ”splitting” regularization coefficient respectively.
Based on the present SB scheme, we proposed a depth related adaptive regularized split Bregman (DARSB) method to overcome the ill-posedness of the inverse problem in Eq. (4). Meanwhile, our method involves on the adaptive regularization parameter estimation with adjusting it in a closed form in each iteration, where Morozovs discrepancy principle is applied to provide a modular solver to update the nanophosphor density ρ [29].
2.3.1. Deduction of the proposed method
An auxiliary variable x and another auxiliary variable y are applied to represent Aρ and ρ respectively. Then, the Eq. (7) can be transformed into:
| (8) |
With the Bregman function J(ρ, x, y) and the corresponding Bregman distance defined as:
| (9) |
| (10) |
the following iterative framework is deduced based on the SB method and the alternating direction method (ADM) [21, 29]:
| (11) |
| (12) |
| (13) |
| (14) |
Hence, Eq. (7) can be transformed into the problem of tackling the above subproblem (11)–(14) efficiently. The subproblem with respect to ρ is solved by preconditioned conjugate gradient method with the backtracking operation to guarantees the global convergence [30]. Meanwhile we apply the nonnegative constraint with respect to ρ in subproblem (11). Eq. (12) can be solved by shrinkage as follows:
| (15) |
where shrink(ρi, δ) = sign(ρi)max(0, |ρi|δ).
For the minimization problem concerning xk+1, we have to analyze the problem that whether to satisfy the discrepancy principle, which is realized by the following two situations in each iteration [29]:
if , set λk+1 = 0 and xk+1 = Aρk+1 + bk;
if set:
| (16) |
2.3.2. Parameter selection
During the above algorithm, the choice of the noise dependent upper bound c is still undetermined. This parameter can reflect and constrain the error between the actual solution and the reconstructed one to a reasonable level, which is normally proportional to the noise variance and still an open problem [29]. Here we estimate it by referring to the minimum of the iteratively. Meanwhile, we introduce two parameters β1 and β2 when calculating the regularization parameter adaptively. It is obvious that β2 is the weight of the difference between y and ρ while β1 is the weight of the difference between x and Aρ. We set β1 = 1010*SNR × β2, β = 10−3, where the signal-noise ratio (SNR) of the optical signal is obtained by setting the maximum of the local variance as the variance of the signal while the minimum as the variance of the noise [31]. Even though the convergence of the proposed method can be guaranteed by the condition that β1 and β2 > 0 [32], a relatively higher SNR represents the nearer distance between Aρ and ϕ, which results in a relatively larger β1 to control the variable x. All the settings of these parameters are obtained empirically.
2.3.3. Evaluation standard
In order to value our reconstruction results more clearly and further explain the validity of our proposed method, we propose two benchmarks that are regularly applied in optical imaging. The first one is the location error of the Euclidean distance between the actual source position and the reconstructed source position as follows [33]:
| (17) |
where (x, y, z) is the center coordinate of the reconstruction source with the maximum density and (x0, y0, z0) is that of the actual source center.
We also introduce DC (dice coefficient) [34] to compare the similarity of the reconstructed results and the actual source distribution, which is obtained as follows:
| (18) |
where |RS| and |AS| represent the number of tetrahedral-elements in reconstructed results and the actual source correspondingly, while |RS ∩ AS| is the number of tetrahedral-elements shared by reconstructed results and the actual source. The larger value of DC can reflect that the reconstructed results are more similar to the actual source.
To further evaluate the accuracy of the reconstruction, the MSE (mean square errors) is applied in our experiments as follows:
| (19) |
where is the true density while is the reconstructed density on the kth mesh element. N is the number of elements where .
Then the relative intensity error between the actual source and the reconstructed one is applied and defined as [11]:
| (20) |
where is the true density while is the reconstructed density on the kth mesh element respectively, and is the number of elements where . The relative intensity error can accurately reveal the intensity error between the actual source and the reconstructed one in the actual region and can be seen as a combination of the relative error of the power density and the measurement of overlapped region, both of which are used to reflect the real reconstruction performance in [35]. The smaller intensity error can indicate the better quantitative reconstruction results.
3. Experiment
3.1. Simulation study
Based on the above system test, we conducted simulation study and compared our method with the traditional SB method to further validate the feasibility and effectiveness of our proposed method. We used four different cylinder phantoms (phantom A, B, C and D) in the simulation study. The phantom with the size of a 30 mm diameter and 30 mm height contained a small cylinder with a 4 mm diameter and 4 mm height to represent the nanophosphors, whose centers were set to (15, 15, 20) mm, (15, 11.25, 20) mm, (15, 7.5, 20) and (15, 3.75, 20) mm respectively, as shown in Figs 3 (a), (b), (c) and (d). The cylinder phantom was applied to mimic the muscle tissue, whose absorption and reduced scattering coefficients of the phantom were set to 0.013 mm−1 and 0.93 mm−1 respectively [36]. The X-ray attenuation coefficient was set to 0.0475 mm−1 [37]. The light yield ε was set to 0.15 cm3/mg [38].
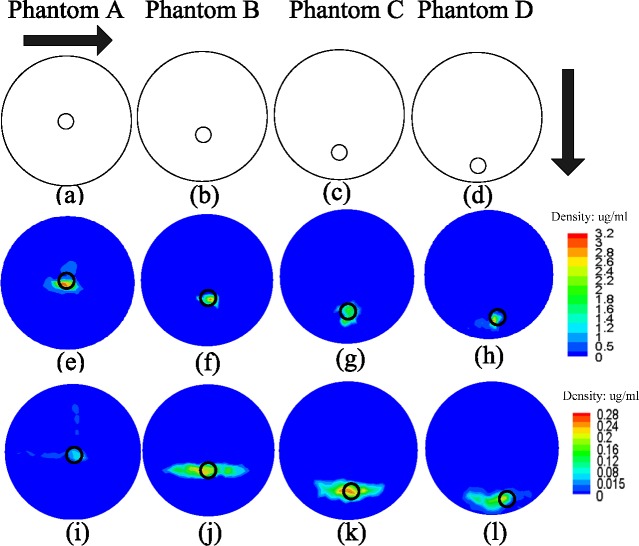
Fig. 3.
Reconstruction results of the two methods. (a), (b), (c) and (d) show the configuration of the phantoms in the slice of z = 20 mm. (e), (f), (g) and (h) show the reconstruction results of the proposed method while (i), (j), (k) and (l) show the reconstruction results of the SB method at the corresponding slice.
We applied the distribution of the X-ray beam in the above X-ray beam assessment as well as the distances of the X-ray source, X-ray detector and the stage to ensure the validity of the simulation. The phantom was supposed to move with step size of the width of the X-ray beam. The simulation data was acquired by employing the light yield ε, the optical parameters, X-ray attenuation coefficient, the discretized information of the phantoms and the system matrix A calculated by the Eq. (4). It is reported that measurements at two orthogonal projections are enough to reconstruct an X-ray luminescence optical tomography (XLOT) image of a single target [39] or even more targets with certain strategy. Hence the simulation was conducted with the assumption of scanning the phantom at two perpendicular directions presented by the black arrows in Fig. 3. During the simulation, we obtained 9 projections by moving the phantom 9 times with the step size of the width of the X-ray beam for each direction. The SB method was applied in the l1-regularized problem of Eq. (6) and the parameters applied in the method are regularization coefficient and “splitting” regularization, which were empirically set as 2×10−2 and 10−6 correspondingly [21].
The reconstruction results were obtained as shown in Fig. 3. Figures 3(a), 3(b), 3(c) and 3(d) show the configuration of the phantoms in the slice of z = 20 mm. Figures 3(e), 3(f), 3(g) and 3(h) show the reconstruction results of the proposed method while Figures 3(i), 3(j), 3(k) and 3(l) show the reconstruction results of the proposed method at the corresponding slice. The location error and the intensity error from both methods were calculated as shown in Table 1. For each phantom, the proposed method has a better performance on location error, DC, MSE and intensity error than SB method. Moreover, the proposed method can better reveal the contour of the nanophorsphors than the traditional split method as shown in Fig. 3, which can be also seen in DC results in Table 1. This is mainly caused by the introduction of the weighting scheme and the adaptive regularization parameter estimation, which overcome the ill-posed problem in the reconstruction. Meanwhile, as shown in Table 1, the reconstruction results including location error, DC, MSE and intensity error become worse when nanophosphors locate deeper in the phantom. This can be explained by the facts that more energy of the X-rays is lost when the depth of the nanophosphors is increasing, which means that less energy of the X-rays is used to excite the nanophosphors.
Table 1. Reconstruction errors of the two methods.
| Proposed method | SB method | |||||||
|---|---|---|---|---|---|---|---|---|
| Location error (mm) | DC | MSE (µg) | Intensity error | Location error (mm) | DC | MSE (µg) | Intensity error | |
| A | 0.37 | 76.36% | 0.17 | 3.90% | 0.97 | 66.64% | 0.17 | 3.92% |
| B | 1.16 | 73.46% | 0.19 | 4.74% | 1.30 | 65.00% | 0.20 | 4.76% |
| C | 1.35 | 72.43% | 0.20 | 5.78% | 1.70 | 64.18% | 0.22 | 5.86% |
| D | 1.57 | 70.37% | 0.21 | 6.71% | 1.64 | 63.64% | 0.24 | 6.92% |
Furthermore, we applied the reconstruction under different noise level to test the robustness of the proposed method. The noise of different levels was added which followed the normal distribution with a mean of 0 and the standard deviation varied from 10% to 40% of the average of the surface measurements with a 10% interval. The reconstruction location errors remain the same under all of the noise levels in each phantom. Meanwhile, there is a little difference in the DC, MSE and intensity error as shown in Table 2. The DC, MSE and intensity errors stay the same level in each phantom, which can indicate that the measurement noise affect the imaging quality with little fluctuation. Hence it can be induced that the proposed method is robust to measurement noise.
Table 2.
Reconstruction errors of the method of different noise levels
| phantom | A | B | C | D | |
|---|---|---|---|---|---|
| DC | 76.26% | 73.26% | 72.03% | 70.17% | |
| 10% | MSE (µg) | 0.17 | 0.19 | 0.20 | 0.21 |
| Intensity error | 3.90% | 4.74% | 5.78% | 6.71% | |
| DC | 75.46% | 72.84% | 71.91% | 69.32% | |
| 20% | MSE (µg) | 0.17 | 0.19 | 0.21 | 0.21 |
| Intensity error | 3.90% | 4.75% | 5.79% | 6.72% | |
| DC | 76.82% | 72.76% | 71.27% | 69.64% | |
| 30% | MSE (µg) | 0.17 | 0.20 | 0.21 | 0.21 |
| Intensity error | 3.91% | 4.75% | 5.80% | 6.81% | |
| DC | 75.76% | 73.07% | 72.13% | 69.77% | |
| 40% | MSE (µg) | 0.18 | 0.20 | 0.21 | 0.22 |
| Intensity error | 3.91% | 4.76% | 5.82% | 6.81% |
3.2. Phantom experiment
Based on the above simulation study, we conducted a physical phantom experiment in our imaging system to further evaluate our proposed imaging strategy. A polyoxymethylene made cylinder phantom with a 20 mm diameter and 20 mm height was applied to mimic biological tissues. The absorption and reduced scattering coefficients of the phantom were set to 0.025 mm−1 and 1.12 mm−1 respectively, which were measured by diffuse optical tomography. The nanophosphors were put into a plastic capillary with a 1 mm radius and 3 mm height, which was embedded in the phantom.
During the experiment, we used the X-ray source to excite the nanophosphors from two perpendicular directions and the CCD camera to collect the luminescent photons emitted from the phantom. The image acquisition system was enclosed in a light-tight environment to avoid the outside light effect. Before the luminescence signal collection, we measured the X-ray beams with the same methods applied in the above imaging system test to obtain the width of the X-ray beam formed by the collimator. The width of the X-ray beam was 0.5 mm at the end of the collimator. During the luminescence signal collection, the phantom was moved with the step size of the X-ray beam. The exposure time was set to 2 s. It only took about 56 s to complete the data collection without considering the time of phantom movement. The fusion images of the collected data from one direction are shown in Fig. 4. Figures 4(a)–4(n) show the fusion images of the phantom when it moves at the direction parallel to the X-ray source. It can be observed that with the movement of the phantom, the collected data have changed obviously. If the center of the nanophosphors was near the X-rays beams, the collected data was becoming larger because more nanophosphors were excited by the X-rays. Then, the computed tomography (CT) projections were first performed (50 kVp, 1.0 mA, 360 views with 1° intervals) and were reconstructed by the filtered back-projection method to get the physical structure and the corresponding X-ray attenuation coefficient of the phantom. The center of the capillary in the phantom was (42.67, 45.81, 21.79) mm, which was obtained from the CT reconstruction results. In the inverse reconstruction, the cylinder phantom was discretized into 56621 tetrahedral-elements and 11009 nodes from the CT results by AMIRA. From the measured data, the distribution of the luminescent sample could be reconstructed by the proposed method.
Fig. 4.
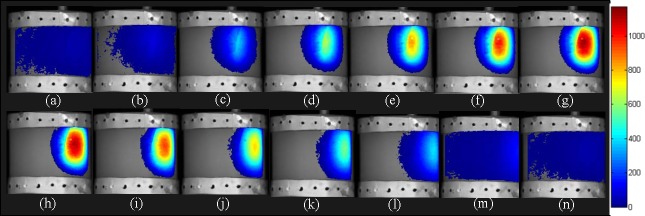
Fusion images of the collected data from one direction. (a)–(n) show the fusion images of the phantom when it moves at the direction parallel to the X-ray source.
In the experiment, in order to further validate the accuracy of the proposed XLCT imaging, we compared the results in which the X-ray beams were approximate as parallel ones. We also compared the results of the proposed method with the traditional SB method. Figure 5 shows the results in the slices of z = 21.79 mm and x = 42. 67 mm respectively represented by red dotted lines shown in Fig. 5(a). Figure 5(a) shows the micro-CT result on the x-z plane. Figures 5(b) and 5(c) show the reconstruction results of the traditional SB method with fan-shaped X-rays model and parallel X-rays model respectively while Figures 5(d) and 5(e) show the results of the proposed method with fan-shaped X-rays model and parallel X-rays model respectively. The reconstruction errors are shown in Table 3. It can be observed that the results of the fan-shaped X-rays model were better than the results of the parallel X-rays model, which means that the model of the accurate attenuation of the X-rays can help improve the reconstruction effectively. Meanwhile, the results from two different methods were consistent with the simulation experiments. The reconstruction results from the proposed method have better performance than SB method in the location error. Moreover, the proposed method can better reveal the contour of the nanophorsphors than the traditional split method as shown in Fig. 5. Moreover, the reconstruction results with the parallel X-rays model are sparser than that with fan-shaped X-rays model as shown in Fig. 5. The parallel X-rays model is less accurate than the fan-shaped X-rays one, and the scanning area is disagree with actual experiment system. This may cause the sparser reconstruction results in the parallel X-rays model.
Fig. 5.

Reconstruction results of the phantom experiments in the slices of z=21.79 mm and x=42. 67 mm respectively represented by red dotted lines. (a) shows the micro-CT result on the x–z plane. (b) and (c) show the reconstruction results of the traditional SB method with fan-shaped X-rays model and parallel X-rays model respectively while (d) and (e) show the results of the proposed method with fan-shaped X-rays model and parallel X-rays model respectively.
Table 3.
Reconstruction errors of the two methods in different models
| Proposed method | SB method | |||
|---|---|---|---|---|
| X-ray | Location error (mm) | DC | Location error (mm) | DC |
| Fan-shaped X-ray | 1.02 | 59.47% | 1.15 | 45.68% |
| Parallel X-ray | 1.26 | 38.02% | 1.67 | 27.52% |
The results show that the distribution of the nanophosphors in the phantom can be revealed by our proposed method in the XLCT imaging system. However, due to the ill-posed problem in the phantom reconstruction and the measurement errors in the process of the data collection, the reconstruction error was slightly bigger than in the simulation experiments, which was normal in the phantom experiment. The light yield ε of the nanophosphors need related information of the X-ray energy, which couldn’t be directly measured in our present system conditions. Hence, the unit of Fig. 5 was ignored and the comparison of quantity results as well as MSE results was not discussed and will be studied in future.
4. Conclusion
In this paper, a narrow beam XLCT imaging modality is proposed, in which the fan-shaped X-rays distribution is modeled and a depth related adaptive regularized split Bregman (DARSB) method is proposed to overcome the ill-posedness of reconstruction. The simulation and phantom experiments were conducted in our imaging system, which could perform conventional CT imaging and X-ray luminescence imaging. The simulation experiments show that the proposed method can achieve better results both in the location error, DC, MSE and the intensity error than the traditional SB method. The simulation experiments showed that our proposed method was stable and robust against different measurement noise levels. The phantom experiment can obtain the location error of 1.02 mm and further validate that the incorporation of fan-shaped X-ray beams in our model can achieve better results than the parallel X-rays.
The cone beam XLCT can be viewed as one of the optical imaging modality such as biolu-minescence tomography (BLT) and fluorescence molecular tomography (FMT), whose reconstruction quality are relatively lower than that of narrow beam XLCT. However, the imaging quality and scanning time of the narrow beam XLCT is closely related to the beam width and sampling [40]. For example, C. M. Carpenter et. al. reported that objects as small as 1 mm in size could be resolved using a 1 mm beam width [40] and that the phantom was translated 26 times in increments of 1 mm and was rotated 24 times to cover 360° [7]. However, the scanning time in our imaging system could be shortened with the relatively larger scanning area of X-rays. Meanwhile, the scanning only performed from two perpendicular directions to accomplish the reconstruction. Even though the scanning time in our phantom experiment was shorter than the cone beam XLCT imaging [9], it cannot indicate that the scanning time in our system is less than the cone beam XLCT because different nanophosphors were applied and the scanning time is related to the size of the object. Nonetheless, compared with the traditional narrow beam XLCT imaging, the scanning time in our proposed imaging modality is greatly decreased. However, the effects of the width of the X-ray beam on the number of projections as well as the results still need further study and research.
There are still several topics that need our further study. First, The spatial resolution along the longitudinal (z axis) direction is not good as that in the transverse plane (x-y plane) as shown in the phantom results. Because the scanning was conducted in the transverse plane, the spatial resolution in the plane can be improved by the fan beam scan. However, we didn’t realize the scanning along the longitudinal direction, which may restrict the improvement along this direction. Hence we will further study how to conduct the scanning along the longitudinal direction and obtain more data from different planes, which is limited by our present experiment conditions. Second, with the development of XLCT imaging, the scanning strategy and reconstruction methods have been proposed in different systems, several of which have already been applied to in vivo small animal imaging [19]. Nevertheless, each system has its own advantages and disadvantages and can be affected by different conditions. The comparison of different scanning strategies and the scopes of application in different systems such as pencil beam XLCT, narrow beam XLCT and cone beam XLCT imaging still need our further research. Thus, we can further develop an optimal XLCT imaging system to achieve good in vivo small animal imaging with the minimum scanning time. Meanwhile, compared with pencil beam XLCT, the scanning time and X-ray dose can be reduced in the cone beam XLCT. The X-ray dose of narrow-beam XLCT may be less than that of pencil beam, more than that of cone beam. However, since we can’t measure the X-ray dose in our present system conditions, we will investigate it in the future.
Acknowledgments
This work was supported by the Program of the National Basic Research and Development Program of China (973) under Grant No. 2011CB707702, the National Natural Science Foundation of China under Grant Nos. 81090272, 81227901 61471279, the National Key Technology Support Program under Grant No. 2012BAI23B06, the Beijing Municipal Natural Science Foundation under Grant No. 7142012 and the Fundamental Research Funds for the Central Universities.
References and links
- 1.Ying T., He C. W., Xian L. X., Yao F., “Preparation and luminescence property of Gd2O2S: Tb X-ray nano-phosphors using the complex precipitation method,” J. Alloys Compd. 433(1), 313–317 (2007). 10.1016/j.jallcom.2006.06.075 [DOI] [Google Scholar]
- 2.Jie S., Dong S. L., Hua Y. C., “Luminescent rare earth nanomaterials for bioprobe applications,” Dalton Trans. 42,5687–5697 (2008). [DOI] [PubMed] [Google Scholar]
- 3.Chen H., Moore T., Qi B., Colvin D. C., Jelen E. K., Hitchcock D. A., He J., Mefford O. T., Gore J. C., Alexis F., Anker J. N., “Monitoring ph-triggered drug release from radioluminescent nanocapsules with x-ray excited optical luminescence,” ACS nano 7(2), 1178–1187 (2013). 10.1021/nn304369m [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sudheendra L., Das G. K., Li C., Stark D., Cena J., Cherry S., Kennedy I. M., “Nagdf4: Eu3+ nanoparticles for enhanced x-ray excited optical imaging,” Chem. Mater. 26(5), 1881–1888 (2014). 10.1021/cm404044n [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wang C., Volotskova O., Lu K., Ahmad M., Sun C., Xing L., Lin W., “Synergistic assembly of heavy metal clusters and luminescent organic bridging ligands in metalCorganic frameworks for highly efficient x-ray scintillation,” J. Am. Chem. Soc. 136(17), 6171–6174 (2014). 10.1021/ja500671h [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Osakada Y., Pratx G., Sun C., Sakamoto M., Ahmad M., Volotskova O., Ong Q., Teranishi T., Harada Y., Xing L., Cui B., “Hard x-ray-induced optical luminescence via biomolecule-directed metal clusters,” Chem. Commun. 50(27), 3549–3551 (2014). 10.1039/c3cc48661c [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pratx G., Carpenter C. M., Sun C., Rao R. P., Xing L., “Tomographic molecular imaging of x-ray-excitable nanoparticles,” Opt. Lett. 35(20), 3345–3347 (2010). 10.1364/OL.35.003345 [DOI] [PubMed] [Google Scholar]
- 8.Li C., Di K., Bec J., Cherry S. R., “X-ray luminescence optical tomography imaging: experimental studies,” Opt. Lett. 38(13), 2339–2341 (2013). 10.1364/OL.38.002339 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chen D., Zhu S., Yi H., Zhang X., Chen D., Liang J., Tian J., “Cone beam x-ray luminescence computed tomography: A feasibility study,” Med. Phys. 40(3), 031111 (2013). 10.1118/1.4790694 [DOI] [PubMed] [Google Scholar]
- 10.Liu X., Liao Q., Wang H., “Fast x-ray luminescence computed tomography imaging,” IEEE Trans. Biomed. Eng. 61(6), 1621–1627 (2014). 10.1109/TBME.2013.2294633 [DOI] [PubMed] [Google Scholar]
- 11.Cong W., Wang C., Wang G., “Stored luminescence computed tomography,” Appl. Opt. 53(25), 5672–5676 (2014). 10.1364/AO.53.005672 [DOI] [PubMed] [Google Scholar]
- 12.Klose A. D., Ntziachristos V., Hielscher A. H., “The inverse source problem based on the radiative transfer equation in optical molecular imaging,” J. Comput. Phys. 202(1), 323–345 (2005). 10.1016/j.jcp.2004.07.008 [DOI] [Google Scholar]
- 13.Soubret A., Ripoll J., Ntziachristos V., “Accuracy of fluorescent tomography in the presence of hetero-geneities: study of the normalized born ratio,” IEEE Trans. Medical Imaging 24(10), 1377–1386 (2005). 10.1109/TMI.2005.857213 [DOI] [PubMed] [Google Scholar]
- 14.Hyde D., Schulz R., Brooks D., Miller E., Ntziachristos V., “Performance dependence of hybrid x-ray computed tomography/fluorescence molecular tomography on the optical forward problem,” J. Opt. Soc. Am. A 26(4), 919–923 (2009). 10.1364/JOSAA.26.000919 [DOI] [PubMed] [Google Scholar]
- 15.Yi H., Chen D., Li W., Zhu S., Wang X., Liang J., Tian J., “Reconstruction algorithms based on l1-norm and l2-norm for two imaging models of fluorescence molecular tomography: a comparative study,” J. Biomed. Opt. 18(5), 056013 (2013). 10.1117/1.JBO.18.5.056013 [DOI] [PubMed] [Google Scholar]
- 16.Zhang Q., Qu X., Chen D., Chen X., Liang J., Tian J., “Experimental three-dimensional bioluminescence tomography reconstruction using the lp regularization,” Adv. Sci. Lett. 16(1), 125–129 (2012). 10.1166/asl.2012.3265 [DOI] [Google Scholar]
- 17.Lin Y., Barber W. C., Iwanczyk J. S., Roeck W., Nalcioglu O., Gulsen G., “Quantitative fluorescence tomography using a combined tri-modality ft/dot/xct system,” Opt. Express 18(8), 7835–7850 (2010). 10.1364/OE.18.007835 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Feng J., Jia K., Yan G., Zhu S., Qin C., Lv Y., Tian J., “An optimal permissible source region strategy for multispectral bioluminescence tomography,” Opt. Express 16(20), 15640–15654 (2008). 10.1364/OE.16.015640 [DOI] [PubMed] [Google Scholar]
- 19.Chen D., Zhu S., Chen X., Chao T., Cao X., Zhao F., Huang L., Liang J., “Quantitative cone beam x-ray luminescence tomography/x-ray computed tomography imaging,” Appl. Phys. Lett. 105(19), 191104 (2014). 10.1063/1.4901436 [DOI] [Google Scholar]
- 20.Osher S., Burger M., Goldfarb D., Xu J., Yin W., “An iterative regularization method for total variation-based image restoration,” Multiscale Model. Sim. 4(2), 460–489 (2005). 10.1137/040605412 [DOI] [Google Scholar]
- 21.Goldstein T., Osher S., “The split bregman method for l1-regularized problems,” SIAM J. Imaging Sci. 2(2), 323–343 (2009). 10.1137/080725891 [DOI] [Google Scholar]
- 22.Yin W., Osher S., Goldfarb D., Darbon J., “Bregman iterative algorithms for l1-minimization with applications to compressed sensing,” SIAM J. Imaging Sci. 1(1), 143–168 (2008). 10.1137/070703983 [DOI] [Google Scholar]
- 23.Abascal J. J., Chamorro-Servent J., Aguirre J., Arridge S., Correia T., Ripoll J., Vaquero J. J., Desco M., “Fluorescence diffuse optical tomography using the split bregman method,” Med. Phys. 38(11), 6275–6284 (2011). 10.1118/1.3656063 [DOI] [PubMed] [Google Scholar]
- 24.Liu B., Zou Y. M., Ying L., “Sparsesense: application of compressed sensing in parallel mri,” in Information Technology and Applications in Biomedicine, 2008. ITAB 2008. International Conference on, (IEEE,), pp. 127–130. [Google Scholar]
- 25.Feng J., Qin C., Jia K., Zhu S., Liu K., Han D., Yang X., Gao Q., Tian J., “Total variation regularization for bioluminescence tomography with the split bregman method,” Appl. Opt. 51(19), 4501–4512 (2012). 10.1364/AO.51.004501 [DOI] [PubMed] [Google Scholar]
- 26.Yang A. Y., Sastry S. S., Ganesh A., Ma Y., “Fast l1-minimization algorithms and an application in robust face recognition: A review,” in Image Processing (ICIP), 2010 17th IEEE International Conference on, (IEEE, 2010), pp. 1849–1852. [Google Scholar]
- 27.Ahn S., Chaudhari A. J., Darvas F., Bouman C. A., Leahy R. M., “Fast iterative image reconstruction methods for fully 3d multispectral bioluminescence tomography,” Phys. Med. Biol. 53(14), 3921 (2008). 10.1088/0031-9155/53/14/013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gilles J., The Bregman Cookbook (2011).
- 29.He C., Hu C., Zhang W., Shi B., Hu X., “Fast total-variation image deconvolution with adaptive parameter estimation via split bregman method,” Math. Probl. Eng. 2014, 617026 (2014). 10.1155/2014/617026 [DOI] [Google Scholar]
- 30.Eisenstat S. C., Walker H. F., “Globally convergent inexact newton methods,” SIAM Journal on Optimization 4(2), 393–422 (1994). 10.1137/0804022 [DOI] [Google Scholar]
- 31.Zhang N., Deng Z.-S., Wang F., Wang X.-Y., “The effect of different number of diffusion gradients on snr of diffusion tensor-derived measurement maps,” J. Biomed. Sci. Eng. 2(2), 96 (2009). 10.4236/jbise.2009.22018 [DOI] [Google Scholar]
- 32.Eckstein J., Bertsekas D. P., On the douglas rachford splitting method and the proximal point algorithm for maximal monotone operators, Math. Program. 55, 293–318 (1992). 10.1007/BF01581204 [DOI] [Google Scholar]
- 33.Zhang B., Yang X., Qin C., Liu D., Zhu S., Feng J., Sun L., Liu K., Han D., Ma X., Zhang X., Zhong J., Li X., Yang X., Tian J., “A trust region method in adaptive finite element framework for bioluminescence tomography,” Opt. Express 18(7), 6477–6491 (2010). 10.1364/OE.18.006477 [DOI] [PubMed] [Google Scholar]
- 34.Dice L. R., “Measures of the amount of ecologic association between species,” Ecology 26(3), 297–302 (1945). 10.2307/1932409 [DOI] [Google Scholar]
- 35.Zhang J., Chen D., Liang J., Xue H., Lei J., Wang Q., Chen D., Meng M., Jin Z., Tian J., “Incorporating mri structural information into bioluminescence tomography: system, heterogeneous reconstruction and in vivo quantification,” Biomed. Opt. Express 5(6), 1861–1876 (2014). 10.1364/BOE.5.001861 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Song X., Wang D., Chen N., Bai J., Wang H., “Reconstruction for free-space fluorescence tomography using a novel hybrid adaptive finite element algorithm,” Opt. Express 15(26), 18300–18317 (2007). 10.1364/OE.15.018300 [DOI] [PubMed] [Google Scholar]
- 37.Dogdas B., Stout D., Chatziioannou A. F., Leahy R. M., “Digimouse: a 3d whole body mouse atlas from ct and cryosection data,” Phy. Med. Biol. 52(3), 577 (2007). 10.1088/0031-9155/52/3/003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Cong W., Shen H., Wang G., “Spectrally resolving and scattering-compensated x-ray luminescence/fluorescence computed tomography,” J. Biomed. Opt. 16(6), 066014 (2011). 10.1117/1.3592499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Li C., Davalos A. M., Cherry S. R., “Numerical and experimental studies of x-ray luminescence optical tomography for small animal imaging,” in SPIE BiOS, (International Society for Optics and Photonics, 2013), pp. 85781B. [Google Scholar]
- 40.Carpenter C., Pratx G., Sun C., Xing L., “Limited-angle x-ray luminescence tomography: methodology and feasibility study,” Phys. Med. Biol. 56(12), 3487 (2011). 10.1088/0031-9155/56/12/003 [DOI] [PMC free article] [PubMed] [Google Scholar]