Non-contact scanning diffuse correlation tomography system for three-dimensional blood flow imaging in a murine bone graft model

Abstract

A non-contact galvanometer-based optical scanning system for diffuse correlation tomography was developed for monitoring bone graft healing in a murine femur model. A linear image reconstruction algorithm for diffuse correlation tomography was tested using finite-element method based simulated data and experimental data from a femur or a tube suspended in a homogeneous liquid phantom. Finally, the non-contact system was utilized to monitor in vivo blood flow changes prior to and one week after bone graft transplantation within murine femurs. Localized blood flow changes were observed in three mice, demonstrating a potential for quantification of longitudinal blood flow associated with bone graft healing.

1. Introduction

Annually over 500,000 and 2.2 million bone graft procedures are performed in the United States and worldwide, respectively [1, 2]. Although transplantation of autologous bone grafts (i.e., autografts), isolated from non-load-bearing regions of the skeleton, offer excellent healing, tissue volume is limited by donor site morbidity. Therefore, for critical-sized bone defects requiring large tissue volumes, the current clinical gold standard involves the use of processed cadaveric allografts [1]. Allografts, however, result in 60% 10-year post-implantation failure rates due to poor integration and remodeling into host tissue, which is due in part to poor vascularization [3–5].

Blood flow is important for multiple phases in bone healing since blood vessels deliver oxygen, nutrients, growth factors, and circulating cells to the graft sites [6]. However, skeletal blood flow has not been widely studied due to limitations with existing techniques. Labeled microsphere administration is generally considered the gold standard technique for blood flow quantification, but is regarded as experimentally difficult and requires sacrifice of animals [6]. Laser Doppler imaging is a non-invasive technique to measure two-dimensional blood flow, but is limited due to shallow penetration depths [7]. Positron emission tomography is another in vivo imaging technique that provides a three-dimensional map of absolute flow rates, but is expensive and subject to the availability of radioisotopes (e.g., ¹⁵O water) [8, 9]. Doppler ultrasound is limited in quantifying blood flow velocity of blood vessels smaller than 100 ~200 μm [10–12]. Furthermore, measurement of skeletal blood flow by Doppler ultrasound is not feasible because the bone acts as an acoustic barrier [13].

Diffuse correlation spectroscopy (DCS) and tomography (DCT) are deep-tissue, non-invasive techniques that quantify microvascular blood flow [14]. They are suitable for longitudinal monitoring studies since they do not use ionizing radiation or contrast agents and are inexpensive to implement. DCS, which quantifies bulk blood flow with the simplified assumption of homogeneous media, has been applied to tumors, brain and skeletal muscle in animals and humans in vivo [15–21]. Furthermore, it has been validated by comparison with laser Doppler flowmetry [22, 23], Doppler ultrasound [17, 24–27], arterial-spin labeled magnetic resonance imaging [28–31], xenon computed tomography (CT) [32], and fluorescent microsphere measurements [20]. DCT, which provides three-dimensional blood flow images, has been limited to applications in rat brain [33, 34], due in part to the difficulties of obtaining large spatial data sets necessary for reliable image reconstruction and good signal-to-noise ratios.

In this study, we developed a non-contact system to provide DCT of murine femurs, towards the goal of monitoring temporal and spatial blood flow changes during bone graft healing. Several types of non-contact DCS or DCT systems have been developed and utilized by others [33–36]. One type projected an image of a fixed distribution of source and detector fibers onto the tissue surface through a conventional camera with crossed polarizers for rat brains and murine tumors [17, 33, 34]. Another type featured the separation of optical paths between sources and detectors for larger source-detector separations suitable for human tissue applications [35] and its extension to collect large spatial data sets using a linear motorized stage [36]. Our approach is unique in that it utilizes galvanometer-based optical scanning which enables collection of large spatial data sets for preclinical applications, it is easily incorporated into the existing DCS system, and it is flexible in that the source-detector separations and spatial scanning parameters are easily modifiable. Moreover, we have optimized the DCT experimental setup and image reconstruction algorithms for small animal leg imaging.

The paper is structured as follows: In Section 2, methods regarding the instrumentations, basic theory of DCS and DCT, comparison between a contact and a non-contact system, generation of simulated data sets from heterogeneous flow distribution, measurements of tissue phantoms made with a murine femur or a tube, and in vivo measurements on murine legs before and after allograft surgery are presented. In Section 3, we show the equivalent performance between a contact and a non-contact system, reconstruction results using simulated data, depth-resolved 3D DCT images of tissue phantoms, and in vivo temporal and spatial blood flow changes in murine allografts. A discussion of the results is presented in Section 4.

2. Methods

2.1 Diffuse correlation instrument

The diffuse correlation instrument generally consists of a light source, multiple photon-counting detectors and a correlator (Fig. 1(a)). A continuous-wave, long-coherence-length (> 5m) diode laser working at 785 nm (DL785-120-SO, Crystal Laser, Reno, NV) is utilized as a light source. A contact probe containing optical fibers is placed in contact with the in vivo tissue of interest. Multi-mode fibers deliver near-infrared photons from the light source to the tissue. Photons propagated through tissue are collected from the tissue surface at different source-detector separations with single-mode fibers. Signals from each source-detector separation are detected by four photon-counting avalanche photodiodes (SPCM-AQ4C, Excelitas Technologies, Waltham, MA) and relayed to a 4-channel correlator board (Correlator.com, Bridgewater, NJ), which outputs the intensity temporal auto-correlation function_{$g_{\text{2}}$}.

Fig. 1.

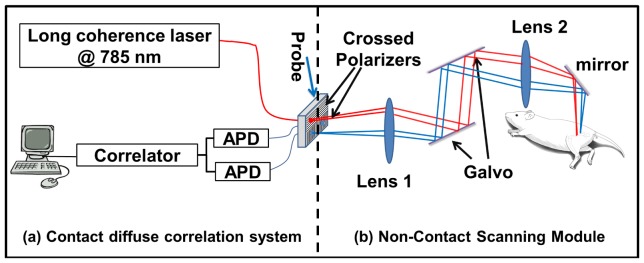
Setup of a non-contact scanning system. (a) The instrumentation for a contact diffuse correlation system includes a long coherence-length laser, a probe, two avalanche photodiodes (APDs) and a correlator. (b) The scanning module for non-contact detection interfaces with the diffuse correlation system via crossed polarizers placed at the probe surface. Two lenses are utilized to image the probe onto the detection plane with 1:1 magnification and a dual-axis scanning mirror galvanometer (galvo) system scans the probe position over the imaging plane.

2.2 Non-contact scanning module

To reconstruct three-dimensional blood flow images, diffuse correlation measurements at multiple source-detector combinations covering a large field of view are required. A non-contact scanning module that provides a large field of view, high positional accuracy, versatility of source-detector separation choices, and easy incorporation into an existing instrument is developed as an additional component added after the probe (Fig. 1(b)). Two identical lenses (LBF254-100-B, focal length f = 100 mm, Thorlabs, Newton, NJ) were utilized to image the probe onto the scanning plane. The lens placed near the probe collimated light from the multi-mode fiber and the second lens focused the collimated beam onto the scanning plane. A dual-axis scanning mirror galvanometer system (GVS012, Thorlabs, Newton, NJ) placed between the two lenses was used to redirect the collimated beam so that the probe could be imaged at different positions in the scanning plane. To minimize direct reflection from the scanning surface, crossed polarizers (APIR29-020, American Polarizers, Inc., Reading, PA) were placed before the source and detectors. Since the polarization of directly reflected light was set by the first polarizer, yet that of diffused light was randomized, the crossed polarizers greatly suppressed direct reflection while letting enough diffused signal pass. This scanning system had a capability to scan over an area of 30 mm x 30 mm with spatial resolution of 0.02 mm. The scanning system has no magnification (1:1), thus the source-detector separations were determined by those in the probe and could be easily modified for different applications. For this application, we utilized 3.0 mm and 4.2 mm source-detector separations.

2.3 Correlation diffusion equation

In dynamic light scattering, electric field auto-correlation function is defined as G₁(r,τ) ≡ <E*(r,t)·E(r,t + τ)>, where E(r,t) is the electric field at position r and time t, τ is the delay time, _* denotes complex conjugate and < > denotes integration over t. In highly scattering media (e.g., tissue) the propagation of G₁ can be described by the correlation diffusion equation, as follows [37],

$$\nabla ·\left(D\left(r\right)\nabla G_1\left(r,\tau \right)\right)-\left(v{\mu }_a\left(r\right)+\frac{1}{3}v{\mu }_s{}^{\prime }\left(r\right){\kappa }_0^2\alpha \langle \Delta r^2\left(r,\tau \right)\rangle \right)G_1\left(r,\tau \right)=-vS{\delta }^3\left(r-r_s\right).$$ (1)

G₁ is a function of both spatial position r and delay time τ. In this equation, μ_a and μ_s′ are the absorption and reduced scattering coefficient of the medium respectively, ν is the speed of light in the medium, D ≡ ν/(3(μ_a + μ_s′ )) is the photon diffusion coefficient, κ₀ = 2π/λ is the wave vector of the photon where λ is the wavelength in the tissue, α is the fraction of moving scatterers and <Δr²(r,τ)> is the mean–squared displacement of scatterers, Sδ³(r-r_s) is a point source located at r_s with the source strength S.

For geometries with simple boundary conditions such as infinite or semi-infinite geometries, the analytical solutions have been derived [14]. The following is the analytic solution for the semi-infinite geometry:

$$\begin{array}{l}{G}_1\left(\mathbf{r},\tau \right)=\frac{vS}{4\pi D}\left[\frac{\exp \left(-K\left(\tau \right)r_1\right)}{r_1}-\frac{\exp \left(-K\left(\tau \right)r_b\right)}{r_b}\right],\\ \text{where}K(\tau )=\sqrt{\left({\mu }_a+\frac{1}{3}{{\mu }_s}^{\prime }{\kappa }_0^2\alpha \langle \Delta r^2\left(r,\tau \right)\rangle \right)v/D},\\ r_1=\left|r-r_s+z_{tr}\hat{\mathbf{n}}\right|\\ r_b=\left|r-r_s-\left(z_{tr}+2z_b\right)\hat{\mathbf{n}}\right|,\end{array}$$ (2)

In Eq. (2), $\hat{\mathbf{n}}$ is the unit vector pointing away from the turbid media boundary, z_tr ≡ 1/ (μ_a + μ_s′) is the depth where the source is considered isotropic, z_b = 2(1 + R_eff) / [3μ_s′ (1-R_eff)] is the extrapolation distance from the boundary, R_eff ≈-1.440n⁻² + 0.710n⁻¹ + 0.668 + 0.0636n is the effective reflection coefficient to account for the index mismatch between the tissue and air boundary and n is the refraction index of the tissue. <Δr²> can be expressed into different forms based on the flow model used: for the case of random flow model, <Δr²> = <V ²> τ², where <V ²> is the second moment of flow distribution. In the case of diffusive motion, such as Brownian motion, <Δr²> = 6D_bτ, where D_b is the Brownian diffusion coefficient. In practice, the Brownian motion model fits the observed auto-correlation decay of in vivo measurement better than random flow motion [14]. Here, the Brownian motion model is assumed and αD_b is referred to as the dynamic parameter of the medium that represents flow. For more complex geometries, numerical methods such as finite difference method (FDM) or finite element method (FEM) are usually utilized to solve the equation for G₁.

As is pointed out in the Section 2.1, the instrument provides measurements of the normalized intensity auto-correlation function g₂(τ); g₂(τ) ≡ <I(t)·I(t + τ)>/<I(t)>² where I(t) = |E(r,t)|². The connection between the electric field auto-correlation and the intensity auto-correlation functions is provided by Siegert relation [38],

$$g_2\left(\tau \right)=1+\beta {\left|g_1\left(\tau \right)\right|}^2$$ (3)

where the normalized electric field temporal auto-correlation, g₁(τ) ≡ G₁(r,τ)/ G₁(r,0), can be calculated from experimental data g₂. In Eq. (3), β is a parameter primarily determined by the optical setup of the system, and is inversely proportional to the number of speckles in the detection area. For a contact system with a single mode fiber, β ≈ 0.5 as there are two independent linear polarization modes of speckle. For the proposed non-contact system, β ≈ 1.0 because the polarizers only allow one linearly polarized mode to pass.

2.4 Diffuse correlation tomography

With the diffusion correlation equation, the normalized temporal auto-correlation function g₁ can be calculated if the flow, αD_b, is known. In practice, however, g₁ can be obtained from diffuse correlation measurement of g₂, while the flow distribution is unknown. The goal is to reconstruct the unknown distribution of flow based on the experimentally measured g₁ (i.e., solve the inverse problem).

To solve the inverse problem, each experimentally measured temporal auto-correlation function is divided into two parts, i.e., the contribution from homogeneous background and the perturbation from heterogeneity in flow, using a perturbation method. In this paper, the Rytov approximation was used to expand the temporal auto-correlation as g₁(r_s,r_d,τ) = g_1,0(r_s,r_d,τ)exp(ϕ(r_s,r_d,τ)), where g_1,0(r_s,r_d,τ) is the contribution from the homogeneous background and ϕ(r_s,r_d,τ) is the perturbation from heterogeneity of flow. r_s is the position of the source and r_d is the position of the detector. For computational simplicity, one representative data point from the correlation curve at a fixed delay time τ₀ is chosen for tomographic reconstruction, instead of calculating ϕ(r_s,r_d,τ) over the range of τs. Here, τ₀ which is the time when g_1,0, the calculated correlation curve of the background, decays to e⁻¹ is chosen since it yields the optimal data set according to Zhou et al. [34].

By following the similar procedure in diffuse optical tomography [39] with the assumption that absorption and scattering coefficients are homogeneous and known, the perturbation, ϕ, can be expressed as follows:

$$\begin{array}{l}\varphi \left({\mathbf{r}}_{\text{si}},{\mathbf{r}}_{\text{di}},{\tau }_0\right)\equiv ln\frac{g_1\left({\mathbf{r}}_{\text{si}},{\mathbf{r}}_{\text{di}},{\tau }_0\right)}{g_{1,0}\left({\mathbf{r}}_{\text{si}},{\mathbf{r}}_{\text{di}},{\tau }_0\right)}\\ =-\frac{1}{G_{1,0}\left({\mathbf{r}}_{\text{si}},{\mathbf{r}}_{\text{di}},{\tau }_0\right)}{\displaystyle \underset{\Omega }{\int }H\left(\mathbf{r},{\mathbf{r}}_{\text{di}},{\tau }_0\right)\frac{2v{\mu }_s{}^{\prime }{\kappa }_0^2{\tau }_0}{D}\Delta \left(\alpha D_b\left(\mathbf{r}\right)\right)G_1\left({\mathbf{r}}_{\text{si}},\mathbf{r},{\tau }_0\right)dV.}\end{array}$$ (4)

In Eq. (4), i denotes the index for source-detector pair, and r is a position in the volume Ω. G_1,0(r_si,r_di,τ₀) is the solution to Eq. (1) with source at r_si and detector at r_di, and G_1,0(r_si,r,τ₀) is the solution to Eq. (1) with source at r_si and detector at r. H(r,r_di,τ₀) is the Green’s function for Eq. (1) with source at r and detector at r_di. To calculate the integral in Eq. (4), finite element mesh is used. First, the volume Ω is discretized into subspace: Ω¹,…,Ω^h,…, Ω^L with nodes: r₁,…, r_j,…, r_N, where L is the total number of subspaces and N is the total number of nodes. In each subspace Ω^h, the functions G, H and Δ(αD_b) can be expressed as f ^h(r) = ∑_j u_j^h(r,r_j) f (r_j), where f (r_j) is function values at node r_j and u_j^h(r,r_j) is the shape function [40]. Thus, Eq. (4) can be expressed in a matrix form as follows:

$$\varphi \left({\mathbf{r}}_{\text{si}},{\mathbf{r}}_{\text{di}},{\tau }_0\right)=\ln \frac{g_1\left({\mathbf{r}}_{\text{si}},{\mathbf{r}}_{\text{di}},{\tau }_0\right)}{g_{1,0}\left({\mathbf{r}}_{\text{si}},{\mathbf{r}}_{\text{di}},{\tau }_0\right)}={\displaystyle \sum _{\text{j}}^N{W}_{\text{ij}}}\left({\mathbf{r}}_{\text{si}},{\mathbf{r}}_{\text{di}},{\mathbf{r}}_{\text{j}},{\tau }_0\right)\Delta \left(\alpha D_b\left({\mathbf{r}}_{\text{j}}\right)\right).$$ (5)

In Eq. (5), W_ij establishes the link between the flow perturbation in the j^th voxel, Δ(αD_b(r_j)), and the measurement perturbation at the i^th source-detector pair. W_ij is calculated as follows:

$$W_{ij}\left({\mathbf{r}}_{\text{si}},{\mathbf{r}}_{\text{di}},{\mathbf{r}}_{\text{j}},{\tau }_0\right)=\frac{-1}{G_{1,0}\left({\mathbf{r}}_{\text{si}},{\mathbf{r}}_{\text{di}},{\tau }_0\right)}{\displaystyle \sum _{h=1}^L{\displaystyle \underset{{\Omega }^h}{\int }\frac{2v{\mu }_s{}^{\prime }{\kappa }_0^2{\tau }_0}{D}}{H}^h\left(\mathbf{r},{\mathbf{r}}_{\text{di}},{\tau }_0\right)G_1^h\left({\mathbf{r}}_{\text{si}},\mathbf{r},{\tau }_0\right)u_{\text{j}}^{h}dV.}$$ (6)

In the calculation of W, H^h and G^h are also further expressed using nodal values and shape functions. Nodal values were obtained directly from Eq. (2). W is often called the sensitivity matrix or the weight matrix as it describes how sensitive the measurement is to the small changes in flow.

After weight matrix W is built, the last step to obtain the spatial distribution of flow change, Δ(αD_b(r)), is to solve the linear equations listed in Eq. (5). Since the equations are usually ill-posed (i.e., the number of unknowns is much larger than that of linear independent equations), Tikhonov regularization is used to stabilize the matrix inversion:

$$\Delta \left(\alpha D_b\left(\mathbf{r}\right)\right)=W^T{\left(W·W^T+\eta ·I\right)}^{-1}·\varphi ,$$ (7)

where T indicates a matrix transpose and η is the regularization parameter. In this paper, a homogeneous regularization parameter was used in the reconstruction and L-curve analysis was performed to find the best value of η for reconstruction as proposed by Zhou et al. [34].

2.5 Comparison between a non-contact and a contact system

To ensure that the quantitative performance of the non-contact system was equivalent to that of the contact system over the physiological flow range typically observed in vivo, both systems were directly compared following a method developed by Lin et al. [35]. In this method, the Brownian motion of particles inside liquid phantom was increased by raising the temperature of the phantom gradually, which provided continuous flow changes over the physiological range. Concurrent measurements on a liquid phantom with μ_a = 0.1 cm⁻¹ and μ_s′ = 8.0 cm⁻¹ were performed. The liquid phantom was made by mixing distilled water with nigrosin (Sigma-Aldrich, St. Louis, MO) as an absorbing agent and Intralipid (Fresenius Kabi, Uppsala, Sweden) as a scattering agent. The flow of the liquid phantom was changed gradually by increasing the temperature from 276.1K to 304.1K in 35 minutes. The temperature of the liquid phantom was increased by adding hot water to a tank surrounding the liquid phantom every 15 minutes and the temperature was monitored continuously using a thermometer (PS0614, Kent Scientific, Torrington, CT). The same integration time (2 s) and the source-detector separation (4.2 mm) were utilized for both the contact and the non-contact measurements as shown in Fig. 2. Room light was turned off during the measurements.

Fig. 2.

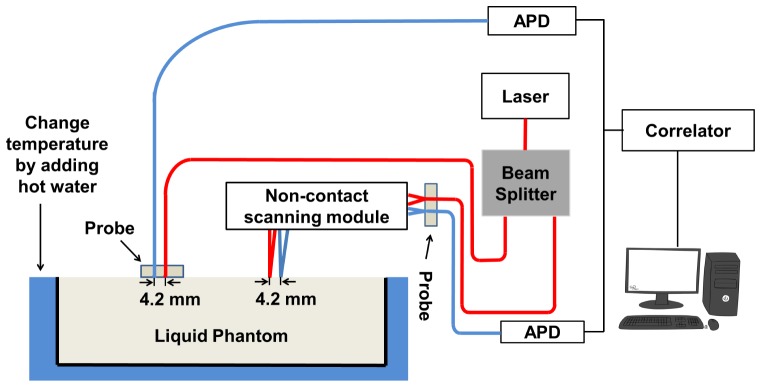
Experimental setup to compare a contact and a non-contact system. Contact and non-contact measurements were carried out concurrently on the same liquid phantom. The temperature of the liquid phantom was changed by adding hot water to the tank outside the container of liquid phantom every 15 minutes. (APD: avalanche photodiode)

The experimental data were fitted to the semi-infinite geometry solution in Eq. (2) to extract the flow, αD_b. Regression analysis and Bland-Altman plot were utilized to compare αD_b at different temperatures measured by the contact and the non-contact system.

2.6 DCT of simulated heterogeneous flow distributions

To test the performance of the DCT algorithm, image reconstructions were performed on a series of simulated data sets described in Fig. 3 and Table 1. g₁ at multiple combinations of source-detector pairs from a three-dimensional map with heterogeneous distribution of αD_b were simulated using a FEM-based solver of Eq. (1) modified from NIRFAST, a software package for diffuse optical tomography [41]. The same mesh (x:-8.5 mm to 8.5 mm, y: −17.5 mm to 20.5 mm, z: 0 mm to 8.0 mm, total number of nodes: 136831, total number of elements: 673162) was used for all simulations. Figure 3(a) and 3(b) illustrates the side and the top view of the three-dimensional αD_b map consisting of a cylinder of 1.2 mm diameter and 20 mm length simulating a long bone (Region 2) and the surrounding homogeneous medium simulating skeletal muscle (Region 1). Figure 3(c) shows the dense coverage of the source-detector pairs from scanning a source-detector pair of 3 mm separation with step size Δx of 0.35 mm and Δy of 0.70 mm. Noise was not added in the simulated data to test the inherent limitation of the linear reconstruction algorithm for the bone graft geometry.

Fig. 3.

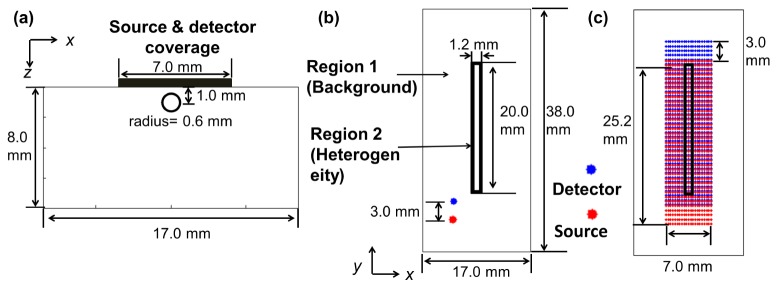
Geometry for data simulation. A cylinder of 1.2 mm diameter and 20 mm length (Region 2) simulating a bone was embedded in a homogeneous background media (Region 1) simulating surrounding muscle. (a) Side view (x-z plane) of the simulation geometry. (b) Top view (x-y plane) of the simulation geometry. (c) Source and detector positions in x-y plane. Source-detector separation of 3 mm was used throughout the simulation.

Table 1. Regional optical and flow parameters utilized to generate simulated data sets (Background and Heterogeneity columns), and the assumed homogeneous μ_s′ for the reconstruction algorithm (right-most column). Homogeneous μ_a = 0.1 cm⁻¹ was assumed for reconstruction of all four simulated data sets.

Simulation #	Background (Region 1)			Heterogeneity (Region 2)			Reconstruction
	μa(1) (cm−1)	μs′ (1) (cm−1)	αDb(1) (x10−8 cm2/s)	μa(2) (cm−1)	μs′ (2) (cm−1)	αDb(2) (x10−8 cm2/s)	μs′ (cm−1)
1	0.1	20.0	1.0	0.1	20.0	0.25	20.0
2	0.1	8.0	1.0	0.1	8.0	0.25	8.0
3	0.1	8.0	1.0	0.1	20.0	1.0	8.0
4	0.1	8.0	1.0	0.1	20.0	0.25	8.0

In order to explore the effect of different μ_s′ between bone and muscle (20.0 cm⁻¹ and 8.0 cm⁻¹ [42]) in the reconstructed αD_b images using the linear reconstruction algorithm based on the assumption of homogeneous background, four simulated data sets with various parameter assignments were produced as shown in Table 1. μ_a was fixed as 0.1 cm⁻¹ based on [42]. Simulation #1 produced a data set similar to the experiment with ex vivo bone immersed in a liquid phantom described in Section 2.7, where αD_b was lower in the bone (i.e., αD_b = 0.25x10⁻⁸ cm²/s in region 2, αD_b = 1.0x10⁻⁸ cm²/s in region 1), but μ_s′ of both regions were set to be 20.0 cm⁻¹. Simulation #2 was the same as #1 except μ_s′ were set to be 8.0 cm⁻¹ in both regions. Simulation #3 produced a data set with no αD_b contrast, but with different μ_s′ in each region. Simulation #4 included both αD_b contrast and μ_s′ differences.

For the DCT image reconstruction, a finite element mesh (x: −5.5 mm to 5.5 mm, y: −15.0 mm to 19.0 mm, z: 0 mm to 5.0 mm, total number of nodes: 80669, total number of elements: 374631) was used to reconstruct the weight matrix W. Note that this mesh was different from the mesh previously used to generate simulated data in terms of coverage and fineness of the mesh. For reconstruction of simulation #1, μ_s′ = 20.0 cm⁻¹ was used in the reconstruction mesh. For reconstruction #2-4, μ_s′ = 8.0 cm⁻¹ was assumed. The initial guess of αD_b was 1.0x10⁻⁸ cm²/s for all cases.

After reconstructing a three-dimensional αD_b map for each simulation, αD_b values in region 2 were averaged to compare with the expected values (Table 1, αD_b⁽²⁾ column). Furthermore, relative blood flow (rBF) was calculated to quantify the changes before and after the αD_b perturbation in a longitudinal study:

$$rBF\left(\mathbf{r}\right)=\frac{\alpha D_b{\left(\mathbf{r}\right)}_{\left(\text{After perturbation}\right)}}{\alpha D_b{\left(\mathbf{r}\right)}_{\left(\text{Before perturbation}\right)}}.$$ (8)

Simulation #3 (no αD_b contrast) and #4 (αD_b contrast) together mimicks a hypothetical longitudinal study situation in which measurements are performed before and after a local flow decrease in the bone region (e.g., immediately after an allograft surgery). A three-dimensional rBF image was obtained by dividing the reconstructed αD_b values from simulation #4 by those from simulation #3. rBF values in region 2 were averaged and compared with the expected value (rBF = 0.25).

2.7 DCT of a tissue phantom with an ex vivo murine femur

To test the performance of the DCT reconstruction algorithm in the presence of realistic experimental noise, a tissue phantom was constructed by suspending an isolated murine femur in a liquid turbid medium. After harvesting a femur from a mouse, soft tissue debris attached to the femur was cleaned. Then the femur was suspended in a homogeneous liquid phantom with a thin wire going through the medullary cavity of the bone. The shaft of the femur has a cylindrical shape with about 1.2 mm diameter and 20 mm length. The dimension of liquid phantom was 100 mm x 70 mm x 60 mm in x, y, z direction. The longest axis of the femur was aligned in the y direction and the center of bone was 1.0 mm under the liquid phantom surface (i.e., z = 1.0 mm). The liquid phantom was made to match the absorption and scattering values of bone reported in literature [42], with μ_a = 0.1 cm⁻¹ and μ_s′ = 20.0 cm⁻¹. This approach of matching optical properties between the bone and the surrounding medium simulated an idealized experimental situation for testing the linear reconstruction algorithm, which assumed homogeneous optical properties throughout the reconstruction volume.

The optical measurements were performed by scanning the surface of the turbid medium with the probe, covering the horizontal range x from −3.5 mm to 3.5 mm and the vertical range y from −12.6 mm to 15.6 mm. The step size for scanning was 0.35 mm in x direction and 0.70 mm in y direction. At each position, one auto-correlation curve was obtained with an integration time of 2 seconds. Data were taken at two source-detector separations, but only scanning data from 3.0 mm source-detector separation were utilized in the reconstruction for this preliminary study.

For the DCT image reconstruction, a finite element mesh was used (x: −4.5 mm to 4.5 mm, y: −13.5 mm to 16.5 mm, z: 0 mm to 6 mm, total number of nodes: 50060, total number of elements: 227788) to reconstruct the weight matrix W. For optical properties, μ_a = 0.1 cm⁻¹ and μ_s′ = 20.0 cm⁻¹ were assumed. The background flow value was determined from a separate DCS measurement on the homogeneous liquid phantom before suspension of the femur, which was αD_b = 0.82x10⁻⁸ cm²/s.

2.8 DCT of a tissue phantom with a tube

Although the use of an actual murine femur in the tissue phantom mimicked in vivo measurement geometry closely, it was difficult to modulate the flow within the bone. Therefore, another type of tissue phantom was constructed using a slightly turbid silicone rubber tube with an inner diameter of 1.0 mm (1972T4, McMaster Carr, Elmhurst, IL) instead of a femur. Two experiments were performed using the optical and flow parameters corresponding to simulation #3 and #4 (see Table 1). Lower flow inside the tube was achieved by adding 2% methyl cellulose to the liquid phantom to increase viscosity, thus decreasing Brownian motion of scatterers [15]. Separate measurements on the liquid phantom yielded αD_b = 0.90x10⁻⁸ cm²/s for liquid phantom without methyl cellulose and αD_b = 0.19x10⁻⁸ cm²/s for phantom with 2% methyl cellulose.

The optical scan covered an area of x from −3.5 mm to 3.5 mm and y from −7.0 mm to 10.0 mm. The x scan step size was 0.35 mm and the y scan step size was 0.70 mm. One measurement was made at each position with integration time of 2 seconds.

For DCT reconstruction, a finite element mesh (x: −4.0 mm to 4.0 mm, y: −8 mm to 10.5 mm, z: 0 mm to 5 mm, total number of nodes: 52681, total number of elements: 244168) was used. The optical properties of the reconstruction regions were assumed to be homogeneous, with μ_a = 0.1 cm⁻¹ and μ_s′ = 8.0 cm⁻¹.

2.9 DCT of in vivo murine legs before and after allograft surgery

For the in vivo experiment, three mice were scanned 5 days before and one week after an allograft surgery. All procedures in the animal study were approved by the University Committee on Animal Resource (UCAR) at the University of Rochester.

The details of the allograft surgery were described in Hoffman et al. [43–45]. To summarize, the allograft surgery was performed by removing a 5 mm diaphyseal segment of bone from the femur of the left hindlimb of a BALB/c mouse and replacing it with a decellularized bone segment from a C57BL/6 mouse (allograft). An intra-medullary pin through the host bones and the new allograft segment was placed to stabilize the graft and facilitate graft-host union.

Before DCT scanning, the mouse was placed on a warming pad and anesthetized with continuous isoflurane administration. Fur was removed from the scanning site 24 hours prior to baseline measurements using Nair (Church & Dwight Co., Inc., Princeton, NJ). Scanning field of view was adjusted such that the femur was located at the center of scanning area and the long axis was aligned with the y direction, as shown in Fig. 4. For the second DCT scan, electric clippers were used to remove any regrown fur. A two dimensional scan was carried out covering an area of x from −3.5 mm to 3.5 mm and y from −7.0 mm to 10.0 mm. The x step size was 0.35 mm and the y step size was 0.70 mm. In total, measurements were made at 441 different positions with 2 source-detector separations and 2 seconds of integration time. After the measurement, the mouse was kept warm until it recovered from the anesthesia. The scanning time was approximately 18 minutes and the whole procedure took less than 40 minutes for each mouse. Only scanning data at 3.0 mm source-detector separation were used in the reconstruction.

Fig. 4.

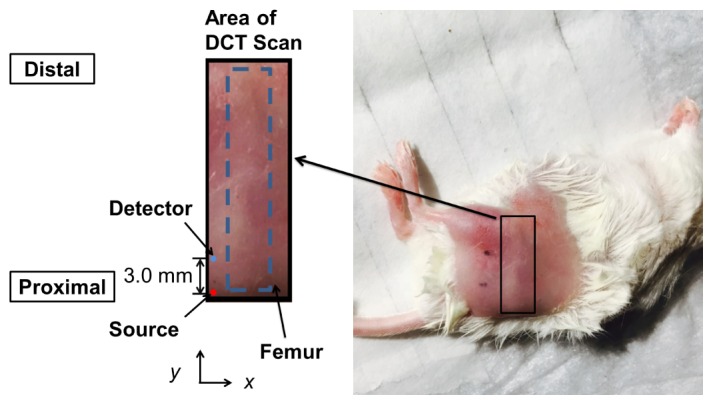
Example DCT scan area on mouse. The dotted blue line indicates the approximate location of the femur with respect to the scanning area.

For DCT image reconstruction, a finite element mesh was used (x: −4.0 mm to 4.0 mm, y: −8 mm to 10.5 mm, z: 0 mm to 5 mm, total number of nodes: 52681, total number of elements: 244168) to reconstruct the weight matrix, W. The optical properties of the reconstruction region were assumed to be homogeneous, with μ_a = 0.1 cm⁻¹ and μ_s′ = 8.0 cm⁻¹. For each scan, first bulk αD_b was fitted to the semi-infinite geometry solution in Eq. (2) at each source-detector pair, then bulk values were averaged over all pairs to yield a background homogeneous αD_b needed for DCT reconstruction.

3. Results

3.1 The performance of a non-contact system is equivalent to that of a contact-system

Typical normalized intensity auto-correlation functions measured by the non-contact system and contact system are shown in Fig. 5(a). Note that experimental β of the non-contact and the contact system is close to 1.0 and 0.5 respectively, as mentioned in Section 2.3. A linear relationship between αD_b measured by the contact system and non-contact system was observed as shown in Fig. 5(b). Linear regression yielded a slope of 0.99 with high coefficient of determination R² = 0.87 (p < 0.0001). The agreement between the two methods can be assessed by a Bland-Altman plot, constructed by plotting the average of the two variables along the x-axis and the difference between the two variables along the y-axis [46], as shown in Fig. 5(c). 95% limits of agreement were computed by the mean difference 1.96 standard deviation of the difference (dotted line). We can conclude that the contact and the non-contact systems generally agree since 96% of data lies within 95% limits of agreement.

Fig. 5.

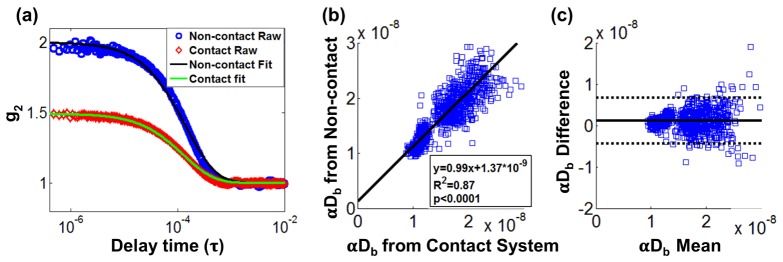
Comparison of concurrent measurements between a non-contact system and a contact system on the liquid phantom: (a) Typical normalized intensity auto-correlation function g₂ from a non-contact and a contact system. Blue circles are measured data from a non-contact system. Red diamonds are measured data from a contact system. Solid lines are the corresponding semi-infinite fits to measured data from each system. (b) Linear regression analysis on extracted αD_b from each system. (c) Bland-Altman plot with x-axis showing average αD_b from a contact and a non-contact system, and y-axis showing the αD_b difference between two systems. Dotted lines denotes the 95% confidence interval of the difference.

From these results, it can be concluded that the performance of the non-contact system is comparable to the contact system. Lin et al. [35] also reported similar results comparing contact and non-contact systems for much larger source-detector separation (26 mm) than used in this study (4.2 mm).

3.2 Three-dimensional flow image reconstruction of simulated data sets

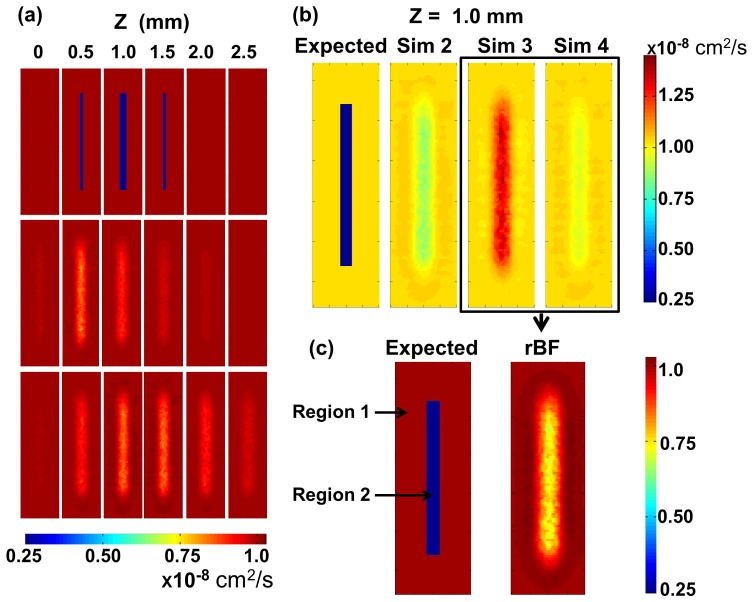
In Fig. 6(a), three-dimensional images are shown as a series of 8 mm x 30 mm image slices at different depths (z) of 0.5 mm interval. The top row images are the expected flow distributions. The middle and the bottom row images are the reconstructed αD_b images from simulation #1 and #2 respectively. The reconstructed images show that the extent of flow heterogeneity is larger than the expected size (i.e., 1.2 mm diameter) and the flow value inside the cylinder is underestimated (0.91x10⁻⁸ cm²/s vs expected 0.25x10⁻⁸ cm²/s). This is in line with the observations from Zhou et al. [34] and other diffuse optical tomography results [47] that the point spread function of the diffuse optical techniques is large and the reconstructed values are usually underestimated. Interestingly, the depth of the cylinder in simulation #1 with global μ_s′ = 20.0 cm⁻¹ was underestimated (0.57 mm vs. expected 1.0 mm), yet that of simulation #2 with global μ_s′ = 8.0 cm⁻¹ was overestimated (1.24 mm). The reconstructed images from simulation #3 and #4 (not shown) looked similar to the z-distribution of simulation #2.In Fig. 6(b), representative αD_b slices at z = 1.0 mm from four simulations are shown side by side to demonstrate the effect of μ_s′ differences between regions. When no difference was present, reconstructed αD_b in the cylindrical region was lower than the background as expected (simulation #2, mean αD_b in region 2 = 0.88x10⁻⁸ cm²/s). However, μ_s′ differences in the absence of αD_b contrast between two regions (simulation #3) resulted in the apparent reconstructed αD_b increase in the cylindrical region. When both μ_s′ differences and αD_b contrast were present (simulation #4), reconstructed αD_b was lower in the cylindrical region, but the contrast (0.94x10⁻⁸ cm²/s) was less than that of simulation #2. For the longitudinal study, the accurate quantification of flow changes from the baseline may still be possible even though the accuracy of absolute αD_b is compromised due to systematic error of the reconstruction method. Therefore, the distribution of relative flow was computed by dividing reconstructed αD_b map of simulation #4 with that of simulation #3, and compared with the expected rBF map in Fig. 6(c). rBF in the cylindrical region was 0.78 as opposed to the expected rBF of 0.25.

Fig. 6.

DCT reconstruction from simulated data sets. (a) z slices of αD_b at different depths for expected value (Top), Simulation #1 (middle, global μ_s′ = 20.0 cm⁻¹) and Simulation #2 (Bottom, global μ_s′ = 8.0 cm⁻¹). (b) z slices of αD_b at 1.0 mm for expected value and simulation #2-4. In simulation #3 and #4, μ_s′ = 8.0 cm⁻¹ and 20.0 cm⁻¹ were assigned for region 1 and 2 respectively simulating muscle and bone. For simulation #3, αD_b = 1.0x10⁻⁸ cm²/s was assigned in both regions. For simulation 4, αD_b = 0.25x10⁻⁸ cm²/s was assigned in region 2. (c) Expected relative blood flow rBF (Left) and rBF calculated by taking the ratio between αD_b of simulation #4 and simulation #3 (Right). (Sim: simulation)

3.3 Three-dimensional flow image reconstruction of a tissue phantom with a murine femur

Figure 7 shows the reconstructed αD_b images in different layers of the tissue phantom at 0.5 mm increments from the surface of the liquid phantom. The photograph on the left shows the position of the bone with respect to the scanning region. At z = 0.5 and 1.0 mm, αD_b distribution with a lower value than the background is observed at the approximate region that corresponds to the spatial extent of the bone in x-y plane, with the narrower width at the center and wider width at the end of the bone. As the bone is solid and, therefore, has a much smaller diffusion coefficient than the liquid phantom, it is expected to exhibit lower flow than the surrounding liquid phantom. The average reconstructed z depth of the bone region was 0.7 mm, which was smaller than the expected depth of 1.0 mm.

Fig. 7.

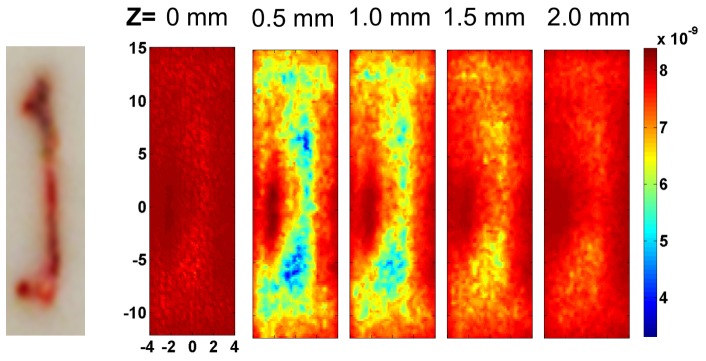
DCT reconstruction results from tissue phantom measurements. The photograph on the left shows the position of the bone with respect to the scanning area. Reconstructed images of αD_b are shown at different z = 0 mm, 0.5 mm, 1.0 mm, 1.5 mm and 2.0 mm with the same color bar.

3.4 Three-dimensional flow image reconstructions of a tissue phantom with a tube

Figure 8 shows the experimental analogue of Fig. 6(c). rBF images are presented in different layers of the tissue phantom at 0.5 mm increments from the surface of the liquid phantom inthe presence of μ_s′ differences between regions. Lower relative flow (rBF = 0.68) in the tube region was observed, but the extent was underestimated when compared to the expected relative flow (rBF = 0.22).

Fig. 8.

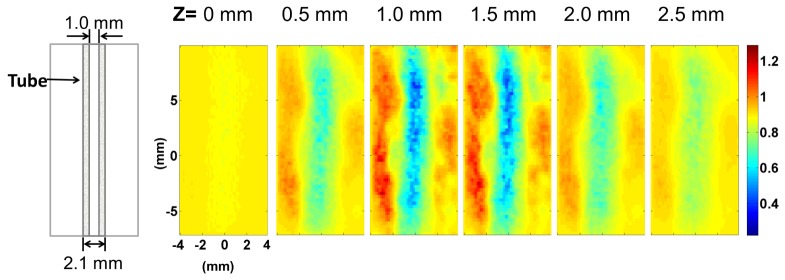
Reconstructed rBF from a tube phantom experiment. The left-most diagram illustrates the position of the tube as seen from the top (x-y plane). Reconstructed images of rBF are shown at different z = 0 mm, 0.5 mm, 1.0 mm, 1.5 mm, 2.0 mm and 2.5 mm with the same color bar.

3.5 Three-dimensional blood flow image reconstructions of in vivo murine leg before and after allograft surgery

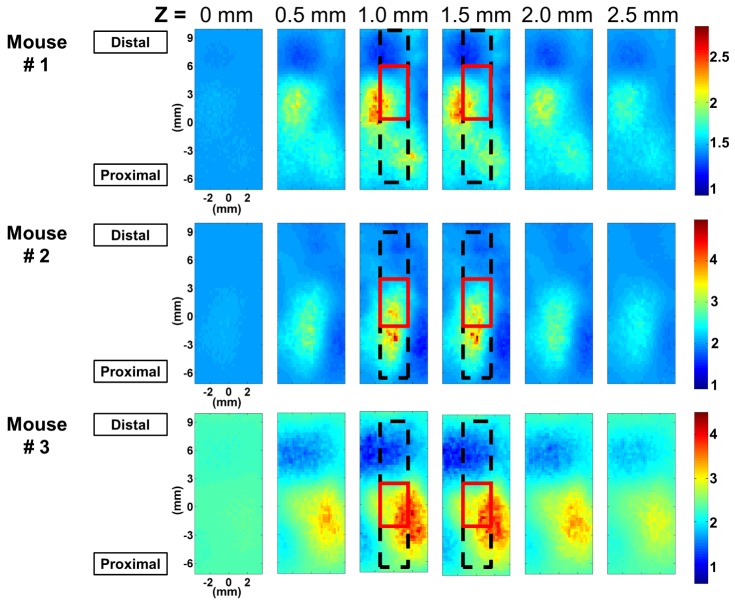
In Fig. 9, rBF images of all three mice at different depths (0 mm, 0.5 mm, 1 mm, 1.5 mm, 2.0 mm and 2.5 mm below the scanning surface) are shown. rBF images were calculated by dividing reconstructed αD_b from measurements taken one week after surgery with that from measurements before surgery. The approximate location of the femur and the graft is outlined with a black dashed line and a solid red line respectively. For every mouse, overall elevation of blood flow was observed compared to the pre-surgical state (1.5 ~2 times). In addition, localized blood flow changes near the graft were clearly captured for all three mice imaged, with the maximum rBF value ranging from 3 to 5.

Fig. 9.

Spatial distribution of blood flow ratio between post- and pre-surgery (rBF) at different depths for three different mice show different localized regions of blood flow increase. The black dotted line and the red solid line indicate the approximate location of the femur and the graft respectively.

4. Discussion

In this study, we demonstrated a galvanometer-based non-contact diffuse correlation tomography system that can provide large spatial data sets with easy instrumental implementation and flexibility, which in turn provides more spatially resolved information in three-dimensional blood flow images of murine femurs. Previous DCT works have been performed with a limited number of spatial data sets for rat brain imaging [33, 34]. Recently, new techniques based on speckle-contrast have been emerging as an alternative for deep-tissue blood flow imaging [48–51]. This can provide large spatial data sets using a CCD-based system, which can yield resolution equivalent to the traditional diffuse correlation tomographic approaches. However, these works were focused on applications in the human scale and the full capability of improving resolution has not been explicitly demonstrated as of yet.

Compared to laser Doppler imaging or speckle contrast imaging, the large data set DCT approach is ideally suited for monitoring the blood flow of the murine bone graft model because of the requirements for relatively deep penetration depth and a large field of view. The murine femur is approximately 1-2 mm deep with respect to the tissue surface, and the entire hindlimb is approximately 5 mm thick. The location of the femur requires relatively deep tissue penetration of light. The length of the femur is approximately 15 - 20 mm with the implanted graft being 5 mm long. This configuration requires not only depth penetration, but also a relatively large field of view to cover the whole femur region. We can provide this large field of view through the galvanometer-based scanning system.

At the present time, the utilized DCT instrumentation and algorithm are not fully optimized and need further improvements. The optical throughput of the current scanning module was lower than that of the contact system due to low transmission of polarizers (30% at 785nm) and insufficient optimization of optical components for light collection efficiency. While the light loss due to crossed polarizers is unavoidable in our scanning design (i.e., 9% transmission after two polarizers), the light throughput in other optical components can be improved with a better design. In the experiments presented here, no optical components were added to equalize the signal-to-noise at different source-detector separations, resulting in superior signal-to-noise ratio for 3 mm separation compared to that for 4.2 mm. For this preliminary study, we focused on using only 3 mm separation data to simplify the analysis. Testing new optical designs to improve the light throughput and to equalize the signal-to-noise at multiple separations is ongoing.

The most notable discrepancy between reconstructed and expected flow distribution using simulated data was the underestimation of flow contrast between the heterogeneity and the surrounding medium. Our current algorithm was based on a linear Rytov approximation which usually underestimates flow values [39]. Based on simulations (not shown), inclusion of more source-detector separations in the DCT reconstruction can improve the accuracy of reconstructed flow values. Another discrepancy was the depth position of the heterogeneity which may be due to the use of constant Tikhonov regularization. This can be improved with spatially variant regularization [52]. In the future, the strategy to optimally combine data from multiple separations with varying signal-to-noise ratios will be developed by inspecting sensitivity matrices of various optical and flow parameters, in addition to incorporating an iterative reconstruction scheme.

Another improvement for DCT reconstruction to be made is the incorporation of heterogeneous distribution of absorption and reduced scattering within the algorithm. In the current reconstruction, absorption and scattering were assumed to be homogeneous throughout. In the ex vivo murine femur tissue phantom experiment, absorption and scattering of the liquid phantom was matched with reported values of bone in literature to create an ideal experimental condition. For the animal study, absorption and scattering coefficients were assumed to match those of muscle, and the potential scattering coefficient differences between the muscle and the bone was not incorporated in the reconstruction algorithm. The impact of this assumption on the quantification of absolute and relative blood flow was studied using a series of numerical simulations and tissue phantom experiments implementing scattering coefficient differences between the muscle and the bone (see Sections 2.6 and 3.2). We showed that relative flow was more robust and reliable compared to the absolute flow, which was susceptible to the optical property differences between the bone and the surrounding tissue. One way to improve this limitation in absolute flow recovery is to use mouse-specific anatomical information from other imaging modalities such as micro-CT, and to assign specific absorption and scattering coefficients from literature in different tissues such as muscle and bone. Another way is to combine DCT with diffuse optical tomography (DOT) and assign the three-dimensional absorption and scattering coefficient map based on DOT reconstruction before performing DCT reconstruction.

Albeit current limitations, we demonstrated superior lateral resolution in a realistic scale tissue phantom with an immersed murine femur using a large spatial data set. In addition, DCT images from before and after allograft surgery revealed overall elevation of blood flow level after surgery and spatially localized flow increases within the femur and/or the surrounding tissue. The ability to reliably and longitudinally monitor blood flow in the murine segmental bone defect model is important as the therapeutic efficacy of various tissue engineering approaches to enhance allograft healing is being assessed using this model [43–45, 53]. In particular, the number and size of blood vessels during bone repair and regeneration have been extensively quantified using end-point assays such as histology or micro-CT with a lead-chromate contrast agent [54]. However, blood flow, which dictates the rate of delivery of oxygen, nutrients, growth factors and circulating cells necessary for healing, is not readily available for quantification. Despite the difficulties, blood flow in the region surrounding a bone injury is thought to be increased due to inflammation and metabolic demands in the early phase of healing [6]. In the later phase of healing, blood flow is expected to increase within the bone graft after the establishment of new penetrating blood vessels from existing vessels [6]. Our preliminary DCT images taken one week after allograft surgery suggest that blood flow needed for healing may be increased in the tissue surrounding the bone graft, considering the limited depth resolution of current analysis. The longitudinal monitoring showing spatial evolution of blood flow in the same mouse at different healing phases may reveal the interplay between the surrounding tissue and graft, and may yield quantitative parameters to predict therapeutic efficacy in the future.

5. Summary

In summary, we have constructed a scanning non-contact DCT system with galvanometer mirrors and verified that our non-contact system performed equivalently to a contact system. We also demonstrated the feasibility of three-dimensional flow imaging with our new DCT system from a tissue phantom with a femur and a tube, and in vivo murine legs. Overall blood flow after 1 week post-allograft surgery on murine legs increased by 1.5 to 2 times from the baseline (i.e., before surgery) blood flow in all three mice. In addition, higher relative blood flow (maximum 3 to 5 times from the baseline) was observed in a focused spatial region near the graft in each mouse. Our system demonstrated a potential for longitudinal study of blood flow changes during bone graft healing.