Fronto-parietal and cingulo-opercular network integrity and cognition in health and schizophrenia

Abstract

Growing evidence suggests that coordinated activity within specific functional brain networks supports cognitive ability, and that abnormalities in brain connectivity may underlie cognitive deficits observed in neuropsychiatric diseases, such as schizophrenia. Two functional networks, the fronto-parietal network (FPN) and cingulo-opercular network (CON), are hypothesized to support top-down control of executive functioning, and have therefore emerged as potential drivers of cognitive impairment in disease-states. Graph theoretic analyses of functional connectivity data can characterize network topology, allowing the relationships between cognitive ability and network integrity to be examined. In the current study we applied graph analysis to pseudo-resting state data in 54 healthy subjects and 46 schizophrenia patients, and measured overall cognitive ability as the shared variance in performance from tasks of episodic memory, verbal memory, processing speed, goal maintenance, and visual integration. We found that, across all participants, cognitive ability was significantly positively associated with the local and global efficiency of the whole brain, FPN, and CON, but not with the efficiency of a comparison network, the auditory network. Additionally, the participation coefficient of the right anterior insula, a major hub within the CON, significantly predicted cognition, and this relationship was independent of CON global efficiency. Surprisingly, we did not observe strong evidence for group differences in any of our network metrics. These data suggest that functionally efficient task control networks support better cognitive ability in both health and schizophrenia, and that the right anterior insula may be a particularly important hub for successful cognitive performance across both health and disease.

1. Introduction

Functional magnetic resonance imaging (fMRI) research has provided evidence of stable, intrinsic functional networks in the human brain (Fox et al., 2005). These functional networks are detectable both during the performance of cognitive tasks (Dosenbach et al., 2006) and while an individual is at rest (Power et al., 2011). These networks appear to support an array of cognitive functions, such as executive functioning, sensory perception, and motor control, and therefore represent important targets for understanding how healthy cognition occurs, and how abnormal cognition can lead to the symptoms observed in clinical populations. One pervasive aspect of mental illness is cognitive deficits (Green, Kern, & Heaton, 2004). Individuals diagnosed with schizophrenia, bipolar disorder, and major depression all display impairments in a multitude of higher-order cognitive domains, including memory, processing speed, and cognitive control (Heinrichs & Zakzanis, 1998; Martinez-Aran et al., 2004; Snyder, 2013). Of all these psychopathologies, patients with schizophrenia consistently exhibit, on average, the most severe cognitive deficits (Hill et al., 2013). These deficits, and the variance shared among them, are associated with impairments in everyday functioning (Sheffield et al., 2014), contributing to the disabling nature of the disorder (Bowie et al., 2008). While researchers have historically attempted to find differential cognitive deficits in schizophrenia, it is increasingly clear that patients are impaired relative to controls on the majority of neuropsychological tasks. This finding has led some to hypothesize that schizophrenia is characterized by a generalized cognitive deficit thought to reflect common psychological or neurobiological mechanisms contributing to performance across cognitive domains (Dickinson & Harvey, 2009). The generalized cognitive deficit makes schizophrenia an ideal population for studying a wide range of individual differences in overall cognitive ability, and this conceptualization of the generalized deficit can be operationalized as the shared variance across tasks that assess different domains of cognition, which we will refer to as global or overall cognition.

Importantly, two functional networks, the fronto-parietal network (FPN) and the cingulo-opercular network (CON), display increased activity during the performance of many complex cognitive tasks (Dosenbach et al., 2006), and the strength of their within-network connectivity predicts cognitive performance (Kelly, Uddin, Biswal, Castellanos, Milham, 2008; Rypma et al., 2006; Seeley et al., 2007; Song et al., 2008), implicating them as part of “task-positive” or “task control” systems that may underlie global cognition. In fact, these networks are hypothesized to represent a dual-system of top-down control that supports cognitive ability, given their pattern of activation and connectivity during task performance (Dosenbach, Fair, Cohen, Schlaggar, & Petersen, 2008). More specifically, the FPN is thought to be involved in trial-by-trial control during task, facilitating the selective attention of trial-specific information, while the CON is thought to facilitate the maintenance of task-relevant goals and the incorporation of error information to adjust behavior (Cocchi, Zalesky, Fornito, & Mattingley, 2013). Therefore, together, these two large-scale networks are globally relevant to wide range of cognitive functions, making them excellent candidates for better understanding individual differences in overall cognitive ability.

Research also suggests that specific brain regions within the FPN and CON play especially important roles in the coordination of information transfer between networks (Dosenbach et al., 2007). In particular, the anterior insula (AI) and dorsal anterior cingulate cortex (DACC) are hypothesized to serve as core hubs within the CON, and the dorsolateral prefrontal cortex (DLPFC) represents a hub within the FPN. Each hub is thought to serve different functions within each network, to support cognitive performance. Given the current conceptualization that multiple brain networks are necessary for higher-order cognition (Cocchi, Zalesky, Fornito, & Mattingley, 2013), hub-ness may be an especially important metric for understanding how communication between networks supports cognitive ability. Previous work suggests that the DACC facilitates outcome-monitoring by evaluating the result of an individual’s actions, and facilitating the resolution of conflict during task (i.e. conflict-monitoring) (Botvinick, Cohen, & Carter, 2004). The AI marks information as salient for additional processing and is thought to communicate with multiple large-scale networks to facilitate the utilization of salient information for attention and working memory processes (Menon & Uddin, 2010). The DLPFC maintains task representations and may bias information in line with task-related goals (Miller & Cohen, 2001). Therefore, the putative role of each hub suggests that, together with other regions within the FPN and CON, these hubs facilitate top-down control to support function across many cognitive domains.

Given this conceptualized role of the FPN and CON in global cognition, it has been argued that abnormalities in the control provided by these networks contributes to mental illness (Cole, Repovs, & Anticevic, 2014). One piece of evidence supporting this notion is abnormal connectivity within and between these networks in schizophrenia. Studies have found reduced connectivity between the FPN and CON (Repovs, Csernansky, & Barch, 2011) and between the CON and the striatum in patients (Tu, Hsieh, Li, Bai, & Su, 2012), as well as reduced connectivity within the FPN (Woodward, Rogers, & Heckers, 2011). In addition, connectivity between major hubs within these networks is reduced (Meyer-Lindenberg et al., 2001; White, Joseph, Francis, & Liddle, 2010). These findings, taken together with the deficits in overall cognition in schizophrenia, make this an excellent population in which to elucidate the relationship between functional networks and global cognition. Therefore, the current study aims to test the hypothesis that FPN and CON abnormalities are associated with shared task variance across many cognitive domains (i.e., global cognition), implicating them as a hypothesized source of the generalized cognitive deficit in schizophrenia.

To date, literature relating cognition and network-specific functional connectivity has largely quantified ‘abnormalities’ as significant differences in the magnitude of average correlation coefficients within and between networks. Recent application of graph theory analysis to functional connectivity data allows for more sophisticated measurement of brain networks, including global and local efficiency of information processing, and the role of hubs (Bullmore & Sporns, 2012; Rubinov & Sporns, 2010). These metrics can be correlated with psychological measures to assess relationships between brain and behavior. In fact, a previous study revealed a significant negative correlation between the characteristic path length of the whole brain network and IQ in a small group of healthy individuals (van den Heuvel, Stam, Kahn, & Hulshoff Pol, 2009), suggesting that more strongly integrated whole brain networks support better cognitive functioning. Efficiency metrics (both global and local) are calculated by taking the inverse of path length between nodes within a network, and therefore quantify how strongly (or efficiently) information can be transferred throughout the network. Given this conceptualization of efficiency metrics, as well as previous findings of a relationship between path length and cognitive ability, these metrics were selected as putatively important for understanding individual differences in overall cognitive functioning in both health and disease. Similarly, the degree to which hub nodes communicate with other networks not only influences the efficiency of a network, but is also a meaningful factor in cognitive functioning, leading us to utilize a metric of hub-ness known as the participation coefficient to quantify the integrity of our a priori hubs. Finally, while several studies have reported abnormal graph metrics in schizophrenia (Alexander-Bloch et al., 2010; Liu et al., 2008; Lynall et al., 2010; Rubinov et al., 2009), very few have assessed how the observed abnormalities are related to behavior. Therefore, the current study aims to assess network topology in healthy controls and individuals with schizophrenia, and measure the relationship between functional network metrics and global cognitive ability.

Finally, much of the graph theory literature focuses almost exclusively on the whole-brain. Thus, we extend this research by constructing graphs of specific functional networks: the FPN, the CON, and the auditory network (AUD), which serves as a comparison network hypothesized not to be related to the current measures of cognition. We hypothesized that patients with schizophrenia would show reduced efficiency of the FPN, CON, and whole brain relative to healthy controls. Given our hypothesis that network integrity underlies performance across many cognitive domains, we quantified shared variance from five different cognitive tasks to use as our measure of global cognition. We expected that efficiency of the whole brain, FPN, and CON, but not the AUD, would be associated with global cognition across all subjects. Finally, we aimed to examine the role of functional hubs within these networks, focusing our analyses on the DACC, AI, and the DLPFC, given their conceptualization as key hubs within the FPN and CON, based on priori research (Dosenbach et al., 2007). We hypothesized that cognition would be associated with the extent to which these regions participate with other networks in the brain.

2. Methods and Materials

2.1 Subjects and Procedure

120 subjects (60 schizophrenia; 60 healthy controls) were recruited as part of the Cognitive Neuroscience Test Reliability and Clinical Applications for Schizophrenia (CNTRACS) initiative (Gold, 2012). Subjects were run through identical protocol across five study sites: Washington University in St Louis, Rutgers University, University of California-Davis, University of Minnesota-Twin Cities, and the Maryland Psychiatric Research Center at the University of Maryland. All subjects signed written informed consent before participating in the study. Exclusion criteria for all subjects included endorsement of serious head injury, neurological disease, intellectual disability, or pervasive developmental disorder. Subjects were excluded if they indicated substance dependence in the past 6 months and/or substance abuse in the past month, or if they failed a drug and alcohol screen administered on the day of testing. All subjects were native English speakers and scored at least a six on the Wechsler Test of Adult Reading (WTAR), a measure of premorbid IQ (Weschler, 2001).

All subjects completed the Structured Clinical Interview of the DSM-IV (SCID; (First, Spitzer, Gibbon, & Williams, 1995)). Controls were excluded if they had a history of serious mental illness (e.g. bipolar disorder or any psychotic disorder), were currently experiencing an episode of major depression, or were currently taking psychotropic or cognition-enhancing medications. Patients were included if they met criteria for schizophrenia or schizoaffective disorder, were not currently experiencing an episode of major depression, did not anticipate any medication changes within a month, and had stable outpatient or partial hospital status. Of our schizophrenia patients, 85% were taking an atypical antipsychotic, 4% were taking a typical antipsychotic, 7% were taking both an atypical and a typical antipsychotic, and complete medication information was not available for 4% (two patients).

A total of 16 subjects (13 schizophrenia, 3 healthy controls) were excluded from our study, either due to incomplete or unusable data. Of these 16 subjects, 7 schizophrenia patients and 2 healthy controls had excessive movement (motion parameters outlined in more detail in section 2.4), 2 schizophrenia subjects moved out of imaging field-of-view to an excessive degree during the scan session, 1 schizophrenia subject was removed due to being an outlier (>3 SD) in the relationship between fMRI and behavioral data (p<.001 in multivariate Mahalanobis distance relative to other subjects), 2 schizophrenia subjects were excluded after Eprime crashed and data collection could not be completed, 1 schizophrenia subject was excluded after failing the drug test during session two, and 1 healthy control was excluded for not completing all tasks within the scanner.

2.2 Procedure

All subjects included in the final analysis completed two cognitive tasks outside of the scanner (verbal learning and processing speed) and three cognitive tasks inside the scanner (episodic memory, visual integration, and goal maintenance). Outside of the fMRI scanner, all subjects completed two cognitive tasks: the Hopkins Verbal Learning Task (HVLT; (Brandt, 1991)) and the Symbol-Coding task from the Brief Assessment of Cognition in Schizophrenia (BACSsc; (Keefe et al., 2004)). While in the MRI scanner, all subjects performed three additional cognitive tasks, the behavioral data from which is used in the current study. Subjects performed the Dot-Probe Expectancy Task (DPX; (Henderson et al., 2012)), the Relational and Item-Specific Encoding Task (RISE; (Ragland et al., 2012)), and the Jittered Orientation Visual Integration Task (JOVI; (Silverstein et al., 2012)), all of which have been validated in schizophrenia as part of the CNTRACS initiative. Each of these tasks is described in more detail below. We detected two outliers in our healthy control group through box-plots, one for the DPX task (score = −5.42; group mean = 0.39; standard deviation = 1.37) and the other for the RISE (score = −0.19; group mean = 2.42; standard deviation = 0.72). In addition, a single subject in our schizophrenia group did not complete the HVLT. Therefore, any analyses that include measures of overall cognition include only 100 subjects (46 schizophrenia; 54 controls).

2.3 Cognitive Tasks

The HVLT is a test of verbal learning and memory that measures one’s ability to recall a list of 12 orally presented words, both immediately and after a 20–25 minute delay. The BACSsc is a measure of processing speed that requires subjects to map the numbers 1–9 onto corresponding symbols as quickly as possible for 90 seconds. Both tasks have been validated and reveal large effect sizes for deficits in schizophrenia (Dickinson, Ramsey, & Gold, 2007; Kern et al., 2011). The DPX is a task of goal maintenance during which subjects observe sequentially presented symbols, and must indicate ‘target’ if they see a target-cue (‘A’) followed by a target-probe (‘X’). Performance on the DPX indexes the hit-rate for ‘AX’ pairs relative to the false-alarm rate for ‘BX’ pairs, during which the pre-potent response to ‘X’ must be inhibited. The RISE is a measure of episodic and relational memory with three outcome measures: recognition for items following item-specific encoding (IRIE), item recognition for items following relational encoding (IRRE) and associative recognition for item pairs from the relational encoding condition (AR). For all three sub-tasks in the RISE, d’prime was taken as the outcome variable. Finally, the JOVI is a measure of visual integration that requires subjects to indicate the direction in which an egg-shaped stimulus is pointing. The stimulus is comprised of a closed contour containing Gabor elements that is embedded within randomly oriented Gabors. Manipulation of visual integration requirements is achieved by adding orientational jitter to the contour elements, such that 0° jitter forms a smooth shape and +/−15–16° jitter is very difficult to discern. Accuracy for +/−9–10° jitter is presented here, as it yielded the largest effect size between groups. Our measure of global cognition in the current study was calculated using a principal axis factor analysis that included performance across all of these cognitive tasks, under the assumption that shared task variance reflects a common neurobiological process.

2.4 fMRI data acquisition, pre-processing and motion-correction

Imaging data was collected in a single session, using a consistent imaging protocol across sites. fMRI scans were collected with gradient-echo BOLD acquisitions using echo-planar imaging (TR = 2000 ms, TE = 30 ms, 77° flip angle, FOV = 220×220 mm, 3.43 mm in-plane voxels, 32 axial-oblique slices approximately parallel with the anterior/posterior commissure, 4 mm thickness with no gap). There were 4 runs of the DPX (each 180 frames), 4 runs of the RISE (IRIE: 1 run, 237 frames; IRAE: 2 runs, each 252 frames; AR: 1 run, 171 frames), and 3 runs of the JOVI (each 239 frames). The order of the tasks was counterbalanced across subjects. Additionally, each session included a 3D T1-weighted scan (MPRAGE: TR = 2300 ms, TE ~ 3.0 ms, TI = 900 ms, 9° flip angle, FOV = 256 × 240 mm, 1.0 mm in-plane voxels, 176 slices, 1.0 mm slice thickness, GRAPPA/SENSE factor = 2, 5:17 min acquisition), and a T2-weighted scan. Three sites used a Siemens 3T TimTrio magnet, with a 12-channel head coil; one site used a Siemens 3T Allegra magnet with a circularly polarized (CP) transmit/receive coil; one site used a Philips 3T Achieva magnet with an 8-channel head coil.

To address hardware differences across sites, we used AGAR phantom data collected at each scan session, as recommended by fBIRN, to perform quality assurance of scanners across sites (Friedman & Glover, 2006). We examined signal-to-fluctuation-noise ration (SFNR), static spatial signal-to-noise ratio (SNR), percent fluctuation, drift and smoothness (FWHM in the X, Y and Z directions), as defined by Friedman and Glover (2006). For all metrics, we saw main effects of site (all p’s <.001), but no main effects of group (all p’s>.20) and no interactions between group and site (all p’s >.2). Principal components analysis on these QA metrics revealed two main components that accounted for 94% of the variance: one that reflected SNR, SFNR and smoothness, and one that reflected fluctuation and drift. When included as predictors in our regression analyses (as described in section 3.4, 3.5, and 3.6), all relationships remained significant (and in some cases even more significant), suggesting that these scanner differences were not driving our main findings.

Imaging data was processed similar to methods used in previous work (Mamah, Barch, & Repovs, 2013) (Anticevic et al., 2014). Processing steps were completed using MatLab code and included: 1) slice timing correction, 2) removal of the first five images from each run to allow data to reach a steady state, 3) rigid body motion correction, 4) normalization of data to a whole brain mode value of 1000, 5) registration of structural (T1) image to Talairach (Washington University 711-2b atlas) coordinate space using a 12-parameter affine transform, and 6) co-registration of functional volumes to the atlas space structural image using 3mm cubic resampling. A finite impulse response (FIR) was used to model the hemodynamic response function.

To improve signal-to-noise ratio, remove possible sources of spurious correlations and task activation induced correlation, additional preprocessing steps were applied to functional images before functional connectivity analyses: 1) spatial smoothing using a Gaussian kernel of 6mm FWHM, 2) high-pass and low-pass filtering with 0.009–0.08 Hz cut-off frequencies, 3) removal of nuisance variables, global signal and task response using multiple regression with the following predictors: a) six rigid body motion correction parameters, b) ventricle, c) white matter, d) whole brain signals and their first derivatives, and e) task appropriate event regressors using unassumed, delta-function modeling of task response across 9 functional frames. All regressors were applied in a single regression step across concatenated runs of the same task; all further steps and analyses were conducted on the residual signal. The resulting, largely task-independent timeseries from all the tasks were then combined into one ‘pseudo-resting state’ timeseries spanning approximately 60 minutes of data. Importantly, task data was regressed out of the timeseries in order to provide an approximation of resting state data, given our interest in the stable, intrinsic functional networks often observed using resting state data. In light of a recent study validating this approach by showing strong similarities in network identification and stability between task and resting-state fMRI data (Cole, Bassett, Power, Braver, & Petersen, 2014), we believe this method provides a reasonable approximation of resting-state BOLD signal, allowing us to observe intrinsic functional networks. We applied the motion-correction procedures suggested by Power et al. (Power, Barnes, Snyder, Schlaggar, & Petersen, 2012) in which bad frames were identified and excluded based on movement (if the sum of the displacement across all six rigid body movement correction parameters exceeded 0.2mm) and movement-related intensity changes (if the root mean square (RMS) of difference in intensity between the current and preceding frame normalized by overall image intensity was more than 1.6 of the median across the run). Frames marked as bad were interpolated before temporal filtering, and excluded from nuisance signal regression and computation of correlation matrices.

2.5 Graph Analysis

Network nodes were determined using the atlas of 264-ROIs published by Power et al. (2011). Using convergence from meta-analytic data and functional connectivity mapping, Power and colleagues identified 264 putative functional areas spanning the cerebral cortex, cerebellum, and subcortical structures. Each node was assigned membership to its most likely functional network, based on 13 networks commonly discussed in the literature (visual, auditory, dorsal attention, ventral attention, sensory/somatomotor hand, sensory/somatomotor mouth, default mode, fronto-parietal, cingulo-opercular, memory retrieval, salience, subcortical, and cerebellar). Node assignments for the FPN, CON, and AUD networks were used to construct our network graphs. ROIs for each node were 6mm spheres in 711-2b space.

To ensure that only gray matter signal was included in analysis, the a priori defined 264 ROIs were masked with each individual’s gray matter mask derived from a high resolution T1 structural image using FreeSurfer tissue segmentation. Nine of the 264 ROIs (leaving N = 255) were dropped from our analyses due to lack of overlap with the gray matter mask in some of the subjects. Of the nodes that were dropped, two had “uncertain” network assignments (according to Power et al. 2011), one from the auditory network, three from the default mode network, one from the visual network, and one from the memory retrieval network.

BOLD timecourses for each node were computed by averaging timeseries for all voxels within each node. These average timeseries were then correlated, resulting in a 255×255 whole brain correlation matrix. We then thresholded the whole brain graph by identifying the top 10%-2% highest correlation coefficients (in 1% increments), resulting in nine graphs per subject in which weak or negative correlations were replaced by zeros. All other correlation values were maintained, resulting in a weighted, undirected graph. Thresholding is a standard method in the functional connectivity graph theory literature (Bassett et al., 2009; Bullmore & Sporns, 2009; Lynall et al., 2010; Power et al., 2011; Power, Schlaggar, Lessov-Schlaggar, & Petersen, 2013) as it serves several methodological purposes (Power, Fair, Schlaggar, & Petersen, 2010): 1) it eliminates negative correlations which currently have unclear meaning in graph analysis of functional network topology, 2) it is thought to eliminate small correlation coefficients that likely represent noise, resulting in graphs with only the strongest relationships, leading to more robust functional networks, 3) unlike absolute thresholding (e.g. only including correlation coefficients > .30), it allows for comparison of graphs across groups that may have different distributions of correlation magnitude, a common finding in the schizophrenia literature (Fornito, Yoon, Zalesky, Bullmore, & Carter, 2011). All analyses in this report use the average of graph metrics calculated across 10%-5% thresholds; in other words, graph metrics were first calculated from individual graphs at each threshold value (e.g. global efficiency when maintaining 5% of the edges), and the resulting graph metrics from each threshold were then averaged to yield a single metric of interest. This range of thresholds was chosen based on the stability of our metrics across this range (as can be seen in Figure 1). The 5% threshold corresponded to a minimum r-value of 0.19 in both the schizophrenia and healthy control groups, while the 10% threshold corresponded to a minimum r-value of 0.12 in both groups. Additionally, when using the thresholded whole-brain graphs in the community detection algorithm (described in section 2.6), we found the greatest similarity in the number of communities to our a priori networks for graphs across this range (Figure 2).

Figure 1.

Average graph metrics plotted at each threshold, from 10% - 2%. Dashed lines indicate schizophrenia subjects and solid lines indicate healthy controls. Particularly for the metrics of local and global efficiency, average efficiency appears to be the most stable in the 10% - 5% range. Given that there is no “correct” threshold, this stability, in addition to the number of modules detected in this range (Figure 2), led to our decision to include only those thresholds in the presented Results.

SZ = schizophrenia; HC = healthy controls; WB = whole brain; FPN = fronto-parietal network; CON = cingulo-opercular network; AUD = auditory network; dACC = dorsal anterior cingulate cortex; rAI = right anterior insula; lAI = left anterior insula; rdlPFC = right dorsolateral prefrontal cortex; ldlPFC = left dorsolateral prefrontal cortex

Figure 2.

Average number of communities, as calculated by Louvain’s modularity algorithm, plotted for each group, for each threshold (10% - 2%). Given that Power et al (2011) estimated 13 functional networks, we wanted to select a range of thresholds that provided a similar community structure. The lowest threshold (10%) yielded approximately 8 communities, which is 5 communities less than Power’s. Therefore, if this range is used as our deviation from 13, then the upper limit of communities should be approximately 18, which corresponds to a threshold of 5%. This, along with the data provided in Figure 1, led to our decision to include only threshold 10%-5% in our presented Results.

From the thresholded whole brain graph, we extracted nodes from our a priori networks to create network-specific graphs for the FPN(25×25), the CON(14×14) and the AUD(13×13) for each subject. The auditory network was included as a negative experimental control network, as we did not believe that efficiency of the AUD should influence cognitive performance. Due to this conceptual consideration, as well as the similarity in the size of the graph with the CON, the AUD was chosen as our control. Graph metrics were then calculated separately for each graph. 2.6 Graph Metrics

On each of our four graphs, we calculated the metrics of global efficiency and local efficiency (Bullmore & Sporns, 2009; Power et al., 2013). Nodes comprising specific networks (e.g. the FPN) were isolated from the whole brain graph prior to computation of global and local efficiency. We chose to isolate these networks before calculating efficiency, as opposed to calculating the efficiency for all nodes in the whole brain and then isolating nodes from specific networks, for two main reason: 1) conceptually, we were interested in how efficient nodes within a network were with one another, not taking into account relationships with the rest of the brain that could influence a network’s efficiency, and 2) practically, in the Brain Connectivity Toolbox, global efficiency is a single metric calculated for the whole network, and therefore we could not calculate the global efficiency of a single network without running the algorithm on nodes only in that network. Participation coefficient was calculated using the whole brain graph, as it is a measure of between-network connectivity.

Conceptually, both local and global efficiency are metrics of functional integration that are dependent on an estimate of path length. In anatomical networks, path length represents the physical distance between nodes, with shorter paths leading to more efficient information transfer. In functional networks, path length is dependent on the strength of correlation between nodes, such that stronger statistical dependency indicates a shorter path (Rubinov & Sporns, 2010). Therefore, both local and global efficiency represent the potential for a network to integrate information across nodes; however “efficiency” in functional networks is not a reflection of speed or physical distance, but rather a statistical association that serves as an estimate of a network’s potential for information transfer. Global efficiency provides a single metric for the entire network. This metric is the inverse average shortest path length of all pairs of nodes in the network, such that the shorter the average path length between all nodes in a network, the higher the global efficiency. Global efficiency is thought to represent integration of network-wide communication. In contrast, local efficiency is computed using information about the path length between the neighbors of a single node. Local efficiency is measured on a nodal basis, such that every node has its own measure representing the inverse average path length between neighbors of a node, with stronger nodal connections contributing more to the local efficiency. Therefore local efficiency is averaged across all the nodes in a network to obtain a single measure, which represents the potential for local information transfer (Bullmore & Sporns, 2009, 2012).

In addition to efficiency, we also measured the participation coefficient for our five a priori hub nodes: DACC, right DLPFC, left DLPFC, right AI, and left AI. Participation coefficient is a measure of how many communities, within an individual subject, that a node is functionally connected to, and is thought to be a more accurate representation of “hub-ness” than degree-based measures (Power et al., 2013). Nodes with high participation are often referred to as “hubs”. In order to obtain a node’s participation coefficient we first calculated the modularity of the whole brain network using Louvain’s community-detection algorithm. In this case, a ‘community’ is a mathematically-determined network of nodes that are strongly interconnected, and the algorithm works to maximizes within-community connectivity and minimizes between-community connectivity to determine the community structure of the whole brain. This algorithm was applied to each individual’s whole brain graph, to take into account individual differences in community structure. Module (i.e. community) assignments were then run through a participation algorithm that determined the participation coefficient of each node (for full details on algorithms and Matlab functions, see (Rubinov & Sporns, 2010)).

2.7 Data Analysis

All graph metrics were computed using the Brain Connectivity Toolbox version 2013_12_25 (Rubinov & Sporns, 2010). Statistical analyses were performed using SPSS version 20. Tests of group differences in demographics and task performance were computed using one-way Analysis of Variance (ANOVA), and group differences in average graph metrics were analyzed using three separate MANOVAs. To test the relationship between graph metrics and cognition, separate linear regressions were performed with group, graph metric, and group x metric interactions as predictor variables, each including two steps: in step 1 we entered the variables for group and the graph metric, and in step 2 we entered the group × metric interaction. This method allowed us to model the relationship between graph metrics and cognition while controlling for group membership. Regressions all predicted a variable representing the shared variance across the following task performance measures: BACSsc, HVLT-R, DPX, JOVI Jitter 9, and RISE IRRE. To obtain this measure of shared variance, we performed a principal axis factor analysis for all subjects including these five variables and saved the scores from the first factor (the only factor with an eigenvalue > 1). Only a single RISE outcome measure was included, as the RISE measures are highly inter-correlated and we did not want to bias our factor structure. To correct for multiple comparisons, we used Bonferroni Correction on our a priori hypotheses. For global and local efficiency, significance was set at p<.017 (.05/3; AUD was our negative control network so we did not include it in the correction), and for participation coefficient significance was considered at p<.01 (.05/5; given that there were five a priori hubs). We also performed mediation in SPSS using macros provided by Preacher & Hayes (Preacher & Hayes, 2004). Post-hoc analyses of differences in strength of correlation coefficients was computed using methods from Meng and colleagues (Meng, Rosenthal, & Rubin, 1992).

3. Results

3.1 Demographics

Patients with schizophrenia had significantly lower personal education (F(1,101)=6.8, p=.01) and significantly lower Socio-Economic Status (SES; F(1,101)=32.1, p<.001) than healthy controls (Table 1). Groups did not differ on age, gender, ethnicity, parental education (as a proxy for developmental SES), or pre-morbid IQ (all p’s>.21).

Table 1.

Subject Demographics

Demographics Mean (Standard Deviation)	Healthy Controls n = 54	Schizophrenia n = 46	Statistics
Age (years)	35.3 (12.0)	34.1 (11.5)	F(1,98) = 0.6, p = .45
Gender (male/female)	39/15	37/9	X2 = 0.9, p = .34
Ethnicity (%Caucasian/%African American)	59%/31%	59%/28%	X2 = 5.7, p = .22
Subject Education (years)**	15.4 (2.6)	14.1 (2.3)	F(1,98) = 1.7, p = .01
Subject SES ***	38.3 (10.3)	24.5 (5.8)	F(1,98) = 29.9, p<.001
Pre-morbid IQ (WTAR)	38.3 (10.3)	35.9 (9.5)	F(1,98) = .07, p = .24
Father Education (years)	14.5 (3.1)	14.3 (3.2)	F(1,89) = .001, p = .77
Mother Education (years)	13.7 (3.3)	14.0 (2.4)	F(1,97) = 3.0, p = .74
Positive Symptoms	-	10.1 (5.4)
Negative Symptoms		7.5 (2.3)
Disorganized Symptoms		5.1 (1.8)
Depressive Symptoms		7.7 (3.6)
Manic Symptoms		4.8 (1.5)

Demographics and clinical characteristics of patients with schizophrenia and healthy controls. SES = socio-economic status, measured using the Hollingshead Index as updated using occupational prestige ratings based on the 1989 general social survey (Hollingshead, 1958); WTAR = Wechsler Test of Adult Reading; Symptom scores within the schizophrenia group were calculated using the Brief Psychiatric Rating Scale (BPRS)

^***p<.001,

^**p<.01,

^*p<.05

3.2 Behavioral Data

Schizophrenia participants displayed significant deficits on all cognitive tasks (all F’s>7.12, all p’s<.01; Figure 3). Principal axis factor analysis revealed only one factor with an eigenvalue>1 that explained 40% of the variance across tasks, with schizophrenia participants having significantly lower factor scores than healthy controls (F(1,98)=34.34, p<.001). This factor score reflected the variance associated with performance on tasks from different cognitive domains (verbal memory, episodic memory, processing speed, goal maintenance, and visual integration), and therefore served as a measure of individual differences in global cognitive ability.

Figure 3.

Cohen’s d effect size of differences in cognitive performance between patients with schizophrenia and healthy control subjects. Negative effect sizes represent worse performance in the patient group, compared to controls. BACSsc = Brief Assessment of Cognition in Schizophrenia Symbol Coding; HVLT-R = Hamilton Verbal Learning Test-Revised; IRIE = Item Recognition for Item Encoding from the RISE; IRRE = Item Recognition for Relational Encoding from the RISE; AR = Associative Recognition from the RISE; DPXDP = Dot Probe Expectancy Task d’prime; JOVI Jit9 = Jittered Orientation Visual Integration at a jitter of 9°

*** p<.001, ** p<.01

3.3 Group Differences in Graph Metrics

Across the four sets of graphs (whole brain, FPN, CON, and AUD), we observed a significant main effect of group for local efficiency (F(4,98)=3.00, p=.02; partial η²=0.11) and a trend level group difference in global efficiency (F(4,98)=2.37, p=.06; partial η²=0.09). Examination of the efficiency for each graph revealed that group differences in local efficiency were driven by lower metrics in the FPN, CON, and AUD in patients with schizophrenia relative to controls, and group differences in global efficiency were being driven by lower metrics in the FPN and AUD in patients with schizophrenia, though none of the individual univariate between-subjects effects were significant (p’s>.10; Figure 4). This finding indicated an overall trend for patients to have lower local and global efficiency relative to controls. No main effect of group was observed for participation coefficients across the five a priori nodes (F(5,97)=1.65, p=.15; partial η²=0.08).

Figure 4.

Group differences in graph metrics. A) Trend towards a main effect of group in global efficiency and B) Significant main effect of group for local efficiency. C) No significant main effect of group for participation coefficients. FPN = fronto-parietal network; CON = cingulo-opercular network; AUD = auditory network; dACC = dorsal anterior cingulate cortex; rAI = right anterior insula; lAI = left anterior insula; rdlPFC = right dorsolateral prefrontal cortex; ldlPFC = left dorsolateral prefrontal cortex

3.4 Global Efficiency Predicting Cognition

Whole brain global efficiency significantly predicted global cognition across both groups, as evidenced by a significant main effect of whole brain global efficiency (β=16.91, t(97)=3.15, p=.002) but no significant group × efficiency interaction (p=.94). Looking at individual networks, global efficiency of the FPN (β=3.39, t(97)=2.69, p=.008) and the CON (β=2.42, t(97)=2.87, p=.005) each significantly predicted global cognition (Figure 5; Figure A1) even after correcting for multiple comparisons, but again we observed no significant group × efficiency interactions (FPN: p=.51; CON: p=.63), suggesting a similar relationship between global efficiency and cognitive ability across groups. In contrast, global efficiency of the AUD showed no significant relationship with cognition (β=1.01, t(2,97)=1.20, p=.23) and no significant interaction with group (p=.78). Although FPN and CON global efficiency significantly predicted cognition and AUD global efficiency did not, follow-up analyses revealed that the magnitude of the relationship between FPN global efficiency and cognition was not significantly greater than the relationship between AUD global efficiency and cognition (t(2,98)=1.44, p=.15). The same was true for the CON (t(2,98)=1.48, p=.14).

Figure 5.

Relationship between cognition and global efficiency of a priori networks for all subjects, visualized using residual values after controlling for group. Cognitive ability was significantly positively associated with global efficiency of the A) whole brain, B) fronto-parietal network, and C) cingulo-opercular network, but not D) the auditory network. Trend lines indicate the linear regression line of the relationship between that network’s global efficiency and cognition for all subjects.

3.5 Local Efficiency Predicting Cognition

Local efficiency of the whole brain network significantly predicted cognition across both groups (β=4.75, t(97)=2.75, p=.007), with no significant group × efficiency interaction (p=.97). For the FPN, local efficiency nominally reached our corrected level of significance (correction method explained in section 2.7; β=2.50, t(97)=2.43, p=.017), but CON local efficiency did not significantly predict cognition (β=1.51, t(97)=1.78, p=.08). Local efficiency of the AUD did not significantly predict cognition (β=1.37, t(97)=1.63, p=.11; Figure 6; Figure A2), and the magnitude of the relationship between FPN local efficiency and cognition was not significantly greater than for AUD local efficiency (t(2,98)=0.77, p=.44). Again, no significant interactions with group were observed for local efficiency, pointing to a similar relationship between network metrics and cognition for patients and controls (for relationships between graph metrics and cognition separated by group, see Table 2).

Figure 6.

Relationship between cognition and local efficiency of a priori networks for all subjects, visualized using residual values after controlling for group. Cognitive ability was significantly positively associated with local efficiency of the A) whole brain and B) fronto-parietal network, but did not reach significance for C) cingulo-opercular network or D) the auditory network. Trend lines indicate the linear regression line of the relationship between that network’s local efficiency and cognition for all subjects.

Table 2.

Correlation (Pearson’s r) Between Cognition and Graph Metrics for each Group

	Controls	Schizophrenia
Whole Brain Global Efficiency	.31*	.30*
FPN Global Efficiency	.31*	.24
CON Global Efficiency	.23	.32*
Whole Brain Local Efficiency	.28*	.26
FPN Local Efficiency	.25	.23
Right Anterior Insula Participation Coefficient	.18	.32*

We performed bivariate correlations between our cognition variable (variance shared across tasks, i.e. the first factor), separately for our control group and our schizophrenia group. We observed small to medium effect sizes for the relationship between cognitive ability and each graph metric, within each group. All effect sizes were positive, suggesting that across both groups, higher efficiency and a higher participation coefficient are associated with better cognitive ability.

^*p<.05

3.6 Participation Coefficient Predicting Cognition

Participation of the right anterior insula significantly predicted cognition (β=1.08, t(97)=2.50, p=.01), meeting significance after correcting for multiple comparisons (Figure 7; Figure A3). There was no significant interaction with group (p=.37). Participation of the other a priori nodes were not significant predictors of cognition (all p’s>.24).

Figure 7.

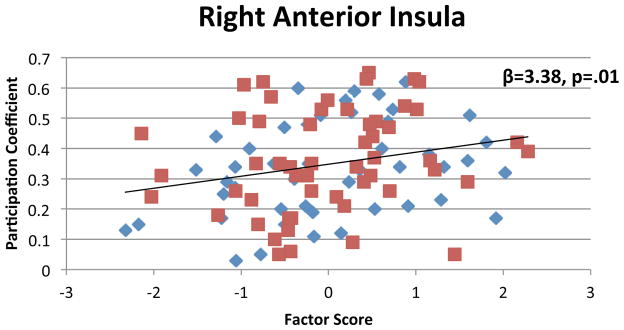
Relationship between cognition and the participation coefficient of the right anterior insula, visualized using residual values after controlling for group. Right anterior insula participation significantly predicted cognition across all subjects. Trend line indicates the linear regression line for all subjects.

3.7 Graph Metrics Predicting Specific Task Performance

Although the aim of this study was to assess relationships between graph metrics and global cognition, we also analyzed relationships between graph metrics and performance on specific cognitive tasks, using the same methods as described above. We found that processing speed performance was significantly predicted by whole brain global efficiency (p=.005) and local efficiency (p=.002), FPN global efficiency (p=.01) and local efficiency (p=.012), and CON global efficiency (p=.01). Verbal learning was significantly predicted by right AI participation (p=.006), whole brain global efficiency (p=.006) and local efficiency (p=.03), and CON global efficiency (p=.002). Finally, visual integration was significantly predicted by whole brain global efficiency (p=.017) and local efficiency (p=.001), FPN global efficiency (p=.008), and CON global efficiency (p=.002) and local efficiency (p<.001). No other significant relationships were observed between graph metrics and performance on specific individual tasks.

3.8 Mediation of Graph Metrics in Predicting Cognition

All graph metrics are calculated from each individual’s whole brain correlation matrix, meaning that they may be inter-dependent. For instance, the participation of a single hub could greatly affect the efficiency of a network, if that network’s characteristic path length is largely dependent on a specific node. Therefore shared variance between metrics may help reveal important network features that would elucidate their relationship with cognitive ability. Given our findings that both global efficiency of the CON and participation of the rAI (a hub within the CON) significantly predict cognition, we ran a mediation analysis to examine whether these relationships were independent.

Using formal mediation analysis, with group included as a covariate, we assessed whether the participation coefficient of the rAI mediated the relationship between CON global efficiency and cognition. This analysis revealed that the rAI did not significantly mediate the relationship between CON global efficiency and cognition (95% CI[−.43, .51]). In this model, the effect of rAI participation on cognition (t=2.51, p=.01) and the direct effect of CON global efficiency on cognition (t=2.35, p=.005) both remained significant, suggesting that the degree to which the rAI communicates with other networks, and the efficiency of information transfer within the CON, make independent contributions to global cognition.

3.9 Motion Analysis

We assessed group differences in motion, as well as relationships between motion, cognition, and functional network topology, in order to determine whether motion was impacting our results – a common concern for functional connectivity data, particularly with clinical populations. Our measure of motion took into account both the number of frames removed for being above a frame displacement of 0.2mm and the normalized displacement between voxels from one frame to the next (above 1.6), for each subject. These motion metrics were used to determine when frames should be eliminated, and when more than 50% of frames were flagged to be eliminated, a subject was excluded from the study.

We found that schizophrenia patients trended towards moving more than controls (t(101) = 1.86, p = .07), in that there was a trend for more frames to be excluded based on our motion criteria. Motion was not significantly related to overall cognition in either group (schizophrenia: r = −.23, p = .11; controls: r = −.22, p = .11), however when the groups were combined, this relationship reached significance (r = −.28, p < .01). In schizophrenia patients, we found that motion was significantly associated with rAI participation (r = −.35, p = .01), and when subjects were included together, we observed a significant relationship between motion and FPN global efficiency (r = −.21, p = .04). However when motion was included in the regression analysis of rAI participation predicting overall cognition and FPN global efficiency predicting overall cognition, relationships between cognition and graph metrics remained significant (rAI: t(99) = 2.24, p = .03; FPN global efficiency: t(99) = 2.31, p = .02).

4. Discussion

The current study utilized novel graph theory analysis of specific functional networks to assess the relationship between efficiency of control networks, participation of hubs within those networks, and cognitive ability in healthy individuals and patients with schizophrenia. This represents one of the first studies to not only measure network topology of a priori functional networks, but also to assess the relationship between those metrics and a complex behavioral measure of cognitive ability. This approach was used to better understand how network integrity relates to cognition in both health and disease-states, in order to gain insight into a broad range of individual differences in global cognitive ability. Given the conceptualization of the FPN and CON as top-down control networks that affect multiple domains of cognition, our measure of cognition reflected shared variance in performance across five tasks that assessed different domains of cognitive function.

4.1 Network efficiency and cognition

Our findings suggest that both the local and global efficiency of specific functional networks contribute to cognitive ability in both healthy individuals and people with schizophrenia. In line with our hypothesis, efficiency of the whole brain, FPN, and CON significantly positively predicted cognition, suggesting that the strength of functional integration within the whole brain and these higher-order cognitive networks are crucial for supporting better cognitive functioning. Importantly, global and local efficiency of our “comparison” network -- the auditory network -- did not significantly predict cognitive ability, providing some specificity to our findings regarding task-positive graphs.

Brain network efficiency is hypothesized by Bullmore & Sporns (2012) to reflect an economic trade-off between wiring cost and an adaptive topology that facilitates connectivity between multiple neuronal populations; the resulting topology appears to balance short and long-distance connections to maximize information integration. Therefore, the observed positive relationship between cognition and efficiency of central executive networks suggests that more robust information transfer within these networks supports better global cognitive ability. These findings replicate previous research showing a negative relationship between characteristic path length and IQ in healthy individuals (van den Heuvel et al., 2009), and extend these findings by revealing that greater efficiency of specific central executive networks is associated with better cognitive functioning. These findings also support the practical and conceptual use of efficiency of individual functional networks in the understanding of cognitive performance and impairments, in both health and disease-states.

4.2 Participation and cognition

In addition to characterizing the efficiency of networks, graph analysis allows for a better understanding of the role of specific functional areas that are particularly important for integrating information across the whole-brain, called hubs. The participation coefficient is one way of quantifying this role, as it measures the number of communities a node shares a functional edge with, outside of that node’s main community. Our a priori hypothesis was that participation of the AI, DACC, and DLPFC would all be associated with cognition, given their putative role as core hubs within the CON and FPN. However, we only observed a significant relationship between cognition and the extent to which the rAI communicated with other communities. Previous work has suggested that the AI aids in domain-free attentional control, based in part on meta-analysis of 10 task-based imaging studies that revealed reliable start-cue and error-related activity in bilateral AI, as well as sustained activation throughout most tasks (Dosenbach et al., 2006). Some researchers have therefore argued that the AI is responsible for basic computational processes related to task-level control and focal attention that are applied to most goal-oriented behaviors (Nelson et al., 2010), implicating this region in the successful performance of a multitude of cognitive functions. Our findings support this interpretation of AI function, given that our measure of cognition reflected shared variance across many different cognitive tasks. Interestingly, participation of the rAI did not significantly mediate the relationship between cognition and CON global efficiency, and both CON efficiency and rAI participation significantly predicted cognition in the same model, indicating independent effects of participation and global efficiency on cognition. This finding points to an interesting relationship between within-network and between-network properties in supporting cognitive ability, such that both methods of functional communication may be independently necessary for cognitive performance across many goal-directed tasks.

4.3 The role of network integrity in schizophrenia

Previous research has found that patients with schizophrenia show reduced activation of regions within the FPN and CON during many different tasks (Meyer-Lindenberg et al., 2001; White et al., 2010), and have reduced connectivity both within and between these networks when measured at rest (Repovs et al., 2011). These networks are considered crucial players in top-down task control across different cognitive domains (Dosenbach et al., 2006), and top-down control is hypothesized to serve a fundamental role in mental health (for review, see (Cole, Repovs, et al., 2014)). Several graph theory studies in schizophrenia have revealed reduced small-worldness and reduced clustering in schizophrenia compared to controls (Liu et al., 2008; Rubinov et al., 2009). In addition a meta-analysis suggested that the right insula has reduced activation in schizophrenia patients during a variety of executive function tasks (Minzenberg, Laird, Thelen, Carter, & Glahn, 2009). In fact, a recent study using Granger analysis and confirmatory Structural Equation Modeling found that the rAI had disrupted functional connectivity with the central executive and default mode networks in schizophrenia (Moran et al., 2013), while another study using Granger analysis of resting state in schizophrenia revealed a failure of the insula to influence the DLPFC -- a region within the FPN (Palaniyappan, Simmonite, White, Liddle, & Liddle, 2013).

Given this background, we were surprised to observe a lack of robust group differences in network metrics, though there were trends for reduced local and global efficiency of the FPN, CON, and AUD in schizophrenia. This is particularly surprising given the worse behavioral performance on all tasks in the schizophrenia group and the relationships between graph metrics and cognition. One possible explanation for the differences in our results and those of previous studies is differing methodologies. Given that graph analysis of functional connectivity data is still a relatively young field, methodological choices can vary widely between studies, and it is not yet fully clear how specific methodological choices influence patterns of group differences. For example, Lynall and colleagues (2010) found significantly reduced small-worldness and clustering in schizophrenia, but they analyzed only 72 brain regions, thousands fewer connections in their whole brain matrix than in the current study, which used 255 regions validated from Power et al (2011). It is possible that we would have found more evidence for overall reduced global or local efficiency had we used a smaller number of regions, but we felt that the choice to use a published and validated parcellation system was an important one. Additionally, choices about methods for motion correction can greatly influence results. The current dataset utilized a much more stringent motion correction protocol than is common in the schizophrenia literature. Individual differences in motion did not impact our observed relationships between network metrics and cognition. However, motion was significantly negatively correlated with our FPN global efficiency, rAI participation, and trended towards being significantly greater in the schizophrenia group. Therefore, previous studies using less stringent motion correction may have found greater evidence for reduced clustering or other metrics in part because of confounds associated with movement. Our sample was also comprised of relatively high functioning patients with schizophrenia, who could tolerate over an hour in an MRI scanner while completing multiple cognitive tasks. This characteristic of our sample may have reduced our power to detect more robust group differences, which might be observable in schizophrenia patients who are more impaired. Further, the existing literature is not completely homogenous, as some studies have not found group differences in FPN and CON connectivity (Fornito et al., 2011), and Lynall et al (2010) found slightly increased global efficiency in schizophrenia, as compared to controls.

Undoubtedly much more work must be done to determine best practices in graph theory analysis of functional connectivity. Nonetheless, our data clearly support the hypothesis that efficiency of specific functional networks and the participation of the rAI are important for understanding cognitive ability across the spectrum of health and disease, but also suggest that the generalized cognitive deficit in schizophrenia cannot be fully understood through this lens of network efficiency and node participation.

4.4 Limitations

One potential limitation of our study was the use of pseudo-resting state data. One concern is that this approach may not sufficiently approximate resting state data and could be influenced by task performance. However, this concern is mitigated by the aggregation of data across three different tasks, making it more likely that the residual correlational structure (i.e. functional connectivity) is reflecting signal that is common across all tasks. This concern is further mitigated by recent work showing strong similarities in the patterns of functional connectivity generated by resting state and task data residuals (Cole, Bassett, et al., 2014). That said, the possibility remains that our pseudo-resting state data was a noisier or less precise estimate of intrinsic neural fluctuation than is ‘pure’ resting state data, which may have reduced our power to detect group differences in graph metrics in our study. An additional limitation is that our schizophrenia patients were all taking antipsychotic medications, though previous studies do not suggest that such cognitive deficits are due to antipsychotic medications (Goldberg & Weinberger, 1996; Keefe et al., 2007). Studies showing reductions in graph metrics in schizophrenia have also included patients taking antipsychotic medications (Lynall et al., 2010; Bassett et al., 2009), suggesting that antipsychotics cannot explain our lack of group differences, although there is some evidence that resting state functional connectivity is altered following six weeks of antipsychotic treatment in formerly drug naive patients (Lui et al., 2010).

4.5 Conclusions

This study demonstrates that efficiency of the whole brain, FPN and CON are significantly positively associated with cognitive ability in both health and schizophrenia, corroborating and extending prior research on the importance of these functional networks in supporting cognitive performance. In addition, our finding of a relationship between participation of the rAI and cognition points to this region’s critical role in coordinating information transfer throughout the whole brain.

• Global and local efficiency of functional brain networks predicts cognitive ability

• Participation of the right anterior insula predicts cognitive ability

• Network metrics may help explain the general cognitive deficit in schizophrenia