Large Ca²⁺-dependent facilitation of Ca_V2.1 channels revealed by Ca²⁺ photo-uncaging

Abstract

Key points

• Ca_V2.1 channels constitute a dominant Ca²⁺ entry pathway into brain neurons, triggering downstream Ca²⁺-dependent processes such as neurotransmitter release.

• Ca_V2.1 is itself modulated by Ca²⁺, resulting in activity-dependent enhancement of channel opening termed Ca²⁺-dependent facilitation (CDF).

• Real-time Ca²⁺ imaging and Ca²⁺ uncaging here reveal that CDF turns out to be strikingly faster, more Ca²⁺ sensitive, and larger than anticipated on previous grounds.

• Robust resolution of the quantitative profile of CDF enables deduction of a realistic biophysical model for this process.

• These results suggest that Ca_V2.1 CDF would figure most prominently in short-term synaptic plasticity and cerebellar Purkinje cell rhythmicity.

Abstract

Ca_V2.1 (P-type) voltage-gated Ca²⁺ channels constitute a major source of neuronal Ca²⁺ current, strongly influencing rhythmicity and triggering neurotransmitter release throughout the central nervous system. Fitting with such stature among Ca²⁺ entry pathways, Ca_V2.1 is itself feedback regulated by intracellular Ca²⁺, acting through calmodulin to facilitate channel opening. The precise neurophysiological role of this calcium-dependent facilitation (CDF) remains uncertain, however, in large measure because the very magnitude, Ca²⁺ dependence and kinetics of CDF have resisted quantification by conventional means. Here, we utilize the photo-uncaging of Ca²⁺ with Ca_V2.1 channels fluxing Li⁺ currents, so that voltage-dependent activation of channel gating is no longer conflated with Ca²⁺ entry, and CDF is then driven solely by light-induced increases in Ca²⁺. By using this strategy, we now find that CDF can be unexpectedly large, enhancing currents by as much as twofold at physiological voltages. CDF is steeply Ca²⁺ dependent, with a Hill coefficient of approximately two, a half-maximal effect reached by nearly 500 nm Ca²⁺, and Ca²⁺ on/off kinetics in the order of milliseconds to tens of milliseconds. These properties were established for both native P-type currents in cerebellar Purkinje neurons, as well as their recombinant channel counterparts under heterologous expression. Such features suggest that CDF of Ca_V2.1 channels may substantially enhance the regularity of rhythmic firing in cerebellar Purkinje neurons, where regularity is believed crucial for motor coordination. In addition, this degree of extensive CDF would be poised to exert large order-of-magnitude effects on short-term synaptic plasticity via rapid modulation of presynaptic Ca²⁺ entry.

Introduction

Ca_V2.1 channels are perhaps the most abundant voltage-gated Ca²⁺ channel in the mammalian brain (Mori et al. 1991), furnishing a dominant Ca²⁺ entry pathway into presynaptic release terminals (Hillman et al. 1991; Dunlap et al. 1995; Westenbroek et al. 1995; Craig et al. 1998), as well as into somatic and postsynaptic compartments (Regan, 1991; Usowicz et al. 1992; Indriati et al. 2013). These channels thereby constitute the pre-eminent trigger of neurotransmitter release in the CNS (Uchitel et al. 1992), initiate Ca²⁺-dependent forms of synaptic and developmental plasticity (Zucker & Regehr, 2002; Finch et al. 2012; Lamont & Weber, 2012; Miyazaki et al. 2012; Wheeler et al. 2012), and support and modulate dendritic Ca²⁺ spiking important for motor coordination (Womack & Khodakhah, 2002, 2004). In all, dynamic regulation of Ca_V2.1 activity is probably a significant contributor to the complexity and richness of neurophysiology and neurocomputation.

Early studies in squid reported that the amplitude of voltage-gated Ca²⁺ currents changed little with altered stimulation patterns, suggesting that other Ca²⁺-dependent processes were responsible for differing forms of rapid Ca²⁺-dependent plasticity (Charlton et al. 1982). For example, paired-pulse facilitation of synaptic efficacy has been attributed to the accumulation of residual Ca²⁺ that primes Ca²⁺ triggering sites for vesicle release, and short-term synaptic depression has been explained in terms of vesicle depletion (Regehr, 2012). These mechanisms have attracted considerable interest because short-term synaptic plasticity is considered to be essential for the neurocomputational repertoire of the brain (Abbott & Regehr, 2004). That said, if the amplitude of Ca_V2.1 currents were variably modulated by recent activity, an additional and powerful class of plasticity mechanisms would arise.

More recently, rapid voltage-dependent inactivation (VDI) has been identified in Ca_V2.1 channels paired with certain auxiliary β subunits (De Waard & Campbell, 1995). In certain contexts where such subunits predominate, it has been argued that such VDI could underlie forms of short-term synaptic depression (Patil et al. 1998). Apart from VDI, Ca²⁺–calmodulin (Ca²⁺–CaM) regulation of Ca_V2.1 channels has emerged as another potential mechanism supporting activity-dependent plasticity (Lee et al. 2000; DeMaria et al. 2001). Intriguingly, CaM regulation of Ca_V2.1 exhibits a bipartite format relating to the lobes of an indwelling CaM bound to the intracellular carboxy tail of channels (DeMaria et al. 2001; Erickson et al. 2001). Ca²⁺ binding to the C-terminal lobe of CaM induces CDF, whereas Ca²⁺ binding to the N-terminal lobe of CaM induces a Ca²⁺-dependent inactivation (CDI) (DeMaria et al. 2001). Indeed, there have been hints that such forms of regulation are at play within neuronal preparations (Borst & Sakmann, 1998; Xu et al. 2007; Mochida et al. 2008; Adams et al. 2010; Catterall et al. 2013), and there have been significant efforts to clarify the structure–function underpinnings of such channel regulation (DeMaria et al. 2001; Lee et al. 2003; Kim et al. 2008; Mori et al. 2008).

Nonetheless, progress has been stymied by the inability to quantify CDF and CDI in more than a cursory qualitative manner. Even the coarse Ca²⁺ sensitivity and magnitude of these forms of regulation remain obscure, complicating efforts to ascribe physiological relevance and decipher structure–function mechanisms. These limitations are particularly acute for CDI of Ca_V2.1 channels, which can only be robustly induced when large Ca²⁺ currents are present with minimal levels of Ca²⁺ buffering (Soong et al. 2002). Thus, the levels of Ca²⁺ required for CDI may exceed physiological bounds.

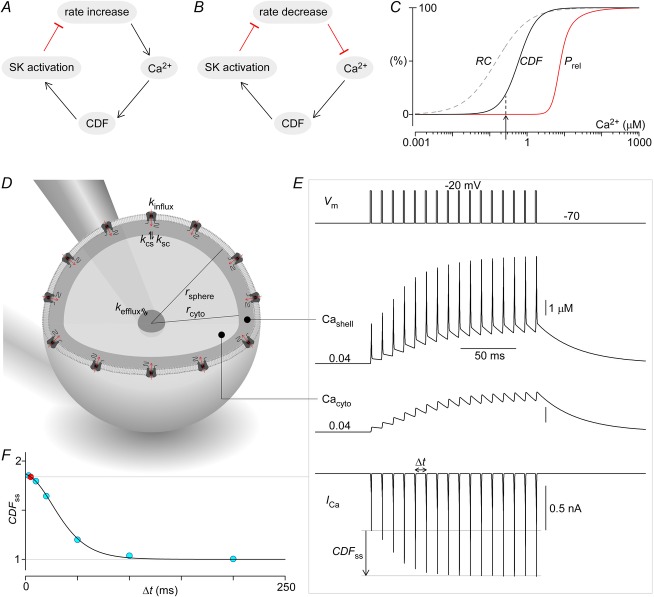
To overcome these limitations, we scrutinized the obstacles to determining the Ca²⁺ sensitivity of Ca_V2.1 regulation as illustrated in Fig.1A. One typically quantifies channel regulation by measuring whole-cell Ca²⁺ currents (I), whose magnitude is specified by channel activation gating (top left box) that is modulated by a CaM regulatory system (top right box in red). However, the Ca²⁺ concentration at the inner mouth of the channel, labelled as nanodomain Ca²⁺ in Fig.1B, constitutes the actual input to the CaM regulatory module, and this nanodomain Ca²⁺ is difficult to measure and control. The challenges arise because nanodomain Ca²⁺ results from the superposition of local Ca²⁺ fluxing through a ‘home’ channel (Fig.1B, red arrow) and global Ca²⁺ sources comprising other Ca²⁺ channels, transport pathways and internal stores. The local Ca²⁺ input is complex, reflecting stochastic channel gating, as well as local diffusion and Ca²⁺ buffering near the channel mouth (Fig.1A, ‘local’ pathway). The global Ca²⁺ input derives from the activity of other Ca²⁺ channels and sources at a distance, as shaped by cellular Ca²⁺ diffusion, geometry and buffering (Fig.1A, ‘global’ pathway). There are numerous unknowns among these multiple determinants of local and global Ca²⁺ inputs. Moreover, the relevant nanodomain Ca²⁺ concentration cannot be measured in most instances, because commonly used Ca²⁺ fluorescent dyes only furnish readouts of spatially averaged global Ca²⁺ (Fig.1B, light-shaded region), and more intricate near-field measurements are currently impractical for the present question (Tay et al. 2012). For CDF, further challenges arise because channel facilitation transpires rapidly over a time scale similar to the growing opening of channels following the onset of a voltage step (Fig.1A, ‘activation gating’). Hence, it is difficult to disambiguate the contributions of CaM-mediated CDF and voltage activation. As a result, previous attempts to quantify CDF have done so indirectly, either by estimating the degree to which channels can be prefacilitated during a preceding voltage step (DeMaria et al. 2001; Chaudhuri et al. 2007; Adams et al. 2010), or by monitoring the gradual increase in currents in response to a train of brief voltage steps (Lee et al. 2000, 2003; Chaudhuri et al. 2007). Though useful for appraising relative changes in CDF, such methods do not quantify the absolute extent of CDF, and can only assess regulation over a narrow voltage range near the midpoint of voltage activation.

Figure 1. Ca²⁺ sources influencing Ca_V2.1 opening.

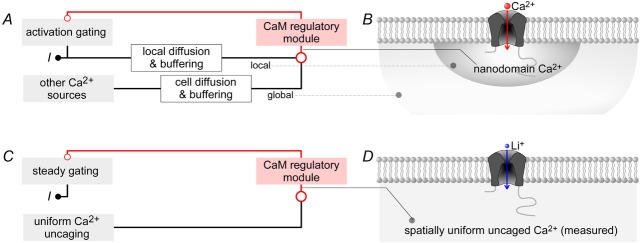
A and B, Ca²⁺–CaM regulation of channels arises from a superposition of local and global Ca²⁺ sources. Ca_V2.1 channels stimulated by a voltage step give rise to Ca²⁺ current I, which is proportional to channel activation gating. The Ca²⁺ current, shaped by local diffusion and buffering, creates a local nanodomain Ca²⁺ signal that feeds into the CaM regulatory module, which bestows feedback modulation on activation gating. Concurrently, Ca²⁺ from distant channels shaped by cell diffusion and buffering creates a global Ca²⁺ signal which is also an input into the CaM regulatory module. C and D, simplified scheme employing Li⁺ as charge carrier. Stimulating Ca_V2.1 here gives rise to Li⁺ current I, which is allowed to reach steady state (steady gating) before Ca²⁺ is uncaged to influence the CaM regulatory module. Importantly, in this system, Ca²⁺ uncaging generates the only Ca²⁺ signal, which is spatially uniform and measurable.

Thus appraised, we here devised strategies to directly measure and control nanodomain Ca²⁺ while recording Ca_V2.1 whole-cell currents at steady state with respect to activation gating. Figure1C and D schematizes the overall approach, where Li⁺ is substituted for Ca²⁺ as charge carrier through these channels (Fig.1D). In so doing, Ca²⁺ influx through channels no longer triggers CaM regulation, and channel gating is uncoupled from induction of the CaM regulatory module (Fig.1C). Instead, uniformly dialysed DM-nitrophen (caged Ca²⁺) is photolysed to abruptly produce spatially uniform Ca²⁺ elevations throughout the cytoplasmic compartment, including the channel nanodomain (Fig.1D). Furthermore, ratiometric Ca²⁺ fluorescent dyes permit real-time measurement of Ca²⁺ concentration. Accordingly, we directly control and measure the Ca²⁺ input to the CaM regulatory module (Fig.1C) (Tadross et al. 2013; Ben-Johny et al. 2014). Importantly, photo-uncaging can be produced well after channels have achieved steady state with respect to voltage activation, so that the changes in Ca_V2.1 current directly reflect the effects of CaM regulation alone (Fig.1C, steady gating).

Using this approach, we now find that CDF of Ca_V2.1 is larger, faster and more Ca²⁺ sensitive than expected. Importantly, the properties of CDF render Ca²⁺ current modulation particularly strong during physiological spike-like voltage stimuli. By contrast, CDI turns out to be more than 50-fold less Ca²⁺ sensitive, such that CDF can, in many instances, develop in isolation from CDI. Our results pertain to both recombinant Ca_V2.1 channels and native Ca_V2.1 currents within cerebellar Purkinje neurons. Moreover, Ca_V2.1 behaviour in both contexts could be quantitatively predicted by a common biophysical model of Ca_V2.1 gating and CDF, gleaned from extensive experimental constraints. Overall, CDF of Ca_V2.1 channels is well positioned to influence activity-dependent processes throughout the CNS.

Methods

Molecular biology

The parental human Ca_V2.1 clones were gifts from Dr Terry Snutch (University of British Columbia). The exact splice background (Soong et al. 2002) used was: Δ10A (+G); 16⁺/17⁺; Δ17A (−VEA); −31* (−NP); 37a (EFa) or 37b (EFb); 43⁺/44⁺; 47⁻ or 47⁺. Henceforth, for compactness, we will refer to the main constructs as EFa −47, EFb +47 and EFb −47. The entire channel ORF was transferred into the pEGFP-N3 vector (Clontech, Mountain View CA) with restriction enzymes Nhe1/XbaI for ease of mutagenesis (enhanced green fluorescent protein (eGFP) coding sequence replaced). The EFb variant in this same background was generated by transferring the relevant region from our Ca_V2.1 EFb clone (Soong et al. 2002) with XhoI/BglII. The pore mutants were all generated by overlap extension PCR, as previously described (Ho et al. 1989). The primers used to generate E1A were: CCCGTCCGACAGAACTGCCTC (flank1_F), GATCAGTCCACCCTgCCATGGTTATGC (E1A_R), GCATAACCATGGcAGGGTGGACTGATC (E1A_F) and TAGGGTCCCTCCCGGCTCAG (flank1_R). The PCR product containing the mutation was then transferred back into our channel backbone with AgeI/PvuI. E2A was generated with the same flanking primers and restriction enzymes, with these overlap primers: CCTGACGGGCGcAGACTGGAAC (E2A_F) and GTTCCAGTCTgCGCCCGTCAGG (E2A_R). The primers for E3A were AACAGGCCCGCTACCACG (flank3_F), CCAGCCTgCTCCCGTGGAC (E3A_R), GTCCACGGGAGcAGGCTGG (E3A_F) and GAAGTTATTCCCAAACTCAGTCACGAGG (flank3_R), and transferred with enzymes PvuI/EcoRV. The primers for E4A were TGTTCTGGGCAGCATCACCG (flank4_F), GCCAAGCTgCCCCGG TGG (E4A_R), CCACCGGGGcAGCTTGGC (E4A_F) and CAGCTTCTTGGCCTTGCTCTGC (flank4_R), and inserted with enzymes EcoRV/BglII. All mutants were verified by Sanger sequencing.

Cell culture and transfection

Human embryonic kidney 293 (HEK 293, ATCC) cells were cultured under sterile conditions on glass coverslips in 60 mm plates at 37°C with 5% CO₂, and transiently transfected with a calcium phosphate protocol (Brody et al. 1997). We used 2–5 μg of cDNA encoding the desired channel α₁ subunit, with 4 μg each of rat brain β2a and α2δ subunits. SV40 T-antigen, 1 μg, and cyan fluorescent protein (CFP), 1 μg, were also co-transfected to enhance expression and identify transfected cells. For experiments not involving Ca²⁺ uncaging, β2a-IRES2-eGFP was used in place of β2a plus CFP to identify transfected cells. All constructs were driven by a CMV promoter, and cells were used for electrophysiology 1–3 days after transfection.

Dissociated Purkinje neurons

Cerebellar Purkinje neurons were isolated from postnatal day (P) 14–18 C57/B6 mice (Jackson Labs, Bar Harbor ME) as previously described (Adams et al. 2010). Animals were handled according to protocols approved by the Johns Hopkins University's Animal Care and Use Committee. Briefly, mice were anesthesized with isoflurane, and swiftly decapitated with a guillotine. Purkinje neurons were then enzymatically dissociated from cerebellar cortex and plated on poly-d-lysine-coated glass-bottom dishes (In Vitro Scientific, Sunnyvale CA). Cells were allowed to recover for 1 h at room temperature before experimentation.

Electrophysiology

For both HEK 293 cells and Purkinje neurons, whole-cell recordings were obtained using Axopatch 200 or 200A amplifiers (Molecular Devices, Sunnyvale CA) at room temperature. Electrodes were pulled (model P-97, Sutter Instruments, Novato CA) from borosilicate glass capillaries (MTW 150-F4, World Precision Instruments, Sarasota FL) and fire-polished with a microforge (Narishige, Tokyo) to achieve resistances of 1–3 MΩ before series resistance compensation of 70–80%. Currents were low-pass filtered at 5 kHz, and leak-subtracted with a P/4–P/8 protocol. Data acquisition (digitized with ITC-18 (Instrutech, Longmont CO)) and analysis of electrophysiological data were done with custom software written in MATLAB (MathWorks, Natick MA).

Whole-cell solutions

Internal solutions

For the Ca²⁺ block and pre-pulse CDF characterizations, the internal solution contained (in mm): 135 CsMeSO₃, 5 CsCl, 1 MgCl₂, 4 MgATP, 1 EGTA, 10 Hepes, with pH titrated to 7.4 with CsOH, and adjusted to 295 mosmol l⁻¹ with glucose. For Ca²⁺-uncaging experiments the internal solution contained: 135 mm CsCl, 40 mm Hepes (pH 7.4), 1–2 mm citrate, 5 μm Fluo-2 (TefLabs, Austin TX) + 5 μm Fluo-2 Low Affinity (TefLabs), 2.5 μm Alexa568 (Invitrogen, Waltham MA), 2 mm DM-Nitrophen (DMNP-EDTA) (Invitrogen) and 0.25–1 mm CaCl₂. The two Ca²⁺ dyes with different Ca²⁺ sensitivities were combined with Alexa568 for increased dynamic range of ratiometric Ca²⁺ detection. Calibration of premixed stocks of Fluo/Alexa was performed both in vitro with droplets and also in vivo by patching HEK 293 cells in the whole-cell configuration with internal solutions containing different free Ca²⁺ concentrations, buffered by either 5 mm EGTA, 5 mm HEDTA, or 5 mm NTA. Free Ca²⁺ concentrations were calculated with MaxChelator (Stanford).

External solutions

For characterizations of CDF with the pre-pulse protocol, the bath solution contained (in mm): 140 TEA-MeSO₃, 10 Hepes (pH 7.4 with TEA-OH) and 5 CaCl₂ or 5 BaCl₂, adjusted to 295 mosmol l⁻¹ with glucose. For Ca²⁺ block experiments, bath solution contained (in mm): 80 TEA-MeSO₃, 10 Hepes (pH 7.4), 80 LiCl and 0.5–2.5 CaCl₂ buffered by 5 EGTA, 5 HEDTA or 5 NTA depending on the desired concentration of free Ca²⁺ (295 mosmol l⁻¹ with glucose). Free Ca²⁺ concentrations of these solutions were calculated using MaxChelator (Stanford). For Ca²⁺-uncaging experiments, bath solution contained (in mm): 80 TEA-MeSO₃, 10 Hepes (pH 7.4), 80 LiCl and 2 EGTA (295 mosmol l⁻¹ with glucose). Unless otherwise specified, all reagents were obtained from Sigma-Aldrich.

Ca²⁺ imaging and uncaging

All Ca²⁺-uncaging experiments were done on a Nikon TE2000-U inverted microscope with a 40×/1.3 Plan Fluor objective as previously described (Tadross et al. 2013). Briefly, dyes are excited by a 514 nm argon laser, with the resulting fluorescence obtained at two channels after splitting by a 545 DCLP dichroic mirror, and filtering either with 545/40BP (Fluo) or 580LP (Alexa568). Brief UV pulses were generated by a UV flash photolysis system (Cairn Research, Kent, England), with varying UV intensities achieved by adjusting the voltage (50–200 V) and total capacitance (500–4000 μF) of the capacitor bank. The fluorescence of our two dyes as a function of Ca²⁺ is a superposition of the Ca²⁺ response of each dye, and exhibits the following relation:

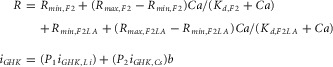where R is the measured green/red fluorescence ratio. We determined R_min and R_max of Fluo-2 (F2) and Fluo-2 Low Affinity (F2LA) dyes by whole-cell dialysis of HEK 293 cells with carefully buffered Ca²⁺ solutions, containing each dye and verified that the in vivo K_d values for both dyes (0.39 and 6.7 μm) were the same as the in vitro K_d values provided by the manufacturer (TEFLabs). Intracellular Ca²⁺ concentration (Ca) was then determined from the measured R by numerically inverting the above equation.

Simulations: Ca_V2.1 channel models

The basic unfacilitated channel model consists of six states, with four transitions amongst five closed states before a final transition to the open state. The parameters of these rate constants were chosen such that they fit both the steady-state open probability (P_o) versus voltage relations (Fig.5E) as well as the kinetics of channel activation and deactivation in response to voltage steps (Fig.5B).

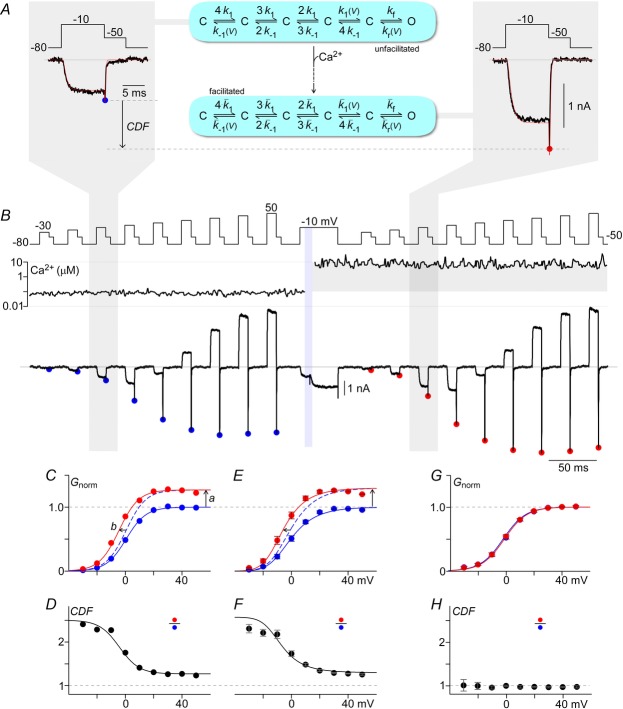
Figure 5. Contrasts between facilitated and non-facilitated channels at various potentials.

A and B, protocol to define conductance–voltage (G–V) curves of unfacilitated and facilitated channels. Li⁺ tail currents from Ca_V2.1 EFa E3A are elicited at −50 mV after 10 ms step depolarizations ranging from −30 to 50 mV. The peak tail currents before (blue) and after (red) Ca²⁺ uncaging are marked with filled circles. Ca²⁺ is uncaged during a 40 ms voltage step at −10 mV to monitor progression of CDF. A, expanded view of tail currents (black) after voltage steps to −10 mV before (left) and after (right) Ca²⁺ uncaging. A kinetic model of Ca_V2.1 channel gating is illustrated (middle), with simulation results (red, left and right) overlaid on the data. Parameters for model shown in Fig.6C, exemplar G–V from B. The peak of the tail currents, normalized to the peak currents after steps to 40 and 50 mV at baseline Ca²⁺ (blue), provides an assessment of how the voltage activation curve changes in response to Ca²⁺ (red). Two effects are seen: an increase in G_max (a), and a left shift of ∼5 mV (b). D, CDF vs. voltage from B. E and F, similarly, population data (mean ± SEM) with n = 7 cells where Ca²⁺ was raised > 3 μm. Smooth fit lines are from simulations of the channel model illustrated in A (middle). G and H, population data for Ca_V2.1 EFb E3A (mean ± SEM) with Ca²⁺ uncaged to > 3 μm for n = 7 cells.

The full channel model with CDF consists of 3 × 6 states, as illustrated in Fig.8B. The horizontal transitions within the first two rows of states are identical to that of the basic unfacilitated model. The last row of states, however, represents the facilitated mode, with 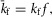and 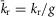, such that the facilitated channel has a larger maximal P_o and increased open times. Additionally, the rate of transitions between the closed states were boosted slightly (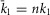; ; 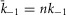n = 1.1) to match the kinetics of voltage activation when channels are fully facilitated (Fig.5B, right). The vertical transitions between states of the three rows are determined by the kinetics of CDF (Fig.8). As there was no discernible voltage dependence to CDF (Fig.7F), the vertical transitions across each of the columns of states are identical, with the exception of the lower-right transition between the open states of rows 2 and 3 where 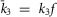and 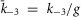to maintain the necessary path independence. This model is easily represented as a system of differential equations, which was numerically integrated in MATLAB with a stiff ODE solver (ode23s). The channel open probability P_o is the probability of residing in any of the three open states, and the simulated macroscopic current is then: 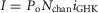, where i_GHK is the voltage-dependent unitary current and N_chan represents the number of channels.

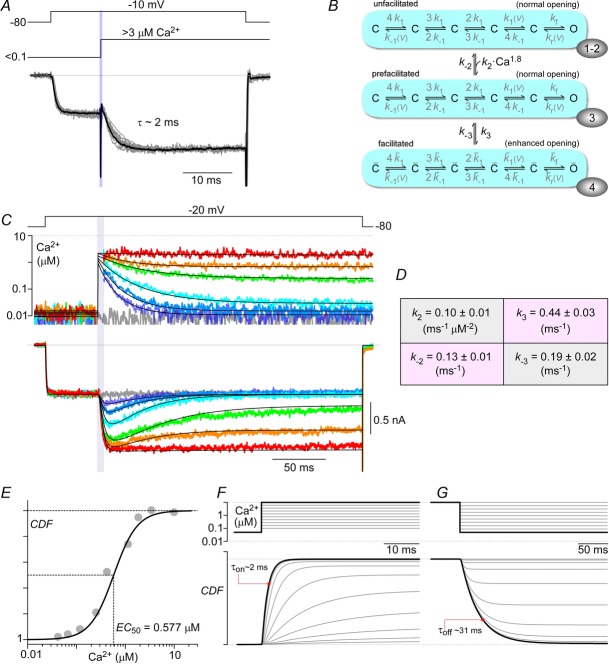
Figure 8. Dynamic Ca²⁺ responsiveness of CDF.

A, saturating on-kinetics of CDF. Individual normalized current records (grey) from 10 cells, where intracellular Ca²⁺ was uncaged to >3 μm, are shown overlaid together with their average (black line), fitted by a single exponential with τ = 2 ms. B, Ca_V2.1 channel model, where the vertical Ca²⁺-dependent transitions have 3 states (rows), with transitions between 2nd and 3rd rows having no Ca²⁺ dependence. The correspondence of these three gating modes to previously described conformations underlying CaM regulation of Ca²⁺ channels (Tadross et al. 2008) is denoted by the numbers within ovoids at the lower right edge of each gating mode. Conformation 1 corresponds to a channel in which the C-terminal lobe of Ca²⁺-free CaM (apoCaM) is bound to a channel pre-association site; conformation 2 depicts a channel wherein this lobe of apoCaM transiently unbinds from the pre-association site; conformation 3 displays a channel where this transiently unbound lobe of CaM complexes with Ca²⁺, and conformation 4 represents the channel after the Ca²⁺-saturated lobe of CaM has interacted with a channel effector site to produce facilitation. For simplicity, conformations 1 and 2 have been combined in simulations used in the present study. C, examplar traces from a single cell, where a family of time-varying Ca²⁺ inputs by Ca²⁺ uncaging (second row) trigger a corresponding family of kinetically distinct CDF records (last row). The continuous black lines on the Ca²⁺ and current axes represent the fit to the Ca²⁺ waveforms used as the input and the output of the channel model, respectively. Parameters for the model are shown in D (mean ± SEM), obtained from fitting n = 8 cells. E, these parameters yield a Ca²⁺ sensitivity curve matching data from Fig.3E (grey circles). F and G, simulations of step increases and decreases of intracellular Ca²⁺ show that the maximal ‘on’ and ‘off’ responses have time constants of 2 ms and 31 ms.

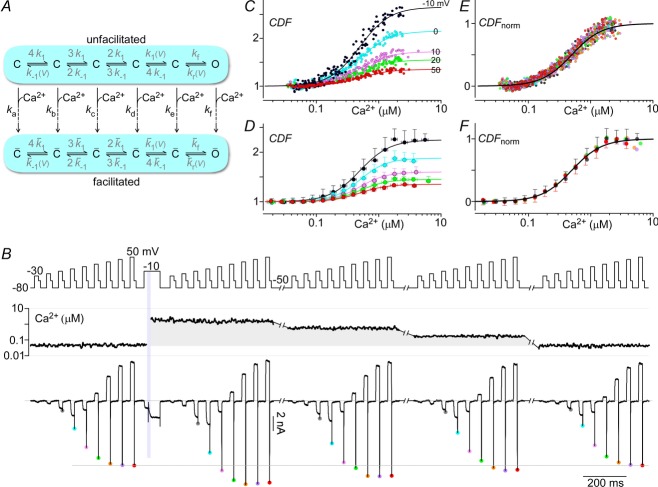
Figure 7. Voltage insensitivity of Ca²⁺-driven conversion to facilitated channels.

A, diagram of channel model illustrating the possibility of having multiple rate constants (k_a–k_f) driving channels towards facilitated states. B, multiple G–V curves are obtained with tail protocols before and after uncaging Ca²⁺. As the intracellular Ca²⁺ concentration drops over time, the peak tail currents correspondingly decrease. C, the peak Li⁺ currents plotted against the intracellular Ca²⁺ charts out the steady-state CDF vs. Ca²⁺ curves for the voltages assessed. D, normalized CDF vs. Ca²⁺ for voltages from −10 to 50 mV show that CDF at different voltages have the same Ca²⁺ sensitivity. E and F, as above, population data (mean ± STD) shown for n = 7 cells. All fits are Hill equations with n_Hill = 1.8 and EC₅₀ = 0.5 μm.

In Figs5, 6 and 8, [Ca²⁺] and transmembrane voltage were supplied as inputs into the model, with the channel currents calculated as above, where:

Figure 6. Physiologically relevant action potential waveforms have significant CDF.

A, parameters of channel model illustrated in Fig.5A in the unfacilitated and facilitated states. B and C, Ca_V2.1 E3A permeating Li⁺ currents are triggered by action potential waveforms recorded from cerebellar Purkinje neurons. Stimulated currents are steady at baseline Ca²⁺ (C, left). Ca²⁺ uncaging in the midst of the ∼50 Hz train causes large enhancement of Li⁺ current (C, right). An expanded view of traces before and after Ca²⁺ elevation (black) are shown in B, with simulation results overlaid (red). D and E, population data (mean ± SEM) for peak Li⁺ current as a function of time with n = 5 cells.

The voltage-dependent unitary current (i_GHK) consists of a superposition of two GHK equations, because Ca_V2.1 E3A channels permeate both inward Li⁺ and outward Cs⁺ currents with relative permeabilities P₁ and P₂. Furthermore, outward current declines relative to expected GHK current at more depolarized voltages due to voltage-dependent pore block, represented here by b, a voltage-dependent Boltzmann factor.

Physiological model

A spherical cell/synapse was divided into three symmetrical compartments, representing a thin shell near the membrane, the cytosol and a reservoir for Ca²⁺ efflux (Fig.1D). Ca_V2.1 channels provide Ca²⁺ influx into the shell compartment, and the resulting Ca²⁺ can then diffuse into the remaining compartments, informed by the following differential equations:

where 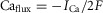, where F is Faraday's constant, and 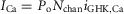. P_o is determined from the 18-state model described above, where V was provided as an input, and Ca_shell was used as the Ca²⁺ signal to facilitate Ca_V2.1 channels. This 20-state model was then solved numerically with MATLAB using the stiff ODE solver as before.

Results

Minimizing Ca²⁺ block of Li⁺ currents carried by Ca_V2.1 channels

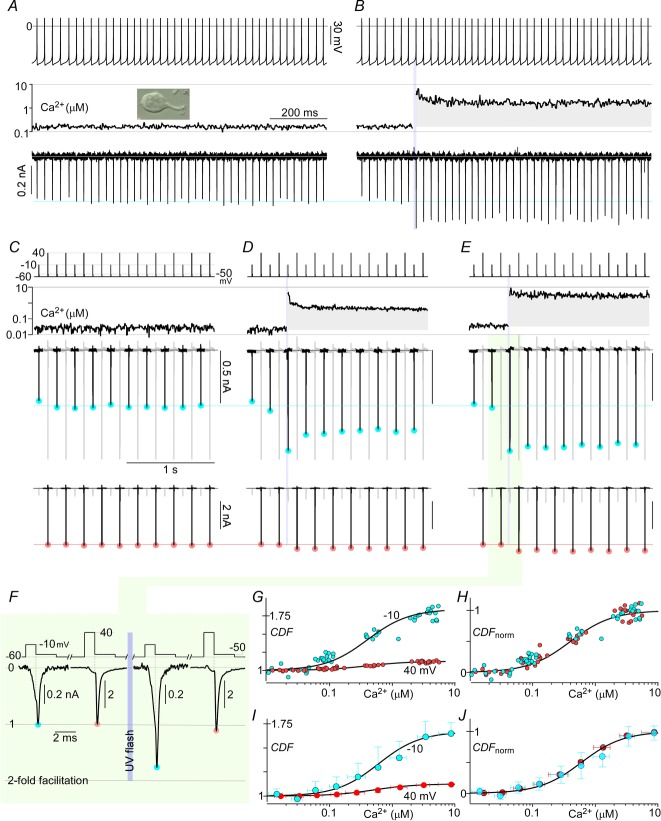
Figure 2A summarizes our initial attempt to utilize Ca²⁺ photo-uncaging to investigate CaM regulation of Ca_V2.1 channels fluxing Li⁺. Recombinant channels were heterologously expressed in HEK 293 cells. The left subpanel displays a robust Li⁺ current evoked by step depolarization to −10 mV. Current decays minimally during the voltage step, as expected for channels coexpressed with β_2a auxiliary subunits to minimize VDI (Patil et al. 1998). Though Ca²⁺-loaded DM-nitrophen was present in the internal solution, intracellular Ca²⁺ concentration remained low throughout (∼0.1 μm) in the absence of ultraviolet (UV) illumination. The right subpanel summarizes the result during a subsequent voltage pulse during which Ca²⁺ was uncaged by a brief UV pulse (at vertical violet bar). Prior to uncaging, the initial current waveform (black trace) precisely tracked the control response from the left subpanel (reproduced as grey trace), substantiating minimal rundown. By contrast, upon Ca²⁺ uncaging to nearly 10 μm, the current abruptly decreased to a nadir in less than a few milliseconds, followed by slow recovery over tens of milliseconds. The precipitous decrement of current might have initially appeared perplexing because it occurred far too quickly to be explained by a slow CDI process (DeMaria et al. 2001). The subsequent recovery of current could have arisen from CDF developing over this unspecified inhibitory process. By recalling classic studies of ion permeation through L-type Ca²⁺ channels (McCleskey & Almers, 1985; Hess et al. 1986), we soon suspected that the Li⁺ flux through Ca_V2.1 might be exquisitely susceptible to block by Ca²⁺ binding to the pore (Fig. 2A, right subpanel diagram). The quick decline of current upon Ca²⁺ uncaging would accord with the sub-millisecond equilibration of Ca²⁺ block of monovalent currents fluxing through Ca²⁺ channels.

Figure 2. Relieving Ca²⁺ blockade of Li⁺ current.

A, Li⁺ permeation through Ca_V2.1 is blocked by Ca²⁺. Ca_V2.1 EFa fluxes Li⁺ current in response to a step depolarization at baseline intracellular Ca²⁺ (left). A brief UV pulse (violet bar) induces a step-like elevation of intracellular Ca²⁺ in the midst of the voltage step, resulting in a rapid block of Li⁺ current, followed by CDF (right). B, characterization of Ca²⁺ block. Li⁺ currents from voltage ramps were obtained in the presence of varying amounts of Ca²⁺ in the bath (Ca_o). Normalized peak currents show the decrement in peak currents of Ca_V2.1 in response to Ca²⁺. Exemplar current–voltage (I–V) traces (right) from the last trace of each Ca²⁺ solution (coloured circles, left) show explicitly the reduction in current amplitude without shifting of the reversal potential. C, similar traces for Ca_V2.1 E3A show a reduced Ca²⁺ sensitivity to block (left), and a left-shifting of the reversal potential (right). D, diagram of Ca_V2.1 channel highlighting the four glutamates (E1–E4) forming the selectivity filter (top). Population (mean ± SEM) Ca²⁺ block data for Ca_V2.1 (bottom): wild-type (WT; IC₅₀ = 0.8 μm; n = 7), E1A (IC₅₀ = 7 μm; n = 5), E2A (IC₅₀ = 8 μm; n = 5), E3A (IC₅₀ = 35 μm; n = 5), E4A (IC₅₀ = 10 μm; n = 5). Fits to binding curves all have Hill coefficient of 1.

To test this hypothesis, and to minimize the potential confounding effects on characterizing CaM regulation, we investigated Ca²⁺ block of Ca_V2.1 channels. The fractional decrement of peak Li⁺ currents (evoked by voltage ramps) was characterized as a function of Ca²⁺ added to the bath (Fig.2B). Consistent with previous studies on Ca_V1.2 channels (Yang et al. 1993), Ca_V2.1 exhibited a high affinity for Ca²⁺, with an IC₅₀ of ∼0.8 μm. Aware that permeation is markedly influenced by four specific glutamate residues in the selectivity filter of L-type channels (Ellinor et al. 1995), we reasoned that substituting alanines for the corresponding glutamates in Ca_V2.1 (Fig.2D, top) might also attenuate Ca²⁺ block. Accordingly, E→A substitutions were introduced into each of four homologous domains, and Ca²⁺ block was then quantified. Figure 2C summarizes the outcome for E→A substitution in domain III (E3A). Indeed, Ca²⁺ block was markedly reduced compared to wild-type Ca_V2.1. Nearly 30% of the initial current amplitude was maintained despite 104 μm Ca²⁺ in the bath. As expected, the reversal potential for E3A was also left-shifted relative to wild-type, with Cs⁺ being the main intracellular cation. There was also asymmetry with respect to the effects of alanine substitutions in the various Ca_V2.1 domains (Fig.2D, bottom). Notably, E3A was least sensitive to Ca²⁺ block (IC₅₀ of 35 μm), whereas mutations in other domains (E1A, E2A, E4A) yielded smaller IC₅₀ values of 7, 8 and 10 μm, respectively. Indeed, this rank order was similar to that in Ca_V1.2 (Ellinor et al. 1995) and Ca_V1.3 (Tadross et al. 2013). That said, we chose the E3A variant for subsequent Ca²⁺-uncaging experiments, presuming that the confounding decrement of current in Fig.2A (right subpanel) was indeed due to Ca²⁺ block.

Steady-state Ca²⁺ sensitivity of Ca_V2.1 CaM regulation revealed by Ca²⁺ uncaging

Before performing Ca²⁺ uncaging experiments with the E3A variant, we first verified that the pore mutation did not significantly alter CDF, a plausible expectation given that the molecular determinants of CDF reside within the channel carboxy terminus rather than the permeation pathway (DeMaria et al. 2001; Lee et al. 2003; Mori et al. 2008). For this purpose, we used a well-established prepulse protocol to coarsely estimate CDF as triggered by Ca²⁺ itself fluxing through channels (DeMaria et al. 2001; Chaudhuri et al. 2004). Corresponding wild-type Ca_V2.1 currents are displayed in Fig.3A. Upon presentation of an isolated test pulse to 5 mV (left subpanel), the activation of Ca²⁺ current follows a biphasic time course. The first phase comprises an initial rapid increase of current owing to the comparatively speedy voltage activation of channels, initially all in their ‘unfacilitated’ condition (Fig.3A, τ_fast). A subsequent second phase of current increase (Fig.3A, τ_slow) reflects the slower facilitation of channel opening by ongoing Ca²⁺ entering through channels. To characterize facilitation more fully, we examined facilitation produced during brief voltage prepulses, using a variation of this initial protocol. In the example shown (Fig.3A, right subpanel, black trace), the test-pulse current following a prepulse exhibits a much reduced slow-activation phase, because many channels have already undergone facilitation during the prepulse. For reference, the test-pulse current without prepulse has been reproduced in grey. The extent of prepulse facilitation (the metric CDF) turns out to be proportional to the area between black and grey traces ΔQ (right subpanel, shaded red area) divided by τ_slow (from left subpanel) (Chaudhuri et al. 2004). Plots of CDF as a function of prepulse voltage then yield the bell-shaped relation shown in Fig.3B, averaged over multiple E3A (red) and wild-type (black) Ca_V2.1 currents. This bell-shape accords with CDF reflecting a genuine Ca²⁺-triggered process, because CDF mirrors the amplitude of prepulse Ca²⁺ currents elicited at various prepulse voltages (Brehm & Eckert, 1978). When Ba²⁺ was substituted as charge carrier, the bell-shaped augmentation was largely eliminated (Fig.3B, open symbols) because Ba²⁺ binds poorly to CaM (Chao et al. 1984). Importantly, the CDF profiles for E3A and wild-type Ca_V2.1 channels were indistinguishable, permitting use of the E3A construct to gauge CDF in subsequent Ca²⁺-uncaging experiments.

Figure 3. Steady-state Ca²⁺ sensitivity of Ca_V2.1 CaM regulation revealed by Ca²⁺ uncaging.

A, characterization of CDF using the prepulse protocol. With Ca²⁺ as the charge carrier, a step depolarization to 5 mV induces an inward current with rapid and slow components due to a superposition of voltage activation and CDF (left). With a preceding voltage step to 20 mV, sufficient Ca²⁺ enters to partially facilitate the channels, such that the subsequent step to 5 mV has a markedly blunted slow component (right). The area between the two current traces (ΔQ), divided by τ_slow, gives an approximation of the CDF triggered by the prepulse. B, population data (mean ± SEM) for CDF vs. prepulse voltage of the pore mutant E3A (red, n = 9) and WT (black, n = 8). The open circles denote the use of Ba²⁺ as the charge carrier (incapable of triggering CDF), while the filled circles denote the use of Ca²⁺. C, E3A mutant permeating Li⁺ current shows negligible Ca²⁺ block. Ca²⁺ uncaging during a voltage step of a CDF-incapable splice variant of Ca_v2.1 (EFb −47) induces neither block nor CDF (middle, right). D, Ca²⁺ uncaging with the EFa variant (−47) showcases large and rapid induction of CDF (middle, right). E, population data for Ca_V2.1 EFa −47 (black circles, mean ± STD, n = 12 cells), quantifying CDF as a function of different uncaged Ca²⁺ concentrations during voltage steps to −10 mV yields a Ca²⁺ sensitivity curve, with EC₅₀ = 0.6 μm and n_Hill = 1.8. Population data for Ca_V2.1 EFb −47 (grey circles, mean ± STD, n = 17 cells) show complete absence of CDF. F, similar experiments with Ca_V2.1 EFa −47 coexpressed with CaM₁₂₃₄, a mutant CaM incapable of binding Ca²⁺, resulted in the elimination of CDF (mean ± STD, n = 7 cells). G, similar experiments with Ca_V2.1 EFa –47 carrying an I(0)A mutation at the IQ domain show a knockout of CDF (mean ± STD, n = 8 cells).

Turning in earnest towards Ca²⁺ uncaging, we initially measured the effects of Ca²⁺ elevation on a splice variant of Ca_V2.1 thought to exhibit far weaker CDF (EFb −47) (Chaudhuri et al. 2004). Results from this construct explicitly test whether the E3A pore mutation suffices to minimize Ca²⁺ block effects in the precise configuration of uncaging protocols. Figure3C (left subpanel) displays exemplar Li⁺ currents through EFb −47 channels bearing the E3A pore mutation. Ca²⁺ remains low throughout (∼0.1 μm) in the absence of uncaging. Upon Ca²⁺ uncaging to just over 1 μm (middle subpanel, vertical violet bar), Li⁺ current appeared unchanged, demonstrating minimal Ca²⁺ block. Yet stronger Ca²⁺ elevation (right subpanel) also negligibly impacted Li⁺ current, substantiating insignificant Ca²⁺ block at levels approaching 10 μm. Likewise, Ca²⁺ elevations over a similar range produced imperceptible effects on a related EFb +47 splice variant of Ca_V2.1 (Chaudhuri et al. 2004) (data not shown). Having confirmed that Ca²⁺ block effects were adequately blunted by E3A mutation, we focused again on the prototypic Ca_V2.1 variant (EFa −47) that exhibits robust CDF, as shown earlier in Fig.3A and B. Figure3D summarizes the effects of Ca²⁺ uncaging, specifically on a version of these prototypic channels containing the E3A mutation. The left subpanel shows steady Li⁺ current evoked without Ca²⁺ uncaging. By contrast, upon Ca²⁺ uncaging (middle subpanel, grey-shaded region), a nearly two-fold augmentation of current was rapidly produced (red-shaded region). Stronger and more sustained Ca²⁺ elevation (right subpanel) induced a still larger and more sustained elevation of current. These effects directly substantiate a fully legitimate CDF process, one that appears considerably larger than previously estimated by indirect means such as in Fig.3B (Lee et al. 2000; DeMaria et al. 2001; Chaudhuri et al. 2005). Data obtained from multiple cells and uncaging experiments are summarized in Fig.3E. For EFa −47 channels, the steady-state relation between CDF and [Ca²⁺] defines a Hill function with a maximum of 2.22, midpoint EC₅₀ of approximately 0.5 μm, and Hill coefficient n_Hill of 1.8 (red curve). CDF was here defined as the ratio of currents evoked before and after Ca²⁺ uncaging at steady state. For EFb −47 channels, CDF was negligibly elevated for [Ca²⁺] up to 10 μm (grey relation). Reassuringly, CDF was essentially eliminated in EFa −47 channels coexpressed with a dominant-negative CaM molecule (Fig.3F), confirming CaM as the sensor for CDF as found in previous studies (DeMaria et al. 2001; Chaudhuri et al. 2005, 2007). Moreover, no appreciable CDF was observed for EFa −47 channels bearing an isoleucine to alanine substitution within an IQ domain in the Ca_V2.1 carboxy terminus (Fig.3G), an outcome that fits with previous characterization of this mutant using more indirect measures (DeMaria et al. 2001).

Beyond the large magnitude of CDF, another unexpected observation was the absence of CDI (Lee et al. 1999; DeMaria et al. 2001) in all the records shown thus far, even though the E3A mutant was capable of undergoing CDI (Fig.4B and C). In particular, there was no hint of current decline in either EFb −47 or EFa −47 records after Ca²⁺ uncaging to several micromolar (Fig. 3C and D, rightmost subpanels). It turns out that Ca²⁺ elevations greater than 10 μm are required to trigger CDI (Fig.4D and E). Owing to technical constraints, it was difficult to uncage Ca²⁺ to such large concentrations, while reliably achieving low baseline [Ca²⁺] prior to uncaging. For this reason, we focused the remainder of experiments on the CDF process, which could be studied in isolation because of the low Ca²⁺ sensitivity of the CDI mechanism.

Figure 4. High Ca²⁺ requirements for CDI.

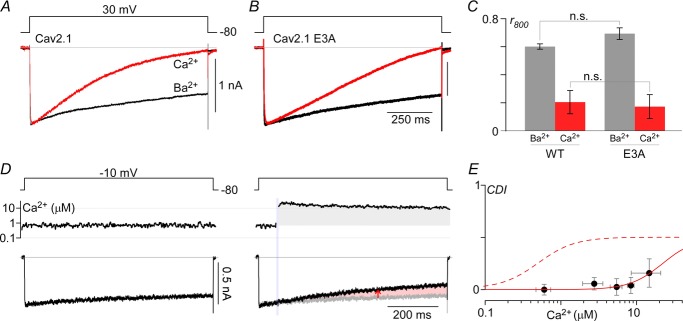
A, exemplar currents from Ca_V2.1 permeating either Ca²⁺ (red) or Ba²⁺ (black) during a 1 s depolarization to 30 mV. B, similar protocol for Ca_V2.1 E3A. In both cases, 40 Ca²⁺/40 Ba²⁺ (mm) were used to increase current density. C, population data for WT and E3A channels, plotting the ratio of currents at 800 ms to peak current for Ba²⁺ and Ca²⁺ (mean ± SEM). Both WT and E3A have n = 5 cells each, with comparison between E3A and WT done using unpaired Student's t test (P > 0.05). D, Li⁺ currents through Ca_V2.1 EFb E3A channels are stable at ∼0.7 μm (left). Uncaging Ca²⁺ to ∼14 μm elicits a small amount of CDI (right). E, compiling traces from n = 19 cells where Ca²⁺ was uncaged to various levels yields a Ca²⁺ dose–response curve for CDI (red continuous line), defined here as CDI = r_400,before – r_400,after (red arrow in D), where r₄₀₀ = I(t_uncaging)/I(t_{uncaging + 400ms}). E, data points shown are mean ± STD, where fit is a Hill function with n_Hill = 2, IC₅₀ = 22 μm. Fit for CDF's Ca²⁺ sensitivity is reproduced as red dashed line for comparison.

Contrasts between fully facilitated and non-facilitated channels at various voltages

Thus far, our data nicely revealed features of CDF, but only as viewed during voltage steps to −10 mV. We therefore sought next to examine the contrasts in opening at different voltages, as exhibited by unfacilitated Ca_V2.1 channels compared to those fully facilitated by Ca²⁺. In particular, Li⁺ currents evoked before Ca²⁺ uncaging (Fig.5A, left subpanel, black trace) reflect the opening and closing of channels governed by transitions among closed states (C) and a predominant open configuration (O) that comprise an unfacilitated mode of gating (middle subpanel, top) (Chaudhuri et al. 2007). Most of the transitions are voltage dependent, while the final transition into O is largely voltage insensitive (Chaudhuri et al. 2007). By contrast, after strong uncaging to fully facilitate channels with respect to Ca²⁺, Li⁺ currents evoked by an identical voltage pulse protocol (right subpanel, black trace) would largely reflect transitions within a ‘facilitated’ gating mode (middle subpanel, bottom), where opening is favoured over that in the unfacilitated mode (middle subpanel, top). That said, a critical feature of CDF concerns the relative advantage in opening between these two gating modes over a range of voltages.

Figure 5B displays the results of a protocol that specifically reveals this advantage. Tail Li⁺ currents through Ca_V2.1 EFa E3A −47 channels were evoked immediately following a series of brief activating voltage pulses ranging from −30 to 50 mV, initially in the absence of Ca²⁺ uncaging (blue circles). The response for the activating pulse to −10 mV (highlighted in grey zone) is displayed on an expanded scale in Fig.5A (left subpanel, black trace). Plotting the peak amplitude of these tail currents as a function of voltage in corresponding activating pulses (Fig.5C, blue symbols and relation) yields the steady-state voltage activation profile of unfacilitated channels. For convenient comparison across cells, the data have been normalized to the largest tail current amplitude. Immediately following acquisition of this initial set of tail currents, current was evoked by a sustained voltage pulse to −10 mV, and Ca²⁺ uncaged to 3.4 μm to produce the usual facilitation of current (note events in Fig.5B near vertical violet bar) as illustrated previously in Fig.3D. As this level of Ca²⁺ saturated facilitation with respect to Ca²⁺ (Fig.3E), subsequent acquisition of tail currents (Fig.5B, red circles) sufficed to approximate the steady-state voltage activation profile for fully facilitated channels (Fig.5C, red symbols and relation). These data have been normalized to the maximal tail current before Ca²⁺ uncaging. Viewed in this way, one can readily deduce that CDF produces both an absolute upward scaling of the voltage activation profile (Fig.5C, effect a) and a hyperpolarizing shift of the relation (effect b) (Chaudhuri et al. 2007). Dividing the relations for facilitated and unfacilitated channels yields the fractional increase in open probability produced by CDF as a function of voltage (Fig.5D). These results were fully corroborated over multiple cells (Fig. 5E and F). Intriguingly, the net result of effects a and b is to produce a Boltzmann-like CDF profile (Fig.5D and F). To confirm that all effects under this protocol were strictly related to CDF, we replicated experiments using Ca_V2.1 EFb E3A −47 channels (which lack facilitation, Fig.3C), and observed a complete absence of CDF behaviour (Fig.5G and H).

Two notable features merit attention. First, the magnitudes of CDF at voltages less than zero are remarkably larger than expected from traditional protocols (Fig.3A), reaching values exceeding two. CDF values of this order are consistent with the results of Ca²⁺ uncaging experiments performed earlier during step depolarizations to −10 mV (Fig.3D, right subpanel), but now we can appreciate that such large facilitation would extend over a range of voltages less than zero. Second, physiological activation of Ca_V2.1 channels, such as during neuronal action potentials, would draw heavily from this hyperpolarized voltage range, so one might expect the effects of CDF to be especially pronounced during physiological spike activation.

To explore further this inference about action potential behaviour, we constructed channel kinetic mechanisms corresponding to the gating modes in Fig.5A, using the parameters in Fig.6A. Quantitative simulations reproduced several important features: the whole-cell current waveforms evoked in Fig.5A (red curves) and B; all the voltage activation and CDF profiles in Fig.5E and F; and published single-channel open times (Chaudhuri et al. 2007). As previously suggested (Chaudhuri et al. 2007), differences between unfacilitated and facilitated gating modes were mainly restricted to the rightmost opening and closing steps according to fixed scaling factors f and g (Figs 5A and 6A). With our gating mechanisms thus established, we turned to predictions of the maximal impact of CDF on currents evoked by physiological action potential waveforms, taken from cerebellar Purkinje neurons (Chaudhuri et al. 2005). For channels resident within the unfacilitated mode, simulated activation by a typical neuronal action potential (Fig.6B, left, red curve) predicts well the actual Ca_V2.1 current (black trace). Upon maximal Ca²⁺-induced conversion towards the facilitated mode, the corresponding simulated current increases by nearly twofold (Fig.6B, right, red curve). This outcome fits with the intuition that CDF could strongly enhance currents during physiological activation. That said, Fig.6C tests experimentally for CDF during trains of action potential waveforms. For an exemplar cell, with Li⁺ currents fluxing through recombinant Ca_V2.1 EFa E3A −47 channels, evoked currents remained steady over multiple action potential waveforms in the absence of Ca²⁺ uncaging (left subpanel), substantiating stability of the preparation. By contrast, upon uncaging to a saturating level of Ca²⁺, corresponding currents increased by nearly twofold (Fig.6C, right subpanel). The impact of CDF on current is further emphasized by the expanded time base plots of exemplar currents evoked just before and after Ca²⁺ uncaging (Fig.6B, black traces, corresponding to Fig.6C responses shaded in green). Additionally, data averaged over many cells confirmed that full induction of CDF can strongly amplify spike current (Fig. 6D and E).

Voltage insensitivity of Ca²⁺-driven conversion to facilitated channels

Still uncertain, though, is whether strong interconversion towards the facilitated mode would actually be produced by physiological Ca²⁺ elevations. In particular, only at a fixed potential of −10 mV has the Ca²⁺ dependence of CDF been determined (Fig.3E). This Ca²⁺ sensitivity reflects the steady-state distribution of channels between upper and lower modes (Fig.7A), as governed by vertical transitions aligned with closed and/or open states most heavily populated at −10 mV (say, for example, k_d transitions). At different potentials, the most frequented closed and/or open states may differ considerably, emphasizing different vertical transitions (for example, k_a, k_b, k_c, k_e or k_f) that may yield alternative Ca²⁺ sensitivities, knowledge of which would be fundamental to appreciating the physiological relevance of CDF. Accordingly, we took advantage of the fact that it takes 1–3 min for Ca²⁺ to return to baseline after large Ca²⁺ uncaging events, owing to the relatively slow diffusion of fresh DM-nitrophen from the pipette into the cell interior. Figure7B displays results for an exemplar cell undergoing such a protocol. As Ca²⁺ gradually recedes, we could continue periodic assessment (every 5–30 s) of voltage activation curves using a tail-current protocol (format as in Fig.5B). In this manner, we could assess the status of near steady-state channel partitioning between unfacilitated and facilitated configurations, over a broad range of smoothly waning Ca²⁺ levels. Most of this partitioning would occur at the holding potential of −80 mV (5–30 s sojourns), punctuated by significant visitations to a wide range of other potentials during the tail-current protocols that last ∼0.5 s. If the vertical transitions in Fig.7A were appreciably different, we would anticipate CDF–Ca²⁺ relations that deviate considerably from those obtained at −10 mV throughout (Fig.3E). Figure7C displays the result for this exemplar cell, where fold increase in tail-current amplitude is plotted versus Ca²⁺ concentration. For example, for responses following brief activation to 0 mV, tail-current amplitudes denoted by the cyan symbols in Fig.7B were normalized to that seen before Ca²⁺ uncaging, and these normalized amplitudes were then plotted against corresponding Ca²⁺ concentrations to yield the cyan CDF–Ca²⁺ relation in Fig.7C. Analogous analysis yielded CDF–Ca²⁺ curves relating to different activation potentials (other coloured relations in Fig.7C). Normalizing all of these relations yields the single Ca²⁺ response profile in Fig.7E, which is indistinguishable from the steady-state function obtained at −10 mV in Fig.3E (EC₅₀ = 0.5 μm and n_Hill = 1.8). Note that currents obtained after Ca²⁺ returned to baseline (Fig.7B, far right) were indistinguishable from those obtained before uncaging (Fig.7B, far left), excluding appreciable run-down phenomena and permitting fold changes in tail current amplitude to be directly attributed to CDF. Averaged data from seven cells fully corroborated this finding (Fig.7D and F). Thus, Ca²⁺-driven conversions between unfacilitated and facilitated conformations (Fig.7A) are insensitive to membrane potential.

Dynamic Ca²⁺ responsiveness of CDF

The key remaining biophysical unknown concerned the temporal response of CDF to Ca²⁺ signals. Uncaging Ca²⁺ during a sustained voltage step allows direct millisecond resolution of CDF induction. In this regard, a first important set of observations emerged when we overlaid multiple current traces of Ca_V2.1 EFa E3A −47 channels (Fig.8A, grey waveforms) corresponding to different-sized Ca²⁺ steps exceeding 3 μm (Fig.8A). The black waveform shows the average of these. These data indicate that CDF can evolve quickly with a monoexponential time constant τ ∼2 ms (Fig.8A), and that τ does not further decrease with larger Ca²⁺ steps. The latter property implicates the existence of a Ca²⁺-independent and rate-limiting step leading to the facilitated mode of gating. Thus, a minimal mechanism would in reality require three modes of gating (Fig.8B), as follows. The transition from unfacilitated (top) to prefacilitated modes of gating (middle) would be Ca²⁺ dependent. Notably, the propensity for opening in these two gating modes would be largely equivalent, so as to allow for the rate limitation of a subsequent transition (Ca²⁺ independent) to an outright facilitated mode with enhanced opening (bottom). These three gating modes correspond to previously described conformations underlying CaM regulation of Ca²⁺ channels (Tadross et al. 2008) (see legend, Fig.8B). Elucidating this simple three mode mechanism would permit prediction of how CDF evolves in response to the complex Ca²⁺ waveforms present physiologically in neurons.

Towards this end, Ca²⁺ photo-uncaging was used to deliver Ca²⁺ waveforms with variable magnitudes and time courses as shown in Fig.8C (top), while simultaneously recording currents (below). The different Ca²⁺ waveforms were produced by varying UV pulse intensity. Weak pulses liberated comparatively few Ca²⁺ ions that could be rapidly buffered via free cytoplasmic DM-nitrophen, yielding weaker Ca²⁺ transients with rapid decays. Strong pulses would uncage so many Ca²⁺ ions that free cytoplasmic DM-nitrophen would be consumed, such that minutes might be required to rebind released Ca²⁺ ions via fresh DM-nitrophen diffusion from the pipette. Moderate UV pulses would produce Ca²⁺ transients with intermediate properties.

Given this rich data set, we proceeded to constrain parameters by fitting Ca²⁺ waveforms with double exponential functions (Fig.8C, top, smooth curves), and then inputting these functions to the kinetic scheme in Fig.8B. The parameters (Fig.8D) were then adjusted until simulated outputs matched both experimental kinetic data (Fig.8C, bottom, smooth curves) and steady-state Ca²⁺ responsiveness (Fig.8E, smooth curve) determined earlier. By repeating this procedure for additional cells, we obtained the final mean parameters for intermodal exchange shown in Fig.8D (from n = 8 cells). Our model also incorporates a Ca²⁺ concentration exponent n_Hill of 1.8. Rate constants within the various gating modes were identical to those established in Fig.6A. With these parameters, the simulated time course of CDF in response to Ca²⁺ step increases and decreases can be shown in Fig. 8F and G. The maximal predicted ‘on’ and ‘off’ responses exhibit time constants of 2 ms and 31 ms, respectively, seemingly fast enough for physiological relevance.

Devising strategies for resolving native Ca_V2.1 properties

Use of the Ca_V2.1 E3A construct permitted Li⁺ currents to be directly studied in Ca²⁺ uncaging experiments, allowing unprecedented access to the Ca²⁺ dependence of CDF. However, the strategies employed thus far could not be used to study native Ca_V2.1 channels because of the problem of Ca²⁺ block (i.e. Fig.2A, right subpanel). It was nonetheless crucial to substantiate our biophysically rigorous understanding of recombinant Ca_V2.1 channels in the native setting.

We thus devised a ‘sparse-tail-current’ variant of our Ca²⁺ uncaging protocol. If Ca²⁺ (rather than Li⁺) could be used as the charge carrier, then little Ca²⁺ block would occur upon uncaging of intracellular Ca²⁺ (Yang et al. 1993), even in native channels with wild-type permeation properties. However, Ca²⁺ influxing through channels would constitute local Ca²⁺ sources with attendant elevations of nanodomain Ca²⁺ that would be difficult to measure with bulk-distributed Ca²⁺ fluorescent dyes (Tay et al. 2012). Indeed, this complexity, as outlined earlier in Fig.1A, motivated our use of Li⁺ currents in the first place. If, however, we applied only brief voltage pulses separated by comparatively long periods of quiescence (Fig.9A, left subpanel), we might be able to assess the propensity for opening (during brief voltage pulses) while the spatially uniform global Ca²⁺ component specifies the extent of CDF during brief opening (owing to the predominance of global Ca²⁺ during long interpulse segments). Importantly, bulk-distributed Ca²⁺ fluorescent dye would reliably measure this global Ca²⁺ concentration (Fig.9A, right subpanel). Figure 9B schematizes further the hoped-for outcome. Brief (1 ms) activating pulses would be alternately presented to 0 and 60 mV, with long (>50 ms) quiescent periods separating pulses. Also obtained would be corresponding tail currents, proportional to the open probability at the end of 1 ms activating voltage pulses. These tail currents (cyan circle after 0 mV pulse; rose circle after 60 mV pulse) would thus monitor the extent of CDF at two key points along the overall voltage-dependent profile of CDF (i.e. Fig.5F). A critical point is that although Ca²⁺ influx during channel openings would sharply increase nanodomain Ca²⁺ via a local component (Fig. 9B, yellow shaded area), this local perturbation would rapidly dissipate such that nanodomain Ca²⁺ during most of the period preceding voltage pulses would be equivalent to the global Ca²⁺ component measured by bulk Ca²⁺ fluorescent dye (grey shaded area). Moreover, it is precisely this preceding global Ca²⁺ concentration that should specify the extent of CDF reflected in tail currents, because the change in CDF that occurs during a 1 ms voltage pulse should be small, as follows. First, the Ca²⁺ entry during 1 ms activating voltage pulses would be limited, because there would be little Ca²⁺ influx during 60 mV steps (near the reversal potential), or voltage activation would be comparatively slow at 0 mV. Second, even under saturating Ca²⁺, CDF can increase no faster than specified by a ∼2 ms time constant (Fig.8A), and the voltage pulses in question only span 1 ms. All told, if all these scenarios were to hold true, then the CDF versus Ca²⁺ relations deduced via this variant protocol should accord with those obtained more directly using Li⁺ currents fluxing through Ca_V2.1 E3A channels (Fig.7E).

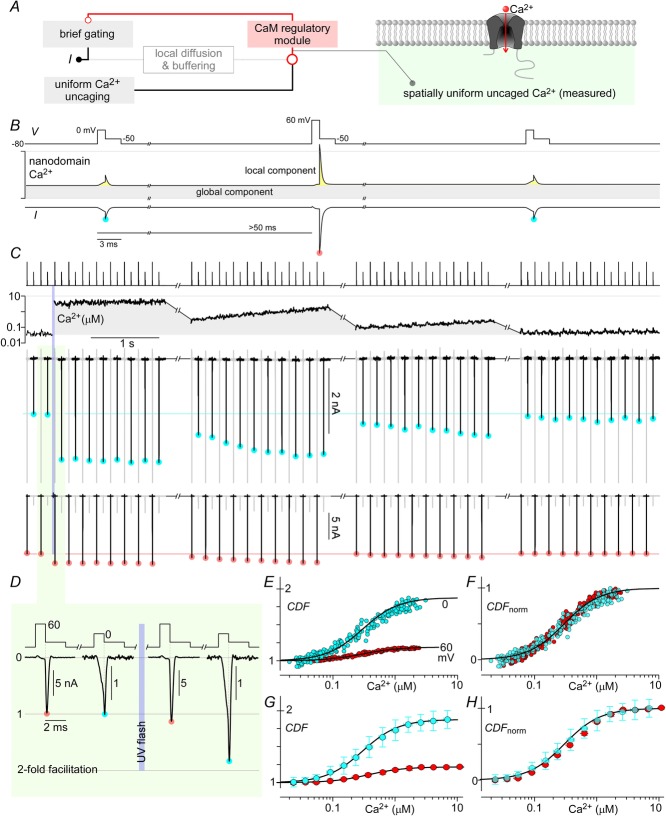
Figure 9. Towards resolving native Ca_V2.1 CDF.

A and B, schema outlining the strategy to resolve Ca²⁺ dependence of native Ca_V2.1 channels. A modified tail current protocol with very brief steps to 0 or 60 mV for 1 ms (brief gating) before eliciting tail currents at −50 mV minimizes the impact of local Ca²⁺ on the CaM regulatory module whilst still allowing assessment of the channel's state at two voltages. Uniform Ca²⁺ uncaging then provides an independent and measurable input to the regulatory module, pushing channels into the facilitated mode. C, exemplar traces from a single cell, illustrating Ca²⁺ tail currents evolving with time and global Ca²⁺. Voltage pulse protocol is displayed in the top row, and global Ca²⁺ in the second row. Tail currents triggered by preceding step to 0 mV are scaled up for clarity and shown in black in the third row (tails triggered by preceding 60 mV steps in grey), with cyan circles marking the peaks. The last row shows the tail currents triggered by preceding 60 mV steps in black, with peaks marked by red circles. D, expanded time frame views of tail currents before and after Ca²⁺ uncaging, normalized to peak levels at baseline Ca²⁺. E, steady-state CDF vs. Ca²⁺ curves at the two voltages assessed are obtained by plotting normalized peak tail currents against instantaneous Ca²⁺ levels. F, CDF vs. Ca²⁺ curves of the 2 voltages are normalized, showing the same Ca²⁺ sensitivity. G and H, population data (mean ± STD) show similar results, with n = 9 cells. Fitted curves have n_Hill = 1.5, EC₅₀ = 0.3 μm.

Figure 9C displays the experimental outcome for an exemplar cell expressing Ca_V2.1 EFa −47 channels fluxing Ca²⁺. The voltage pulse protocol is displayed in the top row, with the global Ca²⁺ concentration readout shown below in the second row. The same resulting tail-current traces are displayed at two gains in the remaining rows. In the third row, the higher-gain trace shows well the smaller tail currents following pulses to 0 mV (black segments of trace, cyan circles) and the segments containing the larger tail currents after 60 mV pulses are plotted in grey and clipped to the frame. The fourth row plots the lower-gain trace optimized for display of larger tail currents after 60 mV pulses (black segments of trace, rose circles), and the segments containing tails after 0 mV pulses are shown in grey. With this setup in mind, the manifestation of CDF can be readily appreciated. Prior to Ca²⁺ uncaging, tail currents remain steady between pulses and immediately following Ca²⁺ uncaging (vertical violet bar) there is strong CDF as demonstrated by the substantial enhancement of tail currents following pulses to both 0 and 60 mV. This observation is corroborated by expanded time base displays of current immediately before and after the uncaging event (Fig.9D), which support nearly twofold enhancement of tails following 0 mV pulses. Following Ca²⁺ uncaging, global Ca²⁺ levels gradually relaxed over the course of minutes, as shown in the remainder of Fig.9C via a display of four time segments punctuated by time-axis breaks. Likewise, tail current amplitudes diminished in parallel with the decline of Ca²⁺, where the horizontal cyan and rose lines reference amplitudes before Ca²⁺ elevation. Importantly, upon the return of Ca²⁺ to baseline (rightmost segment), tail currents were closely similar to those prior to uncaging, allowing interpretation of intervening currents in terms of CDF apart from run-down. We thus plotted fold increase in tail current amplitude as a function of instantaneous Ca²⁺ to obtain the quasi-steady-state CDF–Ca²⁺ correlations in Fig.9E. Reassuringly, the functions for 0 and 60 mV closely resembled the actual steady-state relations obtained using the original protocol with Li⁺ currents (Fig.7C). As expected, the larger CDF observed for 0 versus 60 mV pulses reflects the voltage dependence of unfacilitated versus facilitated modes of gating (Fig.5A and F). Indeed, amplitude scaling of both plots (Fig.9F) furnished a normalized relation tightly resembling that obtained at steady state (Fig.7E), with nearly the same half-Ca²⁺ level (EC₅₀ = 0.3 μm) and slightly diminished Hill coefficient of 1.5 (compared with EC₅₀ = 0.5 μm and n_Hill = 1.8 in Fig.7E). The small differences here may reflect imperfect exclusion of the local Ca²⁺ component in this sparse-tail-current protocol. Similar analysis in multiple cells furnished equivalent results (Fig.9G and H). Thus, we established that this sparse-tail-current protocol could assess CDF–Ca²⁺ relations with near quantitative precision while employing Ca²⁺ as the charge carrier through channels.

Prominent CDF in native Ca_V2.1 in cerebellar Purkinje neurons

Thus armed, we turned to characterization of CDF in native Ca_V2.1 currents in cerebellar Purkinje neurons, renowned for the predominance of these Ca²⁺ channels (Mintz et al. 1995). Acutely dissociated neurons from P14–P18 mice were used (Fig.10A, inset), so as to maximize the presence of EFa versus EFb variants (∼85% EFa transcripts; Chang et al. 2007). Although the presence of CDF in these currents had been detected previously (Chaudhuri et al. 2005; Adams et al. 2010), the means of quantification and characterization were indirect, the extents of CDF seemingly modest, and the quantitative dependence on Ca²⁺ concentration unspecified.

Figure 10. CDF in native Ca_V2.1 channels within cerebellar Purkinje cells.

A, acutely dissociated Purkinje cells were identified by their large size and tear-drop shape (picture inset). Ca_V2.1 Ca²⁺ currents stimulated by ∼50 Hz action potential waveforms are stable and show little facilitation near baseline Ca²⁺. B, Ca²⁺ uncaging in the midst of the action potential train triggers large CDF. C–E, Ca²⁺ sensitivities of CDF at 2 voltages were determined with a protocol similar to that in Fig.9C. Steady currents are seen in the absence of uncaging (C), while uncaging to different Ca²⁺ levels triggers large increases in current (D and E). F, tail currents around the time of Ca²⁺ uncaging are shown with expanded time base, normalized to the peak levels prior to uncaging. G, relative increase in peak tail currents plotted against Ca²⁺ for the above exemplar cell yields steady-state CDF vs. Ca²⁺ curves for −10 and 40 mV. H, data in G, normalized, demonstrate the same Ca²⁺ sensitivity for the two voltages. I and J, population data (mean ± STD) show similar results, with n = 5 cells. Fitted curves have n_Hill = 1.3, EC₅₀ = 0.5 μm.

To corroborate directly the existence of strong CDF in native Ca_V2.1 channels, we evoked native Ca²⁺ currents with trains of action potential waveforms (50 Hz), and simultaneously introduced Ca²⁺ uncaging events. During baseline conditions without uncaging (Fig.10A), currents appeared steady (horizontal cyan line) from the beginning to end of a train, and Ca²⁺ readouts remained constant near 0.1 μm. Thus, it appeared that the local Ca²⁺ component (Fig.9B) was insufficient to trigger appreciable CDF under these conditions. In the next train of action potentials (Fig.10B), currents were initially indistinguishable from those in the previous train (horizontal cyan line). However, upon strong uncaging to several micromolar Ca²⁺ (vertical violet bar), pronounced ∼1.6× amplification of currents was produced, indicating the potential for large native CDF matching that observed in previous figures for recombinant channels.

To quantify the Ca²⁺ sensitivity of this CDF, we applied the sparse-tail-current protocol devised in Fig.9B. Results from a single exemplar Purkinje neuron are reported in Fig.10C–E, using the same display format as in Fig.9C. Absent Ca²⁺ uncaging (Fig.10C) currents remained steady and bulk Ca²⁺ persisted near 0.1 μm, all indicative of a stable baseline. Upon moderate Ca²⁺ uncaging (Fig.10D), currents exhibited modest amplification which decayed as Ca²⁺ levels relaxed. Upon intense Ca²⁺ uncaging (Fig.10E), currents manifested marked and sustained enhancement of nearly twofold for −10 mV pulses. This modulation can be further appreciated in the expanded time base plots of currents immediately before and after uncaging (Fig.10F). Because of slow drift of currents following large Ca²⁺ elevations in these neurons, we could not in general compile traces over the course of minutes (as in Fig.9C), but were instead limited to analysing data from several trace segments, each containing a different-sized uncaging event. Using this strategy in this exemplar neuron, plots of fold enhancement of tail currents as a function of Ca²⁺ yield the CDF–Ca²⁺ relations in Fig.10G. Reassuringly, these bear a strong resemblance to those obtained for recombinant Ca_V2.1 channels (Fig.9E) and amplitude scaling yields an aggregate normalized relationship (Fig.10H, EC₅₀ = 0.5 μm and n_Hill = 1.3) closely similar to that of recombinant channels undergoing the same protocol (Fig.9F). Population data from n = 5 neurons replicate these findings (Fig.10I and J) and firmly establish strong native CDF, whose parameters largely accord with those of recombinant channels. Compared to recombinant channels, the slightly diminished maximal CDF in native currents (Fig.10I) fits with a modest fraction of Ca_V2.1 EFb variants that lack CDF (∼15% transcripts; Chang et al. 2007).

Discussion

This study reveals the long-sought speed and extent of Ca²⁺-dependent facilitation (CDF) of Ca_V2.1 channels. Using Ca²⁺ photo-uncaging as a signal generator of intracellular Ca²⁺, we demonstrate that CDF is considerably larger, faster, and more Ca²⁺ sensitive than previously imagined. This performance profile positions Ca_V2.1 channels for extensive CDF under neurophysiological activity, offering the potential for strong activity-dependent adjustment to downstream signalling pathways. Additionally, the new and extensive Ca²⁺ and electrophysiological constraints furnished by our approach significantly advance mechanistic understanding of this regulatory system, which is formalized by a realistic biophysical model of Ca_V2.1 gating and CDF. Overall, these findings hold key implications for CDF in relation to structural determinants, functional mechanisms and neurophysiological roles, as follows.

Structural determinants of CDF

During baseline characterization via Ca²⁺ uncaging, important aspects of the structural basis of CDF were refined. From qualitative measures of CDF, the carboxy tail of Ca_V2.1 has previously been suggested to be essential for CDF (Mori et al. 2008), just as for CaM regulation of Ca_V1 channels (Ben-Johny et al. 2013). In this regard, a first advance in the present study was to revise previous suggestions that alternative splicing at exon 37 (encoding EFa or EFb modules within the carboxy tail) enables or disables CDF, but in a manner modulated by inclusion of exon 47 on the extreme channel carboxy terminus (Chaudhuri et al. 2004). Using the higher-resolution Ca²⁺ uncaging assay used here, we now demonstrate that the EFa/EFb module fully switches CDF on and off (Fig.3C and E), and that inclusion or exclusion of exon 47 does not affect Ca_V2.1 CDF. This simplifying feature strengthens the view that CDF may be exquisitely tuned in the human brain, since the EFa:EFb variant ratio is regulated in an age-specific, region-specific and sex-specific manner (Chaudhuri et al. 2004, 2005; Chang et al. 2007). Furthermore, the complete switching of CDF at the EF locus offers a simple strategy to create transgenic animal models that lack or possess CDF, thereby aiding clarification of its physiological role. Similarly, one wonders whether diseases of aberrant splicing (Tazi et al. 2009) might act at this EF locus. Second, beyond the EF element, substituting alanine for the central isoleucine within the IQ domain also eliminates CDF under the Ca²⁺ uncaging regime (Fig.3G), affirming further the critical role of the IQ element for CDF (DeMaria et al. 2001; Lee et al. 2003; Mori et al. 2008). Third, the elimination of CDF by the Ca²⁺-insensitive mutant CaM₁₂₃₄ (Fig.3F) consolidates the role of Ca²⁺-free CaM (apoCaM) as a resident CDF sensor bound to the channel carboxy terminus (DeMaria et al. 2001). Finally, our finding of a Hill coefficient near 2 for CDF–[Ca²⁺] relations (Figs 3E and 6F) affirms previous conclusions that CDF is predominantly triggered by Ca²⁺ binding to the C-terminal lobe of CaM (DeMaria et al. 2001), which contains two highly cooperative EF-hand Ca²⁺ binding sites.

Advances in functional mechanisms

Our experiments confirm an ‘enhanced-opening’ mechanism of CDF whereby the maximal open probability of channels at saturating depolarization is enhanced (Chaudhuri et al. 2007). That said, with the improved resolution in the present study, we now also detect a 5 mV left shift of the voltage activation relation (Fig.5C and E) (Borst & Sakmann, 1998), whereas our previous study lacked the sensitivity to detect this effect (Chaudhuri et al. 2007). Though modest, it is this shift in voltage dependence that amplifies CDF significantly during physiological patterns of activation (Figs 5D and F, and 6B and E). These effects could be almost entirely explained by enhancing the last transition to the open state (Fig.5, k_f) while reducing the closing rate from the open state (k_r), leaving all other transitions largely unchanged.

As for the Ca²⁺-induced transitions among unfacilitated and prefacilitated modes of gating (vertical arrows in Fig.8B), we find that these transitions can be approximated as the same, regardless of position along the activation pathway. Physically speaking, this feature suggests that Ca²⁺ binding to calmodulin is largely insensitive to the status of voltage activation. We further suggest that the transitions between prefacilitated and facilitated gating modes are also insensitive to voltage activation, except when the actual open states are reached (Fig.8B; also, see ‘Simulations: Ca_V2.1 channel models’ in Methods). This latter attribute hints that the binding of Ca²⁺–CaM to a channel effector site is mainly sensitive to the final concerted opening step, rather than movements of voltage-sensing paddles.

Together, all these features can be incorporated within an explicit biophysical gating mechanism (Fig.8B), arguably the most extensive for calmodulin regulation of any channel. Indeed, the CDI of Ca_V1.2/3 channels, as triggered by the C-lobe of CaM (Peterson et al. 1999; Yang et al. 2006), may turn out to be described by an analogous mechanism (Fig.8B), except that k_f/k_r in the bottom gating mode would be reduced, and the modes would be described as non-inactivated, pre-inactivated, and inactivated.

A final novel functional feature concerns the stark contrast in the Ca²⁺ sensitivity of CDF versus CDI (Fig. 4E), far more than imagined previously. Whereas the EC₅₀ for CDF is ∼0.5 μm Ca²⁺, the corresponding value for CDI would approximate ∼22 μm. Recalling the earlier finding that Ca_V2.1 CDI is triggered by Ca²⁺ binding to the N-lobe of CaM (DeMaria et al. 2001), as well as the mechanistic framework developed previously (Tadross et al. 2008), we suggest that this relative Ca²⁺ insensitivity of CDI may arise from a far greater channel affinity for the N-terminal lobe of apoCaM compared with Ca²⁺–CaM. The wide divergence of EC₅₀ values for CDF and CDI would allow facilitation to develop in isolation over sustained periods of Ca²⁺ elevation of less than ∼10 μm (Tanaka et al. 2007). The induction of CDI might be reserved for clustered channels positioned at local subcompartments where Ca²⁺ may achieve concentrations exceeding that in bulk cytoplasm. The previous observation that CDI is only apparent in a fraction of cerebellar Purkinje neurons (Chaudhuri et al. 2005) may coincide with this large EC₅₀ for CDI, and the sporadic attainment of these Ca²⁺ levels. Interestingly, previous estimates of Ca²⁺ sensitivity for CDF and CDI in the calyx of Held (EC₅₀ values of 2.5 μm and 6 μm, respectively; Lin et al. 2012) are lower than the estimates provided here. This apparent discrepancy is most likely the result of differences in channel isoform expression. For example, calyces from young, P8–P10 rats used in the previous report express a significant percentage of Ca_V2.2 and Ca_V2.3 channels (Iwasaki & Takahashi, 1998; Wu et al. 1998, 1999; Chaudhuri et al. 2005), which do not have appreciable CDF (Liang et al. 2003) and may have lower Ca²⁺ requirements for CDI than Ca_V2.1 (Nakamura et al. 2008). In contrast, the Ca²⁺ currents recorded from Purkinje neurons isolated from older animals (P14–P18) in our present study are predominantly from the facilitating EFa subtype of Ca_V2.1 (Regan, 1991; Chang et al. 2007), allowing a more specific assessment of the Ca²⁺ responsiveness of Ca_V2.1 channels. Furthermore, Lin et al. used the ratio of cumulative Ca²⁺ current during the first 3 ms of a 20 ms test pulse with or without Ca²⁺ uncaging (Q_3ms,Ca/Q_3ms,ctrl) as their metric for CDF. However, our measure of CDF kinetics (τ_on ∼2 ms, Fig.8) indicates that a significant fraction of channels shift into the facilitated state within the first 3 ms of a test pulse. Because their baseline measure (Q_3ms,ctrl) includes prefacilitated channels, their assay likely underestimates the magnitude and sensitivity of CDF.

Neurophysiological implications

Our experiments in cerebellar Purkinje neurons (Fig.10) not only substantiate the existence of CDF within these neurons (Chaudhuri et al. 2005), but reveal just how large CDF can be in this setting (∼1.8× in Fig.10G and I). The similarity of Ca²⁺ sensitivity for CDF in these neurons (EC₅₀ ∼0.5 μm in Fig.10J), compared to that for recombinant channels (∼0.5 μm in Fig.7F), further supports CaM as the Ca²⁺ sensor for CDF (Chaudhuri et al. 2005). Given the prominence of Ca²⁺ signalling in Purkinje neurons (Gruol et al. 2012), along with the primacy of Ca_V2.1 as a Ca²⁺ entry portal in this locus (Usowicz et al. 1992; Hartmann & Konnerth, 2005), the CDF of Ca_V2.1 channels seems particularly well poised for physiological influence in this context.

A first potential role concerns recent exciting findings that coordinated motor control may require cerebellar Purkinje neurons to spontaneously fire simple spikes with regular and uniform rate (Hoebeek et al. 2005; Otis & Jen, 2006; Walter et al. 2006). Empirically speaking, this requirement can be verified by correlating altered coordination with pharmacological and/or genetic modulation of spike regularity (Walter et al. 2006). From the theoretical standpoint, the need for constant spiking may relate to promising synchronization encoding mechanisms wherein motor information is conveyed through selected deep cerebellar nuclei only at appropriate times, in particular when inhibitory inputs from multiple convergent Purkinje neurons become synchronized (Medina & Khodakhah, 2012; Person & Raman, 2012a). Achieving such synchrony, for example following a shared complex-spike phase reset among convergent Purkinje neurons, would require these neurons to manifest a regular and uniform spontaneous simple spike rate (Person & Raman, 2012b). We can connect this fundamental substrate of motor coordination to Ca_V2.1 CDF by noting that phasic activation of small-conductance Ca²⁺-activated K⁺ channels (SK channels), which drives after-hyperpolarization following spikes, is a prime determinant of spontaneous simple spike rate (Swensen & Bean, 2003). Moreover, the dominant trigger of SK channels involves preferential Ca²⁺ signalling from colocalized Ca_V2.1 channels fluxing peak Ca²⁺ current during the repolarizing phase of spikes (e.g. Fig.5B) (Swensen & Bean, 2003; Womack et al. 2004). Accordingly, attenuation of either SK or Ca_V2.1 channels, such as in heritable forms of ataxia, begets rate variability and motor dyscoordination (Otis & Jen, 2006). We suggest that a potential role of Ca_V2.1 CDF could be to enhance the regularity of simple spike rate in an elegant servo control mechanism, as follows: perturbations increasing the spiking rate would heighten global Ca²⁺, boost Ca_V2.1 CDF and SK channel activation, and thereby downwardly restore rate towards an intrinsic setpoint (Fig.1A). Conversely, transient rate decreases would lower global Ca²⁺, weaken CDF and SK channel activity, and consequently upwardly restore rate (Fig.1B). Thus, we hypothesize that Ca_V2.1 CDF may play a role in optimizing motor coordination. Indeed, the postnatal developmental increase of CDF (due to switching from Ca_V2.1 EFb to EFa variants; Chaudhuri et al. 2005) closely parallels the time course of motor coordinative improvements (Arata & Ito, 2005)11.

Figure 11. Neurophysiological implications of Ca_V2.1 CDF.

A, diagram illustrating the role of CDF in homeostatic rate control of Purkinje cells. Increased rate of Purkinje cell spiking elevates global Ca²⁺, facilitating Ca_V2.1 opening via CDF. Increased Ca_V2.1 activity in turn activates colocalized SK channels, resulting in stronger membrane hyperpolarization that then reduces spiking rate. B, similarly, decreased spiking rate leads to lower global Ca²⁺, reduced CDF, and less SK activation, finally resulting in weaker hyperpolarization and restoration of spiking rate. C, Ca²⁺ dose–response curves for CDF (continuous black line) and neurotransmitter secretion (red line). Additionally, Ca²⁺ sensitivity of paired-pulse facilitation due to residual Ca²⁺ (Regehr et al. 1994) (dashed line) shows an additional mechanism specifying the extent of transmitter release. D, generic nerve terminal is modelled as a sphere with Ca_V2.1 channels uniformly expressed on the membrane. A thin shell compartment adjacent to the membrane forms the nanodomain within which the CDF Ca²⁺ sensor CaM, which acts as a channel subunit, actually senses Ca²⁺. Ca²⁺ within the shell compartment can diffuse to and from the much larger cytosolic compartment. The cytosolic compartment is in turn connected to a third and much larger compartment representing the axon branch itself. The Ca²⁺ concentration within this axonal compartment is set at a fixed resting level, and thus serves to returns Ca²⁺ within the terminal back to its resting levels after periods of activity. The parameters for this system are: r_sphere = 8 μm, r_cyto = 7.9 μm, N_chan = 60,000, k_sc = k_cs = 6 × 10⁻¹³ dm³ ms⁻¹, and k_efflux = 6 × 10⁻¹⁴ dm³ ms⁻¹, with the parameters adjusted such that simulations in E match data from Cuttle et al. (1998). Note that the simulated volume is larger than physical terminals because Ca²⁺ buffers are not explicitly modelled here. E, simulations of the system in D in response to 100 Hz step depolarizations to −20 mV. Ca_V2.1 currents are elicited (bottom row) by the voltage stimulation (top row), which results in a build-up of Ca²⁺ in both the shell (second row) and cytosolic (third row) compartments. The increased Ca²⁺ induces CDF of Ca_V2.1 channels, resulting in gradual amplification of I_Ca, Ca_shell and Ca_cyto. F, CDF at steady state is inversely related to stimulation frequency (blue circles and continuous line), largely due to frequency-dependent accumulation of residual Ca²⁺ (100 Hz example in red).

Secondly, given the predominance of Ca_V2.1 channels in triggering transmitter release across the CNS (Uchitel et al. 1992; Wheeler et al. 1994; Dunlap et al. 1995), CDF might contribute presynaptically to short-term synaptic plasticity, either to boost outright facilitation or to buffer the extent of depression. Indeed, trains of spike-like depolarizations induce large 1.8× facilitation of rat (P9–P17) Ca_V2.1 currents in the calyx of Held (Cuttle et al. 1998). Given that neurotransmitter release probability is proportional to Ca²⁺ concentration to the third or fourth power (Schneggenburger & Neher, 2000; Xu et al. 2007), this CDF could orchestrate order-of-magnitude (Fig.10G–J, 1.8⁴ ∼10) modulation of synaptic strength. Of note, reports of weaker CDF in calyceal Ca_V2.1 currents restricted experiments to conditions minimizing vesicle depletion (Muller et al. 2008), with the result that Ca²⁺ levels (252 nm) may have been insufficient to recruit much of CDF by our Ca²⁺ sensitivity measures (arrow in Fig.1C). Additionally, it is worth noting that whereas CaM is well accepted as the trigger for Ca_V2.1 CDI in the calyx (Xu et al. 2007; Nakamura et al. 2008), neuronal calcium sensor-1 (NCS-1) has been proposed to mediate CDF (Tsujimoto et al. 2002). However, biophysical studies in other cell types suggest NCS-1 alters Ca_V2.1 current, with little to no effect on CDF (Weiss et al. 2010; Yan et al. 2014). As such, we propose that CaM is the predominant molecular sensor for Ca_V2.1 CDF in the calyx, although NCS-1 may modulate Ca_V2.1 currents indirectly through other pathways (Weiss et al. 2010). More broadly, we anticipate a strong contribution of CDF to synaptic plasticity at other synapses. When we embedded our in silico channel mechanism (Fig.8B) within a generic three-compartment spherical terminal (Fig.1D), we reproduced (Fig.1E) both the kinetics and magnitude of experimentally observed CDF in the calyx (Cuttle et al. 1998). In this scheme (Fig.1D), Ca²⁺ enters initially through Ca_V2.1 channels into a submembranous shell compartment, followed by rapid diffusion into a larger cytosolic compartment. This cytosolic space is in turn connected with an efflux pathway into a large axonal compartment set at resting Ca²⁺. When simulated Ca_V2.1 channels are opened with a 1 ms depolarization to −20 mV (Fig.1E, top), peak Ca²⁺ currents (bottom row) caused Ca²⁺ elevation in the shell and cytoplasmic compartments (Ca_shell and Ca_cyto in rows 3–4). The shell compartment experiences large Ca²⁺ spikes coincident with channel opening, each followed by rapid relaxation to the cytosolic (global) pedestal. The global cytoplasmic Ca²⁺ rises with each stimulus during a 100 Hz train, eventually reaching a quasi plateau where Ca²⁺ influx matches its efflux. Interestingly, even though CaM physically senses local Ca²⁺ within the shell, it is the global Ca²⁺ component in this compartment that drives much of CDF when brief spikes are sufficiently spread out. Thus, the time course of CDF tracks the rise and fall of global Ca²⁺, much as in our sparse-tail protocol (Fig.9A). Altering stimulus frequency reveals that CDF quickly decays with slower pacing (Fig.1F), projecting substantial contributions to short-term synaptic plasticity.

In this light, it is worth quantifying how CDF fits with other facilitatory mechanisms underlying rapid synaptic upregulation (Fig.1C). The red curve plots the Ca²⁺ sensitivity of outright neurotransmitter release, presumably as specified by Ca²⁺ binding properties at C2 sites on synaptotagmin (Schneggenburger & Neher, 2000). High Ca²⁺ concentrations (>10 μm) may be required for this process, such as produced by clusters of Ca_V2.1 channels near neurotransmitter vesicle complexes (Sheng et al. 2012). However, accumulation of ‘residual’ presynaptic Ca²⁺ from prior activity (Zucker & Regehr, 2002), insufficient to trigger release, may nonetheless preload unspecified high-affinity Ca²⁺ binding sites (Regehr et al. 1994; Awatramani et al. 2005) to boost ensuing release according to a residual Ca²⁺ (RC) mechanism (Fig.1C, dashed RC curve). Here, our Ca²⁺ uncaging experiments project Ca_V2.1 CDF as another relevant system, in this case with intermediate Ca²⁺ sensitivity (Fig.1C, black curve). Of note, synapses in the calyx of Held of transgenic mice lacking Ca_V2.1 (compensated by Ca_V2.2) exhibit little to no short-term synaptic facilitation (Inchauspe et al. 2007). That said, we do not believe that RC and CDF need be one and the same process, as synaptic paired-pulse facilitation in the calyx of Held can be observed in the absence of CDF (Muller et al. 2008). Overall, it seems likely that CDF and RC processes will differ in their relative contributions at various synapses, and the RC category may encompass several as yet loosely defined processes. That said, our extensive biophysical clarification of Ca_V2.1 CDF, in both recombinant and native currents, now leaves little doubt that this Ca²⁺ regulation will figure prominently in the CNS.

Glossary

CaM

calmodulin

CDF

calcium-dependent facilitation

CDI

calcium-dependent inactivation

RC

residual calcium mechanism of paired-pulse facilitation

VDI

voltage-dependent inactivation

Additional information

Competing interests

The authors have no conflicts of interest to declare.

Author contributions

All experiments were performed in the Calcium Signals Laboratory at the Johns Hopkins University School of Medicine. S.-R.L. created pore mutants, performed electrophysiological experiments, analysed data and wrote the code for the simulations; P.J.A. isolated cerebellar Purkinje neurons, and advised on their electrophysiological characterization. S.-R.L. and D.T.Y. conceived and designed the project, created figures, and wrote the initial manuscript. S.-R.L. and P.J.A. critically reviewed and revised the manuscript and gave final approval of the version to be published.

Funding

This study was supported by grants from NIMH (D.T.Y.), Parkinson Society Canada (P.J.A.) and NIH MSTP grant (S.-R.L.).