Fast, accurate evaluation of exact exchange: The occ-RI-K algorithm

Abstract

Construction of the exact exchange matrix, K, is typically the rate-determining step in hybrid density functional theory, and therefore, new approaches with increased efficiency are highly desirable. We present a framework with potential for greatly improved efficiency by computing a compressed exchange matrix that yields the exact exchange energy, gradient, and direct inversion of the iterative subspace (DIIS) error vector. The compressed exchange matrix is constructed with one index in the compact molecular orbital basis and the other index in the full atomic orbital basis. To illustrate the advantages, we present a practical algorithm that uses this framework in conjunction with the resolution of the identity (RI) approximation. We demonstrate that convergence using this method, referred to hereafter as occupied orbital RI-K (occ-RI-K), in combination with the DIIS algorithm is well-behaved, that the accuracy of computed energetics is excellent (identical to conventional RI-K), and that significant speedups can be obtained over existing integral-direct and RI-K methods. For a 4400 basis function C₆₈H₂₂ hydrogen-terminated graphene fragment, our algorithm yields a 14 × speedup over the conventional algorithm and a speedup of 3.3 × over RI-K.

I. INTRODUCTION

The widespread adoption of Kohn-Sham density functional theory^1,2 (DFT) has allowed for electronic structure calculations of reasonable accuracy to be performed on systems of unprecedented size.^3–5 Perdew’s famous “Jacob’s ladder” analogy elegantly captures the different components of the ideal high-accuracy density functional.⁶ A crucial component of this hierarchy is the so-called “hybrid functionals,” containing a weighted contribution from the exact exchange energy. The importance of including exact exchange was initially recognized by Becke,^7,8 and exact exchange has since become a core component of a huge number of widely used modern density functionals.^9–13

Unfortunately, exact exchange requires the computation of the numerous and expensive four-center two-electron repulsion integrals (ERIs),

$${\displaystyle \left(\mu \lambda |\nu \sigma \right)=\int \int d{\mathit{r}}_{1}d{\mathit{r}}_2{\varphi }_{\mu }^{\ast }\left({\mathit{r}}_1\right){\varphi }_{\lambda }\left({\mathit{r}}_1\right){\mathit{r}}_{12}^{-1}{\varphi }_{\nu }{\left({\mathit{r}}_2\right)}^{\ast }{\varphi }_{\sigma }\left({\mathit{r}}_2\right),}$$ (1)

to construct the exchange matrix, K,

$${\displaystyle K_{\mu \nu }=\sum _{\lambda \sigma }\left(\mu \lambda |\nu \sigma \right)P_{\lambda \sigma }.}$$ (2)

This is in contrast to highly efficient linear scaling evaluation of the classical Coulomb interactions, where four center ERIs can be rigorously avoided by multipole expansions of long-range interactions¹⁴ and rigorous reformulation of the short-range interactions (the “J-matrix engine”^15,16). Naïve construction of the full two-electron integral tensor scales as the fourth power of molecular size. However, it was demonstrated by Almlöf early in the development of the direct SCF method that the number of numerically significant two-electron integrals scales asymptotically only quadratically with molecular size, as there are linear number of overlapping pairs of Gaussian atomic orbitals (AOs).¹⁷ This locality is most commonly exploited via the use of Schwarz-inequality based integral bounds,^18,19 though tighter bounds on numerically significant integrals have been further developed.^20–22

In addition, the density matrix, $\rho \left(\mathbf{r},{\mathbf{r}}^{\prime }\right)$, itself decays exponentially with distance, |r − r′|, in the position representation for systems with a non-negligible HOMO-LUMO gap.^3,23,24 For electronic structure theory based on localized AO basis functions, this translates into sparsity of the density matrix in the AO representation, as well as potential localization of the molecular orbitals (MOs). This sparsity is basis-set dependent and has been studied empirically.^25,26 For appropriate insulating systems and compact basis sets, significant sparsity is present and may be exploited to formulate efficient conditionally linear-scaling integral-driven algorithms.^27–29 Such methods make hybrid DFT calculations possible on very large insulating systems, provided the basis set is compact.

However, the situation worsens dramatically in larger basis sets for two reasons. First, the number of significant two-electron integrals scales as the fourth power of the mean number of basis functions on a single atomic center, leading to a tremendous pre-factor increase. Second, as larger basis sets contain additional diffuse functions, the condition number of the overlap matrix becomes larger, leading to decreased sparsity as well, and thus loss of effectiveness of linear scaling. The combination of these two factors makes large basis exact exchange calculations almost prohibitively more expensive than small basis set calculations. Unfortunately, hybrid functionals must be used with basis sets of at least triple-zeta quality to obtain adequately converged thermodynamic quantities.^30,31 In smaller basis sets, there is no accuracy advantage to hybrid functionals. For the same reason, it has been shown that in order to obtain relatively basis-set independent functional parameters, density functionals should be trained (and thus used) with triple-zeta or larger basis sets.³² Functionals trained close to the basis set limit yield significantly inferior performance in smaller basis sets.^13,33,34 This paper attempts to make progress on the challenging problem of constructing the K matrix in these large basis sets.

Methods based on the resolution of the identity (RI) approximation (also frequently referred to as the “density fitting” or DF approximation) offer the best-established avenue to reducing the computational cost of large basis set DFT calculations. These methods expand the atomic orbital “primary basis” products as linear combinations of “auxiliary basis” functions,

$${\displaystyle {\varphi }_{\mu }^{\ast }\left({\mathit{r}}_1\right){\varphi }_{\lambda }\left({\mathit{r}}_1\right)=\sum _Q{C}_Q^{\mu \lambda }{\chi }_Q\left({\mathit{r}}_1\right).}$$ (3)

Highly efficient RI algorithms have been developed for the Coulomb problem,^35,36 along with the auxiliary Coulomb fitting basis sets necessary to use such algorithms.^37–39 Turning to exchange, for which appropriate auxiliary basis sets are also available,^40,41 the RI approximation results in a much more tractable expression for the K matrix in which only three and two-center quantities are present,

$${\displaystyle K_{\mu \nu }=\sum _{\lambda \sigma }\sum _{PQ}{C}_P^{\mu \lambda }{C}_Q^{\nu \sigma }\left(P|Q\right)P_{\lambda \sigma }.}$$ (4)

By reducing the dimensionality of the AO basis quantities, these methods attain significant improvements in performance for large basis sets. This comes at a formal cost; the subsequent recombination of these lower-dimensional quantities exhibits fourth-order scaling. However, the fact that the relevant quantities can be compressed in earlier steps by transformation to the MO basis allows for a significant advantage in the prefactor of the calculation.^40,42 It should be noted that while RI-based algorithms for constructing K are necessarily significantly more complex than those used for J, the underlying approximation is the same.

Extensive effort has been devoted to lowering the scaling of RI-SCF. These approaches may be broadly classified into two categories: local fit metrics^43–46 and local fit domains.^42,47–50 In the local fit metric approach, the fit coefficients are determined by minimizing the self-repulsion between the fitted and exact densities as measured by a rapidly decaying local analog of the Coulomb operator, rather than the more typical full Coulomb metric. Local fit domain approximations are applied by expanding a given primary basis product only with the auxiliary basis functions within a predefined spatial domain; they differ from local metrics in that locality is achieved explicitly through a constraint rather than implicitly through the decay of the metric.

Two alternative approaches to the problem of large basis set K matrix calculations should be mentioned. The first is the Cholesky decomposition (CD), which has been shown to be equivalent to RI expansion of the two-electron integrals in a customized auxiliary basis.⁵¹ It may thus be regarded as an idealization of the RI approximation in some sense, and the algorithms based on CD and RI are often closely related.⁵² A second related approach is the pseudospectral or “semi-numerical” approach introduced to quantum chemistry by Friesner⁵³ and substantially improved by Neese et al.⁵⁴ Pseudospectral methods apply numerical quadrature to one of the two electronic coordinates in two-electron integral formula (1). In essence, this replaces a given two-electron integral with a large number of one-electron integrals resembling nuclear attraction integrals. When initially compared to the RI-K method, the pseudospectral approach was found to yield comparable speedups and accuracy,⁵⁵ while subsequent work has found superior speedups for large systems.⁵⁶

While efforts to reduce the scaling of RI-K are necessary in the long run, in this work, we focus on reducing the prefactor of the calculation. Combined with the already significant prefactor advantage of standard RI-K, we obtain a method that outperforms linear scaling integral evaluation and existing alternative RI methods for systems of up to 4400 basis functions in quadruple-zeta quality basis sets and even outperforms conventional algorithms in small double-zeta basis sets for a surprisingly large size regime. We achieve this by introducing a framework in which one constructs a much smaller “economized” exchange matrix that nonetheless yields energies, orbital first variations, and direct inversion of the iterative subspace (DIIS) error vectors that are exact. Within this framework, we then adapt the RI-K method to yield a new algorithm, termed the occupied orbital RI-K (occ-RI-K) method, which is intrinsically more efficient than RI-K. While our new approach can be combined with local RI approximations through the use of localized MOs, here we concentrate on the standard global Coulomb RI approximation. We demonstrate that the resulting algorithm is both faster and more accurate than our previous implementation based on the pair atomic RI approximation,⁴² as well as much faster and just as accurate as RI-K itself.

II. THEORY

A. Economization of the K matrix

Using standard spin-orbital notation, the exchange energy, E_K, which enters a global hybrid functional in scaled form (i.e., 0.54E_K for M06-2X¹⁰ or 0.2E_K for B3LYP^8,64,65) can be written in terms of K, defined in Eq. (2), as follows:

$${\displaystyle E_K=-\sum _{\mu \nu i}{c}_{\mu i}{K}_{\mu \nu }{c}_{\nu i},}$$ (5)

where we have expanded the AO density matrix $P_{\mu \nu }=\sum _i{c}_{\mu i}{c}_{\nu i}$ in terms of the MO coefficients c_μi. Evidently to evaluate the energy, it is possible to simply evaluate the diagonal elements of the exchange matrix in the occupied block, K_ii, rather than the full matrix in the AO representation, K_μν.

However, more information is required to evaluate the orbital gradient of E_K, as needed for performing a SCF calculation. Variations of the MO coefficients away from our current set are given as a unitary transformation, U, which is parameterized in terms of the exponential of a skew-symmetric matrix composed of mixings, Δ_ai, between occupied orbitals, i, and empty orbitals, a,

$${\displaystyle U=exp\left[\mathrm{\Delta }-{\mathrm{\Delta }}^T\right].}$$ (6)

It is then straightforward to show⁵⁷ that

$${\displaystyle \frac{\partial E_K}{\partial {\mathrm{\Delta }}_{ai}}=2K_{ai}.}$$ (7)

Evidently the gradient of the exact exchange energy requires only the occupied-virtual block, K_ia, rather than the full matrix in the AO representation, K_μν. Together, the energy and the gradient require only K_iν rather than the full K_μν.

The DIIS method introduced by Pulay is perhaps the most widely used convergence acceleration method.^58,59 For SCF convergence acceleration, the standard form of DIIS⁵⁹ accumulates a sequence of error vectors defined as the AO-basis representation of the commutator $[\hat{f},\hat{\rho }]$. The commutator, which is proportional to the SCF orbital gradient (cf. Eq. (7) for the exact exchange gradient), vanishes at SCF convergence. The AO basis commutator at the m^th iteration is

$${\displaystyle {\mathbf{e}}_m={\mathbf{F}}_m{\mathbf{P}}_m\mathbf{S}-\mathbf{S}{\mathbf{P}}_m{\mathbf{F}}_m,}$$ (8)

where S is the AO overlap matrix. DIIS extrapolation to obtain a new candidate solution is performed by minimizing a weighted linear combination of error vectors, $\sum _m{w}_m{\mathbf{e}}_m$, subject to the normalization constraint, $\sum _m{w}_m=1$. The extrapolated Fock matrix, $F_{\mathit{extrap}}=\sum _m{w}_m{\mathbf{F}}_m$, is then diagonalized to define the updated density matrix, P_m+1, and thus F_m+1, etc.

Since the Fock matrix appears in Eq. (8) only when multiplied by the density matrix, a sequence of DIIS iterates can be correctly evaluated using only the occupied row-block of the K matrix. This yields exactly the same set of DIIS coefficients as if the full K-matrix was used to evaluate the error vector. Hence, construction of the full AO-basis K-matrix is potentially wasteful, as only the entries K_iν are required to obtain an exact DIIS error vector and exchange energy. In addition, it is trivial to show that the occupied eigenvalues are exactly reproduced. This is all that is typically required in a standard DFT calculation, and therefore, exact exchange algorithms can and should be developed to exploit this fact. There are two caveats to note. First, diagonalization steps that neglect the virtual-virtual part of K will not be identical with steps that include it. Second, the virtual eigenvalues will not be exactly reproduced, and thus, a single full K-build is required for post-SCF purposes such as double hybrid density functional theory or the random phase approximation. We note that Eq. (8) suggests that all other components of the Fock matrix, not just the exchange matrix, may be utilized in half-transformed form; however, this would likely be a much more drastic approximation, as the virtual-virtual block of the Fock matrix is qualitatively correct when only the virtual-virtual contribution from K is neglected. Assessment of this more aggressive approach is beyond the scope of this work.

The compressed K-matrix, K_iν, can be employed to build an AO basis quantity as follows. We partition the exchange operator into terms involving projectors onto the occupied subspace (the projector is $\hat{\rho }$ of course) and the virtual subspace (the projector is $\hat{q}=(1-\hat{\rho })$),

$${\displaystyle \hat{K}=(\hat{\rho }+\hat{q})\hat{K}(\hat{\rho }+\hat{q})}$$ (9)

$${\displaystyle =\hat{\rho }\hat{K}\hat{\rho }+\hat{q}\hat{K}\hat{\rho }+\hat{\rho }\hat{K}\hat{q}+\hat{q}\hat{K}\hat{q}.}$$ (10)

We neglect the final term in Eq. (10) and recombine the projection operators in the remaining terms to obtain a modified exact exchange operator,

$${\displaystyle {\hat{K}}^{\prime }=\hat{\rho }\hat{K}+\hat{K}\hat{\rho }-\hat{\rho }\hat{K}\hat{\rho }.}$$ (11)

Transforming this expression into the AO basis yields our final working expression for ${\hat{K}}^{\prime }$,

$${\displaystyle K_{\mu \nu }^{\prime }=\sum _{\lambda i}{S}_{\mu \lambda }{c}_{\lambda i}{K}_{i\nu }+\sum _{i\lambda }{K}_{\mu i}{c}_{\lambda i}^{\ast }{S}_{\lambda \nu }-\sum _{ij}\sum _{\lambda \sigma }{S}_{\mu \lambda }{c}_{\lambda i}{K}_{ij}{c}_{\sigma j}^{\ast }{S}_{\sigma \nu }.}$$ (12)

The second term is clearly just the transpose of the first, and the final term may be obtained easily from the common intermediate, K_iν. The basic idea of computing just K_iν or, for that matter, just F_iν is of course extremely simple and undoubtedly has been thought of before. It has been employed in the iterative updates of plane-wave DFT calculations,⁶⁰ where the full Fock matrix is enormous and thus, evaluating a narrow rectangular matrix is far preferable to an enormous square matrix. Indeed, the idea of constructing this economized version of K was mentioned briefly by Aquilante et al.,⁶¹ but we have found no prior or subsequent discussion in the literature. The important point that has not yet been accomplished is to demonstrate how formation of an economized K matrix can be used for computational advantage with AO basis sets.

B. The RI approximation

One approach to exploiting the gains in efficiency made possible by the economization of the K matrix is to introduce the RI approximation. This approximation is applied by expanding a given pair of Gaussians in terms of an atom-centered Gaussian auxiliary basis set, as shown in Eq. (3). The expansion coefficients are typically determined by minimizing the self-repulsion of the residual between the exact Gaussian product and its fitted expansion.⁴⁴ This formulation yields the following standard formulation of the coefficients in global Coulomb-metric RI:⁴⁴

$${\displaystyle C_Q^{\mu \lambda }=\sum _P\left(\mu \lambda |P\right){\left(P|Q\right)}^{-1}.}$$ (13)

Global Coulomb RI can be shown to be equivalent to the Dunlap functional for the two-electron integral and thus yields error in the final integral quadratic in the expansion errors of the individual products.⁶²

C. The occ-RI-K algorithm

It is apparent from the above discussion that the problem of the efficient computation of the K matrix now reduces to the problem of computing K_iν. Application of the RI approximation and expressing the density matrix in the MO basis yield the following expression for the K_iν:

$${\displaystyle K_{i\nu }=\sum _{j\lambda \sigma Q\mu }{C}_Q^{\mu \lambda }\left(Q|\nu \sigma \right)c_{\mu i}{c}_{\lambda j}{c}_{\sigma j}.}$$ (14)

In the following discussion of performance, we use the following notation for dimension quantities: N (number of primary basis functions), $\left[\mathrm{NB2}\right]$ (number of significant primary-basis function pairs, which is asymptotically linear in system size), X (number of auxiliary basis functions), and o (number of occupied orbitals). In order to avoid an expensive O(X²) step, we pretransform the three-center integrals prior to the formation of the Coulomb metric RI fit coefficients. For calculations run with realistic basis sets and thresholds, $\left[\mathrm{NB2}\right]\gg o^2$, and thus, pretransforming the integrals renders the O(X²) step relatively unimportant. The resulting algorithm for the formation of K_iν is shown in Table I. With K_iν in hand, the three terms in Eq. (12) can be formed trivially via fast matrix multiplications.

TABLE I.

The occ-RI-K algorithm, omitting the trivial final matrix multiplication steps. The second column gives the operation cost for each step in terms of N (number of primary basis functions), $\left[\mathrm{NB2}\right]$ (number of significant primary-basis function pairs, which is asymptotically linear in system size), X (number of auxiliary basis functions), and o (number of occupied orbitals). The computational cost scaling is given as a power of the size of the molecule, M, assuming a uniform choice of the AO and auxiliary basis sets. Memory demand is indicated in the same way.

Step	Operations	Scaling	Memory
At the start of first SCF iteration
Calculate ${\left(P|Q\right)}^{-1}$	X3	M3	M2
For each SCF iteration
Loop over atomic batches of auxiliary functions P
Calculate $\left(\mu \lambda |P\right)$ in batch	$\left[\mathrm{NB2}\right]X$	M2	M1
$\left(\mu j|P\right)=\sum _{\lambda }\left(\mu \lambda |P\right)c_j^{\lambda }$	$o\left[\mathrm{NB2}\right]X$	M3	M2
Write $\left(\mu j|P\right)$ to disk	oNX	M3	M2 (M3 disk)
$\left(ij|P\right)=\sum _{\mu }\left(\mu j|P\right)c_i^{\mu }$	o2NX	M4	M2
$C_Q^{ij}+=\sum _P\left(ij|P\right){\left(P|Q\right)}^{-1}$	o2X2	M4	M2
Loop over atomic batches of auxiliary functions Q
Read $\left(\nu j|Q\right)$ batch from disk	oNX	M3	M2
$K_{i\nu }+=\sum _Q{C}_Q^{ij}\left(\nu j|Q\right)$	o2NX	M4	M2

If the oNX storage requirement becomes prohibitive, the algorithm can be trivially modified to add an additional level of batching over the occupied orbital index j. This will then necessitate recomputation of the AO three-center integrals once per batch of j values. We have constructed such an implementation, but do not find it necessary to use for the timing experiments presented here. In practice, the disk I/O wall time cost is a negligible fraction of the algorithmic runtime.

We can anticipate the performance gains that can be achieved using occ-RI-K by comparing the three quartic steps in Table I against the two quartic steps of the standard RI-K method. In standard RI-K,⁴⁰ one forms $B_{\mu j}^Q+=\left(\mu j|P\right){\left(P|Q\right)}^{-1/2}$ which requires oNX² operations, followed by $K_{\mu \nu }+=B_{j\mu }^Q{B}_{j\nu }^Q$ which requires oN²X operations. The speedup given by occ-RI-K is therefore approximately

$${\displaystyle s=\frac{N\left(X+N\right)}{o\left(X+2N\right)}.}$$ (15)

If we (conservatively) assume that X ≈ 2N, then the approximate speedup is $s=\frac{3}{4}\left(N/o\right)$, suggesting that occ-RI-K can yield a speedup over RI-K which is 75% of the compression factor associated with calculating K_iν rather than K_μν. For a basis set of typical quadruple-zeta quality, this suggests an asymptotic speedup of roughly a factor of 15 (presuming the cubic steps are negligible, as in the very large molecule limit). The next step is to obtain real-world timings on the basis of an implementation for finite-size molecules and compare against other methods for forming the K matrix.

III. RESULTS AND DISCUSSION

All calculations were performed with a development version of Q-Chem 4.2.⁶³

A. Accuracy

At SCF convergence, the energy errors associated with occ-RI-K are formally equivalent to those of RI-K. However, as RI-K has historically received only minimal accuracy benchmarking, primarily in the context of training auxiliary basis sets,⁴¹ we wish to provide an expanded survey of the accuracy of this approximation. We also wish to provide an in-depth comparison to our recent implementation⁴² of the (also sparsely benchmarked)^49,50 PARI-K algorithm. We now demonstrate that occ-RI-K yields superior accuracy to PARI-K, causing negligible errors with respect to unapproximated integral-direct algorithms for a wide variety of energetic properties. Our test suite is based on that of Mardirossian and Head-Gordon³⁴ and consists of a compilation of many separate sets of energetic reference data spanning thermochemistry and intermolecular interactions. The following test sets have been slightly modified from their original versions: only the first 8 barrier heights from BHPERI are included, the four water 20-mers from WATER27 and interactions containing palladium or iodine in X40, XB18, and XB51 have been excluded. Calculations performed at the B3LYP/def2-QZVPPD^66–68 level of theory yield the results summarized in Table II. While PARI-K yields impressive accuracy in its own right, the accuracy of occ-RI-K is clearly superior. The errors per electron in the absolute energies of all molecules in the test set are quite acceptable, with a mean of 0.7 cal mol⁻¹ electron⁻¹ and a maximum of 3.2 cal mol⁻¹ electron⁻¹. This is significantly lower than the corresponding mean of 2.0 cal mol⁻¹ electron⁻¹ and maximum of 11.8 cal mol⁻¹ electron⁻¹ for PARI-K. Note that in these tests the Coulomb interactions are evaluated by exact methods.

TABLE II.

occ-RI-K vs. PARI-K accuracy comparison over a compilation of test sets, using the B3LYP/def2-QZVPPD level of the theory. Data in kcal/mol.

Dataset	occ-RI-K error	PARI-K error
A21x1269	0.00	0.00
A2470	0.00	0.00
AE1871	0.01	0.01
AlkAtom1972	0.01	0.14
AlkIsomer1172	0.00	0.02
AlkIsod1472	0.00	0.03
Bauza3073,74	0.00	0.00
Butanediol6575	0.00	0.00
BzDC21576	0.00	0.00
CT2077	0.00	0.00
DIE6078	0.00	0.00
DS1479	0.00	0.01
EA1380	0.01	0.01
EIE2281	0.00	0.00
FmH2O1082,83	0.01	0.16
ACONF84,85	0.00	0.01
BHPERI85,86	0.00	0.00
CYCONF85,87	0.00	0.00
G21EA85,88	0.00	0.00
G21IP85,88	0.00	0.00
NBPRC85	0.00	0.02
WATER2785,89	0.00	0.03
NHTBH3885,90	0.01	0.02
HTBH3885,91	0.00	0.01
BH76RC85	0.00	0.00
DBH2486	0.00	0.01
H2O6Bind883,92	0.00	0.05
HB1593	0.00	0.01
HSG94,95	0.00	0.00
HW3096	0.00	0.01
HW6Cl82,83	0.00	0.04
HW6F82,83	0.00	0.04
IP1380	0.00	0.00
NBC1095	0.01	0.01
NC1597	0.00	0.00
Pentane1498	0.00	0.01
RG1099	0.00	0.00
S2295,100	0.00	0.00
S66101,102	0.01	0.00
S66x8101	0.00	0.00
Shields38103	0.01	0.06
Styrene45104	0.00	0.01
SW49Rel345105	0.01	0.00
SW49Bind345105	0.00	0.02
SW49Rel6105	0.00	0.01
SW49Bind6105	0.00	0.04
TA13106	0.00	0.00
BDE99MR107	0.01	0.01
BDE99nonMR107	0.00	0.01
HAT707nonMR107	0.00	0.00
HAT707MR107	0.01	0.01
ISOMERIZATION20107	0.00	0.00
SN13107	0.00	0.00
TAE140nonMR107	0.00	0.01
TAE140MR107	0.01	0.02
X40108	0.00	0.00
XB18109	0.00	0.00
XB51109	0.00	0.01

B. Convergence

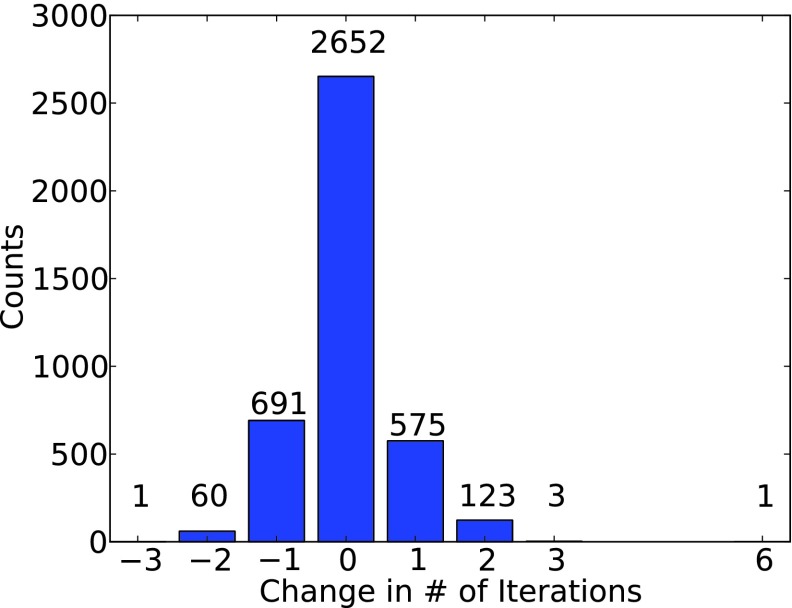
At no point in the course of SCF iteration does the occ-RI-K method explicitly construct the exact Fock matrix, rather we construct a modified Fock matrix that yields the identical orbital gradient and DIIS error vectors and thus converges to the same result as a calculation using the conventional RI-K method. However, the results of the diagonalization updates are not identical, as these depend upon the unoccupied eigenvalues which are not obtained exactly via occ-RI-K. So while the final result (presuming convergence) is not in doubt, the convergence properties of occ-RI-K are an open question. We empirically demonstrate that convergence using occ-RI-K is essentially identical to that of standard DIIS. Over the entire test set, the average number of iterations to convergence with and without occ-RI-K is identically 9.3 iterations. A histogram of the change in SCF iteration count for all calculations in the test set is shown in Fig. 1. Convergence for the vast majority of jobs is completely unaffected, while 752 jobs converge faster with occ-RI-K compared to 702 that converge slower. No job requires more than six additional iterations to converge. We can thus state definitively that occ-RI-K convergence is well-behaved, and on the basis of these statistics, we can simply assess performance based on timing a single K-build.

FIG. 1.

Histogram of change in number of SCF iterations for the calculations in the test set between occ-RI-K and exact integral-direct K.

C. Timings

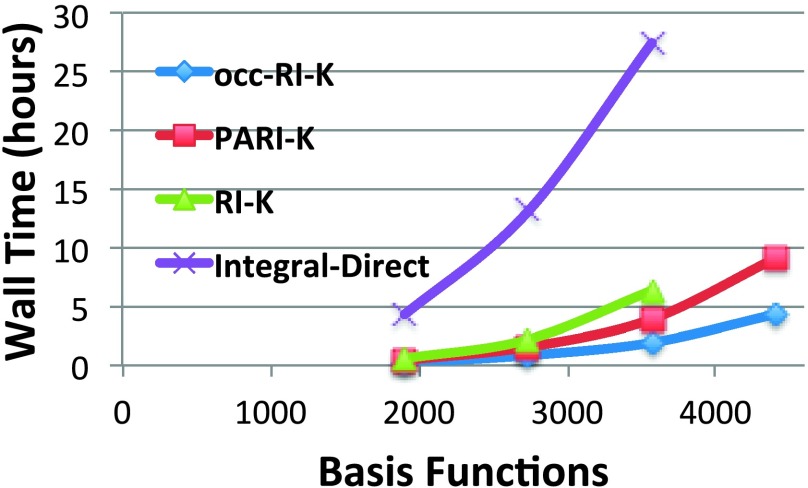
We now demonstrate that occ-RI-K outperforms our recently developed PARI-K algorithm and traditional RI-K. The timings for conventional integral evaluation are shown to reiterate the dramatic advantage of these methods for large basis sets. The systems chosen for comparison are n-by-6 hydrogen-terminated graphene sheets of successively higher depth; we prefer these “somewhat two-dimensional” benchmarks as their size can be increased in a linear fashion but they yield arguably more realistic AO locality than linear systems. The basis set used was the Dunning cc-pVQZ basis set.¹¹⁰ The results of this timing experiment are shown in Fig. 2.

FIG. 2.

Timings for the second K build of various depths of n-by-6 graphene sheets in the cc-pVQZ basis set using a single thread. An integral screening threshold of 10⁻¹⁰ was used for all calculations.

For the largest system treated with the conventional integral code and RI-K, occ-RI-K provides a 14 × speedup, compared to 7 × for PARI and 4 × for RI. We note that the difference between this PARI-K speedup and that reported previously⁴² for the same system/basis set is likely due to a looser screening threshold (10⁻¹⁰ here vs 10⁻¹² in previous work), which accelerates the conventional code relative to PARI and occ-RI-K. The use of a different architecture (AMD Opteron 6376 vs. AMD Opteron 2376 previously) could also play a role.

For the largest system, occ-RI-K outperforms PARI-K by a factor of 2. For the largest system treated with RI-K, occ-RI-K yields a speedup of 3.3 × relative to RI-K. This factor is considerably smaller than our predicted speedup relative to RI-K of about 15 in cc-pVQZ. This reflects the fact that quartic steps do not entirely dominate the calculation for molecules of this size, contrary to what we assumed in the speedup analysis. As a result, the speedups over RI-K will increase further with yet larger size molecules. We demonstrate this trend by considering two linear alkanes, C₃₀H₆₂ and C₇₀H₁₄₂, in the basis sets cc-pVQZ and cc-pVTZ, respectively. For the smaller alkane in the larger basis set, the computational cost is dominated by the lower scaling steps, as shown in Table III. When the system size is increased and the basis set size is reduced, the higher-scaling MO basis steps become much more significant, illustrating the trend of larger speedups with respect to RI-K with increasing system size.

TABLE III.

Contribution of various steps to overall occ-RI-K wall-time for two systems and basis sets. Disk reads/writes are included in overall times for various steps, though their contribution is minor. An integral threshold of 10⁻¹⁰ was employed in both calculations. The total number of basis functions was 3510 and 4088, respectively.

	C30H62/cc-pVQZ		C70H142/cc-pVTZ
Step	Time (s)	% of total	Time (s)	% of total
Calculate $\left(\mu \lambda |P\right)$	955	26	1090	8
$\left(\mu j|P\right)=\sum _{\lambda }\left(\mu \lambda |P\right)c_j^{\lambda }$	1686	46	4294	33
$\left(ij|P\right)=\sum _{\mu }\left(\mu j|P\right)c_j^{\mu }$	174	5	1419	11
$C_Q^{ij}=\sum _P\left(ij|P\right){\left(P|Q\right)}^{-1}$	267	7	3483	27
$K_{i\nu }=\sum _{jQ}{C}_Q^{ij}\left(\nu j|Q\right)$	224	6	1524	12
Speedup relative to RI-K	3.6 ×		5.0 ×

We shall now demonstrate that occ-RI-K can be applied to quite large systems even in small basis sets, while still outperforming conventional SCF. While occ-RI-K has unfavorable asymptotic scaling compared to conventional SCF, in practice this shortcoming is drastically mitigated by two factors. First, the much higher floating point efficiency of standardized linear algebra libraries relative to AO integral evaluation codes coupled with the replacement of extended primary basis function indices with more compact occupied orbital indices yields a much lower prefactor for RI methods that is not overcome by lower-scaling methods until very long length scales. Second, the favorable scaling of conventional K construction is very difficult to attain in practice, as both more diffuse basis sets and tighter integral thresholds than those used in timing benchmark studies must often be used in practical applications.

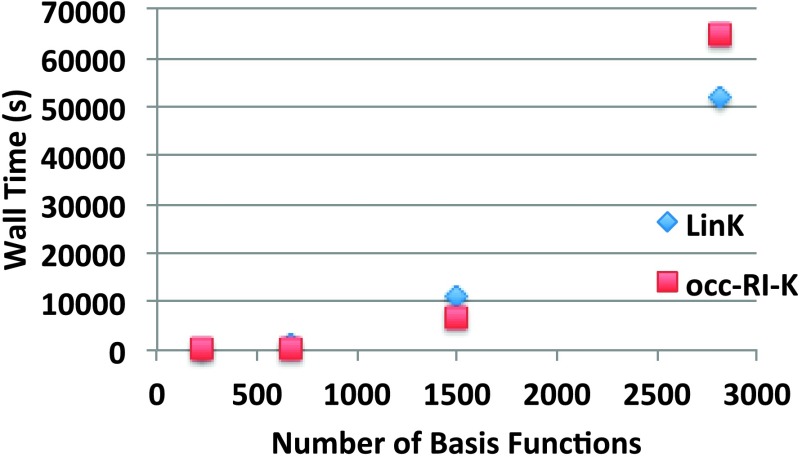
As an illustration of these challenges, we compare the performance of occ-RI-K to that of LinK.²⁹ An integral threshold of 10⁻¹⁰ is often recommended^111,112 to converge SCF energies to 10⁻⁶. The systems on which these comparisons are performed are the octahedral diamondoid model systems used by Strout and Scuseria to model SCF scaling in a previous publication,¹¹¹ treated using the cc-pVDZ basis set.¹¹⁰ Due to the absence of a standard exchange auxiliary fitting basis for this basis set, the double zeta RI-MP2 auxiliary basis set of Weigend was used instead.¹¹³ The results are shown in Fig. 3.

FIG. 3.

Timings for the second K build of various size octahedral diamondoids in the cc-pVDZ basis set using a single thread. The points correspond to n = 2, 3, 4, 5 in the compound series C_(4n³−n)/3H_4n² used by Strout and Scuseria.¹¹¹ An integral screening threshold of 10⁻¹⁰ was used for all calculations.

While occ-RI-K is eventually surpassed by LinK, the first system in which LinK performs better is C₁₆₅H₁₀₀. Thus, even for this very small, compact basis set, a significant size regime exists where occ-RI-K is competitive. We thus assert that occ-RI-K is likely to accelerate a significant subset of everyday quantum chemistry calculations.

IV. CONCLUSIONS

The occ-RI-K method is a new scheme for building the K matrix partially in the MO basis that, combined with the RI approximation, leads to an extremely efficient algorithm that typically outperforms current alternatives. The occ-RI-K method yields extremely accurate energetics (identical to conventional RI-K) and well-behaved convergence (essentially unchanged relative to conventional methods). It yields speedups over conventional integrals and conventional RI-K that increase with the size of the AO basis set. occ-RI-K thus helps to make larger basis set hybrid DFT calculations more feasible, which is desirable for improved accuracy with modern functionals. Whilst we have not treated the case explicitly here as it is a very simple generalization, we note that range-separated hybrid functionals evaluated using occ-RI-K yield an essentially equal speedup over RI-K. Finally, there are very intriguing prospects for employing the economized K framework in lower scaling (conditionally linear scaling) algorithms, using localized orbitals, which will be valuable for the largest molecules.