Synchronized multiartifact reduction with tomographic reconstruction (SMART-RECON): A statistical model based iterative image reconstruction method to eliminate limited-view artifacts and to mitigate the temporal-average artifacts in time-resolved CT

Abstract

Purpose:

In x-ray computed tomography (CT), a violation of the Tuy data sufficiency condition leads to limited-view artifacts. In some applications, it is desirable to use data corresponding to a narrow temporal window to reconstruct images with reduced temporal-average artifacts. However, the need to reduce temporal-average artifacts in practice may result in a violation of the Tuy condition and thus undesirable limited-view artifacts. In this paper, the authors present a new iterative reconstruction method, synchronized multiartifact reduction with tomographic reconstruction (SMART-RECON), to eliminate limited-view artifacts using data acquired within an ultranarrow temporal window that severely violates the Tuy condition.

Methods:

In time-resolved contrast enhanced CT acquisitions, image contrast dynamically changes during data acquisition. Each image reconstructed from data acquired in a given temporal window represents one time frame and can be denoted as an image vector. Conventionally, each individual time frame is reconstructed independently. In this paper, all image frames are grouped into a spatial–temporal image matrix and are reconstructed together. Rather than the spatial and/or temporal smoothing regularizers commonly used in iterative image reconstruction, the nuclear norm of the spatial–temporal image matrix is used in SMART-RECON to regularize the reconstruction of all image time frames. This regularizer exploits the low-dimensional structure of the spatial–temporal image matrix to mitigate limited-view artifacts when an ultranarrow temporal window is desired in some applications to reduce temporal-average artifacts. Both numerical simulations in two dimensional image slices with known ground truth and in vivo human subject data acquired in a contrast enhanced cone beam CT exam have been used to validate the proposed SMART-RECON algorithm and to demonstrate the initial performance of the algorithm. Reconstruction errors and temporal fidelity of the reconstructed images were quantified using the relative root mean square error (rRMSE) and the universal quality index (UQI) in numerical simulations. The performance of the SMART-RECON algorithm was compared with that of the prior image constrained compressed sensing (PICCS) reconstruction quantitatively in simulations and qualitatively in human subject exam.

Results:

In numerical simulations, the 240^∘ short scan angular span was divided into four consecutive 60^∘ angular subsectors. SMART-RECON enables four high temporal fidelity images without limited-view artifacts. The average rRMSE is 16% and UQIs are 0.96 and 0.95 for the two local regions of interest, respectively. In contrast, the corresponding average rRMSE and UQIs are 25%, 0.78, and 0.81, respectively, for the PICCS reconstruction. Note that only one filtered backprojection image can be reconstructed from the same data set with an average rRMSE and UQIs are 45%, 0.71, and 0.79, respectively, to benchmark reconstruction accuracies. For in vivo contrast enhanced cone beam CT data acquired from a short scan angular span of 200^∘, three 66^∘ angular subsectors were used in SMART-RECON. The results demonstrated clear contrast difference in three SMART-RECON reconstructed image volumes without limited-view artifacts. In contrast, for the same angular sectors, PICCS cannot reconstruct images without limited-view artifacts and with clear contrast difference in three reconstructed image volumes.

Conclusions:

In time-resolved CT, the proposed SMART-RECON method provides a new method to eliminate limited-view artifacts using data acquired in an ultranarrow temporal window, which corresponds to approximately 60^∘ angular subsectors.

1. INTRODUCTION

Over the past decade or so, significant progress has been made in tomographic reconstruction using either analytical image reconstruction formulae (see Ref. 1 and references therein) or model based iterative image reconstruction methods.^2–5 Many of these new reconstruction methods have been directly exploited to either improve temporal resolution^6,7 or reduce radiation dose.⁸

Regarding the reconstruction of a static image object using an analytical reconstruction method, the Tuy data sufficiency condition⁹ is of fundamental importance. It states that, to enable a mathematically exact reconstruction of a point inside the image object, every plane passing through that point must intersect the scanning trajectory at least once.¹⁰ This data sufficiency condition determines the minimum angular span of view angles in a data acquisition required for accurate reconstruction of a region of interest inside an image object. Violation of the Tuy condition leads to image object distortion and shading artifacts in the reconstructed images (these multifaceted artifacts are referred to as limited-view artifacts in this paper). To accurately reconstruct the entire image object from fan beam projections, the Tuy condition becomes the so-called short scan condition, requiring that the angular span of view angles must be at least 180^∘ + γ_m, where γ_m is the full fan angle. In the case where the angular span is less than 180^∘ + γ_m, new analytical image reconstruction algorithms have been developed^11–16 to accurately reconstruct a portion of the image object albeit not the entire image object. This has been referred to as super-short scan reconstruction in literature. However, when the angular span falls below 180^∘ − γ_m, using the Tuy data sufficiency condition, it is straightforward to show that even the super-short scan reconstruction algorithms fail to reconstruct the relevant image content inside the scanned field of view (FOV) without limited-view angle artifacts.

A new challenge encountered in time-resolved computed tomography (CT) is the inevitable temporal-average effects during data acquisition and image reconstruction processes even if the angular span of the acquired data does satisfy the Tuy condition, as the acquired data are not compatible with the most fundamental assumption in tomographic reconstruction: the image object does not change during the acquisition of a complete data set for reconstruction. A consequence of violating the above static object assumption is that only a temporally averaged image can be reconstructed using data acquired from a certain span of view angles, no matter if the angular span of the acquired data satisfies the Tuy data sufficiency condition or not. The image artifacts associated with this temporal averaging process include distortion, shading, and streak artifacts in the reconstructed images. These artifacts are collectively referred to as temporal-average artifacts in this paper. The temporal window, i.e., the time elapsed during the acquisition of data within a certain angular span, is used as a surrogate metric to indicate the severity of temporal-average artifacts: a wider temporal window results in more severe temporal-average artifacts in the reconstructed images.

In current CT data acquisition systems, once the gantry rotation speed and detector readout rate are selected for a data acquisition, a wider temporal window allows the tube-detector assembly to travel through a greater angular span and vice versa. Thus, the temporal window and the angular span of a CT data acquisition are inherently correlated with one another. This inherent correlation dictates a coupling between temporal-average artifacts and limited-view artifacts. Specifically, when the temporal window width of the acquired data used in a reconstruction increases, the temporal-average artifacts become more severe and the associated limited-view artifacts become less pronounced. On the contrary, a narrower temporal window results in less severe temporal-average artifacts but more pronounced limited-view artifacts.

When a prior CT image of the same image object can be properly incorporated into the dynamic CT reconstruction process, the aforementioned coupling between temporal-average artifacts and limited-view artifacts can be somewhat decoupled from one another in some specific applications.^7,17,18 Recently, it has been shown that, when the angular span is not significantly shorter than 180^∘ − γ_m (for a 60^∘ fan angle, this coincides with one half of the short scan angular span), the entire image object may be reconstructed without limited-view angle artifacts using the prior image constrained compressed sensing (PICCS) algorithm provided that the prior image used to constrain the reconstruction is not contaminated by the limited-view artifacts.^7,18 However, to the best of the authors’ knowledge, there is no work published yet to show that time-resolved CT images can be reconstructed without severe limited-view angle artifacts when the angular span of the data is significantly below 180^∘ − γ_m.

The purpose of this paper is to present a model based iterative image reconstruction algorithm that allows one to reconstruct dynamically changing objects with negligible limited-view artifact using data from an angular span much shorter than 180^∘ − γ_m. The proposed algorithm, synchronized multiartifact reduction with tomographic reconstruction (SMART-RECON), utilizes both spatial and temporal similarity information among different time frames to eliminate limited-view artifacts with data acquired over an angular span as short as approximately 60^∘.

2. METHODS AND MATERIALS

2.A. Mathematical notation for iterative reconstruction

In this paper, a monochromatic x-ray beam is assumed. This allows the CT reconstruction problem to be linearized, so that the spatial distribution of the attenuation coefficients of an image object, $\mu \left(\overrightarrow{x}\right)$, can be reconstructed from a set of line integral measurements,

$${\displaystyle y_i={\int }_{{\ell }_i}\mathit{\mu }\left(\overrightarrow{x}\right)\mathrm{d}\ell ,(i=1,2,\dots ,N),}$$ (1)

where N is the total number of line integrals. In a digital image representation, the image function, $\mu \left(\overrightarrow{x}\right)$, can be represented by the superposition of a series of basis functions, $B_j\left(\overrightarrow{x}\right)$,

$${\displaystyle \mathit{\mu }\left(\overrightarrow{x}\right)=\sum _{j=1}^M{X}_j{B}_j\left(\overrightarrow{x}\right),(j=1,2,\dots ,M).}$$ (2)

As a result, the image is represented by M numbers, X_j, and these numbers can be arranged as a column vector $\overrightarrow{X}={(X_1,X_2,\dots ,X_M)}^{\mathrm{tr}}$ to represent the image, where (⋅)^tr denotes a matrix transpose operation. Substituting Eq. (2) into Eq. (1) yields

$${\displaystyle y_i=\sum _j{A}_{ij}{X}_j={\left[\mathbf{A}\overrightarrow{X}\right]}_i,}$$ (3)

where the N × M matrix, $A_{ij}={\int }_{{\ell }_i}\mathrm{d}{\ell }_i{B}_j\left(\overrightarrow{x}\right)$, is referred to as the image system matrix. Therefore, the forward model of the tomographic image reconstruction problem [Eq. (1)] can be written as

$${\displaystyle \overrightarrow{y}=\mathbf{A}\overrightarrow{X},}$$ (4)

where the column vector $\overrightarrow{y}={(y_1,y_2,\dots ,y_N)}^{\mathrm{tr}}$.

2.B. Spatial–temporal image matrix for time-resolved CT imaging

In time-resolved contrast enhanced CT image acquisitions, contrast material progressively enhances the vasculature while the x-ray tube travels from the starting angular position, θ₀, to the ending angular position, θ_f, resulting in an angular span of Θ = [θ₀, θ_f]. In practice, regardless of the actual value of the total angular span, Θ, the temporal window can be retrospectively shortened in image reconstruction. For example, the total angular span Θ = [θ₀, θ_f] may be evenly divided into a union of disjoint segments Θ_τ (τ = 1, 2, …, T) each covering a temporal window Δt,

$${\displaystyle \mathrm{\Theta }=[{\theta }_0,{\theta }_f]=\bigcup _{\tau =1}^T{\mathrm{\Theta }}_{\tau },}$$ (5)

where Θ_τ = [θ_tτ−0.5Δt, θ_tτ+0.5Δt]. Each small segment of view angle span Θ_τ corresponds to an image time frame to be reconstructed and thus there are a total number of T image frames to be reconstructed. Using the column vector notation introduced in Subsection 2.A, these image time frames are denoted as ${\overrightarrow{X}}^{\tau }(\tau =1,2,\dots ,T)$. All image time frames can be grouped together to form the following M × T spatial–temporal image matrix:

$${\displaystyle \mathbf{X}=({\overrightarrow{X}}^1,{\overrightarrow{X}}^2,\dots ,{\overrightarrow{X}}^T)=\left(\begin{array}{cccc}\hfill X_1^1\hfill & \hfill X_1^2\hfill & \hfill \cdots \hfill & \hfill X_1^T\hfill \\ \hfill X_2^1\hfill & \hfill X_2^2\hfill & \hfill \cdots \hfill & \hfill X_2^T\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill X_M^1\hfill & \hfill X_M^2\hfill & \hfill \cdots \hfill & \hfill X_M^T\hfill \end{array}\right).}$$ (6)

In this spatial–temporal image matrix, each column of the spatial–temporal matrix X represents one image vector at a given time frame while each row of the spatial–temporal matrix represents the dynamic change of a given pixel/voxel from one time frame to another. Thus, the spatial–temporal matrix X gives a complete spatial and temporal representation of the image object.

2.C. Forward model of the spatial–temporal image matrix

For each individual time frame, ${\overrightarrow{X}}^{\tau }$, the projection data acquired within the temporal window, [t_τ − 0.5Δt, t_τ + 0.5Δt], form a subcolumn data vector ${\overrightarrow{y}}^{\tau }$. The corresponding rows in system matrix A in Eq. (4) form a subsystem matrix A^τ for the τth time frame. (Note, in this paper, superscripts denote the time frame, while subscripts denote the vector component.) Using this notation, we have the following forward projection model for each time frame:

$${\displaystyle \left(\begin{array}{c}\hfill {\overrightarrow{y}}^1\hfill \\ \hfill {\overrightarrow{y}}^2\hfill \\ \hfill ⋮\hfill \\ \hfill {\overrightarrow{y}}^T\hfill \end{array}\right)=\left(\begin{array}{c}\hfill {\mathbf{A}}^1{\overrightarrow{X}}^1\hfill \\ \hfill {\mathbf{A}}^2{\overrightarrow{X}}^2\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{A}}^T{\overrightarrow{X}}^T\hfill \end{array}\right).}$$ (7)

The above T individual forward models can be written in a compact form as follows:

$${\displaystyle \overrightarrow{\mathcal{Y}}=\mathcal{A}\overrightarrow{\mathbf{X}}.}$$ (8)

Here, we introduced the following notations:

$${\displaystyle \overrightarrow{\mathcal{Y}}=\sum _{\tau =1}^T{\hat{e}}_{\tau }⨂{\overrightarrow{y}}^{\tau },\mathcal{A}=I_T⨂{\mathbf{A}}^{\tau },\overrightarrow{\mathbf{X}}=\mathrm{vec}\left(\mathbf{X}\right).}$$ (9)

In these equations, ⨂ denotes the Kronecker direct product operation, ${\hat{e}}^{\tau }={(0,0,\dots ,0,1_{\tau },0,\dots ,0)}^{\mathrm{tr}}$ is the τth standard column basis in a T dimensional space, I_T is the T × T identity matrix, and vec(X) is the vectorization operation of the spatial–temporal matrix introduced in Eq. (6). Note that the dimension of the column vector $\overrightarrow{\mathcal{Y}}$ is N and the dimension of the column vector ${\overrightarrow{y}}^{\tau }$ for an individual time frame is N/T. The dimension of the vector $\overrightarrow{\mathbf{X}}$ is MT and the dimension of the modified system matrix $\mathcal{A}$ in Eq. (8) is N × MT.

2.D. Nuclear norm of the prior image augmented spatial–temporal image matrix: Regularizer in SMART-RECON

As discussed in the Introduction, when the angular span of the acquired data in a temporal window does not satisfy the Tuy condition, limited-view artifacts appear. When a prior CT image of the same image object without limited-view artifacts is available for use in the reconstruction, limited-view artifacts can be mitigated using the PICCS algorithm^4,7,18 for an angular span greater than 180^∘ − γ_m. In this paper, the core idea is still to use the prior image to help reduce limited-view artifacts, but in a fundamentally different way such that the proposed algorithm may be used to eliminate limited-view artifacts down to an angular span much shorter than 180^∘ − γ_m. In this paper, the prior image column vector, ${\overrightarrow{X}}^p$, is used to augment the target spatial–temporal image matrix X to generate an augmented spatial–temporal matrix X_A as follows:

$${\displaystyle {\mathbf{X}}_A=\left({\overrightarrow{X}}^p\right|\mathbf{X})≕\left(\begin{array}{ccccc}\hfill X_1^p\hfill & \hfill X_1^1\hfill & \hfill X_1^2\hfill & \hfill \cdots \hfill & \hfill X_1^T\hfill \\ \hfill X_2^p\hfill & \hfill X_2^1\hfill & \hfill X_2^2\hfill & \hfill \cdots \hfill & \hfill X_2^T\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill X_M^p\hfill & \hfill X_M^1\hfill & \hfill X_M^2\hfill & \hfill \cdots \hfill & \hfill X_M^T\hfill \end{array}\right),}$$ (10)

where ≕ stands for a definition. The nuclear norm of this matrix, i.e., ‖X_A‖_∗, is used to regularize the reconstruction of the spatial–temporal matrix, X; namely, the regularizer is given as

$${\displaystyle \mathrm{\Psi }\left(\mathbf{X}\right)=\Vert {\mathbf{X}}_A{\Vert }_{\ast }=\Vert \mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\mathrm{tr}}{\Vert }_{\ast }=\sum _r{\sigma }_r,}$$ (11)

where X_A = UΣV^tr is the singular value decomposition (SVD) of the matrix X_A. In this decomposition, U and V are two orthogonal matrices, Σ = diag{σ_r} is a diagonal matrix. The values σ_r (r = 1, 2, …) are also known as the singular values of the prior image augmented spatial–temporal image matrix X_A. Throughout this paper, although it is not necessary, the filtered backprojection (FBP) reconstruction from all available time-frames was used to generate the prior image.

2.E. SMART-RECON: Objective function and numerical implementation

In CT data acquisitions, noise always presents in acquired data. Using a quadratic approximation,^2,3 noise can be incorporated into the iterative image reconstruction process by introducing a statistical weight to the data fidelity term. In this paper, the same strategy was used to handle the noise in the measured data. Using the notation introduced above, the proposed statistical model based iterative reconstruction algorithm, SMART-RECON, can be formulated as the following convex optimization problem:

$${\displaystyle \tilde{\mathbf{X}}=\underset{\mathbf{X}}{\arg \hspace{0.17em}\min }\left[\frac{\text{1}}{\text{2}}{(\overrightarrow{\mathcal{Y}}-\mathcal{A}\overrightarrow{\mathbf{X}})}^{\mathrm{tr}}\text{D}(\overrightarrow{\mathcal{Y}}-\mathcal{A}\overrightarrow{\mathbf{X}})+\lambda \Vert {\mathbf{X}}_A{\Vert }_{\ast }\right].}$$ (12)

The parameter λ is introduced to control the balance between the data fidelity term and the regularizer strength and the diagonal noise matrix D has the inverse of the noise variance of the log-transformed data as its diagonal elements.

The above convex optimization problem can be solved using the recently developed alternated updating method¹⁹ to decompose the original optimization problem into two subproblems,

$${\displaystyle {\overrightarrow{\mathbf{X}}}^{\left(k\right)}=\underset{\overrightarrow{\mathbf{X}}}{\arg \hspace{0.17em}\min }\frac{\text{1}}{\text{2}}{(\overrightarrow{\mathcal{Y}}-\mathcal{A}\overrightarrow{\mathbf{X}})}^{\mathrm{tr}}\text{D}(\overrightarrow{\mathcal{Y}}-\mathcal{A}\overrightarrow{\mathbf{X}}),}$$ (13)

$${\displaystyle {\mathbf{X}}^{(k+1)}=\underset{\mathbf{X}}{\arg \hspace{0.17em}\min }\frac{1}{2}\Vert \mathbf{X}-{\mathbf{X}}^{\left(k\right)}{\Vert }_F^2+\lambda \mathrm{\Psi }\left(\mathbf{X}\right),}$$ (14)

where $\Vert \mathbf{X}{\Vert }_F^2≕\sum _{ij}{X}_{ij}^2$ is the Frobenius norm of the real matrix X. In the first equation, a noise weighted data fidelity constraint was imposed on the reconstruction of each individual time frame to generate an intermediate image column vector ${\overrightarrow{\mathbf{X}}}^{\left(k\right)}$ with MT rows. This image vector was converted back to its M × T dimensional spatial–temporal matrix form, X^(k). In the second equation, the nuclear norm ‖X_A‖_∗ was then used as the regularizer to define a modified denoising problem, Eq. (14). In the context of this paper, this modified denoising problem is solved to suppress both limited-view artifacts and image noise. To help gain some intuitive understanding, one can consider the static case, namely, there is no dynamic change of the image content from one time frame to another. In this case, there should be no difference between the prior image and the individual image columns, as both the prior image column and each individual column represent the same image object. In other words, the rank of the matrix X_A should be one to minimize its nuclear norm since there is only one independent image column. In practice, however, since each individual image column can only be generated using the acquired data within a narrow angular span, these individual image columns are thus contaminated with limited-view artifacts. As a result, the rank of the limited-view artifacts contaminated matrix X_A deviates from the ideal value of one and thus the nuclear norm of the matrix increases. Therefore, the result of enforcing a minimal nuclear norm is to mitigate the limited-view artifacts. In this sense, the parameter λ is used to control trade-off between the temporal fidelity and the level of limited-view artifacts in the reconstructed images.

Although a closed-form solution (the pseudoinverse) does exist for the problem in Eq. (13), we use the following gradient descent update sequence to iteratively solve the problem in Eq. (13) together with the problem in Eq. (14) as shown in the pseudocode of the numerical workflow. The quadratic problem in Eq. (13) can be easily solved iteratively using the following update sequence:

$${\displaystyle {\overrightarrow{\mathbf{X}}}^{\left(k\right)}={\overrightarrow{\mathbf{X}}}^{(k-1)}+\delta {\mathcal{A}}^{\mathrm{tr}}\text{D}\left[\overrightarrow{\mathcal{Y}}-\mathcal{A}{\overrightarrow{\mathbf{X}}}^{(k-1)}\right].}$$ (15)

After the kth iteration of the image column vector $\overrightarrow{\mathbf{X}}$, i.e., ${\overrightarrow{\mathbf{X}}}^{\left(k\right)}$, is computed using the above formula, it is converted back to its spatial–temporal matrix form X^(k). The parameter δ is the updating step size. It was empirically fixed to 0.25 in this study. The modified denoising problem in Eq. (14) is then solved to obtain the denoised spatial–temporal matrix denoted by X^(k+1),

$${\displaystyle {{\mathbf{X}}_{\mathbf{A}}}^{(k+1)}={\mathrm{SV\; T}}_{\lambda }\left({{\mathbf{X}}_{\mathbf{A}}}^{\left(k\right)}\right)≕\left(\widetilde{{\overrightarrow{X}}^p}\right|{\mathbf{X}}^{(k+1)}),}$$ (16)

where the singular value thresholding (SVT) function SV T_λ(X) is defined as follows:²⁰

$${\displaystyle {\mathrm{SV\; T}}_{\lambda }\left(\mathbf{X}\right)=\mathbf{U}{(\mathbf{\Sigma }-\lambda \mathbf{I})}_{+}{\mathbf{V}}^{\mathrm{tr}},}$$ (17)

$${\displaystyle {(\mathbf{\Sigma }-\lambda \mathbf{I})}_{+}=\{\begin{array}{l}{\sigma }_i-\lambda ,{\sigma }_i\ge \lambda \hfill \\ 0,{\sigma }_i<\lambda \hfill \end{array},}$$ (18)

where U, V, and Σ = diag{σ_r} are the SVD of X and I is an identity matrix. This two-step optimization strategy has been proven to be linearly convergent.¹⁹ For convenience, the pseudocode of the algorithm is summarized as follows:

Algorithm I.

SMART-RECON algorithm.

1: k = 0

2: ${\mathbf{X}}_A^{\left(k\right)}\leftarrow \left[{\overrightarrow{X}}^p|{\mathbf{X}}^{\left(k\right)}\right]$

3: while$\left|\right|{\overrightarrow{\mathbf{X}}}^{\left(k\right)}-{\overrightarrow{\mathbf{X}}}^{(k-1)}|{|}_2^2\ge \epsilon$ do

4: ${\overrightarrow{\mathbf{X}}}^{\left(k\right)}\leftarrow {\overrightarrow{\mathbf{X}}}^{(k-1)}+\delta {\mathcal{A}}^{\mathrm{tr}}\text{D}[\overrightarrow{\mathcal{Y}}-\mathcal{A}{\overrightarrow{\mathbf{X}}}^{(k-1)}]$

5: ${\mathbf{X}}_A^{\left(k\right)}\leftarrow \left[{\overrightarrow{X}}^p|{\mathbf{X}}^{\left(k\right)}\right]$

6: ${\mathbf{X}}_A^{(k+1)}\leftarrow {\mathrm{SV\; T}}_{\lambda }\left[{\mathbf{X}}_A^{\left(k\right)}\right]$

7: ${\mathbf{X}}^{(k+1)}\leftarrow {\mathbf{X}}_A^{(k+1)}$

8: k = k + 1

9: end while

In this paper, the SMART-RECON algorithm was implemented using compute unified device architecture (CUDA) technology on a local workstation equipped with two graphic processing unit (GPU) cards (GTX Titan Z and GTX 980, NVIDIA Corporation). The SVD procedure was implemented using the CULA linear algebra library (EM Photonics, Inc.). Note that there is no need to perform a full SVD in SV T_λ(X), since only those singular values above the selected regularization parameter λ are needed as shown in Eq. (18). However, in the application presented in our paper, the difference between a full SVD and an economical SVD is negligible from computation load standpoint since we only have 3–5 time image columns and thus only 3–5 singular values. Therefore, in this paper, we performed a full SVD in our GPU implementation of the algorithm.

2.F. Validation methods

To validate that the proposed SMART-RECON method is able to eliminate limited-view and to mitigate temporal-average artifacts, both numerical simulations with ground truth and in vivo experimental data were used.

2.F.1. Numerical simulations

In numerical simulations, a sequence of time-resolved human cerebral angiograms with a peak iodinated contrast enhancement of 400 HU were used to generate synthesized fan-beam projection data by a forward projection procedure. The peak enhancement is similar to a CT angiography acquisition at 80 kVp (mean beam energy at 50 keV) using an intravenous contrast injection protocol and a 350 mg I/ml contrast solution. Poisson noise was added to the numerical simulation data by assuming of an entrance photon fluence of 5.5 × 10⁵ photons/ray to make the noise level in the FBP image of the angiogram similar to the noise level in a clinical CT angiogram. The total view angle span in the numerical simulations was restricted to the short scan angular span with a fan angle of γ_m = 60^∘. An image matrix size of 320 × 320, corresponding to a 0.5 mm² pixel size, was used in image reconstruction. Over the short scan angular span with 888 detector elements crossing the entire scanning field of view, 656 view angles were acquired.

To validate the proposed SMART-RECON method, the projection data for each of the four 60^∘ angular sectors were generated from angiograms with an abrupt change in contrast enhancement from one angular sector to another. Note that the purpose of this validation was to demonstrate the following two key points: (1) SMART-RECON is able to reconstruct images without noticeable limited-view artifacts from data acquired in an ultranarrow temporal window corresponding to one quarter of the short scan angular span; (2) temporal fidelity within each ultranarrow temporal window can be reconstructed with high accuracy. The purpose of selecting such an abrupt intersector contrast change in the simulations is to provide a more challenging test for the algorithm and also to have known truth for contrast enhancement at each individual time frame.

Limited-view artifacts are primarily assessed by subjective visual assessment and further quantified using the relative root mean square error (rRMSE) metric with the noiseless angiograms as ground truth for each of the four image frames. The rRMSE is defined as follows:

$${\displaystyle \mathrm{rRMSE}=\frac{\sqrt{\sum _i{\left(I_i-I_i^{\mathrm{truth}}\right)}^2}}{\sum _i\left|I_i^{\mathrm{truth}}\right|}\times 100\%,}$$ (19)

where I is the image being assessed, I^truth is the ground truth reference image, and the subscript i denotes the pixel location in the image. Although the rRMSE metric also provides a quantification of temporal fidelity, it is well-known that the rRMSE metric is not sensitive to local reconstruction errors. In this paper, the temporal fidelity of two sampled regions of interest (ROIs) in the reconstructed angiograms was further quantified by the universal quality index (UQI)²¹ relative to the ground truth angiograms. The UQI is defined as follows:

$${\displaystyle \mathrm{UQI}=\frac{4{\sigma }_{xy}\overline{x}\overline{y}}{\left({\sigma }_x^2+{\sigma }_y^2\right)\left[{\left(\overline{x}\right)}^2+{\left(\overline{y}\right)}^2\right]},}$$ (20)

where the subscripts x and y denote the input image and the ground truth image for comparison, ${\sigma }_{x/y}^2$ denotes the variance of x or y, $\overline{x}$ and $\overline{y}$ denote the mean values of x and y, respectively, and σ_xy denotes the covariance of x and y, defined as follows: ${\sigma }_{xy}=(1/(N-1))\sum _{i=1}^N(x_i-\overline{x})(y_i-\overline{y})$. The UQI has a dynamic range of [ − 1, 1] and is unitless.

For comparison, the rRMSE and UQI were calculated for the short scan FBP reconstruction result (where only a single image can be reconstructed), for the PICCS reconstruction for each of the four time frames, and for the SMART-RECON images at each of the four time frames. More details of the PICCS implementation are described in Refs. ^{7, 18}, and ²².

2.F.2. Validation using in vivo experimental data

Although these numerical simulations have the advantage of including a known ground truth to quantify performance of the SMART-RECON algorithm, they do have potential limitations: the assumption of an unrealistically abrupt contrast enhancement change from one time frame to another, relatively sparse image content in the angiograms, an overly simplified Poisson noise model, and it is a purely two dimensional simulated image slice, not the more clinically relevant cone beam image volume case. To address these potential limitations in numerical simulations and to demonstrate the applicability of SMART-RECON to in vivo human subject case, a deidentified clinical contrast enhanced cone-beam C-arm CT data set was retrospectively reconstructed using SMART-RECON. Data were acquired using a C-arm image acquisition platform (Artis zee, Siemens AX, Forcheim, Germany). The angular span of the data acquisition was the short scan angular span with a 20^∘ cone angle (Θ = 180^∘ + γ_m = 200^∘ total). The total data acquisition time was 4.3 s and a total of 248 cone beam projections were acquired. Each cone beam projection includes 1024 × 960 measured line integrals. An image matrix size of 512 × 512 × 400 was used to reconstruct the entire image volume for each time frame. Using the conventional FBP reconstruction, only one image volume with a reconstruction temporal window of 4.3 s can be reconstructed. The endpoint of applying the SMART-RECON method to the same data set is to demonstrate that three image time frames can be reconstructed with clear difference in contrast enhancement and without noticeable limited-view artifacts. For comparison, both CT numbers and noise standard deviations were measured in different ROIs in the FBP, PICCS, and SMART-RECON images.

3. RESULTS

3.A. Numerical results

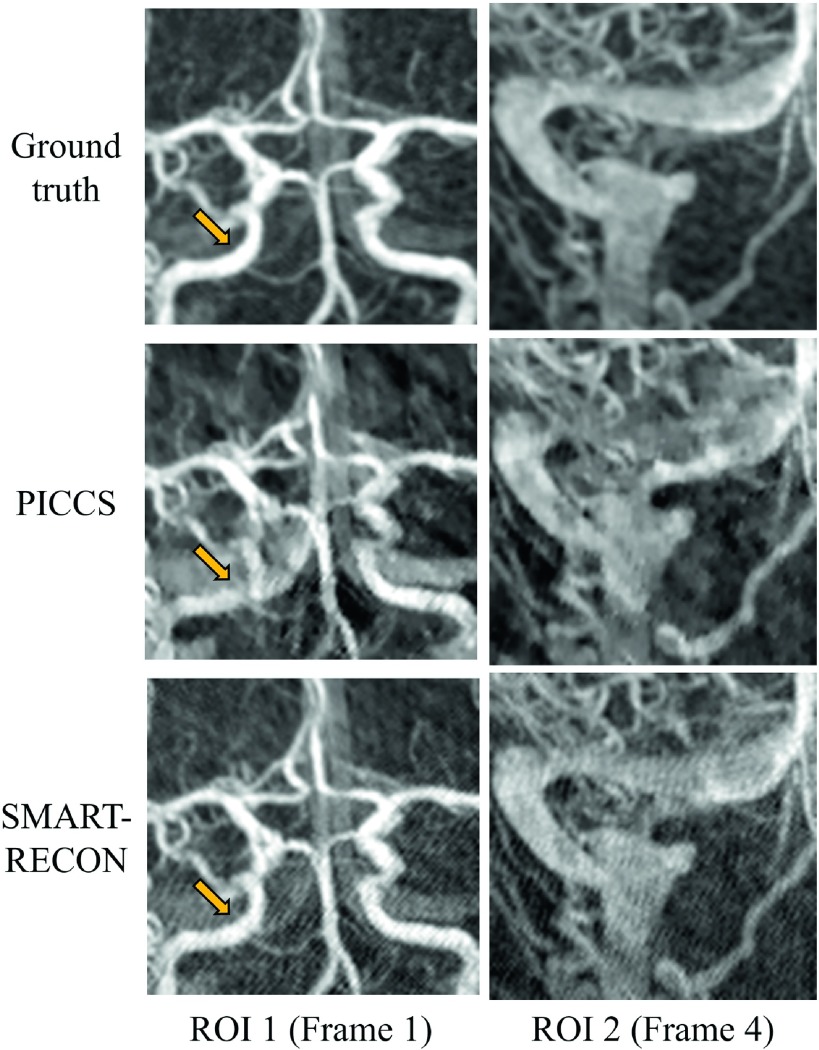
Numerical simulation results are presented in Fig. 1. The first row shows the reference angiographic images for each time frame, the second and third rows show the corresponding time frames reconstructed with the PICCS and SMART-RECON methods, respectively. The reference images were reconstructed using FBP from noisy projection data covering the entire short scan angular span for each of the individual image time frames. As one can visually observe in Fig. 1, SMART-RECON enables a clear reconstruction of arteries and veins with good quality for all four time frames. On the other hand, although images reconstructed with PICCS demonstrate reduced limited view artifacts and image noise, the reconstruction quality of smaller arteries and veins in local areas is poor. Additionally, the PICCS images still demonstrate noticeable temporal averaging artifacts, which the SMART-RECON images do not. To help visualize the differences, two different regions of interest were magnified and presented in Fig. 2.

FIG. 1.

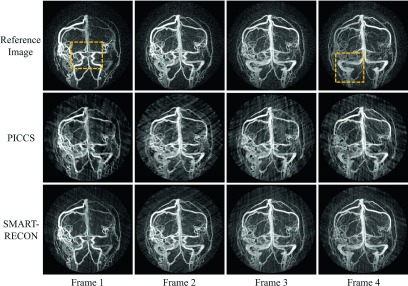
Image results for four time frames for the numerical simulation studies. All images are shown with a W/L: 2000/100.

FIG. 2.

The ROIs indicated in Fig. 1 are displayed here enlarged.

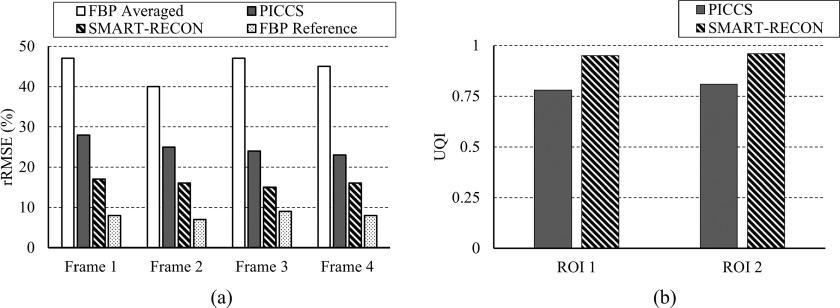
The rRMSEs were calculated for the respective time frames reconstructed with PICCS and SMART-RECON to provide an overall quantification of reconstruction accuracy. Only by using the entire angular range, Θ, can a FBP image be reconstructed without limited-view artifacts, but this averages all the temporal information in the temporal window in which data are acquired, thus introducing a temporal error between this temporally averaged FBP image and the noiseless ground truth at each time frame. The rRMSE of this temporally averaged FBP image was calculated for the corresponding noiseless ground truth image at four time frames. The rRMSE for the short scan FBP from temporal-averaged projection data and PICCS and SMART-RECON from projection data for one specific time frame are presented in Fig. 3. As one can observe in this figure, the short scan FBP images from the temporally averaged projection data deviate from the truth with significant temporal averaging errors. As a comparison, one can observe in Fig. 3 that SMART-RECON enables the reconstruction of all four time frames with the lowest rRMSE since the SMART-RECON suppresses both limited-view artifacts and temporally average artifacts during reconstruction. To benchmark the potential impact of the added noise in projection data on the rRMSE of the reconstructed image without temporal average, a FBP reconstruction was applied to the ground truth projection data with added noise to generate a reference FBP image and its rRMSE was calculated and presented in Fig. 3.

FIG. 3.

Quantitative comparison between temporal averaged FBP image, FBP reconstructed image for each segments, and SMART-RECON images for each segments was plotted.

The differences between the PICCS reconstruction and SMART-RECON for the two marked ROIs were highlighted by the calculation of local UQI indices over two marked regions on time frames 1 (ROI 1) and 4 (ROI 2) (Fig. 1) presented in Fig. 3. As one can observe that SMART-RECON enables almost perfect reconstruction for the marked ROIs with a UQI of 0.95 and 0.96 while the corresponding UQIs for PICCS reconstruction are 0.78 and 0.81, respectively. The results indicate that SMART-RECON enables reconstruction with high temporal fidelity. In comparison, the temporally averaged FBP reconstruction had a UQI of 0.71 and 0.79 in the same two ROIs.

In numerical simulations, it has been found that 15 − 20 iterations of data fidelity enforcement are sufficient to reach the empirical stopping criterion, i.e., difference between two consecutive iterations is negligible in visual observations. Using our computational facility described at the end of Sec. 2, it takes 1 s to execute a complete iteration. In all presented results, to be more conservative, 50 iterations of data fidelity enforcement were used. As a result, the total reconstruction time for all four time frames is 50 s. Note that no specific code optimization has been applied to the current numerical implementation.

3.B. In vivo cone beam CT results

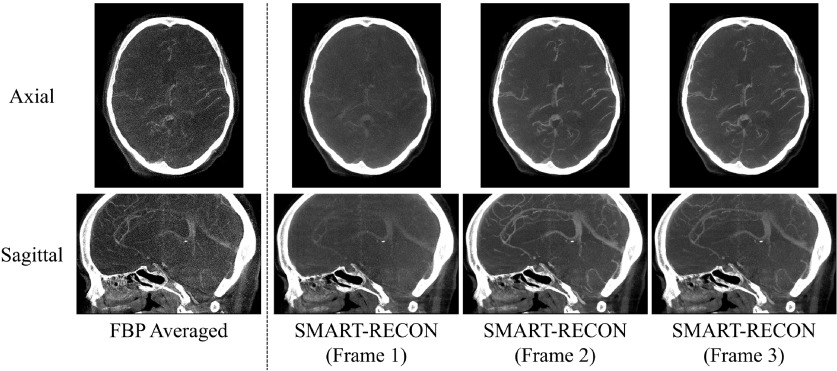
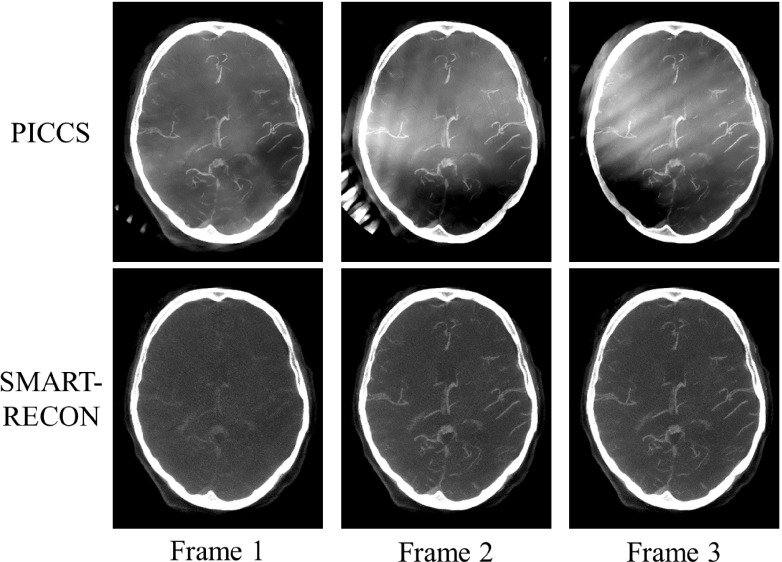
Rather than the single image volume that can be reconstructed by FBP using the acquired short scan data, SMART-RECON enables us to reconstruct several different image volumes with clear changes in the contrast of the vasculature. In this in vivo human subject case, three time frames, each time frame corresponds to a temporal window of 1.43 (=4.3/3) s and an angular span of 66^∘ (=200^∘/3), were found to be an excellent balance between limited-view artifacts and temporal-average artifacts that are reflected in the difference in contrast enhancement in each individual reconstructed time frame. As an example, the mean measured value of a major vessel in the FBP average image was 349 HU, but the mean value for the same vessel in the three SMART-RECON time frames was 218, 383, and 302 HU. Representative axial and sagittal image slices from the reconstructed SMART-RECON image volumes were presented in Fig. 4. To help visualize the contrast differences in the three time frames, a thin slab (10 × 0.5 mm = 5 mm) maximal intensity projection (MIP) was used in Fig. 4. As one can observe in the presented images, there are no limited-view artifacts present in SMART-RECON, and the difference in vascular contrast can be clearly observed from time frames 1 to 3. To estimate noise performance, the standard deviation in a ROI placed over the relatively uniform soft tissue area was measured for the three reconstructed image frames. The noise standard deviation for the FBP reconstruction over the entire short scan angular range is 126 HU while the noise standard deviations for the three time frames are 39, 41, and 38 HU, respectively. On average, a factor of 3.1 noise reduction has been achieved in SMART-RECON reconstruction. For comparison, PICCS images were also generated for the three time frames and are compared to the SMART-RECON images in Fig. 5. As clearly shown in this figure, using the same short scan FBP image volume as the prior image and the same projection data set from the three 66^∘ angular span, PICCS algorithm does not enable an acceptable reconstruction of the three time frames with clear difference in contrast enhancement and without limited-view artifacts. In contrast, the presented SMART-RECON method in this paper does enable time-resolved reconstruction of three image volumes with clear difference in contrast enhancement and without limited-view artifacts.

FIG. 4.

Image results for three time frames from the in vivo human study. All images are shown with W/L: 1000/300 HU.

FIG. 5.

A comparison between PICCS reconstructions for the three time frames and those reconstructed with SMART-RECON. All images shown with W/L: 1000/300 HU.

To reconstruct the three image volumes with matrix size of 256 × 256 × 256 (FOV diameter =25.6 cm) using 248 × 616 × 480 line integrals, it takes 30 s to execute a complete iteration for a total computation time of 7.5 min with 15 iterations of the data fidelity enforcement to achieve empirical convergence, i.e., the difference between the two iterations is negligible in visual observations.

4. DISCUSSION AND CONCLUSIONS

In this paper, a new iterative image reconstruction method, SMART-RECON, was developed and validated to enable time-resolved CT reconstruction without limited-view artifacts using data from an angular span that is significantly below 180^∘ − γ_m. The mitigation of the limited-view artifacts in SMART-RECON was achieved by minimizing the nuclear norm of the augmented spatial–temporal image matrix. The temporal fidelity was maintained by imposing data fidelity on each given time frame using the data from the corresponding temporal window. A balance is sought by SMART-RECON by varying the regularization parameter λ to eliminate limited-view artifacts while to maintain temporal fidelity for each temporal window.

Numerical simulations in two dimensional time-resolved angiograms with Poisson noise added to the projection data were performed to quantify the performance of SMART-RECON in a case with known ground truth. The potential limitations of numerical simulations were complemented with the retrospective in vivo human subject study from a contrast enhanced cone beam CT data set. Validation results from numerical simulations demonstrate that SMART-RECON is able to eliminate limited-view artifacts for an angular span as short as 60^∘ when the Tuy data sufficiency condition is severely violated. Numerical simulation results also demonstrated high reconstruction accuracy for SMART-RECON which indicates that the contrast dynamics of the image object have been restored with high accuracy quantified by both rRMSE and UQIs. In vivo experimental results demonstrated that SMART-RECON may be readily applied to clinical cone beam CT data acquisitions as well. With a single short scan acquisition, the current FBP can only generate one image volume with temporal-average artifact over a temporal window of 4.3 s. Using the proposed SMART-RECON, three image volumes without limited-view artifacts, each volume corresponds to an angular span of 66^∘, can be reconstructed to show the contrast dynamic change and each time frame corresponds to a temporal window of about 1.43 s.

There are several limitations to the current study. (1) The selection of reconstruction parameters is empirical in this preliminary study; specifically, the updating step size δ was fixed at 0.25 in both numerical simulation and in vivo human subject cases to guarantee convergence. The regularizer strength λ was also fixed to be 10% of the largest singular value (0.12 for numerical simulations and 0.1 for human studies). (2) The minimum viable angular span will have to be systematically investigated for a specific clinical application/task to determine a meaningful lower limit. (3) The multitude of spatial and temporal regularizers presented in the literature has not yet been investigated but could be readily incorporated into SMART-RECON to potentially further improve image quality. (4) In addition to the time-resolved CT scenario presented here, other potential applications of the SMART-RECON algorithm will have to be further investigated. These concerns are beyond the scope of this short communication, but we hope to address them in future studies.

In conclusion, a new method was proposed and validated in this paper to enable the reconstruction of time-resolved CT images using data from an angular span of significantly below 180^∘ − γ_m that severely violates the Tuy data sufficiency condition.