Drug Screening Boosted by Hyperpolarized Long-Lived States in NMR

Abstract

Transverse and longitudinal relaxation times (T_1ρ and T₁) have been widely exploited in NMR to probe the binding of ligands and putative drugs to target proteins. We have shown recently that long-lived states (LLS) can be more sensitive to ligand binding. LLS can be excited if the ligand comprises at least two coupled spins. Herein we broaden the scope of ligand screening by LLS to arbitrary ligands by covalent attachment of a functional group, which comprises a pair of coupled protons that are isolated from neighboring magnetic nuclei. The resulting functionalized ligands have longitudinal relaxation times T₁(¹H) that are sufficiently long to allow the powerful combination of LLS with dissolution dynamic nuclear polarization (D-DNP). Hyperpolarized weak “spy ligands” can be displaced by high-affinity competitors. Hyperpolarized LLS allow one to decrease both protein and ligand concentrations to micromolar levels and to significantly increase sample throughput.

Introduction

The first step of drug discovery is commonly referred to as lead identification. Screening techniques such as enzyme-linked immunosorbent assays (ELISA),[1] surface plasmon resonance (SPR, also known under the trade name Biacore),[2] isothermal titration calorimetry (ITC),[3] fluorescence anisotropy,[4] and an ever-expanding range of nuclear magnetic resonance (NMR) techniques[5] allow one to recognize ligands or fragments thereof in extensive libraries of chemical compounds. The binding of a ligand to a target protein:

(1)

can be described by a dissociation constant K_D that gives a measure of the affinity:[6]

(2)

in which [L], [P], and [PL] are the respective concentrations of the free ligand, the free protein, and the protein–ligand complex, and k_on and k_off are second- and first-order rate constants of the association and dissociation reactions. In NMR, a first-order exchange rate is defined as k_ex=(k_on[P]+k_off). If the binding site of the protein is saturated by excess ligand, that is, if [PL]≪[L], one has k_ex≈k_off. Typically, good drugs have small dissociation constants with K_D<1 μm.

Because one can choose from a wide range of observable parameters, NMR spectroscopy offers several methods to study interactions between small ligand molecules and macromolecular targets. It is possible to extract dissociation constants[7] and to obtain structural information about the protein and its complex.[8] Provided the exchange between the free and bound forms of the ligand is faster than the difference of their resonance frequencies,5a, [9] i.e., when k_ex≈k_off≫(π/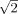)Δν, where Δν is the chemical shift difference (in Hz) of the signals in the bound and free states, any observable quantity ξ^obs, be it a frequency or a relaxation rate, is determined by a weighted average of the free and bound forms:[10]

(3)

for which X^bound and X^free are the mole fractions of the bound and free ligands. The larger the contrast,

(4)

the more sensitive the frequency or relaxation rate is to ligand–protein binding. This expression is more general than the definition of contrast that we proposed in our first report on the subject.[11]

Several NMR methods based on such a contrast are extensively used nowadays to determine dissociation constants of ligand–protein interactions. The quantity ξ^obs can be determined by the chemical shifts of one or more selected nuclei of either target proteins[12] or ligands,[13] the translational or rotational diffusion constant of the ligand,[14] the auto-relaxation rates T₁, T₂ and T_1ρ, the rate of magnetization transfer by cross-relaxation (Overhauser effect) between protons belonging to the ligand,[15] the saturation transfer from proteins to ligands determined by difference spectroscopy,[16] or “water-LOGSY” that exploits differences of the rate of transfer of magnetization from bulk water to free or bound ligands by cross-relaxation.[17] Several of these methods rely on differences in rotational correlation times between the free ligand and the protein–ligand complex.[18]

We recently demonstrated that so-called long-lived states (LLS), also known as singlet states (SS) in isolated two-spin systems, can be used very effectively to investigate protein–ligand interactions.[11] Indeed, the protracted lifetimes T_LLS of these nuclear spin states are exquisitely sensitive to binding to a protein, giving a dramatic contrast between the lifetimes T_LLS of the bound and free forms. Similar rules apply to the lifetimes T_LLC of so-called long-lived coherences (LLC).[19] A drawback of both LLS and LLC methods is that the ligands should contain reasonably isolated two-spin systems. We show in this work that it is possible to overcome this limitation by covalent attachment of a “spin-pair label” carrying an isolated two-spin system.

The requirement of rapid exchange underlying Equation (3) implies that “direct” NMR binding experiments cannot be used for ligands with strong affinities (K_D<100 μm), although good drugs typically have much smaller dissociation constants K_D<1 μm. Fortunately, so-called “competition binding” experiments can be used to determine small dissociation constants K_D of competitors that can displace weak “spy ligands” from the binding sites of target proteins. We show here how a weak ligand with a spin-pair label capable of sustaining an LLS or LLC can be used as a “spy ligand” in competition experiments. If a competitor partly displaces the spy ligand, the lifetimes T_LLS and T_LLC of the spy ligand can be dramatically extended. A set of 1D experiments allows one to screen and rank extensive libraries of compounds. Such “indirect” competition binding experiments[20] open the way to the identification of high-affinity ligands with K_D<1 μm, typical of effective drugs. Remarkably, competition binding experiments can also be used to determine poor binding constants K_D>10 mm that are typical of weakly binding “lead compounds” that tend to be difficult to identify in the early stages of drug discovery.[21]

It is clearly desirable to use low concentrations of both proteins and ligands, not only to save expensive materials, but also to avoid protein aggregation and problems with mixtures (“cocktails”) in the manner of combinatorial chemistry. The quest for low ligand concentrations is generally limited by poor sensitivity of NMR. At concentrations [L]<100 μm, NMR spectra with sufficient signal-to-noise ratios require extensive signal averaging. Hyperpolarization of nuclear spins by dissolution dynamic nuclear polarization (D-DNP)[22] can overcome this problem. By microwave irradiation of samples at temperatures close to T=1.2 K, the polarization of electron spins can be transferred to protons or other nuclei, followed by rapid dissolution of the hyperpolarized samples and their transfer to a high-resolution NMR spectrometer for detection. The technique has not been very popular for ¹H and ¹⁹F nuclei so far, because rapid T₁ relaxation tends to cause loss of polarization during the transfer from the polarizer to the spectrometer. Enhancements ε_DNP up to five orders of magnitude can be obtained for nuclei with low gyromagnetic ratios, while enhancements 100<ε_DNP<1000 can be achieved for ¹H or ¹⁹F nuclei.[23] Spin-pair-labeled molecules containing isolated spins designed for LLS and LLC experiments also feature fairly long T₁ values which also makes them suitable for dissolution DNP.

Long-lived states experiments

Long-lived states (LLS), first described by Levitt and co-workers,[24] have the unique property that their populations relax with time constants that can be much longer than longitudinal relaxation time constants (T_LLS≫T₁). For pairs of protons, T_LLS/T₁ ratios as large as 60 have been observed in R–CH=CH–R’ systems. To perform an LLS experiment, one has to: 1) Start with a system comprising two nonequivalent spins and convert their populations into a density operator corresponding to a singlet–triplet imbalance (Figure 1 a, 1–2);24a, [25] 2) Sustain the LLS by suppressing the effects of the chemical shift difference (Figure 1 a, 2–3), usually by applying a resonant radiofrequency (rf) field during a sustaining time τ_m, with the carrier (ν_rf) placed halfway between the chemical shifts of the two spins;24a,d, [26] LLS are efficiently sustained by an rf field that is at least five times larger than the chemical shift difference between the two spins. 3) After turning off the resonant rf field, a suitable pulse sequence can convert the singlet–triplet imbalance back to observable magnetization (Figure 1 a, 3–4). The lifetime of the LLS can be determined by fitting the signal intensities recorded as a function of τ_m to the exponential function exp(−τ_m/T_LLS).

Figure 1.

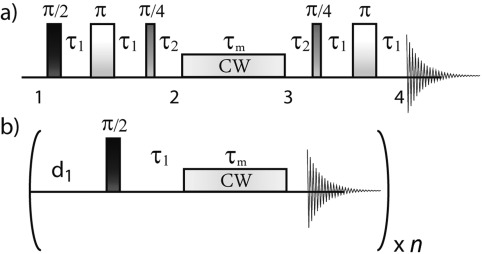
Experiments for long-lived states (LLS) and long-lived coherences (LLC). a) Pulse sequence used to excite, sustain, and observe LLS.[25] An rf field is applied between time points 2 and 3 with the carrier halfway between the chemical shifts of the two spins in order to make them effectively equivalent. The conversion is most efficient if τ₁=1/4 J_IS and τ₂=1/2Δν_IS. b) Pulse sequence designed to excite, sustain, and detect LLC. Typically, τ₁=1/2Δν_IS to achieve an efficient conversion of I_y+S_y into I_x−S_x, and d₁=5T₁. A variant for single-scan LLC spectroscopy is described in the Supporting Information.

On the other hand, long-lived coherences (LLC)[19] have the property that they relax with time constants that can be much longer than transverse relaxation time constants (T_LLC≫T₂). The principles of LLC spectroscopy are briefly reviewed in the Supporting Information.

Results and Discussion

Enhanced contrast of LLS

In direct titration experiments, i.e., in the absence of competitors, the relaxation rate of a (weak or intermediate) spy ligand is measured by titration as a function of the protein-to-ligand ratio. An LLS associated with a ligand L bound to a target protein P will relax faster, that is, T_LLS^bound≪T_LLS^free. The relaxation properties of free and bound ligands contribute to increase the contrast C(T_LLS) of the method. According to Equation (4), one may define the contrast as:

(5)

where R_LLS^obs and T_LLS^obs are the averaged parameters observed for the rapid equilibrium between free and bound forms of the ligand in the sense of Equation (3), while R_LLS^free and T_LLS^free refer to the free ligand in the absence of protein. By analogy, an expression for the contrast C(T_LLC) of long-lived coherences can be derived from Equation (5) by replacing LLS with LLC.

To demonstrate the enhancement of the contrast C(T_LLS) with respect to the contrast C(T₁) and C(T_1ρ), binding experiments were carried out for a 1 mm solution of the tripeptide ligand glycine-glycine-arginine (GGR) in the presence of its protein target trypsin in the range 0.5<[P]<50 μm, using various methods (T_LLS, nonselective T₁ and nonselective T_1ρ). Figure 2 shows that the LLS method can work with a protein–ligand ratio that is ∼25-fold lower than required for the well-known nonselective T_1ρ method, whereas the nonselective T₁ contrast remains below C(T₁)<10 % even at the highest protein concentration [P]=50 μm.

Figure 2.

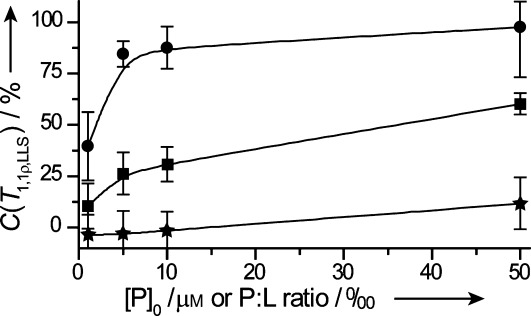
Contrast of life-times T_LLS, T₁, and T_1ρ of ligands binding to proteins. Experimental contrast for T_LLS (•), non-selective T_1ρ (▪), and non-selective T₁ (★) methods for the diastereotopic pair of protons on the middle glycine residue of the tripeptide GGR in a solution with a fixed concentration [L]=1 mm and a variable trypsin concentration 0.5 μm<[P]₀<50 μm in D₂O at 8 °C at 11.7 T (500 MHz for protons).

Spin-pair labeling

A drawback of screening by LLS or LLC is that the ligands must carry a pair of nonequivalent spins −1/2. We therefore developed a synthetic labeling strategy comprising two steps: 1) the identification of a “spy ligand” that binds weakly to the target protein, and 2) the functionalization (see Supporting Information) of this ligand by attaching a “spin-pair label” that can carry LLS or LLC. By way of illustration, 3-bromothiophene-2-carboxylic acid (“BT”), which is known to have long lifetimes T_LLS and T_LLC,[27] was covalently attached to the tripeptide GGR, a weak binder for trypsin. The resulting spin-pair-labeled tripeptide is henceforth called BT-GGR.

Despite some steric effects and long-range dipolar relaxation mechanisms in the spin-pair-labeled tripeptide BT-GGR, the two aromatic protons of the bromothiophene group retain a remarkably long lifetime T_LLS^free(BT)=11.7±0.7 s. In this particular peptide, the diastereotopic pairs of α-protons on the two glycine residues of BT-G₁G₂R can also be used to excite LLS and have lifetimes T_LLS^free(G₁)=10.4±0.5 s and T_LLS^free(G₂)=9.3±0.5 s (see Figure 3 b).

Figure 3.

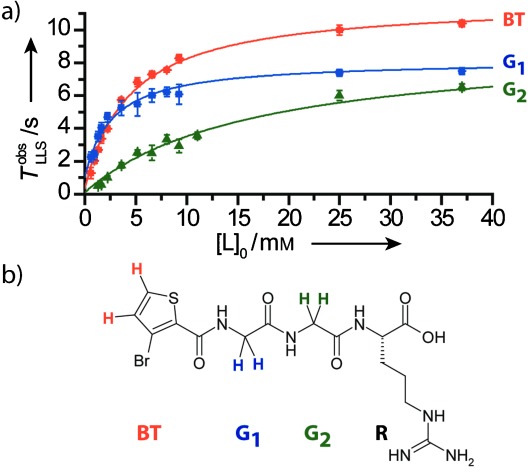
LLS titration experiments. a) Observed LLS lifetimes of the three proton pairs on the spin-pair-labeled tripeptide BT-GGR as a function of the ligand concentration, in the presence of 25 μm trypsin in D₂O at 25 °C and 11.7 T (500 MHz for protons). b) Pairs of protons capable of sustaining LLS in BT-GGR: on bromothiophene BT (orange), on the N-terminal glycine G₁ (blue) and on central glycine G₂ (green) which is close to the arginine residue that binds to the protein.

The observed averaged relaxation rate of LLS in the presence of a protein can be derived from Equation (3), using the definition of K_D of Equation (2) and assuming saturation, i.e., [L]₀≫[PL], so that [L]₀−[PL]≈[L]₀:

(6)

If one measures R_LLS^obs as a function of the concentration [L]₀ of a ligand while [P]₀ is kept constant, it is possible to determine K_D by fitting to Equation (6). The spin-pair-labeled spy ligand L=BT-GGR was added to a solution of [P]₀=25 μm trypsin over a range 0.5<[L]₀<40 mm. At each concentration [L]₀, the observed relaxation times T_LLS^obs=1/R_LLS^obs of three different pairs of protons (belonging to the bromothiophene group and to the middle and the terminal glycines) were measured using the pulse sequence of Figure 1. Figure 3 a shows how the titration curves can be fitted to Equation (6). As expected, nearly the same dissociation constants were obtained for the three proton pairs that can sustain LLS in BT-GGR: K_D(BT)=0.18±0.03 mm, K_D(G₁)=0.24±0.01 mm, K_D(G₂)=0.21±0.02 mm. The LLS fitted lifetime of G₂ (i.e., the glycine closest to the arginine) in the bound form (T_LLS^bound(G₂)=16±1 ms) is shorter than for the two other LLS sites (T_LLS^bound(BT)=90±20 ms, T_LLS^bound(G₁)=110±40 ms). This shorter T_LLS^bound is believed to be due to the fact that the arginine, and thus also the glycine G₂, enter more deeply into the active site of trypsin.

Competition binding experiments

Once a weak ligand has been identified and characterized by titration, it can be used as a “spy ligand” in competition experiments.[20] When stronger ligands are added, the lifetime T_LLS^obs of the spy ligand give information about the dissociation constant K_D^strong of the competitor. Note that the competitor need not contain any spin pairs that can sustain an LLS or LLC. Moreover, as the changes in T_LLS^obs need only be observed for the weak ligand, there are no requirements for the stronger ligands to fulfill the fast-exchange condition. This implies that the accessible range of dissociation constants K_D^strong of the competitor can lie in a range 0.1 nm<K_D^strong<100 nm. When K_D^strong<0.1 nm, one can detect a large effect on the lifetime T_LLS^obs of the weak spy ligand, but it is not possible to rank the ligands according to their affinities. As the strong competitors themselves need not be observed directly, their concentration can also be lowered, typically to the same level as the concentration of the protein, that is, to [L]₀≈[P]₀, which may typically be in the single-digit micromolar range.

When a stronger competitor blocks the active site of the protein, the weak spy ligand will no longer have free access to its target. The concentration [P]_free of the protein that remains free to bind the weak ligand can be derived from the definition of the dissociation constant K_D^strong of the competitor:

(7)

where b=([P]₀+[L^strong]₀+K_D^strong) and [L^strong]₀ is the total concentration of the competitor. As the amount of free available protein decreases, the effects of the protein on the lifetime T_LLS^obs of the weak spy ligand will be less pronounced. Here, the approximation that the binding sites are saturated by ligands cannot be made, since [L^strong]₀≈[P]₀. To describe the relaxation rate R_LLS^obs of the weak spy ligand in competition experiments, [P]₀ in Equation (6) must be replaced by [P]_free of Equation (7).

Once the dissociation constant K_D^weak of the weak spy ligand and its LLS lifetime in the bound form T_LLS^bound are known, it is possible to optimize [L^strong]₀ and [P]₀ to rank strong competitors according to their binding strengths. Figure 4 shows the calculated T_LLS^obs(BT) of the bromothiophene protons in BT-GGR if [P]₀=25 μm and [L^strong]₀=50 μm as function of K_D^strong. Under these conditions, T_LLS^obs changes dramatically between K_D^strong=100 μm and K_D^strong=1 μm.

Figure 4.

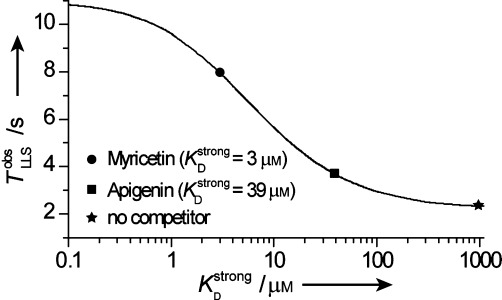
Influence of a competitor on the LLS lifetime of a weak ligand. The LLS lifetimes T_LLS^obs of the pair of aromatic protons of the bromothiophene spin-pair label as a function of the dissociation constant of a competing stronger ligand, calculated using Equations (6) and (7). The parameters of the weak ligand BT-GGR were obtained from the fit of the data in Figure 3: K_D=0.2 mm, T_LLS^bound=0.1 s, T_LLS^free=11 s, [L]₀=0.5 mm, [P]₀=25 μm, and [L^s]₀=50 μm. The three points correspond to T_LLS^obs in the presence of myricetin (K_D^strong=3 μm, •), apigenin (K_D^strong=39 μm, ▪) and in the absence of any competitor (★) calculated for these conditions.

A library of competing ligands can thus be ranked according to their affinities by observing the LLS signal of the weak spy ligand. Under the conditions shown in Figure 4, one can easily rank competing ligands with great accuracy provided 1 μm<K_D^strong<100 μm. Note that the LLS sequence of Figure 1 can be used with a single sustaining delay τ_m. This strategy is compatible with dissolution DNP, as discussed below. As T_LLS^obs of the weak spy ligand is longer in the presence of a stronger competitor, the LLS signal intensity of the spy ligand after a suitably chosen delay τ_m will be higher. LLS spectra with τ_m=3 s were recorded with 0.5 mm BT-GGR, in the presence of [P]₀=25 μm trypsin with four different competitors, all with [L^strong]₀=50 μm: myricetin (K_D^strong=3 μm), morin (K_D^strong=30 μm), apigenin (K_D^strong=39 μm)[28] and benzamidine (K_D^strong=39 μm).[29] Figure 5 a shows three of these five LLS spectra, obtained either without competitor, with apigenin, or with myricetin. Figure 5 b shows the signal intensities of the weak spy ligand BT-GGR in the presence of one of the four competing ligands. The same kind of information can be derived from the lifetimes of long-lived coherences (Figure 5 c,d).

Figure 5.

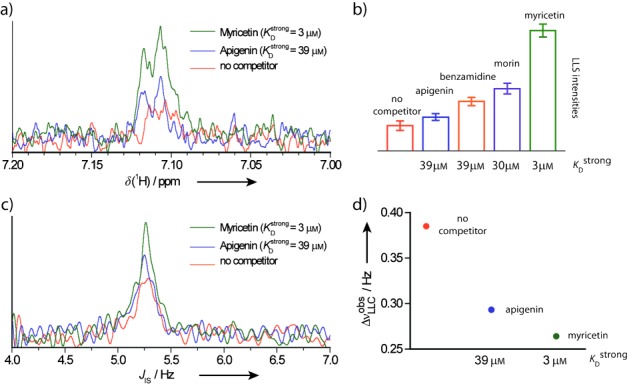
LLS and LLC competition binding experiments. a) Signals of one of the two aromatic protons of bromothiophene of 0.5 mm of the weak spy ligand BT-GGR in the presence of 25 μm trypsin, using the LLS sequence of Figure 1 with a sustaining time τ_m=3 s in D₂O at 25 °C and 11.7 T (500 MHz for protons) 1) in the absence of any competitor (orange), 2) in competition with 50 μm of the intermediate ligand apigenin (blue), and 3) in competition with 50 μm of the stronger ligand myricetin (green). b) Peak intensities of one of the aromatic protons of BT-GGR under the same conditions as in panel a), without competitor or in the presence of apigenin, benzamidine, morin, or myricetin. The better the binding, the smaller the dissociation constant, and the more intense the LLS signal of the displaced spin-pair-labeled spy ligand BT-GGR. c) LLC spectra of the two aromatic protons of the bromothiophene group of BT-GGR acquired with the “on-the-fly” sequence shown in Figure S2b of the Supporting Information, under the same conditions as in panel a). The stronger the binding of competitors, the greater the displacement of the spy ligand BT-GGR, the narrower the peaks in its LLC spectra, and the more intense the signals. d) Line widths of LLC peaks [Δν_LLC^obs=1/(πT_LLC^obs)].

Hyperpolarization by dissolution DNP

Ligands with covalently attached spin-pair labels such as BT-GGR contain spins with long T₁ values and are therefore suitable for hyperpolarization by dissolution DNP. Provided T₁(¹H)>1 s, a sufficient fraction of the hyperpolarized magnetization can be preserved during transfer from the DNP polarizer to the NMR spectrometer.

In a glass-forming solvent mixture H₂O/D₂O/[D₆]DMSO (v/v/v=5:35:60), 10 mm BT-GGR was dissolved with 25 mm 4-hydroxy-2,2,6,6-tetramethylpiperidine-1-oxyl (TEMPOL). Five frozen beads (50 μL) of this solution were loaded together with five frozen beads (50 μL) of 3 m ascorbate[30] into a home-built DNP polarizer[31] operating at B₀=6.7 T and T=1.2 K. The sample was irradiated with microwaves at a frequency f_μW=188.3 GHz and power P_μW=100 mW. Unlike trityl radicals, the nitroxyl radical TEMPO is an efficient polarizing agent for ¹H spins, because it has a broad ESR line Δω_ESR>ω₀(¹H).[32] At B₀=6.7 T, a proton polarization up to P(¹H)=90 % can be obtained,31b while P(¹H) is only ∼40 % in polarizers operating at B₀=3.35 T. After ∼15 min of microwave irradiation, a steady-state proton polarization P(¹H) is reached. The DNP sample can be rapidly dissolved in 0.7 s with 5 mL of hot D₂O (P=1 MPa, T=400 K) and transferred to a 11.7 T NMR spectrometer in 4.5 s through a “magnetic tunnel” so that B₀>0.8 T during transfer, which is particularly important to preserve the polarization of ¹H and ¹⁹F nuclei.[33] A fraction (400 μL) of the hyperpolarized solution is then injected in ∼2 s into a 5 mm NMR tube containing 250 μL D₂O and, depending on the conditions, 3.65 μm trypsin and 3.65 μm of a competitor such as myricetin. After injection, the final solution has a concentration of 1.4 μm protein, 1.4 μm competitor, and 120 μm hyperpolarized spy ligand BT-GGR. After a 3 s interval to allow proper mixing, a reference free induction decay is observed in 0.5 s after exciting transverse magnetization with a single 5° pulse to control the quality of the hyperpolarized sample and to normalize the signal intensity of the spy ligand to its known concentration. This is immediately followed by an LLS sequence as described in Figure 1 with a fixed sustaining time τ_m=3 s.

The DNP enhancements of the aromatic protons of the spin-pair-labeled spy ligand BT-GGR were on the order of ε_DNP=100–200, relative to Boltzmann equilibrium at 25 °C and 11.7 T (500 MHz for protons). A significant fraction of the proton hyperpolarization was lost during the 10 s interval between dissolution and signal acquisition, but a faster sample injection device[33] could decrease this interval to 1.2 s.

Figure 6 shows DNP-enhanced LLS spectra of 1) 120 μm of the spin-pair-labeled spy ligand BT-GGR in the absence of protein, 2) the same upon addition of 1.4 μm trypsin, and 3) the same with further addition of 1.4 μm myricetin as competitor. A dramatic decrease of the LLS signal intensity stemming from BT-GGR is observed upon adding trypsin. The contrast defined in Equation (5) is C(T_LLS)=75 %. Addition of an equimolar amount of the competitor myricetin leads to a partial displacement of the spy ligand that can be readily detected by the revival of its LLS signal. With only 120 μm of the spin-pair-labeled spy ligand BT-GGR, the DNP-enhanced LLS spectrum of Figure 6 recorded in a single scan after τ_m=3 s has a signal-to-noise ratio (SNR) of 130. Under the same conditions, but without DNP, an accumulation of 225 transients for ∼1 h was necessary to reach the same SNR. A DNP-enhanced LLS spectrum of BT-GGR with a concentration as low as 10 μm could be recorded with an SNR of 16. Clearly, DNP allows one to decrease the concentration of ligands, but the protein concentration should not be further decreased. In fact, according to Equation (6), the contrast C_LLS would decrease if the limit K_D+[L₀]≈K_D were to be reached. Without DNP, using a 50-fold increase in ligand concentration (Figure 5), 256 transients had to be accumulated in 100 min to obtain an SNR of 8. The experimental conditions can be adapted depending on the primary objective: low concentrations of either protein or ligand, rapid throughput, high sensitivity for the displacement by a competitor or high SNR. In Figure 6, the conditions were optimized for high SNR and high contrast upon addition of a competitor, albeit at the expense of a slightly higher ligand concentration and longer polarization buildup time. To attain faster throughput, one could polarize at a higher temperature T=4.2 K and B₀=6.7 T, where proton polarization P(¹H)=25 % can be reached by DNP in ∼2 min.31b The price to pay would be an approximate threefold lower SNR. Similarly, at T=1.2 K and B₀=3.35 T, as in commercially available DNP polarizers, P(¹H)=40 % can be reached in ∼6 min.[34]

Figure 6.

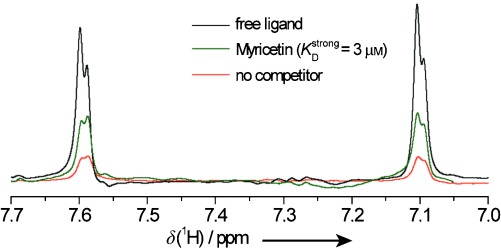
DNP-enhanced LLS competition binding experiments. DNP-enhanced LLS spectra of the two aromatic protons of bromothiophene in BT-GGR 120 μm after a sustaining time τ_m=3 s, 1) without protein (black), 2) in the presence of 1.4 μm trypsin (orange), 3) with 1.4 μm trypsin and 1.4 μm myricetin as competitor (green). All spectra were acquired in a single scan in D₂O, at 25 °C and 11.7 T (500 MHz for protons).

Conclusions

The covalent attachment of “spin-pair labels” such as bromothiophene (BT) permits one to broaden the scope of the LLS and LLC screening methods to virtually any weak ligand in the fast exchange regime. By way of example, bromothiophene carboxylic acid was attached to the N terminus of a tripeptide, but other “spin-pair labels” could be designed. Spy ligands with higher sensitivity to binding could be engineered with the following features: 1) spy ligands with enhanced T_LLS^free, 2) LLS functionalizing groups closer to the binding site, 3) the use of nearly equivalent spins.[35] Our labels are far less bulky than chromophores used in fluorescence experiments, and should not induce significant steric impediments to binding. Relative to other NMR screening methods, LLS and LLC offer much improved contrast. For the same ligand concentration (i.e., for the same experimental time), the protein concentrations can be greatly decreased, giving access to poorly soluble protein targets and decreasing the risk of aggregation. When used in competition mode, both LLS and LLC methods allow one to rank high-affinity ligands using simple 1D experiments. Because there are few protons in the spin-pair label, they tend to have long T₁ relaxation times, so that drug screening experiments using LLS or LLC can be, in principle, readily coupled to D-DNP. Currently, access to this technology remains limited to a few specialized groups, but a dedicated LLS-DNP screening apparatus could be made commercially available in the near future. As demonstrated below, this approach allows one to decrease the concentrations of spy ligands, competitors and target proteins. In our current setup, the time required for transfer from the polarizer to the detection magnet is similar to T₁(¹H) of the spy ligand. An acceleration of the transfer would benefit the remaining proton polarization and thus the SNR. Such improvements would allow either a further decrease in ligand concentration or an increase in sample throughput.

Experimental Section

Samples: BT-GGR (see Supporting Information for details about the synthesis) was titrated over the range 0.5<[L]₀<40 mm into 25 μm type IX-S trypsin from porcine pancreas (Sigma–Aldrich). As internal concentration standard, 5 mm tert-butyl alcohol (>99.5 %, Sigma–Aldrich) was added. Five solutions containing 0.5 mm BT-GGR and 25 μm trypsin in D₂O were prepared for competition experiments: 1) without competitor, 2) with 50 μm myricetin (>96 %, Sigma–Aldrich), 3) with 50 μm morin hydrate (Sigma–Aldrich), 4) with 50 μm apigenin (>97 %, Sigma–Aldrich), and 5) with 50 μm benzamidine hydrochloride (>99 %, Sigma–Aldrich).

Experimental procedures: During the titrations, 2 μL aliquots of 150 mm BT-GGR were added to 300 μL of the starting solution. The lifetimes T_LLS^obs were determined by single-exponential fitting of signal intensities observed with the LLS sequence of Figure 1, setting the sustaining field strength B₁=5Δν_IS, and using N=10 different delays τ_m=n₁Δτ_m with Δτ_m=T_LLS^expected/10 and n₁=1, 3, 6, 10, 15, 21, 29, 37, 46, 56. All measurements were performed at 25 °C on a 500 MHz (11.7 T) Avance Bruker spectrometer equipped with an inverse detection 5 mm CryoProbe.

Dissolution-DNP experiments: Solutions of 10 mm BT-GGR in the glass-forming mixture H₂O/D₂O/[D₆]DMSO (v/v/v=5:35:60) were doped with 25 mm TEMPOL (Sigma–Aldrich). Five frozen beads of 10 μL each of this mixture were inserted with five frozen beads of 10 μL each containing 3 m ascorbate in D₂O to scavenge the radicals after dissolution. DNP was performed at 1.2 K and 6.7 T in a home-built polarizer by applying CW microwave irradiation at f_μW=188.3 GHz and P_μW=100 mW. The beads were dissolved together in 0.7 s with 5 mL D₂O, preheated at T=400 K at P=1.0 MPa, and transferred in 4.5 s by pressurizing with helium gas at 0.6 MPa to an 11.7 T Bruker magnet via a 1.5 mm inner-diameter PTFE tube running through a magnetic tunnel of 5 m length. After injection in 2 s into NMR tubes containing 250 μL of D₂O to allow field-frequency locking before and during injection, plus 1) 250 μL of 3.65 μm trypsin, or 2) 250 μL of 3.65 μm trypsin and 3.65 μm myricetin. A 5° detection pulse was applied to record a hyperpolarized ¹H signal for reference, followed by a single LLS sequence with a sustaining delay τ_m=3 s.

Supporting Information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

miscellaneous_information