A Memory of Errors in Sensorimotor Learning

Abstract

The current view of motor learning suggests that when we revisit a task, the brain recalls the motor commands it previously learned. In this view, motor memory is a memory of motor commands, acquired through trial-and-error and reinforcement. Here we show that the brain controls how much it is willing to learn from the current error through a principled mechanism that depends on the history of past errors. This suggests that the brain stores a previously unknown form of memory, a memory of errors. A mathematical formulation of this idea provides insights into a host of puzzling experimental data, including savings and meta-learning, demonstrating that when we are better at a motor task, it is partly because the brain recognizes the errors it experienced before.

How does the brain alter behavior after experiencing an error? Classic theories assumed that the brain learns some fraction of the error regardless of its history or magnitude (1, 2). However, recent experiments (3–6) demonstrate that the brain learns relatively more from small errors than large errors, and can modulate its error-sensitivity (7–9).

Understanding error-sensitivity is important because it may provide insight into the phenomena of ‘savings’ and ‘meta-learning’. Savings refers to the observation that when a subject adapts to perturbation (A), and then the perturbation is removed (i.e., washout), they exhibit faster readaptation to (A)(10). Remarkably, savings of (A) is present even when washout is followed by adaptation to (-A), a perturbation in the opposite direction (11, 12). Current error-dependent models of learning cannot account for these observations (13, 14), nor explain meta-learning, where prior exposure to a random perturbation produces savings (15, 16).

Let us begin with a standard model of motor learning (17–20) in which on trial n, a perturbation x is imposed on action u so that the sensory consequences are y⁽ⁿ⁾=u⁽ⁿ⁾+x⁽ⁿ⁾. Based on its belief about the environment x̂⁽ⁿ⁾, the learner predicts the sensory consequences ŷ⁽ⁿ⁾=u⁽ⁿ⁾+x̂⁽ⁿ⁾, and then updates its belief from the prediction error e⁽ⁿ⁾=y⁽ⁿ⁾−ŷ⁽ⁿ⁾. Such learning typically depends on a decay factor a, and error-sensitivity η:

$${\widehat{x}}^{(n+1)}=a{\widehat{x}}^{(n)}+{\eta }^{(n)}{e}^{(n)}$$ (1)

Consider an environment in which the perturbations persist from trial to trial, and another environment in which the perturbations switch (Fig. 1A). In a slowly switching environment, the brain should learn from error because the perturbations are likely to persist (learning from error in one trial will improve performance on the subsequent trial). However, in a rapidly switching environment the brain should suppress learning from error because any learning will be detrimental to performance on subsequent trials.

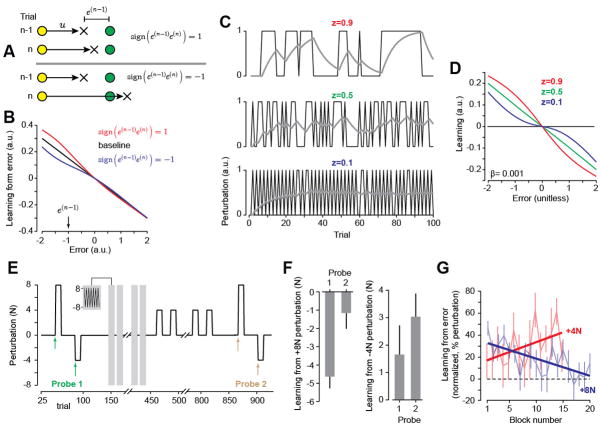
Fig. 1.

History of error alters error-sensitivity. A. Reaching paradigm with force field perturbations. The yellow circles note a perturbations state, and z indicates probability of remaining in that state. The slow, medium and rapidly switching environments are shown. One group of subjects was trained in each environment. We measured error-sensitivity via probe trials in which subjects experienced a constant perturbation, sandwiched between two error-clamp trials. B. Movement trajectories in the perturbation trial of the probe trials. Trajectories were averaged over 5 successive presentations of the probe. The errors in probe trials did not differ between groups. C. Learning from error in the probe trials, measured as the change in force from the trial prior to the trial after the perturbation. D. Learning from error in the probe trials, plotted as a percentage of the ideal force (left). Error-sensitivity η was measured as the trial-to-trial change in the percentage of ideal force divided by error (right). E. Change in error-sensitivity between the baseline block and the last 5 error-clamp triplets. Data are mean ± SEM.

Three groups of subjects (n = 9 per group) made reaching movements while experiencing force perturbations from either a slow, medium, or rapidly switching environment (Fig. 1A). The mean of the perturbations was zero for all blocks (consisting of 30 trials). We measured error in a given trial and then computed the amount that was learned from that error (probe trials, purple bars, Fig. 1A). To quantify learning from error on trial n, we measured the change in force from the trial before to the trial after the perturbation, f⁽ⁿ⁺¹⁾(t)−f⁽ⁿ⁻¹⁾(t) (Fig. 1C). In block 1, learning from error was similar in the three groups (p > 0.99), and in all probe trials the perturbation produced similar errors (Fig. 1B, RM-ANOVA, effect of group p > 0.8, interaction, p > 0.7). However, subjects that experienced the slowly switching environment increased their learning from error (Fig. 1C), whereas those who experienced the rapidly switching environment suppressed this learning.

We measured the force produced on a given trial and computed a coefficient representing percent ideal (Fig. 1D). RM-ANOVA indicated a significant block by group interaction (p < 0.05), suggesting that the history of perturbations altered the amount of learning from error. Post-hoc tests showed that in the slowly switching environment subjects learned more from error than in the rapidly switching environment (p < 0.03). This change in error-sensitivity developed gradually with training (Fig. 1D). The slowly switching environment induced an increase in error-sensitivity (Fig. 1E, changes in sensitivity from the first half to second half of the experiment, ANOVA, p < 0.05).

Is control of error-sensitivity local to the experienced errors? In Exp. 2, subjects performed rapid out-and-back movements for which no visual feedback was available during the outward part of the reach, with the aim of hitting a target at the turn-around point of their movement. An occasional perturbation altered the feedback regarding hand position at the turn-around point (Fig. 2A). We measured the relationship between error e⁽ⁿ⁾ and learning from error (change in reach extent).

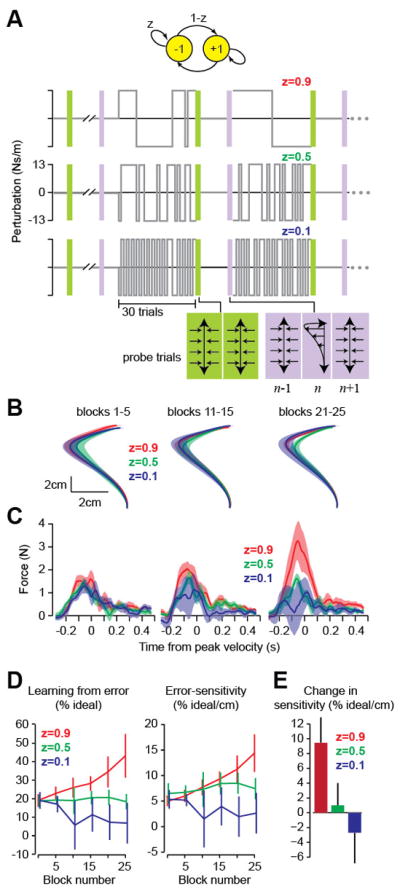
Fig. 2.

Error-sensitivity is a local function of experienced errors. A. Paradigm with visuomotor gain perturbations. B. Perturbation schedule. Dashed lines indicate changes in the statistics of the environment. C. Error-sensitivity averaged over all error-sizes measured over each environment block. D. Learning from error measured at various error sizes. E. Error-sensitivity as a function of error magnitude. F. Probability of error.

Group 1 (n = 10) experienced a perturbation schedule that transitioned from slow, medium, to rapid switching (Fig. 2B) whereas Group 2 (n = 10) experienced the reverse. In Group 1, error-sensitivity decreased whereas in Group 2 error-sensitivity increased (Fig. 2C). We measured the mean error-sensitivity in each environment, resulting in 3 measurements for each subject across the experiment. RM-ANOVA showed a significant main effect of group (p < 0.005) and block (p < 0.001) and group by block interaction (p < 0.001). As the statistics of the perturbation changed, so did the error-sensitivity.

We measured learning from error as a function of error in each environment (Fig. 2D). A given error produced greater learning when that error was experienced in a slow switching environment (Fig. 2D, red line) (RM-ANOVA main effects of error size p < 10⁻⁴, and environment p < 0.001, posthoc between slow vs. medium or fast, p < 0.001). We quantified error-sensitivity at each error size (Fig. 2E) and found that error-sensitivity had not changed globally, but predominantly for smaller error sizes. RM-ANOVA of the absolute sensitivities between 0.25 and 2cm showed a significant main effect of environment (p < 10⁻⁴), as well as a significant environment by error size interaction (p < 0.05). We found a significant difference in error-sensitivity across environments for an error-size of 0.25cm (p < 0.05), but no significant difference for an error-size of 2cm (p > 0.1). Interestingly, the small error sizes for which the subjects had shown the largest change in error-sensitivity were also the most frequent errors (Fig. 2F). This hinted that control of error-sensitivity was a function of error.

Current models of sensorimotor learning assume that error-sensitivity η⁽ⁿ⁾ is independent of error e⁽ⁿ⁾. This is true for state-space models of learning (18, 21–24), as well as Kalman filter models of learning (5, 25–27). However, suppose that sensory prediction errors are encoded in the nervous system with a set of basis elements where each basis element g_i has a preferred error ĕ_i. Further suppose that error-sensitivity is determined by a population coding:

$$\begin{array}{ll}\hfill \eta \left(e^{(n)}\right)& =\sum _i{w}_i{g}_i\left(e^{(n)}\right)\\ \hfill g_i\left(e^{(n)}\right)& =exp\frac{-{\left(e^{(n)}-{\stackrel{⌣}{e}}_i\right)}^2}{2{\sigma }^2}\end{array}$$ (2)

On trial n−1 the motor command u⁽ⁿ⁻¹⁾ produces an error e⁽ⁿ⁻¹⁾, as illustrated in the top part of Fig. 3A. The nervous system learns from this error and produces motor command u⁽ⁿ⁾ on the subsequent trial, resulting in e⁽ⁿ⁾. In a slowly switching environment (top part of Fig. 3A), e⁽ⁿ⁾ has the same sign as e⁽ⁿ⁻¹⁾. In this case, error-sensitivity should increase around e⁽ⁿ⁻¹⁾ (Fig. 3B, red line). On the other hand, in a rapidly switching environment (Fig. 3A, bottom), e⁽ⁿ⁾ has a different sign than e⁽ⁿ⁻¹⁾. In this case, error-sensitivity should decrease:

$${\mathbf{w}}^{(n+1)}={\mathbf{w}}^{(n)}+\beta \text{sign}(e^{(n-1)}{e}^{(n)})\frac{\mathbf{g}\left(e^{(n-1)}\right)}{{\mathbf{g}}^T\left(e^{(n-1)}\right)\mathbf{g}\left(e^{(n-1)}\right)}$$ (3)

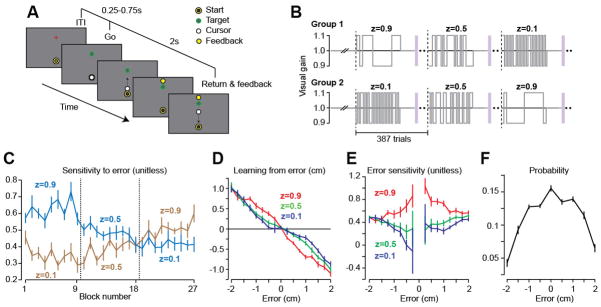
Fig. 3.

Theoretical model and Experiment 3. A. On trial n−1, the motor command u⁽ⁿ⁻¹⁾ is generated, resulting in error e⁽ⁿ⁻¹⁾=−1. If the error in trial n is of the same sign as e⁽ⁿ⁻¹⁾, then error-sensitivity should increase (top). However, if the error experienced in trial n has a different sign than e⁽ⁿ⁻¹⁾ then error-sensitivity should decrease (bottom). B. Learning from error following experience of two consecutive errors from (A).. Error sensitivity around e⁽ⁿ⁻¹⁾ increases if sign (e⁽ⁿ⁻¹⁾e⁽ⁿ⁾)=1 and decreases otherwise. C. Model performance for slow, medium, and rapidly switching environments (gray line represents x̂⁽ⁿ⁾). However, learning from error (D) is increased in the slow switching environment and decreased in the rapidly switching environment. E. Experiment 3 perturbation protocol. F. Single-trial learning from a +8N perturbation and a −4N perturbation in Probes 1 and 2. Learning is increased for the −4N perturbation, while simultaneously decreased for a +8N perturbation. G. Learning from error normalized by the perturbation magnitude (4 or 8N) in the first trial of each repetition of the rapid (blue) and slowly switching (red) environments. Learning increased in the slowly switching (4N) environment but decreased when the perturbation was rapidly switching (8N). Error bars are SEM.

In Eq. (3), $\mathbf{w}={[\begin{array}{cccc}{w}_1& w_2& \cdots & w_N\end{array}]}^T,\mathbf{g}={[\begin{array}{cccc}{g}_1& g_2& \cdots & g_N\end{array}]}^T$, and superscript T is the transpose operator. This rule is similar to the RPROP algorithm, a heuristic for adjusting the learning rate of machines (28), but has the unique feature of assuming that error-sensitivity is via population coding of the error space.

Eqs. (1–3) represent a learner that stores two kinds of memory: a memory of the state of environment (x̂, Eq. 1), and a memory of errors (w, Eq. 3). We simulated the model (Fig. 3C, gray line) and found that in the slow switching environment error-sensitivity increased in the neighborhood of the experienced errors, whereas in the rapidly changing environment error-sensitivity decreased (Fig. 3D).

Our model made a critical prediction: if the brain controlled error-sensitivity via memory of errors, then it should be possible to simultaneously increase sensitivity for one error, while decreasing it for another. In Exp. 3 we considered an isometric task in which subjects (n = 16) produced a force to match a target (16N) in the face of a perturbation. The perturbations were designed so that, according to our model, subjects would increase their sensitivity to −4N errors, while simultaneously decreasing their sensitivity to +8N errors.

In the baseline block we probed sensitivity to +8N and −4N perturbations (Probe 1, Fig. 3E). The resulting learning from error is plotted in Fig. 3F (Probe 1). At baseline, subjects responded to the +8N and −4N perturbations by learning a fraction of each error (Fig. 3F). We next produced 20 repetitions of a rapidly switching environment in which the perturbations were ±8N (Fig. 3E, inset). After a period of washout, we then produced 15 repetitions of a slowly switching environment in which the perturbations were 0N or +4N. The critical aspect of our design was that the subjects were never exposed to a −4N perturbation. They nevertheless experienced −4N errors (because removal of a learned +4N perturbation results in −4N error).

The 8N environment induced a decrease in sensitivity to a +8N error, and subsequent exposure to the +4N environment resulted in an increase in sensitivity to a −4N error (Fig. 3G, RM-ANOVA showed a significant main effect of perturbation (p < 0.03) as well as a perturbation by block interaction, p < 0.01). The critical question, however, was whether both of these changes in sensitivity were simultaneously present. Following the slowly switching block of perturbations, we again probed sensitivity to +8N and −4N errors (Probe 2, Fig. 3E). Compared to the baseline block (Probe 1), learning from a +8N error had decreased (p < 0.005), while simultaneously, learning from a −4N error had increased (p < 0.05) (Fig. 3F). When we ran our model on the same sequence of errors that subjects had experienced, the change in error-sensitivity predicted by the model was highly correlated with the change observed in our subjects (R² = 0.65; p < 10⁻⁸, Fig. S1), suggesting that history of error induced changes in error-sensitivity in the region of the experienced errors.

This new model of learning provided new insights on a wide range of puzzling experiments, including the phenomena of savings and meta-learning (Supporting Online Materials, Fig. S2). It predicted that when one is better at a task than before, it is not because the brain recalled the motor commands, but because it recognized the errors -- the errors for which error-sensitivity had been altered. In addition, the model predicted that savings and meta-learning could be blocked by controlling the errors that are experienced during learning.

In Exp. 4 volunteers participated in a visuomotor rotation experiment (Figs. 4A and S4, n = 10 per group). The control group (ANA) experienced a +30° perturbation followed by extended washout and then relearning of +30°, a protocol that should produce savings (13). According to our model, savings occurs because during the initial exposure to (A) the stable sequence of perturbations increase error-sensitivity, and these errors are re-visited in the subsequent test of (A). If so, we should be able to block savings by presenting (A) gradually (GNA group, Fig. S4), preventing prior exposure to errors that are visited at onset of (A).

Fig. 4.

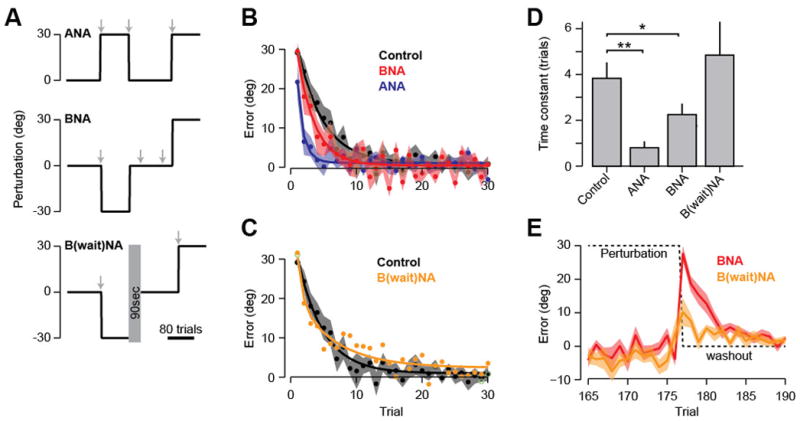
Saving occurs only when previously experienced errors are re-visited. A. A visuomotor perturbation experiment. Gray arrows indicate 1–2 minute set-breaks. B. Performance in the final +30° perturbation. ANA and BNA groups show savings, i.e., faster learning of the perturbation compared to control (naive). Exponential fits are shown for the group data. C. The B_waitNA group does not exhibit savings. D. Exponential time constants are compared to controls (*p < 0.05, **p < 0.01). A lower time constant indicates faster learning. E. Comparison of the errors (i.e., after-effects) experienced by the BNA and B_waitNA groups. The B_waitNA group experienced smaller errors due to the presence of the set-break.

Furthermore, we should be able to produce savings in a very different way: expose subjects to perturbation (B) and then present sudden washout (Fig. 4A, BNA). During washout they are exposed to a sequence of stable errors, which increase error-sensitivity for those errors. Importantly, the washout-induced after-effects are errors that are also experienced during subsequent test of (A). If the meta-learning in BNA is due to errors that are experienced during washout of (B), we should be able to eliminate it by reducing the washout-induced errors. In B_waitNA, a wait period was inserted between −30° training and washout, reducing the size of after-effects associated with the transition from −30° to washout (Fig. 4E). We also tested this idea in a different way: gradual washout (B) (Group BGNA, Fig. S4). In summary, the model predicted savings in ANA but not GNA, meta-leaning in BNA but not B_waitNA and BGNA. Our experimental results confirmed these predictions (Figs. 4C, 4D, S4).

We found that during learning, the brain controlled error-sensitivity in a principled way: learning more from error when perturbations were likely to persist, and less when perturbations were likely to change. Error-sensitivity modulation was specific to the experienced errors, suggesting that training produced a memory of errors. This idea accounted for a host of puzzling observations, including saturation of error-sensitivity (5, 6, 29), the phenomenon of meta-learning (16), examples of savings (10–12), and reinforced repetition (15).

The model predicted that meta-learning vanishes when a small delay or gradual washout alters the history of errors (Fig. 4A), demonstrating that savings depends crucially on the memory of errors that is accumulated during training. This memory of errors likely exists in parallel with the two traditional forms of motor memory, memory of perturbations (23) and memory of actions (30).

In our model, we chose to describe the learner as a process with a single time-scale. However, data suggest that learning from error depends on a fast and a slow process with different error-sensitivities (23, 25, 31). We speculate that the memory of errors exerts its influence through the error-sensitivity of the fast process, and its manipulation through history of errors may be a useful strategy to speed recovery during rehabilitation (32).