Abstract
One critical approach to preclinical evaluation of anti-tuberculosis (anti-TB) drugs is the study of correlations between drug exposure and efficacy in animal TB infection models. While such pharmacokinetic/pharmacodynamic (PK/PD) studies are useful for the identification of optimal clinical dosing regimens, they are resource intensive and are not routinely performed. A mathematical model capable of simulating the PK/PD properties of drug therapy for experimental TB offers a way to mitigate some of the practical obstacles to determining the PK/PD index that best correlates with efficacy. Here, we present a preliminary physiologically based PK/PD model of rifampin therapy in a mouse TB infection model. The computational framework integrates whole-body rifampin pharmacokinetics, cell population dynamics for the host immune response to Mycobacterium tuberculosis infection, drug-bacteria interactions, and a Bayesian method for parameter estimation. As an initial application, we calibrated the model to a set of available rifampin PK/PD data and simulated a separate dose fractionation experiment for bacterial killing kinetics in the lungs of TB-infected mice. The simulation results qualitatively agreed with the experimentally observed PK/PD correlations, including the identification of area under the concentration-time curve as best correlating with efficacy. This single-drug framework is aimed toward extension to multiple anti-TB drugs in order to facilitate development of optimal combination regimens.
Keywords: Rifampin, PKPD, Tuberculosis, Mice, Immune response, Modeling
Introduction
A major aim of anti-tuberculosis (anti-TB) drug development is the identification of new combination regimens to better treat drug-susceptible and drug-resistant TB, including TB in human immunodeficiency virus (HIV) co-infected patients [1]. In order to accelerate the development process relative to sequential single-drug replacement in current three- and four-drug regimens, a Critical Path to TB Drug Regimens (CPTR) initiative is underway in which the unit of development is an entirely novel multidrug combination [2]. Presently, several novel anti-TB drug combinations have been tested in mice [3, 4, 5] and a first multidrug early bactericidal activity (EBA) study has been completed in humans [6].
Beyond the identification of specific drugs to test in combination, there remains the problem of dose optimization which is important both for the therapeutic benefits and as a means to conserve the effective use of the drugs [7]. However, the problem of identifying optimized regimens for TB is especially difficult due in part to the large number of possible doses and schedules of administration that arise from multidrug combinations, but also due to an incomplete understanding of the relationships among the set of pharmacokinetic (PK), pharmacodynamic (PD), and disease related elements that influence the outcomes of the relevant experiments. These difficulties are illustrated by the continuing investigations of standard anti-TB regimens that have been in clinical use for more than 30 years [8, 9, 10]. Our focus here is dose optimization in mouse TB infection models, as they are the primary animal models in the noted regimen-based initiative [11].
Antimicrobial PK/PD methods provide the current basis for preclinical dose optimization of single anti-TB drugs [12, 13, 14]. These methods include measurements and analysis of drug concentration-time profiles and dose fractionation studies to determine correlations between efficacy and various PK/PD indices descriptive of drug exposure and effect. Although preclinical PK/PD data have been informative for optimal dosing in TB patients [15], the resource intensive requirements of in vivo anti-TB PK/PD studies often leads to their consideration as a secondary investigation; for example, following an unexpected pattern of drug behavior observed in clinical testing [16]. The multidimensional exposure-efficacy relationships needed to characterize the three- and four-drug combinations used to treat TB would require even greater experimental resources. Preclinical anti-TB combination studies are currently performed using a limited range of doses that are determined primarily from single-drug studies for new drugs, or from previously optimized regimens for existing drugs [4, 17].
Mathematical modeling and simulation provides a complementary approach to experimental methods that may mitigate some of the practical obstacles to combination regimen based development. Compartmental PK/PD modeling is the most commonly used approach to describe and predict drug exposure-efficacy relationships [18]. These models, typically consisting of one or more compartments for drug concentration kinetics combined with effect compartments for the drug-bacteria interaction, have been used to predict optimal PK/PD indices for a variety of antimicrobial drugs in both in vitro and in vivo systems [19, 20, 21]. However, these conventional PK/PD models aim at reducing the complexity of the drug-biological system interactions to a minimal set of free parameters whose values are specified by data from the types of experiments that are to be simulated. This limits their application to quantitative descriptions of a relatively small number of model variables with a narrowly defined set of experimentally measurable endpoints. In contrast, physiologically based PK/PD models [22] incorporate mechanistic descriptions of the exposure-efficacy relationships using variables and parameters that have physiological and biochemical interpretations. This provides for the experimental measurement of internal model components and a predictive capability beyond the experimental designs used for model development.
As a step toward a mathematical and computational modeling framework capable of describing and predicting PK/PD relationships for preclinical anti-TB regimen-based development, we constructed a physiologically based PK/PD model for rifampin in Mycobacterium tuberculosis infected mice, including a population model for the host-immune response to infection. As an initial application, we calibrated the model to a subset of experimental data from a rifampin PK/PD study in mice by Jayaram et al. [12] and simulated a separate dose fractionation experiment to determine an optimal PK/PD index for efficacy of rifampin against TB-infected mice.
Materials and methods
Pharmacokinetic/pharmacodynamic model
The mathematical PK/PD model was constructed by combining a physiologically based pharmacokinetic (PBPK) model for rifampin in mice [23] with a host-effect model (TB model) describing M. tuberculosis infection in the lungs of mice [24]. The PBPK model provided rifampin concentration-time profiles for the major tissues and organs, including plasma and lungs, for single and multiple oral dosing. The TB model provided the dynamics in the lungs of (i) intra- and extra-cellular bacteria, (ii) resting, activated, and infected macrophages, (iii) CD4+ and CD8+ T cells, and (iv) the cytokines IL-2, IL-10, IL-12, and IFN-γ. Both the PBPK and TB models consisted of physiologically parameterized ordinary differential equations, and the two models were combined through terms for drug-induced killing of the intra- and extra-cellular bacteria.
The drug-bacteria interaction in the lungs was described with a sigmoidal killing term [25] added to the existing equations for bacterial dynamics given in Friedman et al. [24]; these new equations for bacterial cell density (B) as a function of time (t) took the form,
| (1) |
The total rifampin concentration in lungs, CLU (with fLU the corresponding free fraction), was determined from the PBPK model equation,
| (2) |
where VLU is lung tissue volume, QC is cardiac output, CV is rifampin concentration in venous blood, and PLU is the rifampin lung/blood partition coefficient. There were three bacterial cell density equations described by (1); one each for extracellular bacteria and intracellular bacteria in activated or infected macrophages. The first term on the right-hand side of equation (1) represents the bacterial dynamics in the host environment in the absence of drug, with the explicit form for each of the three bacterial subpopulations given by the corresponding equations in Friedman et al. [24]. The drug effect parameters, kmax, EC50, and γ, represent the maximum kill rate, half-maximum effect drug concentration, and Hill coefficient, respectively. These parameters were further distinguished as corresponding to either extracellular bacteria, Ex, or intracellular bacteria, In (for bacteria inside either activated or infected macrophages); in the equation for extracellular bacteria, , and γ = γEx, and for both equations describing intracellular bacteria, , and γ = γIn.
The complete set of PK/PD model equations were obtained by combining all the equations listed in the respective publications for the separate PBPK [23] and TB [24] models into a single model structure, with the only modification being to the three original bacterial dynamics equations to include drug-induced bacterial killing as described above. A diagram of the complete model structure together with the full set of equations is given in the Appendix. We refer the reader to the original model publications [23, 24] for additional equation details. The complete set of parameter values were specified first as baseline values, followed by modification of some of these values through model calibration to various sets of in vivo experimental data. The initial conditions for the TB model were specified in Friedman et al. [24] at day seven of infection, with values appropriate for low-dose aerosol exposure to M. tuberculosis. The initial drug concentrations in all PBPK model compartments were set to zero.
Baseline parameter values
Baseline values for the TB model parameters and the initial cell densities and cytokine concentrations, were chosen as those specified for young mice in Friedman et al. [24]. With the exception of mean body weight, baseline values for the PBPK model parameters were chosen as the mean values listed in Lyons et al. [23]. Mean body weight was set to 21g [26] as representative of the seven- to nine-week old male and female BALB/c mice used for the in vivo measurements in Jayaram et al. [12]. A baseline value for fLU was set from the rifampin unbound fraction in plasma (f plasma ) obtained from Jayaram et al. [12], as fLU = f plasma · BP/PLU [27], where BP is the rifampin blood/plasma ratio, and PLU is the rifampin lung/blood partition coefficient. Baseline values for the drug effect parameters were set from the corresponding terms in the dose-response curves for in vitro killing kinetics assays given in Jayaram et al. [12]; the batch culture results were used for the extracellular values, and the macrophage infection model results were used for the intracellular values.
Model calibration
The PK/PD model calibration was performed using a Bayesian Markov chain Monte Carlo (MCMC) procedure [28, 29] applied sequentially to a set of in vivo data for rifampin in BALB/c mice reported in Jayaram et al. [12]. A first calibration to dose-ranging pharmacokinetic data in uninfected mice was followed by a second calibration to dose-response data in M. tuberculosis aerosol infected mice.
The data obtained from the in vivo dose-ranging and dose-response studies in Jayaram et al. [12] consisted of, respectively; (i) mean values for 72-hour rifampin plasma concentration-time measurements after single oral doses of 0.33, 10, 90, 270, and 810 mg/kg, and (ii) mean lung CFU counts from mice treated with rifampin for 1 or 2 weeks, where treatment started on day 28 of infection using doses in a range of 1 to 270 mg/kg, administered orally 6 days/week. The numerical values for these data were obtained here from the corresponding published graphs by digital extraction using g3data [30, 31] (we note that the original individual data were not available (R. Shandil, personal communication)). The 72-hour rifampin plasma concentration-time measurements corresponding to the 10, 90, and 270 mg/kg doses were chosen as the calibration data from the dose-ranging study, consistent with the results in Jayaram et al. [12] indicating that a non-compartmental model with a 12-hour elimination half-life best described the mouse pharmacokinetics. The dose-response data exhibited a large amount of variability over the two-week treatment interval, particularly in the low doses; as such, we limited the calibration data to the one-week treatment group with lung CFU counts measured on days 28 and 35 post infection.
The model parameters chosen for calibration were those in the drug-bacteria interaction terms, for which the baseline values were specified using in vitro data, together with additional parameters that were found to most sensitively affect model predictions for rifampin plasma concentration and total bacterial cell density (the latter was calculated as the sum of the intra- and extracellular subpopulations). The sensitive parameters were identified using a Monte Carlo (MC) sensitivity analysis, where each MC iteration consisted of a simulation of the time-course of chosen model variables, with the parameter values set by random draws from uniform distributions bounded by ±10% of their baseline mean values. Parameter sensitivity was assessed from correlation coefficients calculated, at specified time points, between the sampled parameter values and model output resulting from 10,000 MC iterations.
The Bayesian procedure included the specification of prior parameter distributions, a likelihood function, and an error term accounting for model and measurement uncertainty. For those parameters subject to calibration, the prior distributions were chosen as uniform, , with mean (M) set to the baseline parameter value, and standard deviation (SD) set from a coefficient of variation (CV = SD/M) chosen from a range of 30–50% to represent the uncertainty in the mean (the arises from parameterization of U in terms of M and SD). All other model parameters that were not subject to calibration were held at their baseline values (see Appendix). The calibration was implemented using MCMC simulation, with log-transformed experimental calibration data, and a normal likelihood with a log uniform error variance bounded between 0.01 and 3.3 [32]. The joint posterior parameter distribution was sampled using five independent Markov chains, with convergence assessed using the Gelman-Rubin potential scale reduction factor (R) [33]. The calibrated model was obtained by replacing the prior mean parameter values with their corresponding marginal posterior means, together with the remaining uncalibrated parameters set at their default baseline values.
PK/PD model simulations
Using the calibrated PK/PD model, simulations were run for total lung CFU’s (calculated as the product of total bacterial cell density and lung tissue volume) and rifampin concentration in plasma corresponding to the dose-ranging and dose-response studies used for model calibration. A simulation of the experimental dose-fractionation study described in Jayaram et al. [12] was also run to determine a PK/PD model prediction of the PK/PD index which best correlated with bactericidal efficacy. For each dosage regimen in the dose-fractionation simulation, the PK/PD indices; AUC24/MIC, Cmax/MIC, and T>MIC, were calculated using the experimentally measured MIC = 1mg/L in serum [12], and the model simulated rifampin plasma concentration-time output (making no distinction between plasma and serum measurements). Here, MIC is the minimum inhibitory concentration, AUC24 is the 24-hour area under the concentration-time curve, Cmax the peak concentration, and T>MIC is the percentage of time the plasma concentration exceeds the MIC. The relationship between the model predicted total lung CFU’s and each PK/PD index was summarized by a fit to a sigmoid inhibitory Emax model of the form , where E is the log10 CFU, Emax is the maximum log10 CFU reduction, X is a PK/PD index, X50 is the value of X at half-maximum effect, and n is a shape parameter (this is a similar analysis of the model simulated data as was originally applied to the corresponding experimental data). The PK/PD index best characterizing the bactericidal effect was selected as the index with the highest correlation between the fitted Emax equation and the model predicted data, as determined by visual inspection and calculated coefficient of determination, R2, and coefficient of variation, CV = (root mean square error)/(mean of dependent variable).
To illustrate additional model features of the immune response we simulated the time course of total lung CFU’s together with corresponding cytokine concentrations and macrophage and T cell densities following daily 10 mg/kg oral dosing starting on day 28 post-infection.
Computational software
MCSim v5.4.0 [34] was used for all PK/PD model simulations, including the MC and MCMC simulations. R v2.15.2 [35], including the CODA package [36], was used for statistical calculations.
Results
Calibration
The rifampin PBPK model parameters; fraction of dose absorbed, total clearance, oral absorption rate, and muscle/blood partition coefficient, were shown previously [23] to have the highest correlation with the PBPK model predictions of rifampin plasma concentration, and were included here for calibration to the dose-ranging data. The MC sensitivity analysis for total bacterial cell density was performed with simulations of 6 day/week oral dosing starting on day 28 post-infection. Separate MC simulations were run for each of 1, 30, 90, and 270 mg/kg oral doses. Pearson correlation coefficients between the sampled parameters and predictions of total bacterial cell density were calculated at days 28 and 35 post-infection. Parameters with correlations of absolute value greater than 0.3, at either of the time points and for any of the doses, were considered sensitive. The TB model parameters; bacterial growth rate inside infected macrophages, rate of infection of resting macrophages, saturation for infection of resting macrophages, and maximal carrying capacity of infected macrophages, as well as the drug effect parameter, maximum kill rate for intracellular bacteria, were found to be sensitive for predictions of total bacterial cell density, and were included together with the remaining parameters in the drug-bacteria interaction terms for calibration to the dose-response data.
The baseline mean parameter values that were used to specify the prior distributions for the calibrated PK/PD model parameters are shown in Table 1. The prior mean distributions and summary statistics of the marginal posterior mean distributions are shown for the calibrated PK/PD model parameters in Table 2. For the pharmacokinetic dose-ranging calibration, each of the five Markov chains were generated from 100,000 MCMC iterations, keeping every fifth iteration of the final 10,000. Convergence was obtained as R = 1 for every sampled parameter. The marginal posterior mean values and SD’s were calculated from the aggregate of the five chains. While both fraction of dose absorbed and plasma clearance were updated, it is only the ratio CL/F that is identifiable in the present study, and while each value changed separately from prior to posterior, the prior and posterior ratios remained approximately equal.
Table 1.
PK/PD parameter baseline mean values for Bayesian prior distributions.
| Parameter (units) | Mean | Source | ||
|---|---|---|---|---|
| PBPK model parameters | ||||
| Fa | Fraction of rifampin dose absorbed | 1 | [23] | |
| ka | Oral rifampin absorption rate (1/d) | 38.64 | [23] | |
| CLC | Total rifampin clearance (L/d/kg0.75) | 0.96 | [23] | |
| PM | Rifampin muscle/blood partition coefficient | 0.76 | [23] | |
| Drug-bacteria parameters | ||||
| fLU | Fraction of rifampin free in lung | 0.3 | [23, 12] | |
|
|
Maximum kill rate for extracellular bacteria (1/d) | 13.82 | [12] | |
|
|
Half-maximum effect conc. for extracellular bacteria (mg/L) | 1.24 | [12] | |
| γEx | Hill coefficient for extracellular bacteria | 0.7 | [12] | |
|
|
Maximum kill rate for intracellular bacteria (1/d) | 1.21 | [12] | |
|
|
Half-maximum effect conc. for intracellular bacteria (mg/L) | 3.38 | [12] | |
| γIn | Hill coefficient for intracellular bacteria | 0.48 | [12] | |
| TB model parameters | ||||
| αI | Bacterial growth rate inside infected macrophages (1/d) | 0.5 | [24] | |
| k1 | Rate of infection of resting macrophages (1/d) | 0.4 | [24] | |
| c1 | Saturation for infection of resting macrophages (cell/mL) | 106 | [24] | |
| N | Maximal carrying capacity of an infected macrophage | 25 | [24] | |
Table 2.
Calibration to in vivo dose-ranging and dose-response measurements obtained from Jayaram et al. [12]: prior distributions and posterior distribution summaries.
| Parametera (units) | Prior | Posteriorb | |
|---|---|---|---|
| PBPK model parameters | |||
| F a | U(0.48, 1.0)c | 0.59(0.07) | |
| ka (1/d) | U(18.0, 59) | 36(10) | |
| CLC (L/d/kg0.75) | U(0.46, 1.5) | 0.58(0.06) | |
| PM | U(0.10, 1.4) | 1.1(0.2) | |
| Drug-bacteria parameters | |||
| fLU | U(0.14, 0.46) | 0.28(0.08) | |
|
|
U(1.8, 26) | 17(6) | |
|
|
U(0.17, 2.3) | 1.0(0.6) | |
| γEx | U(0.09, 1.3) | 0.62(0.3) | |
|
|
U(0.16, 2.3) | 2.0(0.2) | |
|
|
U(0.45, 6.3) | 4.5(1) | |
| γIn | U(0.06, 0.9) | 0.72(0.10) | |
| TB model parameters | |||
| αI (1/d) | U(0.24, 0.76) | 0.58(0.1) | |
| k1 (1/d) | U(0.05, 0.75) | 0.55(0.1) | |
| c1 (cell/mL) | U(1.3 ×105,1.9 ×106) | 5.0 ×105(3 ×105) | |
| N | U(12, 38) | 29(5) | |
U(a,b); Uniform distribution over [a, b].
Parameter definitions are given in Table 1.
Mean(SD).
Truncated to exclude values greater than 1.
The prior baseline mean values of the PBPK model parameters shown in Table 1 were replaced with their corresponding marginal posterior mean values shown in Table 2 for use in the second calibration to the dose-response data. For the calibration to the dose-response data, each of the five Markov chains were generated from 200,000 MCMC iterations, keeping every fifth iteration of the final 10,000. Convergence was obtained as R < 1.06 for every sampled parameter. The marginal posterior mean values and SD’s were calculated from the aggregate of the five chains. The fully calibrated model was obtained using the posterior mean values in Table 2, with the remaining uncalibrated parameters kept at their baseline mean values.
Figure 1 shows simulations of rifampin plasma concentration-time profiles and lung CFU killing kinetics using the calibrated PK/PD model, together with the corresponding mean experimental data from the dose-ranging and dose-response studies in Jayaram et al. [12]. The simulated values of rifampin plasma concentration reasonably approximate the absorption and elimination behavior of the intermediate doses, but show larger deviations from experiment for the low and high doses. The simulation for the 810 mg/kg dose describes the rate of elimination, but over-predicts Cmax, while the 0.33 mg/kg matches the early absorption data, but over-predicts the rate of elimination. For the dose-response data simulations, the CFU counts on day 28 and the range of CFU counts on day 35 are well simulated by the model, but large deviations from model simulaitons are evident in the day 42 CFU data points, reflecting the large variation in this experimental data.
Fig. 1.
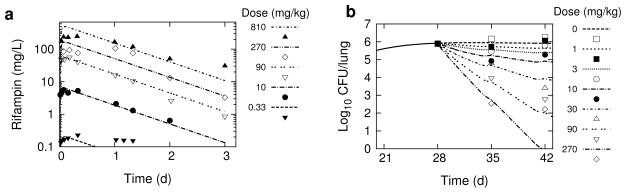
Simulations of rifampin in vivo dose-ranging and dose-response studies. The dashed lines are simulation outputs, and the data points are replotted experimental data digitally extracted from the corresponding plots in Jayaram et al. [12]. a 72-hour rifampin plasma concentration-time profiles following single oral doses of 0.33, 10, 90, 270, and 810 mg/kg. b Total lung CFU’s following 6-day/week dosing of 0, 1, 3, 10, 30, 90 and 270 mg/kg, starting day 28 post-infection.
Simulation of dose-fractionation study
The PK/PD model simulation of the dose-fractionation study described in Jayaram et al. [12] consisted of simulations for total lung CFU’s on day 34 post-infection, following rifampin dosing starting on day 28 post-infection with total doses of 2, 6, 18, 60, 180, 540, 1080, 1620, 3240, and 4860 mg/kg. Each total dose was fractionated one, three, or six times in 144 hours (6 days). For example, the 180 mg/kg total dose was administered as a single dose on day 28, or as 60 mg/kg doses on each of days 28, 30, and 32, or as 30 mg/kg doses on each of days 28 through 33. Single-dose amounts of 1080, 1620, 3240, and 4860 mg/kg, and three-dose amounts of 1080 and 1620 mg/kg, were excluded from the simulations to match the same excluded dosing described in the original experimental study [12]. AUC24 was calculated for each dosage regimen by numerical integration of the rifampin plasma concentration-time curve over the 144 h time interval, divided by 6. Cmax was identified as the highest predicted rifampin plasma concentration during the 144h interval. T>MIC was calculated as the percentage of time the rifampin concentration in plasma was greater than the MIC over the 144 h interval.
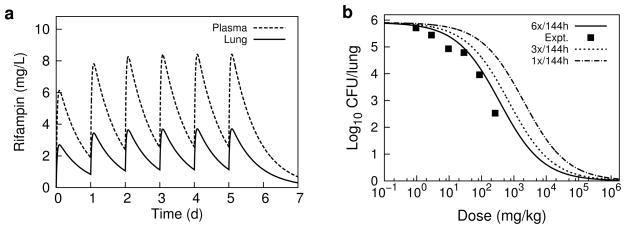
Figure 2 shows the simulation results for model predicted log10 CFU’s plotted against each PK/PD index together with the Emax model fits to the simulation data. Table 3 shows the Emax model and goodness of fit values for the PK/PD model simulated dose-fractionation data and the corresponding experimentally observed data from Jayaram et al. [12]. The experimental data points used for this analysis were digitally extracted from FIG. 2, FIG. 6B, and FIG. 6C of Jayaram et al. [12]. We note a discrepancy between the same AUC/MIC data plotted in FIG. 2 and FIG. 6A, with our results in Table 3 conforming to the FIG. 2 in vivo data as the correct values (there was an approximate factor of 5 shift between the data points in each figure with a likely plotting error in the horizontal axis of FIG 6A). From simulation output for AUC24 and corresponding dose (Dose (mg/kg)), we determined the relationship AUC24 = α · Dose, where α = 11.7, 6.08, or 2.08 (kg/L), for 6, 3, or 1 day/week dosing, respectively. Using this result in the Emax equation for AUC24/MIC we established the dose-response curves, shown together with the corresponding 6x/week experimental data from Jayaram et al. [12] in Figure 3.
Fig. 2.
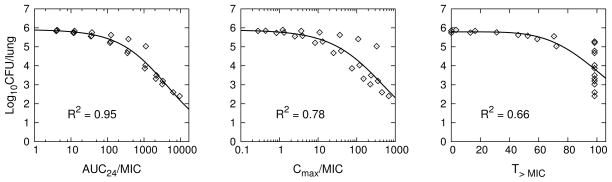
PK/PD model simulation of the experimental rifampin dose-fractionation study for TB infected BALB/c mice described in Jayaram et al. [12]. Individual data points (⋄) were PK/PD model generated, with each point obtained from the simulation of total lung CFU’s and corresponding PK/PD index calculated from simulated plasma concentrations for each dosage regimen of the dose-fractionation study. Solid lines are Emax equation fits (Table 2) to the PK/PD model generated data points.
Table 3.
Fit of to PK/PD model predicted (Figure 2) and experimentally observed [12] mouse rifampin dose-fractionation data (E = log10 CFU, Emax = maximum E, X is a PK/PD index, X50 is the value of X at E = Emax/2, and n is a shape parameter.)
| X | Emax | X50 | n | R2 | CV% | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Pred. | Obs. | Pred. | Obs. | Pred. | Obs. | Pred. | Obs. | Pred. | Obs. | |
| AUC24/MIC | 5.9 | 5.9 | 4.3 ×103 | 3.9 ×103 | 0.65 | 0.70 | 0.95 | 0.95 | 5.4 | 6.0 |
| Cmax/MIC | 5.9 | 6.2 | 5.0 ×102 | 2.8 ×102 | 0.63 | 0.57 | 0.78 | 0.81 | 11 | 9.1 |
| T>MIC | 5.8 | 5.7 | 1.1 ×102 | 1.1 ×102 | 4.8 | 11 | 0.66 | 0.46 | 14 | 18 |
Fig. 3.
PK/PD model simulations. a Total rifampin plasma and lung concentration-time profiles following 10 mg/kg, 6 times/week daily oral dosing. b Dose-response curves for reduction in lung CFU counts following one week of oral rifampin doses administered 1, 3, or 6 times in TB-infected BALB/c mice. Experimental data (Expt.) digitally extracted and replotted from the corresponding non-zero dosing (6x/week) results in Jayaram et al. [12] (the zero dose value was approximately 6.21 log10CFU).
The pattern of simulated output for the individual mice, and the correlation of PK/PD indices with efficacy in the order AUC24/MIC > Cmax/MIC > T>MIC, closely match the experimental results presented in Jayaram et al. [12] (these latter experimental results were not included in our model development or calibration procedure, but were kept as separate independent data used only for comparison to the corresponding computational simulations). While there is overall qualitative agreement between our simulated results and experimental measurement, we find disagreement in the dose fractionation results with a higher than observed prediction of AUC24/MIC for a 1-log CFU reduction. From our Emax equation for AUC24/MIC, a 1-log10 CFU reduction requires AUC24/MIC = 368; the corresponding value reported in Jayaram et al. [12] was 271. The difference between these observed and predicted values can be partially attributed to the error in modeling the rifampin plasma concentration-time profiles, most notably seen in the over-prediction of exposure for the higher doses. In the PK/PD correlation analysis of Jayaram et al. [12], the PK plasma exposure values were determined by simulation using a one-compartment model with first-order absorption and elimination, similar to assumptions made in our PBPK model; as such, we expect similar plasma modeling errors. However, the bacterial killing kinetics were experimental values in Jayaram et al. [12] while here they were model predicted, based on calibration to the dose-response data in Jayaram et al. [12]. The over-prediction of drug exposure in the high dose measurements would lead to an under-prediction of the true rate of bacterial killing, resulting in over-prediction of exposure necessary for the 1-log CFU reduction.
Simulation of host response
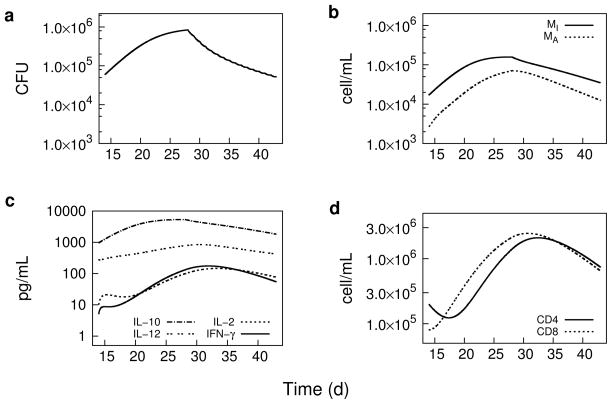
Figure 4 shows the PK/PD model predicted bacterial kinetics and corresponding host response from day 14 through day 42 post-infection, with daily 10 mg/kg rifampin oral dosing beginning on day 28 post-infection. The macrophage cell densities and IL-10 concentration are most clearly seen as directly responsive to the decrease in bacterial load as expected from the location of M. tuberculosis primarily in macrophages, and as IL-10 (and IL-12) are secreted by the macrophages. Also, a lag time relative to bacterial load is seen in the response of the T cells and the T cell derived IL-2 and IFN-γ cytokines, as expected due to time required for T cells to detect and process regulatory signals from the reduction in bacterial stimuli.
Fig. 4.
PK/PD model simulations during days 13 to 44 of pulmonary bacterial load, cytokine concentrations, and macrophage and T cell densities (cells per mL of lung tissue) following a two-week daily 10 mg/kg oral dose of rifampin beginning on day 28 post-aerosol infection in TB-infected BALB/c mice. a Bacterial load (sum of intra- and extracellular bacteria). b Cell densities of infected (MI ) and activated (MA) macrophages. c Cytokine (IL-10, IL-2, IL-12, and IFN-γ) concentrations. d Cell densities of CD4+ and CD8+ T cells.
Discussion
The complexities of anti-TB drug therapy, including host effects and the need for multidrug combinations, strains the capabilities of conventional PK/PD modeling and analysis methods for identifying new optimal regimens. Physiologically based PK/PD modeling can be viewed as a multiscale approach [37] that provides for integration of the multiple aspects of dose-optimization including efficacy, host-toxicity, antimicrobial resistance, and possible drug-drug interactions. PK/PD models for drug treatment of TB that include multiscale descriptions of the host-drug-bacteria interactions are available in the literature [38, 39]. However, while the disease components of these models are physiologically based, the pharmacokinetic components are either empirical models used to describe a single drug [38], or descriptions of combination therapy using efficacy parameters without consideration of the actual dose or drug concentration kinetics [39]. While these models provide useful insights into drug therapy for TB, we envision a computational framework capable of describing whole-body multidrug PK/PD interactions which requires a more detailed pharmacokinetic description than was used in the available examples. Our objective here was to establish, for a single drug, the essential computational aspects of such a multidrug framework.
We constructed a PK/PD model for rifampin in TB-infected mice by combining models for drug disposition and disease through drug-bacteria interaction terms. The model equations were numerically evaluated in a computational framework that included MC simulations to assess parameter sensitivity, and MCMC simulations for a Bayesian calibration procedure that provided for incorporation of experimental data from in vitro and in vivo measurements. While we considered only a single drug in the present study, the model structure can incorporate multiple drugs through expansion of the pharmacokinetic component to include additional PBPK models for each drug of interest. These separate PBPK models can be linked through tissue and organ compartments that correspond to target sites for PK and PD interactions in a manner described by numerous examples for PBPK modeling of chemical mixtures [28, 40, 41]. As rifampin is a potent cytochrome P450 (CYP) enzyme inducer [42], inclusion of CYP enzyme induction [43] into the present PBPK model and combining with PBPK models for commonly co-administered antiretroviral drugs could serve as an application to modeling dose adjustments required for treatment of TB and human immunodeficiency virus (HIV) co-infections [44]. The primary aim of accounting for physiological detail in such a modeling framework is to better translate preclinical experimental data to the clinical setting. PBPK modeling is becoming established in drug development through it’s increasing use for in vitro in vivo extrapolation and interspecies scaling [45]. Additionally, the physiologically based framework described here contains basic modeling elements for novel anti-TB drug therapies such as those related to host-directed adjunct therapies [46] and alternate routes of administration [47].
Our initial application of the computational framework was the simulation of experiments described in a PK/PD study of rifampin in M. tuberculosis infected mice [12]. In vitro measurements of protein binding and M. tuberculosis killing kinetics in batch culture and in macrophages, together with previously specified PBPK model parameter values, were used to specify prior parameter distributions that were subsequently updated by Bayesian calibration to in vivo dose-ranging and dose-response measurements. While the experimental measurements provided by Jayaram et al. [12] presented an integrated set of data with respect to bacterial strain, mouse models, and methods of analysis; data from separate experiments such as from hollow fiber systems [48] could also be used to inform prior parameter distributions. The parameters chosen for calibration were determined from a ranking of those most sensitive to the experimental data used for calibration and for which experimental measurements were most uncertain. For the PBPK model we restricted calibration to sensitive drug-dependent parameters while leaving the measured drug independent physiological parameters at their baseline values. The calibrated model was used to simulate the experimental dose-fractionation study described in Jayaram et al. [12], with a measured MIC incorporated into calculations for the associated PK/PD indices. The simulated output clearly indicated a concentration-dependent behavior, with the AUC24/MIC best correlating with lung CFU’s in agreement with the results in Jayaram et al. [12]. The predicted dose-response curve shown in Figure 3 (derived from the Emax model fit to AUC24/MIC simulated data) shows the standard 10 mg/kg dose well below the maximum response, the complete curve showing a wide range over several orders of magnitude for the dose. This result agrees with other experimental studies indicating rifampin under-dosing for TB in mice [49], and illustrates partly the motivation for recent and ongoing high-dose rifampin clinical trials [50, 51].
While the PK/PD model presented here is a first iteration of model development, combining previously disparate mathematical descriptions for the host-drug-bacteria subcomponents, these preliminary simulations indicate the utility of a computational PK/PD approach to obtain results that are consistent with an otherwise resource intensive dose-fractionation experiment. Additionally, consideration of the differences between the PK/PD model predictions and experimental observations provides a means to improve the model and the hypotheses from which the mathematical statements are derived. In conventional PK/PD modeling, differences between prediction and experimental observation are addressed by changes to the model, using alternate variables and parameterizations, without a necessarily corresponding physiological interpretation. For systems-based modeling, changes to the model are constrained by biological and physiological hypotheses and experimentally measured parameter values. In our case, further investigation of the model hypotheses is suggested by the higher than observed prediction of AUC24/MIC for a 1-log CFU reduction. The PBPK submodel may be improved, as we discussed in an earlier publication [23], with a more detailed description of enterohepatic circulation that may better simulate the plasma concentration-time profiles. The mathematical TB model [24] was developed to describe early and stationary phase bacterial growth. Experimental data describing drug induced bacterial killing and the simultaneous dynamics of T cells, macrophages, and cytokines is not currently available for mice in the anti-TB drug literature. Such data would be highly beneficial to better test the model predictions and to further understand the host effect during drug treatment.
Two important areas of investigation that were not addressed by our model are the characteristic biphasic killing kinetics observed with prolonged drug treatment [52], and postantibiotic effect (PAE) which refers to delayed regrowth of bacteria after drug exposure [53]. These effects would be important for describing the full time course of anti-TB treatment, including accounting for intermittent or missed doses. PK/PD models for rifampin therapy in human TB described by Goutelle et al. [38], explained the biphasic killing kinetics as arising from an initial rapid killing of a large extracellular bacterial population followed by a slower killing of a protected intracellular subpopulation. However, the extracellular bacterial population in standard mouse TB infection models are a much smaller fraction of the total than in humans [54], and preliminary simulations with our PK/PD model (data not shown) do not account adequately for initial rapid killing and longer term persistence. This suggests other mechanisms for bacterial persistence, such as cellular level stochastic processes related to phenotypic heterogeneity [55, 56, 57], may be necessary to explain the long-term M. tuberculosis killing kinetics in mice. A significant PAE for rifampin against M. tuberculosis has been observed in vitro [58], and including a PAE in the model would provide a mechanism for growth inhibition during low or absent drug concentrations. Examples of PK/PD modeling with a PAE are available in the literature [59, 60] and could be included here as a refinement of our current description of the drug-bacteria interaction.
While systems based modeling may be used to explore a wider range of questions for a particular experimental system than conventional PK/PD modeling, the emphasis on physiological description limits the range of systems to which the model can be applied. The TB infection model [24] was developed using data from standard mouse strains such as C57BL/6 or BALB/c, and would not apply directly to mouse strains with highly differing immune responses, such as gamma-interferon knockout (GKO) mice [61], or the necrotic granuloma forming C3HeB/FeJ [62] mice. The dose, route, and bacterial strain used for infection also play an important role in determining the host immune response [63]. These differences in mouse strain, bacterial strain, and other experimental conditions would require, minimally, modification of initial conditions and various parameter values, together with the appropriate experimental measurements on which to base these modifications. While not implemented in this model, the physiologically based nature of the model parameters provides a mechanism to incorporate mouse intra- and inter-individual variability through MC simulation. Such variability was accounted for previously in the PBPK model [23]; however, information on the variability of the TB model parameters was not provided for the published model used here [24]. Such data would be highly beneficial to better test the model predictions and to further understand the host effect during drug treatment. The motivation to obtain such parameter variability data, as well as data corresponding to immune system components during drug treatment, demonstrates the idea of model-directed experimentation, which provides support for further physiologically based model development and a potential better understanding of the experimental system as a whole.
Acknowledgments
The authors wish to thank Scott Irwin and Mary Ann De Groote (Colorado State University (CSU)), Joanne Turner (The Ohio State University), and Radha Shandil (formerly AstraZeneca, Bangalore, India) for helpful discussions. The authors also thank Brad Reisfeld and Raymond Yang (CSU) for a careful review and editing of an earlier version of this manuscript. This work was supported by National Institutes of Health Grant Number K25AI089945.
Appendix
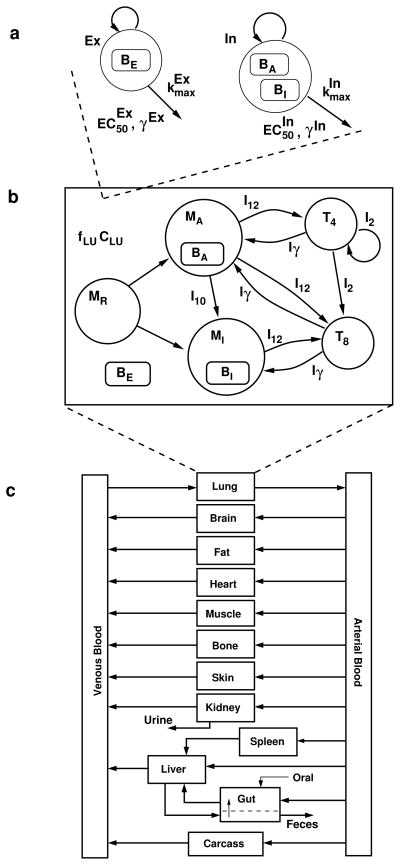
The PK/PD model used in the present work is described by equations (3–23) and the corresponding compartmental structure shown in Figure 5. The equations are those from Friedman et al. [24] and Lyons et al. [23] together with the modifications described in the Materials and methods.
Fig. 5.
PK/PD model structure. a Intracellular (In) and extracellular (Ex) bacterial populations and killing kinetics parameters. BE : extracellular bacteria, BA: bacteria residing in activated macrophages, BI : bacteria residing in infected macrophages, kmax: maximum kill rate, EC50: half-maximum effect drug concentration, and γ: Hill coefficient. b Lung compartment with free rifampin drug concentration (fLU CLU ) together with cell and cytokine populations (adapted from Friedman et al. [24]). MR,MA, and MI : resting, activated, and infected macrophages. I10,I12,I2, and Iγ : IL-10, IL-12, IL-2, and IFN-γ. T4 and T8: CD4+ and CD8+ T cells. c Rifampin PBPK model compartments and blood flow (adapted from Lyons et al. [23]).
Pharmacodynamics: TB model
The TB model and drug-bacteria interactions are described by equations (3–13). The variable names, descriptions, and initial conditions used in the the present work are shown in Table 4. The parameter values that were not updated in the Bayesian calibration are shown in Table 5, while the updated parameters are the posterior mean values shown in Table 2.
Table 4.
PD model variables and initial conditions (day 7 post-infection) used in the present work. The variable names, descriptions, and values are from Friedman et al. [24].
| Variable (units) | Value | |
|---|---|---|
| BI | Density of bacteria residing in infected macrophages (cell/mL) | 36000 |
| BA | Density of bacteria residing in activated macrophages (cell/mL) | 1000 |
| BE | Density of extracellular bacteria (cell/mL) | 1000 |
| MI | Density of infected macrophages (cell/mL) | 1800 |
| MA | Density of activated macrophages (cell/mL) | 200 |
| MR | Density of resting macrophages (cell/mL) | 5 ×105 |
| I10 | Concentration of IL-10 (pg/mL) | 100 |
| I12 | Concentration of IL-12 (pg/mL) | 50 |
| I2 | Concentration of IL-2 (pg/mL) | 10 |
| Iγ | Concentration of IFN-γ (pg/mL) | 5 |
| T4 | Density of CD4+ T cells (cell/mL) | 2 ×105 |
| T8 | Density of CD8+ T cells (cell/mL) | 8 ×104 |
Table 5.
Baseline PD model parameters that were not updated in the Bayesian calibration procedure. The parameter names, descriptions, and values are from Friedman et al. [24].
| Parameter (units) | Value | |
|---|---|---|
| αE | Growth rate of BE (1/d) | 0 |
| αA | Growth rate of BA (1/d) | 0 |
| k2 | Burst rate of infected macrophages (1/d) | 0.81139 |
| k3 | Activation rate of infected macrophages (1/d) | 0.023415 |
| k4 | Deactivation rate of activated macrophages (1/d) | 0.28876 |
| k5 | Take up of BE by activated macrophages (mL/cell/d) | 8.1301 ×10−5 |
| k6 | Rate of activation of resting macrophages (1/d) | 0.077068 |
| k7 | IL-10 production rate by infected macrophages (pg/mL/cell) | 0.50610 |
| k8 | IL-12 production rate by activated macrophages (pg/cell/d) | 0.28503 |
| k9 | IL-12 production rate by resting macrophages (pg/cell/d) | 5 ×10−4 |
| k10 | IL-2 production rate by T 4 (pg/cell/d) | 2.1873 ×10−4 |
| k11 | Loss of IL-2 due to proliferation of T 4 (pg/cell/d) | 1.6383 ×10−4 |
| k12 | Loss of IL-2 due to proliferation of T 8 (pg/cell/d) | 1.6383 ×10−5 |
| k13 | Rate of proliferation of T 4 by IL-2 (mL/pg/d) | 0.16383 |
| k14 | Rate of proliferation of T 8 by IL-2 (mL/pg/d) | 0.016383 |
| c2 | Saturation for activation of infected macrophages (pg/mL) | 50 |
| c3 | IFN-γ inhibition for deactivation of activated macrophages | 3 |
| c4 | Saturation for deactivation of activated macrophages (pg/mL) | 1 |
| c5 | Saturation for activation of resting macrophages (cell/mL) | 105 |
| c6 | IFN-γ saturation for activation of resting macrophages (pg/mL) | 20 |
| c7 | Saturation for IL-10 inhibition by IL-10 (pg/mL) | 5000 |
| c8 | Saturation for IL-12 inhibition by IL-10 (pg/mL) | 200 |
| c9 | Saturation for IL-12 production by resting macrophages (cell/mL) | 5000 |
| c10 | Saturation for T cell proliferation by IL-2 (pg/mL) | 50 |
| c11 | Saturation for IFN-γ production by T cells and IL-12 (cell/mL) | 50 |
| n1 | Average number of BI in an infected macrophage | 20 |
| n2 | Average number of BA in an activated macrophage | 5 |
| n3 | Threshold at which a resting macrophage becomes infected | 10 |
| μMA | Death rate of activated macrophages (1/d) | 0.015 |
| μMI | Death rate of infected macrophages (1/d) | 0.2 |
| μ10 | Decay rate of IL-10 (1/d) | 7.23 |
| μ12 | Decay rate of IL-12 (1/d) | 1.188 |
| μ2 | Decay rate of IL-2 (1/d) | 1.188 |
| μγ | Decay rate of IFN-γ (1/d) | 3 |
| μT4 | Death rate of T 4 (1/d) | 0.33 |
| μT8 | Death rate of T 8 (1/d) | 0.33 |
| λu | Rate of IFN- γ production by T 4 (pg/cell/day) | 1.24 ×10−4 |
| λy | Rate of IFN- γ production by T 8 (pg/cell/day) | 1.24 ×10−4 |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
The functions λi(t), i = {x,y,z,u} were implemented here as λi(t) = λi ·θ(t −tdelay), where tdelay = 14 days, and θ(x) = 1(0) for x ≥ 0(x < 0) is a step function.
Pharmacokinetics: PBPK model
The PBPK model is described by equations (14–23) with initial conditions all set to zero. The subscripts, T, on the tissue volumes, VT, drug concentrations, CT, blood flow rates, QT, and tissue/blood partition coefficients, PT, denote abbreviations for the model compartments as; V : venous blood, LU: lung, A: arterial blood, BR: brain, F: fat, SK: skin, K: kidney, S: spleen, G: gut, GL: gut lumen, L: liver, LA: hepatic artery, CR: carcass. Fractional tissue volumes, VTC, and blood flow rates, QTC, were scaled to total values as VT = VTC · BW and QT = QCC · BW 0.75. BW is body weight, and QCC is an allometric coefficient for cardiac output. Fractional clearance was also scaled as CL = CLC · BW 0.75. Drug concentration in plasma was determined from concentration in venous blood as Cplasma = CV /BP. The parameter values that were not updated in the Bayesian calibration are shown in Tables 6 and 7, while the updated parameters are given in Table 2.
Table 6.
Baseline anatomical/physiological PBPK model parameters that were not updated in the Bayesian calibration procedure. The parameter names, descriptions, and values are from Lyons et al. [23].
| Parameter (units) | Value | |
|---|---|---|
| QCC | Cardiac output (L/d/kg0.75) | 396 |
| kF | Gut lumen transit rate (1/d) | 14.4 |
| Fractional tissue volumesa | ||
| VLUC | Lung | 0.007 |
| VBRC | Brain | 0.017 |
| VFC | Fat | 0.07 |
| VHC | Heart | 0.005 |
| VMC | Muscle | 0.384 |
| VBC | Bone | 0.107 |
| VSKC | Skin | 0.165 |
| VKC | Kidney | 0.017 |
| VSC | Spleen | 0.0035 |
| VGC | Gut | 0.042 |
| VLC | Liver | 0.055 |
| VVC | Venous blood | 0.0327 |
| VAC | Arterial blood | 0.0163 |
| VCRC | Carcass | 0.0785 |
| Fractional blood flowsb | ||
| QBRC | Brain | 0.033 |
| QFC | Fat | 0.09 |
| QHC | Heart | 0.066 |
| QMC | Muscle | 0.159 |
| QBC | Bone | 0.11 |
| QSKC | Skin | 0.058 |
| QKC | Kidney | 0.091 |
| QSC | Spleen | 0.01 |
| QGC | Gut | 0.13 |
| QLAC | Hepatic artery | 0.02 |
| QCRC | Carcass | 0.233 |
Fraction of body weight.
Fraction of cardiac output.
Table 7.
Baseline rifampin-dependent PBPK model parameters that were not updated in the Bayesian calibration procedure. The parameter names, descriptions, and values are from Lyons et al. [23].
| Parameter (units) | Value | |
|---|---|---|
| fR | fractional renal clearance | 0.19 |
| kr | Gut reabsorption rate (1/d) | 4.08 |
| Partition coefficients | ||
| BP | Blood/plasma | 0.9 |
| PLU | Lung/blood | 0.49 |
| PBR | Brain/blood | 0.11 |
| PF | Fat/blood | 0.34 |
| PH | Heart/blood | 0.74 |
| PB | Bone/blood | 0.22 |
| PSK | Skin/blood | 0.76 |
| PK | Kidney/blood | 0.59 |
| PS | Spleen/blood | 0.25 |
| PG | Gut/blood | 0.74 |
| PL | Liver/blood | 3.1 |
| PCR | Carcass/blood | 0.59 |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
The summation in equation (14) is over all tissues draining into the venous blood compartment; for liver, QL = (QLA + QS + QG). The symbols AOD and AGL in equations (21–23) are the amounts of drug input to the gut and in the gut lumen. The delta function in equation (23) describes pulsed oral bolus dosing (D = dose), with times of administration, tn, n = 0,…,nmax − 1, with nmax the maximum number of doses in the treatment interval.
References
- 1.Laurenzi M, Ginsberg A, Spigelman M. Challenges associated with current and future TB treatment. Infect Disord Drug Targets. 2007;7(2):105–119. doi: 10.2174/187152607781001817. [DOI] [PubMed] [Google Scholar]
- 2.Spigelman M, Woosley R, Gheuens J. New initiative speeds tuberculosis drug development: novel drug regimens become possible in years, not decades. Int J Tuberc Lung Dis. 2010;14(6):663–664. [PubMed] [Google Scholar]
- 3.Nuermberger E, Tyagi S, Tasneen R, Williams KN, Almeida D, Rosenthal I, Grosset JH. Powerful bactericidal and sterilizing activity of a regimen containing PA-824, moxifloxacin, and pyrazinamide in a murine model of tuberculosis. Antimicrob Agents Chemother. 2008;52(4):1522–1524. doi: 10.1128/AAC.00074-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tasneen R, Li SY, Peloquin CA, Taylor D, Williams KN, Andries K, Mdluli KE, Nuermberger EL. Sterilizing activity of novel TMC207- and PA-824-containing regimens in a murine model of tuberculosis. Antimicrob Agents Chemother. 2011;55(12):5485–5492. doi: 10.1128/AAC.05293-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Williams K, Minkowski A, Amoabeng O, Peloquin CA, Taylor D, Andries K, Wallis RS, Mdluli KE, Nuermberger EL. Sterilizing activities of novel combinations lacking first- and second-line drugs in a murine model of tuberculosis. Antimicrob Agents Chemother. 2012;56(6):3114–3120. doi: 10.1128/AAC.00384-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Diacon AH, Dawson R, von Groote-Bidlingmaier F, Symons G, Venter A, Donald PR, van Niekerk C, Everitt D, Winter H, Becker P, Mendel CM, Spigelman MK. 14-day bactericidal activity of PA-824, bedaquiline, pyrazinamide, and moxifloxacin combinations: a randomised trial. Lancet. 2012;380(9846):986–993. doi: 10.1016/S0140-6736(12)61080-0. [DOI] [PubMed] [Google Scholar]
- 7.Mouton JW, Ambrose PG, Canton R, Drusano GL, Harbarth S, MacGowan A, Theuretzbacher U, Turnidge J. Conserving antibiotics for the future: new ways to use old and new drugs from a pharmacokinetic and pharmacodynamic perspective. Drug Resist Updat. 2011;14(2):107–117. doi: 10.1016/j.drup.2011.02.005. [DOI] [PubMed] [Google Scholar]
- 8.Chang KC, Leung CC, Grosset J, Yew WW. Treatment of tuberculosis and optimal dosing schedules. Thorax. 2011;66(11):997–1007. doi: 10.1136/thx.2010.148585. [DOI] [PubMed] [Google Scholar]
- 9.De Groote MA, Gruppo V, Woolhiser LK, Orme IM, Gilliland JC, Lenaerts AJ. Importance of confirming data on the in vivo efficacy of novel antibacterial drug regimens against various strains of Mycobacterium tuberculosis. Antimicrob Agents Chemother. 2012;56(2):731–738. doi: 10.1128/AAC.05701-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Grosset J, Almeida D, Converse PJ, Tyagi S, Li SY, Ammerman NC, Pym AS, Wallengren K, Hafner R, Lalloo U, Swindells S, Bishai WR. Modeling early bactericidal activity in murine tuberculosis provides insights into the activity of isoniazid and pyrazinamide. Proc Natl Acad Sci USA. 2012;109(37):15,001–15,005. doi: 10.1073/pnas.1203636109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ginsberg A. The TB Alliance: overcoming challenges to chart the future course of TB drug development. Future Med Chem. 2011;3(10):1247–1252. doi: 10.4155/fmc.11.82. [DOI] [PubMed] [Google Scholar]
- 12.Jayaram R, Gaonkar S, Kaur P, Suresh BL, Mahesh BN, Jayashree R, Nandi V, Bharat S, Shandil RK, Kantharaj E, Balasubramanian V. Pharmacokinetics-pharmacodynamics of rifampin in an aerosol infection model of tuberculosis. Antimi-crob Agents Chemother. 2003;47(7):2118–2124. doi: 10.1128/AAC.47.7.2118-2124.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jayaram R, Shandil RK, Gaonkar S, Kaur P, Suresh BL, Mahesh BN, Jayashree R, Nandi V, Bharath S, Kantharaj E, Balasubramanian V. Isoniazid pharmacokinetics-pharmacodynamics in an aerosol infection model of tuberculosis. Antimicrob Agents Chemother. 2004;48(8):2951–2957. doi: 10.1128/AAC.48.8.2951-2957.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Shandil RK, Jayaram R, Kaur P, Gaonkar S, Suresh BL, Mahesh BN, Jayashree R, Nandi V, Bharath S, Balasubramanian V. Moxifloxacin, ofloxacin, sparfloxacin, and ciprofloxacin against Mycobacterium tuberculosis: evaluation of in vitro and pharmacodynamic indices that best predict in vivo efficacy. Antimicrob Agents Chemother. 2007;51(2):576–582. doi: 10.1128/AAC.00414-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pasipanodya J, Gumbo T. An oracle: antituberculosis pharmacokinetics-pharmacodynamics, clinical correlation, and clinical trial simulations to predict the future. Antimicrob Agents Chemother. 2011;55(1):24–34. doi: 10.1128/AAC.00749-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ahmad Z, Peloquin CA, Singh RP, Derendorf H, Tyagi S, Ginsberg A, Grosset JH, Nuermberger EL. PA-824 exhibits time-dependent activity in a murine model of tuberculosis. Antimicrob Agents Chemother. 2011;55(1):239–245. doi: 10.1128/AAC.00849-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tasneen R, Williams K, Amoabeng O, Minkowski A, Mdluli KE, Upton AM, Nuermberger EL. Contribution of the nitroimidazoles PA-824 and TBA-354 to the activity of novel regimens in murine models of tuberculosis. Antimicrob Agents Chemother. 2015;59(1):129–135. doi: 10.1128/AAC.03822-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Meibohm B, Derendorf H. Basic concepts of pharmacokinetic/pharmacodynamic (PK/PD) modelling. Int J Clin Pharmacol Ther. 1997;35(10):401–413. [PubMed] [Google Scholar]
- 19.Katsube T, Yamano Y, Yano Y. Pharmacokinetic-pharmacodynamic modeling and simulation for in vivo bactericidal effect in murine infection model. J Pharm Sci. 2008;97(4):1606–1614. doi: 10.1002/jps.21062. [DOI] [PubMed] [Google Scholar]
- 20.Katsube T, Yano Y, Yamano Y, Munekage T, Kuroda N, Takano M. Pharmacokinetic-pharmacodynamic modeling and simulation for bactericidal effect in an in vitro dynamic model. J Pharm Sci. 2008;97(9):4108–4117. doi: 10.1002/jps.21265. [DOI] [PubMed] [Google Scholar]
- 21.Nielsen EI, Cars O, Friberg LE. Pharmacokinetic/pharmacodynamic (PK/PD) indices of antibiotics predicted by a semimechanistic PKPD model: a step toward model-based dose optimization. Antimicrob Agents Chemother. 2011;55(10):4619–4630. doi: 10.1128/AAC.00182-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tan YM, Clewell H, Campbell J, Andersen M. Evaluating pharmacokinetic and pharmacodynamic interactions with computational models in supporting cumulative risk assessment. Int J Environ Res Public Health. 2011;8(5):1613–1630. doi: 10.3390/ijerph8051613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lyons MA, Reisfeld B, Yang RS, Lenaerts AJ. A physiologically based pharmacokinetic model of rifampin in mice. Antimicrob Agents Chemother. 2013;57(4):1763–1771. doi: 10.1128/AAC.01567-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Friedman A, Turner J, Szomolay B. A model on the influence of age on immunity to infection with Mycobacterium tuberculosis. Exp Gerontol. 2008;43(4):275–285. doi: 10.1016/j.exger.2007.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Vaddady PK, Lee RE, Meibohm B. In vitro pharmacokinetic/pharmacodynamic models in anti-infective drug development: focus on TB. Future Med Chem. 2010;2(8):1355–1369. doi: 10.4155/fmc.10.224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Charles River Laboratories Inc. Charles River Laboratories Research Models & Services. 2006 http://www.criver.com.
- 27.Gibaldi M, Perrier D. Pharmacokinetics. Marcel Dekker, Inc; New York, NY: 1982. [Google Scholar]
- 28.Cheng S, Bois FY. A mechanistic modeling framework for predicting metabolic interactions in complex mixtures. Environ Health Perspect. 2011;119(12):1712–1718. doi: 10.1289/ehp.1103510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bernillon P, Bois FY. Statistical issues in toxicokinetic modeling: a Bayesian perspective. Environ Health Perspect. 2000;108(Suppl 5):883–893. doi: 10.1289/ehp.00108s5883. [DOI] [PubMed] [Google Scholar]
- 30.Frantz J. G3data, Version 1.5.2, Software. 2012 https://github.com/pn2200/g3data.git.
- 31.Bauer B, Reynolds M. Recovering data from scanned graphs: performance of Frantz’s g3data software. Behav Res Methods. 2008;40(3):858–868. doi: 10.3758/brm.40.3.858. [DOI] [PubMed] [Google Scholar]
- 32.Chiu WA, Okino MS, Evans MV. Characterizing uncertainty and population variability in the toxicokinetics of trichloroethylene and metabolites in mice, rats, and humans using an updated database, physiologically based pharmacokinetic (PBPK) model, and Bayesian approach. Toxicol Appl Pharmacol. 2009;241(1):36–60. doi: 10.1016/j.taap.2009.07.032. [DOI] [PubMed] [Google Scholar]
- 33.Gelman A, Carlin JB, Stern HS, Rubin DB. Bayesian Data Analysis. 2. Chapman and Hall/CRC; Boca Raton, FL: 2003. [Google Scholar]
- 34.Bois FY, Maszle DR. MCSim: A Monte Carlo simulation program. Journal of Statistical Software. 1997;2(i09):1–60. [Google Scholar]
- 35.R Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing; Vienna, Austria: 2012. http://www.R-project.org. [Google Scholar]
- 36.Plummer M, Best N, Cowles K, Vines K. CODA: Convergence diagnosis and output analysis for MCMC. R news. 2006;6(1):7–11. [Google Scholar]
- 37.van der Graff PH, Benson N. Systems pharmacology: bridging systems biology and pharmacokinetics-pharmacodynamics (PKPD) in drug discovery and development. Pharm Res. 2011;28(7):1460–1464. doi: 10.1007/s11095-011-0467-9. [DOI] [PubMed] [Google Scholar]
- 38.Goutelle S, Bourguignon L, Jelliffe RW, Conte JE, Maire P. Mathematical modeling of pulmonary tuberculosis therapy: Insights from a prototype model with rifampin. J Theor Biol. 2011;282(1):80–92. doi: 10.1016/j.jtbi.2011.05.013. [DOI] [PubMed] [Google Scholar]
- 39.Magombedze G, Garira W, Mwenje E. Mathematical modeling of chemotherapy of human TB infection. J Biol Syst. 2006;14:509–553. [Google Scholar]
- 40.Yang RS, El-Masri HA, Thomas RS, Dobrev ID, Dennison JE, Bae DS, Campain JA, Liao KH, Reisfeld B, Andersen ME, Mumtaz M. Chemical mixture toxicology: from descriptive to mechanistic, and going on to in silico toxicology. Environ Toxicol Pharmacol. 2004;18(2):65–81. doi: 10.1016/j.etap.2004.01.015. [DOI] [PubMed] [Google Scholar]
- 41.Mumtaz M, Fisher J, Blount B, Ruiz P. Application of physiologically based pharmacokinetic models in chemical risk assessment. J Toxicol. 2012;2012:904, 603. doi: 10.1155/2012/904603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Baciewicz AM, Chrisman CR, Finch CK, Self TH. Update on rifampin, rifabutin, and rifapentine drug interactions. Curr Med Res Opin. 2013;29(1):1–12. doi: 10.1185/03007995.2012.747952. [DOI] [PubMed] [Google Scholar]
- 43.Raybon JJ, Pray D, Morgan DG, Zoeckler M, Zheng M, Sinz M, Kim S. Pharmacokinetic-pharmacodynamic modeling of rifampicin-mediated Cyp3a11 induction in steroid and xenobiotic X receptor humanized mice. J Pharmacol Exp Ther. 2011;337(1):75–82. doi: 10.1124/jpet.110.176677. [DOI] [PubMed] [Google Scholar]
- 44.Dooley KE, Flexner C, Andrade AS. Drug interactions involving combination antiretroviral therapy and other anti-infective agents: repercussions for resource-limited countries. J Infect Dis. 2008;198(7):948–961. doi: 10.1086/591459. [DOI] [PubMed] [Google Scholar]
- 45.Rowland M, Peck C, Tucker G. Physiologically-based pharmacokinetics in drug development and regulatory science. Annu Rev Pharmacol Toxicol. 2011;51:45–73. doi: 10.1146/annurev-pharmtox-010510-100540. [DOI] [PubMed] [Google Scholar]
- 46.Gonzalez-Juarrero M. Immunity to TB and targets for immunotherapy. Immunotherapy. 2012;4(2):187–199. doi: 10.2217/imt.11.168. [DOI] [PubMed] [Google Scholar]
- 47.Gonzalez-Juarrero M, Woolhiser LK, Brooks E, DeGroote MA, Lenaerts AJ. Mouse model for efficacy testing of antituberculosis agents via intrapulmonary delivery. Antimicrob Agents Chemother. 2012;56(7):3957–3959. doi: 10.1128/AAC.00464-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Srivastava S, Gumbo T. In vitro and in vivo modeling of tuberculosis drugs and its impact on optimization of doses and regimens. Curr Pharm Des. 2011;17(27):2881–2888. doi: 10.2174/138161211797470192. [DOI] [PubMed] [Google Scholar]
- 49.de Steenwinkel JE, Aarnoutse RE, de Knegt GJ, Ten Kate MT, Teulen M, Verbrugh HA, Boeree MJ, van Soolingen D, Bakker-Woudenberg IA. Optimization of the rifampin dosage to improve the therapeutic efficacy in tuberculosis treatment, using a murine model. Am J Respir Crit Care Med. 2013 doi: 10.1164/rccm.201207-1210OC. [DOI] [PubMed] [Google Scholar]
- 50.Radboud University. ClinicalTrials.gov [Internet] Bethesda (MD): National Library of Medicine (US); 2013. Pharmacokinetics and pharmacodynamics of high versus standard dose rifampicin in patients with pulmonary tuberculosis (High RIF) Available from:. http://clinicaltrials.gov/ct2/show/results/NCT00760149, nLM Identifier: NCT00760149. [Google Scholar]
- 51.Radboud University. ClinicalTrials.gov [Internet] Bethesda (MD): National Library of Medicine (US); 2014. Safety, tolerability, extended early bactericidal activity and PK of higher doses rifampicin in adults with pulmonary TB (HR1) Available from:. http://clinicaltrials.gov/ct2/show/results/NCT00760149, nLM Identifier: NCT00760149. [Google Scholar]
- 52.McCune RM, Tompsett R. Fate of Mycobacterium tuberculosis in mouse tissues as determined by the microbial enumeration technique. I. The persistence of drug-susceptible tubercle bacilli in the tissues despite prolonged antimicrobial therapy. J Exp Med. 1956;104(5):737–762. doi: 10.1084/jem.104.5.737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Craig WA. Pharmacokinetic/pharmacodynamic parameters: rationale for antibacterial dosing of mice and men. Clin Infect Dis. 1998;26(1):1–10. doi: 10.1086/516284. [DOI] [PubMed] [Google Scholar]
- 54.Hoff DR, Ryan GJ, Driver ER, Ssemakulu CC, De Groote MA, Basaraba RJ, Lenaerts AJ. Location of intra- and extracellular M. tuberculosis populations in lungs of mice and guinea pigs during disease progression and after drug treatment. PLoS ONE. 2011;6(3):e17, 550. doi: 10.1371/journal.pone.0017550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Dhar N, McKinney JD. Microbial phenotypic heterogeneity and antibiotic tolerance. Curr Opin Microbiol. 2007;10(1):30–38. doi: 10.1016/j.mib.2006.12.007. [DOI] [PubMed] [Google Scholar]
- 56.Rocco A, Kierzek AM, McFadden J. Slow protein fluctuations explain the emergence of growth phenotypes and persistence in clonal bacterial populations. PLoS ONE. 2013;8(1):e54, 272. doi: 10.1371/journal.pone.0054272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Wakamoto Y, Dhar N, Chait R, Schneider K, Signorino-Gelo F, Leibler S, McK-inney JD. Dynamic persistence of antibiotic-stressed mycobacteria. Science. 2013;339(6115):91–95. doi: 10.1126/science.1229858. [DOI] [PubMed] [Google Scholar]
- 58.Gumbo T, Louie A, Deziel MR, Liu W, Parsons LM, Salfinger M, Drusano GL. Concentration-dependent Mycobacterium tuberculosis killing and prevention of resistance by rifampin. Antimicrob Agents Chemother. 2007;51(11):3781–3788. doi: 10.1128/AAC.01533-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Geli P, Andersson M, Svensson A, Andersson DI. A multi-type branching model with varying environment for bacterial dynamics with postantibiotic effect. J Theor Biol. 2009;256(1):58–64. doi: 10.1016/j.jtbi.2008.09.023. [DOI] [PubMed] [Google Scholar]
- 60.Geli P. Modeling the mechanism of postantibiotic effect and determining implications for dosing regimens. J Math Biol. 2009;59(5):717–728. doi: 10.1007/s00285-009-0249-8. [DOI] [PubMed] [Google Scholar]
- 61.Lenaerts AJ, Gruppo V, Brooks JV, Orme IM. Rapid in vivo screening of experimental drugs for tuberculosis using gamma interferon gene-disrupted mice. Antimicrob Agents Chemother. 2003;47(2):783–785. doi: 10.1128/AAC.47.2.783-785.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Pan H, Yan BS, Rojas M, Shebzukhov YV, Zhou H, Kobzik L, Higgins DE, Daly MJ, Bloom BR, Kramnik I. Ipr1 gene mediates innate immunity to tuberculosis. Nature. 2005;434(7034):767–772. doi: 10.1038/nature03419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Flynn JL. Lessons from experimental Mycobacterium tuberculosis infections. Microbes Infect. 2006;8(4):1179–1188. doi: 10.1016/j.micinf.2005.10.033. [DOI] [PubMed] [Google Scholar]