Abstract
White matter (WM) lesions are thought to play an important role in multiple sclerosis (MS) disease burden. Recent work in the automated segmentation of white matter lesions from MRI has utilized a model in which lesions are outliers in the distribution of tissue signal intensities across the entire brain of each patient. However, the sensitivity and specificity of lesion detection and segmentation with these approaches have been inadequate. In our analysis, we determined this is due to the substantial overlap between the whole brain signal intensity distribution of lesions and normal tissue. Inspired by the ability of experts to detect lesions based on their local signal intensity characteristics, we propose a new algorithm that achieves lesion and brain tissue segmentation through simultaneous estimation of a spatially global within-the-subject intensity distribution and a spatially local intensity distribution derived from a healthy reference population. We demonstrate that MS lesions can be segmented as outliers from this intensity model of population and subject (MOPS). We carried out extensive experiments with both synthetic and clinical data, and compared the performance of our new algorithm to those of state-of-the art techniques. We found this new approach leads to a substantial improvement in the sensitivity and specificity of lesion detection and segmentation.
I. INTRODUCTION
Multiple Sclerosis (MS) is a chronic demyelinating disease of the central nervous system (CNS). It is the major cause of non-traumatic neurological disability in young adults in North America and Europe, affecting more than 2.5 million individuals. The pathological hallmark of MS is the presence of focal areas of inflammatory-mediated demyelination of the brain and spinal cord white matter [1]. Although the cause of MS is still unknown, several reports suggest the disease may be caused by the complex interplay among genetic, environmental and immunological factors.
Since magnetic resonance imaging (MRI) was introduced in the early 1980s to diagnose and assess MS, MRI has become the primary imaging modality to monitor the natural history of the disease and to evaluate the efficacy of treatment in longterm therapeutic studies. Post-mortem studies showed a close relationship between lesions seen on T2-weighted (T2w) MRI and plaques of MS [2], [3]. MRI has become a valuable tool for the assessment of patients with MS, aiding in forming a diagnosis [4], monitoring disease progression [5] and assessing disease burden [6].
Focal MS lesions on conventional T2w brain images appear as bright areas, with a diameter larger than 3mm [4], and are often referred to as T2-hyperintense lesions. Hyperintensities in the brain are more common in the WM regions, the inner surface of the corpus callosum, the juxtacortical gray-white junction, the infratentorial brain regions, and the spinalcord [7]. Some of the T2-hyperintense lesions may resolve and fade over time [8]. T2-hyperintense lesions in patients with MS are nonspecific for the underlying pathology, which may include varying degrees of inflammation, demyelination, gliosis, edema, Wallerian degeneration, and axonal loss. A subset of T2-hyperintense MS lesions may appear hypointense on corresponding T1-weighted images.
Quantitative data in MS is essential to understanding the natural history of the disease and to monitoring the effects of available therapies. Conventional MRI-based measures [9] includes CNS atrophy [10] and MS lesion counting (e.g., T2w hyperintense lesion count). In numerous clinical trials, the assessment of MRI lesion load has provided an effective measure of disease. However, the quantitative analysis of lesion load is not without difficulties. For example, because the natural change in lesion load year-to-year is generally small, variations in lesion-load measurements must be reduced as much as possible. Ideally, measurement errors should be significantly less than the natural variability that occurs in individual patients over time [11].
Standard image analysis methods currently utilized in clinical trials are largely manual. Manual segmentation is difficult, time-consuming and costly. Errors occur due to low lesion contrast and unclear boundaries caused by changing tissue properties and partial volume effects. Segmentation inconsistencies are common even among qualified experts. Many studies have investigated the wide variability inherent to manual MS lesion segmentation, finding an inter-rater volume variability of 14% and an intra-rater volume variability of 6.5% [12]. Furthermore, during the third year of a longitudinal interferon beta-1b study [13], the authors attributed a significant decrase in MS lesion volume to a methodological change applied by a single observer who performed the measurements. Because the same change was applied consistently to all scans, it did not affect the intergroup differences that were identified, but it stressed the need for rigorous quality control checks during long-term studies.
Validation of segmentation in medical imaging is a challenging task due to the scarcity of an appropriate reference standard to which results of any segmentation approach can be compared. Comparing the results of segmentation to histology is helpful, but rarely available for clinical data, and relating histology to MRI can be difficult [14]. Consequently, validation studies typically rely on expert evaluation of the imaging data. Given the intra- and inter-expert variability of manual segmentation, it is challenging to distinguish which dissimilarities between manual and automatic segmentations are caused by errors in the segmentation algorithm or by variability in the manual segmentation.
Given that expert measurements are highly variable, any validation should always evaluate automatic segmentation accuracy against a series of repeated measurements by multiple-experts. These multiple expert segmentations can be combined using STAPLE [15] which provides an optimal weighting of each expert segmentation based on the comparison of each segmentation to a hidden reference standard segmentation. The confidence of the expert performance estimates can also be estimated [16], indicating whether or not sufficient data is available to have high confidence in both the reference standard and the expert performance assessments. Ultimately, the best automated segmentation algorithm should have an accuracy similar to that of the best expert segmentations, but with higher reproducibility.
To reduce the intra- and inter-rater variability inherent in manual lesion segmentation, many semiautomatic methods have been proposed. However, these algorithms require the human rater to first identify the location of each lesion, and then estimate lesion boundaries based on a local intensity threshold [12], region growing [17], fuzzy connectedness [18], intensity gradient [19] or statistical shape priors [20]. Although semiautomatic lesion segmentation has demonstrated reduced intra-rater variability, inter-rater variability is still an issue due to the initialization by manual lesion identification. Given this, there is a significant need for an automated method for MR brain image quantification that can analyze large amounts of multi-spectral MR data in a reproducible way while correlating closely with expert image analyses.
The development of fully automated MS lesion segmentation methods has been an area of vigorous research in the medical imaging community over the past 20 years [21]. Techniques for automated MS lesion segmentation generally modify intensity-based classifiers (originally applied to tissue segmentation in the healthy adult brain) to model brain abnormalities on MRI as an additional class. Kamber et al. [22] proposed a model that compensated for the tissue class intensity overlap by using a probabilistic model of the location of MS lesions. By confining the search for MS lesions to those regions with at least a 50% prior probability of being white matter, the incorrect classification of grey matter as MS lesion was significantly reduced. Wells et al. [23] used a Parzen Estimator and bias field correction to identify major brain tissues and separate them from the lesions. A similar approach is proposed by [24] where a Parzen density estimator is used to classify the major brain tissues and an elastically registered template is used to distinguish the healthy gray matter (GM) from WM combined with MS lesions. Lesions are then separated from WM using a minimum distance classifier. In [25], the classifier intensity feature space was extended by using a distance map generated from an anatomical template. This method iterates between kNN classification and elastic registration of the digital template to the hard segmentation of the MS brain generated by the classifier to refine the segmentation of structures and lesions. Zijdenbos et al. [26] developed an automatic pipeline based on a supervised Artificial Neural Network (ANN) classifier and validated it extensively on a multi-center clinical trial. To improve the accuracy of MS lesion segmentation, Wei et al. [27] combined the statistical classification obtained using [23] with the anatomical context provided by a tissue atlas that explicitly modeled the distribution of tissues within the patients brain [25], and an heuristic connectivity-based partial volume effect correction component [28]. Wu et al. [29] extended this approach to segment MS lesions into three subtypes (gadolinium-enhancing lesions, T1 black holes and T2 hyperintense lesions).
More recently, Shiee et al. [30] proposed a topologically consistent MS brain tissue segmentation algorithm. Geremia et al. [31] proposed an MS lesion segmentation algorithm based on a discriminative random decision forest. The method uses multi-channel MR intensities (i.e., T1w, T2w and FLAIR scans), as well as a symmetry feature.
In Van Leemput et al. [32] an approach was proposed where MS lesions were modeled as intensity outliers with respect to a global gaussian mixture model (GMM) initialized by an aligned probabilistic tissue atlas. Such probabilistic tissue atlases are generated by registering a large number of subjects together, assigning voxels to different tissue types, and averaging tissue classes over subjects, irrespective of their intensity. Similarly, [33] used a trimmed likelihood estimator (TLE) to estimate a 10-component GMM and then modeled MS lesions as GM intensity outliers on an enhanced FLAIR image. Additional methods further combine a TLE with a mean shift algorithm [34] or a hidden markov chain [35].
Any such segmentation algorithm estimates an optimal boundary between tissue types on a given feature space. Thus, tissue classification relies on contrast between tissue types (e.g., WM and MS lesions) on a particular feature space. All state-of-the-art, fully automatic MS lesion segmentation algorithms described above are based on the MS patient, MRI-derived, intensity feature space (Figure 1). It has been previously described how the MS lesion intensity distribution overlaps with that of healthy tissue [22], [24]. This limitation, in turn, results in MS lesion segmentation that is generally inaccurate.
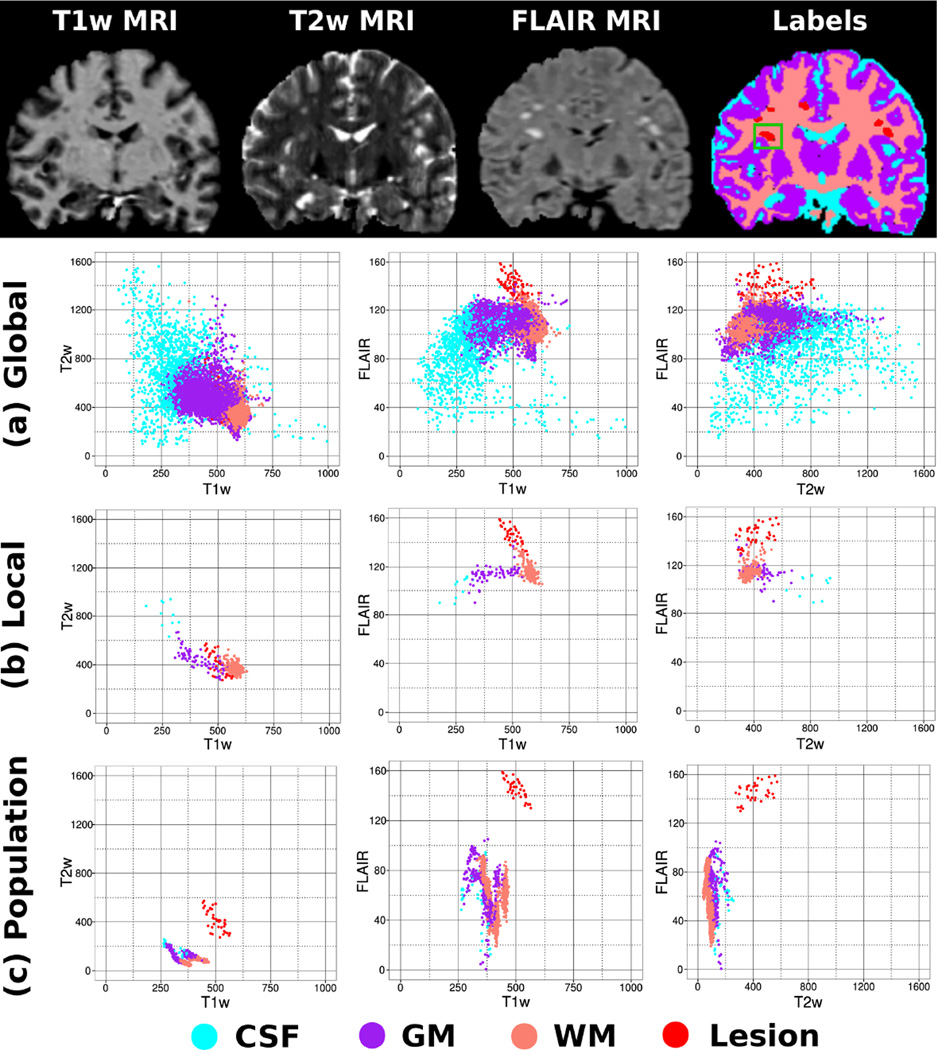
Fig. 1.
Comparison between a tissue intensity scatterplot derived from (a) the subject under analysis, (b) the local neighbourhood delimited by the green square and derived from (c) an aligned reference healthy population. First row: Coronal slice (T1w, T2w and FLAIR) of an MS patients brain and the corresponding tissue segmentation (GM, WM, CSF and MS lesions). Second row: Tissue intensity scatterplot derived from the MS patients brain MRIs. Third row: Tissue intensity scatterplot derived from the MS patients brain MRI region delimited by the green box. Fourth row: Tissue intensity scatterplot estimated in the green bounding box from an aligned healthy reference population. In this case, the red dots correspond to the intensities of the MS lesion surrounded by the green box. It is apparent that the local intensity from a reference population offers a better lesion intensity separation than that obtained by either global or local intensity distribution derived from the subject under study.
Approaches aimed at reducing the extent of lesion false positives are usually based on post-processing steps; namely, experimentally tuned morphological operators, connectivity rules, and minimum size thresholds, among others. Due to the heterogeneous intensity profile of MS lesions, however, these post-processing steps may have to be re-tuned based on the individual features of each case, or tailored to different subjects for varying degrees of lesion burden.
To address these limitations, we propose augmenting the imaging data used to identify lesions to include both an intensity model of the patient under consideration and a collection of intensity and segmentation templates that provide a model of normal tissue. We call this combination a Model of Population and Subject (MOPS) intensities. Unlike the classical approach where lesions are characterized by their intensity distribution compared to all brain tissues, MOPS aims to distinguish locations in the brain with an abnormal intensity level when compared with the expected value in the same location in a healthy reference population (Figure 1c). This is achieved by a tissue mixture model which combines the MS patient global tissue intensity model with a population local tissue intensity model derived from a reference database of MRI scans of healthy subjects.
II. MATERIAL & METHODS
In this section, we first recap the well-established global GMM model of brain tissue segmentation explored in several works including [23]. We then introduce a local intensity prior probability and spatial tissue class prior estimated from a healthy reference population. These two models form the foundation of our coupled local and global GMM tissue model introduced in Section II-D. Section II-E describes the algorithm that detects MS lesions. Finally, we describe the Brainweb and MS Grand Challenge datasets, widely used in the evaluation of state-of-the-art MS lesion segmentation algorithms, used to evaluate the proposed algorithm.
A. Reference Population
We collected data from 15 volunteers on a 3T clinical MR scanner from GE Medical Systems (Waukesha, WI, USA) using an 8-channel receiver head coil and three different pulse sequences: a T1-weighted MPRAGE (Magnetization Prepared Rapid Acquisition Gradient Echo) sequence; a T2-weighted scan from an FSE (Fast Spin Echo) sequence; and a FLAIR scan, also run with an FSE sequence. We acquired the T1w sequence axially; the T2w and FLAIR sequences were sagitally acquired. All sequences were acquired with a matrix size of 256x256 and a field of view of 28 cm. Slice thickness was 1.3 mm for the T1w-MPRAGE sequence; 1 mm for the T2w-FSE sequence; and 2 mm for the FLAIR-FSE sequence. The MPRAGE parameters were TR 10/TE 6 ms with a flip angle of 8. For the FSE, the paramenters were TR 3000/TE 140 ms with an echo train length of 15.
After image acquisition, we aligned the T2w and FLAIR images to the T1w scan. Last, a trained expert manually segmented the intra-cranial volume, CSF, GM and WM tissues [36].
To achieve accurate alignment between healthy volunteers and a patient with MS, we used the nonlinear registration algorithm proposed by [37], which, although not intrinsic to our method, was selected because it is robust in the presence of WM lesions. We note, however, that other non-linear registration approaches are compatible with our technique [38], [39].
The MRI intensity scale in conventional structural imaging has no absolute, physical meaning. Instead, images are formed with contrast related to spin density as well as T1 relaxation and T2 relaxation, yet without quantifying the precise value of these parameters. As a consequence, image intensities and contrast are dependent on the particular pulse sequence, static magnetic field strength, and imaging parameter settings such as flip angle.
For accurate and reproducible segmentation, it is important that the location of boundaries between structures in the images can be detected, despite potential variations in signal intensity. This can be achieved by creating new images in which the intensities between subjects are at comparable levels. For this purpose, we used a linear transformation to find a match between the median intensity of each modality and reference subject, and those found in the scans of the subject of interest.
B. Global GMM MRI Brain Tissue Segmentation
Consider a multispectral grayscale MRI (i.e., T1w, T2w and FLAIR) formed by a finite set of N voxels. Our aim is to assign each voxel i to one of K classes (i.e., GM, WM and CSF) considering the observed intensities Y = {y1, …, yN} with yi ∈ ℝm. Both observed intensities and hidden labels are considered to be random variables denoted respectively as Y = {Y1, …, YN} and Z = {Z1, …, ZN}. Each random variable Zi = ek = {zi1, …, ziK} is a K-dimensional vector with each component zik being 1 or 0 according whether Yi did or did not arise from the kth class.
It is assumed that the observed data Y is described by the conditional probability density function f(Y|Z,φY), which incorporates the image formation and noise models and depends on some parameters φY. In addition, the hidden labels are assumed to be drawn according to a certain parametric probability distribution f(Z|φZ), which depends on parameters φZ.
To segment the observed image Y is to propose an estimate Ẑ of Z on the basis of Y. To this end, the parameter ψ = {φz1,…,φZK;φY1, …, φYK} must be estimated in some manner. If the underlying tissue segmentation Z was known, estimation of the model parameters would be straightforward. However, only the image Y is directly observed, making it necessary to tackle this problem as one involving missing data. The Expectation-Maximization (EM) algorithm is the best candidate for model fitting. The EM algorithm finds the parameters that maximize the complete data log-likelihood by iteratively maximizing the expected value of the log-likelihood log(f(Y, Z|ψ)) of the complete data {Y, Z}, where the expectation is based on the observed data Y and the estimated parameters ψ(m) obtained in the previous iteration m.
E-Step: The E-step requires the computation of the conditional expectation of log (LC(ψ)) given Y, using ψ(m) for ψ, which can be written as
As the complete-data log likelihood, log LC(ψ), is linear in the hidden labels zij, the E-Step simply requires the calculation of the current conditional expectation of Zi given the observed data Y. Then:
that corresponds to the posterior probability that the ith member of the sample belongs to the j class.
M-Step: The M-step on the mth iteration requires the maximization of Q(ψ; ψ(m)) with respect to ψ over the parameter space to give the updated estimate ψ(m+1).
The mixing proportions πk are calculated as follows:
The update of φy on the M-step of the (m + 1)th iteration is estimated by maximizing log LC(φ) with respect φy:
Consider that f(Yi|Zi = ek, φYk) is described by a Gaussian distribution parametrized by φYk = {μk, Σk}
with μk and Σk being respectively the intensity mean vector and covariance matrix for tissue k. Thus, the update equations may be written as:
C. Local Reference Population GMM Intensity Tissue Model
Consider a reference population P formed by R healthy subjects aligned to the subject of interest. Each reference subject is composed by a multispectral grayscale MRI V (i.e., T1w, T2w and FLAIR) and the corresponding tissue segmentation L (i.e., GM, WM and CSF), thus P = {V, L} = {V1, …, VR; L1, …, LR}. Each reference grayscale MRI Vr = {Vr1, …, VrN} is formed by a finite set of N voxels with Vri ∈ ℝm. Also, each reference tissue segmentation Lr = {Lr1, …, LrN} is formed by a finite set of N voxels with Lri = ek = {lri1, …, lriK} is a K-dimensional vector with each component lrik being 1 or 0 according whether Vri did or did not arise from the kth class.
At each voxel i, the reference population P intensity distribution will be modeled as a Gaussian Mixture Model parametrized by ξi = {πPi; μPi, ΣPi}. Where πPi, μPi and ΣPi are respectively the population tissue mixture vector, the population mean intensity vector and the population intensity covariance matrix at voxel i. Because {V, L} are observed variables, ξi can be derived using the following expressions:
| (1) |
| (2) |
| (3) |
where p(Lij = ek) is the probability of voxel i of the jth reference subject belong to tissue k given by Lj, and 𝒩ℛ is the neighborhood centered in voxel i of radius ℛ voxels.
Once the local tissue model is estimated from P, the intensity likelihood of Y can be derived as:
with f(Zi = ek|ξik) = πPik.
D. Coupling Global and Local Models
Consider that, in addition to the patient scan Y, we observe an aligned reference of R healthy subjects P = {V, L} = {V1, …, VR; L1, …, LR}.
As in Section II-B, segmenting the observed data Y implies the estimation of parameters ψ.
The observed population data P is conditionlly independent of the observed patient scan Y formation model parametrized by ψ.
| (4) |
Since the underlying tissue segmentation Z is unknown, the EM algorithm will be used to find the parameters that maximize the complete log-likelihood.
E-Step: The E-step requires the computation of the conditional expectation of log (LC(ψ)) given Y and P, using the current parameter estimate ψ(m).
As in Section II-B, the complete log-likelihood is linear in the hidden labels zij. Again, the E-step requires the calculation of the current conditional expectation of Zi given the observed data Y:
| (5) |
M-Step: Because the local reference population model parameter ξ is constant, the Maximization step will consist of the maximization of Q(ψ; ψ(m)) with respect to ψ, which results in the same update equations obtained in Section II-B.
| (6) |
| (7) |
| (8) |
In order to be robust to the presence of outliers, we used a trimmed likelihood estimator (TLE) to estimate ψ. The TLE was proposed as a modification of the Maximum Likelihood Estimator in the presence of outliers in the observed data [40]. Using the TLE, the complete log-likelihood (4) can be expressed as:
where for a fixed ψ, f(Yv(1) , Znu(1)|ψ, ξ1) ≤ … ≤ f(Yv(N), Znu(N) | ψ, ξN) for i = 1, …, N. With v = v(1), …, v(N) being the corresponding permutation of indices sorted by their probability f(Yv(i), Pv(i), Zv(i)|ψ), and h is the trimming parameter corresponding to the percentage of values included in the parameter estimation. In other words, now the likelihood is only computed using the voxels that are more likely to belong to the proposed model.
The TLE was computed using the FAST-TLE algorithm, in which iteratively the N – h voxels with the highest estimated likelihood according to (4) were selected to estimate ψ(m+1) using the update equations (6), (7), (8). These two steps were iterated until convergence.
E. MS Lesion Detection
Based on (4), it follows intuitively that the local intensity model downweights the likelihood of those voxels having an abnormal intensity given the reference population. Since MRI structural abnormalities will show an abnormal intensity level compared to similarly located brain tissues in healthy subjects, we seek to identify MS lesions by searching for areas with low likelihood LC(ψ) (Figure 2).
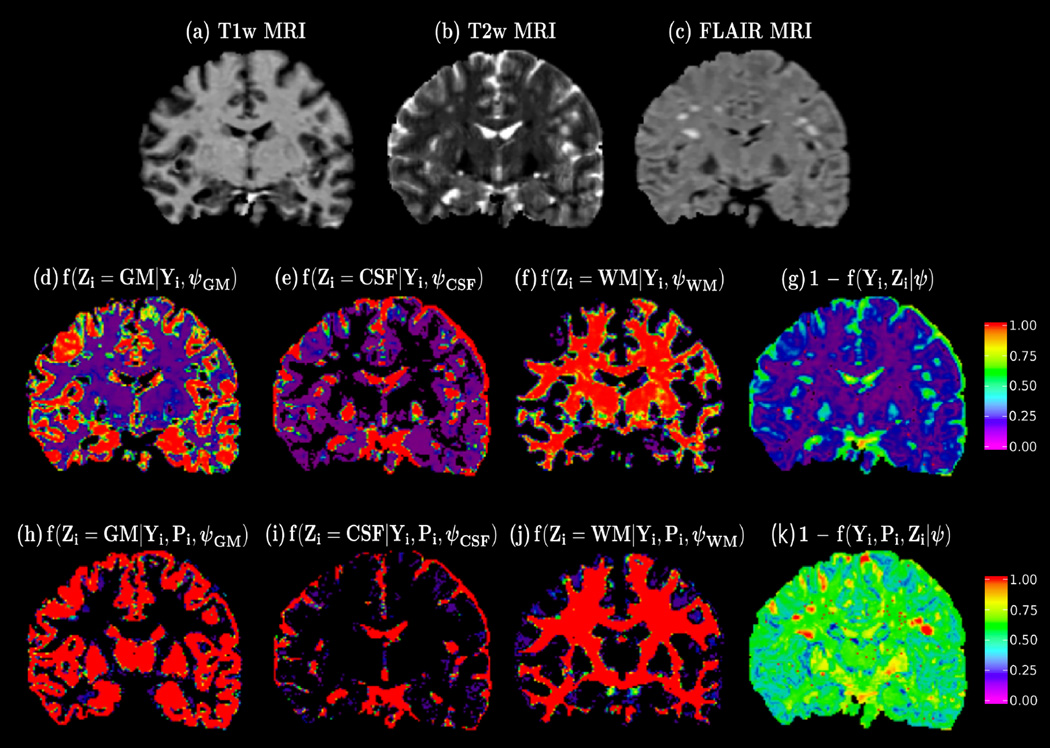
Fig. 2.
Top row: Coronal slice of a patient with MS, (a) T1w MRI, (b) T2w MRI and (c) FLAIR MRI. Middle row: (d,e,f) maximum a posteriori (MAP) tissue probabilities and (g) voxel lesion probability estimated using a global intensity model. Bottom row: (h,i,j) MAP tissue probabilities and (j) voxel lesion probability estimated using MOPS. Observe the improved MS lesion sensitivity of the voxel lesion probability derived from our proposed model (k) compared to the one achieved by a global intensity model (g).
We define a voxels lesion probability as 1–f(Yi, Pi, Zi|ψ). We obtained a set of MS lesion candidate voxels C by selecting those voxels with a lesion probability greater than a given decision threshold (1 – f(Yi, Pi, Zi|ψ) > threshold).
1) MS WM T2w Hyperintense Lesion Segmentation by Graph-Cuts
Structural MRI from MS patients is not only sensitive to WM T2 hyperintense lesions, but also to cortical lesions [41], basal ganglia T2 hypointensities [42], dirty-appearing WM [43] and WM T1w hypointense lesions [44], among others. We used a Graph-Cuts algorithm to classify the set of MS lesion candidate voxels C into WM T2w hyperintense lesions or other MS structural abnormalities.
Let C be the set of all MS lesion candidate voxels, and consider the neighborhood system represented by a set 𝒩 of all pairs {c, d} of neighboring elements in C. Also consider ℒ = ℒ1, …, ℒC to be a binary vector whose components ℒc specify assignments to pixels c in C. Vector ℒ defines a segmentation where each ℒc can be either classified as WM T2 hyperintense MS lesions (𝒪) or other MS abnormalities (ℬ). The energy function we aim to minimize with the graph cut [45] has the form:
| (9) |
The term RC (Vc), referred to as the regional term, expresses how the voxel c fits into given models of the object and background and is encoded in the graph through the t-links. The coefficient λ ≥ 0 specifies the relative importance of the region properties term versus the boundary properties term. Consider that RC (·) reflects on the manner in which the intensity of pixel c fits into given Gaussian models of WM T2 hyperintense MS lesions and other abnormalities:
where yc is the intensity vector of voxel c, {μ𝒪, Σ𝒪} and {μℬ, Σℬ} are respectively the intensity mean and covariance matrices which parametrize the respective WM T2 hyperintense MS lesions and other MS abnormalities Gaussian intensity models.
The WM T2 hyperintense MS lesions and other MS abnormalities Gaussian model parameters were initialized using the partition of C obtained by estimating an Otsu threshold [46] using the FLAIR scan of the MS patient. The partition with the highest intensity was used to initialize the gaussian model parameters for the WM T2 hyperintense MS lesions.
The term B{c,d}, known as the boundary term, reflects the similarity of the voxels c and d. Hence, the n-links that connect the neighboring voxels are comparatively large when c and d are similar but close to zero otherwise. To compute these n-links, we used the following function:
| (10) |
This function penalizes for discontinuities between voxels of different intensities, as well as voxels located in different regions.
The max-flow algorithm proposed in [47] was used to compute the optimal cut of the described graph.
F. Evaluation Datasets
We evaluated our MS lesion segmentation algorithm using both synthetic and clinical data.
1) BrainWeb Synthetic Dataset
BrainWeb is a synthetic brain phantom developed by the McConnell Brain Imaging Center (Montreal, Qc. Canada). It contains a set of realistic MRI data volumes produced by an MRI simulator [48].
The MS brain phantom is based on the healthy phantom, which have been added MS lesions to obtain three MS phantoms with different MS lesion volumes: mild (0.4cm3), moderate (3.5cm3) and severe (10.1cm3). Full 3D MRI scans have been simulated using three sequences (T1w, T2w and PD weighted) and a variety of noise and intensity non-uniformity levels. The MS BrainWeb dataset allows the evaluation of any MS lesion segmentation algorithm in a setting where the ground truth is known.
2) MS Grand Challenge Clinical Dataset
At the 2008 MS lesion segmentation challenge held during the Medical Imaging Computing and Computer Assisted Intervention conference (MICCAI 2008) [49], the University of North Carolina at Chapel Hill (UNC) and Boston Childrens Hospital (BCH) released a publically available clinical database of MS MRI scans1 that contains anatomical MRI scans from 51 subjects with MS. Each case in this database is comprised of a single T1w, T2w, and FLAIR MRI scan. All scans were re-oriented to axial orientation, and the T2w and FLAIR scans were rigidly registered to the corresponding T1w image. Scans were re-sliced at a 0.5 × 0.5 × 0.5mm resolution with cubic spline interpolation.
Due to the presence of intensity inhomogeneity artifacts and noise in the MRI scans, in advance of further analysis both patients with MS and healthy volunteers scans were processed to compensate for the effect of intensity inhomogeneity [50] as well as for thermal noise [51].
Images from MS patients were placed into two groups: a 20-subject training group and a 31-subject testing group, which was the balance of the original 51 subject study cohort. MS lesion manual reference data was only available for those subjects in the training group. Organizers retained and withheld access to the manual lesion segmentations from the testing group. To evaluate the performance of participant segmentation algorithms, competitors were asked to upload their automatic segmentations of the testing data into the challenge website2 where they were automatically evaluated. Results for each of the competitor algorithms on the testing data are publicly available, allowing for a truly objective comparison.
III. RESULTS
A. Synthetic Data Evaluation
Using the BrainWeb T1w and T2w MR images with 3% noise and 20% inhomogeneity with the three available lesion loads (mild, moderate and severe), and fixing the local neighborhood size R to a value of 2 voxels; multiple MS T2w hyperintense lesion segmentations were obtained with our combined mixture model (Section II-D) with varying voxel lesion probability threshold values 1 – f(Yi, Pi, Zi|ψ) > threshold. Additionally, another set of MS T2w hyperintense lesion segmentations were generated using the global mixture model (Section II-B) with varying voxel lesion probability threshold values 1 – f(Yi, Zi|ψ) > threshold.
The resulting lesion segmentations were compared to the BrainWeb MS lesion ground truth by means of the lesion true positive rate (LTPR), lesion false positive rate (LFPR), sensitivity and specificity . A lesion in the manual reference segmentation is considered detected when any part of it is present in the automatic segmentation. The LTPR is thus measured by dividing the number of detected lesions in the segmentation that overlap with a lesion in the reference segmentation by the number of overall lesions in the manual reference segmentation. By contrast, the LFPR is measured by dividing the number of lesions in the segmentation that do not overlap with any lesion in the reference segmentation with the number of overall lesions in the segmentation.
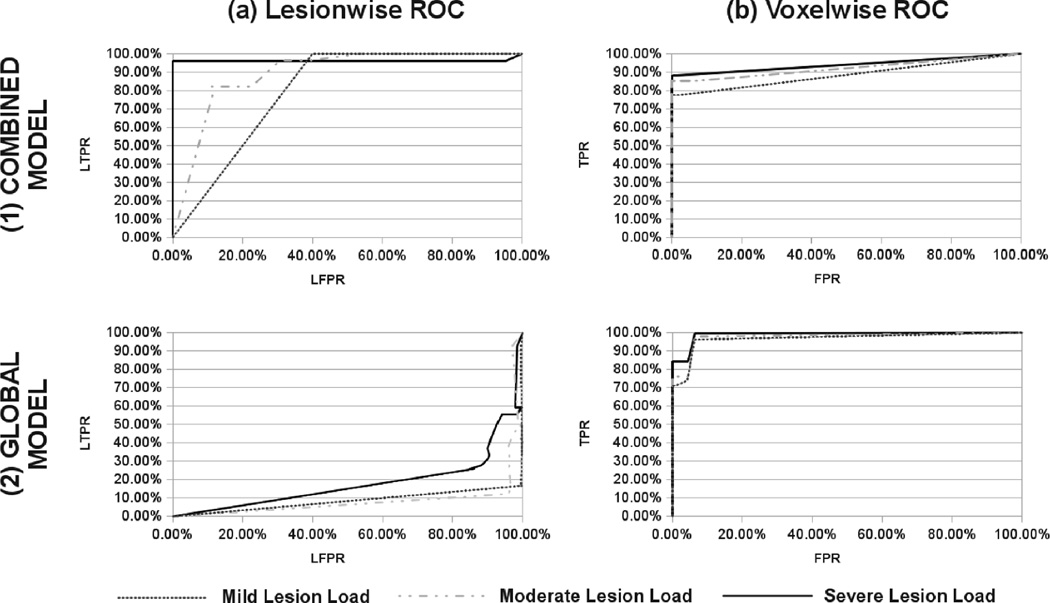
Figure 3 shows the receiver operating curve (ROC) for our combined intensity model classifier (Fig.3.(1)) and a global intensity model classifier (Fig.3.(2)) using both lesionwise (LTPR and LFPR) and voxelwise (Sensitivity and Specificity) metrics. As expected, due to the significant overlap between the global intensity distribution of MS lesions and those of healthy tissues, our proposed algorithm achieved a better lesion detection rate while maintaining a lower lesion false positive rate (Fig.3.(1a) and Fig.3.(2a)). It can also be seen that our algorithm not only detects more MS lesions from the ground truth, but is also more sensitive and specific for lesion voxels (Fig.3.(1b) and Fig.3.(2b)).
Fig. 3.
MS lesion segmentation ROC comparison between our combined local/global intensity model and a global intensity model for three different lesion load atlases (mild, moderate and severe lesion load). Given a fixed complete likelihood threshold, both lesionwise metrics (1a and 2a) and voxelwise metrics (1b and 2b) show our MS lesion segmentation to be more sensitive and specific than those achieved by a global intensity model.
Based on a neighborhood size of ℛ = 2 voxels and the optimal complete likelihood threshold chosen by the evaluation of the ROC curve in Fig.3, we compared the MS lesion segmentation achieved by our combined intensity model with a global intensity model under different conditions of noise and intensity inhomogeneity. Estimated MS lesion segmentation was compared to the ground truth by means of the dice similarity coefficient [52] between the automatic segmentation and the BrainWeb ground truth.
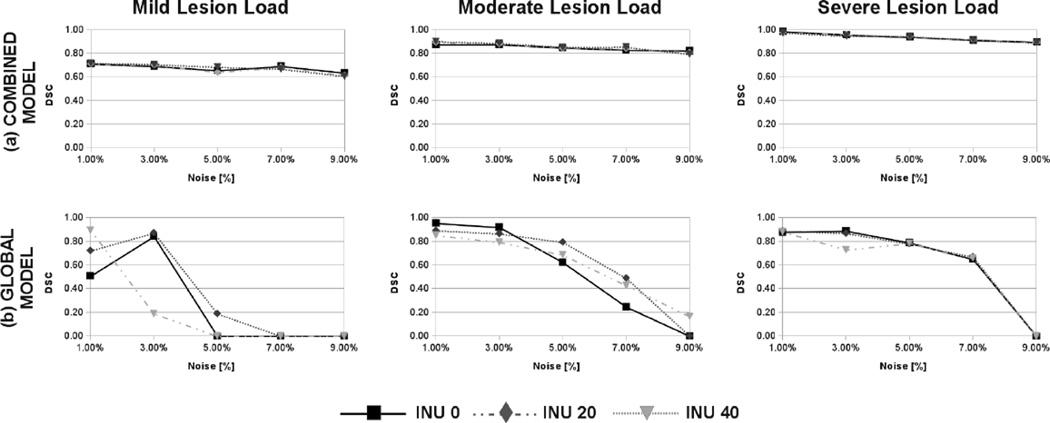
Results in Fig.4 show that our combined intensity model is robust to the presence of noise and intensity inhomogeneity artifact in the image while achieving a comparable or superior DSC than that achieved by the MS lesion segmentation based in a global intensity model.
Fig. 4.
BrainWeb MS lesion DSC for mild, moderate and severe lesion load for different levels of noise and intensity inhomogeneity using our combined intensity model (a) and a global intensity model (b). For any lesion load our MS lesion segmentation algorithm is more robust to the presence of noise and intensity inhomogeneity in the scans than the subject global model.
B. Clinical Data Evaluation
1) MS Grand Challenge Training Results
By fixing the neighborhood size ℛ = 2 voxels, for each subject in the Grand Challenge training dataset, two different sets of MS lesion segmentations were generated with varying threshold values on the complete likelihood estimated using our proposed combined intensity model f(Y, P, Z|ψ) and a global intensity model f(Y, Z|ψ), respectively.
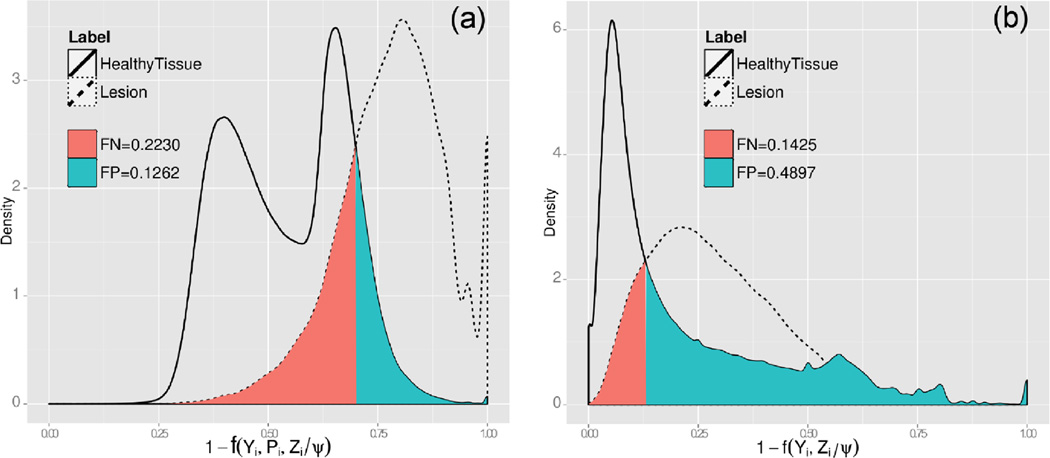
Using the manual MS lesion segmentation reference, we estimated the voxel lesion probability density function for healthy voxels and lesion voxels for both our combined intensity model and the global intensity model. As a result of the existing intensity overlap between healthy tissues and MS lesions, the classifier based in the global intensity model misclassified 48% of healthy tissue voxels as lesions, whereas our combined intensity model classifier misclassified only 12% of tissues labeled as healthy tissues. Thus, our combined global and local intensity model results are more specific towards MS lesion voxels (Figures 2 and 5).
Fig. 5.
(a) Combined model lesion probability density function and (b) global model lesion probability density function. In both figures (a) and (b), the solid and dotted line plot respectively represent the lesion probability density function estimated from voxels manually labeled as MS lesions or as healthy tissue. Like in Figure 2(g), for a global intensity model the lesion probability density function for MS lesions and healthy voxels completely overlaps, which will result in increased FP.
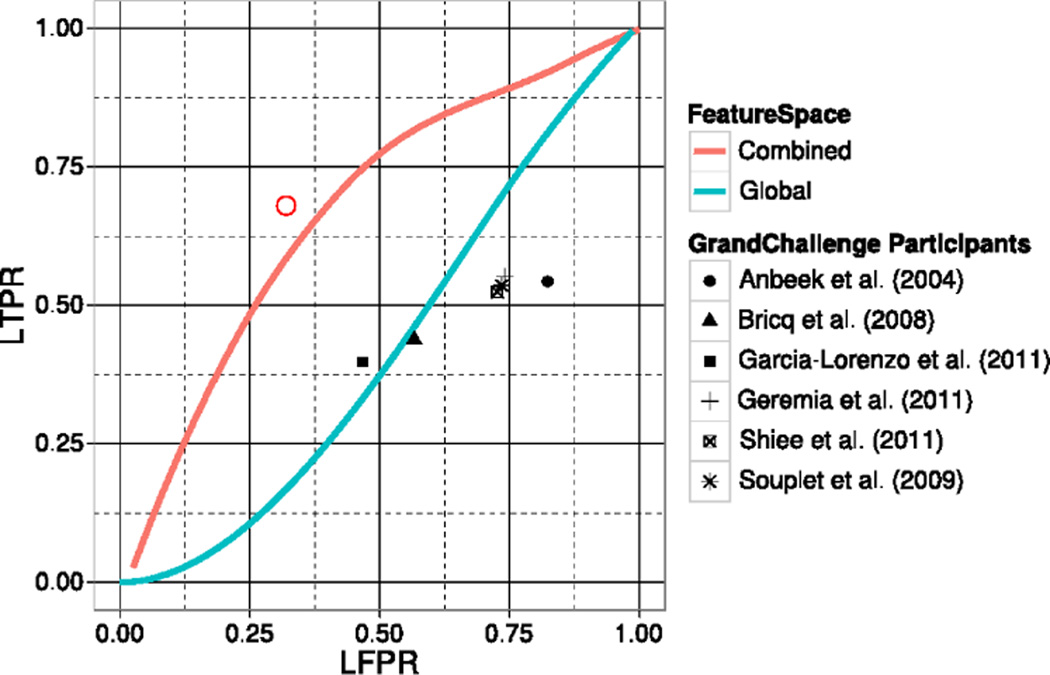
To evaluate the accuracy of our lesion detection, the automatic MS lesion segmentations were compared to the manual MS lesion reference by means of the LTPR and LFPR. Figure 6 shows the lesionwise ROC curves for the MS lesion classifier based on our combined intensity model and, when compared to state-of-the-art techniques, a global intensity model. Because MS lesion intensities overlap with those seen healthy brain tissues, algorithms that model MS lesions as global intensity outliers will both fail to identify WM abnormalities and misclassify hypo and hyperintense areas as lesions, thereby increasing the number of lesion false positives. On the other hand, because our coupled model includes a local intensity model derived from a healthy population; all locations depicting an abnormal intensity level compared to the expected intensity level in the healthy population will be identified as a lesion. This effect is seen in Figure 6, which shows how our coupled model is not only more sensitive to MS lesions but also more specific.
Fig. 6.
MS lesion detection ROC comparison between our combined local/global intensity model and a global intensity model. Reported operating point for several Grand Challenge participant algorithms is overlayed. The red circle represents the operating point for a manual rater (LTPR=0.68 and LFPR=0.32) reported by the Grand Challenge organizers.
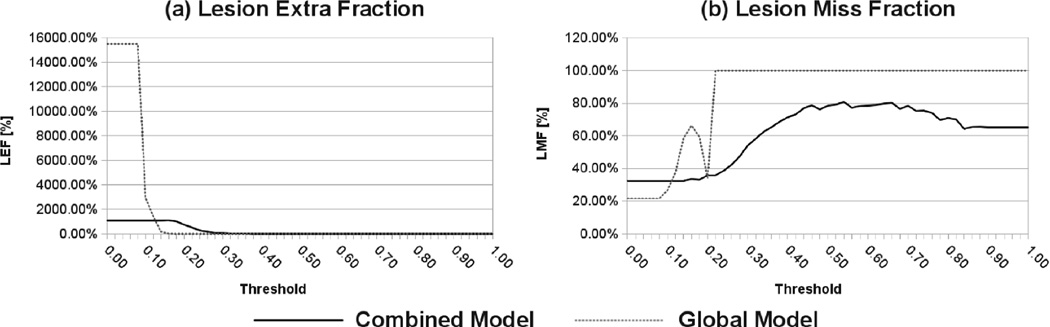
To evaluate the accuracy of the detected MS lesion boundaries compared to the manual reference, we computed for each correctly detected MS lesion, the lesion extra fraction and the lesion miss fraction , where M̄ ⋂ A are the number of voxels in Mthe automatic lesion segmentation that do not overlap with the detected manual lesion segmentation; M ⋂ Ā are the number of voxels in the detected manual lesion segmentation that do not overlap with the automatic lesion segmentation; and M is the voxel size of the detected lesion.
Fig.7 shows the average LEF (Fig.7a) and the average LMF (Fig.7b) respectively over the 20 scans for different voxel lesion probability threshold values. As expected, because of the existing overlap between the intensity distribution of MS lesions and healthy tissues; the lesion segmentation based on a global intensity model needs a much higher threshold to detect lesions. Furthermore, for any given voxel lesion probability threshold value, the lesion segmentation based on our combined intensity model achieves a lower missed fraction. To summarize, our combined intensity model not only achieves better lesion sensitivity and specificity compared to the global intensity model, but is also more accurate at estimating the extent of MS lesions when compared to manual raters.
Fig. 7.
MS lesion segmentation LEF and LM F comparison between our combined local/global intensity model and a global intensity model.
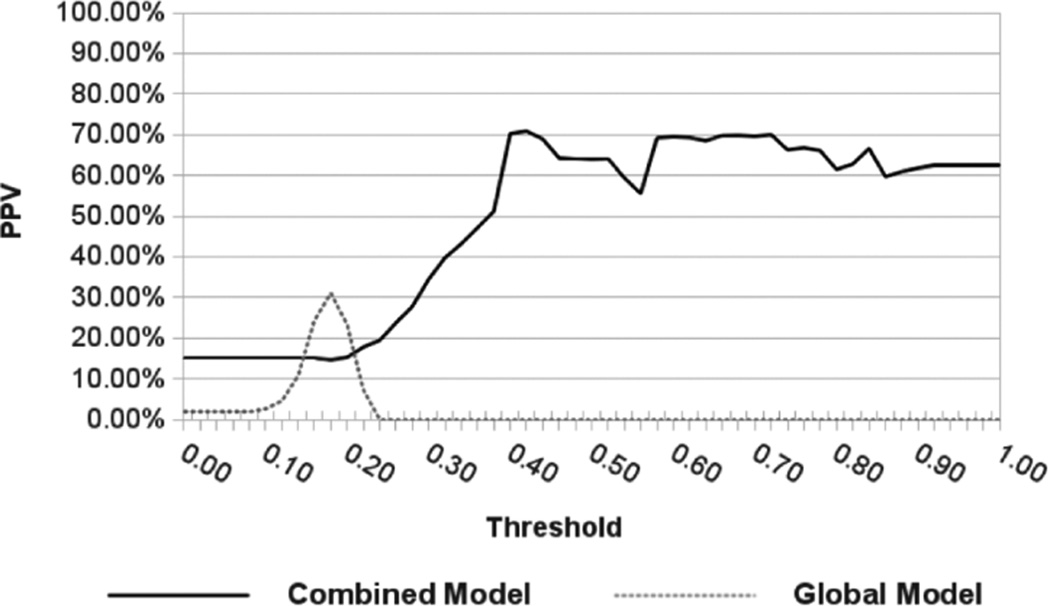
We compared the accuracy of automatic lesion segmentation based on our combined intensity model and on a global intensity model by means of the positive predictive value . Results in Fig.8 show how the MS lesion segmentation based on our combined intensity model achieves a maximum average PPV of 70.88%, which compares favourably to a maximum average value of 31.05% obtained by the MS lesion segmentation based on a global intensity model.
Fig. 8.
MS lesion segmentation PPV comparison between our combined local/global intensity model and a global intensity model.
In the last experiment, we studied the effect of the population registration algorithm on the resulting automatic MS lesion segmentation. Fixing the neighborhood radius ℛ = 2 voxels and a voxel lesion probability threshold as 1 – f(Yi, Pi, Zi|ψ) > 0.73, we generated the MS lesion segmentation of each subject in the training dataset by using our combined tissue intensity model. We compared the effect of using the reference population aligned with SyN [53] or a polyaffine block matching algorithm [37]. Table I shows the average LTPR and LFPR. Computed p-values for the paired, two tailed t-test show no significant differences in the results achieved with different registration algorithms.
TABLE I.
Comparison of MS lesion segmentation using the coupled local/global intensity model using ℛ = 2 voxels. Using different registration algorithms for the alignment of the reference population does not show significant differences in the estimated MS lesion segmentations.
| Block Matching | SyN | p-value | |
|---|---|---|---|
| LTPR | 62.94 ± 19.13 | 60.72 ± 20.13 | 0.94 |
| LFPR | 35.58 ± 24.48 | 41.70 ± 28.01 | 0.15 |
2) MS Grand Challenge Test Results
Each subject MS lesion segmentation was generated using T1w, T2w and FLAIR scans. Algorithm parameters were fixed to neighborhood radius ℛ = 2 voxels and a voxel lesion probability threshold as 1 – f(Yi, Pi, Zi|ψ) > 0.73. Remaining outliers were classified as either WM T2 hyperintense MS lesions or other MS abnormalities using the graph-cuts algorithm described in Section II-E1. Resulting segmentations were uploaded to the Grand Challenge website for automatic evaluation.
Single BCH and UNC raters independently made two manual MS lesion references for each subject from the MS Grand Challenge test group, which were not made available to the participants. Hence, the MS Grand Challenge database allows the comparison of different segmentation algorithms in a truly objective way. Grand Challenge organizers evaluate the quality of the submitted MS lesion segmentations by means of four metrics: absolute volume difference, average distance, LTPR and LFPR. Metrics were normalized between 0 and 100 considering 90 to be the experts agreement [49], where the experts’ agreement was computed as: 60% of volume difference, 75% of average distance, 68% LTPR and 32% LFPR.
Our results in Figure 6 compare favorably to those reported by all methods, independently of lesions modeled as an additional class ([30], [31] and [54]), or as outliers from a global GMM ([35], [33] and [34]).
Further, LTPR and LFPR results achieved by the state-of-the-art segmentation, closely match the ROC curve for the global intensity model depicted in Figure 6. These results suggest that all the aforementioned lesion segmentation methods, independently of the classification algorithm used, are reaching the segmentation accuracy limit that results from using a global intensity model.
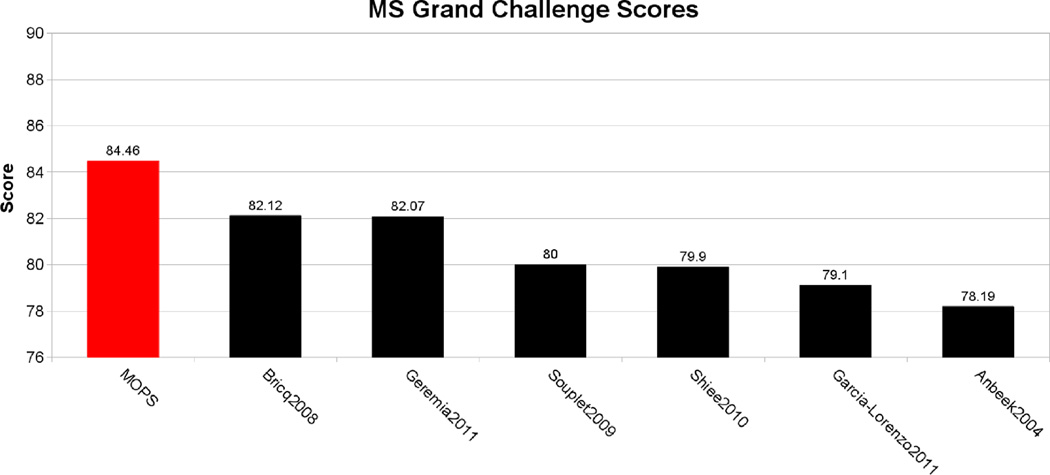
MOPS achieved a score of 84.5, which ranks our algorithm as the best performing of all of the 17 participant lesion segmentation algorithms. Figure 9 compares our score against these algorithms.
Fig. 9.
Grand Challenge score comparison between our proposed algorithm and several state-of-the-art segmentation methods. Grand Challenge organizers reported a score of 90 as the performance of an average human rater.
IV. DISCUSSION
In this paper we proposed a novel automatic algorithm for segmenting MR images of patients with multiple sclerosis (MS). This algorithm uses an approach that combines a global intensity model and a local intensity model derived from an aligned set of healthy reference subjects. Specifically, MS lesions are segmented as outliers within the combined local/global intensity Gaussian Mixture Model (GMM). These outliers not only include WM T2 hyperintense lesions, but also cortical lesions, hypointense basal ganglia and voxels that do not follow the proposed model such as vessels or intensity artifacts. A graph-cuts algorithm is used to extract WM T2 hyperintense lesions from the estimated outliers.
The proposed segmentation algorithm does not model MS lesions as global intensity outliers within each subjects MRI, but rather as local intensity outliers based on an aligned healthy population. This approach not only proves to be highly robust to noisy data, but also allows significantly improved specificity with respect to MS lesions while maintaining a comparable sensitivity to state-of-the-art algorithms. Thus, white matter (WM) lesions should not be considered as intensity outliers but instead as local population intensity outliers.
Until recently, we have been limited in our ability to validate and compare several MS lesion segmentation algorithms because there has been no common database at our disposal. However, with the introduction of the MS Grand Challenge test database, we now are able to perform a truly objective evaluation and comparison of several highly advanced algorithms in current use.
Existing MS lesion detection algorithms can be divided into two categories: 1) those that model MS lesions as outliers from the normal intensity distribution of the individual under consideration (i.e, Van Leemput et al. [32], Garcia-Lorenzo et al. [34], Bricq et al. [35] and Souplet et al. [33]); and 2) those that model lesions as an additional class within a tissue segmentation algorithm (i.e., Shiee et al. [30] and Geremia et al. [31]). Regardless of how MS lesions are modeled, all of these segmentation algorithms are primarily based on MRI global intensity features.
In contrast, our modeling of MS lesions as population local intensity outliers results in detection rates that are consistently more specific, and at least equally sensitive to, those produced by classical methods which depend heavily on ad hoc rules to detect lesions, or on various other post-processing steps aimed at improving the accuracy of MRI segmentation and MS lesion detection.
Given this, we believe our highly robust method offers a viable, flexible solution to the MRI segmentation of MS patients precisely because there are no ad hoc rules in place that can estimate WM lesion candidates. As a result, our algorithm is not tied to a specific imaging protocol. In this setting, we are thus free to operate independently of existing protocols and, moreover, with any advanced imaging technique (i.e., diffusion MRI, magnetization transfer imaging (MTI)) whose goal is to achieve accurate MS lesion segmentation when a reference of healthy subjects is available.
Furthermore, because our combined global/local tissue intensity model is able to detect abnormal local intensities when compared to a healthy reference population, our algorithm is not limited to MS lesion segmentation. Instead, it could be generalized for the detection of multiple brain abnormalities such as brain tumors, harmatomas and cysts, and potentially could also be used to perform tissue segmentation in patients who have undergone brain surgery.
Acknowledgments
This research was supported in part by NIH grants R01 NS079788, R01 LM010033, R01 EB013248, P30 HD018655, and by a research grant from the Boston Childrens Hospital Translational Research Program. Xavier Tomas-Fernandez was supported by a research grant from Caja de Ahorros y Pensiones de Barcelona and a DuPre Fellowship from the Multiple Sclerosis International Foundation (MSIF).
Footnotes
REFERENCES
- 1.Compston A, Coles A. Multiple sclerosis. Lancet. 2008 Oct;372(9648):1502–1517. doi: 10.1016/S0140-6736(08)61620-7. [DOI] [PubMed] [Google Scholar]
- 2.Young I, Hall A, Pallis C, Bydder G, Legg N, E R. Nuclear magnetic resonance imaging of the brain in multiple sclerosis. Lancet. 1981 Nov; doi: 10.1016/s0140-6736(81)91273-3. [DOI] [PubMed] [Google Scholar]
- 3.Steward W, Halland L, Berry K, Paty D. Correlation between NMR scan and brain slice data in multiple sclerosis. Lancet. 1984;324(8399):412. doi: 10.1016/s0140-6736(84)90584-1. [DOI] [PubMed] [Google Scholar]
- 4.Polman CH, Reingold SC, Banwell B, Clanet M, Cohen Ja, Filippi M, Fujihara K, Havrdova E, Hutchinson M, Kappos L, Lublin FD, Montalban X, O’Connor P, Sandberg-Wollheim M, Thompson AJ, Waubant E, Weinshenker B, Wolinsky JS. Diagnostic criteria for multiple sclerosis: 2010 revisions to the McDonald criteria. Ann. Neurol. 2011 Feb;69(2):292–302. doi: 10.1002/ana.22366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Paty DW, Li DK, Oger JJ, Kastrukoff L, Koopmans R, Tanton E, Zhao GJ. Magnetic resonance imaging in the evaluation of clinical trials in multiple sclerosis. Ann. Neurol. 1994 Jan;36(Suppl):S95–S96. doi: 10.1002/ana.410360721. [DOI] [PubMed] [Google Scholar]
- 6.Sperling RA, Guttmann CR, Hohol MJ, Warfield SK, Jakab M, Parente M, Diamond EL, Daffner KR, Olek MJ, Orav EJ, Kikinis R, Jolesz FA, Weiner HL. Regional magnetic resonance imaging lesion burden and cognitive function in multiple sclerosis: a longitudinal study. Arch. Neurol. 2001 Jan;58(1):115–121. doi: 10.1001/archneur.58.1.115. [DOI] [PubMed] [Google Scholar]
- 7.Barkhof F, Simon JH, Fazekas F, Rovaris M, Kappos L, de Stefano N, Polman CH, Petkau J, Radue EW, Sormani MP, Li DK, O’Connor P, Montalban X, Miller DH, Filippi M. MRI monitoring of immunomodulation in relapse-onset multiple sclerosis trials. Nat. Rev. Neurol. 2012 Jan;8(1):13–21. doi: 10.1038/nrneurol.2011.190. [DOI] [PubMed] [Google Scholar]
- 8.Guttmann CR, Ahn SS, Hsu L, Kikinis R, Jolesz Fa. The evolution of multiple sclerosis lesions on serial MR. AJNR. Am. J. Neuroradiol. 1995 Aug;16(7):1481–1491. [PMC free article] [PubMed] [Google Scholar]
- 9.Filippi M, Valsasina P, Rocca MA. MRI of Grey Matter Damage Magnetic Resonance Imaging of Grey Matter Damage in People with MS. Int. Ms J. 2007;14:12–21. [PubMed] [Google Scholar]
- 10.Bermel RA, Bakshi R. The measurement and clinical relevance of brain atrophy in multiple sclerosis. Lancet Neurol. 2006 Feb;5(2):158–170. doi: 10.1016/S1474-4422(06)70349-0. [DOI] [PubMed] [Google Scholar]
- 11.Wei X, Guttmann CR, Warfield SK, Eliasziw M, Mitchell RJ. Has your patient’s multiple sclerosis lesion burden or brain atrophy actually changed? Mult. Scler. 2004 Aug;10(4):402–406. doi: 10.1191/1352458504ms1061oa. [DOI] [PubMed] [Google Scholar]
- 12.Filippi M, Horsfield MA, Bressi S, Martinelli V, Baratti C, Reganati P, Campi A, Miller DH, Comi G. Intra- and inter-observer agreement of brain MRI lesion volume measurements in multiple sclerosis. A comparison of techniques. Brain. 1995 Dec;118(Pt 6):1593–1600. doi: 10.1093/brain/118.6.1593. [DOI] [PubMed] [Google Scholar]
- 13.Paty DW, Li D. Interferon beta-1b is effective in relapsingremitting multiple sclerosis: II. MRI analysis results of a multicenter, randomized, double-blind, placebo-controlled trial. Neurology. 1993 Apr;43(4):662–662. doi: 10.1212/wnl.43.4.662. [DOI] [PubMed] [Google Scholar]
- 14.Clarke LP, Velthuizen RP, Camacho MA, Heine JJ, Vaidyanathan M, Hall LO, Thatcher RW, Silbiger ML. MRI segmentation: methods and applications. Magn. Reson. Imaging. 1995 Jan;13(3):343–368. doi: 10.1016/0730-725x(94)00124-l. [DOI] [PubMed] [Google Scholar]
- 15.Warfield SK, Zou KH, Wells WM. Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation. IEEE Trans. Med. Imaging. 2004 Jul;23(7):903–921. doi: 10.1109/TMI.2004.828354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Akhondi-Asl A, Warfield SK. Simultaneous truth and performance level estimation through fusion of probabilistic segmentations. IEEE Trans. Med. Imaging. 2013 Oct;32(10):1840–1852. doi: 10.1109/TMI.2013.2266258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ashton Ea, Takahashi C, Berg MJ, Goodman A, Totterman S, Ekholm S. Accuracy and reproducibility of manual and semiautomated quantification of MS lesions by MRI. J. Magn. Reson. Imaging. 2003 Mar;17(3):300–308. doi: 10.1002/jmri.10258. [DOI] [PubMed] [Google Scholar]
- 18.Udupa JK, Wei L, Samarasekera S, Miki Y, van Buchem Ma, Grossman RI. Multiple sclerosis lesion quantification using fuzzyconnectedness principles. IEEE Trans. Med. Imaging. 1997 Oct;16(5):598–609. doi: 10.1109/42.640750. [DOI] [PubMed] [Google Scholar]
- 19.Grimaud J, Lai M, Thorpe J, Adeleine P. Quantification of MRI lesion load in multiple sclerosis: a comparison of three computer-assisted techniques. Magn. Reson. 1996;14(5):495–505. doi: 10.1016/0730-725x(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 20.Shepherd T, Prince SJD, Alexander DC. Interactive lesion segmentation with shape priors from offline and online learning. IEEE Trans. Med. Imaging. 2012 Sep;31(9):1698–1712. doi: 10.1109/TMI.2012.2196285. [DOI] [PubMed] [Google Scholar]
- 21.García-Lorenzo D, Francis S, Narayanan S, Arnold DL, Collins DL. Review of automatic segmentation methods of multiple sclerosis white matter lesions on conventional magnetic resonance imaging. Med. Image Anal. 2013 Jan;17(1):1–18. doi: 10.1016/j.media.2012.09.004. [DOI] [PubMed] [Google Scholar]
- 22.Kamber M, Shinghal R, Collins DL, Francis GS, Evans aC. Model-based 3-D segmentation of multiple sclerosis lesions in magnetic resonance brain images. IEEE Trans. Med. Imaging. 1995 Jan;14(3):442–453. doi: 10.1109/42.414608. [DOI] [PubMed] [Google Scholar]
- 23.Wells WM, Grimson WL, Kikinis R, Jolesz Fa. Adaptive segmentation of MRI data. IEEE Trans. Med. Imaging. 1996 Jan;15(4):429–442. doi: 10.1109/42.511747. [DOI] [PubMed] [Google Scholar]
- 24.Warfield S, Dengler J, Zaers J, Guttmann CR, Wells WM, Ettinger GJ, Hiller J, Kikinis R. Automatic identification of gray matter structures from MRI to improve the segmentation of white matter lesions. J. Image Guid. Surg. 1995;1(6):326–338. doi: 10.1002/(SICI)1522-712X(1995)1:6<326::AID-IGS4>3.0.CO;2-C. [DOI] [PubMed] [Google Scholar]
- 25.Warfield SK, Kaus M, Jolesz FA, Kikinis R. Adaptive, template moderated, spatially varying statistical classification. Med. Image Anal. 2000 Mar;4(1):43–55. doi: 10.1016/s1361-8415(00)00003-7. [DOI] [PubMed] [Google Scholar]
- 26.Zijdenbos AP, Forghani R, Evans AC. Automatic “pipeline” analysis of 3-D MRI data for clinical trials: application to multiple sclerosis. IEEE Trans. Med. Imaging. 2002 Oct;21(10):1280–1291. doi: 10.1109/TMI.2002.806283. [DOI] [PubMed] [Google Scholar]
- 27.Wei X, Warfield SK, Zou KH, Wu Y, Li X, Guimond A, Iii JPM, Benson RR, Wolfson L, Weiner HL, Guttmann CRG. Quantitative Analysis of MRI Signal Abnormalities of Brain White Matter With High Reproducibility and Accuracy. J. Magn. Reson. Imaging. 2002;209:203–209. doi: 10.1002/jmri.10053. [DOI] [PubMed] [Google Scholar]
- 28.Guttmann CR, Kikinis R, Anderson MC, Jakab M, Warfield SK, Killiany RJ, Weiner HL, Jolesz Fa. Quantitative follow-up of patients with multiple sclerosis using MRI: reproducibility. J. Magn. Reson. Imaging. 1999 Apr;9(4):509–518. doi: 10.1002/(sici)1522-2586(199904)9:4<509::aid-jmri2>3.0.co;2-s. [DOI] [PubMed] [Google Scholar]
- 29.Wu Y, Warfield SK, Tan IL, Wells WM, Meier DS, van Schijndel Ra, Barkhof F, Guttmann CRG. Automated segmentation of multiple sclerosis lesion subtypes with multichannel MRI. Neuroimage. 2006 Sep;32(3):1205–1215. doi: 10.1016/j.neuroimage.2006.04.211. [DOI] [PubMed] [Google Scholar]
- 30.Shiee N, Bazin P-L, Ozturk A, Reich DS, Calabresi PA, Pham DL. A topology-preserving approach to the segmentation of brain images with multiple sclerosis lesions. Neuroimage. 2010 Jan;49(2):1524–1535. doi: 10.1016/j.neuroimage.2009.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Geremia E, Clatz O, Menze BH, Konukoglu E, Criminisi A, Ayache N. Spatial decision forests for MS lesion segmentation in multi-channel magnetic resonance images. Neuroimage. 2011 Jul;57(2):378–390. doi: 10.1016/j.neuroimage.2011.03.080. [DOI] [PubMed] [Google Scholar]
- 32.Van Leemput K, Maes F, Vandermeulen D, Colchester A, Suetens P. Automated segmentation of multiple sclerosis lesions by model outlier detection. IEEE Trans. Med. Imaging. 2001 Aug;20(8):677–688. doi: 10.1109/42.938237. [DOI] [PubMed] [Google Scholar]
- 33.Souplet J. Ph.D. dissertation. Universite de Nice-Sophia Antipolis; 2009. ÉEvaluation de l’atrophie et de la charge lésionnelle sur des séquences IRM de patients atteints de sclérose en plaques. [Google Scholar]
- 34.Garcia-Lorenzo D, Prima S, Arnold D, Collins D, Barillot C. Trimmed-Likelihood Estimation for Focal Lesions and Tissue Segmentation in Multi-Sequence MRI for Multiple Sclerosis. IEEE Trans. Med. Imaging. 2011 Feb;(c):1–13. doi: 10.1109/TMI.2011.2114671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bricq S, Collet C, Armspach J. Image Process. 2008. ICIP 2008. 15th IEEE Int. Conf. i. Vol. 1. IEEE; 2008. Markovian segmentation of 3D brain MRI to detect multiple sclerosis lesions; pp. 733–736. [Google Scholar]
- 36.Makris N, Meyer JW, Bates JF, Yeterian EH, Kennedy DN, Caviness VS. MRI-Based topographic parcellation of human cerebral white matter and nuclei II. Rationale and applications with systematics of cerebral connectivity. Neuroimage. 1999 Jan;9(1):18–45. doi: 10.1006/nimg.1998.0384. [DOI] [PubMed] [Google Scholar]
- 37.Suarez RO, Commowick O, Prabhu SP, Warfield SK. Automated delineation of white matter fiber tracts with a multiple region-of-interest approach. Neuroimage. 2012 Feb;59(4):3690–3700. doi: 10.1016/j.neuroimage.2011.11.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Klein A, Andersson J, Ardekani BA, Ashburner J, Avants B, Chiang M-C, Christensen GE, Collins DL, Gee J, Hellier P, Song JH, Jenkinson M, Lepage C, Rueckert D, Thompson P, Vercauteren T, Woods RP, Mann JJ, Parsey RV. Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. Neuroimage. 2009 Jul;46(3):786–802. doi: 10.1016/j.neuroimage.2008.12.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Akselrod-Ballin A, Bock D, Reid RC, Warfield SK. Accelerating image registration with the Johnson-Lindenstrauss lemma: application to imaging 3-D neural ultrastructure with electron microscopy. IEEE Trans. Med. Imaging. 2011 Jul;30(7):1427–1438. doi: 10.1109/TMI.2011.2125797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Neykov N, Filzmoser P, Dimova R, Neytchev P, Cs F. Robust fitting of mixtures using the trimmed likelihood estimator. Comput. Stat. Data Anal. 2007 Sep;52(1):299–308. [Google Scholar]
- 41.Geurts JJG, Roosendaal SD, Calabrese M, Ciccarelli O, Agosta F, Chard DT, Gass A, Huerga E, Moraal B, Pareto D, Rocca Ma, Wattjes MP, Yousry Ta, Uitdehaag BMJ, Barkhof F. Consensus recommendations for MS cortical lesion scoring using double inversion recovery MRI. Neurology. 2011 Feb;76(5):418–424. doi: 10.1212/WNL.0b013e31820a0cc4. [DOI] [PubMed] [Google Scholar]
- 42.Ceccarelli A, Rocca Ma, Neema M, Martinelli V, Arora A, Tauhid S, Ghezzi A, Comi G, Bakshi R, Filippi M. Deep gray matter T2 hypointensity is present in patients with clinically isolated syndromes suggestive of multiple sclerosis. Mult. Scler. 2010 Jan;16(1):39–44. doi: 10.1177/1352458509350310. [DOI] [PubMed] [Google Scholar]
- 43.Moore GRW, Laule C, Mackay A, Leung E, Li DKB, Zhao G, Traboulsee aL, Paty DW. Dirty-appearing white matter in multiple sclerosis: preliminary observations of myelin phospholipid and axonal loss. J. Neurol. 2008 Nov;255(11):1802–1811. doi: 10.1007/s00415-008-0002-z. discussion 1812. [DOI] [PubMed] [Google Scholar]
- 44.Bitsch A, Kuhlmann T. A longitudinal MRI study of histopathologically defined hypointense multiple sclerosis lesions. Ann Neurol. 2001;49:793–816. doi: 10.1002/ana.1053. [DOI] [PubMed] [Google Scholar]
- 45.Greig D, Porteous B, Seheult A. Exact maximum a posteriori estimation for binary images. R. Stat. Soc. Ser. 1989;51(2):271–279. [Google Scholar]
- 46.Otsu N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man. Cybern. 1975;SMC-9(1):62–66. [Google Scholar]
- 47.Boykov Y, Veksler O, Zabih R. Fast approximate energy minimization via graph cuts. IEEE Trans. Pattern Anal. Mach. Intell. 2001;23(11):1222–1239. [Google Scholar]
- 48.Kwan RK, Evans AC, Pike GB. MRI simulation-based evaluation of image-processing and classification methods. IEEE Trans. Med. Imaging. 1999 Nov;18(11):1085–1097. doi: 10.1109/42.816072. [DOI] [PubMed] [Google Scholar]
- 49.Styner M, Lee J, Chin B, Chin M, Commowick O, Tran H-h, Markovic-Plese S, Jewells V, Warfield S. 3D segmentation in the clinic. A grand challenge: MS lesion segmentation. Midas J. 2008:1–5. [Google Scholar]
- 50.Mangin J. Entropy minimization for automatic correction of intensity nonuniformity. Proc. IEEE Work. Math. Methods Biomed. Image Anal. MMBIA-2000 (Cat. No.PR00737), vol. 00. IEEE Comput. Soc. 2000:162–169. [Google Scholar]
- 51.Whitaker R, Xue X. Variable-conductance, level-set curvature for image denoising. Image Process. 2001. Proceedings. 2001 Int. Conf. 2001;3:142–145. [Google Scholar]
- 52.Dice LR. Measures of the Amount of Ecologic Association Between Species. Ecology. 1945 Jul26(3):297. [Google Scholar]
- 53.Avants BB, Epstein CL, Grossman M, Gee JC. Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Med. Image Anal. 2008 Mar;12(1):26–41. doi: 10.1016/j.media.2007.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Anbeek P, Vincken KL, van Osch MJP, Bisschops RHC, van der Grond J. Probabilistic segmentation of white matter lesions in MR imaging. Neuroimage. 2004 Mar;21(3):1037–1044. doi: 10.1016/j.neuroimage.2003.10.012. [DOI] [PubMed] [Google Scholar]