Model-based Reconstruction of Objects with Inexactly Known Components

Abstract

Because tomographic reconstructions are ill-conditioned, algorithms that incorporate additional knowledge about the imaging volume generally have improved image quality. This is particularly true when measurements are noisy or have missing data. This paper presents a general reconstruction framework for including attenuation contributions from objects known to be in the field-of-view. Components such as surgical devices and tools may be modeled explicitly as part of the attenuating volume but are inexactly known with respect to their locations poses, and possible deformations. The proposed reconstruction framework, referred to as Known-Component Reconstruction (KCR), is based on this novel parameterization of the object, a likelihood-based objective function, and alternating optimizations between registration and image parameters to jointly estimate the both the underlying attenuation and unknown registrations. A deformable KCR (dKCR) approach is introduced that adopts a control point-based warping operator to accommodate shape mismatches between the component model and the physical component, thereby allowing for a more general class of inexactly known components. The KCR and dKCR approaches are applied to low-dose cone-beam CT data with spine fixation hardware present in the imaging volume. Such data is particularly challenging due to photon starvation effects in projection data behind the metallic components. The proposed algorithms are compared with traditional filtered-backprojection and penalized-likelihood reconstructions and found to provide substantially improved image quality. Whereas traditional approaches exhibit significant artifacts that complicate detection of breaches or fractures near metal, the KCR framework tends to provide good visualization of anatomy right up to the boundary of surgical devices.

INTRODUCTION

The ill-conditioned nature of the tomographic reconstruction problem is well-known and all approaches must contend with the implicit noise amplification. Traditional filtered-backprojection techniques include apodized filters and statistical methods rely on general image priors [1, 2] that enforce desirable image properties like smoothness, edge-preservation, etc. More specific information has also been included in iterative approaches such as anatomical boundary information [3] and even prior scans of the same patient anatomy. [4–6] In this work, we consider a technique for including specific attenuation knowledge for a portion of the imaging volume. Applications where such knowledge is available is potentially widespread in both diagnostic imaging in the presence of surgical devices like fixation hardware, joint prostheses, etc. or in interventional imaging where such devices are being placed, or where surgical tools like biopsy needles are present in the field-of-view. Since such components are manufactured, they are potentially very well described with CAD models and details of their composition. However, where the components lie within the volume with respect to location and pose is unknown. Moreover, certain components are often inexactly known since they are intentionally formed into a new shape during surgical placement. Such is the case for fixation rods in vertebral fusion (see Figure 1) that are bent to enforce a specific spine curvature. Similar deformations may be found with surgical tools like flexible biopsy needles which can bend upon insertion into the patient.

Figure 1.

Surgical hardware utilized in vertebral fusion including (left-to-right) a set screw, a polyaxial pedicle screw, and a fixation rod. These components are connected together into an assembly during a spine fusion procedure to fix the relative position of adjacent vertebra (far right). Highly detailed CAD models and material compositions are known for these components yielding an opportunity for integration of prior information in reconstruction. However, the fixation rod is rarely placed in a patient without modification. It is routinely formed during an interventional procedure to enforce a specific spine curvature. Thus, methods seeking to incorporate this prior knowledge of components must accommodate potential deformations.

While prior work by Snyder et al. [7] has endeavored to include such prior information about known components through a constrained optimization approach, that work has not been generalized to multi-component scenarios such as the spine complex in Figure 1, nor to the case of inexactly known components requiring deformable registrations. We have proposed a distinct approach [8] that models the object as the composition of an arbitrary number of (inexactly) known components and the underlying patient anatomy. Ambiguities for these components including pose, position, and deformations are estimated simultaneously with the background as part of an unconstrained optimization. We illustrate the performance of this technique on low-dose acquisitions that include spine hardware in the field-of-view. Such data are particularly challenging due to the limitations of data fidelity particularly in those measurements that include ray-paths through metal components.

METHODS

The key element of the KCR framework is a decomposition of the object into known components and background anatomy. Mathematically, we represent the attenuation coefficients in a voxelized volume as the vector

$$\mu ({\mu }_{*},\mathrm{\Lambda })=\left(\prod _{n=1}^N\mathbf{D}\right\{\mathbf{W}\left({\lambda }^{(n)}\right)s^{(n)}\left\}\right){\mu }_{*}+\sum _{n=1}^N\mathbf{W}\left({\lambda }^{(n)}\right){\mu }_I^{(n)}$$

$$\mathrm{\Lambda }={\left\{{\lambda }^{(n)}\right\}}_{n=1}^N,$$

where μ_* denotes a traditional voxelization of the background anatomy and μ_I⁽ⁿ⁾ represents a spatial distribution of attenuation for the n^th known component. To combine known components and background, the components is registered within the image volume using the parameterized operator, W(λ⁽ⁿ⁾). This registration operator is general and each component has its own parameter vector, λ⁽ⁿ⁾, that defines the particular transformation applied to that component. We denote the ensemble of parameter vectors for all known components by Λ. For rigid transformations each component’s parameter vector contains a set of (six, in 3D) translation and rotation values to place the component arbitrarily within the field-of-view. For non-rigid registration, the vector contains more general parameter values to accommodate specific warping modes – a specific parameterization of the deformation is discussed below. The transformed components are added to a modified patient background that has had a (transformed) mask, s⁽ⁿ⁾, applied. Note the use of the diagonal matrix operator, D{}, above, to mathematically apply this mask. In effect, this mask zeros out the part of the background to which the component is being added and tends to be largely binary – though non-binary masks can account for partial volume effects at the edges of the component (i.e., each voxel is potentially a mixture of both background attenuation and the component) and for porous devices where there is mixing with the anatomy. Note that the object model is completely specified by μ_* and Λ.

To complete the object model, it remains to specify the registration operator. For a traditional rigid registration operator, it is straightforward to relate the parameter vector λ⁽ⁿ⁾ to a point-to-point mapping between the original image and the transformed image. We find transformed image values using a B-spline approximation kernel [9], which ensures differentiability of the object model with respect to the transformation parameters (which is important for the eventual joint estimation based, in part, on gradient-based optimizations).

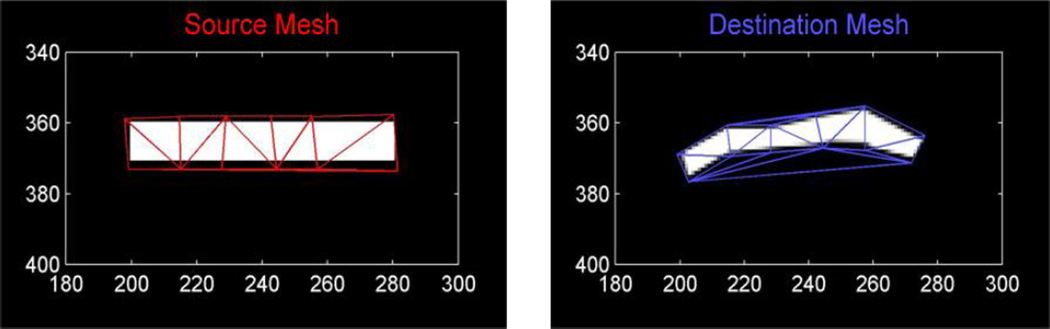
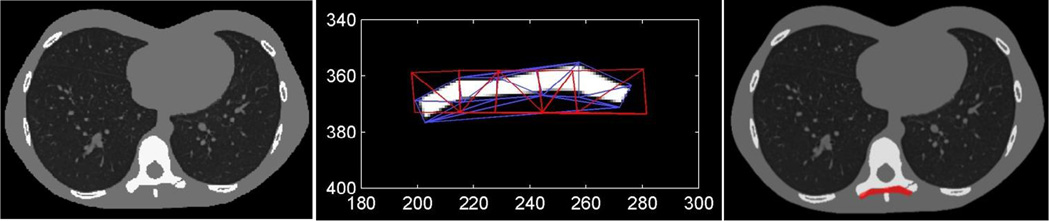
In our initial studies of deformable registration, we have adopted a warping operator based on control points. This operator is illustrated in Figure 2. Control points are defined on the source image (e.g., the component model) which form a source mesh. Corresponding points are defined for a destination image, forming an analogous destination mesh. These two meshes define a point-to-point mapping where every triangle in the source image maps to a triangle in the destination image. Thus, the transform is piecewise affine over each triangular region. (While this mapping is strictly nondifferentiable at triangle boundaries, we have found that the interior volumes dominate the derivative calculations and the mild nondifferentiability is not a problem in practice for optimization.) Again, values in the transformed (destination) image are found by applying a B-spline approximation kernel to neighborhoods of points in the source image using the triangle-based point mapping defined by the two meshes. While one might consider the parameters of this deformation model to be both the source and control points, we have adopted a framework where the source mesh is a part of the component model and the destination control points are the parameters of the object model, Λ. Although, the deformation studies in this paper focus on the 2D problem, these methods may also be extended to the 3D case where source and destination meshes form a mapping based on tetrahedra.

Figure 2.

Illustration of the control point-based warping operator. Control points on an image form a source mesh. Corresponding points which have been translated form a destination mesh. These meshes specify a point-to-point mapping based on triangles, which, in turn, may be used to interpolate values for the destination image.

From this object model, it is straightforward to adopt a forward model for the measurement vector, y, to adopt a noise model, and to derive a likelihood function for the unknown parameters. This process leads one to the implicitly defined Known-Component Reconstruction (KCR) estimator

$$\{{\hat{\mu }}_{*},\hat{\mathrm{\Lambda }}\}=\underset{{\mu }_{*},\mathrm{\Lambda }}{\text{arg max}}\mathrm{\Phi }({\mu }_{*},\mathrm{\Lambda };y)=\underset{{\mu }_{*},\mathrm{\Lambda }}{\text{arg max}}L({\mu }_{*},\mathrm{\Lambda };y)-\beta R({\mu }_{*}),$$

which represents a joint estimation of both the background anatomy and the registration parameters. The objective function is comprised of a log-likelihood term (L), a regularization term (R) to penalize noisy images, and a regularization parameter, β, to control the noise-resolution tradeoff. (In this work, we have concentrated on quadratic roughness penalties.) When the object model includes a deformable registration operator, we refer to the reconstruction approach as deformable KCR (dKCR), whereas the rigid transformation-only variant is labeled (simply) KCR. The authors have developed a custom algorithm for maximization of the above objective for both the KCR and dKCR cases based on alternating optimizations of the registration and image parameters using a quasi-Newton approach and separable quadratic surrogates updates [10], respectively.

RESULTS

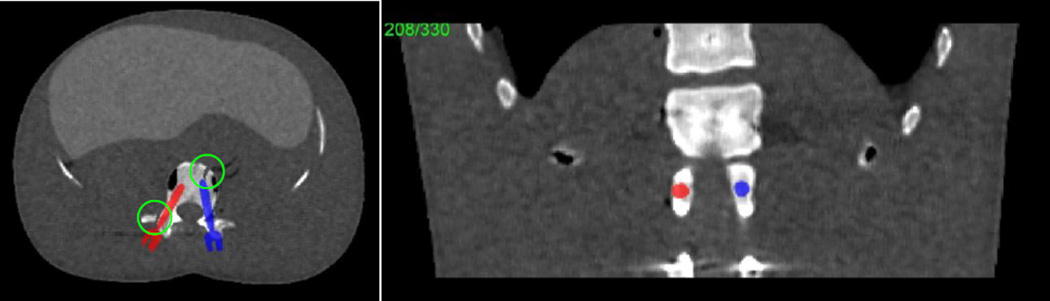
In this work, we present the application of the KCR framework to two scenarios: 1) an application of KCR to bilateral pedicle screw placement in the lumbar spine that relies on two-component rigid registration; and 2) an application of dKCR for a trauma fixation plate placement on the thoracic spine that relies on deformable registration. The phantom for the pedicle screw investigation is shown in Figure 3. Two single-component screws are placed bilaterally within a lumbar vertebra and are displayed as an overlay image. The attenuation profiles of each pedicle screw and the associated component mask were derived from 3D CAD models and the known (titanium) composition. Small fractures near the screws are simulated and illustrated in the axial slice. Using this phantom, an attenuation volume was created and projection data was simulated. We considered a C-arm system geometry and 1 mm voxels. Data acquisitions used a monoenergetic model with 10⁴ photons per (1.552 mm square) detector element and Poisson noise.

Figure 3.

Digital phantom used in the bilateral pedicle screw placement scenario with an overlay display of the known components. Each screw represents a known component and has six degrees of freedom associated with its position in the imaging volume. Green circles illustrate small simulated fractures of the vertebra.

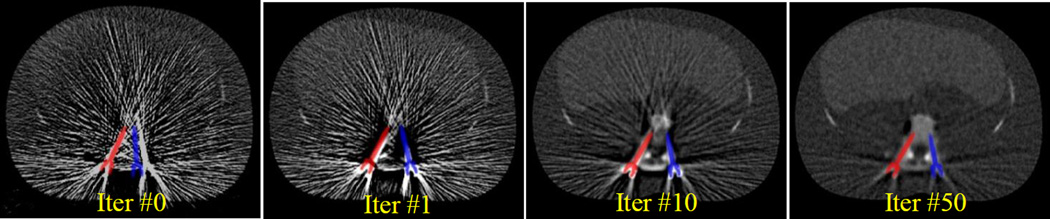
Reconstructions of data were performed using filtered-backprojection (FBP), a quadratically penalized-likelihood estimator (with no component knowledge), and the KCR approach. The FBP image was used to initialize both iterative methods and we attempted to select a regularization parameter that would provide similar spatial resolution for all approaches. Figure 4 shows a sampling of KCR iterations, and the joint nature of the estimation is apparent (with both registration updates and image improvements with each successive iteration). We note that since the object parameterization explicitly separates the background anatomy and the known components, it is straightforward to create (color) overlay images of the screw in the patient anatomy (one may always recreate attenuation images if desired).

Figure 4.

Sample KCR iterations for the bilateral pedicle screw placement scenario. The initial image shows the starting guess for the two pedicle screw positions overlaid on a filtered-backprojection reconstruction of phantom data. Note the joint nature of the reconstruction problem with each iteration updating both the registration estimates and the background image. Successive iterations improve both the pose and location estimates of the screws as well as improving image quality through streak reduction.

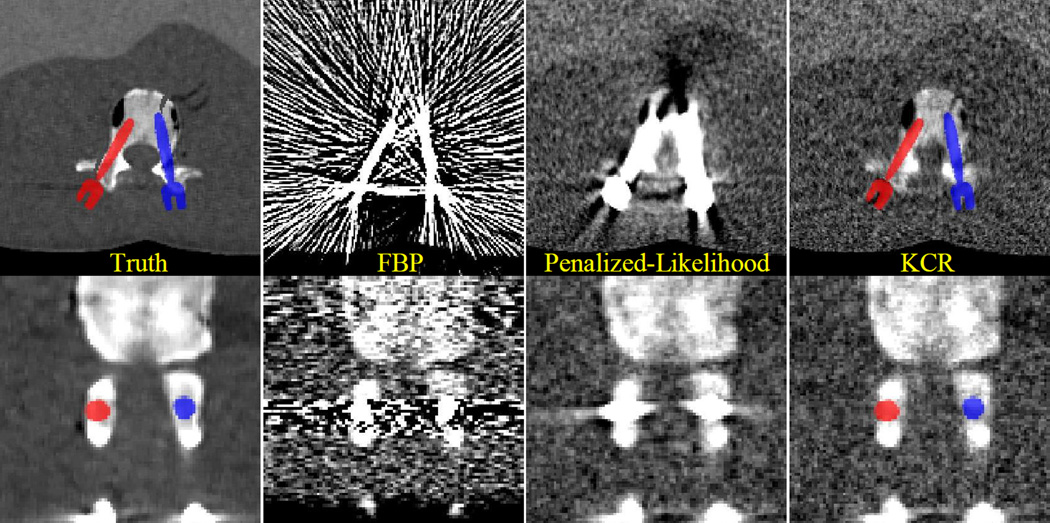
Figure 5 illustrates the relative comparison of the reconstruction approaches against the true image volume in (zoomed) axial and coronal slices. While FBP reconstructions are plagued by significant streak artifacts due to photon starvation (particularly, along the long axes of the screws), the penalized-likelihood approach greatly mitigates streak artifacts due to noise. However, significant biases still remain in proximity to the screws disallowing visualization of the simulated fractures. With KCR, image quality is dramatically improved with better image quality even at the boundaries of the screws. We see the anterior fracture is well visualized, while the lateral fracture is difficult to diagnose. This suggests the need for greater exposure and less regularization for improved spatial resolution in this particular region.

Figure 5.

A comparison of reconstruction approaches for the bilateral pedicle screw placement scenario. Severe streak artifacts are present in the FBP volume due to photon starvation in measurements containing rays passing through the pedicle screws. While the image is greatly improved using a statistical approach, artifacts remain in proximity to the devices, dramatically reducing the utility of the images for detecting breaches. In comparison, the KCR images are essentially streak-free and allow for visualization of anatomy very close to the implant. Specifically, the anterior simulated fracture is evident only in the KCR image. The lateral fracture remains difficult to visualize suggesting increased exposure/reduced regularization may be necessary.

In the fixation plate scenario, a 2D deformable component is used in a simulated application to the thoracic spine. This is illustrated in Figure 6 with the use the same rectangular plate example as was used in the deformation example in Figure 2. The titanium plate is parameterized with 12 control points and is placed on the posterior surface of the vertebra. A small fracture is placed on the transverse process of the vertebra to investigate image quality near the metal component. For data generation, we adopt a C-arm geometry with 0.766 mm detector pixels, 0.8 mm voxels, a monoenergetic beam, 10⁴ photons per detector element, and Poisson noise.

Figure 6.

Illustration of the phantom used in the fixation plate scenario. A single slice containing a thoracic vertebra is selected and modified to contain a small fracture in the transverse process (left). A rectangular block of titanium is deformed and placed on the posterior surface of the vertebra to simulate a fixation plate (right). The source and destination meshes are shown overlaid on the deformed component (center).

As in the previous scenario, we present a sampling of dKCR iterations in Figure 7. The dKCR algorithm is initialized with a flat plate and a FBP reconstruction. Over successive iterations the plate is deformed via improved estimates of the positions of the destination control points. With this improved component knowledge a better to fit the data and object model is possible and updates to the patient anatomy result in greatly improved image quality.

Figure 7.

Illustration of dKCR iterations in the deformable fixation plate example starting with a flat plate on a single slice FBP data set. Successive iterations move the destination control points to accommodate and estimate the particular deformation. With an improved estimate of the component, the background image is updated with consequent improvements in image quality.

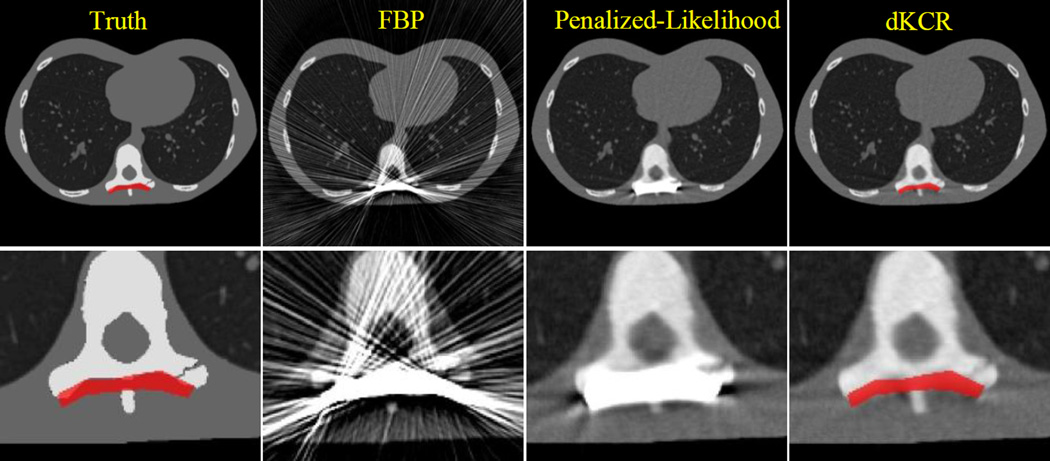
A comparison of reconstruction methods for the deformable component scenario is presented in Figure 8. Again, we have attempted to approximately match spatial resolution in all cases. The rank-order performance of the reconstruction approaches is the same as before. While FBP suffers from substantial streak artifacts, the penalized-likelihood method successfully mitigates the severe streaking across the entire axial slice. However, artifacts still remain in close proximity to the fixation plate, and there is significant "blooming" around the implant that obscures nearby anatomy. Both FBP and penalized-likelihood do not provide sufficient image quality to diagnose the fracture in the transverse process. In the penalized-likelihood image, it is unclear whether the dark bands near the implant are artifact or anatomy. In the dKCR image, artifacts are much reduced and the simulated fracture is more apparent. Moreover, the estimate of the plate deformation is a very good match to the actual deformation that was used to create the data.

Figure 8.

Comparison of different reconstruction methods for the 2D deformable component scenario. Zoomed versions of each case are shown in the lower row of images. While the FBP image is plagued by significant streak artifacts, there is significant reduction of streaks when a statistical approach is used. However, the penalized-likelihood approach still exhibits difficulty resolving details near the boundary of the simulated device; whereas the dKCR approach provides improved quality, better resolving a simulated fracture. We note that not only is image quality improved through the introduction of component knowledge, the deformations estimated by the dKCR approach provide an accurate estimate of the particular deformations that were applied to the component.

DISCUSSION

This paper has presented a general framework called known-component reconstruction, for incorporating an arbitrary number of known components within a penalized-likelihood framework. Such components need not be known exactly and may be rigidly (KCR) or non-rigidly deformed (dKCR) to fit within the volume. This approach appears to work particularly well in the case of photon-starved or missing data scenarios as is found with metal surgical devices within the field-of-view; however, the technique is generally applicable to any kind of component including those comprised of heterogeneous attenuation values. In the case of metal spine hardware, the KCR approaches appear to allow for imaging right to the boundary of metal devices – which would have particular impact if applied clinically for tasks such as the detection of pedicle screw breaches, assessing osteolysis around implants, and biopsy needle guidance (all traditionally difficult imaging tasks due to metal artifacts). Moreover, the joint registration-reconstruction of KCR has additional advantages over traditional methods. The registration estimates themselves may have value for quantitative assessments of surgical deliveries (in comparison with positions in preoperative plans). Similarly, because KCR explicitly decomposes the object into background and component, overlay images and segmentation of components is facilitated. (A benefit for images with high dynamic range, like those with metal in the field-of-view.) Future work includes an extension to 3D deformable registrations, smoother deformation models based on B-splines, and an analysis of deformation model mismatch and application to real data.