Computational study of peptide permeation through membrane: Searching for hidden slow variables

Abstract

Atomically detailed molecular dynamics trajectories in conjunction with Milestoning are used to analyze the different contributions of coarse variables to the permeation process of a small peptide (N-acetyl-L-tryptophanamide, NATA) through a 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) membrane. The peptide reverses its overall orientation as it permeates through the biological bilayer. The large change in orientation is investigated explicitly but is shown to impact the free energy landscape and permeation time only moderately. Nevertheless, a significant difference in permeation properties of the two halves of the membrane suggests the presence of other hidden slow variables. We speculate, based on calculation of the potential of mean force, that a conformational transition of NATA makes significant contribution to these differences. Other candidates for hidden slow variables may include water permeation and collective motions of phospholipids.

1. Introduction

Permeation of small molecules through membranes has attracted considerable experimental and theoretical attention in the past [1–9]. Determination of permeation coefficients and rates of small molecules through biological membranes is clearly important for evolutionary studies [4,6], for investigations of pollutants [10–13], and for research of drug delivery [14–17]. In the present manuscript we focus on the passive permeation of a small peptide through a membrane. Amino acids are the building blocks of proteins and their transport into primitive cells that lacks transport machinery is necessary fuel for protein synthesis. Experimentally we note the pioneering work of Deamer and co-workers that measured passive permeation of peptides and amino acids through lipid bilayers [6] and follow up studies of others [9,18,19]. Experimentally, the process is frequently characterized by the permeation coefficient, P. It is defined as P = J/Δc where J is the reactive flux (number of molecules passing a unit area, in a unit time). The number of molecules per unit volume is the concentration c, and the concentration difference between the solutions at the two sides of the membrane is Δc. For simplicity we set the concentration of the permeant on one side of the membrane to be zero and hence Δc = c.

Past theoretical studies of permeation focus on a one dimensional solubility diffusion model (SDM). The potential of mean force W (Z) and a diffusion constant D (Z) are computed along the axis perpendicular to the membrane surface Z and are used in a 1D overdamped Langevin model to estimate the permeation coefficient, P: [3]

$$P={\left[\underset{Z_1}{\overset{Z_2}{\int }}\frac{\text{exp}[\beta \Delta W(Z)]}{D(Z)}\mathit{\text{dZ}}\right]}^{-1}$$ (1)

where ΔW (Z) are the changes in the potential of mean force, Z₁ and Z₂ are the bilayer boundaries, and β is the inverse temperature. The potential of mean force can be computed with umbrella sampling [20], or the blue moon approach [21]. This is a sensible choice that has been used successfully for permeation studies of small solutes[2,22–30]; however, it may be incomplete since the position of the center of mass of the permeant along the membrane normal is assumed to be the only slow variable of the translocation process There can be other slow variables that affect the permeation coefficient. For example, permeant orientation, conformational transitions of the permeant, and density fluctuations of the solution may all be coupled to the transport. If their corresponding relaxation times are long compared to typical MD simulations of membranes (a few to hundreds of nanoseconds) then their sampling must be explicitly enhanced, or longer simulations must be conducted. The sampling of more than a single variable can be enhanced by methods such as TAMD [31], TAMC [32], Metadynamics [33] and Milestoning [34]. Milestoning has the advantage that it makes it possible to compute the kinetics. Furthermore, the dynamics in Eq. (1) is assumed to be of a particular (diffusive) type. For example, no memory effects are considered while passing over a free energy barrier.

A variable that impacts the average we compute and is not sampled appropriately in a straightforward MD simulation is called a Hidden Slow Variable (HSV). During a simulation a HSV is restricted to only a subset of the thermally available conformations. As the experimentally measured observable depends on the HSV, results of MD simulations are influenced by the initial conditions or on the length of the trajectories. Different simulations may have different “frozen” values and hence different permeation times and/or free energy landscapes. Since simulations of membranes are expensive, careful evaluation of the presence of HSV in permeation calculations is not routinely done. In the present manuscript we examine this possibility for the permeation of a molecule of a moderate size through a DOPC membrane.

To determine the presence of HSV the sensitivity of the results to initial conditions is examined. Ergodic measures can be used[35] to assess relaxation times, however, membrane simulations offer an additional interesting option. We expect the bilayer membrane to be symmetric (on the average) with respect to its center. Averages computed with simulations should show a similar behavior approaching the membrane center from below or from above (the membrane plane center is at Z=0). The calculation reported in reference [9] indicated that the free energy barrier for both directions is similar, however it was not identical and the overall mean first passage time differed by a factor of about 150 (difference from hours to minutes).

What is (or are) the HSV that can explain this difference? We discuss in the present manuscript two candidates for HSV. The first is the overall orientation of the molecule and the second is a conformational transition within the molecule. The molecule under consideration, NATA (N-acetyl-L-tryptophanamide), is not spherically symmetric and can change conformation from a helical turn to an extended chain state. From the current and prior simulations [9], we know that the backbone polar group is kept as close as possible to the aqueous solution. Hence, the molecule is undergoing significant orientation shift when passing the membrane center when the direction of the nearby water interface changes. The reorientation makes the permeation more complex and is likely to affect permeation time.

The other candidate for HSV is the internal torsion ψ of NATA which is a good order parameter for the conformational transition from a α-helix to an extended chain state. The conformational change impacts the overall size of the permeant and the number of exposed hydrogen bonding groups and hence is likely to impact permeation as well.

Yet another potential contribution includes slow relaxation of the membrane itself. It is known that the membrane fluctuates on a broad range of time scales that extend to hours and days (e.g., for phospholipid flips[36]). It is possible that the two halves of the membrane that were used in the simulations have significantly different packing and chain configurations. Connecting alternate membrane states may require long relaxation times to make them similar on the average. Finally, the presence of permeating water molecules may reduce the energy of dangling hydrogen bonds in the small solute (at the cost of transporting water molecules to hydrophobic environments). In the present manuscript we examined (at least to some degree) the first two options and we leave the last complex option of membrane motion for future work.

The energetic and kinetic contributions of the proposed HSVs to the permeation process are evaluated by explicit calculations of the kinetic and (or) calculation of the potential of mean force. In the present manuscript we show that the contributions of orientation and conformational transitions are reducing the variance between the permeation results of the two layers. However they are unlikely to explain all the observed differences. So, while more insight into the mechanism of the transport has been obtained the search for HSVs that impact permeation is not over.

We examine the coupling of the translocation process to other slow variables (in addition to Z) by Milestoning theory [37]. Milestoning enables the investigation of stochastic dynamics in multi-dimensional systems at highly extended time scales. It provides the free energy landscape (similar to umbrella sampling), and also computes directly the kinetics without using additional phenomenological modeling of the dynamics as in Eq. (1).

We mention two recent attempts to introduce additional variables besides the Z coordinate to permeation studies. Jo et al. used a two-dimensional view of the flip-flop of cholesterol between the two leaflets of the bilayer [38]. They computed a two-dimensional free energy by umbrella sampling that included the Z coordinate and the tilt angle of the cholesterol ring. With this free energy surface, the string method [39] was used to compute most probable flip-flop paths. In another more recent study, and closer to the problem of molecular permeation, Laio and collaborators used metadynamics to enhance the sampling of permeation of ethanol through a POPC bilayer [40]. The results of these sampling are used to obtain equilibrium free energy estimates. The free energy landscape and a maximum likelihood procedure to estimate a diffusion tensor are combined in a kinetic Monte Carlo scheme to estimate permeation times.

2. Milestoning

In this section we define and briefly explain the main components of Milestoning; for more details see [9,37].

Milestoning is a theory and an algorithm to compute kinetics and thermodynamics based on atomically detailed simulations. It consists of the following steps (Figure 1): (a) Anchor definition, (b) Definition of milestones, (c) Sampling transitions between milestones, and (d) Solving the Milestoning equation. Each of these steps is further discussed below:

1. Anchor definition. Anchors are phase space points that are defined in a reduced reaction space and provide a coarse sample for the process at hand. The set of anchors is denoted by Y_i while the set of the atomically detailed phase space points is denoted by X_n. In the present manuscript we use only the coordinates to define anchors. Anchors can be determined by prior thermodynamic sampling (e.g. by replica exchange[41,42]), by reaction path calculations [43,44], or by chemical intuition[34,45]. For example, studies of peptide folding and unfolding in an explicit solvent use only the backbone dihedral angles of the peptide as the coarse variables [42,46]. In the present example we use chemical intuition to choose the variables that define the reaction space as explained in the Methods section.

2. Definition of milestones. Every configuration of the atomically detailed simulation is mapped into a domain of a single anchor (or at most two) making it possible to define a trajectory in anchor space. A transition between anchor domains is determined by passing a milestone, a hypersurface separating the spaces of two anchors. We denote a milestone between anchors i and j by M_ij. It is the set of points that are closer to the anchors i and j compared to any other milestone k. The distance of point Y at milestone M_ij from anchor i is d(Y,Y_i)² = (Y – Y_i)^t (Y – Y_i) + Δ² and from anchor j is d(Y,Y_j)² =(Y–Y_j)^t(Y–Y_j) where Δ is a constant shift (0.1 Å in the present simulation) to avoid milestone crossing [47].

3. Sampling transitions between milestones. In Milestoning we do not compute atomically detailed trajectories from the reactant to the product states. Instead we compute trajectories between milestones. Trajectories initiated at milestone M_ij are integrated forward in time until they hit for the first time another milestone M_ij. The identity of the terminating milestone and the time of termination are recorded for further processing. In particular we are interested in the kernel function K_{ij jk}(t) which is the probability density (in time) that a trajectory started at milestone ij will hit for the first time milestone jk exactly after time t. It is estimated numerically as K_ij,jk (t) ≃ n_ij,jk (t) n_ij where n_ij is the number of trajectories initiated at milestone ij and n_{ij jk} (t) is the number of trajectories initiated at ij that hit for the first time milestone jk exactly after time t. The trajectories are initiated at M_ij from a first hitting point distribution (FHPD [37,47,48]), which is the probability density of phase space points that hit for the first time milestone M_ij (the last milestone that they cross previously was different from M_ij). For complex systems the analytical form of the FHPD is not known. We approximate it by the equilibrium distribution with filtering based on backward trajectories (Figure 1).

4. Solving the Milestoning equation. With the kernel K_{ij jk}(t) we consider the Milestoning equation[49]

$$q_{\mathit{\text{ij}}}(t)=p_{\mathit{\text{ij}}}\delta (t^{+})+\sum _{\mathit{\text{ki}}}\underset{0}{\overset{t}{\int }}{q}_{\mathit{\text{ki}}}(t\text{'})K_{\mathit{\text{ki,ij}}}(t-t\text{'})\mathit{\text{dt}}\text{'}$$ (2)

where P_ij is an initial condition (the probability that the last milestone that was crossed at time t=0 was ij). The number of trajectories that passes milestone ij per unit time (the flux) at time t is q_ij(t) which is the vector of functions of length of the number of milestones that we seek. The Milestoning equation is a convolution that can be solved with Laplace transform techniques to obtain quantities of interest [37,50]. For example, we consider the overall mean first passage time (MFPT). It is the average first time the system hits the last milestone f after being initiated according to the probability vector p_ij≡(p)_ij

$${\langle \tau \rangle }_{\mathit{\text{ij}}\to f}={(\mathbf{p})}_{\mathit{\text{ij}}}{(\mathbf{I}-\mathbf{K})}^{-1}\mathbf{t}$$ (3)

where 〈τ〉_ij→f is the MFPT for the transition from milestone ij to f, I is the identity matrix, and K is the stationary transition matrix given by ${(\mathbf{K})}_{\mathit{\text{ij,km}}}=\underset{0}{\overset{\infty }{\int }}{K}_{\mathit{\text{ij,km}}}(t)\mathit{\text{dt}}$. The matrix K is chosen such that K_f,kl=0 ∀kl , an absorbing boundary condition. Finally, t is a vector with the lifetimes of all the milestones ${(\mathbf{t})}_{\mathit{\text{ij}}}=\sum _{\mathit{\text{jk}}}\underset{0}{\overset{\infty }{\int }}t{K}_{\mathit{\text{ij,jk}}}(t)\mathit{\text{dt}}$. We can also use the Milestoning equation to determine the stationary (time independent) fluxes q_stat between the milestones. The stationary flux is determined by the matrix equation

$${\mathbf{q}}_{\mathit{\text{stat}}}(\mathbf{I}-\mathbf{K})=0$$ (4)

To obtain the stationary state we set a cyclic boundary condition.

$$K_{\mathit{\text{f,lm}}}=\left\{\begin{array}{cc}1\hfill & \hfill \mathit{\text{lm}}=\mathit{\text{ij}}\hfill \\ 0\hfill & \hfill \text{otherwise}\hfill \end{array}\right\}$$

Finally the stationary probability and the free energy that the last milestone that was passed is ij, is given by

$${({\mathbf{p}}_{\mathit{\text{stat}}})}_{\mathit{\text{ij}}}={({\mathbf{q}}_{\mathit{\text{stat}}})}_{\mathit{\text{ij}}}{(\mathbf{t})}_{\mathit{\text{ij}}}{F}_{\mathit{\text{ij}}}=-kT\text{log}\left[{({\mathbf{p}}_{\mathit{\text{stat}}})}_{\mathit{\text{ij}}}\right]$$ (5)

The stationary flux, q_stat, is determined up to a multiplicative positive constant c. Hence if q is a solution so is cq. A way of fixing the value of c is to require that the sum over all probabilities (Eq. (5)) is equal one. However, for stationary fluxes and studies of relative fluxes, this is not convenient. Most of the times (an exception is described below) we set the flux at the first milestone to unity, i.e. q₁=1.

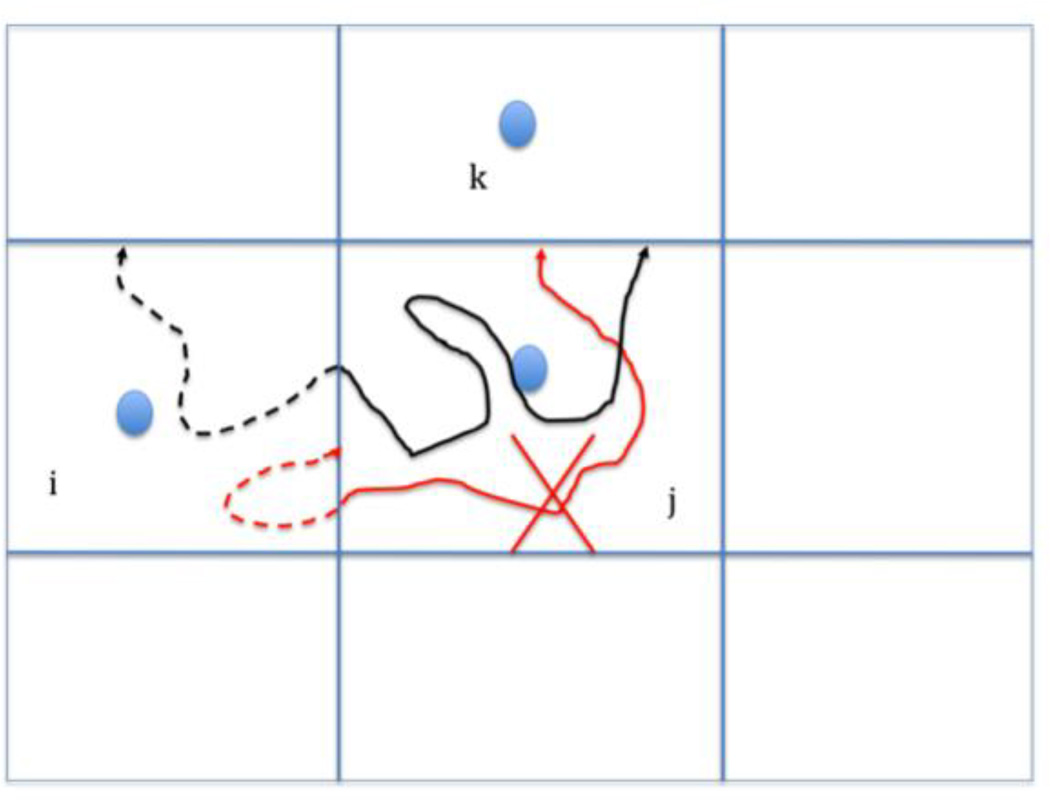
Figure 1.

A schematic representation of the Milestoning algorithm. The blue filled circles denote anchors and the straight blue lines represent the milestones (interfaces) separating the different anchor domains. In Milestoning we estimate the probability that a trajectory initiated at a milestone ij will hit for the first time another milestone jk at time t. We estimate this probability by running a large number of trajectories from ij and record the number of and times of trajectories that hit milestone jk for the first time. The black and red curves are trajectories initiated at milestone ij and terminated at milestone jk. The dashed lines denote time-backward trajectories and are used to check if the initial phase space points are sampled from a first hitting distribution. The black trajectory is acceptable (the backward trajectory reached a different milestone before hitting again the initial milestone) while the red trajectory is not (it returns to the initiating milestone, before hitting another milestone). See Method and reference [37] for more details.

The transitions between milestones are quantified by the stationary fluxes and create a kinetic network. The network is analyzed to elucidate mechanisms of reaction and the contributions of alternative reaction spaces [46]. We will use these tools to better understand the permeation process through the membrane.

Since the most common experimental observable for membrane transport is the permeation coefficient, P, we outline below the direct calculations of P using Milestoning. The permeation coefficient is defined as the flux normalized (divided) by the concentration difference in steady state conditions. The fundamental entity of Milestoning is the flux, q, given by Eq. (4) and normalized such that the initial flux is unity. The final flux q_f under stationary conditions is the permeation coefficient once written in the proper units. We write p=(J₁/c)q_f where q₁=1. The flux J₁ is the number of molecules that pass in unit area and unit time through the first milestone and c is the concentration gradient. The first milestone is in aqueous solution (Fig. 2), which makes it possible to estimate its entry flux from a free diffusion model.

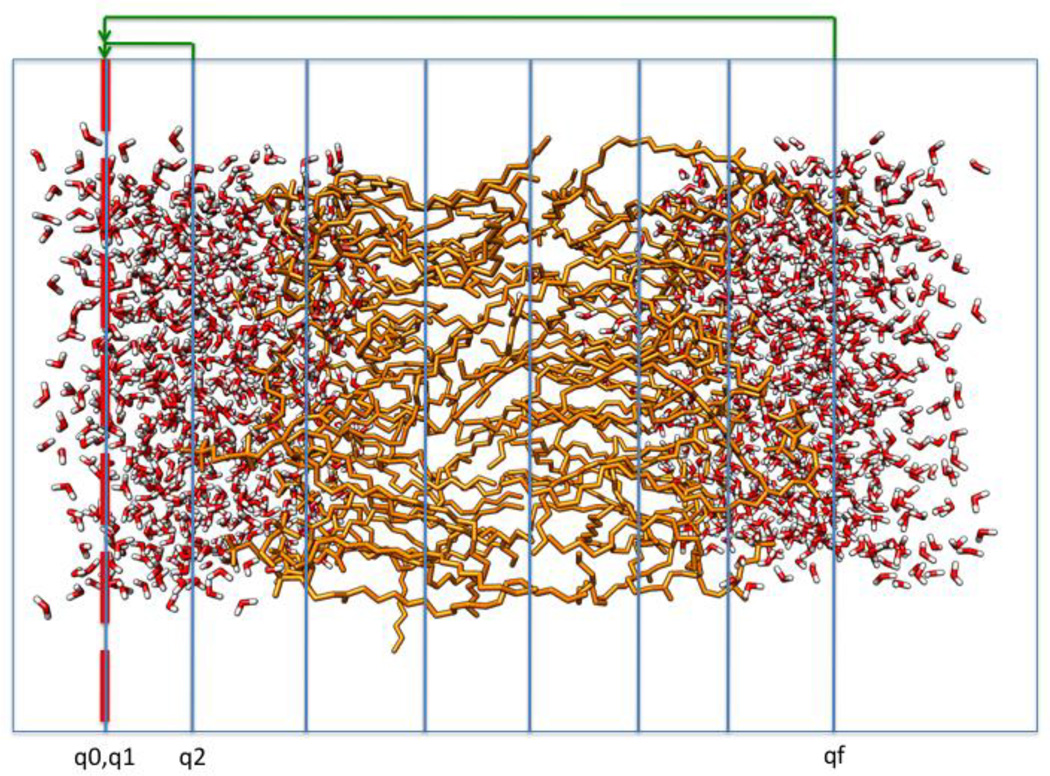
Figure 2.

A schematic representation of the system used to compute the permeation coefficient. We used one-dimensional set up of milestones denoted by blue lines in the figure. We also used cyclic boundary conditions in which trajectories that reach the last milestone q_f are returned to the first milestone q₁ with probability one. Trajectories that return from milestone q₂ to milestone q₀ are also returned with probability one to q₁. See text for more details.

The concentration c is the number of molecules divided by volume c=n/V. The flux is J=n/(At) where A is a cross section of the volume and t is the time. Therefore we have J/c=l/t. We estimate this diffusion flux with over damped Langevin dynamics in one dimension. The only required parameter for the Langevin Eq. is the diffusion constant, D. It is extracted from atomically detailed simulations of the permeant in aqueous solution (see Methods).

To model P we set dual cyclic boundary conditions. The first condition (as discussed immediately after Eq. (4)) is on the final milestone. Every molecule that makes it to the final milestone is moved to the first milestone, i.e.

$$K_{f,\mathit{\text{ij}}}=\left\{\begin{array}{cc}1\hfill & \hfill \mathit{\text{ij}}=1\hfill \\ 0\hfill & \hfill \mathit{\text{otherwise}}\hfill \end{array}\right\}$$

The second adjustment is to add a solvent milestone (number 0) to which the first membrane milestone (milestone 2) is connected. Milestone 0 has the same physical location as milestone 1 but the velocity has an opposite direction. In milestone 1 the velocity is pointing to the membrane and in milestone 0 it is pointing to the solvent. Milestones 0 and 1 are a pair of directional milestones [47]. A molecule that arrives to milestone 0 is moved with probability one to milestone 1 (Fig. 2):

$$K_{0,\mathit{\text{ij}}}=\left\{\begin{array}{cc}1\hfill & \hfill \mathit{\text{ij}}=1\hfill \\ 0\hfill & \hfill \mathit{\text{otherwise}}\hfill \end{array}\right\}$$

To summarize, the permeation coefficient is given by the following formulaes

$$P=q_f^{\prime }$$ (6)

where q’_f is determined by

$$\mathbf{q}\text{'}(\mathbf{I}-\mathbf{K})=\mathbf{0}\&{q\text{'}}_1=J_1/c_w$$ (7)

where c_w is the concentration of NATA in aqueous solution.

3. Methods

3.1 Molecular Dynamics

The starting set of configurations was taken from simulations performed previously[9]. Briefly, the simulation box contains 40 DOPC lipid molecules, 1542 water molecules and 2 NATA (N-acetyl-L-tryptophanamide) molecules. The size of the simulation cell is 37×37×75 Å, with the Z axis perpendicular to the bilayer surface. The side chain and backbone atoms of NATA are modeled with the OPLS united-atom force field [51] and the Berger force field [52] parameters were used for the lipid molecules. Water molecules were represented with the SPC model [53]. Periodic boundary conditions were applied in the three spatial directions. The long-range component of the electrostatics interaction was calculated using the smooth Particle Mesh Ewald method [54] with a grid of 32×32×64 as implemented in the program MOIL[55] including the newest GPU implementation of the program.[56] The real space cutoff for the electrostatics and the van der Waals interactions was set to 9.0 Å. In all the simulations we constrain water bond lengths and angle with a matrix version[57] of the SHAKE algorithm[58], and r-RESPA[59] was used to have a dual time stepping; the reciprocal-space component of the Ewald sum was evaluated every 4 fs and the rest of the forces were evaluated every 1 fs.

3.2 Initial Flux

To compute the initial flux, J₁, we first estimated the diffusion constant of NATA in aqueous solution. We simulated NATA in a box of water of 64×64x64 ų for a period of 300 picoseconds (ps) (trajectory length of 300 ps is probably more than what was required). The time step was 0.5ps, and the grid for Particle Meshed Ewald was 64³. We calculated the diffusion coefficient from the relationship 2Dt=〈x²〉.

The diffusion constant is used in over-damped Langevin simulations to estimate the incoming flux to the first milestone. The simulations are conducted in a one-dimensional box [0,l] with a test boundary at l. Initial coordinates in the box are distributed uniformly in the interval [0,l] and trajectories are conducted until they “hit” l. Their time is recorded and they are terminated. Displacements for Brownian trajectories are generated from a normal distribution with zero mean and variance of 2D δt where δt is the time step. Trajectories are conducted to estimate J₁/c_w as n_p/n at the absorbing boundary where n_p is the number of trajectories that hit l per unit time under constant flux conditions and n is the total number of trajectories.

More formally, we define the ratio of the total number of trajectories that hit l at time t normalized by the total number of trajectories as $N(t)/N_{\mathit{\text{total}}}=[\sum _i\delta (t-t_i)]/N_{\mathit{\text{total}}}$ where the index i is running over the individual trajectories and N_total is the total number of trajectories. Since we seek an expression for a steady state flux an average over the time origin, τ, is computed, where τ is equally distributed along the time line. We have

$$\frac{J_1}{c_w}=\frac{{\langle N(t+\tau )\rangle }_{\tau }}{N_{\mathit{\text{total}}}}=\frac{\sum _{i,j}\delta (t-(t_i+{\tau }_j))}{\sum _{i,j}1}$$ (8)

The simulations are conducted until J₁/c_w converges to a stationary value. Note that the calculations associated with Eq. (8) are inexpensive. The permeation coefficient is finally computed as outlined in Eq. (6) and Eq. (7). Note that the ratio does not depend on the box length as long as the condition of constant concentration is kept. Hence, doubling the length of the box doubles the number of trajectories.

3.3 Definitions of the Milestones

In a previous paper[9] we performed umbrella sampling[20] and Milestoning[37,60] simulations to determine the potential of mean force of insertion of NATA molecules into the system and the kinetic of permeation along the Z coordinate. Specifically, two NATA molecules were inserted (one in each leaflet) and the separation between their centers of mass was kept at Δz = 32 Å by applying a harmonic restraining force constant of 7 kcal/mol Å⁻² to each molecular center of mass. This separation distance was large enough that their correlation can be ignored. The location of the biasing potential was displaced by 1 Å in consecutive windows of the umbrella sampling simulation. The use of two NATA molecules allowed us to cover the range from z = −32 Å to z = 32 Å with only 33 windows. Each of these simulations was run for 50 ns.

Here we go beyond the one-dimensional permeation coordinate used previously. Starting configurations for the current work were selected from the last 5 ns configurations saved of the previous 50 ns simulations. We sample structures at fixed values of the normal to the membrane, from z = −30 Å to z = 30 Å with a 2 Å separation between them. We also added a new coarse variable that measures molecular orientation. Specifically, let us denote as r_orient=r_back–r_side the vector connecting the two centers of mass of the backbone, r_back, and the side chain, r_side. Then, the second coarse-grained coordinate that we use to assess the molecular orientation is

$$z_{\mathit{\text{orient}}}=r_{\mathit{\text{orient}}}^t\cdot e_z$$

where e_z is a unit vector along the Z axis (the normal to the membrane plane).

For a given value of z we sampled seven different values of the orientational coordinate ranging from z_orient = −6 Å to z_orient = −6 Å with a 2 Å separation. The combination of z and z_orient values we are considering gives a total of 217 different anchors, evenly distributed in the two-dimensional space defined by these two coordinates (those anchors are shown in Figure 3).

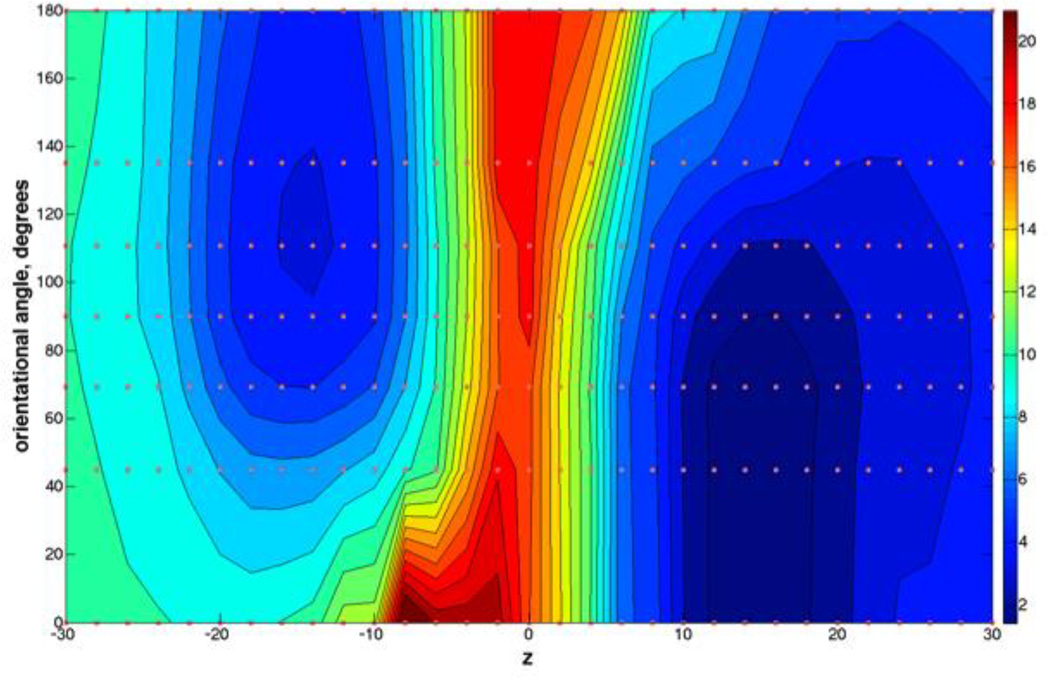
Figure 3.

The two-dimensional free energy surface for the permeation of NATA through a DOPC bilayer, along the membrane axis Z and the orientational coordinate of NATA (expressed as an angle in this and the next figures). The free energy landscape is a solution of the Milestoning equation, Eq. (5). The energy units are in kcal/mole and the color code is provided in the sidebar (blue corresponds to more probable configurations of the system, and red to less populated). The figure also shows (brown dots) the location of the anchors used in the simulation. If the permeant orientation were the HSV that influences the asymmetry in the free energy landscape our explicit enhanced sampling of the orientation would yield a symmetric graph with respect to the membrane center. This is not the case. The minimum on the right is deeper and the permeation on the left side is faster. The difference in well depths of about 3 kcal/mol can explain the difference in the kinetics of the two halves. See text for more details.

From this set of anchors we constructed a set of 1512 milestones (interfaces dividing domains associated with these anchors). These sets of milestones were constructed such that every anchor i connects directly with 8 adjacent anchors, and the interface corresponding to the transition i→j is different from the interface associated with the transition j→i (See 2.b). The anchors at the borders of the z and z_orient two-dimensional space are connected with five other anchors (or only three if the anchors are at the corners).

3.4 First Hitting Point Distribution

Having defined this set of milestones, we approximate the FHPD distribution by sampling configurations with Boltzmann weights (canonical ensemble) that are harmonically restrained to the neighborhood of each of the milestones, as described in[9,47]. Initial configurations for this sampling were taken from the last 5 ns of the 50 ns restrained simulations performed previously. The canonically restrained distribution in the two-dimensional milestones was generated by computing 7 ns of iso-kinetic trajectories in each of the milestones that was shown to yield the canonical distribution[61]. The two NATA molecules were constrained in these simulations. In total, we performed 1512/2=756 of such simulations since we exploit the presence of two permeating NATA molecules in a single membrane. The 7 ns timescale was enough to provide a thorough sampling on these more spatially localized milestones. From these sampling simulations about 1000 configurations were saved for the next step of calculations in which we filter from the ensemble of canonically sampled structures, the first hitting point distribution [37,47,48].

Specifically, starting from the configurations saved in the sampling step we removed the harmonic constraint in one of the two NATA molecules and performed “backward” MD simulations in the system (the harmonic constraint was maintained on the second molecule). During the simulation we check if the unconstrained solute hits a neighboring milestone before hitting the initial milestone (Figure 1). If this was the case, the initial configuration and velocities (drawn according to a Maxwell distribution at 300 K) are considered a first hitting point for this current milestone and the phase space data is saved for the final step of the Milestoning procedure. If during this backward simulation the unconstrained permeant hits the starting milestone first before hitting a neighboring one, then we stop this trajectory and discard this phase space point. This process was repeated until we collected from 100 to 480 first hitting point configurations for each milestone.

3.5 Computing the Transition Kernel

In the final step, we performed unconstrained simulations starting with the first hitting points obtained from the previous step. In this case, we performed “forward” MD simulations by reversing the sign of the initial set of velocities saved in the previous step. The run is stopped when a neighboring milestone is hit regardless of whether the initial milestone is crossed or not during the simulation. The information saved in this step is the identity of the neighboring milestone that is hit and the time it took for this to happen. We extract the matrix (K)_ij,jk and the vector of the lifetimes of the milestones – (t)_ij. The matrix and the vector are used in the Milestoning calculation outlined in Eq. (2)–(7).

Overall we have run a total of 119,819 trajectories with accumulated simulation time of 5.2 microseconds. The average time per trajectory was 43 picoseconds. Hence the simulations exploit parallelization very efficiently since the trajectories are independent.

3.6 MaxFlux

The calculation of kinetic networks in general and the present investigation in particular can be complex and difficult to analyze. A useful interpretation tool is the extraction of reaction coordinates and specific mechanisms. While “best” reaction coordinate is debatable[39,62–68], a useful choice would be a pathway that carries the maximum flux (MaxFlux[69]) of trajectories from reactants (one side of the membrane) to products (the other side of the membrane) and therefore makes the most significant contribution to the reaction. In the present network, the nodes are the anchors and the weight of the edges connecting two anchors i and j are the net fluxes w_ij=q_ij–q_ij where q_ij and q_ij are the stationary fluxes going from anchor domains i→j and from anchors j→i, respectively[37]. Those fluxes are obtained by solving the Milestoning equations (section 2.d). Given the net fluxes the MaxFlux path on the network is computed using the following algorithm: [37]

1. Find the edge with the smallest weight on the graph that corresponds to the milestone with the smallest flux. Mark that edge for elimination.

2. Check if there is still a path connecting the initial and final state after removing the edge marked in the previous step. If there is still a path, then remove the edge from the graph. If there is no such a path, then this edge is essential for the MaxFlux path; thus it is kept, but is not considered any longer for removal in step 1.

3. Return to step 1 until a continuous path from reactant to product was determined.

The collection of all edges that remain after running the algorithm is the MaxFlux path connecting the initial and final states in the discrete representation of the process given by the Milestoning calculation. In this discrete representation a transition state is the edge in the MaxFlux path with the smallest weight (flux). A second best MaxFlux path can be obtained by eliminating the transition state (edge along the path with minimal weight) found in the first MaxFlux path since our focus is typically on the bottleneck or the edge with the lowest flux. A third best MaxFlux path is obtained by further eliminating the transition state of the second best MaxFlux path, and the process can be repeated to obtain additional paths.

5. Results

5.1. Free energy and Permeation Pathways

The equilibrium probability distribution for the system was obtained by solving the Milestoning equation (Equation (5)). The corresponding 2D free energy surface as a function of the membrane axis Z and the orientational direction is shown in Figure 3 and Figure 4. Figure 3 shows the probability distributions obtained by solving the Milestoning equations for the whole membrane, and Figure 4 shows an average of the results over the two halves of the membrane permeation in Figure 3, i.e. enforcing the expected symmetry. In the most populated regions at the interface between the polar and hydrophobic groups of the membrane (at about |Z|=15 Å), the permeant favors an orientation in which most of its backbone atoms point to the closest water phase (orientational angle larger than 90° on the left side and smaller than 90° on the right side). There is an increase of free energy when the permeant moves from that region to the center of the bilayer. This barrier region is narrower when the orientational angle is between 65° and 115° (Figure 4). This equilibrium view of the permeation process suggests that at the center of the membrane NATA prefers an orientation where the indole ring and polar atoms are perpendicular to the membrane normal. More tilted orientations at the center of the bilayer are less beneficial for transmembrane diffusion.

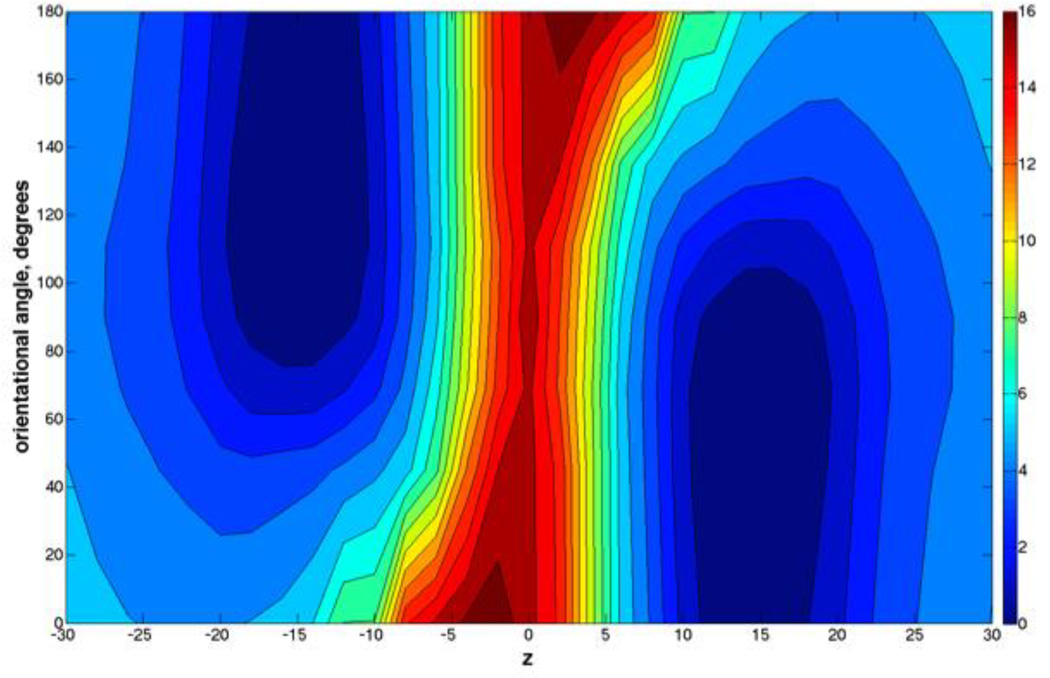
Figure 4.

The two-dimensional free energy surface for the permeation of NATA through a DOPC bilayer, along the membrane axis z and the orientational coordinate of NATA described in the text. At the center of the membrane z = 0 Å. An orientation of 90° corresponds to a NATA molecule being perpendicular to the membrane axis. In the figure, blue corresponds to more probable configurations of the system, and red to less populated. The plot is a symmetric average of the results of Fig. 2.

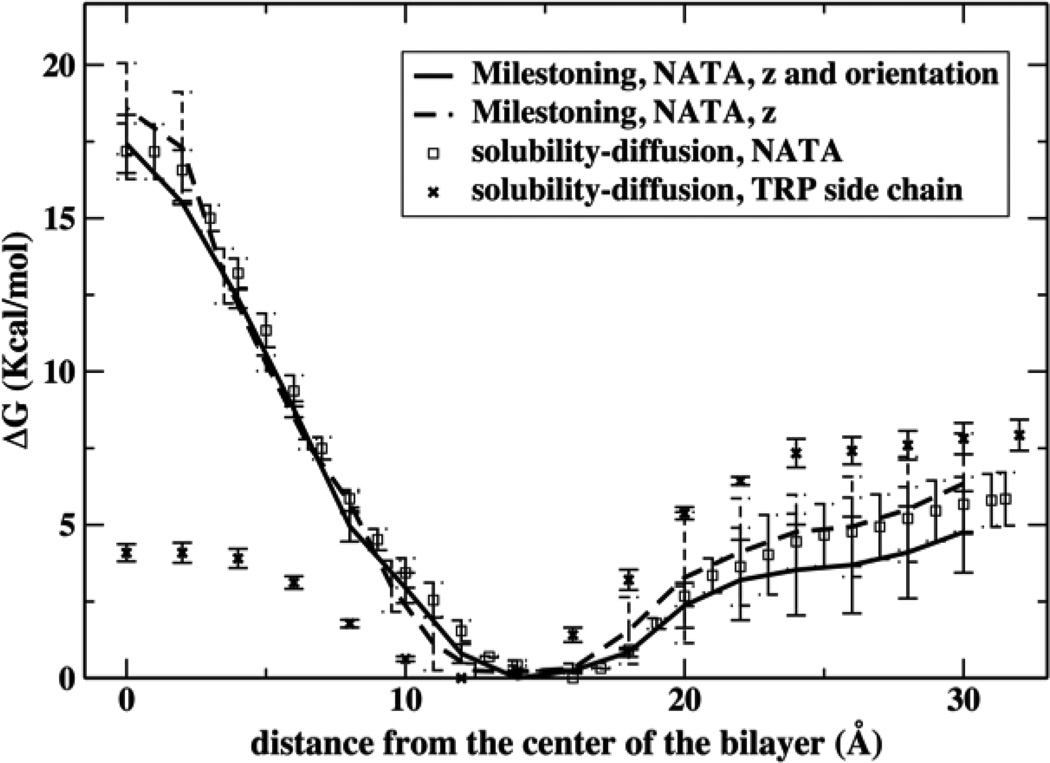
To compare with previous free energy profile estimates we sum the probabilities along the orientation coordinate and took the logarithm to obtain a one dimensional free energy profile along the membrane axis Z. Figure 5 shows the current results for NATA permeation compared with our previous Milestoning estimates using a one dimensional reaction coordinate, and results using the solubility diffusion model (SDM). Qualitatively they all show a preferential location of NATA to be at the interface between the hydrophobic tail and the glycerol region of the lipids. A barrier is present at the center of the bilayer with a relative free energy in the range between 16.5 to 20 kcal/mol. The figure also displays the free energy profile for the indole ring of tryptophan. This less hydrophilic permeant compared to NATA shows a smaller barrier at the center. Note the lower variance of the SDM results. We should keep in mind however, that the SDM is a simpler equilibrium model that is based on overdamped Langevin model throughout the process. Its simplicity is of course an advantage, and makes the estimate of a fewer parameters more stable statistically. However, it is not clear if the model is correct dynamically (neglect of memory effects). It is also not obvious how to use a SDM or a similar model to incorporate other HSVs. The calculation of diffusion constant and the MFPT theory for diffusion in high dimension is still under investigation [70] while the Milestoning algorithm is straightforward even in high dimension and for arbitrary (classical) dynamics. We therefore discuss in details only the Milestoning results.

Figure 5.

One-dimensional free energy profile for the permeation of NATA and an indole ring. The current results using a two dimensional description of the permeation process and then reducing the profile to one dimension are shown in the solid line. Previous one-dimensional results using Milestoning are shown with dash line and the solubility diffusion model is presented with square symbol. Also shown is the permeation free energy profile for tryptophan side chain with x symbol.

5.2. Mean first passage time

The mean first passage times for permeation of NATA from the water phase to the center of the bilayer were computed using Eq. (3) and the results are shown in Table 1. The permeation time ranges from 5 minutes to about 2 hours while the experimental times are of order of a few hours[9]. The previous one-dimensional results using Milestoning showed a larger value for one of the layers and a larger discrepancy between the timing of the two layers. The estimate using the solubility-diffusion equations is slightly faster than our current results. But the results for the three methods are similar. Clearly the slower permeation for the positive side of the membrane repeats in all simulations. As we discussed earlier for the free energy, the SDM shows smaller variance that is likely associated with a simpler model. Milestoning is more accurate in principle and more easily extendable to higher dimensions.

Table 1.

Overall permeation time for NATA through DOPC membrane. Dual time estimates are provided by the calculation of the mean first passage time from the aqueous solution at top or bottom to the center of the membrane (at Z=0).

Method	Average permeation time (in hours)	Time for individual leaflets (in hours)
2D Milestoning	1.0	1.9, 0.09
1D Milestoning	3.8	7.5, 0.05
Solubility-diffusion	0.23	0.41, 0.05

5.3. MaxFlux results

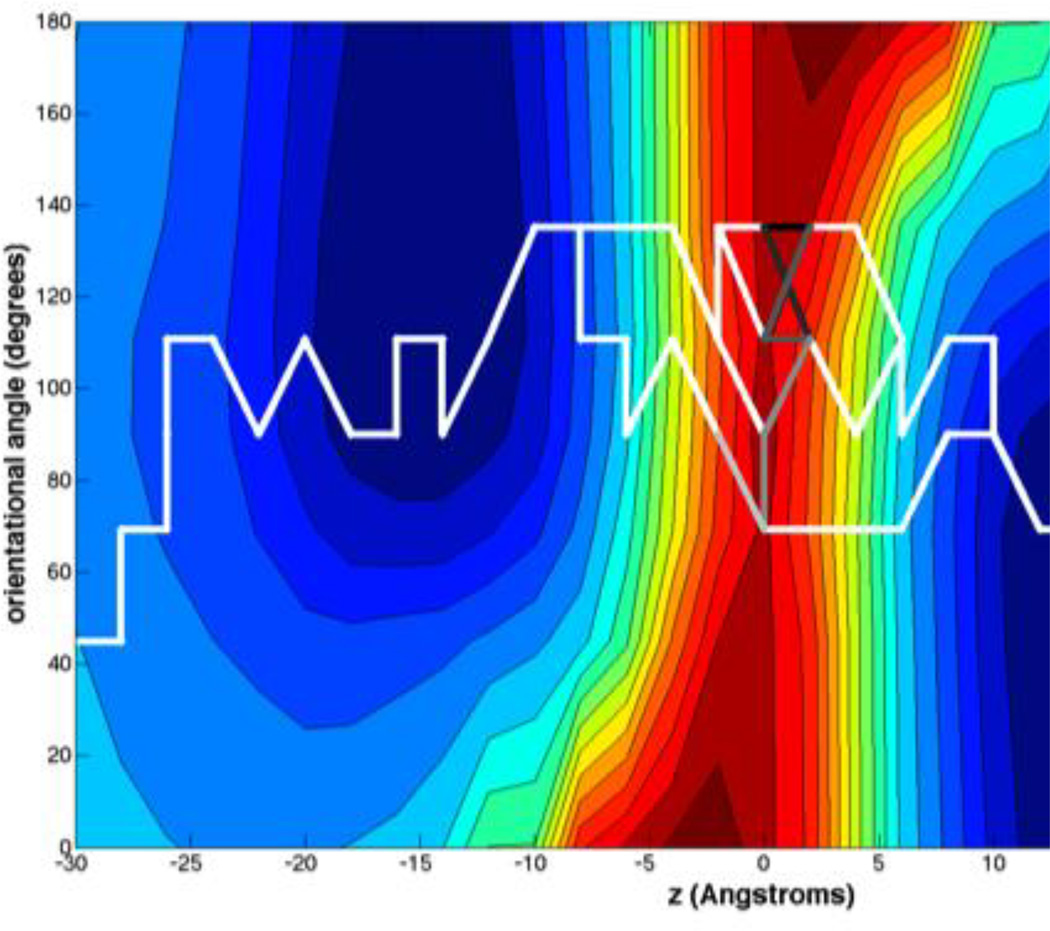
Figure 6 shows the Maxflux paths obtained by applying the Maxflux algorithm described in the method section to the two dimensional network of anchors in the Z and Z’ space. The figure displays the seven best Maxflux paths that are represented in the figure by the collection of edges that remain after solving the algorithm. The difference of the magnitude of the flow between the first and seventh best MaxFlux paths is a factor of ten, so many of these paths should be relevant for the permeation process. The different paths only differ in the central region of the membrane, in which an orientational flip-flop occurs and the permeant leaves one leaflet and enters the second one. For all the paths shown when the permeant moves from z= −8 Å to z = 14 Å, the orientational angle changes by 90 degrees from 135° to 45°. At the membrane center (z = 0 Å) four anchors are involved in the paths with orientational angles of 69°, 90°, 111° and 135°. For the path with maximum flux (represented with the black segment in the figure) the orientational flip-flop only occurs after the permeant has crossed through the membrane center. We computed the best MaxFlux for trajectories moving in the opposite direction and found similar results: that the permeant starts to rotate only after it has passed the center of the bilayer. The transition state of all of the MaxFlux paths (colored with different shades of gray) involves anchors at z = 0 Å (all seven of them), z = 2 Å (five of them) and z = −2 Å (one of them), so for 5 paths the transition state is observed after the permeant has just crossed the center of the membrane.

Figure 6.

The seven best MaxFlux paths for permeation of NATA through the membrane. Note the overall curved shape of the path that tends to visit the minima on the left and on the right when crossing the central barrier. The transition state for each of the paths are colored with different grays (the fastest the transition the darkest the gray color). The paths are not symmetric with respect to the center due to discretization (grid) errors.

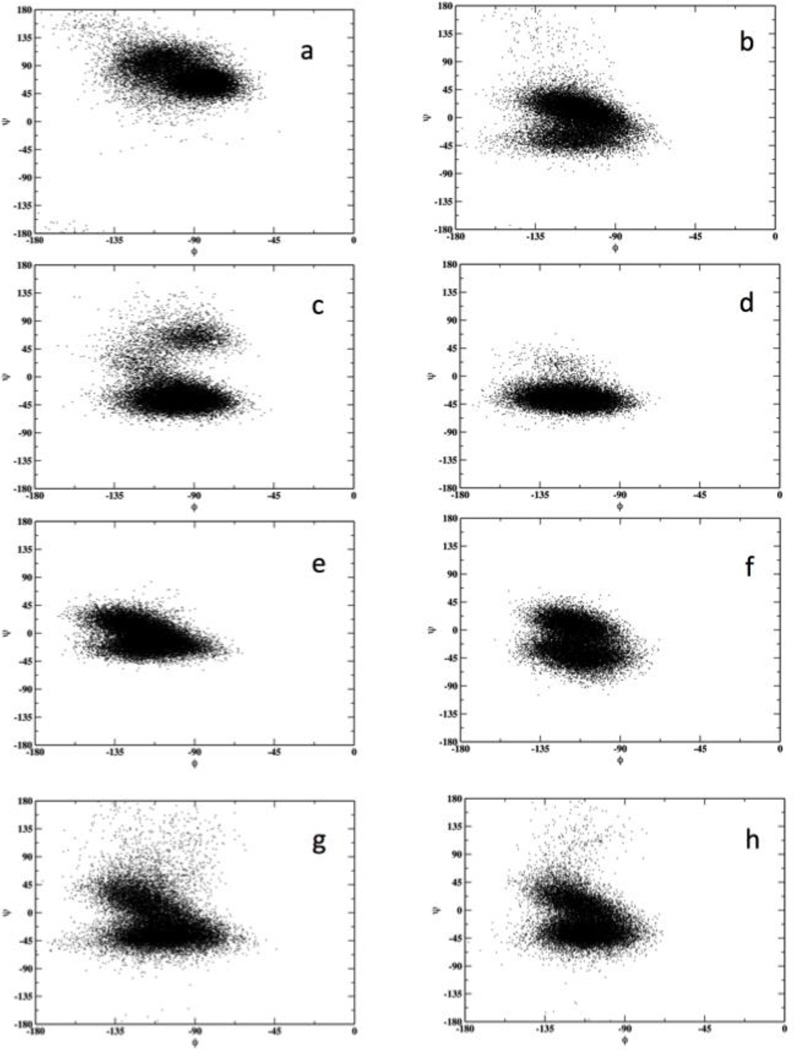
5.4 Backbone torsion angles

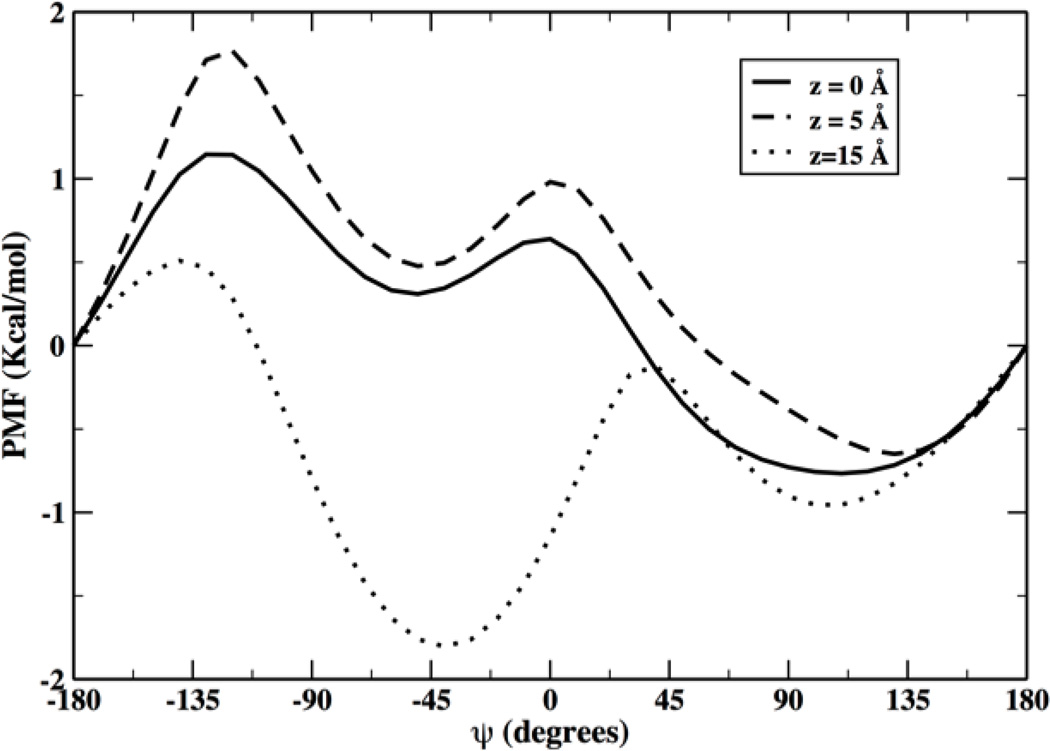
Figure 7 shows representative variations of the backbone dihedral angles of NATA molecules while moving inside the membrane. When the molecule is deeper inside the negative Z layer (left panels, a and c) it tends to obtain an extended conformation while it is more helical in areas of the bilayer closer to the water phase (e). The right panel (positive Z layer) shows a different behavior close to the membrane center with a more helical conformation. The next figure (Figure 8) shows the potential of mean force along the dihedral ψ angle for fixed Z values. An extended conformation at small absolute Z values is more stable according to these calculations.

Figure 7.

Sampling of the backbone dihedral angles (φψ) of NATA for different locations along the Z axis. The left side panels correspond to the layer with negative values of Z and the right side to positive values. (a) and (b) |Z| = 0 Å, (c) and (d) |Z| = 4 Å, (e) and (f) |Z| = 15 Å, (g) and (h) |Z| = 30 Å. Positive Z values correspond to slower permeation.

Figure 8.

Potential of mean force for NATA along the dihedral angle ψ for three different locations inside the membrane (z = 0 Å, z = |5| Å and z = |15|). The potential of mean force was computed with no presence of permeating water molecules at the membrane center (which sometimes are seen to follow NATA towards the center of the membrane[9]).

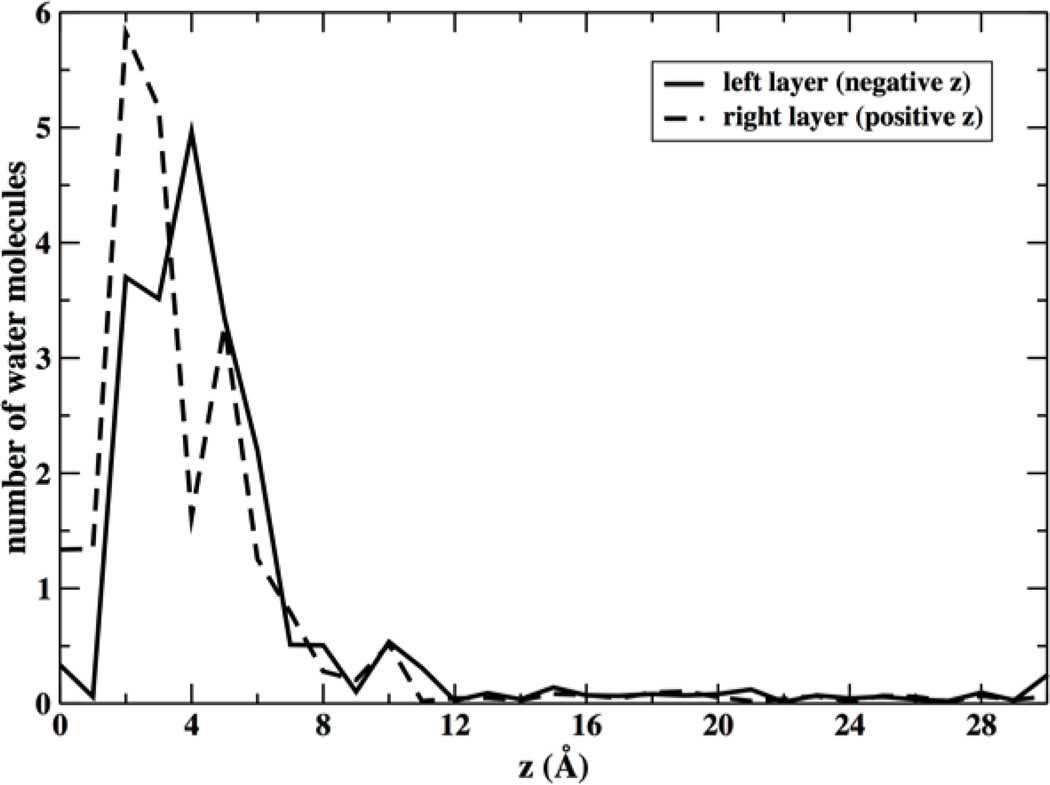
The negative Z layer explored the extended conformation but the positive layer significantly less. We also observed that the latter layer showed more water molecules coming closer to the center than the negative layer (Figure 8). The difference between the helical and the extended chain configuration is of order of 1 kcal/mol when NATA is closer to the membrane center. If we assume that the energy difference between conformers reduces the overall barrier by the same amount, we expect a transition speedup of about exp(1/0.6)=5.3 at 300 K. This factor is lower than the observed speedup of ~20 in the permeation times (Table 1). Hence the conformational transition does not provide the complete answer to the permeation asymmetry of the two layers.

5.5 Permeation coefficient

We computed the permeation coefficient as described in the Milestoning and Method sections. The diffusion constant, D, of NATA in aqueous solution was estimated from the relations 2Dt=〈x²〉 to be 1.6·10⁻⁵cm²_/s. The estimate of J₁/c_w based on one dimensional diffusion model (Eq. (8)) gives J₁/c_w=251 cm/sec.

The Milestoning calculation provides two permeation coefficients estimated for each of the two halves of the membrane. The two results are used to grasp the values of the error bars for P. The permeability coefficient obtained from the Milestoning calculations are 8.8·10⁻¹⁰cm_/s and 4.3·10⁻¹¹cm/s for the first and second membrane halves respectively. The difference is quite large and suggests that we can determine the permeability coefficient only up to a factor of 20. A similar accuracy is obtained for the SDM in which the corresponding values are 1.91·10⁻¹⁰cm/s and 2.63·10⁻¹¹cm/s for both sides of the membrane. The difference here is smaller (a factor of about 10) but still significant and is within the difference between the two technologies. Given that the computational technologies are very different we find the agreement quite satisfactory. Unfortunately there are no measurements for the permeation coefficient of NATA. However, we reported in section 5.2 (and in reference [9]) a comparison between experimental measurements and simulations of the first passage time.

6. Discussions and conclusions

As discussed in the Introduction atomically detailed simulations of molecular permeation frequently use a model that is inherently one-dimensional. The model considers explicitly only the center of mass of the permeant and its projection along the normal to the membrane, Z. This choice implies that all other degrees of freedom are fast to relax on the Molecular Dynamics time scale and are in local equilibrium with the fixed value of Z. If this is not the case and there are Hidden Slow Variables (HSV) in the system then computations of averages will show high variance and will not be accurate, even if the time scale of the HSV is much shorter than the time scale of the transition along Z. We expect significant deviations from one-dimensional picture for larger and more complex permeant, such as the system studied here.

To determine the presence of additional HSV (besides Z) MD simulations are conducted independently for each of the membrane layers. In equilibrium the properties of each half must be the same. If the two MD averages show significant deviations then there must be HSV in the system that are sampled differently at each half. The computed MFPT for NATA permeation differed for both sides by a factor of about 150 in our previous 1D Milestoning[9]. We therefore searched for plausible slow coarse variables that may influence the rate.

If we identify these variables correctly then we could enhanced their sampling in a similar fashion to what we have done for the Z coordinate, by enhanced sampling techniques such us umbrella sampling [20], metadynamics [71], TAMD [31], TAMC [32] and Milestoning [42]. The advantage of using Milestoning in higher dimension is that the kinetic calculations are straightforward. This is not the case for SDM and variants since Jacobian factors and diffusion tensors require additional considerations. The enhancement of sampling should prevent dependence on initial conditions.

How do we identify these coarse variables? In the present manuscript we consider two options. We evaluate one of them in full (orientation) and for the second (backbone dihedral angles) we estimate the free energy landscape. We assumed that molecular orientation was a HSV and computed two dimensional free energy landscape and MFPT using Milestoning. The kinetic asymmetry of the halves was reduced from a factor of 150 (1D Milestoning), to about 20 (2D Milestoning). Although this 7.5 reduction of the MFPT asymmetry indicates that the orientation is a HSV, the fact that that the asymmetry did not vanish suggests that it is not the only HSV that contributes to the differences between the MFPTs. We also examined the energy landscape of the peptide conformational transition at different depths of the membrane. While some small differences were observed for the transition between the helix and the extended chain (of order of 1 kcal/mole) they are probably not sufficient to explain the factor of 20 of difference in MFPT passing each of the layers. Hence, our investigations, while providing considerable insight into the mechanism and pathways of the permeation, did not identify quantitatively all the sources that contribute to the permeation rate of NATA and that can explain the differences between the membrane layers.

We finally speculate on other candidates to HSVs that can be investigated in future work. For example, we observed in our simulations a different number of permeating water molecules that attach themselves to the translocating peptide. A larger number of water molecules is found in the layer in which the peptide permeates more slowly. It is not obvious if the water permeation is associated with the conformational change of the peptide. Hence water presence and peptide conformation may be strongly coupled and not independent, a possibility that we will explore in the future. Yet another possibility is that the phospholipid conformations and packing are different at each leaflet and the relaxation from one packing state to another is long on the MD time scale for each milestone slice. For each of the milestone we consider 7 ns in the two dimensional milestones and 50 ns for the one dimensional milestones calculated previously[9].

While the present manuscript is at least partially negative in the sense that it did not quantify all the factors that affect the permeation rate of NATA through a DOPC membrane we hope that it will help point out key challenges in membrane simulations and provide guidelines when quantitative prediction (and estimation of error bars) of permeation can be made.

Figure 9.

Average number of water molecules that penetrate inside the hydrophobic core of the membrane (within 10 Å from the membrane center) as a function of the location of the center of mass of the permeating NATA molecule z. As the permeant is getting closer to the membrane center (z=0) the number of water molecules at the hydrophobic core increases first but then decay when NATA is at the center. This decay is slightly different for the two layers.