Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2015 Jul 2;6(14):2826–2832. doi: 10.1021/acs.jpclett.5b01164

Anomalous Behavior of the Homogeneous Ice Nucleation Rate in “No-Man’s Land”

Hartawan Laksmono †, Trevor A McQueen ‡,§, Jonas A Sellberg ‡,∥, N Duane Loh †,⊥, Congcong Huang #, Daniel Schlesinger ∥, Raymond G Sierra †, Christina Y Hampton †, Dennis Nordlund #, Martin Beye ‡,∇, Andrew V Martin ○, Anton Barty ○, M Marvin Seibert ◆, Marc Messerschmidt ◆,, Garth J Williams ◆, Sébastien Boutet ◆, Katrin Amann-Winkel ∥,⊗ , Thomas Loerting ⊗ , Lars G M Pettersson ∥, Michael J Bogan †, Anders Nilsson ‡,∥,#,*
PMCID: PMC4507474  PMID: 26207172

Abstract

graphic file with name jz-2015-01164k_0003.jpg

We present an analysis of ice nucleation kinetics from near-ambient pressure water as temperature decreases below the homogeneous limit TH by cooling micrometer-sized droplets (microdroplets) evaporatively at 103–104 K/s and probing the structure ultrafast using femtosecond pulses from the Linac Coherent Light Source (LCLS) free-electron X-ray laser. Below 232 K, we observed a slower nucleation rate increase with decreasing temperature than anticipated from previous measurements, which we suggest is due to the rapid decrease in water’s diffusivity. This is consistent with earlier findings that microdroplets do not crystallize at <227 K, but vitrify at cooling rates of 106–107 K/s. We also hypothesize that the slower increase in the nucleation rate is connected with the proposed “fragile-to-strong” transition anomaly in water.

Understanding the phase transition from supercooled water or amorphous ice to crystalline ice is key to various fields ranging from cryobiology to atmospheric and astrophysical sciences.1−5 Accurate determination of ice nucleation kinetics and the involved structural transformation is essential for modeling atmospheric cloud formation and the corresponding thermostatting effects on the world climate. Most experimental studies of homogeneous ice nucleation (where ice here refers to crystalline ice unless noted otherwise) have been limited to temperatures above the homogeneous nucleation temperature (TH) of ∼232 K6−11 and below the homogeneous crystallization temperature (TX) of ∼160 K.12 This limitation is due to rapid crystallization upon deep supercooling which also prevents measurements of bulk water properties using standard techniques. In the context of ice nucleation, TH and TX correspond, respectively, to the median temperature limit of metastability of micrometer-sized liquid droplets at moderate cooling rates (from ∼1 K/min to ∼100 K/s) and to where amorphous ice crystallizes upon heating.1,8,11 Thus, the temperature region below TH and above TX is referred to as “no-man’s land”. As water is supercooled toward “no-man’s land”, the decrease in diffusivity (D) becomes more pronounced which may have a significant effect on the ice nucleation kinetics. There have been several simulations that observe in detail the formation of ice nuclei.11,13,10,14−18 However, the lack of direct measurements of the nucleation rate, the diffusivity and the solid–liquid (where solid refers to crystalline ice) water interfacial free energy (σsl) limits our knowledge on ice nucleation kinetics within this important region of the water phase diagram.

There have been several attempts to circumvent the limitation set by TH to achieve deeper supercooling and observe homogeneous ice nucleation events in “no-man’s land”. This is often done by increasing the sample cooling rate and reducing the sample dimensions to nanometer sizes that effectively decreases the nucleation probability.19−21 However, reducing the sample volume to such small dimensions also dramatically increases the surface-to-volume ratio and the sample internal pressure due to the reduced radius of curvature (described by the Young–Laplace equation). This may alter D, and thereby the bulk homogeneous ice nucleation rate (J), significantly22 such that it is no longer representative of bulk water at ambient pressure. For microdroplets, attempts to scale the nucleation rate with the surface area instead of volume improves the general agreement between different data sets,3,4 but surface nucleation has not been observed directly in such experiments.23 When applied to nanodroplets, the 2.5 nm subsurface layer used to analyze surface nucleation effects4 is about the size of the nanodroplets themselves, which makes the definition of subsurface volume ambiguous in nanodroplets.21 Therefore, using nanodroplets in ice nucleation experiments may represent water at significantly different conditions than in microdroplets that better represent bulk water at ambient pressure.

Within the framework of classical nucleation theory (CNT),24,25 the formation of an ice nucleus in metastable supercooled water requires overcoming a thermodynamic energy barrier (ΔF*) that includes the Gibbs free energy change to form bulk ice and the Gibbs free energy increase associated with making an interface. This ΔF* is strongly dependent on σsl and to some extent on the increase in pressure via the change in chemical potential difference between solid and liquid phases (Δμsl)2,26−28 (see Supporting Information). In addition, formation of a nucleus also requires overcoming the kinetic barrier (Δf*) that accounts for the movement of water molecules across the solid–liquid water interface, which can be estimated from D in liquid water.29 As mentioned previously, pressure increase may also significantly alter liquid water D,22,30 and thus change the Δf* considerably (see Supporting Information). Also interestingly, D of water at ambient pressure has a peculiar behavior as the temperature approaches TH. Below the melting point, D decreases more rapidly with decreasing temperature than what is expected from the Arrhenius equation,22,29 and this behavior is categorized as that of a “fragile” liquid.31,32 Based on the “fragile” liquid concept, D is expected to decrease even more strongly as the temperature decreases toward and below TH, but this has not been experimentally verified. Near the glass transition temperature (Tg) of ∼136 K,33−35 liquid water has been proposed to behave like a “strong” or even “superstrong” liquid,1,36,37 which would mean that the temperature dependence of D follows (in contrast to a “fragile” liquid) the Arrhenius equation with an energy barrier higher than that of a higher-temperature “fragile” liquid. Within “no-man’s land”, D has been proposed to approach an Arrhenius-like temperature dependence as the temperature is decreased, thus water becomes a “strong” liquid, with a crossover temperature TC at ∼228 K.31,37,38 Overall, the ice nucleation rate is expected to increase as temperature decreases and approaches TH, reach a maximum below TH, and then decrease with further temperature decrease toward Tg. However, in light of the possible large variation of D at ambient pressure and the corresponding effect on Δf* over a wide temperature range, particularly near TH, it is less certain how fast the nucleation rate changes as it approaches and crosses TH.

We recently developed a new method, based on evaporative cooling and ultrafast probing, that allows studies of supercooled water and ice formation at temperatures where ice is formed very rapidly.39 Here, we present an analysis of the ice nucleation kinetics of near-ambient pressure water as it approaches and enters into “no-man’s land”. We are also adding additional information obtained from hyperquenching experiments of micrometer-sized water droplets in order to place upper and lower limits on the maximum nucleation rate40−44 at temperatures further into “no-man’s land”. These limits can be defined based on the observation that essentially all droplets crystallize in huge ensembles of droplets of 3 μm in diameter, when they are cooled at 104 K/s, whereas crystallization was not detected when cooled at 107 K/s through the 70 K broad “no-man’s land”.40−44

The experiments were conducted using a gas dynamic virtual nozzle (GDVN)45 to generate, in vacuum, a train of microdroplets with uniform diameter of 9 or 12 μm that are subsequently probed by X-rays. The droplets cool evaporatively, decreasing their temperature as they travel farther from the nozzle and spend longer time in vacuum. This results in cooling rates of 103–104 K/s around TH prior to crystallization. Hard X-ray laser pulses, each ∼50 fs in duration, from LCLS were used to probe the structure of individual droplets at various distances from the nozzle exit, hence varying the droplet temperature. The scattering patterns from individual droplets hit by the X-ray pulse were recorded over an estimated temperature range of 227–252 K (Figure 1) and sorted according to whether they consisted of only diffuse rings indicating scattering from pure liquid water or contained intense and discrete Bragg reflections that indicate diffraction from ice crystals.39 We collected at least 1800 individual scattering patterns at each distance or temperature. As the droplets spend more time in vacuum and evaporatively cool, the fraction of ice-containing shots (fice) remains near zero for about 1.2 and 3 ms travel time for the 9 and 12 μm droplets, respectively (Figure 1). This fraction increases rapidly to 0.2 in the next 1 ms for both droplet sizes and to 0.97 in the next 2 ms for 12 μm droplets. The error bars in fice represent the standard deviation of individual recordings collected at each distance and include variations in the hit rate and droplet trajectory jitters. The droplet trajectory jitter is expected to arise from jet breakup to form droplets and from the freezing process of the droplets. The onset temperatures where ice is first detected on these time scales are 232 and 230 K for the 9 and 12 μm droplets, respectively. We use fice to estimate J assuming, as in other nucleation rate studies,19−21,46−49 that the nucleation rate follows Poisson statistics and the observed Bragg reflections expected from ice in each shot originate from single nuclei (see Experimental Section). Here, we obtain ice nucleation rates ranging from 2.1 × 1011 to 3.6 × 1012 cm–3s–1 as the temperature decreases from 232 to 227 K (Figure 2a,b). The error bars on the nucleation rate (Figure 2a) account for the standard deviation in fice and the uncertainty in how many ice nuclei exist in each droplet that shows Bragg reflections (see Experimental Section).

Figure 1.

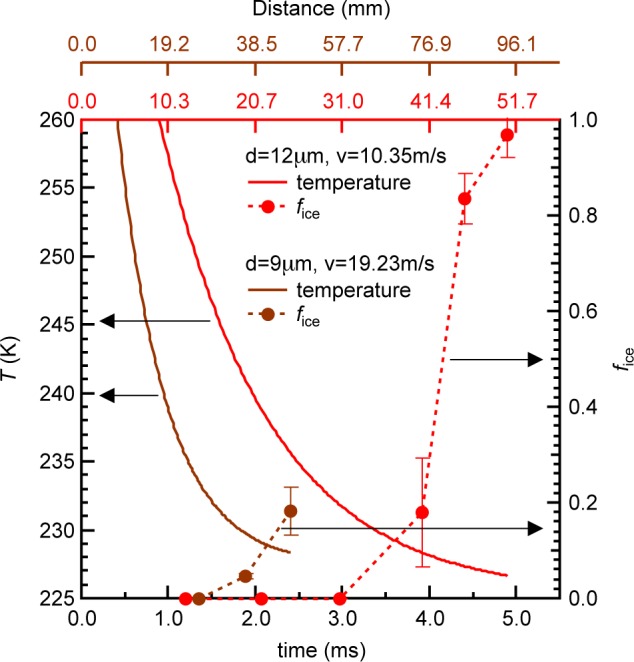
Figure 1

Open in a new tab

Droplet temperature as a function of travel time (or distance traveled) in vacuum for water microdroplets with diameters of 9 μm (brown solid line) and 12 μm (red solid line). The temperature was obtained using the Knudsen theory of evaporation.39 The ice ratio (fice) (dashed line) increased rapidly as the 9 and 12 μm droplets’ travel time in vacuum increased beyond 2 and 4 ms, respectively. The error bars in fice are the standard deviation of individual recordings at each distance, to account for hit rate variations, and droplet trajectory jitters due to jet breakup and droplet freezing.

Figure 2.

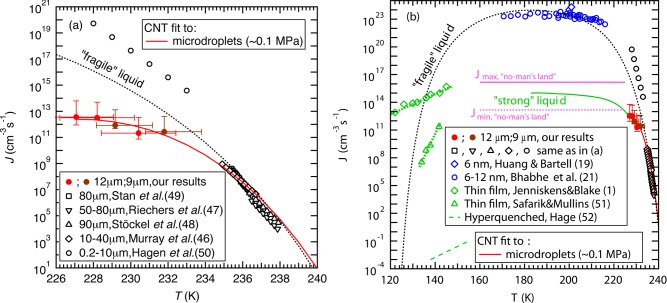
Figure 2

Open in a new tab

Comparison of measured homogeneous ice nucleation rates (J) of water. (a) J within microdroplets (227–240 K) measured by Stan et al.,49 Riechers et al.,47 Stöckel et al.,48 Murray et al.,46 and Hagen et al.,50 are compared to our data (brown and red filled circles with a fit shown with a red line), which suggest slower increase in J below TH than previous data from Hagen et al.50 that is excluded from the CNT fits. The vertical error bars account for the standard deviation in fice and the uncertainty in how many ice nuclei exist in each droplet that shows Bragg reflections (see Experimental Section), while the horizontal error bars account for the uncertainty in the temperature estimation.39 (b) Comparison of J measured using microdroplets (227–240 K), nanodroplets (170–215 K) by Bhabhe et al.,21 and vapor-deposited thin films (120–150 K) by Jenniskens and Blake1 and Safarik and Mullins,51 and hyperquenched droplets (138–155 K) by Hage et al.52 The data of microdroplets (red solid line) and nanodroplets (blue symbols) follow different trajectories where the nanodroplet data might be affected by the large surface area to volume ratio and elevated internal pressure. An upper limit for the nucleation rate maximum within “no-man’s land” Jmax (pink solid line) and a corresponding lower limit Jmin (pink dashed line) were calculated from hyperquenching experiments on microdroplets as described in the text.40−44 The expected CNT behavior for a “fragile” (black dotted line) and a “strong” (green solid line) liquid are included as guides to the eye. We follow Jenniskens and Blake1 to obtain the “fragile liquid” CNT curve (see Supporting Information for fitting parameters), and we also include an expected extension of the nucleation rate into “no-man’s land” (green curve) based on the requirement to lie between the upper and lower limits from hyperquenched microdroplets.

The obtained nucleation rates are consistent with earlier hyperquenching experiments on micrometer-sized droplets;40–44 indeed, practically all evaporatively cooled droplets crystallize at cooling rates of up to 104 K/s. Going beyond this earlier work,40–44 this suggests that the crystallization of droplets observed in these experiments takes place only slightly below TH ∼ 232 K. Since droplets cooled faster by only 3 orders of magnitude vitrify completely, this suggests that the maximum of the homogeneous ice nucleation rate is located below 227 K and most likely not too far below. This suggestion finds confirmation in the nucleation rate data from the current measurements (red and brown filled circles) in Figure 2a, which turns out to be quite insensitive to temperature in the 227–232 K interval. Connecting all data-points measured on microdroplets together with the hyperquenching experiments it would be consistent to assume that the nucleation rate further bends down and eventually flattens out as the temperature is lowered beyond 227 K as indicated by the red line in Figure 2a.

Figure 2b shows ice nucleation rates plotted as a function of temperature for previous studies (black, blue, and green symbols). Data above TH(46−50) (Figure 2a) represent the current state of rate measurements (see ref (40) for an exhaustive list of recent measurements) and are, within the uncertainties due to both temperature and cooling rate, consistent with each other and with the qualitative picture of how the nucleation rate should increase with decreasing temperature as described earlier. As temperature decreases below TH, data from both Hagen et al.’s50 and our experiments result in higher rates than those above TH. However, our measurements yield a 3–7 orders of magnitude lower rate and show weaker temperature dependence than the data of Hagen et al. Notably, Hagen et al. relied on using a droplet growth model50 that may introduce large uncertainties in the estimation of the temperature and droplet size.46 In addition, Riechers et al.47 have reported a slow-down in the rate increase similar to the present study, albeit to lesser extent, as temperature decreases toward TH, which they attributed to a rapid decrease in D.

Ice nucleation experiments from nanodroplets of 6–12 nm diameter allow rate measurements at temperatures between 170 and 215 K, which is well below TH (Figure 2b). These rates (∼1023 cm–3 s–1) are much higher than those from microdroplets and appear less dependent on temperature.19−21 The observation that microdroplets vitrify entirely at cooling rates of 107 K/s sets an upper limit to the maximum nucleation rate within the “no-man’s land” of ∼1016 cm–3 s–1 (see Jmax-limit in Figure 2b). At a rate of q ≈ 107 K/s, it takes Δt ≈ 7 μs to cool through the ∼230 to ∼160 K interval. Assuming that a single nucleation event (N = 1) already suffices to crystallize a droplet of radius ⟨r⟩, one obtains Jmax = N/[(4/3)π⟨r⟩3Δt] ≈ 1.1 × 1016 cm–3 s–1 for ⟨r⟩ = 1.5 μm. This estimate represents a hard limit for the maximum nucleation rate of microdroplets within the “no-man’s land” for bulk water at p ≤ 1 bar. That is, the nucleation rate of microdroplets of 3–12 μm diameter is at least 7 orders of magnitude lower than the one in nanodroplets of 6–12 nm diameter. This discrepancy may be attributed to the much higher surface-to-volume ratio that affects the internal pressure of the nanodroplets and potentially increases surface nucleation (see Supporting Information on nucleation rate sensitivity to pressure). Given these differences between nano- and microdroplets, we only compare our data against those from previous microdroplet experiments where we expect to have similar conditions.46−48

The minimal nucleation rate reached in the “no-man’s land”, Jmin = 1.1 × 1013 cm–3 s–1, is calculated analogously using q ≈ 104 K/s. This is very close to the nucleation rates measured in the present work on evaporatively cooled microdroplets and suggests that indeed the nucleation rate does not need to increase very much in the “no-man’s land” compared to its value at 227 K.

The crystallization kinetics of hyperquenched glassy water to cubic ice was measured by Hage et al.52 on layers of many micrometers in thickness, who report that it takes about 104 seconds to reach full crystallization of a volume of about 10–2±1 cm3 at 140 K and about 103 seconds at 146 K. Both nucleation and growth are diffusion-controlled under these conditions, and so it is not straightforward to extract nucleation rates from the data. Hage et al.52,53 also report that not only crystallization rates, but even the mechanism of crystallization as inferred from the Avrami-exponent is significantly altered when comparing annealed and unannealed films. Assuming only a single nucleation event, i.e., growth being much faster than nucleation, the nucleation rate calculates to J ∼ 10–1±1–10–3±1 cm–3s −1 at 155–138 K.53 Nucleation rates around Tg have also been measured on much thinner annealed amorphous thin films.1,51 Although these rates are much lower than those of nanodroplets as expected, the measured rates (J ∼ 107–1011 cm–3 s–1) by Safarik and Mullins51 are higher by 10 orders of magnitude than the nucleation rates deduced here from the data of Hage et al.52,53 and even comparable to those of microdroplets above TH (≤ ∼ 1010 cm–3 s–1). Jenniskens and Blake1 measured rates (J ∼ 1012–1015 cm–3s–1) that are even higher than our rates below TH, which is problematic considering that amorphous ice can be observed up to 160 K under similar time scales.12 The huge discrepancy between the different data sets suggests that different mechanisms of crystallization were probed in these studies. Thin film nucleation rates that are greater than or equal to ∼ 1011 cm–3s–1 seem unlikely considering that in these experiments the sample is heated at much lower rates (∼0.1–1 K/s) than the cooling rates (≥ ∼ 103 K/s) required to measure nucleation rates ≥ ∼ 1011 cm–3s–1 from microdroplets within “no-man’s land”. It might be possible that their films were preseeded with ice contamination, and so their rates might be limited by growth rather than by nucleation. However, the submicrometer sample thickness used in these thin film experiments may reduce sample volume significantly and thus potentially allow such high nucleation rate measurement. In addition, the rates measured in these experiments on submicrometer samples1,51 differ by 4–7 orders of magnitude and show very different temperature dependence. Although it is unclear why there are such large differences in the crystallization studies on submicrometer films1,51 and much thicker films,52,53 different sample preparation and measurement techniques in these experiments can affect the resulting rates. More nucleation rate studies are necessary to understand the differences between these results and, more importantly, to improve our understanding of water and crystallization kinetics near Tg.

To account for the results of previous rate measurements, Jenniskens and Blake have considered liquid water as either “fragile” or “strong”,1 which is associated with how the diffusivity D changes with temperature. By assuming the temperature-dependent D of a “fragile” liquid within the CNT framework, one can connect most nucleation rate data within “no-man’s land” to those at higher temperatures,19−21,46−49,51 with the exception of the data from Hagen et al.50 for reasons discussed above and also our present data. At low temperatures near Tg, liquid water has been shown to behave like a “strong” liquid by recent dielectric relaxation and calorimetric measurements.36 This “strong” description of water predicts nucleation rates that show a temperature dependence similar to the one given by Jenniskens and Blake.1 In contrast, the rates reported by Safarik and Mullins51 exhibit a temperature dependence that is closer to that of a “fragile” than a “strong” liquid.

The current nucleation rate measurements in conjunction with previous microdroplet measurements46−49 and the nucleation rate limits within “no-man’s land” deduced from the hyperquenching experiments pioneered by Mayer,40−44 however, show a slower than expected nucleation rate increase as temperature decreases toward and crosses TH giving a hint of an anomalous behavior. This slower increase makes the nucleation rate deviate away from the CNT-predicted rate of a “fragile” liquid and move toward that of a “strong” liquid just below TH (Figure 2b). We suggest that an expected rapid decrease in liquid water diffusivity D(22,29) may lead to a significant increase in Δf*, which can explain the slow nucleation rate increase just below TH. In addition, recent ultrafast X-ray scattering measurements have shown a continuous but accelerated change toward a low-density liquid at similar temperatures.39 We thus hypothesize that these observations might be related to the possible “fragile-to-strong” liquid transition37,38 and the findings from molecular dynamics (MD) simulations using the mW water model54 that suggest that the structural transformation controls the ice crystallization rate in “no-man’s land”.10 By contrast, the nucleation rate measurements from nanodroplets appear to follow the CNT-predicted nucleation rate of a “fragile” liquid at temperatures below TH. Thus, we also hypothesize that the pressure increase within the nanodroplets may have kept the liquid as a “fragile” liquid rather than transitioning into a “strong” liquid within the temperature range of these measurements in “no-man’s land”. However, further investigations at a wider range of temperatures and pressures are needed to definitively understand the anomalous water properties and their influence on ice nucleation kinetics, particularly within “no-man’s land”.

In conclusion, we extend ambient pressure nucleation rate measurements to ∼227 K, well below TH and within “no-man’s land”, and observe a slower increase in nucleation rate compared to that expected from prior measurements. Overall, the microdroplet ice nucleation rate data in “no-man’s land” appear consistent with the hypothesis of supercooled water at ambient pressure crossing over from being a “fragile” liquid to a “strong” liquid just below TH.31,37,38,55 However, more work is needed in the future to clearly determine if this indeed is the case.

Experimental Section

X-ray scattering from deionized water (PURELAB Ultra Genetic, resistivity 18.2 MΩcm at 298 K) droplets of 9 and 12 μm diameters upon deep supercooling (<255 K) was measured at the LCLS Coherent X-ray Imaging instrument (CXI).56 A 9.4 keV photon energy and 50 fs nominal pulse duration X-ray laser with spot size of ∼1 μm2 (9 μm droplets) and ∼10 μm2 (12 μm droplets) at the interaction point were used. The Cornell-SLAC pixel array detector (CSPAD) located 132 mm (9 μm droplets) and 139 mm (12 μm droplets) downstream from the interaction point was used to record single-pulse scattering patterns from individual droplets at 120 Hz repetition rate. A 3-axis motorized sample stage was used to control the distance between the nozzle and the interaction point, and thus to determine the droplet temperature. The temperature estimate was based on the Knudsen theory of evaporative cooling with a calibration made by comparing the liquid water wide-angle scattering signal in this experiment against larger microdroplets evaporating in vacuum with diameters of 34 and 37 μm as well as against synchrotron measurements using a cooling cell down to 251 K.39 The evaporative cooling model was further verified through MD simulations of droplet cooling.39 The temperature difference between core and surface within 9 and 12 μm droplets is less than 1 K after 2 ms of travel time. In addition, we estimate the droplet internal pressure to be ∼0.03 MPa, primarily due to surface tension exerting Laplace pressure on the droplet. We assumed this to be a good approximation to ambient pressure (∼0.1 MPa). Finally, data at each distance were sorted according to water-only or ice-containing scattering patterns, and was then used to estimate the fraction of ice-containing shots (fice). Further details are given in the Supporting Information of ref (39). The final data with their respective accuracy are tabulated in Supporting Information.

We used fice to calculate the ice nucleation rate (J) at time tn+1/2 using

graphic file with name jz-2015-01164k_m001.jpg

(refs (21 and 46)) where Vdrop is the droplet volume, and subscripts n and n+1 represent successive measurements. The corresponding temperature, tn+1/2, is obtained from the droplet temperature estimate. We assume, as in other nucleation rate studies,19−21,46−49 that nucleation is a stochastic process that follows Poisson statistics, that diffraction collected in each shot comes from a single crystal, that the growth of a nucleus to a detectable size is much faster than formation of a nucleus, and that the difference in ice nucleation rate is negligible between adjacent data points (i.e., that the temperature difference between adjacent data points is small). These are reasonable assumptions because the cooling rate is slow when ice nucleation occurs (Figure 1) and our measurements generally are limited by thermodynamics (although kinetics becomes increasingly important upon decreasing temperature). In addition, we can detect ice crystals as small as ∼50 nm in diameter and detect ice in the droplet above 0.05% by mass.39 However, our detection limit is much larger than the estimated critical ice nucleus diameter of ∼2.5 nm. Although the structure of a critical ice nucleus has not been determined experimentally, simulations suggest that the critical ice nucleus is rich in cubic ice.14 The average of the ice-containing diffraction patterns, however, shows a hexagonal ice pattern,39 but we cannot exclude that the heat released during growth effectively anneals the ice nuclei into hexagonal ice crystals. Moreover, we observed ∼30 Bragg reflections on average in diffraction patterns classified as hexagonal ice compared to ∼2 Bragg reflections expected on average from a randomly oriented perfect hexagonal ice crystal. These extra Bragg reflections might be due to dendritic growth with defects where the heat release during rapid growth could lead to splitting of the original nucleus into several crystallites. Alternatively, the observed Bragg reflections might originate from ∼15 individual nuclei. We thus account for the possibility of observing ∼15 nuclei in the upper nucleation rate error bar in addition to the fice uncertainty. Finally, we note that the crystallization times may represent a combination of nucleation and growth at the lowest temperature of ∼227 K (see Supporting Information).

Acknowledgments

We acknowledge the Office of Basic Energy Sciences (BES) through SSRL, the AMOS program within the Chemical Sciences, Geosciences, and Biosciences Division of the Office of Basic Energy Sciences, the Department of Energy through the SLAC Laboratory Directed Research and Development Program, the National Science Foundation (US) (Grant No. CHE-0809324 and NSF award 1231306), the Austrian Science Fund FWF (bilateral Austrian-French project I1392 and Firnberg project T463) and the Swedish Research Council for financial support. Portions of this research were carried out at LCLS at SLAC National Accelerator Laboratory. LCLS is an Office of Science User Facility operated for the DOE Office of Science by Stanford University. We wish to thank D. Schafer and M. Hayes for mechanical support; W. Ghonsalves, F. Hoeflich, C. Caronna, and J. Feldkamp for software support; the SLAC detector group for CSPAD support; D. Deponte, H. Nakatsutsumi, K. Beyerlein, and C. Gati for nozzle support; D. Starodub, C. Stan, and C. A. Angell for valuable discussions; and B. Wyslouzil for providing nanodroplet nucleation rate data from refs (20 and 21) and for discussions. N.D.L. acknowledges the support from the Lee Kuan Yew Postdoctoral Fellowship.

Supporting Information Available

CNT that accounts for increased pressure, discussion on crystallization time that may represent nucleation and growth at the lowest temperature of ∼227 K, analysis of nucleation rate sensitivity to increased pressure according to CNT, table of experimental data and calculated ice nucleation rates, and table of thermophysical and transport properties of water. The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.5b01164.

The authors declare no competing financial interest.

Supplementary Material

jz5b01164_si_001.pdf (916.1KB, pdf)

References

  1. Jenniskens P.; Blake D. F. Crystallization of Amorphous Water Ice in the Solar System. Astrophys. J. 1996, 473, 1104–1113 10.1086/178220. [DOI] [PubMed] [Google Scholar]
  2. Murray B. J.; O’Sullivan D.; Atkinson J. D.; Webb M. E. Ice Nucleation by Particles Immersed in Supercooled Cloud Droplets. Chem. Soc. Rev. 2012, 41, 6519–6554 10.1039/c2cs35200a. [DOI] [PubMed] [Google Scholar]
  3. Tabazadeh A.; Djikaev Y. S.; Reiss H. Surface Crystallization of Supercooled Water in Clouds. Proc. Natl. Acad. Sci. U. S. A. 2002, 99, 15873–15878 10.1073/pnas.252640699. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Kuhn T.; Earle M. E.; Khalizov A. F.; Sloan J. J. Size Dependence of Volume and Surface Nucleation Rates for Homogeneous Freezing of Supercooled Water Droplets. Atmos. Chem. Phys. 2011, 11, 2853–2861 10.5194/acp-11-2853-2011. [DOI] [Google Scholar]
  5. Morris G. J.; Acton E.; Murray B. J.; Fonseca F. Freezing Injury: The Special Case of the Sperm Cell. Cryobiology 2012, 64, 71–80 10.1016/j.cryobiol.2011.12.002. [DOI] [PubMed] [Google Scholar]
  6. Mason B. J. The Supercooling and Nucleation of Water. Adv. Phys. 1958, 7, 221–234 10.1080/00018735800101237. [DOI] [Google Scholar]
  7. Cwilong B. M. Sublimation in a Wilson Chamber. Proc. R. Soc. London, Ser. A 1947, 190, 137–143 10.1098/rspa.1947.0066. [DOI] [PubMed] [Google Scholar]
  8. Mossop S. C. The Freezing of Supercooled Water. Proc. Phys. Soc., London, Sect. B 1955, 68, 193–208 10.1088/0370-1301/68/4/301. [DOI] [Google Scholar]
  9. Mishima O.; Stanley H. E. The Relationship between Liquid, Supercooled and Glassy Water. Nature 1998, 396, 329–335 10.1038/24540. [DOI] [Google Scholar]
  10. Moore E. B.; Molinero V. Structural Transformation in Supercooled Water Controls the Crystallization Rate of Ice. Nature 2011, 479, 506–508 10.1038/nature10586. [DOI] [PubMed] [Google Scholar]
  11. Moore E. B.; Molinero V. Ice Crystallization in Water’s “No-Man’s Land. J. Chem. Phys. 2010, 132, 244504. 10.1063/1.3451112. [DOI] [PubMed] [Google Scholar]
  12. Smith R. S.; Kay B. D. The Existence of Supercooled Liquid Water at 150 K. Nature 1999, 398, 788–791 10.1038/19725. [DOI] [Google Scholar]
  13. Matsumoto M.; Saito S.; Ohmine I. Molecular Dynamics Simulation of the Ice Nucleation and Growth Process Leading to Water Freezing. Nature 2002, 416, 409–413 10.1038/416409a. [DOI] [PubMed] [Google Scholar]
  14. Moore E. B.; Molinero V. Is It Cubic? Ice Crystallization from Deeply Supercooled Water. Phys. Chem. Chem. Phys. 2011, 13, 20008–20016 10.1039/c1cp22022e. [DOI] [PubMed] [Google Scholar]
  15. Li T.; Donadio D.; Russo G.; Galli G. Homogeneous Ice Nucleation from Supercooled Water. Phys. Chem. Chem. Phys. 2011, 13, 19807–19813 10.1039/c1cp22167a. [DOI] [PubMed] [Google Scholar]
  16. Li T.; Donadio D.; Galli G. Ice Nucleation at the Nanoscale Probes No Man’s Land of Water. Nat. Commun. 2013, 4, 1887. 10.1038/ncomms2918. [DOI] [PubMed] [Google Scholar]
  17. Sanz E.; Vega C.; Espinosa J. R.; Caballero-Bernal R.; Abascal J. L. F.; Valeriani C. Homogeneous Ice Nucleation at Moderate Supercooling from Molecular Simulation. J. Am. Chem. Soc. 2013, 135, 15008–15017 10.1021/ja4028814. [DOI] [PubMed] [Google Scholar]
  18. Espinosa J. R.; Sanz E.; Valeriani C.; Vega C. Homogeneous Ice Nucleation Evaluated for Several Water Models. J. Chem. Phys. 2014, 141, 18C529. 10.1063/1.4897524. [DOI] [PubMed] [Google Scholar]
  19. Huang J.; Bartell L. S. Kinetics of Homogeneous Nucleation in the Freezing of Large Water Clusters. J. Phys. Chem. 1995, 99, 3924–3931 10.1021/j100012a010. [DOI] [Google Scholar]
  20. Manka A.; Pathak H.; Tanimura S.; Wölk J.; Strey R.; Wyslouzil B. E. Freezing Water in No-Man’s Land. Phys. Chem. Chem. Phys. 2012, 14, 4505–4516 10.1039/c2cp23116f. [DOI] [PubMed] [Google Scholar]
  21. Bhabhe A.; Pathak H.; Wyslouzil B. E. Freezing of Heavy Water (D2O) Nanodroplets. J. Phys. Chem. A 2013, 117, 5472–5482 10.1021/jp400070v. [DOI] [PubMed] [Google Scholar]
  22. Prielmeier F. X.; Lang E. W.; Speedy R. J.; Lüdemann H.-D. The Pressure Dependence of Self-Diffusion in Supercooled Light and Heavy Water. Berichte der Bunsengesellschaft für Phys. Chemie 1988, 92, 1111–1117 10.1002/bbpc.198800282. [DOI] [Google Scholar]
  23. Duft D.; Leisner T. Laboratory Evidence for Volume-Dominated Nucleation of Ice in Supercooled Water Microdroplets. Atmos. Chem. Phys. 2004, 4, 1997–2000 10.5194/acp-4-1997-2004. [DOI] [Google Scholar]
  24. Debenedetti P. G.Metastable Liquids: Concepts and Principles; Princeton University Press: Princeton, NJ, 1997. [Google Scholar]
  25. Frenkel J.Kinetic Theory of Liquids; Oxford University Press: Oxford, U.K., 1946. [Google Scholar]
  26. Němec T. Estimation of Ice–water Interfacial Energy Based on Pressure-Dependent Formulation of Classical Nucleation Theory. Chem. Phys. Lett. 2013, 583064–68 10.1016/j.cplett.2013.07.085. [DOI] [Google Scholar]
  27. Turnbull D.; Fisher J. C. Rate of Nucleation in Condensed Systems. J. Chem. Phys. 1949, 17, 71–73 10.1063/1.1747055. [DOI] [Google Scholar]
  28. Chushak Y.; Bartell L. S. Crystal Nucleation and Growth in Large Clusters of SeF6 from Molecular Dynamics Simulations. J. Phys. Chem. A 2000, 104, 9328–9336 10.1021/jp002107e. [DOI] [Google Scholar]
  29. Price W. S.; Ide H.; Arata Y. Self-Diffusion of Supercooled Water to 238 K Using PGSE NMR Diffusion Measurements. J. Phys. Chem. A 1999, 103, 448–450 10.1021/jp9839044. [DOI] [Google Scholar]
  30. Abramson E. H.; Brown J. M.; Slutsky L. J. The Thermal Diffusivity of Water at High Pressures and Temperatures. J. Chem. Phys. 2001, 115, 10461–10463 10.1063/1.1418244. [DOI] [Google Scholar]
  31. Angell C. A. Water II Is a “Strong” Liquid. J. Phys. Chem. 1993, 97, 6339–6341 10.1021/j100126a005. [DOI] [Google Scholar]
  32. Angell C. A. Formation of Glasses from Liquids and Biopolymers. Science 1995, 267, 1924–1935 10.1126/science.267.5206.1924. [DOI] [PubMed] [Google Scholar]
  33. Johari G. P.; Hallbrucker A.; Mayer E. The Glass–liquid Transition of Hyperquenched Water. Nature 1987, 330, 552–553 10.1038/330552a0. [DOI] [Google Scholar]
  34. McMillan J. A.; Los S. C. Vitreous Ice: Irreversible Transformations during Warm-Up. Nature 1965, 206, 806–807 10.1038/206806a0. [DOI] [Google Scholar]
  35. Elsaesser M. S.; Winkel K.; Mayer E.; Loerting T. Reversibility and Isotope Effect of the Calorimetric Glass → Liquid Transition of Low-Density Amorphous Ice. Phys. Chem. Chem. Phys. 2010, 12, 708–712 10.1039/B917662D. [DOI] [PubMed] [Google Scholar]
  36. Amann-Winkel K.; Gainaru C.; Handle P. H.; Seidl M.; Nelson H.; Böhmer R.; Loerting T. Water’s Second Glass Transition. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 17720–17725 10.1073/pnas.1311718110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Speedy R. J. Evidence for a New Phase of Water: Water II. J. Phys. Chem. 1992, 96, 2322–2325 10.1021/j100184a056. [DOI] [Google Scholar]
  38. Ito K.; Moynihan C. T.; Angell C. A. Thermodynamic Determination of Fragility in Liquids and a Fragile-to-Strong Liquid Transition in Water. Nature 1999, 398, 492–495 10.1038/19042. [DOI] [Google Scholar]
  39. Sellberg J. A.; Huang C.; McQueen T. A.; Loh N. D.; Laksmono H.; Schlesinger D.; Sierra R. G.; Nordlund D.; Hampton C. Y.; Starodub D.; et al. Ultrafast X-Ray Probing of Water Structure below the Homogeneous Ice Nucleation Temperature. Nature 2014, 510, 381–384 10.1038/nature13266. [DOI] [PubMed] [Google Scholar]
  40. Kohl I.; Bachmann L.; Hallbrucker A.; Mayer E.; Loerting T. Liquid-like Relaxation in Hyperquenched Water at ≤ 140 K. Phys. Chem. Chem. Phys. 2005, 7, 3210–3220 10.1039/b507651j. [DOI] [PubMed] [Google Scholar]
  41. Mayer E. Hyperquenching of Water and Dilute Aqueous Solutions into Their Glassy States: An Approach to Cryofixation. Cryo-Letters 1988, 9, 66–77. [Google Scholar]
  42. Mayer E. New Method for Vitrifying Water and Other Liquids by Rapid Cooling of Their Aerosols. J. Appl. Phys. 1985, 58, 663–667 10.1063/1.336179. [DOI] [Google Scholar]
  43. Mayer E.; Brüggeller P. Vitrification of Pure Liquid Water by High Pressure Jet Freezing. Nature 1982, 298, 715–718 10.1038/298715a0. [DOI] [Google Scholar]
  44. Brüggeller P.; Mayer E. Complete Vitrification in Pure Liquid Water and Dilute Aqueous Solutions. Nature 1980, 288, 569–571 10.1038/288569a0. [DOI] [Google Scholar]
  45. DePonte D. P.; Weierstall U.; Schmidt K.; Warner J.; Starodub D.; Spence J. C. H.; Doak R. B. Gas Dynamic Virtual Nozzle for Generation of Microscopic Droplet Streams. J. Phys. D: Appl. Phys. 2008, 41, 195505. 10.1088/0022-3727/41/19/195505. [DOI] [Google Scholar]
  46. Murray B. J.; Broadley S. L.; Wilson T. W.; Bull S. J.; Wills R. H.; Christenson H. K.; Murray E. J. Kinetics of the Homogeneous Freezing of Water. Phys. Chem. Chem. Phys. 2010, 12, 10380–10387 10.1039/c003297b. [DOI] [PubMed] [Google Scholar]
  47. Riechers B.; Wittbracht F.; Hütten A.; Koop T. The Homogeneous Ice Nucleation Rate of Water Droplets Produced in a Microfluidic Device and the Role of Temperature Uncertainty. Phys. Chem. Chem. Phys. 2013, 15, 5873–5887 10.1039/c3cp42437e. [DOI] [PubMed] [Google Scholar]
  48. Stöckel P.; Weidinger I. M.; Baumgärtel H.; Leisner T. Rates of Homogeneous Ice Nucleation in Levitated H2O and D2O Droplets. J. Phys. Chem. A 2005, 109112540–2546 10.1021/jp047665y. [DOI] [PubMed] [Google Scholar]
  49. Stan C. A.; Schneider G. F.; Shevkoplyas S. S.; Hashimoto M.; Ibanescu M.; Wiley B. J.; Whitesides G. M. A Microfluidic Apparatus for the Study of Ice Nucleation in Supercooled Water Drops. Lab Chip 2009, 9, 2293–2305 10.1039/b906198c. [DOI] [PubMed] [Google Scholar]
  50. Hagen D. E.; Anderson R. J.; Kassner J. L. Homogeneous Condensation—Freezing Nucleation Rate Measurements for Small Water Droplets in an Expansion Cloud Chamber. J. Atmos. Sci. 1981, 38, 1236–1243. [DOI] [Google Scholar]
  51. Safarik D. J.; Mullins C. B. The Nucleation Rate of Crystalline Ice in Amorphous Solid Water. J. Chem. Phys. 2004, 121, 6003–6010 10.1063/1.1779171. [DOI] [PubMed] [Google Scholar]
  52. Hage W.; Hallbrucker A.; Mayer E.; Johari G. P. Crystallization Kinetics of Water below 150 K. J. Chem. Phys. 1994, 100, 2743–2747 10.1063/1.466468. [DOI] [Google Scholar]
  53. Hage W.; Hallbrucker A.; Mayer E.; Johari G. P. Kinetics of Crystallizing D2O Water near 150 K by Fourier Transform Infrared Spectroscopy and a Comparison with the Corresponding Calorimetric Studies on H2O Water. J. Chem. Phys. 1995, 103, 545–550 10.1063/1.470140. [DOI] [Google Scholar]
  54. Molinero V.; Moore E. B. Water Modeled as an Intermediate Element between Carbon and Silicon. J. Phys. Chem. B 2009, 113, 4008–4016 10.1021/jp805227c. [DOI] [PubMed] [Google Scholar]
  55. Starr F.; Angell C. A.; Nave E.; Sastry S.; Scala A.; Sciortino F.; Stanley H. E. Recent Results on the Connection between Thermodynamics and Dynamics in Supercooled Water. Biophys. Chem. 2003, 105, 573–583 10.1016/S0301-4622(03)00067-X. [DOI] [PubMed] [Google Scholar]
  56. Boutet S.; Williams G. J. The Coherent X-Ray Imaging (CXI) Instrument at the Linac Coherent Light Source (LCLS). New J. Phys. 2010, 12, 035024. 10.1088/1367-2630/12/3/035024. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz5b01164_si_001.pdf (916.1KB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES